Traceability of optical frequency to SI second via UTC(NIM)

Absolute frequency measurement of an optical clock is a milestone towards the redefinition of second in the International System of Units. This work summarizes briefly the measurement of frequency ratio between an optical clock and the second, applying the frequency comparison link from UTC(NIM) to International Atomic Time. Some strategies and suggestions are proposed to reduce the uncertainty introduced by the measurement system and dead time, which guided the frequency measurement of three optical clocks at 10⁻¹⁶ level in the past 3 years.

Introduction

Since 1967, the second of the International System of Units (SI) is defined according to the 9,192,631,770 Hz hyperfine transition of ¹³³Cs. Currently, Cesium fountain clocks realize the second to an accuracy of 10⁻¹⁶. It is the most precisely measured unit among the SI units. However, in the last decade, optical frequency standards have achieved accuracies of 10⁻¹⁸ or even 10⁻¹⁹ [1, 2]. The International Committee for Weights (CIPM) recommends a roadmap for the redefinition of SI second using optical transition [3]. In preparation, the absolute frequency of an optical clock (OC) needs to be accurate to 10⁻¹⁶ level. Measuring directly the frequency ratio between an OC and a cesium fountain clock imposes very high demands on local cesium fountain clocks, of which only a few in the world have this capability. Hence, in recent years, some laboratories in the world have performed another scheme, tracing the optical frequency to the International Atomic Time (TAI) to get absolute frequency of an optical clock [4–8].

In China, more than 10 OCs of different types are being developed at several research institutes. At the National Institute of Metrology (NIM), the cesium fountain clock NIM5 with an uncertainty of 9 × 10⁻¹⁶ reports regularly to the International Bureau of Weights and Measures (BIPM) [9]. With its successor NIM6, the uncertainty has been improved to 5.8 × 10⁻¹⁶. Nevertheless, both are currently unavailable for high-level (<5 × 10⁻¹⁶) precision measurements. We focus on the second feasible scheme, tracing an optical frequency to the SI second using the frequency comparison link from real-time realization of the Coordinated Universal Time (UTC) UTC(NIM) to TAI.

Fundamental scheme

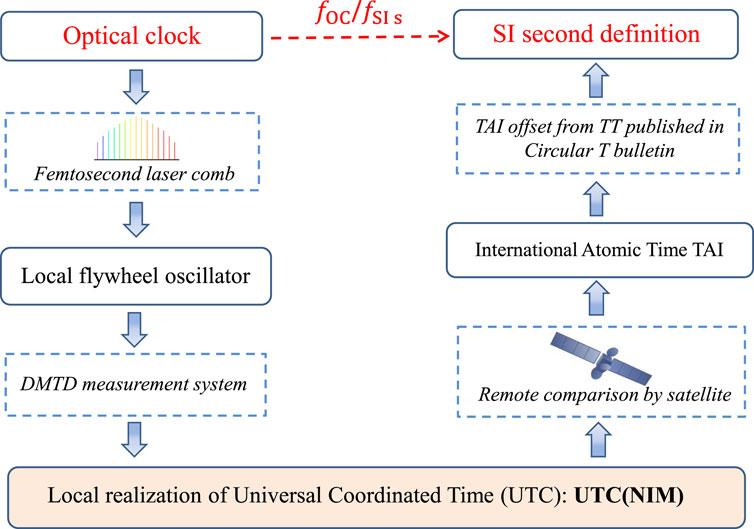
Compared with absolute frequency measurements of an OC obtained directly using a cesium fountain clock, the method discussed below is slightly complicated. Its remarkable advantage is that the measurement uncertainty is no longer limited by the performance of the local cesium fountain clock or even whether such a clock is needed. The traceability link (Figure 1) contains five key nodes: an OC, a local flywheel oscillator (LFO), UTC(NIM), TAI, and SI second definition (SI s). Four procedures are used to measure the frequency ratios between any pair of consecutive nodes. A femtosecond optical frequency comb system measures the frequency ratio of the optical and the microwave frequencies, which originate from the OC and LFO. A dual mixer time difference (DMTD) system is used to measure the frequency difference between multiple hydrogen masersand the reference UTC(NIM). It is therefore the preferred solution of measuring the frequency ratio of a LFO and UTC(NIM). Meanwhile, we maintain remote frequency comparison links by satellite to participate in the TAI cooperation, and to keep time and frequency comparison with the cooperative partners in China. The frequency ratio of the UTC(NIM) and TAI are taken from Circular T, a monthly publication of the BIPM. It uses the weighted average of clock readings to calculate monthly the Échelle Atomique Libre (EAL) from more than 400 atomic clocks in worldwide, and then generate the TAI by steering the EAL frequency to the weighted average frequency of available primary and secondary frequency standards (PSFS) maintained in a few countries. Similarly, the fractional frequency deviation between TAI and the SI second is also published in Circular T, which should be currently the best time reference.

FIGURE 1

FIGURE 1. Schematic of optical frequency traceability.

If an OC can continuously run over a complete 1-month period of TAI reporting, its absolute frequency may be evaluated using

$\frac{y_{\mathrm{O}\mathrm{C}}}{y_{\mathrm{S}\mathrm{I}\mathrm{s}}}=\frac{y_{\mathrm{O}\mathrm{C}}}{y_{\mathrm{L}\mathrm{F}\mathrm{O}}}\times \frac{y_{\mathrm{L}\mathrm{F}\mathrm{O}}}{y_{\mathrm{U}\mathrm{T}\mathrm{C}\left(\mathrm{N}\mathrm{I}\mathrm{M}\right)}}\times \frac{y_{\mathrm{U}\mathrm{T}\mathrm{C}\left(\mathrm{N}\mathrm{I}\mathrm{M}\right)}}{y_{\mathrm{T}\mathrm{A}\mathrm{I}}}\times \frac{y_{\mathrm{T}\mathrm{A}\mathrm{I}}}{y_{\mathrm{S}\mathrm{I}\mathrm{s}}},(1)$

where $y_{\mathrm{O}\mathrm{C}}$ and $y_{\mathrm{S}\mathrm{I}\mathrm{s}}$ are respectively the OC frequency and the SI second definition (specifically, 1 Hz), and $y_{\mathrm{L}\mathrm{F}\mathrm{O}}$, $y_{\mathrm{U}\mathrm{T}\mathrm{C}\left(\mathrm{N}\mathrm{I}\mathrm{M}\right)}$, and $y_{\mathrm{T}\mathrm{A}\mathrm{I}}$ represent respectively the frequencies of the LFO, UTC(NIM), and TAI. In practice, however, the continual running of an OC over a 1-month reporting period is still difficult because of its inherent principle of operation and the state-of-the-art technology. On the right-hand side of Eq. 1, the four factors (the measured frequency ratios) may have potential dead times, implying

$\frac{y_{\mathrm{O}\mathrm{C}}}{y_{\mathrm{S}\mathrm{I}\mathrm{s}}}=\frac{y_{\mathrm{O}\mathrm{C}}\left(∆t_{\mathit{1}}\right)}{y_{\mathrm{L}\mathrm{F}\mathrm{O}}\left(∆t_{\mathit{1}}\right)}\times \frac{y_{\mathrm{L}\mathrm{F}\mathrm{O}}\left(∆t_{\mathit{1}}\right)}{y_{\mathrm{L}\mathrm{F}\mathrm{O}}\left(∆t_{\mathit{2}}\right)}\times \frac{y_{\mathrm{L}\mathrm{F}\mathrm{O}}\left(∆t_{\mathit{2}}\right)}{y_{\mathrm{U}\mathrm{T}\mathrm{C}\left(\mathrm{N}\mathrm{I}\mathrm{M}\right)}\left(∆t_{\mathit{2}}\right)}\times \frac{y_{\mathrm{U}\mathrm{T}\mathrm{C}\left(\mathrm{N}\mathrm{I}\mathrm{M}\right)}\left(∆t_{\mathit{2}}\right)}{y_{\mathrm{U}\mathrm{T}\mathrm{C}\left(\mathrm{N}\mathrm{I}\mathrm{M}\right)}\left(∆t_{\mathit{3}}\right)}\times \frac{y_{\mathrm{U}\mathrm{T}\mathrm{C}\left(\mathrm{N}\mathrm{I}\mathrm{M}\right)}\left(∆t_{\mathit{3}}\right)}{y_{\mathrm{T}\mathrm{A}\mathrm{I}}\left(∆t_{\mathit{3}}\right)}\times \frac{y_{\mathrm{T}\mathrm{A}\mathrm{I}}\left(∆t_{\mathit{3}}\right)}{y_{\mathrm{T}\mathrm{A}\mathrm{I}}\left(∆t_{\mathit{4}}\right)}\times \frac{y_{\mathrm{T}\mathrm{A}\mathrm{I}}\left(∆t_{\mathit{4}}\right)}{y_{\mathrm{S}\mathrm{I}\mathrm{s}}\left(∆t_{\mathit{4}}\right)},(2)$

where $∆t_i$ (i = 1, 2, 3, 4) denote the live measurement time intervals for the four frequency ratios to be measured (Eq. 1, right-hand side). Figure 2 shows a schematic of the live measurement time intervals and dead times between the traceability link from the OC frequency to the SI second definition (SI s) via the LFO and UTC(k). In principle, we may not need the LFO in this traceability link. Due to its robustness is stronger than that of the UTC(NIM), the hydrogen maser as an LFO is widely used to the traceability of the OC frequency to the SI definition of second.

FIGURE 2

FIGURE 2. Time allocations of live measurements and dead times.

Measurement of four frequency ratios

Measuring the four frequency ratios appearing in Eq. 1 are key parts in tracing the OC frequency to the SI definition of second by UTC(NIM). Any one ratio measurement contributes to the uncertainty of the final result, specifically, the OC absolute frequency. Each method of measurement as well as its corresponding uncertainty is discussed below.

Femtosecond optical frequency comb

The microwave frequency (10 MHz or 100 MHz) originating from a LFO (in general, a high-performance hydrogen maser) is first synthesized to a higher frequency, which is the frequency reference for the measured OC frequency. Second, the femtosecond optical frequency comb measures accurately the frequency deviation from the higher frequency to the OC frequency. Such frequency ratios between the OC and the LFO may be calculated directly using the frequency deviation. The uncertainty introduced by a femtosecond optical frequency comb may be negligible compared to the 1-part-in-10¹⁶ accuracy for the frequency ratio measurement. Note that depending on the specific scheme, the microwave frequency distribution and synthesis may introduce a certain uncertainty, which is generally estimated to be close to a few parts in 10¹⁶ in this measurement.

Dual mixer time difference measurement system

The multi-channel measurement system (TSC MMS, Symmetricom, United States) is based on the DMTD measurement principle and is used in our time keeping laboratory. From the technical specifications, the Allan deviation of the system noise is less than 3 × 10⁻¹³ with an averaging time of 1 s. Up until the averaging-time closure of 10⁴ s, the Allan deviation theoretically achieves 3 × 10⁻¹⁷, which is satisfactory for our optical frequency measurements. In contrast, if measurement times are shorter than 10⁴ s, the uncertainty with 10⁻¹⁶ level could be introduced to measurement result.

Remote comparison by satellite

A physical time scale UTC(NIM) is compared continuously with TAI via a time-and-frequency transfer link via satellite. BIPM collects clock readings and time comparison data at 5-day intervals from time laboratories around the world and then calculates the monthly UTC. With a delay of 30–45 days, BIPM publishes in the Circular T bulletin the time difference between the UTC(NIM) and UTC for the 5-day intervals over the last month. The difference reflects the mean frequency difference between the UTC(NIM) and TAI resulting from having only a difference attributed to a leap second between them. The relationship between the uncertainty associated with frequency transfer and averaging time is reported in detail in reference [10]. Specifically, a ∼30-day comparison achieves an uncertainty of ∼2 × 10⁻¹⁶ corresponding to a minimum of u_A 0.3 ns.

Fractional frequency deviation of international atomic time relative to SI second

TAI is a realization of Terrestrial Time (TT), a coordinate time with scale unit the SI second in the geocentric reference system [11]. The fractional frequency deviation of TAI relative to TT is published in Circular T bulletin monthly. Its uncertainty is generally ∼2 × 10⁻¹⁶, which depends on the number of available primary and secondary frequency standards and the uncertainty of each in that period.

Strategies to reduce the uncertainty introduced by dead times

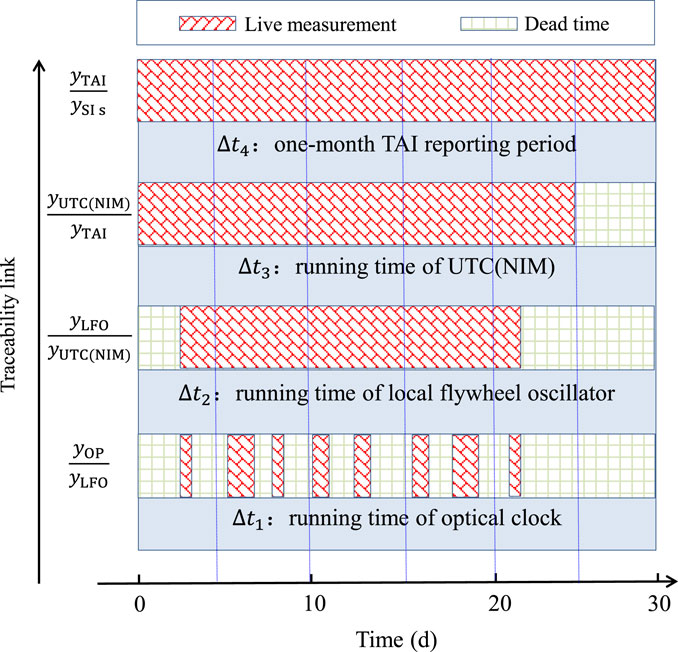
The absolute frequency measurement of an OC is only at several parts in 10¹⁶ because of the current performance of cesium fountain clocks. The dead time in this measurement should be rigorously considered because almost all OCs operate only in the intermittent mode, which could introduce the uncertainty of a few parts in 10¹⁶. We have focused on using a 1-month TAI reporting period (30 days in general) to complete the absolute frequency measurement and achieve an uncertainty of a few parts in 10¹⁶. The continuous running time of the OC is generally much shorter than 30 days (Figure 2). In this traceability link, the uncertainty contributed by live measurements has been considered in the above section. The duration of the dead time in each four-frequency-ratio measurement is closely related to the uncertainty of the final result. In addition, the frequency noise of the LFO, UTC(NIM), and TAI is the main contributor to the uncertainty. In general, the frequency stability of the above-mentioned three in turn become better. Here, $∆t_{\mathit{1}}$ is the sum of all running time segments of the OC obtained in actual operations. The total running time of the LFO $∆t_{\mathit{2}}$ corresponds to the start- and end-times of the OC and is set to minimize the uncertainty for the frequency ratio $\frac{y_{\mathrm{L}\mathrm{F}\mathrm{O}}\left(∆t_{\mathit{1}}\right)}{y_{\mathrm{L}\mathrm{F}\mathrm{O}}\left(∆t_{\mathit{2}}\right)}$ in Eq. 2. Similarly, $∆t_{\mathit{3}}$ is the minimum range covering $∆t_{\mathit{2}}$, and its endpoints must satisfy the 5-day interval reported in the Circular T bulletin. Finally, $∆t_{\mathit{4}}$ is the 1-month TAI reporting period of possibly 30 days.

A more accurate absolute frequency measurement of the OC may be performed based on the above strategy to minimize the uncertainty introduced by dead times. To enhance the measurement capability further, no suitable ideas have been found for TAI and UTC(NIM) because they are relatively unalterable and more complex to perform. The two feasible strategies given below are helpful in optical frequency measurements.

Increasing the operation time of optical clock

In a 1-month TAI reporting period, increasing the operation rate of the OC shortens dead times in the measurements of $\frac{y_{\mathrm{O}\mathrm{C}}}{y_{\mathrm{L}\mathrm{F}\mathrm{O}}}$. In addition, data from more measurements of the fractional frequency difference between OC and LFO are significant in generating more accurate evaluations of noise characteristics of the LFO. Using a weighted method to combine the various measurement results from different 1-month TAI reporting periods is also an optional solution.

Enhancing the frequency stability of local flywheel oscillator

At the fixed operation rate of an OC over a 1-month TAI reporting period, improving the frequency stability of LFO has an extraordinary effect to reduce the uncertainty introduced by measurement dead time between LFO and OC. In our works, the noise model of hydrogen maser as LFO is evaluated accurately by fitting its frequency stability curve respect to sampling time. The short-term frequency stability of hydrogen maser was evaluated by referring to the optical clock based on a continuous measurement period. The middle-term frequency stability was obtained by comparing two identical type hydrogen masers using DMTD system. The long-term frequency stability was measured using UTC as the reference. Therefore, combining several hydrogen masers as a combined LFO will enhance its frequency stability, meanwhile it could be also helpful to decrease the frequency drift of the LFO.

Applications

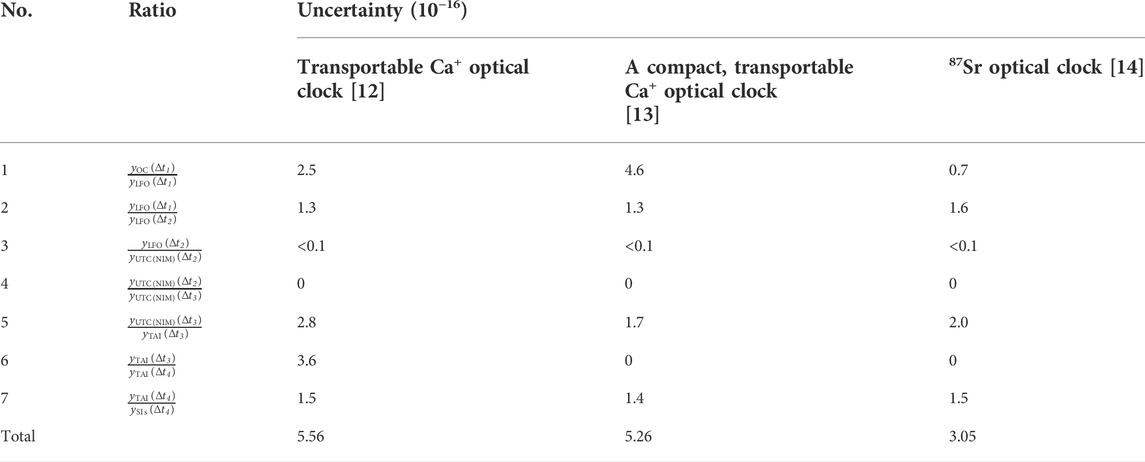
Applying the proposed method, the absolute frequencies of three optical clocks, including two Ca⁺ optical clocks developed by Innovation Academy for Precision Measurement Science and Technology of Chinese Academy of Sciences (APM) [12, 13], and a ⁸⁷Sr optical clock developed by NIM [14], were measured at 10⁻¹⁶ level in the past 3 years.

The uncertainty details of traceability link about these optical clock are listed in Table 1. In these three measurements, the uptime rates of three optical clocks are respectively ∼75% over 20-day period, ∼92% over 35-day period and ∼56% over 30-day period. Total running time of optical clock is recorded as $∆t_1$, and then we deliberately arranged $∆t_2=∆t_3$ to avoid introducing uncertainty in UTC(NIM) extrapolation, therefore the uncertainty attributed to the fourth term $\frac{y_{\mathrm{U}\mathrm{T}\mathrm{C}\left(\mathrm{N}\mathrm{I}\mathrm{M}\right)}\left(∆t_2\right)}{y_{\mathrm{U}\mathrm{T}\mathrm{C}\left(\mathrm{N}\mathrm{I}\mathrm{M}\right)}\left(∆t_3\right)}$ is always zero. The time interval $∆t_4$ is determined according to the Circular T bulletin corresponding to each measurement time period. In our measurement, $∆t_4$ is respectively 35 days (Circular T 385), 35 days (Circular T 396) and 30 days (Circular T 391). Both the capability of femtosecond optical frequency comb and dispersion of measurement data are main contributors to the uncertainty of frequency ratio measurement between the OC and the LFO. There is significant difference in the uncertainty of the first term $\frac{y_{\mathrm{O}\mathrm{C}}\left(∆t_1\right)}{y_{\mathrm{L}\mathrm{F}\mathrm{O}}\left(∆t_1\right)}$ due to different comb used in each measurement. The noise model of hydrogen maser (VCH-1013M) as LFO used in three measurements were evaluated with DMTD and comb measurement data. The 100 numerical simulated masers according to above the noise model were used to calculate the uncertainty of dead time. In addition, evaluating frequency drift of the maser introduce also a certain uncertainty of the second term $\frac{y_{\mathrm{L}\mathrm{F}\mathrm{O}}\left(∆t_1\right)}{y_{\mathrm{L}\mathrm{F}\mathrm{O}}\left(∆t_2\right)}$. Due to higher uptime rates of optical clocks, the uncertainty attributed to dead time is smaller in three measurements, but it is still main contributor to final measurement result. Frequency comparison between hydrogen maser and UTC(NIM) is continuously performed using DMTD method, since the uncertainty of that can be ignored (<1 × 10⁻¹⁷). In the Circular T with no. 385, 396 and, 391, the uncertainty u_A of the time difference between the UTC(NIM) and TAI is 0.3 ns, attributing to satellite time and frequency transfers. It leads to the uncertainty of the fifth term is 2.8 × 10⁻¹⁶ corresponding to $∆t_3$ = 20 days, 1.7 × 10⁻¹⁶ corresponding to $∆t_3$ = 35 days and 2.0 × 10⁻¹⁶ corresponding to $∆t_3$ = 30 days, respectively. When $∆t_3\ne ∆t_4$, the extrapolation uncertainty of TAI frequency average over time peirod $∆t_3$ to $∆t_4$ need to be evaluated using the above maser frequency extrapolation method. In the first measurement, the uncertainty is 3.6 × 10⁻¹⁶ corresponding to TAI extrapolation 15 days. The uncertainty of the last term $\frac{y_{\mathrm{T}\mathrm{A}\mathrm{I}}\left(∆t_4\right)}{y_{\mathrm{S}\mathrm{I}\mathrm{s}}\left(∆t_4\right)}$ can be directly found in Circular T bulletin.

TABLE 1

TABLE 1. Uncertainty of optical frequency traceability link.

Summary

Realizing absolute frequency measurements of an OC at low 10⁻¹⁶ level remains a challenging task for most research groups. Due to performance limitations in local cesium fountain clocks at NIM, applying the frequency comparison link between UTC(NIM) and TAI to measure precisely the optical frequency is currently a more feasible scheme. This work expressed the principle of absolute frequency measurement, and proposed several strategies to reduce the uncertainty introduced by the measurement system and dead time, according to our practical experience of absolute frequency measurement of three optical clocks at 10⁻¹⁶ level.

Author contributions

All authors listed have made a substantial, direct, and intellectual contribution to the work and approved it for publication.

Funding

This research was funded by the National Key R&D Program of China with grant no. 2021YFB3900701 and 2021YFF0600102 and the National Science Foundation of China with grant no. 61905231.

Acknowledgments

The authors would like to thank Professor Yiqiu Wang for his long-term support and guidance to the time and frequency research work of NIM, especially for his effective advises on the reconstruction of UTC(NIM) at NIM new campus. Currently UTC(NIM) has been operating continuously and stably, the work presented in this paper is one of its applications. We sincerely wish Professor Wang a happy 90th birthday.

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Reference

1. Brewer SM, Chen JS, Hankin AM, Clements ER, Leibrandt DR, Wineland D, et al. Al⁺²⁷ quantum-logic clock with a systematic uncertainty below 10^-18. Phys Rev Lett (2019) 123:033201. doi:10.1103/physrevlett.123.033201

PubMed Abstract | CrossRef Full Text | Google Scholar

2. Huang Y, Zhang B, Zeng M, Hao Y, Zhang H, Guan H, et al. A liquid nitrogen-cooled Ca⁺ optical clock with systematic uncertainty of 3×10^-18 (2021). doi:10.21203/rs.3.rs-333884/v1

CrossRef Full Text | Google Scholar

3. Riehle F, Gill P, Arias F, Robertsson L. The CIPM list of recommended frequency standard values: Guidelines and procedures. Metrologia (2018) 55:188–200. doi:10.1088/1681-7575/aaa302

CrossRef Full Text | Google Scholar

4. Hachisu H, Ido T. Intermittent optical frequency measurements to reduce the dead time uncertainty of frequency link. Jpn J Appl Phys (2015) 54:112401. doi:10.7567/jjap.54.112401

CrossRef Full Text | Google Scholar

5. Lodewyck J, Bilicki S, Bookjans E, Robyr JL, Shi C, Vallet G, et al. Optical to microwave clock frequency ratios with a nearly continuous strontium optical lattice clock. Metrologia (2016) 53:1123–30. doi:10.1088/0026-1394/53/4/1123

CrossRef Full Text | Google Scholar

6. Dubé P, Bernard JE, Gertsvolf M. Absolute frequency measurement of the ⁸⁸Sr⁺ clock transition using a GPS link to the SI second. Metrologia (2017) 54:290–8. doi:10.1088/1681-7575/aa5e60

CrossRef Full Text | Google Scholar

7. Pizzocaro M, Bregolin F, Barbieri P, Rauf B, Levi F, Calonico D, et al. Absolute frequency measurement of the¹S⁰-³F⁰ transition of ¹⁷¹Yb with a link to international atomic time. Metrologia (2020) 57:035007. doi:10.1088/1681-7575/ab50e8

CrossRef Full Text | Google Scholar

8. Kim H, Heo MS, Park CY, Yu DH, Lee WK. Absolute frequency measurement of the ¹⁷¹Yb optical lattice clock at KRISS using TAI for over a year. Metrologia (2021) 58:055007. doi:10.1088/1681-7575/ac1950

CrossRef Full Text | Google Scholar

9. Fang F, Li M, Lin P, Chen W, Liu N, Lin Y, et al. NIM5 Cs fountain clock and its evaluation. Metrologia (2015) 52:454–68. doi:10.1088/0026-1394/52/4/454

CrossRef Full Text | Google Scholar

10. Panfilo G, Parker TE. A theoretical and experimental analysis of frequency transfer uncertainty, including frequency transfer into TAI. Metrologia (2010) 47:552–60. doi:10.1088/0026-1394/47/5/005

CrossRef Full Text | Google Scholar

11. Arias EF, Panfilo G, Petit G. Timescales at the BIPM. Metrologia (2011) 48:S145–53. doi:10.1088/0026-1394/48/4/s04

CrossRef Full Text | Google Scholar

12. Huang Y, Zhang H, Zhang B, Hao Y, Gao K. Geopotential measurement with a robust, transportable Ca⁺ optical clock. Phys Rev A (2020) 102:050802. doi:10.1103/PhysRevA.102.050802

CrossRef Full Text | Google Scholar

13. Cao J, Yuan J, Wang S, Zhang P, Yuan Y, Liu D, et al. A compact, transportable optical clock with 1×10⁻¹⁷ uncertainty and its absolute frequency measurement. Appl Phys Lett (2022) 120:054003. doi:10.1063/5.0079432

CrossRef Full Text | Google Scholar

14. Yige L, Q W, Fei M, Cao S, Wang Y, Ye L, et al. A ⁸⁷Sr optical lattice clock with 2.9×10^-17 uncertainty and its absolute frequency measurement. Metrologia (2021) 58:035010. doi:10.1088/1681-7575/abf33e

CrossRef Full Text | Google Scholar