Assessing delivered pulse-energies by a nonlinear model

Short-duration and high-amplitude electric pulses have recently been used for two different biological tasks: stimulating physiological actions such as heart rate or defibrillation and invoking cell annihilation, as in cancer treatment or atrial fibrillation ablation, by electroporation. However, the physics behind the influence of such pulses has been controversial due to the linear methods used in the analyses. We present the results of a simple nonlinear model to study this situation. Results for the specific nonlinear model show that, below a certain pulse duration, stimulating threshold levels increase rapidly, while the delivered energies reach the lowest plateau. This renders former energy estimates based on linear models, which show a distinct minimum in the calculated delivered energy at a certain amplitude which is invalid for the real nonlinear case. It is notable that these results explain why short high-amplitude pulses are more beneficial to the patient than lower and longer ones in pacing. However, these pulses should not be too high, since no additional energy reduction is achieved and electroporation processes could occur. To further reduce the tissue burden, a train of pulses is necessary, but delivered energies become higher. Considering this case, we clarify the difficulty of reaching threshold at the end of the nth pulse for n > 2 not previously reached and find the “best” conditions for such a train of pulses.

Introduction

There has been a substantial increase in recent applications of nanosecond-duration high-intensity pulses in medicine and biophysics. This field is called “nanosecond pulsed electric field” (nsPEF). Applications are divided between two types of pulse-energy, depending on the influence of the tissue. One type is pacing by a either single nsPEF or by a burst or a train of nsPEFs stimulations, such as in a heart implantable cardioverter defibrillator (ICD [1, 2]) in which the task is to use the electric field amplitude to cross a threshold (open a voltage-gated channel) with as little energy delivered to the tissue by the pulse(s) as possible in order to avoid accompanying harm such as pain or electroporation.

The other type is electroporation [3–6]. Electroporation by intense pulsed electric fields (PEF) has recently become the major application of nanosecond-PEF (nsPEF). It is used in medicine for many therapeutic tasks, including electrochemotherapy and gene transfer. Newer applications of this method have been used for tumor and heart ablation procedures. While these issues are beyond the scope of the present work, we note that the physical interactions of the pulses with the tissue are quite different in these applications. This procedure exploits the focused energy, the high electric field of the pulse, its time duration, and other details such as the rise and fall times (see [7] for discussion). These cause electroporation, a process by which pores are created in the cell in order to either insert compounds (such as medications) into it or for “irreversible electroporation” to induce cell death (judicial cell death) [8] by apoptosis, necrosis, or newer methods such as pyroptosis or necroptosis [9]. Judicial cell death has recently been used to eliminate tumors [10, 11] and heart atrial or ventricular fibrillation ablations [12]. Note that Joule heating is worsened when the energy is tightly focused, so longer duration treatments and lower pulse repetition rates would constitute a preferable treatment. It should be noted that, over the past decade and a half, extensive research has teased out and maximized the therapeutic efficiency of different pulses and waveforms, including packets/bursts of pulses, mono- vs. biphasic, and the introduction of asymmetric delays to reduce tissue heating. Heating is a major problem in pulse treatment. This issue has recently been discussed from several points of view [13]. Furthermore, a combination of shorter, high-voltage pulses with longer, low-voltage pulses has investigated the domination of the electrophoretic effect in gene/molecule uptake (see, e.g., [14] for a clear presentation of the subject and [15] for recent advances in it).

We are here interested in the application of electric pulses for simulation. For the benefit of the patient, the delivered pulse(s) should have as low energy as possible to avoid pain or other problems, but be “strong” enough to pass a threshold and cause the required effect.

It has been shown experimentally [16] for patients that increasing the amplitude of an applied single pulse and decreasing its duration leads to a “gentler” influence of the defibrillator than that obtained using regular defibrillating pulses, in that it lowers the electrical energy delivered (EED). This feature of lowering EED was sought in defibrillation to avoid cell damage [17], pain, tachycardia, re-fibrillation, and even mortality [18], all of which can arise from high-energy-delivering pulses. Recently [16, 19], a group succeeded in using nanosecond pulses to stimulate and defibrillate rabbit hearts. It turned out that the defibrillation energy was approximately an order of magnitude lower than that for a millisecond defibrillation. However, the authors of the papers [16, 19] could not explain the reason for such a beneficial outcome, since current knowledge based on linear models predicts that, as a function of pulse duration (and the corresponding amplitude), an EED minimum should exist, and, for shorter (and higher) pulses, the delivered energy must increase! Such an increase, however, does not occur during experimentation. Experiments also show that, while in pulse durations above ∼100 nS, the stimulation-causing-excitation threshold is lower than the electroporation threshold, the opposite is true for much shorter pulse durations [16, 19]. Previous studies of biphasic ns pulse or buffer conductivity and pulse duration found that, for durations lower than 100 ns (depending on local conductivity conditions), a phenomenon like shock formation could cause the electroporation threshold to increase due to a) bypassing the capacitance of the outer membrane and b) causing a reverse uptake of ions into the cytosol instead of leakage into the bulk media. These issues are beyond the scope of this work.

For a linear circuit, the electrical power delivered (P) is proportional to I²R where I is the current and R is the resistivity of the circuit. For this linear case, consider, for example, the Weiss strength–duration rule (see, e.g., [20] and references therein) for a current pulse delivered to a device in order to reach a threshold value $\left(I_{th}\right)$—$I_{th}=R_b\left(1+\frac{C_r}{T}\right)$—where $T$ is the duration time of a rectangular current pulse of amplitude $I_{th}.$, $R_b$ is the “rheobase,” which is a stimulus strength (i.e., current), and $C_r$ is the “chronaxie,” which is characteristic time. Both are constants for a specific system. For a current pulse of constant amplitude $I_{th}$, the energy delivered is $E_{th}={I_{th}}^{2}RT={R_b}^2{\left(1+\frac{C_r}{T}\right)}^{2}RT$. Note that the energy becomes infinite for T→0. This energy has a minimum value for $T=C_r$ which is given by $E_{th\mathit{min}}=4{R_b}^{2}R{C}_r$. From its relation to T, $T=C_r{R}_b$/$\left(I_{th}-R_b\right)$ and as a function of $I_{th},$ $E_{th}={I_{th}}^{2}R{C}_r{R}_b$/$\left(I_{th}-R_b\right)$ (see, e.g., [11]).

However, biological systems are always nonlinear. For a nonlinear system, the power–current dependence is not so simple and the delivered energy acquires a different form. Thus, although the Weiss or Lapique strength–duration rules were shown to be good approximations even for a nonlinear system [21], the delivered energy is a completely different matter.

We used the FitzHugh nonlinear model in its excitable mode, stimulated by a single pulse or by a train of pulses to force it to reach a threshold. The model is used to simulate, for example, an organ under external pacing, such as a fibrillating heart receiving a single pulse or a train of pulses by a defibrillator to terminate the malfunction. We will attempt a possible explanation of the EED problem, based on the nonlinearity of the device–patient interaction. Note that we are only looking for a possible physical explanation and not for an exact replication of an event. Our approach is similar to Izhikevich’s explanations of other nonlinear phenomena [22].

Our results will explain why, in pacing, short pulses of high amplitudes are more beneficial to the patient than lower and longer ones.

A short train of pulses is considered next. Such a pacing is necessary to further ease strain on the patient. However, we explain why the time intervals between pulses reduce the pulses’ threshold-crossing effect. Consequently, we present the optimal conditions for such a short train of pulses.

The model

The FitzHugh (FH) model without diffusion (D = 0) is based on the following system of nonlinear equations:

$\dot{v}=v\left(v-a\right)\left(1-v\right)-w+I\left(t\right),(1)$

$\dot{w}=\epsilon \left(v-dw\right),$

where v can be seen as the action-potential AP appearing in the organ, while the other variable, w, is an auxiliary variable that simulates inhibition; $\epsilon \ll 1,a$ and d are constant parameters. $I\left(t\right)$ is the stimulating current, which in the present case is a square pulse or a train of square pulses, each of amplitude I (constant) and duration T, applied by the stimulator. For negative a-values, system (1) is an oscillator while, for positive a-values, system (1) is in its excitable state. Here, we use only the excitable state of the system, whose behavior is as follows. With no external drive $I\left(t\right)$ = 0, the system is idle, its AP residing at a steady state value (here = 0). Under a single short-pacing current pulse, the response depends on the forcing magnitude. If the latter is below a certain value called “threshold,” only a small AP can be induced. However, if it is above threshold, a real single regular AP pulse is created, after which the cell returns to the idle state. Note that the threshold here is not absolute: it is represented in phase space (w, v) by a so-called repeller line, (R-line). An R-line for excitable systems is a very narrow band of phase space overlapping a (threshold) line, a band at which trajectories change direction in a smooth, albeit rather abrupt, manner. The difference between an R-line and a true threshold is discussed in [21]. Since thresholds in biological systems are of the R-type, we only consider an example of one.

We assume that the present situation of the system (organ) can be simulated by the resting state (v = w = 0) of the model, and that the aim of the pulse(s) application is to cause the system to reach its threshold (or, more exactly, the R-line).

We show that, for the nonlinear system, the energy needed for the task decreases with a decrease in pulse duration and reaches a steady plateau instead of a minimum and increasing again for lower durations.

A single pulse

We consider a single unidirectional rectangular current pulse ($I\left(t\right)=I_{th}$), a constant, delivered to the model for a duration of T time units, where T is the time duration needed for the current of amplitude $I_{th}$ to reach threshold. In contrast to the linear case, the electrical energy delivered is given by:

$E_{th}={\int }_0^T{I}_{th}vdt=I_{th}{\int }_0^{T}v\left(t\right)dt,(2)$

where $v\left(t\right)$ is the solution of system (1), representing the transmembrane potential difference of monopolar electrodes and is not equal to $IR$ for a constant $R$, as for the linear case.

The minimal (asymptotic) energy (E_m) for the pulse to reach threshold can be approximated as follows.

For a very large I (that is $I\gg v,w$), Eq. 1 becomes $\dot{v}≌I\left(t\right)$ or $v≌It$. The threshold $v=v_{th}$ reached at $t=T$ resides approximately at the $w=0$ line in phase space. Therefore, we obtain $IT≌v_{th}$ and $E_m≌\frac{{\left(IT\right)}^2}{2}={v_{th}}^2/2$. Note that, since the product IT is a constant = $v_{th}$ and the minimal energy depends only on it, then, above a certain amplitude I, this $E_{th}$ will not change. Thus, below a certain T (to match $v_{th}/$ I), all threshold reaching pulses will deliver approximately the same (minimal) energy, E_m.

Calculations for the case: a = 0.12, $\epsilon =0.01$, d = 3 yielded $v_{th}$ $≌$ 0.192. Hence, an approximation for $E_m\text{\hspace{0.17em}is\hspace{0.17em}}{E}_m≌$ 0.016.

The system was run numerically for each I with increasing T values until threshold (repeller) was reached. $E_{th}$ was then calculated by Eq. 2.

For Is that are too small, the system cannot reach threshold for even very large Ts. For the case studied, it was checked that, to achieve threshold passage, I should be larger than 0.0147.

Figure 1 shows $I_{th}$ as a function of T. The hyperbolic shape is apparent. To reach threshold, lower pulse durations entail higher pulse amplitudes. As shown in [12], the linear approximation to this strength–duration curve is very good. The lower asymptote, as mentioned previously, is 0.02.

FIGURE 1

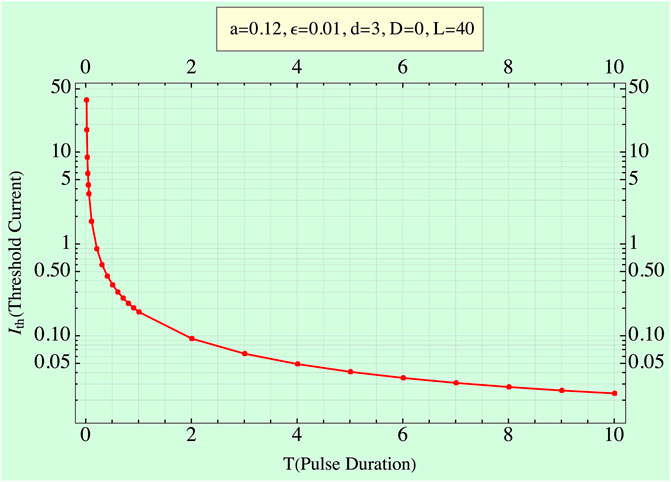
FIGURE 1. Strength–duration curve: input current, $I_{th}$ (semi-logarithmic scale) of single-pulse stimulation at threshold as a function of pulse duration $T$. Parameters used for the calculation are displayed in the figure. Apparently, higher pulses need shorter durations for threshold crossing. Note that there is a lower limit (asymptote) for the pulse duration, below which, regardless of the pulse amplitude, no crossing is possible.

Figures 2A,B depict $E_{th}$ as functions of $I_{th}$ and T respectively

FIGURE 2

FIGURE 2. Numerically calculated threshold energy (Eqs 1,2) (semi-logarithmic scale) as a function of (A) the minimum current input intensity $I_{th}$, and of (B) pulse duration T for a single rectangular pulse. The parameters used for the calculation are displayed in the figure. Delivered energies decrease with decreasing pulse durations and increasing pulse amplitudes up to a certain level. The energy exhibits a plateau of ≌0.016 for high values of ${\mathrm{I}}_{\text{th}}$ and low pulse durations.

It is evident (Figure 2) that no pure “minimum” point arises. The energy reaches a minimum asymptote at E ≌0.016 as expected. Higher I values simply imply lower T’s but ∼ equal energies. Thus, increasing I values always lead to lower or equal energies, validating the experimental measurements of [16 and 19].

A train of pulses

The use of a very short single pulse to achieve the intended result is somewhat problematic since generating such a high amplitude pulse would call for very high electric fields (typically from 1 to over 50 kV/cm to obtain results [23]). This requirement can be overcome [24, 25] by applying a fast train of shorter pulses [26]. However, such an application procedure may increase the total EED to the subject, as has been observed experimentally in a stimulation of cardiomyocytes [27] by a single and a train of two and three rectangular pulses. Here, the train of multiple pulses led to the reduction of the stimulation threshold voltage compared to a single pulse, while there was no reduction in the delivered energies compared to a single-pulse stimulation.

To assess the energy increase using several pulses in succession, we again consider the stimulation of our nonlinear model.

For a train of pulses, the energy delivered to reach the threshold should be:

$E_{th}=I_{th}{\displaystyle {\sum }_{i=1}^n}{\int }_{ti}^{ti+T}v\left(t\right)dt,(3)$

where ti is the initial time of the ith pulse and n marks the pulse number at threshold passing.

Here, the application rate (or duty cycle: DC) in addition to the T and I parameters plays a crucial role, since, during the time between pulses, the action potential v and w move in phase space opposite to the direction of the repeller (see Figure 5), increasing the distance (both in phase space and in terms of v) to the threshold. This inter-pulse-interval-dependence causes a prolongation of T or an amplification of $I_{th}$ and an increase of EED.

Two pulses

As an example, Figure 3 depicts the situation of a train of two pulses of the same amplitude in the attempt to reach threshold at the end of the second pulse with a DC of 0.5. Two cases are shown, one for short-duration pulses (T = 1) and the other for large duration (T = 10).

FIGURE 3

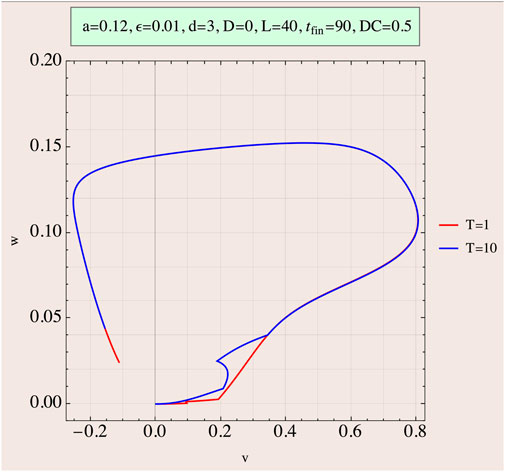
FIGURE 3. Phase portrait (w as a function of v) of two rectangular pulses just passing threshold at the termination of the second pulse. Duty cycle (DC) is 0.5 (interpulse duration equals pulse application time). Two cases, one T = 1 (red line) and one T = 10 (blue line), are displayed. The effect of the interpulse time following first pulse termination is evident as the phase portrait line moves to smaller v values, away from the repeller, and the second pulse’s amplitude therefore increases, so that the sum lengths of the two pulses in the T = 10 case is higher than the single pulse of the T = 1 case.

The phase-space development is revealing. For the short duration case, T = 1, the interpulse interval also equals 1. Therefore, in this case, the decrease in v during this I = 0 period is minimal and thus the necessary amplitude of each of the two pulses is approximately half of the amplitude of the single pulse needed to achieve threshold. Consequently, the EED in this case is only slightly higher than that of the single-pulse case. On the other hand, for the T = 10 case, the interpulse interval also equals 10, causing a larger decrease of v in this period, leading to an increase of the two pulses’ amplitudes to become almost the same height of the single pulse with a much higher EED. Delivered energies are calculated by Eq. 3.

Results are shown in Figure 4.

FIGURE 4

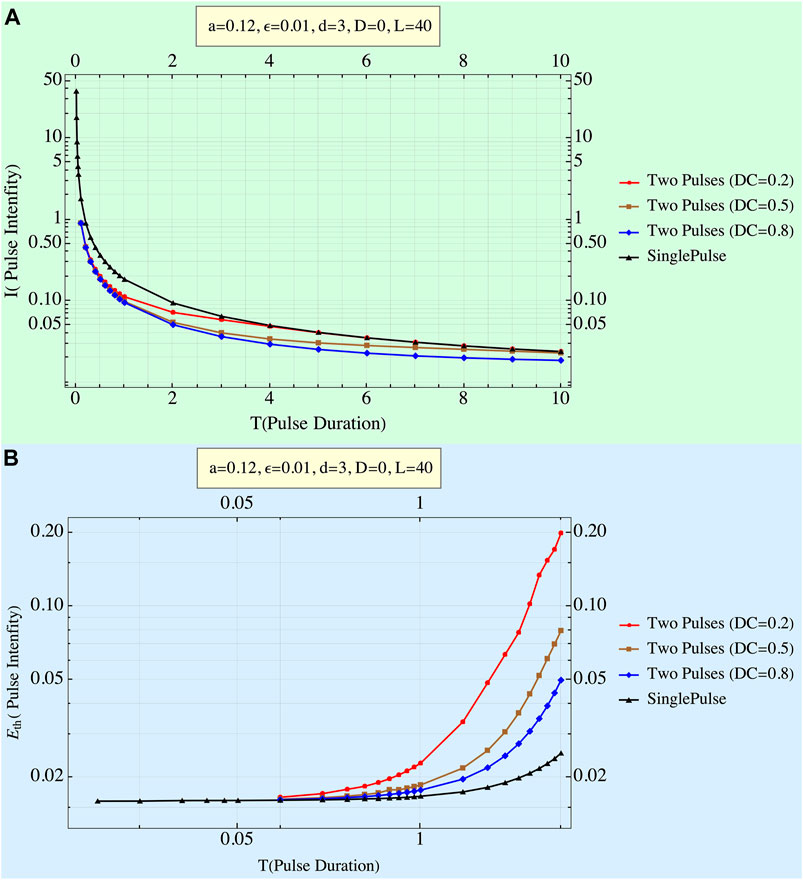
FIGURE 4. (A) Train of two pulses’ strength–duration curve: pulse amplitude of each of a train of two rectangular pulses when threshold is achieved at the termination of the second pulse. Note that the amplitude of each of the twin pulses depends on the duty cycle: the higher it is (and the lower the interpulse interval is), the higher the amplitude. As pulse duration increases, deviations from the repeller grow until, eventually, a single pulse of the twin becomes high enough to induce threshold passage by itself. (B) EED as a function of pulse duration for different values of duty cycle (DC). System parameters are displayed. The twin pulse’s delivered energies are always higher than those of the single pulse, and the effect of the duty cycle is noticeable, especially for long durations.

Figure 4 depicts the influence of both the pulse duration and the DC on the height of each of the two pulses and the transition from a half to almost a full size of the single-pulse amplitude. EEDs are seen to increase both with pulse duration and decrease with the DC.

An example of this behavior is given in Figure 5, where the ratio of the single to double pulse amplitudes for DC = .5 is depicted in Figure 5A as a function of T, showing this ratio’s decrease from 2 to 1. At a ratio of 1, there is, of course, no need for the second pulse, since the first has already overcome the threshold. The related delivered energies are shown in Figure 5B. It is evident that, for T’s smaller than 0.2, these energies barely differ from those for a single pulse, while the energies of the two-pulse train increase rapidly for higher T values reaching ∼ three times higher for T = 10.

$\mathrm{n}\left(>2\right)\text{\hspace{0.17em}pulses}.$

For a train of n (>2) pulses, we have calculated an approximation for $I_{thn}$, as follows.

FIGURE 5

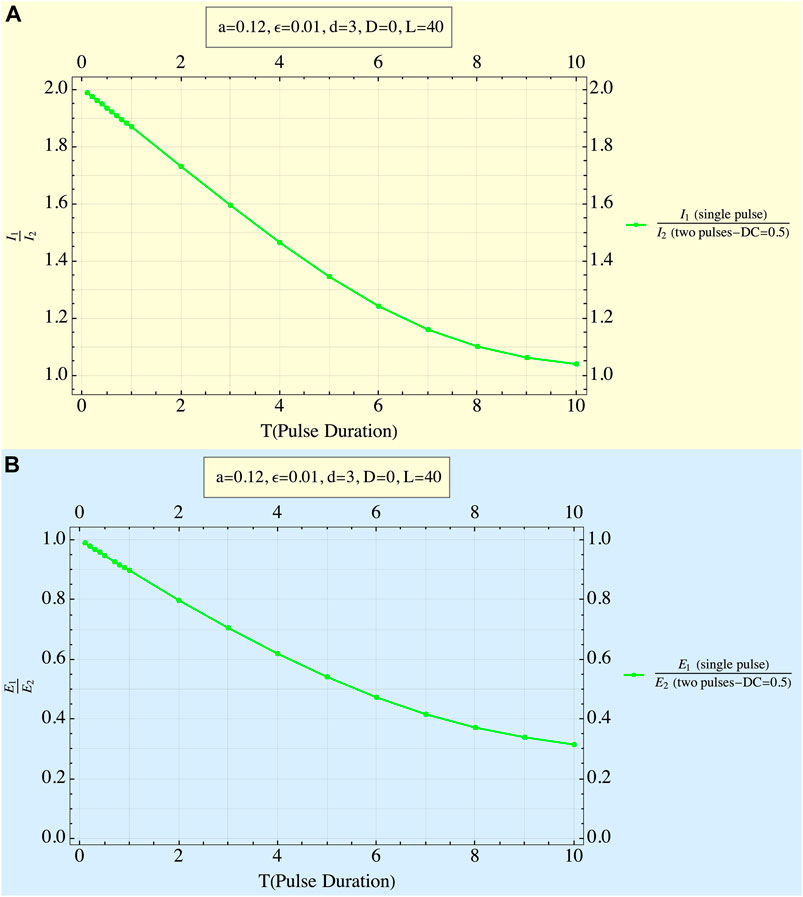
FIGURE 5. Ratio of the amplitude of a single pulse to that of the two pulses to reach threshold. (A) Ratio of input currents as a function of pulse duration. Displayed results correspond to DC of 0.5. Other system parameters are displayed in the figures. At very low pulse durations, the amplitude of each of the twin pulses is almost half of the single-pulse stimulation case. Sizes of the twin pulses increase with pulse durations (and the I₁/I₂ ratio decreases), first linearly, and reaching asymptotically the size of a single pulse. (B) Ratio of EEDs as a function of pulse duration. Displayed results correspond to DC of 0.5. Other system parameters are displayed in the figures. The higher the pulse duration, the greater is the delivered energy needed by the twin pulses w. r. t. the single-pulse case. Changes are similar to Figure 5A.

In the FHN system for a constant $I\left(t\right)=I$ (direct current), there is a limit to I, denoted by $I_0$, below which the system cannot reach threshold, no matter how long the current is applied. In the Appendix, we show that, below $I_0$, the system approaches a steady state—for our case, $\left(a=0.12;d=3\right),I_0=0.016$. Thus, in order for a single DC or a prolonged single pulse to achieve threshold, its amplitude should at least be above $I_0$.

For such a train, there are limits to I and T; outside such limits, the system will not pass threshold at the end of the nth pulse, even under the “best” conditions. The latter are: 1) to be as close to, but slightly above, $I_0$ $.$ keeping the amplitude just above $I_0$; 2) to keep the lowest inter-pulse intervals.

We can derive an approximation for the best conditions. Recall [21] that, according to Weiss for the linear case, and as a good approximation also for the nonlinear case, the amplitude, $I_{th}$ of a single pulse of a short duration T, in order to pass threshold, should be: $I_{th}\approx \frac{a}{T}$. Therefore, for a train of very short n pulses, and for very short interpulse intervals, the required amplitude of each pulse of the train in order to not pass threshold until the end of the train and to pass threshold exactly at this end should be approximately $I_{thn}{=I}_{th}/n$ $\approx a/Tn$. The limiting value of $I_{thn}$ for the FHN case, below which threshold passing is unattainable, is again approximately 0.016. Therefore, $Tn$ should be approximately higher than $b=\frac{a}{I_{th}}$ in order for only the last pulse to cross threshold. The condition for T is therefore:

$T\approx \frac{b}{n}.(4)$

Note that the exact numerical value of b is less important in general. It is important to note that, for n pulses, the lower limit for I does not change, while the limit for T changes like 1/n.

As an example of the use of Eq. 4, we have calculated for n = 5 in the FHN case that $T_{no}\approx 4.2$ or $T_{no}n\approx 21$, meaning that b ∼ 21. Therefore, for any n there, T should be longer than 21/n. Indeed, for n = 10, calculations show that $T_{no}\text{\hspace{0.17em}should\hspace{0.17em}be}\approx 2.1$.

For n = 20, T should be $\approx 1.05$ for $I_{thn}\approx 0.018$

What happens if we keep $I_{thn}Tn\approx c\text{\hspace{0.17em}for\hspace{0.17em}}c=0.016x21=0.336$, like for n = 5 to take $I=0.033,T\approx 2.1$?

Let us try for I = 0.033: n = 10, T $\text{should\hspace{0.17em}be}\sim 0.68$ (it turned out to be 0.675), and n = 20, T should be ∼0.34 (it turned out to be 0.3398).

However, it seems that a better approximation would be if $I_{thn}Tn$ behaved like a hyperbole $I_{thn}Tn-k=h/\left(I_{thn}-0.016\right)$, where k and h are constants to be derived from the model.

So let us try n = 5; I = 0.066 and then $\frac{h}{I-0.016}=0.0144$ or 0.2104 = $I_{thn}Tn$

The result for T indicates that k should be ∼0.183:

$I_{thn}Tn-0.183=\frac{7.2x{10}^{-4}}{\left(I_{thn}-0.016\right)}.$

This approximation appears to be rather good. It was checked for a number of n and I values, with very good outcomes for T. Additionally, for n > 3, the range of values in the vicinity of the best conditions where threshold is achieved exactly at the termination of the nth pulse is rather small.

Discussion

The reason for the discrepancy between the linear and nonlinear energy results stems can be explained as follows. The energy calculation in the linear case is based on $=I^{2}RT$, where $R$ is the system’s resistance. However, for a nonlinear system such a constant “resistance” mode, the system is no longer valid. Instead, resistors in models of nonlinear devices were replaced by variable resistors (see, e.g., the model of McNeal (1976) [28] of a myelinated axon).

Thus, our results show that the energy needed for a single pulse to pass threshold in a nonlinear system asymptotically reaches the lowest plateau above a certain pulse amplitude.

Although nsPEF is less efficient at neurostimulation, they can be employed to minimize painful side effects [29, 30]. These experimental findings cannot be explained by our results. A puzzling experimental result is that, contrary to longer pulse applications, under very short pulses the electroporation threshold is lower than that of stimulation–excitation. There is thus enough energy or pulse amplitude and duration [7] for electroporation to occur. No involuntary muscle contractions or pain arises which would be due to excitation. The reason for this “threshold reversal” is unclear. A very convincing argument [31] is that the discrepancy can be explained by the difference in the time constants $\left({\mathrm{\tau }}^{\prime }s\right)$ for each process (electroporation or stimulation). The argument is that $\tau$ of electroporation $\left({\mathrm{\tau }}_e\right)$ is smaller than that of stimulation $\left({\mathrm{\tau }}_s\right)$. The durations of the nanoseconds-pulses used are shorter than ${\tau }_s$ but larger than ${\tau }_e.$ Therefore, for such short pulses, electroporation would arise before stimulation, even if the latter does occur, supporting the observed “threshold reversal.”

As expected for the train of pulses, the DC, in addition to the T and I parameters, is very important. Figures 4 and 5 depict the train of the two pulses’ situation. T marks the abscissa, and the train period p is the identifying parameter. Thus, the duty cycle is T/p. It is seen that: 1) as expected, the larger p is, the closer one gets to the single pulse; 2) the T prolongation effect is substantial, causing energy increase much above that of a single pulse—the higher the frequency (lower the period p), the higher the effect; 3) above a certain T (below a certain I), excitation is no longer possible. The reason for the difficulty of reaching threshold at the end of the nth pulse for n > 2 can be seen in phase space; for conditions “outside” the best ones, on the one hand, threshold can already be achieved before n, and, on the other hand, n movements away from the repeller during the interpulse intervals dictate that the repeller can never be reached.

The benefit of multiple short pulses with relatively high duty cycle—closely clustered short pulses (the “best conditions”)—becomes evident. Not only do they not require high electric fields for their generation, but they are also shown to deliver almost minimal energy to the patient. If the aim is to deliver a train of n pulses, care should be taken to keep close to the “best” conditions—to maintain amplitudes just above the lower limit of a direct current excitation and use a high DC. On the other hand, for electroporation treatment, short DCs are recommended ([32] and references therein).

The interaction of a periodic pacer with a nonlinear system is a very important line of study in many fields. It has been pursued intensively since Winfree’s seminal work [33]. One of the methods of analyzing this problem was the interesting device of time crystals, which fully describes the phase response of the oscillation. A recent study of such an interaction [34] gives a full pictorial usage of such time crystals. However, since the present work treats only a single or a small number of pacing pulses, it does not use this method.

Calculations were carried out for only one nonlinear system (the FH); however, since the FH is a good representative of this category and the basic understanding of the delivered energy behavior is made clear, it may constitute ample proof of the results for general nonlinear systems of this sort.

Our model does not include diffusion, which could have altered the outcome. However, we wanted to compare our nonlinear system’s response to the former linear approach which does not involve diffusion, and (based on some preliminary results) the alterations by diffusion incorporation seem small.

Data availability statement

The raw data supporting the conclusion of this article will be made available by the authors, without undue reservation.

Author contributions

AR conceived the study. DB, IA, ES, YB, RR, and RT performed calculations and wrote the article. All authors contributed to the article and approved the submitted version.

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article or claim that may be made by its manufacturer is not guaranteed or endorsed by the publisher.

References

1. Weiss R, Knight BP, Gold MR, Leon AR, Herre JM, Hood M, et al. Safety and efficacy of a totally subcutaneous implantable-cardioverter defibrillator. Circulation (2013) 128:944–53. doi:10.1161/circulationaha.113.003042

PubMed Abstract | CrossRef Full Text | Google Scholar

2. Casiola M, Xiao S, Pakhomov AG. Damage-free peripheral nerve stimulation by 12-ns pulsed electric field. Sci Rep (2017) 7:10453. doi:10.1038/s41598-017-10282-5

PubMed Abstract | CrossRef Full Text | Google Scholar

3. Beebe SJ, Joshi R, Schoenbach KH, Xiao S. Ultrashort electric pulse effects in biology and medicine. New York: Springer (2021).

Google Scholar

4. Damijan M. Switzerland: Springer Nature (2022).Handbook of electroporation

Google Scholar

5. Joshi RP, Schoenbach KH. Electric fields in biological cell and membranes. In: Electromagnetic fields in biological systems. Boca Raton: CRC Press (2011). p. 71–114.

Google Scholar

6. Joshi RP, Schoenbach KH. Bioelectric effects of intense ultrashort pulses. Crit Rev Bio-Medical Eng (2010) 38:255–304. doi:10.1615/critrevbiomedeng.v38.i3.20

PubMed Abstract | CrossRef Full Text | Google Scholar

7. Schoenbach KH, Joshi RP, Beebe SJ, Baum C. A scaling law for membrane permeabilization with nanopulses. IEEE Trans Dielectr Electr Insula (2009) 16:1224–35. doi:10.1109/tdei.2009.5293932

CrossRef Full Text | Google Scholar

8. Napotnik TB, Polajzˇer T, Miklavcˇicˇ D. Cell death due to electroporation – a review. Bioelectrochemistry (2021) 141:107871. doi:10.1016/j.bioelechem.2021.107871

PubMed Abstract | CrossRef Full Text | Google Scholar

9. Lv Y, Zhang Y, Rubinsky B. Molecular and histological study on the effects of electrolytic electroporation on the liver. Bioelectrochemistry (2019) 125:79–89. doi:10.1016/j.bioelechem.2018.09.007

PubMed Abstract | CrossRef Full Text | Google Scholar

10. Chan KY, Jang MJ, Yoo BB, Greenbaum A, Ravi N, Wu WL, et al. Engineered AAVs for efficient noninvasive gene delivery to the central and peripheral nervous systems. Nat Neurosci (2017) 20(8):1172–9. doi:10.1038/nn.4593

PubMed Abstract | CrossRef Full Text | Google Scholar

11. See e.g., Zou H, Gan XL, Linghu LJ, Zhang Y. Intense nanosecond pulsed electric fields promote cancer cell apoptosis through centrosome-dependent pathway involving reduced level of PLK1. Eur Rev Med Pharmacol Sci (2013) 17:152–60. https://www.europeanreview.org/wp/wp-content/uploads/152-160.pdf

PubMed Abstract | Google Scholar

12. Althoff TF, Mont L. Novel concepts in atrial fibrillation ablation-breaking the trade-off between efficacy and safety. J Arrhythmia (2021) 37:904–11. doi:10.1002/joa3.12592

CrossRef Full Text | Google Scholar

13. Milestone W, Hu Q, Loveless AM, Garner AL, Joshi RP. Modeling coupled single cell electroporation and thermal effects from nanosecond electric pulse trains. J Appl Phys (2022) 132:094701. doi:10.1063/5.0107544

CrossRef Full Text | Google Scholar

14. Yarmush ML, Golberg A, Serˇsa G, Kotnik T, Miklavčič D. Electroporation-based technologies for medicine: Principles, applications, and challenges. Annu Rev Biomed Eng (2014) 16:295–320. doi:10.1146/annurev-bioeng-071813-104622

PubMed Abstract | CrossRef Full Text | Google Scholar

15. Wang F, Lin S, Yu Z, Wang Y, Zhang D, Cao C, et al. Recent advances in microfluidic-based electroporation techniques for cell membranes. Lab Chip (2022) 22:2624–46. The Royal Society of Chemistry. doi:10.1039/d2lc00122e

PubMed Abstract | CrossRef Full Text | Google Scholar

16. Varghese F, Ju N, Xie F, Philpott JM, Pakhomov AG, Zemlin CW. Low-energy defibrillation with nanosecond electric shocks. Cardiovas Res (2017) 113:1789–97. doi:10.1093/cvr/cvx172

PubMed Abstract | CrossRef Full Text | Google Scholar

17. Walcott GP, Killingsworth CR, Ideker RE. Do clinically relevant transthoratic defibrillation energies cause myocardial damage and dysfunction? Resuscitation (2003) 59:59–70. doi:10.1016/s0300-9572(03)00161-8

PubMed Abstract | CrossRef Full Text | Google Scholar

18. Tan VH, Wilton SB, Kuriachan V, Sumner GL, Exner DV. Impact of programming strategies aimed at reducing nonessential implantable cardioverter defibrillator therapies on mortality A systematic review and meta-analysis. Circ arrhythmia Electrophysiol (2014) 7:164–70. doi:10.1161/circep.113.001217

PubMed Abstract | CrossRef Full Text | Google Scholar

19. Semenov I, Grigoryev S, Neuber JU, Zemlin CW, Pakhomova ON, Casciola M, et al. Excitation and injury of adult ventricular cardiomyocytes by nano-to millisecond electric shocks. Sci Rep (2018) 8:8233. doi:10.1038/s41598-018-26521-2

PubMed Abstract | CrossRef Full Text | Google Scholar

20. Abalkhail TM, MacDonald DB, AlThubaiti I, AlOtaibi FA, Stigsby B, Mokeem AA, et al. Intraoperative direct cortical stimulation motor evoked potentials: Stimulus parameter recommendations based on rheobase and chronaxie. Clin Neurophys (2017) 128:2300–8. doi:10.1016/j.clinph.2017.09.005

PubMed Abstract | CrossRef Full Text | Google Scholar

21. Rabinovitch A, Braunstein D, Biton Y, Friedman M, Aviram I. The weiss–lapicque and the lapicque–blair strength—Duration curves revisited. Biomed Phys Eng Express (2016) 2:015019. doi:10.1088/2057-1976/2/1/015019

CrossRef Full Text | Google Scholar

22. Izhikevich EM, FitzHugh R. FitzHugh-Nagumo model. Scholarpedia (2006) 1(9):1349. doi:10.4249/scholarpedia.1349

CrossRef Full Text | Google Scholar

23. Pakhomov AG, Xiao S, Novickij V, Casciola M, Semenov I, Mangalanathan U, et al. Excitation and electroporation by MHz bursts of nanosecond stimuli. Biochem Biophys Res Commun (2019) 518:759–64. doi:10.1016/j.bbrc.2019.08.133

PubMed Abstract | CrossRef Full Text | Google Scholar

24. Novickij V, Grainys A, Butkus P, Tolvaišienė S, Švedienė J, Paškevičius A, et al. High-frequency submicrosecond electroporator. Biotechnol Biotec Eq (2016) 30:607–13. doi:10.1080/13102818.2016.1150792

CrossRef Full Text | Google Scholar

25. Ryan HA, Hirakawa S, Yang E, Zhou C, Xiao S. High-voltage, multiphasic, nanosecond pulses to modulate cellular responses. IEEE Trans Biomed Circuits Syst (2018) 12:338–50. doi:10.1109/tbcas.2017.2786586

PubMed Abstract | CrossRef Full Text | Google Scholar

26. Sözer EB, AndreiPakhomov GAG, Semenov I, Casciola M, Kim V, Vernier PT, et al. Analysis of electrostimulation and electroporation by high repetition rate bursts of nanosecond stimuli. Bioelectrochemistry (2021) 140:107811. doi:10.1016/j.bioelechem.2021.107811

PubMed Abstract | CrossRef Full Text | Google Scholar

27. Laasmaa M, Lu P, Veletić M, Louch WE, Bergsland J, Balasingham I, et al. Energy-efficiency of cardiomyocyte stimulation with rectangular pulses. Sci Rep (2019) 9:13307. doi:10.1038/s41598-019-49791-w

PubMed Abstract | CrossRef Full Text | Google Scholar

28. McNeal DR. Analysis of a model for excitation of myelinated nerve. IEEE Trans Biomed Eng (1976) 23:320–37. doi:10.1109/tbme.1976.324593

PubMed Abstract | CrossRef Full Text | Google Scholar

29. Kim V, Gudvangen E, Kondratiev O, Redondo L, Xiao S, Pakhomov AG. Peculiarities of neurostimulation by intense nanosecond pulsed electric fields: How to avoid firing in peripheral nerve fibers. Int J Mol Sci (2021) 22:7051. doi:10.3390/ijms22137051

PubMed Abstract | CrossRef Full Text | Google Scholar

30. Casciola M, Shu Xiao S, Pakhomov AG. Damage-free peripheral nerve stimulation by 12-ns pulsed electric field. Sci Rep (2017) 7:10453. doi:10.1038/s41598-017-10282-5

PubMed Abstract | CrossRef Full Text | Google Scholar

31. Pakhomov AG, Pakhomova ON. The interplay of excitation and electroporation in nanosecond pulse stimulation. Bioelectrochemistry (2020) 136:107598. doi:10.1016/j.bioelechem.2020.107598

PubMed Abstract | CrossRef Full Text | Google Scholar

32. Aycock KN, Zhao Y, Lorenzo MF, Davalos RV. A theoretical argument for extended interpulse delays in therapeutic high-frequency irreversible electroporation treatments. IEEE Trans Biomed Eng (2021) 68:1999–2010. doi:10.1109/TBME.2021.3049221

PubMed Abstract | CrossRef Full Text | Google Scholar

33. Winfree AT. The geometry of biological time. New York: Springer (1980).

Google Scholar

34. Himona G, Kovanis V, Kominis Y. Time crystals transforming frequency combs in tunable photonic oscillators. Chaos (2023) 33(4):043134. doi:10.1063/5.0141114

PubMed Abstract | CrossRef Full Text | Google Scholar