Rational solitons for non-local Hirota equations: Robustness and cascading instability

The Hirota equation is a higher-order non-linear Schrödinger equation by incorporating third-order dispersion. Two pairs of non-local Hirota equations are studied. One is a parity transformed conjugate pair, and the other is a conjugate PT-symmetric pair. For the first pair, rational solitons are derived by the Darboux transformation, and are shown computationally to exhibit robust propagation properties. These rational solitons can exhibit both elastic and inelastic interactions. One particular case of an elastic collision between dark and “anti-dark” solitons is demonstrated. For the second pair, a “cascading mechanism” illustrating the growth of higher-order sidebands is elucidated explicitly for these non-local, conjugate PT-symmetric equations. These mechanisms provide a theoretical confirmation of the initial amplification phase of the growth-and-decay cycles of breathers. Such repeated patterns will serve as a manifestation of the classical Fermi-Pasta-Ulam-Tsingou recurrence.

1 Introduction

The non-linear Schrödinger (NLS) equation is an intensively studied, completely “integrable” equation. Physically, it describes various non-linear propagation phenomena in hydrodynamics (oceanic waves), Kerr media, optical pulses and plasma physics [1–7]. Solitons, breathers and rogue waves have been established theoretically as exact solutions, and also observed experimentally in water channels and optical fibers [3, 7–20]. From the perspective of mathematical physics, these three kinds of non-linear wave modes can be derived by elegant techniques like Darboux and Hirota transformations applied to NLS-type equations [20–28]. Existence of solitons is usually attributed to a balance between non-linearity and dispersion [21–25]. Rogue waves are unexpectedly large displacements from an otherwise tranquil background, and usually have peak amplitudes more than twice the significant wave height [26]. While the generation mechanism and growth process of rogue waves are still under intense debates, one school of thought has associated these rogue modes with the amplification and decay of breathers of the underlying evolution equations under periodic boundary conditions [5, 9, 13, 29]. Breathers generally initiate from the growth phase of small perturbation due to modulation instability. Subsequent amplification demands the restoration of non-linear effects and saturation of the growth phase. Typically higher harmonics attain the same order of magnitude as the fundamental frequency at the maximum displacement of the breather [20].

An immediate and widely studied extension of NLS is the Hirota equation, which incorporates third order dispersion [30, 31].

$i{q}_t+\frac{1}{2}{q}_{xx}+{\left|q\right|}^{2}q+i\epsilon \left(q_{xxx}+6{\left|q\right|}^2{q}_x\right)=0.(1)$

This equation was first introduced in the 1970s, and has been shown to possess multi-solitons, doubly periodic patterns and rogue wave modes [32–35].

Recently there have been tremendous interest in non-local evolution equations, especially those from the NLS family [36–38]. For example, rational soliton solutions for focusing and defocusing NLS equations have been studied [37, 38]. One motivation is the existence of purely real spectra for parity-time-symmetric (PT-symmetric), non-Hermitian systems [39–42]. As optics is widely believed to be a plausible testing ground for such PT-symmetric systems, it is natural to consider extensions relevant to this branch of physics. One physical interpretation of a complex potential is that the real and imaginary parts may correspond to the self-phase modulation and gain/loss respectively [43].

The counterpart of a parity symmetry principle in optics is the condition n(–r) = n*r), where n and r are the refractive index profile and the position vector respectively. Such condition cannot hold for naturally occurring materials, but can be fabricated for metamaterials with modern technology [44]. Indeed these special modulations of gain and loss mechanisms permit novel phenomena like switching and symmetry breaking. Transformation optics can be further advanced. Another exciting development arises from electronic circuits. A dynamical model is a sequence of dimers, consisting of a pair of split-ring resonantors, one with gain and the other with the identical amount of loss [45]. The absence or presence of non-linearity then generates intriguing properties of the spectrum and oscillating modes known as breathers.

Third order dispersion will be needed for short (femtosecond) pulses. Hence we shall consider models of non-local Hirota equations in this work. Indeed integrable non-local Hirota equations have been demonstrated [46]. In this paper, we will focus on two cases of non-local Hirota equations including a parity transformed conjugate pair and a conjugate PT-symmetric pair [46]. For the case of a parity transformed conjugate pair, the first- and second-order rational solutions will be studied. While for a conjugate PT-symmetric pair, the cascading mechanism will be investigated. In terms of analytical progress, symmetry broken and preserving soliton solutions, breather and rogue wave solutions have been obtained [47, 48].

The sequence of presentation in this paper can now be explained. The first- and second-order rational soliton solutions are derived (Section 2). The robustness of the rational solution also is studied. The cascading mechanism of a conjugate PT-symmetric pair non-local Hirota equation is elucidated (Section 3). Finally, conclusions are drawn (Section 4).

2 A parity transformed conjugate pair non-local Hirota equation

A parity transformed, conjugate pair of non-local Hirota equation [46] is given as

$i{q}_t\left(x,t\right)+\alpha \left[q_{xx}\left(x,t\right)+2\kappa q^2\left(x,t\right)r\left(x,t\right)\right]$

$-\beta \left[q_{xxx}\left(x,t\right)+6\kappa q\left(x,t\right)r\left(x,t\right)q_x\left(x,t\right)\right]=0,(\mathrm{2a})$

$i{r}_t\left(x,t\right)-\alpha \left[r_{xx}\left(x,t\right)+2\kappa q\left(x,t\right)r^2\left(x,t\right)\right]-\beta \left[r_{xxx}\left(x,t\right)+6\kappa \beta q\left(x,t\right)r\left(x,t\right)r_x\left(x,t\right)\right]=0,(\mathrm{2b})$

where $r\left(x,t\right)=q^{*}\left(-x,t\right)$, and α, β are real numbers. In contrast with works in the literature on non-local, non-linear Schrödinger equation [37, 38], Eq. 2 incorporates third order dispersion and a special form of “self-steepening” cubic non-linearity which maintains the appropriate parity and symmetry. Furthermore, we shall demonstrate that exact, rational solutions with displacements both below and above a mean level will exist for Eq. 2. These entities will bear resemblance to similar units for the non-linear Schrödinger case, and can be termed “dark” and “anti-dark” solitons (for below and above mean level respectively). The parity transformed conjugate pair non-local Hirota equation admits the Lax pair

${\mathrm{\Phi }}_x=U\mathrm{\Phi },{\mathrm{\Phi }}_t=V\mathrm{\Phi },(3)$

where $\mathrm{\Phi }=\mathrm{\Phi }\left(x,t\right)$ is a column vector function,

$U=\left(\begin{array}{cc}i\lambda & i\kappa r\left(x,t\right)\\ iq\left(x,t\right)& -i\lambda \end{array}\right),(\mathrm{4a})$

$\begin{array}{l}V={\lambda }^3\left(\begin{array}{cc}-4\beta & 0\\ 0& 4\beta \end{array}\right)+{\lambda }^2\left[\begin{array}{cc}2i\alpha & -4\beta \kappa r\left(x,t\right)\\ -4\beta \kappa q\left(x,t\right)& -2i\alpha \end{array}\right]\\ +\lambda \left[\begin{array}{cc}2\beta \kappa q\left(x,t\right)r\left(x,t\right)& 2i\alpha \kappa r\left(x,t\right)+2i\beta \kappa r_x\left(x,t\right)\\ 2i\alpha q\left(x,t\right)-2i\beta q_x\left(x,t\right)& -2\beta \kappa q\left(x,t\right)r\left(x,t\right)\end{array}\right]\\ +\left[\begin{array}{cc}-i\kappa r\left(\alpha q-\beta q_x\right)-i\beta \kappa q{r}_x& 2\beta {\kappa }^{2}q{r}^2+\alpha \kappa r_x+\beta \kappa r_{xx}\\ 2\beta \kappa q^{2}r-\alpha q_x+\beta q_{xx}& i\kappa r\left(\alpha q-\beta q_x\right)+i\beta \kappa q{r}_x\end{array}\right],\end{array}(\mathrm{4b})$

The compatibility condition of Eq. 3, namely, $U_t-V_x+\left[U,V\right]=0$, gives rise to Eq. 2. Through the loop group method, the Darboux matrix for Eq. 3 can be represented as

$T^{\left[1\right]}=I-\frac{\left({{\lambda }_1}^{*}+{\lambda }_1\right)z_1\left(x,t\right){z_1}^{†}\left(-x,t\right)\sigma }{\left(\lambda +{{\lambda }_1}^{*}\right){z_1}^{†}\left(-x,t\right)\sigma z_1\left(x,t\right)},(5)$

where $\sigma =\mathrm{d}\mathrm{i}\mathrm{a}\mathrm{g}\left(1,-\kappa \right),z_1\left(x,t\right)=v\left(x,t\right)\mathrm{\Phi }\left(x,t\right),$ $\mathrm{\Phi }\left(x,t\right)$ is a solution of Eq. 3 with $\lambda ={\lambda }_1$, and $v\left(x,t\right)$ is a non-zero function, $†$ denotes the Hermite conjugation.

We can use Eq. 5 to get a new solution of Eq. 3, i.e.,

${\mathrm{\Phi }}_x^{\left[1\right]}=U\left(q^{\left[1\right]};\lambda \right){\mathrm{\Phi }}^{\left[1\right]},{\mathrm{\Phi }}_t^{\left[1\right]}=V\left(q^{\left[1\right]};\lambda \right){\mathrm{\Phi }}^{\left[1\right]},(6)$

where ${\mathrm{\Phi }}^{\left[1\right]}=T^{\left[1\right]}\mathrm{\Phi }$. The entities ${\mathrm{\Phi }}^{\left[j\right]}\left(j=\mathrm{1,2},\dots ,N\right)$ denote N different solutions of Eq. 3 with the initial solution q(x, t) and $\lambda ={\lambda }_j$. The N-fold Darboux matrix can be expressed as

$T^{\left[N\right]}=I-Z\left(x,t\right)M^{-1}{\left(\lambda I+S\right)}^{-1}{Z}^{†}\left(-x,t\right)\sigma ,(7)$

and the N-fold Darboux transformation between old and new potential functions is

$q^{\left[N\right]}=q+\frac{2\det \left[\begin{array}{cc}M& {Z_1}^{†}\left(-x,t\right)\\ Z_2\left(x,t\right)& 0\end{array}\right]}{\det M},(8)$

where

$S=\mathrm{d}\mathrm{i}\mathrm{a}\mathrm{g}\left({{\lambda }_1}^{*},{{\lambda }_2}^{*},\dots ,{{\lambda }_N}^{*}\right),(\mathrm{9a})$

$Z\left(x,t\right)=\left[z_1\left(x,t\right),z_2\left(x,t\right),\dots ,z_N\left(x,t\right)\right],z_j\left(x,t\right)=v_j\left(x,t\right){\mathrm{\Phi }}_j\left(x,t\right)(\mathrm{9b})$

$M={\left(M_{jk}\right)}_{N\times N},M_{jk}={z_j}^{†}\left(-x,t\right)\sigma z_k\left(x,t\right)/\left({\lambda }_j+{{\lambda }_k}^{*}\right)(\mathrm{9c})$

where $v_j\left(x,t\right)$ denotes a non-zero function, and $Z_j\left(x,t\right)$ is the jth row of Z(x, t).

We now start from the plane wave solution $q=\rho \exp \left(2i\alpha \kappa {\rho }^{2}t\right)$ of Eq. 2 for the iteration process of the Darboux transformation (Eq. 8), where ρ denotes the amplitude of the plane wave. We can postulate $\mathrm{\Phi }=GH\mathrm{\Psi }$ with

$G=\left[\begin{array}{cc}1& 0\\ 0& \rho \exp \left(2i\alpha \kappa {\rho }^{2}t\right)\end{array}\right],H=\left(\begin{array}{cc}i\kappa \rho & i\kappa \rho \\ -i\lambda +{\mu }_1& -i\lambda +{\mu }_2\end{array}\right),(10)$

and hence Ψ satisfies the equation as follows:

${\mathrm{\Psi }}_x=\widehat{U}\mathrm{\Psi },{\mathrm{\Psi }}_t=\widehat{V}\mathrm{\Psi },(11)$

where

$\widehat{U}=\mathrm{d}\mathrm{i}\mathrm{a}\mathrm{g}\left({\mu }_1,{\mu }_2\right),\widehat{V}=2\left(\alpha \lambda +2i\beta {\lambda }^2-i\beta \kappa {\rho }^2\right)\widehat{U}+i\alpha \kappa {\rho }^{2}I,(\mathrm{12a})$

${\mu }_1=-\sqrt{-{\lambda }^2-\kappa {\rho }^2},\hspace{1em}{\mu }_2=\sqrt{-{\lambda }^2-\kappa {\rho }^2}.(\mathrm{12b})$

Thus, we can construct the solution of Eq. 3 as

$\mathrm{\Phi }=GHQ,Q=\mathrm{d}\mathrm{i}\mathrm{a}\mathrm{g}\left(Q_1,Q_2\right),(\mathrm{13a})$

$Q_1=\exp \left[{\mu }_{1}x+2\left(\alpha \lambda +2i\beta {\lambda }^2-i\beta \kappa {\rho }^2\right){\mu }_{1}t+i\alpha \kappa {\rho }^{2}t\right],(\mathrm{13b})$

$Q_2=\exp \left[{\mu }_{2}x+2\left(\alpha \lambda +2i\beta {\lambda }^2-i\beta \kappa {\rho }^2\right){\mu }_{2}t+i\alpha \kappa {\rho }^{2}t\right].(\mathrm{13c})$

Setting

$v_1\left(x,t\right)=\exp \left(-i\alpha \kappa {\rho }^{2}t\right),\lambda =i\rho \sqrt{\kappa }h,l_1={\chi }_1\exp \left({\eta }_1\right),l_2=-{\chi }_2\exp \left({\eta }_2\right),(\mathrm{14a})$

${\chi }_{1,2}=\frac{1}{\sqrt{h\pm \sqrt{h^2-1}}\sqrt{h^2-1}},{\eta }_{1,2}=\pm \rho \sqrt{\kappa }\sqrt{h^2-1}F,(\mathrm{14b})$

and we can establish

$z_1\left(x,t\right)=v_1\left(x,t\right)\mathrm{\Phi }\left(\begin{array}{c}{l}_1\\ l_2\end{array}\right)=G\left[\begin{array}{c}i\left({\chi }_1\exp \left(B\right)-{\chi }_2\exp \left(-B\right)\right)\kappa \rho \\ \rho \sqrt{\kappa }\left({\chi }_2\exp \left(B\right)-{\chi }_1\exp \left(-B\right)\right)\end{array}\right],(15)$

where $B=\rho \sqrt{\kappa }\sqrt{h^2-1}\left[x+2ih\alpha \sqrt{\kappa }\rho t-2i\left(1+2h^2\right)\beta \kappa {\rho }^{2}t+F\right]$, and F is an arbitrary complex number.

To derive the higher-order rational solutions of Eq. 2, we set

$h=1+{\epsilon }^2,F_j={\displaystyle \sum }_{k=1}^j{s}_k{\epsilon }^{2\left(k-1\right)},G^{-1}{z}_1\left(x,t,\epsilon \right)={\displaystyle \sum }_{k=1}^{+\infty }{f}_k\left(x,t\right){\epsilon }^{2k},(16)$

where s_k is arbitrary complex constant. Consequently, the general rational solutions of Eq. 1 can be obtained by

$q^{\left[N\right]}=\rho \exp \left(2i\alpha \kappa {\rho }^{2}t\right)\frac{\det \left[A-\frac{2}{\rho }{{\mathrm{\Xi }}_1}^{†}\left(-x,t\right){\mathrm{\Xi }}_2\left(x,t\right)\right]}{\det A},(17)$

where

$\mathrm{\Xi }\left(x,t\right)=\left[f_0\left(x,t\right),f_1\left(x,t\right),\dots ,f_{N-1}\left(x,t\right)\right],(\mathrm{18a})$

$A={\left(A_{jk}\right)}_{N\times N},A_{jk}=\frac{1}{2\rho }{{\displaystyle \sum }_{i_1=0}^{j+k-2}{\displaystyle \sum }_{i_2=\max \left(0,i_1-j+1\right)}^{\min \left(k-1,i_1\right)}\left(-\frac{1}{2}\right)}^{i_1}{C}_{i_1}^{i_2}{f}_{j-1-i_1+i_2}^{†}\left(-x,t\right)f_{k-1-i_2}\left(x,t\right),(\mathrm{18b})$

${\mathrm{\Xi }}_j\left(x,t\right)$ is the jth row of $\mathrm{\Xi }\left(x,t\right)\left(j=1,2\right)$.

2.1 First-order rational soliton solution

The first-order rational soliton solution [49, 50] with s₁ = i can be obtained as

$q=-\rho \frac{-3+4{\rho }^2+2i\left(-1+\rho \right){{\mathrm{\Omega }}_2}^{*}+{\mathrm{\Omega }}_1\left[-2i\left(1+\rho \right)+{{\mathrm{\Omega }}_2}^{*}\right]}{1+4{\rho }^2-2i\rho {\mathrm{\Omega }}_1+\left(2i\rho +{\mathrm{\Omega }}_1\right){{\mathrm{\Omega }}_2}^{*}}\exp \left(i\gamma t\right),(\mathrm{19a})$

${\mathrm{\Omega }}_1=2\rho x-\left(4\alpha {\rho }^2-12i\beta {\rho }^3\right)t,{\mathrm{\Omega }}_2=-2\rho x-\left(4\alpha {\rho }^2-12i\beta {\rho }^3\right)t,(\mathrm{19b})$

where $\gamma =2\alpha \kappa {\rho }^2$. On computing the modulus of the complex valued envelope q of Eq. 19a, both dark solitons (with maximum displacements below the mean position) and “anti-dark” solitons (those with displacements above the mean) are possible. A rational dark soliton and a rational anti-dark soliton can collide elastically (Figure 1A).

FIGURE 1

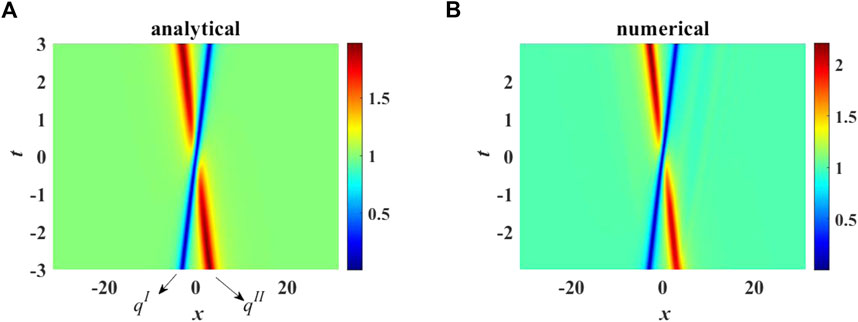
FIGURE 1. (A) Analytical and (B) Numerical elastic interaction between a rational dark soliton and a rational anti-dark soliton. Parameters chosen are κ = −1, α = 1, β = 0.001, ρ = 1.

In particular, q^I being a dark soliton maintains its shape after the collision at t = 0. Furthermore, q^II being an anti-dark soliton also remains unchanged after the collision. To substantiate this dynamical property, we use the asymptotic analysis to investigate the rational soliton solutions.

(1) Along the line ${\mathrm{\Omega }}_1\sim 0\mathrm{a}\mathrm{s}\left|x\right|\to \infty$

$q\to q^I:=-\rho \frac{2i\left(-1+\rho \right)+{\mathrm{\Omega }}_1}{2i\rho +{\mathrm{\Omega }}_1}\exp \left(i\gamma t\right).(20)$

(2) Along the line ${\mathrm{\Omega }}_2\sim 0$ as $\left|x\right|\to \infty$

$q\to q^{II}:=-\rho \frac{-2i\left(1+\rho \right)+{{\mathrm{\Omega }}_2}^{*}}{-2i\rho +{{\mathrm{\Omega }}_2}^{*}}\exp \left(i\gamma t\right).(21)$

To study the computational robustness of the rational soliton, we employ the split-step Fourier method for the simulations of Eq. 2. The linear part is solved in Fourier space while the non-linear part is handled by the fourth-order Runge-Kutta method. The mesh size in x direction is 0.0614, and the step size in t axis is equal to 5 × 10⁻⁴. The initial condition is selected as the rational soliton solution at t = −3 plus a small perturbation. The analytical prediction agrees well with the numerical results (Figure 1B). The significant interactions between the two localized modes (dark and anti-dark solitons) occur at t = 0. After this elastic collision, the two solitons then propagate with their original shapes and velocities.

2.2 Second-order rational soliton solution

For N = 2 in Eq. 17, we can get the second-order rational soliton solution for Eq. 2. The expressions for the second-order rational soliton solution are given by

$f_0=\left[\begin{array}{c}\kappa \rho \left(-i+2i{s}_1\sqrt{\kappa }\rho +2ix\sqrt{\kappa }\rho -4\alpha \kappa {\rho }^{2}t+12\beta \kappa \sqrt{\kappa }{\rho }^{3}t\right)\\ \sqrt{\kappa }\rho +2\left(s_1+x\right)\kappa {\rho }^2+4i\alpha \kappa \sqrt{\kappa }{\rho }^{3}t-12i\beta {\kappa }^2{\rho }^{4}t\end{array}\right],(\mathrm{22a})$

$f_1=\left(\begin{array}{c}{f}_{11}\\ f_{21}\end{array}\right),(\mathrm{22b})$

$f_{11}=\frac{1}{12}\kappa \rho \left\{3i+2\sqrt{\kappa }\rho \left[\begin{array}{l}3i\left(s_1+4s_2+x\right)-6i\left({\left(s_1+x\right)}^2-5i\alpha t\right)\sqrt{\kappa }\rho \\ +2\left(2i{\left(s_1+x\right)}^3+12\left(s_1+x\right)\alpha t+57\beta t\right)\kappa {\rho }^2\\ -24\left(\alpha \left({\left(s_1+x\right)}^2-i\alpha t\right)+3\left(s_1+x\right)\beta \right)t\kappa \sqrt{\kappa }{\rho }^3\\ +24t\left(-2it\left(s_1+x\right){\alpha }^2+3\left({\left(s_1+x\right)}^2-2i\alpha t\right)\beta \right){\kappa }^2{\rho }^4\\ +8t^2\left(4{\alpha }^{3}t+27i\beta \left(4/3\left(s_1+x\right)\alpha +\beta \right)\right){\kappa }^2\sqrt{\kappa }{\rho }^5\\ -144\beta t^2\left(2{\alpha }^{2}t+3i\left(s_1+x\right)\beta \right){\kappa }^3{\rho }^6+864\alpha {\beta }^2{\kappa }^3\sqrt{\kappa }{\rho }^7{t}^3\\ -864{\beta }^3{\rho }^8{t}^3\end{array}\right]\right\},(\mathrm{22c})$

$\begin{array}{l}{f}_{21}=-\frac{\sqrt{\kappa }\rho }{4}+\frac{1}{2}\left(s_1+4s_2+x\right)\kappa {\rho }^2+\left[{\left(s_1+x\right)}^2+5i\alpha t\right]{\kappa }^{3/2}{\rho }^3\\ +\frac{1}{3}\left[2\left(s_1+x\right)\left({\left(s_1+x\right)}^2+6i\alpha t\right)-57i\beta t\right]{\kappa }^2{\rho }^4\\ +4it\left[\alpha \left({\left(s_1+x\right)}^2+i\alpha t\right)-3\left(s_1+x\right)\beta \right]{\kappa }^{5/2}{\rho }^3\\ -4t\left[2{\alpha }^2\left(s_1+x\right)t+3i{\left(s_1+x\right)}^2\beta -6\alpha \beta t\right]{\kappa }^3{\rho }^6\\ +\frac{4}{3}{t}^2\left[-4i{\alpha }^{3}t+9\beta \left(4\alpha \left(s_1+x\right)-3\beta \right)\right]{\kappa }^{7/2}{\rho }^7\\ +24\beta t^2\left[2i{\alpha }^{2}t-3\beta \left(s_1+x\right)\right]{\kappa }^4{\rho }^8-144i\alpha {\beta }^2{\kappa }^{9/2}{\rho }^9{t}^3+144i{\beta }^3{\kappa }^5{\rho }^{10}{t}^3.\end{array}(\mathrm{22d})$

Both propagating and transient pulses are possible for these second-order solutions (Figure 2). By varying the parameters s₁ and s₂, these rational solutions may exhibit novel dynamical properties, e.g., collision between two solitons as an example of “propagating” modes (Figure 2A).

FIGURE 2

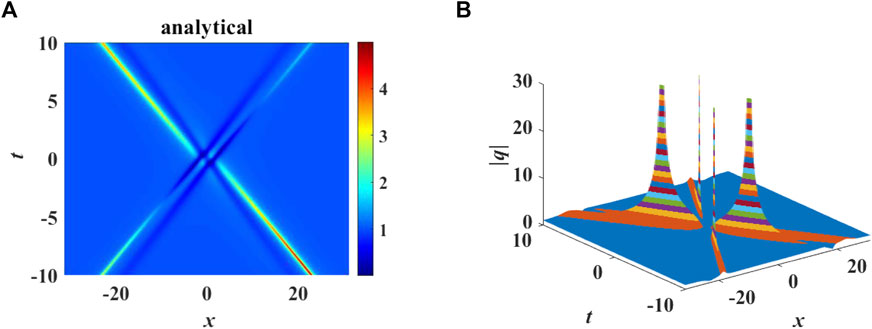
FIGURE 2. (A) Inelastic collision between two solitons with parameters κ = −1, α = 1, β = 0.001, s₁ = 0.1i, s₂ = 4i, ρ = 1. (B) Second-order rational soliton solution with parameters κ = −1, α = 1, β = 0.001, s₁ = 2i, s₂ = 0, ρ = 1.

By choosing different values of the parameters, we obtain rational solutions with combined-peak-valley profiles (Figure 2B). Indeed as many as four transient pulses can appear. These pulses will be loosely termed “rogue waves” in the present context. This whole sequence of mode interactions can be interpreted as rogue modes on a two-soliton background.

To gain further insight, we shall use pole analysis [51] in the complex plane to study the locations of maximum displacements of these transient pulses. The underlying conjecture is that the maximum displacement of these rogue modes in the physical plane will coincide with the turning points of the trajectories in the complex plane, if the spatial variable x is allowed to be complex (while time t remains real). The poles of the exact solutions occur at the roots of the denominator. Numerical computations show excellent agreements between the physical locations of the largest amplitude of the rogue modes and the real parts of the poles in the complex plane (Table 1).

TABLE 1

TABLE 1. Comparison of the locations of maximum displacements in Figure 2B and the locations of poles of Eq. 17 with N = 2.

3 A non-local, conjugate PT-symmetric pair of Hirota equations

We now turn the attention to a non-local, conjugate PT-symmetric pair of Hirota equations given by [46].

$q_t\left(x,t\right)=i\alpha \left[q_{xx}\left(x,t\right)-2\kappa q{\left(x,t\right)}^{2}r\left(x,t\right)\right]$

$-\beta \left[q_{xxx}\left(x,t\right)-6\kappa q\left(x,t\right)r\left(x,t\right)q_x\left(x,t\right)\right],(\mathrm{23a})$

$-r_t\left(x,t\right)=i\alpha \left[r_{xx}\left(x,t\right)-2\kappa r{\left(x,t\right)}^{2}q\left(x,t\right)\right]$

$+\beta \left[r_{xxx}\left(x,t\right)-6\kappa r\left(x,t\right)q\left(x,t\right)r_x\left(x,t\right)\right],(\mathrm{23b})$

where $r\left(x,t\right)=q\left(-x,-t\right)$, κ, α, β are complex numbers. Equation 23 can reduce to Eq. 1 on setting $r\left(x,t\right)=q^{*}\left(x,t\right),\kappa =-1,\alpha =1/2,\beta =\epsilon$.

3.1 Robustness of soliton solution

Soliton solution of Eq. 23 has already been given earlier in the literature [52]:

$q\left(x,t\right)=\frac{2i\left({\lambda }_2-{\lambda }_1\right)}{\exp \left({\theta }_1\right)+\exp \left({\theta }_2\right)},{\theta }_j=2i{\lambda }_j\left[x+2{\lambda }_j\left(\alpha +2\beta {\lambda }_j\right)t\right].(24)$

To test the robustness of these localized modes, we still employ the split-step Fourier scheme as described above. The numerical simulations confirm the existence of sturdy propagation of pulses (Figure 3).

FIGURE 3

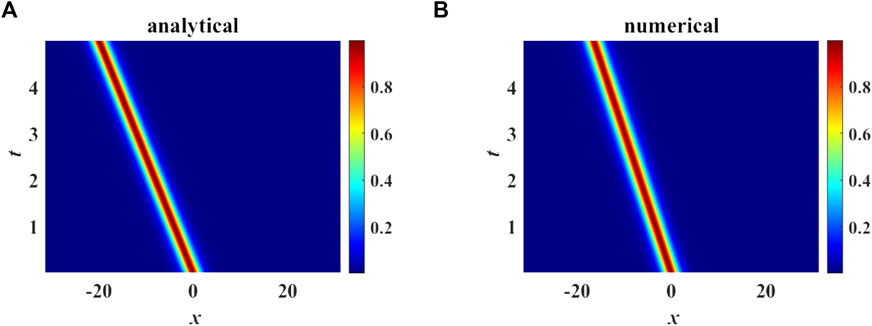
FIGURE 3. (A) Analytical and (B) Numerical soliton. Parameters chosen are κ = −1, α = 1, β = 0.001, λ₁ = 1 − 0.5i, λ₂ = 1 + 0.5i.

3.2 Cascading instability

An issue of current interest in non-linear science is the instability and recurrence of localized modes. More precisely, breathers under periodic conditions can recur in the propagation variable of the NLS equation. Experimentally, this phenomenon has been observed in hydrodynamic wave channels and optical fibers. Theoretically, the initial phase of recurrence has been confirmed by the cascading mechanism. All these studies can be taken as manifestations of the classical physical problem of Fermi-Pasta-Ulam-Tsingou recurrence (FPUT). It will be illuminating to consider if all these principles can be applied to non-local evolution equations. We shall adopt the present non-local Hirota equation as a pilot test case.

A brief remark on the cascading mechanism is in order. Small disturbances on a continuous background will be amplified due to modulation instability. Higher-order modes exponentially small initially will grow at a faster rate. Eventually all modes attain roughly the same order of magnitude. A breather is then formed which then decays subsequently. Growth resumes at small amplitude and FPUT will arise. We shall start quantifying FPUT for non-local equations by looking at the modulation instability process, which describes the growth of the first order sideband. We begin with a continuous wave background, i.e.,

$q\left(x,t\right)=\rho \exp \left[i\left({\gamma }_{1}x+{\gamma }_{2}t\right)\right],(\mathrm{25a})$

$r\left(x,t\right)=\rho \exp \left[-i\left({\gamma }_{1}x+{\gamma }_{2}t\right)\right],(\mathrm{25b})$

where ${\gamma }_2=-\alpha {{\gamma }_1}^2+\beta {{\gamma }_1}^3-2\alpha \kappa {\rho }^2+6\beta {\gamma }_1\kappa {\rho }^2$, and ρ, γ₁ denote the amplitude and wave number of the continuous wave respectively. The perturbed states are expressed as

$q\left(x,t\right)=\left[\rho +u_1\left(x,t\right)\right]\exp \left[i\left({\gamma }_{1}x+{\gamma }_{2}t\right)\right],(\mathrm{26a})$

$r\left(x,t\right)=\left[\rho +u_2\left(x,t\right)\right]\exp \left[-i\left({\gamma }_{1}x+{\gamma }_{2}t\right)\right].(\mathrm{26b})$

Here $u_1\left(x,t\right)$ and $u_2\left(x,t\right)=u_1\left(-x,-t\right)$ denote the perturbations. The Fourier modes of the perturbations have the following forms:

$u_1\left(x,t\right)=u_{11}\exp \left[i\left(\eta x+\mathrm{\Omega }t\right)\right]+u_{12}\exp \left[-i\left(\eta x+\mathrm{\Omega }t\right)\right],(\mathrm{27a})$

$u_2\left(x,t\right)=u_{11}\exp \left[-i\left(\eta x+\mathrm{\Omega }t\right)\right]+u_{12}\exp \left[i\left(\eta x+\mathrm{\Omega }t\right)\right].(\mathrm{27b})$

Modulation instability will arise when Ω has a non-zero imaginary part, i.e.,

$\mathrm{\Gamma }=\left|\mathrm{I}\mathrm{m}\left(\mathrm{\Omega }\right)\right|=\left|\left(\alpha -3\beta {\gamma }_1\right)\eta \right|\sqrt{-{\eta }^2-4\kappa {\rho }^2},(28)$

which requires κ < 0. Next, we conduct a simulation with the continuous wave perturbed by a single Fourier mode, represented as a cosine function, i.e.,

$q\left(x,t\right)=\rho \exp \left[i\left({\gamma }_{1}x+{\gamma }_{2}t\right)\right]+\mu \cos \left(\eta x\right),(\mathrm{29a})$

$r\left(x,t\right)=\rho \exp \left[-i\left({\gamma }_{1}x+{\gamma }_{2}t\right)\right]+\mu \cos \left(\eta x\right),(\mathrm{29b})$

where μ and η represent the amplitude and wave number of perturbation. Typical FPUT patterns are observed (Figure 4) with the perturbation wave number within the unstable regime of modulation instability, where the threshold of the wave number is 2 (Figure 5A). A breather first appears at about 3.5 time units. At 10.5 time units, the second breather occurs, which can be interpreted as a manifestation of FPUT. However, the wave profile of the second breather has a non-zero angle with respect to t axis, which is caused by the third order dispersion. This also leads to the asymmetry pattern with regard to the axis x = 0.

FIGURE 4

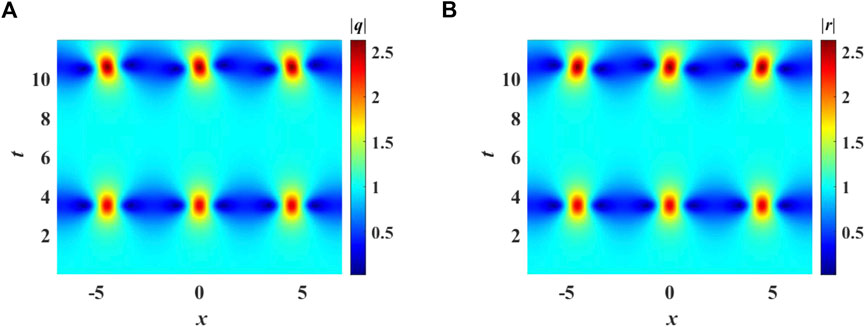
FIGURE 4. FPUT with parameters α = 1, β = 1 × 10⁻⁶, κ = −1, ρ = 1, γ₁ = 0, μ = 0.01, η = 1.4. (A) Modulus of waveguide, |q|; (B) |r|.

FIGURE 5

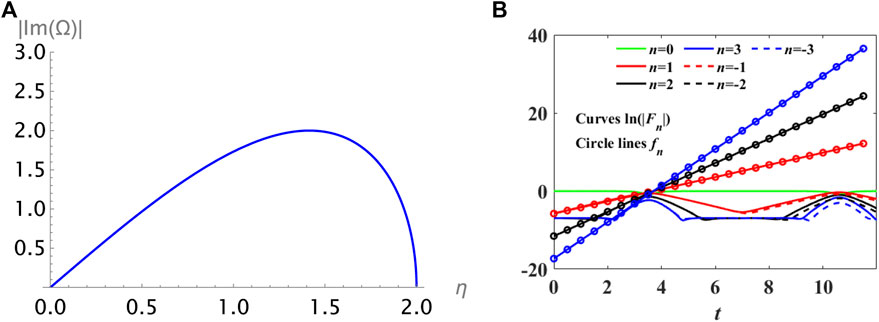
FIGURE 5. (A) Growth rate of modulation instability with parameters α = 1, β = 1 × 10⁻⁶, κ = −1, ρ = 1, γ₁ = 0; (B) Comparison between the numerical spectra and the cascading mechanism prediction.

As a step in theoretical modelling, we shall perform the cascading mechanism analysis to predict the growth of the high-order sidebands observed in FPUT. For this purpose, the complex envelopes q (x, t) and r (x, t) in Eq. 23 are expanded as

$q\left(x,t\right)=\rho \left[B_0\left(t\right)+{\displaystyle \sum }_{j=1}^{\infty }{B}_{\pm j}\left(t\right)\exp \left(\pm ij\eta x\right)\right]\exp \left(i{\gamma }_{1}x\right),(\mathrm{30a})$

$r\left(x,t\right)=\rho \left[B_0\left(-t\right)+{\displaystyle \sum }_{j=1}^{\infty }{B}_{\pm j}\left(-t\right)\exp \left(\mp ij\eta x\right)\right]\exp \left(-i{\gamma }_{1}x\right).(\mathrm{30b})$

To investigate the growth of the second-order sideband (or harmonic), we truncate Eq. 30 at the second order, i.e.,

$q\left(x,t\right)=\rho \left[B_0\left(t\right)+B_{\pm 1}\left(t\right)\exp \left(\pm i\eta x\right)+B_{\pm 2}\left(t\right)\exp \left(\pm 2i\eta x\right)\right]\exp \left(i{\gamma }_{1}x\right),(\mathrm{31a})$

$r\left(x,t\right)=\rho \left[B_0\left(-t\right)+B_{\pm 1}\left(-t\right)\exp \left(\mp i\eta x\right)+B_{\pm 2}\left(-t\right)\exp \left(\mp 2i\eta x\right)\right]\exp \left(-i{\gamma }_{1}x\right).(\mathrm{31b})$

On setting

$B_0\left(t\right)=\exp \left(i{\gamma }_{2}t\right),B_1=a_1\exp \left(i{\gamma }_{2}t+\mathrm{\Gamma }t\right),B_{-1}=a_1\exp \left(i{\gamma }_{2}t-\mathrm{\Gamma }t\right),(32)$

substituting Eq. 31 together with Eq. 32 into Eq. 23, linearization yields

$\left(6i{a_1}^2\alpha \kappa {\rho }^3-18i{a_1}^2\beta {\gamma }_1\kappa {\rho }^3-12i{a_1}^2\beta \eta \kappa {\rho }^3\right)\exp \left(2\mathrm{\Gamma }t+i{\gamma }_{2}t\right)+\rho {B_2}^{\prime }\left(t\right)=0,(\mathrm{33a})$

$\left(6i{a_1}^2\alpha \kappa {\rho }^3-18i{a_1}^2\beta {\gamma }_1\kappa {\rho }^3+12i{a_1}^2\beta \eta \kappa {\rho }^3\right)\exp \left(-2\mathrm{\Gamma }t+i{\gamma }_{2}t\right)+\rho {B_{-2}}^{\prime }\left(t\right)=0.(\mathrm{33b})$

Integration to Eq. 33 will lead to

$B_2\left(t\right)=-\frac{6i{a_1}^2\left(\alpha -3\beta {\gamma }_1-2\beta \eta \right)\kappa {\rho }^2\exp \left[\left(2\mathrm{\Gamma }+i{\gamma }_2\right)t\right]}{2\mathrm{\Gamma }+i{\gamma }_2},(\mathrm{34a})$

$B_{-2}\left(t\right)=-\frac{6i{a_1}^2\left(\alpha -3\beta {\gamma }_1+2\beta \eta \right)\kappa {\rho }^2\exp \left[\left(-2\mathrm{\Gamma }+i{\gamma }_2\right)t\right]}{-2\mathrm{\Gamma }+i{\gamma }_2}.(\mathrm{34b})$

Similarly, we can repeat the steps above to obtain the growth of higher-order sidebands. Proceeding by mathematical induction, the growth rate of the nth-order sideband is proportion to nη, i.e.,

$B_n\left(t\right)=a_n\exp \left[\left(n\mathrm{\Gamma }+i{\gamma }_2\right)t\right],n=\mathrm{1,2,3}\dots (35)$

The corresponding analytical spectra of nth-order sideband are

$f_n=\ln \left[B_n\left(t\right)\right]=n\mathrm{\Gamma }\left(t-t_n\right),t_n=-\frac{\ln \left(\left|a_n\right|\right)}{n\mathrm{\Gamma }},(36)$

where t_n is the time taken for the perturbations to grow to an amplitude of unity. The spectra of the sidebands are expressed as

$F_0=\frac{1}{L}\underset{-L/2}{\overset{L/2}{{\displaystyle \int }}}q\left(x,t\right)dx,(\mathrm{37a})$

$F_n=\frac{1}{L}\underset{-L/2}{\overset{L/2}{{\displaystyle \int }}}q\left(x,t\right)\exp \left(-in\frac{2\pi }{L}x\right)dx,\hspace{1em}n=\pm 1,\pm 2,\dots (\mathrm{37b})$

where the entities $F_n$ are supposed to be computed numerically but $f_n$ should be associated with the analytical formula (Eq. 36). The comparisons between the cascading mechanism prediction (Eq. 36, circle lines in Figure 5B) and the numerical spectral modes calculations (curves in Figure 5B) display excellent agreement. In particular, the first breather has a symmetric spectrum, while the second-order mode exhibits an asymmetry spectrum owing to the third-order dispersion effect.

4 Conclusion

Two pairs of non-local Hirota equations are studied:

• One as a parity transformed conjugate pair.

• One as a conjugate PT-symmetric pair.

Using the Darboux transformation, the first- and second-order rational soliton solutions for a parity transformed conjugate pair non-local Hirota equation have been derived. These solutions can describe both the elastic and inelastic interactions between two solitons, as well as the rogue waves arise from the interactions between two solitons. One particular case of elastic collision between dark and “anti-dark” solitons is demonstrated analytically. Furthermore, the elastic interaction between the two solitons still can appear even though the two solitons propagate with perturbations, i.e., the robustness of the elastic interaction is tested numerically. Finally, a “cascading mechanism” illustrating the growth of higher-order sidebands is elucidated explicitly for a conjugate PT-symmetric pair of non-local Hirota equations. We conjecture that similar analytical and computational properties can also be found for higher-order non-local Schrödinger equations. Further research efforts in these rich areas will definitely be worthwhile.

Data availability statement

The original contributions presented in the study are included in the article/supplementary material, further inquiries can be directed to the corresponding author.

Author contributions

KWC proposed to study these non-local problems. HMY conducted the calculation of the soliton solutions, while QP was responsible for the robustness test. All authors contributed to the article and approved the submitted version.

Funding

Partial financial support has been provided by the Research Grants Council General Research Fund contracts HKU17200718 and HKU17204722.

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

1. Dysthe KB. Note on a modification to the nonlinear Schrödinger equation for application to deep water waves. Proc R Soc Lond A. Math Phys Sci (1979) 369(1736):105–14. doi:10.1098/rspa.1979.0154

CrossRef Full Text | Google Scholar

2. Chabchoub A, Kibler B, Finot C, Millot G, Onorato M, Dudley JM, et al. nonlinear Schrödinger equation and the propagation of weakly nonlinear waves in optical fibers and on the water surface. Ann Phys (2015) 361:490–500. doi:10.1016/j.aop.2015.07.003

CrossRef Full Text | Google Scholar

3. Dudley JM, Dias F, Erkintalo M, Genty G. Instabilities, breathers and rogue waves in optics. Nat Photon (2014) 8(10):755–64. doi:10.1038/nphoton.2014.220

CrossRef Full Text | Google Scholar

4. Akhmediev N, Ankiewicz A. Dissipative solitons: From optics to biology and medicine, Springer Science & Business Media (2008). 751.

Google Scholar

5. Akhmediev N, Ankiewicz A, Soto-Crespo JM. Rogue waves and rational solutions of the nonlinear Schrödinger equation. Phys Rev E (2009) 80(2):026601. doi:10.1103/physreve.80.026601

PubMed Abstract | CrossRef Full Text | Google Scholar

6. Akhmediev N, Ankiewicz A, Taki M. Waves that appear from nowhere and disappear without a trace. Phys Lett A (2009) 373(6):675–8. doi:10.1016/j.physleta.2008.12.036

CrossRef Full Text | Google Scholar

7. Kibler B, Fatome J, Finot C, Millot G, Dias F, Genty G, et al. The Peregrine soliton in nonlinear fibre optics. Nat Phys (2010) 6(10):790–5. doi:10.1038/nphys1740

CrossRef Full Text | Google Scholar

8. Costa A, Osborne AR, Resio DT, Alessio S, Chrivì E, Saggese E, et al. Soliton turbulence in shallow water ocean surface waves. Phys Rev Lett (2014) 113(10):108501. doi:10.1103/physrevlett.113.108501

PubMed Abstract | CrossRef Full Text | Google Scholar

9. Chabchoub A, Hoffmann N, Akhmediev N. Rogue wave observation in a water wave tank. Phys Rev Lett (2011) 106(20):204502. doi:10.1103/physrevlett.106.204502

PubMed Abstract | CrossRef Full Text | Google Scholar

10. Onorato M, Residori S, Bortolozzo U, Montina A, Arecchi F. Rogue waves and their generating mechanisms in different physical contexts. Phys Rep (2013) 528(2):47–89. doi:10.1016/j.physrep.2013.03.001

CrossRef Full Text | Google Scholar

11. Bailung H, Sharma S, Nakamura Y. Observation of Peregrine solitons in a multicomponent plasma with negative ions. Phys Rev Lett (2011) 107(25):255005. doi:10.1103/physrevlett.107.255005

PubMed Abstract | CrossRef Full Text | Google Scholar

12. Baronio F, Degasperis A, Conforti M, Wabnitz S. Solutions of the vector nonlinear schrödinger equations: Evidence for deterministic rogue waves. Phys Rev Lett (2012) 109(4):044102. doi:10.1103/physrevlett.109.044102

PubMed Abstract | CrossRef Full Text | Google Scholar

13. Chabchoub A, Hoffmann N, Onorato M, Akhmediev N. Super rogue waves: Observation of a higher-order breather in water waves. Phys Rev X (2012) 2(1):011015. doi:10.1103/physrevx.2.011015

CrossRef Full Text | Google Scholar

14. Herink G, Kurtz F, Jalali B, Solli DR, Ropers C. Real-time spectral interferometry probes the internal dynamics of femtosecond soliton molecules. Science (2017) 356(6333):50–4. doi:10.1126/science.aal5326

PubMed Abstract | CrossRef Full Text | Google Scholar

15. Xu G, Gelash A, Chabchoub A, Zakharov V, Kibler B. Breather wave molecules. Phys Rev Lett (2019) 122(8):084101. doi:10.1103/physrevlett.122.084101

PubMed Abstract | CrossRef Full Text | Google Scholar

16. Dudley JM, Genty G, Mussot A, Chabchoub A, Dias F. Rogue waves and analogies in optics and oceanography. Nat Rev Phys (2019) 1(11):675–89. doi:10.1038/s42254-019-0100-0

CrossRef Full Text | Google Scholar

17. Akhmediev N, Soto-Crespo J, Ankiewicz A. How to excite a rogue wave. Phys Rev A (2009) 80(4):043818. doi:10.1103/physreva.80.043818

CrossRef Full Text | Google Scholar

18. Bonatto C, Feyereisen M, Barland S, Giudici M, Masoller C, Leite JRR, et al. Deterministic optical rogue waves. Phys Rev Lett (2011) 107(5):053901. doi:10.1103/physrevlett.107.053901

PubMed Abstract | CrossRef Full Text | Google Scholar

19. Frisquet B, Kibler B, Morin P, Baronio F, Conforti M, Millot G, et al. Optical dark rogue wave. Scientific Rep (2016) 6(1):20785–9. doi:10.1038/srep20785

CrossRef Full Text | Google Scholar

20. Kedziora DJ, Ankiewicz A, Akhmediev N. Second-order nonlinear Schrödinger equation breather solutions in the degenerate and rogue wave limits. Phys Rev E (2012) 85(6):066601. doi:10.1103/physreve.85.066601

PubMed Abstract | CrossRef Full Text | Google Scholar

21. Ablowitz M, Prinari B, Trubatch A. Soliton interactions in the vector NLS equation. Inverse Probl (2004) 20(4):1217–37. doi:10.1088/0266-5611/20/4/012

CrossRef Full Text | Google Scholar

22. Zhang Y, Tao X, Yao T, He J. The regularity of the multiple higher-order poles solitons of the NLS equation. Stud Appl Math (2020) 145(4):812–27. doi:10.1111/sapm.12338

CrossRef Full Text | Google Scholar

23. Newell AC. Solitons in mathematics and physics. Philadelphia: SIAM (1985).

Google Scholar

24. Ablowitz MJ, Biondini G, Ostrovsky LA. Optical solitons: Perspectives and applications. Chaos: Interdiscip J Nonlinear Sci (2000) 10(3):471–4. doi:10.1063/1.1310721

PubMed Abstract | CrossRef Full Text | Google Scholar

25. Kodama Y. Optical solitons in a monomode fiber. J Stat Phys (1985) 39(5):597–614. doi:10.1007/bf01008354

CrossRef Full Text | Google Scholar

26. Solli DR, Ropers C, Koonath P, Jalali B. Optical rogue waves. Nature (2007) 450(7172):1054–7. doi:10.1038/nature06402

PubMed Abstract | CrossRef Full Text | Google Scholar

27. Chowdury A, Kedziora D, Ankiewicz A, Akhmediev N. Breather solutions of the integrable quintic nonlinear Schrödinger equation and their interactions. Phys Rev E (2015) 91(2):022919. doi:10.1103/physreve.91.022919

PubMed Abstract | CrossRef Full Text | Google Scholar

28. Wang L, Zhang J-H, Wang Z-Q, Liu C, Li M, Qi F-H, et al. Breather-to-soliton transitions, nonlinear wave interactions, and modulational instability in a higher-order generalized nonlinear Schrödinger equation. Phys Rev E (2016) 93(1):012214. doi:10.1103/physreve.93.012214

PubMed Abstract | CrossRef Full Text | Google Scholar

29. Akhmediev N, Soto-Crespo JM, Ankiewicz A. Extreme waves that appear from nowhere: On the nature of rogue waves. Phys Lett A (2009) 373(25):2137–45. doi:10.1016/j.physleta.2009.04.023

CrossRef Full Text | Google Scholar

30. Kodama Y, Hasegawa A. Nonlinear pulse propagation in a monomode dielectric guide. IEEE J Quan Elect (1987) 23(5):510–24. doi:10.1109/jqe.1987.1073392

CrossRef Full Text | Google Scholar

31. Gedalin M, Scott T, Band Y. Optical solitary waves in the higher order nonlinear Schrödinger equation. Phys Rev Lett (1997) 78(3):448–51. doi:10.1103/physrevlett.78.448

CrossRef Full Text | Google Scholar

32. Hirota R. Exact N-soliton solutions of the wave equation of long waves in shallow-water and in nonlinear lattices. J Math Phys (1973) 14(7):810–4. doi:10.1063/1.1666400

CrossRef Full Text | Google Scholar

33. Chow KW. A class of doubly periodic waves for nonlinear evolution equations. Wave Motion (2002) 35(1):71–90. doi:10.1016/s0165-2125(01)00078-6

CrossRef Full Text | Google Scholar

34. Ankiewicz A, Soto-Crespo J, Akhmediev N. Rogue waves and rational solutions of the Hirota equation. Phys Rev E (2010) 81(4):046602. doi:10.1103/physreve.81.046602

PubMed Abstract | CrossRef Full Text | Google Scholar

35. Li C, He J, Porsezian K. Rogue waves of the Hirota and the maxwell-bloch equations. Phys Rev E (2013) 87(1):012913. doi:10.1103/physreve.87.012913

PubMed Abstract | CrossRef Full Text | Google Scholar

36. Ablowitz MJ, Musslimani ZH. Integrable nonlocal nonlinear Schrödinger equation. Phys Rev Lett (2013) 110(6):064105. doi:10.1103/physrevlett.110.064105

PubMed Abstract | CrossRef Full Text | Google Scholar

37. Xu T, Li L, Li M, Li C, Zhang X. Rational solutions of the defocusing non-local nonlinear schrödinger equation: Asymptotic analysis and soliton interactions. Proc R Soc A (2021) 477(2254):20210512. doi:10.1098/rspa.2021.0512

CrossRef Full Text | Google Scholar

38. Li M, Xu T, Meng D. Rational solitons in the parity-time-symmetric nonlocal nonlinear Schrödinger model. J Phys Soc Jpn (2016) 85(12):124001. doi:10.7566/jpsj.85.124001

CrossRef Full Text | Google Scholar

39. Sinha D, Ghosh PK. Symmetries and exact solutions of a class of nonlocal nonlinear Schrödinger equations with self-induced parity-time-symmetric potential. Phys Rev E (2015) 91(4):042908. doi:10.1103/physreve.91.042908

PubMed Abstract | CrossRef Full Text | Google Scholar

40. Bender CM, Boettcher S, Meisinger PN. PT-symmetric quantum mechanics. J Math Phys (1999) 40(5):2201–29. doi:10.1063/1.532860

CrossRef Full Text | Google Scholar

41. Bender CM, Dunne GV. Large-order perturbation theory for a non-Hermitian PT-symmetric Hamiltonian. J Math Phys (1999) 40(10):4616–21. doi:10.1063/1.532991

CrossRef Full Text | Google Scholar

42. Sarma AK, Miri M-A, Musslimani ZH, Christodoulides DN. Continuous and discrete Schrödinger systems with parity-time-symmetric nonlinearities. Phys Rev E (2014) 89(5):052918. doi:10.1103/physreve.89.052918

PubMed Abstract | CrossRef Full Text | Google Scholar

43. Li Y-Q, Liu W-J, Wong P, Huang L-G, Pan N. Dromion structures in the(2+1)-dimensional nonlinear Schrödinger equation with a parity-time-symmetric potential. Appl Math Lett (2015) 47:8–12. doi:10.1016/j.aml.2015.02.002

CrossRef Full Text | Google Scholar

44. Castaldi G, Savoia S, Galdi V, Alu A, Engheta N. PTMetamaterials via complex-coordinate transformation optics. Phys Rev Lett (2013) 110(17):173901. doi:10.1103/physrevlett.110.173901

PubMed Abstract | CrossRef Full Text | Google Scholar

45. Lazarides N, Tsironis G. Gain-driven discrete breathers inPT-symmetric nonlinear metamaterials. Phys Rev Lett (2013) 110(5):053901. doi:10.1103/physrevlett.110.053901

PubMed Abstract | CrossRef Full Text | Google Scholar

46. Cen J, Correa F, Fring A. Integrable nonlocal Hirota equations. J Math Phys (2019) 60(8):081508. doi:10.1063/1.5013154

CrossRef Full Text | Google Scholar

47. Li N-N, Guo R. Nonlocal continuous Hirota equation: Darboux transformation and symmetry broken and unbroken soliton solutions. Nonlinear Dyn (2021) 105(1):617–28. doi:10.1007/s11071-021-06556-3

CrossRef Full Text | Google Scholar

48. Xu Z, Chow K. Breathers and rogue waves for a third order nonlocal partial differential equation by a bilinear transformation. Appl Math Lett (2016) 56:72–7. doi:10.1016/j.aml.2015.12.016

CrossRef Full Text | Google Scholar

49. Zhang G, Yan Z, Chen Y. Novel higher-order rational solitons and dynamics of the defocusing integrable nonlocal nonlinear Schrödinger equation via the determinants. Appl Math Lett (2017) 69:113–20. doi:10.1016/j.aml.2017.02.002

CrossRef Full Text | Google Scholar

50. Zhang H-Q, Gao M. Rational soliton solutions in the parity-time-symmetric nonlocal coupled nonlinear Schrödinger equations. Commun Nonlinear Sci Numer Simulation (2018) 63:253–60. doi:10.1016/j.cnsns.2018.02.029

CrossRef Full Text | Google Scholar

51. Liu T, Chiu T, Clarkson P, Chow K. A connection between the maximum displacements of rogue waves and the dynamics of poles in the complex plane. Chaos: Interdiscip J Nonlinear Sci (2017) 27(9):091103. doi:10.1063/1.5001007

PubMed Abstract | CrossRef Full Text | Google Scholar

52. Xia Y, Yao R, Xin X. Darboux transformation and soliton solutions of a nonlocal Hirota equation. Chin Phys B (2022) 31(2):020401. doi:10.1088/1674-1056/ac11e9

CrossRef Full Text | Google Scholar