- Institute of Laser and Micro/Nano Engineering, College of Electronics and Information Engineering, Sichuan University, Chengdu, Sichuan, China
Underwater imaging is a challenging task because of the effects of scattering and absorption in water. Ghost imaging (GI) has attracted increasing attention because of its simple structure, long range, and achievability under weak light intensity. In an underwater environment, conventional imaging is limited by low sensitivity, resulting in fuzzy images, while ghost imaging can solve this problem. This study proposes underwater laser ghost imaging based on Walsh speckle patterns. According to the simulated and experimental results, noise resistance and a low sampling rate of ghost imaging based on Walsh speckle patterns are proved. As the turbidity of the underwater environment increases, the imaging quality of ghost imaging based on Walsh speckle patterns decreases. However, it remains much better than that of ghost imaging based on random speckle patterns and Hadamard speckle patterns, whereas conventional imaging is no longer distinguishable. Ghost imaging based on Walsh speckle patterns can be performed with a sampling rate lower than 10%, and the peak signal-to-noise ratio and the structural similarity of the results increase by 150.15% and 396.66%, respectively, compared with random speckle pattern ghost imaging. An identifiable image of ghost imaging based on Walsh speckle patterns can be reconstructed with a sampling rate of 6% in a turbid water environment, which is simulated with the concentration of the milk powder not higher than 11.0 g/L. This method promotes the further development of optical imaging technology for underwater targets with a low sampling rate based on ghost imaging.
1 Introduction
Ghost imaging (GI) is a non-point-to-point imaging technique that has attracted increasing attention in the field of optical imaging. GI comprises two optical paths: the signal arm, in which the laser is modulated by the object and the total light intensity is collected by a bucket detector without spatial resolutions, and the reference arm, in which the laser is not modulated by the object and the spatial resolution is received by an array detector. GI was first proposed in 1995 using entangled photon pairs generated from the spontaneous parametric down-conversion technology. It was considered a phenomenon in the quantum realm [1]. Later, an experiment of GI with a classical light source proved that GI is not limited to the quantum realm [2, 3]. In 2008, computational GI (CGI) was proposed, and a spatial light modulator (SLM) was used to produce a spatial structure modulation to the laser [4]. With the pre-computed intensity fluctuation patterns, CGI can be performed by only one bucket detector, which means the reference arm can be omitted, and the experimental configuration can be simplified significantly. Before the SLM was used, researchers used a rotating ground glass to produce a speckle distribution, and the imaging quality was limited to the uncertainty of the random speckle patterns. With the use of the SLM, digital micro-mirror device, digital light projector, and other devices, the distribution of speckle patterns can be preset, which can improve the imaging quality of GI. Speckle patterns of a random distribution were used in early CGI experiments. The sampling rate was limited by the Nyquist theorem, which means a large number of samples were required to get an ideal reconstructed image. Orthogonal speckle patterns, such as a distribution of Hadamard [5–13], Walsh [13–17], Russian Dolls [18], Haar wavelet [19], and hybrid types [20], have been widely used in GI in recent years. Theoretically, GI based on orthogonal speckle patterns could achieve a perfect image of the object when the sampling rate is 1. There is a possibility to further reduce the sampling rate of GI using the properties of the orthogonal matrix. Due to the advantages and breakthroughs in key technologies, GI has been applied in some real environments, such as turbulent atmospheres [21], speckle media [22], underwater environments [23–31], super-resolved quantum [32], and microscopy field [33]. GI has the advantage of anti-disturbance, which provides a better option for underwater optical imaging. If the speckle patterns with a special structure, such as Walsh, are used for GI, better imaging quality can be obtained in complex environments, which will open a new way for the practical application of GI.
In this study, we propose an underwater laser GI scheme based on Walsh speckle patterns. The effects of random, Hadamard, and Walsh speckle patterns on the imaging quality of GI are simulated, and the results show that GI based on Walsh speckle patterns is resistant to noise and its sampling rate is low. The experimental results show that when the sampling rate is 10%, its peak signal-to-noise ratio (PSNR) increases by 150.15% and its structural similarity (SSIM) increases by 396.66% compared with GI based on random speckle patterns. The object could be identified at a low sampling rate in high turbid water in which milk concentration is not higher than 11.0 g/L, although the imaging quality of GI based on the Walsh speckle patterns decreases with the increase in the turbidity of the underwater environment.
Section 2 presents the design of the Walsh speckle patterns and the GI principle. The simulation and underwater experiment of laser GI based on Walsh speckle patterns have been given in Section 3. Finally, the concluding remarks are presented in Section 4.
2 Theory
The working principle of CGI is that the laser is modulated by an SLM (4), the resulting speckle patterns are projected onto the object, and the total intensity is collected by a bucket detector. The transmission distribution of the object is
The light intensity collected by a bucket detector is formed into a
The mean value of the m bucket detectors is
The mean value of the speckle patterns is
Using the second-order correlation calculation, GI is [3]
The Hadamard matrix is orthogonal with elements of +1 and −1. The low-order Hadamard matrix is defined as [5, 9, 11, 13]
and the higher-order Hadamard matrix can be expressed as
where
When the Hadamard matrix is used as the speckle patterns for acquisition, the variance of the matrix is [29]
However, the correlation GI is
The Walsh matrix can be formed by the Hadamard matrix in the order of the number of sign changes of each row in the Hadamard matrix. For example, the third-order Hadamard matrix is expressed as
At this point, the third-order Walsh matrix is expressed as
As an orthogonal matrix, the Walsh matrix is also orthogonal to each other for all the row or column vectors. When using Hadamard speckle patterns and Walsh speckle patterns for GI, the −1 elements are experimentally replaced by the 0 elements, which did not affect the imaging quality.
The speckle pattern distribution of each sheet and the corresponding detected buckets for GI using different speckle patterns are shown in Figure 1. Figure 1A shows the case of random speckle patterns, Figure 1B shows the case of Hadamard speckle patterns, and Figure 1C shows the case of Walsh speckle patterns.
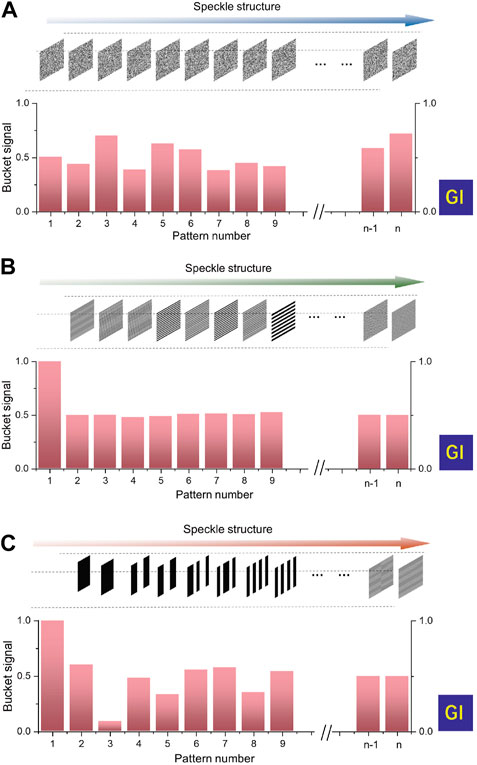
FIGURE 1. Speckle distribution of each sheet and corresponding bucket detector for ghost imaging using different patterns. (A) Random, (B) Hadamard, and (C) Walsh speckle patterns.
We characterize the image quality by the PSNR and the SSIM. The PSNR is defined as [9]
The SSIM is defined as [13]
where
3 Simulation and experiment
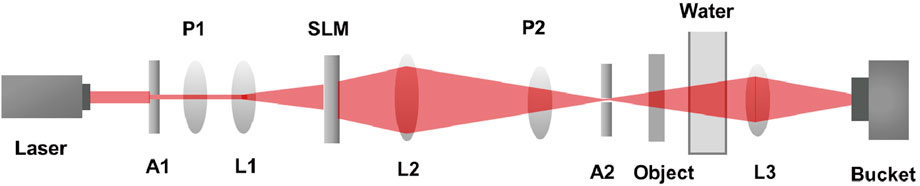
The experimental scheme of underwater laser GI based on Walsh speckle patterns is shown in Figure 2. A laser with a collimation system (Fuzhe Laser Technology FU532D12-BD43) is used as the light source, and a polarizer P1 combined with a polarizer P2 is used to adjust the light intensity. A transmissive liquid crystal SLM (UPOLabs RSLM1024) is used to generate the speckle patterns, and the distribution of speckle patterns is generated by a connected computer and then input on the screen of SLM. A power meter (OPHIR PD300-3W-V1 and OPHIR StarLite) is used as the bucket detector, which is connected to the computer to gather the signals of the light power. The 4 cm × 4 cm thick paper is placed as an “object” plane, as shown in Figure 2. The resolution of the projected speckle patterns is 128 pixels × 128 pixels. Lens 1 has a focal length of 10 cm, lens 2 has a focal length of 15 cm, and lens 3 has a focal length of 10 cm. The size of the liquid container is 210 mm × 315 mm × 41 mm.
3.1 Simulated results without noise
Simulated results of laser GI based on different speckle patterns are shown in Figure 3. The objects are images of the text “GI,” text “ILMNE,” tumor map, and cell map. As the sampling rate increases, the imaging quality of GI based on different speckle patterns is all improved, and the GI based on Hadamard and Walsh speckle patterns recovers the object perfectly when the sampling rate is 1. There is a large amount of random background noise in the imaging results of random speckle pattern GI, which makes the imaging quality of random speckle pattern GI low. In contrast, for GI based on the Hadamard speckle patterns, periodic ghosting exists in the reconstructed images at low sampling rates. When the sampling rate is 0.5, the result consists of the object and the ghosting of the object shifted by half position. The imaging results of GI based on the Hadamard speckle patterns at lower sampling rates are composed of more ghosting together in superposition, which makes the object unable to be distinguished, and it could be fatal in practical applications. The periodic ghosting in GI based on the Walsh speckle patterns occurs only at very low sampling rates, such as 1%, whereas the reconstructed target remains recognizable even at a low sampling rate, such as 5%. At the sampling rate of 10%, GI based on Walsh speckle patterns can meet the basic requirements.
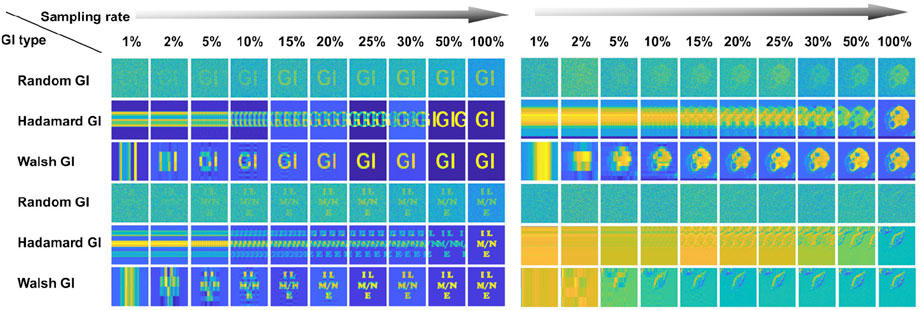
FIGURE 3. Simulated results of laser GI based on random, Hadamard, and Walsh speckle patterns in the noiseless environment.
Figure 4 shows the evaluation of the imaging quality of laser GI using the PSNR and the SSIM in the noiseless environment. GI based on both Hadamard speckle patterns and Walsh speckle patterns performs a perfect recovery when the sampling rate is 1, but GI based on Walsh speckle patterns shows its advantage over others at low sampling rates. It is also observed that at the sampling rate of an integer power of 0.5, the imaging quality of GI based on Walsh speckle patterns is much higher than that of the other nearby sampling rates due to the characteristics of the Walsh speckle pattern construction itself.
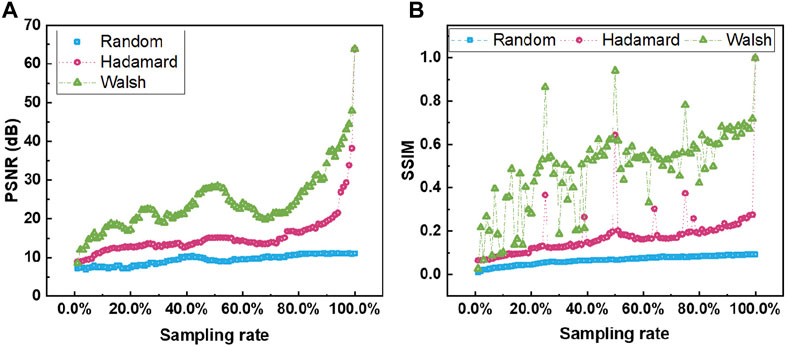
FIGURE 4. (A) PSNR indicator and (B) SSIM indicator vs sampling rates of laser GI based on random, Hadamard, and Walsh speckle patterns in the noiseless environment.
3.2 Simulated results with noise
To test and compare the anti-disturbance of laser GI based on random, Hadamard, and Walsh speckle patterns, we performed a simulation by adding a portion of random noise to the bucket detector to simulate the fluctuations in the real environment. Figure 5 shows the imaging results of GI based on three types of speckle patterns when 1.0% random fluctuations (generated by the randn function of MATLAB R2022a) are added to the bucket. For the Hadamard configuration, the reconstructed images are apparently clearer than those of the random speckle patterns, but owing to the periodic ghosting at subsampling rates, the SSIM of GI based on the Hadamard speckle patterns is not much higher than the SSIM of GI based on the random speckle patterns. As mentioned previously, there is no periodic ghosting when the Hadamard matrix is re-ranged in a Walsh order, which can be seen in Figure 5; the image quality of GI based on Walsh speckle patterns is better than that of the other two types, even with a partial noise; and GI based on Walsh speckle patterns can be performed at a subsampling rate.
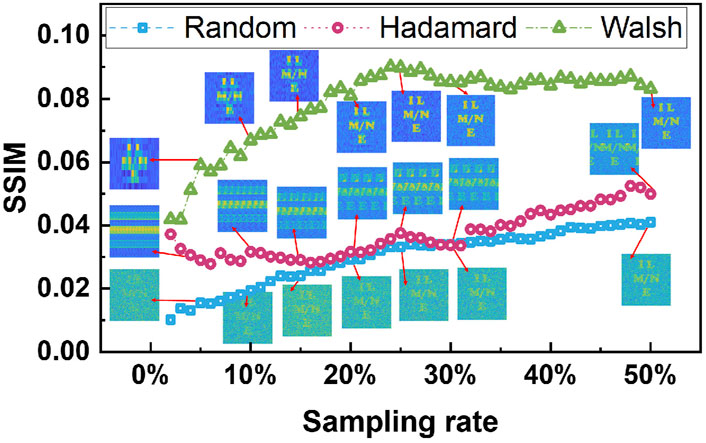
FIGURE 5. Simulated results of SSIM indicator vs. sampling rates of laser GI based on random, Hadamard, and Walsh speckle patterns at the 1% noise environment.
With 0.5%, 1%, 1.5%, 2%, 2.5%, and 3% noises added to the bucket of laser GI based on Walsh speckle patterns, an intuitive comparison of reconstructed images in different sampling rates and noise added is shown in Figure 6A, and the scatter plots of PSNR and SSIM are shown in Figures 6B, C. With the increasing noise, the imaging quality of GI based on Walsh speckle patterns decreased, which can be indicated from the direct image comparison and the imaging quality evaluations. The imaging quality is slightly improved by increasing the sampling rate at the same noise, but it cannot match the significant impact of the random noise with the 3% noise added to the bucket; no matter how much the sampling rate increases, the reconstructed image is recognizable but full of random noise; and the PSNR and the SSIM are severely affected.
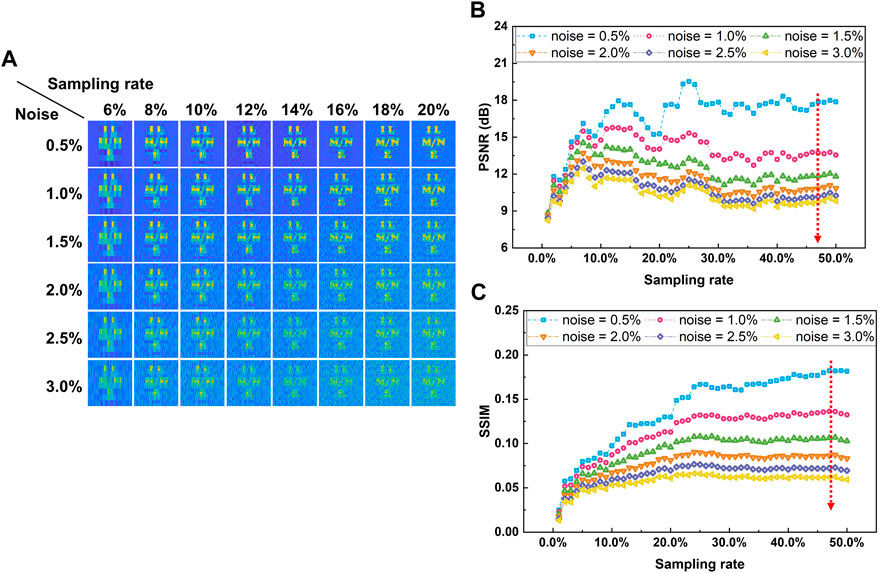
FIGURE 6. (A) Simulated results of laser GI based on Walsh speckle patterns under different random noise. (B) PSNR indicator and (C) SSIM indicator vs. sampling rates under different random noise and sampling rates.
3.3 Experimental results in the air
Experimental results of laser GI based on random and Walsh speckle patterns in the air environment are shown in Figure 7. The results of this experiment are similar to the simulated results with noise in some way. The experimental imaging results of laser GI based on Walsh speckle patterns are similar to the simulated results with the noise of 1.5%, indicating that the fluctuation of the surrounding environment is inevitably present in the actual experiment. It can be predicted that the appearance of noise is also inevitable and more obvious in the turbid underwater. The imaging results are shown in Figure 7A, combined with the data analysis of the SSIM in Figure 7B and the PSNR in Figure 7C, showing that laser GI based on Walsh speckle patterns works better in practice. However, the target text “GI” in the reconstructed image of laser GI based on random speckle patterns is close to being drowned in the background noise in a subsampling rate, and the PSNR of laser GI based on random speckle patterns does not present an expected rising trend in a low sampling rate that may be caused by introducing more noise with the increase in the sampling rate. Clear images are performed in GI based on Walsh speckle patterns at the sampling rate of 20% but not for GI based on Walsh speckle patterns, and it can meet the basic requirements at a low sampling rate of 10%. The PSNR and the SSIM of GI based on Walsh speckle patterns are 13.39 dB and 0.042, respectively. The PSNR and SSIM of GI based on random speckle patterns are 5.35 dB and 0.008, respectively. It means that the use of Walsh speckle patterns on GI can increase the PSNR and SSIM by 150.15% and 396.66%, respectively.
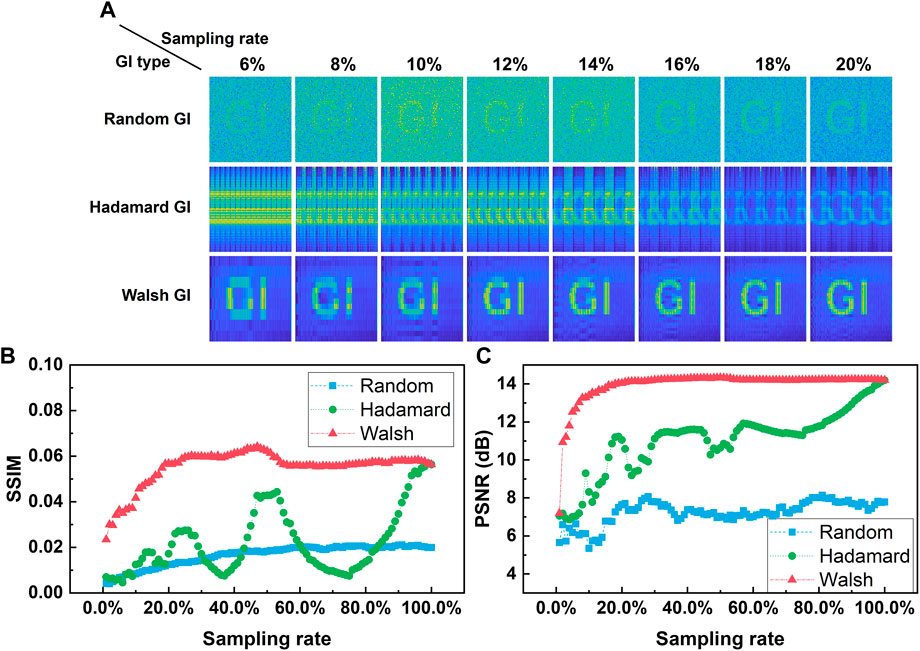
FIGURE 7. (A) Experimental results of laser GI based on random speckle patterns, Hadamard speckle patterns, and Walsh speckle patterns in the air. (B) SSIM indicator and (C) PSNR indicator vs sampling rates of laser GI based on random, Hadamard, and Walsh speckle patterns in the air.
3.4 Experimental results in the turbid water
The disturbance in turbid water is much higher than that in the air, under the premise of uniform turbidity, and to simulate and quantify the turbidity in water, 0.4, 0.6, 0.8, 1, 1.2, 2, 3, 4, 5, 6, 11, 22 g of milk powder are mixed to 2 L of pure water. The solution was stirred by Meiyingpu H05-1 constant temperature magnetic stirrer. The corresponding concentrations are 0.2, 0.3, 0.4, 0.5, 0.6, 1, 1.5, 2, 2.5, 3, 5.5, and 11 g/L. The protein content of the milk powder used is 21.2/100 g, and the fat content is 19.3/100 g. Both are the key elements that contribute to the turbidity solution. The imaging results of underwater laser GI based on Walsh speckle patterns are shown in Figure 8. With the increase in the milk powder concentration, the light passing through the turbid solution becomes weaker. As the measurement value of the bucket gradually becomes smaller, the visibility of the target text “GI” in the reconstructed image reduced, finally fading into the background. It can be inferred that with an ultra-high precision bucket detector, the underwater laser GI may go further with higher turbidity until the light intensity is reduced to a threshold where the bucket detector cannot distinguish the fluctuation of the light from the background noise.
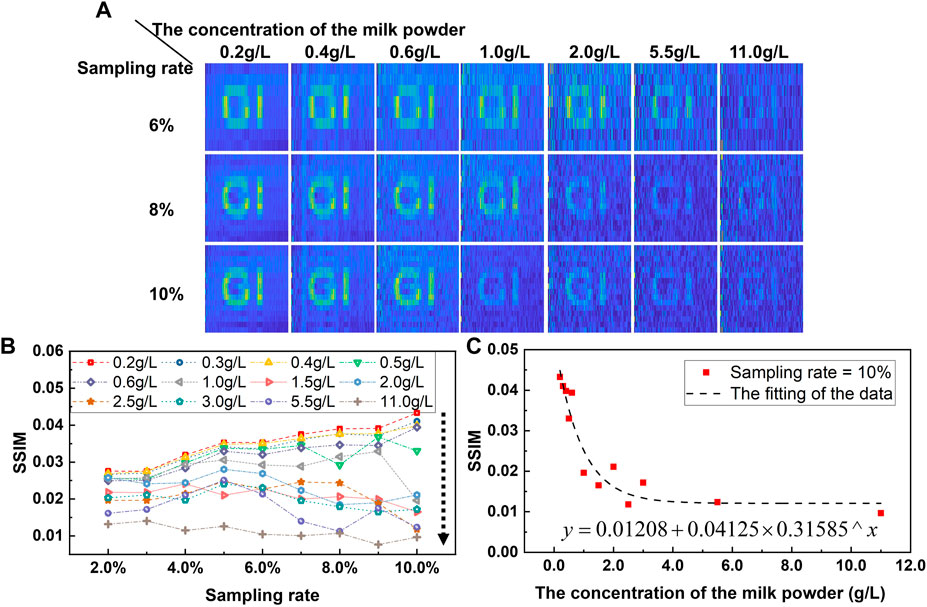
FIGURE 8. (A) Experimental results of laser GI based on Walsh speckle patterns in the turbidity water. (B) SSIM indicator vs sampling rates in the different turbidity water. (C) SSIM indicator vs the concentrations of the milk powder when the sampling rate is 10%.
Figure 8B shows the SSIM of different turbidity water under different sampling rates. The imaging quality of laser GI based on Walsh speckle patterns decreases with increasing turbidity. Although the increasing sampling rate improves the imaging quality, the impact of turbidity is more significant. To further reveal the relationship between the SSIM and the turbid water in a quantitative way, we take GI based on Walsh speckle patterns at a 10% sampling rate as an example and perform the SSIM scatter plot as shown in Figure 8C. While fitting the SSIM and the concentration of the milk powder, we find that it presents an approximate power series curve decline trend. The imaging quality of laser GI based on Walsh speckle patterns is excellent at the low milk powder concentration, whereas imaging could be achieved at the high milk powder concentration. According to the fitting function curve, the SSIM no longer drastically changes when the concentration of the milk powder is higher than 4 g/L, which means the increasing concentration of the effect of the milk powder on the transmitted light intensity will reach a relatively stable threshold, and the succeeding increase in milk powder slightly contributes to the transmittance. In other words, GI can be reconstructed even in an extremely turbid water environment as long as the light transmission is weak. This proves another advantage of GI based on Walsh speckle patterns: it can be achieved in a weak light intensity.
4 Conclusion
In this study, an underwater laser GI method based on Walsh speckle patterns is proposed. Random speckle patterns are affected by the environmental noise of the same property. Hadamard speckle patterns have overlapping noise at low sampling. However, Walsh speckle patterns make low-frequency information at the front end and high-frequency information at the back end. Therefore, GI based on Walsh speckle patterns can be achieved at a low sampling rate and is less affected by noise. As the turbidity of the underwater environment increases, the imaging quality of laser GI based on Walsh speckle patterns decreases, whereas conventional imaging is no longer distinguishable. GI based on Walsh speckle patterns can be performed when the sampling rate is lower than 10%. Its PSNR increases by 150.15%, and its SSIM increases by 396.66% compared with random speckle pattern GI. Even in a turbid water environment, in which the concentration of the milk powder is not higher than 11.0 g/L, a recognizable image was acquired. This illustrates the potential of the proposed method for rapid imaging under turbid water. This paper lays the foundation for researchers to study underwater GI, and the use of speckle pattern distribution of specific structures, such as Walsh, is a growing trend. In future work, the practical application of GI in complex environments is the future research direction. It will be of great significance to achieve high-quality imaging in an ultra-harsh environment by combining the optimization of front-end schemes, such as speckle pattern designs, and image reconstruction techniques, such as fast transformation [5, 16], compressed sensing [13, 28], and neural network [30, 34].
Data availability statement
The original contributions presented in the study are included in the article/Supplementary Material. Further inquiries can be directed to the corresponding author.
Author contributions
MY: idea construction, simulation calculation, experiment completion, manuscript drawing, and initial manuscript completion. YW: assisted in completing the experiment and revising the manuscript. GF: idea construction, data check, and manuscript revision.
Funding
This research was financially supported by the National Key Research and Development Program of China under Grant No. 2022YFB3606300 and National Natural Science Foundation of China under Grant No. U2230129.
Acknowledgments
The authors wish to thank Prof. Houkun Liang, Sichuan University, for his help in the experiment.
Conflict of interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Publisher’s note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
References
1. Pittman TB, Shih YH, Strekalov DV, Sergienko AV. Optical imaging by means of two-photon quantum entanglement. Phys Rev A (1995) 52(5):R3429–32. doi:10.1103/physreva.52.r3429
2. Bennink RS, Bentley SJ, Boyd RW. Two-photon" coincidence imaging with a classical source. Phys Rev Lett (2002) 89(11):113601. doi:10.1103/physrevlett.89.113601
3. Valencia A, Scarcelli G, D’Angelo M, Shih Y. Two-photon imaging with thermal light. Phys Rev Lett (2005) 94(6):063601. doi:10.1103/physrevlett.94.063601
4. Shapiro JH. Computational ghost imaging. Phys Rev A (2008) 78(6):061802. doi:10.1103/physreva.78.061802
5. Wang L, Zhao SM. Fast reconstructed and high-quality ghost imaging with fast walsh–hadamard transform. Photon Res (2016) 4(6):240–4. doi:10.1364/prj.4.000240
6. Wang L, Zou L, Zhao SM. Edge detection based on subpixel-speckle-shifting ghost imaging. Opt Commun (2018) 407:181–5. doi:10.1016/j.optcom.2017.09.002
7. Yu WK. Super sub-nyquist single-pixel imaging by means of cake-cutting hadamard basis sort. Sensors [Internet] (2019) 19(19):4122. doi:10.3390/s19194122
8. Yuan X, Zhang LH, Chen J, Wang KM, Zhang DW. Multiple-image encryption scheme based on ghost imaging of hadamard matrix and spatial multiplexing. Appl Phys B (2019) 125(9):174–13. doi:10.1007/s00340-019-7286-9
9. Wu H, Wang RZ, Li CS, Chen MY, Zhao GP, He ZY, et al. Influence of intensity fluctuations on hadamard-based computational ghost imaging. Opt Commun (2020) 454:124490. doi:10.1016/j.optcom.2019.124490
10. Wu H, Zhao GP, Wang RZ, Xiao HP, Wang DD, Liang J, et al. Computational ghost imaging system with 4-connected-region-optimized hadamard pattern sequence. Opt Lasers Eng (2020) 132:106105. doi:10.1016/j.optlaseng.2020.106105
11. Zhang LH, Wang Y, Ye HL, Xu RC, Zhang DW. Research on camouflaged encryption scheme based on hadamard matrix and ghost imaging algorithm. Curr Opt Photon (2021) 5(6):686–98.
12. Gao ZJ, Yin JH, Bai YF, Fu XQ. Imaging quality improvement of ghost imaging in scattering medium based on hadamard modulated light field. Appl Opt (2020) 59(27):8472–7. doi:10.1364/ao.400280
13. Vaz PG, Amaral D, Requicha Ferreira LF, Morgado M, Cardoso J. Image quality of compressive single-pixel imaging using different hadamard orderings. Opt Express (2020) 28(8):11666–81. doi:10.1364/oe.387612
14. Olivieri L, Totero Gongora JS, Pasquazi A, Peccianti M. Time-resolved nonlinear ghost imaging. ACS Photon (2018) 5(8):3379–88. doi:10.1021/acsphotonics.8b00653
15. Ma HY, Sang AJ, Zhou C, An XF, Song LJ. A zigzag scanning ordering of four-dimensional Walsh basis for single-pixel imaging. Opt Commun (2019) 443:69–75. doi:10.1016/j.optcom.2019.02.041
16. Ma HY, Sang AJ, Zhou C, An XF, Zhao XW, Song LJ. High-efficiency reconstruction of ghost imaging based on equivalent deformation of 2d Walsh transform. J Opt (2020) 22(12):125702. doi:10.1088/2040-8986/abc95d
17. Totero Gongora JS, Olivieri L, Peters L, Tunesi J, Cecconi V, Cutrona A, et al. Route to intelligent imaging reconstruction via terahertz nonlinear ghost imaging. Micromachines (2020) 11(5):521. doi:10.3390/mi11050521
18. Sun MJ, Meng LT, Edgar MP, Padgett MJ, Radwell N. A Russian Dolls ordering of the hadamard basis for compressive single-pixel imaging. Scientific Rep (2017) 7(1):3464. doi:10.1038/s41598-017-03725-6
19. Yu Z, Gao C, Wang XQ, Zhao H, Yao ZH. Hadamard-haar (2d) dual domain ghost imaging. Opt Laser Tech (2022) 155:108413. doi:10.1016/j.optlastec.2022.108413
20. Wang XX, Tao Y, Yang FB, Zhang YW. An effective compressive computational ghost imaging with hybrid speckle pattern. Opt Commun (2020) 454:124470. doi:10.1016/j.optcom.2019.124470
21. Hardy ND, Shapiro JH. Reflective ghost imaging through turbulence. Phys Rev A (2011) 84(6):063824. doi:10.1103/physreva.84.063824
22. Bina M, Magatti D, Molteni M, Gatti A, Lugiato LA, Ferri F. Backscattering differential ghost imaging in turbid media. Phys Rev Lett (2013) 110(8):083901. doi:10.1103/physrevlett.110.083901
23. Chen Q, Mathai A, Xu XP, Wang X. .A study into the effects of factors influencing an underwater, single-pixel imaging system’s performance. Photonics (2019) 6(4):123. doi:10.3390/photonics6040123
24. Yin MQ, Wang L, Zhao SM. Experimental demonstration of influence of underwater turbulence on ghost imaging. Chin Phys B (2019) 28(9):094201. doi:10.1088/1674-1056/ab33ee
25. Zhang Y, Li WD, Wu HZ, Chen YH, Su XY, Xiao Y, et al. High-visibility underwater ghost imaging in low illumination. Opt Commun (2019) 441:45–8. doi:10.1016/j.optcom.2019.02.036
26. Luo CL, Wan WX, Chen SY, Long AF, Peng LN, Wu SF, et al. High-quality underwater computational ghost imaging with shaped lorentz sources. Laser Phys Lett (2020) 17(10):105209. doi:10.1088/1612-202x/abb094
27. Li MD, Mathai A, Lau SLH, Yam JW, Xu XP, Wang X. Underwater object detection and reconstruction based on active single-pixel imaging and super-resolution convolutional neural network. Sensors (2021) 21(1):313. doi:10.3390/s21010313
28. Wang T, Chen MY, Wu H, Xiao HP, Luo SJ, Cheng LL. Underwater compressive computational ghost imaging with wavelet enhancement. Appl Opt (2021) 60(23):6950–7. doi:10.1364/ao.431712
29. Yang X, Liu Y, Mou XY, Hu TY, Yuan F, Cheng E. Imaging in turbid water based on a hadamard single-pixel imaging system. Opt Express (2021) 29(8):12010–23. doi:10.1364/oe.421937
30. Yang X, Yu ZY, Xu L, Hu JM, Wu L, Yang CH, et al. Underwater ghost imaging based on generative adversarial networks with high imaging quality. Opt Express (2021) 29(18):28388–405. doi:10.1364/oe.435276
31. Wang MQ, Bai YF, Zou XPF, Peng MD, Zhou LY, Fu Q, et al. Effect of uneven temperature distribution on underwater computational ghost imaging. Laser Phys (2022) 32(6):065205. doi:10.1088/1555-6611/ac6ac3
32. Moodley C, Forbes A. Super-resolved quantum ghost imaging. Scientific Rep (2022) 12(1):10346–9. doi:10.1038/s41598-022-14648-2
33. Olivieri L, Gongora JST, Peters L, Cecconi V, Cutrona A, Tunesi J, et al. Hyperspectral terahertz microscopy via nonlinear ghost imaging. Optica (2020) 7(2):186–91. doi:10.1364/optica.381035
Keywords: underwater imaging, ghost imaging, single-pixel imaging, Walsh speckle patterns, laser imaging
Citation: Yang M, Wu Y and Feng G (2023) Underwater environment laser ghost imaging based on Walsh speckle patterns. Front. Phys. 11:1106320. doi: 10.3389/fphy.2023.1106320
Received: 23 November 2022; Accepted: 13 January 2023;
Published: 26 January 2023.
Edited by:
Guorui Zhou, China Academy of Engineering Physics, ChinaReviewed by:
Dan Dan, Xian Institute of Optics and Precision Mechanics, (CAS), ChinaBernhard Johan Hoenders, University of Groningen, Netherlands
Ma Hongyang, Qingdao University of Technology, China
Valeria Rodríguez-Fajardo, Colgate University, United States
Copyright © 2023 Yang, Wu and Feng. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Guoying Feng, Z3VvaW5nX2ZlbmdAc2N1LmVkdS5jbg==
 Mochou Yang
Mochou Yang Yi Wu
Yi Wu