Nuclear fission properties of super heavy nuclei described within the four-dimensional Langevin model

1 Introduction

Nuclear fission is a fundamental phenomenon that brings us enormous energy in the form of nuclear energy. There is abundant data on the fission of some significant nuclei, such as neutron-induced fission on ²³⁵U or ²³⁸Pu for the safe and efficient use of nuclear energy. However, it is still difficult to predict or measure observables such as the distribution of fission fragment yield or the total kinetic energies (TKEs) and their correlations accurately enough even today [1–3]. For example, radioactivities of the heavy actinide nuclei often make it difficult to measure fission-related quantities with good accuracy. From the theoretical side, it has been known that average mass numbers of the heavy and light fragments and TKE has an anomalous trend superposed on a systematical one.

Information on nuclear fission is essential not only for the development of nuclear energy but also in nuclear astrophysics, such as the r-process (rapid neutron capture process) nucleosynthesis. The concept of r-process with fission recycling has a long history after Burbidge-Burbidge proposed it in 1957 [4]. Since then, the r-process sites have been hot topics in astrophysics. A few astronomical phenomena, such as type-II supernovae and neutron star mergers, have been enthusiastically studied as their actual site. In 2017, this situation on the r-process drastically changed. The gravitational wave from GW170817 [5] elucidated that one of the r-process sites was neutron star mergers. Now the r-process is believed to be the origin of heavy elements during neutron star (NS) mergers. Under the extremely high neutron flux produced by NS-NS or NS-BH (black hole) mergers, the r-process synthesizes various superheavy nuclei (SHN). Then the fission fragments from SHNs are considered to be seed nuclei of the subsequent r-process path [6, 7]. Several fission recyclings have been expected to take place in the r-process. It opened a new era for the r-process and has required nuclear physicists to access more information on the nuclear fission of superheavy elements because that brings a significant ambiguity among nuclear inputs of the r-process simulations.

In the r-process environment, fission yields provide information [8] on which nuclei will be the dominant seed nuclei of the r-process. TKEs are also essential to estimate the number of neutrons emitted by fission recycling and how much energy is released as a local source of heating. Some use a microscopic approach as density functional theory [9] to predict these, while we use the Langevin model of the macroscopic-microscopic approaches here.

The Langevin approach [10] is successfully applied in various branches of theoretical physics and chemistry for many years. In nuclear physics, this approach is used to describe fission or fusion processes at the excitations well above the fission barrier [11–21]. The approach describes quite well the mass distributions and kinetic energies of fission fragments, the multiplicities of emitted neutrons, and other observable of fission or fusion processes.

Our Langevin model can simultaneously reproduce fission yields and TKEs well without parameter adjustments [18, 20, 22]. Thus we can provide reliable fission properties of superheavy elements (SHEs) at low excitation energies [23, 24] where the experiments are challenging.

This paper is organized as follows. In Section 2, we briefly introduce our four-dimensional Langevin model used to predict features of the SHN fission and Brosa model [25], which is used to analyze the TKEs. In Section 3, we show fission fragment mass distributions (FFMDs) and the total kinetics energies (TKEs) released in the nuclear fission of actinides to SHEs. We also display the fragment deformations of these nuclei. Based on those results, we found the systematics in the FFMDs and TKEs. We summarize our results in Sec.4.

2 Models

2.1 4D Langevin model

We have simulated nuclear fission process using the four-dimensional Langevin model [22]. In this model, we solve the equations for the time evolution of the nuclear shape of a compound system. As a shape parametrization, we use the two-center shell model (TCSM) with four independent parameters {q_μ, μ = 1⋯4} = {z₀/R₀, δ₁, δ₂, α}. The central potential in TCSM consists of two oscillator potentials, smoothly joint by the fourth order polynomial in z, see left part of Figure 1. Here z₀/R₀ corresponds to the distance between the centers of oscillator potentials with R₀ = 1.2 A^1/3, where R₀ is the radius of the compound nucleus having a mass number A.

FIGURE 1

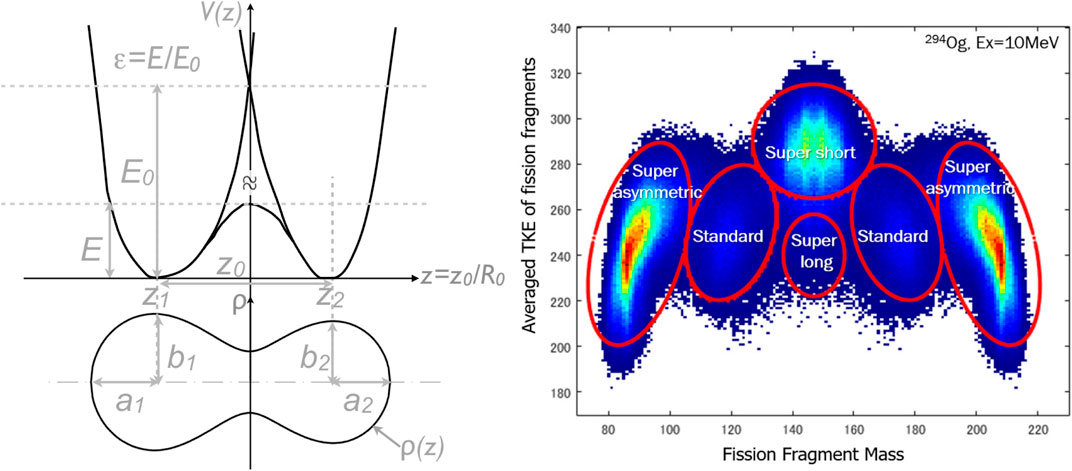
FIGURE 1. Left: The lower part shows the shape of a²³⁶U nucleus calculated by the TCSM. The upper part is the corresponding potential. Right: TKE distribution of fission fragments with our fission modes in the case of ²⁹⁴Og as compound nucleus at E_x = 10 MeV.

The two independent parameters, δ_i (i = 1, 2) denote the deformation of outer tips of the two fragments. The parameter α is the mass asymmetry defined as α = (A₁−A₂)/(A₁+A₂), where A_i (i = 1, 2) denote mass numbers of the fission fragments. The fifth (neck) parameter ϵ is defined as the ratio of the intercept of the harmonic oscillator potentials and that of the connecting function. Note that we fixed the neck parameter of the TCSM shape parametrization as ϵ = .35 in all calculations. This value was fixed in the earlier works [12] within the Langevin approach by fitting the fission fragment mass distributions of actinide nuclei to experimental results.

The Langevin equations are the first-order stochastic differential equations for the collective variables q_μ and the conjugated momenta p_μ:

$\frac{d{q}_{\mu }}{dt}={\left(m^{-1}\right)}_{\mu \nu }{p}_{\nu },(1)$

$\frac{d{p}_{\mu }}{dt}=-\frac{\partial F\left(q,T\right)}{\partial q_{\mu }}-\frac{1}{2}\frac{\partial {\left(m^{-1}\right)}_{\nu \sigma }}{\partial q_{\mu }}{p}_{\nu }{p}_{\sigma }-{\gamma }_{\mu \nu }{\left(m^{-1}\right)}_{\nu \sigma }{p}_{\sigma }+g_{\mu \nu }{R}_{\nu }\left(t\right),$

where we assume the sums over the repeated indices. In the Langevin equations, the F (q, T) is the temperature-dependent free energy of the system, and γ_μν and ${({\text{m}}^{-1})}_{\mu \nu }$ correspond to the friction and inverse of mass tensors, while g_μν is the strength of he random force.

We calculate the free energy F (q, T) by the sum of liquid drop deformation energy and the temperature dependent shell correction δF (q, T). The details on the damping of shell correction δF (q, T) with the excitation energy can be found in our previous publication [26]. The single particle energies are calculated by Pashkevich code [27] for the deformed Woods-Saxon potential. For this, we expand the TCSM shapes in series in Cassini ovaloids (up to 20 deformation parameters were included) and run the code for the deformed shape given by these 20 deformation parameters. The single particle energies and wave functions are calculated by the expansion of wave functions in the oscillator basis. The 15 oscillator shells were included for the actinide nuclei, and 20 shells for super-heavies. The parameters of the Woods-Saxon potential and pairing interaction can be found in [27]. The accuracy and reliability of this code were confirmed by the few decades’ experience of calculations of fission barrier heights and comparison with the experimental data. The position of the peaks in mass distributions of fission fragments is defined mainly by the shell effects in the deformation energy. The widths of the peaks and the pre-scission kinetic energies are more sensitive to friction and inertia tensors. Larger friction leads to the broader peaks and smaller pre-scission kinetic energy. However, friction or inertia are not the adjustable quantities. They have a clear physical meaning and should be calculated within the reliable theoretical models.

In the present work, we calculate the collective inertia tensor m_μν, by the widely used macroscopic Werner-Wheeler approximation [28]. This approximation does not contain any adjustable parameter. For the friction tensor γ_μν, we applied the popular wall-and-window formula [29, 30] with the commonly accepted reduction factor k_s = .27. This value was suggested immediately after formulation of wall formula, since the wall formula friction turned out to be too large for application in nuclear physics.

The random force g_μνR_ν(t) is given by the product of white noise R_ν(t) and the temperature-dependent strength factors g_μν. For the relation between the factors g_μν, the temperature, and friction tensor γ_μν, we use the modified Einstein relation,

$g_{\mu \sigma }{g}_{\sigma \nu }=T^{*}{\gamma }_{\mu \nu },\text{with}{T}^{*}=\frac{\hslash \omega }{2}\coth \frac{\hslash \omega }{2T},(2)$

where T* is the effective temperature [31, 32]. The application of effective temperature makes the width of the yields somewhat larger at small excitation energies and improves the agreement with the experimental data. The parameter ω is the local frequency of collective motion. At large excitation energies, T* is close to T. At T = 0 the effective temperature T* turns into ℏω/2. In principle, ω is deformation dependent, but the account of this dependence is too time-consuming. It was found in [33] within the linear response theory that at the ground state of ²²⁴Th the frequency ω varies in the limits 1 MeV < ℏω < 2 MeV depending on the excitation energy. We have checked that the position of peaks in the mass distributions of considered here nuclei does not depend on the value of ω in this region. Only the width of peaks gets smaller by few percents in case of ℏω = 1 MeV compared with case ℏω = 2 MeV. To make the computations faster, in all calculations below, the parameter ω was kept constant ℏω = 2 MeV.

All other parameters that appear in the transport coefficients are fixed outside of Langevin approach. Thus, the set of parameters was fixed and used for calculations for all nuclei from ²³⁶U to ³⁰⁶122.

For given nucleons number we can vary only the excitation energy. For high excitations the shell effects are washed out and the fission is mass-symmetric. That is only low excitations where one can see a structure in the mass distributions.

The temperature T in Eq. 2) is related to the internal excitation energy E* by,

$E^{*}=E_{gs}+E_x-\frac{1}{2}{m}_{\mu \nu }^{-1}{p}_{\mu }{p}_{\nu }-V_{\mathit{pot}}\left(q,T=0\right)=a{T}^2,(3)$

where V_pot means the potential energy and a is the level density parameter.

Initially, we set the momenta p_μ to be zero and start calculations from the ground state deformation. We continue the Langevin calculations until the trajectories come to the “scission point”, where the neck radius becomes r_neck = 0 fm. We have checked that the replacement of r_neck = 0 fm by r_neck = 1 fm or r_neck = 2 fm has a negligible small effect on the mass distributions.

At the scission point, the solutions of Langevin equations supply the complete information on the system, its shape, collective velocities, and excitation energy. This information makes it possible to calculate the multiple moments of density distributions, the mass distributions, the total kinetic energy, and the excitation energies of fission fragments. To get stable results, we start the calculations for 10⁵–10⁶ trajectories. More details can be found in our earlier publications [18, 20, 22, 23].

2.2 Brosa-like mode decomposition

We can understand fission properties using the Brosa model when we analyze the fission observables such as fission yields, TKEs, and prompt neutrons. The most popular Brosa model [25] consists of the standard I (ST1) and II (ST2) modes for asymmetric fission components and the supershort (SS) and superlong (SL) modes for symmetric components.

ST1 mode appears around the double magic nucleus with a spherical shape (¹³²Sn) and around its counterpart. The experimental characteristics of ST1 are high TKE and fewer prompt neutrons. On the other hand, Z = 54 shell closure governs ST2 mode. In ST2 mode, fission fragments favor octupole deformations. TKE and prompt neutron multiplicity of ST2 are intermediate values. In our analysis, we combine these modes and treat them as standard (ST) modes. SS mode is more compact than the standard modes. SS gives higher TKEs and emits a smaller number of neutrons. In contrast, SL has an elongated shape compared to the standard modes. As a result, the TKE of SL becomes lower, and the fission fragments with SL mode emit more prompt neutrons. In addition to these modes, we can observe the super-asymmetric mode in the nuclear fission of superheavy nuclei as shown in the right part of Figure 1.

In the following section, we analyze the TKE following the above Brosa-like model.

3 Calculated results and discussion

This section reports the fission simulations of important actinides, more heavy nuclei for which the experimental information is available, and selected SHEs that demonstrate the role of the shell effects in the fission yields. The calculations were done with the same set of parameters for all nuclei. Figure 2 displays the fission fragment mass yields at the excitation energies slightly above the fission barrier. Note, that the reference data of ²³⁶U to ²⁵²Cm are from the JENDL/FPY-2011 [34] and those reference data are for post-neutron emission. The peaks of mass disstribution are not symmetric with respect to A/2 and are shifted a little bit to the left. Our distribution are calculated for the pre-neutron emission and are symmetric with respect to A/2. The reference data of ^256−259Fm, ²⁶⁰Md, and ²⁵⁹Lr are the experimental data of spontaneous fission [35–37]. These data and our calculations are both for pre-neutron emission. In this case the position of peaks is perfectly reproduced.

FIGURE 2

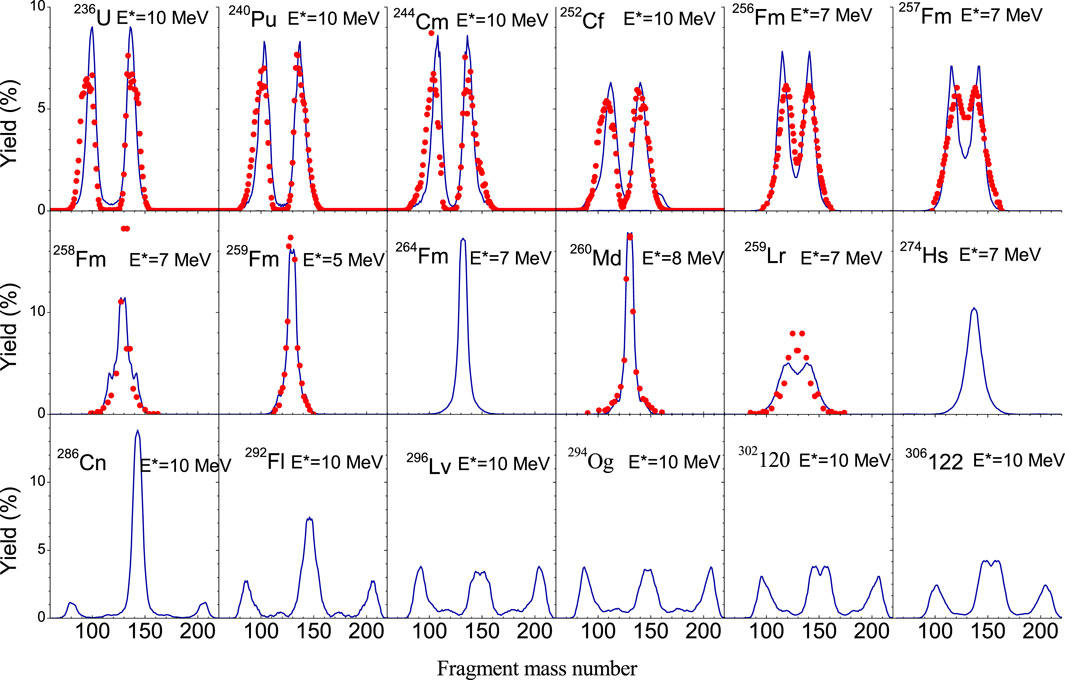
FIGURE 2. Calculated fission fragment mass distributions of ²³⁶U to ³⁰⁶122 (blue) and the available experimental data (red points) for the thermal neutrons induced fission of ²³⁵U - ²⁵²Cf after prompt neutron emissions JENDL/FPY-2011 [34] and for spontaneous fission of ²⁵⁶Fm - ²⁵⁹Lr [35–37].

On average, our calculations reproduce quite well the peak width and position for nuclear fission of ²³⁶U to ²⁵⁹Lr, including Fm-isotopes, as a compound system. The transition from mass-asymmetric to mass-symmetric distribution between ²⁵⁷Fm and ²⁵⁸Fm is also qualitatively reproduced, though the transition is not as sharp as in experiments on spontaneous fission [37]. The similar mild transition from asymmetric to symmetric yield between ²⁵⁶Fm and ²⁵⁸Fm was obtained also in a resent work [38] within a Metropolis method for strongly damped fission dynamics. The transition from asymmetric to symmetric yield in Fermium isotopes was qualitatively reproduced also in [39] within the time-dependent generator-coordinate formalism and in [40] within the three-dimensional Langevin approach. The mildness of transition could be related to the fact that the calculations were done at the finite excitation energies, which partly suppresses the shell effects.

In the region of light super-heavies, the fragment yields are mass symmetric, like in the case of ²⁷⁴Hs. For heavier SHEs the strongly mass asymmetric peaks appear in mass distributions at A_H ≈ 208. For the nuclei from ²⁹⁶Lv to ³⁰⁶122, the symmetric and strongly mass asymmetric peaks are approximately of the same magnitude. In the case of ³⁰²120 and ³⁰⁶122, the symmetric peak is split into two components. In ³⁰²120 and ³⁰⁶122, the mean fragment mass of the lighter middle peak becomes almost constant at A_F = 144 as in the case of the middle peaks of ²⁷⁴Hs to ²⁹⁶Lv and the heavier peaks in actinides. On the other hand, the heavier middle peaks in ³⁰²120 and ³⁰⁶122 clearly deviate from A_F = 144 as shown in Figure 3.

FIGURE 3

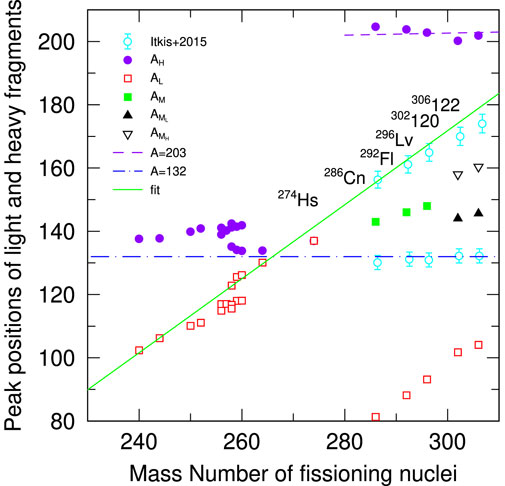
FIGURE 3. Averaged peak positions of light and heavy fragments as a function of a compound nuclear mass. Light blue symbols with error bars are experimental data measured by Itkis et al. The other symbols are our calculations. The subscripts of symbol legends, H, L, M, M_H and M_L, denote the heaviest peak, the lightest peak, the middle peak, the heavier middle peak, and the lighter middle peak in mass numbers.

The heavy fragment with A_H ≈ 208 was found recently [21] in Langevin calculations with the so-called Fourier shape parametrization. The ²⁰⁸Pb was obtained also as the main fission fragment of ²⁹⁴Og in [41] assuming the cluster radioactivity as an important decay mode in super-heavy nuclei.

In experimental work of Itkis group [42] the mass symmetric fission of Hassium isotopes was found in reactions ²²Ne + ²⁴⁹Cf →²⁷¹Hs and ²⁶Mg + ²⁴⁸Cm →²⁷⁴Hs and the mass asymmetric fission with the main fragment close to ²⁰⁸Pb in reactions ³⁶S + ²³⁸U →²⁷¹Hs and ⁵⁸Fe + ²⁰⁸Pb →²⁶⁶Hs. At the same time, the later experimental results of Itkis [43] show ¹³²Sn as the main fragment of mass asymmetric fission of super-heavy nuclei.

The reason of the difference may be the fact that the calculations and experiment are done not for the same process. The calculations are carried out for the fission of a completely equilibrated compound nucleus. Whereas in Itkis experiments, the super-heavy system is created in the fusion-fission reactions between heavy ions. The re-separation of ions can happen at each stage of the evolution of the combined system from the touching configuration till the separation of fission fragments. The main part of fission fragments comes from the quasi-fission events. It is not clear how well the quasi-fission events are separated in the experiment from the true fission events. This uncertainty could be the reason for disagreement between experimental and calculated results. The question, what is the main fission fragment of fission of super-heavy nuclei,¹³²Sn or ²⁰⁸Pb, still has to be clarified both from the experimental and theoretical sides.

To summarize the fission mass yields, we plot the averaged peak positions in Figure 3. Filled circles, open squares, filled squares, filled triangles, and open triangles denote the averaged mass of the heaviest peak A_H, the lightest peak A_L, the middle peak A_M (three peak FFMD case), the lighter middle peak $A_{M_L}$ and the heavier middle peak $A_{M_H}$, respectively. Open circles with error bars are the measured averaged peaks [43] but at high E_x compared to our results at E_x = 7 MeV. The experimental values lie along the extrapolation line of the averaged mass systematics of actinides. In our calculations, the shell structures of A_F = 132–144 govern fission fragments with the heaviest peak position in actinides and the middle peaks (A_M and $A_{M_L}$) in SHEs. However, the heaviest and lightest peaks in SHEs behave quite differently than in actinides. Our calculations suggest the strong influence of the double shell closure of ¹³²Sn and the deformed shell at Z_H = 54 in actinides as experiments, while the dominant shell changes to the double-shell closure of ²⁰⁸Pb.

To investigate the Brosa-like fission modes defined in the previous section, we plot the TKEs as a function of fission fragment mass number in Figure 4. We define the total kinetic energy of fission fragments by the sum of the pre-scission kinetic energy and the energy of Coulomb repulsion of fragments just before the scission in approximation of point charges,

$TKE=K{E}_{\mathit{pre}}+e^2{Z}_L{Z}_H/D.(4)$

Here KE_pre is the kinetic energy of relative motion of future fragments in fission direction, and D is the distance between the centers of mass of parts nucleus to the left and to the right from the neck.

FIGURE 4

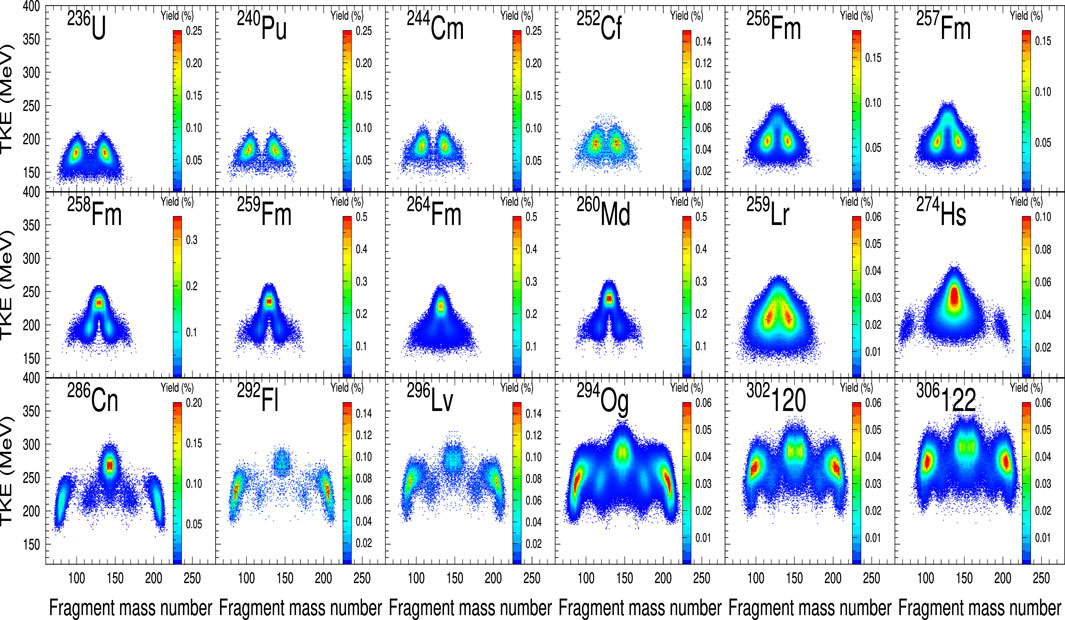
FIGURE 4. Fission fragment’s TKE distributions of ²³⁶U to ³⁰⁶122 at low excitation energy just above their fission barrier height using the four-dimensional Langevin model.

It is seen from Figure 4 that the fission modes continuously change from the standard mode to the coexisting standard mode and supershort mode in actinides from ²³⁶U to ²⁵⁹Lr. SHEs clearly have a different mode component from that in actinides. We find the super asymmetric mode, which commonly appears in SHEs, in ²⁷⁴Hs, while the super asymmetric components in the fission yield of ²⁷⁴Hs are too small to see in Figure 2. The other fission modes in SHEs seem to be in common with those in actinides. We also find that the dominant mode gradually changes from the super short to super asymmetric from ²⁷⁴Hs to ²⁹²Fl.

In Figure 5, we display the quadrupole moments Q₂₀ to elucidate which nuclear shell structure affects nuclear fissions in actinides and SHEs.

FIGURE 5

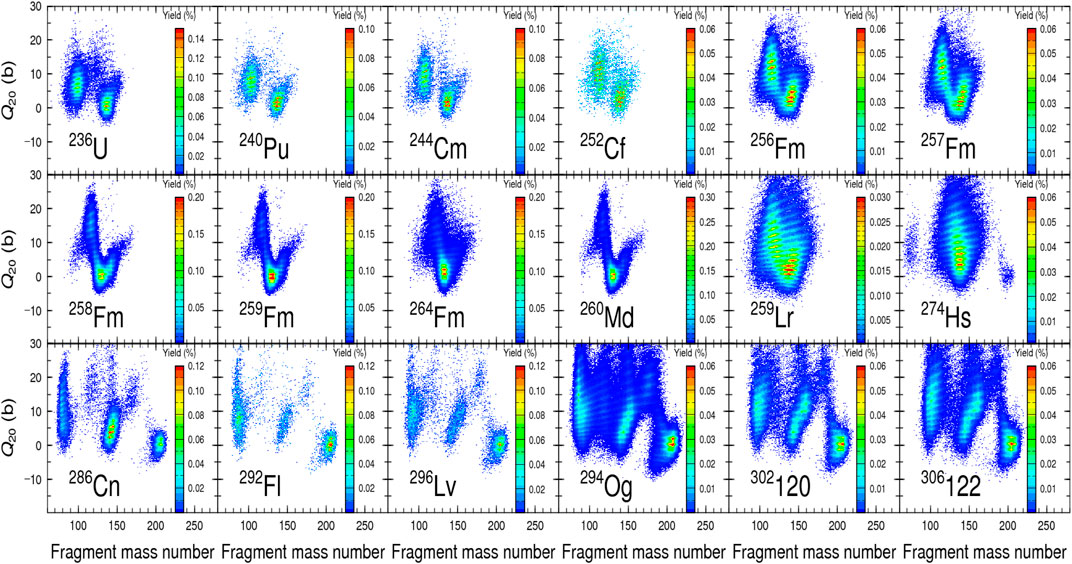
FIGURE 5. Quadrupole moment (Q₂₀) distributions of ²³⁶U to ³⁰⁶122 at low excitation energy just above their fission barrier height using the four-dimensional Langevin model.

We calculate the quadrupole (Q₂₀) and octupole (Q₃₀) momentum of each fragment shape just before scission, as follows. First, we define the volume density as

${\rho }^i\left(\mathbf{r}\right)=A_i\frac{1_{\mathbf{r}\subset V_i}}{V_i},1_{\mathbf{r}\subset V_i}=\left\{\begin{array}{c}1:\mathbf{r}\subset V_i\hfill \\ 0:\mathbf{r}⊈V_i.\hfill \end{array}\right.(5)$

where r is the distance from the center of each fragment, and V_i is the volume of each fragment.

We calculate the Q₂₀ and Q₃₀ using the sharp-cut approximation of the fission fragment just before scission.

$Q_{20}^i=\sqrt{\frac{5}{16\pi }}\int {\rho }^i\left(\mathbf{r}\right)\left(2z^2-x^2-y^2\right)d^{3}r,Q_{30}^i=\sqrt{\frac{7}{16\pi }}\int {\rho }^i\left(\mathbf{r}\right)\left(2z^2-3z\left(x^2+y^2\right)\right)d^{3}r.(6)$

Actinides from ²³⁶U to ²⁵⁹Lr show a similar trend of the Q₂₀. We found that Q₂₀ localize around (A_F, Z_F) = (132, 50) with Q₂₀ = 0, and spreads to (A_F, Z_F) = (140, 52–56) where both of the Q₂₀ and Q₃₀ develop well at the ground state. Such a deformed shape is compatible with a fragment shape at scission. We also find the common structure in Q₂₀ of SHEs from ²⁷⁴Hs to ³⁰⁶122. In SHEs, the double-closed shell of ²⁰⁸Pb becomes dominant as the mass number increases instead of ¹³²Sn, though we can observe both influences on Q₂₀. In the nuclear fission of SHEs, spherical fragments with Q₂₀ = 0 appear at A_F ≃ 208.

In the same manner, as Figures 2, 4, 5, the octupole moment Q₃₀ of major actinides and SHEs are illustrated in Figure 6. In contrast to the strongly mass-dependent Q₂₀, the octupole moments Q₃₀ are almost constant as Q₃₀ ≃ 2 b^3/2 for all nuclei picked up in Figure 6. Those Q₃₀ values are consistent with experiments [44] and recent results [45] with time-dependent density functional theory, which describes quantum dynamics well. We also find that the Q₃₀s of ²⁹⁴Og, ³⁰²120, and ³⁰⁶122 become larger than that of Uranium. Such strong octupole deformations in these nuclei result in fission fragments with A_F = 140 to 160. Thus, fission fragment shapes strongly depend on the mass number of a fissioning nucleus.

FIGURE 6

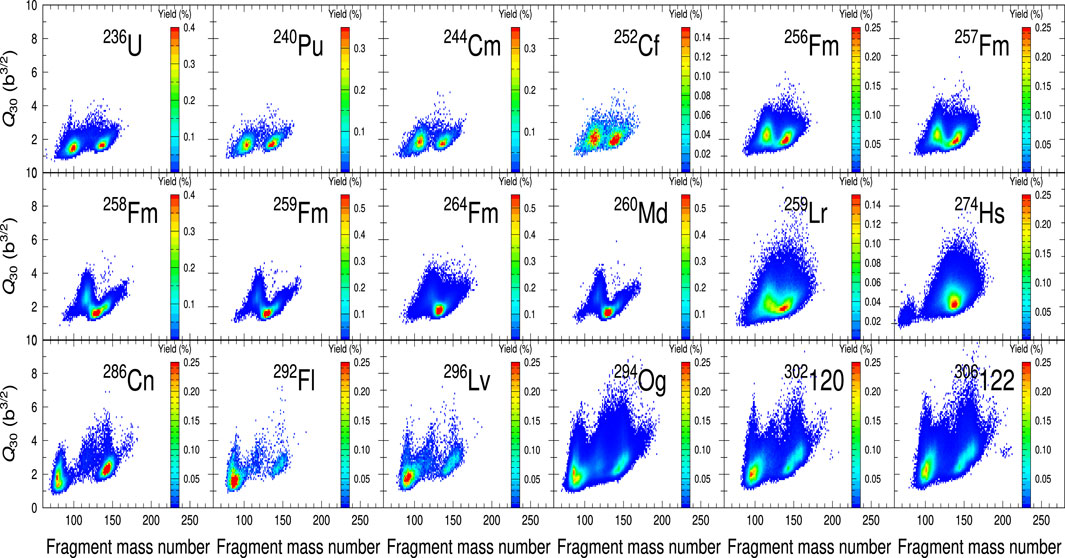
FIGURE 6. Octupole moment (Q₃₀) distributions of ²³⁶U to ³⁰⁶122 at low excitation energy just above their fission barrier height using the four-dimensional Langevin model.

Figure 7 summarizes the Brosa-like fission modes shown in Figure 4. The lower panel shows the fission modes observed in our results of nuclear fissions at E_x = 7 MeV. The upper panel corresponds to a similar plot as the lower panel but for the fission fragments at Ex = 7, 10, and 30 MeV in the case of SHEs. Reference values are taken from the previous works by Brosa (with open squares and open diamonds) [25] and Itkis et al. (with open and filled triangles) [43]. The other symbols are all our results. For the details of those symbols, see the legend in Figure 7.

FIGURE 7

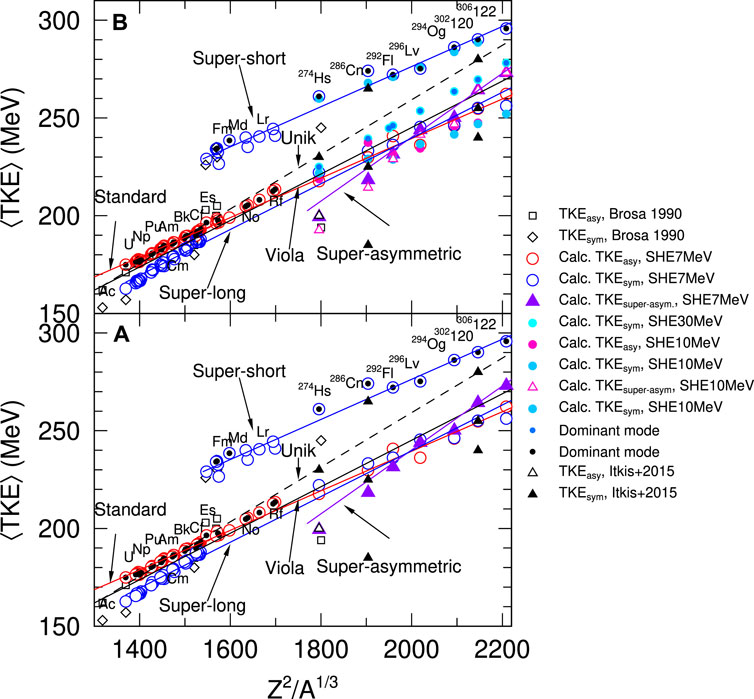
FIGURE 7. The systematics in averaged TKE as a function of Z²/A^1/3.(A) TKE systematics at E_x = 7 MeV. (B) The same plot as (B) but at E_x = 7, 10, and 30 MeV.

We carefully included experimental data of Itkis et al. [43]. For ²⁷⁴Hs case, we took a higher symmetric component of ²⁷⁴Hs, which was produced via ²⁶Mg + ²⁴⁸Cm as a black filled-triangle because the lower symmetric component corresponds to a liquid-drop-like state. The averaged TKE of the asymmetric component of ²⁷⁴Hs corresponds to the maximum yields. In their experiments, the symmetric components are very sparse for the nuclear fission of ²⁸⁶Cn at E_lab = 232 MeV and ³⁰²120 at E_lab = 328 MeV. So we only plot the asymmetric components with three filled triangles for each nucleus. In Itkis’s measurements, the TKE can be fitted with three Gaussian components, i.e., lower, Viola-like (middle), and higher components. Among those mean asymmetric-TKEs, Viola-like and higher components agreed well with our calculations.

We marked each dominant mode in centered black dots. The standard mode distributes along the solid red line in all actinides. The symmetric modes change from superlong to supershort at Es, though these two modes are on each mode’s expected lines. Extending our focus from the actinides to SHEs, we find that actinides and SHEs have common systematics for the standard, the superlong, and supershort modes. In addition to them, the super asymmetric mode merges. In Figures 7A,B, we also investigated the changes in the TKE systematics accompanied by the change in Ex. The systematics for E_x = 7 MeV is almost the same as that for E_x = 10 MeV, though the TKEs become lower at E_x = 10 MeV. At E_x = 30 MeV, all modes except for the symmetric mode suddenly disappear, i.e., we cannot see any asymmetric component in SHEs at E_x = 30 MeV. In order to clarify what happens at E_x = 30 MeV, we plot the fission fragment mass distribution and TKE(A) in Figure 8 for ²⁹⁶Lv as a representative case.

FIGURE 8

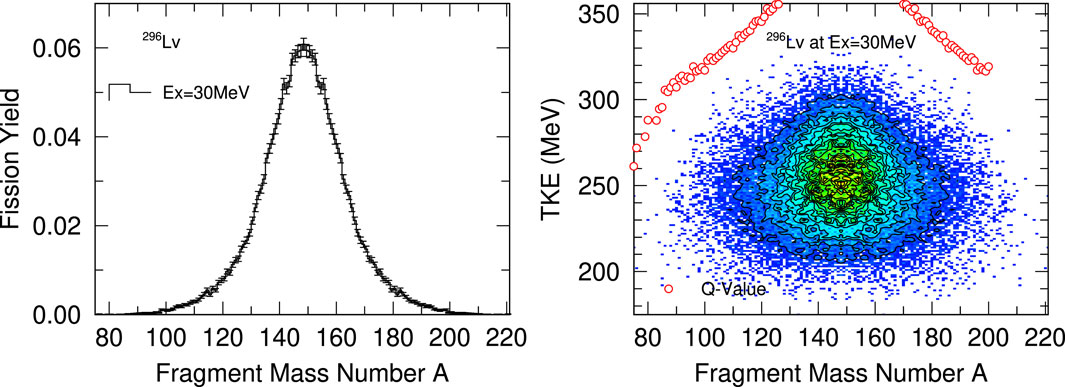
FIGURE 8. TKEs and FFMD of nuclear fission of ²⁹⁶Lv at Ex = 30 MeV. (Right panel) TKE distribution color map calculated by the Langevin model with the Q-values. (Left panel) Fission fragment mass distribution as a function of fission fragment mass number.

As shown in Figure 7B, we found that the asymmetric mode does not appear in the TKE systematics at E_x = 30 MeV. To understand it, we plot the FFMD and the TKE distributions in the case of ²⁹⁶Lv in Figure 8. Compared to the FFMDs at low E_x shown in Figure 2, FFMD at the high E_x of Figure 8 spreads over a broader mass range. The TKEs of these fission fragments show that the high excitation energy washes out the shell structure, and the system becomes a liquid-drop-like state.

At the end of this section, we focus on the influence of the shell effects on nuclear fission in SHEs. Figure 9 is the shell energy color map on the nuclear chart with the positions of sub and main peaks of FFMDs. The shell energy was taken from the KTUY mass formula [46] consisting of a gross term, an even-odd term, and a shell term. Their shell energy was obtained with spherical single-particle potentials. They treated deformed nuclei as a superposition of spherical nuclei. The resulting KTUY mass formula agrees with experimental masses very well within about 500 keV. In the case of Z = 120, these isotopes have four peak structures in the FFMDs, as seen in Figure 3. In Figure 9, pairs of filled triangles correspond to the main peaks, while those of open triangles are the sub-peak positions. We plot solid lines based on the assumption that the ratio of proton to neutron density is unchanged (UCD). In SHEs, the double shell closure of ²⁰⁸Pb governs nuclear fissions instead of ¹³²Sn in actinides, as discussed in Figure 5. The UCD lines of two Z = 120 isotopes, ^302,308120, come very close to ²⁰⁸Pb. The shell correction energy there is much smaller than in the other regions. It makes fission fragments there very stable. However, this situation drastically changes when the isotopes become more neutron-rich. In ^322–338120, the positions of the main and sub-peaks approach each other. That is because the UCD lines of those nuclei are no longer close to ²⁰⁸Pb.

FIGURE 9

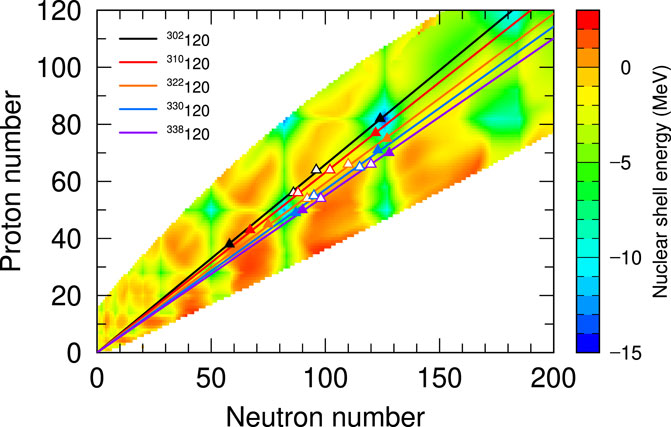
FIGURE 9. Peak positions in the nuclear fission of five isotopes with Z = 120 on the shell energy color map calculated by Koura et al.

4 Summary

Nuclear fission is still a challenging research topic even today. The number of prompt neutrons emitted from fission fragments is essential information to operate nuclear reactors and develop advanced reactors. To improve the prediction of prompt neutrons [47], we need an integrated understanding of the fission phenomenon based on nuclear physics. Especially, precise prediction of the TKE is crucial because it turns into the excitation energy of a fission fragment that emits prompt neutrons. In this paper, we systematically simulated nuclear fissions in actinides and SHEs. The fission model we used here is the four-dimensional Langevin model. Our previous works found that it can reproduce quite well representative characteristics of nuclear fission in actinides.

The main focus of the current paper is demonstrating the results of a systematic survey of fission properties from actinides to SHEs. We showed the fission yield FPY(A), the total kinetic energy TKE(A), the quadrupole moment Q₂₀(A), and the octupole moment Q₃₀(A) of each fragment produced by nuclear fission of ²³⁶U to ³⁰⁶122 as a compound system.

As a result, our Q₃₀ values are consistent with those of the microscopic model and previous experiments. We also found that the double closed shell of ¹³²Sn and deformed shell at Z = 54 affect the nuclear fission of actinides and SHEs, though those impacts become weaker in SHEs. Instead, the double-closed shell of ²⁰⁸Pb is dominant in SHEs. Based on the above surveys, we derived two systematics in the averaged peak position of fission yield and the averaged TKE of each component of the Brosa-like model. This two systematics help evaluate the vital fission fragments and interpolate/extrapolate the averaged TKE. For the fission recycling in the r-process, we need to elucidate the fission properties of more neutron-rich SHEs than the nuclei we picked up in this paper. We have started expanding the survey for those nuclei and will report it elsewhere.

Data availability statement

The raw data supporting the conclusion of this article will be made available by the authors, without undue reservation.

Author contributions

CI, FI, and SC contributed to the conception and design of the study. CI, FI, and SC designed the procedure of the study. CI and SC wrote the first draft of the manuscript. All authors contributed to code development, performing calculations, making figures, manuscript revision, reading, and approving the submitted version.

Funding

The authors declare that this study has been supported by Grants-in-Aid for Scientific Research (C) No. 18K03642 and the Grands-in-Aid for Scientific Research (B) No. 21H01856 from Japan Society for the Promotion of Science. The subject theme of the adopted project is improving the Langevin model and understanding fission mechanisms.

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

1. Andreyev AN, Nishio K, Schmidt K-H. Nuclear fission: A review of experimental advances and phenomenology. Rep Prog Phys (2017) 81(1):016301. doi:10.1088/1361-6633/aa82eb

PubMed Abstract | CrossRef Full Text | Google Scholar

2. Schunck N, Regnier D. Theory of nuclear fission. Prog Part Nucl Phys (2022) 125:103963. doi:10.1016/j.ppnp.2022.103963

CrossRef Full Text | Google Scholar

3. Bender M, Bernard R, Bertsch G, Chiba S, Dobaczewski J, Dubray N, et al. Future of nuclear fission theory. J Phys G: Nucl Part Phys (2020) 47(11):113002. doi:10.1088/1361-6471/abab4f

CrossRef Full Text | Google Scholar

4. Margaret Burbidge E, Burbidge GR, Fowler WA, Hoyle F. Synthesis of the elements in stars. Rev Mod Phys (1957) 29:547–650. doi:10.1103/revmodphys.29.547

CrossRef Full Text | Google Scholar

5. Abbott BP, Abbott R, Abbott TD, Acernese F, Ackley K, Adams C, et al. GW170817: Observation of gravitational waves from a binary neutron star inspiral. Phys Rev Lett (2017) 119:161101. doi:10.1103/PhysRevLett.119.161101

PubMed Abstract | CrossRef Full Text | Google Scholar

6. Beun J, McLaughlin GC, Surman R, Hix WR. Fission cycling in a supernovarprocess. Phys Rev C (2008) 77:035804. doi:10.1103/physrevc.77.035804

CrossRef Full Text | Google Scholar

7. Goriely S, Sida J-L, Lemaitre J-F, Panebianco S, Dubray N, Hilaire S, et al. New fission fragment distributions andr-process origin of the rare-earth elements. Phys Rev Lett (2013) 111:242502. doi:10.1103/physrevlett.111.242502

PubMed Abstract | CrossRef Full Text | Google Scholar

8. Giuliani SA, Martinez-Pinedo G, Wu M-R, RobledoLuis M. Fission and the r-process nucleosynthesis of translead nuclei in neutron star mergers. Phys Rev.C (2020) 102:045804. doi:10.1103/physrevc.102.045804

CrossRef Full Text | Google Scholar

9. Schunck N, Robledo LM. Microscopic theory of nuclear fission: A review. Rep Prog Phys (2016) 79:116301. doi:10.1088/0034-4885/79/11/116301

PubMed Abstract | CrossRef Full Text | Google Scholar

10. Langevin P. Sur la theorie du mouvement Brownien. C.R Acad Sci (Paris) (1908) 146530.

Google Scholar

11. Davies KTR, Sierk AT, Nix JR. Effect of viscosity on the dynamics of fission. Phys Rev C (1976) 13:2385–403. doi:10.1103/physrevc.13.2385

CrossRef Full Text | Google Scholar

12. Wada T, Abe Y, Carjan N. One-body dissipation in agreement with prescission neutrons and fragment kinetic energies. Phys Rev Lett (1993) 70:3538–41. doi:10.1103/physrevlett.70.3538

PubMed Abstract | CrossRef Full Text | Google Scholar

13. Fröbrich P, Gontchar II. Langevin description of fusion deep-inelastic collisions and heavy-ion-induced fission. Phys Rep (1998) 282:131–237. doi:10.1016/s0370-1573(97)00042-2

CrossRef Full Text | Google Scholar

14. Pomorski K, Bartel J, Richert J, Dietrich K. Evaporation of light particles from a hot, deformed and rotating nucleus. Nucl Phys A (1996) 605:87–119. doi:10.1016/0375-9474(96)00180-7

CrossRef Full Text | Google Scholar

15. Asano T, Wada T, Ohta M, Ichikawa T, Yamaji S, Nakahara H. Dynamical calculation of multi-modal nuclear fission of fermium nuclei. J Nucl Radiochem Sci (2004) 5(1):1–5. doi:10.14494/jnrs2000.5.1

CrossRef Full Text | Google Scholar

16. Adeev GD, Karpov AV, Nadtochy PN, Vanin DV. Multidimensional stochastic approach to the fission dynamics of excited nuclei. Fiz Elem Chastits Yadra[phys Part Nucl (2005) 3636:732378.

Google Scholar

17. Aritomo Y, Chiba S, Ivanyuk FA. Fission dynamics at low excitation energy. Phys Rev C (2014) 90:054609. doi:10.1103/physrevc.90.054609

CrossRef Full Text | Google Scholar

18. Usang MD, Ivanyuk FA, Ishizuka C, Chiba S. Analysis of the total kinetic energy of fission fragments with the Langevin equation. Phys Rev C (2017) 96:064617. doi:10.1103/physrevc.96.064617

CrossRef Full Text | Google Scholar

19. Sierk AJ. Langevin model of low-energy fission. Phys Rev C (2017) 96:034603. doi:10.1103/physrevc.96.034603

CrossRef Full Text | Google Scholar

20. Usang MD, Ivanyuk FA, Ishizuka C, Chiba S. Correlated transitions in TKE and mass distributions of fission fragments described by 4-D Langevin equation, Vol. 9. Springer Nature (2019).

Google Scholar

21. Kostryukov PV, Dobrowolski A, Nerlo-Pomorska B, Warda M, Xiao ZG, Chen YJ, et al. Potential energy surfaces and fission fragment mass yields of even-even superheavy nuclei. Chin Phys C (2021) 45:124108. doi:10.1088/1674-1137/ac29a3

CrossRef Full Text | Google Scholar

22. Ishizuka C, Usang MD, Ivanyuk FA, Maruhn JA, Nishio K, Chiba S. Four-dimensional Langevin approach to low-energy nuclear fission of ²³⁶U. Phys Rev C (2017) 96:064616. doi:10.1103/physrevc.96.064616

CrossRef Full Text | Google Scholar

23. Ishizuka C, Zhang X, Usang MD, Ivanyuk FA, Chiba S. Effect of the doubly magic shell closures in ¹³²Sn and ²⁰⁸Pb on the mass distributions of fission fragments of superheavy nuclei. Phys Rev C (2020) 101:011601. doi:10.1103/physrevc.101.011601

CrossRef Full Text | Google Scholar

24. Ivanyuk FA, Radionov SV, Ishizuka C, Chiba S. The Langevin approach for fission of heavy and super-heavy nuclei. submitted Acta Physica Pol B (2022).

Google Scholar

25. Ulrich B, Grossmann S, Mueller A. Nuclear scission. Nucl scission. Phys Rep (1990) 197(4):167–262. doi:10.1016/0370-1573(90)90114-h

CrossRef Full Text | Google Scholar

26. Ivanyuk FA, Ishizuka C, Usang MD, Chiba S. Temperature dependence of shell corrections. Phys Rev C (2018) 97:054331. doi:10.1103/physrevc.97.054331

CrossRef Full Text | Google Scholar

27. Pashkevich VV. On the asymmetric deformation of fissioning nuclei. Nucl Phys A (1971) 169:275–93. doi:10.1016/0375-9474(71)90884-0

CrossRef Full Text | Google Scholar

28. Werner FG, Wheeler JA. Superheavy nuclei. Phys Rev (1958) 109:126–44. doi:10.1103/physrev.109.126

CrossRef Full Text | Google Scholar

29. Blocki J, Boneh Y, Nix JR, Randrup J, Robel M, Sierk AJ, et al. One-body dissipation and the super-viscidity of nuclei. Ann Phys (1978) 113(2):330–86. doi:10.1016/0003-4916(78)90208-7

CrossRef Full Text | Google Scholar

30. Sierk AJ, Rayford Nix J. Fission in a wall-and-window one-body-dissipation model. Phys Rev C (1980) 21:982–7. doi:10.1103/physrevc.21.982

CrossRef Full Text | Google Scholar

31. Werner E, Wio HS, Hofmann H, Pomorski K. Nuclear dissipation with residual interactions studied by means of the Mori formalism. Z Phys A - Atoms Nuclei (1981) 299:231–9. doi:10.1007/bf01443940

CrossRef Full Text | Google Scholar

32. Hofmann H, Kiderlen D. A self-consistent treatment of damped motion for stable and unstable collective modes. Int J Mod Phys E (1998) 7:243–74. doi:10.1142/s0218301398000105

CrossRef Full Text | Google Scholar

33. Hofmann H, Ivanyuk FA, Yamaji S, Rummel C. Nuclear fission: The ”onset of dissipation” from a microscopic point of view. Phys Rev C (2011) 64:054316. doi:10.1103/physrevc.64.054316

CrossRef Full Text | Google Scholar

34. Katakura J. JENDL FP decay data file 2011 and fission yields data file 2011 (JAEA-Data/Code 2011-025). Tokai-mura, Japan (2012). 1–81.

Google Scholar

35. Hulet EK, Wild JF, Dougan RJ, Lougheed RW, Landrum JH, Dougan AD, et al. Spontaneous fision properties of ²⁵⁸Fm, ²⁵⁹Md, ²⁶⁰Md, ²⁵⁸No, and ²⁶⁰[104]: Bimodal fission. Phys Rev.C (1989) 40(2):770–84. doi:10.1103/physrevc.40.770

PubMed Abstract | CrossRef Full Text | Google Scholar

36. Hamilton TM, Gregorich KE, Lee DM, Czerwinski KR, Hannink NJ, Kacher CD, et al. Spontaneous fission properties of ²⁵⁹Lr₁₀₃. Phys Rev.C (1992) 46:1873–9. doi:10.1103/physrevc.46.1873

CrossRef Full Text | Google Scholar

37. Lane MR, Gregorich KE, Lee DM, Mohar MF, Hsu M, Kacher CD, et al. Spontaneous fision properties of ²⁶²Rf₁₀₄. Phys Rev.C (1996) 53:2893–9. doi:10.1103/physrevc.53.2893

CrossRef Full Text | Google Scholar

38. Albertsson M, Carlson BG, Dössing T, Moller P, Randrup J, Aberg S. Super-short fission mode in fermium isotopes. Phys Rev C (2021) 104:064616. doi:10.1103/physrevc.104.064616

CrossRef Full Text | Google Scholar

39. Regnier D, Dubray N, Schunk N. From asymmetric to symmetric fission in the fermium isotopes within the time-dependent generator-coordinate-method formalism. Phys Rev C (2019) 99:024611. doi:10.1103/physrevc.99.024611

CrossRef Full Text | Google Scholar

40. Miyamoto Y, Aritomo Y, Tanaka S, Hirose K, Nishio K. Origin of the dramatic change of fission mode in fermium isotopes investigated using Langevin equations. Phys Rev C (2019) 99:051601. doi:10.1103/physrevc.99.051601

CrossRef Full Text | Google Scholar

41. Matheson Z, Jiuliani SA, Nazarewicz W, Sadhukhan J, Schunk N. Cluster radioactivity of ²⁹⁴Qg₁₁₈. Phys Rev C (2019) 99:041304. (R).

Google Scholar

42. Itkis IM, Kozulin EM, Itkis MG, Knyazheva GN, Bogachev AA, Chernysheva EV, et al. Fission and quasifission modes in heavy-ion-induced reactions leading to the formation of Hs*. Phys Rev C (2011) 83:064613. doi:10.1103/physrevc.83.064613

CrossRef Full Text | Google Scholar

43. Itkis MG, Vardaci E, Itkis IM, Knyazheva GN, Kozulin EM. Fusion and fission of heavy and superheavy nuclei (experiment). Nucl Phys A (2015) 944:204–37. Special Issue on Superheavy Elements. doi:10.1016/j.nuclphysa.2015.09.007

CrossRef Full Text | Google Scholar

44. Yokoyama R, Ideguchi E, Simpson GS, Tanaka M, Nishimura S, Doornenbal P, et al. Beta-gamma spectroscopy of the neutron-rich ¹⁵⁰Ba. Prog Theor Exp Phys (2018) 2018(4):04. doi:10.1093/ptep/pty037

CrossRef Full Text | Google Scholar

45. Scamps G, Simenel C. Impact of pear-shaped fission fragments on mass-asymmetric fission in actinides, Vol. 564. Springer Nature (2018).

Google Scholar

46. Koura H, Tachibana T, Uno M, Yamada M. Nuclidic mass formula on a spherical basis with an improved even-odd term. Prog Theor Phys (2005) 113(2):305–25. doi:10.1143/ptp.113.305

CrossRef Full Text | Google Scholar

47. Capote R, Chen YJ, Hambsch FJ, Kornilov N, Lestone J, Litaize O, et al. Prompt fission neutron spectra of actinides. Nucl Data SheetsSpecial Issue Nucl React Data (2016) 131:1–106. doi:10.1016/j.nds.2015.12.002

CrossRef Full Text | Google Scholar