Quantitative and qualitative analyses of the mKdV equation and modeling nonlinear waves in plasma

1 Introduction

The propagation of nonlinear structures in electron–positron (EP) plasmas is quite different from that in ordinary electron–ion (EI) plasmas because of the same mass of both the species. In a number of interesting physical situations, EP plasmas have been observed and investigated. The examples include pulsar environments, supernovae, active galactic nuclei, and cluster explosions [1–4]. Many astrophysical plasmas are an admixture of mainly electrons and positrons having a small fraction of ions, whereas the converse is true for the laboratory plasmas where the positron concentration is very low.

Many approaches have been proposed to create laboratory EP plasmas over the past few decades [5–7]. In initial experiments, relativistic positrons from radioactive neon gas were trapped directly into a magnetic mirror (MM) [5, 6]. Tsytovich and Wharton [7] suggested trapping positrons in an MM from a LINAC source. Later on, Boehmer [8] employed cyclotron heating to trap moderated positrons from a radioactive source and to heat the trapped positrons to relativistic energies. The most successful experimental approach, to obtaining positron plasmas, however, has turned out to be the scattering from a buffer gas into a Penning trap. In this case, the positron density is large enough to study the collective modes in plasmas [9]. It is important to note that pair annihilation can take place in EP plasmas. It is, therefore, a prerequisite that, for the study of collective modes in such plasma, the annihilation time scale ought to be much longer than the time scale for plasma effects, which is typically the inverse of the plasma frequency [9]. It is quite common in astrophysical and laboratory plasmas to have ions in addition to electrons and positrons, and, therefore, it is important to understand the linear and nonlinear behavior in electron–positron–ion (EPI) plasmas. Many studies have been carried out in the past few decades to investigate the linear and nonlinear wave propagation in EPI plasmas that highlight the importance of the inclusion of positrons in the system [10–18].

The observations of geophysical and laboratory plasmas have indicated the presence of two populations of electrons, namely, cold and hot electrons. Examples include hot cathode discharge plasmas, solar wind at about 1 AU, turbulent plasma for thermonuclear interest, and strongly interacting beam plasma systems [19]. In collisionless plasmas of space, Earth’s bow shock [20], and in the up/downstream of interplanetary shocks [21], two-temperature plasmas have been observed. Moreover, this type of plasmas has been observed in heliospheric termination shock [22], planetary magnetospheres [23], and space plasmas [24]. Additionally, different missions such as Polar [25], Geotail [26], FAST [27], and S3 − 3 [28] observed and discovered the two populations of electrons in the auroral zone and magnetosphere. The investigation of the linear ion acoustic wave (IAW) in plasma of two population electrons has a significant impact on its characteristics [29]. Many authors studied the ion acoustic solitons in plasma of two population electrons and reported many interesting facts about them [30–32].

No well-established methods have been developed, so far, that can solve all nonlinear differential equations arising in mathematics, physics, engineering, and biological sciences. Concerted efforts have thus been made to develop various analytical techniques to study nonlinear phenomena. Some of these methods include the homogeneous balance method [33–35], hyperbolic tangent expansion method [36–38], trial function method [39, 40], nonlinear transformation method [41, 42], and sine–cosine method [43]. Although, soliton and shock solutions have been obtained, periodic solutions could not be found by these methods. Porubov et al. [44, 45] obtained some exact periodic solutions for some nonlinear wave equations using the Weierstrass elliptic function which involved complicated deductions. Fu et al. [46] proposed the Jacobi elliptic function expansion method (JEFEM) and applied it to some nonlinear wave problems. In addition to shock and solitary wave solutions, various periodic solutions, based on the Jacobi elliptic sine function, were also found [46]. To discuss all three possible waveforms (for traveling wave solution), we use JEFEM to present all possible analytic solutions of the mKdVE. These include both bounded and unbounded periodic solutions. In recent years, theory of the dynamical system has generated a lot of interest in the study of nonlinear equations arising in plasma physics and fluid mechanics [47–56].

Saha and Chatterjee [57] used bifurcation of the phase portrait to analyze the qualitative behavior of the dust ion acoustic traveling wave solution of the modified Kadomtsev–Petviashvili equation (mKPE). The authors showed the existence of periodic, solitary, and kink wave solutions using the theory of the dynamical system by investigating the nature of the critical points. Analytical traveling wave solution of the mKPE is also obtained, and the two approaches are shown to be consistent. This work [57] is a generalization of the work presented by Samanta et al [52] who identified two solutions instead of three, using bifurcation analysis. Tamang et al; [53] used the planar dynamical system approach to present nonlinear homoclinic and nonlinear periodic trajectories of the modified mKdVE and generalized Gardner equation (GGE). A few articles, in which Asit Saha [52, 53, 57] is one of the authors, bifurcation has been used to identify the wave profiles and their properties depending on the parameter values. It may be noted that the bifurcation of the wave structure, as mentioned in these articles, should not be confused with the bifurcation diagram. We know that the qualitative behavior of the phase portraits such as periodic, solitary, or kink depends on the characterizing parameters of the problem. The phase portraits are drawn for some discrete values of the parameters without any prior knowledge of their behaviors. The qualitative change occurring in the phase diagrams is observed visually depending on the closed, homoclinic, or heteroclinic orbits.

Let us first recall the procedure adopted in these studies. A model nonlinear partial differential equation (PDE) is initially transformed into a nonlinear ordinary differential equation (ODE) using a traveling wave solution. The ODE is then formulated in terms of the corresponding dynamical system, and the phase plane diagram is drawn near the critical points using linear stability analysis. The solution behavior is based on the nature of the critical points, and the wave behavior is predicted from the phase diagram. For example, the center in the phase space corresponds to the closed orbit representing the periodic wave, the homoclinic orbit representing the solitary wave, and heteroclinic orbits corresponding to the kink (or shock) wave front. The closed-domain traveling wave solution generally corresponds to these waveforms. The stability of the wave solution is determined from the critical point and the Jacobian matrix. The phase diagram and the corresponding wave nature are determined for specifically choosing the parameters.

The aforementioned analysis raises a few questions for further thinking: a) Can we choose a set of premeditated parameters which gives rise to the wave structure of our choice? b) Can we divide the whole range of a parameter into sub-intervals with different topological behaviors (if so)? Can we know the behavior of the solution for some choice of the parameters without actually experimenting it through the phase plane diagram? Can we guess the behavior for a continuous spectrum of the parameter of interest instead of its discrete values? The answer to these questions lies in stability and bifurcation theory, which, to our understanding, has not been given due importance. The issues raised previously are addressed in this work besides finding the exact analytical solution. After taking up the analytical solution and the solution behavior of mKdVE, we show that the two approaches lead to same conclusions and corroborate each other. We are lucky to find the exact solution here; however, in more complex problems involving higher-order non-linearities, where analytical solution is not possible, the qualitative solution gives us all the physics we need to know.

In the present paper, no heteroclinic orbit appears, and, therefore, no shock solution exists for all possible parameters of the mKdVE. The existence of periodic (bounded and unbounded) and solitary wave solutions is found both mathematically and qualitatively. The bifurcation points are identified at which the topological behavior of the wave form changes, that is, the switch of the dynamical behavior from periodic to solitary waves or the other way round. A complete range of the important parameters like α, β, δ, γ, μ, and ν have been specified from the bifurcation diagram predicting the behavior in advance without any fear of wrong conclusion or incomplete conclusion (leaving some values of the parameters unattended). In passing, we note that the homoclinic behavior mentioned in [57] is actually from 0.8 < q < 1.0, instead of, q $>-1$. The important conclusions and observations highlighting important physical features are discussed in the concluding section. The analysis presented here will be useful to explore the physical behaviors in the problems with greater complexities in some future works where the analytical solution is not a possibility.

The paper is organized as follows: in Section 2 and Section 3, we present a set of model equations and derive the mKdVE using the reductive perturbation technique (RPT) [58–60]. In Section 4, we present the analytical solutions of the mKdVE using the JEFEM. All possible analytic solutions including bounded periodic solutions, solitary solutions, and unbounded periodic solutions are found. Section 5 explores the qualitative behavior of the mKdVE using the planar theory of the dynamical system. In Section 5, we present the results and discussion of both the quantitative and qualitative analyses using the plasma parameters that are consistent with the satellite observations of space plasmas. The main findings of the paper are recapitulated in Section 7.

2 Basic set of equations

We consider multicomponent plasma comprising hot and cold electrons, warm adiabatic ions, and isothermal positrons. In order to study the nonlinear behavior of the IAWs, we employ the following set of normalized fluid equations [32]:

${\partial }_t{n}_i+{\partial }_x\left(n_i{u}_i\right)=0,(1)$

${\partial }_t{u}_i+u_i{\partial }_x{u}_i=-{\partial }_x\varphi -\frac{5}{3}\delta n_i^{-1/3}{\partial }_x{n}_i,(2)$

${\partial }_x^2\varphi =-\rho =n_e-\left(1-\alpha \right)n_i-n_p,(3)$

where n_e = n_h + n_c.

The cold and hot populations of electrons and positrons are assumed to be inertialess on the ion time scale and assumed to follow the Maxwell–Boltzmann distribution function and are given as [32]

$n_p=\exp \left(-\gamma \varphi \right),(4)$

$n_c=\mu \exp \left(\frac{\varphi }{\mu +\nu \beta }\right),(5)$

$n_h=\nu \exp \left(\frac{\beta \varphi }{\mu +\nu \beta }\right),(6)$

and

$n_e=1+\varphi +\frac{\left(\mu +\nu {\beta }^2\right)}{2{\left(\mu +\nu \beta \right)}^2}{\varphi }^2+\frac{\left(\mu +\nu {\beta }^3\right)}{6{\left(\mu +\nu \beta \right)}^3}{\varphi }^3+\cdots .(7)$

In the aforementioned equations, n_i is the density of ions normalized by n_i0; u_i is the fluid velocity of the ion species normalized by ion acoustic speed C_i; n_c0, n_h0, and n_i0 are the equilibrium densities of two electron populations and the ion component, respectively; ϕ is the electrostatic potential normalized by thermal potential T_eff/e; α is the equilibrium density ratio of positron to electron species; ν is the equilibrium density ratio of hot electrons to the total electron number density; μ is the equilibrium density ratio of cold electrons to the total electron number density; β is the ratio of cold to hot electron temperatures; and δ is the ratio of ion to electron effective temperature. In the aforementioned equations, time and space coordinates have been normalized by the inverse of the ion–plasma frequency ${\omega }_{pi}^{-1}$ and Debye length λ_D, respectively, whereas electron densities n_h and n_c are normalized by n_e0. Here, β = T_c/T_h, α = n_po/n_eo, μ = n_co/n_eo, ν = n_ho/n_eo, δ = T_i/T_eff, γ = T_eff/T_p, T_eff = T_hT_h/(μT_h + νT_c), $c_i={(T_{\mathit{eff}}/m_i)}^{1/2}$, ${\omega }_{pi}^{-1}={(4\pi n_{eo}{e}^2/m_i)}^{-1/2}$, and ${\lambda }_D={(T_{\mathit{eff}}/\left(4\pi n_{eo}{e}^2\right))}^{1/2}$.

3 Derivation of the mKdVE

Before deriving the mKdV equation, we remark that in some cases, it so happens that the nonlinear term in the KdV equation becomes identically zero because of the value of plasma parameters. As a consequence, no solitary wave is possible. This necessitates to consider the next-order (higher-order) non-linearity to balance dispersion in the governing equation leading to the mKdV equation. Moreover, it is worthwhile to explore the effect of cubic non-linearity on the formation of nonlinear structures, which becomes possible with the mKdV equation. For that, the following stretched coordinates ξ and τ are introduced [32]

$\left\{\begin{array}{c}\hfill \xi =\epsilon \left(x-\lambda t\right),\hfill \\ \tau ={\epsilon }^{3}t,\hfill \end{array}\right.,(8)$

where λ indicates the phase velocity and ɛ is a small and real perturbation parameter. We next expand the physical variables in Eqs. (4)–(7) as follows:

$\left\{\begin{array}{c}\hfill n_i=1+ϵn_{i1}+{ϵ}^2{n}_{i2}+{ϵ}^3{n}_{i3}+\cdots ,\hfill \\ u_i=ϵu_{i1}+{ϵ}^2{u}_{i2}+{ϵ}^3{u}_{i3}+\cdots ,\hfill \\ \varphi =ϵ{\varphi }_1+{ϵ}^2{\varphi }_2+{ϵ}^3{\varphi }_3+\cdots ,\hfill \\ \rho =ϵ{\rho }_1+{ϵ}^2{\rho }_2+{ϵ}^3{\rho }_3+\cdots .\hfill \end{array}\right.(9)$

Substituting Eqs (8)–(9) into Eqs (1)–(3) and equating the terms with same power of ϵ will yield the following equations in the lowest order, that is, O (ϵ²)

$\begin{array}{ll}\hfill u_{i1}& =\lambda n_{i1}=\frac{3\lambda }{\left(3{\lambda }^2-5\sigma \right)}{\varphi }_1,\hfill \\ \hfill \lambda & =\sqrt{\frac{\left(1-\alpha \right)}{\left(1+\alpha \gamma \right)}+\frac{5\delta }{3}}.\hfill \end{array}(10)$

For the next higher-order equations, that is, O (ϵ³), and after substituting the values of n_i1, u_i1, and λ, we obtain

$u_{i2}=\frac{\left(81{\lambda }^3-18\lambda \right)}{2{\tilde{\lambda }}^2}{\varphi }_1^2-\frac{15\delta }{2{\tilde{\lambda }}^3}{\varphi }_1^2+\frac{3}{\tilde{\lambda }}{\varphi }_2,(11)$

$n_{i2}=\frac{\left(81{\lambda }^2-15\delta \right)}{2{\tilde{\lambda }}^3}{\varphi }_1^2+\frac{3}{\tilde{\lambda }}{\varphi }_2,(12)$

$\alpha {\gamma }^2-\frac{\left(\mu +\nu {\beta }^2\right)}{{\left(\mu +\nu \beta \right)}^2}+\frac{81\left(1-\alpha \right){\lambda }^2}{{\tilde{\lambda }}^3}-\frac{15\delta \left(1-\alpha \right)}{{\tilde{\lambda }}^3}=0,(13)$

where $\tilde{\lambda }=(3{\lambda }^2-5\delta )$.

To the next higher-order equation of ϵ, that is, O (ϵ⁴), we obtain

${\partial }_{\tau }{n}_{i1}-\lambda {\partial }_{\xi }{n}_{i3}+{\partial }_{\xi }\left(u_{i2}{n}_{i1}\right)+{\partial }_{\xi }\left(n_{i2}{u}_{i1}\right)+{\partial }_{\xi }{u}_{i3}=0,(14)$

$\begin{array}{ll}\hfill & {\partial }_{\tau }{u}_{i1}-\lambda {\partial }_{\xi }{u}_{i3}+u_{i1}{\partial }_{\xi }{u}_{i2}+u_{i2}{\partial }_{\xi }{u}_{i1}+{\partial }_{\xi }{\varphi }_3-\frac{5}{9}\delta n_{i2}{\partial }_{\xi }{n}_{i1}+\frac{5}{3}\delta {\partial }_{\xi }{n}_{i3}-\frac{5}{9}\delta n_{i1}{\partial }_{\xi }{n}_{i2}+\frac{10}{27}\delta n_{i1}^2{\partial }_{\xi }{n}_{i1}=0,\hfill \end{array}(15)$

and

$\begin{array}{ll}\hfill & {\partial }_{\xi }^2{\varphi }_1+\left(1-\alpha \right)n_{i3}-\alpha \gamma {\varphi }_3-\frac{1}{6}\alpha {\gamma }^3{\varphi }_1^3+\alpha {\gamma }^2{\varphi }_1{\varphi }_2-{\varphi }_3-\frac{\left(\mu +\nu {\beta }^2\right){\varphi }_1{\varphi }_2}{{\left(\mu +\nu \beta \right)}^2}-\frac{1}{6}\frac{\left(\mu +\nu {\beta }^3\right){\varphi }_1^3}{{\left(\mu +\nu \beta \right)}^3}=0.\hfill \end{array}(16)$

Differentiating Eqs (11), (12) and using Eq. (13), the following mKdVE is obtained:

${\partial }_{\tau }{\varphi }_1+A{\varphi }_1^2{\partial }_{\xi }{\varphi }_1+B{\partial }_{\xi }^3{\varphi }_1=0,(17)$

with

$\begin{array}{ll}\hfill A& =\frac{{\left(3{\lambda }^2-5\delta \right)}^2}{18\left(1-\alpha \right)\lambda }\left[\frac{6561\left(1-\alpha \right){\lambda }^4}{2{\tilde{\lambda }}^5}-\frac{2565\left(1-\alpha \right)\delta {\lambda }^2}{2{\tilde{\lambda }}^5}-\frac{486\left(1-\alpha \right){\lambda }^2}{{\tilde{\lambda }}^4}+\frac{225{\delta }^2\left(1-\alpha \right)}{2{\tilde{\lambda }}^5}+\frac{30\left(1-\alpha \right)\delta }{{\tilde{\lambda }}^4}-\frac{\alpha {\gamma }^3}{2}-\frac{1}{2}\frac{\left(\mu +\nu {\beta }^3\right)}{{\left(\mu +\nu \beta \right)}^3}]\right]\hfill \end{array}(18)$

and

$B=\frac{{\left(3{\lambda }^2-5\delta \right)}^2}{18\left(1-\alpha \right)\lambda }.(19)$

4 Solution to the mKdVE via JEFEM

Considering the mKdV Eq. (17), we obtain

${\partial }_{\tau }{\varphi }_1+A{\varphi }_1^2{\partial }_{\xi }{\varphi }_1+B{\partial }_{\xi }^3{\varphi }_1=0,(20)$

where ${\varphi }_1\equiv {\varphi }_1\left(\xi ,\tau \right)$.

Substituting the traveling wave solution ϕ₁ = ψ(η), where η = k (ξ − uτ), into Eq. (20), the following Duffing equation is obtained [61–66]:

$\ddot{\psi }+p\psi +q{\psi }^3=0,(21)$

where $\ddot{\psi }\equiv d^2\psi /d{\eta }^2$, $p=-u/\left(B{k}^2\right)$, and $q=A/\left(3B{k}^2\right)$.

4.1 Periodic solution to the mKdVE

For the JEFEM, we consider the ansatz

$\psi \left(\eta \right)=\sum _{j=0}^n{a}_{j}S{n}^j\left(\eta \right),(22)$

where Sn(η) ≡ Sn(η, m) indicates the modulus of the JEF such that 0 ≤ m ≤ 1.

Inserting Eq. (22) in Eq. (21) and using the balancing principle (higher non-linearity gives 3n, while higher derivative gives n + 2), we find n = 1; thus, Eq. (22) reduces to

$\psi \left(\eta \right)=a_0+a_{1}Sn\left(\eta \right).(23)$

Substituting Eq. (23) into Eq. (21) and equating the terms of the same orders to zero, we obtain

$\left\{\begin{array}{c}\hfill a_0=0,a_1=\pm \sqrt{\frac{-6B}{A}}mk,\hfill \\ u=-B{k}^2\left(1+m^2\right).\hfill \end{array}\right.(24)$

Note that the velocity u is a free parameter. Thus, from Eq. 24, we can obtain the value of k as follows:

$k=\sqrt{-\frac{u}{B\left(1+m^2\right)}},(25)$

leading to the following new form of a₁

$a_1=\pm \sqrt{\frac{6u}{A\left(1+m^2\right)}}m.(26)$

Thus, the periodic solution to the mKdVE can be expressed as

$\psi \left(\xi ,\tau \right)=\pm \sqrt{\frac{6u}{A\left(1+m^2\right)}}mSn\left[\sqrt{\frac{-u}{B\left(1+m^2\right)}}\left(\xi -u\tau \right)\right].(27)$

However, knowing that B > 0 and u > 0, this solution can only exist for A < 0. Eq. (28), therefore, takes the following form:

$\psi \left(\xi ,\tau \right)=\mp \sqrt{\frac{6u}{A\left(1+m^2\right)}}mSn\left[\sqrt{\frac{u}{B\left(1+m_1^2\right)}}\left(\xi -u\tau \right)\right],(28)$

where m₁ = 1 − m. However, this is the unbounded periodic solution which is of little physical significance. Thus, we can consider a new ansatz

$\psi \left(\eta \right)=\sum _{j=0}^n{b}_{j}C{n}^j\left(\eta \right).(29)$

Applying Eq. (29) to Eq. (21) and by applying the balancing principle, we obtain n = 1, which leads to

$\psi \left(\eta \right)=b_0+b_{1}Cn\left(\eta \right).(30)$

Substituting Eq. (30) into Eq. (21) yields

$\left\{\begin{array}{c}\hfill b_0=0,b_1=\pm \sqrt{\frac{6B}{A}}km,\hfill \\ u=B{k}^2\left(2m^2-1\right),\hfill \end{array}\right.,(31)$

with

$\left\{\begin{array}{c}\hfill b_0=0,b_1=\pm \sqrt{\frac{6u}{A\left(2m^2-1\right)}}m,\hfill \\ k=\sqrt{\frac{u}{B\left(2m^2-1\right)}},\hfill \end{array}\right.(32)$

Accordingly, the periodic Cn solution reads

$\psi \left(\xi ,\tau \right)=\pm \sqrt{\frac{6u}{A\left(2m^2-1\right)}}mCn\left[\sqrt{\frac{u}{B\left(2m^2-1\right)}}\left(\xi -u\tau \right)\right].(33)$

The solution given by Eq. (33) demands u > 0, A > 0, and 2m² − 1 > 0 or u > 0, A < 0, and 2m² − 1 < 0. The first choice gives the bounded Cn periodic solution, whereas the second choice leads to the solution

$\psi \left(\xi ,\tau \right)=\pm \sqrt{\frac{6u}{A\left(2m^2-1\right)}}mnC\left[\sqrt{\frac{u}{B\left(2m_1^2-1\right)}}\left(\xi -u\tau \right)\right],(34)$

where nC = 1/Cn. Equation 34 reveals unbounded periodic solutions for 0.29 < m < 0.7071 and bounded periodic solutions for 0 < m < 0.29. Remember that the wave profile depends on the phase and the modulus of the JEF. Note that hitherto invisible behavior for the second choice emerges for some range of the parameter values of m, which is also of physical significance (bounded periodic solution).

4.2 Shock solution to the mKdVE

First, we note that the elliptic Jacobi functions become hyperbolic functions at m = 1. When m = 1, the solution Eq. (27) reduces to the shock wave solution

$\psi \left(\xi ,\tau \right)=\pm \sqrt{\frac{3u}{A}}\tanh \left[\sqrt{\frac{-u}{2B}}\left(\xi -u\tau \right)\right].(35)$

For the real solution to this equation, we have two choices i) B < 0 and A > 0 and ii) B > 0 and A < 0. The first choice is not possible for the values of the plasma parameters of this problem, and the second choice gives the unbounded periodic solution. Thus, it eliminates the possibility of the shock wave structure.

4.3 Solitary wave solution to the mKdVE

For m = 1, the solution Eq. 33 reduces to the solitary wave solution

$\psi \left(\xi ,\tau \right)=\pm \sqrt{\frac{6u}{A}}sech\left[\sqrt{\frac{u}{B}}\left(\xi -u\tau \right)\right].(36)$

We note that based on the solution Eq. (33), the solitary wave solution is only possible for A > 0 and 2m² − 1 > 0. Thus, the analytical analysis using the JEFEM shows periodic and solitary solutions and no shock wave solution. The method also reveals unbounded periodic solutions which are presented for mathematical interest.

5 Qualitative analysis of the mKdVE (traveling wave solution)

For brevity, we take BC = A here and rewrite Eq. (20) in the following form:

${\partial }_{\tau }\psi +A{\psi }^2{\partial }_{\xi }\psi +B{\partial }_{\xi }^3\psi =0.(37)$

According to the Lie symmetry method, Eq. (37) is invariant under the translational symmetry. For the invariant traveling wave solution, taking

$\eta =k\left(\xi -u\tau \right)$

in Eq. (37) yields the following standard Duffing equation Eqs (61)–(66).

$\ddot{\psi }=\frac{u}{B}\psi -\frac{C}{3}{\psi }^3,(38)$

where k = 1. Differential Eq. (38) is now expressed as an autonomous system of first-order equations (dynamical system)

$\left\{\begin{array}{c}\dot{\psi }=z=f\left(\psi ,z\right),\hfill \\ \hfill \dot{z}=\frac{u}{B}\psi -\frac{C}{3}{\psi }^3=g\left(\psi ,z\right).\hfill \end{array}\right.(39)$

The Hamiltonian function (total energy) of the aforementioned system reads as follows:

$H\left(\psi ,z\right)=\frac{z^2}{2}-\frac{u}{2B}{\psi }^2+\frac{C}{12}{\psi }^4.(40)$

The dynamical system Eq. 39 reveals three equilibrium points (stationary solutions):

$\left\{\begin{array}{c}\left({\psi }_1,z_1\right)=\left(\mathrm{0,0}\right),\hfill \\ \hfill \left({\psi }_2,z_2\right)=\left(\sqrt{\frac{3u}{BC}},0\right),\hfill \\ \hfill \left({\psi }_3,z_3\right)=\left(-\sqrt{\frac{3u}{BC}},0\right).\hfill \end{array}\right.(41)$

The nature of the equilibrium can be determined from the eigenvalues of the Jacobian matrix at the location of the critical points. The eigenvalues of the Jacobian matrix of stationary solutions turn out to be

$\left\{\begin{array}{c}{\lambda }_1=\pm \sqrt{\frac{u}{B}},\hfill \\ \hfill {\lambda }_{\mathrm{2,3}}=\pm i\sqrt{\frac{2u}{B}}.\hfill \end{array}\right.(42)$

The first stationary solution is a saddle, while the second and third are centers. The local behavior of the solution at the saddle point (hyperbolic point) matches with the global behavior of the Hartman–Grobman theorem. For the centers (non-hyperbolic point), the Hartman–Grobman theorem does not apply [67], and we use the energy method. Since the Hamiltonian function Eq. (40) is conserved $\frac{dH}{d\psi }=0$, closed orbits are represented by the center. We make a remark that for the traveling wave solution, we expect only three types of the waves, namely, periodic, solitary, or the shock waves. Furthermore, we discuss the qualitative behavior of the solution for a continuous range of the characteristic parameters with the help of bifurcation diagrams (branches). The results of bifurcation analysis are provided in Figures 8F, 9F, 10.

6 Results and discussion

6.1 Analytical approach

In this section, we will discuss the graphs of the numerically investigated parametric regimes for which we obtain solitonic, shock, and periodic solutions of the mKdVE admitted by the JEFEM. We mention at the outset that for the present model, the mKdVE does not admit any shock solutions; however, it allows the formation of solitonic and periodic solutions. It is also apt to mention here that the most important plasma parameters of the model are the positron concentration, α, and the percentage of cold and hot electrons present in the system represented by the parameters μ and ν, respectively.

The JEF, Sn, gives unbounded periodic solutions for A < 0 for all values of 0 < m < 1 (an outcome of Sn property). When m = 1, the corresponding tanh solution (shock wave) does not exist for the parametric values of the present model. The function, Cn, clearly gives bounded periodic solutions for A > 0 and 2m² − 1 > 1, that is, m > 0.707. Finally, when A < 0 and 2m² − 1 < 0, Cn gives the unbounded periodic solution for 0.29 < m < 0.707 and bounded periodic solution for 0 < m < 0.29. The unexpected periodic solution suddenly emerges depending on the value of the modulus of Jacobi elliptic function (eccentricity of the ellipse) that strongly influences the behavior of the wave. Once again, this conclusion comes from the property of the Cn function with imaginary argument. The corresponding solitonic solution, sec h (limiting the solution of Cn when m reaches 1), exists for A > 0. From the aforementioned discussion, we conclude that for A > 0, bounded periodic Cn and solitary (sec h) wave solutions exist. For A < 0, there are unbounded periodic solutions because Sn, Cn, and tanh have imaginary arguments. An exception in the case of A < 0 comes from nC for which the bounded periodic solution exists for a range of small values of m. As m reaches closer to zero, elliptic Jacobi functions tend to yield trigonometric functions and the unbounded periodic solutions become bounded periodic functions. The mathematical reason is that in nC, it is the complimentary of m, that is, m₁ that matters instead of m. The fate of the waveforms depends on the sign of the non-linearity coefficient A and the value of m. For all the cases, the amplitude needs to be real for physical solutions. We once again emphasize that unbounded solutions are not physical. The shock solution does not appear for any choice of parameters of the problem. We now proceed to the discussion of the figures and emphasize that the reader should look at them in the light of aforementioned explanation. Here, we plot only the positive solutions.

The Sn periodic solution for μ = 0.1 and α = 0.1 is shown in Figure 1. These values yield A < 0, which corresponds to the unbounded periodic solution. If we keep α the same and choose μ > 0.17, the non-linearity coefficient A becomes greater than zero and Sn function offers no solution. Physically, this means that the change in values of the positron concentration will change the range of A for which it goes from positive to negative, turning the unbounded periodic solution into no solution. The aforementioned analysis is true for all values of m. Before discussing Figure 2, we recall that the periodic solution, Cn, exists, in principle, for both A ≶ 0 subject to (2m² − 1) ≶ 0. For A > 0 (μ > 0.17), the Cn solution gives the bounded periodic solution—the physically plausible solution (Figure 3). For A < 0 (μ = 0.1) and 0.29 < m < 0.707, we obtain the unbounded periodic solution (Figure 2), whereas for 0 < m < 0.29, the solution turns into the bounded periodic solution (Figure 4). The former solution is not physical, whereas the latter is physical. The interesting physical solution emerges suddenly because of small values of m, and the Jacobi function approaches the trigonometric function which is certainly bounded.

FIGURE 1

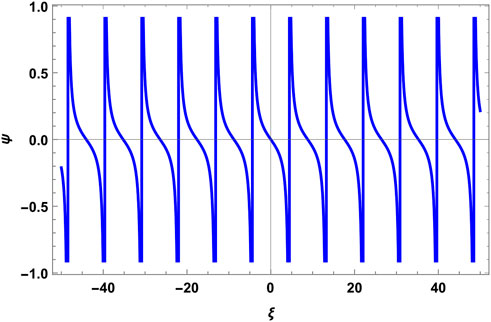
FIGURE 1. Periodic solution Sn for plasma parameters α =0.1, β =0.026, γ =0.7, δ =0.01, μ =0.1, ν =0.9, and $m=\frac{1}{3}$. Here, A <0 and 0< m <1.

FIGURE 2

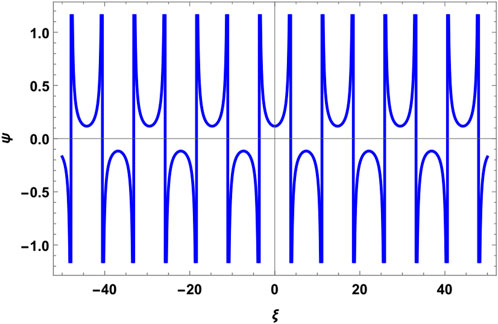
FIGURE 2. Periodic solution Cn for plasma parameters α =0.1, β =0.026, γ =0.7, δ =0.01, μ =0.1, ν =0.9, and $m=\frac{1}{3}$. Here, A <0 and 0.29< m <0.707.

FIGURE 3

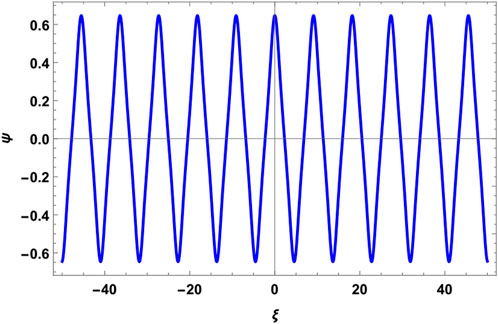
FIGURE 3. Periodic solution Cn for plasma parameters α =0.3, β =0.026, γ =0.7, δ =0.01, μ =0.1, ν =0.9, and m =0.8. Here, A >0 and 2m²−1>0.

FIGURE 4

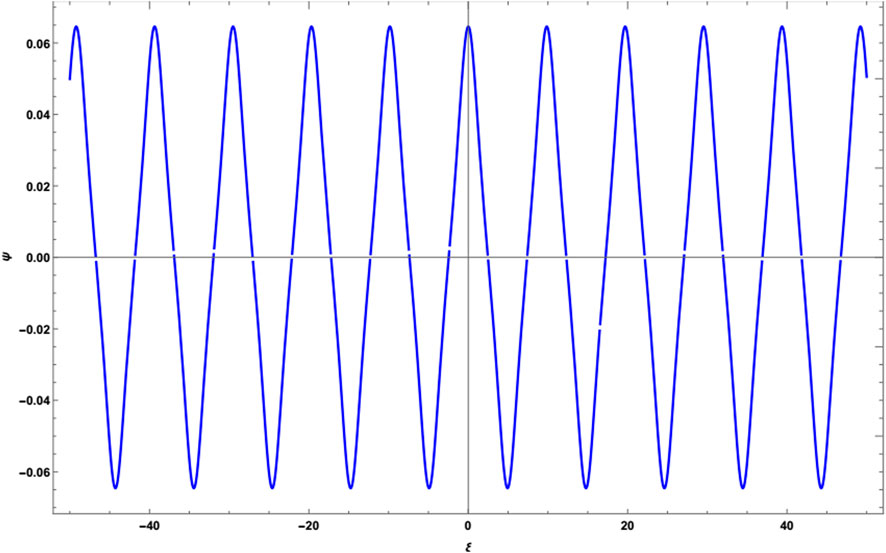
FIGURE 4. Periodic solution Cn for plasma parameters α =0.1, β =0.026, γ =0.7, δ =0.0, μ =0.1, ν =0.9, and m =0.2. Here, A <0 and 0< m <0.29.

The Jacobi functions turn into hyperbolic functions for m = 1. In this case, the bounded Cn function becomes sech function representing the solitary wave solution. This is substantiated in Figure 5 by choosing α = 0.1 and μ = 0.2 (A > 0). However, for α = 0 and μ = 0.2, A becomes negative, and the solitary solution does not exist. However, if we increase μ to 0.25, A becomes positive, and the solitary wave appears once again. These observations lead us to the physics of the plasma. The addition of positrons admits a solitary wave for a less percentage of cold electrons in comparison with ordinary (EI) plasma. Figures 5–7 plot the acoustic solitary wave for both EPI and EI plasmas for the set of values which admits solitary waves. It is found that the inclusion of positrons mitigates the amplitude of the solitary wave significantly. The solitary wave solution is another physical solution in addition to the two discussed previously. It may be added that the unbounded periodic solutions are interesting from the mathematical standpoint and add to the understanding of various possibilities of physical parameters of the problem and cannot be summarily toned down even from the point of view of physicists.

FIGURE 5

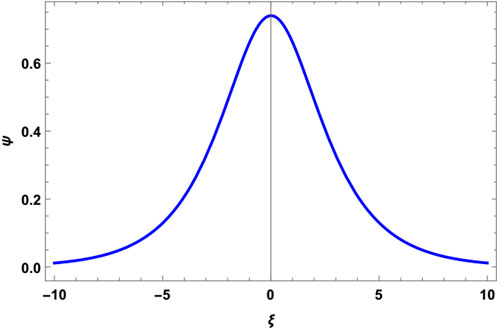
FIGURE 5. Soliton profile for plasma parameters α =0.1, β =0.026, γ =0.7, δ =0.01, μ =0.2, ν =0.8, and m =1. Here, A >0 and 2m²−1>0.

FIGURE 6

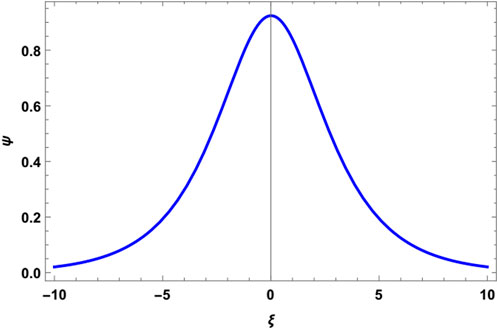
FIGURE 6. Soliton profile for plasma parameters α =0.0, β =0.026, γ =0.7, δ =0.01, μ =0.25, ν =0.75, and m =1. Here, A >0 and 2m²−1>0.

FIGURE 7

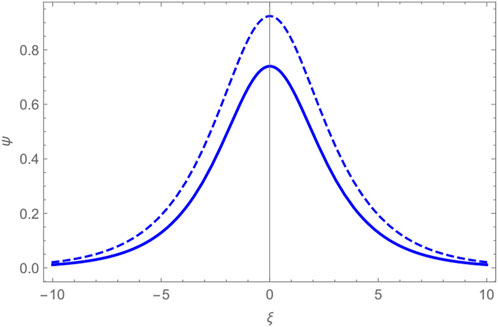
FIGURE 7. Comparison of two periodic waves: the dashed line represents α =0 and thick line represents α =0.1 drawn for A >0 and 2m²−1>0.

All solutions that have been discussed so far theoretically are supported by the dynamical system via the phase plane analysis and the bifurcation diagrams. The topological behavior (local behavior) near the equilibrium points in the phase plane provides the wave patterns representing the solution to the mKdVE, and the bifurcation diagrams predict the behavior for the continuous spectrum of the physical parameters of the problem. The dynamical system approach is presented in the following section.

6.2 Dynamical system and bifurcation diagram

6.2.1 Variation with respect to α

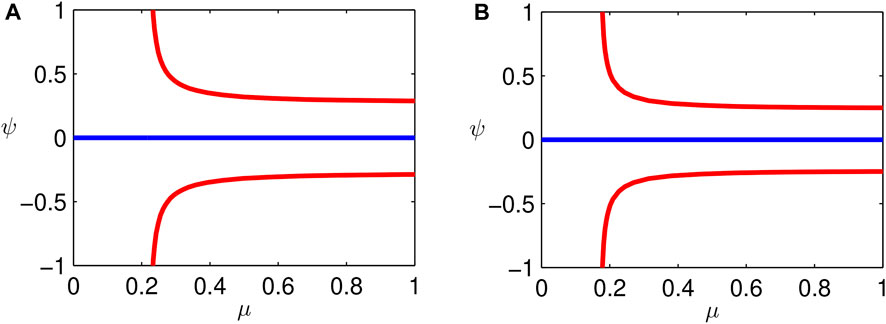
The phase portrait in the (ψ, z) plane is given by Figure 8A. In this figure, the center corresponds to the closed orbits having a finite period, and the homoclinic orbits (saddle is connected to itself) correspond to the solitary wave with an infinite period. The two pairs of homoclinic orbits represent rarefaction and compression waves, and the orbit outside the homoclinic orbit corresponds to a super periodic wave. No heteroclinic orbit (two or more saddles and at least one center in the phase plane) suggests that no traveling shock wave solution is expected for the mKdVE for this choice of parameters. This observation is in conformity with the analytical observation made previously. Figure 8B is the solitary wave representing the homoclinic orbit that satisfies the boundary conditions at infinity for mKdVE. Figure 8F gives the bifurcation diagram for α in the α − ψ plane, keeping other parameters fixed. The bifurcation diagram defines the solution behavior over a continuous range 0 < α < 1. For 0 < α < 0.3, there is only one saddle point at (0,0), whereas for α ≥ 0.3, there is a saddle at (0,0) and centers at $\pm \sqrt{\frac{3u}{BC}}$ (Figures 8E, F). The phase portraits give the solution behavior for the specific choice of α parameter, whereas the bifurcation diagrams predict the solution behavior for all possible choices of this parameter. The qualitative behavior for other values of α (including α = 0.3) is determined from the bifurcation diagram. For instance, at α = 0.5, the bifurcation diagram shows the existence of two centers (red branches) and one saddle (blue branch). Similarly, for α = 0.1, there is only one singular point, saddle, which is unstable equilibrium. The value of α = 0.3 corresponds to two bifurcation points (−0.64, 0) and (0.64,0). The behavior for this value of α is also supported by the bifurcation diagram, that is, Figure 8F. A single saddle point (which does exist in the phase plane) has two branches. One branch moves toward the critical point (stable branch), and the other (unstable branch) moves away from the critical point. The one which moves away from the saddle point gives the periodic wave of infinite amplitude (the singular solution). Moreover, the inset branches of the saddle show the stable manifold, and outset branches are the unstable manifold (see Figure 8E). From the foregoing analysis, the sensitivity of the positron concentration is evident. The switching of the dynamical behavior takes place at the parametric value α = 0.3. For the range 0 < α < 0.3, there is only saddle (showing unbounded periodic solutions) and two centers (closed orbits) for α ≥ 0.3. It may further be noted that for 0 < α < 0.3 and A < 0, unbounded periodic solutions are obtained as shown in Figure 8E, whereas for α ≥ 0.3, the bounded periodic solutions are obtained as shown in Figures 8C, D. These observations are in conformity with the analytical results given previously in Section 4.

FIGURE 8

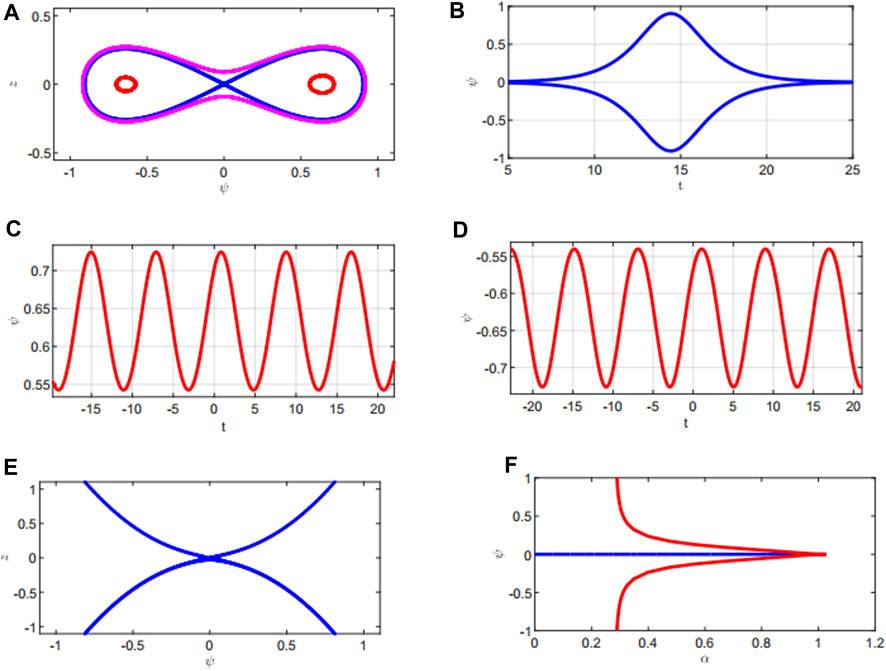
FIGURE 8. (A) Phase plane diagram in the (ψ, z) plane for α =0.3 and A >0. (B) Solitary wave. (C)–(D) Periodic wave for α =0.3 and A >0. (E) Phase plane diagram in the (ψ, z) plane for α =0.1 and A <0. (F) Bifurcation diagram between α and ψ keeping other parameters as β =0.026, δ =0.01, γ =0.7, ν =0.9, and μ =0.1.

6.2.2 Variation with respect to β

Similar analysis is repeated for β = 0.1 in Figure 9. The analysis shows two centers and one saddle in the phase plane. According to the physics of these critical points, they correspond to close orbits and homoclinic orbit, respectively (Figure 9A). The homoclinic orbit represents the solitary wave structure of the wave form shown in Figure 9B. The value β = 0.01 reveals only one critical point—saddle point (unstable equilibrium). These observations are authenticated from the bifurcation diagram (Figure 9F), showing a saddle at (0,0) for 0 < β < 0.02 and centers at $\pm \sqrt{\frac{3u}{BC}}$ for β ≥ 0.02. The value of β = 0.026 corresponds to two bifurcation points (−0.64, 0) and (0.64,0) (Figure 9F). We further observe that the non-linearity coefficient A < 0 for 0 < β < 0.02 gives rise to unbounded periodic solutions (Figure 9E), and for A > 0, the bounded periodic solution is obtained, as shown in Figures 9C, D. We conclude that the nature of these critical points, for the continuous range of their values, can be forecasted without actually experimenting for the specific values of these parameters from the phase plane analysis or analytic considerations.

FIGURE 9

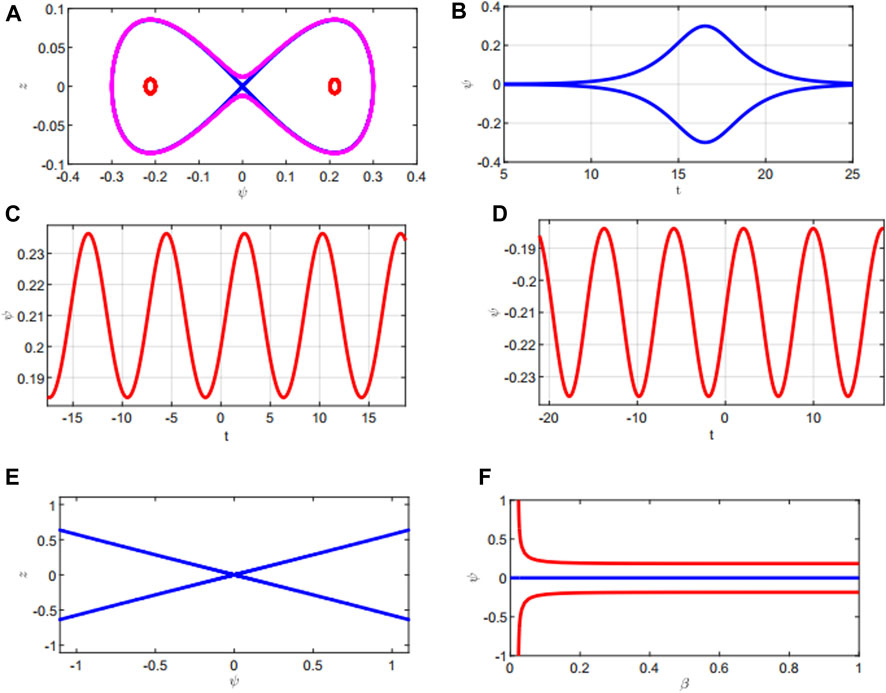
FIGURE 9. (A) Phase plane diagram in the (ψ, z) plane for β =0.1 and A >0. (B) Solitary wave. (C)–(D) Periodic wave for β =0.1 and A >0. (E) Phase plane diagram in the (ψ, z) plane for β =0.01 and A <0. (F) Bifurcation diagram between β and ψ keeping other parameters as α =0.3, δ =0.01, γ =0.7, ν =0.9, and μ =0.1.

6.2.3 Variation with respect to μ

First, we recall that variation of positron concentration (μ) in the system changes the range of percentage of cold electrons for which the periodic or solitary waves exist. The bifurcation diagram between μ and ψ is shown in Figures 10A, B) for different values of α (positron concentration). It is observed that the region for the existence of solitary wave increases with α. From the bifurcation diagram, we infer that an increase in positron concentration gives solitary behavior for lesser percentage of cold electrons μ. The branch points with respect to μ for α = 0.0 and α = 0.1 are (±0.97, 0) and (±0.94, 0), respectively (Figures 10A, B). This observation is in agreement with the analytic results obtained previously. The wave forms for saddles in Figures 8E, 9E are not presented since they correspond to unbounded periodic solutions and are of little physical significance.

FIGURE 10

FIGURE 10. Bifurcation diagram between μ and ψ. (A) α =0.0; (B) α =0.1.

6.2.4 Some significant observations of bifurcation analysis

The bifurcation diagrams provide the solution behavior for a continuous range of physically important parameters, namely, α, β, and μ. Another important aspect of even greater significance is that the bifurcation theory predicts and identifies the switching of the solution behavior from one topological space to another when the value of a parameter crosses some threshold value. For example, the bifurcation diagram predicts the change in behavior from periodic to solitary at α = 0.3 and β = 0.026. Similarly, a cut off from the periodic to solitary waves with respect to μ for α = 0.0 and α = 0.1 comes at (±0.97, 0) and (±0.94, 0), respectively. Moreover, the bifurcation theory plays an important role in the analysis of highly nonlinear models whose analytical solution is not possible. It is effective to probe the stability of the solution by investigating the equilibrium curves drawn versus characterized parameters in advance without plotting the topological structures.

7 Summary and conclusion

The nonlinear ion acoustic waves in unmagnetized collisionless plasma consisting of two populations of electrons (cold and hot), positrons, and warm adiabatic ions are investigated. The mKdVE is derived using multi-scale analysis and solved by the Jacobi elliptic function expansion method. The bounded periodic and solitary solutions are obtained. In addition to that, unbounded periodic solutions (of little physical significance) also appear in the solution. No shock wave is found for any value of plasma parameters.

The dynamical system theory and the bifurcation analysis are applied to determine the qualitative behavior of the mKdVE. The behaviors are determined from the nature of the critical points and the corresponding phase plane diagrams. The centers and homoclinic orbits ensure periodic and solitary wave behaviors, whereas the absence of heteroclinic orbit confirms the non-existence of the shock wave and corroborates the analytical results. A complete convergence between the analytical results and the qualitative behavior is established. In the end, we conclude with the remark that the qualitative behavior is useful when the closed-form solutions of the nonlinear differential equations are known and crucial and when analytic solutions are not possible. The results presented here provide a general framework and can be used to study a variety of plasma waves in laboratory, space, and astrophysical plasmas.

Data availability statement

The original contributions presented in the study are included in the article/Supplementary Material; further inquiries can be directed to the corresponding author.

Author contributions

All authors listed have made a substantial, direct, and intellectual contribution to the work and approved it for publication.

Acknowledgments

The authors express their gratitude to Princess Nourah bint Abdulrahman University Researchers Supporting Project number (PNURSP2023R17), Princess Nourah bint Abdulrahman University, Riyadh, Saudi Arabia.

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

1. Goldreich P, Julian WH. Pulsar electrodynamics. Astrophys J (1996) 157:869. doi:10.1086/150119

CrossRef Full Text | Google Scholar

2. Sturrock PA. A model of pulsars. Astrophys J (1971) 164:529. doi:10.1086/150865

CrossRef Full Text | Google Scholar

3. Michel FC. Theory of pulsar magnetospheres. Rev Mod Phys (1982) 54:1–66. doi:10.1103/revmodphys.54.1

CrossRef Full Text | Google Scholar

4. Michel FC. Theory of neutron star magnetosphere. Chicago: Chicago University Press (1991).

Google Scholar

5. Gibson G, Jordan WC, Lauer EJ. Containment of positrons in a mirror machine. Phys Rev Lett (1960) 5:141–4. doi:10.1103/physrevlett.5.141

CrossRef Full Text | Google Scholar

6. Gibson G, Jordan WC, Lauer EJ. Particle behavior in static, axially symmetric, magnetic mirror and cusp geometries. Phys Fluids (1963) 6:116. doi:10.1063/1.1724497

CrossRef Full Text | Google Scholar

7. Tsytovich V, Wharton CB. Comments Plasma Phys Controlled Fusion (1978) 4:91.

8. Weiss A, Ottewitte E. “Slow Positron Beam Techniques for Solids and Surfaces,” in Fifth International Workshop, Jackson Hole, WY, August 1992 (AIP Conference Proceedings, Hardcover) (1992).

Google Scholar

9. Zank GP, Hargreaves RG. Linear and nonlinear modes in nonrelativistic electron-positron plasmas. Phys Rev E (1995) 51:6079–90. doi:10.1103/physreve.51.6079

CrossRef Full Text | Google Scholar

10. Rizzato FB. Weak nonlinear electromagnetic waves and low-frequency magnetic-field generation in electron-positron-ion plasmas. J Plasma Phys (1988) 40:289–98. doi:10.1017/s0022377800013283

CrossRef Full Text | Google Scholar

11. Berezhiani VI, El-Ashry MY, Mofiz UA. Theory of strong-electromagnetic-wave propagation in an electron-positron-ion plasma. Phys Rev E (1994) 50:448–52. doi:10.1103/physreve.50.448

CrossRef Full Text | Google Scholar

12. Popel SI, Vladimirov SV, Shukla PK. Ion-acoustic solitons in electron–positron–ion plasmas. Phys Plasmas (1995) 2:716–9. doi:10.1063/1.871422

CrossRef Full Text | Google Scholar

13. Wang Y, Zhou Z, Jiang X, Zhang H, Jiang Y, Hou C, et al. Cylindrical Kadomtsev–Petviashvili equation for relativistically magnetosonic solitary wave in the collisionless plasma. Phys Lett A (2006) 355:386–9. doi:10.1016/j.physleta.2006.03.001

CrossRef Full Text | Google Scholar

14. Moslem WM, Kourakis I, Shukla PK, Schlickeiser R. Nonlinear excitations in electron-positron-ion plasmas in accretion disks of active galactic nuclei. Phys Plasmas (2007) 14:102901. doi:10.1063/1.2795127

CrossRef Full Text | Google Scholar

15. Masood W, Jehan N, Mirza AM, Sakanaka PH. Planar and non-planar ion acoustic shock waves in electron–positron–ion plasmas. Phys Lett A (2008) 372:4279–82. doi:10.1016/j.physleta.2008.03.058

CrossRef Full Text | Google Scholar

16. Masood W, Jehan N, Mirza AM. A new equation in two dimensional fast magnetoacoustic shock waves in electron-positron-ion plasmas. Phys Plasmas (2010) 17:032314. doi:10.1063/1.3322885

CrossRef Full Text | Google Scholar

17. Masood W, Rizvi H. Effect of nonthermal electrons on the propagation characteristics and stability of two-dimensional nonlinear electrostatic coherent structures in relativistic electron positron ion plasmas. Phys Plasmas (2011) 18:062304. doi:10.1063/1.3591343

CrossRef Full Text | Google Scholar

18. Khalid S, Qureshi MNS, Masood W. Alfvenic perturbations with finite Larmor radius effect in non-Maxwellian electron–positron–ion plasmas. AIP Adv (2020) 10:025002. doi:10.1063/1.5141891

CrossRef Full Text | Google Scholar

19. Buti B. Ion-acoustic holes in a two-electron-temperature plasma. Phys Lett A (1980) 76:251–4. doi:10.1016/0375-9601(80)90483-1

CrossRef Full Text | Google Scholar

20. Feldman WC, Anderson RC, Bame SJ, Gary SP, Gosling JT, McComas DJ, et al. Electron velocity distributions near the Earth's bow shock. J Geophys Res–space (1983) 88:96–110. doi:10.1029/ja088ia01p00096

CrossRef Full Text | Google Scholar

21. Mace RL, Hellberg MA. Higher-order electron modes in a two-electron-temperature plasma. J Plasma Phys (1990) 43:239–55. doi:10.1017/s0022377800014768

CrossRef Full Text | Google Scholar

22. Berthomier M, Pottelette R, Malingre M, Khotyaintsev Y. Electron-acoustic solitons in an electron-beam plasma system. Phys Plasmas (2000) 7:2987–94. doi:10.1063/1.874150

CrossRef Full Text | Google Scholar

23. Verheest F, Hellberg MA, Lakhina GS. Necessary conditions for the generation of acoustic solitons in magnetospheric and space plasmas with hot ions. Astrophys Space Sci (2007) 3:15–20. doi:10.5194/astra-3-15-2007

CrossRef Full Text | Google Scholar

24. Saha A, Tamang J. Effect of q-nonextensive hot electrons on bifurcations of nonlinear and supernonlinear ion-acoustic periodic waves. Adv Space Res (2019) 63:1596–606. doi:10.1016/j.asr.2018.11.010

CrossRef Full Text | Google Scholar

25. McFadden JP, Carlson CW, Ergun RE, Mozer FS, Muschietti L, Roth I, et al. J Geophys Res-space (2003) 108.

26. Matsumoto H, Kojima H, Miyatake T, Omura Y, Okada M, Nagano I, et al. Electrostatic solitary waves (ESW) in the magnetotail: BEN wave forms observed by GEOTAIL. Geophys Res Lett (1994) 21:2915–8. doi:10.1029/94gl01284

CrossRef Full Text | Google Scholar

27. Ergun RE, Carlson CW, McFadden JP, Mozer FS, Delory GT, Peria W, et al. FAST satellite observations of large-amplitude solitary structures. Geophys Res Lett (1998) 25:2041–4. doi:10.1029/98gl00636

CrossRef Full Text | Google Scholar

28. Temerin M, Cerny K, Lotko W, Mozer FS. Observations of double layers and solitary waves in the auroral plasma. Phys Rev Lett (1982) 48:1175–9. doi:10.1103/physrevlett.48.1175

CrossRef Full Text | Google Scholar

29. Goswami BN, Buti B. Ion acoustic solitary waves in a two-electron-temperature plasma. Phys Lett A (1976) 57:149–50. doi:10.1016/0375-9601(76)90195-x

CrossRef Full Text | Google Scholar

30. Balaku TK, Hellberg MA. Phys.Plasmas (2012) 19:012106.

31. Panwar A, Ryu CM, Bains AS. Oblique ion-acoustic cnoidal waves in two temperature superthermal electrons magnetized plasma. Phys Plasmas (2014) 21:122105. doi:10.1063/1.4903848

CrossRef Full Text | Google Scholar

32. Rehman MA, Mishra MK. Ion-acoustic Gardner Solitons in electron-positron-ion plasma with two-electron temperature distributions. Phys Plasmas (2016) 23:012302. doi:10.1063/1.4939802

CrossRef Full Text | Google Scholar

33. Wang M. Phys Lett A (1995) 199:169.

34. Wang M, Zhou YB, Li ZB. Application of a homogeneous balance method to exact solutions of nonlinear equations in mathematical physics. Phys Lett A (1996) 216:67–75. doi:10.1016/0375-9601(96)00283-6

CrossRef Full Text | Google Scholar

35. Yang L, Zhu Z, Wang Y. Exact solutions of nonlinear equations. Phys Lett A (1999) 260:55–9. doi:10.1016/s0375-9601(99)00482-x

CrossRef Full Text | Google Scholar

36. Yang L, Liu J, Yang K. Exact solutions of nonlinear PDE, nonlinear transformations and reduction of nonlinear PDE to a quadrature. Phys Lett A (2001) 278:267–70. doi:10.1016/s0375-9601(00)00778-7

CrossRef Full Text | Google Scholar

37. Parkes EJ, Duffy BR. Travelling solitary wave solutions to a compound KdV-Burgers equation. Phys Lett A (1997) 229:217–20. doi:10.1016/s0375-9601(97)00193-x

CrossRef Full Text | Google Scholar

38. Fan E. Extended tanh-function method and its applications to nonlinear equations. Phys Lett A (2000) 277:212–8. doi:10.1016/s0375-9601(00)00725-8

CrossRef Full Text | Google Scholar

39. Hirota R. Exact N-soliton solutions of the wave equation of long waves in shallow-water and in nonlinear lattices. J Math Phys (1973) 14:810–4. doi:10.1063/1.1666400

CrossRef Full Text | Google Scholar

40. Kudryashov NA. Exact solutions of the generalized Kuramoto-Sivashinsky equation. Phys Lett A (1990) 147:287–91. doi:10.1016/0375-9601(90)90449-x

CrossRef Full Text | Google Scholar

41. Otwinowski M, Paul R, Laidlaw WG. Exact travelling wave solutions of a class of nonlinear diffusion equations by reduction to a quadrature. Phys Lett A (1988) 128:483–7. doi:10.1016/0375-9601(88)90880-8

CrossRef Full Text | Google Scholar

42. Liu SK, Fu ZT, Liu SD, Zhao Q. Appl Math Mech (2001) 22:326–31. doi:10.1023/a:1015514721870

CrossRef Full Text

43. Yan C. A simple transformation for nonlinear waves. Phys Lett A (1996) 224:77–84. doi:10.1016/s0375-9601(96)00770-0

CrossRef Full Text | Google Scholar

44. Porubov AV. Periodical solution to the nonlinear dissipative equation for surface waves in a convecting liquid layer. Phys Lett A (1996) 221:391–4. doi:10.1016/0375-9601(96)00598-1

CrossRef Full Text | Google Scholar

45. Porubov AV, Velarde MG. Exact periodic solutions of the complex Ginzburg–Landau equation. J Math Phys (1999) 40:884–96. doi:10.1063/1.532692

CrossRef Full Text | Google Scholar

46. Fu Z, Liu S, Liu S, Zhaoa Q. New Jacobi elliptic function expansion and new periodic solutions of nonlinear wave equations. Phys Lett A (2001) 290:72–6. doi:10.1016/s0375-9601(01)00644-2

CrossRef Full Text | Google Scholar

47. Jiménez-Lozano J, Sen M. Streamline topologies of two-dimensional peristaltic flow and their bifurcations. Chem Eng Process (2010) 49:704–15. doi:10.1016/j.cep.2009.10.005

CrossRef Full Text | Google Scholar

48. Ullah K, Ali N. Stability and bifurcation analysis of stagnation/equilibrium points for peristaltic transport in a curved channel. Phys Fluids (2019) 31:073103. doi:10.1063/1.5097555

CrossRef Full Text | Google Scholar

49. Ullah K, Ali N. Bifurcation and stability analysis of stagnation points for an asymmetric peristaltic transport. Can J Phys (2020) 98:172–82. doi:10.1139/cjp-2019-0062

CrossRef Full Text | Google Scholar

50. Ehsan T, Asghar S, Anjum HJ. Identification of trapping in a peristaltic flow: A new approach using dynamical system theory. Phys Fluids (2020) 32:011901. doi:10.1063/1.5128417

CrossRef Full Text | Google Scholar

51. Yasmeen S, Asghar S, Anjum HJ, Ehsan T. Analysis of Hartmann boundary layer peristaltic flow of Jeffrey fluid: Quantitative and qualitative approaches. Commun Nonlinear Sci (2019) 76:51–65. doi:10.1016/j.cnsns.2019.01.007

CrossRef Full Text | Google Scholar

52. Samanta UK, Saha A, Chatterjee P. Phys Plasmas (2013) 20:022111.

53. Tamang J, Saha A. Bifurcations of small-amplitude supernonlinear waves of the mKdV and modified Gardner equations in a three-component electron-ion plasma. Phys Plasmas (2020) 27:012105. doi:10.1063/1.5115821

CrossRef Full Text | Google Scholar

54. Tamang J, Abdikian A, Saha A. Phase plane analysis of small amplitude electron-acoustic supernonlinear and nonlinear waves in magnetized plasmas. Phys Scripta (2020) 95:105604. doi:10.1088/1402-4896/abb05b

CrossRef Full Text | Google Scholar

55. Abdikian A, Tamang J, Saha A. Supernonlinear wave and multistability in magneto-rotating plasma with (r, q) distributed electrons. Phys Scripta (2020) 96:095605. doi:10.1088/1402-4896/ac07b7

CrossRef Full Text | Google Scholar

56. Pradhan B, Abdikian A, Saha A. Waves in random and complex media (2022). doi:10.1080/17455030.2022.2070796

CrossRef Full Text | Google Scholar

57. Saha A, Chatterjee P. Dust ion acoustic travelling waves in the framework of a modified Kadomtsev-Petviashvili equation in a magnetized dusty plasma with superthermal electrons. Astrophys Space Sci (2014) 349:813–20. doi:10.1007/s10509-013-1685-x

CrossRef Full Text | Google Scholar

58. El-Tantawy SA. Rogue waves in electronegative space plasmas: The link between the family of the KdV equations and the nonlinear Schrödinger equation. Astrophysics Space Sci (2016) 361:164. doi:10.1007/s10509-016-2754-8

CrossRef Full Text | Google Scholar

59. El-Tantawy SA. Effect of ion viscosity on dust ion-acoustic shock waves in a nonextensive magnetoplasma. Astrophysics Space Sci (2016) 361:249. doi:10.1007/s10509-016-2831-z

CrossRef Full Text | Google Scholar

60. El-Tantawy SA, Carbonaro P. Phys Lett A (2016) 380:1627.

61. Salas AH, El-Tantawy SA. On the approximate solutions to a damped harmonic oscillator with higher-order nonlinearities and its application to plasma physics: Semi-analytical solution and moving boundary method. Eur Phys J Plus (2020) 135:833. doi:10.1140/epjp/s13360-020-00829-3

CrossRef Full Text | Google Scholar

62. Salas AH, El-Tantawy SA, Noufe HA. Math Probl Eng (2021) 2021:8875589.

63. El-Tantawy SA, Salas AH, Alharthi MR. Math Probl Eng (2021) 2021:6678102.

64. NoufeAljahdaly H, El-Tantawy SA. On the multistage differential transformation method for analyzing damping duffing oscillator and its applications to plasma physics. Mathematics (2021) 9:432. doi:10.3390/math9040432

CrossRef Full Text | Google Scholar

65. Alvaro H, Sales A. El-tantawy “analytical solutions of some strong nonlinear oscillators.” engineering problems - uncertainties, constraints and optimization techniques. IntechOpen (2022). doi:10.5772/intechopen.97677

CrossRef Full Text | Google Scholar

66. Alvaro HS, Mamon AH, BadriahAlotaibi M, LamiaaEl-Sherif S, El-Tantawy SA. Analytical and numerical approximations to some coupled forced damped duffing oscillators. Symmetry (2022) 14:2286. doi:10.3390/sym14112286

CrossRef Full Text | Google Scholar

67. Seydel R. Practical bifurcation and stability analysis. Springer Science & Business Media (2009).

Google Scholar