Few-femtosecond X-ray pulse generation and pulse duration control in a seeded free-electron laser

With the development of ultrafast science, free-electron lasers (FELs) with ultrashort pulses have become a state-of-the-art tool in ultrafast phenomena studies. In an externally seeded FEL, the output pulse duration is usually determined both by the seed laser pulse duration and FEL amplification process, which can hardly reach the timescale of a few femtoseconds. In this study, through a simple method of changing the relative time delay and correspondingly the pulse energy of the two seed lasers employed in a seeded FEL, we demonstrated the possibility of generating few-femtosecond soft X-ray pulses and controlling the final FEL pulse durations. Based on theoretical calculations and practical experiments, we conducted a detailed study on the capabilities and limitations to this method with the parameters of the Shanghai Soft X-ray FEL Facility. Start-to-end simulations indicate that we can achieve ultrashort soft X-ray FEL pulses with the pulse duration down to 5.2 fs, and the final pulse durations can also be controlled in terms of relative time delays.

1 Introduction

The X-ray free-electron laser (XFEL) with high brightness, short pulse durations, superior coherence, and wide tuning ranges has become a powerful tool in numerous scientific research areas, such as molecular, atomic, and electronic motions. Comparing with synchrotron radiation, the XFEL has extraordinary advantages of high resolution in both temporal and spatial dimensions. Today, with the realization of a high-gain free-electron laser, several large-scale FEL facilities around the world have been built up to provide XFEL pulses [1–6]. XFELs usually have a pulse duration of tens to hundreds of femtoseconds. To shorten the pulse length down to a few femtoseconds or even sub-femtosecond timescale, several approaches have been proposed [7–13]. Ultrashort X-ray pulses having a few to tens of femtoseconds can image the dynamics of individual nanostructures and protein nanocrystals, which will promote a promising development in the fields of structural biology, medicine dynamics, and neuroscience [14–21].

The basic working scheme of XFELs is self-amplified spontaneous emission (SASE) [22–24], which has a relatively low temporal coherence and high pulse-energy fluctuations since the initial signal is derived from a shot noise of the electron beam. Throughout the last decade, the self-seeding method [25–29] has been proven highly effective to significantly increase the temporal coherence of the SASE XFEL pulses. Using a monochromator and a bypass chicane implemented between two undulator sections, the self-seeding method can obtain monochromatic light from the SASE FEL pulse developed in the up-front undulator section and amplify it to saturation in the subsequent undulator section. However, there are still noticeable shot-to-shot fluctuations in the output pulse energy. Another effective way to improve the temporal coherence and stability of high-gain FELs is through the external seeding strategy, which includes the high-gain harmonic generation (HGHG) [30–34] and the echo-enabled harmonic generation (EEHG) [35–41]. EEHG is also one of the most promising configurations for generating a fully coherent FEL radiation at the Shanghai High-Repetition-Rate XFEL and Extreme Light Facility (SHINE) [42]. Although they can hardly reach tender X-ray and hard X-ray regimes, the externally seeded FELs can produce fully coherent soft X-ray radiation pulses. The pulse duration in a seeded soft X-ray FEL is usually determined both by the seed laser pulse duration and FEL amplification process, which can hardly reach the timescale of a few femtoseconds [43–46]. The latest study has found that externally seeded FELs can generate few-femtosecond extreme-ultraviolet FEL pulses with the superradiant cascade technique, but the duration of these pulses cannot be flexibly controlled [47].

In this paper, a simple method has been studied for generating few-femtosecond soft X-ray pulses and controlling the final FEL pulse durations in an externally seeded FEL. The method is mainly based on the EEHG scheme. By changing the relative time delay of the two seed lasers employed in EEHG, there will appear a finite bunched part in the electron beam, which can radiate ultrashort soft X-ray FEL pulses, and the pulse durations can be varied in terms of different relative time delays. Through theoretical calculations and practical experiments, we conduct a detailed study on the performance of the method in both the single-stage EEHG and the cascaded EEHG–HGHG scheme based on the Shanghai Soft X-ray FEL Facility (SXFEL).

2 Theoretical analysis and optimization

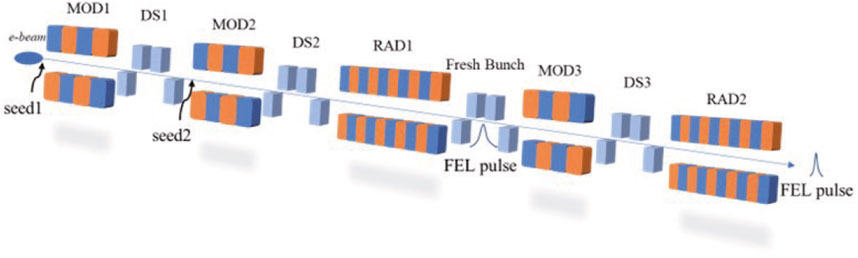
The principles of EEHG have been promoted for a decade, which primarily focuses in producing fully coherent soft X-ray FEL pulses. The cascaded EEHG–HGHG scheme was proposed then to further extend the photon energy coverage and obtain a narrower spectrum. SXFEL can work both on the SASE and external seeding modes, in which the single-stage EEHG scheme and cascaded EEHG–HGHG scheme are all applicable. The schematic layout of the cascaded EEHG–HGHG in SXFEL is shown in Figure 1. The whole beamline comprised an EEHG as the first stage and an HGHG as the second stage, with a fresh-bunch chicane located in between. The first-stage EEHG setup consists of two modulation sections (MOD1 and MOD2), two dispersion sections (DS1 and DS2), and an FEL radiator (RAD1). The second-stage HGHG setup consists of a modulator (MOD3), a dispersion section (DS3), and a final FEL radiator (RAD2). The electron beam from the upstream LINAC will first go through the EEHG-FEL setup to generate an initial radiation pulse in RAD1. With appropriate delays of the electron beam in the fresh-bunch chicane, the first-stage EEHG-FEL radiation pulse will slip ahead into the head of the electron beam and work as a seed laser in the following HGHG-FEL setup.

FIGURE 1

FIGURE 1. Schematic layout of the SXFEL-UF.

In a typical EEHG scheme, assuming a seed laser with a Gaussian power profile of an rms width σ_s and central wavelength λ_s, the electric field distribution along the electron beam can be characterized as

$E\left(s\right)=E_0{e}^{-s^2/4{\sigma }_s^2}{e}^{i\left(k_{s}s+{\varphi }_0\right)},(1)$

where s is the longitudinal coordinate along the electron bunch, E₀ is the peak electric field intensity, k_s = 2π/λ_s is the wavenumber of the seed laser, and ϕ₀ is the initial carrier-envelope phase of the laser. As to the energy exchange in the modulator, the energy modulation Δγ for an electron beam with central kinetic energy γ can be given as

$\mathrm{\Delta }\gamma \left(s\right)={\int }_0^z\frac{eK\left[JJ\right]}{2\gamma m{c}^2}E\left(s\right)dz,(2)$

where K is the unitless undulator parameter (K = 0.934Bλ_u with B in Tesla and λ_u in centimeter), and [JJ] and z characterize the modified Bessel factor [JJ] = J₀ [K²/(4 + 2K²)] − J₁ [K²/(4 + 2K²)] and the length of the modulator, respectively. Normally, the two seed lasers employed in the two modulators in EEHG should be synchronized, interacting in the same position within the electron bunch, so that the EEHG effect can be fulfilled at the most. However, in the proposed method, to generate ultrashort EEHG FEL pulses, two seed lasers are designed to have a relative time delay of δs, and in the overlapped area, the laser intensities are set to optimized values for given dispersive strengths of chicanes. Under this condition, the maximum bunching factor will appear in the intermediate position s + δs/2. Considering the situation here, the energy modulation in the first modulator (MOD1) can be written as$\mathrm{\Delta }{\gamma }_1=\frac{eK[JJ]}{2\gamma m{c}^2}E(s)z$, while in the second modulator (MOD2), $\mathrm{\Delta }{\gamma }_2=\frac{eK[JJ]}{2\gamma m{c}^2}E(s+\delta s)z$. The maximum bunching factor is optimized at the new modulation position s + δs/2. To satisfy the modulation strength requirements at this position, the pulse energy of the seed lasers should change simultaneously, according to the relative time delay of the two seed lasers. At the exit of the second dispersion section (DS2), the bunching factor of the hth harmonic number at the selected modulation position can be similarly written as

$b_h\left(s\right)=\left|{\exp }^{-{\left[-B_1+\left(m-1\right)B_2\right]}^2/2}{J}_m\left[-\left(m-1\right)A_2\left(s+\delta s\right)B_2\right]\times J_{-1}\left\{-A_1\left(s\right)\left[-B_1+\left(m-1\right)B_2\right]\right\}\right|,(3)$

where h = m − 1 with an integer m. A = Δγ/σ_γ denotes the modulation amplitude in the modulators, and B = R₅₆k_sδ_γ/γ, where R₅₆ represents the dispersive strength of the chicanes. Δγ is the modulation depth. δ_γ is the slice energy spread. After the fresh-bunch chicane, the first-stage EEHG-FEL radiation will interact with a fresh part of the electron beam in MOD3 in the second-stage HGHG with an amplitude of $\mathrm{\Delta }\gamma =\frac{eK[JJ]}{2\gamma m{c}^2}E(s^{\prime })z$ at the new position s′. After DS3, the bunching factor can be described as

$b\left(s^{\prime }\right)=\left|{\exp }^{-B_3^2/2}{J}_n\left(nA\left(s^{\prime }\right)B_3\right)\right|.(4)$

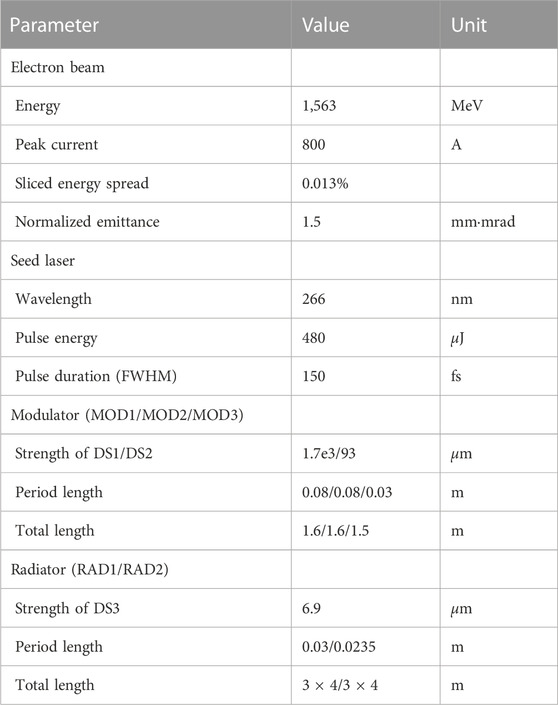
Here, we adopt the configurations of the SXFEL-UF to conduct the calculations of our proposed method. The calculations are performed based on the cascaded EEHG-HGHG scheme with relative time delays of 0, 120, and 300 fs. For the 120-fs case, the maximum energy modulation amplitudes A₁ and A₂ of the two seed lasers are both 4.8. For the 300-fs case, the maximum energy modulation amplitudes A₁ and A₂ are both 15.7. At the local manipulation position, the energy modulation amplitudes are all optimized to be 4. The energy modulation amplitude in MOD3 is about 5. The strength of DS1 is about 5.38. The harmonic number of the first stage EEHG is 20 and that of the second stage HGHG is 5. Hence, the total frequency up-conversion number is 100. Using the aforementioned theory, the squared bunching factors at the entrance of RAD1 and RAD2 with different time delays are shown in Figures 2A,C. The peak power of the seed lasers is also shown in Figure 2A. We can see that the smaller the relative time delay, the lower the peak power. In addition, we can obtain a qualitative analysis of the pulse durations based on the bunching factor distributions. Figure 2B shows a local enlarged image of Figure 2A that shows the bunching factor distributions in the overlapped region. One can find out that with the increase of the relative time delay, the pulse durations of the first-stage EEHG and the second-stage HGHG will both be shortened. We can also see that the first-stage EEHG has several side peaks, while the second-stage HGHG does not. To make comparisons, the squared bunching factors of the single-stage EEHG with the parameters optimized for the harmonic number of 100 are shown in Figure 2D, where one can also find that the bunching factor distributions under longer time delays will have narrower pulse durations. Also, the final pulse duration is comparable to that in the cascaded EEHG-HGHG scheme. However, considerable side peaks appeared in the single-stage EEHG scheme will result in similar longitudinal profiles of the FEL output, while in the cascaded EEHG-HGHG scheme, an isolated pulse can be generated.

FIGURE 2

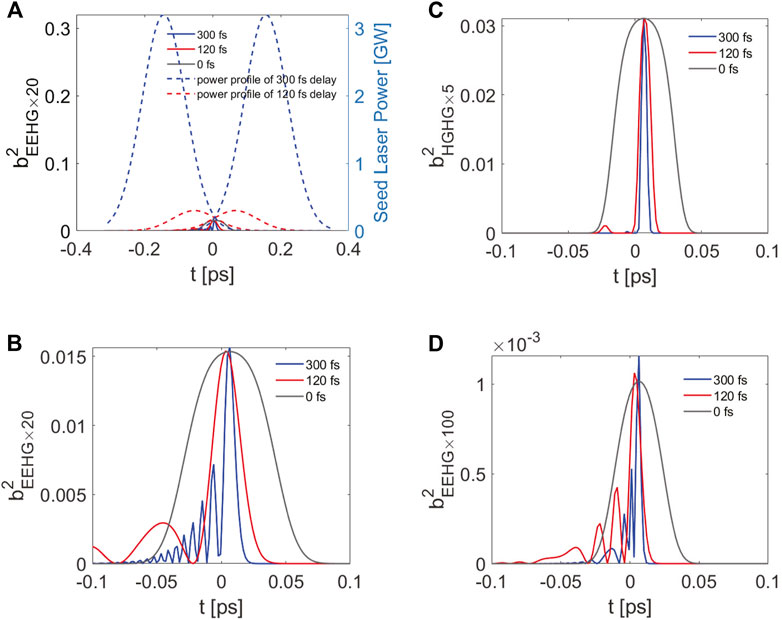
FIGURE 2. (A) Squared bunching factors of the cascaded scheme at the entrance of RAD1 with different time delays and the corresponding power profiles of the seed lasers. (B) Zoomed bunching factors of Figure 2A. (C) Squared bunching factors of the cascade scheme at the entrance of RAD2 with different relative time delays of the two seed lasers. (D) Squared bunching factors of the single-stage EEHG scheme at the entrance of the radiator with different relative time delays of the two seed lasers.

Generally, the dispersion strength B₂ of DS2 in the first-stage EEHG setup is critical to bunching properties. We demonstrate the optimization results of the bunching factor distributions with respect to different B₂ values, as shown in Figure 3. Figure 3A shows a large-scale three-dimensional scanning map. In addition, we select the right hot spot to be the optimized value of B₂ for a higher bunching factor and narrower width, which is 0.29 in dimensionless. Figure 3B shows the projection around the white dashed line. We can clearly see that there are many satellite side peaks along the bunching factor distributions. In addition, the satellite side peaks arising here can barely be eliminated. The reason is that, in the EEHG mechanism, the bunching properties are sensitive to the second modulation amplitude A₂, which is gradually changing with respect to their longitudinal positions due to the practical power profile of the overlapped seed laser part. Furthermore, the satellite peaks will appear when the changing amplitudes A₂ meet the local optimized conditions for a fixed given B₂ value. However, in the cascaded EEHG-HGHG scheme, even though the side peaks are nearly inevitable in the first-stage EEHG, by selecting an appropriate dispersion strength of DS3, they can be eliminated in the second-stage HGHG. In MOD3, the modulation amplitudes are relatively large at the main peak and relatively small at the side peaks. After DS3, with an R₅₆ value optimized for the main peak, density modulation at the main peak will show a higher bunching factor than that at the side peaks. Hence, the main peak will generate ultrashort FEL pulses in RAD2 without side peaks. The strength of DS3 is set to be 0.24 to meet the optimized condition of the HGHG section and eliminate the side peaks from EEHG.

FIGURE 3

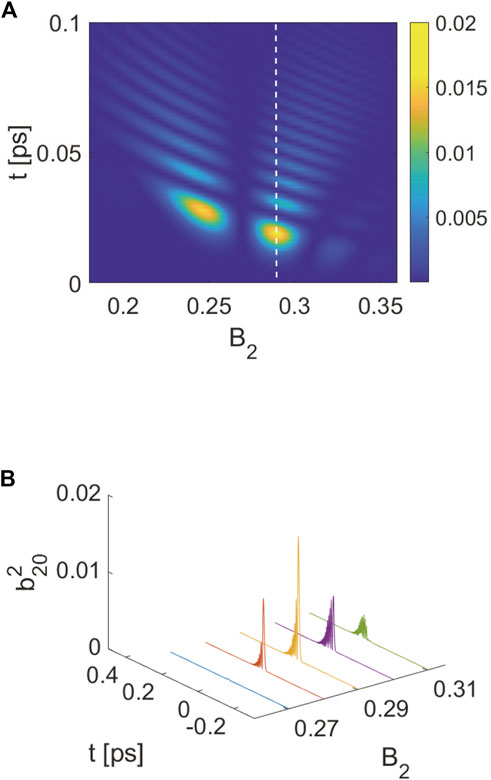
FIGURE 3. Optimization of B₂ of EEHG. (A) Squared bunching factor distributions with respect to different dispersion strengths B₂. The white dashed line is the optimized strength of DS2. (B) Projection around the white dashed line.

3 Experiments at the soft X-ray free-electron laser test facility

With the aforementioned theoretical analysis, we have conducted calculations and experiments at the Shanghai Soft X-ray Free-Electron Laser Test Facility (SXFEL-TF) to demonstrate the performance of the method. The parameters of the SXFEL-TF are shown in Table 1. Cascaded EEHG–HGHG is the basic working scheme at the SXFEL-TF, in which the harmonic number of the first-stage EEHG is 6 and that of the second-stage HGHG is 5. We can eventually achieve 8.8-nm soft x-ray FEL radiation from the 264-nm ultra-violet external seed laser. Based on the typical parameters and configurations of the SXFEL-TF, we conducted the numerical calculations and practical experiments for our method with different relative time delays of the two seed lasers employed in the first-stage EEHG. The results are shown in Figure 4. In the calculations, the squared bunching factors after the first-stage sixth harmonic EEHG and after the second-stage fifth harmonic HGHG with respect to different time delays are shown in Figures 4A,B. We can see that although the maximum bunching factors are basically the same, the approximately equivalent pulse durations of the first-stage EEHG and the second-stage HGHG are both shorter for the relatively larger time delay of 133 fs. In comparison, the squared bunching factors of the single-stage 30th harmonic EEHG are shown in Figure 4C. We can clearly see that there exist side peaks beside the main bunching peak for the 133-fs time delay case, while for cascaded EEHG-HGHG, the final bunching factor distributions shown in Figure 4B are much cleaner.

TABLE 1

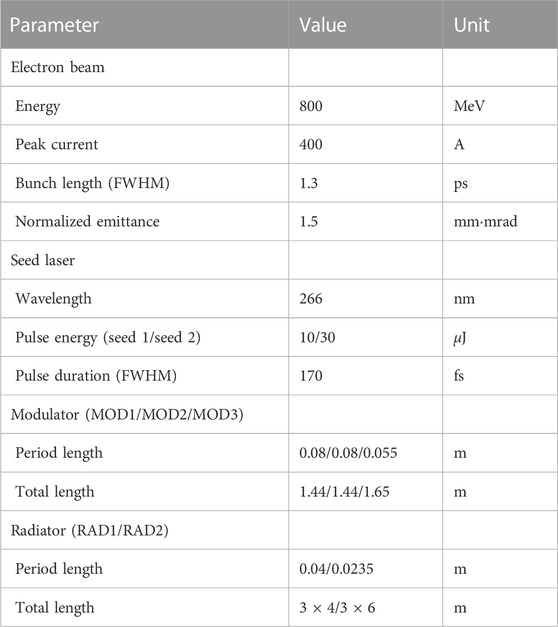
TABLE 1. Parameters for the SXFEL-TF experiments.[49].

FIGURE 4

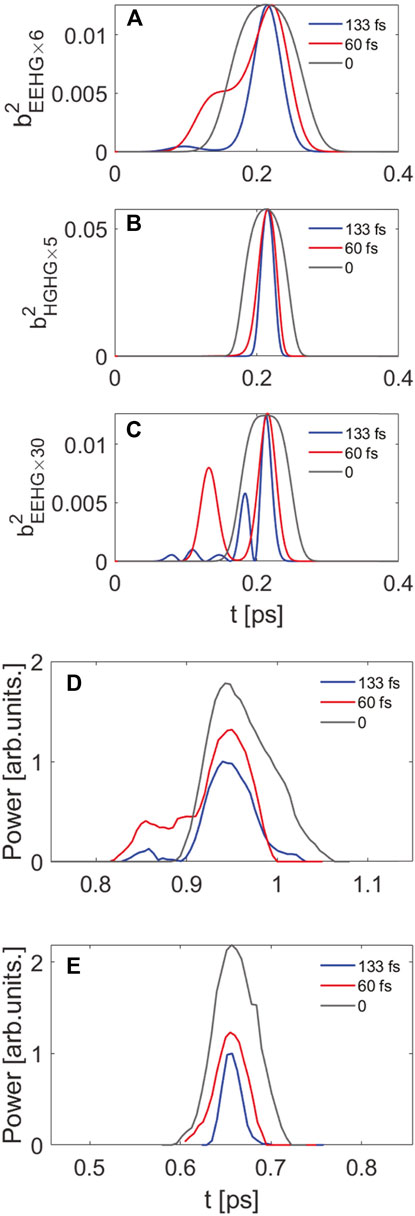
FIGURE 4. (A) Squared bunching factors of the first-stage EEHG with different time delays. (B) Squared bunching factors of the second-stage HGHG with different time delays. (C) Squared bunching factors of the single-stage EEHG with different time delays. Experimental results of the normalized reconstructed FEL power profiles for different time delays: (D) the first-stage EEHG-FEL pulses; (E) the second-stage HGHG-FEL pulses.

In the experiments, with the increase of the relative time delay of the two seed lasers, the pulse energy was also increased. The pulse energy is 30 μJ for the relative time delay of 133 fs, while for the 60-fs case, it is 10 μJ. The results of the experiments are shown in Figures 4D,E. We have reconstructed the normalized FEL radiation profiles with the relative time delay 0 fs, 60 fs, and 133 fs [48,49]. The power profiles shown in Figure 4D correspond to the first-stage EEHG, while Figure 4E corresponds to the second-stage HGHG. Figure 4D shows that there exist small side peaks in the first-stage EEHG radiation with the time delay being 60 fs and 133 fs, while Figure 4E shows that the second-stage HGHG can deliver single spike pulses with narrower durations. The duration of the FEL pulse from the first stage is about 85 fs (FWHM) for the 0-fs time delay case, and around 58 fs (FWHM) for the 60-fs and 133-fs delay cases, as shown in Figure 4D. The FEL pulse durations from RAD2 will further be shortened due to the pulse shortening effect [49–51]. The final pulse duration for the 0-fs time delay is about 57 fs (FWHM), for the 60-fs time delay is about 41 fs (FWHM), and for the 133-fs time delay is about 25 fs (FWHM), as shown in Figure 4E. These experimental results demonstrate that the proposed method can be used for pulse duration control in a seeded FEL by changing the relative time delay of the two seed lasers. However, the shortest pulse duration is limited to about 25 fs due to the slippage effect, which is about 18 fs in RAD2 in accordance with this experiment.

4 Three-dimensional simulations based on the soft X-ray free-electron laser user facility

With a shorter radiation wavelength, it is possible to further reduce the output pulse duration due to the shorter slippage length. Here, we adopt the main parameters of the SXFEL user facility (SXFEL-UF), as shown in Table. 2, to perform three-dimensional start-to-end simulations. The schematic layout of the SXFEL-UF is shown in Figure 1. The initial beam is generated by Astra [52], a program package imitating the beam dynamics from a photoinjector, taking into consideration the space charge effects. The acceleration process in the LINAC is conducted with the beam tracking code ELEGANT [53], considering the coherent synchrotron radiation (CSR) and incoherent synchrotron radiation (ISR) effects. The final FEL amplification process is simulated by the 3D time-dependent code GENESIS [54]. Figure 5 shows the longitudinal phase space and current distribution of the electron beam using the end of the LINAC. In our simulations when generating shorter FEL pulses, the relative time shift should increase. At the same time, to keep a relatively large bunching factor at the local overlapped area, the energy modulation amplitudes increase too, and the pulse energy of the seed lasers should increase correspondingly. To maintain reasonable seed laser pulse energy, the maximum relative time delay of the two seed lasers is set to be 300 fs. To satisfy the modulation strength requirements at this position, the pulse energy of the seed lasers should change simultaneously with the relative time delay of the seed lasers changing. Thus, the two seed lasers employed in the first-stage EEHG both have a pulse duration of 150 fs (FWHM) and a maximal pulse energy of 480 μJ.

TABLE 2

TABLE 2. Parameters for the start-to-end simulations.

FIGURE 5

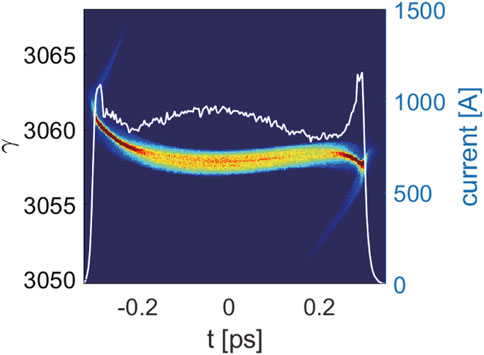
FIGURE 5. Longitudinal phase space and current distribution of the electron beam by the end of the LINAC of the SXFEL-UF.

Figure 6 shows the FEL performances in the first and second stages. At the entrance of RAD1, the maximum bunching factor is about 9%, as shown in Figure 6A. Figure 6B shows an ultrafast 13.3 nm radiation with a peak power of about 300 MW, and a pulse duration of about 36 fs (FWHM) is generated through RAD1. We can see that there exist satellite side peaks. The corresponding spectrum is shown in Figure 6C. After DS3, the maximum bunching factor at the entrance of RAD2 is about 1.2%, and a final FEL pulse at 2.66 nm is obtained over a 200-MW peak power through RAD2, as shown in Figures 6D,E. The final FEL pulse duration can also be efficiently shortened to about 5.2 fs. The corresponding spectrum is shown in Figure 6F. For seeded FELs, the dispersion strength has an important impact on the output pulse properties [45,46]. Thus, to obtain a shorter pulse duration, the R₅₆ value of DS3 is chosen to be a little bit weaker than the calculated optimized value, and the bunching factor is also smaller than the calculation results. According to the equations in Section 2, this weaker R₅₆ value will be of significant benefit to smearing out the density modulation of the side peaks, thus shortening the final FEL pulse duration in RAD2.

FIGURE 6

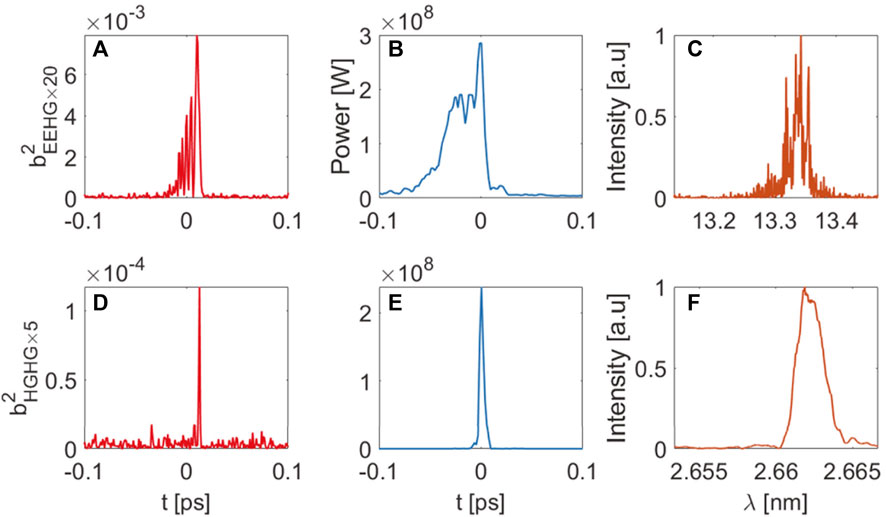
FIGURE 6. (A) Squared bunching factor of the simulation results at the entrance of RAD1 with a harmonic number of 20. (B) Power of the EEHG-FEL radiation. (C) Spectrum of the EEHG-FEL radiation. (D) Squared bunching factor of the simulation results at the entrance of RAD2 with a harmonic number of 5. (E) Power of the HGHG-FEL radiation. (F) Spectrum of the HGHG-FEL radiation.

The evolution of the pulse duration and the corresponding spectrum along RAD2 has also been shown in Figure 7. The FEL radiation pulse has a pulse duration of about 4.41 fs at the exit of the first undulator segment. After that, the pulse duration is increased by approximately 1.12 fs per undulator segment and finally increases to about 5.2 fs after a total of four undulator segments, as shown in Figure 7B. Due to the slippage effects, the pulse duration of the final FEL at the exit of RAD2 will always be several times the slippage length, which will be a limitation to generate even shorter FEL radiation pulses.

FIGURE 7

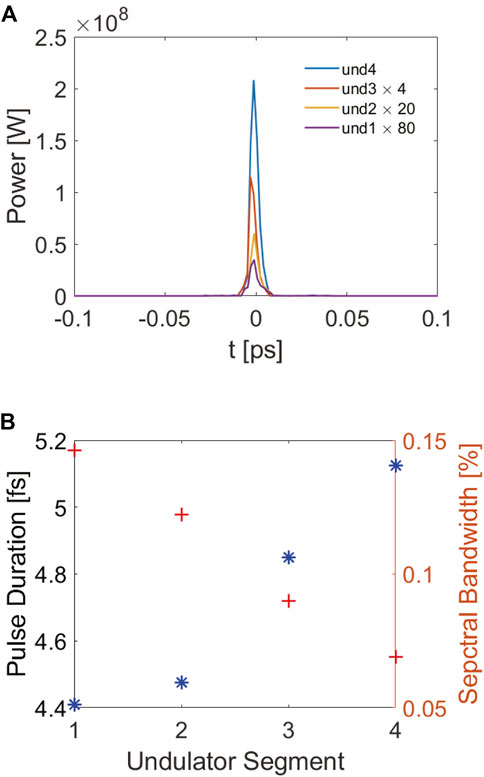
FIGURE 7. (A) Radiation power profiles at various undulator segments along RAD2. (B) FEL pulse duration and spectral bandwidth evolutions at various undulator segments along RAD2.

We also provide the simulation results of controlling the final FEL pulse durations at a wavelength of 2.66 nm with different time delays from 120 fs to 300 fs. Figure 8 shows that for the relative time delay of 120-fs case, the final pulse duration from RAD2 is about 65 fs. Also, with the increase of the relative time delay, the pulse duration can gradually be decreased. For the 300-fs time delay, the final FEL pulse duration is only about 5.2 fs, as we have presented previously. Moreover, to maintain the optimized condition of the bunching factor, the pulse energy of the seed lasers should be increased accordingly. In our simulation, the seed laser pulse energy for 120-fs time delay is about 30 μ J, while for the 300-fs time delay, it is increased to more than 480 μ J. The required seed laser pulse energy grows rapidly with the increase of the relative time delay.

FIGURE 8

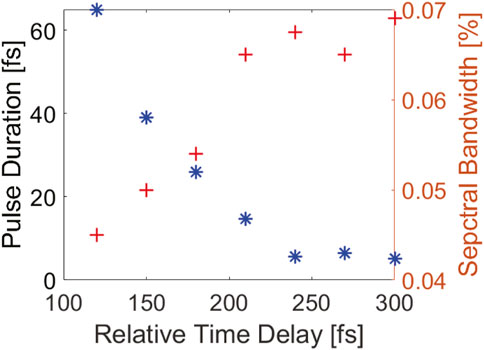
FIGURE 8. FEL pulse duration and spectral bandwidth with respect to different relative time delays between the two seed lasers.

5 Conclusion

In this article, we have studied a simple method to generate few-femtosecond fully coherent ultrashort soft X-ray FEL pulses and control the final FEL pulse durations in a seeded FEL. This method also holds promising prospects for generating fully coherent ultrashort FEL radiation pulses in high-repetition-rate FEL facilities. By changing the relative time delay and correspondingly the pulse energy of the two seed lasers employed in EEHG, bunching properties of the electron beam can be manipulated and ultrashort FEL pulses can be generated. Based on the SXFEL, we studied the performances of the method through theoretical analysis, numerical simulations, and practical experiments. The experimental results are consistent with the theories and simulations. The simulation results indicate that an isolated 5.2-fs FEL pulse at 2.66 nm can be obtained with a peak power of about 200 MW, and the pulse duration is controllable with respect to the relative time delay. The final output FEL radiation pulse duration is essentially limited by the slippage length in the radiator, indicating that even shorter pulses can be generated at higher harmonics.

Data availability statement

The raw data supporting the conclusion of this article will be made available by the authors, without undue reservation.

Author contributions

WF and CF contributed to the conception and design of the study. WF performed the statistical analysis. WF, CF, and ZQ wrote the first draft of the manuscript. CF and ZQ conducted the experiments. MZ and CF are the supervisors. All authors contributed to manuscript revision, reading, and approved the submitted version.

Funding

This work is supported by the National Natural Science Foundation of China (12122514 and 11975300) and the Shanghai Science and Technology Committee Rising-Star Program (20QA1410100).

Acknowledgments

The authors would like to thank the SXFEL group on the experiments.

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

1. Emma P, Akre R, Arthur J, Bionta R, Bostedt C, Bozek J, et al. First lasing and operation of an ångstrom-wavelength free-electron laser. Nat Photon (2010) 4:641–7. doi:10.1038/nphoton.2010.176

CrossRef Full Text | Google Scholar

2. Ishikawa T, Aoyagi H, Asaka T, Asano Y, Azumi N, Bizen T, et al. A compact X-ray free-electron laser emitting in the sub-ångström region. Nat Photon (2012) 6:540–4. doi:10.1038/nphoton.2012.141

CrossRef Full Text | Google Scholar

3. Allaria E, Castronovo D, Cinquegrana P, Craievich P, Dal Forno M, Danailov MB, et al. Two-stage seeded soft-X-ray free-electron laser. Nat Photon (2013) 7:913–8. doi:10.1038/nphoton.2013.277

CrossRef Full Text | Google Scholar

4. Kang HS, Min CK, Heo H, Kim C, Yang H, Kim G, et al. Hard X-ray free-electron laser with femtosecond-scale timing jitter. Nat Photon (2017) 11:708–13. doi:10.1038/s41566-017-0029-8

CrossRef Full Text | Google Scholar

5. Milne CJ, Schietinger T, Aiba M, Alarcon A, Alex J, Anghel A, et al. SwissFEL: The Swiss X-ray free electron laser. Appl Sci (Switzerland) (2017) 7:720–57. doi:10.3390/app7070720

CrossRef Full Text | Google Scholar

6. Decking W, Abeghyan S, Abramian P, Abramsky A, Aguirre A, Albrecht C, et al. A MHz-repetition-rate hard X-ray free-electron laser driven by a superconducting linear accelerator. Nat Photon (2020) 14:391–7. doi:10.1038/s41566-020-0607-z

CrossRef Full Text | Google Scholar

7. Giannessi L, Musumeci P, Spampinati S. Nonlinear pulse evolution in seeded free-electron laser amplifiers and in free-electron laser cascades. J Appl Phys (2005) 98:043110. doi:10.1063/1.2010624

CrossRef Full Text | Google Scholar

8. Yan J, Deng HX, Wang D, Dai ZM. EEHG-assisted FEL schemes for attosecond X-ray pulses generation. Nucl Instr Methods Phys Res Section A: Acc Spectrometers, Detectors Associated Equipment (2010) 621:97–104. doi:10.1016/j.nima.2010.06.099

CrossRef Full Text | Google Scholar

9. Huang S, Ding Y, Huang Z, Marcus G. Generation of subterawatt-attosecond pulses in a soft x-ray free-electron laser. Phys Rev Acc Beams (2016) 19:080702. doi:10.1103/PhysRevAccelBeams.19.080702

CrossRef Full Text | Google Scholar

10. Tanaka T, Rebernik Ribič P. Shortening the pulse duration in seeded free-electron lasers by chirped microbunching. Opt Express (2019) 27:30875. doi:10.1364/oe.27.030875

PubMed Abstract | CrossRef Full Text | Google Scholar

11. Duris J, Li S, Driver T, Champenois EG, MacArthur JP, Lutman AA, et al. Tunable isolated attosecond X-ray pulses with gigawatt peak power from a free-electron laser. Nat Photon (2020) 14:30–6. doi:10.1038/s41566-019-0549-5

CrossRef Full Text | Google Scholar

12. Maroju PK, Grazioli C, Di Fraia M, Moioli M, Ertel D, Ahmadi H, et al. Attosecond pulse shaping using a seeded free-electron laser. Nature (2020) 578:386–91. doi:10.1038/s41586-020-2005-6

PubMed Abstract | CrossRef Full Text | Google Scholar

13. Xiao Y, Feng C, Liu B. Generating isolated attosecond x-ray pulses by wavefront control in a seeded free-electron laser. Ultrafast Sci (2022) 2022:9812478. doi:10.34133/2022/9812478

CrossRef Full Text | Google Scholar

14. Clark JN, Beitra L, Xiong G, Higginbotham A, Fritz DM, Lemke HT, et al. Ultrafast three-dimensional imaging of lattice dynamics in individual gold nanocrystals. Science (2013) 341:56–9. doi:10.1126/science.1236034

PubMed Abstract | CrossRef Full Text | Google Scholar

15. Hantke MF, Hasse D, Maia FR, Ekeberg T, John K, Svenda M, et al. High-throughput imaging of heterogeneous cell organelles with an X-ray laser. Nat Photon (2014) 8:943–9. doi:10.1038/nphoton.2014.270

CrossRef Full Text | Google Scholar

16. Kupitz C, Basu S, Grotjohann I, Fromme R, Zatsepin NA, Rendek KN, et al. Serial time-resolved crystallography of photosystem II using a femtosecond X-ray laser. Nature (2014) 513:261–5. doi:10.1038/nature13453

PubMed Abstract | CrossRef Full Text | Google Scholar

17. Clark JN, Beitra L, Xiong G, Fritz DM, Lemke HT, Zhu D, et al. Imaging transient melting of a nanocrystal using an X-ray laser. Proc Natl Acad Sci United States America (2015) 112:7444–8. doi:10.1073/pnas.1417678112

PubMed Abstract | CrossRef Full Text | Google Scholar

18. Van Der Schot G, Svenda M, Maia FR, Hantke M, Deponte DP, Seibert MM, et al. Imaging single cells in a beam of live cyanobacteria with an X-ray laser. Nat Commun (2015) 6:5704–9. doi:10.1038/ncomms6704

PubMed Abstract | CrossRef Full Text | Google Scholar

19. Gorman MG, Briggs R, McBride EE, Higginbotham A, Arnold B, Eggert JH, et al. Direct observation of melting in shock-compressed bismuth with femtosecond X-ray diffraction. Phys Rev Lett (2015) 115:095701. doi:10.1103/PhysRevLett.115.095701

PubMed Abstract | CrossRef Full Text | Google Scholar

20. Fletcher LB, Lee HJ, Döppner T, Galtier E, Nagler B, Heimann P, et al. Ultrabright X-ray laser scattering for dynamic warm dense matter physics. Nat Photon (2015) 9:274–9. doi:10.1038/nphoton.2015.41

CrossRef Full Text | Google Scholar

21. Ekeberg T, Svenda M, Abergel C, Maia FR, Seltzer V, Claverie JM, et al. Three-dimensional reconstruction of the giant mimivirus particle with an X-ray free-electron laser. Phys Rev Lett (2015) 114:098102–6. doi:10.1103/PhysRevLett.114.098102

PubMed Abstract | CrossRef Full Text | Google Scholar

22. Kondratenko AM, Saldin EL. Generation of coherent radiation by a relativistic electron beam in an ondulator. Part Acc Print (1980) 10:207–216.

Google Scholar

23. Bonifacio R, Pellegrini C, Narducci LM. Collective instabilities and high-gain regime in a free electron laser. Opt Commun (1984) 50:373–8. doi:10.1016/0030-4018(84)90105-6

CrossRef Full Text | Google Scholar

24. Andruszkow J, Aune B, Ayvazyan V, Baboi N, Bakker R, Balakin V, et al. First observation of self-amplified spontaneous emission in a free-electron laser at 109 nm wavelength. Phys Rev Lett (2000) 85:3825–9. doi:10.1103/PhysRevLett.85.3825

PubMed Abstract | CrossRef Full Text | Google Scholar

25. Geloni G, Kocharyan V, Saldin E. A novel self-seeding scheme for hard X-ray FELs. J Mod Opt (2011) 58:1391–403. doi:10.1080/09500340.2011.586473

CrossRef Full Text | Google Scholar

26. Amann J, Berg W, Blank V, Decker FJ, Ding Y, Emma P, et al. Demonstration of self-seeding in a hard-X-ray free-electron laser. Nat Photon (2012) 6:693–8. doi:10.1038/nphoton.2012.180

CrossRef Full Text | Google Scholar

27. Stoupin S, Blank VD, Terentyev SA, Polyakov SN, Denisov VN, Kuznetsov MS, et al. Diamond crystal optics for self-seeding of hard X-rays in X-ray free-electron lasers. Diamond Relat Mater (2013) 33:1–4. doi:10.1016/j.diamond.2012.12.009

CrossRef Full Text | Google Scholar

28. Zhang K, Qi Z, Feng C, Deng H, Wang D, Zhao Z. Extending the photon energy coverage of an x-ray self-seeding FEL via the reverse taper enhanced harmonic generation technique. Nucl Instr Methods Phys Res Section A: Acc Spectrometers, Detectors Associated Equipment (2017) 854:3–10. doi:10.1016/j.nima.2017.02.039

CrossRef Full Text | Google Scholar

29. Inoue I, Osaka T, Hara T, Tanaka T, Inagaki T, Fukui T, et al. Generation of narrow-band X-ray free-electron laser via reflection self-seeding. Nat Photon (2019) 13:319–22. doi:10.1038/s41566-019-0365-y

CrossRef Full Text | Google Scholar

30. Yu LH. Generation of intense uv radiation by subharmonically seeded single-pass free-electron lasers. Phys Rev A (1991) 44:5178–93. doi:10.1103/PhysRevA.44.5178

PubMed Abstract | CrossRef Full Text | Google Scholar

31. Yu LH, Ben-Zvi I. High-gain harmonic generation of soft X-rays with the ”fresh bunch” technique. Nucl Instr Methods Phys Res Section A: Acc Spectrometers, Detectors Associated Equipment (1997) 393:96–9. doi:10.1016/S0168-9002(97)00435-X

CrossRef Full Text | Google Scholar

32. Dattoli G, Ottaviani PL. Design considerations for x-ray free electron lasers. J Appl Phys (1999) 86:5331–6. doi:10.1063/1.371528

CrossRef Full Text | Google Scholar

33. Liu B, Li WB, Chen JH, Chen ZH, Deng HX, Ding JG, et al. Demonstration of a widely-tunable and fully-coherent high-gain harmonic-generation free-electron laser. Phys Rev Spec Top - Acc Beams (2013) 16:020704. doi:10.1103/PhysRevSTAB.16.020704

CrossRef Full Text | Google Scholar

34. Allaria E, Badano L, Bassanese S, Capotondi F, Castronovo D, Cinquegrana P, et al. The FERMI free-electron lasers. J Synchrotron Radiat (2015) 22:485–491. doi:10.1107/S1600577515005366

PubMed Abstract | CrossRef Full Text | Google Scholar

35. Xiang D, Stupakov G. Echo-enabled harmonic generation free electron laser. Phys Rev Spec Top - Acc Beams (2009) 12:030702. doi:10.1103/PhysRevSTAB.12.030702

CrossRef Full Text | Google Scholar

36. Zhao ZT, Wang D, Chen JH, Chen ZH, Deng HX, Ding JG, et al. First lasing of an echo-enabled harmonic generation free-electron laser. Nat Photon (2012) 6:360–3. doi:10.1038/nphoton.2012.105

CrossRef Full Text | Google Scholar

37. Xiang D, Colby E, Dunning M, Gilevich S, Hast C, Jobe K, et al. Evidence of high harmonics from echo-enabled harmonic generation for seeding X-Ray free electron lasers. Phys Rev Lett (2012) 108:024802. doi:10.1103/PhysRevLett.108.024802

PubMed Abstract | CrossRef Full Text | Google Scholar

38. Hemsing E, Dunning M, Hast C, Raubenheimer TO, Weathersby S, Xiang D. Highly coherent vacuum ultraviolet radiation at the 15th harmonic with echo-enabled harmonic generation technique. Phys Rev Spec Top - Acc Beams (2014) 17:070702. doi:10.1103/PhysRevSTAB.17.070702

CrossRef Full Text | Google Scholar

39. Hemsing E, Dunning M, Garcia B, Hast C, Raubenheimer T, Stupakov G, et al. Echo-enabled harmonics up to the 75th order from precisely tailored electron beams. Nat Photon (2016) 10:512–5. doi:10.1038/nphoton.2016.101

CrossRef Full Text | Google Scholar

40. Ribič PR, Roussel E, Penn G, De Ninno G, Giannessi L, Penco G, et al. Echo-enabled harmonic generation studies for the FERMI free-electron laser. Photonics (2017) 4:19. doi:10.3390/photonics4010019

CrossRef Full Text | Google Scholar

41. Feng C, Deng H, Zhang M, Wang X, Chen S, Liu T, et al. Coherent extreme ultraviolet free-electron laser with echo-enabled harmonic generation. Phys Rev Acc Beams (2019) 22:050703. doi:10.1103/PhysRevAccelBeams.22.050703

CrossRef Full Text | Google Scholar

42. Zhu ZY, Zhao ZT, Wang D, Liu Z, Li RX, Yin LX, et al. Sclf: An 8-GEV CW SCRF linac-based x-ray FEL facility in Shanghai. In: Proceedings of the 38th International Free-Electron Laser Conference, FEL 2017; 20-25 August 2017; Santa Fe, NM, United States (2017). p. 182–184. doi:10.18429/JACoW-FEL2017-MOP055

CrossRef Full Text | Google Scholar

43. Haixiao D, Xingtao W, Zhimin D. Short-pulse length effects of the seed laser in high-gain harmonic generation free-electron laser. Phys Rev Spec Top - Acc Beams (2008) 11:040703. doi:10.1103/PhysRevSTAB.11.040703

CrossRef Full Text | Google Scholar

44. Labat M, Joly N, Bielawski S, Szwaj C, Bruni C, Couprie ME. Pulse splitting in short wavelength seeded free electron lasers. Phys Rev Lett (2009) 103:264801. doi:10.1103/PhysRevLett.103.264801

PubMed Abstract | CrossRef Full Text | Google Scholar

45. Gauthier D, Ribič PR, De Ninno G, Allaria E, Cinquegrana P, Danailov MB, et al. Spectrotemporal shaping of seeded free-electron laser pulses. Phys Rev Lett (2015) 115:114801. doi:10.1103/PhysRevLett.115.114801

PubMed Abstract | CrossRef Full Text | Google Scholar

46. Finetti P, Höppner H, Allaria E, Callegari C, Capotondi F, Cinquegrana P, et al. Pulse duration of seeded free-electron lasers. Phys Rev X (2017) 7:021043. doi:10.1103/PhysRevX.7.021043

CrossRef Full Text | Google Scholar

47. Mirian NS, Di Fraia M, Spampinati S, Sottocorona F, Allaria E, Badano L, et al. Generation and measurement of intense few-femtosecond superradiant extreme-ultraviolet free-electron laser pulses. Nat Photon (2021) 15:523–9. doi:10.1038/s41566-021-00815-w

CrossRef Full Text | Google Scholar

48. Zeng L, Feng C, Gu D, Wang X, Zhang K, Liu B, et al. Online single-shot characterization of ultrafast pulses from high-gain free-electron lasers. Fundam Res (2022) 2:929–36. doi:10.1016/j.fmre.2022.01.027

CrossRef Full Text | Google Scholar

49. Feng C, Liu T, Chen S, Zhou K, Zhang K, Qi Z, et al. Coherent and ultrashort soft x-ray pulses from echo-enabled harmonic cascade free-electron lasers. Optica (2022) 9:785. doi:10.1364/optica.466064

CrossRef Full Text | Google Scholar

50. Ratner D, Fry A, Stupakov G, White W. Laser phase errors in seeded free electron lasers. Phys Rev Spec Top - Acc Beams (2012) 15:030702. doi:10.1103/PhysRevSTAB.15.030702

CrossRef Full Text | Google Scholar

51. Wang G, Feng C, Zhang T, Wang D, Deng H. Study on the seed laser phase error multiplication in seeded free electron lasers. Nucl Instr Methods Phys Res Section A: Acc Spectrometers, Detectors Associated Equipment (2014) 737:237–41. doi:10.1016/j.nima.2013.11.020

CrossRef Full Text | Google Scholar

52. Floettmann K. ASTRA users manual (1999). Available at: https://www.desy.de/∼mpyflo/ (Accessed March, 2017).

Google Scholar

53. Borland M. Elegant: A flexible SDDS-compliant code for accelerator simulation. In: Proceedings of 6th International Computational Accelerator Physics Conference; 11-14 September 2000; Darmstadt, Germany (2000). 1–11. doi:10.2172/761286

CrossRef Full Text | Google Scholar

54. Reiche S. Genesis 1.3: A fully 3D time-dependent FEL simulation code. Nucl Instr Methods Phys Res Section A: Acc Spectrometers, Detectors Associated Equipment (1999) 429:243–8. doi:10.1016/S0168-9002(99)00114-X

CrossRef Full Text | Google Scholar