Tunable non‐Hermitian skin effects in Su‐Schrieffer‐Heeger‐like models

Wu, Shi-Qiao; Xu, Yadong; Jiang, Jian-Hua

doi:10.3389/fphy.2023.1123596

ORIGINAL RESEARCH article

Front. Phys., 14 February 2023
Sec. Condensed Matter Physics
Volume 11 - 2023 | https://doi.org/10.3389/fphy.2023.1123596

Tunable non-Hermitian skin effects in Su-Schrieffer-Heeger-like models

Shi-Qiao Wu*

Yadong Xu

Jian-Hua Jiang

Institute of Theoretical and Applied Physics, School of Physical Science and Technology & Collaborative Innovation Center of Suzhou Nano Science and Technology, Soochow University, Suzhou, China

The flourishment of non-Hermitian topology has promoted the development of skin effect, a well-known feature of the non-Hermitian systems, by which the bulk states evolve from extended to localized toward boundaries. However, in previous works, the scenarios are usually delicately designed with intricate parameters to explore the skin effects. In this work, we propose a simple paradigm to implement tunable non-Hermitian skin effects in one and two-dimensional Su-Schrieffer-Heeger (SSH)-like tight-binding models. Skin modes with distinct dimensions can be predicted irrespective of the non-Hermitian systems are topological or not. They also have no relations with the coupling values, but only are dependent on the scaling factors of non-reciprocal hopping terms. Furthermore, by engineering the hopping configurations, the skin modes could be predicted at expected edges or corners, featuring skin effects hierarchical. These tunable non-Hermitian skin effects and higher-dimensional non-Hermitian skin effects can be exploited to guide waves into targeted regions and may have useful applications when realized in metamaterials.

Introduction

The most remarkable hallmark of topological phases of matter is the scattering-free transportation behavior dictated by the topological properties of bulk bands [1, 2]. In non-Hermitian systems, bulk states also become localized, resulting in the breakdown of conventional bulk-edge correspondence. Hence, edge properties cannot be dictated by their bulks any more. In non-Hermitian systems, eigenenergy of bulk bands own real and imaginary values simultaneously. And their eigenvectors are not mutually orthogonal any more. These intriguing characters prompt non-Bloch band theory in energy-nonconservative systems. Based on the non-Hermitian band theory, many exotic phenomena can be well resolved with skin effects for example, which are usually implemented by introducing asymmetry couplings [3–23] or onsite gain and loss [24–36]. A variety of works [5, 11, 16, 17, 19, 20, 31, 34, 36] have been dedicated to the exploration of skin modes and non-Hermitian topological properties in non-Hermitian systems during the past decade. Recently, [17] theoretically proposed a new mechanism defined as hybrid skin topological principle to achieve skin modes, which are induced by the intricate interplay of non-Hermitian topology and net non-reciprocal pumping. Furthermore, [3] experimentally studied the transformation of topological states from localized to extended resort to the non-Hermitian skin modes. The intriguing phenomena have also been verified in an active mechanical experiment. More recently, Zeng et al. found energy-dependent skin modes in one-dimensional (1D) system with non-reciprocal hopping beyond the nearest-neighboring sites. Inverse participation ratio was also calculated to characterize the localization of the skin localized states. In these non-Hermitian works, skin effects are mainly explored by delicately setting specific hopping amplitudes and non-Hermitian strength [3, 4, 8, 16–18, 20, 21]. This may impede the experimental implementation at the same time due to the strict requirement of tuning fine parameters. A pressing task that how to decrease the difficulty of tuning parameters to realize skin modes then was put forward. Besides, it can easily be found that the study on skin modes in the lattice with non-reciprocity between all the nearest-neighboring (NN) lattice sites has typically been ignored and related mechanism of skin effect in these cases still remains elusive.

In this work, we study the tunable non-Hermitian skin effects (NHSE) in 1D and 2D SSH-like tight-binding models. In particular, we show that the emergence of skin effect is mainly induced by the scaling factors of unequal forward and backward hoppings for intracell and intercell terms. In our scheme, inequivalence of forward and backward hopping terms breaks the standard bulk-boundary correspondence, leading to the emergence of skin effects in 1D SSH-like lattices and higher-dimensional skin effect in 2D SSH-like lattices. It can be found that no matter the systems are in topological or trivial phase, the profiles of the skin modes are almost the same in 1D or 2D SSH-like lattice models, apart from the survival of zero-energy topological modes in the topological phase. Furthermore, the profiles of skin modes can also be tuned feasibly by judiciously reconfiguring the scaling factors configuration. With no need of delicate design of hopping amplitudes, our results provide a promising paradigm to realize NHSE, which may be potentially implemented in photonic systems [24, 37–48], phononic systems [25, 29, 32, 49–52] and electrical circuits [53–57].

Tunable NHSE in 1D SSH-like model

We consider a general 1D SSH-like tight-binding lattice model as illustrated by the schematics in Figure 1A. And the Hamiltonian of the 1D SSH-like model in momentum space can be read as,

H = [\begin{array}{c} 0 & t_{1} + t_{2} e^{- i k_{x}} \\ {m t}_{1} + n t_{2} e^{i k_{x}} & 0 \end{array}] (1)

where $k_{x}$ is the Bloch wave vector. $t_{1}$ and ${m t}_{1}$ represent leftward and rightward coupling coefficients of the intracell hopping terms. For the intercell hoppings, the leftwards and rightwards coupling amplitudes are denoted as ${n t}_{2}$ and $t_{2}$ , respectively. If $m = n = 1$ , it will restore to standard SSH model. In this scenario, we first set $t_{1} = 2$ and $t_{2} = 1$ . In Hermitian model, all the eigenenergy of the Hamiltonian are real. However, the introduction of non-Hermiticity in non-Hermitian Hamiltonian makes the eigenenergy complex. The complexity of eigenenergy enable multiple exotic phenomena and versatile properties in non-Hermitian systems. Obviously, Eq. 1 is a non-Hermitian Hamiltonian. To explore the skin effects, we plot both of the energy spectra and intensity profiles of all the eigenstates of Eq. 1 for different sets of $m$ and $n$ . The band structure of the unit cell under PBC and the energy spectra of the open chain (comprise 40 primitive units) under OBC can be attained by diagonalizing their Hamiltonians in momentum space, and we plot them by black and blue dots in complex-energy planes in Figures 1B–D for three sets of parameters $m = 5, n = 10;$ $m = 10, n = 10$ and $m = 10, n = 5$ , respectively. From the energy spectra plots, it can be found that both the spectra under PBC and OBC are symmetric with respect to zero energy, which is direct manifestation of preserved chiral symmetry [58, 59]. It can also be found that as long as scaling factor $m$ differentiate $n$ , the spectra under PBC form two isolated circles [black dots in Figures 1B, D], otherwise they would become two symmetric arcs [black dots in Figure 1C]. For all the three cases, the spectral shapes under OBC look like two symmetric arcs. That is to say, if the scaling factors $m$ and $n$ are not the same, the spectra of the primitive unit of the non-Hermitian system under PBC are complex, which is a hallmark of non-Hermitian system in the presence of non-Hermiticity. The highly sensitive character of complex energy to the boundary conditions is an obvious indicator of skin effect in non-Hermitian model. It should be noticed that the spectra in Figure 1C are very similar to those in Hermitian systems because of the emergence of line gap [see Figures 1B, D].

FIGURE 1

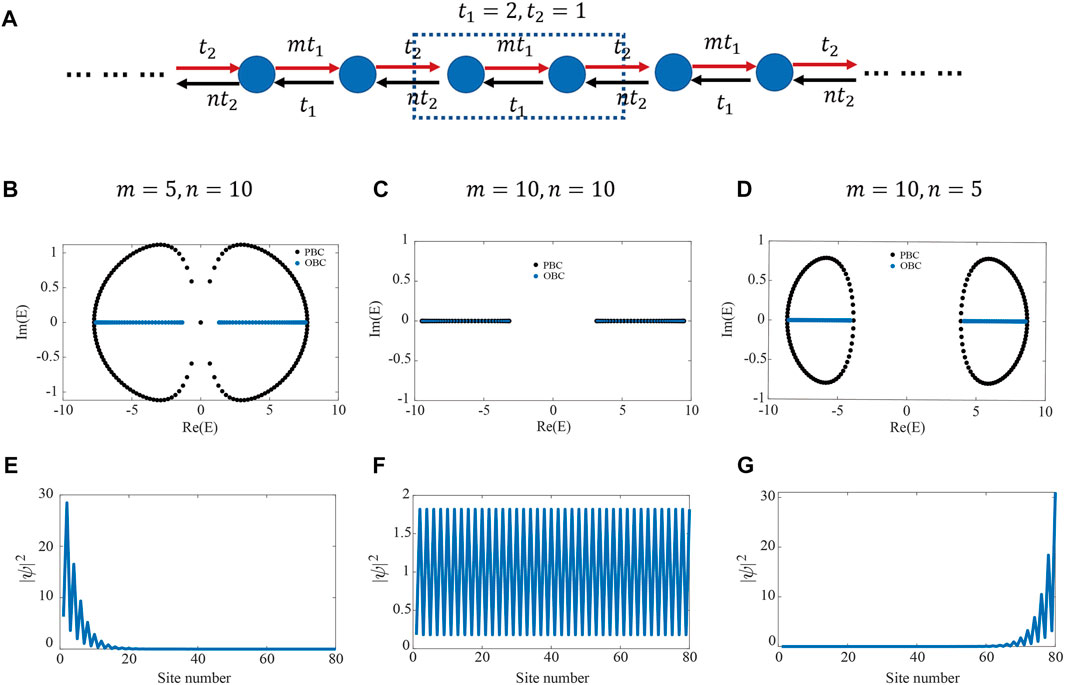
FIGURE 1. (A) Schematics of a 1D non-Hermitian SSH-like model with non-reciprocal hoppings between NN sites. Dashed rectangle encloses the unit cell. Blue dots denote sublattice sites. Leftward hoppings of intracell and intercell are represented by symbols $t_{1}$ and $n t_{2}$ while $m t_{1}$ and $t_{2}$ for rightward hoppings. The scaling factors of hoppings terms within and across unit cells are separately denoted as $m$ and $n$ . The complex spectra under PBC and OBC and superimposed intensity profiles under an open chain are calculated and exhibited in (B) (E) for the case of $m = 5, n = 10$ , in (C) (F) for $m = 10, n = 10$ , and in (D) (G) for $m = 10, n = 5$ .

Moreover, the skin effect can also be directly revealed by examining the superimposed intensity profiles of all the eigenstates. In fact, the most rigorous method to affirm skin effect of the non-Hermitian systems is to check the profile of every eigenfunction of all the eigenstates. As the procedure in previous works [3, 10, 17, 32, 36], the superposition of all the eigenstates profiles can also demonstrate the phenomenology attribute of the skin effect. In Figures 1E–G, wo plot ${|ψ|}^{2} = \sum_{i = 1}^{N} {|ψ_{i}|}^{2}$ , where N = 80 is the number of the eigenstates as the 1D lattice model consists of 40 primitive cells. Obviously, the intensity profiles decay exponentially from left ending or right ending rapidly into the bulk region [in Figures 1E, G], respectively, which is direct observation of the skin modes. In the scenario of $m = 5, n = 10$ , intercell hopping scaling factor $n$ is larger than intracell hopping scaling factor $m$ , then skin modes show up and collapse toward the left ending as the leftward hopping term $n t_{2}$ points to. Instead, if $m = 10, n = 5$ , the skin modes dwell at the right ending [in Figure 1G], which is the consequence of scaling factor $m$ larger than $n$ . When $m = n = 10$ , both the scaling factors are identical, the summation of squared amplitude of all the eigenstates uniformly distributed along lattice sites [see Figure 1F], manifesting the vanishment of skin effect. In addition, the energy spectra [Figure 1C] under different boundary conditions are almost the same, indicating the inexistence of skin effect. So far, we have discovered that the skin modes can be tuned by the scaling factors $m$ and, but contribution of the parameters $t_{1}$ and $t_{2}$ still remains elusive.

In the following, we go on to consider the same sets of parameters $m$ and $n$ as the cases above in the 1D non-Hermitian SSH-like chain, but reverse the values of $t_{1}$ and $t_{2}$ , i.e., $t_{1} = 1$ and $t_{2} = 2$ . The localized behavior of superimposed intensity profiles of all the eigenstates at each side of the 1D lattice also persists as long as parameters $m$ and $n$ are unequal, as shown in Figures 2B–L. Furthermore, the intensity profiles under the situation of $m = n = 10$ are also uniform along lattice sites [see Figure 2G]. The spectra in Figures 2A, F, K are almost identical to those in Figures 1B–D, except for emergent zero-energy states under OBC, which are induced by topological property. To further figure it out, we also plot the real part of the eigenenergy vs. state number in Figures 2C, H, M, in which two degenerate eigenstates remain at the middle of the band gap. The squared amplitudes of the two eigenstates pinned at zero energy are respectively plotted in the lowest two rows in Figure 2. It is particularly noted that in the case of Figure 2F, even the skin modes disappear [Figure 2G], zero-energy eigenstates still manifest localized phenomena [Figures 2I, J]. The abnormal behavior is triggered by the topological property of the system and have no relation with the skin modes. It is worth mentioning that topological edge states will typically exist if $t_{1} < t_{2}$ . And skin effect occurs, which is driven by the non-Hermiticity if the condition of $m \neq n$ is satisfied. In contrast to the topological boundary states in Hermitian systems, here the profiles of the degenerate zero-energy topological boundary states assemble at the same ending of the 1D non-Hermitian SSH-like chain. From the study above, we notice that the skin modes are determined by scaling factors $m$ and $n$ instead of hopping amplitudes $t_{1}$ and $t_{2}$ . In fact, the physical consequences still maintain if $t_{1}$ and $t_{2}$ are arbitrarily assigned.

FIGURE 2

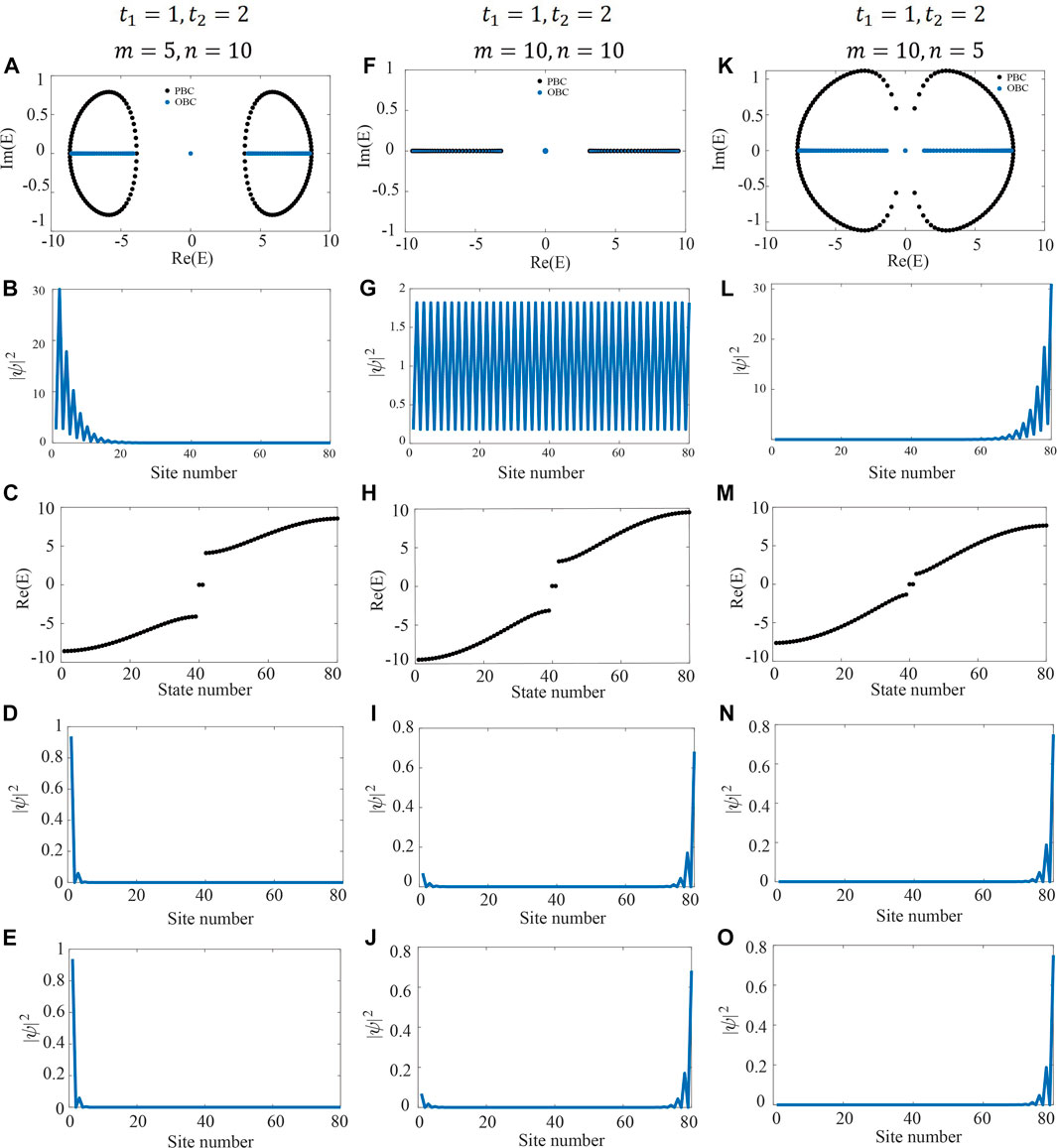
FIGURE 2. We consider three sets of $m$ and $n$ with $t_{1} = 1$ and $t_{2} = 2$ . In subpictures (A)–(E), we respectively plot and show the energy spectra, summed intensity profile of all the eigenstates, the real part of eigen energy and intensity profile of in-gap eigenstates in the scenario of $m = 5, n = 10$ . Similar calculations are also conducted and the results are displayed in (F)–(J) and (K)–(O) separately for the cases of $m = 10, n = 10$ and $m = 10, n = 5$ . The energy spectra in complex-energy planes under the condition of $t_{1} = 1$ , $t_{2} = 2$ are very similar to those in the schemes of $t_{1} = 2$ , $t_{2} = 1$ except for the emergence of zero-energy eigenstates, which essentially are topological states and can be understandable due to larger intercell hopping $(t_{2})$ over the intracell $(t_{1})$ .

Tunable higher-dimensional NHSE in 2D SSH-like model

The higher-dimensional NHSE (HD-NHSE) is the counterpart of NHSE in the higher-dimensional system. In this section, we proceed by extending the 1D SSH-like model into 2D, as illustrated in Figure 3A. Through the Fourier transformation of the real-space Hamiltonian, the Hamiltonian in reciprocal space can be expressed as follows,

H = [\begin{array}{c} 0 & 0 & - t_{x 1} - t_{x 2} e^{- i k_{x}} & t_{y 1} + t_{y 2} e^{- i k_{y}} \\ 0 & 0 & p_{3} t_{y 3} + p_{4} t_{y 4} e^{i k_{y}} & m_{3} t_{x 3} + m_{4} t_{x 4} e^{i k_{x}} \\ {- m}_{1} t_{x 1} {- m}_{2} t_{x 2} e^{i k_{x}} & t_{y 3} + t_{y 4} e^{- i k_{y}} & 0 & 0 \\ p_{1} t_{y 1} + p_{2} t_{y 2} e^{i k_{y}} & t_{x 3} + t_{x 4} e^{- i k_{x}} & 0 & 0 \end{array}] (2)

FIGURE 3

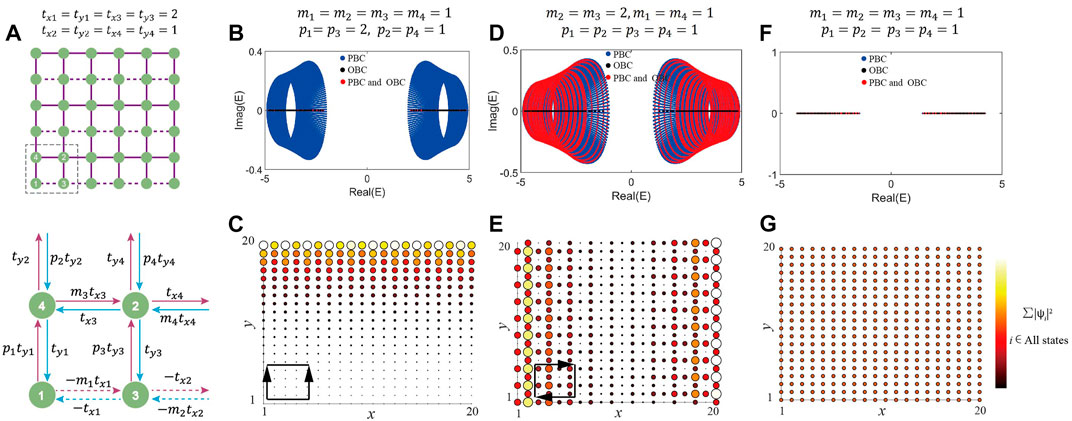
FIGURE 3. (A) Illustration of a 2D SSH-like lattice model with dashed box highlighting the primitive cell. The enlarged inset clearly shows the detail of non-reciprocal hoppings between NN sites. Positive and negative hoppings are denoted by solid and dashed lines. Under double PBCs (blue dots), double OBCs (black dots) and $y$ -OBC/ $x$ -PBC (red dots), we respectively plot eigenenergy in the complex-energy planes for three sets of ratio coefficients [(B) (D) (F)]. Accordingly, the intensity profiles of all the eigenmodes are also respectively summed and plotted in subfigure (C), (E), and (G) with dots representing amplitude of skin mode intensity. The insets depict the forming mechanism of skin modes.

In the remain of the main text, we set intracell hopping parameters $t_{x 1} = t_{y 1} = t_{x 3} = t_{y 3} = 2$ and intercell hopping parameters $t_{x 2} = t_{y 2} = t_{x 4} = t_{y 4} = 1$ . Then the system is in trivial phase, which imposes no effect on the research of skin effect, as evidenced by the study of 1D non-Hermitian lattice above. Within each plaquette of the 2D SSH-like model, there exists eight scaling factors, which are termed as $m_{1}$ , $m_{3}$ , $p_{1}$ , $p_{3}$ for intracell hoppings and $m_{2}$ , $m_{4}$ , $p_{2}$ , $p_{4}$ for intercell hoppings. The configurations of scaling factors can be tuned flexibly to reconfigure the intensity profile of the eigen modes. If all the scaling factors are the same, then the system returns to the conventional quadrupole model with quantized moment. In addition, the system still preserves chiral symmetry ${\bar{σ}}_{z} H (k_{x}, k_{y}) {\bar{σ}}_{z} = - H (k_{x}, k_{y})$ , ${\bar{σ}}_{z} = σ_{z} \otimes Ι$ , in which $σ_{z}$ is the third Pauli matrix and $Ι$ is $2 \times 2$ identity matrix, as evidenced by symmetry energy spectra with respective to the real axes in the complex-energy plane.

First, we consider a hopping configuration, as shown by the inset in Figure 3C. Net non-reciprocal pumping vanishes along $x$ direction because of $m_{1} = m_{2} = m_{3} = m_{4}$ . As for $y$ direction, net non-reciprocity pumping can be formed due to the instructively interfere ( $p_{1} > p_{2} a n d p_{3} > p_{4}$ ). Then the eigen modes can accumulate toward the upper boundary of the finite-sized lattice consisting of $10 \times 10$ units [see Figure 3C], resulting in the skin modes. To investigate the origin of the skin effect in this 2D lattice model, energy spectra with three types of boundary conditions including double OBCs, double PBCs, and $y$ -OBC $/ x$ -PBC are plotted. Generically, the trajectory of energy spectra would transform from closed loops (under double PBCs) into open lines or arcs (under double OBCs) if a system owns skin effect, while the $y$ -OBC $/ x$ -PBC is the transition boundary condition between them. In Figure 3B, the spectra between double PBCs (blue dots) and double OBCs (black dots) vary greatly, which further substantiate the skin effect in this case. Based on the recognition of the hopping configuration in Figure 3C, the net non-reciprocities generate in $x$ direction ( $m_{1} \neq m_{2}, m_{3} \neq m_{4}$ ) but cancel in $y$ direction ( $p_{1} = p_{2} = p_{3} = p_{4}$ ). Skin modes hence manifest as boundary localized modes at left and right boundaries of the lattice simultaneously [in Figure 3E]. The area of the energy spectra in Figure 3D shrinks from large loop to segment along with the decrease of PBC dimensions. In contrast, if the scaling factors are all the same along both directions, which is the 2D extension of the sample in Figure 1F, then the eigen modes are uniformly distributed along lattice sites [Figure 3G] and the spectra are identical arcs under different boundary conditions [Figure 3F]. Up to now, we have found that the law of adopting scaling factors to expect skin modes also works in 2D generic non-reciprocal lattice.

In addition to the 1D edge-toward NHSE, HD-NHSE with 2D corner-toward skin modes can also be judiciously designed and predicted by configuring the scaling factor profiles. In Figure 4, three configurations are delicately designed to induce three types of HD-NHSE with various corner-toward localized modes, including diagonally distributed skin corner modes [Figure 4C], parallelly distributed skin corner modes [Figure 4E] and isolated skin corner modes [Figure 4G]. These skin modes are generated by intersection of net non-reciprocal pumping along different directions. The energy spectra of the three settings are also numerically calculated, and respectively plotted in Figures 4B–F. Under double PBCs, the spectra consist of a number of large loops and these loops become small when $y$ -directed dimension turns into OBC, and eventually they degenerate to be arcs under double OBCs, obvious indicator of HD-NHSE, i.e., skin corner modes in 2D systems. Similar skin modes can also be achieved when other sets of parameters $t_{1}$ and $t_{2}$ are taken into account. According to the principle of generating skin effects in 1D and 2D SSH-like models, skin surface modes, higher-dimensional skin hinge modes and higher-dimensional skin corner modes can also be constructed and realized in 3D counterpart of SSH-like models.

FIGURE 4

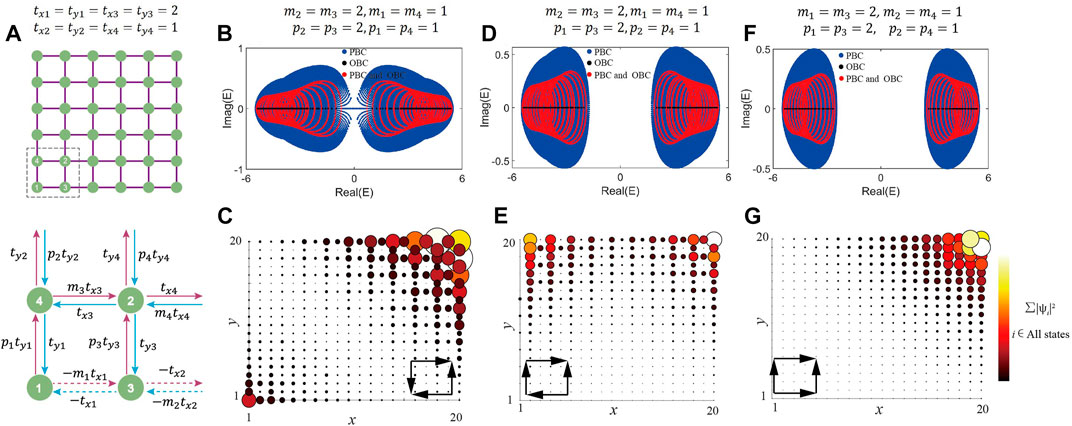
FIGURE 4. (A) Diagram of a 2D SSH-like lattice model with its primitive unit in the inset below the main panel. (B)–(C) Complex energy spectra under three different boundary conditions and HD-NHSE with skin modes at two diagonal corners. (D)–(E) Complex energy spectra and HD-NHSE with skin modes at two parallel corners. (F)–(G) Complex energy spectra and HD-NHSE with skin modes at an isolated corner. The insets inside panels (C), (E) and (G) schematically show the net non-reciprocal pumping directions.

Though similar skin modes have been realized in theoretical work [17] and observed in experiment [3]. Whereas the non-reciprocity strength in these works seriously influences the effect of skin modes. And this further imposes more stringent demand to the realization in experiment. In comparison, in our proposed scheme, the expected skin modes are mainly induced by the scaling coefficient of left- and right-toward (upper- and lower-toward) hopping terms rather than their hopping amplitudes. This would dramatically expand the parameters threshold ranges and be beneficial to the experimental implementation. Our proposal offers new theoretical route to realize skin effects and provide a blueprint to study non-Hermitian topological property, which may further inspire potential application.

Conclusion and outlook

In conclusion, we numerically investigated the NHSE in 1D SSH-like model and HD-NHSE in 2D SSH-like model. Here, the non-Hermiticity are introduced by the non-reciprocal hoppings of both intercell and intracell sites. Non-reciprocity inevitably contributes to the formation of non-zero net non-reciprocal pumping and result in the emergence of skin modes. Furthermore, the energy spectra and skin modes can be easily regulated by configuring the pumping pattern. Our study provides useful and feasible designs for generating controllable NHSE that can be potentially realized in various physical platforms such as electrical circuits, sonic crystals, and electromagnetic metamaterials. In addition, our findings also provide alternative degree of freedom to realize non-Hermiticity.

Data availability statement

The raw data supporting the conclusion of this article will be made available by the authors, without undue reservation.

Author contributions

All authors listed have made a substantial, direct, and intellectual contribution to the work and approved it for publication.

Funding

The authors acknowledge support from National Natural Science Foundation of China (Grant Nos. 12074281 and 12047541), the Jiangsu specially appointed professor funding, and the Academic Program Development of Jiangsu Higher Education (PAPD).

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

1. Hasan MZ, Kane CL. Colloquium: Topological insulators. Rev Mod Phys (2010) 82:3045–67. doi:10.1103/revmodphys.82.3045