Experiments probing clustering effects in explosive nucleosynthesis

1 Introduction

It has long been known that nuclei can exhibit a number of nuclear structure effects. One common effect is the tendency to form sub-clusters of strongly-bound groups of nucleons. One of the most common types of clusters is the formation of α particles that may additionally be joined by one or two valence nucleons. In fact, the tendency to form α clusters is even imprinted on the solar abundances (see Figure 1), which show peaks for the light elements of nuclei composed of integer numbers of α particles. Nuclear states with this high degree of clusterization often also exhibit larger charge radii, high degrees of deformation, and enhanced emission rates of particle clusters.

FIGURE 1

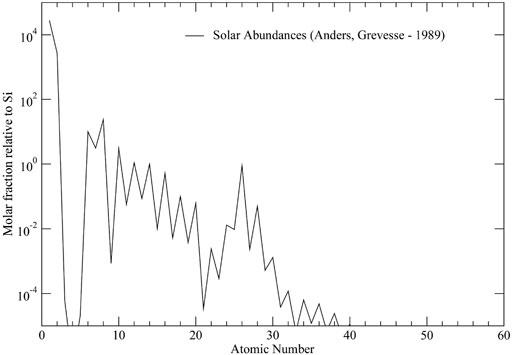
FIGURE 1. The solar abundances from data tabulated in Ref. [1]. The enhanced stability exhibited by α-cluster nuclei in imprinted directly onto the abundance pattern.

It is often observed that cluster states will appear near the cluster threshold and can therefore greatly enhance astrophysical reaction rates. The most famous example of such a state is the Hoyle state in ¹²C, which enables the triple α process to form carbon and bypass the A = 8 abundance gap [2]. Other processes involving cluster states were also found to be important in the nucleosynthesis occurring in the first generation of stars [3]. A somewhat less explored topic is the role that cluster structure may play in explosive environments such as novae, X-ray bursts, and supernovae. The primary goal of this manuscript is to discuss such topics and provide examples of experiments probing the cluster structure of nuclei important to explosive nucleosynthesis.

2 Explosive nucleosynthesis

Explosive nucleosynthesis occurs in a number of environments, and the burning is driven by a variety of phenomena. One common trigger is accretion-driven nuclear fuel consumption such as in novae, type Ia supernovae, and X-ray bursts. These can occur in binary systems with hydrogen being accreted from one star onto its compact and further-evolved companion. The material accumulates in a thin layer but quickly compresses and heats as a result of the large surface gravity. Thermonuclear burning of the hydrogen ignites this surface fuel, and an astrophysical explosion results. Since convection can be significant, the nuclear burning typically involves subsequent proton-induced reactions on stable seed nuclei producing neutron-deficient nuclei, which can undergo subsequent reactions before decaying. The nucleosynthesis produces exotic nuclei up to roughly Ca in a nova explosion [4] and up to nuclei around Sn in an X-ray burst [5]. The exotic nuclei then decay back to stability producing the final abundance pattern of the explosion.

While the nucleosynthesis is driven by the compression and heating of a hydrogen-rich layer, the influence of α-cluster nuclei also have a dramatic impact. For instance in novae, the temperatures are not hot enough for a full rapid-proton (rp) capture process to occur, and the nucleosynthesis proceeds through a series of nuclear cycles [similar to the Hot CNO (HCNO) cycles] that ultimately lead to the production of heavier nuclei. Each of these cycles (as shown in Figure 2) is closed by a (p, α) reaction, and the existence of α-cluster resonances in these reactions can greatly increase their rates. Type I X-ray bursts also occur in accreting binaries and emit X-rays with light curves lasting 10–100 s and recurring with periods of hours to days. The peak of the burst is initiated with the αp process [¹⁴O(α, p)¹⁷F(p, γ)¹⁸Ne(α, p)²¹Na(p, γ)²²Mg…], which eventually transitions to the rp capture process leading to heavy element production (See Figure 3). Recent sensitivity studies have shown that a number of these (α, p) reactions along with a handful of others can have dramatic effects on the observed X-ray burst light curve [7, 8]. These important (α, p) reactions could be strongly enhanced by α cluster resonances. Finally, supernovae type Ia (SNIa) are also accretion-driven phenomena. When a CO white dwarf accretes enough mass from its companion star, thermonuclear supernova explosions can occur. Type Ia supernovae always reach approximately the same brightness and are therefore considered the astronomer’s standard candle. A recent sensitivity study [9] found five nuclear reactions to be the most critical to determine for SNIa nucleosynthesis: ¹²C(α, γ)¹⁶O, ¹²C+¹²C, ²⁰Ne(α, p), ²⁰Ne(α, γ), and ³⁰Si(p, γ). Of these five, four are strongly influenced by the existence of clusterized states in the compound nucleus.

FIGURE 2

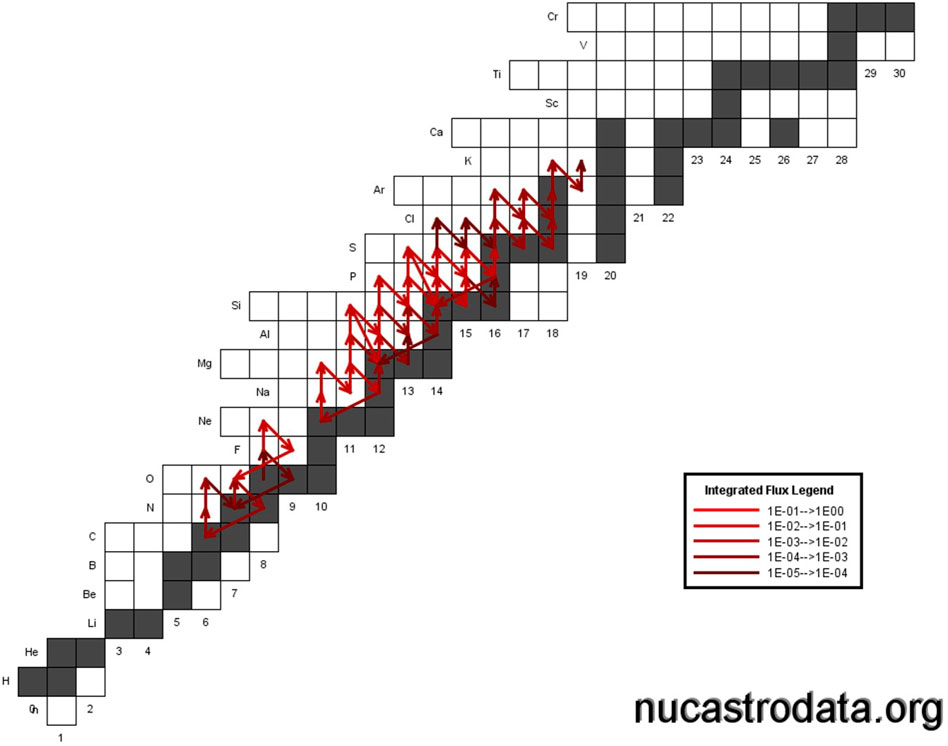
FIGURE 2. A snapshot of the nuclear reaction flow of an energetic nova explosion. The color of the arrows indicates the fraction of the total integrated flow (i.e., flux) that proceeds through a given reaction. Pronounced cycling can occur with individual cycles closed by (p, α) reactions.

FIGURE 3

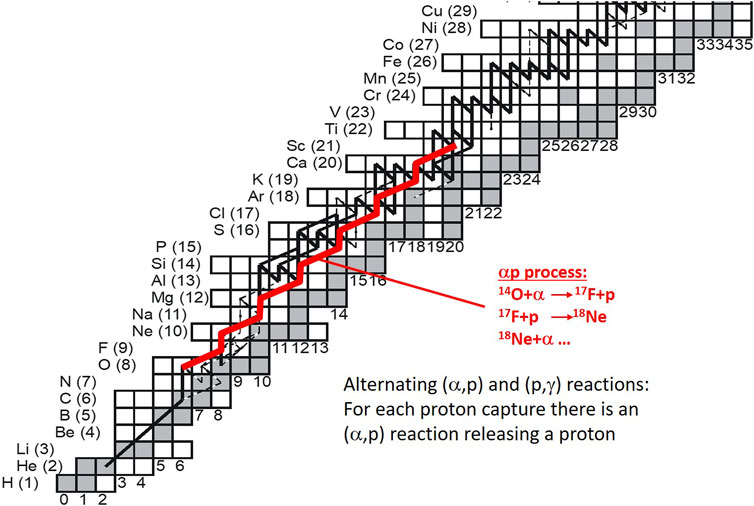
FIGURE 3. The αp process in an accreting neutron star [6].

Core-collapse supernovae (CCSN) are, however, an entirely different phenomenon. Stars with more than about eight times the mass of our Sun may collapse to form core-collapse supernovae. As such a star collapses and compresses the core to nuclear densities, the equation of state becomes stiff and a shock wave is formed. Elements in and around the core are rapidly photo-dissociated back to free protons, neutrons and α particles. A significant fraction of the protons convert to neutrons inside the core, resulting in a burst of electron neutrinos. This burst then produces a neutrino-driven wind that could be strong enough that sufficient neutrino-nucleon interactions occur, powering the nuclear reaction network in the (photo-dissociated) outer layer of the core. While the core is ultimately doomed to further collapse into a neutron star or black hole, the layers outside undergo nucleosynthesis in α-rich zones that initially are dominated by quasi-static equilibrium burning [10]. As these zones ultimately cool, an α-rich freeze-out occurs that ultimately determines the final abundances of observable nuclei such as ⁴⁴Ti and ⁵⁶Ni. The α-induced nuclear reactions occurring within these zones would be strongly-influenced by cluster states necessitating a good understanding of these to interpret the nucleosynthetic signatures produced by such events.

3 Astrophysical reaction rates

3.1 Calculation of stellar reaction rates

The rate of thermonuclear reactions per unit of stellar volume for reactions of the type: a + X → Compound nucleus → Y + b is given by [11] as

$r=\frac{N_a{N}_X}{1+{\delta }_{aX}}<\sigma v>.(1)$

In this equation N_aN_X is the product of the number densities of the two nuclei in the entrance channel, the Kronecker delta, δ_aX, is 1 if the reacting nuclei are identical and 0 otherwise, and $<\sigma v>$ is the product of the reaction cross section σ and the center-of-mass velocity v averaged over the Maxwell-Boltzmann energy distribution at a stellar temperature T:

$\begin{array}{ccc}\hfill <\sigma v>& =\hfill & {\left(\frac{8}{\pi \mu {\left(kT\right)}^3}\right)}^{\frac{1}{2}}{\int }_0^{\infty }E\sigma \left(E\right)\exp \left(-\frac{E}{kT}\right)dE\hfill \\ \hfill & =\hfill & \frac{6.1968\times 10^{-14}}{A^{\frac{1}{2}}{T}_9^{\frac{3}{2}}}{\int }_0^{\infty }E\sigma \left(E\right)\exp \left(-\frac{11.605E}{T_9}\right)dE{\mathrm{c}\mathrm{m}}^3/\sec .\hfill \end{array}(2)$

In Eq. 2, E is the center-of-mass energy in MeV, T₉ = T/10⁹ K, k is the Boltzmann constant, μ is the reduced mass, and A is the reduced mass in atomic mass units [12].

Gamow first showed, in connection with the problem of alpha decay, that the probability for two particles of Z_a and Z_X moving with relative velocity v to penetrate their electrostatic repulsion is proportional to the factor

$\mathrm{P}\mathrm{e}\mathrm{n}\mathrm{e}\mathrm{t}\mathrm{r}\mathrm{a}\mathrm{t}\mathrm{i}\mathrm{o}\mathrm{n}\propto \exp \left(-\frac{2\pi Z_a{Z}_X{e}^2}{\hslash v}\right).(3)$

It follows that the cross sections for nuclear reactions will also tend to be proportional to such a factor, since reactions can hardly occur unless particles penetrate this repulsion. It is, therefore, convenient to factor out this term and express the nuclear cross section in terms of the astrophysical S-factor, S(E) as follows:

$\sigma \left(E\right)=\frac{1}{E}\exp \left(-2\pi \eta \right)S\left(E\right),(4)$

where $\eta =\frac{Z_a{Z}_X{e}^2}{\hslash v}$ is the Sommerfeld parameter. The exponential term exp(−2πη) corrects, in a first-order approximation, for the influence of the Coulomb barrier in cases where electron screening can be ignored. At the high temperatures characterizing explosive nucleosynthesis environments, electron screening is rarely an issue. The factor $\frac{1}{E}$ arises from the fact that the quantum-mechanical interaction between two particles is always proportional to a geometrical factor πλ², where λ is the de Broglie wavelength:

$\pi {\lambda }^2\propto {\left(\frac{1}{p}\right)}^2\propto \frac{1}{E}.(5)$

The advantage of writing the cross section in this way is that two of the strongly energy-dependent factors appearing in the nuclear cross sections are factored explicitly, leaving a residual function of energy, S(E), which usually exhibits a much weaker energy dependence. Under the above assumptions, the S-factor would represent the intrinsically nuclear parts of the probability for the occurrence of a nuclear reaction, whereas the other two explicit factors represent well-known energy dependences that are non-nuclear in nature. Because of this weak energy dependence, the S-factor is often used to extrapolate measured cross sections to astrophysical energies [11]. If Eq. 4 is inserted into Eq. 2, then the reaction rate per particle pair becomes

$<\sigma v>={\left(\frac{8}{\pi \mu {\left(kT\right)}^3}\right)}^{\frac{1}{2}}{\int }_0^{\infty }S\left(E\right)\exp \left(-\frac{E_G^{1/2}}{E^{1/2}}-\frac{E}{kT}\right)dE,(6)$

where $E_G=2\mu {(\pi e^2{Z}_a{Z}_X/\hslash )}^2$ is the Gamow energy [12]. By taking the first derivative of the integrand in Eq. 6, one can find E_o, the most effective energy for thermonuclear reactions at a given temperature T:

$E_o={\left(\frac{E_G^{1/2}kT}{2}\right)}^{2/3}=1.22{\left(Z_a^2{Z}_X^{2}A{T}_6^2\right)}^{1/3}\mathrm{k}\mathrm{e}\mathrm{V}.(7)$

Since the integrand in Eq. 6 decreases exponentially for all energies outside of the Gamow window, E_o ±Δ where

$\mathrm{\Delta }=4{\left(\frac{kT{E}_o}{3}\right)}^{1/2},(8)$

the stellar reaction rate at any temperature depends mostly on the S-factor in the Gamow window. The thermonuclear reaction rate is, therefore, very sensitive to the properties of resonances which lie in the Gamow window.

3.2 Resonant reactions

For low energy reactions involving light ions, such as those reactions in the HCNO cycle, the cross section will be dominated by the properties of just a few resonances. Direct capture can also contribute but is typically not important for reactions occurring in explosive nucleosynthesis. The nuclear cross section for a resonant reaction can be expressed in the Breit-Wigner form [13]:

$\sigma \left(E\right)=\frac{{\lambda }^2}{4\pi }\frac{2J+1}{\left(2J_a+1\right)\left(2J_X+1\right)}\frac{{\mathrm{\Gamma }}_a\left(E\right){\mathrm{\Gamma }}_b\left(E\right)}{{\left(E-E_{\mathit{res}}\right)}^2+{\left(\mathrm{\Gamma }\left(E\right)/2\right)}^2},(9)$

where J, J_a, and J_X are the spins of the resonance and the two incident nuclei, respectively. E_res is the center-of-mass resonance energy. Γ_a, Γ_b, and Γ are the partial widths in the entrance and exit channel and the total width, respectively. If Eq. 9 is inserted into Eq. 2, we get a general expression for the reaction rate per particle pair through a single resonance:

$<\sigma v>={\left(\frac{8}{\pi \mu {\left(kT\right)}^3}\right)}^{\frac{1}{2}}{\int }_0^{\infty }\frac{{\lambda }^2}{4\pi }\frac{\omega E{\mathrm{\Gamma }}_a\left(E\right){\mathrm{\Gamma }}_b\left(E\right)}{{\left(E-E_{\mathit{res}}\right)}^2+{\left(\mathrm{\Gamma }\left(E\right)/2\right)}^2}\exp \left(-\frac{E}{kT}\right)dE(10)$

where $\omega =\frac{2J+1}{(2J_a+1)(2J_X+1)}$. If the resonance is isolated and narrow, this expression reduces to

$<\sigma v>={\left(\frac{2\pi }{\mu kT}\right)}^{3/2}{\hslash }^2{\left(\omega \gamma \right)}_{\mathit{res}}\exp \left(-\frac{E_{\mathit{res}}}{kT}\right),(11)$

where (ωγ)_res is the resonance strength for the resonance:

${\left(\omega \gamma \right)}_{\mathit{res}}=\frac{2J_{\mathit{res}}+1}{\left(2J_a+1\right)\left(2J_X+1\right)}\frac{{\mathrm{\Gamma }}_a{\mathrm{\Gamma }}_b}{{\mathrm{\Gamma }}_{\mathit{res}}}.(12)$

For several non-overlapping resonances this can be generalized to

$<\sigma v>={\left(\frac{2\pi }{\mu kT}\right)}^{3/2}{\hslash }^2\sum _i{\left(\omega \gamma \right)}_i\exp \left(-\frac{E_i}{kT}\right).(13)$

If, on the other hand, the resonances are broad, then Eq. 10 must be integrated taking the energy dependence of the widths into account. The most commonly used method to parameterize the widths is in terms of the reduced width ${\theta }_{\ell }^2$ [13]:

${\mathrm{\Gamma }}_{\ell }\left(E\right)=\frac{2\hslash c}{R_n}{\left(\frac{2E}{\mu c^2}\right)}^{1/2}{P}_{\ell }\left(\zeta ,\rho \right){\theta }_{\ell }^2.(14)$

Here Γ_ℓ is the partial width in the relevant reaction channel for the ℓ^th partial wave, R_n is the radius of the relevant reaction channel, and P_ℓ is the penetrability for the ℓ^th partial wave in a given reaction channel:

$P_{\ell }=\frac{1}{F_{\ell }^2\left(\zeta ,\rho \right)+G_{\ell }^2\left(\zeta ,\rho \right)}.(15)$

The functions F_ℓ(ζ, ρ) and G_ℓ(ζ, ρ) are the regular and irregular Coulomb wavefunctions, which are solutions to the Schrödinger equation with a Coulomb potential. The arguments of the Coulomb functions are given by

$\begin{array}{ccc}\hfill \zeta & =\hfill & \frac{Z_a{Z}_X\alpha }{2}\sqrt{\frac{2\mu c^2}{E}}\hfill \\ \hfill \rho & =\hfill & k{R}_n=\frac{\sqrt{2\mu c^{2}E}}{\hslash c}{R}_n\hfill \end{array}(16)$

where α is the fine structure constant. The physical interpretation of the partial width is that it is the product of two probabilities. The first is the reduced width ${\theta }_{\ell }^2$ which is the square of the probability amplitude obtained by the overlap (inner product) of the compound nuclear state with the state given by the two particles in the entrance channel with relative angular momentum ℓ. The second factor is the penetrability P_ℓ and is the probability of the two particles occurring within the nuclear volume and subsequently penetrating through the Coulomb and angular momentum barriers. At energies that are small compared to the sum of the Coulomb and centrifugal barriers, the penetration factor decreases very rapidly with increasing relative orbital angular momentum. Because of this, in calculations of reaction rates, usually only the minimum possible partial wave allowed by angular momentum coupling and parity conservation is used. This parameterization of the partial particle widths is particularly convenient for expressing the energy dependence of the widths. Since the only non-explicit energy dependence is contained in the penetrability, we can obtain the partial width at any energy from the width on resonance by scaling

${\mathrm{\Gamma }}_{\ell }\left(E\right)={\mathrm{\Gamma }}_{\ell }\left(E_{\mathit{res}}\right)\frac{P_{\ell }\left(E\right)}{P_{\ell }\left(E_{\mathit{res}}\right)}\sqrt{\frac{E}{E_{\mathit{res}}}}.(17)$

The use of the ratios of penetrabilities makes the expression for Γ_ℓ(E) relatively insensitive to the value of the nuclear radius chosen.

3.3 Effects of clustering

From the discussion above, it is clear that the presence of nuclear levels providing resonances to astrophysical reactions has a profound effect on the production of nuclei and nuclear burning during explosive nucleosynthesis. In many cases, the nuclear reaction rates are not known and must be estimated from level properties that are inputted into the reaction rate formalism described in the previous section. Nuclear models provide valuable input to the predictions of these level properties. The nuclear shell model continues to be one of the most valuable tools for describing and predicting nuclear levels that may provide important astrophysical resonances [14]. Other models are required to describe collective states such as rotational and vibrational excitations. These are typically less important for astrophysics owing to the high angular momentum typically required to excite such levels. Nuclear cluster states do not traditionally fall into any of these categories. In fact, the single-particle picture described by the nuclear shell model completely fails to predict these important states such as the Hoyle state, and nuclear cluster models are required to understand the Hoyle state properties [15].

Nuclear reactions involving α particles in the entrance and exit channels may also be dramatically enhanced by nuclear cluster states providing resonances. This can primarily be seen through Eq. 14 where the α particle width, Γ_α is shown to depend directly on the α reduced with ${\theta }_{\alpha }^2$,

${\mathrm{\Gamma }}_{\alpha }\propto {\theta }_{\alpha }^2.(18)$

These α-particle reduced widths may be much larger for α-cluster states such that resonances provided by such states may dominate the α-induced reaction rates (e.g., see Ref. [16]). Traditional shell model approaches [17], however, greatly under-predict α-particle reduced widths in the sd shell [18], but new approaches utilizing a cluster-nucleon configuration interaction model seem to better describe the effects of clusterization [19].

4 Experiments probing cluster resonances

4.1 Nova burning

A number of different experimental studies of astrophysical interest probe cluster structure in nuclei. For instance for novae, it was mentioned above that cycling through (p, α) reactions could be strongly impacted by cluster structure. Mostly these involve (p, α) reactions on $T_z=\frac{1}{2}$ nuclei producing α conjugate compound nuclear states with relatively strong α clusterization. Examples include (p, α) reactions on ¹⁵N, ²³Na, ²⁷Al, ³¹P, and ³⁵Cl producing compound nuclei ¹⁶O, ²⁴Mg, ²⁸Si, ³²S, and ³⁶Ar, respectively (see Figure 2). These compound nuclei were found to exhibit strong clustering effects indicated by ${\theta }_{\alpha }^2$ extracted from experiments that were many times shell-model predictions [18]. The cycling reactions have been shown to affect the final produced abundances in a number of sensitivity studies. Despite this importance, many of these (p, α) reactions are relatively poorly known. For many of these, the primary difficulty arises in producing a robust target with relatively few impurities or spectator nuclei. For instance, to study the (p, α) reactions on ³¹P and ³⁵Cl, targets were made either via ion implantation or vacuum evaporation of molecules containing the target of interest [20, 21]. Ultimately background from reactions on spectator nuclei limited the measurements such that upper limits of resonance strengths were extracted for most of the resonances of interest.

An alternative approach was recently published in Ref. [22] that alleviated the need for difficult targets. The (p, α) reactions on ³¹P and ³⁵Cl were measured in inverse kinematics by bombarding a differentially-pumped hydrogen target with energetic beams of ³¹P and ³⁵Cl (see Figure 4). Since both the beam and target were relatively pure, a greater sensitivity could be obtained resulting in some (p, α) resonances being measured for the first time. As the beam traversed the extended gas target, it would lose energy until a resonance was reached in the (p, α) cross section. Therefore resonance energies could be determined from the physical position that the reaction was observed to occur in the target. This was extracted by determining the reaction vertex from the reaction kinematics as measured in the angle/energy spectrum observed by the silicon-strip detectors placed directly in the gas (see Figure 4). Since the target was an extended volume of gas, the reaction vertex could be physically moved around the target by changing the beam energy, which in turn could be used to measure the stopping power of the beam in the gas as a function of energy. Figure 4 shows the reaction vertex extracted for two different beam energies. Such analysis was important to determine the solid angle efficiencies of the measurements.

FIGURE 4

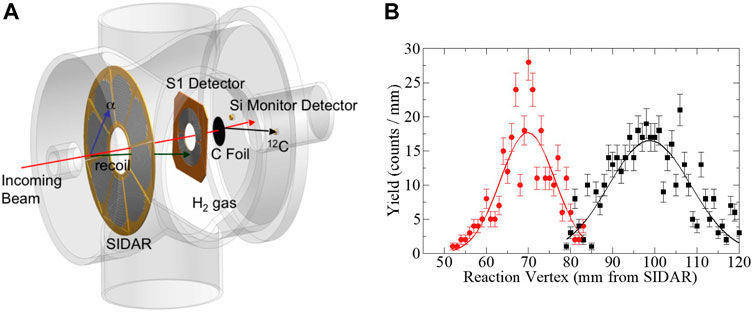
FIGURE 4. (A) Experimental setup used to measure the ³¹P(p, α)²⁸Si reaction. The ³¹P beam bombarded a differentially-pumped hydrogen containing target chamber in which various silicon detectors were placed [22]. (B) The vertex of the (p, α) reactions could be reconstructed from reaction kinematics. The vertex moved as expected when the beam energy was changed.

4.2 The αp process

In accreting X-ray binaries, the αp process initiates the peak of the burst by linking the initial burning through the HCNO cycles to the rp process that produces elements up to roughly the mass of Sn (see Figure 3). Possible breakout reactions of the αp process are ¹⁵O(α, γ)¹⁹Ne and ¹⁸Ne(α, p)²¹Na, and the importance of these reactions has been affirmed by a number of sensitivity studies [7, 8, 23]. The rates of these reactions are largely determined by the α-cluster structure of the compound nuclei, and a number of experiments have been performed or are under development to probe this structure. One particular question that has garnered a great deal of attention is the measurement of the α-branching ratio for the 4.03-MeV ¹⁹Ne level, which is expected to make a dominant contribution to the astrophysical ¹⁵O(α, γ)¹⁹Ne rate [24–28]. The only successful measurement thus far was reported in Ref. [27] and made use of the TwinSol [29] magnetic separator at the University of Notre Dame. Tritons from the ¹⁹F(³He,t)¹⁹Ne reaction were separated and identified in TwinSol in coincidence with decay α particles detected in silicon detectors facing the target (see Figure 5). The primary limitation was the large flux of δ electrons produced when the beam impinged on the target that could “pile-up” into the energy range of interest for the decay α particles [27]. To help reduced this background and increase the sensitivity of the measurements, a new device is being constructed that takes advantage of the recent conversion of TwinSol to TriSol [30]. The idea is to create a helical spectrometer out of the first TriSol solenoid to detect the decay α particles after magnetically separating them from the delta electrons (see Figures 5, 6). The α particles would spiral in the magnetic field to ultimately be detected near the solenoid axis in a silicon detector array named the Solenoid Spectrometer for Nuclear Astrophysics and Decays (SSNAPD). The device is currently under construction and is expected to begin measurements in 2024. Other studies of the α-branching ratio are also being pursued by the GADGET group [31, 32] and using the SABRE detector [33].

FIGURE 5

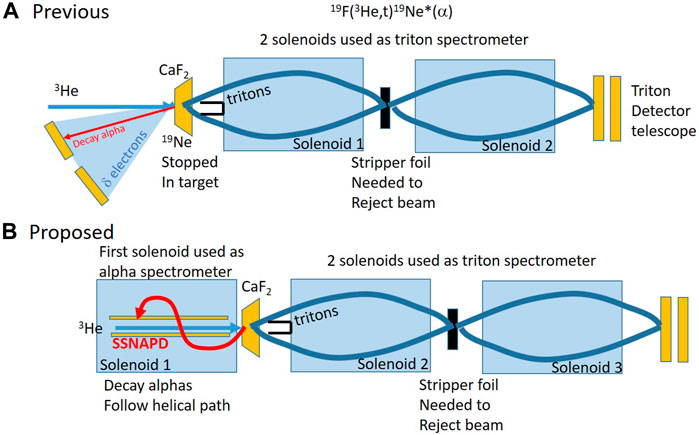
FIGURE 5. (A) The α widths of ¹⁹Ne levels were previously measured [27] utilizing the ¹⁹F(³He,t)¹⁹Ne reaction. Tritons populating ¹⁹Ne levels were separated by the TwinSol separator in coincidence with decay α particles detected in Si detectors. (B) The SSNAPD detector would alleviate background coming from the blinding rate of δ electrons hitting the Si detector by magnetically analyzing light charged particles leaving the target.

FIGURE 6

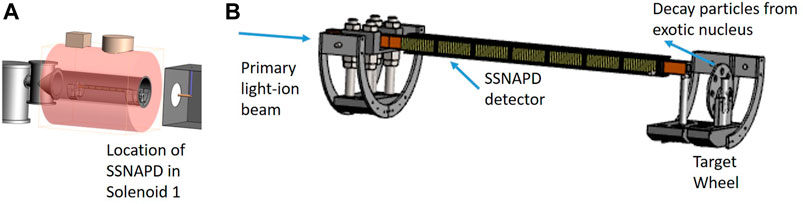
FIGURE 6. (A) The SSNAPD detector would sit on axis at the center of TriSol solenoid 1. (B) The beam is tuned through SSNAPD to bombard a target at the exit of the solenoid. Decay particles would spiral backwards in the solenoidal magnetic field to be detected back on axis by SSNAPD.

While indirect techniques are important, many reactions in the αp process can be measured directly at existing or future exotic beam facilities. The compound nuclei produced in these (α, p) reactions are two valence neutrons short of being α conjugate nuclei, and the presence of α clustering paired with these valence neutrons could significantly enhance the astrophysical reaction rates [34]. A major challenge in performing these direct cross section measurements, however, is that the studies have to be performed in inverse kinematics, and therefore some sort of He target is required. Ideally the He target should be localized such that reaction kinematics can be exploited to identify the reactions of interest, and the existence of spectator target nuclei should be minimized to avoid significant backgrounds. The Jet Experiments in Nuclear Structure and Astrophysics (JENSA) gas-jet target was developed and constructed for this purpose [35, 36]. JENSA uses He injected at high pressures through a laval nozzle to achieve a supersonic flow of gas before it is recirculated, compressed, and re-injected. A number of (α, p) reaction studies have been performed using JENSA including ²⁶Al(α, p)²⁹Si and ³⁴Ar(α, p)³⁷K (see Figure 7). In the figure, protons from the ³⁴Ar(α, p)³⁷K reaction were detected while bombarding the JENSA He target with energetic ³⁴Ar beams produced at the ReA3 facility [37] at Michigan State University. ³⁴Ar(α, p)³⁷K events were identified by their dstinctive reaction kinematics (Figure 7).

FIGURE 7

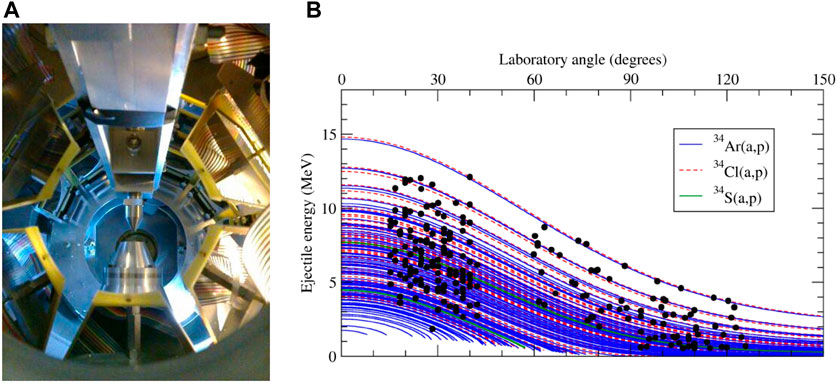
FIGURE 7. (A) He gas is injected from the top and captured for recirculation by a receiver at the bottom of JENSA. The beam is tuned down the center of the apparatus. The interaction point is surrounded by arrays of silicon-strip detectors. (B) Protons from (α, p) reactions are plotted along with calculated kinematic lines for reactions on the beam constituents.

An alternative approach that has been applied with significant success is the use of active targets in which the detector gas serves as both the target of the measurement and the reaction detector as well. Recent examples include ²²Mg(α, p)²⁵Al that was studied with both the Active Target - Time Projection Chamber [38] and the MUlti-Sampling Ionization Chamber [39]. Another recent example was a¹⁸Ne(α, p)²¹Na study [40] performed with the ANASEN [41] detector.

4.3 Supernovae Ia

As described above, SNIa are also an accretion-driven phenomenon that could be strongly impacted by nuclear cluster states. Some of the most important reactions are ¹²C(α, γ)¹⁶O, ¹²C+¹²C, ²⁰Ne(α, p), ²⁰Ne(α, γ), and ³⁰Si(p, γ) [9]. Of the five, four are expected to be strongly influenced by nuclear clusterization. As opposed to the previous section, these reactions involve stable beams and targets with the main challenge being the exceedingly low cross sections in the astrophysical energy ranges of interest combined (in some cases) with difficult gas- or enriched-targets.

Recently the ²⁰Ne(α, p)²³Na reaction was studied using the windowless gas target Rhinoceros (Rhino) [42, 43]. Previous estimates of its astrophysical rate were based upon studies of the inverse reaction ²³Na(p, α)²⁰Ne, which ignores contributions populating excited ²³Na states. Rhino was run with ^natNe gas at 10 Torr of pressure, and charged particle yields were measured at six angles via ruggedized Si surface barrier detectors as a function of beam energy from 3.5–6.0 MeV (see Figure 8). Significant yield was observed populating the first excited state of ²³Na, which indicates the importance of including this channel. This data is still under analysis but the (α, p) reaction was observed down to roughly 4 MeV bombarding energies.

FIGURE 8

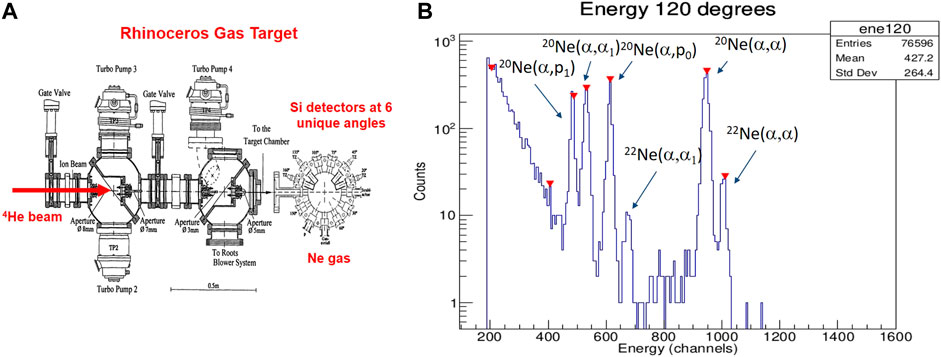
FIGURE 8. (A) The windowless gas target Rhino. The beam enters from the left through a series of pumping apertures entering a target chamber filled with 10 Torr of target gas. Silicon detectors detect charged particles from produced nuclear reactions. (B) The charged particle spectrum from ⁴He+Ne reactions observed at 120 degrees at a bombarding energy of 5.745 MeV.

The ¹²C+¹²C fusion reaction is also of critical importance. Numerous reaction channels are open, and the reaction cross section exhibits a complicated pattern indicating the importance of interference superimposed unto complex and possibly molecular-like resonances. This complicated reaction mechanism combined with rather low cross sections has resulted in the rate being experimentally constrained on only the rather high side of astrophysical energies [44, 45]. Complicating the situation further was a recent Trojan Horse style measurement [46] that indicated the rate was actually 1-2 orders of magnitude larger than previous estimates at astrophysical energies. These conflicting claims created a critical need for actual cross section measurements (or at least upper limits) in the low-energy range. Such measurements have begun at the University of Notre Dame [47], and first measurements have extracted cross sections lower than the Trojan Horse estimates.

4.4 Core-collapse supernovae

After the bounce of massive-star collapse, there exists a phase of nuclear re-combination when the temperature is dropping known as α-rich freezeout. During this phase, α-induced reactions can strongly impact the production of radioisotopes (such as ²⁶Al, ⁴⁴Ti, and ⁵⁶Ni) that are used as observational tracers of the accompanying nucleosynthesis and as diagnostics of explosion energetics. Such α-induced reactions are strongly impacted by α-cluster resonances and understanding their impact is critical to using radioisotope observations to understand CCSN.

²⁶Al is one radioisotope produced primarily in massive stars. Its production occurs in three specific environments: core hydrogen burning, C/Ne convective shell burning and explosive C/Ne shell burning [48]. ²⁶Al is produced in all of these environments via the ²⁵Mg(p,γ)²⁶Al reaction and is destroyed primarily via β decay to ²⁶Mg. ²⁵Mg, which is seed nuclei for ²⁶Al, is either present in the initial abundance of the star or is generated via the ²⁴Mg(p,γ)²⁵Al(β⁺)²⁵Mg reactions. A sensitivity study published in Ref. [49] sought to determine which reaction rates and their uncertainties influenced the final abundance of ²⁶Al in the burning environments described above. For explosive C/Ne burning, this study found that one of the most influential rates, when varied, was the ²⁵Mg(α,n)²⁸Si reaction rate. As mentioned above, this reaction destroys seed ²⁵Mg nuclei which would otherwise go on to produce ²⁶Al. In convective C/Ne shell burning both the ²⁵Mg(α,n)²⁸Si and ²⁶Mg(α,n)²⁹Si reactions were found to impact the final abundance of ²⁶Al. These reactions produce neutrons that destroy ²⁶Al via neutron capture reactions.

Despite the importance of these reactions, there have been relatively few measurements [50, 51] of the total ²⁵Mg(α,n)²⁸Si and ²⁶Mg(α,n)²⁹Si reaction cross sections in the energy range 2.5–3.5 MeV appropriate for high temperature explosive burning conditions, and adopted reaction rates [52] are based upon statistical model calculations. A new technique was recently used to validate the cross section data based upon measurements with the Active Target High Efficiency detector for Nuclear Astrophysics (ATHENA) [53]. ^25,26Mg beams were used to bombard 225 Torr of He gas in the ATHENA detector, and (α, n) reactions were identified using the sudden change in ionization that occurs for the reaction recoils compared with the beam (see Figure 9). Reaction cross sections have been measured in the 3–5 MeV range and are being prepared for publication [54].

FIGURE 9

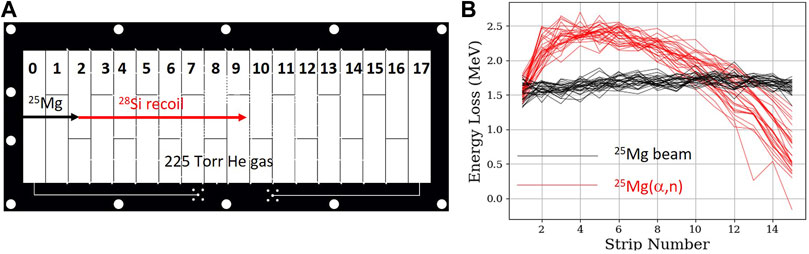
FIGURE 9. (A) The segmented anode of the ATHENA active target detector. ^25,26Mg ions enter the chamber, and electrons liberated by their ionization are collected on the segmented anode. (B) A sudden increase in ionization is observed when an (α, n) reaction occurs.

While this is one example, there are a number of other nuclear reactions that have been identified to affect radioisotope production in CCSN. Many of these could be strongly impacted by cluster structure and resonances. The ⁴⁴Ti(α, p)⁴⁷V, ⁴⁰Ca(α, γ)⁴⁴Ti, ⁴⁰Ca(α, p)⁴³Sc, ¹⁷F(α, p)²⁰Ne, and ²¹Na(α, p)²⁴Mg reactions were identified by Magkotsios et al. [10] as affecting ⁴⁴Ti and ⁵⁶Ni production. On the other hand, Subedi, Meisel, and Merz [55] identified ¹³N(α, p)¹⁶O, ¹⁷F(α, p)²⁰Ne, ⁵²Fe(α, p)⁵⁵Co, ⁵⁶Ni(α, p)⁵⁹Cu, and ³⁹K(p, α)³⁶Ar as some of the most important α-cluster reactions. While studies do not always agree on the most important reactions to constrain, it is clear that α-clusterized nuclei are important for nucleosynthesis in CCSN.

5 Conclusion

The cluster structure in nuclei has great impact on a number of explosive astrophysical scenarios. In fact cluster resonances near the threshold may dominate the reaction flow and determine the reaction path in many helium-rich environments. Because of the difficulties in studying exotic nuclei with significant clusterization of importance for explosive burning, indirect methods are becoming increasingly a vital tool in the nuclear physicists toolkit.

In this manuscript, numerous explosive astrophysical cases have been described along with a flavor of the types of nucleosynthesis that is expected to occur. Example experiments have been mentioned for each along with the primary challenges and opportunities. It is clear that as next-generation facilities are coming online, we need to continue to develop the experimental tools required to advance such studies.

Data availability statement

The raw data supporting the conclusion of this article will be made available by the authors, without undue reservation.

Author contributions

The author confirms being the sole contributor of this work and has approved it for publication.

Funding

This research was supported by the National Science Foundation under Grant Nos. PHY-2011890 and PHY-2117687.

Acknowledgments

The work described here was due to the contributions of numerous others. While I have attempted to describe representative examples of theoretical studies and measurements, I have undoubtedly omitted many outstanding and important contributions to the field. I especially would like to thank H. Schatz, B. Moazen, K. Chipps, C. Boomershine, and D. Blankstein for allowing me to describe work they have performed.

Conflict of interest

The author declares that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

1. Anders E, Grevesse N. Abundances of the elements: Meteoritic and solar. Geochimica et Cosmochimica Acta (1989) 53:197–214. doi:10.1016/0016-7037(89)90286-X

CrossRef Full Text | Google Scholar

2. Beck C. Clustering in stable and exotic light nuclei. In: W Schroeder, editor. Nuclear particle correlations and cluster Physics. Singapore: World Scientific (2017). p. 179–201. doi:10.1142/9789813209350_0007

CrossRef Full Text | Google Scholar

3. Wiescher M, Clarkson O, deBoer RJ, Denisenkov P. Nuclear clusters as the first stepping stones for the chemical evolution of the universe. The Eur Phys J A (2021) 57:24. doi:10.1140/epja/s10050-020-00339-x

CrossRef Full Text | Google Scholar

4. José J, Hernanz M. Nucleosynthesis in classical novae: Co versus one white dwarfs. Astrophysical J (1998) 494:680–90. doi:10.1086/305244

CrossRef Full Text | Google Scholar

5. Schatz H, Aprahamian A, Barnard V, Bildsten L, Cumming A, Ouellette M, et al. End point of the rp process on accreting neutron stars. Phys Rev Lett (2001) 86:3471–4. doi:10.1103/PhysRevLett.86.3471

PubMed Abstract | CrossRef Full Text | Google Scholar

6. Schatz H, Bildsten L, Cumming A, Wiescher M. The rapid proton process ashes from stable nuclear burning on an accreting neutron star. Astrophysical J (1999) 524:1014–29. doi:10.1086/307837

CrossRef Full Text | Google Scholar

7. Parikh A, José J, Moreno F, Iliadis C. The effects of variations in nuclear processes on type i x-ray burst nucleosynthesis. Astrophysical J Suppl Ser (2008) 178:110–36. doi:10.1086/589879

CrossRef Full Text | Google Scholar

8. Cyburt RH, Amthor AM, Heger A, Johnson E, Keek L, Meisel Z, et al. DEPENDENCE OF x-RAY BURST MODELS ON NUCLEAR REACTION RATES. Astrophysical J (2016) 830:55. doi:10.3847/0004-637x/830/2/55

CrossRef Full Text | Google Scholar

9. Parikh A, José J, Seitenzahl IR, Röpke FK. The effects of variations in nuclear interactions on nucleosynthesis in thermonuclear supernovae. Astron Astrophysics (2013) 557:A3. doi:10.1051/0004-6361/201321518

CrossRef Full Text | Google Scholar

10. Magkotsios G, Timmes FX, Hungerford AL, Fryer CL, Young PA, Wiescher M. Trends in 44ti and 56ni from core-collapse supernovae. Astrophysical J Suppl Ser (2010) 191:66–95. doi:10.1088/0067-0049/191/1/66

CrossRef Full Text | Google Scholar

11. Clayton DD. Principles of stellar evolution and nucleosynthesis. Cambridge: Cambridge University Press (1983).

Google Scholar

12. Rolfs CE, Rodney WS. Cauldrons in the cosmos. Chicago: University of Chicago Press (1988).

Google Scholar

13. Blatt JM, Weiskopf VF. Theoretical nuclear Physics. New York: John Wiley & Sons (1952).

Google Scholar

14. Martínez-Pinedo G, Langanke K. Shell model applications in nuclear astrophysics. Physics (2022) 4:677–89. doi:10.3390/physics4020046

CrossRef Full Text | Google Scholar

15. Chernykh M, Feldmeier H, Neff T, von Neumann-Cosel P, Richter A. Structure of the hoyle state in ¹²C. Phys Rev Lett (2007) 98:032501. doi:10.1103/PhysRevLett.98.032501

PubMed Abstract | CrossRef Full Text | Google Scholar

16. Long AM, Adachi T, Beard M, Berg GPA, Couder M, deBoer RJ, et al. α-unbound levels in ³⁴Ar from ³⁶Ar(p,t)³⁴Ar reaction measurements and implications for the astrophysical ³⁰S(α,p)³³Cl reaction rate. Phys Rev C (2018) 97:054613. doi:10.1103/PhysRevC.97.054613

CrossRef Full Text | Google Scholar

17. Chung W, van Hienen J, Wildenthal B, Bennett C. Shell-model predictions of alpha-spectroscopic factors between ground states of 16 ≤ A ≤ 40 nuclei. Phys Lett B (1978) 79:381–4. doi:10.1016/0370-2693(78)90387-8

CrossRef Full Text | Google Scholar

18. Carey TA, Roos PG, Chant NS, Nadasen A, Chen HL. Alpha-particle spectroscopic strengths using the (p, pα) reaction at 101.5 mev. Phys Rev C (1984) 29:1273–88. doi:10.1103/PhysRevC.29.1273

CrossRef Full Text | Google Scholar

19. Volya A, Tchuvil’sky YM. Nuclear clustering using a modern shell model approach. Phys Rev C (2015) 91:044319. doi:10.1103/PhysRevC.91.044319

CrossRef Full Text | Google Scholar

20. Iliadis C, Giesen U, Görres J, Graff S, Wiescher M, Azuma R, et al. The reaction branching 31p (p, γ)/31p (p, α) in the rp-process. Nucl Phys A (1991) 533:153–69. doi:10.1016/0375-9474(91)90824-p

CrossRef Full Text | Google Scholar

21. Ross JG, Görres J, Iliadis C, Vouzoukas S, Wiescher M, Vogelaar RB, et al. Indirect study of low-energy resonances in 31P(p, alpha)28Si and 35Cl(p, alpha)32S. Phys Rev C (1995) 52:1681–90. doi:10.1103/PhysRevC.52.1681

CrossRef Full Text | Google Scholar

22. Moazen B, Matei C, Bardayan DW, Blackmon J, Chae K, Chipps K, et al. Direct studies of low-energy resonances in 31p (p, α) 28si and 35cl (p, α) 32s. Eur Phys J A (2011) 47:66–7. doi:10.1140/epja/i2011-11066-7

CrossRef Full Text | Google Scholar

23. Meisel Z, Merz G, Medvid S. Influence of nuclear reaction rate uncertainties on neutron star properties extracted from x-ray burst model–observation comparisons. Astrophysical J (2019) 872:84. doi:10.3847/1538-4357/aafede

CrossRef Full Text | Google Scholar

24. Magnus P, Smith M, Howard A, Parker P, Champagne A. Measurement of ¹⁵o(α, γ)¹⁹ne resonance strengths. Nucl Phys A (1990) 506:332–45. doi:10.1016/0375-9474(90)90390-8

CrossRef Full Text | Google Scholar

25. Davids B, van den Berg AM, Dendooven P, Fleurot F, Hunyadi M, de Huu MA, et al. Astrophysical rate of¹⁵O(α,γ)¹⁹Ne via the (p, t) reaction in inverse kinematics. Phys Rev C (2003) 67:065808. doi:10.1103/PhysRevC.67.065808

CrossRef Full Text | Google Scholar

26. Rehm KE, Wuosmaa AH, Jiang CL, Caggiano J, Greene JP, Heinz A, et al. Branching ratio Γ_α/Γ_γ of the 4.033 mev 3/2⁺ state in ¹⁹Ne. Phys Rev C (2003) 67:065809. doi:10.1103/PhysRevC.67.065809

CrossRef Full Text | Google Scholar

27. Tan WP, Fisker JL, Görres J, Couder M, Wiescher M. O15(α,γ)Ne19 breakout reaction and impact on x-ray bursts. Phys Rev Lett (2007) 98:242503. doi:10.1103/PhysRevLett.98.242503

PubMed Abstract | CrossRef Full Text | Google Scholar

28. Bardayan DW, Chipps KA, Ahn S, Blackmon JC, Greife U, Jones KL, et al. Particle decay of astrophysically-important 19ne levels. J Phys Conf Ser (2019) 1308:012004. doi:10.1088/1742-6596/1308/1/012004

CrossRef Full Text | Google Scholar

29. Lee M, Becchetti F, O’Donnell T, Roberts D, Zimmerman J, Guimarães V, et al. Study of nuclear reactions with intense, high-purity, low-energy radioactive ion beams using a versatile multi-configuration dual superconducting-solenoid system. Nucl Instr Methods Phys Res Section A: Acc Spectrometers, Detectors Associated Equipment (1999) 422:536–40. doi:10.1016/S0168-9002(98)01081-X

CrossRef Full Text | Google Scholar

30. O’Malley P, Ahn T, Bardayan D, Brodeur M, Coil S, Kolata J. Trisol: A major upgrade of the twinsol rnb facility. Nucl Instr Methods Phys Res Section A: Acc Spectrometers, Detectors Associated Equipment (2023) 1047:167784. doi:10.1016/j.nima.2022.167784

CrossRef Full Text | Google Scholar

31. Mahajan R, Adams A, Allmond J, Alvarez Pol H, Argo E, Ayyad Y, et al. Measuring the ¹⁵O(α,γ)¹⁹Ne reaction in type I X-ray bursts using the GADGET II TPC: Software. EPJ Web Conf (2022) 260:11034. doi:10.1051/epjconf/202226011034

CrossRef Full Text | Google Scholar

32. Wheeler T, Adams A, Allmond J, Alvarez Pol H, Argo E, Ayyad Y, et al. Measuring the ¹⁵O(α, γ)¹⁹Ne reaction in type I X-ray bursts using the GADGET II TPC: Hardware. EPJ Web Conf (2022) 260:11046. doi:10.1051/epjconf/202226011046

CrossRef Full Text | Google Scholar

33. Good EC, Sudarsan B, Macon KT, Deibel CM, Baby LT, Blackmon JC, et al. Sabre: The silicon array for branching ratio experiments. Nucl Instr Methods Phys Res Section A, Acc Spectrometers, Detectors Associated Equipment (2021) 1003:165299. doi:10.1016/j.nima.2021.165299

CrossRef Full Text | Google Scholar

34. Kubono S, Binh DN, Hayakawa S, Hashimoto H, Kahl D, Yamaguchi H, et al. Role of clusters in nuclear astrophysics with cluster nucleosynthesis diagram (cnd). J Phys Conf Ser (2013) 436:012071. doi:10.1088/1742-6596/436/1/012071

CrossRef Full Text | Google Scholar

35. Chipps K, Greife U, Bardayan D, Blackmon J, Kontos A, Linhardt L, et al. The jet experiments in nuclear structure and astrophysics (jensa) gas jet target. Nucl Instr Methods Phys Res Section A: Acc Spectrometers, Detectors Associated Equipment (2014) 763:553–64. doi:10.1016/j.nima.2014.06.042

CrossRef Full Text | Google Scholar

36. Schmidt K, Chipps K, Ahn S, Bardayan D, Browne J, Greife U, et al. Status of the jensa gas-jet target for experiments with rare isotope beams. Nucl Instr Methods Phys Res Section A: Acc Spectrometers, Detectors Associated Equipment (2018) 911:1–9. doi:10.1016/j.nima.2018.09.052

CrossRef Full Text | Google Scholar

37. Leitner D. State-of-the-art post-accelerators for radioactive beams. Nucl Instr Methods Phys Res Section B: Beam Interactions Mater Atoms (2013) 317:235–41. XVIth International Conference on ElectroMagnetic Isotope Separators and Techniques Related to their Applications, December 2–7, 2012 at Matsue, Japan. doi:10.1016/j.nimb.2013.07.071

CrossRef Full Text | Google Scholar

38. Randhawa JS, Ayyad Y, Mittig W, Meisel Z, Ahn T, Aguilar S, et al. First direct measurement of ²²Mg(α,p)²⁵Al and implications for x-ray burst model-observation comparisons. Phys Rev Lett (2020) 125:202701. doi:10.1103/PhysRevLett.125.202701

PubMed Abstract | CrossRef Full Text | Google Scholar

39. Jayatissa H, Avila ML, Rehm KE, Mohr P, Meisel Z, Chen J, et al. Study of the ²²mg waiting point relevant for x-ray burst nucleosynthesis via the ²²Mg(α,p)²⁵Al reaction. arXiv:2211.00628 (2022).

Google Scholar

40. Anastasiou M, Wiedenhöver I, Blackmon JC, Baby LT, Caussyn DD, Hood AA, et al. Measurement of the ¹⁸Ne(α,p)²¹Na reaction with the anasen active-target detector system at E_c.m. = 2.5 − −4 mev. Phys Rev C (2022) 105:055806. doi:10.1103/PhysRevC.105.055806

CrossRef Full Text | Google Scholar

41. Koshchiy E, Blackmon J, Rogachev G, Wiedenhöver I, Baby L, Barber P, et al. Anasen: The array for nuclear astrophysics and structure with exotic nuclei. Nucl Instr Methods Phys Res Section A: Acc Spectrometers, Detectors Associated Equipment (2017) 870:1–11. doi:10.1016/j.nima.2017.07.030

CrossRef Full Text | Google Scholar

42. Hammer J. Investigations of astrophysically interesting nuclear reactions by the use of gas target techniques. In: Proceedings of the International workshop XXVI on gross properties of nuclei and nuclear excitations; 11-17 Jan 1998; Hirschegg (Austria) (1998).

Google Scholar

43. Kölle V, Kölle U, Braitmayer S, Mohr P, Wilmes S, Staudt G, et al. Capture reactions at astrophysically relevant energies: Extended gas target experiments and geant simulations. Nucl Instr Methods Phys Res Section A: Acc Spectrometers, Detectors Associated Equipment (1999) 431:160–76. doi:10.1016/S0168-9002(99)00247-8

CrossRef Full Text | Google Scholar

44. Becker HW, Kettner K, Rolfs C, Trautvetter H. The12c+ 12c reaction at subcoulomb energies (ii). Z für Physik A Atoms Nuclei (1981) 303:305–12. doi:10.1007/bf01421528

CrossRef Full Text | Google Scholar

45. Jiang CL, Rehm KE, Back BB, Janssens RVF. Expectations for ¹²C and ¹⁶O induced fusion cross sections at energies of astrophysical interest. Phys Rev C (2007) 75:015803. doi:10.1103/PhysRevC.75.015803

CrossRef Full Text | Google Scholar

46. Tumino A, Spitaleri C, La Cognata M, Cherubini S, Guardo G, Gulino M, et al. An increase in the 12c+ 12c fusion rate from resonances at astrophysical energies. Nature (2018) 557:MISC6–8. doi:10.35352/gioenia.v52i382.86

CrossRef Full Text | Google Scholar

47. Tan WP, Boeltzig A, Dulal C, deBoer RJ, Frentz B, Henderson S, et al. New measurement of ¹²C +¹²C fusion reaction at astrophysical energies. Phys Rev Lett (2020) 124:192702. doi:10.1103/PhysRevLett.124.192702

PubMed Abstract | CrossRef Full Text | Google Scholar

48. Limongi M, Chieffi A. The nucleosynthesis of 26al and 60fe in solar metallicity stars extending in mass from 11 to 120 m: the hydrostatic and explosive contributions. Astrophysical J (2006) 647:483–500. doi:10.1086/505164

CrossRef Full Text | Google Scholar

49. Iliadis C, Champagne A, Chieffi A, Limongi M. The effects of thermonuclear reaction rate variations on 26al production in massive stars: A sensitivity study. Astrophysical Journal Suppl Ser (2011) 193:16. doi:10.1088/0067-0049/193/1/16

CrossRef Full Text | Google Scholar

50. Van der Zwan L, Geiger KW. Cross Sections for the ²⁵Mg(α,n)²⁸Si Reaction for E_α < 4.8 MeVn)28si reaction for e_α < 4.8mev. Nucl Sci Eng (1981) 79:197–201. doi:10.13182/nse81-a27408

CrossRef Full Text | Google Scholar

51. Anderson M, Mitchell L, Sevior M, Sargood D. 25Mg (α, n)28Si and 26Mg(α, n)29Si as neutron sources in explosive neon burningn)²⁸si and ²⁶mg(α,n)²⁹si as neutron sources in explosive neon burning. Nucl Phys A (1983) 405:170–8. doi:10.1016/0375-9474(83)90330-5

CrossRef Full Text | Google Scholar

52. Angulo C, Arnould M, Rayet M, Descouvemont P, Baye D, Leclercq-Willain C, et al. A compilation of charged-particle induced thermonuclear reaction rates. Nucl Phys A (1999) 656:3–183. doi:10.1016/S0375-9474(99)00030-5

CrossRef Full Text | Google Scholar

53. Blankstein D, Bardayan D, Allen J, Boomershine C, Callahan L, Carmichael S, et al. Athena: An active target detector for the measurement of total cross sections. Nucl Instr Methods Phys Res Section A: Acc Spectrometers, Detectors Associated Equipment (2023) 1047:167777. doi:10.1016/j.nima.2022.167777

CrossRef Full Text | Google Scholar

54. Blankstein D. Active Target Measurement Of The ^25,26mg(Α,N)^28,29si Total Cross Section. Ph.D. thesis. Indiana: University of Notre Dame (2023).

Google Scholar

55. Subedi SK, Meisel Z, Merz G. Sensitivity of 44ti and 56ni production in core-collapse supernova shock-driven nucleosynthesis to nuclear reaction rate variations. Astrophysical J (2020) 898:5. doi:10.3847/1538-4357/ab9745

CrossRef Full Text | Google Scholar