- 1Department of Mathematics, Saveetha School of Engineering, SIMATS, Chennai, Tamil Nadu, India
- 2Department of Mathematics, College of Science Al-Zulfi, Majmaah University, Al-Majmaah, Saudi Arabia
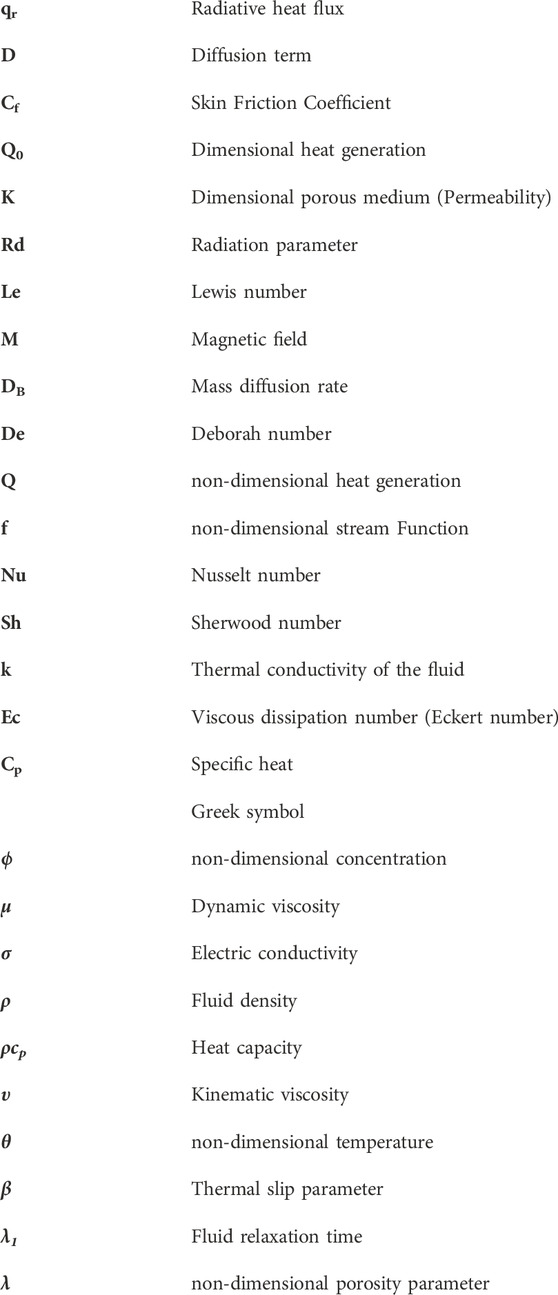
Maxwell fluids display viscous flow on a long timescale but exhibit additional elastic resistance during rapid deformations. Among various types of rate-type fluids, the Maxwell fluid has achieved prominence in numerous study fields. This viscoelastic fluid has viscous and elastic properties. Due to their reduced complexity, this Maxwell fluid is utilized used in the polymeric industries. We have established a mathematical model based on the applications. This article examines the mathematical and graphical analysis for steady-state magnetohydrodynamic flow in a horizontal flat plate of Maxwell viscoelastic fluid for a permeable medium with heat and thermal radiation. The non-dimensional and similarity transformation used to frame the partial differential equations with restored ordinary differential equations. The shooting technique is originated to find solutions to nonlinear boundary value problems with the help of MATLAB software via the Runge-Kutta Fehlberg method. The primary idea behind this strategy is to change the boundary conditions of boundary value problems into initial value problems. Several plots illustrate the leading parameters such as Prandtl number (Pr), Deborah number (De), Eckert number (Ec), heat generation (Q), radiation (Rd), Lewis number (Le), magnetic parameter (M), and thermal slip condition (β) on the velocity profile and energy transfer behaviour. We validated our results with published work. The most significant impact of this study is that the Nusselt number drops as the Eckert number rises and climbs when heat radiation increases. The skin friction coefficient increases as Deborah number increases.
1 Introduction
Numerous natural phenomena, such as the flight of birds, the swimming of fish, and the evolution of the weather, are studied with fluid dynamics. Researchers have become interested in free convective transport with saturated porous media due to its applications, which include petroleum reservoirs, geothermal processes, chemical catalytic reactors, and nuclear waste deposits. Standard procedures in nature and industry include the extrusion of metals and plastics, drying and cooling, paper and textiles. Flow models in porous media have biologically relevant applications in brain tissue diffusion, tissue development, bioheat transfer in tissues, blood flow in tumors, and bioconvection. Mabood and Shateyi [1] studied temperature for concentration flow affecting a stretched sheet based on the radiation effect. Dawar et al. [2] addressed the MHD flow on copper-nanofluid across a horizontal plate under the influence of solar light. Nath et al. [3] discussed the analytical solutions for Maxwell fluids in a microchannel with a zeta perspective. Lin et al. [4] considered the possibility of mixed-convectional fluids with an arbitrary Prandtl value. The above research’s drawback is that non-Newtonian flow on a flat plate needs to be included.
The study of fluid flows and energy in a non-Newtonian fluid has gathered considerable notice due to its many engineering applications. The majority of investigations in the literature involve conventional Newtonian fluids. It is common knowledge that the bulk of fluids encountered in non-Newtonian is the process of terms under parameter estimations. Oil engineering, biology, physiology, technology, and industry utilize these fluids. Maxwell fluids are a subclass of non-Newtonian fluids that accurately capture fluids’ pseudo-plastic and dilatant properties. Adegbie et al. [5] discovered the behaviour of heat and mass transport in Maxwell fluid flow with the impact of thermo-physical parameters over a flat melting surface. Mustafa et al. [6] researched the flux as non-Fourier in thermal variables for the rotation of Maxwell fluid flow. It was derived by Shafique et al. [7] within the context of a rotating frame. Olabode et al. [8] studied Maxwell fluids with the impact on temperature-dependent variable characteristics and the influence of quadratic thermo-solutal convection. Heyhat and Khabazi [9] observed the non-isothermal flow of Maxwell fluid over fixed horizontal plates influenced by a transverse magnetic field. In the above articles, authors used Maxwell fluid on different geometries but not on a flat plate. So, Maxwell fluid flow on the flat plate must be included with the existing.
Porous medium is a material that contains either connected or unconnected voids (pores) spread in a regular or random pattern. These pores may contain various fluids, including air, water, oil, etc. If pores represent a percentage of the bulk volume, a composite network capable of fluid transport can be constructed. The permeability of the porous medium was the partial and overall bulk quantity of volume. The structure of the porous material determines permeability, a measure of the material’s mean square pore diameter. The following authors included porous media in their study.
Bhattacharyya [10] investigated chemically reactive flow’s first-order diffusion equations across a porous flat plate focused on force and changing wall concentration. Sadia et al. [11] examined the convection of energy–mass transfer with generalized Maxwell fluid impact, chemical reaction and exponential heating utilizing fractional derivatives models such as Caputo–Fabrizio. Shenoy [12] researched heat transport in non-Newtonian fluids throughout porous media. In the above research, a few authors have used a porous medium in different geometries, especially not in flat plates over Maxwell fluid.
Radiation is the energy transfer from a body via electromagnetic radiation emission or absorption. Thermal radiation spreads in the absence of substances through the vacuum of space. In contrast to conduction and convection, heat radiation can be concentrated in a limited area using reflecting mirrors, which produce focused solar energy. Venkatadri et al. [13] discussed the melting energy transfer investigation through an exponentially widening permeable sheet. In contrast, radiative heat flux was present in an MHD. Mahanthesh et al. [14] conducted research on the study of nonlinear convective flow in a nano Maxwell fluid combined with nonlinear radiation. According to the research by Kumar et al. [15], the properties of mass transfer on the 3D flow on a horizontal plate with a chemical reaction were investigated. Hsiao [16] described a thermal extrusion system that combines electrical MHD heat transfer with Maxwell fluid, considered radiative and viscous dissipation. In the above research, the authors have used radiation and heat generation in other fluids that flow on a flat porous medium.
Reddy et al. [17] published the outcomes of a numerical computation study on how thermal outlines along the side walls of an annular enclosure made up of various hybrid nanofluids with insulated horizontal borders are affected by axially variable temperature. Sankar et al. [18] investigated free convection heat transport in an annular cylindrical chamber with distinct heat sources on the inner wall. On the other hand, the exterior wall is cooled isothermally to a lower temperature. Makinde and Sankar [19] investigated two thermal conditions in which the opposite wall of a cylinder is insulated while the inner or outer wall of the cylinder is continuously heated. Sudarmozhi et al. [20] inspected the possessions of heat generation, thermal radiation, and also with the consideration of chemical reaction on double diffusion in a porous MHD Maxwell fluid medium. The dual results of a nanofluid flow on a convectively heated, nonlinearly contracting sheet were examined by Roy and Pop [21]. The double results of MHD mixed convection flow of an Oldroyd-B nanofluid on a shrinking sheet with a heat source and sink were discussed by Roy and Pop [22]. Zahir Shah et al. [23] solved the Darcy–Forchheimer magnetic flow of water-based silver and copper nanofluids by generating entropy. Joule heating and the effects of viscous dissipation were used to analyze the model. Tang et al. [24] looked at the energy transfer and flow of magnetized gold-blood Oldroyd-B nanofluids in narrow stenotic arteries using a computational approach.
Maxwell was the first to model a non-Newtonian fluid; its examples include polymer extrusion, nuclear reactor emergency cooling systems, food processing, and thermal welding. As far as the authors know, Maxwell fluid’s steady-state boundary layer flow across a permeable flat plate with the above-mentioned physical consequences has yet to be documented in the literature. Many authors have conducted a study using different geometries and parameters. But they have yet to study a porous flat plate combining thermal radiation, MHD and heat generation over a Maxwell fluid flow with a moving velocity in the boundary condition (U).
Consequently, the original aim and objective of this research is to analyze a model for the flow of magnetic flow of Maxwell fluid across a porous flat plate and to examine the combined impacts of heat generation, mass diffusion and thermal radiation over the moving flat plate. The governing equations are transmuted to a system of differential equations. The investigation will be conducted numerically using the computing software MATLAB (RKF). Possible flow patterns will also be produced to visualize velocity and temperature flow behaviour. Finally, the numerical values are validated with the current work. Even though similar problems have been covered in existing literature in recent years, it is worth noting that the study provides logical answers to the research questions.
1. What is the increasing effect of the Nusselt number for the Rd versus the magnetic field?
2. What is the decreasing effect of the Nusselt number for the Eckart number versus the magnetic field?
3. How do large values of the De versus the magnetic field affect skin friction?
4. How do large values of the porosity parameter versus the MHD affect skin friction?
2 Mathematical modelling
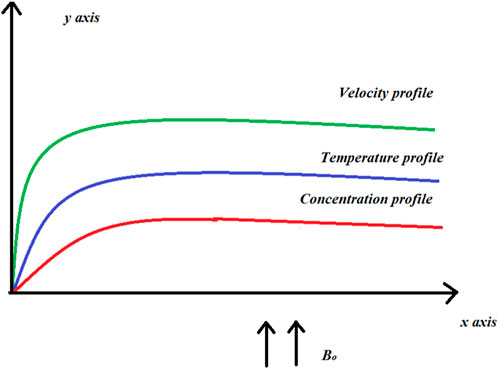
Let’s use the effect of heat generation and radiation on a flat porous plate to define the laminar, two-dimensional, incompressible and steady flow of a non-Newtonian Maxwell fluid. It is supposed that the x-axis is on the plate, the y-axis is perpendicular to the plate, and the flow’s motion is considered towards the positive x-axis. Let u and v be the horizontal and vertical velocity mechanisms along the x and y directions. T is known as temperature, and C is the concentration of the fluid. The geometry of this modelling can be displayed in Figure 1. The wall’s convective boundary conditions affect the local temperature. The flat porous plate is subjected to an MHD with a constant strength of B0 and applied along the y-axis and perpendicular to the plate. And the magnetic Reynolds number is minimal, so the induced magnetic field can be neglected. Let temperature be the constant, and the concentration of the horizontal plate is Tw and Cw that of the ambient fluid known as T∞ and C∞. U is the constant velocity of the free stream, or that of a moving horizontal plate. U∞ denotes free stream velocity. The following are the governing equations, written in Cartesian form, along with the assumptions mentioned above and boundary layer approximations by adding the porous medium, heat generation, and mass equation from Mustafa [25].
The Cauchy equations of motion can be used to derive the boundary layer equations for all viscoelastic fluid. In the presence of an MHD, the y-axis experiences continuous 2D flow. Based on the idea of conventional boundary layers, the equation of continuity can be stated as
The motion equation is formulated for an incompressible viscous fluid based on Newton’s second law of motion, often known as the momentum conservation law. Viscoelastic flows are mathematically fascinating because their spectral features change significantly from the Newtonian case. The Maxwell model has an unrealistic creep function, hence in the presence of a Maxwell fluid, the momentum equation is derived as follows:
The energy conservation principle, which states that the total time rate of change of kinetic and internal energies is equal to the sum of the work done by external forces per unit of time and the sum of the other energies given per unit of time, is the foundation for the heat transfer equation. The heat transport equation can be derived from this method as
qr is the radiative heat flux measured as qr = −(4 σ */3 k*) ∂T 4/∂ y, Rosseland [26] here σ *& k* are the mean absorption coefficient & the Stephan-Boltzmann coefficient, respectively. As resulting Raptis and Perdikis [27], the temperature differences in the flow are consider to be sufficiently small so that T4 may be stated as a linear function of energy. This is skilled by expanding T 4 about the ambient temperature T∞ and then ignoring the squares and higher-order terms to attain
Thus, by using the above.
The medium’s conductivity affects mass diffusion, but the magnetic field does not disturb this process. As a result, when the right conditions are met, the ordinary differential equation can be applied to MHD problems. Fick’s law can calculate the differential equation that describes the field of any component in a moving binary mixture when a fluid is incompressible and does not have an internal mass source.
Concentration Equation,
The boundary conditions associated with the present problem are as below (Mustafa [25])
here
Using the below similarity variables (η & ψ) and dimensionless variables for the energy and flow equations are transferred into ODEs
By introducing Eqs 6a, 6b, the momentum, heat, and mass equations are turned into ordinary differential equations.
In the nonlinear approximation, the issue is regulated by the Prandtl number, the radiation parameter, and the energy ratio parameter.
Dimensionless energy equation,
Dimensionless concentration equation,
The transformed boundary conditions are compact to a dimensionless form
Here
Using Fick’s law and Fourier’s law, the following expressions hold for the local Sherwood number (shx) & the local Nusselt number (Nux), which are given here respectively by
The above-expressed similarity quantities and Nux are simplified by applying the aforementioned dimensionless quantities.
With the presence of the local Reynolds number
3 Method of the solution
This section solves dimensionless governing equations using the MATLAB function Bvp4c and dimensionless boundary value conditions. The MATLAB function bvp4c is the Runge-Kutta-Fehlberg method. To define mesh and control approximation solution mistakes. The comparative error acceptance was set to 10−6. The linked and highly nonlinear modified governing equations make it challenging to obtain closed-form solutions. Consequently, the Runge-Kutta-Fehlberg technique numerically solves these equations with boundary conditions in the symbolic computation software MATLAB. Following is a reduction of the strongly coupled boundary value problem to a system of first-order differential equations:
The substitutions are
Additionally, boundary conditions need to be considered in Eq. 10, as
Choosing the correct finite value of infinity is the most challenging aspect of the procedure. Both the technique’s longitudinal step size of 0.0001 and its tolerance value of 10−6 are highly effective convergence measurements. The exactness of the current approach is evaluated by associating the results to those found in the literature [1]. The parameters effect is examined in the present study to compute the numerical values of Nusselt number and the skin friction as depicted in Figures 1–20.
3.1 Validation
To check the accuracy of our numerical calculations, Table 1 compares the present result and the above work by Mabood et al. The numerical results are compared to Mabood et al. [1] for various Prandtl number values. This comparison demonstrates that the present and earlier studies are in perfect accord.
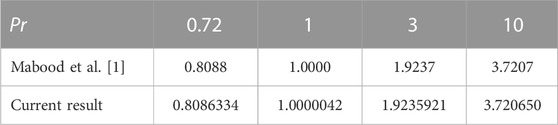
TABLE 1. Assessment of the current results with existing work (Mabood et al. [1]) for heat transfer rate in temperature profile when porous and heat generation parameters are zero.
4 Discussion of results
The current work analyses the boundary layer steady, MHD Maxwell fluid on a permeable flat plate with heat generation and radiation impact. This section discoursed the effects on concentration, temperature and velocity fields by applying the numerical values to different flow parameters. This article examines radiative MHD Maxwell fluid flow on a flat plate on a permeable medium in the occurrence of heat generation impacts. To draw graphs, fixed parameter values are De = 0.1; Pr = 4; Ec = 0.1; Rd = 1; Q = 0.1; M = 0.1; β = 0.2; λ = 0.1; Le = 2.0; the parameter values are taken from formal studies in the literature. These numbers are standard throughout the investigation, except that distinct values are displayed in separate figures.
4.1 Explanation for velocity profile
• The consequences of De on boundary layer velocity are depicted in Figure 2. Due to a rise in Deborah number, the resulting rate also rises. According to the data, Deborah number makes the border layer faster and more efficient. Physically speaking, fluid will reach equilibrium when shear stress is gone. Numerous polymeric liquids exhibit this phenomenon, which the viscous fluid model cannot describe. A more excellent Deborah number estimation will result in a retarding force between two adjacent layers in the flow. As an outcome, the velocity and thickness of the layer decrease. This is because an upsurge in Deborah number implies that the fluid is experiencing a significant viscous force; this force restricts fluid flow.
• The outcome of M on the velocity distribution is depicted in Figure 3. Magnetic fields in electrically conducting liquids produce Lorentz force. The magnetic region slows boundary-layer transport. A magnetic variable weakens boundary layers. Physically, the magnetic parameter possesses Lorentz force, which restricts fluid flow. This Lorentz force provides resistance to the velocity.
• Variations in the velocity distribution on a flat plate for different porosity parameter values are depicted in Figure 4. The graph demonstrates decreasing velocities as λ rises. Increasing the porous media parameter creates resistance to flow, which explains this phenomenon.
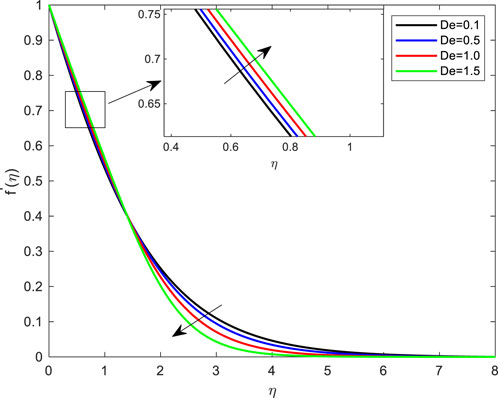
FIGURE 2. Influence of Deborah number on velocity profile with De = 0.1; Pr = 4; Ec = 0.1; Rd = 1; Q = 0.1; M = 0.1; β = 0.2; λ = 0.1; Le = 2.0.
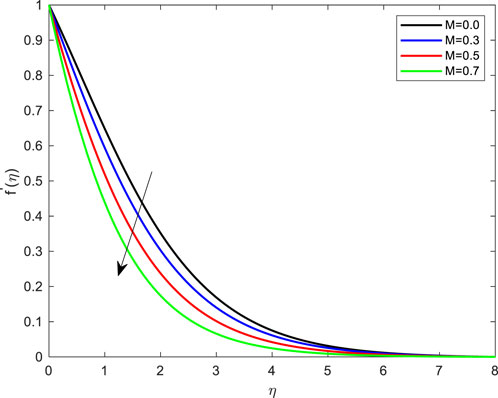
FIGURE 3. Impact of Magnetic field parameter on velocity profile with De = 0.1; Pr = 4; Ec = 0.1; Rd = 1; Q = 0.1; M = 0.1; β = 0.2; λ = 0.1; Le = 2.0.
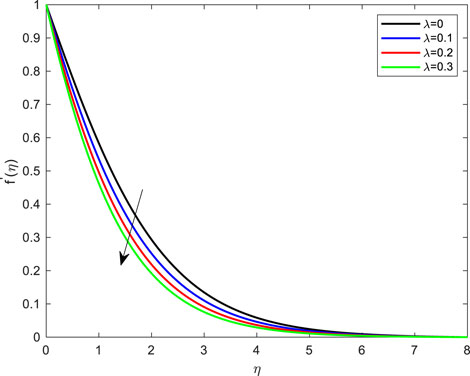
FIGURE 4. Impact of porosity parameter on velocity profile with De = 0.1; Pr = 4; Ec = 0.1; Rd = 1; Q = 0.1; M = 0.1; β = 0.2; λ = 0.1; Le = 2.0.
4.2 Explanation for temperature profile
• The temperature profile for several Prandtl values is shown in Figure 5. Based on the numbers, the temperature falls as the Prandtl number rises. The breadth of the energy boundary layer and the temperature contour decrease as Pr increases. As a result, heat may spread out from the heated area considerably more quickly. Thicker thermal barriers and slower heat transfer occur at lower Prandtl values. Physically, greater Pr values reduce thermal diffusivity, resulting in a diminished capacity for energy transfer. Because Pr is the combination of thermal and momentum diffusivity, this is the case. Small values of Pr thus indicate that thermal diffusivity predominates. For more precise estimates of Pr, momentum diffusivity dominates.
• The inspiration of the Eckert number on the contour of the temperature distribution is depicted in Figure 6. The enthalpy difference is a measurement of the temperature of the flow compared to the point of the energy boundary layer. An upsurge in temperature was observed alongside a rise in Ec. Physically, this is true due to the fact that the occurrence of heat generates heat energy within the fluid. In fluid flow ideas, the Eckert number Ec is used to quantify dissipative effects. Ec measures the energy dissipation of the flow arrangement.
• The temperature outline can be seen in Figure 7 as the heat source/sink values rise. The negative value of Q < 0 is known as heat absorption and the positive value of Q > 0 is known as heat transfer. By increasing the significance of the heat generation parameter, the temperature of the fluid rises due to an associated heat source that generates heat for the fluid; consequently, the temperature of the fluid increases.
• The impact of Rd on the temperature contour is shown in Figure 8. It has been detected that increasing Rd causes a rise in fluid temperature. Physically, this occurs because the fluid absorbs heat from the plate.
• The result of magnetic factors on temperature distributions is depicted in Figure 9. It has been detected that a rise in M causes a rapid rise in fluid temperature. Moreover, it can be got that the imposed MHD has no substantial impact on the thermal boundary layer thickness. This phenomenon generates a minor upsurge in the temperature outline due to the Lorentz force addition to the existing skin friction, which results in a rise in plate heat.
• The temperature delivery on a flat plate for several values of the porous parameters is showed in Figure 10. It was found that raising the value of λ rapidly increases the fluid’s temperature. Due to thermal resistance, the thickness of the thermal boundary layer rises.
• Figure 11 shows the result of β on the temperature outline. The results show that the temperature and momentum boundary layer improve for the rising values of β.
• Deborah’s number effect on fluid temperature is revealed in Figure 12. The Deborah number quantified fluidity. Outcomes show that De has a beneficial impact on the temperature field and boundary layer. Whenever the Deborah number is of the order of 1, assumed a high Deborah number; in other words, high Deborah number flows correspond to solid-like behavior and low Deborah numbers to fluid-like behavior. Due to a rise in the shear stress property of a non-Newtonian fluid, the fluid’s layer becomes slightly adhesive as it moves. As stated previously, because of the resistance, more heat is created.
• As shown in Figure 13, the energy and thermal boundary layer grows with the Lewis number. This behavior is more easily observed in shear-thinning fluids. Physically, the ratio between heat and mass diffusivity is known as the Lewis number.
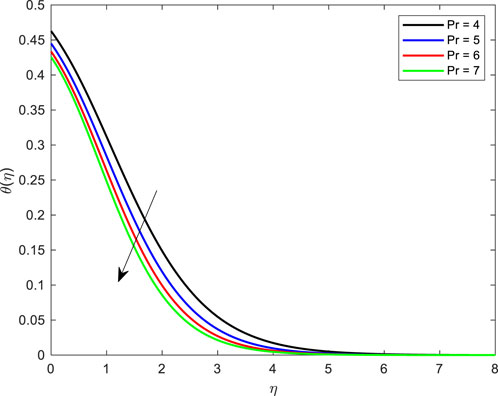
FIGURE 5. Impact of Prandtl number on temperature profile with De = 0.1; Pr = 4; Ec = 0.1; Rd = 1; Q = 0.1; M = 0.1; β = 0.2; λ = 0.1; Le = 2.0.
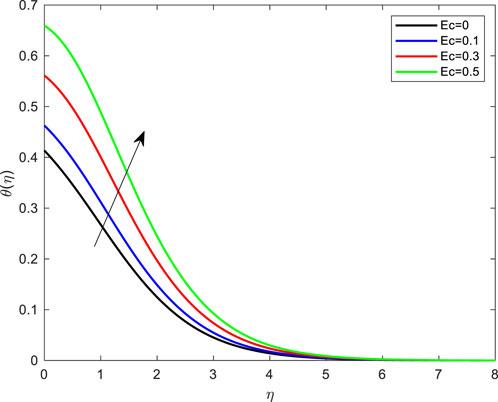
FIGURE 6. Impact of Eckert number on temperature profile with De = 0.1; Pr = 4; Ec = 0.1; Rd = 1; Q = 0.1; M = 0.1; β = 0.2; λ = 0.1; Le = 2.0.
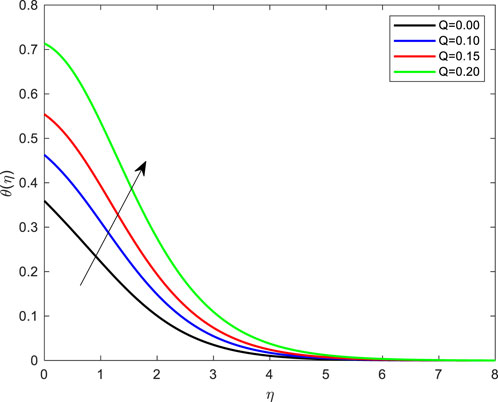
FIGURE 7. Impact of Heat generation on temperature profile with De = 0.1; Pr = 4; Ec = 0.1; Rd = 1; Q = 0.1; M = 0.1; β = 0.2; λ = 0.1; Le = 2.0.
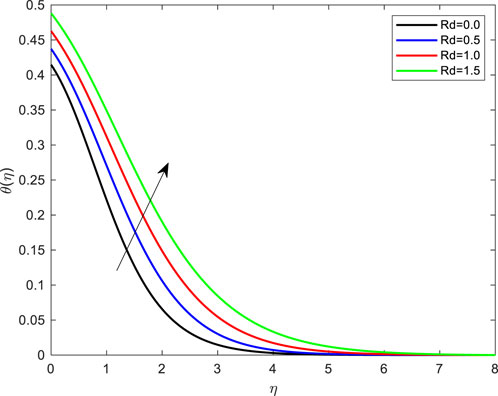
FIGURE 8. Impact of thermal radiation parameter on temperature profile with De = 0.1; Pr = 4; Ec = 0.1; Rd = 1; Q = 0.1; M = 0.1; β = 0.2; λ = 0.1; Le = 2.0.
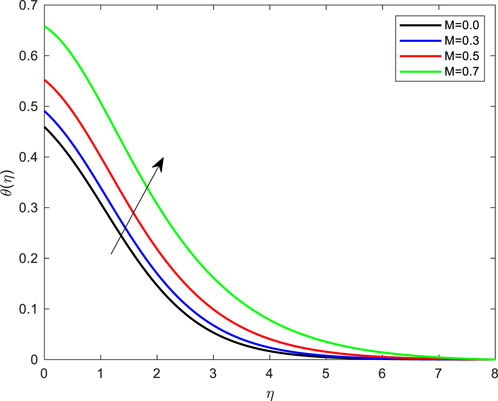
FIGURE 9. Impact of Magnetic field parameter on temperature profile with De = 0.1; Pr = 4; Ec = 0.1; Rd = 1; Q = 0.1; M = 0.1; β = 0.2; λ = 0.1; Le = 2.0.
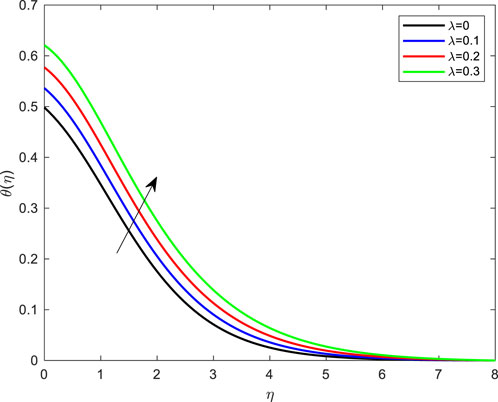
FIGURE 10. Impact of porosity parameter on temperature profile with De = 0.1; Pr = 4; Ec = 0.1; Rd = 1; Q = 0.1; M = 0.1; β = 0.2; λ = 0.1; Le = 2.0.
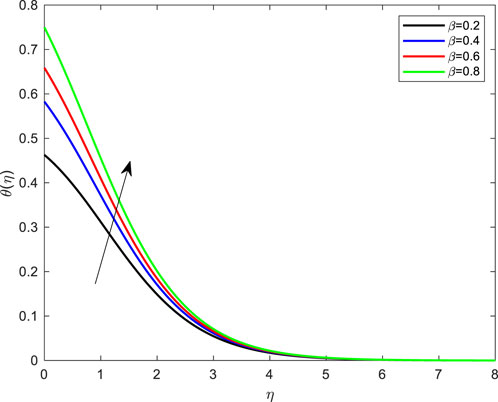
FIGURE 11. Impact of thermal slip condition on temperature profile with De = 0.1; Pr = 4; Ec = 0.1; Rd = 1; Q = 0.1; M = 0.1; β = 0.2; λ = 0.1; Le = 2.0.
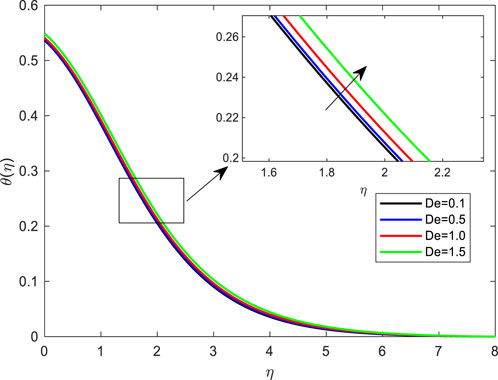
FIGURE 12. Impact of Deborah number on temperature profile with De = 0.1; Pr = 4; Ec = 0.1; Rd = 1; Q = 0.1; M = 0.1; β = 0.2; λ = 0.1; Le = 2.0.
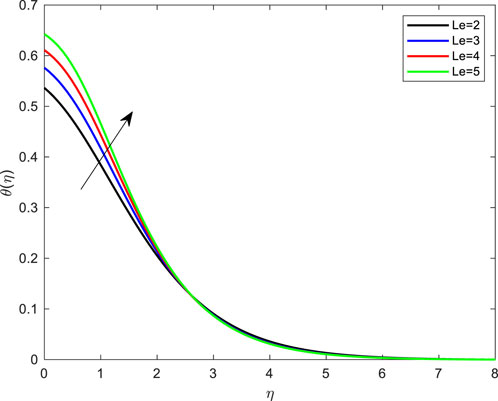
FIGURE 13. Impact of Lewis number on temperature profile with De = 0.1; Pr = 4; Ec = 0.1; Rd = 1; Q = 0.1; M = 0.1; β = 0.2; λ = 0.1; Le = 2.0.
4.3 Explanation for concentration profile
Figure 14 depicts concentration variations as a function of M. Boosting concentration profiles is possible by altering the magnetic parameter values. The concentration distribution changes as the porosity parameter are adjusted, as shown in Figure 15. Figure 16 depicts the impact of Le on sharpness. Higher Lewis numbers decrease concentration and result in a narrower concentration boundary layer. The Le is the ratio between the mass and heat diffusion rates. As the Lewis number rises, the mass diffusivity declines.
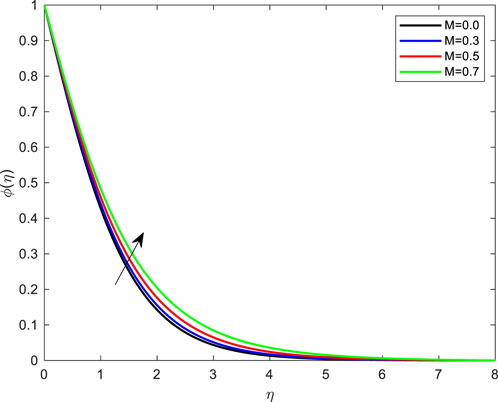
FIGURE 14. Impact of Magnetic field parameter on concentration profile with De = 0.1; Pr = 4; Ec = 0.1; Rd = 1; Q = 0.1; M = 0.1; β = 0.2; λ = 0.1; Le = 2.0.
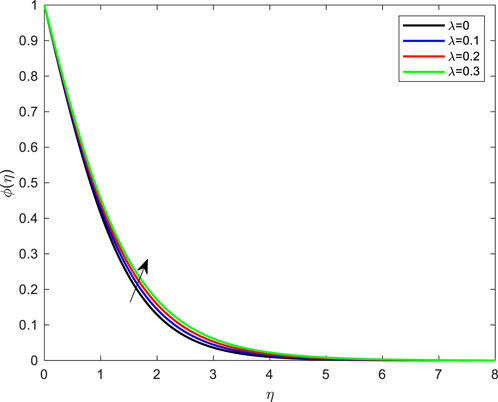
FIGURE 15. Impact of porosity parameter on concentration profile with De = 0.1; Pr = 4; Ec = 0.1; Rd = 1; Q = 0.1; M = 0.1; β = 0.2; λ = 0.1; Le = 2.0.
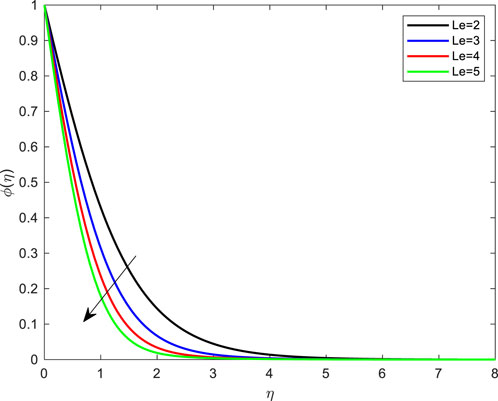
FIGURE 16. Impact of Lewis number on concentration profile with De = 0.1; Pr = 4; Ec = 0.1; Rd = 1; Q = 0.1; M = 0.1; β = 0.2; λ = 0.1; Le = 2.0.
4.4 Explanation for skin friction and Nusselt number profile
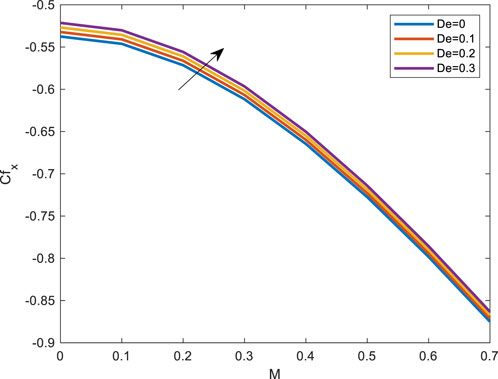
Figure 17 depicts the relationship between the Eckert and Nusselt numbers about M. Nusselt number falls as Ec grows. Figure 18 shows as thermal radiation increases, so do the Nusselt number. The effect of porosity and skin friction is depicted in Figure 19. Skin friction diminishes as the porosity parameter increases. Deborah number (Maxwell’s parameter) and magnetic field skin friction are shown in Figure 20. Skin friction increases as De increases.
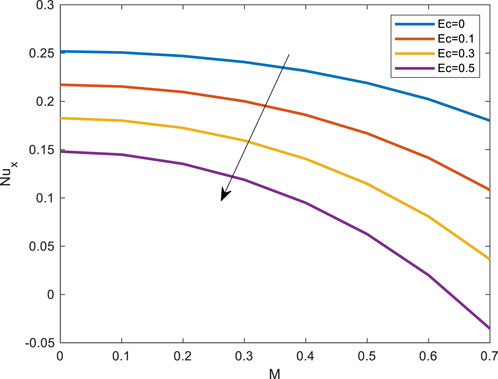
FIGURE 17. Impact of Eckert number over local Nusselt number profile against Magnetic field parameter.
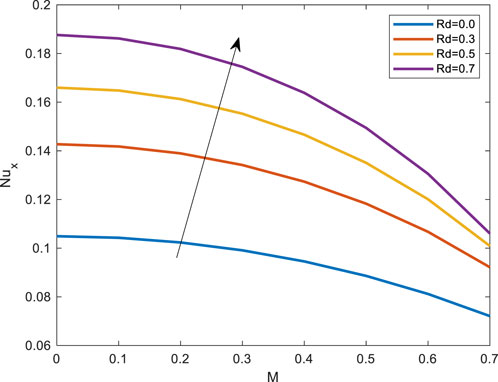
FIGURE 18. Impact of thermal radiation parameter over local Nusselt number profile against Magnetic field parameter.
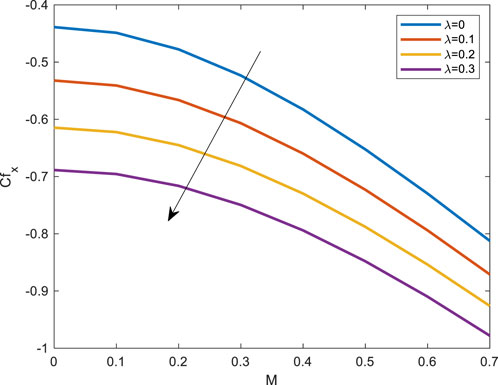
FIGURE 19. Impact of porosity parameter over skin friction profile against Magnetic field parameter.
5 Concluding remarks
This investigation aims to analyze the MHD radiative Maxwell fluid flow with the joint result of heat generation and mass diffusion over a flat porous plate. After converting modelled PDEs into ODEs, the numerical solutions for ongoing boundary value problems are carried out by means of the Runge-Kutta Fehlberg technique in MATLAB software. The skin friction coefficient and Nusselt number in heat transfer for the Maxwell fluid are computed, as well as the effects of the nonlinear solved problem for numerous governing parameters on the flow quantities. The novel findings of this research are to investigate the Nusselt number for the Eckert number versus the MHD and the Nusselt number for the radiation parameter versus the magnetic field. In addition to the skin friction study, investigate the porosity and the Deborah number in the occurrence of a magnetic field. To draw graphs, fixed parameter values are Pr = 4; De = 0.1; Ec = 0.1; Rd = 1; Q = 0.1; M = 0.1; β = 0.2; λ = 0.1; Le = 2.0; Some of the significant critical findings of the paper are giving the answers to the research questions:
• The velocity outline reduced with rising values of Deborah number, magnetic parameter, and porosity parameter.
• Temperature profile values increased with rising Eckert number, heat generation, thermal radiation, Magnetic field parameter, porosity parameter, thermal slip condition, Deborah number, and Lewis number. Still, they decreased with an increasing Prandtl number value.
• The concentration profile increased as the Magnetic field parameter and permeability values increased, whereas the concentration profile decreased when the Lewis number value enlarged.
• The Nusselt number increased as the Eckert number increased, while it decreased for thermal radiation.
• The coefficient of friction declines as the porosity parameter rises, but the coefficient growths as the Deborah number rises.
Applying the Runge-Kutta Fehlberg technique in MATLAB dramatically enhances efficacy and precision. Our outcomes indicate that this strategy is effective and sufficiently potent for solving fluid flow problems.
Data availability statement
The original contributions presented in the study are included in the article/Supplementary Material, further inquiries can be directed to the corresponding author.
Author contributions
KS: similarity transformation and solutions DI: modelling and formulation IK: results and discussion. All authors contributed to the article and approved the submitted version.
Conflict of interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Publisher’s note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
References
1. Mabood F, Shateyi S. Multiple slip effects on MHD unsteady flow heat and mass transfer impinging on permeable stretching sheet with radiation. Model Simulation Eng (2019) 2019:1–11. doi:10.1155/2019/3052790
2. Dawar A, Shah Z, Islam S, Deebani W, Shutaywi M. MHD stagnation point flow of a water-based copper nanofluid past a flat plate with solar radiation effect. J Pet Sci Eng (2023) 220:111148. doi:10.1016/j.petrol.2022.111148
3. Nath AJ, Roy P, Banerjee D, Pati S, Randive PR, Biswas P. Analytical solution to time-periodic electro-osmotic flow of generalized Maxwell fluids in parallel plate microchannel with slip-dependent zeta potential. J Fluids Eng (2023) 145(1):014501. doi:10.1115/1.4055782
4. Lin HT, Chen CC, Yu WS. Mixed convection from a horizontal plate to fluids of any Prandtl number. Wärme-und Stoffübertragung (1989)) 24(4):225–34. doi:10.1007/BF01625498
5. Adegbie KS, Omowaye AJ, Disu AB, Animasaun IL. Heat and mass transfer of upper convected Maxwell fluid flow with variable thermo-physical properties over a horizontal melting surface. Appl Math (2015) 6(08):1362–79. doi:10.4236/am.2015.68129
6. Mustafa M, Hayat T, Alsaedi A. Rotating flow of Maxwell fluid with variable thermal conductivity: An application to non-fourier heat flux theory. Int J Heat Mass Transfer (2017) 106:142–8. doi:10.1016/j.ijheatmasstransfer.2016.10.051
7. Shafique Z, Mustafa M, Mushtaq A. Boundary layer flow of Maxwell fluid in rotating frame with binary chemical reaction and activation energy. Results Phys (2016) 6:627–33. doi:10.1016/j.rinp.2016.09.006
8. Olabode JO, Idowu AS, Akolade MT, Titiloye EO. Unsteady flow analysis of Maxwell fluid with temperature dependent variable properties and quadratic thermo-solutal convection influence. Partial Differential Equations Appl Math (2021) 4:100078. doi:10.1016/j.padiff.2021.100078
9. Heyhat MM, Khabazi N. Non-isothermal flow of Maxwell fluids above fixed flat plates under the influence of a transverse magnetic field. J Mech Eng Sci (2011) 225(4):909–16. doi:10.1243/09544062JMES2245
10. Bhattacharyya K, Boundary layer flow with diffusion and first-order chemical reaction over a porous flat plate subject to suction/injection and with variable wall concentration. Chem Eng Res Bull (2011) 15(1):6–11. doi:10.3329/cerb.v15i1.6464
11. Sadia H, Gul N, Zeb A, Khan ZA. Convection heat–mass transfer of generalized Maxwell fluid with radiation effect, exponential heating, and chemical reaction using fractional Caputo–Fabrizio derivatives. Open Phys (2022) 20(1):1250–66. doi:10.1155/2022/3629416
12. Shenoy AV. Non-Newtonian fluid heat transfer in porous media. In Adv Heat transfer (1994) 24. 101–90.
13. Venkatadri K, Abdul Gaffar S, Rajarajeswari P, Prasad VR, Anwar Bég O, Hidayathulla Khan BM. Melting heat transfer analysis of electrically conducting nanofluid flow over an exponentially shrinking/stretching porous sheet with radiative heat flux under a magnetic field. Heat Transfer (2020)) 49(8):4281–303. doi:10.1002/htj.21827
14. Mahanthesh B, Gireesha BJ, Thammanna GT, Shehzad SA, Abbasi FM, Gorla RS. Nonlinear convection in nano Maxwell fluid with nonlinear thermal radiation: A three-dimensional study. Alexandria Eng J (2018) 57(3):1927–35. doi:10.1016/j.aej.2017.03.037
15. Kumar KG, Rudraswamy NG, Gireesha BJ. Effects of mass transfer on MHD three-dimensional flow of a Prandtl liquid over a flat plate in the presence of chemical reaction. Results Phys (2017) 7:3465–71. doi:10.1016/j.rinp.2017.08.060
16. Hsiao KL. Combined electrical MHD heat transfer thermal extrusion system using Maxwell fluid with radiative and viscous dissipation effects. Appl Therm Eng (2017) 112:1281–8. doi:10.1016/j.applthermaleng.2016.08.208
17. Reddy NK, Swamy HA, Sankar M. Buoyant convective flow of different hybrid nano liquids in a non-uniformly heated annulus. Eur Phys J Spec Top (2021) 230(5):1213–25. doi:10.1140/epjs/s11734-021-00034-y
18. Sankar M, Park J, Do Y. Natural convection in a vertical annuli with discrete heat sources. Numer Heat Transfer, A: Appl (2011) 59(8):594–615. doi:10.1080/10407782.2011.561110
19. Makinde OD, Sankar M. Numerical investigation of developing natural convection in vertical double-passage porous annuli. Defect and Diffusion Forum (2018) 387:442–60. doi:10.4028/www.scientific.net/DDF.387.442
20. Sudarmozhi K, Iranian D, Khan I, Alzahrani J, Al-johani A, Eldin SM. Double diffusion in a porous medium of MHD Maxwell fluid with thermal radiation, heat generation and chemical reaction. Case Stud Therm Eng (2023) 43:102700. doi:10.1016/j.csite.2023.102700
21. Roy NC, Pop I. Dual solutions of a nanofluid flow past a convectively heated nonlinearly shrinking sheet. Chin J Phys (2023) 82:31–40. doi:10.1016/j.cjph.2022.12.008
22. Roy NC, Pop I. Dual solutions of magnetohydrodynamic mixed convection flow of an Oldroyd-B nanofluid over a shrinking sheet with heat source/sink. Alexandria Eng J (2022) 61(8):5939–48. doi:10.1016/j.aej.2021.11.021
23. Shah Z, McCash LB, Dawar A, Bonyah E. Entropy optimization in Darcy–Forchheimer MHD flow of water based copper and silver nanofluids with Joule heating and viscous dissipation effects. AIP Adv (2020) 10(6):065137. doi:10.1063/5.0014952
24. Tang T, Rooman M, Shah Z, Asif Jan M, Vrinceanu N, Racheriu M, Computational study and characteristics of magnetized gold-blood Oldroyd-B nanofluid flow and heat transfer in stenosis narrow arteries. J Magnetism Magn Mater (2023) 569:170448. doi:10.1016/j.jmmm.2023.170448
25. Mustafa M, Khan JA, Hayat T, Alsaedi A. Sakiadis flow of Maxwell fluid considering magnetic field and convective boundary conditions. Aip Adv (2015) 5(2):027106. doi:10.1063/1.4907927
26. Rosseland S. Astrophysik und atom-theoretische Grundlagen. Berlin: Springer (1931). doi:10.1007/978-3-662-26679-3
27. Raptis A, Perdikis C. Viscoelastic flow by the presence of radiation Appl Math Mech. (1998) 78(4):277–9. doi:10.1002/(sici)1521-4001(199804)78:4<277::aid-zamm277>3.0.co;2-f199804).
Nomenclature
Keywords: viscous dissipation, Maxwell fluid, porous medium, magnetic field, horizontal plate
Citation: Sudarmozhi K, Iranian D and Khan I (2023) A steady flow of MHD Maxwell viscoelastic fluid on a flat porous plate with the outcome of radiation and heat generation. Front. Phys. 11:1126662. doi: 10.3389/fphy.2023.1126662
Received: 18 December 2022; Accepted: 10 May 2023;
Published: 08 June 2023.
Edited by:
Ramon Planet, University of Barcelona, SpainReviewed by:
Hina Sadaf, National University of Sciences and Technology (NUST), PakistanSankar M., University of Technology and Applied Sciences, Oman
Zahir Shah, University of Lakki Marwat, Pakistan
Copyright © 2023 Sudarmozhi, Iranian and Khan. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Ilyas Khan, aS5zYWlkQG11LmVkdS5zYQ==
 K. Sudarmozhi
K. Sudarmozhi D. Iranian
D. Iranian Ilyas Khan
Ilyas Khan