A new effective metric for dynamical robustness of directed networks

1 Introduction

In practical applications, power grids [1, 2], communication networks, secure communication [3] and public transportation systems [4, 5] often encounter failures and attacks [6–9]. A failure of a very small fraction of nodes in a network may lead to complete fragmentation of the whole network. Therefore, the robustness of complex networks subjected to failures or attacks is an important issue to study in network science and engineering [10]. Exploring the network robustness can help better understand various networked systems and enable us to design more robust infrastructural or social systems.

In the past 2 decades, the issue of network robustness has attracted a lot of attention [10–15]. Most of the previous works focus on the structural robustness of complex networks, which is defined as the ability to maintaining their functionalities when they are disturbed or attacked [16, 17]. Therein, the failure of a node or an edge in the network is modeled by the removal of the node or the edge. To quantify structural robustness of complex networks, many measures with respect to the network structure have been formulated, such as connectivity, maximum strongly connected subgraph, natural connectivity, and average shortest path [18, 19]. Moreover, a variety of attack strategies, such as random attack and deliberate attack, have been proposed to test the robustness of different kinds of networks [20–22]. The structural robustness of complex networks can also be measured using some metrics derived from statistical physics and percolation theory [23].

Recently, the network robustness with respect to the system dynamics has stimulated even more interest [24–26]. A new concept of dynamical robustness [27] can be used to quantify the ability of a network to maintain its dynamical activities against local perturbations. Different from structural robustness where topological perturbations are considered, dynamical robustness is concerned with the robustness of network dynamics. In [27], node failure is modeled as the inactivation of diffusively coupled oscillators. In [28], dynamical robustness is quantified through the synchronization error as a function of the noise variance, where node failure is modeled by injecting noise into a node. In [29], a mathematical framework is established to quantify the effect of noise injected at one of the nodes on the synchronization performance of coupled dynamical systems. Indeed, noise is inevitable in real-world networks [30, 31]. It is natural to ask whether a networked system subjected to noise can recover to its synchronous state? On the one hand, noise may destroy the network’s stability and prevent network synchronization [32, 33]. On the other hand, noise-induced synchronization can be beneficial for coupled chaotic systems [34]. In order to clarify the influence of noise on the network, in [35] networks of different structure and complexity are analyzed, showing that many networks are better in coping with both intrinsic and extrinsic noise.

Motivated by the above discussions, this article further investigates the dynamical robustness of stochastic complex networks. The network topology is directed and the nodes are higher-dimensional non-linear dynamical systems. Similar to [29], the failure of a node in the network is modeled by injecting noise into the node. However, differing from [29], in this article it is not assumed that the network is symmetric. From a technical perspective, this introduces more challenges than its undirected counterpart [36]. A novel metric measuring the dynamical robustness of a directed networked system with additive noise is formulated. Notice that the proposed robustness metric uncovers the complex interplay between node dynamics and network topology on the overall network robustness.

The main contributions of this article are as follows. First, a mathematical framework is established to examine the dynamical robustness of a directed network of coupled dynamical systems. In this article, the notion of dynamical robustness refers to the ability of a network of coupled dynamical systems to return to its synchronous state when it encounters the disturbance of noise. The new metric is used to characterize the degree to which the networked system withstand failures and perturbations. Assume that the networked system synchronizes before the noise is introduced. The system’s robustness is defined related to the synchronization error of the network. Moreover, different from the methods used for undirected networks, the Laplacian matrix of a directed network is decomposed to two simpler matrices. In the context of mean-square stochastic stability, the new robustness metric is precisely formulated. This metric highlights the importance of the node dynamics in network robustness. Finally, numerical simulations are presented for illustration and verification using three chaotic systems (namely, Rössler system, Chen system and Wang system). The study of dynamical robustness can help better understand the roles of node dynamics and network topology, thereby better designing noise-tolerant networks.

The remainder of this article is organized as follows. Section 2 introduces the notation and some basic graph theory. In Section 3, problem formulation is presented and a new robustness metric is formulated. In Section 4, numerical simulations are shown for illustration and verification. Section 5 concludes the investigation.

2 Preliminaries

2.1 Notation

Let $\mathbb{R}$ denote the set of real numbers, ${\mathbb{R}}^n$ the set of the n-dimensional real vectors, and ${\mathbb{R}}^{n\times m}$ the set of n × m real matrices. Let I_n be the n × n identity matrix, 1_n the column vector of all ones, 0 the zero matrix with appropriate dimensition, and diag (a₁, … , a_n) the n × n diagonal matrix with the diagonal elements being a₁, … , a_n. Let the trace of matrix A be denoted by Tr(A). Moreover, let $‖\cdot ‖$ denote the 2-norm of a matrix or a vector, ⊗ the Kronecker product, and ⊕ the Kronecker sum. Let the superscript T denote the transpose. Let j denote the imaginary unit satisfying j² = −1. For a matrix $A\in {\mathbb{R}}^{m\times n}$, $Vec(A)={[co{l}_1^T(A),\dots ,co{l}_n^T(A)]}^T\in {\mathbb{R}}^{mn}$ is the colum vector of size mn × 1 obtained by stacking all columns of A, where $co{l}_i(A)\in {\mathbb{R}}^m$ denotes the ith column of A.

2.2 Graph theory

A directed graph $\mathcal{G}=(\mathcal{V},\mathcal{E})$ consists of a node set $\mathcal{V}=\{1,\dots ,N\}$ and an edge set $\mathcal{E}=\{(j,i)\}$. Let $\mathcal{A}=(a_{ij})\in {\mathbb{R}}^{N\times N}$ denote the adjacency matrix of a digraph, where a_ij = 1 if there is a directed edge from node j to node i, and a_ij = 0 otherwise. Moreover, a_ii = 0 for all i = 1, … , N. Let $\mathcal{D}=\mathrm{diag}(d_1^{in},\dots ,d_N^{in})$ be the in-degree matrix, where $d_i^{in}$ represents the in-degree of node i. The Laplacian matrix is then defined by $\mathcal{L}=\mathcal{D}-\mathcal{A}$. The Laplacian matrix can be decomposed as $\mathcal{L}=U+\mathrm{\Delta }$, where $U=\frac{1}{2}(\mathcal{L}+{\mathcal{L}}^T)$ is a symmetric matrix and $\mathrm{\Delta }=\frac{1}{2}(\mathcal{L}-{\mathcal{L}}^T)$ is an anti-symmetric matrix satisfying Δ^T = −Δ.

For the anti-symmetric matrix Δ, the following lemma is obtained.

Lemma 1. Let $\mathrm{\Delta }\in {\mathbb{R}}^{N\times N}$ be an anti-symmetric matrix satisfying Δ^T = −Δ. Then, there exists an orthogonal matrix C such that

$\begin{array}{c}\hfill C^T\mathrm{\Delta }C=\mathrm{diag}\left(\mathbf{0},\dots ,\mathbf{0},\left(\begin{array}{cc}\hfill 0\hfill & \hfill b_1\hfill \\ \hfill -b_1\hfill & \hfill 0\hfill \end{array}\right),\dots ,\left(\begin{array}{cc}\hfill 0\hfill & \hfill b_l\hfill \\ \hfill -b_l\hfill & \hfill 0\hfill \end{array}\right)\right),\end{array}(1)$

where 0, … , 0, ±b₁j, … , ±b_lj (b_i ≠ 0) are the eigenvalues of the matrix Δ. Here, $l=\frac{N-r}{2}$ with r being the multiplicity of the zero eigenvalue of Δ.

Proof: Let μ₁ = b₁j be an eigenvalue of Δ and χ₁ the corresponding eigenvector. Let ${\bar{\mu }}_1=-b_1\mathbf{j}$. It follows that Δχ₁ = μ₁χ₁, $\mathrm{\Delta }{\bar{\chi }}_1={\bar{\mu }}_1{\bar{\chi }}_1$, and ${\chi }_1\ne {\bar{\chi }}_1$, where ${\bar{\chi }}_1$ is an eigenvector of Δ associated with ${\bar{\mu }}_1$.

Recall that Δ is anti-symmetric. Consequently, it is a normal matrix and is unitary similar to a diagonal matrix. Particularly, let $P=(0,\dots ,0,{\varsigma }_1,{\bar{\varsigma }}_1,\dots ,{\varsigma }_l,{\bar{\varsigma }}_l)$, where ${\varsigma }_i\in {\mathbb{R}}^N$, ${\bar{\varsigma }}_i\in {\mathbb{R}}^N$, i = 1, … , l, and ${\varsigma }_i\ne {\bar{\varsigma }}_i$. It follows that

$P^{-1}\mathrm{\Delta }P=\mathrm{diag}\left(0,\dots ,0,{\mu }_1,{\bar{\mu }}_1,\dots ,{\mu }_l,{\bar{\mu }}_l\right).(2)$

Let ${\phi }_1=\frac{{\varsigma }_1+{\bar{\varsigma }}_1}{\sqrt{2}}$ and ${\phi }_2=\frac{{\varsigma }_1-{\bar{\varsigma }}_1}{\sqrt{2}\mathbf{j}}$. One has

$\mathrm{\Delta }{\phi }_1=\frac{1}{\sqrt{2}}\left(\mathrm{\Delta }{\varsigma }_1+\mathrm{\Delta }{\bar{\varsigma }}_1\right)=\frac{1}{\sqrt{2}}\left({\mu }_1{\varsigma }_1+{\bar{\mu }}_1{\bar{\varsigma }}_1\right)=-b_1{\phi }_2,$

$\mathrm{\Delta }{\phi }_2=\frac{1}{\sqrt{2}\mathbf{j}}\left(\mathrm{\Delta }{\varsigma }_1-\mathrm{\Delta }{\bar{\varsigma }}_1\right)=\frac{1}{\sqrt{2}\mathbf{j}}\left({\mu }_1{\varsigma }_1-{\bar{\mu }}_1{\bar{\varsigma }}_1\right)=b_1{\phi }_1.$

Because p is a unitary matrix, ${\phi }_1^T{\phi }_1=1$, ${\phi }_2^T{\phi }_2=1$, and ${\bar{\varsigma }}_j^T{\phi }_1=0(j=2,\dots ,l)$. Similarly, φ₃, … , φ_2l have the same property. It follows that C = (0, … , 0, φ₁, … , φ_2l) is an orthogonal matrix, in which the number of zero eigenvalues is r and r + 2l = N. Therefore,

$\begin{array}{c}\hfill C^T\mathrm{\Delta }C=\mathrm{diag}\left(\mathbf{0},\dots ,\mathbf{0},\left(\begin{array}{cc}\hfill 0\hfill & \hfill b_1\hfill \\ \hfill -b_1\hfill & \hfill 0\hfill \end{array}\right),\dots ,\left(\begin{array}{cc}\hfill 0\hfill & \hfill b_l\hfill \\ \hfill -b_l\hfill & \hfill 0\hfill \end{array}\right)\right).\end{array}$

3 The new robustness metric

Consider a directed network consisting of N identical nodes with linearly diffusive couplings, in which each node is an n-dimensional dynamical system. The network can be described by the following coupled stochastic differential equation:

$\begin{array}{cc}\hfill {\dot{x}}_i\left(t\right)& =f\left(x_i\left(t\right)\right)-\alpha \sum _{j=1}^N{l}_{ij}h\left(x_j\left(t\right)\right)+{\upsilon }_i{H}_{\eta }\eta \left(t\right),\hfill \\ \hfill i& =1,\dots ,N,\hfill \end{array}(3)$

where $x_i(t)\in {\mathbb{R}}^n$ is the state vector of node i, f (⋅) a smooth function describing the self-dynamics of each node, α > 0 the coupling strength, l_ij the (i, j)th entry of the Laplacian matrix, and h (⋅) the inner-coupling function of the nodes. The variable υ_i indicates whether node i is subjected to noise. That is, υ_i = 1 when node i is contaminated with additive noise, and υ_i = 0 otherwise. The vector $H_{\eta }\in {\mathbb{R}}^n$ describes how the noise η(t) enters the dynamics of a node, where η(t) is a zero-mean Gaussian white noise with variance $\frac{\theta }{2}$ (θ > 0).

For network (3), $\mathcal{L}=(l_{ij})\in {\mathbb{R}}^{N\times N}$ is the Laplacian matrix defined by l_ij = −1 if there is a directed edge from node j to node i, and l_ij = 0 otherwise, with $l_{ii}=-{\sum }_{j=1,j\ne i}^N{l}_{ij}$, for all i, j = 1, … , N. Therefore, $\mathcal{L}$ is a zero row-sum matrix. Recall from Section 2.2 that $\mathcal{L}=U+\mathrm{\Delta }$, in which $U=\frac{1}{2}(\mathcal{L}+{\mathcal{L}}^T)$ is a symmetric matrix and $\mathrm{\Delta }=\frac{1}{2}(\mathcal{L}-{\mathcal{L}}^T)$ is an anti-symmetric matrix with Δ^T = −Δ. Therefore, network (3) can be rewritten as

$\begin{array}{cc}\hfill {\dot{x}}_i\left(t\right)& =f\left(x_i\left(t\right)\right)-\alpha \sum _{j=1}^N{u}_{ij}h\left(x_j\left(t\right)\right)-\alpha \sum _{j=1}^N{\delta }_{ij}h\left(x_j\left(t\right)\right)\hfill \\ \hfill & +{\upsilon }_i{H}_{\eta }\eta \left(t\right),i=1,\dots ,N,\hfill \end{array}(4)$

where u_ij is the (i, j)th element of U and δ_ij is the (i, j)th element of Δ.

The network is said to achieve synchronization if ${\lim }_{t\to \infty }‖x_i(t)-s(t)‖=0$ for all i = 1, … , N, where s(t) is the solution of $\dot{s}(t)=f(s(t))$ (see [37]).

Define the node synchronization error ξ_i(t) = x_i(t) − s(t). The linearized error system is given by

$\begin{array}{cc}\hfill {\dot{\xi }}_i\left(t\right)& =J_f\left(s\right){\xi }_i\left(t\right)-\alpha \sum _{j=1}^N{u}_{ij}{J}_h\left(s\right){\xi }_j\left(t\right)-\alpha \sum _{j=1}^N{\delta }_{ij}{J}_h\left(s\right){\xi }_j\left(t\right)+{\upsilon }_i{H}_{\eta }\eta \left(t\right),i=1,\dots ,N,\hfill \end{array}(5)$

where $J_f(s)\in {\mathbb{R}}^{n\times n}$ and $J_h(s)\in {\mathbb{R}}^{n\times n}$ are, respectively, the Jacobian matrices of f and h, i.e., $J_f(s)=\frac{\partial f(x)}{\partial x}{|}_{x=s(t)}$ and $J_h(s)=\frac{\partial h(x)}{\partial x}{|}_{x=s(t)}$.

Let $\xi (t)={[{\xi }_1^T(t),\dots ,{\xi }_N^T(t)]}^T\in {\mathbb{R}}^{Nn}$. The linearized error system 5) can be rewritten in a compact form as

$\begin{array}{cc}\hfill \dot{\xi }\left(t\right)& =\left[I_N\otimes J_f\left(s\right)-\alpha U\otimes J_h\left(s\right)-\alpha \mathrm{\Delta }\otimes J_h\left(s\right)\right]\xi \left(t\right)\hfill \\ \hfill & +\left(\upsilon \otimes H_{\eta }\right)\eta \left(t\right),\hfill \end{array}(6)$

where $\upsilon ={[{\upsilon }_1,\dots ,{\upsilon }_N]}^T\in {\mathbb{R}}^N$ denotes the location of the node where noise is injected.

The objective is to provide a thorough analysis of (6) to illustrate the overall effect of noise on network synchronization. Define the network synchronization error as

$\varphi \left(t\right)={‖\xi \left(t\right)‖}^2.(7)$

The expected value of ϕ(t) is given by

$\mathbb{E}\left[\varphi \left(t\right)\right]=\mathbb{E}\left[{\xi }^T\left(t\right)\xi \left(t\right)\right]=\mathbf{Tr}\left(\mathbb{E}\left[\xi \left(\mathit{\text{t}}\right){\xi }^{\mathit{\text{T}}}\left(\mathit{\text{t}}\right)\right]\right).(8)$

Let $\mathrm{\Sigma }(t)=\mathbb{E}[\xi (t){\xi }^T(t)]$. Note that the analysis of the effect of noise injected at the network node can be reduced to the study of the time evolution of the trace of the correlation matrix Σ(t). Since U^T = U and Δ^T = −Δ, one has

$\begin{array}{ll}\hfill \dot{\mathrm{\Sigma }}\left(t\right)& =\mathbb{E}\left[\dot{\xi }\left(t\right){\xi }^T\left(t\right)+\xi \left(t\right){\dot{\xi }}^T\left(t\right)\right]\hfill \\ \hfill & =\left[I_N\otimes J_f\left(s\right)-\alpha U\otimes J_h\left(s\right)-\alpha \mathrm{\Delta }\otimes J_h\left(s\right)\right]\mathrm{\Sigma }\left(t\right)\hfill \\ \hfill & +\mathrm{\Sigma }\left(t\right)\left[I_N\otimes J_f^T\left(s\right)-\alpha U\otimes J_h^T\left(s\right)+\alpha \mathrm{\Delta }\otimes J_h^T\left(s\right)\right]\hfill \\ \hfill & +\left(\upsilon \otimes H_{\eta }\right)\mathbb{E}\left[\eta \left(t\right){\xi }^T\left(t\right)\right]+\mathbb{E}\left[\xi \left(t\right)\eta \left(t\right)\right]\left({\upsilon }^T\otimes H_{\eta }^T\right).\hfill \end{array}(9)$

Notice that the solution of (6) is

$\xi \left(t\right)={\mathrm{\Phi }}_{\xi }\left(t,0\right)\xi \left(0\right)+{\int }_0^t{\mathrm{\Phi }}_{\xi }\left(t,\tau \right)\left(\upsilon \otimes H_{\eta }\right)\eta \left(\tau \right)d\tau ,(10)$

where Φ_ξ(t, τ) is the state transition matrix associated with the state matrix I_N ⊗ J_f(s) − αU ⊗ J_h(s) − αΔ ⊗ J_h(s), and ξ(0) is the initial value. Recall that η(t) is a zero-mean Gaussian white noise with variance $\frac{\theta }{2}$. According to the analysis in [38], $\mathbb{E}\left[\eta (t)\eta (\tau )\right]=\frac{\theta }{2}\delta (t-\tau )$ and $\mathbb{E}\left[\xi (0)\eta (\tau )\right]=\frac{\theta }{2}{\mathbf{1}}_{Nn}$, where δ(t) is the Dirac delta function. Eq. 9 can be rewritten as the following time-varying Lyapunov equation for the time evolution of the correlation matrix:

$\begin{array}{cc}\hfill \dot{\mathrm{\Sigma }}\left(t\right)& =\left[I_N\otimes J_f\left(s\right)-\alpha U\otimes J_h\left(s\right)-\alpha \mathrm{\Delta }\otimes J_h\left(s\right)\right]\mathrm{\Sigma }\left(t\right)\hfill \\ \hfill & +\mathrm{\Sigma }\left(t\right)\left[I_N\otimes J_f^T\left(s\right)-\alpha U\otimes J_h^T\left(s\right)+\alpha \mathrm{\Delta }\otimes J_h^T\left(s\right)\right]\hfill \\ \hfill & +\theta \left(\upsilon {\upsilon }^T\otimes H_{\eta }{H}_{\eta }^T\right).\hfill \end{array}(11)$

Recall the definition of the matrix C in Lemma 1. Particularly, let C = [c₁, … , c_N], $c_i\in {\mathbb{R}}^N$. Let D = C^TΔC, M = C^TUC, $\tilde{C}=C\otimes I_n$, and $\tilde{\mathrm{\Sigma }}(t)={\tilde{C}}^T\mathrm{\Sigma }(t)\tilde{C}$. Multiplying (11) from the left by ${\tilde{C}}^T$ and from the right by $\tilde{C}$ leads to

$\begin{array}{cc}\hfill \dot{\stackrel{̃}{\mathrm{\Sigma }}}\left(t\right)& =\left[I_N\otimes J_f\left(s\right)-\alpha M\otimes J_h\left(s\right)-\alpha D\otimes J_h\left(s\right)\right]\tilde{\mathrm{\Sigma }}\left(t\right)\hfill \\ \hfill & +\tilde{\mathrm{\Sigma }}\left(t\right)\left[I_N\otimes J_f^T\left(s\right)-\alpha M\otimes J_h^T\left(s\right)+\alpha D\otimes J_h^T\left(s\right)\right]\hfill \\ \hfill & +\theta \left(C^T\upsilon {\upsilon }^{T}C\otimes H_{\eta }{H}_{\eta }^T\right).\hfill \end{array}(12)$

Since the trace of a matrix does not change under a similarity transformation, one has $\mathrm{Tr}(\mathrm{\Sigma }(t))=\mathrm{Tr}(\tilde{\mathrm{\Sigma }}(t))$ and $\mathbb{E}\left[\varphi (t)\right]=\mathrm{Tr}(\tilde{\mathrm{\Sigma }}(t))$. Let

$\tilde{\mathrm{\Sigma }}\left(t\right)=\sum _{i,j=1}^N{e}_i{e}_j^T\otimes {\tilde{\sigma }}_{ij}\left(t\right),(13)$

where $e_i\in {\mathbb{R}}^N$ denotes the ith canonical vector and ${\tilde{\sigma }}_{ij}(t)\in {\mathbb{R}}^{n\times n}$ is the (i, j)th block of the matrix $\tilde{\mathrm{\Sigma }}(t)$. It then follows that

$\mathbb{E}\left[\varphi \left(t\right)\right]=\sum _{i=1}^N\mathbf{Tr}\left({\tilde{\sigma }}_{ii}\left(t\right)\right).(14)$

The dynamics of ${\tilde{\sigma }}_{ii}(t)$ are given by

$\begin{array}{cc}\hfill {\dot{\stackrel{̃}{\sigma }}}_{ii}\left(t\right)& =\left[J_f\left(s\right)-\alpha m_{ii}{J}_h\left(s\right)\right]{\tilde{\sigma }}_{ii}\left(t\right)\hfill \\ \hfill & +{\tilde{\sigma }}_{ii}\left(t\right)\left[J_f^T\left(s\right)-\alpha m_{ii}{J}_h^T\left(s\right)\right]+\theta {\left(c_i^T\upsilon \right)}^2{H}_{\eta }{H}_{\eta }^T,\hfill \\ \hfill i& =1,\dots ,N,\hfill \end{array}(15)$

where m_ii is the ith diagonal element of M.

Let ${\zeta }_i(t)={\tilde{\sigma }}_{ii}(t)$, κ_i = αm_ii, and ${\beta }_i=c_i^T\upsilon$. Eq. 15 can be rewritten as

$\begin{array}{cc}\hfill {\dot{\zeta }}_i\left(t\right)& =\left[J_f\left(s\right)-{\kappa }_i{J}_h\left(s\right)\right]{\zeta }_i\left(t\right)\hfill \\ \hfill & +{\zeta }_i\left(t\right)\left[J_f^T\left(s\right)-{\kappa }_i{J}_h^T\left(s\right)\right]+\theta {\beta }_i^2{H}_{\eta }{H}_{\eta }^T,\hfill \\ \hfill i& =1,\dots ,N.\hfill \end{array}(16)$

Rewrite (16) as follows:

$\begin{array}{cc}\hfill Vec\left({\dot{\zeta }}_i\left(t\right)\right)& =\left(\left[J_f\left(s\right)-{\kappa }_i{J}_h\left(s\right)\right]\oplus \left[J_f\left(s\right)-{\kappa }_i{J}_h\left(s\right)\right]\right)\hfill \\ \hfill & \times Vec\left({\zeta }_i\left(t\right)\right)+\theta {\beta }_i^{2}Vec\left(H_{\eta }{H}_{\eta }^T\right),\hfill \\ \hfill i& =1,\dots ,N,\hfill \end{array}(17)$

where Vec indicates matrix vectorization defined in Section 2.1. The solution of (17) is given by

$\begin{array}{cc}\hfill Vec\left({\zeta }_i\left(t\right)\right)& ={\mathrm{\Phi }}_{Vec\left({\zeta }_i\right)}\left(t,0\right)Vec\left({\zeta }_i\left(0\right)\right)\hfill \\ \hfill & +\theta {\beta }_i^2{\int }_0^t{\mathrm{\Phi }}_{Vec\left({\zeta }_i\right)}\left(t,\tau \right)d\tau Vec\left(H_{\eta }{H}_{\eta }^T\right),\hfill \\ \hfill i& =1,\dots ,N,\hfill \end{array}(18)$

where ${\mathrm{\Phi }}_{Vec({\zeta }_i)}(t,\tau )$ is the state transition matrix, which is associated with the state matrix $\left[J_f(s)-{\kappa }_i{J}_h(s)\right]\oplus \left[J_f(s)-{\kappa }_i{J}_h(s)\right]$, and Vec (ζ_i (0)) is the initial value.

Based on (14)–(18), the expectation of the network synchronization error can be rewritten as

$\begin{array}{cc}\hfill \mathbb{E}\left[\varphi \left(t\right)\right]& =\sum _{i=1}^{N}Ve{c}^T\left(I_n\right){\mathrm{\Phi }}_{Vec\left({\zeta }_i\right)}\left(t,0\right)Vec\left({\zeta }_i\left(0\right)\right)\hfill \\ \hfill & +\sum _{i=1}^{N}Ve{c}^T\left(I_n\right)\theta {\beta }_i^2{\int }_0^t{\mathrm{\Phi }}_{Vec\left({\zeta }_i\right)}\left(t,\tau \right)d\tau Vec\left(H_{\eta }{H}_{\eta }^T\right).\hfill \end{array}(19)$

In the following, consider the stochastic linear system (6), where J_f(s) and J_h(s) are Jacobian matrics of f and h evaluated at s(t), respectively. Constant α > 0 is the coupling strength and $\upsilon \in {\mathbb{R}}^N$ denotes the location of the node where noise is injected. The vector $H_{\eta }\in {\mathbb{R}}^n$ describes how the noise η(t) enters the dynamics of a node, where η(t) represents zero-mean Gaussian white noise with variance $\frac{\theta }{2}$. Assume that one of the network nodes denoted by i_noise is contaminated with additive noise. Let $\rho =Ve{c}^T(I_n)Vec({\zeta }_{i_{\mathit{noise}}}(t))$ be the measurement metric of the system error, which is referred to as the robustness metric.

Remark 1. It follows from the above analysis that the robustness of the directed network subjected to noise is quantified by the robustness metric ρ. Here, the networked system synchronizes before noise is introduced. The notion of dynamical robustness refers to the ability of a network of coupled dynamical systems to return to its synchronous state after it encountered the disturbance of noise. The robustness metric ρ is used to characterize the degree to which the networked system withstand failures and perturbations. It is thus defined related to the synchronization error of the network. The smaller the value of ρ, the more robust the network. Furthermore, given the location of the node where noise is injected, the dynamical robustness of the network depends not only on the node dynamics but also on the network topology. In particular, it is determined by the inherent dynamics of the isolated node J_f(s), the inner-coupling function J_h(s), the coupling strength α, the variance θ of the noise, and the network topology. Note that J_f(s) and J_h(s) are the Jacobian matrices of f and h evaluated at s(t), respectively. This implies that the robustness matric ρ is also determined by the synchronization trajectory s(t).

4 Interplay between dynamics and topology

In this section, the effects of node dynamics and network topology on the system robustness are investigated in detail.

4.1 Node dynamics

In the following, three representative non-linear systems, namely, Rössler system, Chen system, and Wang system, are introduced. In simulations, these three systems with chaotic behaviors are adopted as the self-dynamics of the nodes, respectively.

4.1.1 Rössler system

A single Rössler system [39] is described by

$\left\{\begin{array}{c}{\dot{x}}_1=-x_2-x_3,\hfill \\ {\dot{x}}_2=x_1+a{x}_2,\hfill \\ {\dot{x}}_3=b+x_1{x}_3-c{x}_3,\hfill \end{array}\right.(20)$

which has a chaotic attractor when $a=b=\frac{1}{5}$ and c = 9. The Jacobian matrix evaluated at $s(t)={\left[s_1(t),s_2(t),s_3(t)\right]}^T$ is given by

$J_f\left(s\right)=\left[\begin{array}{ccc}\hfill 0\hfill & \hfill -1\hfill & \hfill -1\hfill \\ \hfill 1\hfill & \hfill \frac{1}{5}\hfill & \hfill 0\hfill \\ \hfill s_3\hfill & \hfill 0\hfill & \hfill s_1-9\hfill \end{array}\right].(21)$

4.1.2 Chen system

A single Chen system [40] is described by

$\left\{\begin{array}{c}{\dot{x}}_1=a\left(x_2-x_1\right),\hfill \\ {\dot{x}}_2=\left(c-a-x_3\right)x_1+c{x}_2,\hfill \\ {\dot{x}}_3=x_1{x}_2-b{x}_3,\hfill \end{array}\right.(22)$

which has a chaotic attractor when a = 35, b = 3, and c = 28. The Jacobian matrix evaluated at $s(t)={\left[s_1(t),s_2(t),s_3(t)\right]}^T$ is given by

$J_f\left(s\right)=\left[\begin{array}{ccc}\hfill -35\hfill & \hfill 35\hfill & \hfill 0\hfill \\ \hfill -7-s_3\hfill & \hfill 28\hfill & \hfill -s_1\hfill \\ \hfill s_2\hfill & \hfill s_1\hfill & \hfill -3\hfill \end{array}\right].(23)$

4.1.3 Wang system

A single Wang system [41] is described by

$\left\{\begin{array}{c}{\dot{x}}_1=x_2{x}_3+a,\hfill \\ {\dot{x}}_2=x_1^2-x_2,\hfill \\ {\dot{x}}_3=1-4x_1,\hfill \end{array}\right.(24)$

which has a chaotic attractor when a = 0.006. The Jacobian matrix evaluated at $s(t)={\left[s_1(t),s_2(t),s_3(t)\right]}^T$ is given by

$J_f\left(s\right)=\left[\begin{array}{ccc}\hfill 0\hfill & \hfill s_3\hfill & \hfill s_2\hfill \\ \hfill 2s_1\hfill & \hfill -1\hfill & \hfill 0\hfill \\ \hfill -4\hfill & \hfill 0\hfill & \hfill 0\hfill \end{array}\right].(25)$

4.2 Dynamical robustness beyond directed path graphs

In simulations, consider a directed path graph with five nodes. Assume that θ = 1. The noise is injected into the fourth node and the third state variable of this node, that is the fourth element of υ is one and $H_{\eta }={\left[\mathrm{0,0,1}\right]}^T$.

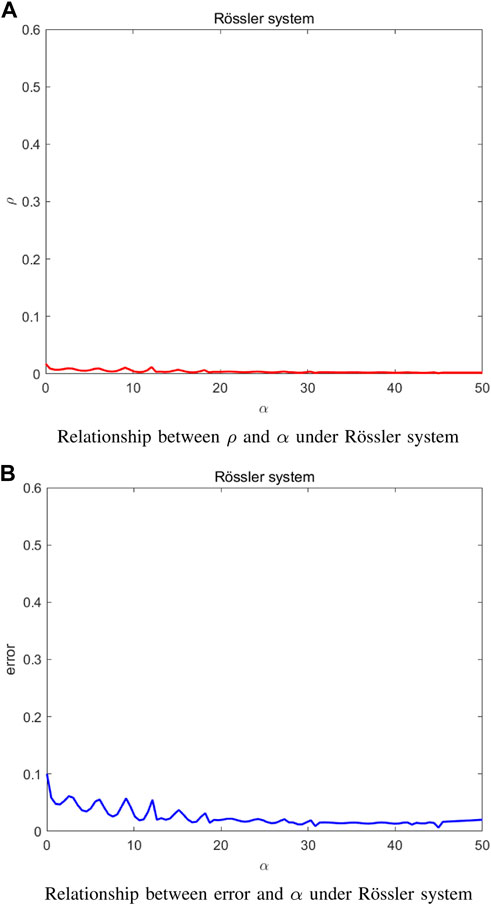
Figure 1 shows the simulation results for the network of Rössler systems. Assume that the nodes are coupled on the second and third variables thereby J_h(s) = [0,0,0; 0.1,0; 0,0,1]^T. As can be seen from Figure 1A, the robustness metric ρ first continuously oscillates and then converges to around zero with the increase of the coupling strength α. As shown in Figure 1B, the synchronization error exhibits a similar behavior.

FIGURE 1

FIGURE 1. The results are obtained under Rössler systems when a directed path graph is considered.

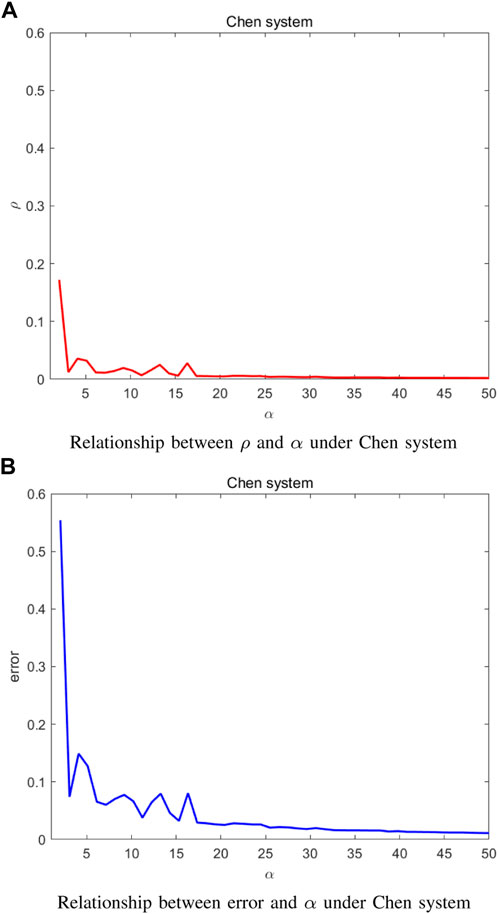
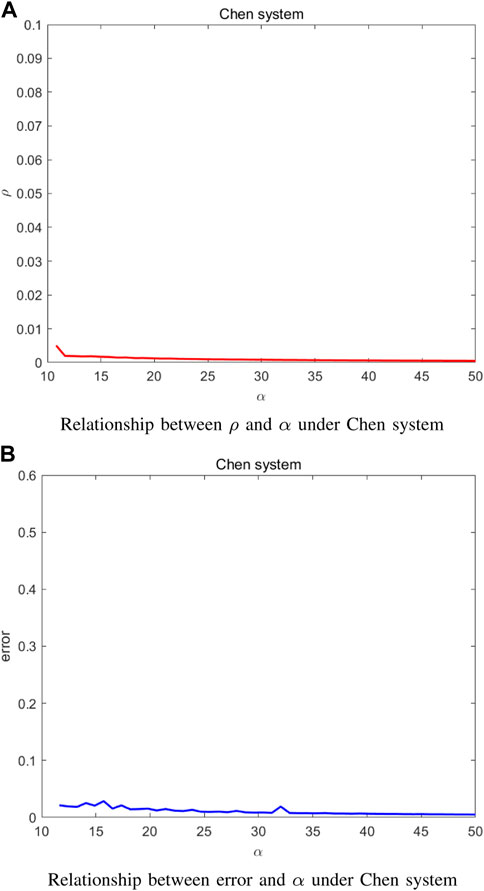
Figure 2 shows the simulation results for the network of Chen systems. Assume that the nodes are coupled through all state variables thereby J_h(s) = [1,0,0;0,1,0;0,0,1]^T. It is interesting to see from Figure 2A that, after a sharp fall, the robustness metric ρ begins to continuously oscillate and then converges to zero with the increase of the coupling strength α. Figure 2B shows that the synchronization error exhibits a similar behavior of the robustness metric.

FIGURE 2

FIGURE 2. The results are obtained under Chen systems when a directed path graph is considered.

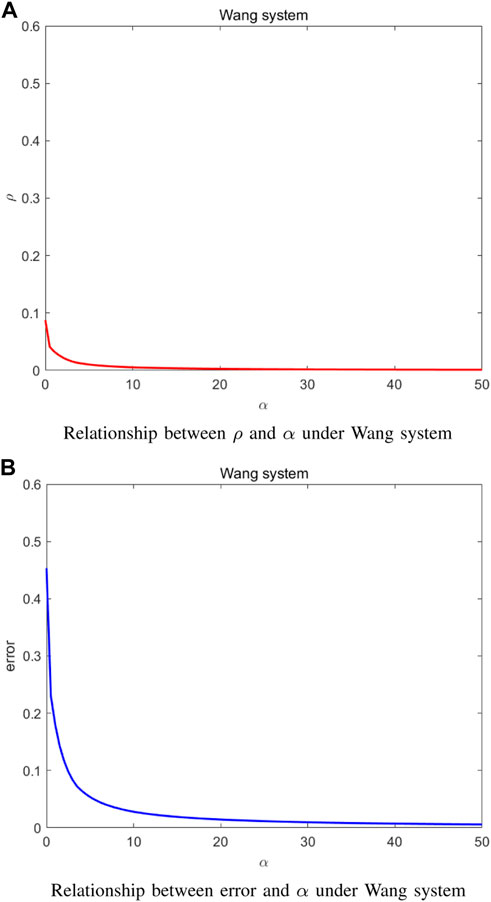
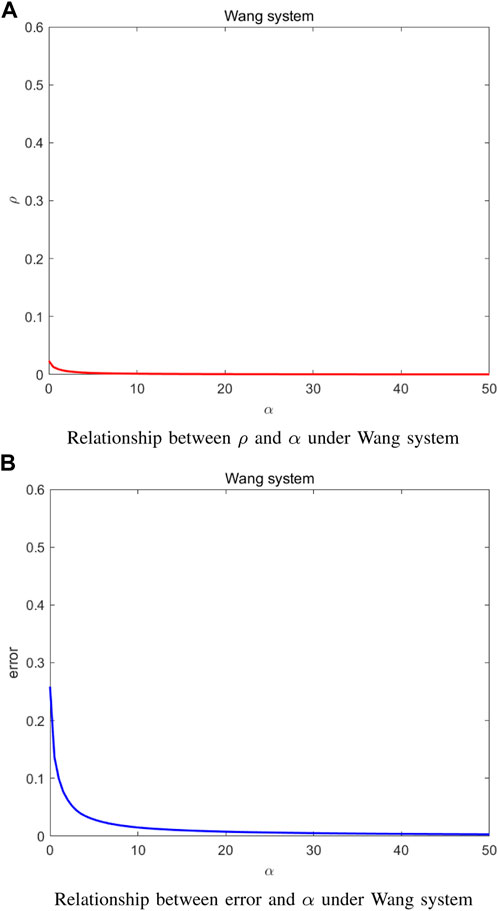
Figure 3 illustrates the results for the network of Wang systems. Assume that the nodes are coupled on the first and third variables thereby J_h(s) = [1,0,0; 0,0,0; 0,0,1]^T. It follows from Figure 3A that the robustness metric first sharply decreases and gradually converges to zero with the increase of the coupling strength. Also, the synchronization error approaches to zero when the coupling strength increases.

FIGURE 3

FIGURE 3. The results are obtained under Wang systems when a directed path graph is considered.

Recall that the networked system synchronizes before the noise is introduced. This means that the choice of J_h(s) in the simulation section can ensure the existence of the synchronized region.

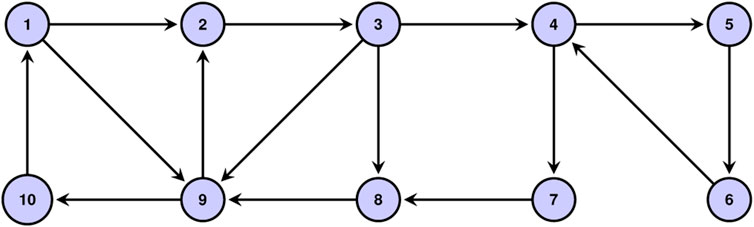
4.3 Dynamical robustness beyond general digraphs

In this subsection, consider a general directed graph [42] as shown in Figure 4. Assume that noise is injected into the fourth node, so the element of υ is one into the fourth row and others are 0. In addition, θ = 1 and $H_{\eta }={\left[\mathrm{0,0,1}\right]}^T$.

FIGURE 4

FIGURE 4. Network topology.

Figures 5A, B are obtained under Rössler systems with J_h(s) = [0,0,0; 0.1,0; 0,0,1]^T. Notice that a much more complex scenario emerges. The robustness metric increases rapidly with intermittent descent when the coupling strength is larger than 19. From Figure 5B, the synchronization error decreases after continuously oscillating. When the coupling strength is larger than 19, the synchronization error begins to increase rapidly with intermittent descent.

FIGURE 5

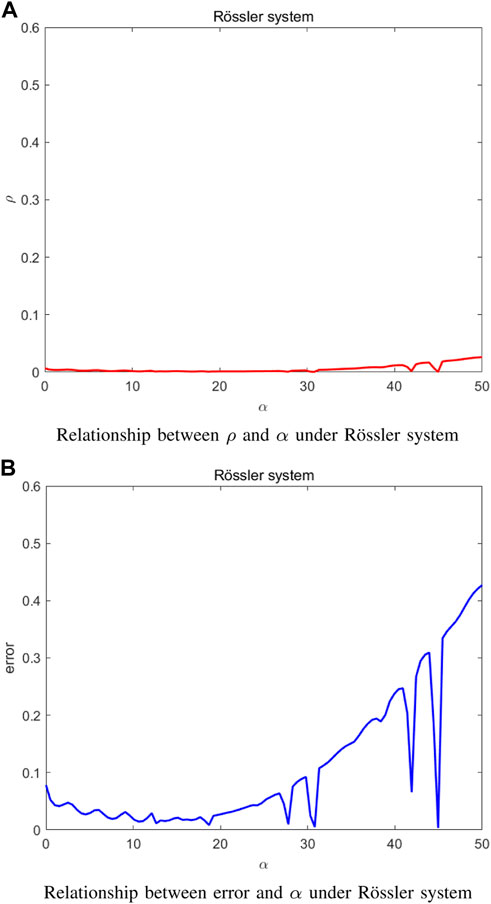
FIGURE 5. The results are obtained under Rössler systems when a general directed graph is considered.

Figures 6A, B are obtained under Chen systems with J_h(s) = [1,0,0; 0.1,0; 0,0,1]^T. After a sharp fall, the robustness metric is monotonically decreasing. The synchronization error exhibits a similar behavior to the robustness metric.

FIGURE 6

FIGURE 6. The results are obtained under Chen systems when a general directed graph is considered.

Figures 7A, B are obtained under Wang systems with J_h(s) = [1,0,0; 0.0,0; 0,0,1]^T. When the coupling strength gradually increases, the curves in Figure 7A and Figure 7B both converge to zero, which illustrates that the network of Wang systems is robust to noise and can reach the synchronization when the coupling strength is enough large.

FIGURE 7

FIGURE 7. The results are obtained under Wang systems when a general directed graph is considered.

In summary, the 10-node network of Rössler systems shows greatly different robustness from other systems.

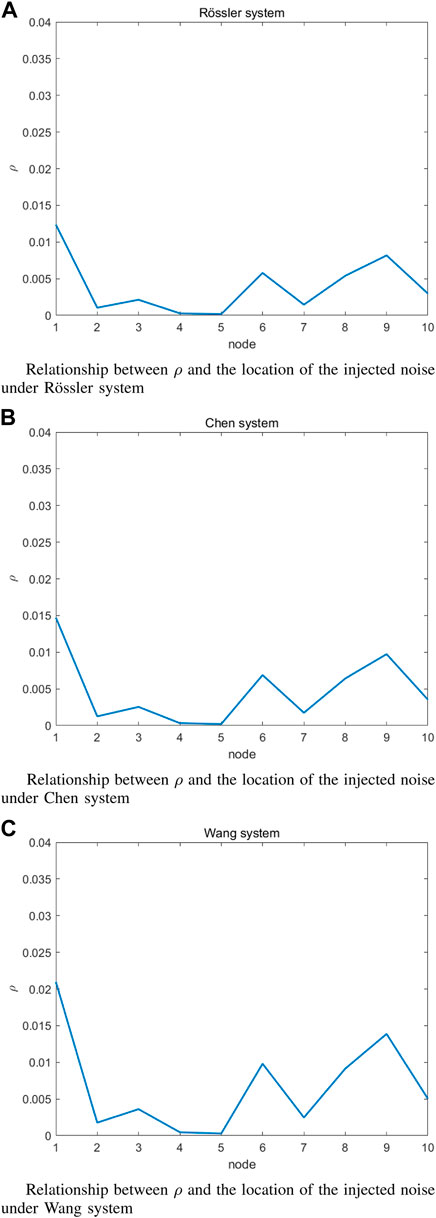
In order to illustrate the effect of the location of the injected noise, the robustness metrics are examined in Figure 8 for Rössler system, Chen system, and Wang system, respectively, all with α = 20. Recall that a smaller value of ρ implies a more dynamically robust network. It is clear that, for Rössler system, Chen system, and Wang system, the network shows a similar robustness. The results shown in Figure 8 provide guidance for minimizing the effect of noise on the network robustness. For example, the network is more robust to noise if node five is subjected to noise. Therefore, node five is the best choice to minimize the effect of noise from the dynamical robustness perspective.

FIGURE 8

FIGURE 8. The main results are obtained under a general directed graph: α = 20.

5 Conclusion

This article investigates the dynamical robustness of a directed network with noise. A novel robustness metric is formulated and analyzed under the framework of mean-square stochastic stability. It is found that the dynamical robustness of the directed network is determined by both the node dynamics and the network topology. Particularly, for networks of Rössler systems, with the increase of the coupling strength, different network topologies show different effects on the robustness metric. While for Wang systems, the robustness to noise is stronger than other systems. These findings demonstrate that node dynamics plays an important role in the network robustness. The results of this study can provide theoretical and technical guidances for designing a dynamically robust networked system.

In the future, it will be interesting to investigate dynamical robustness of higher-order networks [37, 43]. Moreover, it will be interesting to investigate the effects of different types of noise on the network robustness. The dynamical robustness of stochastic complex networks with time-delays [44] or heterogeneous node dynamics [45] are challenging but also worthy of further investigation.

Data availability statement

The original contributions presented in the study are included in the article/supplementary material, further inquiries can be directed to the corresponding author.

Author contributions

All authors designed and did the research. JS and LX did the analytical and numerical calculations. JS, LX, and GC were the lead writer of the manuscript. All authors read and approved the final manuscript.

Funding

This work was supported by the National Natural Science Foundation of China (No. 61973064), Natural Science Foundation of Hebei Province of China (No. F2022501024), Hebei Provincial Postgraduate Student Innovation Ability Training Funding Project (No. CXZZSS2023202), and Hong Kong Research Grants Council under the GRF Grant CityU11206320.

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

1. Wu J, Yu X, Li X. Global frequency synchronization of complex power networks via coordinating switching control. IEEE Trans Circuits Syst Regular Pap (2019) 66:3123–33. doi:10.1109/tcsi.2019.2908085

CrossRef Full Text | Google Scholar

2. Mingotti A, Peretto L, Tinarelli R. Accuracy evaluation of an equivalent synchronization method for assessing the time reference in power networks. IEEE Trans Instrumentation Meas (2018) 67:600–6. doi:10.1109/tim.2017.2779328

CrossRef Full Text | Google Scholar

3. Yu F, Shen H, Yu Q, Kong X, Kumar Sharma P, Cai S. Privacy protection of medical data based on multi-scroll memristive hopfield neural network. IEEE Trans Netw Sci Eng (2022) 1–14:1–14. doi:10.1109/tnse.2022.3223930

PubMed Abstract | CrossRef Full Text | Google Scholar

4. Wu J, Liu M, Sun H, Li T, Gao Z, Wang DZ. Equity-based timetable synchronization optimization in urban subway network. Transportation Res C: Emerging Tech (2015) 51:1–18. doi:10.1016/j.trc.2014.11.001

CrossRef Full Text | Google Scholar

5. Liu T, Ceder A. Synchronization of public transport timetabling with multiple vehicle types. Transportation Res Rec (2016) 2539:84–93. doi:10.3141/2539-10

CrossRef Full Text | Google Scholar

6. Buldyrev SV, Parshani R, Paul G, Stanley HE, Havlin S. Catastrophic cascade of failures in interdependent networks. Nature (2010) 464:1025–8. doi:10.1038/nature08932

PubMed Abstract | CrossRef Full Text | Google Scholar

7. Zhang L, Xiang L, Zhu J. Relationship between fragility and resilience in complex networks. Physica A (2022) 605:128039. doi:10.1016/j.physa.2022.128039

CrossRef Full Text | Google Scholar

8. Mao B, Wu X, Lü J, Chen G. Predefined-time bounded consensus of multiagent systems with unknown nonlinearity via distributed adaptive fuzzy control. IEEE Trans Cybernetics (2022) 1–14. doi:10.1109/tcyb.2022.3163755

CrossRef Full Text | Google Scholar

9. Zhu Y, Xia C-Y, Wang Z, Chen Z. Networked decision-making dynamics based on fair, extortionate and generous strategies in iterated public goods games. IEEE Trans Netw Sci Eng (2022) 9(4):2450–62. doi:10.1109/tnse.2022.3164094

CrossRef Full Text | Google Scholar

10. Lou Y, Wu R, Li J, Wang L, Tang C-B, Chen G. Classification-based prediction of network connectivity robustness. Neural Networks (2023) 157:136–46. doi:10.1016/j.neunet.2022.10.013

PubMed Abstract | CrossRef Full Text | Google Scholar

11. Callaway DS, Newman ME, Strogatz SH, Watts DJ. Network robustness and fragility: Percolation on random graphs. Phys Rev Lett (2000) 85(25):5468–71. doi:10.1103/physrevlett.85.5468

PubMed Abstract | CrossRef Full Text | Google Scholar

12. Wang X, Pournaras E, Kooij RE, Mieghem PV. Improving robustness of complex networks via the effective graph resistance. The Eur Phys J B (2014) 87:221–12. doi:10.1140/epjb/e2014-50276-0

CrossRef Full Text | Google Scholar

13. Liu X, Sun S, Wang J, Xia C. Onion structure optimizes attack robustness of interdependent networks. Physica A (2019) 535:122374. doi:10.1016/j.physa.2019.122374

CrossRef Full Text | Google Scholar

14. Liao L, Shen Y, Liao J. Robustness of dispersal network structure to patch loss. Ecol Model (2020) 424:109036. doi:10.1016/j.ecolmodel.2020.109036

CrossRef Full Text | Google Scholar

15. Huang D, Bian J, Jiang H, Yu Z. Consensus indices of two-layered multi-star networks: An application of Laplacian spectrum. Front Phys (2021) 9:803941. doi:10.3389/fphy.2021.803941

CrossRef Full Text | Google Scholar

16. Liu X, Li D, Ma M, Szymanski BK, Stanley HE, Gao J. Network resilience. Phys Rep (2022) 971:1–108. doi:10.1016/j.physrep.2022.04.002

CrossRef Full Text | Google Scholar

17. Nie S, Wang X-W, Zhang H, Li Q, Wang B. Robustness of controllability for networks based on edge-attack. PLoS ONE (2014) 9:e89066. doi:10.1371/journal.pone.0089066

PubMed Abstract | CrossRef Full Text | Google Scholar

18. Shargel B, Sayama H, Epstein IR, Bar-Yam Y. Optimization of robustness and connectivity in complex networks. Phys Rev Lett (2003) 90(6):068701. doi:10.1103/physrevlett.90.068701

PubMed Abstract | CrossRef Full Text | Google Scholar

19. Schwartz N, Cohen R, Ben-Avraham D, Barabási A-L, Havlin S. Percolation in directed scale-free networks. Phys Rev E (2002) 66(1):015104. doi:10.1103/physreve.66.015104

PubMed Abstract | CrossRef Full Text | Google Scholar

20. Albert R, Jeong H, Barabási A-L. Error and attack tolerance of complex networks. Nature (2000) 406(6794):378–82. doi:10.1038/35019019

PubMed Abstract | CrossRef Full Text | Google Scholar

21. Holme P, Kim BJ, Yoon CN, Han SK. Attack vulnerability of complex networks. Phys Rev E (2002) 65(5):056109. doi:10.1103/physreve.65.056109

PubMed Abstract | CrossRef Full Text | Google Scholar

22. Cohen R, Erez K, Ben-Avraham D, Havlin S. Breakdown of the internet under intentional attack. Phys Rev Lett (2001) 86(16):3682–5. doi:10.1103/physrevlett.86.3682

PubMed Abstract | CrossRef Full Text | Google Scholar

23. Cohen R, Erez K, Ben-Avraham D, Havlin S. Resilience of the internet to random breakdowns. Phys Rev Lett (2000) 85:4626–8. doi:10.1103/physrevlett.85.4626

PubMed Abstract | CrossRef Full Text | Google Scholar

24. Nagata S, Kikuchi M. Emergence of cooperative bistability and robustness of gene regulatory networks. PLoS Comput Biol (2020) 16(6):e1007969. doi:10.1371/journal.pcbi.1007969

PubMed Abstract | CrossRef Full Text | Google Scholar

25. Faci-Lázaro S, Lor T, Ródenas G, Mazo JJ, Soriano J, Gómez-Gardeñes J. Dynamical robustness of collective neuronal activity upon targeted damage in interdependent networks. Eur Phys J Spec Top (2022) 231(3):195–201. doi:10.1140/epjs/s11734-021-00411-7

CrossRef Full Text | Google Scholar

26. Franci A, O’Leary T, Golowasch J. Positive dynamical networks in neuronal regulation: How tunable variability coexists with robustness. IEEE Control Syst Lett (2020) 4(4):946–51. doi:10.1109/lcsys.2020.2997214

CrossRef Full Text | Google Scholar

27. Tanaka G, Morino K, Aihara K. Dynamical robustness in complex networks: The crucial role of low-degree nodes. Scientific Rep (2012) 2(1):232–6. doi:10.1038/srep00232

PubMed Abstract | CrossRef Full Text | Google Scholar

28. Buscarino A, Gambuzza LV, Porfiri M, Fortuna L, Frasca M. Robustness to noise in synchronization of complex networks. Scientific Rep (2013) 3(1):2026–6. doi:10.1038/srep02026

PubMed Abstract | CrossRef Full Text | Google Scholar

29. Porfiri M, Frasca M. Robustness of synchronization to additive noise: How vulnerability depends on dynamics. IEEE Trans Control Netw Syst (2019) 6(1):375–87. doi:10.1109/tcns.2018.2825024

CrossRef Full Text | Google Scholar

30. Chen F, Xiang L, Lan W, Chen G. Coordinated tracking in mean square for a multi-agent system with noisy channels and switching directed network topologies. IEEE Trans Circuits Systems-II: Express Briefs (2012) 59(11):835–9. doi:10.1109/tcsii.2012.2218395

CrossRef Full Text | Google Scholar

31. Hu J, Wu Y, Li T, Ghosh BK. Consensus control of general linear multiagent systems with antagonistic interactions and communication noises. IEEE Trans Automatic Control (2019) 64(5):2122–7. doi:10.1109/tac.2018.2872197

CrossRef Full Text | Google Scholar

32. Meng JH, Riecke H. Synchronization by uncorrelated noise: Interacting rhythms in interconnected oscillator networks. Scientific Rep (2018) 8:6949. doi:10.1038/s41598-018-24670-y

PubMed Abstract | CrossRef Full Text | Google Scholar

33. Zhang C, Yang Y. Synchronization of stochastic multi-weighted complex networks with lévy noise based on graph theory. Physica A (2020) 545:123496. doi:10.1016/j.physa.2019.123496

CrossRef Full Text | Google Scholar

34. Sun Y, Zhao D. Effects of noise on the outer synchronization of two unidirectionally coupled complex dynamical networks. Chaos (2012) 22(2):023131. doi:10.1063/1.4721997

PubMed Abstract | CrossRef Full Text | Google Scholar

35. Cardelli L, Csikász-Nagy A, Dalchau N, Tribastone M, Tschaikowski M. Noise reduction in complex biological switches. Scientific Rep (2016) 6(1):20214–2. doi:10.1038/srep20214

CrossRef Full Text | Google Scholar

36. Sun S, Chen F, Ren W. Distributed average tracking in weight-unbalanced directed networks. IEEE Trans Automatic Control (2020) 66(9):4436–43. doi:10.1109/tac.2020.3046029

CrossRef Full Text | Google Scholar

37. Chen G. Searching for best network topologies with optimal synchronizability: A brief review. IEEE/CAA J Automatica Sinica (2022) 9(4):573–7. doi:10.1109/jas.2022.105443

CrossRef Full Text | Google Scholar

38. Young GF, Scardovi L, Leonard NE. Robustness of noisy consensus dynamics with directed communication. In: Proceedings of the American Control conference (2010). p. 6312–7.

CrossRef Full Text | Google Scholar

39. Rössler OE. An equation for continuous chaos. Phys Lett A (1976) 57:397–8. doi:10.1016/0375-9601(76)90101-8

CrossRef Full Text | Google Scholar

40. Chen G, Ueta T. Yet another chaotic attractor. J Bifurcation Chaos (1999) 9(7):1465–6. doi:10.1142/s0218127499001024

CrossRef Full Text | Google Scholar

41. Wang X, Chen G. A chaotic system with only one stable equilibrium. Commun Nonlinear Sci Numer Simulation (2011) 17:1264–72. doi:10.1016/j.cnsns.2011.07.017

CrossRef Full Text | Google Scholar

42. Song Q, Cao J. On pinning synchronization of directed and undirected complex dynamical networks. IEEE Trans Circuits Syst Regular Pap (2010) 57:672–80. doi:10.1109/tcsi.2009.2024971

CrossRef Full Text | Google Scholar

43. Shi D, Chen G. Simplicial networks: A powerful tool for characterizing higher-order interactions. Natl Sci Rev (2022) 9(5):nwac038–2. doi:10.1093/nsr/nwac038

PubMed Abstract | CrossRef Full Text | Google Scholar

44. Chen F, Chen X, Xiang L, Ren W. Distributed economic dispatch via a predictive scheme: Heterogeneous delays and privacy preservation. Automatica (2021) 123:109356. doi:10.1016/j.automatica.2020.109356

CrossRef Full Text | Google Scholar

45. Chen F, Feng G, Liu L, Ren W. Distributed average tracking of networked Euler-Lagrange systems. IEEE Trans Automatic Control (2015) 60(2):547–52. doi:10.1109/tac.2014.2343111

CrossRef Full Text | Google Scholar