A metamaterial cylindrical shell with multiple graded resonators for broadband longitudinal wave attenuation

This paper investigates a metamaterial cylindrical shell with local resonators for broadband longitudinal wave attenuation. A three-component phononic crystal metamaterial cylindrical shell that opens local resonant bandgaps at low frequencies is formed by periodically inserting a lead column coated with soft rubber into an ordinary cylindrical shell. First, the governing equations of elastic wave propagation in cylindrical shell structures are derived through coordinate transformation. Subsequently, numerical models of the metamaterial cylindrical shell are established, and the dispersion relation and vibration transmission characteristics of this structure are calculated using the Finite Element Method (FEM). Finally, in order to further broaden the bandgaps and the strong suppression range of the structure, a multiple-graded-resonator metamaterial cylindrical shell with three different local resonators is also proposed. These local resonators have different start frequencies and locations of their longitudinal wave bandgaps, so they can be combined to produce a wider overall bandgap. Numerical results show that this kind of multiple-graded-resonator metamaterial cylindrical shell has a good vibration suppression effect on longitudinal waves in the range of approximately 180–710 Hz and the vibration suppression effect can reach −40 dB at best. In addition, experimental results on vibration transmission characteristics show good agreement with the numerical results. This work provides a new idea and method for the development of acoustic metamaterials to obtain broadband and low-frequency bandgaps for cylindrical shell structures.

1 Introduction

In recent years, the issue of mechanical system noise control has attracted an increasing amount of attention in a bid to improve the quality of the environment for people due to stringent legal regulations on noise. Vibration and noise control devices may affect the performance of mechanical systems. Therefore, novel solutions that are simple and easy to apply in engineering problems are needed in order to achieve excellent performance while meeting low noise requirements [1]. Phononic crystal (PC) structures are becoming increasingly interesting as an innovative and efficient noise control solution.

A phononic crystal is an artificial periodic elastic composite structure consisting of two or more materials with elastic wave bandgaps [2]. A periodic arrangement of scatters can prevent the propagation of elastic waves in certain frequency ranges, thus forming directional or complete bandgaps. The bandgaps in PCs can be used for sound insulation and environmental noise control [3–5]. The propagation of acoustic and elastic waves in PCs has attracted considerable attention over the past two decades [6–8]. Wu et al. [9] validated the existence of complete bandgaps and resonance in PC plates with periodic stubbed surfaces using numerical and experimental methods. Badreddine et al. [10] presented hybrid PCs composed of periodic stepped pillars and holes in order to obtain lower and wider bandgaps.

An original and impressive piece of work demonstrated the fact of spectral gaps with a lattice constant two orders of magnitude smaller than the relevant wavelength and presented the concept of a local resonance phononic crystal (LRPC) [11]. LRPC structures have shown particularly great potential in efficiently insulating noise and vibration [12, 13]. In LRPC structures, the existence of the stopband phenomenon is due to the distribution of resonance cells in the host structure at the sub-wavelength scale (i.e., the size is smaller than the wavelength of host structure at the frequency of interest) [14]. The stopbands of LRPCs are almost fully independent of the spatial arrangement of scatters, and the widths of the stopbands are closely related to the filling ratio [15].

In acoustic metamaterial design, a flat host structure is a common type of structure in engineering applications. Many researchers focus on metamaterials with a flat host structure, such as acoustic metamaterial beams [16–18] and plates [19, 20]. However, the range of applications of complete beams and plates in engineering is narrower than that of cylindrical shell structures. Cylindrical shells form the basic structure used in various aircrafts, ships, rockets, and precision instruments, and are widely used in the chemical industry, aerospace, and national defense, among other domains. Therefore, researchers have extensively studied wave propagation in cylindrical shells using analytical and numerical methods. The propagation of axis waves in cylindrically curved panels of infinite length was studied by Pany et al., and their natural frequencies of bending vibration were determined [21]. Recently, the Wave Finite Element Method was utilized by Manconi et al. to analyze wave dispersion in isotropic and orthotropic cylindrical panels and closed cylindrical shells [22]. The stopband behavior of cylindrically curved metamaterial panels in different directions was studied by Nateghi et al., who also discuss the influence of the radius of the cylindrical shell on the bandgaps [23].

The studies mentioned above have mainly focused on the fundamental mechanism of wave propagation in acoustic metamaterials, while other researchers have attempted to adjust the width and location of the bandgaps of acoustic metamaterials by theoretical and experimental methods. In many engineering applications, a broadband resonant metamaterial is more appealing than conventional linear narrow-band metamaterials. Banerjee et al. [24] studied the graded parametrical arrangements of resonating units to modify the ranges of the stopband and transmission band. In addition, Ding et al. [25] proposed a broadband acoustic metamaterial with a space-coiling structure including an impedance-matching layer introduced between the air and the metamaterial. The impedance-matching layer was achieved by specifically designing the parameters of the space-coiling structure to form a gradient index. A hierarchical structure was also constructed to work in broadband, in which the shock wave was resisted in multiple bands, and the relationship between these bands and the hierarchy was thoroughly demonstrated. There is also another way to design multi-resonator metamaterials [26], namely by increasing the number of internal masses arranged in parallel in each metamaterial unit. An acoustic metamaterial plate was designed by integrating mass–spring subsystems with two degrees of freedom with an isotropic plate to act as vibration absorbers. A theoretical model of one-dimensional (1D) periodic graded metacomposites has been studied to investigate and enlarge the bandgaps in which wave propagation is prevented [27].

To the authors’ knowledge, the propagation of longitudinal waves in three-component PC metamaterial cylindrical shells has never been studied in previous work. Motivated by the objective of understanding stopband behavior in PCs for wave propagation, this paper presents a study of the propagation of longitudinal waves in three-component PC metamaterial cylindrical shells based on the local resonance mechanism. First, the finite periodic condition along the circumferential direction of the cylindrical shell is transformed into an infinite periodic condition by coordinate transformation. Subsequently, numerical models for cylindrical shells are established by deriving the dynamic equation and the Bloch periodic condition, the dispersion relation of the unit cell is calculated using the Finite Element Method, and the effects of scatterer radius on stopband behavior are studied. Finally, the suppression of longitudinal waves in a finite periodic metamaterial cylindrical shell structure is further studied to verify the stopband behavior through numerical simulation and experimentation investigating the vibration transmission characteristics.

The paper is structured as follows. Section 2 briefly introduces the cylindrical shell model and presents a derivation of the governing equations of elastic waves. Section 3 presents a calculation of the dispersion relation of the unit cell and the vibration transmission characteristics of the finite structure using the FEM. The multiple-graded-resonator structure is presented and its vibration transmission characteristics are studied via experimentation and simulation in Section 4. Several conclusion are presented in the final section.

2 Theoretical foundation

This section briefly introduces the unit cell for metamaterial cylindrical shells and illustrates the rule of coordinate transformation. Subsequently, the numerical model for the unit cell is established through derivation of the governing equations of elastic waves.

2.1 Coordinate transformation

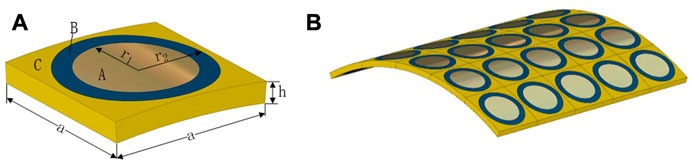
The unit cell of the metamaterial cylindrical shell investigated is as shown in Figure 1A. The lattice constant is a, and the shell thickness is h = 0.1 × a. The radii of the cylindrical shell, the scatterer A, and the connector B are R, r₁, and r₂, respectively. The unit cell is composed of a lead cylinder coated with a silicone rubber layer, arranged periodically in the epoxy resin matrix C. Figure 1B shows the 5 × 5 metamaterial cylindrical shell.

FIGURE 1

FIGURE 1. Metamaterial cylindrical shell: (A) unit cell; (B) 5 × 5 metamaterial cylindrical shell.

To better describe the unit cell of the metamaterial cylindrical shell, it is necessary to convert from the Cartesian coordinate system to the cylindrical coordinate system, in which points are represented by ring coordinate s, axis coordinate y, and transverse coordinate z representing distance from the cylinder center.

The transformation equation is as follows:

$R\theta \to s,z\to y,r\to z(1)$

and the corresponding displacement is given by:

$u_{\theta }\to u,u_z\to v,u_r\to w(2)$

At a given moment, the non-zero strains are therefore:

${\epsilon }_{ss}=-\frac{w}{R}+\frac{\partial u}{\partial s}-z\left(\frac{{\partial }^{2}w}{\partial s^2}+\frac{1}{R}\frac{\partial u}{\partial s}\right){\epsilon }_{yy}=\frac{\partial v}{\partial y}-z\frac{{\partial }^{2}w}{\partial y^2}{\epsilon }_{sy}=\frac{1}{2}\left[\frac{\partial v}{\partial s}+\frac{\partial u}{\partial y}-z\left(2\frac{{\partial }^{2}w}{\partial s\partial y}+\frac{1}{R}\frac{\partial u}{\partial y}\right)\right](3)$

2.2 Derivation of governing equations

In order to obtain the governing equation for the time-harmonic vibration of the cylindrical shell with multiple graded resonators shown in Figure 1B, it is assumed that the shell is very thin. Given this assumption, we can obtain the kinetic energy δT, elastic energy δU, and non-conservative work done δW by the external loads:

$\delta T=-{\int }_s{\int }_y\rho h\ddot{u}\delta udsdy-{\int }_s{\int }_y\rho h\ddot{v}\delta vdsdy-{\int }_s{\int }_y\rho h\ddot{w}\delta wdsdy(4)$

$\delta W=0(5)$

$\delta U={\int }_{-s_0/2}^{+s_0/2}{\int }_{-y_0}^{+y_0}{\int }_{-h/2}^{+h/2}\left[\left({\epsilon }_{ss}\bullet \delta {\epsilon }_{ss}+{\epsilon }_{yy}\bullet \delta {\epsilon }_{yy}+2{\epsilon }_{ss}\bullet \delta {\epsilon }_{yy}\right)\bullet E^{*}+G{\epsilon }_{sy}\bullet \delta {\epsilon }_{sy}\right]dsdydh(6)$

where Poisson’s ratio is denoted by v, Young’s modulus is denoted by E, $E^{*}\equiv \frac{E}{\left(1-v^2\right)}$, and $G=\frac{E}{2\left(1+v\right)}$. By substituting Eq. 3 into Eq. 6 and integrating along the thickness direction, the total strain energy is obtained:

$\delta U={\int }_{-s_0/2}^{+s_0/2}{\int }_{-y_0}^{+y_0}\left(\widehat{E}{U}_1+D{U}_2\right)dsdy(7)$

where $D\equiv \frac{E{h}^3}{12\left(1-v^2\right)}$, $\widehat{E}\equiv \frac{Eh}{1-v^2}$.

$U_1={\left(\frac{\partial u}{\partial s}+\frac{\partial v}{\partial y}-\frac{w}{R}\right)}^2+\frac{1}{2}\left(1-v\right)\left[-4\left(\frac{\partial u}{\partial s}-\frac{w}{R}\right)\frac{\partial v}{\partial y}+{\left(\frac{\partial u}{\partial y}+\frac{\partial v}{\partial s}\right)}^2\right](8)$

$U_2={\left(\frac{{\partial }^{2}w}{\partial s^2}+\frac{{\partial }^{2}w}{\partial y^2}+\frac{1}{R}\frac{\partial u}{\partial s}\right)}^2-2\left(1-v\right)\frac{{\partial }^{2}w}{\partial y^2}\left(\frac{{\partial }^{2}w}{\partial s^2}+\frac{1}{R}\frac{\partial u}{\partial s}\right)+\frac{1}{2}\left(1-v\right){\left(2\frac{{\partial }^{2}w}{\partial s\partial y}+\frac{1}{R}\frac{\partial u}{\partial y}\right)}^2(9)$

Using Hamilton’s principle, we obtain:

${\int }_0^t\left(\delta T-\left(\delta U+\delta W\right)\right)dt=0(10)$

Setting δw, δu, and δv to zero yields the governing equations of an infinitely long cylindrical shell with multiple graded resonators:

$\widehat{E}\left[\begin{array}{c}\frac{{\partial }^{2}u}{\partial s^2}+\frac{1}{2}\left(1-v\right)\frac{{\partial }^{2}u}{\partial y^2}\\ +\frac{1}{2}\left(1+v\right)\frac{{\partial }^{2}v}{\partial s\partial y}-\frac{1}{R}\frac{\partial w}{\partial s}\end{array}\right]+\frac{D}{R^2}\left[\begin{array}{c}\frac{{\partial }^{2}u}{\partial s^2}+\frac{1}{2}\left(1-v\right)\frac{{\partial }^{2}u}{\partial y^2}\\ +R\frac{{\partial }^{3}w}{\partial y^2\partial s}+R\frac{{\partial }^{3}w}{\partial s^3}\end{array}\right]=\rho h\frac{{\partial }^{2}u}{\partial t^2}(11)$

$\widehat{E}\left[\frac{1}{2}\left(1+v\right)\frac{{\partial }^{2}u}{\partial s\partial y}+\frac{{\partial }^{2}v}{\partial y^2}+\frac{1}{2}\left(1-v\right)\frac{{\partial }^{2}v}{\partial s^2}-\frac{v}{R}\frac{\partial w}{\partial y}\right]=\rho h\frac{{\partial }^{2}v}{\partial t^2}(12)$

$-\widehat{E}\left[\frac{1}{R}\frac{\partial u}{\partial s}+\frac{v}{R}\frac{\partial v}{\partial s}-\frac{w}{R^2}\right]+D\left[\frac{{\partial }^{4}w}{\partial s^4}+2\frac{{\partial }^{4}w}{\partial s^2\partial y^2}+\frac{{\partial }^{4}w}{\partial y^4}\right]+\frac{D}{R}\left[\frac{{\partial }^{3}u}{\partial y^2\partial s}+\frac{{\partial }^{3}u}{\partial s^3}\right]=-\rho h\frac{{\partial }^{2}w}{\partial t^2}(13)$

3 Numerical simulation

In this section, the dispersion relation of the unit cell is calculated using the FEM and the effects of scatterer radius on longitudinal wave stopband are discussed. In order to verify the attenuation effect on longitudinal vibration in the finite structure of metamaterial cylindrical shells, we also study the vibration transmission characteristics.

3.1 Calculation and discussion of dispersion relation

In the present work, the COMSOL Multiphysics software package was used to calculate the dispersion relation of metamaterial cylindrical shells by eigenvalue analysis in solid mechanics. The details of the FEM model are as follows: the unit cell is divided into 1,855 nodes, and the number of degrees of freedom is 37,449. In addition, the geometrical and material parameters identified in Figure 1 are given: a = 30 mm, h = 3 mm, r₁ = 10 mm, r₂ = 12 mm, R = 50 mm. The density(ρ) of the scatterer A (made of lead) is 11,600 kg m⁻³, Poisson’s ratio (ν) is 0.369, and Young’s modulus (E) is 40.8 GP. The connector B is made of silicone rubber, ρ = 1,300 kg m⁻³, ν = 0.469, E = 1.175e⁻⁴GP. The cylindrical shell C is made of epoxy resin, ρ = 1,180 kg m⁻³, ν = 0.368, E = 4.35 GP.

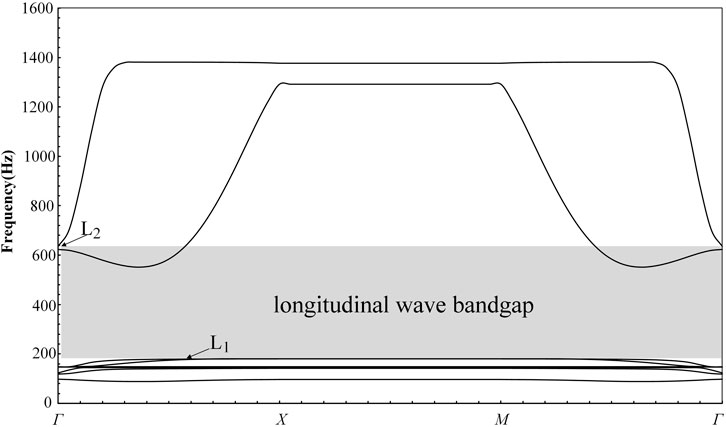
Figure 2 shows the numerical simulation results for the dispersion curves. The dispersion curves exhibit several different propagation waves. The bandgap for longitudinal waves ranges from 188 to 635 Hz because there are no freely propagating solutions in the longitudinal mode.

FIGURE 2

FIGURE 2. Dispersion curves of the unit cell with r₁ = 10 mm.

3.2 Effect of the scatterer radius

In order to obtain a wider longitudinal wave bandgap, we also studied the effect of scatterer radius on stopband behavior. For this purpose, we calculated the dispersion relation for unit cells with scatterer radii of 9, 10, and 11 mm. The bandgaps in the 9, 10, and 11 mm cases fell within the intervals (199,589), (188,635), and (178,711), respectively. It can be seen that with the increase in scatterer radius, the start frequency of the bandgap decreases slightly, while the stop frequency increases greatly. These shifts are caused by the increase in scatterer mass and filling rate, respectively.

3.3 Vibration transmission analysis for the finite periodic structure

The dispersion curves illustrate the frequency location and width of the bandgap. However, the dispersion curves cannot provide a full explanation of the vibration characteristics of the finite periodic structure. To further illustrate the vibration transmission characteristics and validate the accuracy of the bandgap, an analysis of vibration transmission for the finite periodic structure is presented in this section.

The finite periodic metamaterial cylindrical shell consists of 25 unit cells arranged periodically in a 5 × 5 layout along the s and y directions. To determine the transmission coefficient along the ΓX direction, incident longitudinal waves along this axis direction are modeled by applying harmonic displacements $Q_{inc}=q_{inc}{e}^{iwt}$ in the axis direction. The homogeneous parts are the transitional material connecting the periodic structure and the perfectly matched layers (PMLs). The PMLs are applied at both ends of the homogeneous part to prevent reflections by the scattering waves from the domain boundaries. Both the homogeneous parts and the PMLs have the same material parameters as the matrix. In addition, periodic boundary conditions are applied in the plane of the s direction.

The harmonic displacement response occurring along the interface between the homogeneous part and the periodic structure on the right side is represented by $Q_{res}=q_{res}{e}^{iwt}$. The transmission coefficient should be defined as:

$T=20\mathit{lg}\frac{Q_{res}}{Q_{inc}}(14)$

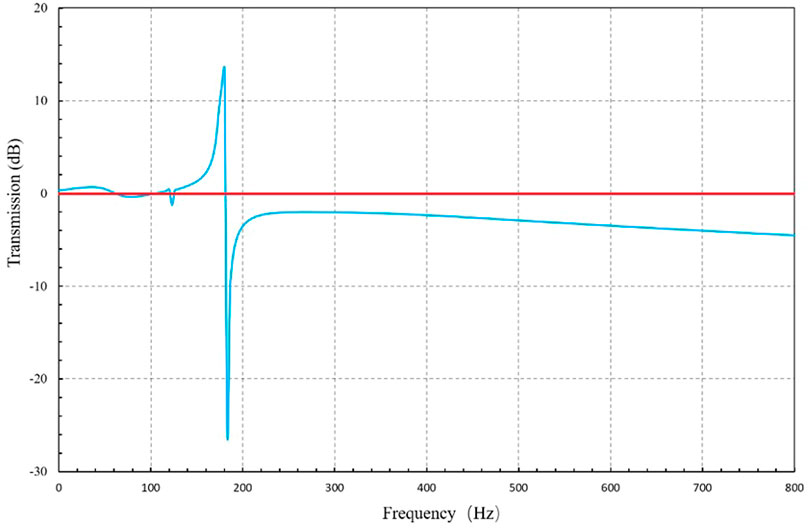
A frequency domain analysis sweeping from 0 to 800 Hz at intervals of 3 Hz was performed, and the simulated transmission coefficient as a function of frequency is plotted in Figure 3. The transmission coefficient agrees well with the corresponding dispersion curves of the unit cell, but the longitudinal wave transmission coefficient exhibits strong attenuation only at the start frequency of the bandgap, due to Fano-like interference phenomena. This shows that the metamaterial cylindrical shell structure has good vibration absorption characteristics.

FIGURE 3

FIGURE 3. Longitudinal transmission coefficient of the cylindrical shell model with r₁ = 10 mm.

4 The multiple-graded-resonator cylindrical shell

In this section, a cylindrical shell structure with multiple graded resonators, composed of scatterers with three different radii, is proposed in order to widen the longitudinal wave bandgaps. Additionally, the vibration transmission characteristics of this structure without a PML are verified via experiments.

As stated in the previous section, due to the presence of Fano-like interference in the metamaterial based on the local resonance mechanism, the longitudinal vibration transmission of the metamaterial only exhibits strong attenuation at the start frequency of the bandgaps. Therefore, we propose a multiple-graded-resonator cylindrical shell structure with a wider range of strong vibration attenuation, developed by combining three kind of metamaterial cylindrical shells with different start frequencies and locations, as shown in Figure 4A.

FIGURE 4

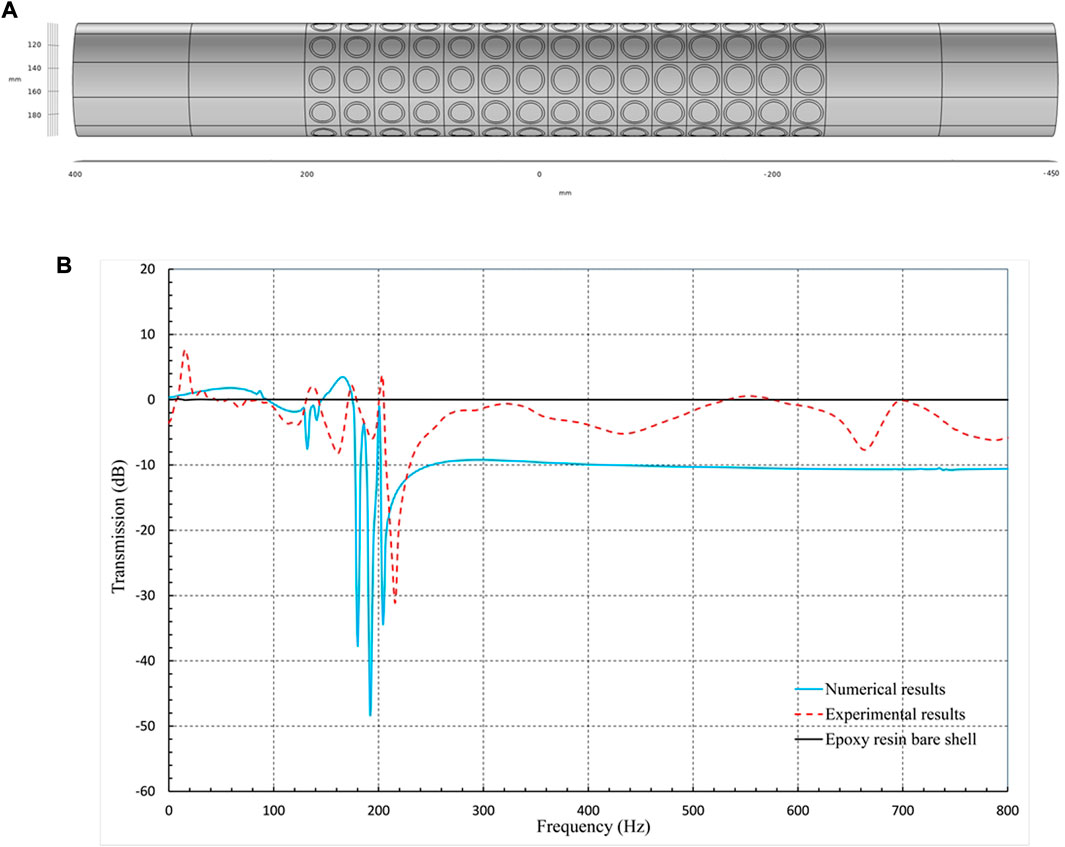
FIGURE 4. Cylindrical shell with multiple graded resonators: (A) the numerical model; (B) longitudinal transmission coefficient.

In order to verify the practical attenuation effect of the longitudinal vibration of this structure, we carried out a vibration attenuation experiment using a Siemens data acquisition instrument (type: LMS SCADAS Mobile). Two accelerometers (type: 356A16 SNLW180872; sensitivity: 98.3 mv/g) were used, with one placed at each end of the model. A hammer (type: PCB 086C01; sensitivity: 11.2 mv/N) was used to strike the model on one side.

The materials of the subject were consistent with those described in Section 3.1, and the components were connected to each other by adhesive bonding. In the experiment, vertical excitation was induced by the hammer hitting the outer surface of one end of the subject, which was freely positioned on a sponge, and the acceleration sensor was used to collect the stable response of the target point in the range 0–800 Hz. Subsequently, the transmission coefficient was obtained using Eq. 14.

Figure 4B shows the comparison between the experimental results and the simulation results on the vibration transmission characteristics of the multiple-graded-resonator structure.

As can be seen, the experimental results on the vibration transmission characteristics exhibit the same trend as the numerical results. In general, although the longitudinal vibration attenuation effect of the actual structure was slightly smaller than the effect in the simulation results, the bandwidth of the actual attenuation was wider. For the actual structure, there were three attenuation peaks at 162, 192, and 216 Hz. The first and third attenuation peaks differed by approximately 15 Hz from the simulation results, in which the corresponding peaks occurred at 178 and 201 Hz. Deviations in the material parameters and manufacturing process may be the main reason for the offset between experimental results and numerical results. In addition, the range of bandgaps of the multiple-graded-resonator cylindrical shell is the superposition of three single-resonator structures, and the strong attenuation range of this multiple-graded-resonator cylindrical shell (180–255 Hz) is approximately triple that of the single-resonator structure (178–199 Hz).

5 Conclusion

The present work investigated the property of longitudinal wave propagation in a metamaterial cylindrical shell. The dispersion curves of the proposed structure were used to analyze stopband behavior. Several numerical and experimental tests were also conducted and the results investigated in detail to study the effectiveness of the proposed structure. The following conclusions resulted from the work:

(1) The metamaterial cylindrical shell structure creates a longitudinal wave bandgap at 188–635 Hz, in which the propagation of longitudinal waves is impossible.

(2) As the scatterer radius is increased, the start frequency of the bandgap decreases slightly, while the stop frequency increases greatly; these shifts are caused by the increase in scatterer mass and filling rate, respectively.

(3) The bandgap range of the multiple-graded-resonator cylindrical shell is the superposition of that of three single-resonator structures, and the strong attenuation range of the multiple-graded-resonator cylindrical shell is triple that of the single-resonator structure. The development of this metamaterial cylindrical shell structure and the use of multiple graded resonators pave the way toward vibration reduction and noise control in the cylindrical shell structure.

Data availability statement

The raw data supporting the conclusion of this article will be made available by the authors, without undue reservation.

Author contributions

JY: Conceptualization, methodology, and writing; KX: Modeling and writing; DY: Modeling, methodology, and writing; LY: Conceptualization, discussions, and editing. All authors contributed to the article and approved the submitted version.

Funding

This work was supported by the National Natural Science Foundation of China (No. 52175121).

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

1. Panza MA. A review of experimental techniques for NVH analysis on a commercial vehicle. Energ Proced (2015) 82:1017–23. doi:10.1016/j.egypro.2015.11.861

CrossRef Full Text | Google Scholar

2. Deymier PA. Acoustic Metamaterials and phononic crystals. Berlin Heidelberg: Springer-Verlag (2013).

Google Scholar

3. Li L, Gang X, Sun Z, Zhang X, Zhang F. Design of phononic crystals plate and application in vehicle sound insulation. Adv Eng Softw (2018) 1(125):19–26. doi:10.1016/j.advengsoft.2018.08.002

CrossRef Full Text | Google Scholar

4. Charles C, Bonello B, Ganot F. Propagation of guided elastic waves in 2D phononic crystals. Ultrasonics (2006) 44(4):e1209–13. doi:10.1016/j.ultras.2006.05.096

PubMed Abstract | CrossRef Full Text | Google Scholar

5. Song Y, Wen J, Yu D, Liu Y, Wen X. Reduction of vibration and noise radiation of an underwater vehicle due to propeller forces using periodically layered isolators. J Sound vibration (2014) 333(14):3031–43. doi:10.1016/j.jsv.2014.02.002

CrossRef Full Text | Google Scholar

6. Yao L, Huang G, Chen H, Barnhart MV. A modified smoothed finite element method (M-SFEM) for analyzing the band gap in phononic crystals. Acta Mech (2019) 230(6):2279–93. doi:10.1007/s00707-019-02396-w

CrossRef Full Text | Google Scholar

7. Yao L, Jiang G, Wu F, Luo J. Band structure computation of two-dimensional and three-dimensional phononic crystals using a finite element-least square point interpolation method. Appl Math Model (2019) 76:591–606. doi:10.1016/j.apm.2019.05.052

CrossRef Full Text | Google Scholar

8. Yao LY, Wu F, Wu G. Numerical study of exterior acoustic problems using a novel finite element-least square point interpolation method with perfectly matched layerfinite element-least square point interpolation method with perfectly matched layer. Eng Anal Boundary Elem (2019) 102:87–96. doi:10.1016/j.enganabound.2019.01.021

CrossRef Full Text | Google Scholar

9. Wu TT, Huang ZG, Tsai TC, Wu TC. Evidence of complete band gap and resonances in a plate with periodic stubbed surface. Appl Phys Lett (2008) 93(11):111902. doi:10.1063/1.2970992

CrossRef Full Text | Google Scholar

10. Badreddine Assouar M, Sun JH, Lin FS, Hsu JC. Hybrid phononic crystal plates for lowering and widening acoustic band gaps. Ultrasonics (2014) 54(8):2159–64. doi:10.1016/j.ultras.2014.06.008

PubMed Abstract | CrossRef Full Text | Google Scholar

11. Liu Z, Zhang X, Mao Y, Zhu YY, Yang Z, Chan CT, et al. Locally resonant sonic materials. science (2000) 289(5485):1734–6. doi:10.1126/science.289.5485.1734

PubMed Abstract | CrossRef Full Text | Google Scholar

12. Liu Z, Chan CT, Sheng P. Analytic model of phononic crystals with local resonances. Phys Rev B (2005) 71(1):014103. doi:10.1103/physrevb.71.014103

CrossRef Full Text | Google Scholar

13. Goffaux C, Sánchez-Dehesa J. Two-dimensional phononic crystals studied using a variational method: Application to lattices of locally resonant materials. Phys Rev B (2003) 67(14):144301. doi:10.1103/physrevb.67.144301

CrossRef Full Text | Google Scholar

14. Claeys CC, Sas P, Desmet W. On the acoustic radiation efficiency of local resonance based stop band materials. J Sound Vibration (2014) 333(14):3203–13. doi:10.1016/j.jsv.2014.03.019

CrossRef Full Text | Google Scholar

15. Zhang X, Liu Y, Wu F, Liu Z. Large two-dimensional band gaps in three-component phononic crystals. Phys Lett A (2003) 317(1-2):144–9. doi:10.1016/j.physleta.2003.08.032

CrossRef Full Text | Google Scholar

16. Chen H, Li XP, Chen YY, Huang G. Wave propagation and absorption of sandwich beams containing interior dissipative multi-resonators. Ultrasonics (2017) 76:99–108. doi:10.1016/j.ultras.2016.12.014

PubMed Abstract | CrossRef Full Text | Google Scholar

17. Sharma B, Sun CT. Impact load mitigation in sandwich beams using local resonators. J sandwich structures Mater (2016) 18:50–64. doi:10.1177/1099636215583171

CrossRef Full Text | Google Scholar

18. Yao DH, Xiong MK, Luo JY, Yao L. Flexural wave mitigation in metamaterial cylindrical curved shells with periodic graded arrays of multi-resonator. Mech Syst Signal Process (2022) 168:108721. doi:10.1016/j.ymssp.2021.108721

CrossRef Full Text | Google Scholar

19. Oudich M, Li Y. Tunable sub-wavelength acoustic energy harvesting with a metamaterial plate. J Phys D: Appl Phys (2017) 50(31):315104. doi:10.1088/1361-6463/aa779d

CrossRef Full Text | Google Scholar

20. He ZC, Xiao X, Li E. Design for structural vibration suppression in laminate acoustic metamaterials. Composites B: Eng (2017) 131:237–52. doi:10.1016/j.compositesb.2017.07.076

CrossRef Full Text | Google Scholar

21. Pany C, Parthan S. Axial wave propagation in infinitely long periodic curved panels. J Vibration Acoust (2003) 125(1):24–30. doi:10.1115/1.1526510

CrossRef Full Text | Google Scholar

22. Manconi E, Mace B. Wave characterization of cylindrical and curved panels using a finite element method. The J Acoust Soc America (2009) 125(1):154–63. doi:10.1121/1.3021418

CrossRef Full Text | Google Scholar

23. Nateghi A, Belle LV, Claeys C, Deckers E, Pluymers B, Desmet W. Wave propagation in locally resonant cylindrically curved metamaterial panels. Int J Mech Sci (2017) 127:73–90. doi:10.1016/j.ijmecsci.2016.07.003

CrossRef Full Text | Google Scholar

24. Banerjee A, Das R, Calius EP. Frequency graded 1D metamaterials: A study on the attenuation bands. J Appl Phys (2017) 122(7):075101. doi:10.1063/1.4998446

CrossRef Full Text | Google Scholar

25. Ding YH, Yi H, Statharas EC, Hong M. A broadband acoustic metamaterial with impedance matching layer of gradient index. Appl Phys Lett (2017) 110(24):241903. doi:10.1063/1.4986472

CrossRef Full Text | Google Scholar

26. Yu X, Lu ZB, Cui FS, Cheng L, Cui Y. Tunable acoustic metamaterial with an array of resonators actuated by dielectric elastomer. Extreme Mech Lett (2017) 12:37–40. doi:10.1016/j.eml.2016.07.003

CrossRef Full Text | Google Scholar

27. An X, Fan H, Zhang C. Wave dispersion in one-dimensional periodic graded metacomposites. J Sound Vibration (2017) 409:217–26. doi:10.1016/j.jsv.2017.08.002

CrossRef Full Text | Google Scholar