- 1Key Laboratory of In-fiber Integrated Optics of Ministry of Education, Harbin Engineering University, Harbin, China
- 2School of Physics, Harbin Institute of Technology, Harbin, China
Non-linear metamaterials hold great promise for enhanced terahertz harmonic generation. Here, we numerically investigate enhanced terahertz third-harmonic generation (THG) by exploiting the symmetry-protected bound states in the continuum (BICs) in graphene grating-like metamaterial. By symmetry breaking of metamaterials, BICs transform into quasi-BICs. The high Q-factor and strong localized field enhancement is achieved at quasi-BICs, leading to a boosted THG process with low incident intensity of fundamental frequency. The THG conversion efficiency reaches 3.1% at an incident intensity of 100 kW/cm2. The remarkably enhanced non-linear optical process in the proposed non-linear metamaterial constitutes an outstanding platform for on-chip terahertz non-linear conversion applications.
1 Introduction
Terahertz electromagnetic waves hold unique opportunities for various important applications, including terahertz communications [1], non-destructive measurements [2], and security imaging [3]. Metamaterials, artificial structural materials, are used for arbitrary manipulation of terahertz waves, taking advantage of its unique electromagnetic properties. Essential functionalities achieved include holograms [4–6], generalized Snell’s law [7], metalenses [8, 9], and wavefront controlling [10, 11]. Furthermore, metamaterials have become instrumental for observing non-linear phenomena, providing a new platform for development of non-linear photonics [12]. Compared to the non-linear bulk crystals, metamaterials can not only enhance the localized density of states but also relax the necessity of phase-matching constraints [13, 14], leading to stronger non-linear processes, which are very interesting for practical applications.
Resonance response, associated with strong localized field confinement, has the potential to improve the non-linear responses. Recently, the bound states in the continuum (BICs), which can completely confine the electromagnetic wave without radiation leakage, have been introduced as strong resonances in metamaterials [15]. The most common approach is to realize symmetry-protected BICs in metamaterials with in-plane inversion symmetry [16]. By assigning the bound state and the continuum to different symmetries, the leakage of the bound state is forbidden due to symmetry incompatibility. True BICs are resonances associated with an infinite quality-factor (Q-factor), considered embedded trapped modes. However, the infinite Q-factor BICs are not available under external excitation. In practice, with the structural perturbations, the BICs can transform into quasi-BICs with a finite Q-factor [17]. For metamaterials supporting symmetry-protected BICs, the distinct quasi-BICs are realized by breaking the symmetry [16]. Although BIC metamaterials are widely used to boost the non-linear response in the optical range [18–20], the Q-factor of quasi-BICs at terahertz frequencies is several orders of magnitude lower than that at optical bands, which limits the research on the terahertz non-linear response. Exploring the efficient terahertz non-linear response remains a basic challenge.
In the paper, we proposed a graphene grating-like metamaterial with BICs for enhancing the terahertz THG response. By symmetry breaking of the metamaterial, the symmetry-protected BICs can make the transition to quasi-BICs. It enables high Q-factor and strong localized field enhancement, improving the light–matter interaction in monolayer graphene. By exploiting the large third-order non-linearity of graphene, the THG non-linear process with lower pump power at quasi-BICs is significantly boosted. Our study reveals that the quasi-BICs can significantly boost the THG in the graphene grating-like metamaterial, which offers an approach to achieve practical non-linear devices for on-chip terahertz non-linear conversion applications.
2 Structural design and simulation
The schematic of the proposed graphene grating-like metamaterial is illustrated in Figure 1A, which contains two monolayer graphene strips, a monolayer graphene nanoribbon, and a metal ground layer separated by the glass spacer layers (where the refractive index of glass is 1.6 [21]). The metamaterial is periodic in the direction of x-axis and considered infinite in the direction of y-axis. As shown in Figure 1B, the structural parameters of the metamaterial include p = 300 nm, w1 = 100 nm, w2 = 90 nm, d = 50 nm, h1 = 12 nm, and h2 = 1,350 nm. The thickness of the metal ground layer is greater than the skin depth to reflect the transmitted waves. The Fermi levels of the monolayer graphene strips and the monolayer graphene nanoribbon are Ef1 and Ef2, respectively At terahertz frequencies, the linear conductivity of graphene can be described by the Drude model as [22, 23]
where e is the electron charge, Ef is the graphene Fermi level, ℏ is the reduced Planck’s constant, ω is the angular frequency of the incident waves, and τ is the carrier relaxation time, which can conform to the following equation τ = μEf/(evf2). The Fermi velocity vf is 106 m/s, and the carrier mobility μ is 1 m2/(V·s), which can be obtained in experiment [24]. The linear conductivity is a complex number, and the imaginary part represents the loss of graphene. In the simulation, we neglected the loss of glass, and the loss of the metamaterial is primarily derived from graphene. The third-order non-linear conductivity of graphene is expressed as [25, 26]
where σ0 = e2/4ℏ, T(x) = 17G(x) - 64G(2x) + 45G(3x), and G(x) = In|(1 + x)/(1 - x)| + iπθ(|x| - 1). θ(z) is the Heaviside step function. The graphene is modeled to be a non-linear surface current, which is calculated by the formula [27].
where EFF and ETH are the electric fields of the fundamental frequency and the third-harmonic wave, respectively. The metamaterial is normally illuminated by a transverse magnetic-polarized wave with an input intensity of 100 kW/cm2 along the direction of z-axis. The finite element method (FEM) is utilized to compute the linear response and third-order non-linear response in the frequency domain. The perfectly matched layer conditions are employed in the direction of z-axis, and the period boundary conditions are employed in the direction of x-axis.
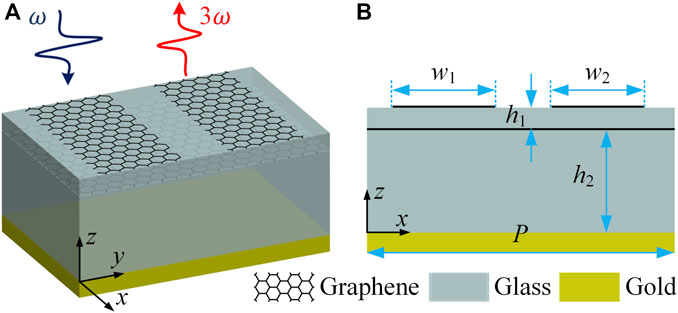
FIGURE 1. (A) Schematic of the designed terahertz non-linear metamaterial. (B) Cross-section of the metamaterial with geometric dimensions.
3 Results and discussion
The linear response for the graphene grating-like metamaterial is first studied. The proposed metamaterial produces symmetry-protected BICs, which can transform into quasi-BICs with high Q-factor and strong localized field enhancement through breaking the symmetry of the metamaterial. The asymmetry property of the metamaterial is controlled by an asymmetric factor defined as α = |w1-w2|/w1, where w1 is fixed. For the metamaterial structure with w2 = 100 nm, the system can be considered a Fabry–Pérot cavity circular structure, producing a Fabry–Pérot resonance mode, which is explained by [28]
where c is the velocity of light in vacuum, w is the width of the graphene strip, and nM is the effective refractive index of Fabry–Pérot resonance modes.
The absorption spectra as a function of frequency with different widths w2 are shown in Figure 2A. When asymmetric factor α = 0 (w2 = 100 nm), the proposed metamaterial meets inversion symmetry. Due to symmetry mismatch between the bound state and the continuum, the leakage at the bound state is forbidden at Γ point. Therefore, the left resonance disappears completely, forming symmetry-protected BICs. By varying the width of graphene 2 (w2) to break the symmetry, the symmetry-protected BICs are perturbed and leak to free space, leading to quasi-BICs with high Q-factors. Notably, the quasi-BICs are essentially Fabry–Pérot resonance modes. The quasi-BICs move from high to low frequency, with the decreasing width w2 explained by Eq. 4. The temporal coupled mode theory is suitable to analyze the coupling in a single-mode optical resonator with multiple ports, and the absorption spectra can be represented by [29].
where δ and γ represent the intrinsic loss and external leakage rates, respectively. ω0 is the resonance angular frequency. Figure 2B shows the Q-factor and the maximum electric field enhancement of the metamaterial versus the asymmetric factor α. The Q-factor and the maximum field enhancement increase gradually as α decreases from 0.2 to 0.04 (corresponding to w2 from 80 to 96 nm). The Q-factor is 72 at the metamaterial of α = 0.2 but can be as high as 109 at α = 0.1 and even 135 at α = 0.04 at the quasi-BICs. Generally, the quasi-BICs have a Q-factor of 104 or more at optical bands. At terahertz spectra, the Q-factor of plasmonic metamaterials is significantly reduced by several orders of magnitude compared to optical bands due to inherent ohmic and radiation losses. The order of magnitude of the Q-factor for the quasi-BICs is comparable to that previously reported [17, 30, 31]. Moreover, the quasi-BICs are not only associated with high Q-factors but also with remarkably strong localized field enhancement, which can significantly enhance the non-linear response of the system.
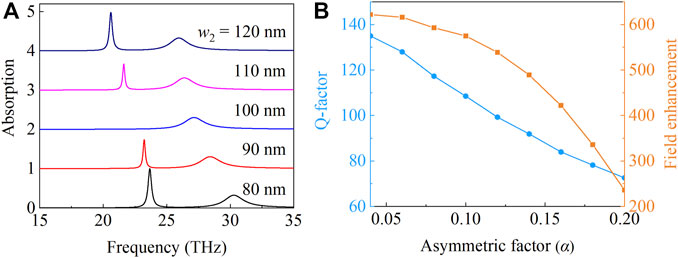
FIGURE 2. (A) Absorption spectra for the metamaterial with p = 300 nm, w1 = 100 nm, h1 = 12 nm, h2 = 1,350 nm, and Ef1 = Ef2 = 1 eV for different widths w2. (B) Corresponding Q-factor and maximum electric field enhancement as a function of the asymmetric factor α.
The quasi-BICs are localized by the Fabry–Pérot cavities, which can be regulated by modulating the graphene Fermi level. In the simulation, the relaxation time is dependent on the Fermi level and changing the Fermi level results in a corresponding variation in the relaxation time. Thus, the effects of time and Fermi level on conversion efficiency are discussed together. The Fermi level can be manipulated by the gate voltage, which can be written as follows [32]:
where ε0 and ε1 are the vacuum permittivity and static permittivity of the glass, respectively. Figure 3A displays the absorption of the quasi-BICs with different Fermi levels Ef1. As the Fermi level decreases, Ef1, the resonance frequency of the quasi-BICs, shows a distinct redshift. It can be attributed to the variation in graphene conductivity resulting from the Fermi level. According to Eq. 2, the metamaterial with low Fermi level can achieve strong non-linear response. However, the absorption of the quasi-BICs is below 20% for the Fermi level Ef1 of 0.2 eV, which is negative for boosting the non-linear response. To improve the absorption of the quasi-BICs for the Fermi level Ef1 = 0.2 eV, the effect of the distance h1 on the absorption is calculated as shown in Figure 3B. Clearly, the absorption at the quasi-BICs increases as distance h1 increases, and the absorption can reach 63% with distance h1 of 52 nm. Moreover, the resonance frequency of the quasi-BICs increases as the distance h1 increases, and it can be explained by the mechanism of the Fabry–Pérot resonance mode. Graphene plasmons can be accompanied by damping effects due to inelastic scattering with phonons and elastic carrier scattering processes when the plasmon energy exceeds 0.2 eV [33]. The resonance frequency of the quasi-BICs is less than 20 THz, corresponding to the plasmon energy of 0.08 eV. Therefore, damping effects in the proposed system can be neglected.
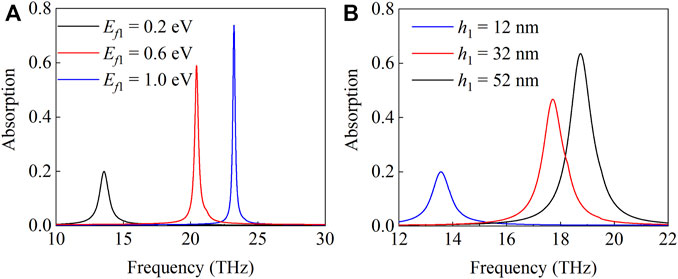
FIGURE 3. (A) Absorption spectra of the metamaterial with p = 300 nm, w1 = 100 nm, w2 = 90 nm, h1 = 12 nm, h2 = 1,350 nm, and Ef2 = 1 eV for different Fermi levels Ef1. (B) Absorption spectra of the metamaterial with p = 300 nm, w1 = 100 nm, w2 = 90 nm, h2 = 1,350 nm, Ef1 = 0.2 eV, and Ef2 = 1 eV for different distances h1.
We next investigate the THG response for the graphene grating-like metamaterial. Utilization of graphene to improve the functionality of absorbers and non-linear effects has been extensively reported in previous works [34–38]. However, the non-linear effects normally require tremendous input radiation intensities to be excited, rendering their practical applications an enormous challenge. The proposed metamaterial with BICs significantly confines the electromagnetic power in subwavelength range, which results in a high Q-factor and strong localized field near the non-linear graphene, enhancing the non-linear effects. Meanwhile, the requirement of complex phase-matching conditions for the proposed metamaterial with ultrathin thickness can be relaxed than for the non-linear body crystals. The fundamental frequency of the incident radiation for the non-linear metamaterial is aligned with the resonance frequency of the quasi-BICs. To represent the power conversion from the fundamental frequency to the third-harmonic wave, the THG conversion efficiency is calculated as η = PTH(3ω)/PFF(ω) [39], where PTH(3ω) is the output THG power for the third-harmonic frequency derived from the integration of the THG power outflow on the top port of the metamaterial and PFF(ω) is the incident power for the fundamental frequency. The parameters are assumed to be p = 300 nm, w1 = 100 nm, w2 = 90 nm, h1 = 52 nm, h2 = 1,350 nm, Ef1 = 0.2 eV, and Ef2 = 1 eV.
Figure 4A depicts the THG conversion efficiency of the graphene grating-like metamaterial versus the fundamental frequency. Obviously, the THG conversion efficiency exhibits a remarkable peak at the resonance frequency of 18.7 THz for the quasi-BICs. The lower or higher fundamental frequencies reduces the THG conversion efficiency, as explained using Eq. 3. With the input intensity around 100 kW/cm2, the graphene grating-like metamaterial exhibits a THG conversion efficiency of 2.8% at the quasi-BICs. The electric-field-enhancement distributions for the graphene grating-like metamaterial at the fundamental frequency and the third-harmonic wave are illustrated in the insets of Figure 4A. The strong localized field enhancement is achieved both at the fundamental frequency and at the third-harmonic wave, which is beneficial for improving the THG response. Figure 4B displays the incident intensity of fundamental frequency dependence of THG conversion efficiency for the graphene grating-like metamaterial. The fundamental frequency is fixed at a resonance frequency of 18.7 THz for the quasi-BICs, and the THG conversion efficiency is significantly enhanced with increasing incident intensity, revealing a squared trend. As shown in the inset of Figure 4B, the corresponding log plot displays a linear relationship with a slope of ∼2 between the THG conversion efficiency and incident intensity, as expected for the THG process.
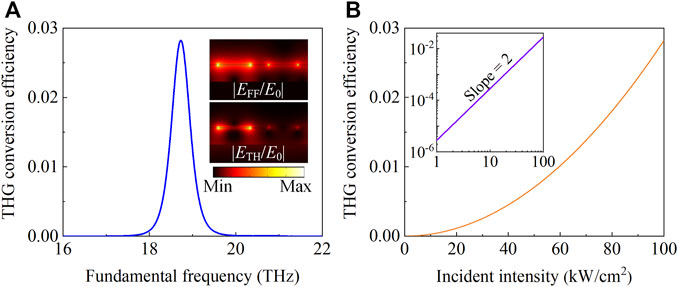
FIGURE 4. (A) THG conversion efficiency against the fundamental frequency for the incident wave. The insets are the enhanced electric field distributions at the fundamental frequency of 18.7 THz and the third-harmonic frequency of 56.1 THz. (B) THG conversion efficiency varies with intensity for the incident wave. The inset is corresponding to the log–log plot. The parameters are p = 300 nm, w1 = 100 nm, w2 = 90 nm, h1 = 52 nm, h2 = 1,350 nm, Ef1 = 0.2 eV, and Ef2 = 1 eV.
Figure 5A displays the THG conversion efficiency for the graphene grating-like metamaterial at Fermi level Ef1 = 0.2, 0.4, and 0.6 eV. As shown in the figure, the THG conversion efficiency of the quasi-BICs increases as the Fermi level Ef1 decreases. At the quasi-BICs, the THG conversion efficiency under the Fermi level Ef1 decreased from 0.6 to 0.2 eV and improved from 0.6% to 2.8%, which is enhanced by more than four times. This significant enhancement can be explained by the increase in third-order non-linear conductivity as the graphene Fermi level decreases, as given by Eq. 2. Particularly, the variation in the Fermi level can have an effect on the carrier mobility. The maximum conversion efficiency in the proposed system is obtained with a fixed Fermi level of 0.2 eV, so the variation of the Fermi level hardly affects the carrier mobility. The THG conversion efficiency for the graphene grating-like metamaterial with different distances h1 is plotted in Figure 5B. It is obvious that the THG conversion efficiency of the quasi-BICs increases as the distance h1 increases, which is caused by the increase in the absorption of the quasi-BICs at the fundamental frequency with the increase in the distance h1, as shown in Figure 3B.
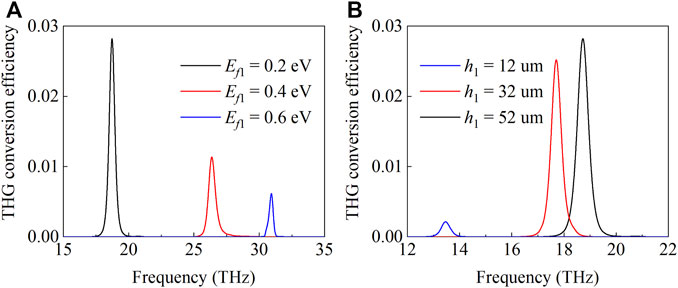
FIGURE 5. THG conversion efficiency spectra for (A) different Fermi levels Ef1 and (B) different distances h1. The other parameters are p = 300 nm, w1 = 100 nm, w2 = 90 nm, h2 = 1,350 nm, and Ef2 = 1 eV.
Based on the aforementioned results, we now investigate how to further enhance the non-linear response of the graphene grating-like metamaterial. As shown in Figure 4B, the THG response has not achieved saturation at the asymmetry factor α = 0.1 (w2 = 90 nm). The transition from BICs to quasi-BICs causes the resonance to decay, resulting in leakage of optical radiation to free space, which can reduce the light–matter interaction in non-linear graphene. To solve this problem, we calculate the THG conversion efficiency for the graphene grating-like metamaterial with different widths w2, as shown in Figures 6A. Figures 6B displays the variation in the THG conversion efficiency at the quasi-BICs with asymmetry factor α ranging from 0.04 to 0.2 (corresponding width w2 from 96 to 80 nm). Remarkably, the THG conversion efficiency can reach 3.1% for the asymmetry factor α of 0.04, which can be largely enhanced by 10% in contrast to the result obtained with the asymmetry factor α of 0.1. The efficiency of the proposed metamaterial is significantly boosted than that of previous ones reported both in simulations [40–46] and experiments [12, 47, 48]. Notably, the THG conversion efficiency at the quasi-BICs can be enhanced at a higher level with the asymmetry factor α close to 0.
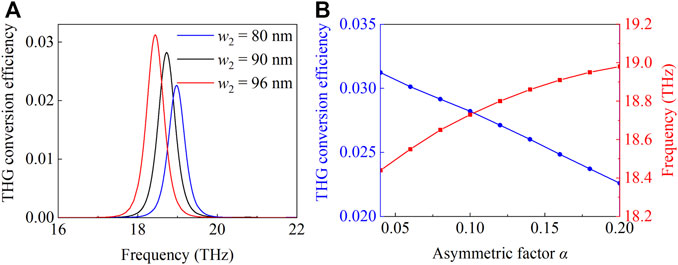
FIGURE 6. (A) THG conversion efficiency versus the fundamental frequency for different widths w2. (B) THG conversion efficiency and fundamental frequency of the quasi-BICs dependence on the asymmetric factor α. The other parameters are p = 300 nm, w2 = 90 nm, h1 = 52 nm, h2 = 1,350 nm, Ef1 = 0.2 eV, and Ef2 = 1 eV.
4 Conclusion
In summary, we theoretically demonstrated a graphene grating-like metamaterial with BICs for enhancing the terahertz THG response. The quasi-BICs with accompanying high Q-factor and strong localized field enhancement can be achieved through symmetry-breaking of metamaterials, producing the strong terahertz THG response. By adjusting the graphene Fermi level and structural parameters, the THG conversion efficiency is further improved. Under the input intensity 100 kW/cm2, a THG conversion efficiency of 2.8% is attained with the asymmetric factor α of 0.1. Moreover, THG conversion efficiency exceeds 3.1% at α of 0.04. The proposed efficiency non-linear metamaterial indicates great promise for on-chip terahertz non-linear conversion applications.
Data availability statement
The original contributions presented in the study are included in the article/Supplementary Material; further inquiries can be directed to the corresponding authors.
Author contributions
BW and LL conceived and led the design. BW, JL, and JlL finished the whole manuscript writing and manuscript modification. JL and JC performed the statistical analysis. JlL and FT performed image processing. WS, JC, and FT contributed to the proofreading and revised the article format. All authors approved the submitted version.
Funding
This work was supported in part by the Natural Science Foundation of Heilongjiang Province, Grant Number LH2019F012, and by the 111 Project of Harbin Engineering University, Grant Number B13015.
Conflict of interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Publisher’s note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
References
1. Koenig S, Lopez-Diaz D, Antes J, Boes F, Henneberger R, Leuther A, et al. Wireless sub-THz communication system with high data rate. Nat Photon (2013) 7:977–81. doi:10.1038/NPHOTON.2013.275
2. Zhong S. Progress in terahertz nondestructive testing: A review. Front Mech Eng-prc (2019) 14:273–81. doi:10.1007/s11465-018-0495-9
3. Berry CW, Wang N, Hashemi MR, Unlu M, Jarrahi M. Significant performance enhancement in photoconductive terahertz optoelectronics by incorporating plasmonic contact electrodes. Nat Commun (2013) 4:1622. doi:10.1038/ncomms2638
4. Guo J, Wang T, Zhao H, Wang X, Feng S, Han P, et al. Reconfigurable terahertz metasurface pure phase holograms. Adv Opt Mater (2019) 7:1801696. doi:10.1002/adom.201801696
5. Rajabalipanah H, Rouhi K, Abdolali A, Iqbal S, Zhang L, Liu S. Real-time terahertz meta-cryptography using polarization-multiplexed graphene-based computer-generated holograms. Nanophotonics (2020) 9:2861–77. doi:10.1515/nanoph-2020-0110
6. Wang R, Ren G, Ren Z, Liu J, Li S, Chen X, et al. Reconstructing subwavelength resolution terahertz holographic images. Opt Express (2022) 30:7137–46. doi:10.1364/OE.453634
7. Yu N, Genevet P, Kats MA, Aieta F, Tetienne J-P, Capasso F, et al. Light propagation with phase discontinuities: Generalized laws of reflection and refraction. Science (2011) 334:333–7. doi:10.1126/science.1210713
8. Wang S, Wu PC, Su V-C, Lai Y-C, Chen M-K, Kuo HY, et al. A broadband achromatic metalens in the visible. Nat Nanotechnol (2018) 13:227–32. doi:10.1038/s41565-017-0052-4
9. Wang R, Han J, Liu J, Tian H, Sun W, Li L, et al. Multi-foci metalens for terahertz polarization detection. Opt Lett (2020) 45:3506–9. doi:10.1364/OL.395580
10. Li J, Li J, Yang Y, Li J, Zhang Y, Wu L, et al. Metal-graphene hybrid active chiral metasurfaces for dynamic terahertz wavefront modulation and near field imaging. Carbon (2020) 163:34–42. doi:10.1016/j.carbon.2020.03.019
11. Zhu S, Quan J, Fu Y, Chen H, Gao L, Xu Y. Anomalous wavefront control of third-harmonic generation via graphene-based nonlinear metasurfaces in the terahertz regime. Opt Express (2022) 30:29246. doi:10.1364/OE.453700
12. Deinert J-C, Alcaraz Iranzo D, Pérez R, Jia X, Hafez HA, Ilyakov I, et al. Grating-graphene metamaterial as a platform for terahertz nonlinear photonics. ACS Nano (2021) 15:1145–54. doi:10.1021/acsnano.0c08106
13. Krasnok A, Tymchenko M, Alu A. Nonlinear metasurfaces: A paradigm shift in nonlinear optics. Mater Today (2018) 21:8–21. doi:10.1016/j.mattod.2017.06.007
14. Gomez-Diaz JS, Tymchenko M, Lee J, Belkin MA, Alù A. Nonlinear processes in multi-quantum-well plasmonic metasurfaces: Electromagnetic response, saturation effects, limits, and potentials. Phys Rev B (2015) 92:125429. doi:10.1103/PhysRevB.92.125429
15. Abujetas DR, van Hoof N, ter Huurne S, Gómez Rivas J, Sánchez-Gil JA. Spectral and temporal evidence of robust photonic bound states in the continuum on terahertz metasurfaces. Optica (2019) 6:996. doi:10.1364/OPTICA.6.000996
16. Koshelev K, Lepeshov S, Liu M, Bogdanov A, Kivshar Y. Asymmetric metasurfaces with high-Q resonances governed by bound states in the continuum. Phys Rev Lett (2018) 121:193903. doi:10.1103/PhysRevLett.121.193903
17. Zhao X, Chen C, Kaj K, Hammock I, Huang Y, Averitt RD, et al. Terahertz investigation of bound states in the continuum of metallic metasurfaces. Optica (2020) 7:1548–54. doi:10.1364/OPTICA.404754
18. Koshelev K, Tang Y, Li K, Choi D-Y, Li G, Kivshar Y. Nonlinear metasurfaces governed by bound states in the continuum. ACS Photon (2019) 6:1639–44. doi:10.1021/acsphotonics.9b00700
19. Huang Z, Wang M, Li Y, Shang J, Li K, Qiu W, et al. Highly efficient second harmonic generation of thin film lithium niobate nanograting near bound states in the continuum. Nanotechnology (2021) 32:325207. doi:10.1088/1361-6528/abfe23
20. Kang L, Bao H, Werner DH. Efficient second-harmonic generation in high Q-factor asymmetric lithium niobate metasurfaces. Opt Lett (2021) 46:633–6. doi:10.1364/OL.413764
21. Gao E, Li H, Liu C, Ruan B, Li M, Zhang B, et al. Dynamically tunable bound states in the continuum supported by asymmetric Fabry-Pérot resonance. Phys Chem Chem Phys (2022) 24:20125–9. doi:10.1039/d2cp02605h
22. Jablan M, Buljan H, Soljacic M. Plasmonics in graphene at infrared frequencies. Phys Rev B (2009) 80:245435. doi:10.1103/PhysRevB.80.245435
23. Wang B, Gai K, Wang R, Yan F, Li L. Ultra-broadband perfect terahertz absorber with periodic-conductivity graphene metasurface. Opt Laser Technol (2022) 154:108297. doi:10.1016/j.optlastec.2022.108297
24. Chen J-H, Jang C, Xiao S, Ishigami M, Fuhrer MS. Intrinsic and extrinsic performance limits of graphene devices on SiO2. Nat Nanotechnol (2008) 3:206–9. doi:10.1038/nnano.2008.58
25. Cheng JL, Vermeulen N, Sipe JE. Third order optical nonlinearity of graphene. New J Phys (2014) 16:053014. doi:10.1088/1367-2630/16/5/053014
26. Guo T, Jin B, Argyropoulos C. Hybrid graphene-plasmonic gratings to achieve enhanced nonlinear effects at terahertz frequencies. Phys Rev Appl (2019) 11:024050. doi:10.1103/PhysRevApplied.11.024050
27. Chatzidimitriou D, Pitilakis A, Kriezis EE. Rigorous calculation of nonlinear parameters in graphene-comprising waveguides. J Appl Phys (2015) 118:023105. doi:10.1063/1.4926501
28. Todorov Y, Andrews AM, Sagnes I, Colombelli R, Klang P, Strasser G, et al. Strong light-matter coupling in subwavelength metal-dielectric microcavities at terahertz frequencies. Phys Rev Lett (2009) 102:186402. doi:10.1103/PhysRevLett.102.186402
29. Zhong H, Liu Z, Liu X, Fu G, Liu G, Chen J, et al. Ultra-high quality graphene perfect absorbers for high performance switching manipulation. Opt Express (2020) 28:37294. doi:10.1364/OE.412861
30. Tan TCW, Plum E, Singh R. Lattice-enhanced fano resonances from bound states in the continuum metasurfaces. Adv Opt Mater (2020) 8:1901572. doi:10.1002/adom.201901572
31. Niu J, Zhai Y, Han Q, Liu J, Yang B. Resonance-trapped bound states in the continuum in metallic THz metasurfaces. Opt Lett (2021) 46:162–5. doi:10.1364/OL.410791
32. Efetov DK, Kim P. Controlling electron-phonon interactions in graphene at ultrahigh carrier densities. Phys Rev Lett (2010) 105:256805. doi:10.1103/PhysRevLett.105.256805
33. Yan H, Low T, Zhu W, Wu Y, Freitag M, Li X, et al. Damping pathways of mid-infrared plasmons in graphene nanostructures. Nat Photon (2013) 7:394–9. doi:10.1038/nphoton.2013.57
34. Hong S-Y, Dadap JI, Petrone N, Yeh P-C, Hone J, Osgood RM. Optical third-harmonic generation in graphene. Phys Rev X (2013) 3:021014. doi:10.1103/PhysRevX.3.021014
35. Mikhailov SA. Quantum theory of third-harmonic generation in graphene. Phys Rev B (2014) 90:241301. doi:10.1103/PhysRevB.90.241301
36. Rostami H, Polini M. Theory of third-harmonic generation in graphene: A diagrammatic approach. Phys Rev B (2016) 93:161411. doi:10.1103/PhysRevB.93.161411
37. Amin M, Farhat M, Baǧcı H. A dynamically reconfigurable Fano metamaterial through graphene tuning for switching and sensing applications. Sci Rep-uk (2013) 3:2105. doi:10.1038/srep02105
38. Chen P-Y, Argyropoulos C, Farhat M, Gomez-Diaz JS. Flatland plasmonics and nanophotonics based on graphene and beyond. Nanophotonics-berlin (2017) 6:1239–62. doi:10.1515/nanoph-2016-0137
39. Nasari H, Abrishamian MS. Nonlinear terahertz frequency conversion via graphene microribbon array. Nanotechnology (2016) 27:305202. doi:10.1088/0957-4484/27/30/305202
40. Liu Y, Zhu S, Zhou Q, Cao Y, Fu Y, Gao L, et al. Enhanced third-harmonic generation induced by nonlinear field resonances in plasmonic-graphene metasurfaces. Opt Express (2020) 28:13234–42. doi:10.1364/OE.391294
41. Liu JQ, Fang JN, Wang DY, Chen S, He MD. Enhanced third-harmonic generation from layered graphene/insulator disks array. J Phys D: Appl Phys (2021) 54:055302. doi:10.1088/1361-6463/abc0bd
42. Jin B, Guo T, Argyropoulos C. Enhanced third harmonic generation with graphene metasurfaces. J Opt (2017) 19:094005. doi:10.1088/2040-8986/aa8280
43. Yu S, Zhang T, Han X, Dai J, Xu K. Inverse design of graphene-assisted metallodielectric grating and its applications in the perfect absorber and plasmonic third harmonic generation. Opt Express (2020) 28:35561–75. doi:10.1364/OE.410107
44. Wang B, Wang R, Yan F, Liu J, Liu J, Sun W, et al. Enhanced terahertz third harmonic generation with high-order guided-mode resonance of graphene plasmonic gratings. Phys Scr (2022) 97:115501. doi:10.1088/1402-4896/ac9560
45. Theodosi A, Tsilipakos O, Soukoulis CM, Economou EN, Kafesaki M. 2D-patterned graphene metasurfaces for efficient third harmonic generation at THz frequencies. Opt Express (2022) 30:460–72. doi:10.1364/OE.445751
46. Wang B, Liu J, Liu J, Liu J, Liu G, Sun W, et al. Enhanced terahertz third-harmonic generation in graphene–metal metasurface with bound states in the continuum. J Appl Phys (2023) 133:023103. doi:10.1063/5.0132059
47. Tielrooij K-J, Principi A, Reig DS, Block A, Varghese S, Schreyeck S, et al. Milliwatt terahertz harmonic generation from topological insulator metamaterials. Light Sci Appl (2022) 11:315. doi:10.1038/s41377-022-01008-y
Keywords: terahertz, third-harmonic generation, bound states in the continuum, graphene, metamaterial
Citation: Wang B, Liu J, Cui J, Liu J, Tian F, Sun W and Li L (2023) Enhanced terahertz third-harmonic generation by bound states in the continuum in graphene grating-like metamaterial. Front. Phys. 11:1135211. doi: 10.3389/fphy.2023.1135211
Received: 31 December 2022; Accepted: 06 March 2023;
Published: 21 March 2023.
Edited by:
Dibakar Roy Chowdhury, Mahindra École Centrale College of Engineering, IndiaReviewed by:
Andrea Marini, University of L'Aquila, ItalyMohamed Farhat, King Abdullah University of Science and Technology, Saudi Arabia
Copyright © 2023 Wang, Liu, Cui, Liu, Tian, Sun and Li. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Weimin Sun, c3Vud2VpbWluQGhyYmV1LmVkdS5jbg==; Li Li, bGlsaS5waHlzQGhpdC5lZHUuY24=
 Baoku Wang
Baoku Wang Jing Liu1
Jing Liu1 Li Li
Li Li