A simple frequency formulation for fractal–fractional non-linear oscillators: A promising tool and its future challenge

This paper proposes a simple frequency formula developed from He’s frequency formulation for fractal systems. In this approach, the initial guess can be judiciously chosen. Even the simplest initial guess leads to a highly accurate approximate solution. A detailed theoretical development is elucidated, and the solving process is given step by step. The simple calculation and reliable results have been merged into an effective tool for deeply studying fractal vibration systems, and the present approach offers a completely new angle for the fast insight into the physical properties of a non-linear vibration system in a fractal space.

1 Introduction

Fractal oscillations not only demonstrate the beauty of mathematics but also reveal the nature of the world and change the way people study nature. Fractal non-linear systems truly describe the dynamic problems of engineering science, and the research on them greatly expands the field of human cognition. The emergence of fractal theory makes us realize that the world is non-linear and fractals are everywhere. Fractal non-linear vibration can be close to practical problems in both depth and breadth, and it explains many phenomena through the fractal theory. Since the birth of the fractal theory, it has been used in engineering and science, for example, the fractal diffusion [1, 2], the fractal rheological model [3], the fractal control [4], the fractal solitary waves [5, 6], and the fractal oscillators [7]. The two-scale fractal calculus is used to describe transport problems in a porous medium, such as the problem of oil extraction and heat transfer of heat pipes. The porous medium is viewed as a fractal space, so non-linear vibrations in the porous medium can be modeled by fractal vibration theory [8, 9].

There are many analytical and numerical methods to find an approximate solution of a differential equation containing fractional derivatives. The homotopy perturbation method contains perturbation parameters, which have been extended to a wide range of physical applications and engineering fields by many researchers [10, 11]. He’s frequency formula is a simple and powerful method for a conservation non-linear oscillator, which has been widely applied to solve non-linear oscillator problems, especially the pull-in instability found in MEMS [12, 13]. It can be extended to the fractal oscillators and non-conservative oscillators [14–21]. The applications of these non-linear oscillations do not have non-linear even functions. El-Dib proposed a modification of He’s method for the case of even non-linearity [22]. The Hamiltonian-based frequency formula is a modification of He’s frequency formula [23]. The most important property of a non-linear system is the relationship between frequency and amplitude, so how to quickly estimate the frequency–amplitude relationship is an urgent problem to study. Many researchers devoted their efforts to studying fractional calculus which provides a powerful tool to characterize the periodic behavior of a non-linear oscillator [24]. He gave a tutorial review on fractal space and fractional calculus [25], Tian et al. established a fractal model for N/MEMS [26], and Li et al. studied the non-linear vibration of nanoparticles in the electrospinning process [27].

There are many analytical solutions for fractal oscillators, but the continuous solution has not been discussed so far. Existing frequency formulas cannot be formulated to correspond to the frequency of the continuous process [28]. Recently, El-Dib proposed an efficient frequency formula, which can be used to obtain successive approximate solutions for the non-linear oscillation [22]. In this paper, we illustrate the frequency formula and extend it in the differential equation with the fractional derivative. The new method will be applied to rapidly predict the frequency characteristics and determine successive approximate solutions of a fractal vibration system.

2 Two-scale fractal theory

As the fractal theory is helpful in establishing a governing equation in a fractal space, it has become a significant topic in both mathematics and mechanical engineering. The two-scale fractal derivative [29] is defined as follows:

$\frac{\mathit{d}\mathit{z}}{\mathit{d}{\mathit{t}}^{\mathit{\phi }}}\left({\mathit{t}}_{\mathbf{0}}\right)=\mathbf{\Gamma }\left(\mathbf{1}+\mathit{\phi }\right)\underset{\begin{array}{c}\mathit{t}-{\mathit{t}}_{\mathbf{0}}\to ∆\mathit{t}\\ ∆\mathit{t}\ne \mathbf{0}\end{array}}{\mathbf{lim}}\frac{\mathit{z}\left(\mathit{t}\right)-\mathit{z}\left({\mathit{t}}_{\mathbf{0}}\right)}{{\left(\mathit{t}-{\mathit{t}}_{\mathbf{0}}\right)}^{\mathit{\phi }}}(1)$

where $\mathit{\phi }\in R$.

When we observe a motion at a large scale, it may be a continuous change, while at a small scale, it may become discontinuous. Therefore, the two-scale fractal theory is a powerful mathematical tool to study the world with greater precision [30].

When $\phi =1$ and $∆t\to 0$, we can easily have $\frac{dz}{d{t}^1}=\mathrm{\Gamma }\left(2\right)\underset{\begin{array}{c}t-t_0\to ∆t\\ ∆t\ne 0\end{array}}{\lim }\frac{z\left(t\right)-z\left(t_0\right)}{t-t_0}=z^{\prime }$. Similarly, when $\phi =2$, $\frac{dz}{d{t}^2}=\mathrm{\Gamma }\left(3\right)\underset{\begin{array}{c}t-t_0\to ∆t\\ ∆t\ne 0\end{array}}{\lim }\frac{z\left(t\right)-z\left(t_0\right)}{{\left(t-t_0\right)}^2}=z^{″}$.

It is worth mentioning that the two-scale fractal derivative agrees with the traditional differential derivative when the fractal dimension $\phi$ is a positive integer.

To better understand the fractional derivative, let us take the function $\mathrm{z}=t^{\mu }$ as an example. Using Eq. 1, we can obtain [31]

$\frac{\mathit{d}}{\mathit{d}{\mathit{t}}^{\mathit{\phi }}}{\mathit{t}}^{\mathit{\mu }}=\frac{\mathbf{\Gamma }\left(\mathbf{1}+\mathit{\mu }\right)\mathbf{\Gamma }\left(\mathbf{1}+\mathit{\phi }-\mathit{N}\right)}{\mathbf{\Gamma }\left(\mathbf{1}+\mathit{\mu }-\mathit{N}\right)}{\mathit{t}}^{\mathit{\mu }-\mathit{\phi }}(2)$

where N is a natural number, $N\le \phi .$

Knowing the fractional derivative of the power function, the derivatives of all elementary functions will also be calculated, with the help of Taylor’s series. For example, we have the following equation:

$\mathit{s}\mathit{i}\mathit{n}\mathit{t}={\displaystyle \sum }_{\mathit{k}=\mathbf{0}}^{\mathbf{\infty }}\frac{{\left(-\mathbf{1}\right)}^{\mathit{k}}}{\left(\mathbf{2}\mathit{k}+\mathbf{1}\right)!}{\mathit{t}}^{\mathbf{2}\mathit{k}+\mathbf{1}}.(3)$

By using Eqs 2, 3, we can obtain

$\frac{\mathit{d}}{\mathit{d}{\mathit{t}}^{\mathit{\phi }}}\mathit{s}\mathit{i}\mathit{n}\mathit{t}={\displaystyle \sum }_{\mathit{k}=\mathbf{0}}^{\mathbf{\infty }}\frac{{\left(-\mathbf{1}\right)}^{\mathit{k}}}{\left(\mathbf{2}\mathit{k}+\mathbf{1}\right)!}\frac{\mathbf{\Gamma }\left(\mathbf{2}+\mathbf{2}\mathit{k}\right)\mathbf{\Gamma }\left(\mathbf{1}+\mathit{\phi }-\mathit{N}\right)}{\mathbf{\Gamma }\left(\mathbf{2}+\mathbf{2}\mathit{k}-\mathit{N}\right)}{\mathit{t}}^{\mathbf{2}\mathit{k}+\mathbf{1}-\mathit{\phi }}(4)$

After simple calculations, it yields the following result:

$\frac{\mathit{d}}{\mathit{d}{\mathit{t}}^{\mathbf{1}}}\mathit{s}\mathit{i}\mathit{n}\mathit{t}={\displaystyle \sum }_{\mathit{k}=\mathbf{0}}^{\mathbf{\infty }}\frac{{\left(-\mathbf{1}\right)}^{\mathit{k}}}{\left(\mathbf{2}\mathit{k}+\mathbf{1}\right)!}\frac{\mathbf{\Gamma }\left(\mathbf{2}+\mathbf{2}\mathit{k}\right)\mathbf{\Gamma }\left(\mathbf{1}+\mathbf{1}-\mathbf{1}\right)}{\mathbf{\Gamma }\left(\mathbf{2}+\mathbf{2}\mathit{k}-\mathbf{1}\right)}{\mathit{t}}^{\mathbf{2}\mathit{k}+\mathbf{1}-\mathbf{1}}=\mathit{c}\mathit{o}\mathit{s}\mathit{t}(5)$

and

$\frac{\mathit{d}}{\mathit{d}{\mathit{t}}^{\mathbf{1.5}}}\mathit{s}\mathit{i}\mathit{n}\mathit{t}={\displaystyle \sum }_{\mathit{k}=\mathbf{0}}^{\mathbf{\infty }}\frac{{\left(-\mathbf{1}\right)}^{\mathit{k}}}{\left(\mathbf{2}\mathit{k}+\mathbf{1}\right)!}\frac{\mathbf{\Gamma }\left(\mathbf{2}+\mathbf{2}\mathit{k}\right)\mathbf{\Gamma }\left(\mathbf{1}+\mathbf{1.5}-\mathbf{1}\right)}{\mathbf{\Gamma }\left(\mathbf{2}+\mathbf{2}\mathit{k}-\mathbf{1}\right)}{\mathit{t}}^{\mathbf{2}\mathit{k}+\mathbf{1}-\mathbf{1.5}}=\frac{\sqrt{\mathit{\pi }}}{\mathbf{2}}{\mathit{t}}^{-\mathbf{0.5}}\mathit{c}\mathit{o}\mathit{s}\mathit{t}(6)$

Also, we can obtain another form of the fractional derivative. It is obvious that the fractal derivative is useful and convenient to study.

3 Successive approximate solutions for fractal non-linear oscillation

We consider a general fractal non-linear oscillator in a fractal space as follows:

$\frac{\mathit{d}}{\mathit{d}{\mathit{t}}^{\mathit{\phi }}}\left(\frac{\mathit{d}\mathit{z}}{\mathit{d}{\mathit{t}}^{\mathit{\phi }}}\right)+\mathit{h}\left(\mathit{z}\right)=\mathbf{0},\mathit{z}\left(\mathbf{0}\right)=\mathit{A},\frac{\mathit{d}\mathit{z}\left(\mathbf{0}\right)}{\mathit{d}{\mathit{t}}^{\mathit{\phi }}}=\mathbf{0}(7)$

where $h\left(z\right)$ is an odd potential function or an odd polynomial as $h\left(z\right)=a_{1}z+a_3{z}^3+\dots +a_{2n+1}{z}^{2n+1}$.

Let $\tau =t^{\phi }$, Eq. 7 can be converted into its differential partner as

${\mathit{z}}^{″}+\mathit{h}\left(\mathit{z}\right)=\mathbf{0},\mathit{z}\left(\mathbf{0}\right)=\mathit{A},{\mathit{z}}^{\prime }\left(\mathbf{0}\right)=\mathbf{0},(8)$

where the derivative of the function $z$ with respect to $\tau$ is defined. Here, $\phi$ is the scale dimension, and t and $\tau$ describe the small and large scales, respectively.

He rewrote Eq. 8 in the following form [12]:

${\mathit{z}}^{″}+\frac{\mathit{h}\left(\mathit{z}\right)}{\mathit{z}}\mathbf{z}=\mathbf{0}(9)$

where the ratio h(z)/z is the equivalent stiffness.

When Eq. 8 is approximated by a linear oscillator:

${\mathit{z}}^{″}+{\mathit{\omega }}^{\mathbf{2}}\mathit{z}=\mathbf{0}(10)$

He has established a simple formula [12].

${{\mathit{\omega }}_{\mathit{H}\mathit{e}}}^{\mathbf{2}}={\left.\frac{\mathit{d}\mathit{h}\left(\mathit{z}\right)}{\mathit{d}\mathit{z}}\right|}_{\mathit{z}=\frac{\mathit{A}}{\mathbf{2}}}(11)$

Following the analysis principle of He’s frequency formula, He and Liu proposed a modified frequency formulation for a fractal vibration in the porous medium [32].

${{\mathit{\omega }}_{\mathit{H}\mathit{L}}}^{\mathbf{2}}=\frac{{\int }_{\mathbf{0}}^{\mathit{A}}{\mathit{z}}^{\mathbf{4}}\mathit{h}\left(\mathit{z}\right)\mathit{d}\mathit{z}}{{\int }_{\mathbf{0}}^{\mathit{A}}{\mathit{z}}^{\mathbf{5}}\mathit{d}\mathit{z}}(12)$

El-Dib established an extended frequency–amplitude formula, which is the best and most efficient formula and can be used to obtain successive approximate solutions for the non-linear oscillations [26]. We extend this method to the fractal system and obtain high-precision approximate frequency.

In the same way as in Eqs 8, 9 can be rewritten as follows:

${\mathit{z}}^{″}+\frac{\mathit{h}\left(\mathit{z}\right)\mathit{z}}{{\mathit{z}}^{\mathbf{2}}}\mathit{z}=\mathbf{0}(13)$

Integrating the numerator and the denominator of the stiffness term, the frequency ${\omega }^2$ with the trial solution $\mathrm{z}=\mathit{z}\left(\mathit{\tau }\right)$ that corresponds to the initial conditions is obtained in the following form:

${\left.{\mathit{\omega }}^{\mathbf{2}}\right|}_{\mathit{z}=\mathit{z}\left(\mathit{\tau }\right)}=\frac{{\int }_{\mathbf{0}}^{\mathit{T}}\mathit{h}\left(\mathit{z}\right)\mathit{z}\mathit{d}\mathit{\tau }}{{\int }_{\mathbf{0}}^{\mathit{T}}{\mathit{z}}^{\mathbf{2}}\mathit{d}\mathit{\tau }}(14)$

where T is the period, $T=\frac{2\pi }{\mathit{\omega }}$.

Let us explain this frequency formula from another angle.

By the comparison of Eqs 8, 10, the error function needs to take the minimum value.

$\mathit{E}\left({\mathit{\omega }}^{\mathbf{2}}\right)=\left|\mathit{h}\left(\mathit{z}\right)-{\mathit{\omega }}^{\mathbf{2}}\mathit{z}\right|(15)$

The mean square error is defined as

$\mathit{M}\mathit{S}\mathit{E}\left({\mathit{\omega }}^{\mathbf{2}}\right)={\int }_{\mathbf{0}}^{\mathit{T}}{\left(\mathit{h}\left(\mathit{z}\right)-{\mathit{\omega }}^{\mathbf{2}}\mathit{z}\right)}^{\mathbf{2}}\mathit{d}\mathit{\tau },={\mathit{\omega }}^{\mathbf{4}}{\int }_{\mathbf{0}}^{\mathit{T}}{\mathit{z}}^{\mathbf{2}}\mathit{d}\mathit{\tau }-{\mathit{\omega }}^{\mathbf{2}}\mathbf{2}{\int }_{\mathbf{0}}^{\mathit{T}}\mathit{h}\left(\mathit{z}\right)\mathit{z}\mathit{d}\mathit{\tau }+{\int }_{\mathbf{0}}^{\mathit{T}}{\mathit{h}}^{\mathbf{2}}\left(\mathit{z}\right)\mathit{d}\mathit{\tau }(16)$

The aforementioned problem is equivalent to the value of ${\omega }^2$, and the function $MSE\left({\omega }^2\right)$ takes the minimum value. After a simple calculation, the minimum point is

$\frac{\mathit{d}\mathit{M}\mathit{S}\mathit{E}\left({\mathit{\omega }}^{\mathbf{2}}\right)}{\mathit{d}{\mathit{\omega }}^{\mathbf{2}}}={\mathit{\omega }}^{\mathbf{2}}\mathbf{2}{\int }_{\mathbf{0}}^{\mathit{T}}{\mathit{z}}^{\mathbf{2}}\mathit{d}\mathit{\tau }-\mathbf{2}{\int }_{\mathbf{0}}^{\mathit{T}}\mathit{h}\left(\mathit{z}\right)\mathit{z}\mathit{d}\mathit{\tau }=\mathbf{0}(17)$

The solution of Eq. 17 is Eq. 14. The aforementioned analysis process verifies the accuracy of the frequency formula. With a suitable chosen trial solution, performing the aforementioned integrals gives the corresponding frequency.

For the non-linear oscillator, $h\left(z\right)=a_{1}z+a_3{z}^3$, we obtain

${{\mathit{\omega }}_{\mathit{H}\mathit{e}}}^{\mathbf{2}}={{\mathit{\omega }}_{\mathit{H}\mathit{L}}}^{\mathbf{2}}={\left.{\mathit{\omega }}^{\mathbf{2}}\right|}_{\mathit{z}=\mathit{Acos}\mathit{\omega }\mathit{\tau }}={\mathit{a}}_{\mathbf{1}}+\frac{\mathbf{3}}{\mathbf{4}}{\mathit{A}}^{\mathbf{2}}{\mathit{a}}_{\mathbf{3}}(18)$

The precision of Eq. 18 can be found by comparing it with the exact frequency [22].

${\mathit{\omega }}_{\mathit{e}\mathit{x}\mathit{c}}=\frac{\mathit{\pi }}{\mathbf{2}{\int }_{\mathbf{0}}^{\mathit{\pi }/\mathbf{2}}\frac{\mathit{d}\mathit{\theta }}{\sqrt{{\mathit{a}}_{\mathbf{1}}+\frac{\mathbf{1}}{\mathbf{2}}{\mathit{A}}^{\mathbf{2}}{\mathit{a}}_{\mathbf{3}}\left(\mathbf{1}+{\mathit{sin}}^{\mathbf{2}}\mathit{\theta }\right)}}}(19)$

4 Application and numerical illustration

In order to illustrate the solution process of the aforementioned method, we consider the following oscillator:

$\frac{\mathit{d}}{\mathit{d}{\mathit{t}}^{\mathit{\phi }}}\left(\frac{\mathit{d}\mathit{z}}{\mathit{d}{\mathit{t}}^{\mathit{\phi }}}\right)+{\mathit{z}}^{\frac{\mathbf{1}}{\mathbf{3}}}=\mathbf{0},\mathit{z}\left(\mathbf{0}\right)=\mathit{A},\frac{\mathit{d}\mathit{z}\left(\mathbf{0}\right)}{\mathit{d}{\mathit{t}}^{\mathit{\phi }}}=\mathbf{0}(20)$

We consider that the general mth-order trial solution which satisfies the initial conditions can be expressed by

${\mathit{z}}_{\mathit{m}}\left(\mathit{\tau }\right)={\displaystyle \sum }_{\mathit{n}=\mathbf{1}}^{\mathit{m}}{\mathit{c}}_{\mathit{n}}\mathbf{cos}\left(\left(\mathbf{2}\mathit{n}-\mathbf{1}\right){\mathit{\omega }}_{\mathit{m}}\mathit{\tau }\right),(21)$

where $\tau =t^{\phi }$ and ${\displaystyle \sum }_{n=1}^m{c}_n=A$.

Using the first-order trial solution, $z_1=\mathit{Acos}{\omega }_1\tau$, and employing Eq. 14, the corresponding frequency is

${\mathit{\omega }}_{\mathbf{1}}=\sqrt{\frac{{\int }_{\mathbf{0}}^{\mathit{T}}{\left({\mathit{z}}_{\mathbf{1}}\right)}^{\frac{\mathbf{4}}{\mathbf{3}}}\mathit{d}\mathit{\tau }}{{\int }_{\mathbf{0}}^{\mathit{T}}{\left({\mathit{z}}_{\mathbf{1}}\right)}^{\mathbf{2}}\mathit{d}\mathit{\tau }}}=\frac{\mathbf{1.076845}}{{\mathit{A}}^{\frac{\mathbf{1}}{\mathbf{3}}}},\mathit{T}=\frac{\mathbf{2}\mathit{\pi }}{{\mathit{\omega }}_{\mathbf{1}}}(22)$

For a comparison between He–Liu’s modification and the present modification, we obtain

${\mathit{\omega }}_{\mathit{H}\mathit{L}}=\sqrt{\frac{{\int }_{\mathbf{0}}^{\mathit{A}}{\mathit{z}}^{\mathbf{4}}\mathit{h}\left(\mathit{z}\right)\mathit{d}\mathit{z}}{{\int }_{\mathbf{0}}^{\mathit{A}}{\mathit{z}}^{\mathbf{5}}\mathit{d}\mathit{z}}}=\frac{\mathbf{1.06066}}{{\mathit{A}}^{\frac{\mathbf{1}}{\mathbf{3}}}}(23)$

The exact frequency of Eq. 20 is ${\omega }_{\mathrm{e}\mathrm{x}\mathrm{c}}$.

${\mathit{\omega }}_{\mathbf{e}\mathbf{x}\mathbf{c}}=\frac{\mathbf{2}\mathit{\pi }}{\mathbf{2}\sqrt{\mathbf{2}}{\int }_{\mathbf{0}}^{\mathit{A}}\frac{\mathbf{d}\mathbf{z}}{\sqrt{{\int }_{\mathit{z}}^{\mathit{A}}{\mathit{s}}^{\frac{\mathbf{1}}{\mathbf{3}}}\mathit{d}\mathit{s}}}}=\frac{\mathbf{1.070451}}{{\mathit{A}}^{\frac{\mathbf{1}}{\mathbf{3}}}}(24)$

So, the relative error in the first-order approximate frequency is given by

$\left|\frac{{\mathit{\omega }}_{\mathbf{e}\mathbf{x}\mathbf{c}}-{\mathbf{\omega }}_{\mathbf{1}}}{{\mathit{\omega }}_{\mathbf{e}\mathbf{x}\mathbf{c}}}\right|\times \mathbf{100}\%=\mathbf{0.5973}\%(25)$

Also, the error in He–Liu’s modification is

$\left|\frac{{\mathit{\omega }}_{\mathbf{e}\mathbf{x}\mathbf{c}}-{\mathbf{\omega }}_{\mathit{H}\mathit{L}}}{{\mathit{\omega }}_{\mathbf{e}\mathbf{x}\mathbf{c}}}\right|\times \mathbf{100}\%=\mathbf{0.9147}\%(26)$

It is noticed that the present method has better precision.

The first-order approximate solution of Eq. 20 is

${\mathit{z}}_{\mathbf{1}}=\mathit{Acos}\left(\frac{\mathbf{1.076845}}{{\mathit{A}}^{\frac{\mathbf{1}}{\mathbf{3}}}}\mathit{\tau }\right),(27)$

that is,

${\mathit{z}}_{\mathbf{1}}=\mathit{Acos}\left(\frac{\mathbf{1.076845}}{{\mathit{A}}^{\frac{\mathbf{1}}{\mathbf{3}}}}{\mathit{t}}^{\mathit{\phi }}\right)(28)$

We consider that the second-order trial solution meeting the initial conditions can be expressed as

${\mathit{z}}_{\mathbf{2}}={\mathit{c}}_{\mathbf{1}}\mathbf{cos}\left({\mathit{\omega }}_{\mathbf{2}}\mathit{\tau }\right)+\left({\mathit{A}-\mathit{c}}_{\mathbf{1}}\right)\mathbf{cos}\left(\mathbf{3}{\mathit{\omega }}_{\mathbf{2}}\mathit{\tau }\right)(29)$

Using a trigonometric formula $\cos \left(3{\omega }_2\tau \right)=4{\mathit{cos}}^3\left({\omega }_2\tau \right)-3\cos \left({\omega }_2\tau \right)$, we have the following equation:

${\mathit{z}}_{\mathbf{2}}=\left(\mathbf{4}{\mathit{c}}_{\mathbf{1}}-\mathbf{3}\mathit{A}\right)\mathbf{cos}\left({\mathit{\omega }}_{\mathbf{2}}\mathit{\tau }\right)+\left({\mathbf{4}\mathit{A}-\mathbf{4}\mathit{c}}_{\mathbf{1}}\right){\mathbf{cos}}^{\mathbf{3}}\left({\mathit{\omega }}_{\mathbf{2}}\mathit{\tau }\right)(30)$

The least-square of the displacement is estimated as follows:

${\int }_{\mathbf{0}}^{\mathit{T}}{\left[\left(\mathbf{4}{\mathit{c}}_{\mathbf{1}}-\mathbf{3}\mathit{A}\right)\mathbf{cos}\left({\mathit{\omega }}_{\mathbf{2}}\mathit{\tau }\right)\right]}^{\mathbf{2}}\mathit{d}\mathit{\tau }={\int }_{\mathbf{0}}^{\mathit{T}}{\left[\left({\mathbf{4}\mathit{A}-\mathbf{4}\mathit{c}}_{\mathbf{1}}\right){\mathbf{cos}}^{\mathbf{3}}\left({\mathit{\omega }}_{\mathbf{2}}\mathit{\tau }\right)\right]}^{\mathbf{2}}\mathit{d}\mathit{\tau },\mathit{T}=\frac{\mathbf{2}\mathit{\pi }}{{\mathit{\omega }}_{\mathbf{2}}}(31)$

The solution of Eq. 31 is $c_1=086038A$, and substituting the value into Eq. 29, we obtain

${\mathit{z}}_{\mathbf{2}}=\mathbf{086038}\mathit{A}\mathbf{cos}\left({\mathit{\omega }}_{\mathbf{2}}\mathit{\tau }\right)+\mathbf{0.13962}\mathit{A}\mathbf{cos}\left(\mathbf{3}{\mathit{\omega }}_{\mathbf{2}}\mathit{\tau }\right)(32)$

Using Eq. 32 and the second-order trial solution, Eq. 14 becomes

${\mathit{\omega }}_{\mathbf{2}}=\sqrt{\frac{{\int }_{\mathbf{0}}^{\mathit{T}}{\left({\mathit{z}}_{\mathbf{2}}\right)}^{\frac{\mathbf{4}}{\mathbf{3}}}\mathit{d}\mathit{\tau }}{{\int }_{\mathbf{0}}^{\mathit{T}}{\left({\mathit{z}}_{\mathbf{2}}\right)}^{\mathbf{2}}\mathit{d}\mathit{\tau }}},\mathit{T}=\frac{\mathbf{2}\mathit{\pi }}{{\mathit{\omega }}_{\mathbf{2}}}(33)$

After integral calculation, the second-order approximate frequency is given by

${\mathit{\omega }}_{\mathbf{2}}=\frac{\mathbf{1.074586}}{{\mathit{A}}^{\frac{\mathbf{1}}{\mathbf{3}}}}(34)$

The percentage relative error in second-order approximate frequency is 0.3863%. Also, the second-order approximate solution of Eq. 20 is

${\mathit{z}}_{\mathbf{2}}=\mathbf{086038}\mathit{A}\mathbf{cos}\left(\frac{\mathbf{1.074586}}{{\mathit{A}}^{\frac{\mathbf{1}}{\mathbf{3}}}}\mathit{\tau }\right)+\mathbf{0.13962}\mathit{A}\mathbf{cos}\left(\frac{\mathbf{3.223758}}{{\mathit{A}}^{\frac{\mathbf{1}}{\mathbf{3}}}}\mathit{\tau }\right)(35)$

This leads to

${\mathit{z}}_{\mathbf{2}}=\mathbf{086038}\mathit{A}\mathbf{cos}\left(\frac{\mathbf{1.074586}}{{\mathit{A}}^{\frac{\mathbf{1}}{\mathbf{3}}}}{\mathit{t}}^{\mathit{\phi }}\right)+\mathbf{0.13962}\mathit{A}\mathbf{cos}\left(\frac{\mathbf{3.223758}}{{\mathit{A}}^{\frac{\mathbf{1}}{\mathbf{3}}}}{\mathit{t}}^{\mathit{\phi }}\right)(36)$

In order to obtain the sequential extended approximate solution and improve the accuracy of the solution, we can use a higher-order trial solution, but the solving process becomes more complex.

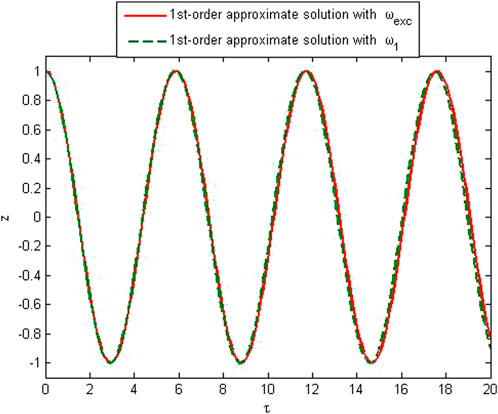
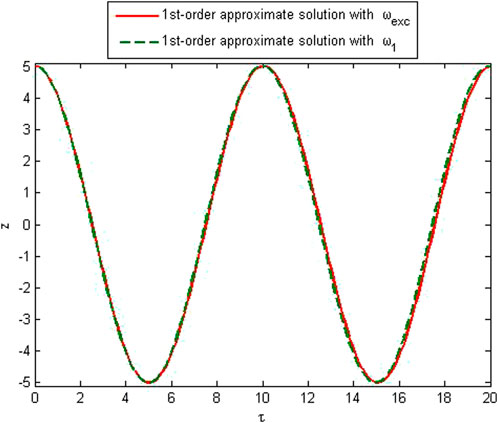
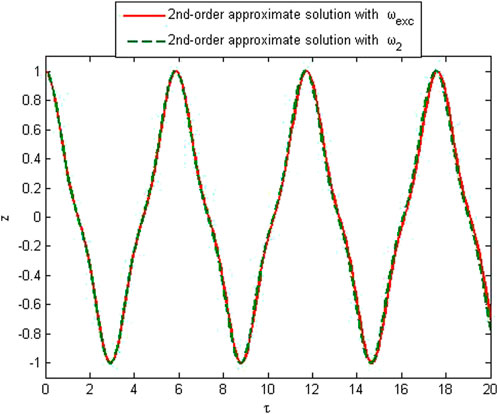
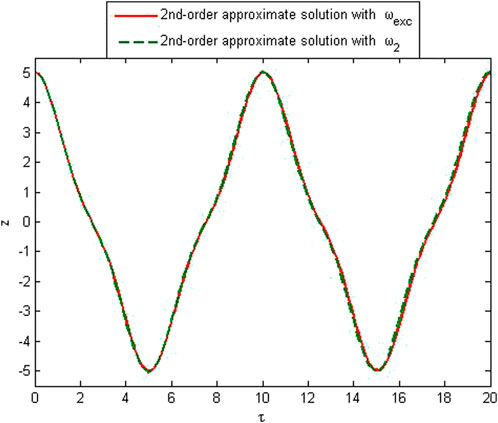
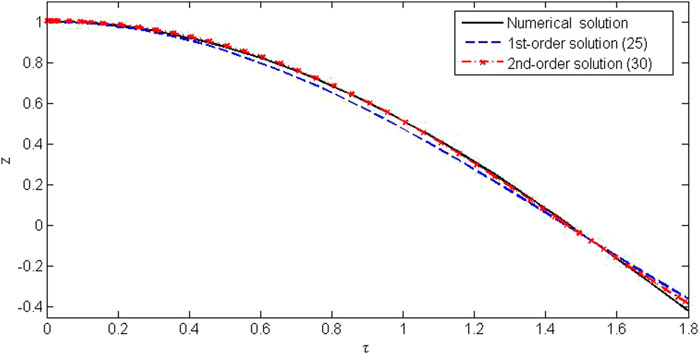
To verify the accuracy of the method, the approximate solution is compared with the exact solution of Eq. 20 in Figures 1–5. The comparison of the approximate frequency with the exact one is made, and relative errors have been found. It is noted that the relative error does not depend upon the amplitude; that is, the error is the same for any value of the amplitude, while it decreases with the increase in the order of approximation. Figures 1, 2 show first-order approximate solutions with different values of the amplitudes. Figures 3, 4 show second-order approximate solutions. A good agreement for various amplitudes of first- and second-order approximate frequencies can be seen from these figures. Figure 5 shows the comparison of the numerical solution obtained by the Matlab solver “ode45” with approximate solutions over a small interval.

FIGURE 1

FIGURE 1. Illustration of the first-order approximate solution with $A=1$.

FIGURE 2

FIGURE 2. Illustration of the first-order approximate solution with $A=5$.

FIGURE 3

FIGURE 3. Illustration of the second-order approximate solution with $A=1$.

FIGURE 4

FIGURE 4. Illustration of the second-order approximate solution with $A=5$.

FIGURE 5

FIGURE 5. Comparison of the numerical solution with first- and second-order solutions for $A=1$

Different values of the fractal exponent $\phi$ are considered for Eq. 28 and shown together in Figure 6. It is observed that the vibration attenuation occurs more, and the oscillation frequency becomes faster for increasing the values of the fractal exponent $\phi$.

FIGURE 6

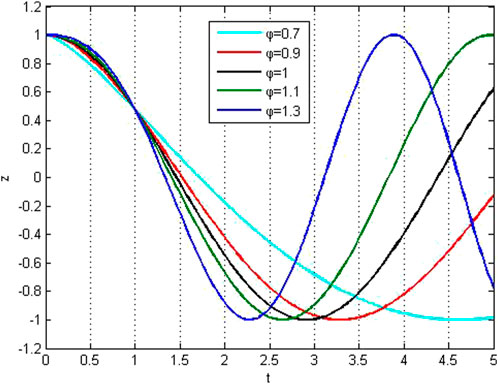
FIGURE 6. Graphing solution (28) for sequences of the parameter φ with $A=1$.

5 Conclusion

In this paper, a high-precision frequency is obtained by a trial solution for the first time ever, and a frequency formula determined by the trial solution is proposed for solving a fractal nonlinear vibration system. The new method is described theoretically, and an example is given to explain in detail the process of finding the higher-order approximate solution and the approximate frequency. The analysis results show that this new method can be used to obtain the frequency with high accuracy and to quickly calculate the high-order continuous solution of the fractal non-linear oscillator. The influence of the fractal derivative order on the periodic motion is visually displayed graphically. It is revealed that the fractal exponent affects the frequency characteristics greatly as that discussed in Refs. [33, 34]. Although we only discuss the oscillator with the non-zero initial condition, it is still valid for the oscillator with zero initial condition as that in micro-electromechanical systems [35], which will be discussed in the next paper.

Data availability statement

The original contributions presented in the study are included in the article/Supplementary Material; further inquiries can be directed to the corresponding author.

Author contributions

All authors listed have made a substantial, direct, and intellectual contribution to the work and approved it for publication.

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

1. Xiao BQ, Huang QW, Yu BM, Long GB, Chen HX. A fractal model for predicting oxygen effective diffusivity of porous media with rough surfaces under dry and wet conditions. Fractals (2021) 29(3):2150076. doi:10.1142/s0218348x21500766

CrossRef Full Text | Google Scholar

2. He JH, Qian MY. A fractal approach to the diffusion process of red ink in a saline water. Therm Sci (2022) 26(3B):2447–51. doi:10.2298/tsci2203447h

CrossRef Full Text | Google Scholar

3. Zuo YT. Effect of sic particles on viscosity of 3-D print paste a fractal rheological model and experimental verification. Therm Sci (2021) 25(3):2405–9. doi:10.2298/tsci200710131z

CrossRef Full Text | Google Scholar

4. Ma HJ. Fractal variational principle for an optimal control problem. J Low Frequency Noise, Vibration Active Control (2022) 41:1523–31. doi:10.1177/14613484221104647

CrossRef Full Text | Google Scholar

5. Wang KL. Exact solitary wave solution for fractal shallow water wave model by He’s variational method. Mod Phys Lett B (2022) 36(7):2150602. doi:10.1142/s0217984921506028

CrossRef Full Text | Google Scholar

6. Wang KL. New variational theory for coupled nonlinear fractal Schrodinger system. Int J Numer Methods Heat Fluid Flow (2022) 32(2):589–97. doi:10.1108/hff-02-2021-0136

CrossRef Full Text | Google Scholar

7. Shen Y, El-Dib YO. A periodic solution of the fractional sine-Gordon equation arising in architectural engineering. J Low Frequency Noise, Vibration Active Control (2021) 40(2):683–91. doi:10.1177/1461348420917565

CrossRef Full Text | Google Scholar

8. He JH, Kou SJ, He CH, Zhang ZW, Gepreel KA. Fractal oscillation and its frequency-amplitude property. Fractals (2021) 29(4):2150105. doi:10.1142/s0218348x2150105x

CrossRef Full Text | Google Scholar

9. Elías-Zúñiga A, Martínez-Romero O, Trejo DO, Palacios-Pineda LM. Exact steady-state solution of fractals damped and forced systems. Results Phys (2021) 28:104580. doi:10.1016/j.rinp.2021.104580

CrossRef Full Text | Google Scholar

10. He CH, El-Dib YO. A heuristic review on the homotopy perturbation method for non-conservative oscillators. J Low Frequency Noise, Vibration Active Control (2022) 41(2):572–603. doi:10.1177/14613484211059264

CrossRef Full Text | Google Scholar

11. He JH, Jiao ML, He CH. Homotopy perturbation method for fractal Duffing oscillator with arbitrary conditions. Fractals (2022) 30(9). doi:10.1142/S0218348X22501651

CrossRef Full Text | Google Scholar

12. He JH. The simplest approach to nonlinear oscillators. Results Phys (2019) 15:102546. doi:10.1016/j.rinp.2019.102546

CrossRef Full Text | Google Scholar

13. He JH, Na Q, He CH, Khaled G. Fast identification of the pull-in voltage of a nano/micro-electromechanical system. J Low Frequency Noise, Vibration Active Control (2022) 41:566–71. doi:10.1177/14613484211068252

CrossRef Full Text | Google Scholar

14. Feng GQ. He’s frequency formula to fractal undamped Duffing equation. J Low Frequency Noise Vibration Active Control (2021) 40:1671–6. doi:10.1177/1461348421992608

CrossRef Full Text | Google Scholar

15. Elias-Zuniga A, Palacios-Pineda LM, Jimenez-Cedeno IH, Martinez-Romero O, Olvera-Trejo D. Analytical solution of the fractal cubic–quintic duffing equation. Fractals (2021) 29(4):2150080. doi:10.1142/s0218348x21500808

CrossRef Full Text | Google Scholar

16. Elias-Zuniga A, Palacios-Pineda LM, Jiménez-Cedeño IH, Martinez-Romero O, Olvera-Trejo D. A fractal model for current generation in porous electrodes. J Electroanalytical Chem (2021) 880:114883. doi:10.1016/j.jelechem.2020.114883

CrossRef Full Text | Google Scholar

17. Qie N, Hou WF, He JH. The fastest insight into the large amplitude vibration of a string. Rep Mechan Eng (2020) 2:1–5. doi:10.31181/rme200102001q

CrossRef Full Text | Google Scholar

18. El-Dib YO. The frequency estimation for non-conservative nonlinear oscillation. Zamm-z Angew Math Mech (2021) 101:101. doi:10.1002/zamm.202100187

CrossRef Full Text | Google Scholar

19. El-Dib YO. The damping Helmholtz–Rayleigh–Duffing oscillator with the non-perturbative approach. Mathematics Comput Simulation (2022) 194:552–62. doi:10.1016/j.matcom.2021.12.014

CrossRef Full Text | Google Scholar

20. El-Dib YO. The simplest approach to solving the cubic nonlinear jerk oscillator with the non-perturbative method. Math Meth Appl Sci (2022) 45:5165–83. doi:10.1002/mma.8099

CrossRef Full Text | Google Scholar

21. Elías-Zúñiga A, Palacios-Pineda LM, Jiménez-Cedeño IH, Martínez-Romero O, Trejo DO. He’s frequency–amplitude formulation for nonlinear oscillators using Jacobi elliptic functions. J Low Frequency Noise, Vibration Active Control (2020) 39(4):1216–23. doi:10.1177/1461348420972820

CrossRef Full Text | Google Scholar

22. El-Dib YO. Insightful and comprehensive formularization of frequency-amplitude formula for strong or singular nonlinear oscillators. J Low Frequency Noise, Vibration Active Control (2022) 42:89–109. doi:10.1177/14613484221118177

CrossRef Full Text | Google Scholar

23. He JH. Hamiltonian approach to nonlinear oscillators. Phys Lett A (2010) 374:2312–4. doi:10.1016/j.physleta.2010.03.064

CrossRef Full Text | Google Scholar

24. Ain QT, He JH. On two-scale dimension and its applications. Therm Sci (2019) 23:1707–12. doi:10.2298/tsci190408138a

CrossRef Full Text | Google Scholar

25. He JH. Fractal calculus and its geometrical explanation. Results Phys (2018) 10:272–6. doi:10.1016/j.rinp.2018.06.011

CrossRef Full Text | Google Scholar

26. Tian D, Ain QT, Anjum N, He CH, Cheng B. Fractal N/MEMS: From pull-in instability to pull-in stability. Fractals (2021) 29(2):2150030. doi:10.1142/s0218348x21500304

CrossRef Full Text | Google Scholar

27. He JH. The simpler, the better: Analytical methods for nonlinear oscillators and fractional oscillators. J Low Frequency Noise Vibration Active Control (2019) 38:1252–60. doi:10.1177/1461348419844145

CrossRef Full Text | Google Scholar

28. Elías-Zúñiga A, Martínez-Romero O, Palacios-Pineda LM, Olvera-Trejo D. New analytical solution of the fractal anharmonic oscillator using an ancient Chinese algorithm: Investigating how plasma frequency changes with fractal parameter values. J Low Frequency Noise, Vibration Active Control (2022) 41(3):833–41. doi:10.1177/14613484211070883

CrossRef Full Text | Google Scholar

29. Elias-Zuniga A. On the two-scale dimension and its application for deriving a new analytical solution for the fractal Duffing’s equation. Fractals (2022) 30(3):2250061. doi:10.1142/S0218348X2250061X

CrossRef Full Text | Google Scholar

30. Elias-Zuniga A, Palacios-Pineda LM, Olvera-Trejo D, Martinez-Romero O. Recent strategy to study fractal-order viscoelastic polymer materials using an ancient Chinese algorithm and He's formulation. J Low Frequency Noise Vibration Active Control (2022) 41(3):842–51. doi:10.1177/14613484221085413

CrossRef Full Text | Google Scholar

31. He JH, El-Dib YO. A tutorial introduction to the two-scale fractal calculus and its application to the fractal Zhiber-Shabat oscillator. Fractals (2021) 29(8):2150268. doi:10.1142/s0218348x21502686

CrossRef Full Text | Google Scholar

32. He CH, Liu C. A modified frequency-amplitude formulation for fractal vibration systems. Fractals (2022) 30(3):2250046. doi:10.1142/S0218348X22500463

CrossRef Full Text | Google Scholar

33. He JH, Moatimid GM, Zekry MH. Forced nonlinear oscillator in a fractal space. Facta Univ Series: Mech Eng (2022) 20(1):1–20.

CrossRef Full Text | Google Scholar

34. Liu FJ, Zhang T, He CH, Tian D. Thermal oscillation arising in a heat shock of a porous hierarchy and its application. Facta Univ Series: Mech Eng (2022) 20(3):633–645.

CrossRef Full Text | Google Scholar

35. Anjum N, He JH, Ain QT, Tian D. Li-He’s modified homotopy perturbation method for doubly-clamped electrically actuated microbeams-based microelectromechanical system. Facta Univ Series: Mech Eng (2021) 19(4):601–612.

CrossRef Full Text | Google Scholar