A modern analytic method to solve singular and non-singular linear and non-linear differential equations

This article circumvents the Laplace transform to provide an analytical solution in a power series form for singular, non-singular, linear, and non-linear ordinary differential equations. It introduces a new analytical approach, the Laplace residual power series, which provides a powerful tool for obtaining accurate analytical and numerical solutions to these equations. It demonstrates the new approach’s effectiveness, accuracy, and applicability in several ordinary differential equations problem. The proposed technique shows the possibility of finding exact solutions when a pattern to the series solution obtained exists; otherwise, only rough estimates can be given. To ensure the accuracy of the generated results, we use three types of errors: actual, relative, and residual error. We compare our results with exact solutions to the problems discussed. We conclude that the current method is simple, easy, and effective in solving non-linear differential equations, considering that the obtained approximate series solutions are in closed form for the actual results. Finally, we would like to point out that both symbolic and numerical quantities are calculated using Mathematica software.

1 Introduction

A differential equation or a system of differential equations, along with proper boundary and initial conditions (ICs), is one of the most common outputs when mathematical modeling describes physical, biological, or chemical phenomena. Finding ordinary or partial differential equations and analyzing their solutions are at the heart of applied mathematics [1].

Since ancient times, differential equations have attracted the interest of researchers and scientists from two sides. The first is how to use them to express phenomena and issues that interest them in their specializations and research. On the other hand, there is the question of how to solve these equations. There are a limited number of differential equations, especially linear ones, whose solutions can be determined using the well-known traditional methods based on finite and simple algebraic operations. In contrast, there are many kinds of differential equations that still require the search for simple and accurate solutions. For this reason, the interest of mathematicians in previous decades was and is still in the investigation for analytical and sometimes numerical methods to solve these forms of differential equations.

Many analytical, numerical, and numero-analytical techniques have been proposed previously and recently to provide solutions for differential equations with initial or boundary conditions, such as the Laplace and Fourier transforms method [2], the Adomian decomposition method [3–5], the variational iteration method [6–8], the homotopy perturbation method [9–11], the homotopy analysis method [12, 13], the differential transformation method [14–16], the finite difference method [17], the predictor–corrector method [18, 19], the first integral method [20, 21], the Adams–Bashforth Molten method [22], the new iterative method [23, 24], the Crank–Nicolson method [25, 26], the reproducing kernel method [27, 28], the Laplace Adomian decomposition method [11, 29, 30], the He–Laplace method [31–33], and others [34–36].

Recently, Eriqat et al. [37] presented a new hybrid method in which they combined the Laplace transform (LT) method with the residual power series (PS) method to establish series solutions of the pantograph equation. This method is called the LRPS method, and it simulates the residual PS method but with a different construction and view. It uses the limit concept instead of the concept of the derivative as in the residual PS method. The LRPS method uses the LT to transfer the given differential equation to a new algebraic equation in a new space. The obtained algebraic equation is solved by assuming that it is a solution that has a Laurent series (LS) form. The values of the coefficients of the LS are determined by utilizing the limit at infinity. Then, the inverse LT is used to transfer the LS, which is the solution of the algebraic equation in the Laplace space, to the initial space. Thus, we have obtained the solution to the original problem in the form of PS.

Indeed, the LRPS method is similar to the He–Laplace method’s [31–33] idea of searching for the solution of differential equations in Laplace space. The He–Laplace technique uses the variational iteration method or homotopy perturbation method to solve the just-transformed Laplace space. In contrast, the LRPS method uses the PS method to solve that equation using the Laurent series instead of the Taylor series. In addition, the LRPS method is just an easy and fast technique for finding the PS solution coefficients of the differential equations.

The LRPS method has won the admiration and interest of many researchers due to its ease, speed, and efficiency in arriving at exact or accurate approximate solutions to many equations. In addition, the LT was employed in dealing with non-linear problems because it is known that the LT deals only with some categories of linear equations. In 2021, El-Ajou [38] adapted the LRPS method to establish solitary solutions of non-linear time-fractional dispersive partial differential equations and to introduce a vector series solution of some types of hyperbolic system of Caputo time-fractional partial differential equations with variable coefficients [39]. Recently, the LRPS method was used for solving time-fractional Navier–Stokes equations [40], fuzzy quadratic Riccati DEs [41], Lane–Emden equations of fractional order [42], a system of fractional initial value problems (IVPs) [43], autonomous n-dimensional fractional non-linear systems [44], and others [45–49].

Despite the extensive publication of research dealing with the new method, all works dealt with specific problems devoid of complexity and generality. Therefore, we aim in this manuscript, first, to employ the LRPS method to provide exact or accurate approximate analytic series solutions to linear ordinary differential equations (ODEs) in their general form, whether their coefficients are constants or analytical functions, which have the following formula:

$\frac{d^{n}y}{d{t}^n}=L_t\left[y\left(t\right)\right]+g\left(t\right),t\ge 0.$(1.1)

Subject to the ICs,

$y\left(0\right)=y_0,y^{\prime }\left(0\right)=y_1,\dots ,y^{\left(n-1\right)}\left(0\right)=y_{n-1},$(1.2)

where $L_t$ is a linear differential operator of order $\left(n-1\right)$ with coefficients being analytic functions. This general equation is difficult to solve by the direct PS method. Herein lays the importance and novelty of the aim of this research.

Since in our world, most events are essentially non-linear and modeled by non-linear equations, the study of non-linear issues is critical in mathematics and physics, engineering, economics, and other disciplines. Solving non-linear problems is difficult, and getting an analytical approximation of a given problem is often more complicated than getting a numerical one. Therefore, the second aim of this paper is to establish analytic approximate solutions to the general form of non-linear ODEs, which have the following form using the proposed method (LRPS method):

$\frac{d^{n}y}{{dt}^n}=f\left(t,y\left(t\right),\frac{dy}{dt},\frac{d^{2}y}{{dt}^2},\dots ,\frac{d^{n-1}y}{{dt}^{n-1}}\right),t\ge 0.$(1.3)

Subject to the ICs,

$y\left(0\right)=y_0,y^{\prime }\left(0\right)=y_1,\dots ,y^{\left(n-1\right)}\left(0\right)=y_{n-1},$(1.4)

where $f$ is an analytic function on $\left[0,\infty \right.)$.

The third objective of this article is to provide a series solution to the singular ODEs, whether linear or non-linear. This type of equation is of great interest to researchers in providing analytical solutions to it, as it appears in the models of many natural phenomena, as well as the difficulty of providing solutions to it.

To determine the efficiency and applicability of the method, we test for three types of errors: exact error, relative error, and residual error. We present the numerical results of the resulting solutions through prepared and organized tables. In addition, we sketch the obtained approximate solution by the proposed method along with the exact solution if we can obtain it to make the comparison on the one hand and to determine the period of convergence to solve the series on the other hand.

2 Basic facts of the LT and PS

In this section, we overview essential facts about the LT and the PS, along with some properties that are needed in this article.

Definition 2.1. [50]). We assume that $y\left(t\right)$ is a continuous function defined for $t\ge 0$ and let $s\in I\subseteq \mathbb{R}$. Then, the LT of $y\left(t\right)$ is the function $\mathrm{Y}\left(\mathrm{s}\right)$, denoted and defined as follows:

$Y\left(s\right)=\mathcal{L}\left[y\left(t\right)\right]\left(s\right)={\displaystyle \underset{0}{\overset{\infty }{\int }}}{e}^{-st}y\left(t\right)dt,$(2.1)

where the improper integral is the convergence on an interval of $s$, which represents the domain of $Y\left(s\right)$.Also, the inverse LT of a function $Y\left(s\right),s\in I$ is the function $y\left(t\right),t\ge 0$ that is denoted and defined as

$y\left(t\right)={\mathcal{L}}^{-1}\left[\mathrm{Y}\left(s\right)\right]\left(\mathrm{t}\right)={\displaystyle \underset{c-i\infty }{\overset{c+i\infty }{\int }}}{e}^{st}\mathrm{Y}\left(s\right)ds,c=\mathrm{R}\mathrm{e}\left(s\right)>c_0,$(2.2)

where $c_0$ lies in the right-half plane of the absolute convergence of the Laplace integral.

Lemma 2.1. [50]). Suppose that $y\left(t\right)$ and $x\left(t\right)$ are both continuous functions defined on $\left[0,\infty \right.)$, $Y\left(s\right)=\mathcal{L}\left[y\left(t\right)\right]$, $X\left(s\right)=\mathcal{L}\left[x\left(t\right)\right]$, and $\eta ,\lambda$ are constants. Then, we have the following properties:

1) $\mathcal{L}\left[e^{\lambda t}y\left(t\right)\right]=Y\left(s-\lambda \right)$

2) $\mathcal{L}\left[t^{n}y\left(t\right)\right]={\left(-1\right)}^n\frac{d^n}{d{s}^n}Y\left(s\right)$

3) $\mathcal{L}\left[y\left(\lambda t\right)\right]=\frac{1}{\lambda }Y\left(\frac{s}{\lambda }\right),\lambda >0$

4) ${\mathcal{L}}^{-1}\left[\eta Y\left(s\right)+\lambda X\left(s\right)\right]=\eta {\mathcal{L}}^{-1}\left[Y\left(s\right)\right]+\lambda {\mathcal{L}}^{-1}\left[X\left(s\right)\right]=\eta y\left(t\right)+\lambda x\left(t\right)$5) $\underset{s\to \infty }{\lim }sY\left(s\right)=y\left(0\right)$

6) $\mathcal{L}\left[y^{\left(n\right)}\left(t\right)\right]=s^n\mathcal{L}\left[y\right]-{\displaystyle \sum _{k=0}^{n-1}}{s}^{n-k-1}{y}^{\left(k\right)}\left(0\right)$

Definition 2.2. [51]). A series that has the representation

${\displaystyle \sum _{n=-\infty }^{\infty }}{c}_n{\left(s-s_0\right)}^n={\displaystyle \sum _{n=1}^{\infty }}\frac{c_{-n}}{{\left(s-s_0\right)}^n}+{\displaystyle \sum _{n=0}^{\infty }}{c}_n{\left(s-s_0\right)}^n$(2.3)

is called the LS about $s=s_0$, where $s$ is the variable and $c_n$'s are the coefficients of the series. The series ${\displaystyle \sum _{n=0}^{\infty }}{c}_n{\left(s-s_0\right)}^n$ is known as the analytic or regular part of the LS, while ${\displaystyle \sum _{n=1}^{\infty }}\frac{c_{-n}}{{\left(s-s_0\right)}^n}$ is known as the singular or the principal part of the LS.

Theorem 2.1. [50]). Let $y\left(t\right)$ be an analytic function defined on the domain $D:{\xi }_1<\left|t-t_0\right|<{\xi }_2$. Then, $y\left(t\right)$ can be expanded as a PS as follows:

$y\left(t\right)={\displaystyle \sum _{n=0}^{\infty }}{c}_n{\left(t-t_0\right)}^n,$(2.4)

which is valid for ${\xi }_1<\left|t-t_0\right|<{\xi }_2$.

Theorem 2.2. If $Y\left(s\right)=\mathcal{L}\left[y\left(t\right)\right]$ has an LS representation about $s=0$,

$Y\left(s\right)=\frac{c_0}{s}+{\displaystyle \sum _{n=1}^{\infty }}\frac{c_n}{s^{n+1}},s>0,$(2.5)

then $c_n=y^{\left(n\right)}\left(0\right),n=\mathrm{0,1,2},\dots .$.Proof. Suppose that $Y\left(s\right)$ can be represented by the LS expansion as in Eq. 2.5. So,

$sY\left(s\right)=c_0+{\displaystyle \sum _{n=1}^{\infty }}\frac{c_n}{s^n},s>0.$(2.6)

According to part (5) of Lemma 2.1, we have $c_0=y\left(0\right).$Multiplying Eq. 2.6 by $s$ gives the following expansion:

$s^{2}Y\left(s\right)-y\left(0\right)s=c_1+{\displaystyle \sum _{n=2}^{\infty }}\frac{c_n}{s^n},s>0.$(2.7)

Using part (5) of Lemma 2.1, it is obvious that

$c_1=\underset{s\to \infty }{\lim }\left(c_1+{\displaystyle \sum _{n=2}^{\infty }}\frac{c_n}{s^n}\right)=\underset{s\to \infty }{\lim }\left(s^{2}Y\left(s\right)-sy\left(0\right)\right)=\underset{s\to \infty }{\lim }s\left(sY\left(s\right)-y\left(0\right)\right)=\underset{s\to \infty }{\lim }s\left(\mathcal{L}\left[y^{\prime }\left(t\right)\right]\right)=y^{\prime }\left(0\right).$

Similarly, multiplying Eq. 2.7 by $s$ gives the following expansion:

$s\left(s^{2}Y\left(s\right)-y\left(0\right)s-y^{\prime }\left(0\right)\right)=c_2+{\displaystyle \sum _{n=3}^{\infty }}\frac{c_n}{s^n},s>0.$(2.8)

Again, by parts (5) and (6) of Lemma 2.1, we have

$c_2=\underset{s\to \infty }{\lim }\left(c_2+{\displaystyle \sum _{n=3}^{\infty }}\frac{c_n}{s^n}\right)=\underset{s\to \infty }{\lim }s\left(s^{2}Y\left(s\right)-sy\left(0\right)-y^{\prime }\left(0\right)\right)=\underset{s\to \infty }{\lim }s\left(\mathcal{L}\left[y^{″}\left(t\right)\right]\right)=y^{″}\left(0\right).$

Now, we can find out the general formula for the coefficient $c_n$. However, we can get it by multiplying Eq. 2.6 by $s^{n+1}$ and taking the limit of the resulting equation as $s\to \infty$; then, we find that $c_n=y^{\left(n\right)}\left(0\right),n=\mathrm{0,1,2},\dots$. Thus, the proof is now complete.

Theorem 2.3. assume that $\mathcal{L}\left[y\left(t\right)\right]=Y\left(s\right)$ can be represented as in Eq. 2.6. If $\left|s\mathcal{L}\left[y^{\left(n\right)}\left(t\right)\right]\right|\le K$, on $0<s\le d$, then the reminder $R_n\left(s\right)$ of the expansion of the LS appearing in Theorem 2.2 will satisfy the relation

$\left|R_n\left(s\right)\right|\le \frac{K}{s^{n+2}},0<s\le d.$(2.9)

Proof.First, we assume that for $r=\mathrm{0,1,2},\dots ,n+1$, $\mathcal{L}\left[y^{\left(r\right)}\left(t\right)\right]\left(s\right)$ is defined on $0<s\le d$. Also, we assume the following:

$\left|s\mathcal{L}\left[\left(y^{\left(n+1\right)}\right)\left(t\right)\right]\right|\le K,0<s\le d.$(2.10)

From the definition of the reminder $R_n\left(s\right)=Y\left(s\right)-{\displaystyle \sum _{i=0}^n}\frac{y^{\left(i\right)}\left(0\right)}{s^{i+1}}$, one can acquire

$s^{n+2}{R}_n\left(s\right)=s^{n+2}Y\left(s\right)-{\displaystyle \sum _{m=0}^n}{s}^{\left(n+1-m\right)}{y}^{\left(m\right)}\left(0\right)=s\left(s^{n+1}Y\left(s\right)-{\displaystyle \sum _{i=0}^n}{s}^{\left(n-m\right)}{y}^{\left(m\right)}\left(0\right)\right)=s\mathcal{L}\left[y^{\left(n+1\right)}\left(t\right)\right].$(2.11)

Eq. 2.10 and Eq. 2.11 lead to the conclusion that $\left|s^{\left(n+1\right)\alpha +1}{R}_n\left(s\right)\right|\le K$. Thus,

$-K\le s^{n+2}{R}_n\left(s\right)\le K,0<s\le d.$(2.12)

The inequality $\left|R_n\left(s\right)\right|\le \frac{K}{s^{n+2}}$ can be discovered by reformulating Eq. 2.12, and so, we got the result.

3 Constructing series solutions to ODEs

In this section, we first use the LRPS method to solve linear ODEs in preparation for solving non-linear ODEs. What is worth noting is the possibility of solving non-linear ODEs, which cannot be carried out using the traditional LT method. We will use the construction that we will get to solve non-linear ODEs when solving singular ODEs, whether linear or non-linear, and this is what we will see in Section 3.3.

3.1 LRPS method for solving linear ODEs

In this section, we demonstrate the steps of the LRPS method for solving linear ODEs. The basic idea of the proposed method is to apply the LT to the linear ODEs and then use the LRPS approach to construct a series solution, in LS form, to the transformed equation. Then, we transform the obtained solution into the required solution in the original space.

To illustrate the idea of the LRPS method in constructing series solutions to the linear ODEs, we consider problems (1.1) and (1.2), considering that $L_t$ is a linear differential operator given by

$L_t=a_{n-1}\left(t\right)\frac{{\mathrm{d}}^{n-1}}{\mathrm{d}{t}^{n-1}}+\dots +a_1\left(t\right)\frac{\mathrm{d}}{\mathrm{d}t}+a_0\left(t\right),$(3.1)

where $a_0\left(t\right),a_1\left(t\right),...,a_{n-1}\left(t\right)$ and $g\left(t\right)$ are arbitrary analytic functions that depend only on $t$, $y\left(t\right)$ is the unknown function of the independent variables $t$, and $I$ is an open interval.

To generate the LRPS solution of the IVP (1.1) and (1.2), first, we apply the LT to both sides of Eq. 1.1 to obtain

$\mathcal{L}\left[y^{\left(n\right)}\left(t\right)\right]=\mathcal{L}\left[L_t\left[y\left(t\right)\right]\right]+\mathcal{L}\left[g\left(t\right)\right],t\in I.$(3.2)

Using ICs (1.2) and some properties of the LT, Eq. 3.2 becomes

$Y\left(s\right)={\displaystyle \sum _{i=0}^{n-1}}\frac{y_i}{s^{i+1}}+\frac{1}{s^n}\mathcal{L}\left[L_t\left[{\mathcal{L}}^{-1}\left[Y\left(s\right)\right]\right]\right]+\frac{G\left(s\right)}{s^n},s>0.$(3.3)

We assume that $Y\left(s\right)$ in Eq. 3.3 has an expansion in the LS form as

$Y\left(s\right)={\displaystyle \sum _{i=0}^{\infty }}\frac{c_i}{s^{1+i}},s>0.$(3.4)

Depending on Theorem 2.3 and the given conditions in Eq. 1.2, the first $n$-coefficients of the expansion (3.4) can be determined, so it can be rewritten as follows:

$Y\left(s\right)={\displaystyle \sum _{i=0}^{n-1}}\frac{y_i}{s^{i+1}}+{\displaystyle \sum _{i=n}^{\infty }}\frac{c_i}{s^{1+i}},s>0.$(3.5)

The $k$th-truncated series of $Y\left(s\right)$ is given by

$Y_k\left(s\right)={\displaystyle \sum _{i=0}^{n-1}}\frac{y_i}{s^{i+1}}+{\displaystyle \sum _{i=n}^k}\frac{c_i}{s^{1+i}},s>0.$(3.6)

Thus, one can conclude

$Y_n\left(s\right)={\displaystyle \sum _{i=0}^{n-1}}\frac{y_i}{s^{i+1}}+\frac{c_n}{s^{1+n}},s>0.$(3.7)

To find the values of the unknown coefficients in series (3.7), we define the Laplace residual function (LRF) of Eq. 3.3 as

$LRes\left(s\right)=Y\left(s\right)-{\displaystyle \sum _{i=0}^{n-1}}\frac{y_i}{s^{i+1}}-\frac{1}{s^n}\mathcal{L}\left[L_t\left[{\mathcal{L}}^{-1}\left[Y\left(s\right)\right]\right]\right]-\frac{G\left(s\right)}{s^n},s>0$(3.8)

and the $k$th LRF as

${LRes}_k\left(s\right)=Y_k\left(s\right)-{\displaystyle \sum _{i=0}^{n-1}}\frac{y_i}{s^{i+1}}-\frac{1}{s^n}\mathcal{L}\left[L_t\left[{\mathcal{L}}^{-1}\left[Y_k\left(s\right)\right]\right]\right]-\frac{G\left(s\right)}{s^n},s>0.$(3.9)

It is clear that ${\mathit{Lim}}_{k\to \infty }{LRes}_k\left(s\right)=LRes\left(s\right)$, $LRes\left(s\right)=0$, and thus, $s^{k}LRes\left(s\right)=0$ for $s>0$ and $k=\mathrm{0,1,2,3},\dots$. Therefore, ${\mathit{Lim}}_{s\to \infty }\left(s^{k}LRes\left(s\right)\right)=0.$ Moreover,

${\mathit{Lim}}_{s\to \infty }\left(s^{k+1}LRes\left(s\right)\right)={\mathit{Lim}}_{s\to \infty }\left(s^{k+1}{LRes}_k\left(s\right)\right)=0,k=\mathrm{1,2,3},\dots$(3.10)

Substituting the first $n$th-truncated series in Eq. 3.7 into the $n$th LRF to obtain

${LRes}_n\left(s\right)=\frac{c_n}{s^{1+n}}-\frac{1}{s^n}\mathcal{L}\left[L_t\left[{\mathcal{L}}^{-1}\left[{\displaystyle \sum _{i=0}^{n-1}}\frac{y_i}{s^{i+1}}+\frac{c_n}{s^{1+n}}\right]\right]\right]-\frac{G\left(s\right)}{s^n},s>0.$(3.11)

Running the inverse LT in Eq. 3.11, we get

${LRes}_n\left(s\right)=\frac{c_n}{s^{1+n}}-\frac{1}{s^n}\mathcal{L}\left[L_t\left[{\displaystyle \sum _{i=0}^{n-1}}\frac{y_i}{i!}{t}^i+\frac{c_n}{n!}{t}^n\right]\right]-\frac{G\left(s\right)}{s^n},s>0.$(3.12)

Since the coefficients of the linear operator in Eq. 3.1 are analytic functions, they can be expressed as

$a_r\left(t\right)={\displaystyle \sum _{j=0}^{\infty }}{\lambda }_{rj}{t}^j,r=\mathrm{0,1},\dots ,n-1,$(3.13)

where

${\lambda }_{rj}=\frac{a_r^{\left(j\right)}\left(0\right)}{j!},r=\mathrm{0,1},\dots ,n-1,j=\mathrm{0,1,2},\dots .$(3.14)

So, the linear operator $L_t$ in Eq. 3.1 can be expressed as

$L_t={\displaystyle \sum _{r=0}^{n-1}}\left({\displaystyle \sum _{j=0}^{\infty }}{\lambda }_{rj}{t}^j\right)\frac{d^r}{{dt}^r}.$(3.15)

Running the operator $L_t$ on Eq. 3.12 according to its new form in Eq. 3.15, we get

${LRes}_n\left(s\right)=\frac{c_n}{s^{1+n}}-\frac{1}{s^n}\mathcal{L}\left[{\displaystyle \sum _{r=0}^{n-1}}{\displaystyle \sum _{j=0}^{\infty }}\left(\frac{c_n{\lambda }_{rj}}{\left(n-r\right)!}{t}^{n+j-r}+{\displaystyle \sum _{i=r}^{n-1}}\frac{{\lambda }_{rj}{y}_i}{\left(i-r\right)!}{t}^{i+j-r}\right)\right]-\frac{G\left(s\right)}{s^n}.$(3.16)

Finally, we run the LT in Eq. 3.16 to obtain the required form of the $n$th LRF:

${LRes}_n\left(s\right)=\frac{c_n}{s^{1+n}}-\frac{G\left(s\right)}{s^n}-\frac{1}{s^n}{\displaystyle \sum _{r=0}^{n-1}}{\displaystyle \sum _{j=0}^{\infty }}\left(\frac{c_n{\lambda }_{rj}}{\left(n-r\right)!}\frac{\left(n+j-r\right)!}{s^{1+n+j-r}}\right.\left.+{\displaystyle \sum _{i=r}^{n-1}}\frac{{\lambda }_{rj}{y}_i}{\left(i-r\right)!}\frac{\left(i+j-r\right)!}{s^{1+j+i-r}}\right).$(3.17)

Now, multiplying Eq. 3.17 by $s^{n+1}$, we get the following function:

$s^{n+1}{LRes}_n\left(s\right)=c_n-sG\left(s\right)-{\displaystyle \sum _{r=0}^{n-1}}{\displaystyle \sum _{j=0}^{\infty }}\frac{c_n{\lambda }_{rj}}{\left(n-r\right)!}\frac{\left(n+j-r\right)!}{s^{n+j-r}}-{\displaystyle \sum _{r=0}^{n-1}}{\displaystyle \sum _{j=0}^{\infty }}{\displaystyle \sum _{i=r}^{n-1}}\frac{{\lambda }_{rj}{y}_i}{\left(i-r\right)!}\frac{\left(i+j-r\right)!}{s^{j+i-r}}.$(3.18)

Taking the limit at infinity to Eq. 3.18, according to Eq. 3.10, we get

$c_n=g\left(0\right)+{\displaystyle \sum _{r=0}^{n-1}}{\lambda }_{r0}{y}_r.$(3.19)

Thus, the first approximation of the solution of Eq. 3.3 is

$Y_n\left(s\right)=\frac{y_0}{s}+\frac{y_1}{s^2}+\frac{y_2}{s^3}+\dots +\frac{y_{n-1}}{s^n}+\frac{1}{s^{n+1}}\left(g\left(0\right)+{\displaystyle \sum _{r=0}^{n-1}}{\lambda }_{r0}{y}_r\right).$(3.20)

Following that, one can find the value of the coefficient $c_{\mathrm{n}+1}$; to do that, we substitute the $\left(n+1\right)$th-truncated series, $Y_{n+1}\left(s\right)=\frac{y_0}{s}+\frac{y_1}{s^2}+\frac{y_2}{s^3}+\dots +\frac{y_{n-1}}{s^n}+\frac{c_n}{s^{n+1}}+\frac{c_{n+1}}{s^{n+2}}$, into the $\left(n+1\right)$th LRF to get the following:

${LRes}_{n+1}\left(s\right)=\frac{c_n}{s^{n+1}}+\frac{c_{n+1}}{s^{n+2}}-\frac{1}{s^n}\mathcal{L}\left[L_t\left[{\mathcal{L}}^{-1}\left[{\displaystyle \sum _{i=0}^{n-1}}\frac{y_i}{s^{i+1}}+\frac{c_n}{s^{1+n}}+\frac{c_{n+1}}{s^{n+2}}\right]\right]\right]-\frac{G\left(s\right)}{s^n}.$(3.21)

Performing the previous steps, we obtain the final form of the $\left(n+1\right)$th LRF:

$\begin{array}{c}{LRes}_{n+1}\left(s\right)=\frac{c_n}{s^{n+1}}+\frac{c_{n+1}}{s^{n+2}}-\frac{G\left(s\right)}{s^n}\\ -\frac{1}{s^n}{\displaystyle \sum _{r=0}^{n-1}}{\displaystyle \sum _{j=0}^{\infty }}\left(\frac{c_{n+1}{\lambda }_{rj}}{\left(n+1-r\right)!}\frac{\left(n+1+j-r\right)!}{s^{2+n+j-r}}+\frac{c_n{\lambda }_{rj}}{\left(n-r\right)!}\frac{\left(n+j-r\right)!}{s^{1+n+j-r}}\right.\left.+{\displaystyle \sum _{i=r}^{n-1}}\frac{{\lambda }_{rj}{y}_i}{\left(i-r\right)!}\frac{\left(i+j-r\right)!}{s^{1+j+i-r}}\right).\end{array}$(3.22)

Again, we multiply Eq. 3.22 by $s^{n+2}$ to obtain

$\begin{array}{c}{s^{n+2}\mathrm{L}\mathrm{R}\mathrm{e}\mathrm{s}}_{n+1}\left(s\right)=c_{n+1}-s^{2}G\left(s\right)+sg\left(0\right)+s{\displaystyle \sum _{r=0}^{n-1}}{\lambda }_{r0}{y}_r\\ -{\displaystyle \sum _{r=0}^{n-1}}{\displaystyle \sum _{j=0}^{\infty }}\left(\frac{c_{n+1}{\lambda }_{rj}}{\left(n+1-r\right)!}\frac{\left(n+1+j-r\right)!}{s^{n+j-r}}+\frac{c_n{\lambda }_{rj}}{\left(n-r\right)!}\frac{\left(n+j-r\right)!}{s^{n+j-r-1}}\right.\left.+{\displaystyle \sum _{i=r}^{n-1}}\frac{{\lambda }_{rj}{y}_i}{\left(i-r\right)!}\frac{\left(i+j-r\right)!}{s^{i+j-r-1}}\right).\end{array}$(3.23)

Computing the limit at infinity to both sides of the last equation and using Eq. 3.10, we get

$c_{n+1}=g^{\prime }\left(0\right)+c_n{\lambda }_{\left(n-1\right)0}+1!{\displaystyle \sum _{r=0}^{n-1}}{\lambda }_{r1}{y}_r+{\displaystyle \sum _{r=0}^{n-2}}{\lambda }_{r0}{y}_{r+1}.$(3.24)

So, the second approximation of the solution of Eq. 3.3 is

$\begin{array}{c}{Y}_{n+1}\left(s\right)=\frac{y_0}{s}+\frac{y_1}{s^2}+\frac{y_2}{s^3}+\dots +\frac{y_{n-1}}{s^n}+\frac{1}{s^{n+1}}\left(g\left(0\right)+{\displaystyle \sum _{r=0}^{n-1}}{\lambda }_{r0}{y}_r\right)\\ +\frac{1}{s^{n+2}}\left(g^{\prime }\left(0\right)+\left(g\left(0\right)+{\displaystyle \sum _{r=0}^{n-1}}{\lambda }_{r0}{y}_r\right){\lambda }_{\left(n-1\right)0}+{\displaystyle \sum _{r=0}^{n-1}}{\lambda }_{r1}{y}_r+{\displaystyle \sum _{r=0}^{n-2}}{\lambda }_{r0}{y}_{r+1}\right).\end{array}$(3.25)

Like the previous steps, we have

$\begin{array}{c}{c}_{n+2}=g^{″}\left(0\right)+c_{n+1}{\lambda }_{\left(n-1\right)0}+c_n{\lambda }_{\left(n-2\right)0}+\frac{2!}{1!}{c}_n{\lambda }_{\left(n-1\right)1}\\ +2!\left({\displaystyle \sum _{r=0}^{n-1}}{\lambda }_{r2}{y}_r+{\displaystyle \sum _{r=0}^{n-2}}{\lambda }_{r1}{y}_{r+1}+{\displaystyle \sum _{r=0}^{n-3}}{\lambda }_{r0}{y}_{r+2}\right).\end{array}$(3.26)

Repeating the steps, one can obtain

$c_{n+3}=g^{‴}\left(0\right)+3!{\displaystyle \sum _{i=0}^2}{\displaystyle \sum _{r=0}^i}\frac{c_{\left(n+2-i\right)}{\lambda }_{\left(n-1-i+r\right)r}}{\left(3-r\right)!}+3!\left({\displaystyle \sum _{i=0}^3}{\displaystyle \sum _{r=0}^{n-1-i}}\frac{{\lambda }_{r\left(3-i\right)}{y}_{\left(r+i\right)}}{i!}\right).$(3.27)

Considering a pattern of the obtained coefficients, we easily deduce the coefficient $c_{n+k}$ as follows:

$c_{n+k}=g^{\left(k\right)}\left(0\right)+k!{\displaystyle \sum _{i=0}^{k-1}}{\displaystyle \sum _{r=0}^i}\frac{c_{\left(n+k-1-i\right)}{\lambda }_{\left(n-1-i+r\right)r}}{\left(k-r\right)!}+k!\left({\displaystyle \sum _{i=0}^k}{\displaystyle \sum _{r=0}^{n-1-i}}\frac{{\lambda }_{r\left(k-i\right)}{y}_{\left(r+i\right)}}{i!}\right),k=\mathrm{0,1},\dots .$(3.28)

According to Eq. 3.14, the recurrence relation (3.28) becomes as follows:

$c_{n+k}=g^{\left(k\right)}\left(0\right)+{\displaystyle \sum _{i=0}^{k-1}}{\displaystyle \sum _{r=0}^i}\left(\begin{array}{c}k\\ r\end{array}\right)c_{\left(n+k-1-i\right)}{a}_{\left(n-1-i+r\right)}^{\left(r\right)}\left(0\right)+\left({\displaystyle \sum _{i=0}^k}{\displaystyle \sum _{r=0}^{n-1-i}}\left(\begin{array}{c}k\\ i\end{array}\right)y_{\left(r+i\right)}{a}_r^{\left(k-i\right)}\left(0\right)\right).$(3.29)

Thus, we can express the $\left(k+1\right.$)th-approximate solution of Eq. 3.3 by the following formula:

$Y_{n+k}\left(s\right)={\displaystyle \sum _{i=0}^{n-1}}\frac{y_i}{s^{i+1}}+{\displaystyle \sum _{i=0}^k}\frac{c_{n+i}}{s^{1+i+n}},s>0,k=\mathrm{0,1},\dots ..$(3.30)

Therefore, the exact solution of Eq. 3.3 can be expressed as

$Y\left(s\right)={\displaystyle \sum _{i=0}^{n-1}}\frac{y_i}{s^{i+1}}+{\displaystyle \sum _{i=0}^{\infty }}\frac{c_{n+i}}{s^{1+i+n}}.$(3.31)

Substituting the result in Eq. 3.29 into Eq. 3.31 and running the inverse LT gives the solutions of IVP (1.1) and (1.2) as follows:

$\begin{array}{c}y\left(t\right)={\displaystyle \sum _{i=0}^{n-1}}\frac{y_i}{i!}{t}^i+{\displaystyle \sum _{i=0}^{\infty }}\frac{t^{i+n}}{\left(i+n\right)!}\left(g^{\left(i\right)}\left(0\right)+{\displaystyle \sum _{j=0}^{i-1}}{\displaystyle \sum _{r=0}^j}\left(\begin{array}{c}i\\ r\end{array}\right)c_{\left(n+i-1-j\right)}{a}_{\left(n-1-j+r\right)}^{\left(r\right)}\left(0\right)+{\displaystyle \sum _{j=0}^i}{\displaystyle \sum _{r=0}^{n-1-j}}\left(\begin{array}{c}i\\ j\end{array}\right)y_{\left(r+j\right)}{a}_r^{\left(i-j\right)}\left(0\right)\right).\end{array}$(3.32)

3.2 The LRPS method for solving non-linear ODEs

This section introduces the steps of the LRPS approach in solving non-linear ODEs. To explain the methodology of the proposed method in constructing series solutions to this class, we consider IVP (1.3) and (1.4).

To generate the LRPS solution of the IVP (1.3) and (1.4), we consider the first step; that is, operating the LT to Eq. 1.3 and utilizing conditions (1.4), we obtain

$Y\left(s\right)={\displaystyle \sum _{i=0}^{n-1}}\frac{y_i}{s^{i+1}}+\frac{1}{s^n}\mathrm{\Psi }\left(s,Y\left(s\right),\frac{dY}{ds},\frac{d^{2}Y}{{ds}^2},\dots ,\frac{d^{m}Y}{{ds}^m}\right),s>0,$(3.33)

where $\mathrm{\Psi }$ is a multivariable function of $s,Y\left(s\right),\frac{dY}{ds},\frac{d^{2}Y}{{ds}^2},$ and $\frac{d^{m}Y}{{ds}^m}$, $m\in \mathbb{N}$.

We assume that $Y\left(s\right)$ given in Eq. 3.33 can be expanded as in Eq. 3.4. According to the conditions given in Eq. 1.4 and Theorem 2.3, series (3.4) also has the form in Eq. 3.5, and the $k$th-truncated series of $Y\left(s\right)$ will be like Eq. 3.6.

To set the values of the unknown coefficients in Eq. 3.6, according to Eq. 3.33, we define the LRF of Eq. 3.33 as

$LRes\left(s\right)=Y\left(s\right)-{\displaystyle \sum _{i=0}^{n-1}}\frac{y_i}{s^{i+1}}-\frac{1}{s^n}\mathrm{\Psi }\left(s,Y\left(s\right),\frac{dY}{ds},\frac{d^{2}Y}{{ds}^2},\dots ,\frac{d^{m}Y}{{ds}^m}\right),s>0$(3.34)

and the kth LRF as

${LRes}_k\left(s\right)=Y_k\left(s\right)-{\displaystyle \sum _{i=0}^{n-1}}\frac{y_i}{s^{i+1}}-\frac{1}{s^n}\mathrm{\Psi }\left(s,Y_k\left(s\right),\frac{d{Y}_k}{ds},\frac{d^2{Y}_k}{{ds}^2},\dots ,\frac{d^m{Y}_k}{{ds}^m}\right),s>0.$(3.35)

According to the form of ${\mathrm{Y}}_k\left(s\right)$ as in Eq. 3.6, it is clear that $\mathrm{\Psi }\left(s,Y_k\left(s\right),\frac{d{Y}_k}{ds},\frac{d^2{Y}_k}{{ds}^2},\dots ,\frac{d^m{Y}_k}{{ds}^m}\right)$ has a finite LS as follows:

$\mathrm{\Psi }\left(s,Y_k\left(s\right),\frac{d{Y}_k}{ds},\frac{d^2{Y}_k}{{ds}^2},\dots ,\frac{d^m{Y}_k}{{ds}^m}\right)={\displaystyle \sum _{i=0}^k}\frac{\varphi \left(c_n,c_{n+1},\dots ,c_{n+i}\right)}{s^{1+i}},s>0,$(3.36)

where $\varphi$ is a multivariable function of $c_n,c_{n+1},\dots ,c_{n+i}$, for $i=\mathrm{0,1},\dots ,k$.

Substituting the expansions (3.6) and (3.36) in (3.35) gives the following expansion form of the $k$th LRF:

${LRes}_k\left(s\right)={\displaystyle \sum _{i=n}^k}\frac{c_i}{s^{1+i}}-{\displaystyle \sum _{i=0}^k}\frac{\varphi \left(c_n,c_{n+1},\dots ,c_{n+i}\right)}{s^{1+n+i}},s>0.$(3.37)

Thus, the $n$th LRF is

${LRes}_n\left(\mathrm{s}\right)=\frac{c_n}{s^{1+n}}-{\displaystyle \sum _{i=0}^k}\frac{\varphi \left(c_n,c_{n+1},\dots ,c_{n+i}\right)}{s^{1+n+i}},s>0.$(3.38)

Now, we multiply Eq. 3.38 by $s^{n+1}$ to get

$s^{n+1}{LRes}_n\left(\mathrm{s}\right)=c_n-{\displaystyle \sum _{i=0}^k}\frac{\varphi \left(c_n,c_{n+1},\dots ,c_{n+i}\right)}{s^i},s>0.$(3.39)

Now, applying the limit as s → ∞ to both sides of Eq. 3.39 and using the fact in Eq. 3.10, we can easily determine the value of $c_n$ by solving the following equation for $c_n$:

$c_n=\varphi \left(c_n\right).$(3.40)

In the same manner, we find the value of the coefficient $c_{n+1}$ by substituting the $\left(n+1\right)$th-truncated series, $Y_n\left(s\right)={\displaystyle \sum _{i=0}^{n-1}}\frac{y_i}{s^{1+i}}+\frac{c_n}{s^{1+n}}$, into the $\left(n+1\right)$th LRF to get the following:

${LRes}_{n+1}\left(s\right)=\frac{c_{n+1}}{s^{2+n}}-{\displaystyle \sum _{i=0}^k}\frac{\varphi \left(c_n,c_{n+1},\dots ,c_{n+i}\right)}{s^{2+n+i}},s>0.$(3.41)

Multiplying $s^{n+2}$ by both sides of Eq. 3.41, we get the following function:

${s^{n+2}LRes}_{n+1}\left(s\right)=c_{n+1}-{\displaystyle \sum _{i=1}^k}\frac{\varphi \left(c_n,c_{n+1},\dots ,c_{n+i}\right)}{s^{i-1}},s>0.$(3.42)

Applying the limit at infinity to Eq. 3.42, we obtain the algebraic equation:

$c_{n+1}=\varphi \left(c_{n+1}\right).$(3.43)

Solving Eq. 3.43 implicitly for $c_{n+1}$ determines the second unknown coefficient in Eq. 3.6.

Similarly, we compute the third coefficient $c_{n+2}$ by substituting the $\left(n+2\right)$th-truncated series, $Y_{n+2}\left(s\right)=\frac{y_0}{s}+\frac{y_1}{s^2}+\frac{y_2}{s^3}+\dots +\frac{y_{n-1}}{s^n}+\frac{c_n}{s^{n+1}}+\frac{c_{n+1}}{s^{n+2}}+\frac{c_{n+2}}{s^{n+3}}$, into the $\left(n+2\right)$th LRF to get the following function:

${LRes}_{n+2}\left(s\right)=\frac{c_{n+2}}{s^{n+3}}-{\displaystyle \sum _{i=0}^k}\frac{\varphi \left(c_n,c_{n+1},\dots ,c_{n+i}\right)}{s^{1+n+i}},s>0.$(3.44)

Multiplying Eq. 3.44 by $s^{n+3}$ gives

$s^{n+3}{\mathrm{L}\mathrm{R}\mathrm{e}\mathrm{s}}_{n+2}\left(s\right)=c_{n+2}-\varphi \left(c_n\right)-\varphi \left(c_{n+1}\right)-\varphi \left(c_{n+2}\right)-{\displaystyle \sum _{i=2}^k}\frac{\varphi \left(c_n,c_{n+1},\dots ,c_{n+i}\right)}{s^{i-2}},s>0.$(3.45)

According to fact (3.10), we obtain

$c_{n+2}=\varphi \left(c_n\right)+\varphi \left(c_{n+1}\right)+\varphi \left(c_{n+2}\right).$(3.46)

Solving Eq. 3.46 for $c_{n+2}$ sets another coefficient in Eq. 3.6.

The value of the third unknown coefficient $c_{n+3}$ can be obtained by similar arguments and by solving the following equation:

$c_{n+3}=\varphi \left(c_n\right)+\varphi \left(c_{n+1}\right)+\varphi \left(c_{n+2}\right)+\varphi \left(c_{n+3}\right).$(3.47)

Considering the pattern of the obtained coefficients, we easily conclude the coefficient $c_{n+k}$ from the following implicit formula of $c_{n+k}$:

$c_{n+k}=\varphi \left(c_n\right)+\varphi \left(c_{n+1}\right)+\varphi \left(c_{n+2}\right)+\varphi \left(c_{n+3}\right)+\dots +\varphi \left(c_{n+k}\right).$(3.48)

Thus, we can express the $\left(k+1\right.$)th-approximate solution of Eq. 3.33 in the following shape:

$Y_{n+k}\left(s\right)={\displaystyle \sum _{i=0}^{n-1}}\frac{y_i}{s^{i+1}}+{\displaystyle \sum _{i=0}^k}\frac{\varphi \left(c_n,c_{n+1},\dots ,c_{n+i}\right)}{s^{1+n+i}},s>0,k=\mathrm{0,1},\dots .$(3.49)

Therefore, the exact analytic solution of Eq. 3.33 is written in a series form:

$Y\left(s\right)={\displaystyle \sum _{i=0}^{n-1}}\frac{y_i}{s^{i+1}}+{\displaystyle \sum _{i=0}^{\infty }}\frac{\varphi \left(c_n,c_{n+1},\dots ,c_{n+i}\right)}{s^{1+n+i}}.$(3.50)

Running the inverse LT to Eq. 3.50 gives the solution of Eq. 1.3 and Eq. 1.4 in a series expansion as

$y\left(t\right)={\displaystyle \sum _{i=0}^{n-1}}\frac{y_i}{i!}{t}^i+{\displaystyle \sum _{i=0}^{\infty }}\frac{\varphi \left(c_n,c_{n+1},\dots ,c_{n+i}\right)}{\left(i+n\right)!}{t}^{i+n}.$(3.51)

3.3 The LRPS method for solving singular-value problems

This section presents the LRPS method’s procedure for handling singular-value problems. To do this, let us consider the following singular-value problem:

$\frac{1}{t^k}\frac{d^{n}y}{d{t}^n}=f\left(t,y\left(t\right),\frac{dy}{dt},\frac{d^{2}y}{d{t}^2},\dots ,\frac{d^{n-1}y}{d{t}^{n-1}}\right),t\in I,m,k\in \mathbb{N}.$(3.52)

Subject to the ICs

$y\left(0\right)=y_0,y^{\prime }\left(0\right)=y_1,\dots ,y^{\left(n-1\right)}\left(0\right)=y_{n-1}.$(3.53)

To solve the initial-singular value problems (3.52) and (3.53), we first multiply Eq. 3.52 by $t^k$ to get

$\frac{d^{n}y}{d{t}^n}=t^{k}f\left(t,y\left(t\right),\frac{dy}{dt},\frac{d^{2}y}{d{t}^2},\dots ,\frac{d^{n-1}y}{d{t}^{n-1}}\right).$(3.54)

Now applying LT to Eq. 3.54 and using ICs (3.53), we get

$Y\left(s\right)={\displaystyle \sum _{i=0}^{n-1}}\frac{y_i}{s^{i+1}}+\frac{1}{s^n}\mathcal{L}\left[{\mathcal{L}}^{-1}\left[\frac{k!}{s^{k+1}}\right]{\mathcal{L}}^{-1}\left[\mathrm{\Psi }\left(s,Y\left(s\right),\frac{dY}{ds},\frac{d^{2}Y}{d{s}^2},\dots ,\frac{d^{m}Y}{d{s}^m}\right)\right]\right],s>0.$(3.55)

Now, suppose that the function Y(s) can be expressed in the form of the expansion of (3.4), and so on. We can complete the steps described in the previous Section 3.2 to obtain the required solution.

4 Applications to linear and non-linear problems

This section presents seven interesting problems with wide applications in physics and other sciences that are discussed and solved by the LRPS method.

Problem 4.1. consider the following composite oscillation equation:

$\frac{d^{2}y}{d{t}^2}-a\frac{dy}{dt}-by\left(t\right)=8,t\ge 0,$(4.1)

with respect to the initial condition

$y\left(0\right)=0,y^{\prime }\left(0\right)=0.$(4.2)

Comparing Eq. 4.1 with Eq. 1.1 concludes that $a_1\left(t\right)=a,a_0\left(t\right)=b,$ and $g\left(x\right)=8.$ Using the results obtained in Section 3.1, we can deduce ${\lambda }_{10}=a,{\lambda }_{11}={\lambda }_{12}={\lambda }_{13}=\dots =0$ and ${\lambda }_{00}=b,{\lambda }_{01}={\lambda }_{02}={\lambda }_{03}=\dots =0$. According to the recurrence relation in Eq. 3.29, we can see that $c_2=8$, $c_3=8a$, $c_4=8\left(b+a^2\right),c_5=8\left(a^3+2ab\right)$, $c_6=8\left(a^4+3a^{2}b+b^2\right)$, $c_7=8\left(a^5+4a^{3}b+3a{b}^2\right)$, $c_8=8\left(a^6+5a^{4}b+6a^2{b}^2+b^3\right)$, $c_9=8\left(a^7+6a^{5}b+10a^3{b}^2+4a{b}^3\right)$, and $c_{10}=8\left(a^8+7a^{6}b+15a^4{b}^2+10a^2{b}^3+b^4\right)$. Therefore, the 10th approximation of the solution of the IVP (4.1) and (4.2) will be as follows:

$\begin{array}{ll}\hfill y_{10}\left(t\right)& =\frac{8}{2!}{t}^2+\frac{8a}{3!}{t}^3+\frac{8\left(b+a^2\right)}{4!}{t}^4+\frac{8\left(a^3+2ab\right)}{5!}{t}^5+\frac{8\left(a^4+3a^{2}b+b^2\right)}{6!}{t}^6+\frac{8\left(a^5+4a^{3}b+3a{b}^2\right)}{7!}{t}^7\hfill \\ \hfill & +\frac{8\left(a^6+5a^{4}b+6a^2{b}^2+b^3\right)}{8!}{t}^8+\frac{8\left(a^7+6a^{5}b+10a^3{b}^2+4a{b}^3\right)t^9}{9!}+\frac{8\left(a^8+7a^{6}b+15a^4{b}^2+10a^2{b}^3+b^4\right)t^{10}}{10!}.\hfill \end{array}$(4.3)

It is easy to check if the exact solution of Eq. 4.1 and Eq. 4.2 is as follows:

$y\left(t\right)=\frac{4}{bc}\left(\left(c+a\right){\mathrm{e}}^{\frac{1}{2}\left(a-c\right)t}+\left(c-a\right){\mathrm{e}}^{\frac{1}{2}\left(a+c\right)t}\right)-\frac{8}{b},c=\sqrt{a^2+4b.}$(4.4)

To analyze the accuracy of the approximate solution in Eq. 4.3 and determine the interval of convergence, we introduce and compute two types of error, actual and relative errors that are defined, respectively, as follows:

$Act.Err.\left(t\right)=\left|y\left(t\right)-y_{10}\left(t\right)\right|$(4.5)

and

$Rel.Err.\left(t\right)=\left|\frac{y\left(t\right)-y_{10}\left(t\right)}{y\left(t\right)}\right|.$(4.6)

For analysis and comparison of the exact and approximate solutions of IVP (4.1) and (4.2), Table 1 shows the numerical results of this problem. It displays the exact and approximate results in addition to the actual and relative errors at different values of $t$ within the interval $\left[\mathrm{0,1}\right]$. The results indicate that the errors increase when the value of t increases. It is known that by increasing the number of terms in the series solution, the error decreases and the convergence period of the truncated series increases. It should be noted that we can extend the convergence period using the multi-stage technique.

TABLE 1

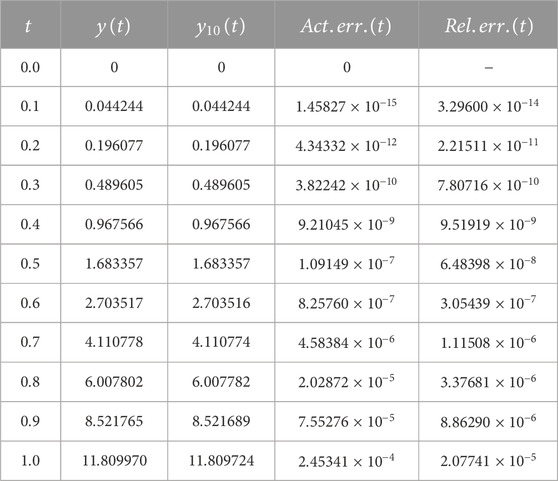
TABLE 1. The exact and the $10$^th approximate solutions of the IVP (4.1) and (4.2) and the actual and relative errors at $a=3$ and $b=-2$.

Problem 4.2. consider the following Bessel’s equation:

$\left(1-t^2\right)y^{″}\left(t\right)-2t{y}^{\prime }\left(t\right)+2y\left(t\right)=0.$(4.7)

Subject to the ICs,

$y\left(0\right)=1,y^{\prime }\left(0\right)=-1.$(4.8)

According to the existence and uniqueness theorem, it is clear that the IVPs (4.7) and (4.8) have a unique solution in the interval $\left(-\mathrm{1,1}\right)$, so we seek to get this solution via the LRPS method. To reach our goal and be able to rely on the construction obtained in Section 3.1, it is necessary to rewrite Eq. 4.7 as follows:

$y^{″}\left(t\right)=\frac{2t}{\left(1-t^2\right)}{y}^{\prime }\left(t\right)-\frac{2}{\left(1-t^2\right)}y\left(t\right),0\le t<1.$(4.9)

Comparing Eq. 4.7 with Eq. 1.1, we find that

$L_t=\frac{2t}{\left(1-t^2\right)}\frac{d}{dt}-\frac{2}{\left(1-t^2\right)},a_1\left(t\right)=\frac{2t}{\left(1-t^2\right)},a_0\left(t\right)=\frac{-2}{\left(1-t^2\right)},$(4.10)

where $a_0\left(t\right)$ and $a_1\left(t\right)$ are analytic functions on $\left[\mathrm{0,1}\right.)$.Since the coefficients of the linear operator in Eq. 4.10 are analytic functions, they can be expressed as McLaurin expansions as follows:

$a_0\left(t\right)={\displaystyle \sum _{j=0}^{\infty }}-2t^{2j},a_1\left(t\right)={\displaystyle \sum _{j=0}^{\infty }}2t^{2j+1}.$(4.11)

So, according to Eq. 4.11 and Eq. 3.14, we have

$\begin{array}{c}{\lambda }_{0\left(2j\right)}=\frac{a_0^{\left(2j\right)}\left(0\right)}{\left(2j\right)!}=-2,{\lambda }_{0\left(2j+1\right)}=\frac{a_0^{\left(2j+1\right)}\left(0\right)}{\left(2j+1\right)!}=0,j=\mathrm{0,1,2},\dots \\ {\lambda }_{1\left(2j\right)}=\frac{a_1^{\left(2j\right)}\left(0\right)}{\left(2j\right)!}=0,{\lambda }_{1\left(2j+1\right)}=\frac{a_1^{\left(2j+1\right)}\left(0\right)}{\left(2j+1\right)!}=2,j=\mathrm{0,1,2},\dots \end{array}.$(4.12)

Comparing with the general formula (3.29), we can find the values of the coefficients as follows:

$\begin{array}{l}{c}_2={\lambda }_{00}{y}_0+{\lambda }_{10}{y}_1=-2,\\ c_3=c_2{\lambda }_{10}+{\lambda }_{01}{y}_0+{\lambda }_{11}{y}_1+{\lambda }_{00}{y}_1=0,\\ c_4=c_3{\lambda }_{10}+c_2{\lambda }_{00}+2!c_2{\lambda }_{11}+2\left({\lambda }_{02}{y}_0+{\lambda }_{12}{y}_1+{\lambda }_{01}{y}_1\right)=-8,\\ c_5=c_4{\lambda }_{10}+c_3{\lambda }_{00}+3c_3{\lambda }_{11}+3c_2{\lambda }_{01}+6c_2{\lambda }_{12}+6\left({\lambda }_{03}{y}_0+{\lambda }_{13}{y}_1+{\lambda }_{02}{y}_1\right)=0\\ c_6=c_5{\lambda }_{10}+c_4{\lambda }_{00}+4c_4{\lambda }_{11}+4c_3{\lambda }_{01}+12c_3{\lambda }_{12}+12c_2{\lambda }_{02}+24c_2{\lambda }_{13}\\ +24\left({\lambda }_{04}{y}_0+{\lambda }_{14}{y}_1+{\lambda }_{03}{y}_1\right)=-144\\ c_7=c_6{\lambda }_{10}+c_5{\lambda }_{00}+5c_5{\lambda }_{11}+5c_4{\lambda }_{01}+20c_4{\lambda }_{12}+20c_3{\lambda }_{02}+60c_3{\lambda }_{13}\\ +60c_2{\lambda }_{03}+120c_2{\lambda }_{14}+120\left({\lambda }_{04}{y}_1+{\lambda }_{05}{y}_0+{\lambda }_{15}{y}_1\right)=0\\ c_8={c_7{\lambda }_{10}+c}_6{\lambda }_{00}+6c_6{\lambda }_{11}+6c_5{\lambda }_{01}+30c_5{\lambda }_{12}+30c_4{\lambda }_{02}+120c_4{\lambda }_{13}+120c_3{\lambda }_{03}\\ +360c_3{\lambda }_{14}+360c_2{\lambda }_{04}+720c_2{\lambda }_{15}+720\left({\lambda }_{05}{y}_1+{\lambda }_{06}{y}_0+{\lambda }_{16}{y}_1\right)=-5760\\ c_9=c_7{\lambda }_{00}+7c_6{\lambda }_{01}+42c_5{\lambda }_{02}+210c_4{\lambda }_{03}+840c_3{\lambda }_{04}+2520c_2{\lambda }_{05}+c_8{\lambda }_{10}+7c_7{\lambda }_{11}+42c_6{\lambda }_{12}\\ +210c_5{\lambda }_{13}+840c_4{\lambda }_{14}+2520c_3{\lambda }_{15}+5040c_2{\lambda }_{16}+5040\left({\lambda }_{07}{y}_0+{\lambda }_{17}{y}_1+{\lambda }_{06}{y}_1\right)=0\\ c_{10}=c_8{\lambda }_{00}+8c_7{\lambda }_{01}+56c_6{\lambda }_{02}+336c_5{\lambda }_{03}+1680c_4{\lambda }_{04}+6720c_3{\lambda }_{05}+20160c_2{\lambda }_{06}+c_9{\lambda }_{10}+8c_8{\lambda }_{11}\\ +56c_7{\lambda }_{12}+336c_6{\lambda }_{13}+1680c_5{\lambda }_{14}+6720c_4{\lambda }_{15}+20160c_3{\lambda }_{16}+40320c_2{\lambda }_{17}\\ +40320\left({\lambda }_{08}{y}_0+{\lambda }_{18}{y}_1+{\lambda }_{07}{y}_1\right)=-403200.\end{array}$

Therefore, the LRPS solution to Problem 4.2 can be expressed in the following series form:

$y\left(t\right)=1-t-t\left(t+\frac{t^3}{3}+\frac{t^5}{5}+\frac{t^7}{7}+\frac{t^9}{9}+\dots \right).$(4.13)

The expansion in (4.13) is the same expansion as that of the function ${\tan }^{-1}\left(t\right)$. Therefore, the exact solution of the IVP (4.7) and (4.8) has the following closed form:

$y\left(t\right)=1-t-t{\tan }^{-1}\left(t\right),0\le t<1.$(4.14)

Table 2 shows the numerical results of Problem 4.2. It shows the exact and approximate results in addition to the actual and relative errors at different values of $t\in \left[\mathrm{0,09}\right]$. The displayed data are acceptable and can be improved by increasing the order of the approximation.

TABLE 2

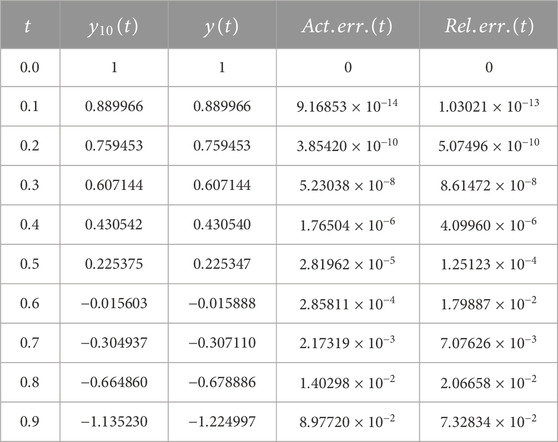
TABLE 2. The exact and the $10$^th approximate solutions of the IVP (4.7) and (4.8) and the actual and relative errors.

Problem 4.3. consider the following non-linear nonhomogeneous ODE:

$y^{\left(3\right)}\left(t\right)+y^2\left(t\right)+\cos t{y}^{\prime }\left(t\right)=1-\cos t.$(4.15)

Subject to the ICs,

$y\left(0\right)=0,y^{\prime }\left(0\right)=1,y^{″}\left(0\right)=0.$(4.16)

Similar to the previous problems, we operate the LT on both sides of Eq. 4.15 and employ the ICs (4.16). Then, we obtain the following equation in the Laplace space:

$Y\left(s\right)=\frac{1}{s^2}-\frac{1}{s^3}\mathcal{L}\left[{\left({\mathcal{L}}^{-1}\left[Y\left(s\right)\right]\right)}^2\right]-\frac{1}{s^3}\mathcal{L}\left[{\mathcal{L}}^{-1}\left[\frac{s}{1+s^2}\right]{\mathcal{L}}^{-1}\left[sY\left(s\right)\right]\right]+\frac{1}{s^4}-\frac{1}{s^2\left(1+s^2\right)},s>0.$(4.17)

We assume that the solution of Eq. 4.17 has the same LS expansion as in Eq. 3.4. According to ICs (4.16), the $k$th-truncated series of $Y\left(s\right)$ becomes

$Y_k\left(s\right)=\frac{1}{s^2}+{\displaystyle \sum _{i=3}^k}\frac{c_i}{s^{1+i}},s>0.$(4.18)

To set the value of the unknown coefficients in series (4.18), we utilize the kth LRF of Eq. 3.17, which is defined as

$\begin{array}{c}{\mathrm{L}\mathrm{R}\mathrm{e}\mathrm{s}}_k\left(\mathrm{s}\right)=Y_k\left(s\right)-\frac{1}{s^2}+\frac{1}{s^3}\mathcal{L}\left[{\left({\mathcal{L}}^{-1}\left[Y_k\left(s\right)\right]\right)}^2\right]+\frac{1}{s^3}\mathcal{L}\left[{\mathcal{L}}^{-1}\left[\frac{s}{1+s^2}\right]{\mathcal{L}}^{-1}\left[s{Y}_k\left(s\right)\right]\right]-\frac{1}{s^4}\\ +\frac{1}{s^2\left(1+s^2\right)},s>0.\end{array}$(4.19)

To determine the coefficient $c_3$, we substitute $Y_3\left(s\right)=\frac{1}{s^2}+\frac{c_3}{s^4}$ into ${\mathrm{L}\mathrm{R}\mathrm{e}\mathrm{s}}_3\left(s\right)$ and run the operators in Eq. 4.19 to get the following rational function:

${\mathrm{L}\mathrm{R}\mathrm{e}\mathrm{s}}_3\left(\mathrm{s}\right)=\frac{c_3}{s^4}-\frac{1}{s^4}+\frac{2}{s^2\left(1+s^2\right)}+\frac{2}{s^6}+\frac{8c_3}{s^8}+\frac{c_3}{{\left(1+s^2\right)}^3}-\frac{3c_3}{s^2{\left(1+s^2\right)}^3}+\frac{20c_3^2}{s^{10}}.$(4.20)

Employing fact (3.10), the solution of the equation $\underset{s\to \infty }{\lim }{s}^4{\mathrm{L}\mathrm{R}\mathrm{e}\mathrm{s}}_3\left(s\right)=0$ for $c_3$ introduces $c_3=-1.$Similarly, to find out the value of the second unknown coefficient $c_4$, we substitute $Y_4\left(s\right)=\frac{1}{s^2}+\frac{1}{s^4}+\frac{c_4}{s^5}$ into the 4^th-LRF to get the following:

$\begin{array}{c}{LRes}_4\left(s\right)=\frac{c_3}{s^5}+\frac{2}{s^6}-\frac{8}{s^8}+\frac{20}{s^{10}}-\frac{1}{{\left(1+s^2\right)}^3}+\frac{3}{s^2{\left(1+s^2\right)}^3}-\frac{2}{s^4+s^6}-\frac{70c_3}{s^{11}}+\frac{10c_3}{s^9}\\ +\frac{c_3}{s^3{\left(1+s^2\right)}^4}-\frac{6c_3}{s{\left(1+s^2\right)}^4}+\frac{s{c}_3}{{\left(1+s^2\right)}^4}+\frac{70c_3^2}{s^{12}},s>0.\end{array}$(4.21)

Utilizing fact (3.10) via Eq. 4.21 gives $c_4=0$. Using the same procedure as mentioned above, we can find more coefficients for series (4.18). Some of them are $c_5=1,c_6=0,c_7=-1,c_8=0,c_9=1,c_{10}=0,c_{11}=-1.$ So, the series solution to Eq. 4.31 has the following LS:

$Y\left(s\right)=\frac{1}{s^2}-\frac{1}{s^4}+\frac{1}{s^6}-\frac{1}{s^8}+\frac{1}{s^{10}}-\frac{1}{s^{12}}+\dots .$(4.22)

Therefore, the LRPS solution to Eq. 4.15 and Eq. 4.16 can be expressed in the following series form:

$y\left(t\right)=t-\frac{t^3}{3!}+\frac{t^5}{5!}-\frac{t^7}{7!}+\frac{t^9}{9!}-\frac{t^{11}}{11!}+\dots ,$(4.23)

which is the expansion of the exact solution $y\left(t\right)=\sin \left(t\right).$

Problem 4.4. consider the following non-linear pantograph equation:

$\frac{d^{2}y}{{dt}^2}=-2y^2\left(\frac{t}{2}\right),t\ge 0.$(4.24)

Subject to the ICs,

$y\left(0\right)=1,y^{\prime }\left(0\right)=0.$(4.25)

Following the same procedure as in the previous problems, we can express the LRPS solution to IVP (4.24) and (4.25) in the form

$y\left(t\right)=1-t^2+\frac{t^4}{12}-\frac{7t^6}{1440}+\frac{127t^8}{1290240}-\frac{10879t^{10}}{7431782400}+\dots .$(4.26)

Since we cannot predict the pattern in the coefficients of the series solution in Eq. 4.26, we cannot reach the exact solution. Therefore, we test the results using the residual and relative errors, which are defined as follows, respectively:

$Res.Err.\left(t\right)=\left|{\mathcal{L}}^{-1}\left[{LRes}_k\left(s\right)\right]\right|=\left|\frac{d^2{y}_k}{{dt}^2}+2y_k^2\left(\frac{t}{2}\right)\right|,$(4.27)

$Rel.Err.\left(t\right)=\left|\frac{y_k\left(t\right)-y_{k/2}\left(t\right)}{y_k\left(t\right)}\right|.$(4.28)

Table 3 shows the numerical results of Problem 4.4. It displays the 10th approximate solution in addition to the residual and relative errors at different values of $t$ within the interval $\left[\mathrm{0,1}\right]$. The results indicate that the LRPS solution is acceptable mathematically in the period $\left[\mathrm{0,1}\right].$

TABLE 3

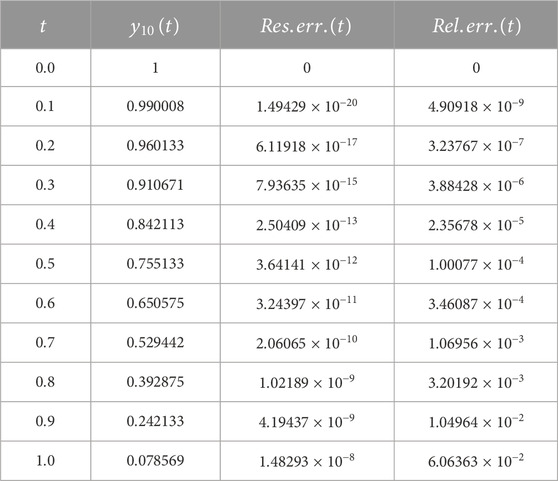
TABLE 3. The $10$^th approximate LRPS solution of the IVP (4.24) and (4.25) and the residual and relative errors.

Problem 4.5. consider the following homogenous linear singular ODE:

$\left(\sin t\right)y^{″}-2\left(\cos t\right)y^{\prime }-\left(\sin t\right)y=0,0<t<\pi ,$(4.29)

with respect to the ICs:

$y\left(0\right)=2,y^{\prime }\left(0\right)=0.$(4.30)

We apply the LT on both sides of Eq. 4.29 and use the ICs in Eq. 4.30 to obtain the following symbolic algebraic equation in the Laplace space:

$\begin{array}{c}\mathcal{L}\left[{\mathcal{L}}^{-1}\left[\frac{1}{1+s^2}\right]{\mathcal{L}}^{-1}\left[s^{2}Y\left(s\right)-2s\right]\right]-2\mathcal{L}\left[{\mathcal{L}}^{-1}\left[\frac{1}{1+s^2}\right]{\mathcal{L}}^{-1}\left[sY\left(s\right)-2\right]\right]\\ -\mathcal{L}\left[{\mathcal{L}}^{-1}\left[\frac{1}{1+s^2}\right]{\mathcal{L}}^{-1}\left[Y\left(s\right)\right]\right]=0,s>0.\end{array}$(4.31)

Suppose that the solution of Eq. 4.31 has a LS expansion as in Eq. 3.4. According to ICs (4.30), the $k$th-truncated series (3.6) can be expressed as

$Y_k\left(s\right)=\frac{2}{\mathrm{s}}+{\displaystyle \sum _{i=2}^k}\frac{c_i}{s^{1+i}},s>0.$(4.32)

To set the unknown coefficient in series (4.32), we define the $k$th LRF of Eq. 4.31 as follows:

$\begin{array}{c}{\mathrm{L}\mathrm{R}\mathrm{e}\mathrm{s}}_k\left(s\right)=\mathcal{L}\left[{\mathcal{L}}^{-1}\left[\frac{1}{1+s^2}\right]{\mathcal{L}}^{-1}\left[s^2{Y}_k\left(s\right)-2s\right]\right]-2\mathcal{L}\left[{\mathcal{L}}^{-1}\left[\frac{1}{1+s^2}\right]{\mathcal{L}}^{-1}\left[s{Y}_k\left(s\right)-2\right]\right]\\ -\mathcal{L}\left[{\mathcal{L}}^{-1}\left[\frac{1}{1+s^2}\right]{\mathcal{L}}^{-1}\left[Y_k\left(s\right)\right]\right],s>0.\end{array}$(4.34)

We substitute $Y_2\left(s\right)=\frac{2}{s}+\frac{c_2}{s^3}$ into ${\mathrm{L}\mathrm{R}\mathrm{e}\mathrm{s}}_2\left(s\right)$ and run the operators in Eq. 4.34 to get the following function:

${\mathrm{L}\mathrm{R}\mathrm{e}\mathrm{s}}_2\left(s\right)=-\frac{2}{{\left(1+s^2\right)}^3}+\frac{4c_2}{{\left(1+s^2\right)}^3}-\frac{4s^2}{{\left(1+s^2\right)}^3}-\frac{c_2{s}^2}{{\left(1+s^2\right)}^3}-\frac{2s^4}{{\left(1+s^2\right)}^3}-\frac{c_2{s}^4}{{\left(1+s^2\right)}^3}.$(4.35)

Solving the equation $\underset{s\to \infty }{\lim }{s}^2{\mathrm{L}\mathrm{R}\mathrm{e}\mathrm{s}}_2\left(s\right)=0$ gives $c_2=-2$. Thus, the first approximation of the solution of Eq. 4.31 is $Y_2\left(s\right)=\frac{2}{s}-\frac{2}{s^3}$.Again, we substitute 3^rd-truncated series, $Y_3\left(s\right)=\frac{2}{s}-\frac{2}{s^3}+\frac{c_3}{s^4}$, into the 3^rd LRF to get the following:

${\mathrm{L}\mathrm{R}\mathrm{e}\mathrm{s}}_3\left(s\right)=\frac{-10}{{\left(1+s^2\right)}^4}+\frac{12c_{3}s}{{\left(1+s^2\right)}^4}-\frac{12s^2}{{\left(1+s^2\right)}^4}+\frac{4c_3{s}^3}{{\left(1+s^2\right)}^4}-\frac{2s^4}{{\left(1+s^2\right)}^4}.$(4.36)

Consequently, the equation $\underset{s\to \infty }{\lim }{s}^3{\mathrm{L}\mathrm{R}\mathrm{e}\mathrm{s}}_3\left(s\right)=0$ gives $c_3=0$.Likewise, we substitute the 4th-truncated series, $Y_4\left(s\right)=\frac{2}{s}-\frac{2}{s^3}+\frac{c_4}{s^5}$, into the 4th LRF to get the following:

$\begin{array}{c}{\mathrm{L}\mathrm{R}\mathrm{e}\mathrm{s}}_4\left(s\right)=\frac{-10}{{\left(1+s^2\right)}^5}-\frac{4c_4}{{\left(1+s^2\right)}^5}-\frac{22s^2}{{\left(1+s^2\right)}^5}+\frac{21c_4{s}^2}{{\left(1+s^2\right)}^5}-\frac{14s^4}{{\left(1+s^2\right)}^5}+\frac{10c_4{s}^4}{{\left(1+s^2\right)}^5}\\ -\frac{2s^6}{{\left(1+s^2\right)}^5}+\frac{c_4{s}^6}{{\left(1+s^2\right)}^5}.\end{array}$(4.37)

Solving the equation $\underset{s\to \infty }{\lim }{s}^4{\mathrm{L}\mathrm{R}\mathrm{e}\mathrm{s}}_4\left(s\right)=0$ gives $c_4=2$. Applying the same procedure for $k=\mathrm{5,6,7,8}$ leads to $c_5=0$, $c_6=-2$, $c_7=0$, and $c_8=2$. Thus, we conclude that the solution of Eq. 4.31 has the following expansion:

$Y\left(s\right)=\frac{2}{s}-\frac{2}{s^3}+\frac{2}{s^5}-\frac{2}{s^7}+\frac{2}{s^9}-\dots .$(4.38)

Applying the inverse LT to Eq. 4.38 gives the LRPS solution to the IVP (4.29) and (4.30) in the following PS form:

$y\left(t\right)=2\left(1-\frac{t^2}{2!}+\frac{t^4}{4!}-\frac{t^6}{6!}+\frac{t^8}{8!}-\dots \right).$(4.39)

It is clear that the closed form of the exact solution of IVP (4.50) and (4.51) is $y\left(t\right)=2\cos \left(t\right)$.

Problem 4.6. consider the following non-homogeneous nonlinear Lane–Emden singular ODE:

$\begin{array}{c}{y}^{″}\left(t\right)+\frac{2}{t}{y}^{\prime }\left(t\right)-t\sin y\left(t\right)=e^{2t}\end{array},t\in \left(\mathrm{0,2}\right),$(4.40)

considering the ICs:

$y\left(0\right)=\mathrm{\pi },y^{\prime }\left(0\right)=0.$(4.41)

Using similar arguments to the previous problem, one can obtain the series solution of the LT of the IVP (4.40) and (4.41) as follows:

$Y\left(s\right)=\frac{\pi }{s}+\frac{\frac{1}{3}}{s^3}+\frac{1}{s^4}+\frac{\frac{12}{5}}{s^5}+\frac{\frac{14}{3}}{s^6}+\frac{\frac{60}{7}}{s^7}+\frac{15}{s^8}+\frac{28}{s^9}+\frac{\frac{2588}{45}}{s^{10}}+\dots .$(4.42)

Applying the inverse LT on Eq. 4.42 gives the LRPS solution of the IVP (4.40) (4.41) in the following series form:

$y\left(t\right)=\pi +\frac{t^2}{6}+\frac{t^3}{6}+\frac{t^4}{10}+\frac{7t^5}{180}+\frac{t^6}{84}+\frac{t^7}{336}+\frac{t^8}{1440}+\frac{647t^9}{4082400}+\dots .$(4.43)

There is no pattern between the series terms in Eq. 4.43. So, it is difficult to predict the exact solution formula. Thus, we suffice with the approximate solution we got for Problem 4.6. It is worth noting that the more terms we calculate for the LRPS solution, the longer the series convergence interval and the higher the accuracy of the solution. Therefore, we test the 8^th approximate LRPS solution for Problem 4.6 using the residual and relative errors, which are defined as follows, respectively:

$\begin{array}{l}Res.Err.\left(t\right)=\left|{\mathcal{L}}^{-1}\left[{LRes}_8\left(s\right)\right]\right|\\ =\left|t-e^{2t}t+2t^2+2t^3+\frac{4t^4}{3}+\frac{2t^5}{3}+\frac{4t^6}{15}+\frac{4t^7}{45}+\frac{8t^8}{315}+\frac{t^9}{1512}-\frac{13t^{10}}{4320}-\frac{1003t^{11}}{255150}-\frac{113221t^{12}}{32659200}\right|,\end{array}$(4.44)

$Rel.Err.\left(t\right)=\left|\frac{y_8\left(t\right)-y_4\left(t\right)}{y_8\left(t\right)}\right|=\left|\frac{\frac{t^6}{84}+\frac{t^7}{336}+\frac{t^8}{1440}+\frac{647t^9}{4082400}}{\pi +\frac{t^2}{6}+\frac{t^3}{6}+\frac{t^4}{10}+\frac{7t^5}{180}+\frac{t^6}{84}+\frac{t^7}{336}+\frac{t^8}{1440}+\frac{647t^9}{4082400}}\right|.$(4.45)

Table 4 shows the numerical results of Problem 4.6. It illustrates the 8^th approximate solution in addition to the residual and relative errors at different values of $t$ within the interval $\left[\mathrm{0,1}\right]$. Similar to the results in the previous tables, the data are good for the period $\left[\mathrm{0,1}\right.$].

TABLE 4

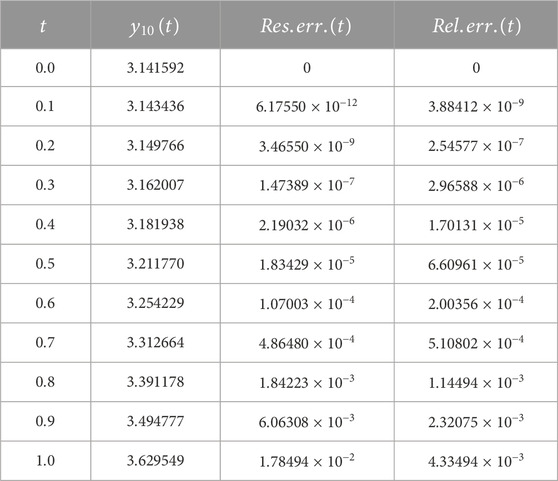
TABLE 4. The $8$^th approximate LRPS solution of the IVP (4.40) and (4.41) and the residual and relative errors.

Problem 4.7. We consider the following micro-electromechanical system (MEMS) [52]:

$y^{″}+y+\frac{\theta }{y-1}=0,\theta >0,$(4.46)

with the ICs:

$y\left(0\right)=y^{\prime }\left(0\right)=0.$(4.47)

This dynamic differential equation is used to describe the wire’s movement as a point mass, where $y$ is the dimensionless distance and $\theta$ is a voltage-related parameter.

Simulating the previous examples, the LT of the IVP (4.46) and (4.47) is given by the following algebraic equation:

$\mathcal{L}\left[{\mathcal{L}}^{-1}\left[s^{2}Y\left(s\right)\right]{\mathcal{L}}^{-1}\left[Y\left(s\right)\right]\right]-s^{2}Y\left(s\right)+\mathcal{L}\left[{\left({\mathcal{L}}^{-1}\left[Y\left(s\right)\right]\right)}^2\right]-Y\left(s\right)+\frac{1}{s^2}=0,s>0.$(4.48)

Applying the arguments and processes of the LRPS method, one can obtain the LRPS solution to the algebraic Eq. 4.48 as follows:

$\begin{array}{c}Y\left(s\right)=\frac{\theta }{s^3}+\frac{\theta \left(\theta -1\right)}{s^5}+\frac{\theta \left(1-2\theta +7{\theta }^2\right)}{s^7}-\frac{\theta \left(1-3\theta +39{\theta }^2-127{\theta }^3\right)}{s^9}\\ +\frac{\theta \left(1-4\theta +168{\theta }^2-1678{\theta }^3+4369{\theta }^4\right)}{s^{11}}+\dots .\end{array}$(4.49)

Applying the inverse LT to Eq. 4.49 gives the LRPS solution of the IVP (4.46) (4.47) as follows:

$\begin{array}{c}y\left(t\right)=\frac{\theta t^2}{2}+\frac{\theta \left(\theta -1\right)t^4}{4!}+\frac{\theta \left(1-2\theta +7{\theta }^2\right)t^6}{6!}-\frac{\theta \left(1-3\theta +39{\theta }^2-127{\theta }^3\right)t^8}{8!}\\ +\frac{\theta \left(1-4\theta +168{\theta }^2-1678{\theta }^3+4369{\theta }^4\right)t^{10}}{10!}+\dots .\end{array}$(4.50)

To test the accuracy of the obtained solution given in (4.50), we compute the residual and relative errors to the 10th approximation of the solution. Table 5 shows the 10th approximate solution in addition to the residual and relative errors at different values of $t$ within the interval $\left[\mathrm{0,1}\right]$. The results indicate that the obtained solution is acceptable mathematically.

TABLE 5

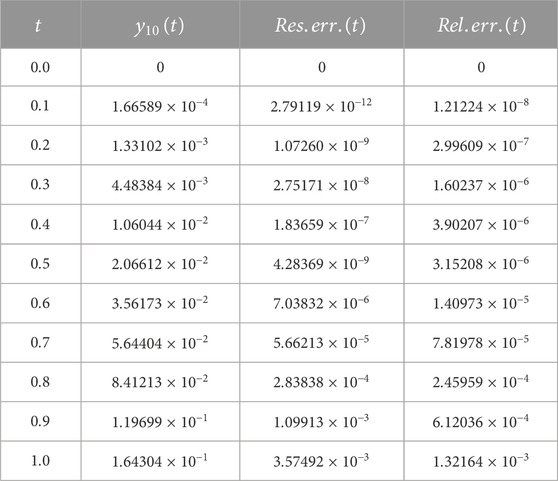
TABLE 5. The $10$^th approximate LRPS solution of the IVP (4.46) and (4.47) and the residual and relative errors.

On the other hand, what specialists in MEMS system implementations are most interested in is the pull-in phenomenon analysis. The MEMS system in Eq. 4.46 and Eq. 4.47 conducts either periodically or unsteadily. This behavior depends on the value of the voltage-related parameter, $\theta$. At small values of $\theta$, the solution of the system is stable and periodic, whereas at large values of $\theta$, it becomes unstable, called pull-in instability. Figure 1 shows that the system is stable and periodic at $\theta$ values less than or equal to the critical value ($\theta =0.203632188$) [52], and it becomes unstable at $\theta$ values greater than the critical one.

FIGURE 1

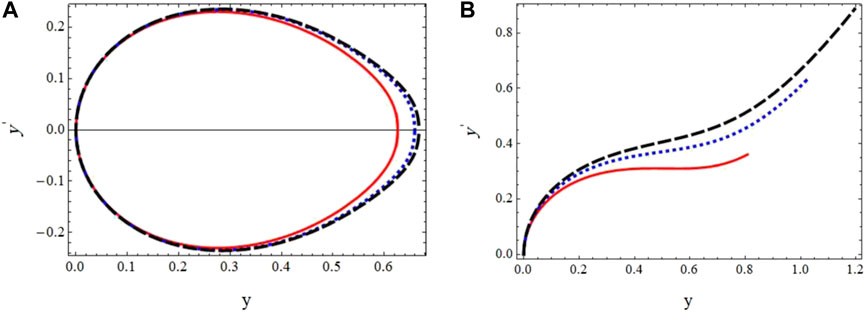
FIGURE 1. Phase trajectories at different values of $\theta$. (A) Solid line: $\theta =0.2$; dotted line: $\theta =0.203$; and dashed line: $\theta =0.203632188$. (B) Solid line: $\theta =0.2037$; dotted line: $\theta =0.25$; and dashed line: $\theta =0.3$.

5 Conclusion

This study aims to test the efficiency of the LRPS method in finding series solutions for ODEs, which are difficult to solve in the analytical methods. We have succeeded in providing a solution to the general form of linear ODEs whose coefficients are analytical functions as an exact solution in a PS form. We also dealt with non-linear ODEs in the proposed technique and found approximate solutions with high accuracy. The biggest surprise is the success of the LRPS method in providing series solutions for the equations about the singular points that coincide with the exact results in some examples. Using the LRPS method, there is no longer an obstacle to obtaining a PS solution for a broad class of ODEs. In addition, the idea of the method circumvented the use of the LT to solve non-linear equations to which the LT is difficult to apply. In addition to the method’s efficiency in arriving at exact solutions, LRPS is easy and fast in finding the coefficients of a series solution. There is no doubt that we can use the new method to solve other sets of equations that we did not have to deal with in previous studies, such as using it to solve partial differential equations, integral equations, integrodifferential equations, and linear or non-linear, as well as algebraic equations. We should not forget that the method has not been applied to solve differential equations with boundary conditions. All these and other topics will be under research by our research team in the next stage.

Data availability statement

The original contributions presented in the study are included in the article/Supplementary Material; further inquiries can be directed to the corresponding author.

Author contributions

All authors listed have made a substantial, direct, and intellectual contribution to the work and approved it for publication.

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

1. King A, Billingham J, Otto S. Differential equations: Linear, nonlinear, ordinary and partial. Cambridge: Cambridge University Press (2003).

Google Scholar

2. Huntley E, Pickering WM, Zinober ASI. The numerical solution of linear time-dependent partial differential equations by the Laplace and fast Fourier transforms. J Comput Phys (1978) 27(2):256–71. doi:10.1016/0021-9991(78)90008-6

CrossRef Full Text | Google Scholar

3. Adomian G. A review of the decomposition method and some recent results for nonlinear equations. Comput Maths Appl (1991) 21(5):101–27. doi:10.1016/0898-1221(91)90220-x

CrossRef Full Text | Google Scholar

4. Evans DJ, Raslan KR. The Adomian decomposition method for solving delay differential equation. Int J Comput Maths (2005) 82(1):49–54. doi:10.1080/00207160412331286815

CrossRef Full Text | Google Scholar

5. Ibijola EA, Adegboyegun BJ, Halid OY. On Adomian Decomposition Method (ADM) for numerical solution of ordinary differential equations. Adv Nat Appl Sci (2008) 2(3):165–70.

Google Scholar

6. He JH. Approximate solution of nonlinear differential equations with convolution product nonlinearities. Comput Methods Appl Mech Eng (1998) 167(1-2):69–73. doi:10.1016/s0045-7825(98)00109-1

CrossRef Full Text | Google Scholar

7. He JH. Variational iteration method–a kind of non-linear analytical technique: Some examples. Int J non-linear Mech (1999) 34(4):699–708. doi:10.1016/s0020-7462(98)00048-1

CrossRef Full Text | Google Scholar

8. Abbasbandy S. Numerical solution of non-linear Klein–Gordon equations by variational iteration method. Int J Numer Methods Eng (2007) 70(7):876–81. doi:10.1002/nme.1924

CrossRef Full Text | Google Scholar

9. Anjum N, He JH, Ain QT, Tian D. Li-He’s modified homotopy perturbation method for doubly-clamped electrically actuated microbeams-based microelectromechanical system. Facta Universitatis, Ser Mech Eng (2021) 19(4):601–12. ‏. doi:10.22190/fume210112025a

CrossRef Full Text | Google Scholar

10. Anjum N, He JH. Homotopy perturbation method for N/MEMS oscillators. In: Mathematical methods in the applied sciences (2020). ‏.

CrossRef Full Text | Google Scholar

11. Saadeh R. Numerical algorithm to solve a coupled system of fractional order using a novel reproducing kernel method. Alexandria Eng J (2021) 60(5):4583–91. doi:10.1016/j.aej.2021.03.033

CrossRef Full Text | Google Scholar

12. Liao W, Zhu J, Khaliq AQ. An efficient high-order algorithm for solving systems of reaction-diffusion equations. Numer Methods Partial Differential Equations (2002) 18(3):340–54. doi:10.1002/num.10012

CrossRef Full Text | Google Scholar

13. Abbasbandy S. Soliton solutions for the Fitzhugh–Nagumo equation with the homotopy analysis method. Appl Math Model (2008) 32(12):2706–14. doi:10.1016/j.apm.2007.09.019

CrossRef Full Text | Google Scholar

14. Pukhov G. Taylor transforms and their application in electrical engineering and electronics (Russian book). Kiev: Izdatel'stvo Naukova Dumka (1978). p. 259. p, In Russian.

Google Scholar

15. Pukhov GE. Differential transformations of functions and equations. Kiev: Naukova Dumka (1980). p. 54–7. (in Russian).

Google Scholar

16. Abbasov TEYMURAZ, Bahadir AR. The investigation of the transient regimes in the nonlinear systems by the generalized classical method. Math Probl Eng (2005) 2005(5):503–19. doi:10.1155/mpe.2005.503

CrossRef Full Text | Google Scholar

17. Chawla M. A fourth-order tridiagonal finite difference method for general non-linear two-point boundary value problems with mixed boundary conditions. IMA J Appl Maths (1978) 21(1):83–93. doi:10.1093/imamat/21.1.83

CrossRef Full Text | Google Scholar

18. Ascher UM, Ruuth SJ, Wetton BT. Implicit-explicit methods for time-dependent partial differential equations. SIAM J Numer Anal (1995) 32(3):797–823. doi:10.1137/0732037

CrossRef Full Text | Google Scholar

19. Burrage K, Tian T. Predictor-corrector methods of runge--kutta type for stochastic differential equations. SIAM J Numer Anal (2002) 40(4):1516–37. doi:10.1137/s0036142900372677

CrossRef Full Text | Google Scholar

20. Feng Z, Knobel R. Traveling waves to a Burgers–Korteweg–de Vries-type equation with higher-order nonlinearities. J Math Anal Appl (2007) 328(2):1435–50. doi:10.1016/j.jmaa.2006.05.085

CrossRef Full Text | Google Scholar

21. Eslami M, Fathi Vajargah B, Mirzazadeh M, Biswas A. Application of first integral method to fractional partial differential equations. Indian J Phys (2014) 88(2):177–84. doi:10.1007/s12648-013-0401-6

CrossRef Full Text | Google Scholar

22. Ascher UM, Petzold LR. Computer methods for ordinary differential equations and differential-algebraic equations. Philadelphia, PA: Society for Industrial and Applied Mathematics (1998). p. 61.

Google Scholar

23. Ostrowski AM. Solution of equations and systems of equations: Pure and applied mathematics: A series of monographs and textbooks, vol. 9. Amsterdam: Elsevier (2016).

Google Scholar

24. Hueso JL, Martínez E, Teruel C. Multipoint efficient iterative methods and the dynamics of Ostrowski's method. Int J Comput Maths (2019) 96(9):1687–701. doi:10.1080/00207160.2015.1080354

CrossRef Full Text | Google Scholar

25. Li D, Zhang C. Nonlinear stability of discontinuous Galerkin methods for delay differential equations. Appl Maths Lett (2010) 23(4):457–61. doi:10.1016/j.aml.2009.12.003

CrossRef Full Text | Google Scholar

26. Zaibin Z, Zhizhong S. A Crank-Nicolson scheme for a class of delay nonlinear parabolic differential equations. J Numerica Methods Comput Appl (2010) 31(2):131.

Google Scholar

27. Zhou Y, Cui M, Lin Y. Numerical algorithm for parabolic problems with non-classical conditions. J Comput Appl Maths (2009) 230(2):770–80. doi:10.1016/j.cam.2009.01.012

CrossRef Full Text | Google Scholar

28. Geng F, Cui M. A reproducing kernel method for solving nonlocal fractional boundary value problems. Appl Maths Lett (2012) 25(5):818–23. doi:10.1016/j.aml.2011.10.025

CrossRef Full Text | Google Scholar

29. Khuri SA. A Laplace decomposition algorithm applied to a class of nonlinear differential equations. J Appl Math (2001) 1(4):141–55. doi:10.1155/s1110757x01000183

CrossRef Full Text | Google Scholar

30. Kiymaz O. An algorithm for solving initial value problems using Laplace Adomian decomposition method. Appl Math Sci (2009) 3:1453–9.

Google Scholar

31. Nadeem M, He JH. He–Laplace variational iteration method for solving the nonlinear equations arising in chemical kinetics and population dynamics. J Math Chem (2021) 59:1234–45. doi:10.1007/s10910-021-01236-4

CrossRef Full Text | Google Scholar

32. Rehman S, Hussain A, Rahman JU, Anjum N, Munir T. Modified Laplace based variational iteration method for the mechanical vibrations and its applications. acta mechanica et automatica (2022) 16(2):98–102. ‏. doi:10.2478/ama-2022-0012

CrossRef Full Text | Google Scholar

33. Anjum N, He JH. Laplace transform: Making the variational iteration method easier. Appl Maths Lett (2019) 92:134–8. ‏. doi:10.1016/j.aml.2019.01.016

CrossRef Full Text | Google Scholar

34. He K, Nadeem M, Habib S, Sedighi HM, Huang D. Analytical approach for the temperature distribution in the casting-mould heterogeneous system. Int J Numer Methods Heat Fluid flow (2022) 32(3):1168–82. ‏. doi:10.1108/hff-03-2021-0180

CrossRef Full Text | Google Scholar

35. Fang J, Nadeem M, Habib M, Karim S, Wahash HA. A new iterative method for the approximate solution of klein-gordon and sine-gordon equations. J Funct Spaces (2022) 2022:1–9. doi:10.1155/2022/5365810‏

CrossRef Full Text | Google Scholar

36. Anjum N, Suleman M, Lu D, He JH, Ramzan M. Numerical iteration for nonlinear oscillators by Elzaki transform. J Low Frequency Noise, Vibration Active Control (2020) 39(4):879–84. ‏. doi:10.1177/1461348419873470

CrossRef Full Text | Google Scholar

37. Eriqat T, El-Ajou A, Oqielat MN, Al-Zhour Z, Momani S. A new attractive analytic approach for solutions of linear and nonlinear neutral fractional pantograph equations. Chaos, Solitons and Fractals (2020) 138:109957. doi:10.1016/j.chaos.2020.109957

CrossRef Full Text | Google Scholar

38. El-Ajou A. Adapting the Laplace transform to create solitary solutions for the nonlinear time-fractional dispersive PDEs via a new approach. The Eur Phys J Plus (2021) 136(2):229–2. doi:10.1140/epjp/s13360-020-01061-9

CrossRef Full Text | Google Scholar

39. El-Ajou A, Al-Zhour Z. A vector series solution for a class of hyperbolic system of Caputo time-fractional partial differential equations with variable coefficients. Front Phys (2021) 9:525250. doi:10.3389/fphy.2021.525250

CrossRef Full Text | Google Scholar

40. Burqan A, El-Ajou A, Saadeh R, Al-Smadi M. A new efficient technique using Laplace transforms and smooth expansions to construct a series solution to the time-fractional Navier-Stokes equations. Alexandria Eng J (2022) 61(2):1069–77. doi:10.1016/j.aej.2021.07.020

CrossRef Full Text | Google Scholar

41. Oqielat MN, El-Ajou A, Al-Zhour Z, Eriqat T, Al-Smadi M. A new approach to solving fuzzy quadratic Riccati differential equations. Int J Fuzzy Logic Intell Syst (2022) 22(1):23–47. ‏. doi:10.5391/ijfis.2022.22.1.23

CrossRef Full Text | Google Scholar

42. Saadeh R, Burqan A, El-Ajou A. Reliable solutions to fractional Lane-Emden equations via Laplace transform and residual error function. Alexandria Eng J (2022) 61(12):10551–62. doi:10.1016/j.aej.2022.04.004

CrossRef Full Text | Google Scholar

43. Salah E, Qazza A, Saadeh R, El-Ajou A. A hybrid analytical technique for solving multi-dimensional time-fractional Navier-Stokes system. AIMS Maths (2023) 8(1):1713–36. doi:10.3934/math.2023088

CrossRef Full Text | Google Scholar

44. Alquran M, Ali M, Alshboul O. Explicit solutions to the time-fractional generalized dissipative Kawahara equation. J Ocean Eng Sci (2022) 1–5. doi:10.1016/j.joes.2022.02.013

CrossRef Full Text | Google Scholar

45. Eriqat T, Oqielat MN, Al-Zhour Z, Khammash G, El-Ajou A, Alrabaiah H. Exact and numerical solutions of higher-order fractional partial differential equations: A new analytical method and some applications‏. Pramana (2022) 96(4):207‏. doi:10.1007/s12043-022-02446-4

CrossRef Full Text | Google Scholar

46. Saadeh R, Ala’yed O, Qazza A. Analytical solution of coupled hirota–satsuma and KdV equations. Fractal and Fractional (2022) 6(12), 694. ‏doi:10.3390/fractalfract6120694

CrossRef Full Text | Google Scholar

47. Saadeh R, Qazza A, Amawi K. A new approach using integral transform to solve cancer models. Fractal and Fractional (2022) 6(9), 490.‏doi:10.3390/fractalfract6090490

CrossRef Full Text | Google Scholar

48. El-Ajou A, Oqielat MN, Al-Zhour Z, Momani S. A class of linear non-homogenous higher order matrix fractional differential equations: Analytical solutions and new technique‏. Fractional Calculus Appl Anal (2020) 23(2), 356–77. doi:10.1515/fca-2020-0017

CrossRef Full Text | Google Scholar

49. Eriqat T, Oqielat MN, Al-Zhour Z, El-Ajou A, Bataineh A. Revisited Fisher’s equation and logistic system model: A new fractional approach and some modifications‏. Int J Dyn Control (2022) 11, 555–63. doi:10.1007/s40435-022-01020-5

CrossRef Full Text | Google Scholar

50. Nagle RK, Saff EB, Snider AD. Fundamentals of differential equations. United States: Pearson (2018).

Google Scholar

51. Zill DG, Shanahan PD. A first course in complex analysis with applications. London: Jones & Bartlett Learning (2013).

Google Scholar

52. Feng GQ, Niu JY. The analysis for the dynamic pull-in of a micro-electromechanical system‏. J Low Frequency Noise, Vibration Active Control (2022) 146134842211455. doi:10.1177/14613484221145588

CrossRef Full Text | Google Scholar