ECMI resonance in AKR revisited: Hyperbolic resonance, harmonics, and wave–wave interaction

1 Introduction

The electron cyclotron maser instability (ECMI) mechanism [1, 13, 20, 32] has, for already close to half a century, been identified as the canonical mechanism of generating AKR, the celebrated “auroral kilometric radiation” [first analyzed by [5], who identified its auroral origin], which is a sporadic narrow-banded intense radio emission [discovered in [6] in their hardly accessible work]. It is emitted preferentially during substorms, the major disturbance [1, 2, 7] in Earth’s magnetosphere.

AKR [for a recent review of observations, cf., e.g., [10]] propagates in the X-mode polarization and is radiated from the auroral zone close to Earth where the magnetic field is strong, and the thermal plasma on various scales becomes locally diluted, frequently with a very small plasma-to-cyclotron frequency ratio ω_e/ω_ce ≪ 1. Under such circumstances, the ECMI sets on if only its necessary and sufficient conditions are both met simultaneously. These refer to the cyclotron resonance of weakly relativistic electrons occupying an excited energy state [first suggested in a more general astrophysical context by [1]] and, for the sufficient condition, to a suitable electronic energy source. In classical physics, an excited non-thermal state is identified with some highly non-thermal electron phase-space distribution function that deviates strongly from a thermal [even anisotropic relativistic, see [11]] Boltzmann–Maxwell distribution. Experimentally, the relevant distribution that would be effective in exciting the ECMI has not been ultimately identified yet. The distribution is conventionally assumed to be kind of a simple (weakly relativistic) loss-cone distribution [cf., e.g., [12, 40]] in phase space as it has frequently been measured [for a typical in situ measurement of the auroral magnetosphere, cf., e.g., [14]] in the presumable AKR source region, an assumption which has, however, been challenged [4, 15].

In a recent note [16], we inspected the paradigmatic mechanism of auroral kilometric radiation, the most intense natural radio emission in near-Earth space. We noted a number of problems with this mechanism that have not been or were at most approximately solved yet. Nevertheless, it seems to be certain that the ECMI is the sole sufficiently strong, and thus reasonable and probable, mechanism that could explain the emission of the surprisingly intense radiation pattern of AKR. Simultaneously, it may also serve as the non-thermal radio emission paradigm in strongly magnetized objects for application in other places in space: planetary magnetospheres in general, extrasolar planetary systems, and probably in astrophysics as well to generate sporadic intense emissions in the radio band, which cannot be understood as synchrotron radiation but must have been caused by unknown non-thermal electron distributions, even though the most effective of these distributions still have to be identified unambiguously.

In the present note, we do not go into the important question of the sufficient condition: what kinds of distributions are responsible for ECMI? We rather deal merely with the necessary condition that has to be clarified first, prior to considering which most probable and experimentally supported phase-space distribution must be chosen to obtain sufficient radiation intensities. Here, we investigate and attempt to answer the following question: given any suitable distribution function, under which conditions can the ECMI become excited and escape into free space, hopefully at the observed large amplitudes? This question is related to the kinetic theory and the condition of resonance between the ECMI-source electrons and the relevant electromagnetic wave mode.

2 Resonance—The necessary condition

The ECMI is a kinetic instability emitted in the X-mode polarization [cf., e.g., [3, 32]]. By reference to observations, it propagates (predominantly) in the electromagnetic X-R mode [3, 17] almost perpendicular to the strong ambient magnetic field $\vec{B}$. In the ECMI, the X-mode is excited when, as noted previously, the electron component in the plasma exhibits a particular momentum space distribution function, representing the equivalent of an elevated energy state of the resonant electron component.

Assume a relativistic electron velocity (momentum) distribution $f_e(\vec{p})$ of such an energetically elevated kind. In a certain range of frequencies ω and wavenumbers $\vec{k}$, it obeys the required property and allows for the excitation of the ECMI with the growth rate:

${\left.\mathrm{\Gamma }\left(\omega ,\vec{k}\right)=-\mathrm{I}\mathrm{m}\mathcal{D}\left(\omega ,\vec{k}\right)/{\partial }_{\omega }\mathrm{R}\mathrm{e}\mathcal{D}\left(\omega ,\vec{k}\right)\right|}_{{\omega }_X}=\sum _n{\mathrm{\Gamma }}_n\left(\omega ,\vec{k}\right)>0.(1)$

Here, $\omega (\vec{k})={\omega }_X(\vec{k})$ is the X-mode frequency as a function of wavenumber $\vec{k}$ and $\mathcal{D}(\omega ,\vec{k})$ is the kinetic dispersion relation, explicitly given in [3, 17] and, for a loss-cone distribution, explicated in [19], taken at the X-mode frequency and wavenumber [for the full magneto-ionic theory¹ of the X-mode in a cold electron–proton plasma, cf., e.g., [20, 21]]. $\mathcal{D}(\omega ,\vec{k})$ results from phase-space integration over the source-electron distribution function $f_e(\vec{p})$ in a homogeneous magnetized plasma and its gyrotropic derivatives with respect to the components p_‖, p_⊥ of $\vec{p}$, a quite involved expression in a non-Maxwellian plasma even for purely perpendicular wave propagation of the X-mode.

In instability, each resonance n provides a positive/negative contribution to the total positive growth rate $\mathrm{\Gamma }(\omega ,\vec{k})>0$ at the particular frequency. This growth rate, being a function of the X-mode frequency ω_X, accordingly exhibits discrete maxima/minima at or near each resonance n, depending on the contribution of ${\mathrm{\Gamma }}_n(\omega ,\vec{k})$ being positive or not at that particular frequency. Plasmas like the upper-auroral substorm-magnetosphere are capable of exciting the ECMI with the growth rate Γ > 0, are dilute with ω_ce ≫ ω_e, and, for the purposes of X-mode propagation, can, sufficiently justified, be considered cold and non-relativistic, as it is the only weakly relativistic non-thermal auroral electron population, not necessarily being of ionospheric origin and responsible for the unstable excitation of the ECMI. However, this may be different in much hotter astrophysical plasmas, where the relativistic modification in the X-R mode dispersion may have to be taken into account, a problem that is ruled out in the context of the magnetosphere. The assumed low-density state relegates the source of AKR and excitation of ECMI to the spatially extended auroral upward-current region and generally excludes the narrow and dense downward-current region, which also implies that the prevalent electron distribution is believed to be of the loss-cone family. This notion has been challenged [16, 35] though not disproved. In this study, no attempt is made to calculate the growth rate for any specific distribution, which leaves this question open.

2.1 Harmonic resonances n > 1

The necessary condition for contributing to instability at the harmonic number n > 1 and parallel or antiparallel propagation is

$\omega -n{\omega }_{ce}/\gamma -k_{\Vert }c{\beta }_{\Vert }=0,(2)$

where k_‖ = k cos θ is the nth resonance in the phase-space integral, with n = ±1, ±2, …, and the cyclotron harmonic number which, in calculating the total growth rate $\mathrm{\Gamma }(\omega ,\vec{k})$ as a function of the X-mode frequency ω = ω_X, is summed over. Because the relativistic factor γ > 1, their fundamental (relativistic) resonant frequency ω_1X = ω_ce/γ at n = 1 is always below the non-relativistic cyclotron frequency ω_ce = eB/m_e and thus confined to the plasma, while in all higher harmonics |n| > 1, the resonant frequencies ω_nX exceed the X-mode stop band ${\omega }_{uh}\le {\omega }_X\le {\omega }_{co}^u$ between the upper hybrid ${\omega }_{uh}={\omega }_{ce}\sqrt{1+{\omega }_e^2/{\omega }_{ce}^2}$ and upper cut-off ${\omega }_{co}^u=\frac{1}{2}{\omega }_{ce}(\sqrt{1+4{\omega }_e^2/{\omega }_{ce}^2}+1)$ frequencies. While the fundamental cannot escape without help, the higher harmonics would naturally radiate away at about the speed of light if excited, having had little time for amplification and thus should generally be rather weak.

In the growth rate sum, each term ${\mathrm{\Gamma }}_n(\omega ,\vec{k})$ gives the contribution of the harmonic resonance n to $\mathrm{\Gamma }(\omega ,\vec{k})$ or, in other words, the growth rate of the harmonic frequency at number n. The harmonic number −∞ < n < ∞ introduces an infinite chain of possible resonances from which the given distribution function $f_e(\vec{p})$ and the available resonant electron energies ${ϵ}_e=m_e{c}^2\gamma (\vec{p})$ must be chosen. For emission, the AKR source must be relativistic [13, 20, 21, 33], which is taken care of in $\gamma (\vec{p})=\sqrt{1+p^2/m_e^2{c}^2}$, and the electron momentum $\vec{p}=m_e\gamma c\vec{\beta }$, where $\vec{\beta }\equiv \vec{v}/c$ is defined.

Working in momentum space $\vec{p}$ is more convenient. It has the advantage that no restriction is to be made on $\vec{p}$ as the fully relativistic momentum spreads the entire space 0 ≤ |p| < ∞, thereby avoiding the inconvenient upper bound on β ≤ 1, the circle of light speed radius in $\vec{\beta }$-space, which apparently excludes any high-speed beams from becoming involved. This artefact disappears in momentum space.

For any γ ≳ 1 and κ_‖ = k_‖c/ω_ce = kc cos θ/ω_ce, the fully relativistic resonance condition reads

$\gamma \left(\vec{p}\right)x-{\kappa }_{\Vert }{p}_{\Vert }/m_{e}c=n,(3)$

where x = ω/ω_ce is the normalized frequency. Introducing the parallel momentum shift $p_0=n{m}_{e}c{\kappa }_{\Vert }/(x^2-{\kappa }_{\Vert }^2)$ yields the resonance line in gyrotropic momentum space (p_‖, p_⊥) which is an ellipse, that is,

$\frac{{\left(p_{\Vert }-p_0\right)}^2}{a_{\Vert p}^2}+\frac{p_{\perp }^2}{a_{\perp p}^2}=1,\mathrm{w}\mathrm{i}\mathrm{t}\mathrm{h}0<p^2<\infty ,(4)$

where the two radii are given by

$a_{\Vert p}^2=m_e^2{c}^2{x}^2\left(n^2+{\kappa }_{\Vert }^2-x^2\right)/{\left(x^2-{\kappa }_{\Vert }^2\right)}^2,(5)$

$a_{\perp p}^2=m_e^2{c}^2\left(n^2+{\kappa }_{\Vert }^2-x^2\right)/\left(x^2-{\kappa }_{\Vert }^2\right).(6)$

For κ_‖ = k_‖ = 0, the ellipse degenerates into an unshifted circle, and all perpendicular harmonic emissions are below x < n for any energy γ. Usually, the resonance ellipse is expressed in $\vec{\beta }$ in the literature. There is a subtle difference between the two representations of $\vec{\beta }$ and $\vec{p}$ resonances. The former is insensitive to the relation between frequency x and parallel wavenumber κ_‖, whereas in the latter, this relation may affect the shape of the resonance curve, a problem we will return to later.

In oblique propagation, the case $x^2>n^2+{\kappa }_{\Vert }^2$ is excluded, as both radii would become imaginary. In order to maintain an ellipse, one requires that $a_{\perp p}^2>0$ is positive, which implies that x > κ_‖ and $n^2>x^2-{\kappa }_{\Vert }^2$. Of course, emission is below

$x<\sqrt{n^2+{\kappa }_{\Vert }^2}.(7)$

The higher the harmonic number, the more oblique the wave mode which contributes. For small obliqueness θ ≲ π/2, the most interesting case is the free space ECMI with ω_Xn = kc. This sets a condition on the angle of emission for extension above harmonic n in the frequency band

$n<\frac{{\omega }_{Xn}}{{\omega }_{ce}}<\frac{n}{|\sin \theta |},(8)$

which is only a narrow range. There is no restriction on any emission below n, other than that the frequency must exceed the upper frequency cut-off ${\omega }_{co}^u$. This gives, for the small ratio ω_e/ω_ce < 1, the auxiliary condition,

$1+\frac{{\omega }_e^2}{{\omega }_{ce}^2}<\frac{{\omega }_{Xn}}{{\omega }_{ce}}=\frac{n}{\gamma }(9)$

for excitation and propagation in the nth harmonic. An upper limit γ ≲ n is set on the electron energy ϵ_e = m_ec²γ in resonance with the nth harmonic to contribute to the radiation near the upper cut-off, meaning that all resonances contribute to radiation in the lowest band of the free-space X-mode which, therefore, will be the most intense.

Below n, resonances and emissions are, in principle, unrestricted. However, the last condition also allows just for a narrow range $|n|<x<\sqrt{2}|n|$ of frequencies above |n|, depending on the electron distribution function and resonant energy γ whether or not it favors ECMI. At higher frequencies above this limit, the resonance condition does not permit radiation, a general necessary condition which is independent of any particle distribution function. It weakly contradicts the claims in the study by [19] while, at the same time, making them precise. Generally, harmonic emissions will always be below the harmonic n with just that the narrow range of oblique emission being above n. Observation of high-frequency bounded radiation can be taken as measurement of n.

However, though harmonic resonances (and in case of causing instability realized as radiation) are possible, they will necessarily be rather weak because the radiation is on the upper X-mode branch where it readily escapes from the source region at light velocity c. The most intense directly excited emission results from below the second harmonic x = ω/ω_ce < 2, just above the upper frequency cut-off,

${\omega }_{co}^u=\frac{1}{2}{\omega }_{ce}\left[{\left(1+4{\omega }_e^2/{\omega }_{ce}^2\right)}^{1/2}+1\right]<{\omega }_{nX},(10)$

where all higher harmonics also contribute if present. In the magnetosphere, only radiation below n = 2 is of interest, being restricted to frequencies ${\omega }_{co}^u<{\omega }_{2X}<2{\omega }_{ce}$ and yielding for the resonant electron energy the upper limit,

$1<\gamma <2/\left(1+{\omega }_e^2/{\omega }_{ce}^2\right).(11)$

This implies that in the auroral AKR source region, electrons of energy ϵ_e = m_eγc² ≲ 0.9 MeV are eligible of directly exciting AKR beneath the second X-mode harmonic in about perpendicular propagation in free space if only their distribution function suites the ECMI. This range of necessary electron energies indeed includes auroral energies, suggesting that second harmonic AKR radiation can naturally originate from the auroral magnetosphere, as was proposed by Wu & Qiu [19] and suggested from observation by [24]. Radiation should, however, be weak for the aforementioned reason of unrestricted escape and lack of spatial amplification. Generally, auroral electron energies are far below this limit [however, for a different observation cf., e.g., [25]]. They barely are capable of exciting higher harmonics. For this simple reason, harmonics n > 2 should be absent in AKR.

2.2 Ultra-relativistic resonance

The absence of any restriction on the momentum $\vec{p}$ suggests that even very high resonant electron momenta/energies could, in general, participate in the ECMI. Turning to the extreme, this raises interest in the ultra-relativistic limit, which, here, is listed for completeness, not for application in the magnetosphere, but will probably be of vital importance in astrophysics.

Ultra-relativistic conditions imply $p^2\gg m_e^2{c}^2$ and $\gamma (\vec{p})=p/m_{e}c$. The resonance ellipse has radii,

$\frac{a_{\Vert p}^2}{m_e^2{c}^2}=\frac{n^2{x}^2}{{\left(x^2-{\kappa }_{\Vert }^2\right)}^2},\frac{a_{\perp p}^2}{m_e^2{c}^2}=\frac{n^2}{x^2-{\kappa }_{\Vert }^2}.(12)$

It degenerates into a circle in perpendicular propagation κ_‖ = 0 of radius a_p = nm_ec/x. Generally, one has

$\frac{\omega }{{\omega }_{ce}}=\frac{n}{p/m_{e}c}+{\kappa }_{\Vert }\cos {\theta }_p,(13)$

where θ_p is the angle of the momenta of the resonant particles. The bounds on either n or p are obtained when replacing the frequency with the upper X-mode cut-off,

$\frac{|n|}{p/m_{e}c}>\left|1+\frac{{\omega }_e^2}{{\omega }_{ce}^2}-{\kappa }_{\Vert }\cos {\theta }_p\right|,|n|>1.(14)$

Remember that n can be both positive and negative as it enters the sum of harmonic growth rates Γ_n. The second condition on n just points out that this limitation applies to all harmonic emissions propagating in the free space X-R mode.

2.3 Resonance at the fundamental

In view of application to the terrestrial magnetosphere, it has been correctly claimed [13] that the (weakly relativistic) ECMI resonance dominates at harmonic number n = 1, the fundamental. The reasons for this are already listed: any higher harmonic barely has time for being amplified substantially before leaving the source. Therefore, the apparent theoretical [19] and suspected or real observationally claimed presence of any intense second harmonic AKR emission in the magnetosphere can hardly be understood as direct excitation.

Restricting to resonance on the lower X-mode branch eliminates all harmonics n > 1. With $0\le \gamma -1=\sqrt{1+p^2/m^2{c}^2}-1\ll 1$, this is true in the auroral region, from where the ECMI wave cannot escape into free space (Figure 1), as this requires traversing the X-mode stop band ${\omega }_{uh}\le \omega \le {\omega }_{co}^u$ between the upper hybrid and upper cut-off frequencies.

FIGURE 1

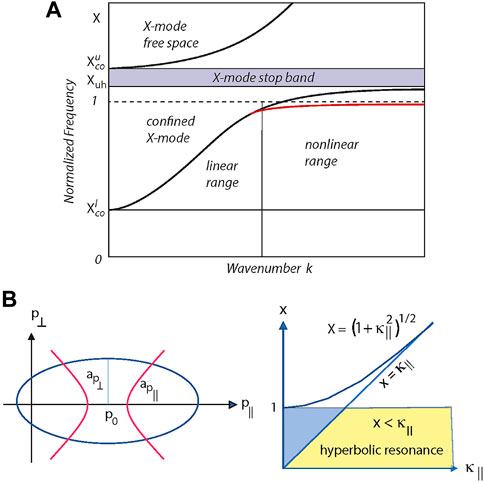
FIGURE 1. (A) Plasma-confined X-mode dispersion relation in the auroral upward-current AKR source region (lower solid curve) under the prevalent low-density plasma condition ω_e ≪ ω_ce. The upper curve is the free-space X-mode. In the stop band between both X-mode branches, the X-mode cannot propagate. Normalization of the frequencies is set to x ≡ ω/ω_ce, with x = 1 being the non-relativistic electron cyclotron frequency which is crossed by the linear lower-branch dispersion curve slightly above the relativistically allowed ECMI resonance. It propagates between the lower cut-off and upper hybrid frequencies. The red line approaching x = 1 is the non-linear X-mode dispersion branch at the maintained resonant frequency x_res ≈ const ≲ 1, stretching out to large wavenumbers k. Note that here on the dotted line, the linear dispersion Eq. 17 is invalid. In this range, both the phase and group velocities of the lower-branch X-mode at resonant frequency, which is held constant remaining below ω_ce, are substantially reduced, with the wave becoming quasi-electrostatic in resonance with an appropriate distribution of electrons. The wave–wave interaction becomes probable here and results in escaping radiation at x ≲ 2 on the free-space upper X-mode branch. For four-wave interaction, higher harmonics may become excited. No deformation of the dispersion relation as a function of propagation angle θ is shown here, which would slightly modify resonance, dispersion, and interaction under large-wavenumber conditions, even switching from elliptic to hyperbolic (for the hyperbolic case, see the following part labels). (B) Different resonance topographies Eq. 5 in dependence on the normalized frequency x = ω/ω_ce in the fundamental band x < 1. Elliptic resonance curves of the sort shown in the left part of the figure occur to the left of the line x = κ_‖ and below the curve $x^2=1+{\kappa }_{\Vert }^2$ in the range x < 1 required by the fully relativistic resonance in the fundamental band n = 1. Hyperbolic resonance is obtained in the yellow part on the right for x < κ_‖ and x < 1. Resonant hyperboles are the kind indicated on the left in red color. Apparently, their range is substantially larger than that of the ellipses. However, its extension depends on the restrictions on the large wavenumbers that emerge from the non-linear evolution of the resonance. The range of resonance is in fact not restricted to proximity to x = 1 as in the weakly relativistic resonance theory. At higher relativistic energy with γ ≫ 1, frequencies well below x = 1 become resonant.

Resonance is generally not restricted to proximity to ω_ce. The lower X-mode branch for zero wavenumber k ≈ 0 starts at the lower cut-off frequency ${\omega }_X>{\omega }_{co}^l=\frac{1}{2}[{({\omega }_{ce}^2+4{\omega }_e^2)}^{1/2}-{\omega }_{ce}]\approx {\omega }_e^2/{\omega }_{ce}$ for small ratios of plasma-to-cyclotron frequency, the parameter range where the ECMI becomes effective. Assuming strictly perpendicular propagation k_‖ = 0, all relativistic factors

$1<\gamma <{\omega }_{ce}^2/{\omega }_e^2(15)$

of electrons in the distribution function could, in principle, participate in the resonance. The oblique relativistic resonance condition for those electrons is given by Eq. 3 with n = 1. The parallel shift (now conventionally expressed in $\vec{\beta }$) becomes ${\beta }_0={\kappa }_{\Vert }/(1+{\kappa }_{\Vert }^2)<1$, and the elliptic radii are

$\frac{a_{\Vert }^2}{m_e^2{c}^2}=\frac{1+{\kappa }_{\Vert }^2-x^2}{{\left(1+{\kappa }_{\Vert }^2\right)}^2},\frac{a_{\perp }^2}{m_e^2{c}^2}=1-\frac{x^2}{1+{\kappa }_{\Vert }^2}.(16)$

With large $\gamma \lesssim {\omega }_{ce}^2/{\omega }_e^2$, the resonance is placed far below ω_ce on the lower X-mode branch by the factor ω_e/ω_ce in frequency, if only sufficiently high-energy electrons would be available, implying that the resonant energy in this case would be high. In the magnetosphere, we have ${\omega }_{ce}^2/{\omega }_e^2\gtrsim 10^2$ or even larger which, well away from the cyclotron frequency, yields ϵ_e = m_eγc² ∼ 50 MeV. Such (about ultra-relativistic) electrons are absent there which, in retrospect, justifies the assumption of proximity of the resonance to ω_ce [we note, however, that high energies have been referred to the study by [25], for apparently observed AKR, whose source the authors attribute to the radiation belts]. In remote astrophysical systems, on the other hand, containing very-high, mostly even ultra-relativistic electrons, proximity to the cyclotron frequency may become spurious, and excitation of lower-branch-trapped long-wavelength k_⊥≳ 0 X-mode waves near the lower cut-off ${\omega }_{co}^l<{\omega }_X^l\ll {\omega }_{ce}$ may become possible or should be the rule. Therefore, the ECMI would include almost the entire lower X-mode branch.

A broad energetic electron distribution may undergo resonance over a large part of the lower X-mode branch contributing to the ECMI and growth of lower-branch X-mode waves in a wide range of frequencies ${\omega }_X^l<{\omega }_X(k)<{\omega }_{ce}$. The wavenumbers in resonance are obtained from the pure lower-branch electron X-mode dispersion relation in perpendicular propagation [3, 17].

$\frac{k^2{c}^2}{{\omega }_{ce}^2}=\frac{\left({\omega }_{co}^{u2}-{\omega }^2\right)\left({\omega }^2-{\omega }_{co}^{l2}\right)}{{\omega }_{ce}^2\left({\omega }_{uh}^2-{\omega }^2\right)},(17)$

where, for our purely electronic purposes, the ion contributions and higher powers of small quantities have been neglected.

This dispersion curve crosses the cyclotron frequency at ω = ω_ce, corresponding to $k_{m\perp }\approx \sqrt{2}{\omega }_e/c$, which is about the inverse electron inertial length λ_e = c/ω_e, setting an upper limit on the resonant wavenumber k_⊥, a large number, respectively, short wavelength indeed. The unstable range Δk_⊥ maps to the energy range Δγ(k_⊥) of resonant electrons

$0<k_{\perp }\left(\omega ,\gamma \right)\lesssim \sqrt{2}/{\lambda }_e.(18)$

Depending on the electron distribution function, instability becomes possible almost everywhere along the lower X-mode branch if only sufficiently large electron energies are available. k_⊥ = 0 corresponds to reflection at the lower X-mode cut-off ${\omega }_{co}^l$ and is clearly outside the unstable wavenumber range.

Near ω ≈ ω_ce, the phase velocity of the X-mode becomes $v_X\approx c/\sqrt{2}$, implying that at an observed frequency ω ≲ ω_ce ≈ 300 kHz, the nominal magnetospheric AKR frequency [5], the phase speed is low enough for the wave to experience several amplifications before leaving the source.

In order to check this, we obtain for the group velocity

$v_{gX}=\frac{d\omega }{d{k}_{\perp }}\approx -2^{3/2}{\left(\frac{{\omega }_e}{{\omega }_{ce}}\right)}^{2}c\ll -c,(19)$

which is much smaller than the velocity of light. For an ECMI growth rate Γ(ω_X), the spatial amplification rate K ≈ −Γ/v_gX becomes

$K\left(\omega \right)\approx \frac{\mathrm{\Gamma }\left(\omega \right)}{2\sqrt{2}c}{\left(\frac{{\omega }_{ce}}{{\omega }_e}\right)}^2,(20)$

a comparably large value. Assuming ω_e/ω_ce ≲ 0.1, as approximately applicable to the auroral source region, the group velocity is just the order of v_gX ≲ 10³ km/s. In the auroral magnetosphere, this compares to the Alfvén velocity v_A, giving roughly K ≳ 2 × 10⁻⁴Γ(ω_X) km⁻¹. So, for a growth rate Γ ∼ 10⁻⁴ω, we have at the nominal emission frequency of ω ∼ 300 kHz that

$K\gtrsim 4\times 10^{-1}{\mathrm{k}\mathrm{m}}^{-1}.(21)$

This corresponds to several e-folding lengths over one wavelength, sufficient for excitation of moderate (or even large) amplitude X-mode waves. Of course, growth rates Γ(ω) of this order may be extreme. Reducing Γ(ω) by two orders of magnitude still gives one e-folding over one wavelength of λ_X ∼ 1 km within the oscillation and growth times. Such amplification rates are still large.

This estimate suggests that the ECMI on the lower X-mode branch is capable of generating rather large amplitude-confined X-mode waves close to the local non-relativistic cyclotron frequency ω_ce predominantly because the group velocity is strongly reduced there, and the wave has sufficient time to grow before leaving the source.

Growth becomes substantial here if the source is sufficiently extended over a number of wavelengths in the direction of propagation about perpendicular to the magnetic field ${\vec{B}}_0$. This very fact makes the ECMI on the lower X-mode branch (see Figure 1) very interesting not just by itself but also for its possible non-linear interaction with the dilute plasma component whose pressure is necessarily low and thus susceptible to large-amplitude electromagnetic radiation and the implications of its ponderomotive force. Modulation instability of the unstable ECMI may become possible, causing chains of solitons and structure in the plasma, effects which have not been considered yet in connection with ECMI but may play an important role if investigating its fine structure [compare Figure 2 in [16]] and the reaction/response of the auroral environment to its presence.

Away from the local cyclotron frequency ω_ce, however, growth is reduced on the X-mode branch where higher-energy electrons γ ≫ 0.1 are required to be present in an excited state, a case barely existing in the auroral region. Here, the group speed increases slightly before dropping to low values when approaching the lower X-mode cut-off. In the auroral magnetosphere, large numbers of relativistic electrons are absent [cf., however, [25], for a counter example]. The relation between k_⊥ and γ is

$k_{\perp }^2{\lambda }_e^2+1\approx \frac{1}{{\gamma }^2}\frac{{\omega }_{ce}^2}{{\omega }_e^2}.(22)$

In the longer-wavelength regime λ_⊥ > λ_e, one has

$1<\gamma \lesssim \frac{{\omega }_{ce}}{{\omega }_e}\left(1-\frac{1}{2}{k}_{\perp }^2{\lambda }_e^2\right)(23)$

between k_⊥ and γ away from the plasma resonance with the resonant frequency reduced due to the increase in the required resonant energy. These wavenumbers define the location of the resonance on the lower X-mode branch according to Eq. 17.

The elliptical nature of the resonance condition is, however, not easily matched by any of the reasonable and measured electron distribution functions in the magnetosphere. Such a distribution should be some kind of a (phase-space-shifted) hollow beam or horseshoe distribution with parallel shift β₀ (in terms of the momentum p₀), where highly diluted regions lacking higher-energy electrons in the hole. Their boundaries are formed by accelerated/scattered cold electron beams [11, 26]. This should provide the required positive β_⊥-space gradient mimicking an excited state of the resonant electrons. The beam nature of the distribution is imposed by the finite displacement ± p₀ along the external field, which is seen in the observer’s frame. This poses the question of the formation of such hollow beam distributions. Reasons for them can be found in the generation of electron holes by strong field-aligned currents and have been attributed to the downward-current region in the auroral magnetosphere [21], where such partial hollows have been assumed, either being electron holes or, if of larger scale, so-called horseshoes.

However, guided by auroral zone observations, it seemed that the prevalent electron distribution of downward shifting electrons, part of which is reflected while another part absorbed by the dense ionosphere below, would become a loss-cone distribution, which is also supported by theory. Numerical calculations based on the resonance ellipse and using observed loss-cones [28] found just very small amplification rates there. Moreover, from VLF observation and theory, it became pretty clear that any loss-cones are readily depleted or strongly reduced by intense interaction and amplification of VLF noise [15]. The latter leaves little rudimentary resonance for the excitation of the ECMI and agrees well with the calculations based on the observed loss-cone.

Other relevant electron source-distributions are caused in the generation of electron holes. These result in strong field-aligned currents which decay into localized electrostatic structures of few Debye length ℓ_‖ ∼ few λ_D extension along the magnetic field but large perpendicular scale ℓ_⊥≫ ℓ_‖ of the order of the perpendicular X-mode wavelength ${\ell }_{\perp }\sim k_{\perp }^{-1}$. Inside those holes, the conditions of excited electron states are satisfied. Here, we do not go into a detailed investigation of this most interesting fact [26] that we had referred to in the earlier work [21]. In the next section, we deal with the question what interests us here the most: the condition of excitation of the ECMI on the lower X-mode branch and its possible escape into free space without requiring any usually evoked propagation effects in inhomogeneous plasmas [18, 19, 29].

Depending on the available electron energy and the excited phase-space distribution function f_e (p_⊥, p_‖), the ECMI will become effective over a large section of the lower X-mode branch to drive the X-mode unstable. The range where this could happen is prescribed by the condition of a dilute plasma with ${\omega }_e^2\ll {\omega }_{ce}^2$ and the additional necessary condition on the distribution function that ∂f_e/∂p_⊥ > 0 in an appropriate range on the resonance curve in the (p_‖, p_⊥)-plane. This resonance line for purely perpendicular propagation is given by

$\sqrt{1+p_{\perp }^2/m^2{c}^2+p_{\Vert }^2/m^2{c}^2}={\omega }_{ce}/{\omega }_X^l\left(k_{\perp }\right),(24)$

with ${\omega }_X^l(k_{\perp })$ being the lower X-mode branch frequency and a function of k_⊥ on the right-hand side. Any of those unstable X-mode waves have of course frequency ${\omega }_X^l<{\omega }_{ce}$ below the non-relativistic cyclotron frequency. They are confined to the plasma and detectable only in situ, unless a mechanism is found which allows them to either escape into free space by tunneling the ECMI-X-mode stop band ${\omega }_{ce}<\omega <{\omega }_{co}^u$ between the cyclotron and upper X-mode cut-off frequencies.

The other possibility is to undergo a three-wave interaction process as we proposed [16] and will be investigated in the following section. However, staying with strictly perpendicular propagation, one may also envisage direct excitation of higher harmonics n > 1 of the cyclotron frequency ${\omega }_X^u=n{\omega }_{ce}/\gamma$. Before returning to the three-wave process, we briefly discuss such an interaction process.

2.4 Wave–wave interaction at the fundamental

From observations, it is not entirely clear whether AKR is observed in the second harmonic or not. Fundamental radiation is trapped below the X-mode stop band (see Figure 1) and escapes only under strongly inhomogeneous conditions which have not been clarified convincingly yet. On the other hand, harmonic radiation when identified appears to be surprisingly intense. For the aforementioned reasons, one may doubt the importance of any direct radiation mechanism. The large growth rates Γ_n ∼ nω_ce and large amplification factors κ_n they require are hard to reproduce in theory. Free-space modes escape quickly before picking up any amplification unless the source extends over very large distances while maintaining all the conditions in favor of excitation. In addition to the obvious confinement of the fundamental ω_X ≲ ω_ce, observation of apparently intense harmonic radiation [cf., e.g., [32]] in the spectrograms poses a problem.

Of course, these conditions refer, in addition, to the required sufficient condition on the electron distribution function in phase space and are, probably, not very easy to satisfy in general. They require rather special electron distribution functions which, in order to contribute efficiently to growth, must adapt to the particular geometry of the resonance curve in phase space. Such distribution functions must possess a positive perpendicular momentum gradient along the phase-space resonance or at least large parts of it in order to pick up the contributions of many electrons along the resonance that are elevated to the higher momentum/energy excitation level.

Here, we are interested in conditions which allow transformation of the ECMI at the lower X-mode branch into the free-space mode. As argued previously, at the lower X-mode branch, the ECMI can indeed attain large amplification because of the comparably slow group velocity under the conditions below ω^l < ω_ce. Since waves can be excited here in any direction perpendicular to the external magnetic field, a three-wave process [9, 33], as suggested by [16], becomes possible where two lower branch modes interact to compensate for their large perpendicular wavenumbers and result in a long wavelength mode at roughly the sum of the two frequencies according to the three-wave interaction conditions of conservation of total energy and momentum

${\omega }_X^u={\omega }_{1X}^l+{\omega }_{2X}^l,k_{\perp }^u=k_{1\perp }^l-k_{2\perp }^l\ll k_{\mathrm{1,2}\perp }^l.(25)$

It generates a long-wavelength $k_{\perp }^u\approx {\omega }_X^u/c$ upper X-mode branch of frequency ${\omega }_X^u\lesssim 2{\omega }_{ce}$ below though near the second harmonic n = 2. This wave has large amplitude, propagates in the free-space mode, can escape without any difficulty from the source region, and does not need any further amplification. The condition under which it may meet the free-space branch is that its frequency must be above the upper X-mode branch cut-off. Since each of the resonant waves on the lower branch satisfies the resonance condition ${\omega }_X^l={\omega }_{ce}/\gamma$, the condition for escape of the ECMI-wave at the upper branch becomes

$\frac{{\gamma }_1+{\gamma }_2}{{\gamma }_1{\gamma }_2}>1+{\omega }_e^2/{\omega }_{ce}^2,(26)$

where the indices refer to the two lower branch waves that participate in the interaction, and we neglect powers of small quantities. If the resonant energies do not differ much, this yields

$1<\gamma <\frac{2}{1+{\omega }_e^2/{\omega }_{ce}^2},(27)$

which of course is the same condition as for direct excitation below the second harmonic n = 2 on the upper X-mode branch given previously. Its meaning in the present case is, however, quite different. The two interacting waves are slow and have grown to large amplitudes. In head-on collisional interaction, they result in large-amplitude escaping radiation just below the second harmonic n < 2. For the small frequency ratio ω_e/ω_ce in the denominator, the marginal relativistic factor is close to γ ≲ 2, or, as already noted, the upper limit on the electron energy is ϵ_e ≲ 0.9 MeV.

Low energies excite the ECMI on the lower X-mode branch close to ω_ce, but higher energies near the upper energy limit also contribute. They shift the resonance down on the lower branch according to ${\omega }_X^l={\omega }_{ce}/\gamma$. Thus, the ECMI can, in principle, become excited almost along the entire lower X-mode branch. Nevertheless, escaping radiation generated via the three-wave collision process is allowed only for those waves excited by electrons of the aforementioned limited energies. Their energy determines the location of the resonance on the lower X-mode branch dispersion relation Eq. 17.

We have ${\omega }^2\ll {\omega }_{co}^{u2}$ and neglect higher powers of ω_e/ω_ce, which is justified in all cases where the ECMI is expected to become effective. In that case, the lower X-mode branch dispersion relation Eq. 17 simplifies yielding

$\frac{k_{\perp }^2{c}^2}{{\omega }_{ce}^2}\approx \frac{{\omega }^2-{\omega }_{co}^{l2}}{{\omega }_{ce}^2}=\frac{1}{{\gamma }^2}-\frac{{\omega }_e^2}{{\omega }_{ce}^2}(28)$

for the relation between k_⊥ and γ, which reproduces condition Eq. 15 while holding all along the lower X-mode branch.

$1<\gamma <\frac{{\omega }_{ce}/{\omega }_e}{\sqrt{k_{\perp }^2{\lambda }_e^2+1}}.(29)$

All wavenumbers,

$k_{\perp }{\lambda }_e\lesssim \frac{{\omega }_{ce}}{{\omega }_e}\left(1-\frac{1}{2}\frac{{\omega }_e}{{\omega }_{ce}}\right)(30)$

are eligible for the three-wave ECMI emission process above the upper cut-off frequency, including almost the entire lower-branch wavenumbers. Combination of the last three conditions on γ and k_⊥ yields that the three-wave interaction will become effective for frequency ratios,

${\omega }_{ce}>\sqrt{3}{\omega }_e,(31)$

a condition that is easily met in the auroral magnetosphere, where, under the conditions when emission of AKR occurs, the electron cyclotron frequency by far exceeds the plasma frequency.

To conclude this section, it is of substantial interest to note that exactly the same non-linear wave–wave interaction mechanism of generation of radiation in the free-space X-mode has been explicated in detail for the Z-mode [35] in the approximate second n = 2 and fourth n = 4 harmonics of the cyclotron frequency. This mechanism would, in principle, compete with the ECMI wave–wave generation mechanism on the lower X-mode branch proposed here; otherwise, the two mechanisms would unfortunately exclude each other. The ECMI works solely under the condition that the ratio ω_e/ω_ce ≪ 1 is small. In this case, the Z-mode becomes confined to a rather narrow region around x ≈ ω_e/ω_ce [3]. On the other hand, in the opposite situation, when this ratio is large, as presumably, for instance, in the downward-current region, the ECMI becomes unimportant, and excitation of the Z-mode dominates (see the discussion below in Section 3.2 on downward currents). This is a very interesting case, indeed, as it predicts that, in that case, AKR could be radiated from non-linear coalescence of Z-modes near the upper hybrid frequency ω ∼ ω_uh. Generation of Z-modes in that case is much less restricted than the ECMI on the X-mode. It is well known that the Z-mode is generated rather frequently by the continuous presence of VLF [15] in the auroral magnetosphere, where it is not necessarily found just in the auroral zone and at extreme magnetic activity but spreads over a wider latitudinal and longitudinal region in space and in time. One expects that by the mechanism of wave–wave interaction in both Z-modes (possibly in the downward-current region outside the upward-current region) and X-modes (preferentially in the upward-current region), intense-escaping AKR is produced at nearly same harmonic frequencies in the free-space X-mode.

2.5 Non-linear evolution

The ECMI-unstable lower X-mode branch beneath ω_X/ω_ce ≡ x = 1 is a slow wave with comparably low phase velocity v_ph = ω/k < c and, in particular, low group speed v_g = ∂ω/∂k < c, both substantially less than the velocity of light. As argued in the previous section, these properties allow the wave to grow and achieve amplitudes which are large enough to violate the linear assumption. In this moderately or large-amplitude state and being unable to leave the plasma below the X-mode stop band, the wave exerts a slowly variable ponderomotive force on the dilute low-pressure plasma background (note that the plasma is generally assumed to be at most temperate in this entire theory; what concerns the wave dispersion, so the background is even assumed to be cold.) The ponderomotive force results from an average over the entire ensemble of unstable waves, thus being the effect of collective action. The variation in the ponderomotive force is slow; it occurs on the ion time scale. The plasma reacts to this force as described by the Sagdeev–Zakharov (slowly variable non-linear Schrödinger) equation [cf., e.g., [33, 34]] by exciting ion acoustic waves which under stationary conditions lead to envelope solitons, density depletions that trap the high-frequency lower-branch X-mode waves. The relative quasi-neutral density modulation δN/N₀ (amplitude of the ion acoustic wave) of these structures, which from pressure balance are density depletions (cavitons), is related to the X-mode amplitude as

$\frac{\delta N}{N_0}\approx -\frac{{ϵ}_0}{4m_i{N}_0{c}_{ia}^2}|\delta E_X{|}^2,(32)$

with c_ia ≪ c being the ion acoustic speed. Trapping of the X-mode inside the density depletions causes a spatial modulation of the wave spectrum (one may note that only the electric field amplitude appears here. The magnetic amplitude of the electromagnetic wave is relativistically small.) At the same time, it leads to two other important effects.

First, trapping of the spectrum of participating X-modes splits the waves into two populations of oppositely directed wavenumbers ± k_tr which bounce back and forth inside the density depletions. Several of these waves will thus participate in the aforementioned three-wave process to cause second harmonic radiation ω_X ≲ 2ω_ce. This leads to losses of wave energy and may ultimately terminate the deepening of the density depletions, i.e., stabilizing the non-linear ion acoustic wave amplitude, even though radiative losses generally remain only weak.

The second interesting effect concerns the trapped wave-mode wavelength λ (or wavenumber k_X). Conservation of caviton shape over the time of caviton formation and evolution implies that the number of waves (wavelengths) inside the cavity is conserved and remains constant. Shrinking the cavity size thus necessarily shortens the wavelengths and increases the wavenumber k_X according to

$k^2\propto {ϵ}_0|\delta E_X{|}^2,(33)$

with the wave energy density on the right-hand side which evolves during non-linear formation of the caviton, i.e., the sum of the individual wave energies ℏω per volume of the caviton with frequency, being conserved. This affects the dispersion of the trapped waves. This is very interesting by itself.

Though the trapped X-mode waves inside the cavitons initially propagate in the linear X-mode on the linear dispersion branch, shrinkage and shortening of wavelength modifies the linear X-mode branch near resonance until it becomes non-linear, a rather complicated process which strongly modifies the linear dispersion. In fact, due to the deviation of the dispersion curve from its linear topology that is caused by the resonant interaction with the energetic source-electron component, the X-mode here becomes quasi-electrostatic, which makes it active in affecting the plasma through its ponderomotive force and particle trapping inside the self-consistently generated cavitons [cf., e.g., [30], for the complete non-linear theory of purely electrostatic waves]. The resonance still occurs beneath though close to ω_ce here (unless a non-linear frequency shift is taken into account, which is assumed of higher order, here, and thus negligible). Constancy of wave frequency implies that the non-linear (about electrostatic) interaction stretches the dispersion curve out to large wavenumbers k_nl which substantially exceed the linear wavenumber k while frequency remaining below the electron cyclotron frequency, thereby avoiding crossing it upward to approach the upper hybrid resonance ω_uh which is not allowed by the resonance condition (as long as it remains linear by itself).

This increase in k → k_nl causes a severe additional reduction of the phase velocity $v_{\mathit{ph,nl}}=\omega /k_{nl}\propto \omega /\sqrt{|E_X{|}^2}$. In addition, the sudden self-consistent trapping of the waves inside the cavitons (resulting from the ponderomotive force) implies a violent retardation of the group speed to v_g ∼ c_ia which adjusts it to the ion acoustic velocity. The slowdown in phase velocity substantially increases the spatial amplification rate, as has been argued previously. As a consequence, the waves locally experience many e-foldings and, consequently, also large wave amplification due to an increase in their e-folding length. As a result of these two effects, the amplitude of the trapped X-mode waves will readily grow to become large, which, on the one hand, causes additional deepening of the cavitons while also strongly supporting the wave–wave interaction and second harmonic radiation ω_X ≲ 2ω_ce. Higher harmonic resonance, as explained previously, has little chance to cause comparably intense radiation. In contrast, resonance x = ω/ω_ce ≲ 1 at the lower X-mode branch amplifies the confined X-modes with short wavelengths [picked up, for instance, from thermal electromagnetic background noise, cf., e.g., [36]] which propagate at strongly reduced phase velocity and experience many e-foldings.

3 Hyperbolic resonance

The non-linear deformation of the linear dispersion has another profound effect on the topology of resonance that so far (at least to our knowledge) has been missed in the literature on the ECMI. This is uncovered when considering the resonance condition (4). The linear-state relativistic resonance is the famous ellipse in $\vec{\beta }$- or $\vec{p}$-space. In the non-linear state, however, there arises the possibility for the ellipse to turn into a hyperbola

$\frac{{\left(p_{\Vert }-p_0\right)}^2}{a_{\Vert p}^2}-\frac{p_{\perp }^2}{a_{\perp p}^2}=1.(34)$

This happens when in Eq. 5, during non-linear evolution and increasing wavenumber κ = kc/ω_ce, the conserved normalized frequency x = ω/ω_ce < κ_‖ for some oblique propagation angle θ drops below the parallel normalized non-linear wavenumber κ_‖ (one may note that this leaves the numerators in Eq. 5 invariant such that only the transverse radius a_⊥p is affected to become imaginary). The condition includes only the parallel wavenumber and is thus simply a condition on the angle θ of propagation, which means that

$\cos \theta >\omega /c{k}_{nl}=\frac{v_{\mathit{ph,nl}}}{c}(35)$

exceeds the ratio of the strongly decreased non-linear phase velocity v_ph,nl to light speed. It states that for the topological switch to take place, the angle of resonance should turn more parallel. This condition is readily satisfied close to the gyrofrequency ω_ce already in the linear regime, as indicated in Figure 1, where the dispersion begins to flatten out shortly before crossing the line x = 1. It essentially excludes perpendicular propagation from hyperbolic resonance, which, however, is clear anyway. The restriction of the resonance to x < 1 in onsetting non-linear evolution and the following smooth increase in wavenumber k → k_nl warrant that this condition is always met at oblique propagation, thus satisfying the aforementioned condition which relaxes in further non-linear evolution. One may note that this important change in the resonance topology occurs when working in the fully relativistic resonance regime, which applications have so far avoided. It is of particular importance in the interesting astrophysical ultra-relativistic regime.

Hence, the transition from linear elliptic to non-linear hyperbolic resonance is quite natural. In its course, the resonating wave becomes increasingly oblique during non-linear interaction. On the other hand, it is clear that this case cannot be realized for any of the resonances n > 1 which are not confined and thus do not interact non-linearly.

Manipulation of the relativistic resonance condition $x\gamma (\vec{p})=1+{\kappa }_{\Vert }{p}_{\Vert }/m_{e}c$ with constant x ≈ 1 yields an upper limit on

$\cos \theta <\frac{\gamma -1}{\gamma {\beta }_{\Vert }}\frac{{\omega }_{ce}}{k_{nl}c}=\frac{{ϵ}_{\mathit{kin}}}{m_e{c}^2{\beta }_{\Vert }}\frac{{\omega }_{ce}}{{\omega }_e}{\left(k_{nl}{\lambda }_e\right)}^{-1},(36)$

where k_nl is the increased non-linear wavenumber. This is, in fact, no serious restriction as long as the right-hand side exceeds unity. Otherwise, it just excludes a range of nearly parallel propagation angles, hence permitting hyperbolic resonance over a wide oblique angular interval Δθ.

3.1 Upward current region

As it turns out, the upward-current region becomes the ideal place for application of the hyperbolic resonance. We shall demonstrate that it is best suited to fit the celebrated loss-cone distribution as the primary source for generation of AKR here.

Observations in the presumable upward-current AKR source region of the auroral magnetosphere [e.g., [24]] suggest that the kinetic energy of source electrons is about ϵ_kin ∼ 10 keV, while the frequency ratio amounts to about ω_ce/ω_e ∼ 10. Parallel speeds of the auroral electrons have been measured to be approximately β_‖ ∼ 10⁻¹. Moreover, the electron inertial length in the diluted upward-current region is of order λ_e ∼ 0.5 km. This yields within the uncertainty of these numbers

$\omega /c{k}_{nl}<\cos \theta <1/k_{nl}{\lambda }_e.(37)$

As the left-hand side readily holds close to x = 1, there are no restrictions on the propagation angle here for any non-linear wavelengths λ_nl ≳ λ_e longer than the electron inertial length, a rather weak condition only. If k_nl would further increase beyond this limit, the hyperbolic resonance becomes more oblique though still covering a large angular interval.

It thus seems natural that the resonance in the upward-current region on the lower X-mode branch, the presumably most important domain of its validity, readily switches from elliptic to hyperbolic, which naturally fits the loss-cone distribution and the interior of the loss-cone well if not much better than the resonant ellipse.

This is shown in Figure 2 as an example of available highest-resolution FAST observations of downward electron fluxes in the upward-current region, performed 2 decades ago [14]. The figure suggests that, in contrast to the usually used resonance ellipse, the hyperbolic resonance conveniently covers the entire inner perpendicular electron flux (velocity space distribution) gradient ∂f_e/∂β_⊥ > 0 offered by the interior of the loss-cone for excitation of the ECMI lower-branch X-mode. This has some clarifying implications on the choice of the source-electron distribution function. Hyperbolic resonance is clearly in favor of the celebrated loss-cone distribution as the main electronic phase-space source-distribution here where it is continuously observed and theoretically supported.

FIGURE 2

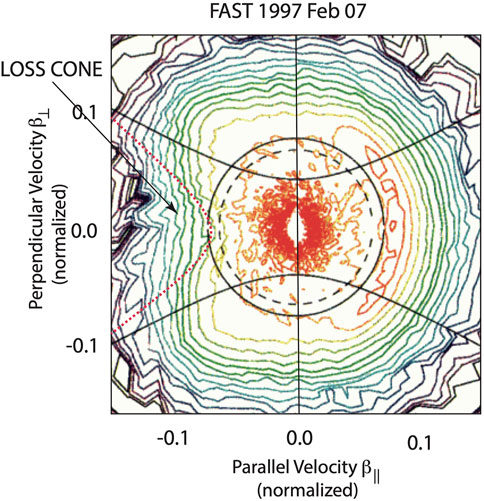
FIGURE 2. Measured loss-cone distribution in the presumable AKR upward-current auroral source region [after 10, which should be consulted for a detailed description of the observations]. The intensity of downward electron fluxes is color-coded (from black to red, covering five orders of flux magnitude), with red having the highest intensities, here, indicating the denser warm auroral-magnetospheric electron background. The comparably wide upward (negative normalized parallel velocities β_‖ = v_‖/c < 0) electron loss-cone is well exhibited. Circles show the theoretical (solid) and observed (dashed) low-speed bounds. At positive parallel speeds, the red banana indicates the high-energy downward auroral electron beam. The two black hyperbolas are theoretical angular limits of inner and outer phase-space regions. The dotted red hyperbola at negative (upward) β_‖ is the resonant hyperbola about along the loss-cone boundary with k_‖c > ω. Positive perpendicular gradients along and inside this hyperbola contribute to resonant ECMI growth. The loss-cone is wide enough to host a continuity of such hyperboles inside its bounds, thus providing the ECMI with a bandwidth Δω at constant frequency ω. Uncertainty of the observations is too large for calculating quantitative numbers (Modified and adapted from Ref. [14]. Courtesy AGU.).

The reasonable conclusion is that in the upward-current region, loss-cone distributions, like those in Figure 2 [14], can under all circumstances drive the lower-branch ECMI just beneath ω ≲ ω_ce (see Figure 1) increasingly unstable and entering its state of non-linear evolution toward large wavenumbers kλ_e < 1. This is expected to happen already for rather moderate amplitudes readily deforming the linear dispersion relation into its non-linear cousin to participate in hyperbolic rather than elliptic resonance.

In the dilute upward-current low-pressure plasma background, it should be stressed that even rather moderately confined ECMI-X-mode amplitudes suffice to enter the non-linear state by choosing a suitable initial wavenumber and frequency interval that the thermal electromagnetic background noise offers for amplification [for the presence of such noise, which for oblique propagation, exists particularly below and close to ω_ce; see [36]].

Such a switch in resonance suites the upward loss-cone distribution quite well for a spectrum Δk_res of wavenumbers k and excitation of a narrow spectral band Δω below ω_ce. These intervals are determined by the angular width of the loss-cone and the steepness of the resonant perpendicular momentum-space gradient.

As described in the caption of Figure 2, the circles separate the loss-cone from the unaffected main plasma distribution at low electron speeds. The observations do not allow for unambiguous identification of a parallel shift p₀ of the distribution. The two black hyperbolic lines drawn map the boundaries of the loss-cone in their upward-directed parts while being artefacts on the downhill side. Tentatively, one resonant hyperbola (red) has been drawn along the boundary of the loss-cone. The entire positive perpendicular momentum/velocity gradient region in the loss-cone could be filled with a continuum of such resonant hyperboles. At any fixed resonant parallel momentum p_‖ with its respective velocity β_‖, the growth rate Γ_n=1 (p_‖, ω) is determined as the function of resonant frequency and provides an estimate of the bandwidth of excitation where observations in situ suggest the AKR source to be of the order of just few kHz in so-called elementary events [cf. the discussion in [16]]. Unfortunately, this is inhibited by the large scatter of data in the iso-flux lines.

Radiation in the fundamental X-mode is confined and cannot escape, at least not locally, unless it becomes scattered and propagates up along though oblique to the magnetic field until becoming gradually transformed to find itself on the free-space X-R mode branch in the magnetospheric tail. Otherwise, the large-amplitude X-mode remains trapped, as described previously, and it undergoes the non-linear wave–wave interaction to generate escaping second harmonic radiation. Presumably, this is the reason for observation of locally intense though (because of their proximity to x = 1) very narrow-band plasma-confined ECMI emissions near the fundamental x ∼ 1 [4, 24] in the upward-current region. The wave–wave interaction of those confined large-amplitude amplified waves transforms the confined X-mode into the free-space escaping X-mode radiation at frequency ω ≲ 2ω_ce below the second harmonic.

3.2 Downward current region

The same hyperbolic resonance condition [36] holds of course also in the downward-current region, but the mostly confirmed and reasonable absence of any loss-cone distribution here demands a different mechanism to cause positive perpendicular phase-space gradients on the source-electron distribution function along the resonance hyperbole. Otherwise, if no appropriate electron distribution becomes available in the downward-current region favorable for hyperbolic resonance, one requires v_ph ∼ kc, in which the resonance returns to elliptic. It seems that this applies indeed to the downward-current region even though this condition is difficult to satisfy. It implies that the lower-branch X-mode waves maintain comparably large phase velocities and that the resonance is replaced away from the electron cyclotron frequency, a condition difficult to achieve.

Unfortunately, no comparably high-resolution measurements of the angular electron fluxes and distribution functions are available yet (at least to our knowledge) here. The precise form of the electron distributions is thus not known and would indeed be worth to be focused on in (hopefully planned and available) future auroral magnetospheric space missions in the spatially rather narrowly extended auroral downward-current regions of which during substorms there are many in a row. Electron fluxes are upward, low energy, spatially highly structured, and highly variable in time. The corresponding upward currents are not smoothly distributed over a wide latitudinal interval as in the upward-current region where the comparable smoothness of the upward sheet current is reflected in the smooth spatial course of the current-transverse magnetic field component that is typical for a broad but unstructured main-field-aligned sheet current.

In contrast to the upward-current region, the downward main-field-aligned currents flow in latitudinally narrow parallel current sheets or current braids which are kept apart by the comparably very strong external geomagnetic field. Accordingly, the current-transverse magnetic field component fluctuates considerably spatially, typical for the presence of many narrow current filaments. The main geomagnetic field is strong enough to compensate for the Lorentz force of these quasi-stationary narrow field-aligned sheet currents which attract each other but cannot merge. Located at the boundary of the auroral cavity, average densities in the downward-current region are comparably high, though still in the range ω_e/ω_ce < 1 [37]. Energies of the upgoing current-carrying current-closing electrons of ionospheric origin are just around ϵ_kin ∼ few keV at most, roughly one order of magnitude less than those in the upward-current region. Related upward velocities β_‖ decrease by a factor of roughly 10, compensating for the decrease in kinetic energy.

The downward currents are intense enough for causing current instability, including reconnection in strong current-parallel guide fields and, in particular, non-linear evolution [38], which structures and deforms the electron distribution function and generates large numbers of (so-called) Debye-scale electrostatic structures [11, 39], ion and electron holes, that propagate along the magnetic field. Debye lengths are in the order of λ_D ≲ 10 m here, depending on the exact spatially variable density and temperature. Whether this is in favor or not of the ECMI remains unclarified. The absence of loss-cones makes the hyperbolic resonance less attractive, requiring rather particular source-electron phase-space distributions. These may be provided by those non-linear Debye-scale structures, current-driven electron holes. It has been suggested [[26] and others] that holes cause violent deformations of the electron distribution function digging phase-space holes into it which contain a highly diluted temperate low-pressure electron population and are bound by denser cold walls in phase space of much higher hole-field-accelerated speed. At these boundaries, the phase-space distribution develops steep gradients which may serve the needs for exciting the ECMI. This model has been used to propose the action of the ECMI here as well, based on elliptic, not hyperbolic resonance [35, 40], in those incomplete hollow-electron phase-space distributions, sometimes called horseshoes.

Observed electron holes extend several λ_D along the magnetic field but are much less restricted in perpendicular extension, which is limited by the width of the unstable field-aligned current filaments and electron gyroradii, the latter being the order of r_ce = β_⊥c/ω_ce ≲ 1 km for the dominant source electrons. Trapping of linearly excited X-modes in these (for the purpose of the ECMI pre-existing) plasma depletions [which result in the non-linear evolution of current instability, for the most recent complete theory cf. [41]] is preferably at k_⊥ > k_‖, i.e., short perpendicular wavelengths and slightly oblique propagation θ ≲ 90°. This is supported close to x = ω_X/ω_ce ∼ 1 on the lower X-mode branch where wavenumbers increase and wave group speeds become low, holding, however, only for the perpendicular wavenumber. This means that κ_‖ < x is a reasonable option inside those holes, whose Debye-structured property applies only to the parallel direction. Consequently, the electron-hole-trapping hypothesis identifies the resonance with an ellipse instead of the hyperbole in the adjacent upward-current region.

The range of X-mode frequencies fits these perpendicular wavelengths, which become trapped in parallel Debye-scale holes. The elliptic resonance condition, applied to the interior of such oblate holes, supports excitation of the ECMI. In contrast to the upward-current region, ECMI is caused at the perpendicular boundary of the phase-space holes, not the general form of the meso-scale electron distribution as this, here, is not of the loss-cone family. Rather, it is self-consistently provided by the self-consistent non-linear evolution of the electron holes. Generation of electron holes and related phase-space distributions of the hollow/horseshoe type is primarily independent on the excitation of the X-mode, being provided by the non-linear evolution of sufficiently strong field-aligned electron currents [as for electrostatic waves has extensively been reviewed by [41]]. It is the particular electron phase-space distribution resulting from this non-linear evolution which, in the downstream-current region, may encourage the excitation of the lower X-mode branch in elliptical or hyperbolic resonance and support their increase to reach large local amplitudes while also experiencing the wave–wave interaction to escape into free space.

The lower-branch hole-trapped X mode has large parallel wavelengths λ_‖ ≫ λ_D along the magnetic field, which by far exceeds the Debye-scale. It overlaps a large number of Debye-scale low-density holes which are densely chained along the magnetic field effectively experiencing an amplification from all those holes along the field over its parallel wavelength. Simultaneously, the wave bounces back and forth synchronously inside all of them in perpendicular direction. Even though each hole contributes differently to the growth of the wave, the concerted action of all holes in the average should lead to a substantial amplification of the X-mode. If this is the case, one expects that observations in situ will detect highly temporarily structured narrow-band and intense confined short perpendicular wavelength X-mode radiation which propagates at group velocity substantially below light speed. Its frequency will be very close to the local electron cyclotron frequency ω ∼ ω_ce. Growing to large amplitude, this slow radiation will again undergo wave–wave interaction to generate second harmonic radiation which escapes from the source and can be observed from remote. The trapped large-amplitude fundamental narrow-band X-mode radiation can, however, be observed only in situ [as for instance in Figure 2 of [4]] where it moves together with the entire chain of holes along the magnetic field. If the remaining radiation trapped for all the life-time of the holes, it will [as has surprisingly been observed, see [42], and references therein] also be transported away from the source by the holes either down to the ionosphere [43] or upward into the magnetosphere. Similar observations in the upper ionosphere [25, 44] have also been reported from DEMETER spacecraft observations.

4 Conclusion

Examination of the fully relativistic resonance condition in ECMI in application to the auroral magnetosphere revealed a so far missed domain where the elliptic resonance can turn into a hyperbolic resonance, thereby becoming topologically completely different and matching the observation of loss-cones in the auroral upward-current region, thus suggesting a number of interesting facts. First, loss-cone distributions with hollow and partially filled loss-cones can, in fully relativistic theory, become efficient sources of rather narrow-band excitation of lower X-mode branch modes which cannot escape from the source region. The bandwidth of frequency of those modes would be determined by the narrow loss-cone boundary at a given wavenumber which, by observation, is of the order of at most few kHz. The ECMI source can only be observed in situ. Second, these locally excited waves have low phase and group velocities, which are trapped in the source region, experience several exponentiations, and evolve to large amplitudes. This generates non-linearities and causes the wavenumbers to shrink further until the non-linear wave becomes trapped in cavities where it undergoes wave–wave interaction to generate second harmonic radiation above the upper X-mode cut-off on the free-space mode from where the radiation escapes. This picture rounds up the theory of AKR excitation by the ECMI in the very low-density upward-current region.

Whether the ECMI can also work in the downward-current region remains uncertain. Primarily, the condition of very low density is not necessarily given there. In that case, ECMI should not evolve. However, the downward-current region is the location of so-called Debye-scale structures, very low-density electron holes which, along the field, are of 10 times the Debye lengths but in perpendicular direction, extend over many electron gyroradii which correspond to the transverse wavelength of the X-mode such that the X-mode fits the hole and in the low-density region can also become amplified and evolve non-linearly, as we have explained in Section 3.2. ECMI-generated AKR could thus also result from here, though in different ways.

In addition, however, in the downward-current region, Z-mode radiation may compete in all those regions which do not experience dilution by Debye structures. Here, the Z-mode propagates and can be excited by VLF, undergo the wave–wave interaction, and radiate at the second and possibly even higher harmonics. This mechanism is not based on the ECMI but deserves to be taken into account when dealing with the downward-current region.

A most interesting observation of AKR is that it seems to weakly leak down into the ionosphere at spacecraft altitudes and even down to the ground under favorable though still unknown condition. These observations raise an interesting question: how can AKR generated at altitudes of at least 1,000 km above ground pass into and even across the ionospheric density screen? Such a passage seems forbidden. However, if generated in density cavities, either self-generated cavities in the upward or within Debye-scale cavities in the downward-current region, then X-modes could possibly be trapped inside those cavities and together with them may become transported down to the ionosphere, where few of them could survive the transport and leak out. This most interesting observation still awaits its theoretical explanation [46].

Author contributions

All authors listed have made a substantial, direct, and intellectual contribution to the work and approved it for publication.

Acknowledgments

This work was part of a brief Visiting Scientist Program (by RAT) at the International Space Science Institute, Bern. The authors acknowledge the interest of the ISSI directorate and the hospitality of the ISSI staff, particularly the assistance of the librarians Andrea Fischer and Irmela Schweitzer and the Systems Administrator Willi Wäfler. We thank the Reviewer for suggesting addition of the lower part in Figure 2 and providing a useful sketch.

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Footnotes

¹It should be noted that the magneto-ionic theory is a fluid theory. It assumes that those wave modes are present, while the hot kinetic plasma component just serves its excitation or damping. In linear dispersion, this permits neglecting all non-linear modifications.

References

1. Twiss RQ. Radiation transfer and the possibility of negative absorption in radio astronomy. Aust J Phys (1958) 11:564. doi:10.1071/PH580564

CrossRef Full Text | Google Scholar

2. Hirshfield JL, Granatstein VI. The electron cyclotron maser--an historical survey. IEEE Trans Microw Theor Tech. (1977) 25:522–7. doi:10.1109/TMTT:1977.1129150

CrossRef Full Text | Google Scholar

3. Melrose DB. Instabilities in space and laboratory plasmas. Cambridge, UK: Cambridge University Press (1986).

Google Scholar

4. Treumann RA. The electron cyclotron-maser for astrophysical application. Astron Astrophys Rev (2006) 13:229–315. doi:10.1007/s00159-006-0001-y

CrossRef Full Text | Google Scholar

5. Gurnett DA. The Earth as a radio source: Terrestrial kilometric radiation. J Geophys Res (1974) 79:4227–38. doi:10.1029/JA079i028p04227

CrossRef Full Text | Google Scholar

6. Benediktov EA, Getmantsev GG, Sazonov YA, Tarasov AF. Kosm Issled Soviet Phys Cosmic Res (1965) 3:614492.

7. Kamide Y, Baumjohann W. Magnetosphere-ionosphere coupling. Berlin, Germany: Springer (1993).

Google Scholar

8. Akasofu S-I. Several `Controversial' issues on substorms. Space Sci Rev (2004) 113:1–40. doi:10.1023/B:SPAC.0000042938.57710.fb

CrossRef Full Text | Google Scholar

9. Akasofu S-I. A review of studies of geomagnetic storms and auroral/magnetospheric substorms based on the electric current approach. Front Astron Space Sci (2020) 7:100. doi:10.3389/fspas.2020.604750

CrossRef Full Text | Google Scholar

10. Yearby KH, Pickett JS. A review of cluster wideband data multi-spacecraft observations of auroral kilometric radiation. J Geophys Res Space Phys (2022) 127:e2021JA029499. doi:10.1029/2021JA029499

CrossRef Full Text | Google Scholar

11. Treumann RA, Baumjohann W. Anisotropic Jüttner (relativistic Boltzmann) distribution. Ann Geophys (2016) 34:737–8. doi:10.5194/angeo-34-737-2016

CrossRef Full Text | Google Scholar

12. Pritchett PL. Electron-cyclotron maser radiation from a relativistic loss-cone distribution. Phys Fluids (1984) 27:2393. doi:10.1063/1.864542

CrossRef Full Text | Google Scholar

13. Wu CS, Lee LC. A theory of the terrestrial kilometric radiation. Astrophys J (1979) 230:621. doi:10.1086/157120

CrossRef Full Text | Google Scholar

14. Delory GT, Ergun RE, Carlson CW, Muschietti L, Chaston CC, Peria W, et al. FAST observations of electron distributions within AKR source regions. Geophys Res Lett (1998) 25:2069–72. doi:10.1029/98GL00705

CrossRef Full Text | Google Scholar

15. LaBelle J, Treumann RA. Auroral radio emissions, 1. Hisses, roars, and bursts. Space Sci Rev (2002) 101:295–440. doi:10.1023/A:1020850022070

CrossRef Full Text | Google Scholar

16. Baumjohann W, Treumann RA. Auroral kilometric radiation – the electron cyclotron maser paradigm. Front Astron Space Sci (2022) 9:1053303. doi:10.3389/fspas.2022.1053303

CrossRef Full Text | Google Scholar

17. Krall NA, Trivelpiece AW. Principles of plasma physics. N.Y.: McGraw-Hill (1973).

Google Scholar

18. Baumjohann W, Treumann RA. Basic space plasma physics. ICP london, 1996. 3rd ed. Singapore: World Scientific (2022).

Google Scholar

19. Wu CS, Qiu XM. Emissions of second-harmonic auroral kilometric radiation. J Geophys Res (1983) 88:10072. doi:10.1029/JA088iA12p10072

CrossRef Full Text | Google Scholar

20. Budden KG. The propagation of radio waves. Cambridge UK: Cambridge University Press (1988).

Google Scholar

21. Treumann RA, Baumjohann W, Pottelette R. Electron-cylotron maser radiation from electron holes: Downward current region. Ann Geophys (2012) 30:119–30. doi:10.5194/angeo-30-119-2012

CrossRef Full Text | Google Scholar

22. Melrose DB. Cyclotron masers and solar spike bursts. Space Sci Rev (1994) 68:159–70. doi:10.1007/BF00749134

CrossRef Full Text | Google Scholar

23. Treumann RA, Baumjohann W. Advanced space plasma physics. London: Imperial College Press (1997).

Google Scholar

24. Pottelette R, Treumann RA. Electron holes in the auroral upward current region. Geophys Res Lett (2005) 32:L12104. doi:10.1029/2005gl022547

CrossRef Full Text | Google Scholar

25. Xiao F, Zhou Q, Su Z, He Z, Yang C, Liu S, et al. Explaining occurrences of auroral kilometric radiation in Van Allen radiation belts. Geophys Res Lett (2016) 43:11971–8. doi:10.1002/2016GL071728

CrossRef Full Text | Google Scholar

26. Muschietti L, Ergun RE, Roth I, Carlson CW. Phase-space electron holes along magnetic field lines. Geophys Res Lett (1999) 26:1093–6. doi:10.1029/1999GL900207

CrossRef Full Text | Google Scholar

27. Ergun RE, Carlson CW, McFadden JP, Mozer FS, Muschietti L, Roth I, et al. Debye-scale plasma structures associated with magnetic-field-aligned electric fields. Phys Rev Lett (1998) 81:826–9. doi:10.1103/PhysRevLett.81.826

CrossRef Full Text | Google Scholar

28. Omidi N, Gurnett DA. Path-integrated growth of auroral kilometric radiation. J Geophys Res (1984) 89:10801. doi:10.1029/JA089iA12p10801

CrossRef Full Text | Google Scholar

29. Zarka P, Le Queau D, Genova F. The maser synchrotron instability in an inhomogeneous medium: Determination of the spectral intensity of auroral kilometric radiation. J Geophys Res (1986) 91:13542. doi:10.1029/JA091iA12p13542

CrossRef Full Text | Google Scholar

30. Louarn P, Roux A, de Ferraudy H, Le Queau D, Andre M, Matson I. Trapped electrons as a free energy source for the auroral kilometric radiation. J Geophys Res (1990) 95:5983. doi:10.1029/JA095iA05p05983

CrossRef Full Text | Google Scholar

31. Lamy L, Zarka P, Cecconi B, Prange R. Auroral kilometric radiation diurnal, semidiurnal, and shorter-term modulations disentangled by Cassini. J Geophys Res (2010) 115:A09221. doi:10.1029/2010JA015434

CrossRef Full Text | Google Scholar

32. Pottelette R, Treumann RA, Berthomier M. Auroral plasma turbulence and the cause of auroral kilometric radiation fine structure. J Geophys Res (2001) 106:8465–76. doi:10.1029/2000JA000098

CrossRef Full Text | Google Scholar

33. Sagdeev RZ, Galeev AA. Nonlinear plasma theory. Los Angeles, CA, USA: W.A. Benjamin Inc. (1969).

Google Scholar

34. Davidson RC. Methods in nonlinear plasma theory. Cambridge, MA, USA: Academic Press (1973).

Google Scholar

35. Yoon PH, LaBelle J, Weatherwax AT. Right-hand polarized 4f_ce auroral roar emissions: 2. Nonlinear generation theory. J Geophys Res (2016) 121:7981–7. doi:10.1002/2016JA022889

CrossRef Full Text | Google Scholar

36. Yoon PH, Lopéz RA. Spontaneous emission of electromagnetic fluctuations in magnetized plasmas. Phys Plasmas (2017) 24:022117. doi:10.1063/1.4976321

CrossRef Full Text | Google Scholar

37. Temerin M, Carlson CW. Current-voltage relationship in the downward auroral current region. Geophys Res Lett (1998) 25:2365–8. doi:10.1029/98GL01865

CrossRef Full Text | Google Scholar

38. Carlson CW, McFadden JP, Ergun RE, Temerin M, Peria W, Mozer FS, et al. FAST observations in the downward auroral current region: Energetic upgoing electron beams, parallel potential drops, and ion heating. Geophys Res Lett (1998) 25:2017–20. doi:10.1029/98GL00851

CrossRef Full Text | Google Scholar

39. Bernstein IB, Greene JM, Kulsrud MD. Exact nonlinear plasma oscillations. Phys Rev (1957) 108:546–50. doi:10.1103/PhysRev.108.546

CrossRef Full Text | Google Scholar

40. Treumann RA, Baumjohann W, Pottelette R. Electron-cylotron maser radiation from electron holes: Upward current region. Ann Geophys (2011) 29:1885–904. doi:10.5194/angeo-29-1885-2011

CrossRef Full Text | Google Scholar

41. Schamel H. Pattern formation in Vlasov-Poisson plasmas beyond Landau caused by the continuous spectra of electron and ion hole equilibria (2022). ArXiv [physics.plasma-ph]. doi:10.48550/arXiv.2110.01433

CrossRef Full Text | Google Scholar

42. LaBelle J, Yearby K, Pickett JS. South Pole station ground-based and cluster satellite measurements of leaked and escaping auroral kilometric radiation. J Geophys Res (2022) 127:e2021JA029399. doi:10.1029/2021JA029399

CrossRef Full Text | Google Scholar

43. Treumann RA, Baumjohann W, LaBelle J, Pottelette R. Downward transport of electromagnetic radiation by electron holes? (2012). ArXiv:1208.3055. doi:10.48550/arXiv.1208.3055

CrossRef Full Text | Google Scholar

44. Parrot M, Berthelier J-J. AKR-like emissions observed at low altitude by the DEMETER satellite. J Geophys Res (2012) 117:10314. doi:10.1029/2012JA017937

CrossRef Full Text | Google Scholar

45. Parrot M, Nemec F, Santolik O. Properties of AKR-like emissions recorded by the low altitude satellite lDEMETER during 6.5 years. J Geophys Res (2022) 127:e30495. doi:10.1029/2022JA030495

CrossRef Full Text | Google Scholar

46. Treumann RA, Baumjohann W. Electron cyclotron maser instability (ECMI) in strong magnetic guide field reconnection. Ann Geophys (2017) 35:999–1013. doi:10.5194/angeo-35-999-2017

CrossRef Full Text | Google Scholar