Homotopy perturbation method-based soliton solutions of the time-fractional (2+1)-dimensional Wu–Zhang system describing long dispersive gravity water waves in the ocean

Physical phenomena and natural disasters, such as tsunamis and floods, are caused due to dispersive water waves and shallow waves caused by earthquakes. In order to analyze and minimize damaging effects of such situations, mathematical models are presented by different researchers. The Wu–Zhang (WZ) system is one such model that describes long dispersive waves. In this regard, the current study focuses on a non-linear (2 + 1)-dimensional time-fractional Wu–Zhang (WZ) system due to its importance in capturing long dispersive gravity water waves in the ocean. A Caputo fractional derivative in the WZ system is considered in this study. For solution purposes, modification of the homotopy perturbation method (HPM) along with the Laplace transform is used to provide improved results in terms of accuracy. For validity and convergence, obtained results are compared with the fractional differential transform method (FDTM), modified variational iteration method (mVIM), and modified Adomian decomposition method (mADM). Analysis of results indicates the effectiveness of the proposed methodology. Furthermore, the effect of fractional parameters on the given model is analyzed numerically and graphically at both integral and fractional orders. Moreover, Caputo, Caputo–Fabrizio, and Atangana–Baleanu approaches of fractional derivatives are applied and compared graphically in the current study. Analysis affirms that the proposed algorithm is a reliable tool and can be used in higher dimensional fractional systems in science and engineering.

1 Introduction

The study of differential equations (DEs) is a pivotal topic as they capture most of the real-world phenomena, i.e., earthquakes [1, 2], natural gas consumption [3, 4], current flow [5], and cooking [6]. These equations can additionally be characterized into linear and non-linear differential equations. Many important and interesting phenomena like electrical circuits [7, 8], DNA sequencing [9, 10], disease modeling and analysis [11, 12], and food chain models [13, 14] are captured through differential equations. Since the order of a DE describes the nature and scope of the captured phenomena, it is therefore important for researchers to cater fractional-order derivatives for a more general study of the physical aspects of the considered phenomena. Fractional models allow better understanding of model dynamics and facilitate researchers to accurately predict changes in the physical systems. The chaos theory [15], nanotechnology [16], fluid flow [17], cosmology [18], and robotics [19] use differential equations for problem formulation. These equations also frequently appear in many branches of mathematics [20, 21], finance [22], economy [23], and biology [24].

The phrase “fractal” was first created in 1975 by mathematician Benoit Mandelbrot [25]. It is a geometric shape that exhibits the same level of non-regularity on all scales. Fractals are infinite patterns, which we frequently see in nature. Snowflakes, trees, mountains, clouds, and coastlines represent fractals as they are highly uneven at both large and small scales. Many important models including the diffusion model of red ink [26] and thin films [27], the vibration model for a concrete beam [28] and electronic devices [29], and the COVID-19 mathematical model [30] contain fractal geometry. The distinction between fractional and fractal is that the former is a statement of a fractional number, while the latter is a geometric figure that is similar at all scales.

The Wu–Zhang system [31] contains non-linear partial differential equations (PDEs) and deals with the motion of water waves in oceans. In 1996, three sets of model equations were first derived by Wu and Zhang and named the Wu–Zhang system of PDEs [31]. This system is used to customize several harbor and coastal designs. This non-linear (2 + 1)-dimensional fractional system describes shallow water dispersive long gravity waves in two horizontal directions, which are given as

$\begin{array}{cc}\hfill & \frac{{\partial }^{\zeta }\mathcal{U}}{\partial {\mathfrak{t}}^{\zeta }}+\mathcal{U}\frac{\partial \mathcal{U}}{\partial x}+\mathcal{V}\frac{\partial \mathcal{U}}{\partial y}+\frac{\partial \mathcal{W}}{\partial x}=0,\hfill \\ \hfill & \frac{{\partial }^{\zeta }\mathcal{V}}{\partial {\mathfrak{t}}^{\zeta }}+\mathcal{U}\frac{\partial \mathcal{V}}{\partial x}+\mathcal{V}\frac{\partial \mathcal{V}}{\partial y}+\frac{\partial \mathcal{W}}{\partial y}=0,\hfill \\ \hfill & \frac{{\partial }^{\zeta }\mathcal{W}}{\partial {\mathfrak{t}}^{\zeta }}+\frac{\partial \left(\mathcal{U}\mathcal{W}\right)}{\partial x}+\frac{\partial \left(\mathcal{V}\mathcal{W}\right)}{\partial y}+\frac{1}{3}\left(\frac{{\partial }^3\mathcal{U}}{\partial x^3}+\frac{{\partial }^3\mathcal{U}}{\partial x\partial y^2}+\frac{{\partial }^3\mathcal{V}}{\partial x^2\partial y}+\frac{{\partial }^3\mathcal{V}}{\partial y^3}\right)=0,\hfill \end{array}(1)$

where $\mathcal{U}$ and $\mathcal{V}$ represent the velocities at the surface of water in x and y directions, while $\mathcal{W}$ depicts the elevation of water waves. The aforementioned WZ system is a time fraction, while Wang and He [32] concluded that when time is fractional, space must also be fractional. This is called Wang–He’s spatiotemporal fractional relationship (for more details see [32]). Due to the substantial importance of WZ systems, many scholars have attempted to solve and analyze these systems through variety of methodologies like mVIM [33], ADM [34, 35], extended tanh and exp–function method [36], and dynamical analysis method [37]. Recently, for more generalized solutions and predictions, the WZ systems are also attempted fractionally by few of the scientists. Kaur and Gupta discussed dispersion analysis of the (2 + 1)-dimensional time-fractional WZ system [38]. Patel and Patel investigated the fractional-order WZ system analytically [39]. Different approaches of fractional derivatives can be utilized, such as Caputo [40], Atangana–Baleanu [41], Caputo–Fabrizio [42], and He’s fractional derivative [43].

In order to solve such highly non-linear fractional systems, many analytical and numerical methodologies are utilized by different researchers. Anjum et al. [44] applied Li–He’s modified homotopy perturbation approach to solve the microelectromechanical system. Baitiche et al. [45] used the monotone iterative method for fractional DEs with non-linearity at the boundary. Do et al. [46] extended Chebyshev wavelets to two-dimensional fractional DEs. Hashemi et al. [47] investigated multi-term FDEs using minimization techniques. Tian and Liu utilized the modified exp-function to fractional PDEs in [48]. Furthermore, to solve complex problems, the enhanced homotopy methods can be found in [49, 50]. In this study, a hybrid algorithm is proposed by mixing the classical homotopy perturbation method [51, 52] with the Laplace transform [53] along with different fractional derivatives (Atangana–Baleanu, Caputo–Fabrizio, and Caputo) for a highly non-linear time-fractional (2 + 1)-dimensional WZ system. In the rest of the paper, Section 2 contains preliminary definitions. Section 3 contains the proposed methodology for handling time-fractional (2 + 1)-dimensional WZ system, whereas proof of convergence and error analysis are given in Section 4. Solution and results and discussion are given in Sections 5 and 6, respectively, while a conclusion is given in Section 7.

2 Basic definitions

Definition 1: For a function $\mathcal{U}(t,x,y)$, the Caputo’s time-fractional derivative ${}^C\mathcal{D}_t^{\zeta }$ is [54]

${}^C\mathcal{D}_t^{\zeta }\mathcal{U}\left(t,x,y\right)=\frac{1}{\mathrm{\Gamma }\left(q-\zeta \right)}{\int }_0^t{\left(t-G\right)}^{q-\zeta -1}{\mathcal{U}}^{\left(q\right)}\left(G,x,y\right)dG,q-1<\zeta \le q.(2)$

Definition 2: According to [55], one can express the Laplace transform L of the function $\mathcal{U}(t,x,y)$ that has been subjected to the Caputo’s time-fractional derivative ${}^C\mathcal{D}_t^{\zeta }$.

$\mathbf{L}\left\{{}^C\mathcal{D}_t^{\zeta }\mathcal{U}\left(t,x,y\right)\right\}=s^{\zeta }\mathbf{L}\left\{\mathcal{U}\left(t,x,y\right)\right\}-{\displaystyle \sum _{p=0}^{q-1}}{s}^{\zeta -p-1}{\mathcal{U}}^{\left(p\right)}\left(0,x,y\right),q-1<\zeta \le q.(3)$

Definition 3: The Caputo–Fabrizio’s time-fractional derivative ${}^{CF}\mathcal{D}_t^{\zeta }$ of a function $\mathcal{U}(t,x,y)$ is [42]

${}^{CF}\mathcal{D}_t^{\zeta }\mathcal{U}\left(t,x,y\right)=\frac{1}{1-\zeta }{\int }_0^t{e}^{\frac{-\zeta \left(t-G\right)}{1-\zeta }}\frac{\partial \mathcal{U}\left(G,x,y\right)}{\partial G}dG,0<\zeta <1.(4)$

Definition 4: The Laplace transform L of the Caputo–Fabrizio’s time-fractional derivative ${}^{CF}\mathcal{D}_t^{\zeta }$ of a function $\mathcal{U}(t,x,y)$ is given as [56]

$\mathbf{L}\left\{{}^{CF}\mathcal{D}_t^{\zeta +q}\mathcal{U}\left(t,x,y\right)\right\}=\frac{s^{q+1}\mathbf{L}\left\{\mathcal{U}\left(t,x,y\right)\right\}-{\displaystyle \sum _{p=0}^q}{s}^{q-p}{\mathcal{U}}^{\left(p\right)}\left(0,x,y\right)}{s+\zeta \left(1-s\right)},0<\zeta \le 1.(5)$

Definition 5: A function $\mathcal{U}(t,x,y)$ in the sense of Atangana–Baleanu’s time-fractional derivative ${}^{AB}\mathcal{D}_t^{\zeta }$ is stated as [41]

${}^{AB}\mathcal{D}_t^{\zeta }\mathcal{U}\left(t,x,y\right)=\frac{\mathbb{K}\left(\zeta \right)}{1-\zeta }{\int }_0^t{E}_{\zeta }\left[-\frac{\zeta {\left(t-G\right)}^{\zeta }}{1-\zeta }\right]\frac{\partial \mathcal{U}\left(G,x,y\right)}{\partial G}dG,0<\zeta \le 1.(6)$

Here, $\mathbb{K}(\zeta )$ is a normalization function with properties $\mathbb{K}(0)$ = $\mathbb{K}(1)$ = 1.

Definition 6: The Laplace transform L connected with Atangana–Baleanu time-fractional derivative ${}^{AB}\mathcal{D}_t^{\zeta }$ of a function $\mathcal{U}(t,x,y)$ can be described as [57]

$\mathbf{L}\left\{{}^{AB}\mathcal{D}_t^{\zeta }\mathcal{U}\left(t,x,y\right)\right\}=AB\left(\zeta \right).\frac{s^{\zeta }\mathbf{L}\left\{\mathcal{U}\left(t,x,y\right)\right\}-s^{\zeta -1}\mathcal{U}\left(0,x,y\right)}{s^{\zeta }\left(1-\zeta \right)+\zeta },0\le \zeta \le 1.(7)$

Here, AB(ζ) is a normalization function.

Definition 7: He’s fractional derivative of a function $\mathcal{U}(t,x,y)$ can be defined by [43]

${\mathcal{D}}_t^{\zeta }\mathcal{U}\left(t,x,y\right)=\frac{1}{\mathrm{\Gamma }\left(q-\zeta \right)}\frac{d^q}{d{t}^q}{\int }_{t_0}^t{\left(G-t\right)}^{q-\zeta -1}\left[{\mathcal{U}}_0\left(G,x,y\right)-\mathcal{U}\left(G,x,y\right)\right]dG,q-1<\zeta \le q.(8)$

Definition 8: The core idea behind the two-scale dimension [58, 59], which commonly arises in the non-linear problem, is that while self-similarity is difficult to uncover in practical applications, fractal structures self-assemble on all scales. Creating models with the two-scale dimension allows for the successful description of various physical events.

Definition 9: A Banach space $\mathbb{B}$ is a normed space ‖. ∥, which is complete with respect to the metric derived from its norm.

3 Hybrid algorithm for (2 + 1)-dimensional time-fractional systems

Consider a (2 + 1)-dimensional, time-fractional system as

$\begin{array}{cc}\hfill & {\mathcal{D}}_t^{\zeta }\mathcal{A}1\left(t,x,y\right)+\mathcal{L}\left[\mathcal{A}r\left(t,x,y\right)\right]+\mathcal{N}\left[\mathcal{A}r\left(t,x,y\right)\right]-\mathfrak{l}\left(t,x,y\right)=0,\hfill \\ \hfill & {\mathcal{D}}_t^{\zeta }\mathcal{A}2\left(t,x,y\right)+\mathcal{L}\left[\mathcal{A}r\left(t,x,y\right)\right]+\mathcal{N}\left[\mathcal{A}r\left(t,x,y\right)\right]-\mathfrak{m}\left(t,x,y\right)=0,\hfill \\ \hfill & {\mathcal{D}}_t^{\zeta }\mathcal{A}3\left(t,x,y\right)+\mathcal{L}\left[\mathcal{A}r\left(t,x,y\right)\right]+\mathcal{N}\left[\mathcal{A}r\left(t,x,y\right)\right]-\mathfrak{n}\left(t,x,y\right)=0,\hfill \\ \hfill & r=\mathrm{1,2,3},t>0,\hfill \\ \hfill & q-1<\zeta \le q,\hfill \end{array}(9)$

that has initial conditions

$\begin{array}{c}\hfill \mathcal{A}1\left(0,x,y\right)=\mathcal{J}1,\\ \hfill \mathcal{A}2\left(0,x,y\right)=\mathcal{J}2,\\ \hfill \mathcal{A}3\left(0,x,y\right)=\mathcal{J}3,\end{array}(10)$

where the unknown functions $\mathcal{A}1(t,x,y)$, $\mathcal{A}2(t,x,y)$, and $\mathcal{A}3(t,x,y)$ have time-fractional derivatives, and ${\mathcal{D}}_t^{\zeta }$, $\mathfrak{l}(t,x,y)$, $\mathfrak{m}(t,x,y)$, and $\mathfrak{n}(t,x,y)$ are some of its known functions. The symbols $\mathcal{N}$ and $\mathcal{L}$ represent non-linear and linear operators, respectively.

The procedure will start by applying the Laplace transform on (9), which gives

$\begin{array}{cc}\hfill & \mathcal{L}\left\{{\mathcal{D}}_t^{\zeta }\left[\mathcal{A}1\left(t,x,y\right)\right]\right\}+\mathcal{L}\left\{\mathcal{L}\left[\mathcal{A}r\left(t,x,y\right)\right]+\mathcal{N}\left[\mathcal{A}r\left(t,x,y\right)\right]-\mathfrak{l}\left(t,x,y\right)\right\}=0,\hfill \\ \hfill & \mathcal{L}\left\{{\mathcal{D}}_t^{\zeta }\left[\mathcal{A}2\left(t,x,y\right)\right]\right\}+\mathcal{L}\left\{\mathcal{L}\left[\mathcal{A}r\left(t,x,y\right)\right]+\mathcal{N}\left[\mathcal{A}r\left(t,x,y\right)\right]-\mathfrak{m}\left(t,x,y\right)\right\}=0,\hfill \\ \hfill & \mathcal{L}\left\{{\mathcal{D}}_t^{\zeta }\left[\mathcal{A}3\left(t,x,y\right)\right]\right\}+\mathcal{L}\left\{\mathcal{L}\left[\mathcal{A}r\left(t,x,y\right)\right]+\mathcal{N}\left[\mathcal{A}r\left(t,x,y\right)\right]-\mathfrak{n}\left(t,x,y\right)\right\}=0.\hfill \end{array}(11)$

Now, by utilizing the basic definitions given in Section 2, we can find the Laplace transform of the fractional derivative. Definition (2) gives

$\begin{array}{c}\hfill \mathcal{L}\left[\mathcal{A}1\left(t,x,y\right)\right]-\left(\frac{1}{s^{\zeta }}\right){\displaystyle \sum _{p=0}^{q-1}}{s}^{\zeta -p-1}\mathcal{A}{1}^{\left(p\right)}\left(0,x,y\right)+\left(\frac{1}{s^{\zeta }}\right)\mathcal{L}\left\{\mathcal{L}\left[\mathcal{A}r\left(t,x,y\right)\right]\right.\\ \hfill \left.+\mathcal{N}\left[\mathcal{A}r\left(t,x,y\right)\right]-\mathfrak{l}\left(t,x,y\right)\right\}=0,\\ \hfill \mathcal{L}\left[\mathcal{A}2\left(t,x,y\right)\right]-\left(\frac{1}{s^{\zeta }}\right){\displaystyle \sum _{p=0}^{q-1}}{s}^{\zeta -p-1}\mathcal{A}{2}^{\left(p\right)}\left(0,x,y\right)+\left(\frac{1}{s^{\zeta }}\right)\mathcal{L}\left\{\mathcal{L}\left[\mathcal{A}r\left(t,x,y\right)\right]\right.\\ \hfill \left.+\mathcal{N}\left[\mathcal{A}r\left(t,x,y\right)\right]-\mathfrak{m}\left(t,x,y\right)\right\}=0,\\ \hfill \mathcal{L}\left[\mathcal{A}3\left(t,x,y\right)\right]-\left(\frac{1}{s^{\zeta }}\right){\displaystyle \sum _{p=0}^{q-1}}{s}^{\zeta -p-1}\mathcal{A}{3}^{\left(p\right)}\left(0,x,y\right)+\left(\frac{1}{s^{\zeta }}\right)\mathcal{L}\left\{\mathcal{L}\left[\mathcal{A}r\left(t,x,y\right)\right]\right.\\ \hfill \left.+\mathcal{N}\left[\mathcal{A}r\left(t,x,y\right)\right]-\mathfrak{n}\left(t,x,y\right)\right\}=0.\end{array}(12)$

The homotopy of the system is

$\begin{array}{c}\hfill {\mathcal{H}}_1=\left(1-s\right)\left(\mathcal{L}\left\{\mathcal{A}1\left(t,x,y\right)\right\}-\mathcal{A}{1}_0\left(t,x,y\right)\right)+s(\mathcal{L}\left\{\mathcal{A}1\left(t,x,y\right)\right\}-\left(\frac{1}{s^{\zeta }}\right){\displaystyle \sum _{p=0}^{q-1}}{s}^{\zeta -p-1}\\ \hfill \left.\mathcal{A}{1}^{\left(p\right)}\left(0,x,y\right)+\left(\frac{1}{s^{\zeta }}\right)\mathcal{L}\left\{\mathcal{L}\left[\mathcal{A}r\left(t,x,y\right)\right]+\mathcal{N}\left[\mathcal{A}r\left(t,x,y\right)\right]-\mathfrak{l}\left(t,x,y\right)\right\}\right),\\ \hfill {\mathcal{H}}_2=\left(1-s\right)\left(\mathcal{L}\left\{\mathcal{A}2\left(t,x,y\right)\right\}-\mathcal{A}{2}_0\left(t,x,y\right)\right)+s(\mathcal{L}\left\{\mathcal{A}2\left(t,x,y\right)\right\}-\left(\frac{1}{s^{\zeta }}\right){\displaystyle \sum _{p=0}^{q-1}}{s}^{\zeta -p-1}\\ \hfill \left.\mathcal{A}{2}^{\left(p\right)}\left(0,x,y\right)+\left(\frac{1}{s^{\zeta }}\right)\mathcal{L}\left\{\mathcal{L}\left[\mathcal{A}r\left(t,x,y\right)\right]+\mathcal{N}\left[\mathcal{A}r\left(t,x,y\right)\right]-\mathfrak{m}\left(t,x,y\right)\right\}\right),\\ \hfill {\mathcal{H}}_3=\left(1-s\right)\left(\mathcal{L}\left\{\mathcal{A}3\left(t,x,y\right)\right\}-\mathcal{A}{3}_0\left(t,x,y\right)\right)+s(\mathcal{L}\left\{\mathcal{A}3\left(t,x,y\right)\right\}-\left(\frac{1}{s^{\zeta }}\right){\displaystyle \sum _{p=0}^{q-1}}{s}^{\zeta -p-1}\\ \hfill \left.\mathcal{A}{3}^{\left(p\right)}\left(0,x,y\right)+\left(\frac{1}{s^{\zeta }}\right)\mathcal{L}\left\{\mathcal{L}\left[\mathcal{A}r\left(t,x,y\right)\right]+\mathcal{N}\left[\mathcal{A}r\left(t,x,y\right)\right]-\mathfrak{n}\left(t,x,y\right)\right\}\right),\end{array}(13)$

where $\mathcal{A}{1}_0$, $\mathcal{A}{2}_0$, and $\mathcal{A}{3}_0$ are initial guesses. Expansion of $\mathcal{A}1(t,x,y)$, $\mathcal{A}2(t,x,y)$, and $\mathcal{A}3(t,x,y)$ in power series with respect to s leads to

$\begin{array}{c}\hfill \mathcal{A}1\left(t,x,y\right)=\mathcal{A}{1}_0\left(t,x,y\right)+s^1\mathcal{A}{1}_1\left(t,x,y\right)+s^2\mathcal{A}{1}_2\left(t,x,y\right)+\dots \\ \hfill \mathcal{A}2\left(t,x,y\right)=\mathcal{A}{2}_0\left(t,x,y\right)+s^1\mathcal{A}{2}_1\left(t,x,y\right)+s^2\mathcal{A}{2}_2\left(t,x,y\right)+\dots \\ \hfill \mathcal{A}3\left(t,x,y\right)=\mathcal{A}{3}_0\left(t,x,y\right)+s^1\mathcal{A}{3}_1\left(t,x,y\right)+s^2\mathcal{A}{3}_2\left(t,x,y\right)+\dots \end{array}(14)$

After substituting Eq. 14 in (13) and then comparing similar coefficients of s, we obtainAt s¹

$\begin{array}{c}\hfill \mathcal{L}\left\{\mathcal{A}{1}_1\left(t,x,y\right)\right\}+\mathcal{A}{1}_0\left(t,x,y\right)-\left(\frac{1}{s^{\zeta }}\right){\displaystyle \sum _{p=0}^{q-1}}{s}^{\zeta -p-1}\mathcal{A}{1}^{\left(p\right)}\left(0,x,y\right)+\left(\frac{1}{s^{\zeta }}\right)\mathcal{L}\left\{\mathcal{L}\left[\mathcal{A}{r}_0\left(t,x,y\right)\right]\right.\\ \hfill \left.+\mathcal{N}\left[\mathcal{A}{r}_0\left(t,x,y\right)\right]-\mathfrak{l}\left(t,x,y\right)\right\}=0,\\ \hfill \mathcal{L}\left\{\mathcal{A}{2}_1\left(t,x,y\right)\right\}+\mathcal{A}{2}_0\left(t,x,y\right)-\left(\frac{1}{s^{\zeta }}\right){\displaystyle \sum _{p=0}^{q-1}}{s}^{\zeta -p-1}\mathcal{A}{2}^{\left(p\right)}\left(0,x,y\right)+\left(\frac{1}{s^{\zeta }}\right)\mathcal{L}\left\{\mathcal{L}\left[\mathcal{A}{r}_0\left(t,x,y\right)\right]\right.\\ \hfill \left.+\mathcal{N}\left[\mathcal{A}{r}_0\left(t,x,y\right)\right]-\mathfrak{m}\left(t,x,y\right)\right\}=0,\\ \hfill \mathcal{L}\left\{\mathcal{A}{3}_1\left(t,x,y\right)\right\}+\mathcal{A}{3}_0\left(t,x,y\right)-\left(\frac{1}{s^{\zeta }}\right){\displaystyle \sum _{p=0}^{q-1}}{s}^{\zeta -p-1}\mathcal{A}{3}^{\left(p\right)}\left(0,x,y\right)+\left(\frac{1}{s^{\zeta }}\right)\mathcal{L}\left\{\mathcal{L}\left[\mathcal{A}{r}_0\left(t,x,y\right)\right]\right.\\ \hfill \left.+\mathcal{N}\left[\mathcal{A}{r}_0\left(t,x,y\right)\right]-\mathfrak{n}\left(t,x,y\right)\right\}=0.\end{array}(15)$

The inverse Laplace transform leads to

$\begin{array}{c}\hfill \mathcal{A}{1}_1\left(t,x,y\right){+\mathcal{L}}^{-1}\left\{\mathcal{A}{1}_0\left(t,x,y\right)-\left(\frac{1}{s^{\zeta }}\right){\displaystyle \sum _{p=0}^{q-1}}{s}^{\zeta -p-1}\mathcal{A}{1}^{\left(p\right)}\left(0,x,y\right)\right\}{+\mathcal{L}}^{-1}\left\{\left(\frac{1}{s^{\zeta }}\right)\right.\\ \hfill \mathcal{L}\{\mathcal{L}\left[\mathcal{A}{r}_0\left(t,x,y\right)\right]+\mathcal{N}\left[\mathcal{A}{r}_0\left(t,x,y\right)\right]-\mathfrak{l}\left(t,x,y\right)\}=0,\\ \hfill \mathcal{A}{2}_1\left(t,x,y\right){+\mathcal{L}}^{-1}\left\{\mathcal{A}{2}_0\left(t,x,y\right)-\left(\frac{1}{s^{\zeta }}\right){\displaystyle \sum _{p=0}^{q-1}}{s}^{\zeta -p-1}\mathcal{A}{2}^{\left(p\right)}\left(0,x,y\right)\right\}{+\mathcal{L}}^{-1}\left\{\left(\frac{1}{s^{\zeta }}\right)\right.\\ \hfill \mathcal{L}\left\{\mathcal{L}\left[\mathcal{A}{r}_0\left(t,x,y\right)\right]+\mathcal{N}\left[\mathcal{A}{r}_0\left(t,x,y\right)\right]-\mathfrak{m}\left(t,x,y\right)\right.\}=0,\\ \hfill \mathcal{A}{3}_1\left(t,x,y\right){+\mathcal{L}}^{-1}\left\{\mathcal{A}{3}_0\left(t,x,y\right)-\left(\frac{1}{s^{\zeta }}\right){\displaystyle \sum _{p=0}^{q-1}}{s}^{\zeta -p-1}\mathcal{A}{3}^{\left(p\right)}\left(0,x,y\right)\right\}{+\mathcal{L}}^{-1}\left\{\left(\frac{1}{s^{\zeta }}\right)\right.\\ \hfill \mathcal{L}\left\{\mathcal{L}\left[\mathcal{A}{r}_0\left(t,x,y\right)\right]+\mathcal{N}\left[\mathcal{A}{r}_0\left(t,x,y\right)\right]-\mathfrak{n}\left(t,x,y\right)\right.\}=0.\end{array}(16)$

At s^k

$\begin{array}{c}\hfill \mathcal{L}\left\{\mathcal{A}{1}_k\left(t,x,y\right)\right\}+\left(\frac{1}{s^{\zeta }}\right)\mathcal{L}\left\{\mathcal{L}\left[\mathcal{A}{r}_{k-1}\left(t,x,y\right)\right]+\mathcal{N}\left[\mathcal{A}{r}_{k-1}\left(t,x,y\right)\right]\right\}=0,\\ \hfill \mathcal{L}\left\{\mathcal{A}{2}_k\left(t,x,y\right)\right\}+\left(\frac{1}{s^{\zeta }}\right)\mathcal{L}\left\{\mathcal{L}\left[\mathcal{A}{r}_{k-1}\left(t,x,y\right)\right]+\mathcal{N}\left[\mathcal{A}{r}_{k-1}\left(t,x,y\right)\right]\right\}=0,\\ \hfill \mathcal{L}\left\{\mathcal{A}{3}_k\left(t,x,y\right)\right\}+\left(\frac{1}{s^{\zeta }}\right)\mathcal{L}\left\{\mathcal{L}\left[\mathcal{A}{r}_{k-1}\left(t,x,y\right)\right]+\mathcal{N}\left[\mathcal{A}{r}_{k-1}\left(t,x,y\right)\right]\right\}=0.\end{array}(17)$

Operating the inverse Laplace transform gives the following:

$\begin{array}{c}\hfill \mathcal{A}{1}_k\left(t,x,y\right){+\mathcal{L}}^{-1}\left\{\left(\frac{1}{s^{\zeta }}\right)\mathcal{L}\left\{\mathcal{L}\left[\mathcal{A}{r}_{k-1}\left(t,x,y\right)\right]+\mathcal{N}\left[\mathcal{A}{r}_{k-1}\left(t,x,y\right)\right]\right\}\right\}=0,\\ \hfill \mathcal{A}{2}_k\left(t,x,y\right){+\mathcal{L}}^{-1}\left\{\left(\frac{1}{s^{\zeta }}\right)\mathcal{L}\left\{\mathcal{L}\left[\mathcal{A}{r}_{k-1}\left(t,x,y\right)\right]+\mathcal{N}\left[\mathcal{A}{r}_{k-1}\left(t,x,y\right)\right]\right\}\right\}=0,\\ \hfill \mathcal{A}{3}_k\left(t,x,y\right){+\mathcal{L}}^{-1}\left\{\left(\frac{1}{s^{\zeta }}\right)\mathcal{L}\left\{\mathcal{L}\left[\mathcal{A}{r}_{k-1}\left(t,x,y\right)\right]+\mathcal{N}\left[\mathcal{A}{r}_{k-1}\left(t,x,y\right)\right]\right\}\right\}=0.\end{array}(18)$

The approximate solution of the given general time-fractional, (2 + 1)-dimensional PDE system is

$\begin{array}{cc}\hfill \tilde{\mathcal{A}}1& =\mathcal{A}{1}_0\left(t,x,y\right)+\mathcal{A}{1}_1\left(t,x,y\right)+\mathcal{A}{1}_2\left(t,x,y\right)+\mathcal{A}{1}_3\left(t,x,y\right)+\cdots ,\hfill \\ \hfill \tilde{\mathcal{A}}2& =\mathcal{A}{2}_0\left(t,x,y\right)+\mathcal{A}{2}_1\left(t,x,y\right)+\mathcal{A}{2}_2\left(t,x,y\right)+\mathcal{A}{1}_3\left(t,x,y\right)+\cdots ,\hfill \\ \hfill \tilde{\mathcal{A}}3& =\mathcal{A}{3}_0\left(t,x,y\right)+\mathcal{A}{3}_1\left(t,x,y\right)+\mathcal{A}{3}_2\left(t,x,y\right)+\mathcal{A}{3}_3\left(t,x,y\right)+\cdots .\hfill \end{array}(19)$

Residual errors of the system are

$\begin{array}{cc}\hfill \mathfrak{R}\mathfrak{e}\mathfrak{s}1& ={\mathcal{D}}_t^{\zeta }\left[\tilde{\mathcal{A}}1\right]+\mathcal{L}\left[\tilde{\mathcal{A}}r\right]+\mathcal{N}\left[\tilde{\mathcal{A}}r\right]-\mathfrak{l}\left(t,x,y\right),\hfill \\ \hfill \mathfrak{R}\mathfrak{e}\mathfrak{s}2& ={\mathcal{D}}_t^{\zeta }\left[\tilde{\mathcal{A}}2\right]+\mathcal{L}\left[\tilde{\mathcal{A}}r\right]+\mathcal{N}\left[\tilde{\mathcal{A}}r\right]-\mathfrak{m}\left(t,x,y\right),\hfill \\ \hfill \mathfrak{R}\mathfrak{e}\mathfrak{s}3& ={\mathcal{D}}_t^{\zeta }\left[\tilde{\mathcal{A}}3\right]+\mathcal{L}\left[\tilde{\mathcal{A}}r\right]+\mathcal{N}\left[\tilde{\mathcal{A}}r\right]-\mathfrak{n}\left(t,x,y\right).\hfill \end{array}(20)$

The same procedure can be extended to a system that comprises more than three equations.

4 Convergence and error analysis of the hybrid algorithm for (2 + 1)-dimensional fractional systems

4.1 Convergence

Theorem 1: If a Banach space has $\mathcal{A}{r}_n(t,x,y)$ and $\mathcal{A}r(t,x,y)$ defined in it for r = 1, 2, 3, then, the series solution of a fractional (2 + 1)-D system in Eq. 19 converges to the solution of (9) for a constant μ ϵ (0,1).

Proof: Let us define the sequence of partial sums of Eq. 19 as Qr_n. To demonstrate that Qr_n(t, x, y) forms a Cauchy sequence in the Banach space, we can proceed by using

$\begin{array}{cc}\hfill \Vert Q{r}_{n+1}\left(t,x,y\right)-Q{r}_n\left(t,x,y\right)\Vert & =\Vert \mathcal{A}{r}_{n+1}\left(t,x,y\right)\Vert \hfill \\ \hfill & \le \mu \Vert \mathcal{A}{r}_n\left(t,x,y\right)\Vert \hfill \\ \hfill & \le {\mu }^2\Vert \mathcal{A}{r}_{n-1}\left(t,x,y\right)\Vert \hfill \\ \hfill & \le \dots \le {\mu }^{n+1}\Vert \mathcal{A}{r}_0\left(t,x,y\right)\Vert .\hfill \end{array}(21)$

If Qr_n and Qr_m are partial sums with n ≥ m and n, m ϵ N, then utilization of triangle inequality gives

$\begin{array}{c}\hfill \Vert Q{r}_n-Q{r}_m\Vert =\Vert \left(Q{r}_n\left(t,x,y\right)-Q{r}_{n-1}\left(t,x,y\right)\right)+\left(Q{r}_{n-1}\left(t,x,y\right)-Q{r}_{n-2}\left(t,x,y\right)\right)\\ \hfill +\cdots +\left(Q{r}_{m+1}\left(t,x,y\right)-Q{r}_m\left(t,x,y\right)\right)\Vert \\ \hfill \le \Vert Q{r}_n\left(t,x,y\right)-Q{r}_{n-1}\left(t,x,y\right)\Vert +\Vert Q{r}_{n-1}\left(t,x,y\right)-Q{r}_{n-2}\left(t,x,y\right)\Vert \\ \hfill +\cdots +\Vert Q{r}_{m+1}\left(t,x,y\right)-Q{r}_m\left(t,x,y\right)\Vert .\end{array}(22)$

From Eq. 21, we get

$\begin{array}{cc}\hfill \Vert Q{r}_n-Q{r}_m\Vert & \le {\mu }^n\Vert \mathcal{A}{r}_0\left(t,x,y\right)\Vert +{\mu }^{n-1}\Vert \mathcal{A}{r}_0\left(t,x,y\right)\Vert +\cdots +{\mu }^{m+1}\Vert \mathcal{A}{r}_0\left(t,x,y\right)\Vert \hfill \\ \hfill & \le \left({\mu }^n+{\mu }^{n-1}+\cdots +{\mu }^{m+1}\right)\Vert \mathcal{A}{r}_0\left(t,x,y\right)\Vert \hfill \\ \hfill & \le {\mu }^{m+1}\left({\mu }^{n-m-1}+{\mu }^{n-m-2}+\cdots +\mu +1\right)\Vert \mathcal{A}{r}_0\left(t,x,y\right)\Vert \hfill \\ \hfill & \le {\mu }^{m+1}\left(\frac{1-{\mu }^{n-m}}{1-\mu }\right)\Vert \mathcal{A}{r}_0\left(t,x,y\right)\Vert .\hfill \end{array}(23)$

Given 0 $<\mu <$ 1, hence, 1 − μ^n−m < 1. Thus, we have

$\begin{array}{c}\hfill \Vert Q{r}_n-Q{r}_m\Vert \le \frac{{\mu }^{m+1}}{1-\mu }\mathit{max}|\mathcal{A}{r}_0\left(t,x,y\right)|,\forall tϵ\left[0,T\right].\end{array}(24)$

Since $\mathcal{A}{r}_0$ is bounded, so

$\underset{n,m\to \infty }{\lim }\Vert Q{r}_n\left(t,x,y\right)-Q{r}_m\left(t,x,y\right)\Vert =0.(25)$

Thus, Qr_n(t, x, y) is a Cauchy sequence in the Banach space, and hence, the given statement is proved.

4.2 Error estimation

Theorem 1: One can determine the maximum absolute truncation error of the solution (19) for a fractional (2 + 1)-dimensional system (9) by using the following expression:

$\left|\mathcal{A}r\left(t,x,y\right)-{\displaystyle \sum _{j=0}^m}\mathcal{A}{r}_j\left(t,x,y\right)\right|\le \frac{{\mu }^{m+1}}{1-\mu }\Vert \mathcal{A}{r}_0\left(t,x,y\right)\Vert .(26)$

Proof: From Eq. 23, we have

$\Vert \mathcal{A}r\left(t,x,y\right)-Q{r}_m\Vert \le {\mu }^{m+1}\left(\frac{1-{\mu }^{n-m}}{1-\mu }\right)\Vert \mathcal{A}{r}_0\left(t,x,y\right)\Vert .(27)$

Since 0 $<\mu <$ 1, therefore, 1 − μ^n−m < 1. Thus, we have

$\left|\mathcal{A}r\left(t,x,y\right)-{\displaystyle \sum _{j=0}^m}\mathcal{A}{r}_j\left(t,x,y\right)\right|\le \frac{{\mu }^{m+1}}{1-\mu }\Vert \mathcal{A}{r}_0\left(t,x,y\right)\Vert .(28)$

5 Solution and analysis of the time-fractional Wu–Zhang system

Consider the following coupled time-fractional (2 + 1)-dimensional WZ system [39]:

$\begin{array}{cc}\hfill & \frac{{\partial }^{\zeta }\mathcal{U}}{\partial {\mathfrak{t}}^{\zeta }}+\mathcal{U}\frac{\partial \mathcal{U}}{\partial x}+\mathcal{V}\frac{\partial \mathcal{U}}{\partial y}+\frac{\partial \mathcal{W}}{\partial x}=0,\hfill \\ \hfill & \frac{{\partial }^{\zeta }\mathcal{V}}{\partial {\mathfrak{t}}^{\zeta }}+\mathcal{U}\frac{\partial \mathcal{V}}{\partial x}+\mathcal{V}\frac{\partial \mathcal{V}}{\partial y}+\frac{\partial \mathcal{W}}{\partial y}=0,\hfill \\ \hfill & \frac{{\partial }^{\zeta }\mathcal{W}}{\partial {\mathfrak{t}}^{\zeta }}+\frac{\partial \left(\mathcal{U}\mathcal{W}\right)}{\partial x}+\frac{\partial \left(\mathcal{V}\mathcal{W}\right)}{\partial y}+\frac{1}{3}\left(\frac{{\partial }^3\mathcal{U}}{\partial x^3}+\frac{{\partial }^3\mathcal{U}}{\partial x\partial y^2}+\frac{{\partial }^3\mathcal{V}}{\partial x^2\partial y}+\frac{{\partial }^3\mathcal{V}}{\partial y^3}\right)=0,0<\zeta \le 1\hfill \end{array}(29)$

that has the initial conditions

$\begin{array}{cc}\hfill \mathcal{U}\left(0,x,y\right)& =-\frac{d+ac}{b}+\frac{2\sqrt{3}}{3}b\tanh \left(bx+cy\right),\hfill \\ \hfill \mathcal{V}\left(0,x,y\right)& =a+\frac{2\sqrt{3}}{3}c\tanh \left(bx+cy\right),\hfill \\ \hfill \mathcal{W}\left(0,x,y\right)& =\frac{2}{3}\left(b^2+c^2\right){\text{sech}}^2\left(bx+cy\right),\hfill \end{array}(30)$

where $\mathcal{U}$ and $\mathcal{V}$ represent the velocity at the surface of water in the x and y directions, respectively, and $\mathcal{W}$ depicts the elevation of the water waves. a, b, c, and d are the non-zero arbitrary constants. The exact solution of (29) at ζ = 1 is

$\begin{array}{cc}\hfill \mathcal{U}\left(t,x,y\right)& =-\frac{d+ac}{b}+\frac{2\sqrt{3}}{3}b\tanh \left(bx+cy+dt\right),\hfill \\ \hfill \mathcal{V}\left(t,x,y\right)& =a+\frac{2\sqrt{3}}{3}c\tanh \left(bx+cy+dt\right),\hfill \\ \hfill \mathcal{W}\left(t,x,y\right)& =\frac{2}{3}\left(b^2+c^2\right){\text{sech}}^2\left(bx+cy+dt\right).\hfill \end{array}(31)$

Solution: The initial step of the He–Laplace procedure is the application of the Laplace transform on both sides of Eq. 29, which gives

$\begin{array}{cc}\hfill & \mathbf{L}\left\{\frac{{\partial }^{\zeta }\mathcal{U}}{\partial {\mathfrak{t}}^{\zeta }}\right\}+\mathbf{L}\left\{\mathcal{U}\frac{\partial \mathcal{U}}{\partial x}+\mathcal{V}\frac{\partial \mathcal{U}}{\partial y}+\frac{\partial \mathcal{W}}{\partial x}\right\}=0,\hfill \\ \hfill & \mathbf{L}\left\{\frac{{\partial }^{\zeta }\mathcal{V}}{\partial {\mathfrak{t}}^{\zeta }}\right\}+\mathbf{L}\left\{\mathcal{U}\frac{\partial \mathcal{V}}{\partial x}+\mathcal{V}\frac{\partial \mathcal{V}}{\partial y}+\frac{\partial \mathcal{W}}{\partial y}\right\}=0,\hfill \\ \hfill & \mathbf{L}\left\{\frac{{\partial }^{\zeta }\mathcal{W}}{\partial {\mathfrak{t}}^{\zeta }}\right\}+\mathbf{L}\left\{\frac{\partial \left(\mathcal{U}\mathcal{W}\right)}{\partial x}+\frac{\partial \left(\mathcal{V}\mathcal{W}\right)}{\partial y}+\frac{1}{3}\left(\frac{{\partial }^3\mathcal{U}}{\partial x^3}+\frac{{\partial }^3\mathcal{U}}{\partial x\partial y^2}+\frac{{\partial }^3\mathcal{V}}{\partial x^2\partial y}+\frac{{\partial }^3\mathcal{V}}{\partial y^3}\right)\right\}=0.\hfill \end{array}(32)$

Utilization of the Laplace transform on the Caputo’s time-fractional derivative (2) leads to

$\begin{array}{ll}\hfill \mathbf{L}\left\{\mathcal{U}\left(t,x,y\right)\right\}& -\frac{1}{s}\left(-\frac{d+ac}{b}+\frac{2\sqrt{3}}{3}b\tanh \left(bx+cy\right)\right)+\left(\frac{1}{s^{\zeta }}\right)\mathbf{L}\left\{\mathcal{U}\frac{\partial \mathcal{U}}{\partial x}+\mathcal{V}\frac{\partial \mathcal{U}}{\partial y}\right.\left.+\frac{\partial \mathcal{W}}{\partial x}\right\}=0,\mathbf{L}\left\{\mathcal{V}\left(t,x,y\right)\right\}\hfill \\ \hfill & -\frac{1}{s}\left(a+\frac{2\sqrt{3}}{3}c\tanh \left(bx+cy\right)\right)+\left(\frac{1}{s^{\zeta }}\right)\mathbf{L}\left\{\mathcal{U}\frac{\partial \mathcal{V}}{\partial x}+\mathcal{V}\frac{\partial \mathcal{V}}{\partial y}+\frac{\partial \mathcal{W}}{\partial y}\right\}=0,\mathbf{L}\left\{\mathcal{W}\left(t,x,y\right)\right\}\hfill \\ \hfill & -\frac{1}{s}\left(\frac{2}{3}\left(b^2+c^2\right){\text{sech}}^2\left(bx+cy\right)\right)+\left(\frac{1}{s^{\zeta }}\right)\times \mathbf{L}\left\{\frac{\partial \left(\mathcal{U}\mathcal{W}\right)}{\partial x}+\frac{\partial \left(\mathcal{V}\mathcal{W}\right)}{\partial y}+\frac{1}{3}\right.\left.\left(\frac{{\partial }^3\mathcal{U}}{\partial x^3}+\frac{{\partial }^3\mathcal{U}}{\partial x\partial y^2}+\frac{{\partial }^3\mathcal{V}}{\partial x^2\partial y}+\frac{{\partial }^3\mathcal{V}}{\partial y^3}\right)\right\}=0.\hfill \end{array}(33)$

We construct homotopies of the aforementioned system as

$\begin{array}{c}{H}_1=\left(1-p\right)\left(\mathbf{L}\left\{\mathcal{U}\left(t,x,y\right)\right\}-{\mathcal{U}}_0\left(t,x,y\right)\right)+p\left(\mathbf{L}\left\{\mathcal{U}\left(t,x,y\right)\right\}-\frac{1}{s}\left(-\frac{d+ac}{b}+\frac{2\sqrt{3}}{3}\right.\right.\hfill \\ \left.b\tanh \left(bx+cy\right))+\left(\frac{1}{s^{\zeta }}\right)\mathbf{L}\left\{\mathcal{U}\frac{\partial \mathcal{U}}{\partial x}+\mathcal{V}\frac{\partial \mathcal{U}}{\partial y}+\frac{\partial \mathcal{W}}{\partial x}\right\}\right),\hfill \\ H_2=\left(1-p\right)\left(\mathbf{L}\left\{\mathcal{V}\left(t,x,y\right)\right\}-{\mathcal{V}}_0\left(t,x,y\right)\right)+p\left(\mathbf{L}\left\{\mathcal{V}\left(t,x,y\right)\right\}-\frac{1}{s}\left(a+\frac{2\sqrt{3}}{3}c\right.\right.\hfill \\ \left.\tanh \left(bx+cy\right))+\left(\frac{1}{s^{\zeta }}\right)\mathbf{L}\left\{\mathcal{U}\frac{\partial \mathcal{V}}{\partial x}+\mathcal{V}\frac{\partial \mathcal{V}}{\partial y}+\frac{\partial \mathcal{W}}{\partial y}\right\}\right),\hfill \\ H_3=\left(1-p\right)\left(\mathbf{L}\left\{\mathcal{W}\left(t,x,y\right)\right\}-{\mathcal{W}}_0\left(t,x,y\right)\right)+p\left(\mathbf{L}\left\{\mathcal{W}\left(t,x,y\right)\right\}-\frac{1}{s}\left(\frac{2}{3}\left(b^2+c^2\right)\right.\right.\hfill \\ {\text{sech}}^2\left(bx+cy\right))+\left(\frac{1}{s^{\zeta }}\right)\mathbf{L}\left\{\frac{\partial \left(\mathcal{U}\mathcal{W}\right)}{\partial x}+\frac{\partial \left(\mathcal{V}\mathcal{W}\right)}{\partial y}+\frac{1}{3}\left(\frac{{\partial }^3\mathcal{U}}{\partial x^3}\right.\right.\left.\left.\left.+\frac{{\partial }^3\mathcal{U}}{\partial x\partial y^2}+\frac{{\partial }^3\mathcal{V}}{\partial x^2\partial y}+\frac{{\partial }^3\mathcal{V}}{\partial y^3}\right)\right\}\right),\hfill \end{array}(34)$

where ${\mathcal{U}}_0(t,x,y)$, ${\mathcal{V}}_0(t,x,y),$ and ${\mathcal{W}}_0(t,x,y)$ are the initial guesses.

$\begin{array}{cc}\hfill {\mathcal{U}}_0\left(t,x,y\right)& =-\frac{d+ac}{b}+\frac{2\sqrt{3}}{3}b\tanh \left(bx+cy\right),\hfill \\ \hfill {\mathcal{V}}_0\left(t,x,y\right)& =a+\frac{2\sqrt{3}}{3}c\tanh \left(bx+cy\right),\hfill \\ \hfill {\mathcal{W}}_0\left(t,x,y\right)& =\frac{2}{3}\left(b^2+c^2\right){\text{sech}}^2\left(bx+cy\right).\hfill \end{array}(35)$

In the next step, we will expand $\mathcal{U}(t,x,y)$, $\mathcal{V}(t,x,y),$ and $\mathcal{W}(t,x,y)$ in Taylor’s series form with respect to p as

$\begin{array}{cc}\hfill \mathcal{U}\left(t,x,y\right)& ={\displaystyle \sum _{m=1}^{\infty }}{p}^m{\mathcal{U}}_m,\hfill \\ \hfill \mathcal{V}\left(t,x,y\right)& ={\displaystyle \sum _{m=1}^{\infty }}{p}^m{\mathcal{V}}_m,\hfill \\ \hfill \mathcal{W}\left(t,x,y\right)& ={\displaystyle \sum _{m=1}^{\infty }}{p}^m{\mathcal{W}}_m.\hfill \end{array}(36)$

Substitution of Eq. 36 into Eq. 34 and then comparison of a similar coefficient with respect to p givesthe first-order problem

$\begin{array}{cc}\hfill & \mathbf{L}\left\{{\mathcal{U}}_1\left(t,x,y\right)\right\}+{\mathcal{U}}_0\left(t,x,y\right)-\frac{1}{s}\left(-\frac{d+ac}{b}+\frac{2\sqrt{3}}{3}b\tanh \left(bx+cy\right)\right)\hfill \\ \hfill & +\left(\frac{1}{s^{\zeta }}\right)\mathbf{L}\left\{{\mathcal{U}}_0\frac{\partial {\mathcal{U}}_0}{\partial x}+{\mathcal{V}}_0\frac{\partial {\mathcal{U}}_0}{\partial y}+\frac{\partial {\mathcal{W}}_0}{\partial x}\right\}=0,\hfill \\ \hfill & \mathbf{L}\left\{{\mathcal{V}}_1\left(t,x,y\right)\right\}-{\mathcal{V}}_0\left(t,x,y\right)-\frac{1}{s}\left(a+\frac{2\sqrt{3}}{3}c\tanh \left(bx+cy\right)\right)\hfill \\ \hfill & \left.+\left(\frac{1}{s^{\zeta }}\right)\mathbf{L}\left\{{\mathcal{U}}_0\frac{\partial {\mathcal{V}}_0}{\partial x}\right.+{\mathcal{V}}_0\frac{\partial {\mathcal{V}}_0}{\partial y}+\frac{\partial {\mathcal{W}}_0}{\partial y}\right\}=0,\hfill \\ \hfill & \mathbf{L}\left\{{\mathcal{W}}_1\left(t,x,y\right)\right\}-{\mathcal{W}}_0\left(t,x,y\right)-\frac{1}{s}\left(\frac{2}{3}\left(b^2+c^2\right){\text{sech}}^2\left(bx+cy\right)\right)\hfill \\ \hfill & \left.+\left(\frac{1}{s^{\zeta }}\right)\mathbf{L}\left\{\frac{\partial {\mathcal{U}}_0{\mathcal{W}}_0}{\partial x}\right.+\frac{\partial {\mathcal{V}}_0{\mathcal{W}}_0}{\partial y}+\frac{1}{3}\left(\frac{{\partial }^3{\mathcal{U}}_0}{\partial x^3}+\frac{{\partial }^3{\mathcal{U}}_0}{\partial x\partial y^2}+\frac{{\partial }^3{\mathcal{V}}_0}{\partial x^2\partial y}+\frac{{\partial }^3{\mathcal{V}}_0}{\partial y^3}\right)\right\}=0,\hfill \end{array}(37)$

with the condition

$\begin{array}{cc}\hfill {\mathcal{U}}_1\left(0,x,y\right)& =0,\hfill \\ \hfill {\mathcal{V}}_1\left(0,x,y\right)& =0,\hfill \\ \hfill {\mathcal{W}}_1\left(0,x,y\right)& =0.\hfill \end{array}(38)$

By operating the inverse Laplace transform, the solution at first order is

$\begin{array}{cc}\hfill {\mathcal{U}}_1\left(t,x,y\right)& =-\frac{4b{d}^2{t}^{2\zeta }\tanh \left(bx+cy\right){\text{sech}}^2\left(bx+cy\right)}{\sqrt{3}\mathrm{\Gamma }\left(2\zeta +1\right)},\hfill \\ \hfill {\mathcal{V}}_1\left(t,x,y\right)& =-\frac{4c{d}^2{t}^{2\zeta }\tanh \left(bx+cy\right){\text{sech}}^2\left(bx+cy\right)}{\sqrt{3}\mathrm{\Gamma }\left(2\zeta +1\right)},\hfill \\ \hfill {\mathcal{W}}_1\left(t,x,y\right)& =\frac{4\left(b^2+c^2\right)d^2{t}^{2\zeta }\left(\cosh \left(2\left(bx+cy\right)\right)-2\right){\text{sech}}^4\left(bx+cy\right)}{3\mathrm{\Gamma }\left(2\zeta +1\right)}.\hfill \end{array}(39)$

The second-order problem is

$\begin{array}{cc}\hfill & \mathbf{L}\left\{{\mathcal{U}}_2\left(t,x,y\right)\right\}+\left(\frac{1}{s^{\zeta }}\right)\mathbf{L}\left\{{\mathcal{U}}_1\frac{\partial {\mathcal{U}}_1}{\partial x}+{\mathcal{V}}_1\frac{\partial {\mathcal{U}}_1}{\partial y}+\frac{\partial {\mathcal{W}}_1}{\partial x}\right\}=0,\hfill \\ \hfill & \mathbf{L}\left\{{\mathcal{V}}_2\left(t,x,y\right)\right\}+\left(\frac{1}{s^{\zeta }}\right)\mathbf{L}\left\{{\mathcal{U}}_1\frac{\partial {\mathcal{V}}_1}{\partial x}+{\mathcal{V}}_1\frac{\partial {\mathcal{V}}_1}{\partial y}+\frac{\partial {\mathcal{W}}_1}{\partial y}\right\}=0,\hfill \\ \hfill & \mathbf{L}\left\{{\mathcal{W}}_2\left(t,x,y\right)\right\}+\left(\frac{1}{s^{\zeta }}\right)\mathbf{L}\left\{\frac{\partial {\mathcal{U}}_1{\mathcal{W}}_1}{\partial x}+\frac{\partial {\mathcal{V}}_1{\mathcal{W}}_1}{\partial y}+\frac{1}{3}\left(\frac{{\partial }^3{\mathcal{U}}_1}{\partial x^3}+\frac{{\partial }^3{\mathcal{U}}_1}{\partial x\partial y^2}+\frac{{\partial }^3{\mathcal{V}}_1}{\partial x^2\partial y}+\frac{{\partial }^3{\mathcal{V}}_1}{\partial y^3}\right)\right\}=0\hfill \end{array}(40)$

that has the condition

$\begin{array}{cc}\hfill {\mathcal{U}}_2\left(0,x,y\right)& =0,\hfill \\ \hfill {\mathcal{V}}_2\left(0,x,y\right)& =0,\hfill \\ \hfill {\mathcal{W}}_2\left(0,x,y\right)& =0.\hfill \end{array}(41)$

The inverse of the Laplace transform gives

$\begin{array}{cc}\hfill {\mathcal{U}}_2\left(t,x,y\right)& =\frac{2bd{t}^{\zeta }{\text{sech}}^2\left(bx+cy\right)}{\sqrt{3}\mathrm{\Gamma }\left(\zeta +1\right)},\hfill \\ \hfill {\mathcal{V}}_2\left(t,x,y\right)& =\frac{2cd{t}^{\zeta }{\text{sech}}^2\left(bx+cy\right)}{\sqrt{3}\mathrm{\Gamma }\left(\zeta +1\right)},\hfill \\ \hfill {\mathcal{W}}_2\left(t,x,y\right)& =-t^{\zeta }\left(\frac{4}{3}d{b}^2\tanh \left(bx+cy\right){\text{sech}}^2\left(bx+cy\right)+\frac{4}{3}{c}^2\right.\hfill \\ \hfill & \left.d\tanh \left(bx+cy\right){\text{sech}}^2\left(bx+cy\right)\right)/\mathrm{\Gamma }\left(\zeta +1\right).\hfill \end{array}(42)$

The same procedure is applied for higher-order problems. Thus, the approximate solution at the higher order of the (2 + 1)-dimensional Wu–Zhang system can be obtained by

$\begin{array}{cc}\hfill \tilde{\mathcal{U}}& ={\displaystyle \sum _{m=0}^{\infty }}{\mathcal{U}}_m\left(t,x,y\right),\hfill \\ \hfill \tilde{\mathcal{V}}& ={\displaystyle \sum _{m=0}^{\infty }}{\mathcal{V}}_m\left(t,x,y\right),\hfill \\ \hfill \tilde{\mathcal{W}}& ={\displaystyle \sum _{m=0}^{\infty }}{\mathcal{W}}_m\left(t,x,y\right).\hfill \end{array}(43)$

By replacing the approximate solutions (43) in the given system (29), we obtain residual errors

$\begin{array}{cc}\hfill & R1=\frac{{\partial }^{\zeta }\tilde{\mathcal{U}}}{\partial {\mathfrak{t}}^{\zeta }}+\tilde{\mathcal{U}}\frac{\partial \tilde{\mathcal{U}}}{\partial x}+\tilde{\mathcal{V}}\frac{\partial \tilde{\mathcal{U}}}{\partial y}+\frac{\partial \tilde{\mathcal{W}}}{\partial x},\hfill \\ \hfill & R2=\frac{{\partial }^{\zeta }\tilde{\mathcal{V}}}{\partial {\mathfrak{t}}^{\zeta }}+\tilde{\mathcal{U}}\frac{\partial \tilde{\mathcal{V}}}{\partial x}+\tilde{\mathcal{V}}\frac{\partial \tilde{\mathcal{V}}}{\partial y}+\frac{\partial \tilde{\mathcal{W}}}{\partial y},\hfill \\ \hfill & R3=\frac{{\partial }^{\zeta }\tilde{\mathcal{W}}}{\partial {\mathfrak{t}}^{\zeta }}+\frac{\partial \tilde{\mathcal{U}}\tilde{\mathcal{W}}}{\partial x}+\frac{\partial \tilde{\mathcal{V}}\tilde{\mathcal{W}}}{\partial y}+\frac{1}{3}\left(\frac{{\partial }^3\tilde{\mathcal{U}}}{\partial x^3}+\frac{{\partial }^3\tilde{\mathcal{U}}}{\partial x\partial y^2}+\frac{{\partial }^3\tilde{\mathcal{V}}}{\partial x^2\partial y}+\frac{{\partial }^3\tilde{\mathcal{V}}}{\partial y^3}\right).\hfill \end{array}(44)$

6 Results and discussion

The objective of this study is to propose a new soliton solution of the non-linear time-fractional Wu–Zhang system. This (2 + 1)-dimensional system describes the phenomena of long dispersive waves. The current section is focused on the numerical and graphical results of the WZ system through a hybrid approach by using homotopy perturbation with the Laplace transform, which is known as the He–Laplace algorithm (method). Initially, solutions are captured through the He–Laplace algorithm, considering the fractional derivative in Caputo sense. The obtained results are then analyzed at both fractional and integral orders. Table 1 depicts the residual error at $\mathcal{U},\mathcal{V},\mathcal{W}$ along with overall system errors at various fractional parameter values. These errors clearly indicate the reliability of proposed methodology across the complete fractional domain. It is also observed that error is reduced when fractional parameter approaches one.

TABLE 1

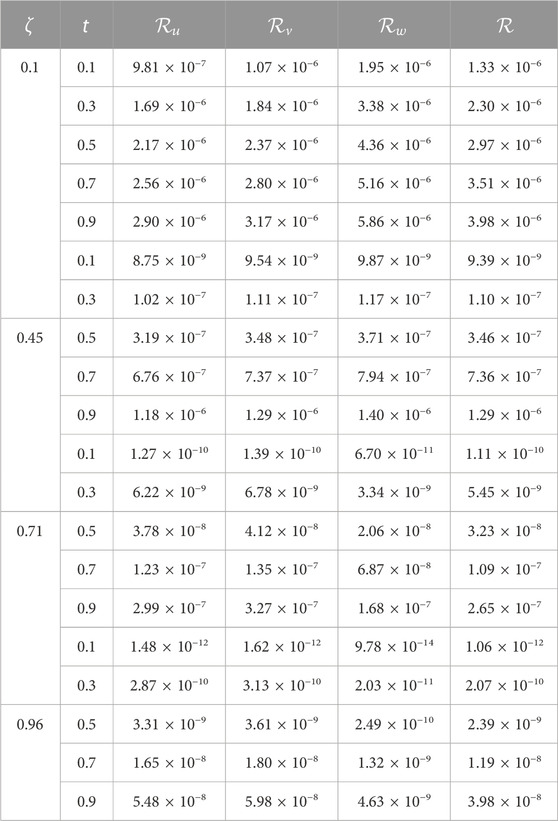
TABLE 1. He–Laplace errors for different values of ζ, when a = d = 0.13, b = 0.11, c = 0.12, x = 3, and y = 6. Here, ${\mathcal{R}}_{\mathit{u}}$, ${\mathcal{R}}_{\mathit{v}}$, ${\mathcal{R}}_{\mathit{w}}$, and $\mathcal{R}$ represent residual errors of $\mathcal{U}$, $\mathcal{V}$, $\mathcal{W}$, and system errors, respectively.

Table 2 shows the comparison of results obtained through He–Laplace and other methods at the integer order that is ζ = 1. This numerical comparison indicates that He–Laplace surpasses other mentioned schemes in terms of accuracy. Figure 1 depicts the He–Laplace solution of the WZ system in 3D at the integer order. This graphical illustration confirms that in the WZ system, surface water velocities in x and y directions are very high, while elevation in water waves decreases with time. Error analysis at ζ = 0.4, 0.8, and 1 as 3D structures can be seen from Figure 2 for $\mathcal{U}$, $\mathcal{V},$ and $\mathcal{W},$ respectively. At ζ = 1, the errors are lesser than ζ = 0.8, and the same can be observed in case of ζ = 0.4.

TABLE 2

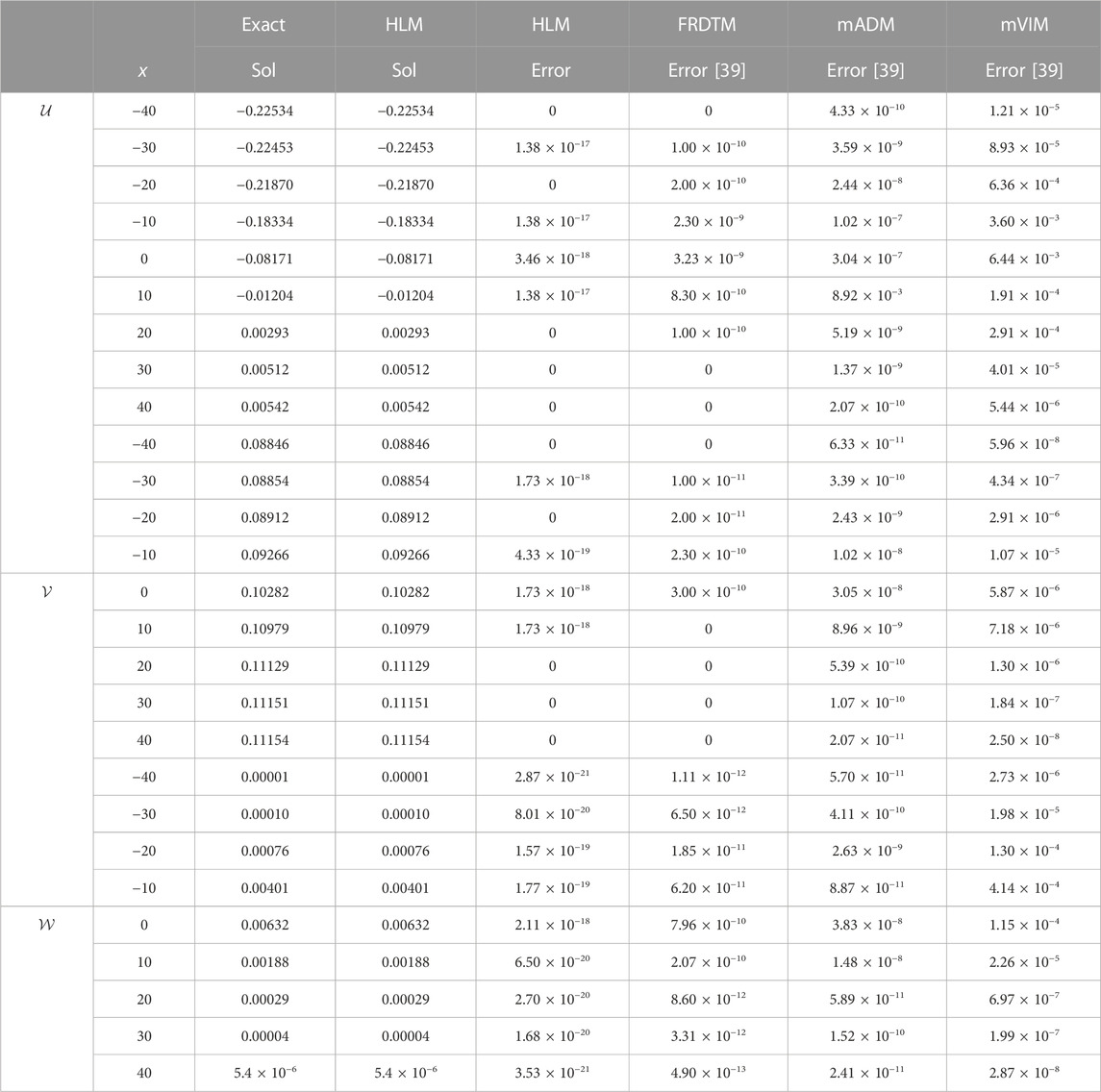
TABLE 2. Error comparison of the He–Laplace algorithm with other methods, when ζ = 1, a = b = 0.1, c = d = 0.01, t = 5, and y = 20.

FIGURE 1

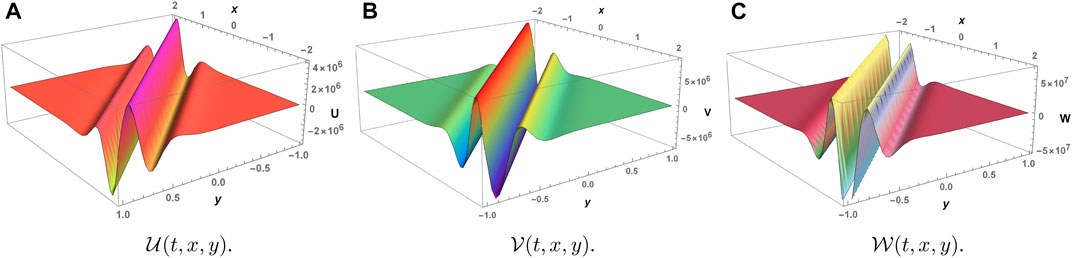
FIGURE 1. Graphical illustration of the He–Laplace solution at ζ = 1, a = c = 2, b = d = 1, and t = 2.

FIGURE 2

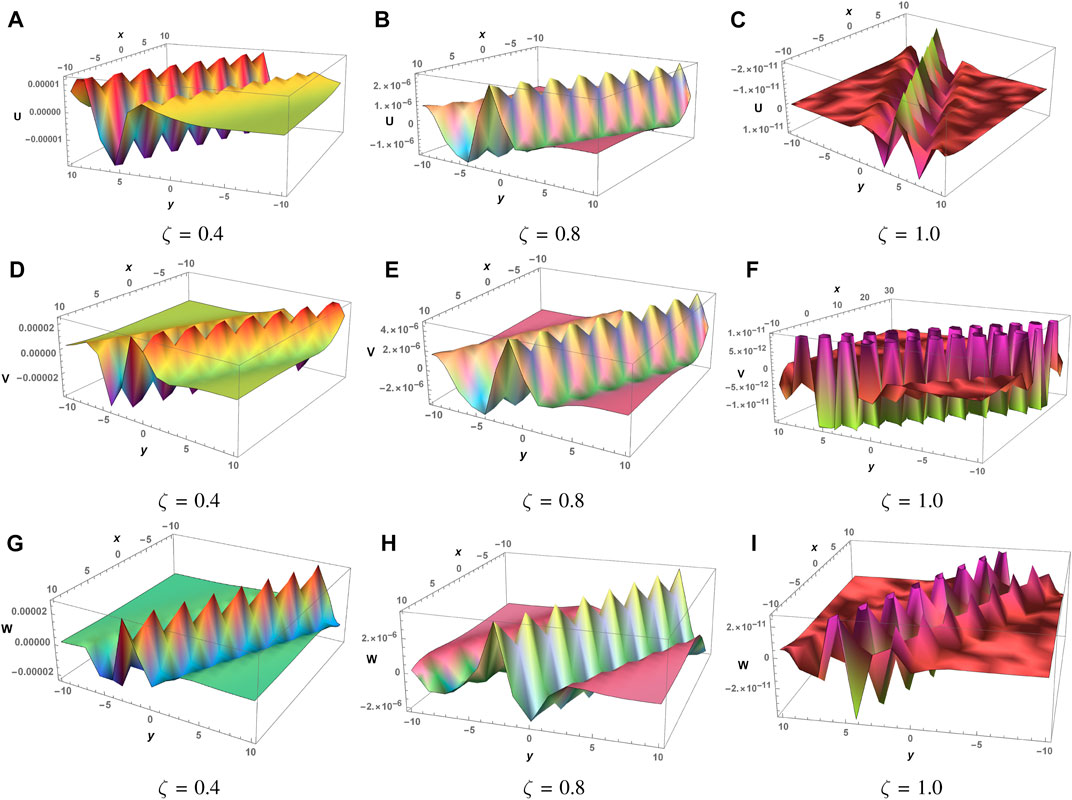
FIGURE 2. Error analysis at different values of the fractional parameter ζ, when a = c = 0.2, b = d = 0.1, and t = 2.

The impact of the fractional parameter on the water surface is depicted in Figure 3. Research findings indicate that a rise in ζ results in a reduction of the water surface velocity, in both the x and y directions. However, water wave elevation $(\mathcal{W})$ shows inverse behavior in this case. Comparative analysis of different fractional derivative approaches (Atangana–Baleanu, Caputo–Fabrizio, and Caputo) on the solution profile can be seen in Figure 4. Analysis of this figure shows that water surface velocities are highest in the Atangana–Baleanu fractional approach as compared to Caputo and Caputo–Fabrizio fractional approaches. On the other hand, $\mathcal{W}$ depicts opposite behavior as compared to $\mathcal{U}$ and $\mathcal{V}$.

FIGURE 3

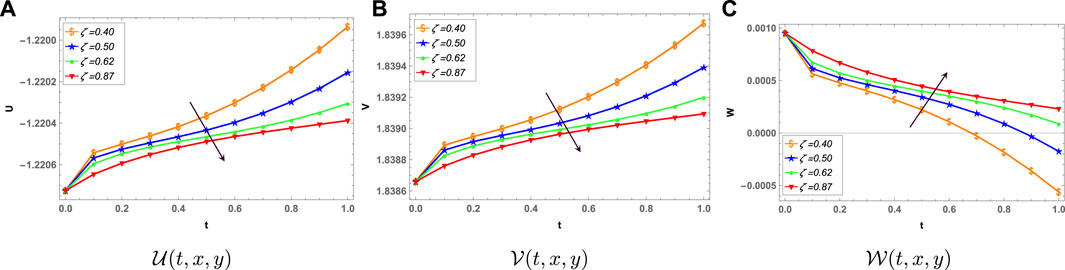
FIGURE 3. Effect of the fractional parameter ζ on the water surface level, when a = 0.8, c = 0.9, b = d = 0.7, y = 3, and x = 2.

FIGURE 4

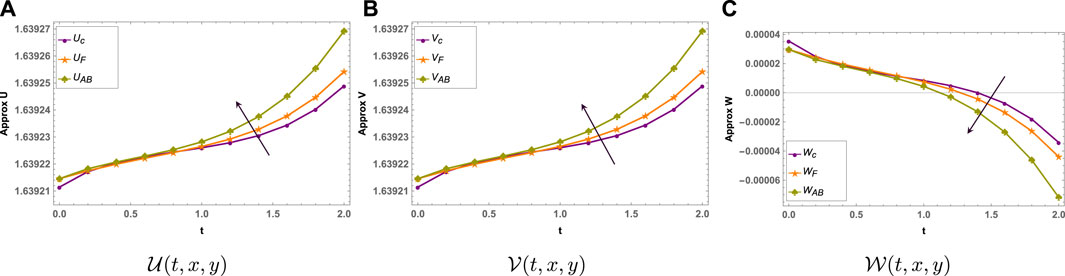
FIGURE 4. Comparison of Caputo, Caputo–Fabrizio, and Atangana–Baleanu fractional derivative approaches on the solution profile, when a = 0.6, b = 0.8, c = 0.9, d = 0.7, y = 2, and x = 5.

7 Conclusion

In this article , a hybrid approach is proposed to solve and analyze the highly non-linear time-fractional (2 + 1)-dimensional WZ system, which is famous for capturing long dispersive waves. A hybrid approach in which homotopy perturbation is combined with the Laplace transform along with different fractional derivatives is proposed for the solution and analysis of the fractional WZ system. Efficiency of the obtained solution is checked over the entire fractional domain to show the validity and convergence of the proposed methodology. Error analysis is also performed in comparison with other well-known numerical methods, which confirms the efficiency of the proposed approach. Graphical analysis shows that water surface velocities increase, while surface elevation decreases, when fractional parameter increases. Also, it is noted that the Atangana–Baleanu approach uplifts water velocities in x and y directions more than Caputo and Caputo–Fabrizio approaches. Analysis of the results also concludes that the proposed method is a reliable technique, which can be extended to more complex fractional systems.

Data availability statement

The original contributions presented in the study are included in the article/Supplementary Material; further inquiries can be directed to the corresponding author.

Author contributions

Conceptualization: MQ. Data curation: EA. Formal analysis: ST. Validation: EA. Writing—original draft: MQ and SS. Writing—review editing: HA and SA. All authors contributed to the article and approved the submitted version.

Funding

This Project is funded by King Saud University, Riyadh, Saudi Arabia.

Acknowledgments

Research Supporting Project number (RSP2023R167), King Saud University, Riyadh, Saudi Arabia.

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Abbreviations

WZ, Wu–Zhang; DEs, differential equations; PDEs, partial differential equations; FDEs, fractional differential equations; HPM, homotopy perturbation method; HLM, He–Laplace method; mVIM, modified variation iteration method; mADM, modified Adomian decomposition method; FRDTM, fractional reduced differential transform method.

References

1. Dzerjinsky RI. The earthquake attributes disjunctive form analysis at the quickest form change directions. In: Lecture notes in networks and systems. Springer International Publishing (2021). p. 96–101.

CrossRef Full Text | Google Scholar

2. Hirano S. Source time functions of earthquakes based on a stochastic differential equation. Scientific Rep (2022) 12(1):3936. doi:10.1038/s41598-022-07873-2

CrossRef Full Text | Google Scholar

3. Zheng C, Wu W-Z, Xie W, Li Q. A MFO-based conformable fractional nonhomogeneous grey Bernoulli model for natural gas production and consumption forecasting. Appl Soft Comput (2021) 99:106891. doi:10.1016/j.asoc.2020.106891

CrossRef Full Text | Google Scholar

4. Liu C, Wu W-Z, Xie W, Zhang T, Zhang J. Forecasting natural gas consumption of China by using a novel fractional grey model with time power term. Energ Rep (2021) 7(788–797):788–97. doi:10.1016/j.egyr.2021.01.082

CrossRef Full Text | Google Scholar

5. Akbar MA, Abdul Kayum M, Osman MS, Abdel-Aty A-H, Eleuch H. Analysis of voltage and current flow of electrical transmission lines through mZK equation. Results Phys (2021) 20:103696. doi:10.1016/j.rinp.2020.103696

CrossRef Full Text | Google Scholar

6. Bidkhori P, Karizaki VM. Diffusion and kinetic modeling of water absorption process during soaking and cooking of chickpea. Legume Sci (2021) 4(1). doi:10.1002/leg3.116

CrossRef Full Text | Google Scholar

7. Ahmadova A, Mahmudov NI. Langevin differential equations with general fractional orders and their applications to electric circuit theory. J Comput Appl Math (2021) 388:113299. doi:10.1016/j.cam.2020.113299

CrossRef Full Text | Google Scholar

8. Khader MM, Gómez-Aguilar JF, Adel M. Numerical study for the fractional RL, RC, and RLC electrical circuits using legendre pseudo-spectral method. Int J Circuit Theor Appl (2021) 49(10):3266–85. doi:10.1002/cta.3103

CrossRef Full Text | Google Scholar

9. Caro LAP, Mendoza R, Mendoza VMP. Application of genetic algorithm with multi-parent crossover on an inverse problem in delay differential equations. In: PROCEEDINGS OF THE INTERNATIONAL CONFERENCE ON MATHEMATICAL SCIENCES AND TECHNOLOGY 2020 (MATHTECH 2020): Sustainable Development of Mathematics and Mathematics in Sustainability Revolution. AIP Publishing (2021).

CrossRef Full Text | Google Scholar

10. Chen Y, Luo Y, Liu Q, Xu H, Zhang D. Any equation is a forest: Symbolic genetic algorithm for discovering open-form partial differential equations (sga-pde) (2021).

Google Scholar

11. Salazar-Viedma M, Gabriel Vergaño-Salazar J, Pastenes L, D’Afonseca V. Simulation model for hashimoto autoimmune thyroiditis disease. Endocrinology (2021) 162(12):bqab190. doi:10.1210/endocr/bqab190

PubMed Abstract | CrossRef Full Text | Google Scholar

12. Guzzi PH, Petrizzelli F, Mazza T. Disease spreading modeling and analysis: A survey. Brief Bioinform (2022) 23(4). doi:10.1093/bib/bbac230

CrossRef Full Text | Google Scholar

13. Sahoo D, Samanta GP. Comparison between two tritrophic food chain models with multiple delays and anti-predation effect. Int J Biomath (2021) 14(03). doi:10.1142/s1793524521500108

CrossRef Full Text | Google Scholar

14. Mondal B, Ghosh U, Rahman MS, Saha P, Sarkar S. Studies of different types of bifurcations analyses of an imprecise two species food chain model with fear effect and non-linear harvesting. Math Comput Simul (2022) 192:111–35. doi:10.1016/j.matcom.2021.08.019

CrossRef Full Text | Google Scholar

15. Ahmad Z, Ali F, Khan N, Khan I. Dynamics of fractal-fractional model of a new chaotic system of integrated circuit with mittag-leffler kernel. Chaos, Solitons and Fractals (2021) 153:111602. doi:10.1016/j.chaos.2021.111602

CrossRef Full Text | Google Scholar

16. Ayub A, Sabir Z, Le D-N, Aly AA. Nanoscale heat and mass transport of magnetized 3-d chemically radiative hybrid nanofluid with orthogonal/inclined magnetic field along rotating sheet. Case Stud Therm Eng (2021) 26:101193. doi:10.1016/j.csite.2021.101193

CrossRef Full Text | Google Scholar

17. Ali Abro K, Atangana A. Dual fractional modeling of rate type fluid through non-local differentiation. In: Numerical methods for partial differential equations (2020).

Google Scholar

18. Shchigolev VK. Fractional-order derivatives in cosmological models of accelerated expansion. Mod Phys Lett A (2021) 36(14):2130014. doi:10.1142/s0217732321300147

CrossRef Full Text | Google Scholar

19. Abed AM, Rashid ZN, Abedi F, Zeebaree SRM, Sahib MA, Mohamad Jawad AJ, et al. Trajectory tracking of differential drive mobile robots using fractional-order proportional-integral-derivative controller design tuned by an enhanced fruit fly optimization. Meas Control (2022) 55(3-4):209–26. doi:10.1177/00202940221092134

CrossRef Full Text | Google Scholar

20. Shokhanda R, Goswami P, He J-H, Althobaiti A. An approximate solution of the time-fractional two-mode coupled Burgers equation. Fractal Fractional (2021) 5(4):196. doi:10.3390/fractalfract5040196

CrossRef Full Text | Google Scholar

21. Habib S, Batool A, Islam A, Nadeem M, Gepreel KA, He J-H. Study of nonlinear Hirota-Satsuma coupled KdV and coupled mkdv system with time fractional derivative. Fractals (2021) 29(05):2150108. doi:10.1142/s0218348x21501085

CrossRef Full Text | Google Scholar

22. Jin T, Yang X. Monotonicity theorem for the uncertain fractional differential equation and application to uncertain financial market. Math Comput Simul (2021) 190:203–21. doi:10.1016/j.matcom.2021.05.018

CrossRef Full Text | Google Scholar

23. Lin Z, Wang H. Modeling and application of fractional-order economic growth model with time delay. Fractal Fractional (2021) 5(3):74. doi:10.3390/fractalfract5030074

CrossRef Full Text | Google Scholar

24. Al-Nassir S. Dynamic analysis of a harvested fractional-order biological system with its discretization. Chaos, Solitons and Fractals (2021) 152:111308. doi:10.1016/j.chaos.2021.111308

CrossRef Full Text | Google Scholar

25. Mandelbrot BB Les objets fractals: Forme, hasard et dimension, Vol. 17 Flammarion Paris (1975).

Google Scholar

26. He J-H, Qian M-Y. A fractal approach to the diffusion process of red ink in a saline water. Therm Sci (2022) 26:2447–51. doi:10.2298/tsci2203447h

CrossRef Full Text | Google Scholar

27. Zhou W, Cao Y, Zhao H, Li Z, Feng P, Feng F. Fractal analysis on surface topography of thin films: A review. Fractal Fractional (2022) 6(3):135. doi:10.3390/fractalfract6030135

CrossRef Full Text | Google Scholar

28. He C-H, Liu C, He J-H, Gepreel KA Low frequency property of a fractal vibration model for a concrete beam. Fractals (2021) 29(05):2150117. doi:10.1142/s0218348x21501176

CrossRef Full Text | Google Scholar

29. Vu CC, Truong TTN, Kim JY. Fractal structures in flexible electronic devices. Mater Today Phys (2022) 27:100795. doi:10.1016/j.mtphys.2022.100795

CrossRef Full Text | Google Scholar

30. Khan H, Ahmad F, Tunç O, Idrees M. On fractal-fractional Covid-19 mathematical model. Chaos, Solitons Fractals (2022) 157:111937. doi:10.1016/j.chaos.2022.111937

PubMed Abstract | CrossRef Full Text | Google Scholar

31. Wu TY, Zhang JE. On modeling nonlinear long waves. In: Mathematics is for solving problems (1996). p. 233–49.

Google Scholar

32. Wang K-L, He C-H. A remark on wang’s fractal variational principle. Fractals (2019) 27(08):1950134. doi:10.1142/s0218348x19501342

CrossRef Full Text | Google Scholar

33. Zayed EME, -Abdel Rahman HM. On solving the kay-burger’s equation and the Wu-zhang equations using the modified variational iteration method. Int J Nonlinear Sci Numer Simulation (2009) 10(9). doi:10.1515/ijnsns.2009.10.9.1093

CrossRef Full Text | Google Scholar

34. Khater MMA, Attia RAM, Lu D. Numerical solutions of nonlinear fractional Wu-zhang system for water surface versus three approximate schemes. J Ocean Eng Sci (2019) 4(2):144–8. doi:10.1016/j.joes.2019.03.002

CrossRef Full Text | Google Scholar

35. Aljahdaly NH, El-Tantawy SA, Wazwaz A-M, Ashi HA. Adomian decomposition method for modelling the dissipative higher-order rogue waves in a superthermal collisional plasma. J Taibah Univ Sci (2021) 15(1):971–83. doi:10.1080/16583655.2021.2012373

CrossRef Full Text | Google Scholar

36. Asgari A, Ganji DD, Davodi AG. Extended tanh method and exp-function method and its application to(2+ 1)-dimensional dispersive long wave nonlinear equations. J Appl Math Stat Inform (Jamsi) (2010) 6.

Google Scholar

37. Zheng H, Xia Y, Bai Y, Lei G. Travelling wave solutions of Wu-zhang system via dynamic analysis. Discrete Dyn Nat Soc (2020) , 2020:1–9. doi:10.1155/2020/2845841

CrossRef Full Text | Google Scholar

38. Kaur B, Gupta RK. Time fractional (2+1)-dimensional Wu-zhang system: Dispersion analysis, similarity reductions, conservation laws, and exact solutions. Comput Math Appl (2020) 79(4):1031–48. doi:10.1016/j.camwa.2019.08.014

CrossRef Full Text | Google Scholar

39. Patel T, Patel H. An analytical approach to solve the fractional-order (2 + 1)-dimensional Wu-zhang equation. Math Methods Appl Sci (2022) 46:479–89. doi:10.1002/mma.8522

CrossRef Full Text | Google Scholar

40. Almeida R. A caputo fractional derivative of a function with respect to another function. Commun Nonlinear Sci Numer Simul (2017) 44:460–81. doi:10.1016/j.cnsns.2016.09.006

CrossRef Full Text | Google Scholar

41. Atangana A, Baleanu D. New fractional derivatives with nonlocal and non-singular kernel: Theory and application to heat transfer model (2016).

CrossRef Full Text | Google Scholar

42. Caputo M, Fabrizio M. A new definition of fractional derivative without singular kernel. Prog Fractional Differ Appl (2015) 1(2):73–85.

Google Scholar

43. Anjum N, Ain QT. Application of He’s fractional derivative and fractional complex transform for time fractional Camassa-Holm equation. Therm Sci (2020) 24:3023–30. doi:10.2298/tsci190930450a

CrossRef Full Text | Google Scholar

44. Anjum N, He J-H, Ain QT, Tian D. Li-He’s modified homotopy perturbation method for doubly-clamped electrically actuated microbeams-based microelectromechanical system. Facta Universitatis, Ser Mech Eng (2021) 19(4):601. doi:10.22190/fume210112025a

CrossRef Full Text | Google Scholar

45. Baitiche Z, Derbazi C, Alzabut J, Esmael Samei M, Kaabar MKA, Siri Z. Monotone iterative method for caputo fractional differential equation with nonlinear boundary conditions. Fractal and Fractional (2021) 5(3):81. doi:10.3390/fractalfract5030081

CrossRef Full Text | Google Scholar

46. Do QH, Ngo HTB, Razzaghi M. A generalized fractional-order Chebyshev wavelet method for two-dimensional distributed-order fractional differential equations. Commun Nonlinear Sci Numer Simul (2021) 95:105597. doi:10.1016/j.cnsns.2020.105597

CrossRef Full Text | Google Scholar

47. Hashemi MS, Hajikhah S, Mustafa Inc. Generalized squared remainder minimization method for solving multi-term fractional differential equations. Nonlinear Anal Model Control (2021) 26(1):57–71. doi:10.15388/namc.2021.26.20560

CrossRef Full Text | Google Scholar

48. Tian Y, Liu J. A modified exp-function method for fractional partial differential equations. Therm Sci (2021) 25:1237–41. doi:10.2298/tsci200428017t

CrossRef Full Text | Google Scholar

49. He J-H, He C-H, Alsolami AA. A good initial guess for approximating nonlinear oscillators by the homotopy perturbation method. Facta Univ. Ser Mech Eng (2023) 21(1):21–9.

Google Scholar

50. He J-H, El-Dib YO. The enhanced homotopy perturbation method for axial vibration of strings. Facta Univ. Ser Mech Eng (2021) 19(4):735–50. doi:10.22190/fume210125033h

CrossRef Full Text | Google Scholar

51. He J-H. Homotopy perturbation technique. Comput Methods Appl Mech Eng (1999) 178(3-4):257–62. doi:10.1016/s0045-7825(99)00018-3

CrossRef Full Text | Google Scholar

52. He C-H, El-Dib YO. A heuristic review on the homotopy perturbation method for non-conservative oscillators. J Low Frequency Noise, Vibration Active Control (2021) 41(2):572–603. doi:10.1177/14613484211059264

CrossRef Full Text | Google Scholar

53. Schiff JL. The Laplace transform. New York: Springer (1999).

Google Scholar

54. Ain QT, Anjum N, Din A, Zeb A, Djilali S, Khan ZA. On the analysis of Caputo fractional order dynamics of Middle East lungs coronavirus (MERS-CoV) model. Alexandria Eng J (2022) 61(7):5123–31. doi:10.1016/j.aej.2021.10.016

CrossRef Full Text | Google Scholar

55. Tuan NH, Mohammadi H, Rezapour S. A mathematical model for COVID-19 transmission by using the caputo fractional derivative. Chaos, Solitons and Fractals (2020) 140:110107. doi:10.1016/j.chaos.2020.110107

PubMed Abstract | CrossRef Full Text | Google Scholar

56. Alizadeh S, Baleanu D, Rezapour S. Analyzing transient response of the parallel RCL circuit by using the caputo-fabrizio fractional derivative. Adv Differ. Equations (2020) 2020, 55, doi:10.1186/s13662-020-2527-0

CrossRef Full Text | Google Scholar

57. Atangana A, Gómez-Aguilar JF. Decolonisation of fractional calculus rules: Breaking commutativity and associativity to capture more natural phenomena. The Eur Phys J Plus (2018) 133(4):166. doi:10.1140/epjp/i2018-12021-3

CrossRef Full Text | Google Scholar

58. Ain QT, He J-H. On two-scale dimension and its applications. Therm Sci (2019) 23:1707–12. doi:10.2298/tsci190408138a

CrossRef Full Text | Google Scholar

59. Anjum N, Ain QT, Li X-X. Two-scale mathematical model for tsunami wave. GEM - Int J Geomathematics (2021) 12(1):10. doi:10.1007/s13137-021-00177-z

CrossRef Full Text | Google Scholar

Nomenclature