High-Q transmission characteristics in terahertz guided-mode magnetic resonance system

Introduction: Guided mode resonance is generated by coupling wave diffractions with the waveguided mode. The guided mode resonances provide narrow-linewidth and resonance intensity for high quality factor (Q-factor) optical resonators.

Methods: we demonstrate the high-Q guided mode resonances propagating on a low-loss, terahertz guided-mode magnetic resonance system, which are periodic square lattices of U-shaped split ring resonators (SRRs) on quartz substrates.

Results: By choosing a judicious array period, two distinct frequency guided mode resonances and a magnetic dipole resonance with high Q-factor are observed. The interaction of the two resonances at similar frequencies produces a total transmission peak.

Discussion: The dependences of the magnetic dipole resonance on the lattice period and structural parameters are investigated and discussed. The frequency difference between these two guided mode resonances widens with increasing Lattice period. The sharp spectral feature of each resonance results in the abrupt degradation of the spectral edge transmission. The proposed scheme is promising for efficient THz sensing, THz switching, and slow-light devices.

1 Introduction

Terahertz (THz) radiation has received great attentions owing to its potential advantages in many frontier fields, such as medical diagnosis, broadband communication, security, national defense, and biomolecular noninvasive sensing [1–4]. As a transition band between electronics and photonics, THz radiation has always been one of the important subjects across different branches of physics such as optics, electromagnetics, and nanophotonics [5–10]. THz technology has achieved significant progress, particularly in THz radiation sources, detectors and application research in sensing and imaging. However, various THz functional devices and physical phenomena are still need to be developed diligently. Especially in THz regime, the realization of the strong field-matter interaction has been in the exploratory stage and is urgent.

Guided mode resonances, arises from the coherent coupling of the grating diffraction field and waveguide modes under the conditions of the phase matching [11–14]^, which can be used to achieve THz resonant metasurfaces with high quality factors and frequency selective responses. Guided mode resonances with high quality-factor (Q-factor) plays an important role for ultra-sensitive label-free sensing. Recently, a variety of guided mode resonances have been presented to operate in the THz band [15–29], contributing greatly to the development of THz high-Q resonance. However, most reported works about THz high Q-factor guided-mode resonances focused on conventional electrical gratings [16–29], and few studies have reported guided-mode resonances in guided mode-magnetic resonance system. Moreover, it is still challenging to achieve both guided-mode resonance and magnetic resonance with ultrahigh-Q and large modulation depth in a resonant system, because the magnetic contribution is negligible in light-matter interactions, since because the effect of light on the magnetic permeability is much weaker than on the electric permittivity [30].

In the paper, we propose a guided-mode magnetic resonance system to produce extremely high Q-factor Fano guided-mode resonance in THz regime. High-Q guided mode resonances and magnetic dipole resonance with ultrahigh-Q and large modulation depth in a resonant system can be achieved in a low-loss, THz guided-mode magnetic resonance system, which are periodic square lattices of U-shaped SRRs on quartz substrates. The effects of lattice period and structural parameters on the magnetic dipole resonance are discussed. Choosing a judicious array period, two distinct different frequency guided mode resonances are observed. The interaction of the two resonances at similar frequencies produces a total transmission peak. The frequency difference between these two guided mode resonances widens with increasing Lattice period. The sharp spectral feature of each resonance results in the abrupt degradation at the spectral edge transmission. The proposed scheme holds great promise for practical applications for ultra-narrow THz filters.

2 Metasurface design and simulation

The proposed THz plasmonic metasurface resonator is depicted in Figure 1, with a sketch of unit cell, the relevant dimensional parameters and the polarization configuration (the electric (E) and magnetic (H) fields of the incident wave). The geometric center of the SRR is placed on orthocenter of the unit cell, as shown by the white dashed line. In contrast to plasmonic based guided-mode resonance devices, the advantage of the proposed structure is that the simple U-shaped SRRs simultaneously acts as low-loss magnetic resonator and a diffraction grating, supporting in the formation of THz guided-mode resonance and enabling distinct properties for transmission. In addition, the proposed structure has the characteristics of simplicity, better homogeneity, and easy processing.^17,18 The optimized geometric parameters of the SRRs involve the super cell lattice constants of P_x = P_y = p = 160 μm, the two arms L_x = 30 μm, the backbone L_y = 50 μm, the split gap s = 40 μm, the width w = 5 μm, and the thickness of metal SRRs is 200 nm. The thickness of the quartz substrate is 300 μm.

FIGURE 1

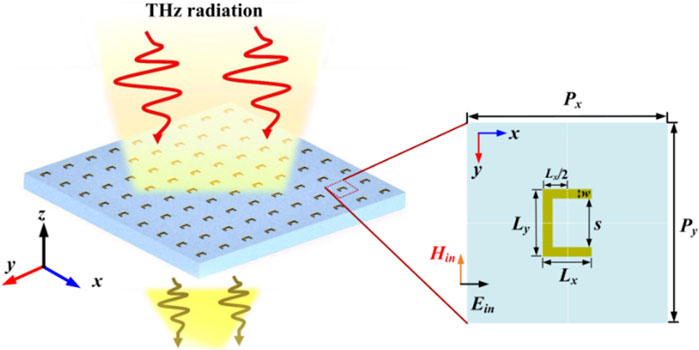
FIGURE 1. Structural schematic of the proposed THz plasmonic metasurfaces, with a unit cell and metal SRR zoomed in. The unit cell includes the relevant dimensional parameters and the polarization configuration.

Numerical simulations were carried out by utilizing commercially full-wave simulation software package COMSOL Multiphysics based on the finite element method (FEM). Periodic boundary conditions in both x and y directions along with perfectly matched layer is the z direction are applied to the metamaterial unit cell. Theoretical simulation techniques can be supported in recent papers [21, 22, 31]. The filtering properties of the resonator can occur normally when an infinite metasurface is fabricated into a finite sample [21, 22, 31]. The relative permittivity of gold is calculated by the Drude model as ε = 1-ω_p²/(ω²+iγ_cω) in the THz regime, with plasma frequency ω_p = 1.37 × 10¹⁶ rad/s and damping rate γ_c = 4.08 × 10¹³ rad/s [22, 32, 33]. The metals have excellent conductivity at THz frequencies, the ohmic losses of most metallic metamaterials are relatively quite low. The quartz substrate is taken as a lossless dielectric with relative electrical permittivity of 2.14 [31]. The plane waves are incident normally to the unit cell along the z direction with the x-polarization (perpendicular to the gap of SRRs). The transmittance coefficient is obtained by calculating the S-parameter.

3 Results and discussions

The transmission spectra with x-polarization incidence is shown in Figure 2A. It can be observed that when the lattice period is 160 μm (shown by the red line), a broadband dipolar resonance and two abrupt ultra-sharp Fano resonances with distinct narrow linewidth are excited at f₁ = 0.886 THz, f₂ = 0.931 THz and f₃ = 0.940 THz with Δf of in the simulated transmission spectra, respectively. The Q-factor is defined as Q = 2πf₀P_S/P_L = f₀/Δf [22], where f₀ is the resonant frequency, P_S and P_L are stored energy and dissipated energy, and Δf is the full width at half maximum. Thus, the Q-factor of the dipole resonance mode f₁ is about 32. Intriguingly, it can also be observed that two abrupt ultrasharp resonances feature with ultrahigh Q-factor as high as 651 and 97 occur at f₂ = 0.931 THz and f₃ = 0.940 THz in the transmission spectra, as shows in Figure 2. Note that the energy radiation loss is generally large in SRRs magnetic resonant systems. The Q-factor of resonance in various THz magnetic systems is often difficult to break the limit of 15 experimentally, and the theoretical Q-factor is less than about 10² [31]. In such cases, the Q-factors of the order of 10³ can be considered as high. The simulated modulation depth [(T_max-T_min)/(T_max + T_min) × 100%] for the three resonances are 90.6%, 95.2%, and 95.3%, respectively. Interestingly, as indicated by the green dot, the interaction of the two resonances at similar frequencies produces a total transmission peak. Interestingly, the THz guided-mode magnetic resonance system exhibits three total transmission peaks in the 0.8 to 1 THz range, which is appropriate for practical application to ultra-narrow multi-band filters.

FIGURE 2

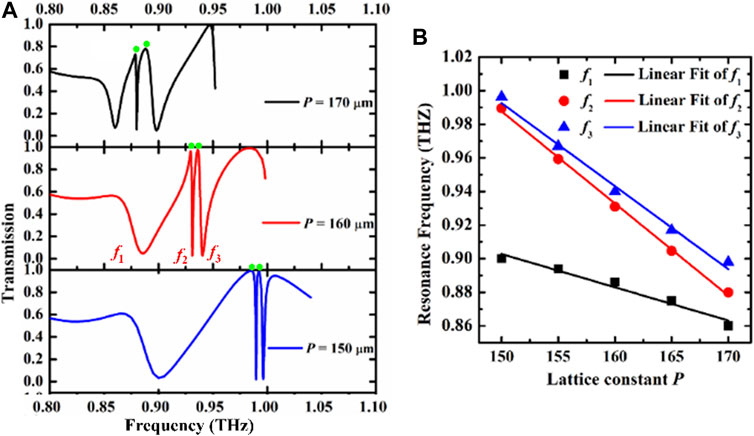
FIGURE 2. (A) The transmission of U-type arrays versus inverse lattice period; (B) The evolutions of resonant frequency of the three modes versus inverse lattice constant.

When the lattice period increases from 150 to 170 μm, all three resonance modes appear distinctly redshift, which is attributed to the reduction of the effective dielectric permittivity of the resonance response due to the geometric scale effect. The magnetic dipole mode becomes sharper, while the f₂ mode and f₃ mode appear the opposite behavior, accompanied by gradually increasing linewidth. When the lattice period is equal to 150 and 160 μm, the resonator exhibits high-Q full-transmittance at the green dot. As the lattice period increases, the peak transmission at the dot shows a gradual decrease, even when the period is equal to 170 μm, the transmission at the green dot can still be maintained at 80%. Figure 2B shows the resonant frequency for each mode as a function of the lattice period P of unit resonator. As seen in the plot, all three modes exhibit a noticeable red shift with increasing lattice constant. The resonant frequencies can be found to shift linearly as the lattice constant changed.

In order to deeply understand the fundamental nature and physical mechanism of these spectral resonances, when the lattice period is 160 μm, the surface current and magnetic field distributions at the three resonant frequencies (f₁, f₂, and f₃) are calculated are given in Figure 3. The induced surface currents on the SRR are schematically illustrated by white arrows. For the resonance f₁, from the Figure 3A, it can be a circular surface currents loop in the SRR are excited. The SRRs allow the formation of the fundamental-order magnetic dipole resonance at 0.886 THz with a circulating current. The fundamental-order magnetic dipole mode can be excited with a high Q-factor, and the physical mechanism is the coherent coupling of the purely magnetic dipole mode and the first-order (0,1) in-plane lattice surface mode [19]. As reported in our previous work [31], the strong coherent coupling between the magnetic dipole mode and the lattice mode enhances the Q-factor. However, in the previous work, for the fundamental-order magnetic dipole mode, we only characterized an experiment without specifically studying the dependence of transmission resonances on the structural parameters or other factors. In the present work, the high-Q transmission properties of the fundamental-order magnetic dipole mode are more theoretically studied and discussed.

FIGURE 3

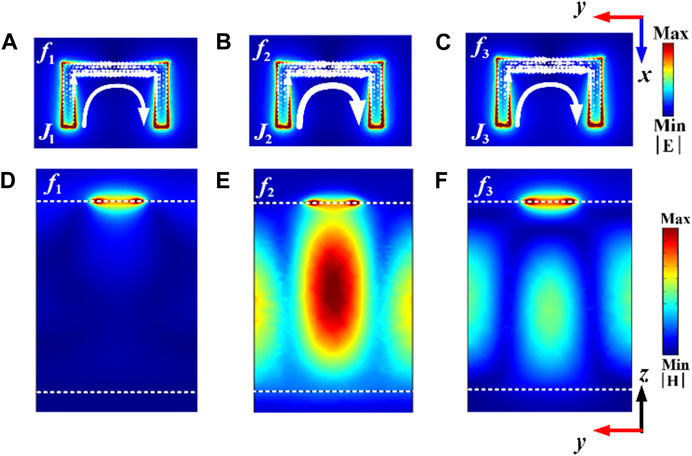
FIGURE 3. (A-C) surface current and (D-F) magnetic field distributions at the three resonance frequencies on the transmission spectra. The simulation results of current and field intensity are in arbitrary units (color coded). Notice the current and electric field intensities of guided-mode resonance f₂ are much larger than f₃. The color bar represents intensity distribution.

In contrast, as for the resonance f₂ of 0.931 THz and the resonance f₃ of 0.940 THz, from Figures 3B, C, it can be seen that the surface current remains a circular surface current loop. The excitation of standing-wave guided-mode make the probing field strongly confined in a gap cavity is observed, as shown in Figures 3E, F. From the electric field distribution in Figure 3D, it can be concluded that the first resonance f₁ among the multiple resonances in Figure 2 originates from the magnetic dipole resonance of the metal ring, and the second resonance f₂ and the third resonance f₃ both exhibit the characteristics of the guided-mode resonances. Unlike the previous guided-mode resonances based on the metal pattern resonators [23–28]^, the metal ring also exhibits strong field distribution. In Figure 3E, the field distribution in the SRRs is similar to that in Figure 3D, which indicates that the magnetic dipoles are involved in the coupling. In Figure 3F, the field distribution at the middle of the metal is obviously different from that in Figures 3D, E, the metal SRR acts as a diffraction grating at resonant frequency f₃. When the incident light impinges on the grating, the in-plane-wavevector-frequency relations of diffraction modes satisfy the dispersion relations of guided-mode resonances, the guided-mode resonance can be launched [34]. The second resonance originates from the Fano-type interference between the guided-mode resonance f₃ and the magnetic dipole, accompanied by the significant electric field enhancement in the substrate layer. The results imply that the photon energy could be strongly confined into the substrate through diffraction coupling, which dramatically increases the energy stored (P_S) by the subwavelength resonators. Resulting in low radiation loss and high Q factor. This implies that the low absorption and radiation losses occurring at resonance make a great contribution to ultra-narrow bandwidths, consequently producing ultrahigh Q-factors of 651 in f₂ mode and 97 in f₃ mode.

With the periodic lattice produced by the SRRs sitting on the substrate, guided-modes are generated in the substrate. The eigenvalue equation of guided-modes is obtained by [35–37].

$\frac{{\gamma }_{1}d}{2}=m\mathrm{\pi }+\arctan \left(\frac{{\gamma }_2}{{\gamma }_1}\right)(1)$

$\frac{{\gamma }_{1}d}{2}=m\mathrm{\pi }+\arctan \left(\frac{{\epsilon }_1{\gamma }_2}{{\epsilon }_2{\gamma }_1}\right)(2)$

Where ${{\gamma }_1}^2=k_0^2{\epsilon }_1-{\beta }^2$, ${{\gamma }_2}^2={\beta }^2-k_0^2{\epsilon }_2$, m is an integer, d is the thickness of the substrate layer, and β is the resonance wavenumbers, which can be described as

$\beta =k_y+2m\mathrm{\pi }/P_g(3)$

k_y is the y-component of the incident wavevector, and P_g is the grating period. The theoretical derivations clearly show that for a guided-mode resonance, the resonance characteristics are strongly dependent on the grating period. Thus, the high-Q resonance response accompanied by a large modulation depth can be modulated and manipulated by changing the lattice period or structural size of the SRRs.

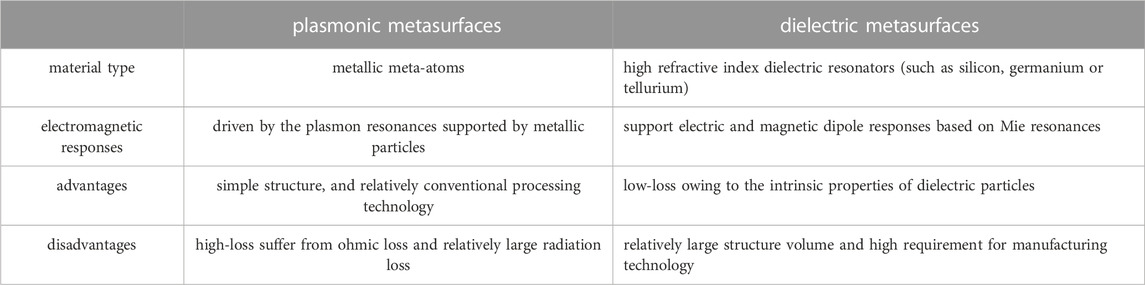
Table 1 summarizes the comparison of the proposed structure and dielectric metasurfaces. The proposed structures can be classified as plasmonic metasurfaces according to the material type, which are composed in metallic unit structures whose optical responses are driven by plasmon resonances supported by metallic particles [38]. For dielectric metasurfaces, the unit structure is composed of high refractive index dielectric resonators, including silicon, germanium or tellurium, where electric and magnetic dipole responses based on Mie resonances can be excited [38, 39].

TABLE 1

TABLE 1. The comparison of the proposed metasurfaces and dielectric metasurfaces.

In terms of high-Q resonance, the disadvantage of plasmonic metasurfaces is that the losses of the structure are usually higher, as metals tend to suffer from ohmic losses. The advantages of the proposed metasurfaces is that the structure is simpleand the processing technology is relatively conventional. However, dielectric metasurfaces have a great advantage for achieving high-Q resonances because the small loss of the structure is related to the intrinsic properties of dielectric particles. The structure volume of the dielectric supersurface is relatively large and have relatively high requirements of processing technology.

The effect of the thickness of substrate d on the three resonances is also investigated. As shown in Figure 4A, as the thickness of substrate increases from 220 to 300 μm, high-Q resonance transmission of three modes can be observed. The Q-factor of the fundamental-order magnetic dipole resonance is essentially constant, even though changing the substrate leads to a change in the line shape of the spectra. It’s different from that the spectra linewidth of the two guided-mode resonances exhibits a decreasing and then increasing feature, and the modulation depth also shows a decreasing and then increasing feature. This may be mainly related to the change of the phase matching conditions of the guided-modes due to the change of the substrate thickness [36]. Figure 4B shows the resonant frequency for each mode as a function of the substrate thickness d. The resonance frequency of the fundamental-order magnetic dipole resonance remains unchangeable, due to the fact that the magnetic resonance of the metal SRRs is mainly determined by the ring current. It can be seen that two guided-modes exhibit a distinct redshift towards low frequencies due to the reduction of the effective dielectric permittivity when the thickness of substrate d increases.

FIGURE 4

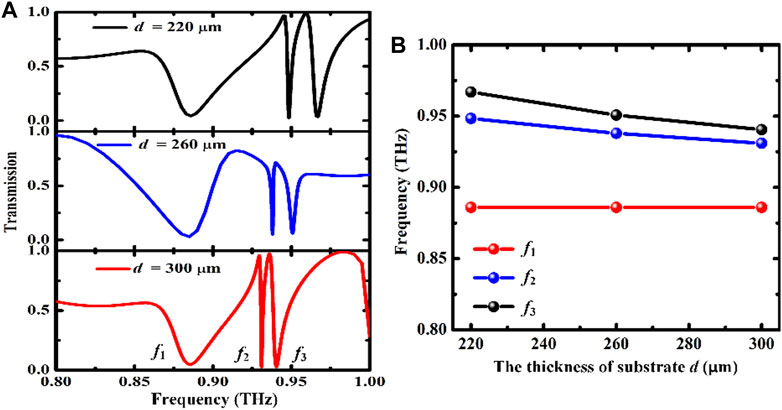
FIGURE 4. (A) Transmission spectra of the proposed scheme as a function of the substrate thickness d; (B) The evolutions of resonant frequency of the three modes when changing the substrate thickness d.

To highlight evolution of the three resonant modes, the lattice period is of great importance to the electromagnetic response of the proposed THz plasmonic metasurfaces. Here the influence of the lattice period P on the spectral response behavior is investigated. The Q-factors and modulation depths are plotted as functions of lattice constant P.

As shown in Figure 5A, when the period increases from 150 to 170 μm, the Q-factor exhibits an interesting exponential growth behavior versus the lattice period P. The dependence of the Q-factor of the f₁ mode on the lattice period P is summarized as Q_f1 = Q₀ + A₁exp [(P + D₁)/B₁], where the coefficients retrieved from numerical fitting are A₁ = 3.12844, B₁ = 6.30738, D₁ = −150.826, respectively, and the fitting R-square is 0.9996, which is very close to unity. The modulation depth of f₁ mode decreases from 93.7% to 81.7%, and the resonance response still maintains a large modulation depth. As shown in Figures 5B, C, when the period increases from 150 μm to 170 μm, the Q-factor of two Fano guided-mode resonances exhibits an exponential decreasing behavior versus the lattice period P. The dependence of the Q-factor of the f₂ mode on the lattice period P is summarized as Q_f2 = Q₂ + A₂exp (P/B₁), where the fitting coefficients are: A₂ = 7.91 × 10¹³, B₂ = −5.84, Q₂ = 565.76, respectively, and the fitting R-square is 0.995. The large modulation depth of f₁ mode decreases from 95.7% to 86.3%. The dependence of the Q-factor of the f₃ mode on the lattice period P is expressed as Q_f3 = Q₃+A₃exp (P/B₃), where the fitting coefficients are: A₃ = 2.91×10¹⁴, B₃ = −5.48, Q₃ = 38.4, respectively, and the fitting R-square is 0.999. The modulation depth of f₁ mode decreases from 95.2% to 90.9%. The exponentially increasing Q-factor rapidly because the cancellation of dipole moment in the U-SRRs is enhanced along with relatively lower radiative loss. However, the Q-factor of two Fano guided-mode resonances decreases exponentially with increasing lattice constant as a consequence of the fact that the diffraction guide mode effect will become weaker, resulting in relatively high radiative loss. It can be seen that the magnetic dipole mode and the Fano guided-mode resonances with extremely high Q-factor and large modulation depth mostly depends on the suitable lattice period.

FIGURE 5

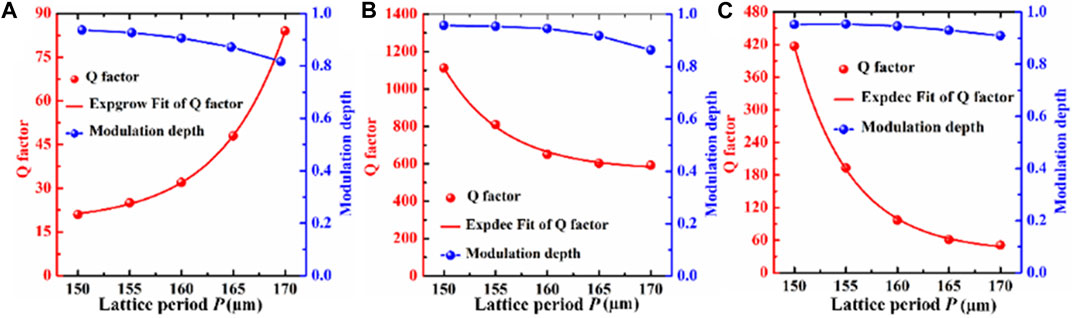
FIGURE 5. (A–C) The evolutions of Q-factors and modulation depth of the three modes versus inverse lattice period, respectively.

To further investigate transmission characteristics of high-Q resonances of THz plasmonic metasurfaces, we performed key parametric study of the effect of the arm L_x, the backbone L_y and split gap s on the behavior of the spectral responses. The simulated transmission spectra as a function of geometric parameters and resonance frequency each in a color map is shown in Figures 6A–C, respectively. Figures 6D–F are the variations of the Q-factor with the change of geometric parameters. As shown in Figure 6A, with the increase of the arm L_x, the transmission spectra of the ω₁ mode and the ω₃ mode exhibit a distinct redshift, while the ω₂ mode exists a slight redshift, and its resonance frequency remains basically unchanged. Interestingly, with the increase of L_x from 15 μm to 35 μm, the resonance linewidth of the ω₁ mode gradually increases, the resonance linewidth of the ω₂ mode shows a slight increase first and then decreases, while the ω₃ mode manifests a clear increase first and then decrease. This is because the loss mechanisms of the three resonances are obviously different. The corresponding Q-factor is shown in Figure 6D, as the L_x of the resonator gradually increases, the resonance linewidth changes differently, and the loss of the resonator is different. The Q-factor of the ω₁ mode gradually decreases from 2400 to 96, and finally in a saturated state, the Q-factor of the ω₂ mode first decreases and then increases from about 4200 to about 900, and the Q-factor of the ω₃ mode also decreases first and then increases from about 400 to about 400.

FIGURE 6

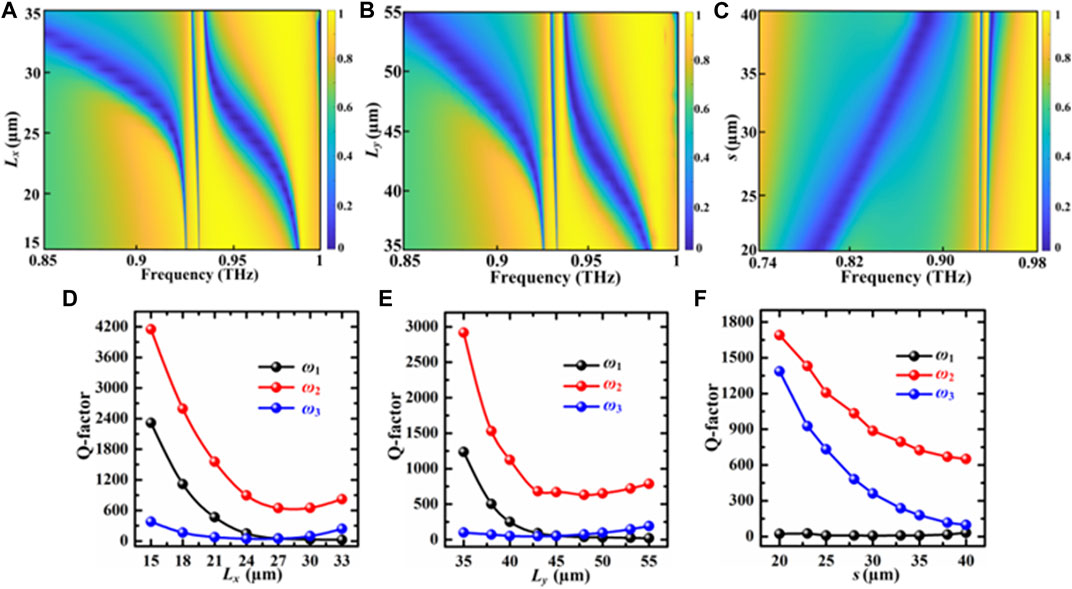
FIGURE 6. (A–C) are the spectral transmission as a function of the operating frequency and structural parameters, respectively at the three geometric parameters of L_x, L_y and s. (D–F) represent the variation of Q-factor with geometric parameters L_x, L_y and s, respectively.

Similarly, as shown in Figure 6B, as the backbone L_y increases from 35 to 55 μm, the transmission spectra of the ω₁ mode and the ω₃ mode also show significant redshift, and the ω₂ mode shows a slight redshift. Due to the increase of radiation damping caused by the size mismatch, all of modes still remain at high level. Figure 6C depicts the simulated transmission spectra for a sweep of the split gap s from 20 to 40 μm. Obviously, both the resonances ω₁ and ω₃ for the SRRs appear distinctly blue shift towards higher frequencies due to the decreased capacitive coupling in the structure when the split gap s is increased, but the resonance frequency of the ω₂ mode remains unchanged. Both the ω₂ and ω₃ modes exhibit gradual broadening as the split gap enlarged. The Q-factor of the magnetic resonance ω₁ and guided mode resonances (ω₂ and ω₃) as a function of split gap s has also been extracted, as shown in Figure 6F. In the ω₁ mode, the Q-factor can be stably maintained during the whole operation, but show a slight floating. However, unlike resonance mode ω₁, the resonance mode ω₂ and ω₃ show a decreasing trend. This is because the excitation principles of magnetic resonance and guided-mode resonance are different in nature.

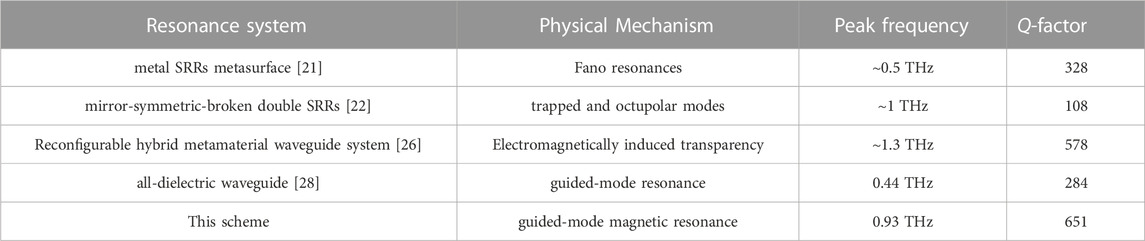
With the increase of the gap s from 20 to 40 μm, the Q-factor of resonance mode ω₂ drops from about 1700 to about 750, and the Q-factor of resonance mode ω₃ is reduced from about 1400 to about 100. The results suggest that proposed THz plasmonic metasurfaces possessing magnetic resonance and double sharp guided-mode resonances with adjustable Q-factor and modulation depth could be used for versatile applications by choosing an appropriate geometric parameter. Table 2 summarizes a comparison of the performance with respect to the state-of-the-art schemes. Compared with previous typical achievements [21, 22, 26, 28], the proposed structure can easy to excite low-loss magnetic dipole mode and guided-mode resonances simultaneously, avoiding a complex patterned metal metamaterial.

TABLE 2

TABLE 2. A comparison of the performance with respect to the state-of-the-art schemes.

4 Potential fabrication process

The proposed structure can be fabricated by regular photolithography technology due to structure feature size exceeding a few micrometers [31], which can support the feasibility of the scheme for measurements. A set of the main feasible steps of the SRRs array metasurfaces production process is shown in Figure 7. In general, Au pattern layer with a thickness of t = 200 nm is deposited on a 300 µm thick quartz substrate. Au is chosen because it is stable and hardly oxidated in air.

FIGURE 7

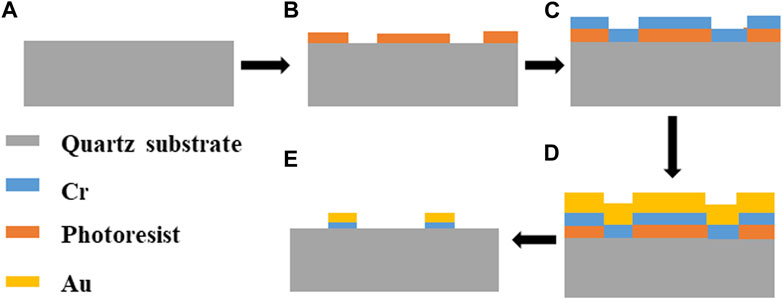
FIGURE 7. Sample fabrication process. (A) Deposition of quartz substrate; (B) Spin coating of photoresist. (C) Magnetron sputtering of Cr; (D) Magnetron sputtering of Au; (E) Target graphic structure obtained by lift-off technique.

As the adhesion between Au and quartz substrate is not strong, the adhesion between Cr and quartz substrate and Au are very good, and Cr is chosen as the adhesion layer [40]. Note that the thickness of the Cr layer is so thin that it has a negligible effect on the resonance. As shown in Figure 7, Firstly, the quartz substrate is pretreated to remove surface contaminants; secondly, the spin coating of photoresist is performed on the quartz substrate [41]; Then, a 10 nm thickness of Cr is grown on the structure surface by using magnetron sputtering to enhance the adhesion of the metal layer to the substrate [42]; Subsequently, the growth of a 200 nm thick metallic film is continued by magnetron sputtering deposition, and the target coating is applied on the mask plate; Finally, the lift-off is used to obtain the target graphic structure by dissolving the photoresist or mechanically removing the metal hard mask using a stripping solution [43]. The potential challenges can arise during the manufacturing process, including the requirement of manufacturing precision and the influence of the fabrication errors on the THz response, and it is important to avoid these whenever possible.

5 Conclusion

To summarize, we have presented an ultra-narrow guided mode resonances and magnetic dipole resonance with an ultrahigh Q-factor and large modulation depth. The proposed structure is composed of a U-shaped SRRs array and a quartz substrate. In THz guided-mode magnetic resonance system, the cavity-enhanced interaction in resonant guided modes brings about ultra-narrowband sharp resonance of large modulation depth at an ultrahigh Q-factor. The transmission dependences of the magnetic dipole resonance and guided-mode resonances on the lattice period and structural parameters are investigated and discussed. The proposed scheme is very promising for development of ultra-narrow multi-band filters at THz frequency.

Data availability statement

The original contributions presented in the study are included in the article/Supplementary Material, further inquiries can be directed to the corresponding author.

Author contributions

FY: Data curation (lead); Investigation (lead); Writing—Original draft (lead). QL: Funding acquisition (lead); Project administration (lead); Resources (lead); Supervision (lead). ZW: Data curation (equal). All authors listed have made a substantial, direct, and intellectual contribution to the work and approved it for publication.

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

1. Kutas M, Haase B, Bickert P, Riexinger F, Molter D, Freymann GV Terahertz quantum sensing. Sci Adv (2020) 6(11):8065. doi:10.1126/sciadv.aaz8065

PubMed Abstract | CrossRef Full Text | Google Scholar

2. Han S, Cong L, Srivastava YK, Qiang B, Rybin MV, Kumar A, et al. All-dielectric active terahertz photonics driven by bound states in the continuum. Adv Mater (2019) 31:1901921. doi:10.1002/adma.201901921

CrossRef Full Text | Google Scholar

3. Nagel M, Bolivar PH, Brucherseifer M, Kurz H, Bosserhoff A, Büttner R. Integrated THz technology for label-free genetic diagnostics. Appl Phys Lett (2002) 80(1):154–6. doi:10.1063/1.1428619

CrossRef Full Text | Google Scholar

4. Tonouchi M Cutting-edge terahertz technology. Nat Photon (2007) 1(2):97–105. doi:10.1038/nphoton.2007.3

CrossRef Full Text | Google Scholar

5. Arikawa T, Hiraoko T, Morimoto S, Blanchard F, Tani S, Tanaka T, et al. Transfer of orbital angular momentum of light to plasmonic excitations in metamaterials. Sci Adv (2020) 6(24):1977. doi:10.1126/sciadv.aay1977

PubMed Abstract | CrossRef Full Text | Google Scholar

6. Valentine J, Zhang S, Zentgraf T, Ulin-Avila E, Genov DA, Bartal G, et al. Three-dimensional optical metamaterial with a negative refractive index. Nature (2008) 455(7211):376–9. doi:10.1038/nature07247

PubMed Abstract | CrossRef Full Text | Google Scholar

7. Gupta M, Srivastava YK, Singh R A toroidal metamaterial switch. Adv Mater (2018) 30(4):1704845. doi:10.1002/adma.201704845

CrossRef Full Text | Google Scholar

8. Cojocari MV, Schegoleva KI, Basharin AA Blueshift and phase tunability in planar THz metamaterials: The role of losses and toroidal dipole contribution. Opt Lett (2017) 42(9):1700–3. doi:10.1364/ol.42.001700

PubMed Abstract | CrossRef Full Text | Google Scholar

9. Seren HR, Zhang J, Keiser GR, Maddox SJ, Zhao X, Fan K, et al. Nonlinear terahertz devices utilizing semiconducting plasmonic metamaterials. Light Sci Appl (2016) 5(5):e16078. doi:10.1038/lsa.2016.78

PubMed Abstract | CrossRef Full Text | Google Scholar

10. Chen H-T, Padilla WJ, Cich MJ, Azad AK, Averitt RD, Taylor AJ A metamaterial solid-state terahertz phase modulator. Nat Photon (2009) 3(3):148–51. doi:10.1038/nphoton.2009.3

CrossRef Full Text | Google Scholar

11. Hayashi S, Nesterenko DV, Rahmouni A, Sekkat Z Observation of Fano line shapes arising from coupling between surface plasmon polariton and waveguide modes. Appl Phys Lett (2016) 108(5):051101. doi:10.1063/1.4940984

CrossRef Full Text | Google Scholar

12. Mendis R, Nag A, Chen F, Mittleman DM A tunable universal terahertz filter using artificial dielectrics based on parallel-plate waveguides. Appl Phys Lett (2010) 97(13):131106. doi:10.1063/1.3495994

CrossRef Full Text | Google Scholar

13. Uddin MJ, Magnusson R Efficient guided-mode-resonant tunable color filters. IEEE Photon Technol. Lett. (2012) 24(17):1552–4. doi:10.1109/lpt.2012.2208453

CrossRef Full Text | Google Scholar

14. Bark HS, Kim GJ, Jeon T-I Transmission characteristics of all-dielectric guided-mode resonance filter in the THz region. Sci Rep (2018) 8(1):13570. doi:10.1038/s41598-018-31931-3

PubMed Abstract | CrossRef Full Text | Google Scholar

15. Uddin MJ, Khaleque T, Magnusson R Guided-mode resonant polarization-controlled tunable color filters. Opt Express (2014) 22(10):12307–15. doi:10.1364/oe.22.012307

PubMed Abstract | CrossRef Full Text | Google Scholar

16. Uddin MJ, Magnusson R Guided-mode resonant thermo-optic tunable filters. IEEE Photon Technol. Lett. (2013) 25(15):1412–5. doi:10.1109/lpt.2013.2266272

CrossRef Full Text | Google Scholar

17. Dobbs DW, Cunningham BT Optically tunable guided-mode resonance filter. Appl Opt (2006) 45(28):7286–93. doi:10.1364/ao.45.007286

PubMed Abstract | CrossRef Full Text | Google Scholar

18. Oulton R, Sorger V, Genov D, Pile D, Zhang X A hybrid plasmonic waveguide for sub-wavelength confinement and long range propagation. Nat Photon (2008) 2(8):496–500. doi:10.1038/nphoton.2008.131

CrossRef Full Text | Google Scholar

19. Rayleigh L On the dynamical theory of gratings. R Soc (1907) 79(532):399–416.

Google Scholar

20. Scalari G, Maissen C, Cibella S, Leoni R, Faist J High quality factor, fully switchable terahertz superconducting metasurface. Appl Phys Lett (2014) 105(26):261104. doi:10.1063/1.4905199

CrossRef Full Text | Google Scholar

21. Srivastava YK, Manjappa M, Cong L, Cao W, Al-Naib I, Zhang W, et al. Ultrahigh-Q Fano resonances in terahertz metasurfaces: Strong influence of metallic conductivity at extremely low asymmetry. Adv Opt Mater (2016) 4:457–63. doi:10.1002/adom.201500504

CrossRef Full Text | Google Scholar

22. Yang S, Tang C, Liu Z, Wang B, Wang C, Li J, et al. Simultaneous excitation of extremely high-Q factor trapped and octupolar modes in terahertz metamaterials. Opt Express (2017) 25(14):15938–46. doi:10.1364/oe.25.015938

PubMed Abstract | CrossRef Full Text | Google Scholar

23. Shin H, Catrysse PB, Fan SH Effect of the plasmonic dispersion relation on the transmission properties of subwavelength cylindrical holes. Phys Rev B (2005) 72(8):085436. doi:10.1103/physrevb.72.085436

CrossRef Full Text | Google Scholar

24. Christ A, Tikhodeev SG, Gippius NA, Kuhl J, Giessen H Waveguide-plasmon polaritons: Strong coupling of photonic and electronic resonances in a metallic photonic crystal slab. Phys Rev Lett (2003) 91(18):183901. doi:10.1103/physrevlett.91.183901

PubMed Abstract | CrossRef Full Text | Google Scholar

25. Zhang J, Cai L, Bai W, Song G Hybrid waveguide-plasmon resonances in gold pillar arrays on top of a dielectric waveguide. Opt Lett (2010) 35(20):3408–10. doi:10.1364/ol.35.003408

PubMed Abstract | CrossRef Full Text | Google Scholar

26. Zhao X, Zhu L, Yuan C, Yao J Reconfigurable hybrid metamaterial waveguide system at terahertz regime. Opt Express (2016) 24(16):18244–51. doi:10.1364/oe.24.018244

PubMed Abstract | CrossRef Full Text | Google Scholar

27. Yannopapas V, Stefanou N Optical excitation of coupled waveguide-particle plasmon modes: A theoretical analysis. Phys Rev B (2004) 69(1):012408. doi:10.1103/physrevb.69.012408

CrossRef Full Text | Google Scholar

28. Bark S, Baek IH, Kim G-R, Jeong YU, Jang K-H, Lee K, et al. Polarization-independent all-dielectric guided-mode resonance filter according to binary grating and slab waveguide dimensions. Opt Express (2021) 29(23):37917–26. doi:10.1364/oe.442858

PubMed Abstract | CrossRef Full Text | Google Scholar

29. Ko H, Razmjooei N, Hemmati H, Magnusson R Perfectly-reflecting guided-mode-resonant photonic lattices possessing Mie modal memory. Opt Express (2021) 29(17):26971–82. doi:10.1364/oe.434359

PubMed Abstract | CrossRef Full Text | Google Scholar

30. Yen TJ, Padilla WJ, Fang N, Vier DC, Smith DR, Pendry JB, et al. Terahertz magnetic response from artificial materials. Science (2004) 303(5663):1494–6. doi:10.1126/science.1094025

PubMed Abstract | CrossRef Full Text | Google Scholar

31. Yan F, Li Q, Hu H, Wang ZW, Tian H, Li L, et al. Terahertz high-Q magnetic dipole resonance induced by coherent Fano interactions. Appl Phys Lett (2022) 121:201704. doi:10.1063/5.0112993

CrossRef Full Text | Google Scholar

32. Liu W, Chen S, Li Z, Cheng H, Yu P, Li J, et al. Realization of broadband cross-polarization conversion in transmission mode in the terahertz region using a single-layer metasurface. Opt Lett (2015) 40(13):3185–8. doi:10.1364/ol.40.003185

PubMed Abstract | CrossRef Full Text | Google Scholar

33. Grady NK, Heyes JE, Chowdhury DR, Zeng Y, Reiten MT, Azad AK, et al. Terahertz metamaterials for linear polarization conversion and anomalous refraction. Science (2013) 340(6138):1304–7. doi:10.1126/science.1235399

PubMed Abstract | CrossRef Full Text | Google Scholar

34. Ren Y, Guo X, Zhang G, Balakin AV, Shkurinov AP, Yu A, et al. Excitation of graphene surface plasmons polaritons by guided-mode resonances with high efficiency. Opt Express (2020) 28(9):13224–33. doi:10.1364/oe.391237

PubMed Abstract | CrossRef Full Text | Google Scholar

35. Song S, Sun F, Chen Q, Zhang Y Contrast-enhanced ultrasound imaging of the vasa vasorum of carotid artery plaque. IEEE Trans Terahertz Sci Technol (2015) 5:131–3. doi:10.4329/wjr.v7.i6.131

PubMed Abstract | CrossRef Full Text | Google Scholar

36. Tomioka T, Kubo S, Nakagawa M, Hoga M, Tanaka T Split-ring resonators interacting with a magnetic field at visible frequencies. Appl Phys Lett (2013) 103:071104. doi:10.1063/1.4818666

CrossRef Full Text | Google Scholar

37. Jeppesen C, Mortensen NA, Kristensen A Capacitance tuning of nanoscale split-ring resonators. Appl Phys Lett (2009) 95:193108. doi:10.1063/1.3263191

CrossRef Full Text | Google Scholar

38. Wang J, Du J. Plasmonic and dielectric metasurfaces: Design, fabrication and applications. Appl Sci (2016) 6(9):239. doi:10.3390/app6090239

CrossRef Full Text | Google Scholar

39. Jahani S, Jacob Z All-dielectric metamaterials. Nat Nanotech (2016) 11:23–36. doi:10.1038/nnano.2015.304

PubMed Abstract | CrossRef Full Text | Google Scholar

40. Bassiri G Diffusion effect of intermetallic layers on adhesion and mechanical properties of electrical contacts (2006).

Google Scholar

41. Zhang X, Sun B, Friend RH, Guo H, Giessen H Metallic photonic crystals based on solution-processible gold nanoparticles. Nano Lett (2006) 6(4):651–5. doi:10.1021/nl052361o

PubMed Abstract | CrossRef Full Text | Google Scholar

42. Li Y, Gao Y, Yao Y, Sun S, Khatiwada D, Pouladi S, et al. Direct synthesis of biaxially textured nickel disilicide thin films by magnetron sputter deposition on low-cost metal tapes for flexible silicon devices. Appl Phys Lett (2019) 114(8):083502. doi:10.1063/1.5080283

CrossRef Full Text | Google Scholar

43. Kim SJ, Lee HE, Choi H, Kim Y, We JH, Shin JS, et al. High-performance flexible thermoelectric power generator using laser multiscanning lift-off process. Acs Nano (2016) 10(12):10851–7. doi:10.1021/acsnano.6b05004

PubMed Abstract | CrossRef Full Text | Google Scholar