- 1Tianjin Key Laboratory of Optoelectronic Detection Technology and System, School of Electronic and Information Engineering, Tiangong University, Tianjin, China
- 2Institute of Fluid Physics, China Academy of Engineering Physics, Mianyang, China
- 3Key Laboratory of Opto-Electronics Information Technology (Ministry of Education), School of Precision Instruments and Opto-Electronic Engineering, Tianjin University, Tianjin, China
A terahertz (THz) fiber is of interest due to low loss and easy beam shaping. Graphene plays an important role in modulating the optical signal. In this paper, a graphene-coated D-shaped THz fiber modulator is proposed. The performance of the proposed modulator is investigated by the finite element method. The inference of geometric parameters of the structure on the proposed modulator is also analyzed, and an optimal structure is obtained. Simulation results show that the confinement loss and the full width at half-maximum (FWHM) can be tuned by adjusting the Fermi level of graphene. The proposed THz fiber modulator shows potential in future THz fiber communications.
1 Introduction
Terahertz (THz) is broadly defined in 0.1 THz to 10 THz, lying between the infrared and microwave range of the spectral region [1]. The increasing efforts in THz science and technology stem from promising applications in spectroscopy, imaging, and communications [2]. In recent years, breakthroughs in THz sources and detectors have greatly promoted the development of this research area. However, the lack of active THz components to realize wave manipulation and modulation has hindered the substantive progression of THz applications. One of the key THz components mostly desired for this field, such as THz imaging and communications [3, 4], is high-performance THz modulators, used to maintain the amplitude, phase, polarization, and propagation of the THz wave. The THz region has a broad range of applications including biotechnology, telecommunication, military, and environmental applications [5–9]. The advances of THz technology and the growing interest in its applications have accelerated the development of THz sources, THz detectors, THz fibers, and other devices [10]. Among them, remarkable progress has been attained in designing effective THz fibers. The THz fiber has been used in many applications, such as filtering, sensing, interferometry, quantum key distribution, and coherent communication [11].
A phase or an amplitude THz modulator requires prohibitively thick crystals or the non-trivial implementation of efficient THz waveguides and their operation at high voltages. To overcome these hurdles, several THz modulators have been reported based on active materials with tunable optical properties, such as the two-dimensional electron gas (2DEG) in InGaAs/GaAs systems, conventional semiconductors, metamaterials, superconductors, and phase-transition materials [12–16].
Graphene, as a two-dimensional semiconductor material, has been proven useful for THz wave modulation due to its unique electrical, optical, and mechanical properties and has great potentialities in the field of thermology, chemistry, electricity, and optics [17–22]. Compared to other materials, graphene with its linear energy dispersion with zero bandgap energy exhibits an ultrahigh carrier mobility to modulate THz wave flexibly, along with a broad spectral response and plasmonics in infrared and THz frequencies [23–25]. Moreover, optical properties of graphene can be easily tuned by altering its Fermi level via electrical means, an optical stimulus, or chemical doping, such as the gate voltage [26] and optical pump [27]. A kind of square porous-core photonic crystal fiber (PCF) for polarization-maintaining terahertz wave guidance proposed in [28] offers a high birefringence of 0.063 and a low EML of 0.081 cm−1 at 1 THz. Moreover, a very low flattened dispersion profile is observed over a wide frequency domain of 0.85–1.9 THz. The zero flattened dispersion can be controlled. Furthermore, a highly birefringent single-mode-suspended core fiber in the THz regime was proposed in [29], which can provide a high birefringence of the order of 10–2 over a wide frequency region in a single-mode operation. [30] proposed an ultrasensitive tunable terahertz (THz) sensor, which consists of single-layer graphene-based gratings integrated with a Fabry–Perot cavity through numerical simulations.
Therefore, the status of the modulators can be controlled based on a graphene switch between the ON and OFF states [31]. Graphene THz modulators have been widely used in the THz region [32]. Meanwhile, THz graphene waveguide modulators have been designed and demonstrated [33].
THz fibers have attracted much attention recently, owing to their performance advantages, including low loss and dispersion, good flexibility of structure, and good confinement ability [34]. The development of 3D printing technology has greatly improved the flexibility of designs and the fabrication of THz fibers, and reduced the material loss and manufacturing cost [35]. In this paper, a graphene-coated D-shaped THz fiber modulator is proposed. The proposed modulator with a single layer of graphene on the surface of the D-shaped fiber can share the advantage of both graphene-based and fiber-structured modulators. The performance of the D-shaped THz graphene fiber-based modulator is investigated by the finite element method. A tunable confinement loss is observed by adjusting the Fermi level of graphene via chemical doping. The confinement loss of Y polarization is higher than that of X polarization at the operating frequency of 0.64 THz.
2 Fiber modulator mode design and principle
A schematic representation of the proposed graphene-coated D-shaped THz fiber modulator is illustrated in Figure 1. It consists of a hollow core surrounded by eleven cladding layers with the same thickness and a graphene layer coated on a micro-bridge. The diameter of the core is noted as D. The cladding layers are a periodic structure of alternating photosensitive resin layers with a high refractive index and air layers with a low refractive index. The thickness of each layer is presented by t. The micro-bridge is introduced into the cladding layers in order to fabricate the stable structure and coat the graphene layer. The thickness of the micro-bridge is t/2. To implement the alternating high-refractive index photosensitive resin and low-refractive index air layers, we first fabricated a thick layer of high-refractive index photosensitive resin via spin coating.
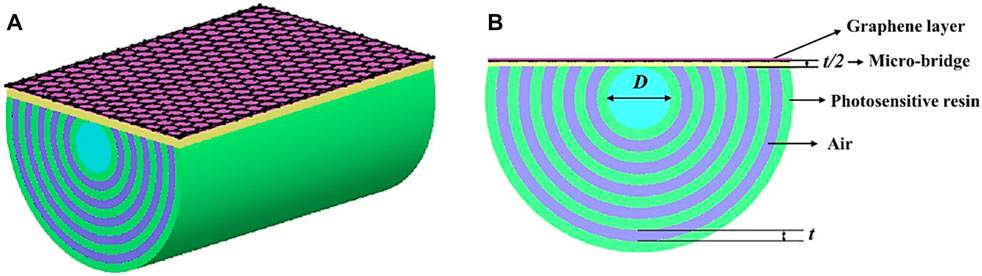
FIGURE 1. (A) 3D view and (B) cross-sectional view of the proposed graphene-coated D-shaped THz fiber modulator.
The micro-bridge was created on top of this thick layer by photolithography and oxygen plasma etching. The micro-bridge acted as a support structure for the remaining fabrication process, which included the deposition of the graphene layer on top of a thin buffer layer and coating this with a relatively thick cladding layer. Once the graphene layer was deposited and coated with the cladding layer, we used another photolithography and oxygen plasma etching process to create air holes in the cladding layer around the micro-bridge. Finally, we removed the micro-bridge to form a suspended photonic crystal membrane structure consisting of the alternating high-refractive index photosensitive resin and low-refractive index air layers, with a graphene layer incorporated within the cladding layer.
High-quality large-area monolayer graphene was grown using the chemical vapor deposition (CVD) method, and stacked multilayers were transferred onto the side-polished region of the fiber for an evanescent field interaction with the guided mode in the fiber [36].
The fiber can be obtained by 3D stereolithography (SLA). In this paper, the refractive index of the air layer and the hollow core are both 1. The absorption coefficient and the refractive index of the photosensitive resin used in this paper can be expressed as in [37].
The relative permittivity of graphene is defined as follows [38, 39]:
where
where
where
The complex refractive index of graphene can be calculated by the relative permittivity of graphene [44]:
where
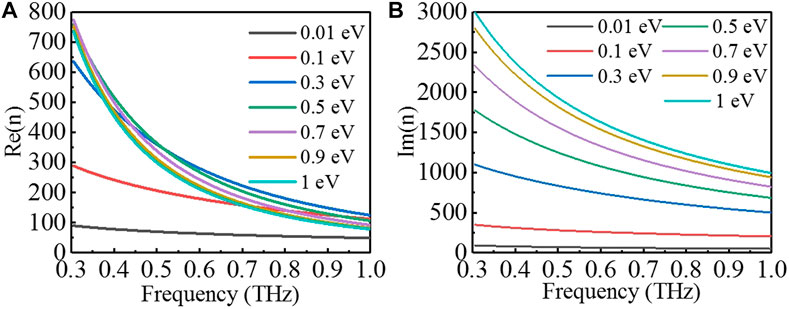
FIGURE 2. (A) Real and (B) imaginary refractive indexes of graphene with different Fermi energy levels versus the frequency.
The confinement loss of the fiber transmission mode in the form of an evanescent wave is an important parameter in terms of the modulator; the effective material loss should be considered in addition to the confinement loss. The effective material loss can be considered in the context of modulator design, but it is usually not a key parameter of concern. Although the effective material loss is an important consideration in optical systems, confinement loss parameters often take priority in modulator design, and the confinement loss expression is as follows [45]:
where
3 Results and discussion
The influence of each parameter of the device structure on the confinement loss and the full width at half-maximum (FWHM) are calculated and analyzed. The thickness of the graphene layer is a single graphene layer of 0.335 nm [46]; the Fermi energy level is 1 eV, and the graphene layer is in the first layer of the cladding layer in this part. The first is the diameter of the core. It can be seen from Figures 3A, B that the confinement loss of the two polarization states decreases with the increasing diameter of the core. When the diameter of the core is greater than 4 mm, the confinement loss is lower with a frequency range of 0.5 THz to 1 THz. Meanwhile, owing to the stronger power guided in the core region at 6 mm, the confinement loss is lower, as shown in Figure 3D and Figure 4. This is because the increasing diameter of the core makes the THz wave less likely to leak from the core to the graphene layer directly above the core.
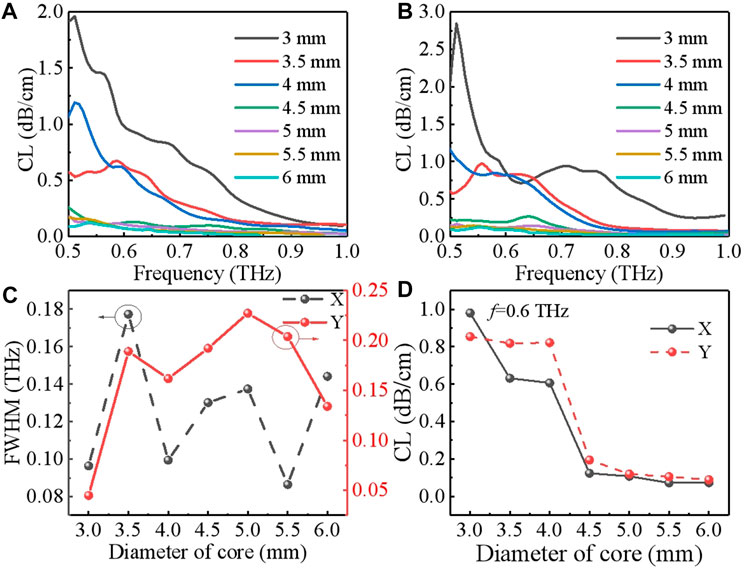
FIGURE 3. (A), (B) Confinement loss versus the frequency for different diameters of the core of X- and Y-polarization; (C) FWHM; (D) confinement loss at 0.6 THz of X- and Y-polarization with different diameters of the core. The remaining structural parameters are 800 μm and 0.335 nm.
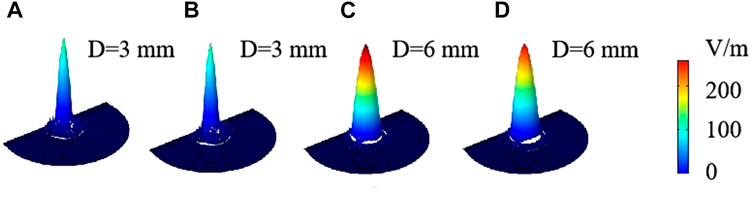
FIGURE 4. Electric field distribution of the fundamental mode with different diameters of the core at 0.6 THz: (A), (C) X polarization and (B), (D) Y polarization.
The depth of polarization states refers to the degree to which the polarization state of a light beam deviates from being fully polarized. Furthermore, the full width at half-maximum is commonly measured as the ratio between the intensity of the polarized component and the total intensity of light. Furthermore, the changes of the FWHM of X- and Y-polarization with the diameter of the core are shown in Figure 3C. The FWHM of X-polarization reaches the middle at 4.5 mm. Moreover, the larger the diameter of the core, the larger the number of modes in the core region. In order to achieve an effective single-mode operation, the diameter of the core should be reduced.
The FWHM of the transmission spectrum in our modulator is primarily affected by two factors: the thickness of graphene coating and the dispersion properties of the fiber. The thickness of graphene coating affects the effective refractive index of the fiber, which, in turn, can shift the frequencies at which resonances occur. Specifically, thicker coatings will shift resonant frequencies to lower values, resulting in a wider bandwidth and a correspondingly smaller FWHM. Conversely, thinner coatings will shift the resonant frequencies to higher values and lead to a narrower bandwidth and a larger FWHM. Anomalous dispersions can be used to compensate for the dispersion of graphene coating, leading to a narrower bandwidth and a smaller FWHM. Other factors that can affect the FWHM include the shape and structure of the fiber, and any impurities or defects present in the material. These factors can introduce additional losses or alter the distribution of the mode field energy within the fiber, leading to changes in the FWHM of the transmission spectrum.
The distribution of the mode field energy in our modulator is determined by a combination of factors, including the geometry and dimensions of the fiber structure, the dispersion properties of the fiber, and the presence of any impurities or defects that may alter the distribution of energy within the fiber. One important factor affecting the distribution of mode field energy is the shape and dimensions of the fiber structure. In our D-shaped fiber modulator, specific shapes and dimensions of the fiber can lead to coupling between different modes within the fiber, resulting in the redistribution of energy within the fiber. Additionally, the thickness of graphene coating can also affect the distribution of the mode field energy by altering the effective refractive index of the fiber and leading to shifts in the resonant frequencies of the device.
Regarding the choice of the photosensitive resin, we selected a specific type of photosensitive resin because it offered a high refractive index, excellent photoresistive properties, and was compatible with our fabrication process. Specifically, the photosensitive resin we used had a refractive index, which is higher than that of air and similar to that of silicon dioxide, making it a good candidate for fabricating a graphene-coated D-shaped terahertz fiber modulator consisting of an alternating high-refractive index and low-refractive index layers.
The confinement loss versus frequency for different thicknesses of the cladding layers of X- and Y-polarization are shown in Figures 5A, B, respectively. When the thickness of the cladding layers is 800 μm, the confinement loss of the two polarization states is lower, owing to the stronger power in the core region, as shown in Figure 5D and Figure 6. Figure 5C shows that the FWHM reaches a minimum at 900 μm.
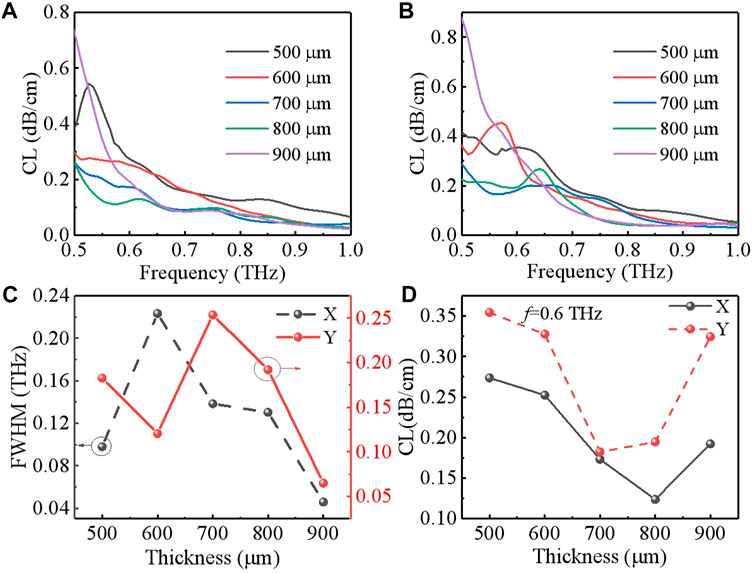
FIGURE 5. (A), (B) Confinement loss versus the frequency for different thicknesses of the cladding layers of X- and Y-polarization; (C) FWHM; (D) confinement loss at 0.6 THz of X- and Y-polarization with different thicknesses of cladding layers. The remaining structural parameters are
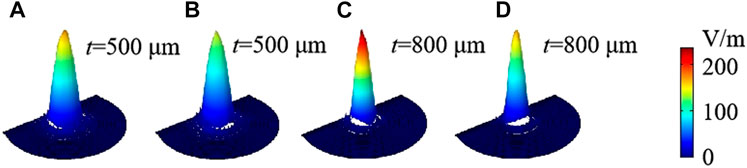
FIGURE 6. Electric field distribution of the fundamental mode with different diameters of the core at 0.6 THz: (A), (C) X polarization and (B), (D) Y polarization.
Different positions of the graphene layer represent the different distances from the core to the graphene layer; the numbers 1 and 5 are used to indicate the different positions of the graphene layer of the D-shaped THz fiber. In particular, region 1 represents that the graphene layer is in the first layer, while region 5 represents that the graphene layer is in the fifth layer, as shown in Figure 7. In Figure 8 and Figure 9, it is clearly observed that when the graphene layer is in the first layer, the confinement loss of the two polarization states is lowest due to the strongest power in the core region and the FWHM of X- and Y-polarization is lowest and greatest, respectively. This is because as the core to the graphene layer decreases, the channel of THz wave leakage from the fiber core to the graphene layer becomes narrower, which makes leakage more difficult. The periodicity of the structure can create photonic band gaps, where certain frequencies are fully reflected, leading to unique transmission behaviors.

FIGURE 7. Different positions of the graphene layer in the fiber: (A) in the first layer, (B) in the second layer, (C) in the third layer, (D) in the fourth layer, and (E) in the fifth layer.
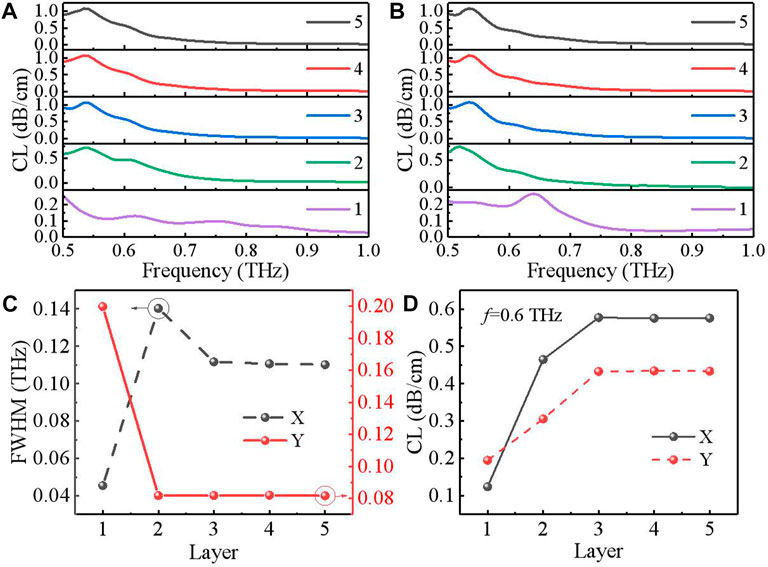
FIGURE 8. (A), (B) Confinement loss versus the frequency for different positions of the graphene layer of X- and Y-polarization. (C) FWHM. (D) Confinement loss at 0.6 THz of X- and Y-polarization with different positions of the graphene layer.

FIGURE 9. Electric field distribution of the fundamental mode with different positions of the graphene layer at 0.6 THz: (A), (C) X polarization and (B), (D) Y polarization.
Based on the aforementioned investigation, an optimized structure of the proposed modulator is obtained. The structural parameters are = 4.5 mm and = 800 μm, and the graphene layer located in the first layer is the cladding layer. The confinement loss versus the frequency of different graphene Fermi levels of X- and Y-polarization is shown in Figures 10A, B, respectively. The confinement loss of X-polarization first increases before 0.6 THz and then decreases in the frequency range of 0.6 THz to 0.67 THz with the Fermi level gradually reducing from 1 eV to 0.01 eV, while it remains stable at other frequencies. The confinement loss of Y-polarization first takes on a loss peak around 0.64 THz when the Fermi level is less than 0.3 eV and then decreases rapidly, reduced to a loss peak with the decreasing Fermi level. These results mean that with the weakening of graphene electric doping, the leakage of the evanescent wave from the core to the graphene layer changes and the confinement loss of the proposed structure decreases. The loss peak in the transmission spectrum of our modulator is a result of several mechanisms that contribute to the attenuation of the signal as it propagates through the fiber. One factor contributing to the loss peak is the coupling between different modes within the fiber. In our modulator, the periodic structure of the graphene coating creates a series of resonant cavities that can couple the energy between different modes within the fiber. This coupling can lead to the energy being lost from the fundamental mode and being transferred to higher-order modes, resulting in increased attenuation at certain frequencies. Another factor contributing to the loss peak is scattering losses due to defects or impurities within the fiber. These defects can scatter energy out of the guided mode and into the surrounding modes or the cladding, resulting in increased attenuation. In our modulator, the use of graphene as a coating helps in reducing absorption losses by providing a highly conductive surface that can efficiently carry current and avoid energy losses due to its resistance.
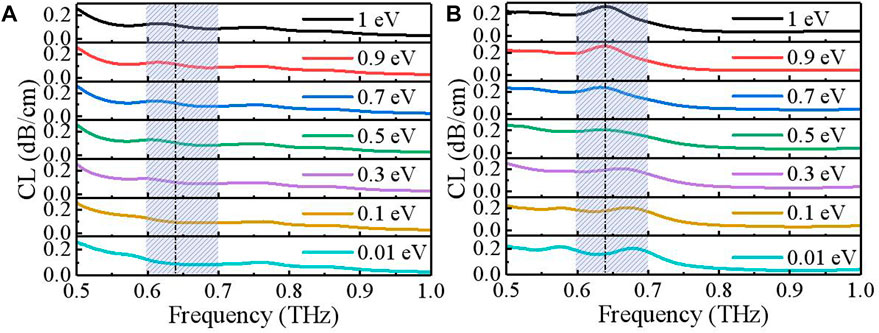
FIGURE 10. (A), (B) Confinement loss versus the frequency for different graphene Fermi levels of X- and Y-polarization.
In order to demonstrate the THz fiber-based modulator, the working frequency used to observe the various confinement losses of X- and Y-polarization is 0.64 THz. The confinement loss of X polarization only has a small frequency shift, as shown in Figure 11A. The extinction ratio mainly affected by the confinement loss in the ON and OFF states is an important parameter in terms of the performance of the modulator. As shown in Figure 11B, the minimum value of the Y-polarization confinement loss is 0.15932 dB/cm and the maximum value is 0.26779 dB/cm. The extinction ratio is 22.55% and the modulation depth is 40.51%. The X-polarization confinement loss has a minimum value of 0.08794 dB/cm and a maximum value of 0.11654 dB/cm. The extinction ratio is 12.23%, and the modulation depth is 24.54%. The two polarization states are both proportional to the Fermi level. In Figure 11C, the minimum value of the Y-polarization FWHM is 0.19974 THz and the maximum value is 0.22881 THz. As can be seen from Figure 11D, when the modulator is in the ON state, the incident THz wave is strongly confined within the core region. However, with the increasing conductivity of graphene, transverse resonant coupling between the core mode and the graphene layer mode is stronger until the OFF state.
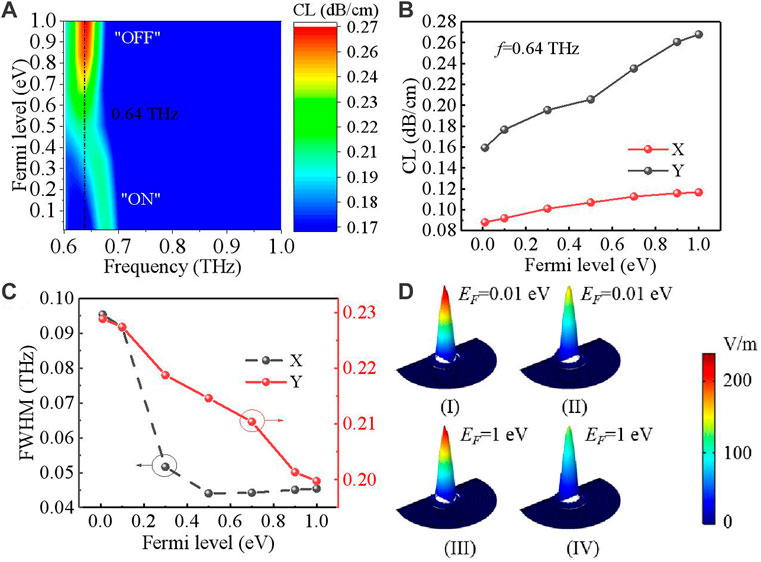
FIGURE 11. (A) 2D contour map of confinement loss; (B) confinement loss at 0.64 THz; (C) FWHM of X- and Y-polarization with different graphene Fermi levels; (D) electric field distribution of the fundamental mode of X polarization (I) and (III) and Y polarization (II) and (IV) at 0.64 THz.
4 Conclusion
In conclusion, a graphene-coated D-shaped THz fiber modulator is proposed. The performance of the D-shaped THz graphene fiber-based modulator is investigated. The inference of geometric parameters of the structure of the proposed modulator is also analyzed, and the optimal structure is obtained. The results show that the confinement loss and the FWHM can be tuned by adjusting the Fermi level of graphene. The modulation depths of the two polarization states at an operating frequency of 0.64 THz are 40.51% and 24.54%, respectively. The proposed THz fiber modulator shows potential in future THz fiber communications.
Data availability statement
The original contributions presented in the study are included in the article/Supplementary Material; further inquiries can be directed to the corresponding author.
Author contributions
Conceptualization: JS; methodology: SW, MS, and LT; software: HB and XGL; validation: LT, XGL, and HB; writing—original draft preparation:SW and MS; writing—review and editing: SW, LT, and PN; visualization: XYL; supervision: PN and JY; project administration: JS and LT. All authors have contributed to the article and approved the submitted version.
Funding
This work was supported by the National Natural Science Foundation of China (61905177, 61901297, 62101518, and 61903273); the Natural Science Foundation of Tianjin City (19JCQNJC01400 and 18JCQNJC70600); the Foundation of the National Key Laboratory of Shock Wave and Detonation Physics (JCKYS2022212001); the Open Research Fund of National Mobile Communications Research Laboratory, Southeast University (2022D12); and the Open Fund of IPOC, BUPT (IP-OC2021B02).
Conflict of interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Publisher’s note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
References
1. Withayachumnankul W, Png GM, Yin XX, Atakaramians S, Jones I, Lin HY, et al. T-ray sensing and imaging. Proc IEEE (2007) 95(8):1528–58. doi:10.1109/JPROC.2007.900325
2. Tonouchi M. Cutting-edge terahertz technology. Nat Photon (2007) 1(2):97–105. doi:10.1038/nphoton.2007.3
3. Kleine-Ostmann T, Nagatsuma T. A review on terahertz communications research. J Infrared Millim Terahertz Waves (2011) 32(2):143–71. doi:10.1007/s10762-010-9758-1
4. Mittleman DM. Twenty years of terahertz imaging Invited. Opt Express (2018) 26(8):9417–31. doi:10.1364/OE.26.009417
5. Habib MA, Anower MS. Low loss highly birefringent porous core fiber for single mode terahertz wave guidance. Curr Opt Photon (2018) 2:215–20. doi:10.3807/COPP.2018.2.3.215
6. Chen D, Tam HY. Highly birefringent terahertz fibers based on super-cell structure. J Lightwave Technol (2010) 28:1858–63. doi:10.1109/jlt.2010.2049338
7. Islam R, Habib MS, Hasanuzzaman GKM, Ahmad R, Rana S, Kaijage SF. Extremely high-birefringent asymmetric slotted-core photonic crystal fiber in THz regime. IEEE Photon Technol. Lett. (2015) 27:2222–5. doi:10.1109/lpt.2015.2457673
8. Hasanuzzaman GKM, Rana S, Habib MS. A novel low loss, highly birefringent photonic crystal fiber in THz regime. IEEE Photon Technol. Lett. (2016) 28:899–902. doi:10.1109/lpt.2016.2517083
9. Rana S, Rakin AS, Subbaraman H, Leonhardt R, Abbott D. Low loss and low dispersion fiber for transmission applications in the terahertz regime. IEEE Photon Technol. Lett. (2017) 29:830–3. doi:10.1109/lpt.2017.2693203
10. Kaijage SF, Ouyang Z, Jin X. Porous-core photonic crystal fiber for low loss terahertz wave guiding. IEEE Photon Technol. Lett. (2013) 25:1454–7. doi:10.1109/lpt.2013.2266412
11. Anthony J, Leonhardt R, Leon-Saval SG, Argyros A. THz propagation in kagome hollow-core microstructured fibers. Opt Express (2011) 19:18470. doi:10.1364/oe.19.018470
12. Zhao YC, Wang L, Zhang YX, Qiao S, Liang SX, Zhou TC, et al. High-speed efficient terahertz modulation based on tunable collective-individual state conversion within an active 3 nm two-dimensional electron gas metasurface. Nano Lett (2019) 19(11):7588–97. doi:10.1021/acs.nanolett.9b01273
13. Watts CM, Shrekenhamer D, Montoya J, Lipworth G, Hunt J, Sleasman T, et al. Terahertz compressive imaging with metamaterial spatial light modulators. Nat Photon (2014) 8(8):605–9. doi:10.1038/nphoton.2014.139
14. Lim WX, Manjappa M, Srivastava YK, Cong LQ, Kumar A, MacDonald KF, et al. Ultrafast all-optical switching of germanium-based flexible metaphotonic devices. Adv Mater (2018) 30(9):1705331. doi:10.1002/adma.201705331
15. Kalhor S, Kindness SJ, Wallis R, Beere HE, Ghanaatshoar M, Degl'Innocenti R, et al. Active terahertz modulator and slow light metamaterial devices with hybrid graphene-superconductor photonic integrated circuits. Nanomaterials (2021) 11(11):2999. doi:10.3390/nano11112999
16. Zhu HF, Li J, Du LH, Huang WX, Liu JB, Zhou JH, et al. A phase transition oxide/graphene interface for incident-angle-agile, ultrabroadband, and deep THz modulation. Adv Mater Inter (2020) 7(24):2001297. doi:10.1002/admi.202001297
18. Lee C, Wei XD, Kysar JW, Hone J. Measurement of the elastic properties and intrinsic strength of monolayer graphene. Science (2008) 321(5887):385–8. doi:10.1126/science.1157996
19. Ferrari AC, Meyer JC, Scardaci V, Casiraghi C, Lazzeri M, Mauri F, et al. Raman spectrum of graphene and graphene layers. Phys Rev Lett (2006) 97(18):187401. doi:10.1103/physrevlett.97.187401
20. Zhao SQ, Wu QQ, Pi JC, Liu JY, Zheng JT, Hou SJ, et al. Cross-plane transport in a single-molecule two-dimensional van der Waals heterojunction. Sci Adv (2020) 6(22):eaba6714. doi:10.1126/sciadv.aba6714
21. Castro Neto AH, Guinea F, Peres NMR, Novoselov KS, Geim AK. The electronic properties of graphene. Rev Mod Phys (2009) 81(1):109–62. doi:10.1103/revmodphys.81.109
22. Stankovich S, Dikin DA, Dommett GH, Kohlhaas KM, Zimney EJ, Stach EA, et al. Graphene-based composite materials. Nature (2006) 442(7100):282–6. doi:10.1038/nature04969
23. Zhong C, Li J, Lin H. Graphene-based all-optical modulators. Front Optoelectronics (2020) 13(2):114–28. doi:10.1007/s12200-020-1020-4
24. Otsuji T, Tombet SAB, Satou A, Fukidome H, Suemitsu M, Sano E, et al. Graphene-based devices in terahertz science and technology. J Phys D-appl Phys (2012) 45(30):9. doi:10.1088/0022-3727/45/30/303001
25. Low T, Avouris P. Graphene plasmonics for terahertz to mid-infrared applications. ACS Nano (2014) 8(2):1086–101. doi:10.1021/nn406627u
26. Novoselov KS, Geim AK, Morozov SV, Jiang D, Zhang Y, Dubonos SV, et al. Electric field effect in atomically thin carbon films. Science (2004) 306(5696):666–9. doi:10.1126/science.1102896
27. Luo ZT, Pinto NJ, Davila Y, Johnson ATC. Controlled doping of graphene using ultraviolet irradiation. Appl Phys Lett (2012) 100(25):253108. doi:10.1063/1.4729828
28. Luo J, Tian F, Li L, Qu H, Zhang J, Yang X, et al. Design and numerical analysis of a THz square porous-core photonic crystal fiber for low flattened dispersion, ultrahigh birefringence. Appl Opt (2017) 56:6993–7001. doi:10.1364/ao.56.006993
29. Luo J, Chen S, Qu H, Su Z, Tian F. Highly birefringent single-mode suspended-core fiber in terahertz regime. J Lightwave Tech (2018) 36(16):3242–8. doi:10.1109/JLT.2018.2834458
30. Yan F, Li L, Wang R, Tian H, Liu J, Liu J, et al. Ultrasensitive tunable terahertz sensor with graphene plasmonic grating. J Lightwave Tech (2019) 37(4):1103–12. doi:10.1109/JLT.2018.2886412
31. Su MY, Yang B, Liu JM, Ye HP, Zhou XX, Xiao JN, et al. Broadband graphene-on-silicon modulator with orthogonal hybrid plasmonic waveguides. Nanophotonics (2020) 9(6):1529–38. doi:10.1515/nanoph-2020-0165
32. Li XG, Feng G, Lin SB. Ultra-wideband terahertz absorber based on graphene modulation. Appl Opt (2021) 60(11):3170–5. doi:10.1364/ao.420143
33. Huang JW, Song ZY. Terahertz graphene modulator based on hybrid plasmonic waveguide. Phys Scr (2021) 96(12):125525. doi:10.1088/1402-4896/ac387d
34. Yang TY, Zhang L, Shi YJ, Liu SD, Dong YM. A highly birefringent photonic crystal fiber for terahertz spectroscopic chemical sensing. Sensors (2021) 21(5):1799. doi:10.3390/s21051799
35. Luo YH, Canning J, Zhang JZ, Peng GD. Toward optical fibre fabrication using 3D printing technology. Opt Fiber Technol (2020) 58:102299. doi:10.1016/j.yofte.2020.102299
36. Bae S, Kim H, Lee Y, Xu XF, Park JS, Zheng Y, et al. Roll-to-roll production of 30-inch graphene films for transparent electrodes. Nat Nanotechnol (2010) 5(8):574–8. doi:10.1038/nnano.2010.132
37. Li JW, Nallappan K, Guerboukha H, Skorobogatiy M. 3D printed hollow core terahertz Bragg waveguides with defect layers for surface sensing applications. Opt Express (2017) 25(4):4126–44. doi:10.1364/oe.25.004126
38. Tang PR, Li J, Du LH, Liu Q, Peng QX, Zhao JH, et al. Ultrasensitive specific terahertz sensor based on tunable plasmon induced transparency of a graphene micro-ribbon array structure. Opt Express (2018) 26(23):30655–66. doi:10.1364/oe.26.030655
39. Chen PY, Alu A. Atomically thin surface cloak using graphene monolayers. ACS Nano (2011) 5(7):5855–63. doi:10.1021/nn201622e
40. Vakil A, Engheta N. Transformation optics using graphene. Science (2011) 332(6035):1291–4. doi:10.1126/science.1202691
41. Fei Z, Rodin AS, Andreev GO, Bao W, McLeod AS, Wagner M, et al. Gate-tuning of graphene plasmons revealed by infrared nano-imaging. Nature (2012) 487(7405):82–5. doi:10.1038/nature11253
42. Bolotin KI, Sikes KJ, Jiang Z, Klima M, Fudenberg G, Hone J, et al. Ultrahigh electron mobility in suspended graphene. Solid State Commun (2008) 146(9-10):351–5. doi:10.1016/j.ssc.2008.02.024
43. Xu W, Zhu ZH, Liu K, Zhang JF, Yuan XD, Lu QS, et al. Dielectric loaded graphene plasmon waveguide. Opt Express (2015) 23(4):5147–53. doi:10.1364/oe.23.005147
44. Chen T, Wang LL, Chen LJ, Wang J, Zhang HK, Xia W. Tunable terahertz wave difference frequency generation in a graphene/AlGaAs surface plasmon waveguide. Photon Res (2018) 6(3):186–92. doi:10.1364/prj.6.000186
45. Habib MA, Anower MS. Design and numerical analysis of highly birefringent single mode fiber in THz regime. Opt Fiber Technol (2019) 47:197–203. doi:10.1016/j.yofte.2018.11.006
Keywords: optical fibers, electro-optic modulators, graphene, Fermi level, terahertz communications
Citation: Wang S, Su M, Tang L, Li X, Li X, Bai H, Niu P, Shi J and Yao J (2023) Graphene-coated D-shaped terahertz fiber modulator. Front. Phys. 11:1202839. doi: 10.3389/fphy.2023.1202839
Received: 09 April 2023; Accepted: 17 May 2023;
Published: 31 May 2023.
Edited by:
Li Li, Harbin Institute of Technology, ChinaReviewed by:
Fengjun Tian, Harbin Engineering University, ChinaPinghui Wu, Quanzhou Normal University, China
Copyright © 2023 Wang, Su, Tang, Li, Li, Bai, Niu, Shi and Yao. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Jia Shi, c2hpamlhQHRpYW5nb25nLmVkdS5jbg==
 Shaona Wang
Shaona Wang Mengya Su1
Mengya Su1 Pingjuan Niu
Pingjuan Niu Jia Shi
Jia Shi