Feasibility study of nuclear excitation by electron capture using an electron beam ion trap

The nuclear excitation by electron capture (NEEC) mechanism is considered to be one of the most effective ways to excite nuclear isomers. Despite being proposed over 50 years ago, direct experimental evidence of NEEC is yet elusive. In this study, we propose an experimental scheme to examine the NEEC process using an electron beam ion trap (EBIT). In an EBIT, highly charged ions are bombarded by an electron beam, which can result in excitation of the nuclei in the trap through mechanisms such as NEEC and Coulomb excitation (CE), etc. Our calculations show that the total rates of NEEC production for some nuclei can reach over 0.1/s, which is higher than these from other mechanisms like CE. The proposed scheme may result in the confirmation of the existence of NEEC, and can also be used to study atomic nuclear excitation related processes.

1 Introduction

Nuclear isomers, being meta-stable states of nuclei, have a profound impact on various fields including nuclear structure models [1,2], nuclear astrophysics [2,3], nuclear lasers [4], nuclear batteries [5], nuclear clocks [6], fine structure measurement [7], and more [8–10]. In order to advance applications in the field of nuclear isomers, it is crucial to understand the mechanisms for exciting or de-exciting them. How to effectively excite the nucleus from the ground state to the isomeric state involves Coulomb excitation (CE) [11], photoabsorption [12], multi-photon excitation [13], and atomic processes related to electron-nucleus interaction. The latter includes nuclear excitation by electron capture (NEEC) [14], nuclear excitation by electronic transition (NEET) [15] and electron bridge (EB) [16]. Some of the more in-depth studies, such as CE and direct γ-photon absorption, their excitation probability is relatively low [17]. Therefore, the potential effective nuclear excitation mechanism of electron coupling in atoms has been considered, especially the NEEC process. NEEC is the inverse process of the internal conversion (IC). The concept of NEEC was first proposed by V.I. Goldanskii et al. in 1976 [14,17]. The principle of NEEC is shown in Figure 1A. Similar to the excitation of atoms in dielectronic recombination [18], where an ion captures a free electron leading to the excitation of the atom, the NEEC is a process in which an ion captures a free electron leading to the resonance excitation of atomic nuclei, which can then be de-excited by emitting γ-ray or IC electrons. For most nuclei, their NEEC resonance cross sections are much larger than the direct photon absorption cross sections, which makes the NEEC to be a promising mechanism for effective nuclear excitation [17]. Just like the “electron captured on nuclei” process [19,20], the NEEC process, which is an “electron captured on atoms” process, play a significant role in the nucleosynthesis in astrophysical environments [21–24], such as in stars like the sun, nova, or supernova explosions.

FIGURE 1

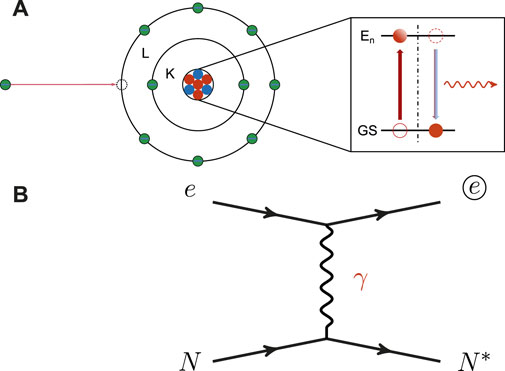
FIGURE 1. (A) The NEEC process of highly charged ions and its energy transition scheme of the nucleus, respectively; (B) The Feynman diagrams of the NEEC. Here, the symbol “ⓔ” indicates that the electron is at an atomically bounded state, while “e” at a continuum state, i.e., a free electron. “N” represents the nucleus is on its ground state (GS), while “N*” on an excited state (E_n). The symbol-γ in the diagram is to indicate the electromagnetic character of the process.

Considerable effort has been devoted to describing the NEEC process theoretically, as well as verifying it experimentally, which include methods of using laser-generated plasma [14,25–30], storage ring [17,31,32], channeling through crystals [33], beam-based scenario [34–36], and so on. In 2018, C. J. Chiara et al. claimed to have discovered the first experimental evidence of NEEC in the isomer depletion of ^93mMo in a beam-based scenario [34]. However, this result was quickly called into questions by subsequent literature for overestimating the theoretical NEEC cross section [35,37] and underestimating the experimental backgrounds [38]. Recently, the isomer beam experiment overturned the previous experimental results [39], but the estimates of the upper limits of their yields remain consistent with the results of theoretical calculations [35,37]. Consequently, the urgent need for experimental confirmation of the NEEC process persists to this day.

In this work, we propose a new experimental scheme for verifying the existence of the NEEC process based on electron beam ion traps (EBIT). The EBIT is a type of ion trap that uses electron beams to trap and confine ions. Traditionally, the EBIT has been used in various fields, from basic atomic and molecular physics to plasma physics [40,41]. By adding an extra electron gun, the modified EBIT is expected to be used to study the nuclear physical processes like the NEEC.

The remaining sections are organized as follows: Section 2 focuses on the theoretical method of calculating the NEEC cross sections for charged ions [31,36,42]. To detect the NEEC process, Section 3 proposes an experimental setup based on an EBIT. The numerical simulation results are provided in Section 4, demonstrating the possibility of NEEC detection. Section 5 presents a potential error budget based on the proposed experimental setup. Lastly, Section 6 provides a summary of this study.

2 NEEC resonance strengths for highly charged ions

The NEEC is a nuclear excitation process in which a free electron is captured by the atom. Its Feynman diagram is shown in Figure 1B, where the original electron e is at continuum state, and the final electron is marked as “ⓔ” to indicate that it is atomically bounded. By transiting the energy released from the free electron, a nuclear isomer could be produced through this process. Because of the energy conservation, one has E_r = E_n − E_b, where E_r is the kinetic energy carried by the free electron, E_b is the binding energy to which the free electron is captured, and E_n is the nuclear excitation energy.

It has been shown theoretically that the cross sections of the NEEC process normally are much higher than the photon absorption cross sections [31,36,42], which makes NEEC a good method to produce nuclear isomers. Furthermore, the nuclear isomer cross sections could be further enhanced if the free electron is captured to a highly charged state. In fact, as shown in Ref. [42], for a certain final electronic configuration ${\alpha }_r$ ($n{l}_j$) and ion charge state q before the electron capture, the NEEC cross section for a nucleus in its ground state initially is written as,

${\sigma }_{\text{NEEC}}^{q,{\alpha }_r}\left(E_e\right)=K\frac{{\lambda }_{\mathrm{e}}^2}{2}{\alpha }_{\text{IC}}^{q,{\alpha }_r}{\mathrm{\Gamma }}_{\gamma }{L}_r\left(E_e-E_r\right),(1)$

where

$K=\frac{\left(2J_E+1\right)\left(2j_c+1\right)}{\left(2J_G+1\right)\left(2j_f+1\right)},(2)$

J_E and J_G are the nuclear spins of the excited and ground states, respectively; j_c and j_f are the total angular momenta of the captured and free electrons, respectively [22]. λ_e is the free electron wavelength, and Γ_γ is the nuclear transition width of the electromagnetic radiation. The partial IC coefficients (ICCs) ${\alpha }_{\text{IC}}^{q,{\alpha }_r}$, depends on the α_r and q. $L_r\left(E_e-E_r\right)$ is a Lorentzian function centered at the resonance energy E_r. The integral of the NEEC cross section ${\sigma }_{\text{NEEC}}^{q,{\alpha }_r}(E_e)$ over the free projectile electron energy E_e is called resonance strength $S_{\text{NEEC}}^{q,{\alpha }_r}$, which can be expressed as

$S_{\text{NEEC}}^{q,{\alpha }_r}=\int {\sigma }_{\text{NEEC}}^{q,{\alpha }_r}\left(E_e\right)d{E}_e=K\frac{{\lambda }_{\mathrm{e}}^2}{2}{\alpha }_{\text{IC}}^{q,{\alpha }_r}{\mathrm{\Gamma }}_{\gamma }.(3)$

Assuming a linear scaling dependence, one can deduce the ICCs for ionized atoms $({\alpha }_{\text{IC}}^{q,{\alpha }_r})$ in Eq. 3 from the ICCs of neutral atoms ${\alpha }_{\mathrm{I}\mathrm{C}}^{q=0,n{l}_j}$ [36],

${\alpha }_{\text{IC}}^{q,{\alpha }_r}={\alpha }_{\text{IC}}^{q=0,n{l}_j}\left(\frac{E_{\mathrm{b}}^{q,{\alpha }_r}}{E_{\mathrm{b}}^{q=0,n{l}_j}}\right)\left(\frac{n_{\mathrm{h}}}{n_{\max }}\right),(4)$

where $E_{\mathrm{b}}^{q,{\alpha }_r}$ and $E_{\mathrm{b}}^{q=0,n{l}_j}$ are the binding energies for ions in the charge state q and neutral atoms, respectively. Their ratio accounts for the increase of the ICCs with the ionization level [24,43]. The ratio between the present n_h and the maximum n_max number of holes in the capture subshell nl_j accounts for the decrease of the ICCs for partially filled subshells [43,44].

The following steps are taken to calculate ${\alpha }_{\text{IC}}^{q,{\alpha }_r}$ in Eq. 4. To obtain the ICCs of neutral atoms, ${\alpha }_{\mathrm{I}\mathrm{C}}^{q=0,n{l}_j}$, the code BrIccFO package is employed [45], which employs the frozen orbital approximation to take into account the effect of the hole. The binding energies $E_{\mathrm{b}}^{q=0,n{l}_j}$ for neutral atoms are taken from tables in Ref. [46], while the ones for highly ionized atoms, $E_{\mathrm{b}}^{q,{\alpha }_r}$, are taken from the NIST database [47].

Isomeric states of nuclei with relatively low nuclear energy levels are chosen as potential candidates for searching NEEC experimentally, and their NEEC excitation resonance strengths are calculated, as listed in Table 1. It can be seen that for most of the longer-lived ($>1$ ms) isomeric states, the NEEC excitation resonance strengths are relatively low, about 10^–6 order of magnitude below, which may be due to the fact that the transition has a high multi-polarity. The ¹⁸¹Ta⁵⁹⁺, which has the relatively high electric transition strength among all the nuclei considered here, has a strength of 4.34 × 10⁻³ b⋅eV. It is mainly due to its very low γ transition multipolarity (E1), as well as its large ICC $({\alpha }_{\text{IC}}^{q=\mathrm{0,3}{p}_{3/2}}=6.72)$. In fact, we have conducted a detailed study of the resonance strengths of NEEC in ¹⁸¹Ta across various charged states and subshells under the ground state assumption (NEEC-GSA) [42]. Figure 2 shows resonance strengths of NEEC for ¹⁸¹Ta’s M, N, O, and P subshells, calculated as a function of the projectile electron energy E_e and the charge states q (1 ≤ q ≤ 59) of ^181mTa ions. It can be founded that the maximum value of the resonance strength is 6 orders of magnitude larger than the minimum one. The maximum resonance strength is typically observed in the inner shell, which corresponds to a higher charged state. This is due to the fact that the electrons in the inner shell are closer to the nucleus, which increases the likelihood of exciting them, as long as the energy conservation principle is satisfied.

TABLE 1

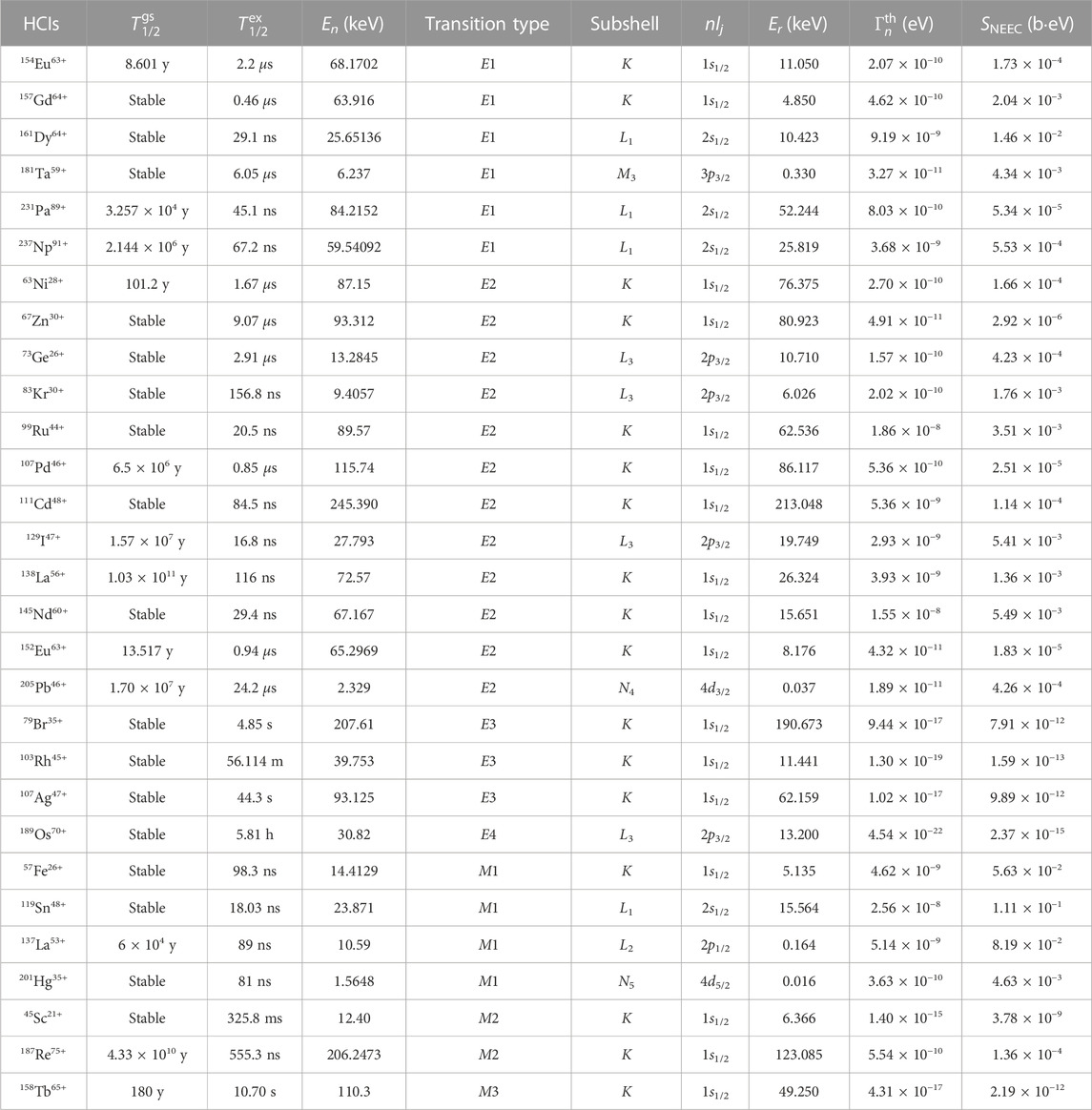
TABLE 1. The NEEC resonance strengths S for several selected heavy HCIs. The first column in the table represents the species of highly charged ions. The second $(T_{1/2}^{\text{gs}})$ and third columns $(T_{1/2}^{\text{ex}})$ are the half-lives of the ground state and isomeric state, respectively. The fourth column (E_n) lists the transition energy of the isomeric state. The 5th column is the electromagnetic transition type. The nl_j represents the quantum state of the subshell where electron capture occurs. The E_r in the 8th column represents the resonant electron beam energy corresponding to NEEC. The ${\mathrm{\Gamma }}_n^{\text{th}}$ represents the width of the level of the isomeric state obtained via theoretical calculations. The S_NEEC is the resonance strength of NEEC.

FIGURE 2

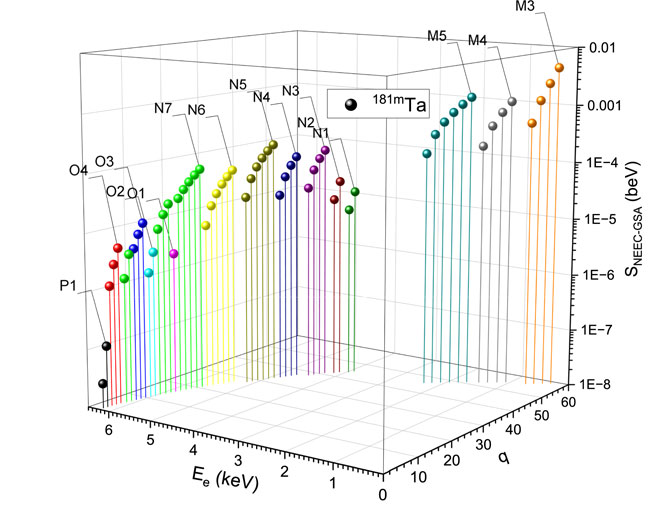
FIGURE 2. NEEC resonance strengths $S_{\text{NEEC}}^{q,{\alpha }_r}$ for captures into M, N, O, and P subshells as a function of the kinetic energy E_e and charge state q of ^181mTa ions under the NEEC-GSA.

Our calculations show that highly charged ions (HCIs), including ¹⁵⁷Gd, ¹⁶¹Dy, ¹⁸¹Ta, ⁸³Kr, ⁹⁹Ru, ¹²⁹I, ¹³⁸La, ¹⁴⁵Nd, ⁵⁷Fe, ¹¹⁹Sn, ¹³⁷La, ²⁰¹Hg, etc., may be very promising in searching for the NEEC process. If they are ionized to HCIs, they are relatively easy to be excited to isomeric states due to their high NEEC resonance strengths, which are further discussed in detail in the subsequent sections.

3 Proposed experimental setup

As shown in the preceding section, the calculation results indicate that the NEEC resonance strengths can be enhanced significantly if HCIs are used, suggesting their potential in NEEC search experiments. An EBIT is a device that utilizes a monoenergetic, high-current-density electron beam to generate and then confine HCIs. With appropriate modifications, the EBITs have the potential to be valuable instruments for investigating NEEC.

The principle we propose for investigating NEEC utilizing an EBIT is illustrated in Figure 3. In contrast to conventional EBIT configurations that employ only one electron gun, our design incorporates two electron guns with varying energies. The electron beams are extracted from the electron guns and accelerated to designed energies, from tens to hundreds keV. Then the electron beams fly into the drift tubes, bombard, and then ionize the atoms there. The product ions undergo triple confinements. Firstly, they are radially confined by the spatial charge of a dense electron beam. The superconducting magnetic field provides further radial and longitudinal confinements. Further longitudinal confinement is achieved by the static electric field of three electrodes in the drift tubes. As the atoms/ions are continuously bombarded by electron beams, they can be stripped to HCIs. If the energy of the electrons matches the NEEC resonance conditions for the electron-HCI, the nuclei can be excited to their isomeric state. By placing a photon detector, such as a High-purity germanium detector, in close proximity, one can monitor the gamma photons emitted by the excited nuclei.

FIGURE 3

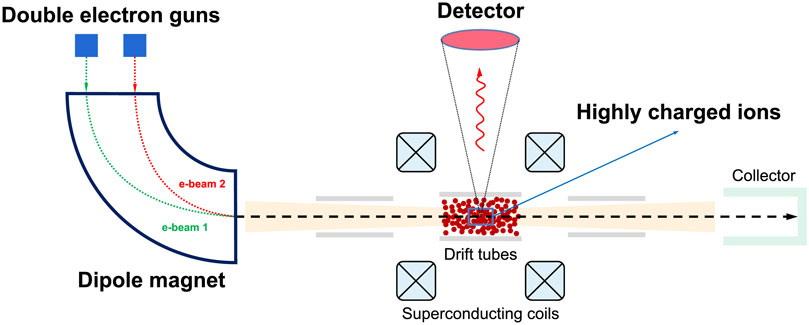
FIGURE 3. The proposed schematic experimental setup. The deflecting dipole magnet is used to converge two electron beams with different energies into a single beam for incidence. When the incident electron beam interacts with atoms in the trap, the atoms can be stripped to form HCIs. The NEEC may occur during the process.

An electron gun can provide a beam density over 10¹³ electrons ⋅s⁻¹cm⁻², with energy fluctuation of tens of eV today. The HCIs can be confined in the trap with a diameter of tens of micrometers, a length of a few centimeters, and a density in the order of 10⁸ cm⁻³. With the help of an EBIT device, HCIs of almost any element in the periodic table can now be produced.

However, the energy required for stripping does not necessarily match that for the resonance. Therefore, to address this issue, in our proposed setup, we use two electron guns. One gun is tuned to strip the atoms to HCIs, while the other is tuned to match the resonance conditions of the NEEC. As shown in Figure 3, the two electron beams from the two electron guns can be deflected by a dipole magnet, converge to be co-axial, and then pass through the confined HCIs area. As an example, for isotope ¹⁸¹Ta, by tuning the first electron gun to 17.721 keV, one can stripe it to ¹⁸¹Ta⁵⁹⁺ [48]. If tuning the second electron gun to 0.33 keV, the 0.33 keV electrons from the 2nd gun can excite ¹⁸¹Ta⁵⁹⁺ to their isomeric state of (9/2⁻, 6.237 keV) with the cross section of 4.34 × 10⁻³ b⋅eV.

4 Estimation of NEEC reaction rates

Consider HCIs that are trapped in an EBIT, as shown in Figure 3. It is assumed that the ions are confined within a cylindrical volume with a radius of R and a length of L cm. Additionally, it is assumed that the electron energy spectrum follows a Gaussian distribution with a width of ϵ_e. The spatial spreading of the electron beam is also assumed to be Gaussian with a width of σ_b. The rate of nuclear isomers generated by the NEEC process for a given electron beam in EBIT can be written using the resonance strength Eq. 3 as

$\begin{array}{cc}\hfill R_{\text{NEEC}}\left(E_e\right)& =\int \frac{j}{e}f\left(E_e-E_r\right)n_i{\sigma }_{\text{NEEC}}\left(E_e\right)LdE\hfill \\ \hfill & =\frac{j}{e}f\left(E_e-E_r\right)n_i{S}_{\text{NEEC}}L,\hfill \end{array}(5)$

where j represents the electron beam current intensity, e is the charge of an electron, n_i represents the density of ion trapped in an EBIT, L is the length of the ion cluster in the trap, E_e is the energy of the electron beam, and f (E_e − E_r) represents the energy distribution of the electron beam.

To ensure practicality, we initially screened candidate nuclei for NEEC studies based on certain criteria. Ideally, we looked for stable isotopes or isotopes with a long lifetime (more than 1 year) to avoid the need for a radioactive ion source. Additionally, we preferred isotopes with relatively lower transition energy (less than 300 keV) since it is hard for typical EBITs to provide electron energies larger than that. We also considered the lifetime of the isomeric state, which should be relatively long but not too long (in the range of tens of nanoseconds to microseconds). A longer lifetime results in a narrower resonance width and smaller reaction yield. However, if the lifetime is too short, it may overlap with the radioactive recombination (RR) process [49,50], which is an atomic process with a short lifetime, typically in order of 10^–14 s [49]. The RR can be a significant background for NEEC studies.

Taking ¹⁸¹Ta as an example, it can be stripped to the 59⁺ valence state, which corresponds to a binding energy of E_b = 5.907 keV. To achieve the highest ratio of expected charge state to all ions, the stripping electron beam energy E_es should be tuned to be 2 ∼ 3 times the ion binding energy E_b, i.e., E_es ≈ (2 ∼ 3)E_b [48]. Ta ions can capture an electron to the 3p_3/2 atomic level (58⁺ charge state) through the NEEC process while being excited from the ground state (J^π = 7/2⁺, stable) to a 6.237 keV isomeric state $(J^{\pi }=9/2^{-},T_{1/2}^{\text{ex}}=6.05\mu \mathrm{s})$. Therefore, for the beam serving as the NEEC resonance beam to match the nuclear excitation resonance condition, its beam energy E_er can be tuned to be 0.33 keV.

Consider that ¹⁸¹Ta ions are trapped in a typical EBIT, and the trapped ions fill a cylindrical volume with a radius of 50 μm and a length of 3 cm. We assume that n_i is 10⁸ cm⁻³ in the ion trap and that a resonant electron beam with a current of 200 mA is incident. The electron beam with an energy spread of under 50 eV (ϵ_e) and a radius of about 50 μm (σ_b) is achievable today. Normally the nuclear energy level width ${\mathrm{\Gamma }}_n^{\text{th}}={\mathrm{\Gamma }}_{\gamma }+{\mathrm{\Gamma }}_{\text{IC}}$ is very narrow compared with the beam energy spread, where Γ_IC represents the IC decay width. For instance, the ¹⁸¹Ta isotope’s total nuclear transition width is approximately ${\mathrm{\Gamma }}_n^{\text{th}}=3.27\times 10^{-11}$ eV, compared with the electron beam energy spread of 50 eV. Therefore, we also need to consider the influence of resonance strength. The value of the resonance strength is calculated to be S_NEEC = 4.34 × 10⁻³ b⋅eV at the resonance energy E_r = 0.33 keV.

The calculated rates based on the above assumptions are listed in Table 2. As an order of magnitude estimation, the distribution of charge states is not considered. Here only one charge state is considered and other charge states are ignored. For ¹⁸¹Ta⁵⁹⁺, the reaction rate is 1.3 × 10⁻²/s for the electron beam with the energy of 0.33 keV, while for the beam of 17.721 keV, the reaction rate can be negligible due to the production rate being below the order of magnitude of 10^–30/s. Therefore, the total reaction rate of NEEC, i.e., R_NEEC = R_NEEC (E_er) + R_NEEC (E_es), is approximately equal to R_NEEC (E_er).

TABLE 2

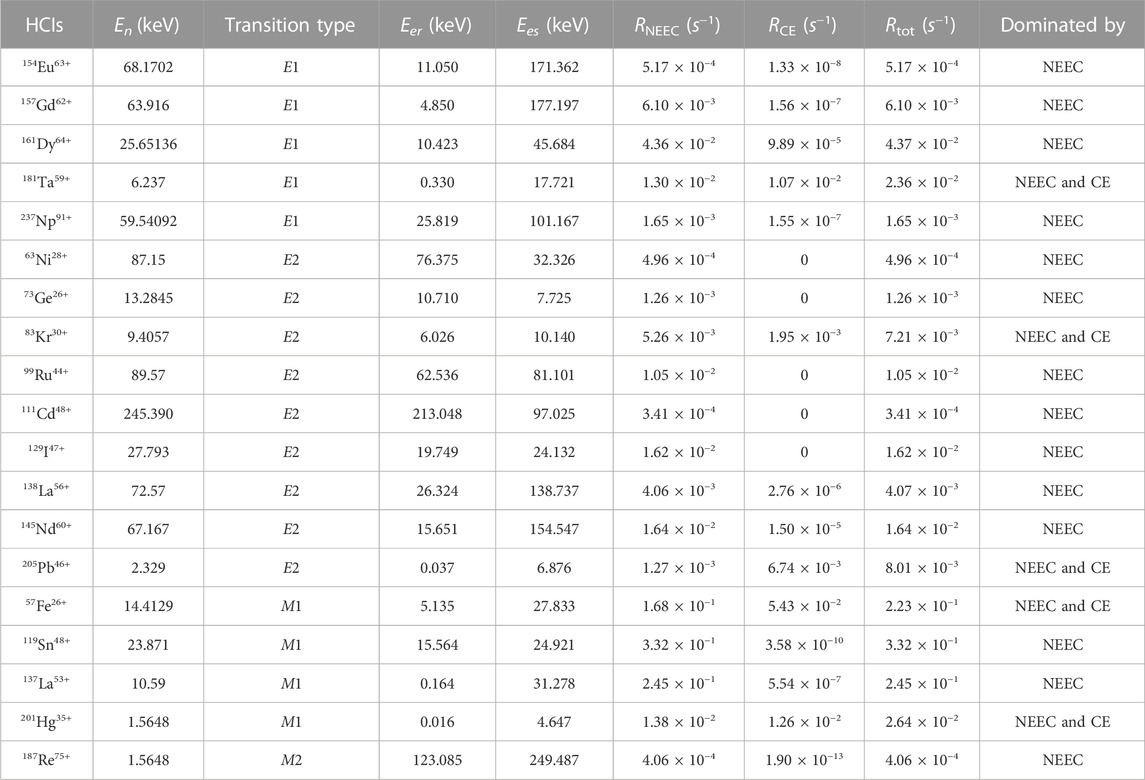
TABLE 2. In a typical EBIT with a length of 3 cm, the ion density n_i is assumed to be 10⁸ cm⁻³. The current of the incident electron beam with an energy broadening of 50 eV is 200 mA. The reaction rates R_NEEC∕CE for NEEC and CE processes at two different electron beam energies of some HCIs in Table 1. Here the contribution to R_NEEC∕CE comes from the both electron beams, E_er and E_es, and R_tot = R_NEEC + R_CE.

The reaction rates of CE, i.e., R_CE (E_e) = In_iσ_CE (E_e)L, I = j/e, are also considered, where CE cross sections were calculated using semi-classical theory [51]. The total reaction rates of CE, i.e., R_CE = R_CE (E_er) + R_CE (E_es) are listed in Table 2 too. For the 0.33 keV beam, the energy is too low and the reaction is forbidden; for the 17.721 keV beam, the CE rate and the NEEC rate are in the same order of 10^–2/s. This nucleus has a relatively high isomer generation rate R_tot = R_CE + R_NEEC in all the nuclei considered in this work. Indeed, some nuclei, such as ⁵⁷Fe, ¹¹⁹Sn, and ¹³⁷La, can be produced at rates greater than 0.1/s.

For other HCIs considered in this work, such as ¹⁵⁴Eu⁶³⁺, ¹⁵⁷Gd⁶²⁺, ²³⁷Np⁹¹⁺, ⁶³Ni²⁸⁺, ¹¹¹Cd⁴⁸⁺, ¹¹⁹Sn⁴⁸⁺, ¹³⁷La⁵³⁺, and ¹⁸⁷Re⁷⁵⁺, their NEEC excitation rates are much greater than the CE, which is very beneficial to prove the existence of the NEEC process. In particular, for ⁶³Ni²⁸⁺, ⁷³Ge²⁶⁺, ⁹⁹Ru⁴⁴⁺, ¹¹¹Cd⁴⁸⁺, and ¹²⁹I⁴⁷⁺ ions, the resonant and stripping electron beam energies are both less than the nuclear excitation energy. This means that the CE excitation is energetically forbidden, and only the NEEC excitation is present.

5 Discussion

The decay of the isomers [52] are mainly through gamma transition and IC (collectively referred to as isomeric transition or IT decay); partly through beta decay such as β −, β +, orbital electron capture on nuclei; and a small amount through alpha decay, neutron emission, neutrino-nucleus processes, etc. However, all of our selected nuclei are stable, and their excited state decay is only IT decay.

The major backgrounds for NEEC searching come from RR and CE processes [50,53,54]. However, it should be noted that the NEEC is a resonance process, while CE processes are not resonance processes. This difference in resonance properties allows for the possibility of distinguishing the resonance peak from the flat background in the NEEC search. We have calculated the excitation rates of the possible CE and NEEC processes for different HCIs separately, as an example shown in Table 2. For most cases where both the electron beams are taken into account and the energies of the beams are smaller than 300 keV, cross sections due to CE are much smaller than the corresponding NEEC process cross sections.

The search for NEEC faces significant interference from the RR process, which is another major background. However, as a broad-resonant process, the RR process has anisotropic angular distributions [50], whereas the distribution of NEEC is isotropic. The combination of an isotropic distribution and a resonance peak can help distinguish the NEEC from the RR process. In addition, since the selected isomers are long-lived, they can be extracted from the ion trap to a clean environment for observation like [39,54] to avoid the interference of other background processes.

There may be competition between the NEEC and stripping processes. The former process involves adding an electron to a HCI, while the latter involves removing one. However, the time scale of nuclear excitation process is much shorter than the time scale required to strip electrons from outside the nucleus at high energies [55,56]. Therefore, the interference between the two processes can be negligible.

The expected thermal motion of ions in the trap is in the order of $<10$ eV, which is smaller than the energy spread of the resonance electron beam at around 50 eV. As a result, the Doppler effect resulting from the ions’ thermal motion in the trap can be considered negligible [57]. Furthermore, other factors may cause changes in nuclear energy levels and their widths, such as the confinement magnet. The Zeeman effect causes energy levels of nuclei and atoms to split, with the energy splits (ΔE ∝B) typically being small due to limited confinement magnetic fields [58]. Therefore, given the electron beam’s energy spread of about 50 eV, the Zeeman effect can also be considered negligible.

Based on the estimated NEEC rates listed in Table 2 which are practically measurable and the controllable background noise signals discussed above, it is promising to search for the NEEC process using the proposed setup.

6 Summary

In summary, we propose an experimental scheme to study NEEC by utilizing an EBIT with two electron beams. The first electron beam strips atoms in the EBIT to high charge states, while the second electron beam matches the energy required for the NEEC process. Our calculations show that this approach yields high cross sections and sufficient reaction products. A resonance strength in the order of magnitude of 10^–3 b⋅eV is achievable by using nuclei like ¹⁸¹Ta⁵⁹⁺, ¹³⁷La⁵³⁺, ¹¹⁹Sn⁴⁸⁺, etc. The proposed scheme can be implemented with minimal modifications to existing EBIT setups, requiring only an additional electron gun and photon detectors. We are confident that our proposed scheme will stimulate additional research on NEEC processes and potentially confirm the existence of this phenomenon, which has been extensively investigated for over 50 years but has yet to be confirmed. Furthermore, we anticipate that our proposed scheme could be adapted to investigate other exotic processes (e.g., the NEET or EB process after further modifications) and potentially contribute to further advances in our understanding of nuclear physics.

Data availability statement

The original contributions presented in the study are included in the article/supplementary material, further inquiries can be directed to the corresponding authors.

Author contributions

This study was proposed by CF, WH, and YM. The theoretical calculations in this manuscript were done by YW under the guidance of CF and also discussed the theory of NEEC with YY, ZM, and WH. ZM and CF provided theoretical support on the CE. The initial draft of this manuscript was written by YW and further revised by CF. All authors contributed to the article and approved the submitted version.

Funding

This work is supported by the National Natural Science Foundation of China (NSFC) under Grant No. 12235003.

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

1. Dracoulis GD, Walker PM, Kondev FG. Review of metastable states in heavy nuclei. Rep Prog Phys (2016) 79:076301. doi:10.1088/0034-4885/79/7/076301

PubMed Abstract | CrossRef Full Text | Google Scholar

2. Walker P, Dracoulis G. Energy traps in atomic nuclei. Nature (1999) 399:35–40. doi:10.1038/19911

CrossRef Full Text | Google Scholar

3. Belic D, Arlandini C, Besserer J, De Boer J, Carroll J, Enders J, et al. Photoactivation of 180 ta m and its implications for the nucleosynthesis of nature’s rarest naturally occurring isotope. Phys Rev Lett (1999) 83:5242–5. doi:10.1103/physrevlett.83.5242

CrossRef Full Text | Google Scholar

4. Tkalya E. Proposal for a nuclear gamma-ray laser of optical range. Phys Rev Lett (2011) 106:162501. doi:10.1103/physrevlett.106.162501

PubMed Abstract | CrossRef Full Text | Google Scholar

5. Carroll JJ. Nuclear structure and the search for induced energy release from isomers. Nucl Instr Methods Phys Res Section B: Beam Interactions Mater Atoms (2007) 261:960–4. doi:10.1016/j.nimb.2007.04.128

CrossRef Full Text | Google Scholar

6. von der Wense L, Seiferle B. The $$^{229}$$Th isomer: Prospects for a nuclear optical clock. The Eur Phys J A (2020) 56:277. doi:10.1140/epja/s10050-020-00263-0

CrossRef Full Text | Google Scholar

7. Flambaum VV. Enhanced effect of temporal variation of the fine structure constant and the strong interaction in ²²⁹Th. Phys Rev Lett (2006) 97:092502. doi:10.1103/PhysRevLett.97.092502

PubMed Abstract | CrossRef Full Text | Google Scholar

8. Banerjee S, Ambikalmajan Pillai MR, Ramamoorthy N. Evolution of tc-99m in diagnostic radiopharmaceuticals. Semin Nucl Med (2001) 31:260–77. doi:10.1053/snuc.2001.26205

PubMed Abstract | CrossRef Full Text | Google Scholar

9. Zhang ZZ, Wang HL, Meng HY, Liu ML. Uncertainty evaluation and correlation analysis of single-particle energies in phenomenological nuclear mean field: An investigation into propagating uncertainties for independent model parameters. Nucl Sci Tech (2021) 32:16. doi:10.1007/s41365-021-00851-9

CrossRef Full Text | Google Scholar

10. Ma Z, Fu C, He W, Ma Y. Manipulation of nuclear isomers with lasers: Mechanisms and prospects. Sci Bull (2022) 67:1526–9. doi:10.1016/j.scib.2022.06.020

CrossRef Full Text | Google Scholar

11. Hayes AB, Cline D, Wu CY, Ai J, Amro H, Beausang C, et al. Breakdown of k selection in ¹⁷⁸Hf. Phys Rev Lett (2006) 96:042505. doi:10.1103/PhysRevLett.96.042505

PubMed Abstract | CrossRef Full Text | Google Scholar

12. Collins CB, Davanloo F, Iosif MC, Dussart R, Hicks JM, Karamian SA, et al. Accelerated emission of gamma rays from the 31-yr isomer of ¹⁷⁸Hf induced by x-ray irradiation. Phys Rev Lett (1999) 82:695–8. doi:10.1103/PhysRevLett.82.695

CrossRef Full Text | Google Scholar

13. Tkalya E. Many-photon excitation of atomic neclei in the hot plasma. Soviet Phys Doklady (1991) 36:467.

Google Scholar

14. Goldanskii VI, Namiot VA. On the excitation of isomeric nuclear levels by laser radiation through inverse internal electron conversion. Phys Lett B (1976) 62:393–4. doi:10.1016/0370-2693(76)90665-1

CrossRef Full Text | Google Scholar

15. Kishimoto S, Yoda Y, Seto M, Kobayashi Y, Kitao S, Haruki R, et al. Observation of nuclear excitation by electron transition in ¹⁹⁷Au with synchrotron x rays and an avalanche photodiode. Phys Rev Lett (2000) 85:1831–4. doi:10.1103/PhysRevLett.85.1831

PubMed Abstract | CrossRef Full Text | Google Scholar

16. Bilous PV, Bekker H, Berengut JC, Seiferle B, von der Wense L, Thirolf PG, et al. Electronic bridge excitation in highly charged ²²⁹Th ions. Phys Rev Lett (2020) 124:192502. doi:10.1103/PhysRevLett.124.192502

PubMed Abstract | CrossRef Full Text | Google Scholar

17. Pálffy A, Evers J, Keitel CH. Isomer triggering via nuclear excitation by electron capture. Phys Rev Lett (2007) 99:172502. doi:10.1103/PhysRevLett.99.172502

PubMed Abstract | CrossRef Full Text | Google Scholar

18. Harman Z, Shah C, González Martínez AJ, Jentschura UD, Tawara H, Keitel CH, et al. Resonance strengths for kll dielectronic recombination of highly charged mercury ions and improved empirical z-scaling law. Phys Rev A (2019) 99:012506. doi:10.1103/PhysRevA.99.012506

CrossRef Full Text | Google Scholar

19. Giannaka P, Kosmas T, Ejiri H. Original e− Capture Cross Sections for Hot Stellar Interior Energies. Particles (2022) 5:390–406. doi:10.3390/particles5030031

CrossRef Full Text | Google Scholar

20. Langanke K, Martínez-Pinedo G, Zegers RGT. Electron capture in stars. Rep Prog Phys (2021) 84:066301. doi:10.1088/1361-6633/abf207

CrossRef Full Text | Google Scholar

21. Helmrich S, Spenneberg K, Pálffy A. Coupling highly excited nuclei to the atomic shell in dense astrophysical plasmas. Phys Rev C (2014) 90:015802. doi:10.1103/PhysRevC.90.015802

CrossRef Full Text | Google Scholar

22. Harston MR, Chemin JF. Mechanisms of nuclear excitation in plasmas. Phys Rev C (1999) 59:2462–73. doi:10.1103/PhysRevC.59.2462

CrossRef Full Text | Google Scholar

23. Gosselin G, Méot V, Morel P. Modified nuclear level lifetime in hot dense plasmas. Phys Rev C (2007) 76:044611. doi:10.1103/PhysRevC.76.044611

CrossRef Full Text | Google Scholar

24. Gosselin G, Morel P. Enhanced nuclear level decay in hot dense plasmas. Phys Rev C (2004) 70:064603. doi:10.1103/PhysRevC.70.064603

CrossRef Full Text | Google Scholar

25. Gunst J, Litvinov YA, Keitel CH, Pálffy A. Dominant secondary nuclear photoexcitation with the x-ray free-electron laser. Phys Rev Lett (2014) 112:082501. doi:10.1103/PhysRevLett.112.082501

CrossRef Full Text | Google Scholar

26. Wu Y, Gunst J, Keitel CH, Pálffy A. Tailoring laser-generated plasmas for efficient nuclear excitation by electron capture. Phys Rev Lett (2018) 120:052504. doi:10.1103/PhysRevLett.120.052504

PubMed Abstract | CrossRef Full Text | Google Scholar

27. Wu D, Bai CL, Sagawa H, Song ZQ, Zhang HQ. Contributions of optimized tensor interactions on the binding energies of nuclei. Nucl Sci Tech (2020) 31:14. doi:10.1007/s41365-020-0727-7

CrossRef Full Text | Google Scholar

28. He YF, Sun B, Ma MJ, Li W, He QY, Cui ZH, et al. Topology optimization of on-chip integrated laser-driven particle accelerator. Nucl Sci Tech (2022) 33:120. doi:10.1007/s41365-022-01101-2

CrossRef Full Text | Google Scholar

29. Lan HY, Wu D, Liu JX, Zhang JY, Lu HG, Lv JF, et al. Photonuclear production of nuclear isomers using bremsstrahlung induced by laser-wakefield electrons. Nucl Sci Tech (2023) 34:74. doi:10.1007/s41365-023-01219-x

CrossRef Full Text | Google Scholar

30. Hu P, Ma ZG, Zhao K, Zhang GQ, Fang DQ, Wei BR, et al. Development of gated fiber detectors for laser-induced strong electromagnetic pulse environments. Nucl Sci Tech (2021) 32:58. doi:10.1007/s41365-021-00898-8

CrossRef Full Text | Google Scholar

31. Pálffy A, Scheid W, Harman Z. Theory of nuclear excitation by electron capture for heavy ions. Phys Rev A (2006) 73:012715. doi:10.1103/PhysRevA.73.012715

CrossRef Full Text | Google Scholar

32. Ma X, Wen WQ, Huang ZK, Wang HB, Yuan YJ, Wang M, et al. Proposal for precision determination of 7.8 ev isomeric state in 229th at heavy ion storage ring. Physica Scripta (2015) T166:014012. doi:10.1088/0031-8949/2015/T166/014012

CrossRef Full Text | Google Scholar

33. Yuan ZS, Kimball JC. First-principles calculation of the cross sections for nuclear excitation by electron capture of channeled nuclei. Phys Rev C (1993) 47:323–8. doi:10.1103/PhysRevC.47.323

CrossRef Full Text | Google Scholar

34. Chiara C, Carroll J, Carpenter M, Greene J, Hartley D, Janssens R, et al. Isomer depletion as experimental evidence of nuclear excitation by electron capture. Nature (2018) 554:216–8. doi:10.1038/nature25483

PubMed Abstract | CrossRef Full Text | Google Scholar

35. Wu Y, Keitel CH, Pálffy A. ^93mMo isomer depletion via beam-based nuclear excitation by electron capture. Phys Rev Lett (2019) 122:212501. doi:10.1103/PhysRevLett.122.212501

PubMed Abstract | CrossRef Full Text | Google Scholar

36. Rzadkiewicz J, Polasik M, Słabkowska K, Syrocki L, Wȩder E, Carroll JJ, et al. Beam-based scenario for ^242mAm isomer depletion via nuclear excitation by electron capture. Phys Rev C (2019) 99:044309. doi:10.1103/PhysRevC.99.044309

CrossRef Full Text | Google Scholar

37. Rzadkiewicz J, Polasik M, Słabkowska K, Syrocki L, Carroll JJ, Chiara CJ. Novel approach to ^93mMo isomer depletion: Nuclear excitation by electron capture in resonant transfer process. Phys Rev Lett (2021) 127:042501. doi:10.1103/PhysRevLett.127.042501

PubMed Abstract | CrossRef Full Text | Google Scholar

38. Guo S, Fang Y, Zhou X, Petrache C. Possible overestimation of isomer depletion due to contamination. Nature (2021) 594:E1–2. –E2. doi:10.1038/s41586-021-03333-5

PubMed Abstract | CrossRef Full Text | Google Scholar

39. Guo S, Ding B, Zhou XH, Wu YB, Wang JG, Xu SW, et al. Probing ^93mMo isomer depletion with an isomer beam. Phys Rev Lett (2022) 128:242502. doi:10.1103/PhysRevLett.128.242502

PubMed Abstract | CrossRef Full Text | Google Scholar

40. Currell F, Fussmann G. Physics of electron beam ion traps and sources. IEEE Trans Plasma Sci (2005) 33:1763–77. doi:10.1109/TPS.2005.860072

CrossRef Full Text | Google Scholar

41. Lapierre A, Crespo López-Urrutia JR, Braun J, Brenner G, Bruhns H, Fischer D, et al. Lifetime measurement of the ar xiv 1{s}^{2}2{s}^{2}2p\phantom{\rule{0.2em}{0ex}}^{2}p_{3/2}^{o} metastable level at the heidelberg electron-beam ion trap. Phys Rev A (2006) 73:052507. doi:10.1103/PhysRevA.73.052507

CrossRef Full Text | Google Scholar

42. Gargiulo S, Madan I, Carbone F. Nuclear excitation by electron capture in excited ions. Phys Rev Lett (2022) 128:212502. doi:10.1103/PhysRevLett.128.212502

PubMed Abstract | CrossRef Full Text | Google Scholar

43. Rysav M, Dragoun O. On the reliability of the theoretical internal conversion coefficients. J Phys G: Nucl Part Phys (2000) 26:1859–72. doi:10.1088/0954-3899/26/12/309

CrossRef Full Text | Google Scholar

44. Raman S, Nestor CW, Ichihara A, Trzhaskovskaya MB. How good are the internal conversion coefficients now? Phys Rev C (2002) 66:044312. doi:10.1103/PhysRevC.66.044312

CrossRef Full Text | Google Scholar

45. Kibédi T, Burrows T, Trzhaskovskaya M, Davidson P, Nestor C. Evaluation of theoretical conversion coefficients using bricc. Nucl Instr Methods Phys Res Section A: Acc Spectrometers, Detectors Associated Equipment (2008) 589:202–29. doi:10.1016/j.nima.2008.02.051

CrossRef Full Text | Google Scholar

46. Larkins F. Semiempirical auger-electron energies for elements 10 - z - 100. At Data Nucl Data Tables (1977) 20:311–87. doi:10.1016/0092-640X(77)90024-9

CrossRef Full Text | Google Scholar

47.[ Dataset] Kramida A, Ralchenko Y, Reader J. NAT. Nist atomic spectra database. version 5.10 (2022). doi:10.18434/T4W30F

CrossRef Full Text | Google Scholar

48. Pálffy A. Theory of nuclear excitation by electron capture for heavy ions. Germany: Justus-Liebig-University Giessen (2006). Ph.D. thesis.

49. Pálffy A, Harman Z, Kozhuharov C, Brandau C, Keitel CH, Scheid W, et al. Nuclear excitation by electron capture followed by fast x-ray emission. Phys Lett B (2008) 661:330–4. doi:10.1016/j.physletb.2008.02.027

CrossRef Full Text | Google Scholar

50. Pálffy A, Harman Z, Scheid W. Quantum interference between nuclear excitation by electron capture and radiative recombination. Phys Rev A (2007) 75:012709. doi:10.1103/PhysRevA.75.012709

CrossRef Full Text | Google Scholar

51. Alder K, Bohr A, Huus T, Mottelson B, Winther A. Study of nuclear structure by electromagnetic excitation with accelerated ions. Rev Mod Phys (1956) 28:432–542. doi:10.1103/revmodphys.28.432

CrossRef Full Text | Google Scholar

52. Sagawa AO. Modern nuclear physics. Singapore: Springer (2021).

Google Scholar

53. Arigapudi SK, Pálffy A. Overlapping resonances in nuclei coupling to the atomic shells. Phys Rev A (2012) 85:012710. doi:10.1103/PhysRevA.85.012710

CrossRef Full Text | Google Scholar

54. Feng J, Wang W, Fu C, Chen L, Tan J, Li Y, et al. Femtosecond pumping of nuclear isomeric states by the coulomb collision of ions with quivering electrons. Phys Rev Lett (2022) 128:052501. doi:10.1103/PhysRevLett.128.052501

PubMed Abstract | CrossRef Full Text | Google Scholar

55. Shang JJS. Modeling plasma via electron impact ionization. Aerospace (2018) 5:2. doi:10.3390/aerospace5010002

CrossRef Full Text | Google Scholar

56. Jonauskas V, Kynienė A, Kučas S, Pakalka S, icv M, Prancikevičius A, et al. Electron-impact ionization of w⁵⁺. Phys Rev A (2019) 100:062701. doi:10.1103/PhysRevA.100.062701

CrossRef Full Text | Google Scholar

57. Beiersdorfer P, Phillips TW, Wong KL, Marrs RE, Vogel DA. Measurement of level-specific dielectronic-recombination cross sections of heliumlike fe xxv. Phys Rev A (1992) 46:3812–20. doi:10.1103/PhysRevA.46.3812

PubMed Abstract | CrossRef Full Text | Google Scholar

58. Zou Y, Hutton R. Physics based on electron beam ion traps*. Physica Scripta (2005) T120:47–52. doi:10.1088/0031-8949/2005/T120/006

CrossRef Full Text | Google Scholar