Generation of polarization-controllable low-frequency THz radiations from single-layer graphene using incommensurate two-color laser pulses

We propose to combine a circularly polarized first-color laser with a linearly polarized second-color laser to control the polarization of THz radiations in the low-frequency region from single-layer graphene. We find that the THz ellipticity can be greatly adjusted by varying the wavelength of second color, and it can be slightly modified by varying the intensity ratio of two colors. We then show that the polarization direction of THz emissions can be dramatically changed by changing the phase difference between two colors. We also identify that the intensity, ellipticity, and polarization direction of THz wave can be changed simultaneously with the time delay between two colors. These can be understood by analyzing the electron currents, intensities of THz emissions in two orthogonal directions, and the phase difference between them. Our proposed scheme can be easily performed in the experiment based on the laser technology nowadays.

1 Introduction

Terahertz (THz) technology has attracted much attention due to its potential applications [1–6] in nonlinear spectroscopy, remote sensing, imaging, antiterrorism detection and biomedicine, and so on. It has also been applied to capture the ultrafast electronic or nonlinear optical response of air and solid materials [7–9]. In past years, THz radiations from different frequency bands have been coherently generated through laser-matter interaction by using gases [10], air plasma [11–13], solids [14], and liquids [15, 16]. With the advancement of optical parametric amplification (OPA) and optical parametric chirped pulse amplification (OPCPA) technologies, it has become mature to precisely synthesize multi-color laser pulses [17–19]. This provides with new opportunities to modify the properties of THz emissions. For example, THz radiations in both low- and high-frequency regions have been enhanced by using two- or three-color linearly polarized laser pulses with air plasma or gases [5, 11–13, 20].

Since the elliptically and circularly polarized THz waves are essential light sources for applications in dichroism [21], THz imaging [22], and polarimetry [23], it is very crucial to control the polarization of THz emissions in the generation process. In general, there are two ways to generate the elliptically polarized THz waves. The first one is using laser-induced gas plasma, which can generate the THz radiations with an ultrabroad bandwidth ($>$50 THz) and has a higher damage threshold. Either circularly polarized few-cycle laser pulses [24, 25] or two-color laser pulses [26, 27] were employed to control the polarization characteristics of the THz waves generated from the gas plasma. The second approach is generating the polarization controllable THz radiations by using functional devices, such as waveplates and polarizers. These devices are usually made by some special materials, for instance, liquid crystal and metamaterials [28–30]. You et al. [28] used two-layer graphene grating to achieve a switchable quarter-wave plate (QWP), which can convert a linear polarization of THz waves to a left- (or right-) handed circular polarization in the ON state. Liu et al. [30] demonstrated that VO₂-based grating structure with a total internal reflection geometry is a powerful device for actively controlling the broadband THz polarization. Elliptically polarized THz waves generated through above two ways are distributed in quite different frequency regions. By using laser-induced gas plasma, THz frequencies can reach 10 THz or above. With functional devices, THz frequencies are mostly limited below 5 THz. But low conversion efficiency and limited solid materials restrict further applications of such low-frequency polarized THz emissions. To overcome these shortcomings, it has been proposed to produce THz emissions with ellipticity through the shift current of solid materials, generated by the coherent evolution of electron and hole wave function in noncentrosymmetric materials [31, 32]. However, how to use centrosymmetric materials to effectively achieve the same goal is still challenging.

Graphene is a representative two-dimensional and centrosymmetric material. THz emissions from graphene have been extensively studied in both theory and experiment [33, 34]. For example, laser pulses with duration of 110 fs at oblique incidence were used to drive the graphene to generate a coherent THz radiation ranging from 0.1 to 4 THz [35] and THz polarization states in vertically grown graphene were well controlled [36]. Single-layer graphene with zero gap is a special centrosymmetric material, and it exhibits weak screening, high damage threshold, and unique optical properties [37, 38]. Thus it is an ideal candidate material to efficiently generate the polarized THz emissions. However, it becomes difficult to directly apply existent (or present-day) methods into the single-layer graphene. If it is used as a functional device, it becomes hard to achieve the THz QWP [28] since it has a very low phase difference due to insufficient thickness. Meanwhile, as a centrosymmetric material, the single-layer graphene cannot generate the shift current with a linearly polarized driving laser, so the polarized THz waves cannot be prompted. It is thus required to come up with new solutions. Two-color scheme has shown its advantages in the THz generation with single-layer graphene. THz intensity can be greatly enhanced due to the weak screening of single-layer graphene [38]. Similar to the laser-induced gas plasma, the frequency regions of THz emissions can be tailored [35]. Furthermore, it has been demonstrated theoretically that the polarization controllable THz waves in the relatively high-frequency regions can be obtained from gases by using two-color laser pulses [39]. Thus, it is desirable to examine whether the two-color scheme is able to control the polarization of low-frequency THz emissions from single-layer graphene.

In this work, we suggest to use incommensurate two-color laser pulses to generate the polarization-controllable THz radiations in the low-frequency regions with the single-layer graphene. Two-color laser pulses consist of a circularly polarized laser and a linearly polarized laser. The article is organized in the following. Section 2 introduces the theoretical methods for simulating the laser-graphene interaction. Section 3 presents the detailed results of ellipticity, electric waveform, and intensity of THz emissions. The simulations are performed by varying the wavelength of the linearly polarized laser, or by varying the intensity ratio, time delay, and relative phase between two colors. Meanwhile, the electron currents and THz radiations in two orthogonal directions are analyzed. And the summary of this paper is given in Section 4.

2 Theoretical methods

We employ the time-dependent tight-binding (T-B) approximation to study the laser-graphene interaction. Band energies near the Dirac points can be precisely calculated unless the applied laser intensity is too higher. Time-dependent Schrödinger equation can be written as [40],

$i\hslash \frac{\partial \psi }{\partial t}=\widehat{H}\left(\mathbf{k}+\mathbf{A}\left(t\right)\right)\psi ,(1)$

where

$\begin{array}{llll}\hfill & \hfill & \hfill \widehat{H}\left(t\right)=& \left[\begin{array}{cc}\hfill 0\hfill & \hfill f\left(\mathbf{k}+\mathbf{A}\left(t\right)\right)\hfill \\ \hfill f^{*}\left(\mathbf{k}+\mathbf{A}\left(t\right)\right)\hfill & \hfill 0\hfill \end{array}\right],\hfill \end{array}(2)$

here A(t) is the vector potential of driving laser, and f(k) is a complex function, which can be written as

$f\left(\mathbf{k}\right)=\gamma \left[e^{{iak}_y/\sqrt{3}}+2e^{{-iak}_y/2\sqrt{3}}\cos \left({ak}_x/2\right)\right],(3)$

where a = 2.46 $\mathring{A}$, γ = −2.9 eV, and $|\mathbf{k}|=\sqrt{k_x^2+k_y^2}$.

We define the time-dependent wave function ${\varphi }_{\mathbf{k}}(t)=C_v^{\mathbf{k}}(t){\varphi }_v^{\mathbf{k}}+C_v^{\mathbf{k}}(t){\varphi }_c^{\mathbf{k}}$ in terms of Bloch basis. Here ${\varphi }_v^{\mathbf{k}}={(\mathrm{1,0})}^T$ and ${\varphi }_c^{\mathbf{k}}={(\mathrm{0,1})}^T$.

By using Bloch basis, Eq. 1 can be transformed as

$i\hslash \frac{\partial {\varphi }_{\mathbf{k}}}{\partial t}={\widehat{H}}_B\left(t\right){\varphi }_{\mathbf{k}}.(4)$

And the corresponding two-band equations are [41–43].

$\begin{array}{cc}\hfill \frac{d}{dt}{C}_v^{\mathbf{k}}\left(t\right)& =\frac{i}{2}\left[-B_1\left(t\right)C_v^{\mathbf{k}}\left(t\right)-B_2\left(t\right)C_c^{\mathbf{k}}\left(t\right)\right],\hfill \\ \hfill \frac{d}{dt}{C}_c^{\mathbf{k}}\left(t\right)& =\frac{i}{2}\left[-B_3\left(t\right)C_v^{\mathbf{k}}\left(t\right)-B_4\left(t\right)C_c^{\mathbf{k}}\left(t\right)\right].\hfill \end{array}(5)$

Here,

$\begin{array}{cc}\hfill B_1\left(t\right)=& -\left[f\left(\mathbf{k}+\mathbf{A}\left(t\right)\right)e^{-i{\theta }_{f\left(\mathbf{k}\right)}}+f^{*}\left(\mathbf{k}+\mathbf{A}\left(t\right)\right)e^{i{\theta }_{f\left(\mathbf{k}\right)}}\right],\hfill \\ \hfill B_2\left(t\right)=& -\left[f\left(\mathbf{k}+\mathbf{A}\left(t\right)\right)e^{-i{\theta }_{f\left(\mathbf{k}\right)}}-f^{*}\left(\mathbf{k}+\mathbf{A}\left(t\right)\right)e^{i{\theta }_{f\left(\mathbf{k}\right)}}\right],\hfill \\ \hfill B_3\left(t\right)=& \left[f\left(\mathbf{k}+\mathbf{A}\left(t\right)\right)e^{-i{\theta }_{f\left(\mathbf{k}\right)}}-f^{*}\left(\mathbf{k}+\mathbf{A}\left(t\right)\right)e^{i{\theta }_{f\left(\mathbf{k}\right)}}\right],\hfill \\ \hfill B_4\left(t\right)=& \left[f\left(\mathbf{k}+\mathbf{A}\left(t\right)\right)e^{-i{\theta }_{f\left(\mathbf{k}\right)}}+f^{*}\left(\mathbf{k}+\mathbf{A}\left(t\right)\right)e^{i{\theta }_{f\left(\mathbf{k}\right)}}\right].\hfill \end{array}(6)$

Next, we define ${\bar{\rho }}_{vv}={(C_v^{\mathbf{k}})}^{†}{C}_v^{\mathbf{k}}$ as the electron population in the valence band, ${\bar{\rho }}_{cc}={(C_c^{\mathbf{k}})}^{†}{C}_c^{\mathbf{k}}$ as the electron (or hole) population in the conduction band, and ${\bar{\rho }}_{cv}={(C_v^{\mathbf{k}})}^{†}{C}_c^{\mathbf{k}}$ as the inter-band polarization. The coupled equations can be obtained as [44].

$\begin{array}{cc}\hfill \frac{d}{dt}{\bar{\rho }}_{cv}\left(t\right)& =-i{B}_4^{*}{\bar{\rho }}_{cv}\left(t\right)+i{B}_1^{*}{\bar{\rho }}_{cv}\left(t\right)\hfill \\ \hfill & -i{B}_3\left(1-f_e\left(t\right)-f_h\left(t\right)\right)-{\gamma }_r{\bar{\rho }}_{cv}\left(t\right),\hfill \\ \hfill \frac{d}{dt}{f}_e\left(t\right)& =2\text{Im}\left[B_3^{*}{\bar{\rho }}_{cv}\left(t\right)\right]-{\gamma }_l{f}_e\left(t\right),\hfill \\ \hfill \frac{d}{dt}{f}_h\left(t\right)& =2\text{Im}\left[-B_2^{*}{\bar{\rho }}_{cv}\left(t\right)\right]-{\gamma }_l{f}_h\left(t\right),\hfill \end{array}(7)$

where $f_e={\bar{\rho }}_{cc}$ and f_h = f_e denote the electron and hole population, respectively, and γ_r and γ_l are the transverse and longitudinal relaxation constants, respectively. In the most simplified case, $\left|f(\mathbf{k})\right|\approx (k^2/2m_u+E_g/2)$ with electron mass of m_u and the band gap energy of E_g, and θ_f(k) = θ_k, where θ_k define the directional angle of vector [k_x, k_y]. The single-electron current can be evaluated as [45].

$j_{\mathbf{k}}\left(t\right)=⟨{\varphi }_{\mathbf{k}}\left(\mathbf{r},t\right)|\widehat{\mathbf{p}}+\mathbf{A}\left(t\right)|{\varphi }_{\mathbf{k}}\left(\mathbf{r},t\right)⟩.(8)$

And the THz field can be calculated via derivative of the electron current:

${\mathbf{E}}_{\text{THz}}\left(t\right)=\xi \left[\frac{d\mathbf{J}}{dt}\right].(9)$

Here the scale factor ξ can be obtained as [38].

${\xi }^2=\frac{{\int }_{-\infty }^{+\infty }{\left|E_x^{\text{L}}\left(t\right)\right|}^{2}dt+{\int }_{-\infty }^{+\infty }{\left|E_y^{\text{L}}\left(t\right)\right|}^{2}dt}{{\int }_{-\infty }^{+\infty }{\left|\frac{d{J}_x\left(t\right)}{dt}\right|}^{2}dt+{\int }_{-\infty }^{+\infty }{\left|\frac{d{J}_y\left(t\right)}{dt}\right|}^{2}dt},(10)$

and the conversion efficiency of THz in the frequency region of ω₁ to ω₂ can be calculated as

$\eta =\sigma \cdot \frac{{\int }_{{\omega }_1}^{{\omega }_2}{\left|E_x^{\text{THz}}\left(\omega \right)\right|}^{2}d\omega +{\int }_{{\omega }_1}^{{\omega }_2}{\left|E_y^{\text{THz}}\left(\omega \right)\right|}^{2}d\omega }{{\int }_0^{+\infty }{\left|E_x^{\text{L}}\left(\omega \right)\right|}^{2}d\omega +{\int }_0^{+\infty }{\left|E_y^{\text{L}}\left(\omega \right)\right|}^{2}d\omega }(11)$

Here $E_i^{\text{L}}(\omega )$ and $E_i^{\text{THz}}(\omega )$ (i = x, y) are Fourier transforms of driving laser and THz fields, respectively, and σ is the light transmission coefficient. For the single-layer graphene, σ is chosen as 100%.

Since the single-layer grapene is thin enough, the propagation of driving laser and THz field in the medium can be neglected.

3 Results and Discussion

3.1 Formulation of incommensurate two-color laser pulses and THz ellipticity

In our simulations, the electric field of two-color laser pulses in two orthogonal x and y directions takes the form in the following:

$\begin{array}{cc}\hfill E_x^{\text{L}}\left(t\right)& =\frac{\sqrt{2}}{2}\sqrt{I_1}f\left(t\right)\cos \left({\omega }_{1}t+{\varphi }_1\right)\hfill \\ \hfill & +\sqrt{I_2}f\left(t-t_d\right)\cos \left[{\omega }_2\left(t-t_d\right)+{\varphi }_2)\right],\hfill \\ \hfill E_y^{\text{L}}\left(t\right)& =\frac{\sqrt{2}}{2}\sqrt{I_1}f\left(t\right)\cos \left({\omega }_{1}t+{\varphi }_1+\pi /2\right),\hfill \end{array}(12)$

where $\frac{\sqrt{2}}{2}\sqrt{I_1}$ is the field amplitude in x or y direction of the circularly polarized laser, $\sqrt{I_2}$ is the field amplitude of the linearly polarized laser, ϕ₁ and ϕ₂ are carrier-envelope phases (CEPs) for circularly and linearly polarized lasers, respectively, t_d is the relative time delay between two-color laser pulses, and f(t) represents a cos⁴ pulse envelope. We set the angular frequency of first color as ω₁ = 0.028 a.u. (1,600 nm), fix the total intensity as I₁ + I₂ = 7.1 × 10¹¹ W/cm², and set t_d = 0 unless otherwise defined. The ellipticity ɛ of THz wave for a given angular frequency ω is defined as

$\begin{array}{cc}\hfill \epsilon & =\tan \chi ,\hfill \\ \hfill \sin 2\chi & =\sin \left(2\beta \right)\sin \delta ,\hfill \\ \hfill \tan \beta & =E_y^{\text{THz}}/E_x^{\text{THz}},\hfill \end{array}(13)$

where $E_y^{\text{THz}}$ and $E_x^{\text{THz}}$ are THz intensities in the x and y directions, respectively, δ is the phase difference between THz waves in the two directions.

Note that Hafez et al. [38] have experimentally demonstrated that emissions from SiO₂, a commonly used substrate for single-layer graphene, are much weaker than that from single-layer graphene in the frequency region of 1–3 THz. So we ignore the effect of substrate on the THz emission in our simulations since we mainly focus on the THz emission near 2 and 3 THz. Damage threshold of material is also considered when we choose the laser parameter. We have checked that the maximum fluence is about 80 mJ/cm² with our laser parameters, which is well below the damage threshold of single-layer graphene [46].

3.2 Comparison of THz generation with one-color circularly polarized laser and incommensurate two-color laser pulses

First, we simulate the THz emissions with the one-color circularly polarized laser only. By varying the full laser duration (in terms of period T of 1600-nm laser), the dependence of THz ellipticity on the frequency are shown in Figure 1A. For each fixed duration, the THz ellipticity is gradually increased from 0 (linearly polarized) to 1 (circularly polarized) with the increase of THz frequency. With the longer duration, the THz ellipticity can quickly reach to 1 at lower THz frequency. For example, for 8 T case (blue line), the ellipticity is dramatically changed in the 0–30 THz frequency band. This means the THz ellipticity in low-frequency regions can be controlled much easier with longer-duration driving laser. We also show the THz yields (i.e., the summed THz intensities in both x and y directions) integrated in the 0–80 THz frequency band as a function of pulse duration in Figure 1B (black points). The THz yields are greatly decreased with the increase of pulse duration. Thus it is not appealing to control the THz ellipticity in the low-frequency regions by solely increasing the duration of one-color circularly polarized laser. Alternatively, we add the second-color linearly polarized laser, take the full duration of first color as 8 T, and set the following parameters: I₂/I₁ = 0.25, ϕ_1,2 = 0, ω₂ = 0.0175 a.u. (2,600 nm), the full duration of second color is also set as 8 T (in term of period T of 1600-nm laser). The resulted THz ellipticity (green line) and THz yields (red point) are plotted in Figures 1A,B, respectively. One can see that the THz ellipticity is effectively changed in an even narrower frequency region (below 10 THz) compared to that obtained with the first color alone. Meanwhile, the THz intensity is remarkably enhanced. Therefore, the generation of polarization controllable THz radiations in the low-frequency regions can be efficiently achieved under the two-color scheme.

FIGURE 1

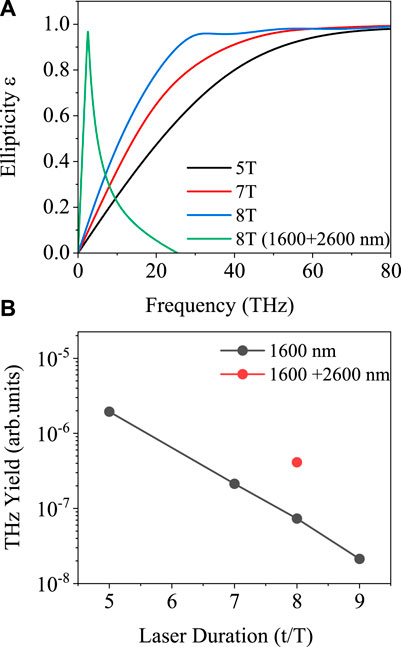
FIGURE 1. (A) Dependence of THz ellipticity on the frequency with different durations of single-color circularly laser and under an incommensurate two-color laser. (B) THz yields integrated below 80 THz (black squares or red circle) as a function of pulse duration. Period T is defined with respect to the 1600-nm laser.

To understand above results, we examine the electron currents versus time, and individual THz spectra in x and y directions with frequency in Figure 2. For the first-color lasers, as shown in Figures 2A,C, the residual current in the x direction is approximately zero while it decreases with the increase of the laser duration in the y direction. This is the consequence of laser symmetry dependence on the width of laser pulse. By introducing a linearly polarized laser in Figure 2E, the residual current in the y direction can be enhanced in comparison with that in Figure 2C. This explains the enhancement of THz yields in Figure 1B by using incommensurate two-color laser pulses. From Figures 2B, D, F, low-frequency THz emissions in the x direction are always weak regardless of pulse duration or two-color combination. In the y direction, they can be modified by changing the laser duration or by changing the form of laser pulses. Besides, the phase difference between THz emissions in the x and y directions is nearly 0.5π in the low-frequency regions (for example, in the 0.1–5 THz region). Thus the THz ellipticity in the interested frequency regions are mostly determined by the THz intensities in the x and y directions. Furthermore, in Figures 2B,D, the cross of THz intensities in the two directions occurs at about 30 THz for 8-T laser while it takes place at 50 THz for 5-T laser. This explains why the frequency region for controlling THz ellipticity in Figure 1A becomes narrower by using a longer pulse duration of first-color field. In Figure 2F, the cross of THz intensities appears in the extremely low-frequency region (approximately 3 THz) with incommensurate two-color laser pulses, leading to the controllable THz ellipticity below 10 THz in Figure 1A.

FIGURE 2

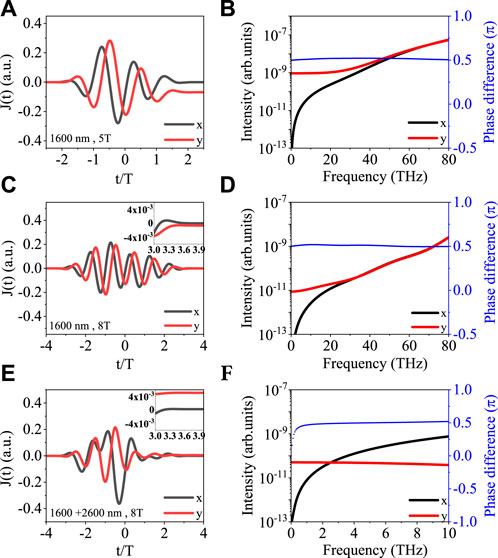
FIGURE 2. Comparison of electron currents (left) and THz intensities (right) in the x and y directions by circularly polarized lasers with full durations of 5 [(A) and (B)] and 8 optical cycles [(C) and (D)] and by an incommensurate two-color laser [(E) and (F)]. In (B), (D) and (F), phase differences between THz emissions in two directions are also shown.

Conversion efficiency is an important factor in the THz generation. Here we gives this value for one set of laser parameters, for example,. For the following laser parameters: I₂/I₁ = 0.25, ϕ_1,2 = 0, t_d = 0, laser duration is 8 T, and wavelength combination of 1,600 + 2,600 nm, according to Eq. 11, we can calculate that the conversion efficiency of 0.1–10 THz emissions is 3.05 × 10⁻⁶, and it is close to 10^–4 for a broad frequency band of 0.1–100 THz.

3.3 Control of ellipticity of low-frequency THz generation by varying two-color parameters

Next, we check how the ellipticity and the polarization direction of THz emissions are modified by varying two-color parameters. We first vary the wavelength of second color λ₂ from 1,200 to 2,600 nm, and the following parameters are fixed: I₂/I₁ = 0.25, ϕ_1,2 = 0, λ₁ = 1,600 nm, and full pulse duration is 8 optical cycles of 1600-nm laser for both colors. The resulted THz ellipticity as a function of THz frequency are plotted in Figure 3A. When the wavelength of second color is 2,200 nm, the maximum THz ellipticity is about 0.75, located at about 6 THz. By further increasing the wavelength, the maximum ellipticity is increased up to 1, and its location goes to a lower frequency. Thus the THz ellipticity in the low-frequency regions (near 5 THz or below) can be tuned by varying the wavelength of linearly polarized second-color laser. We plot the waveforms of electric fields obtained by synthesizing THz emissions centered at 2 THz in Figure 3B. It shows that the THz intensity is increased with the decrease of the wavelength of second color. And the major THz polarization direction is slightly adjusted by the second-color wavelength. We take two examples of 1,600 + 2,600 nm and 1,600 + 2,200 nm to understand the underlying physical mechanism. In Figures 3C,D, the phase differences between THz emissions in the x and y directions are shown. For the case of 1,600 + 2,600 nm, the phase difference is nearly 0.5π while it is about 0.6π for 1,600 + 2,200 nm case by neglecting the results below 1 THz. In these figures, THz intensities in two directions are also plotted. One can see that the interaction of THz intensities in the x and y directions takes place at 2.5 THz for 1,600 + 2,600 nm case, and it is located at 6.5 THz for 1,600 + 2,200 nm case. The ellipticity is determined by both the phase difference and intensities of THz emissions in the x and y directions in Eq. 10 Since the phase difference for 1,600 + 2,600 nm case is closer to 0.5π, the corresponding maximum ellipticity of the former is larger than that for the latter in Figure 3A. Thus, the wavelength of the linearly polarized laser is a key parameter to control the ellipticity of low-frequency THz emissions.

FIGURE 3

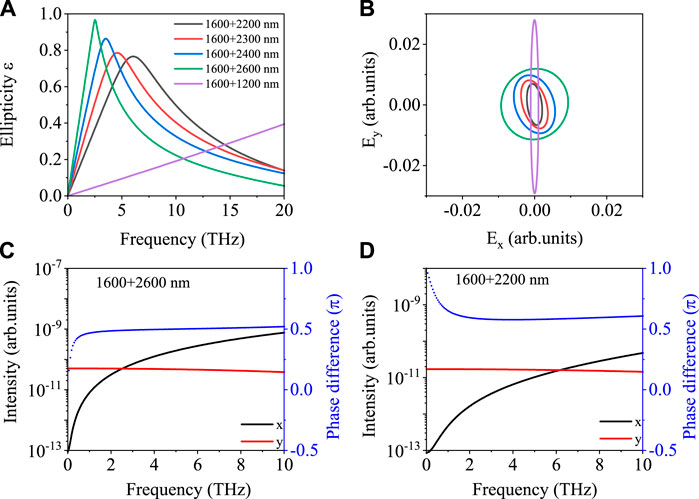
FIGURE 3. (A) The ellipticity dependence of THz radiations below 20 THz on the frequency under different two-color combinations. (B) Corresponding electric waveforms by synthesizing THz field centered at 2 THz (the spectral band is about 1 THz). Intensities of THz emissions in the x and y directions and phase difference of them are shown for 1,600 + 2,600 nm (C) and 1,600 + 2,200 nm (D).

We then change the intensity ratio of two colors, which is defined as α = I₂/I₁. The wavelength of second color is fixed as λ₂ = 2,600 nm, and other parameters remain the same. In Figure 4A, the THz ellipticity in low-frequency regions can be slightly tuned by the α. When α changes from 0.75 to 0.25, the peak position of THz ellipticity is varied in the frequency region of 2–2.5 THz. Its position is almost not changed by further decreasing the value of the α. In Figure 4B, we compare waveforms of electric fields at 2 THz with different α. It shows that larger α results in stronger THz emission. By tuning the α, the polarization direction is not changed much since the ellipticity is relatively large at 2 THz. For example, it is about 0.95 (or 0.82) for α = 0.5 (or 0.25). We employ the same analysis method as in Figure 3 to understand these results. In Figures 4C,D, the phase difference between THz emissions in the x and y directions does not change much for different α. It is about 0.5π for α = 0.25, and this value is about 0.53π when α = 0.5. In these figures, the crossing point of THz emissions in two directions does not change much by varying the α as well. It locates at about 2.5 THz (or 2 THz) for α = 0.25 (or 0.5). Therefore, the THz ellipticity can only be slightly tuned by varying the α in Figure 4A.

FIGURE 4

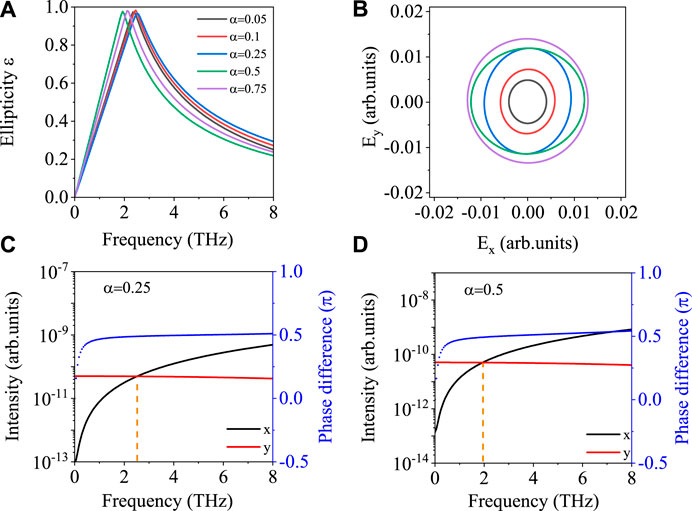
FIGURE 4. Similar figure to Figure 3 except that the intensity ratio α of two colors is varied. (A) The ellipticity of THz radiations below 8 THz as a function of the frequency under different α. (B) Corresponding electric waveforms by synthesizing the THz field centered at 2 THz (the spectral band is about 1 THz). Intensities of THz emissions in the x and y directions and phase difference of them are shown for α = 0.25 (C) and α = 0.5 (D).

From above results, we conclude that the THz ellipticity or intensity can be effectively tuned by varying the wavelength of second color or the intensity ratio of two colors. However, the polarization direction of THz wave can only be slightly modified. We set the phase difference of two colors as a variable to check whether the THz polarization can be significantly changed. The laser parameters are the same as those used in Figure 3 except that ϕ₂ is varied and λ₂ is chosen as 800 nm or 2,600 nm. In Figure 5A, we show the electric waveforms of 2-THz field driven by 1,600 + 800 nm laser pulses. One can clearly see that by changing the ϕ₂ (or the phase difference of two colors), the THz polarization direction can be greatly changed. We have checked that the intensity and the ellipticity of THz wave don’t change much by solely varying the ϕ₂. Meanwhile the THz ellipticity maintains a relatively small value. We select ϕ₂ = 0.42π and 0.63π for detailed analysis. In Figures 5B,C, we show the intensities of THz emissions in the x and y directions, and the phase differences between two directions. In comparison with Figures 3, 4, there are no crossing points between THz intensities in the x and y directions in the frequency regions below 10 THz. And the THz intensities in the x direction are effectively enhanced. The phase difference between two directions is not a constant any more. In Figures 5B,C, the phase difference is linearly varied with the frequency for a fixed ϕ₂. At 2 THz, it is about 0.04π for ϕ₂ = 0.42π while it is 0.98π for ϕ₂ = 0.63π. This illustrates that the phase difference can be dramatically tuned by varying the ϕ₂, which is the major factor to determine the THz polarization direction in Figure 5A. The similar results are shown in Figures 5D–F for 1,600 + 2,600 nm case. The THz polarization direction can be effectively tuned by varying the ϕ₂ as shown in Figure 5D. And the phase difference of THz emissions between two directions is significantly changed at different ϕ₂ as shown in Figures 5E,F. Although the wavelength of second color is different, the THz polarization direction still can be greatly modified and the underlying physical mechanism is not amended. Therefore, it is quite general to control the THz polarization direction through the phase difference between two colors.

FIGURE 5

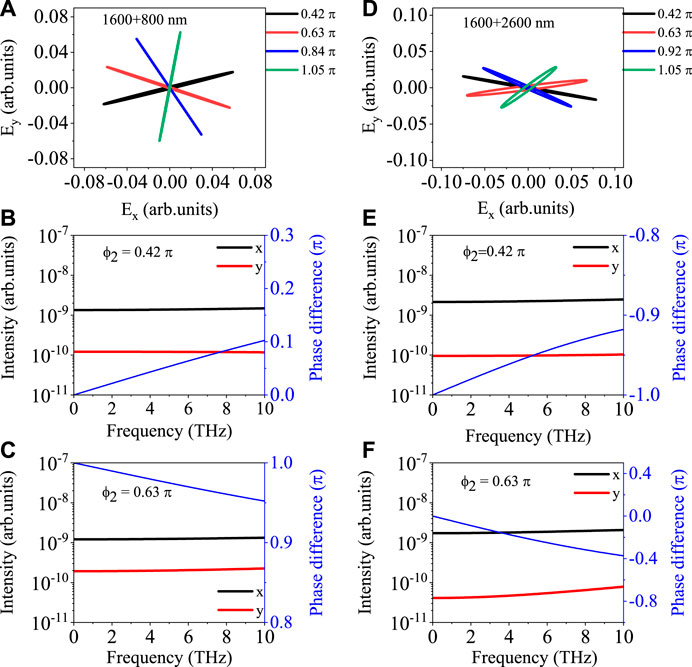
FIGURE 5. Electric waveforms of 2-THz field obtained at different ϕ₂ driven by 1,600 + 800 nm (A) or 1,600 + 2,600 nm laser (D). Intensities of THz emissions in the x and y directions and phase differences between them are shown: (B) ϕ₂ = 0.42π, 1,600 + 800 nm; (C) ϕ₂ = 0.63π, 1,600 + 800 nm; (E) ϕ₂ = 0.42π, 1,600 + 2,600 nm; and (F) ϕ₂ = 0.63π, 1,600 + 2,600 nm.

We also check the effect of relative time delay between two-color laser pulses, which is another important parameter to control the THz polarization. We choose the laser parameters are the same as those in Figure 3 except that t_d is varied in the unit of T, where T is an optical period of fundamental 1600-nm laser, and λ₂ is chosen as 2,600 nm. In Figure 6A, the THz ellipticity in low-frequency regions can be dramatically tuned by the t_d. When t_d is changed from −T to T, peak position of THz ellipticity is greatly shifted and even disappeared. In Figure 6B, we compare waveforms of electric fields at 2 THz with different t_d, which shows that intensity of THz wave and its ellipticity are significantly changed by t_d, for example, intensity of THz wave is stronger when t_d = −T or T, while ellipticity of THz wave is larger at t_d = 0. In Figures 6C,D, we take two examples of t_d = −0.5T and 0.5T for analyzing the generation mechanism. These figures show that THz emissions near 2 THz in two directions do not change much, while their phase differences are dramatically changed, indicating again that the phase difference is mainly responsible for the change of THz polarization direction in Figure 6B. Besides, in 2–5 THz frequency regions, the phase difference is closer to 0.5π for t_d = −0.5T, which explains the maximum ellipticity occurs near 4 THz for t_d = −0.5T in Figure 6A. Therefore, the time delay between two-color laser pulses can also significantly change ellipticity, intensity, and polarization direction of THz wave simultaneously.

FIGURE 6

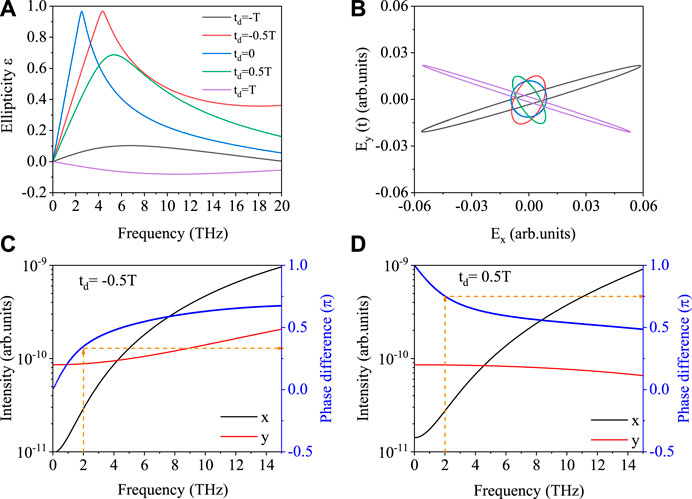
FIGURE 6. (A) Ellipticity dependence of THz radiations below 20 THz on the frequency under different time delays between two-colors. (B) Corresponding electric waveforms by synthesizing THz fields centered at 2 THz (the spectral band is about 1 THz). (C) Intensities of THz emissions in the x and y directions and phase difference of them are shown for (C) t_d = −0.5T and (D) t_d = 0.5T. T is the optical period of 1600-nm laser.

Finally, we remain t_d = 0 and investigate the control of the THz ellipticity and polarization direction by varying the intensity ratio and the phase difference of two colors simultaneously. We focus on 2 THz under the 1,600 + 2,600 nm laser and 3 THz with the 1,600 + 2,400 nm laser. In Figure 7A, we show the dependence of ellipticity of 2-THz field on the intensity ratio α and the CEP ϕ₂ of second color. When ϕ₂ is around 0 or 2π, the ellipticity is close to 1 no matter how the intensity ratio is changed. If ϕ₂ = 1.0π, the ellipticity is increased up to 1 with the increase of the α. For ϕ₂ = 0.5π or 1.5π, the dependence of the ellipticity on the α is similar to the case of ϕ₂ = 1.0π, however, the value of ellipticity is smaller. At other ϕ₂, the THz ellipticity always maintains a very small value. In Figure 7B, we show the similar results for the 3-THz field, which indicates the different dependence of the THz ellipticity on the α and the ϕ₂ from the 2-THz field. We can also see two common things. First, the THz ellipticity has larger value at some selected ϕ₂ only. Second, at some fixed ϕ₂, the strong dependence of THz ellipticity on the α can be seen. We then check the THz polarization direction. In Figure 7C, the electric waveforms of 2-THz field with the same ellipticity of 0.25 are plotted. They are taken from Figure 7A under different combinations of the intensity ratio and the phase difference of two colors, labeled as E_i (i = 1, 2, 3, 4). It clearly demonstrates that the THz polarization direction can be greatly adjusted even though the THz ellipticity and intensity are kept the same. In Figure 7D, the 3-THz fields with the ellipticity of 0.55 are chosen, marked as S_i (i = 1, 2, 3, 4) in Figure 6B, and corresponding electric waveforms show the significant change of THz polarization direction as well.

FIGURE 7

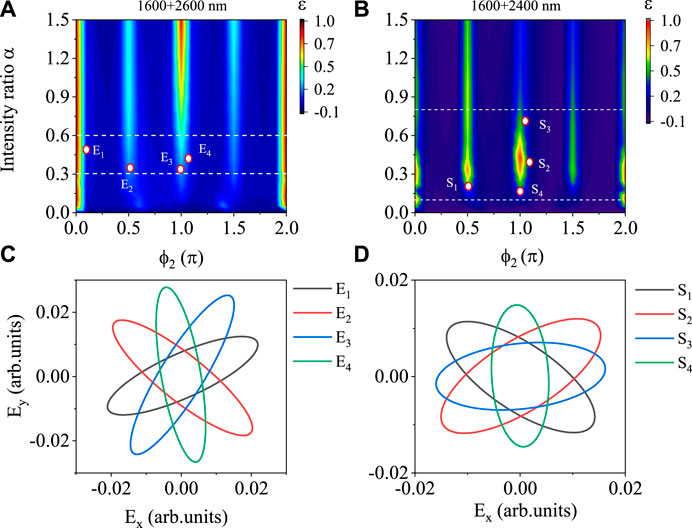
FIGURE 7. (A) The ellipticity of 2-THz field as a function of α and ϕ₂ by 1,600 + 2,600 nm laser. (B) Similar results for 3-THz field by 1,600 + 2,400 nm laser. Electric waveforms for selected points E_i (i = 1, 2, 3, 4) in (A) with the same ellipticity of 0.25 (C) and for selected points S_i (i = 1, 2, 3, 4) in (B) with the same ellipticity of 0.55 (D).

4 Conclusion

In summary, we demonstrated that by using a centrosymmetric solid material it is able to control the ellipticity and the polarization direction of THz emissions in the low-frequency region from single-layer graphene. To efficiently achieve this goal, we employed a scheme of incommensurate two-color laser pulses, which is composed of a circularly polarized first-color laser and a linearly polarized second-color laser. We showed that the two-color laser can enhance the THz intensity and enables to control the THz ellipticity in a much lower frequency region in comparison with the single-color circularly polarized laser. We found that the dramatic change of THz ellipticity can be achieved by varying the wavelength of second color and it can be fine tuned by varying the intensity ratio of two colors. We also showed that the polarization direction of THz emissions can be greatly changed by changing the phase difference between two colors when the THz ellipticity maintains a small value. By varying the phase difference along with the intensity ratio of two colors, untrivial change of THz polarization direction can be realized at higher THz ellipticity. We checked that the relative time delay between two-color laser pulses can change the polarization direction, intensity, and ellipticity of THz emissions at the same time. Meanwhile, we performed the detailed analysis of electron currents and THz emissions in two orthogonal directions. Two-color laser can enhance the residual current in the y direction, the THz ellipticity is mostly determined by the THz intensities in the x and y directions, and the THz polarization direction is closely related to the phase difference between THz emissions in two directions. Note that our proposed scheme can be realized experimentally by combining several techniques available in the labs, such as the generation and measurement of THz emissions from single-layer graphene driven by single-color laser [35, 38, 47], the generation of high-power few-cycle mid-infrared laser pulses [48–50], and the synthesis of two-color laser pulses [51]. And it also increases the operation complication and the cost in the experiment. Our work provides with a new way to use the centrosymmetric solid material to efficiently control the polarization of THz radiations. Compared to the laser-induced gas medium [39], our method can be applied to control the THz polarization in a much lower frequency region.

Data availability statement

The raw data supporting the conclusion of this article will be made available by the authors, without undue reservation.

Author contributions

All authors listed have made a substantial, direct, and intellectual contribution to the work and approved it for publication.

Funding

This work was supported by National Natural Science Foundation of China (Grant Nos 12274230, 12204238, 11964033, and 11834004), Funding of Nanjing University of Science and Technology (Grant No. TSXK2022D005), and Natural Science Foundation of Jiangsu Province (Grant No. BK20220925).

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

1. Cook DJ, Hochstrasser RM. Intense terahertz pulses by four-wave rectification in air. Opt Lett (2000) 25:1210–2. doi:10.1364/OL.25.001210

PubMed Abstract | CrossRef Full Text | Google Scholar

2. Yiwen E, Zhang LL, Tcypkin A, Kozlov S, Zhang CY, Zhang X. Broadband thz sources from gases to liquids. Ultrafast Sci (2021) 2021:9892763. doi:10.34133/2021/9892763

CrossRef Full Text | Google Scholar

3. Kreβ M, Löffler T, Eden S, Thomson M, Roskos HG. Terahertz-pulse generation by photoionization of air with laser pulses composed of both fundamental and second-harmonic waves. Opt Lett (2004) 29:1120–2. doi:10.1364/OL.29.001120

PubMed Abstract | CrossRef Full Text | Google Scholar

4. Kreβ M, Löffler T, Thomson MD, Dörner R, Gimpel H, Zrost K, et al. Determination of the carrier-envelope phase of few-cycle laser pulses with terahertz-emission spectroscopy. Nat Phys (2006) 2:327–31. doi:10.1038/nphys286

CrossRef Full Text | Google Scholar

5. Kim KY, Glownia JH, Taylor AJ, Rodrguez G. Terahertz emission from ultrafast ionizing air in symmetry-broken laser fields. Opt Express (2007) 15:4577–84. doi:10.1364/OE.15.004577

PubMed Abstract | CrossRef Full Text | Google Scholar

6. Xie X, Dai JM, Zhang XC. Coherent control of thz wave generation in ambient air. Phys Rev Lett (2006) 96:075005. doi:10.1103/PhysRevLett.96.075005

PubMed Abstract | CrossRef Full Text | Google Scholar

7. Kim KY, Taylor AJ, Glownia JH, Rodrguez G. Coherent control of terahertz supercontinuum generation in ultrafast laser–gas interactions. Nat Photon (2008) 2:605–9. doi:10.1038/nphoton.2008.153

CrossRef Full Text | Google Scholar

8. Wen H, Wiczer M, Lindenberg AM. Ultrafast electron cascades in semiconductors driven by intense femtosecond terahertz pulses. Phys Rev B (2008) 78:125203. doi:10.1103/PhysRevB.78.125203

CrossRef Full Text | Google Scholar

9. Gaal P, Reimann K, Woerner M, Elsaesser T, Hey R, Ploog KH. Nonlinear terahertz response of n-type gaas. Phys Rev Lett (2006) 96:187402. doi:10.1103/PhysRevLett.96.187402

PubMed Abstract | CrossRef Full Text | Google Scholar

10. Zhou ZY, Zhang DW, Zhao ZX, Yuan JM. Terahertz emission of atoms driven by ultrashort laser pulses. Phys Rev A (2009) 79:063413. doi:10.1103/PhysRevA.79.063413

CrossRef Full Text | Google Scholar

11. Thomson MD, Blank V, Roskos HG. Terahertz white-light pulses from an air plasma photo-induced by incommensurate two-color optical fields. Opt Express (2010) 18:23173–82. doi:10.1364/OE.18.023173

PubMed Abstract | CrossRef Full Text | Google Scholar

12. Zhang L, Wang GL, Zhou XX. Optimized two- and three-colour laser pulses for the intense terahertz wave generation. J Mod Opt (2006) 63:2159–65. doi:10.1080/09500340.2016.1185544

CrossRef Full Text | Google Scholar

13. Kim KY. Generation of coherent terahertz radiation in ultrafast laser-gas interactions. Phys Plasmas (2009) 16:056706. doi:10.1063/1.3134422

CrossRef Full Text | Google Scholar

14. Hauri C, Ruchert C, Vicario C, Ardana F. Strong-field single-cycle thz pulses generated in an organic crystal. Appl Phys Lett (2011) 99:161116. doi:10.1063/1.3655331

CrossRef Full Text | Google Scholar

15. Wang T, Klarskov P, Jepsen PU. Ultrabroadband thz time-domain spectroscopy of a free-flowing water film. IEEE Trans Terahertz Sci Tech (2014) 4:425–31. doi:10.1109/tthz.2014.2322757

CrossRef Full Text | Google Scholar

16. Ponomareva EA, Stumpf SA, Tcypkin AN, Kozlov SA. Impact of laser-ionized liquid nonlinear characteristics on the efficiency of terahertz wave generation. Opt Lett (2019) 44:5485–8. doi:10.1364/ol.44.005485

PubMed Abstract | CrossRef Full Text | Google Scholar

17. Wirth A, Hassan M, Grguraš I, Gagnon J, Moulet A, Luu TT, et al. Synthesized light transients. Science (2011) 334:195–200. doi:10.1126/science.1210268

PubMed Abstract | CrossRef Full Text | Google Scholar

18. Huang SW, Cirmi G, Moses J, Hong K, Bhardwaj S, Birge J, et al. High-energy pulse synthesis with sub-cycle waveform control for strong-field physics. Nat Photon (2011) 5:475–9. doi:10.1038/nphoton.2011.140

CrossRef Full Text | Google Scholar

19. Rossi GM, Mainz R, Yang YD, Scheiba F, Silva MA, Chia SH, et al. Sub-cycle millijoule-level parametric waveform synthesizer for attosecond science. Nat Photon (2020) 14:629–35. doi:10.1038/s41566-020-0659-0

CrossRef Full Text | Google Scholar

20. Zhang L, Wang GL, Zhou XX. Controlling of strong tunable thz emission with optimal incommensurate multi-color laser field. Phys Plasmas (2017) 24:023116. doi:10.1063/1.4976549

CrossRef Full Text | Google Scholar

21. Castro-Camus E, Fu L, Lloyd-Hughes J, Han HH, Jagadish C, Johnston MB. Photoconductive response correction for detectors of terahertz radiation. Appl Phys Lett (2008) 104:053113. doi:10.1063/1.2969035

CrossRef Full Text | Google Scholar

22. Chan WL, Deibel J, Mittleman DM. Imaging with terahertz radiation. Rep Prog Phys (2007) 70:1325–79. doi:10.1088/0034-4885/70/8/R02

CrossRef Full Text | Google Scholar

23. Kanda N, Konishi K, Kuwata-Gonokami M. Terahertz wave polarization rotation with double layered metal grating of complimentary chiral patterns. Opt Express (2007) 15:11117–25. doi:10.1364/OE.15.011117

PubMed Abstract | CrossRef Full Text | Google Scholar

24. Wu HC, MeyerterVehn J, Sheng ZM. Phase-sensitive terahertz emission from gas targets irradiated by few-cycle laser pulses. New J Phys (2008) 10:043001. doi:10.1088/1367-2630/10/4/043001

CrossRef Full Text | Google Scholar

25. Song LW, Bai Y, Xu RJ, Li C, Liu P, Li RX, et al. Polarization control of terahertz waves generated by circularly polarized few-cycle laser pulses. Appl Phys Lett (2013) 103:261102. doi:10.1063/1.4856495

CrossRef Full Text | Google Scholar

26. Dai JM, Karpowicz N, Zhang XC. Coherent polarization control of terahertz waves generated from two-color laser-induced gas plasma. Phys Rev Lett (2009) 103:023001. doi:10.1103/PhysRevLett.103.023001

PubMed Abstract | CrossRef Full Text | Google Scholar

27. Stremoukhov S, Andreev A. Quantum-mechanical fingerprints in generation of elliptical terahertz radiation by extended media interacting with two-color laser field. J Opt Soc Am B (2017) 34:232–7. doi:10.1364/JOSAB.34.000232

CrossRef Full Text | Google Scholar

28. You JW, Panoiu NC. Polarization control using passive and active crossed graphene gratings. Opt Express (2018) 26:1882–94. doi:10.1364/OE.26.001882

PubMed Abstract | CrossRef Full Text | Google Scholar

29. Ji YY, Fan F, Wang XH, Chang SJ. Broadband controllable terahertz quarter-wave plate based on graphene gratings with liquid crystals. Opt Express (2018) 26:12852–62. doi:10.1364/OE.26.012852

PubMed Abstract | CrossRef Full Text | Google Scholar

30. Liu X, Chen X, Parrott EPJ, Han C, Humbert G, Crunteanu A, et al. Invited article: An active terahertz polarization converter employing vanadium dioxide and a metal wire grating in total internal reflection geometry. APL Photon (2018) 3:051604. doi:10.1063/1.5010940

CrossRef Full Text | Google Scholar

31. Wang J, Huang YY, Lei Z, Xi YY, Du WY, Cao XQ, et al. Tunable polarized terahertz wave generation induced by spontaneous polarization-dependent ultrafast shift current from vertically grown ferroelectric sns. Phys Rev B (2022) 106:235308. doi:10.1103/PhysRevB.106.235308

CrossRef Full Text | Google Scholar

32. Xi YY, Zhou YX, Lei Z, Cao XQ, Wang J, Ge YQ, et al. Thickness-dependent terahertz emission from Bi₂S₃ films under excitation below and above the band gap. Phys Rev B (2023) 107:035307. doi:10.1103/PhysRevB.107.035307

CrossRef Full Text | Google Scholar

33. Sensale-Rodriguez B, Yan R, Kelly MM, Fang T, K Tahy Wsh , Jena D, et al. Broadband graphene terahertz modulators enabled by intraband transitions. Nat Commun (2012) 3:780. doi:10.1038/ncomms1787

PubMed Abstract | CrossRef Full Text | Google Scholar

34. Naib IA, Poschmann M, Dignam MM. Optimizing third-harmonic generation at terahertz frequencies in graphene. Phys Rev B (2015) 91:205407. doi:10.1103/PhysRevB.91.205407

CrossRef Full Text | Google Scholar

35. Maysonnave J, Huppert S, Wang F, Maero S, Berger C, de Heer W, et al. Terahertz generation by dynamical photon drag effect in graphene excited by femtosecond optical pulses. Nano Lett (2014) 14:5797–802. doi:10.1021/nl502684j

PubMed Abstract | CrossRef Full Text | Google Scholar

36. Zhu LP, Yao ZH, Huang YY, He C, Quan BG, Li JJ, et al. Circular-photon-drag-effect-induced elliptically polarized terahertz emission from vertically grown graphene. Phys Rev Appl (2019) 12:044063. doi:10.1103/PhysRevApplied.12.044063

CrossRef Full Text | Google Scholar

37. Navaeipour P, Dignam M. Effects of microscopic scattering on terahertz third harmonic generation in monolayer graphene. Phys Rev B (2022) 105:115431. doi:10.1103/PhysRevB.105.115431

CrossRef Full Text | Google Scholar

38. Hafez H, Kovalev S, Deinert J, Mics Z, Green B, Awari N, et al. Extremely efficient terahertz high-harmonic generation in graphene by hot Dirac fermions. Nature (2018) 561:507–11. doi:10.1038/s41586-018-0508-1

PubMed Abstract | CrossRef Full Text | Google Scholar

39. Li YN, Wang GL, Zhang L, Jiao ZH, Zhao SF, Zhou XX. Generating the polarization-controllable thz radiations by incommensurate two-color femtosecond laser fields. Phys Plasmas (2019) 26:073109. doi:10.1063/1.5093145

CrossRef Full Text | Google Scholar

40. Higuchi T, Heide C, Ullmann K, Weber HB, Hommelhoff P. Light-field-driven currents in graphene. Nature (2017) 550:224–8. doi:10.1038/nature23900

PubMed Abstract | CrossRef Full Text | Google Scholar

41. Guan Z, Wang GL, Zhang L, Jiao ZH, Zhao SF, Zhou XX. Broadband terahertz wave generation from monolayer graphene driven by few-cycle laser pulse. Chin Phys Lett (2021) 38:054201. doi:10.1088/0256-307X/38/5/054201

CrossRef Full Text | Google Scholar

42. Guan Z, Liu L, Wang L, Zhao SF, Jiao ZH, Zhou XX. An improved method for the investigation of high-order harmonic generation from graphene. Chin Phys B (2020) 29:104206. doi:10.1088/1674-1056/abab76

CrossRef Full Text | Google Scholar

43. Guan Z, Wang BC, Wang GL, Zhou XX, Jin C. Analysis of low-frequency thz emission from monolayer graphene irradiated by a long two-color laser pulse. Opt Express (2022) 30:26912–30. doi:10.1364/OE.463568

PubMed Abstract | CrossRef Full Text | Google Scholar

44. Tamaya T, Ishikawa A, Ogawa T, Tanaka K. Diabatic mechanisms of higher-order harmonic generation in solid-state materials under high-intensity electric fields. Phys Rev Lett (2016) 116:016601. doi:10.1103/PhysRevLett.116.016601

PubMed Abstract | CrossRef Full Text | Google Scholar

45. Dong FL, Xia QZ, Liu J. Ellipticity of the harmonic emission from graphene irradiated by a linearly polarized laser. Phys Rev A (2021) 104:033119. doi:10.1103/PhysRevA.104.033119

CrossRef Full Text | Google Scholar

46. Zurrón Ó, Picón A, Plaja L. Theory of high-order harmonic generation for gapless graphene. New J Phys (2018) 20:053033. doi:10.1088/1367-2630/aabec7

CrossRef Full Text | Google Scholar

47. Bahk YM, Ramakrishnan G, Choi J, Song H, Choi G, Kim YH, et al. Plasmon enhanced terahertz emission from single layer graphene. ACS Nano (2014) 8:9089–96. doi:10.1021/nn5025237

PubMed Abstract | CrossRef Full Text | Google Scholar

48. Thiré N, Maksimenka R, Kiss B, Ferchaud C, Gitzinger G, Pinoteau T, et al. Highly stable, 15 w, few-cycle, 65 mrad cep-noise mid-ir opcpa for statistical physics. Opt Express (2018) 26:26907–15. doi:10.1364/OE.26.026907

PubMed Abstract | CrossRef Full Text | Google Scholar

49. Alismail A, Wang H, Barbiero G, Altwaijry N, Hussain SA, Pervak V, et al. Multi-octave, cep-stable source for high-energy field synthesis. Sci Adv (2020) 6:eaax3408. doi:10.1126/sciadv.aax3408

PubMed Abstract | CrossRef Full Text | Google Scholar

50. Steinleitner P, Nagl N, Kowalczyk M, Zhang JW, Pervak V, Hofer C, et al. Single-cycle infrared waveform control. Nat Photon (2022) 16:512–8. doi:10.1038/s41566-022-01001-2

CrossRef Full Text | Google Scholar

51. Cirmi G, Mainz RE, Silva-Toledo MA, Scheiba F, Cankaya H, Kubullek M, et al. Optical waveform synthesis and its applications. Laser Photon Rev (2023) 17:2200588. doi:10.1002/lpor.202200588

CrossRef Full Text | Google Scholar