- 1Department of Energy, Politecnico di Milano, Milano, Italy
- 2Center for Proton Therapy, Paul Scherrer Institute, Villigen, Switzerland
- 3Department of Physics, ETH-Hönggerberg, Zurich, Switzerland
- 4Accelerator Technology and Applied Physics Division, Lawrence Berkeley National Laboratory, Livermore, CA, United States
Radionuclides are of paramount importance in nuclear medicine both for clinical uses and radiopharmaceutical production. Among the others, nuclides suitable for theranostics like Copper-64 are particularly attractive since they can play both a diagnostic and therapeutic role. In the last years, the growing demand for these nuclides stimulated the research of new solutions, along with cyclotrons already in use, for their production. In this respect, a promising alternative is laser-driven proton accelerators based on the interaction of superintense laser pulses with target materials. Because of their potential compactness and flexibility, they are under investigation for several applications ranging from materials science to nuclear medicine. Moreover, the use of advanced Double-Layer targets (DLTs) was identified as a viable route to increase the number and energy of the accelerated protons to satisfy the requirements of demanding applications. In this contribution, we numerically investigate the use of DLT-based laser-driven sources for Copper-64 production. We show that activities relevant to pre-clinical studies can be achieved with an existing 150 TW laser and DLTs. Moreover, we extend the discussion by considering a broad range of laser systems by exploiting a theoretical model. Our results can guide the choice of laser and target parameters for future experimental investigations.
1 Introduction
Radioisotopes play a crucial role in nuclear medicine for both diagnostic and therapeutic purposes. In 2023, over 40 million nuclear medicine procedures are performed each year, and demand for radioisotopes is increasing at up to 5% annually [1]. In this framework, access to radioisotopes suitable for advanced applications, such as radiotheranostics, is crucial. Radiotheranostics is a novel approach that combines diagnostic and therapeutic applications using the same radionuclide. Firstly, a patient is diagnosed using a radiopharmaceutical that targets a specific tissue, allowing to determine the extent and severity of the disease, as well as to identify which treatment the patient is likely to respond. Then, once the diagnosis is made, a therapeutic dose of the same or similar radioisotope can be administered to the patient, selectively killing the target cells with reduced radiation damage to the healthy tissue. The diagnostic action typically relies on gamma or positron emission, while the therapeutic effect exploits α or β decay. Among the possible candidate nuclides for radiotheranostics, Copper-64 (64Cu) is considered especially promising thanks to the branching ratio of its decay channels (17.9% probability of β+ decay to 64Ni, 39.0% probability of β− decay to 64Zn), its relatively long half-life of 12.7 h, and the favourable chemistry of copper, which allows for easy labelling with a wide range of biological molecules, such as peptides, antibodies, and proteins [1].
Currently, radioisotepes for nuclear medicine are typically produced using nuclear reactors and conventional accelerators, mostly cyclotrons. Commercial cyclotrons used for radioisotope production are optimized to work with a specific kind of particle (usually protons) and a fixed operating energy (which lies in the range 3–30 MeV) with a typical beam current in the range of 10 μA up to 1 mA, depending on the size of the cyclotron itself [2]. While these accelerators are tailored for their specific purpose and can deliver very high radioisotope activity, their flexibility in terms of the energy and nature of the accelerated particles is narrow. Moreover, their limited availability hinders the widespread accessibility to radioisotopes of interest for emerging applications in radiobiology, medical and clinical research, such as 64Cu radiotheranostics.
Laser-driven ion acceleration is attracting growing interest as a promising solution to circumvent some limitations of conventional accelerators, such as non-tunable energy, high costs, non-portable size, and radioprotection issues. The working principle of laser-driven acceleration is based on the interaction of an ultra-intense ultra-short laser pulse (I
One of the most reliable, robust, and well-understood laser-driven ion acceleration schemes is Target Normal Sheath Acceleration (TNSA). In TNSA, a laser pulse is focused on a micrometric solid target, causing a portion of its energy to be absorbed by the target electron population, which is heated to relativistic energies and expands towards the back of the target, generating a very intense (up to few MV/μm) longitudinal sheath electric field. This sheath field is ultimately responsible for the acceleration of light ions, mostly protons, located on the rear surface of the target. As a result, bunches of light ions (108 up to 1012 protons per shot) with an exponential-like energy distribution and a well-defined cut-off energy (ranging from a few MeV up to several tens of MeV) are emitted towards the direction perpendicular to the target surface.
Thanks to their features, laser-driven ion sources are already of potential practical interest for some applications in the field of ion beam analysis for material characterization [4–7], for which requirements in terms of particle energy and current are not particularly strict. On the other hand, to make laser-driven acceleration attractive for the most challenging applications, including radioisotope production, an enhanced acceleration performance in terms of energy and current of the ion beam is required [8–11].
To address this challenge, different strategies have been considered so far. The first path relies on the continuing advancement in laser technology, especially for what concerns multi-petawatt laser systems with high pulse energy, ranging from tens to hundreds of joule. This approach, however, depends on the availability of a small number of top-class laser facilities, posing an inherent limitation to the widespread diffusion of laser-driven ion sources. The second approach focuses on table-top lasers with peak power of tens to hundreds of terawatts (with laser pulse energies ranging from tens of millijoule to a few joule) and high repetition rates (ranging from Hz to kHz) to provide a practical, compact, and cost-effective alternative to conventional accelerators. In order to meet the requirements about ions energy and number set by the applications even with limited laser pulse energy, the laser-plasma coupling should be enhanced by tailoring the properties of the target. Among the various possibilities, Double-Layer Targets (DLTs) have emerged as one of the most reliable approaches to enhance TNSA performance. DLTs are made of a micrometric solid foil covered with a low-density layer (e.g., near-critical carbon nanofoams [12, 13]), whose electron density is close to the critical density for optical wavelengths. The enhanced laser pulse coupling with the near-critical layer leads to a high conversion efficiency of laser-to-energy into the hot electrons responsible for the TNSA process [14]. In previous works we have experimentally demonstrated the DLT capability of enhancing the acceleration process both in terms of ion current and energy [15–17], and we have proposed the utilization of DLTs as the key factor to fully develop the potential of laser-driven sources for many applications, including Particle Induced X-ray Analysis [5, 18], Photon Activation Analysis [19], and Fast Neutron Resonance Reaction [20].
The production of radioisotopes is a challenging application requiring high proton currents and energies. The use of laser-driven sources for this scope demands considering these important aspects [8, 21]. In this respect, the availability of numerical and theoretical tools that estimate the yields and activities as a function of the laser and target parameters is crucial. They can allow guiding the choice of the parameters, planning future activities and experiments, as well as identifying critical experimental issues to be addressed. For instance, the development of proper target delivery systems that are able to position targets at high repetition rates and compatible with DLTs could be fundamental.
In this work we present numerical and theoretical approaches to explore the potential of DLTs for the laser-driven production of radioisotopes. In particular, we focus on 64Cu, a radionuclide with promising applications in novel techniques like radiotheranostics, as mentioned above. Emphasis is put on the process of proton acceleration and proton-induced 64Cu generation, while issues concerning the radiopharmaceutical preparation and delivery are outside the scope of this work. We make use of 3D Particle-In-Cell (PIC) simulations to model the proton acceleration from a single-layer target and a DLT. We consider a realistic laser parameter and the simulation results are compared with experimental data. Then, we couple the output of the PIC simulations with Monte Carlo simulations to obtain the yield of 64Cu and the associated activity. Finally, we provide an estimate of the activity achievable with multi-joule lasers and DLTs by exploiting a theoretical model. Our results show that a 100 TW class laser equipped with DLTs can provide sufficient activity (i.e., 10 s MBq) for pre-clinical studies. Moreover, we suggest that PW-class lasers in combination with advanced targets could reach the performance conventional accelerators for the production of 64Cu activities relevant for clinical purposes (i.e., 100 s MBq).
2 Results and discussion
2.1 Particle-in-cell simulations and comparison with experimental data
As discussed in Section 1, we performed two 3D PIC simulations with the PICCANTE code [22] to obtain reliable proton energy spectra from both a single-layer target and a DLT. In these simulations, we consider realistic laser parameters achievable with a 150 TW class laser. They are the same exploited in a recently published experimental work by [17]. The p-polarized pulse has a Gaussian envelope, 800 nm wavelength λ, a time duration of 30 fs, 2.8 μm FWHM focal spot and normalized laser intensity a0 = 16. The simulation box is x = 90λ along the laser propagation direction and the lateral dimensions are 60λ in the y and z directions. The spacial resolution is equal to 20 points per λ and the simulation duration is 100λ/c = 267 fs. We impose periodic boundary conditions in all directions.
The front surface of the targets is placed at x = 40λ. The bare target has a thickness of 1.875λ = 1.5 μm and 40nc density (
For the simulation with the DLT, while keeping for the substrate the same parameters set for the single-layer target, we included a realistic three-dimensional nanostructured layer in front of the solid foil. It was obtained through the application of a Diffusion Limited Cluster-Cluster Aggregation (DLCCA) model [23]. The thickness of this layer is equal to 5λ = 4.0 μm and the resulting density is 3nc, partitioned in 2.85nc for a species with Z/A = 0.5 and 0.15nc for a species with Z/A = 1. To simulate the carbon foam, we set 40 macro-electrons, 4 macro-ions with Z/A = 0.5 and 2 macro-ions with Z/A = 1 per cell. A snapshot of the simulation showing the interaction of the laser with the nanostructured DLT is reported in Figure 1A.
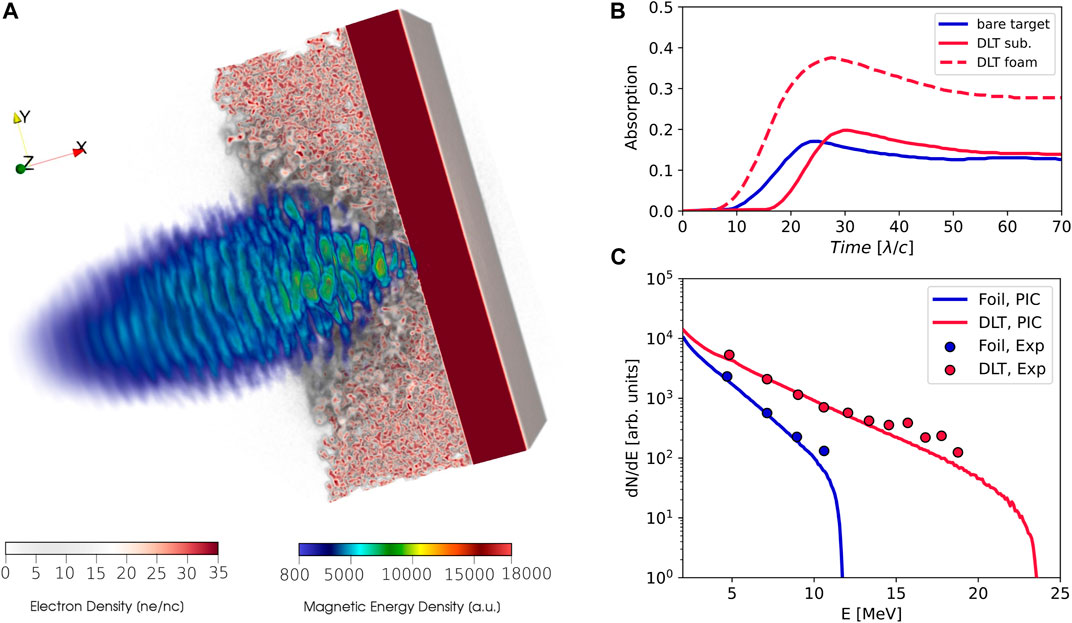
FIGURE 1. 3D PIC simulation results. (A) A snapshot of the laser interaction with the DLT. (B) Fraction of laser energy absorbed by the target normalized to 1 as a function of time. (C) Proton energy spectra obtained from the PIC (lines) and RCF experimental results (dots) from [17].
As shown in Figure 1B, with single-layer targets about 17% of the laser energy is absorbed by hot electrons at maximum (i.e., 25λ/c after the start of the simulation). Similarly, electrons from the DLT substrate absorb about 20% of the laser energy. On the other hand, the nanostructured layer absorbs 40% of the laser energy at 28λ/c. Overall, the presence of the low-density layer allows increasing by a factor of
The proton spectra are retrieved at 70λ/c, and they are reported in Figure 1C with continuous lines. According to the PIC simulations, we can achieve an energy enhancement of about 2 in the presence of the nanostructure, being 11.6 MeV and 23.5 MeV the maximum energies achieved with the single-layer target and DLT, respectively. Moreover, considering protons having energies exceeding 2 MeV, their number is increased by a factor of 2.2 exploiting the DLT.
The proton energy spectra from PIC simulations are compared in Figure 1C with those reported in [17] and obtained with RCF stacks. The PIC results predict exactly the temperatures of the proton spectra for both kinds of targets. The experimental maximum energy of the accelerated protons with the single-layer target is equal to 10.6 MeV, thus resulting in a relative error of
2.2 Monte Carlo simulations of 64Cu radioisotope production
In order to quantify the number of 64Cu isotopes that can be produced with monoenergetic and laser-driven proton sources, we performed Monte Carlo Geant4 [24] simulations. The goal is to compare the number of generated isotopes per unit incident protons (i.e., the yield) with laser-driven proton sources and conventional accelerators. For all irradiation conditions, we consider a pure Ni-64 sample of 5 cm thickness. We neglect the presence of other isotopes since enrichment levels higher than 95% can be achieved in samples for radioisotope production [25, 26]. It is placed 5 cm far from the source.
We performed two simulations with laser-driven protons providing the input proton spectra for single-layer target and DLT obtained from the PIC. Thus, the primary proton energies are sampled from the distributions reported in Figure 1C. The minimum energy is set to 2 MeV since, according to the 64Ni(p, n)64Cu reaction cross section reported in Figure 2A, no radioisotopes are produced below this threshold. Moreover, we carried out nine Monte Carlo simulations with monoenergetic protons having energies between 4 and 20 MeV. The energies provided by cyclotron machines for radioisotope productions usually lie in this range [1]. In the simulations involving laser-driven protons, we neglect the angular divergence of the beam since the irradiated material is large enough so that all particles reach the surface.
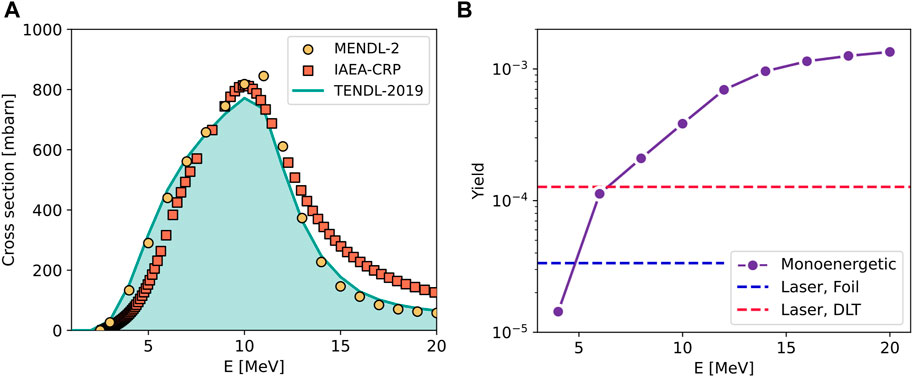
FIGURE 2. Monte Carlo simulation results. (A) 64Ni(p, n)64Cu reaction cross section according to different databases (B) Comparison between the 64Cu yields achieved with the single-layer target and DLT laser-driven sources and monoenergetic protons.
As far as the hadronic processes are concerned, we implemented the G4HadronElasticPhysicsHP and G4HadronPhysicsQGSP_BIC_AllHP physics lists to model elastic and inelastic interactions, respectively. In particular, the second one allowed us to exploit the TENDL-2019 cross section [27] for 64Cu radioisotope production (i.e., the continuous filled line in Figure 2A). For each simulation, a total number of 4 × 107 primary particles were simulated.
The number of produced 64Cu isotopes per unit incident proton is reported in Figure 2. As expected, the yield achieved with monoenergetic protons monotonically increases with the primary particle energy. Around 20 MeV, it reaches a plateau since the proton energy is beyond the region where the cross section lies. Considering the laser-driven source with the single-layer target, the yield is Y = 3.3 × 10−5, thus comparable with that achievable with 4.5 MeV monoenergetic protons. Exploiting the DLT, the yield increases up to Y = 1.3 × 10−4, which is equivalent to the case of a 6.4 MeV monoenergetic proton source.
2.3 Evaluation of the activity for pre-clinical studies
Exploiting the results obtained from Monte Carlo simulations, we can evaluate the activity achievable during irradiation with the laser-driven proton source. To this aim, we assume the same repetition rate of RR = 10 Hz that can be achieved with the laser system [28] considered for PIC simulations. For the single-layer target case, we assume Np = 2.6 × 1010 accelerated protons per shot with energies higher than 2 MeV. This value has been obtained from the experimental scaling reported in [20]. The scaling is valid for 10–100 fs laser pulses and simple foils as targets. Then, we apply the gain factor of 2.2 for the proton number achievable with DLT. Therefore, the number of incident protons per shot with the near-critical nanostructured target is assumed to be 5.74 × 1010.
In order to retrieve the activity A during irradiation, we apply the following simple equation:
where λ = ln(2)/T1/2 is the decay constant and T1/2 = 12.7 h is the half life of 64Cu. The results are reported in Figure 3.
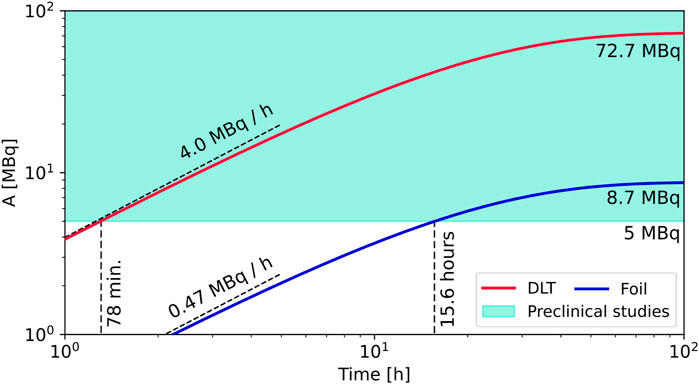
FIGURE 3. Activity as a function of the irradiation time obtained with the laser-driven source exploiting the DLT (red line) and single-layer target (blue line). The coloured green area represents the 5–100 MBq range of activity usually exploited for pre-clinical studies with mice.
First of all, we can notice that the activation rate and the saturation activity are one order of magnitude higher with the DLT compared to the single layer target, achieving approximately 4 MBq/h against 0.5 MBq/h and 73 MBq against 9 MBq, respectively. Overall, the highest activity we can achieve with the considered laser parameters would not allow performing clinical studies on human patients. Indeed, the values usually needed for treatments are of the order of 100 s MBq or higher [1, 29, 30]. They are achieved by exploiting cyclotrons providing 5–20 MeV monoenergetic protons and currents of the order of 10 s of μA. To achieve comparable performances, a more intense laser source and DLTs should be considered, as will be discussed in the next Section.
On the other hand, the activity values usually considered for pre-clinical studies exploiting mouse models lie in the range 5–100 MBq [31–36]. In particular, the indicative threshold of 5 MBq is achieved after 15.6 h of irradiation by exploiting single-layer targets. Vice versa, the same activity can be obtained in 78 min of elapsed time by adopting DLTs. These results show how near-critical nanostructured targets could play a fundamental role to achieve the activities required for pre-clinical studies by increasing the performances of the laser-driven proton source. In principle, a 150 TW class laser equipped with DLTs could provide sufficient 64Cu isotopes for studies with mouse models. Notably, laser systems with parameters coherent with those considered for this study have become commercially available in recent years [37, 38]. On the other hand, important effort must be put in the future to develop target delivery systems compatible with DLTs and high repetition rate operation. This point is currently subject of research [39].
2.4 Analytical estimation of the activity with an analytical model
In the previous Sections, we have studied in detail the process with a fixed set of laser and target parameters by making use of 3D PIC simulations coupled with a Monte Carlo code. This approach is aimed at modeling the laser-driven radioisotope generation with the highest accuracy and demonstrating its potential in the view of practical applications. On the other hand, it would also be very interesting to extend the analysis to different laser and target configurations. In this Section, we aim at finding a suitable estimation of the total yield YT as a function of laser intensity a0 for optimized DLT conditions.
The total 64Cu production yield YT in a semi-infinite, isotopically pure 64Zn converter can be expressed by:
where Nn is the total number of radioisotopes produced upon converter irradiation with Np protons, NAv is the Avogadro’s number, M is the converter atomic mass, ρ is the converter density, f(EP) is the proton spectrum normalized to the total number of protons Np, Sp(E) is the proton linear stopping power of the converter material and σ(E) is the total cross section for the 64Zn(p, n)64Cu reaction, as a function of the proton energy E.
In order to develop an explicit analytical expression for YT we look for some suitable approximation of the integrals in Equation 2. Firstly, let’s define the differential yield g(E) and the monoenergetic yield h(Ep) as:
and
in which Nat = ρ NAv/M in the atomic density of the converter. We decided to approximate the g(E) with a Gaussian function Γ(E):
The values of the parameters Ymax (2.023 × 10−3), E0 (10.25 MeV) and w (4.38 MeV) are obtained with a least square fitting of Γ(E) over the reference g(E). To this purpose, g(E) (Equation 3) is calculated by assuming Nat ≈ 8.379 cm−3 as the atomic density of a pure 64Ni target, S(E) according to the Bethe’s formula for proton stopping power [40], and σ(E) from the TENDL nuclear data library [27].
According to the literature concerning TNSA [3], the normalized proton distribution is modeled as an exponential function characterized by a slope Tp and with a cut-off corresponding to the maximum proton energy ϵM:
The integral
Since Ymax, w and E0 are known, the last step is to express Tp as a function of laser and target parameters. By considering the PIC spectra shown in Figure 1C one can get Tp = 1.86 MeV for the bare foil target and Tp = 3.24 MeV for the DLT. These values are close to the electron temperature in both cases (1.84 MeV and 3.36 MeV respectively), and therefore we assume that Tp ≃ Te, where Te can be estimated through the theoretical model presented in [14]. Although this approximation may seem rather crude it yields reasonable results nonetheless, as detailed in the following.
The comparison between the approximated 64Cu yield achieved with bare targets and DLTs as a function of the normalized laser intensity is reported in Figure 4A. For a0 < 20, there is a remarkable difference between the yields obtained with the two kinds of targets. Indeed, the proton maximum energies are close to the energy range 5–15 MeV where the maximum of the cross section is located. Thus, a strong enhancement of the proton energies with DLTs results in a relevant increment of the yields in comparison with bare targets. On the other hand, the curves of the yields start having the same slope for a0 > 30, highlighting that the maximum proton energies have largely exceeded 15 MeV for both kinds of targets.
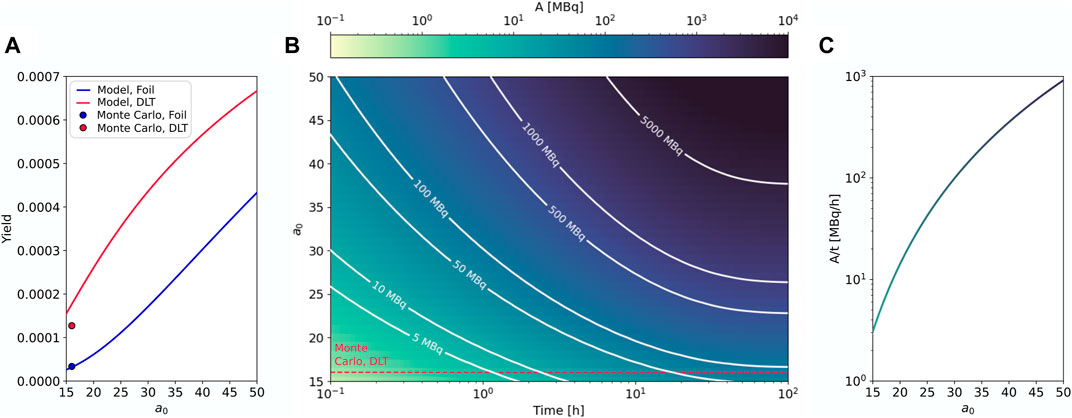
FIGURE 4. Results of the analytical model. (A) 64Cu Yield obtained from the model for the single-layer target (blue line) and DLT (red line) as a function of the normalized laser intensity. The dots correspond to the yields obtained from the MC in Section 2.2. (B) Activity as a function of the irradiation time and normalized laser intensity. White isolines correspond to fixed values of activity. (C) Activity per unit time as a function of the normalized laser intensity at the start of the irradiation.
We notice a fair agreement between the yields from the model and those obtained from the Monte Carlo. They are practically superimposed for the bare-target case. The yield resulting from the Monte Carlo considering the DLT slightly underestimates the analytical estimation. The discrepancy can be ascribed to the approximations introduced in the model to treat the physical processes, as well as to the different shapes of the proton spectrum (resulting from the PIC in the Monte Carlo and purely exponential in the model). In addition, there is a small difference between the target parameters exploited in the PIC simulations and those obtained from the optimization with the model.
By exploiting the analytical yields, we can apply Equation 1 to obtain the activity as a function of the elapsed (i.e., irradiation) time for all values of a0 (corresponding to laser energies in the range 0.7–17.5 J). The results are reported in Figure 4B. Here, we keep constant RR = 10 Hz for all values of normalized laser intensities. While this high repetition rate has not yet been achieved for the higher intensities considered here, we can reasonably assume that laser technology will provide such systems in the future. Indeed, state-of-the-art multi-100 s TW and PW class lasers can work at
The isolines in Figure 4B lie in correspondence with constant values of activity. By way of comparison, we identified the 150 TW (i.e., a0 ∼ 16), DLT case study presented in the previous Sections as a dotted red line. It intercepts the 5 MBq activity isoline at 72 min, which is quite in agreement with the 78 min reported in Section 2.3. We noticed that, considering intensity values between 20 and 50, activities compatible with pre-clinical studies could be achieved in minutes rather than hours. To obtain A ≫ 100 MBq relevant for clinical studies, elapsed times of the order of 1 h or more should be considered. The same result can be deduced also from the activity per unit of elapsed time at the start of the irradiation. By looking at the activity rate as a function of a0 (Figure 4C) one should conclude that a0 > 30 will be sufficient to exceed 100 MBb/h.
3 Conclusion
Laser-driven proton acceleration is promising for several applications, including the production of radioisotopes for nuclear medicine. Although the requirements in terms of proton energy and current are rather challenging, the constant progress in laser technology and advanced target engineering suggests that laser-driven proton sources could play a role in coping with the expected rise of demand for radionuclides.
In this work, we have investigated the production of 64Cu with laser-driven protons for theranostics purposes. Considering a state-of-the-art 150 TW 10 Hz laser system, we numerically assessed the increment in terms of activity achievable by exploiting an advanced DLT rather than a single-layer target. Notably, the activity obtained with DLTs upon irradiation lasting for tens of minutes is of the order of 10 s MBq. In principle, this activity is sufficient for pre-clinical studies with mouse model. In addition, we expanded the analysis to more powerful systems using an approximated analytical model. We showed that laser-driven sources could provide sufficient 64Cu activity for clinical studies in the future. In this respect, advanced DLTs can play a crucial role in efficiently producing radioisotopes for nuclear medicine both in the case of commercial 100 s TW lasers and multi-PW systems.
Data availability statement
The raw data supporting the conclusion of this article will be made available by the authors, without undue reservation.
Author contributions
AM conceived the idea, developed the analytical model, contributed to the Monte Carlo Simulations and co-wrote the manuscript. FM performed the Monte Carlo simulation, contributed to the analytical estimations, and co-wrote the manuscript. AG contributed to the model development and Monte Carlo simulations. AF performed the particle-in-cell simulations. MP supervised the project and all the activities, acquired the funding, and revised the manuscript. All authors contributed to the article and approved the submitted version.
Funding
This project has received funding from the European Research Council (ERC) under the European Union’s Horizon 2022 research and innovation programme (PoC-PANTANI Grant Agreement No. 101069171).
Authors acknowledge the agreement between the Department of Energy at Politecnico di Milano and the Cineca consortium (Casalecchio di Reno, Italy) for access to the high-performance computing machines Marconi100 and Galileo100.
Conflict of interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Publisher’s note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
References
1.IAEA. Copper-64 radiopharmaceuticals: Production, quality control and clinical applications. No. 7 in radioisotopes and radiopharmaceuticals series. Vienna: INTERNATIONAL ATOMIC ENERGY AGENCY (2022).
2. Synowiecki M, Perk L, Nijsen J. Ejnmmi radiopharm. Chem. (2018) 2018:3. doi:10.1186/s41181-018-0038-z
3. Macchi A, Borghesi M, Passoni M. Ion acceleration by superintense laser-plasma interaction. Rev Mod Phys (2013) 85:751–93. doi:10.1103/revmodphys.85.751
4. Barberio M, Veltri S, Scisciò M, Antici P. Laser-accelerated proton beams as diagnostics for cultural heritage. Scientific Rep (2017) 7:40415. doi:10.1038/srep40415
5. Passoni M, Fedeli L, Mirani F. Superintense laser-driven ion beam analysis. Scientific Rep (2019) 9:9202–11. doi:10.1038/s41598-019-45425-3
6. Mirani F, Maffini A, Casamichiela F, Pazzaglia A, Formenti A, Dellasega D, et al. Integrated quantitative pixe analysis and edx spectroscopy using a laser-driven particle source. Sci Adv (2021) 7:eabc8660. doi:10.1126/sciadv.abc8660
7. Puyuelo-Valdes P, Vallières S, Salvadori M, Fourmaux S, Payeur S, Kieffer J-C, et al. Combined laser-based x-ray fluorescence and particle-induced x-ray emission for versatile multi-element analysis. Scientific Rep (2021) 11:9998–10. doi:10.1038/s41598-021-86657-6
8. Sun Z. Review: Production of nuclear medicine radioisotopes with ultra-intense lasers. AIP Adv (2021) 11:040701. doi:10.1063/5.0042796
9. Ledingham K, McKenna P, McCanny T, Shimizu S, Yang J, Robson L, et al. High power laser production of short-lived isotopes for positron emission tomography. J Phys D: Appl Phys (2004) 37:2341–5. doi:10.1088/0022-3727/37/16/019
10. Amato E, Italiano A, Margarone D, Pagano B, Baldari S, Korn G. Future laser-accelerated proton beams at eli-beamlines as potential source of positron emitters for pet. J Instrumentation (2016) 11:C04007. doi:10.1088/1748-0221/11/04/c04007
11. Spencer I, Ledingham K, Singhal R, Mccanny T, McKenna P, Clark E, et al. Laser generation of proton beams for the production of short-lived positron emitting radioisotopes. Nucl Instr Methods Phys Res Section B: Beam Interactions Mater Atoms (2001) 183:449–58. doi:10.1016/s0168-583x(01)00771-6
12. Maffini A, Pazzaglia A, Dellasega D, Russo V, Passoni M. Growth dynamics of pulsed laser deposited nanofoams. Phys Rev Mater (2019) 3:083404. doi:10.1103/physrevmaterials.3.083404
13. Maffini A, Orecchia D, Pazzaglia A, Zavelani-Rossi M, Passoni M. Pulsed laser deposition of carbon nanofoam. Appl Surf Sci (2022) 599:153859. doi:10.1016/j.apsusc.2022.153859
14. Pazzaglia A, Fedeli L, Formenti A, Maffini A, Passoni M. A theoretical model of laser-driven ion acceleration from near-critical double-layer targets. Commun Phys (2020) 3:133–13. doi:10.1038/s42005-020-00400-7
15. Passoni M, Sgattoni A, Prencipe I, Fedeli L, Dellasega D, Cialfi L, et al. Toward high-energy laser-driven ion beams: Nanostructured double-layer targets. Phys Rev Acc Beams (2016) 19:061301. doi:10.1103/physrevaccelbeams.19.061301
16. Passoni M, Arioli F, Cialfi L, Dellasega D, Fedeli L, Formenti A, et al. Advanced laser-driven ion sources and their applications in materials and nuclear science. Plasma Phys Controlled Fusion (2019) 62:014022. doi:10.1088/1361-6587/ab56c9
17. Prencipe I, Metzkes-Ng J, Pazzaglia A, Bernert C, Dellasega D, Fedeli L, et al. Efficient laser-driven proton and bremsstrahlung generation from cluster-assembled foam targets. New J Phys (2021) 23:093015. doi:10.1088/1367-2630/ac1fcd
18. Maffini A, Mirani F, Galbiati M, Ambrogioni K, Gatti F, De Magistris G, et al. Towards compact laser-driven accelerators: Exploring the potential of advanced double-layer targets. EPJ Techn Instrum (2023) 10:15. doi:10.1140/epjti/s40485-023-00102-8
19. Mirani F, Calzolari D, Formenti A, Passoni M. Superintense laser-driven photon activation analysis. Commun Phys (2021) 4:185–13. doi:10.1038/s42005-021-00685-2
20. Mirani F, Maffini A, Passoni M. Laser-driven neutron generation with near-critical targets and application to materials characterization. Phys Rev Appl (2023) 19:044020. doi:10.1103/physrevapplied.19.044020
21. Ruiz C, Benlliure J, Cortina D, González D, Llerena J, Martín L. Development of a multi-shot experiment for proton acceleration. J Phys Conf Ser (2018) 1079:012009. doi:10.1088/1742-6596/1079/1/012009
22. Sgattoni A, Fedeli L, Sinigardi S, Marocchino A, Macchi A, Weinberg V, et al. Optimising piccante-an open source particle-in-cell code for advanced simulations on tier-0 systems. arXiv preprint arXiv:1503.02464 (2015).
23. Fedeli L, Formenti A, Cialfi L, Pazzaglia A, Passoni M. Ultra-intense laser interaction with nanostructured near-critical plasmas. Scientific Rep (2018) 8:3834. doi:10.1038/s41598-018-22147-6
24. Allison J, Amako K, Apostolakis J, Arce P, Asai M, Aso T, et al. Recent developments in geant4. Nucl Instr Methods Phys Res section A: Acc Spectrometers, Detectors Associated Equipment (2016) 835:186–225. doi:10.1016/j.nima.2016.06.125
25. Obata A, Kasamatsu S, McCarthy DW, Welch MJ, Saji H, Yonekura Y, et al. Production of therapeutic quantities of 64cu using a 12 mev cyclotron. Nucl Med Biol (2003) 30:535–9. doi:10.1016/s0969-8051(03)00024-6
26. Avila-Rodriguez MA, Nye JA, Nickles RJ. Simultaneous production of high specific activity 64cu and 61co with 11.4 mev protons on enriched 64ni nuclei. Appl Radiat Isot (2007) 65:1115–20. doi:10.1016/j.apradiso.2007.05.012
27. Koning A, Rochman D, Sublet J-C, Dzysiuk N, Fleming M, Van der Marck S. Tendl: Complete nuclear data library for innovative nuclear science and technology. Nucl Data Sheets (2019) 155:1–55. doi:10.1016/j.nds.2019.01.002
28. Zeil K, Kraft S, Bock S, Bussmann M, Cowan T, Kluge T, et al. The scaling of proton energies in ultrashort pulse laser plasma acceleration. New J Phys (2010) 12:045015. doi:10.1088/1367-2630/12/4/045015
29. Capasso E, Durzu S, Piras S, Zandieh S, Knoll P, Haug A, et al. Role of 64 cucl 2 pet/ct in staging of prostate cancer. Ann Nucl Med (2015) 29:482–8. doi:10.1007/s12149-015-0968-4
30. Avila-Rodriguez M, Rios C, Carrasco-Hernandez J, Manrique-Arias J, Martinez-Hernandez R, Garcia-Perez F, et al. Biodistribution and radiation dosimetry of [64 cu] copper dichloride: First-in-human study in healthy volunteers. EJNMMI Res (2017) 7:98–7. doi:10.1186/s13550-017-0346-4
31. Ferrari C, Niccoli Asabella A, Villano C, Giacobbi B, Coccetti D, Panichelli P, et al. Copper-64 dichloride as theranostic agent for glioblastoma multiforme: A preclinical study. Biomed Research International (2015) 2015:1–6. doi:10.1155/2015/129764
32. Huda P, Binderup T, Pedersen MC, Midtgaard SR, Elema DR, Kjær A, et al. Pet/ct based in vivo evaluation of 64cu labelled nanodiscs in tumor bearing mice. PLoS One (2015) 10:e0129310. doi:10.1371/journal.pone.0129310
33. Khosravifarsani M, Ait-Mohand S, Paquette B, Sanche L, Guérin B. In vivo behavior of [64cu] nota-terpyridine platinum, a novel chemo-radio-theranostic agent for imaging, and therapy of colorectal cancer. Front Med (2022) 9:975213. doi:10.3389/fmed.2022.975213
34. Gutfilen B, Souza SA, Valentini G. Copper-64: A real theranostic agent. Drug Des Dev Ther (2018) 12:3235–45. doi:10.2147/dddt.s170879
35. Keinänen O, Fung K, Brennan JM, Zia N, Harris M, van Dam E, et al. Harnessing 64cu/67cu for a theranostic approach to pretargeted radioimmunotherapy. Proc Natl Acad Sci (2020) 117:28316–27. doi:10.1073/pnas.2009960117
36. Qin C, Liu H, Chen K, Hu X, Ma X, Lan X, et al. Theranostics of malignant melanoma with 64cucl2. J Nucl Med (2014) 55:812–7. doi:10.2967/jnumed.113.133850
37.QUARK. Quark 200/350/500: Ultrafast Ti:sa laser series. Thales (2023). https://perma.cc/48HH-GYG6 (Accessed March 12, 2023).
38. Pulsar TW. Ultra intense ultrafast laser. Amplitude Technologies (2023). https://perma.cc/3K44-N7CV (Accessed March 12, 2023).
39. Gao Y, Bin J, Haffa D, Kreuzer C, Hartmann J, Speicher M, et al. An automated, 0.5 hz nano-foil target positioning system for intense laser plasma experiments. High Power Laser Sci Eng (2017) 5:e12. doi:10.1017/hpl.2017.10
40. Fano U. Penetration of protons, alpha particles, and mesons. Annu Rev Nucl Sci (1963) 13:1–66. doi:10.1146/annurev.ns.13.120163.000245
41. Danson CN, Haefner C, Bromage J, Butcher T, Chanteloup J-CF, Chowdhury EA, et al. Petawatt and exawatt class lasers worldwide. High Power Laser Sci Eng (2019) 7:e54. doi:10.1017/hpl.2019.36
Keywords: laser-driven protons, Copper-64, theranostics, nuclear medicine, Monte Carlo, particle-in-cell
Citation: Maffini A, Mirani F, Giovannelli AC, Formenti A and Passoni M (2023) Laser-driven production with advanced targets of Copper-64 for medical applications. Front. Phys. 11:1223023. doi: 10.3389/fphy.2023.1223023
Received: 15 May 2023; Accepted: 29 June 2023;
Published: 11 July 2023.
Edited by:
Changbo Fu, Fudan University, ChinaReviewed by:
Zilong Chang, Indiana University, United StatesGiulia Festa, Museo Storico della Fisica e Centro Studi e Ricerche Enrico Fermi, Italy
Copyright © 2023 Maffini, Mirani, Giovannelli, Formenti and Passoni. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: F. Mirani, ZnJhbmNlc2NvLm1pcmFuaUBwb2xpbWkuaXQ=
 A. Maffini
A. Maffini F. Mirani
F. Mirani A. C. Giovannelli
A. C. Giovannelli A. Formenti1,4
A. Formenti1,4 M. Passoni
M. Passoni