Bayesian optimization for design of high-repetition-rate laser-driven muon source

1 Introduction

Muons have broad applications in fundamental science such as material science, chemistry, biology, and nuclear physics [1–7], which are produced mainly through the proton-nucleon reactions driven by RF-based accelerators in laboratories [8]. However, the cost of improving the muon beam quality on conventional accelerators is increasingly unaffordable. Thus, new methods of generating compact, dense short muon sources are in high demand.

Over the past years, various muon sources have been developed using different techniques and technologies [9]. Laser-driven muon sources have gained attention due to their promising potential for producing bright and compact muon beams [10, 11]. In the previous work, we proposed a novel scheme for obtaining an unprecedentedly dense and short muon source by using a micro-scale spot, fs-duration 100s-PW-laser-driven proton beam irradiating a typical graphite converter target [12]. However, the scheme is limited by the low repetition rate of the high-power laser. Currently, the 100-PW-class laser can hardly achieve a repetition rate of 1 Hz [13], while the conventional pulsed muon source can already accomplish a repetition rate of more than 10 Hz [14, 15]. Therefore, although the instantaneous flux of the laser-driven muon source is much higher than that of the conventional muon source, the average flux is still much lower than the latter. This implies that the proposed scheme is not currently suitable for some applications that require a high number of muons, such as neutrino generation [10] and fusion catalysis [2]. Therefore, there is an urgent need to develop a high-repetition-rate, high-average-flux muon source for practical use.

With the rapid development of laser technology, several petawatt-class lasers are now capable of delivering laser pulses at a repetition rate of 1 Hz or more [16, 17]. Especially, HAPLS has even reached a repetition rate of 3.3 Hz [18] and is about to reach the target of 10 Hz [19]; ELI-ALPS is also planning to build a 10 Hz, 2 PW laser [19]. Nevertheless, reducing the laser power to increase the repetition rate makes it challenging to obtain the required energy and profile of the proton beam, which is necessary for generating high-quality laser-driven muon sources. Therefore, the laser-driven proton-based high-repetition-rate muon source has still a long way to go before it becomes reality.

In recent years, researchers have demonstrated that it is possible to obtain energetic ion beams by using intense laser interaction with targets of various sizes and compositions. For instance, a linearly polarized laser with focusing intensity of 5 × 10²⁰ W/cm², pulse duration of 550 fs, and energy of 80 J irradiating a nm-scale diamond target can generate a C⁶⁺ beam with cut-off energy of about 1 GeV [20]. Similarly, A nearly-fully-ionized iron ion beam can be accelerated up to 0.9 GeV by using a 200 TW-scale femtosecond (fs) pulsed laser to interact with a micron-thick iron-impurities-coated aluminum foil [21]. Utilizing a 40 fs, 5 × 10²¹ W/cm², 12 J laser hitting a submicron silver target [22] can lead to a 2.2 GeV Ag⁴⁵⁺ beam. In addition, an Al¹¹⁺ beam with a peak energy of 310 MeV can be achieved by combining a 0.12 PW, 650 fs, 80 J linearly polarized laser with a 250 nm flat Al target [23]. For superheavy ions, an ultra-intense laser pulse with focused intensity of 5 × 10¹⁹ W/cm², pulse duration of 1.2 ps and energy of 50 J obliquely irradiating a 2-mm-thick lead target can obtain 46-valent lead ions with peak energy of 430 MeV [24]. A fs-scale laser with intensity of 10²² W/cm² hitting an ultrathin Au target covered with carbon nanotube foams can accelerate 51-valent gold ions to 1.2 GeV [25]. Notably, the mass-energy conversion relation dictates that the kinetic energy threshold of ions required to produce muons by strong interactions in laboratory systems is about 300 MeV [26–28]. Therefore, the experimental realization of GeV heavy ion beams based on high-repetition-rate PW-class laser has made it possible to obtain high-repetition-rate high-average-flux muon sources in the future.

The yield of muon sources is determined by the energy and profile of the driving ions, which are influenced by various laser parameters such as intensity, focal spot, and pulse shape, as well as by the features of the irradiated target such as density, thickness, and shape. This implies that a sizeable number of input parameters must be tuned to optimize the quality of the muon source. Traditionally, researchers have used univariate uniform scans (UUS) around the expected optimal parameters to optimize the process. However, as the number of parameters increases, this approach leads to a sample size explosion, requiring a sample size of the order of 10^N for an UUS based on the control variables method when investigating N parameters. This would quickly exhaust computational and experimental resources. Due to these constraints, only a limited number of parameters can be scanned. To overcome this obstacle, some researchers have employed the optimal value of each preceding variable as a fixed one to study the optimal value of next variable. Nevertheless, this approach cannot be generalized to all cases since input parameters are frequently intertwined with each other. In addition, the laser-ion acceleration process, which precedes the muon generation process, is highly sensitive to the relevant parameters, and slight parameter deviations may lead to significant changes in the acceleration and muon generation outcomes. Therefore, the sampling interval in the sweeping process is difficult to determine, as a large interval is ineffective in searching for the optimal value, while a small interval leads to a substantial increase in the sampling cost. In summary, the traditional one-dimensional optimization method is inadequate for investigating the muon generation process.

Machine learning has demonstrated its superior ability to solve complex problems in various fields such as plasma physics, acceleration science, and light source applications [29–35]. Bayesian optimization [36] is a popular method for quickly searching the parameter space and analyzing the relationship between the coupling of parameters. One of its advantages is that the data points sampled in the previous order can be used to build a surrogate model to deduce the location of the next sampled point, and then the newly sampled points can be applied to optimize the surrogate model so as to find more valuable sample points. Therefore, Bayesian optimization can efficiently find extreme value points and ultimately reduce the sample size. Additionally, the selection of an appropriate acquisition function can avoid being trapped by local optimum.

In this paper, we combine Latin hypercube sampling (LHS) with Bayesian optimization to further enhance the efficiency of sampling. The improved Bayesian optimization sampling (BOS) is applied to simultaneously tune four parameters to obtain the required optimal laser-muon source by using the results of particle-in-cell (PIC) simulations coupled with Monte Carlo (MC) simulations. The dataset obtained by the BOS approach confirms that the radiation pressure acceleration mechanism is a promising approach to generating a significant number of muons. The simulation results indicate that BOS has approximately three times the sampling efficiency compared to the UUS, which greatly reduces the investigation cost. Furthermore, the laser-driven carbon-based muon source deduced by BOS has a higher average flux than the laser-driven proton-based muon source, and this result is obtained within only several tens of simulations.

2 Model and method

2.1 Overview of the scheme

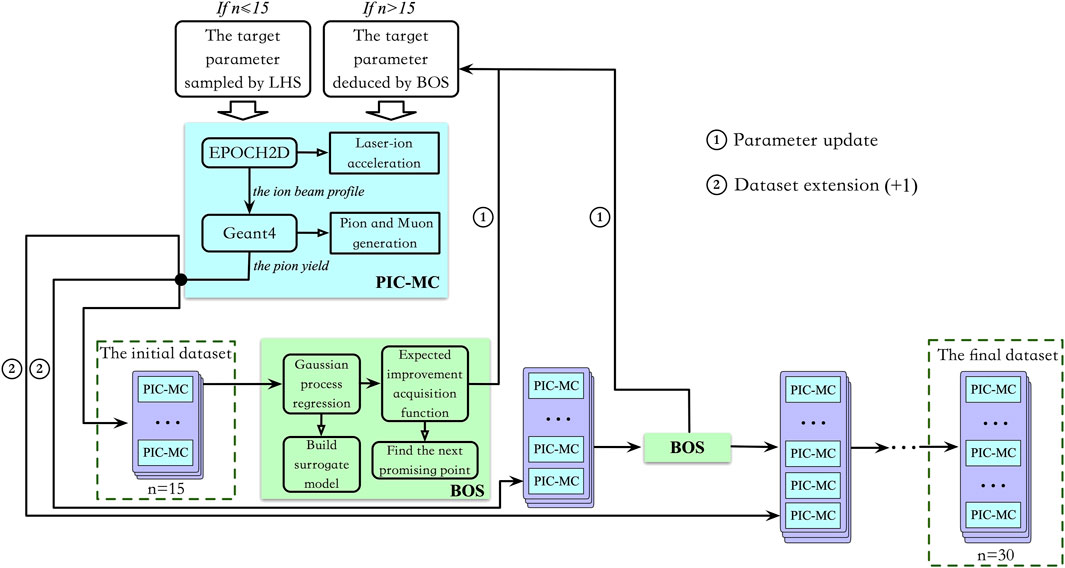
The sketch of the laser-muon sources is depicted in Figure 1, which is composed of the ion acceleration stage and the muon generation stage.

FIGURE 1

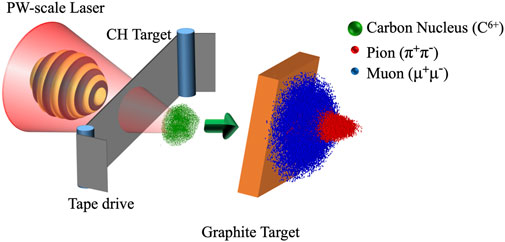
FIGURE 1. Schematics for producing high-repetition-rate high-average-flux muon source using a laser-ion accelerator.

The simulation process begins with the two-dimensional PIC code EPOCH2D [37], which is used to investigate the laser-ion acceleration process. The simulation box has a dimension of 160 μm × 30μm, where a circularly polarized driving laser pulse with a super-Gaussian spatial profile is incident from the left boundary and then irradiates a custom-designed tape drive target system located at 8 μm away from the left boundary. The drive laser has an intensity of I = 2.76 × 10²² W/cm², a wavelength of λ = 0.8 μm, a focal spot radius of 1.2 μm at 1/e² and a trapezoidal pulse duration of 26.7 fs (2.67 fs linear growth—21.36 fs plateau—2.67 fs linear decrease). These parameters correspond to a laser with a peak power of approximately 1.24 PW and total energy of 33 J. It should be noted that the power of the laser to be used ranges from 2 to 3 PW, and it can be generated by upcoming 10 Hz PW-scale laser facilities such as HAPLS and ELI-ALPS [18, 19]. The custom-designed tape drive target system which allows for high repetition rate [38] is composed of two motorized rotating spools and a plastic base supporting the carbon-hydrogen (CH) planar target, in which the density of the carbon ions n_C and hydrogen ions n_H are determined by BOS. Due to the significant increase in computational cost associated with designing the tape drive target size based on its actual dimensions in the simulation, we set the lateral dimension of the target in the simulation to be 10 times the laser focal spot radius. This approach helps to avoid unnecessary waste of computational resources caused by excessive calculations. To ensure that the grid size along the laser propagation direction is less than the laser skin depth, the longitudinal grid number per micron is the minimal integer that is greater than $2\pi /\left(\lambda \sqrt{n_c/n_e}\right)$ per micron, where n_c = 1.74 × 10²¹ cm⁻³ is the plasma critical density and n_e = 6n_C + n_H is the electron density of CH target. The horizontal grid number is set to 32 per micron. In all simulations, Particles are represented by 8 macro-particles in each cell and ions are movable. Opening boundary conditions are used for both electromagnetic fields and particles, and the quantum electrodynamics (QED) module is turned on, while the radiation reaction (RR) effect is considered throughout the simulations.

In the second stage of the experiment, the accelerated ion beams from the former stage impinge onto a 7 mm-thick graphite converter target at a 45-degree angle, triggering the generation of pions via the ion inelastic collision and further production of muons via the pion decay. The MC code Geant4 [39] is utilized to model the conventional beam-converter process. It is important to note that the laboratory ion energy threshold required for pion production is approximately 290 MeV [26–28]. Therefore, we only consider those ions with energy greater than 300 MeV in our simulation of the second stage. To save the computation resources, we randomly sample approximate 10⁹ ions from the energetic laser-driven ion beam. The ions input into the MC simulation are with the same ion energy, position and momentum distributions from the PIC simulation. It should be noted that the total charge of the ions in the simulation is estimated by multiplying the 2D results by 10^–6 [37].

2.2 Pion production model

In the beam-converter interaction process, pions can be produced as soon as the laboratory energy of ions is above 290 MeV which can then decay into muons and muon neutrinos. Because the De-Broglie wavelength of the incoming ions and subsequent collision products is smaller than the average inter-nucleon distance, one can apply MC sampling to determine the point of collision, the type of collision, the momentum of the struck nucleon, and the scattering angles for each collision, where the cross-section of reactions are provided by free-particle collision experiments [40]. However, the beam-converter interaction is much more complicated than collisions between free nucleons. In the converter target, the nucleons are initially bound in their orbits due to the nuclear mean field and thus the collisions will take place within the nuclear medium, in which some of the final states are blocked by other nucleons on account of the Pauli exclusion principle. Furthermore, the initial nucleon distributions will be altered rapidly by the interactions. Therefore, it is necessary to employ models with more accurate nucleon density distribution to calculate the ion-nucleus reactions.

The Liège intranuclear-cascade model (INCL) [41] is suitable for calculating the pion production in the process of ion bombarding the solid target with nucleon number A ≤ 18. Compared with the traditional intranuclear-cascade model, INCL has considered the pion production process and has applied the Hartree-Fock-Bogoliubov calculation method to describe the radial density distribution of protons and neutrons in nucleons [42], which is closer to the experimental results. Meanwhile, the model minimizes the number of model parameters by using the experimental results, e.g., the basic reaction cross-section, and theoretical results, e.g., the stop time, so as to improve the prediction ability of the model. Hence, we use the C++ program block INCL++ [43] based on INCL in the following to calculate the pion production in the process of carbon ion collision.

2.3 Bayesian optimization

Bayesian optimization is an efficient global optimization algorithm, which can find the next evaluation position according to the modelling results of the current sample points, so as to achieve the optimal solution as quickly as possible [44]. It is an operation framework, which can obtain the optimal solution of complex objective functions by evaluating a small number of samples. The core idea is to use the surrogate model to fit the real objective function according to the initial dataset, and then actively select the extreme point of the acquisition function as the next sample point for evaluation, so as to reduce the number of useless sample points greatly through active optimization. The surrogate model will be rebuilt at every iteration, which can improve the accuracy of the model effectively and ultimately provide the maximum search rate in the parameter space. This algorithm is efficient in basic scientific research and particularly in studies requiring significant computational or experimental resources.

In the work performed here, Bayesian optimization is utilized by the authors based on Openturns platform [45]. This algorithm is composed of a Gaussian process regression model [46] and an Expected improvement acquisition function. Gaussian Process Regression, also known as Gaussian Process (GP), is a common non-parametric model belonging to supervised learning. Gaussian Process defines the distribution of functions, such that if we take any two or more points X from the function, the observed output values Y at these points follow a joint (multivariate) Gaussian distribution. In other words, Gaussian Process is defined as a collection of sample points that follow a joint (multivariate) Gaussian distribution. Taking into account factors such as noise in the data points themselves and measurement uncertainty, we assume that the observed values are composed of an independent “signal” term f(x) and a “noise” term ϵ. The noise term ϵ reflects the inherent randomness in the observed values, which is present regardless of the number of observations we make. In this context, the relationship between the input variable x and the output y can be described as follows.

$y=f\left(\mathbf{x}\right)+ϵ,ϵ\sim \mathcal{N}\left(0,{\sigma }_{ϵ}^2\right)(1)$

The function f(x) is distributed as a Gaussian process.

$f\left(\mathbf{x}\right)\sim \mathcal{G\; P}\left(m\left(\mathbf{x}\right),k\left(\mathbf{x},{\mathbf{x}}^{\prime }\right)\right),(2)$

Where $m(\mathbf{x})=\mathbb{E}\left[\mathbf{x}\right]$ represents the mean function of the Gaussian process, and $k\left(\mathbf{x},{\mathbf{x}}^{\prime }\right)=\mathbb{E}\left[(f(\mathbf{x})-m(\mathbf{x}))\left(f\left({\mathbf{x}}^{\prime }\right)-m\left({\mathbf{x}}^{\prime }\right)\right)\right]$ represents the covariance function. In order to avoid expensive posterior computations and perform inference solely based on the covariance function, it is common to set the prior mean function as m(x) = 0. The covariance function k is often referred to as the kernel of the Gaussian process. The choice of the kernel is based on assumptions about the smoothness and patterns in the data, and it directly affects the degree of fit between the Gaussian process and the studied data. Here, we select to use the Matér${\text{n}}_{\frac{3}{2}}$ kernel, which is defined as follows:\

$k\left(\tau \right)={\sigma }^2\left(1+\frac{\sqrt{3}\tau }{\rho }\right)\exp \left(-\frac{\sqrt{3}\tau }{\rho }\right).(3)$

Based on the aforementioned definition, our first step is to sample the function. Although the Gaussian process is continuous, the process of sampling the function is accomplished by computing the function values at a selected set of input points. During this process, we do not aim to consider all mathematically possible functions, so we predict only for a finite number of points and use the covariance matrix generated by the multivariate normal distribution and the kernel to draw the outputs for these points. We define X as a data set matrix with each row representing an input point x_i(i = 1, … ,n). The covariance matrix can then be written as:

$K\left(\mathbf{X},\mathbf{X}\right)=\left[\begin{array}{cccc}\hfill k\left({\mathbf{x}}_1,{\mathbf{x}}_1\right)\hfill & \hfill k\left({\mathbf{x}}_1,{\mathbf{x}}_2\right)\hfill & \hfill \dots \hfill & \hfill k\left({\mathbf{x}}_1,{\mathbf{x}}_n\right)\hfill \\ \hfill k\left({\mathbf{x}}_2,{\mathbf{x}}_1\right)\hfill & \hfill k\left({\mathbf{x}}_2,{\mathbf{x}}_2\right)\hfill & \hfill \dots \hfill & \hfill k\left({\mathbf{x}}_2,{\mathbf{x}}_n\right)\hfill \\ \hfill ⋮\hfill & \hfill ⋮\hfill & \hfill \ddots \hfill & \hfill ⋮\hfill \\ \hfill k\left({\mathbf{x}}_n,{\mathbf{x}}_1\right)\hfill & \hfill k\left({\mathbf{x}}_n,{\mathbf{x}}_2\right)\hfill & \hfill \dots \hfill & \hfill k\left({\mathbf{x}}_n,{\mathbf{x}}_n\right)\hfill \end{array}\right].(4)$

Next, we perform sampling from the multivariate normal distribution of f(x) and denote the sampled function values as f, yielding:

$\mathbf{f}\sim \mathcal{N}\left(\mathbf{0},K\left(\mathbf{X},\mathbf{X}\right)\right)(5)$

Building upon this, incorporating the noise term ϵ corresponds to sampling the output values y, which forms the prior distribution. We assume that the noise ϵ follows an independent and identically distributed Gaussian distribution $p(\epsilon )=\mathcal{M}\left(0,{\sigma }^2\right)$. By applying Bayes’ Rule, we obtain the posterior distribution for the new data set ${\mathcal{D}}_{\star }=\left\{{\mathbf{X}}_{\star },{\mathbf{y}}_{\star }\right\}$ as follows:

$\left[\begin{array}{c}\hfill \mathbf{y}\hfill \\ \hfill {\mathbf{f}}_{\star }\hfill \end{array}\right]\sim \mathcal{N}\left(\mathbf{0},\left[\begin{array}{cc}\hfill K\left(\mathbf{X},\mathbf{X}\right)+{\sigma }^2\mathbf{I}\hfill & \hfill K\left(\mathbf{X},{\mathbf{X}}_{\star }\right)\hfill \\ \hfill K\left({\mathbf{X}}_{\star },\mathbf{X}\right)\hfill & \hfill K\left({\mathbf{X}}_{\star },{\mathbf{X}}_{\star }\right).\hfill \end{array}\right]\right)(6)$

In the equation, f_⋆ represents the predicted function values, i.e.,

$\begin{array}{c}p\left({\mathbf{f}}_{\star }\mid \mathbf{X},\mathit{y},{\mathbf{X}}_{\star }\right)=\mathcal{M}\left(⟨{\mathbf{f}}_{\star }⟩,\mathrm{c}\mathrm{o}\mathrm{v}\left({\mathbf{f}}_{\star }\right)\right)\\ ⟨{\mathbf{f}}_{\star }⟩=K\left({\mathbf{X}}_{\star },\mathbf{X}\right){\left[K\left(\mathbf{X},\mathbf{X}\right)+{\sigma }^2\mathbf{I}\right]}^{-1}\mathbf{y}\\ \mathrm{c}\mathrm{o}\mathrm{v}\left({\mathbf{f}}_{\star }\right)=K\left({\mathbf{X}}_{\star },{\mathbf{X}}_{\star }\right)-K\left({\mathbf{X}}_{\star },\mathbf{X}\right){\left[K\left(\mathbf{X},\mathbf{X}\right)+{\sigma }^2\mathbf{I}\right]}^{-1}K\left(\mathbf{X},{\mathbf{X}}_{\star }\right)\end{array}(7)$

Additionally, The acquisition function is defined as follows.

${\alpha }_t\left(\mathit{x};D_{1:t}\right)=\left\{\begin{array}{c}\left(v^{*}-\xi -{\mu }_t\left(\mathit{x}\right)\right)\varphi \left(\frac{v^{*}-\xi -{\mu }_t\left(\mathit{x}\right)}{{\sigma }_t\left(\mathit{x}\right)}\right)\hfill \\ +{\sigma }_t\left(\mathit{x}\right)\varphi \left(\frac{v^{*}-\mathit{\xi }-{\mu }_t\left(\mathit{x}\right)}{{\sigma }_t\left(\mathit{x}\right)}\right),\hfill & {\sigma }_t\left(\mathit{x}\right)>0\hfill \\ 0,\hfill & {\sigma }_t\left(\mathit{x}\right)=0\hfill \end{array}\right.(8)$

where v* represents the current optimal function value, ϕ(⋅) is the probability density function of the standard normal distribution, and ξ is a balancing parameter utilized to balance the relationship between the local and global search, avoiding getting trapped in local optima.

Meanwhile, in order to improve the efficiency of Bayesian optimization, we utilized the LHS to structure the initial dataset, given that it generates samples that reflect the true underlying distribution and tend to require much smaller sample sizes than simple random sampling. The complete optimization process based on PIC-MC simulation is illustrated below.

As depicted in Figure 2, we first get the target parameters by 15 times LHS, and then apply EPOCH2D to calculate the ion beam profile during the laser-ion acceleration process. After injecting the ion beam profile to Geant4, we obtain the pion and muon yield. The entire physical simulation process is referred to as the “PIC-MC” simulation. In our studies, The 15 sets of pion yield corresponding to the different target parameters made up the initial dataset. Subsequently, a surrogate model was constructed by means of the Gaussian process regression model. Following this model, the Expected improvement acquisition function was employed to determine the next promising sample point. Based on this recommended sample point, we amend the target parameter, e.g., target density and thickness, and run the whole PIC-MC simulation again to calculate the pion yield. The new result extends the dataset, thereby making the surrogate model more accurate. After 15 rounds of BOS, we end up with an optimized dataset and a relatively accurate surrogate model. A similar algorithm has been successfully utilized to eliminate the necessity of parameter scans and reduce the required prior information about the measurement’s behavior, along with associated measurement constraints in particle accelerators [47].

FIGURE 2

FIGURE 2. The flow chart of Bayesian optimization applied in the PIC-MC simulations.

3 Results

In the present work, we apply BOS to investigate the effect of the density of carbon ions and hydrogen ions, as well as the thickness of the CH target and the ion acceleration time on the muon generation. Here, we choose the yield of pion source as the objective function, since maximizing the yield of pion source would be promising to obtain high flux muon and pion beams. In the simulations, the parameter range considered were [0, 100n_c] for the density of the carbon ions n_C and the hydrogen ions n_H, and [0.01 μm, 0.2 μm] for the thickness l of the CH target. The acceleration time t of laser-plasma interaction was in the range of [40T₀, 190T₀], where T₀ = 2.67 fs is the laser period. The size of the initial dataset, which was sampled by LHS, was set as 10, and the total number of simulated samples was 30. To compare the performance, a set of UUS was carried out with 36 sample points, where n_C = 10, 55, 100n_c, n_H = 10, 55, 100n_c, l = 0.01, 0.2 μm and t = 40, 190T₀, respectively.Visualizing sample points in high-dimensional space is challenging. A dimension reduction technique that fails to capture important information can obscure the underlying distribution in low-dimensional representations. This study uses t-Stochastic Neighbor Embedding (t-SNE) [48], a nonlinear dimension reduction technique that converts Euclidean distances of sample points in high-dimensional parameter space into conditional probabilities and characterizes the similarity between points. Gradient descent algorithms were then used to approximate the high-dimensional distribution in low dimensions. The results are shown in Figures 3A, C, where the total yield of π⁺ is represented by color. Figure 3A reveals that the sample points distribution of BOS is uneven, and obvious clustering phenomenon occurs at the points 21, 24, 25, and 27, with the values of these four points being 4.22 × 10⁶, 5.99 × 10⁶, 5.25 × 10⁶ and 5.98 × 10⁶, respectively. Whereas, the sample points distribution of UUS exhibits periodicity and low yield. The maximum value is only 2.99 × 10⁶, which is much less than that of BOS. Figures 3B, D represent the change in particle number versus the sampling sequence. ${\pi }_{\mathit{out}}^{\pm }$ and ${\mu }_{\mathit{out}}^{\pm }$ stand for the particle number of pion and muon beams, where π^± indicates the total pion yield. It is found that the particle numbers of pion and muon beams are positively correlated with the total yield of pions. By comparison, UUS results reveal a suboptimal yield, with only 3 points having a yield greater than 10⁶. In this paper, a sample point with a yield less than 10⁵ is considered as a waste point. As displayed in Figure 3D, the waste point rate of UUS is as high as 83.3%, which represents a huge waste of computational resources. In contrast to UUS, BOS has a much higher sampling efficiency. Besides the maximum point with a yield of 5.99 × 10⁶ found, 19 sample points with yield greater than 10⁶ are obtained via BOS. Furthermore, the BOS with a waste point rate of <30% is more efficient than UUS in numerical and experimental studies.Efficient sampling of complex physical processes is beneficial for investigating the laws of physics and finding the optimal solution, especially when the sample size is finite. Intuitively, the higher the energy and charge of the ion beam, the more advantageous muon production becomes. Radiation pressure acceleration mechanism is expected to produce an energetic and high-charge ion beam, which, in turn, increases the muon production. Therefore, we put the sampled points into the electron density-target thickness phase space and compare it with the radiation pressure acceleration condition a₀λ ≈ π ln_e/n_c, as shown in Figure 4. Figure 4A displays that the sampled points with higher yields are closer to the curve of radiation pressure acceleration condition. Extreme points of yields in the two regions, one with larger and one with smaller target thicknesses, fall around the curve. The results of the initial sampled points in Figures 3A, B indicate that the previous sampling did not find points with high yields in the central region, but only obtained points with high yields at both ends of the region. Therefore, the aggregation of sampled points is observed at both ends of the region. While the current result of the 30-point sampling does not extensively explore the region, subsequent sampling using BOS will be more inclined to explore the region due to its high level of uncertainty. Therefore, the absence of points with high muon yield in this region can be attributed to the limited number of sampling points. To investigate the reasons behind the lower muon yields of certain points on the RPA curve, such as the arrow-marked point in this figure, these points were placed in the acceleration time-target thickness phase space to examine the impact of acceleration time, specifically, the duration of laser-plasma interaction before the ion beam reaches the converter target.Figure 5 illustrates the evolution of energy and charge for the marked points in Figure 4 of the main text. Figure 5A reveals a rapid increase in the cut-off energy of carbon ions before 50T₀, which then approaches saturation with minimal variation thereafter. Conversely, the charge of carbon ions demonstrates stability for a period following a rapid increase before 25T₀, after which it undergoes a rapid decrease after 80T₀, as depicted in Figure 5B. This phenomenon can be attributed to RPA’s ability to maintain a stable acceleration structure and generate a powerful and high-energy ion beam within tens T₀, as depicted in Figure 5C. Over time, the Rayleigh-Taylor-like instability [49, 50] intensifies rapidly, resulting in the deterioration of the acceleration field structure. Subsequently, the acceleration mechanism of laser-driven ions gradually transitions to Target-Normal Sheath Acceleration (TNSA) [51]. While a certain degree of velocity increase still occurs at this stage, TNSA amplifies the divergence angle of the ions. As a result, a substantial portion of high-energy ions is unable to pass through the “collimator.” In this study, our objective is to establish a small-scale muon source with higher yields. To accomplish this, collimator is employed to shield ions with significant divergence angles. The transverse size of the simulation box is comparable to the collimator’s aperture. Thus, it can be observed in Figure 5D that despite the increasing cutoff energy of carbon ions, there is a substantial reduction in the overall number of ions, particularly high-energy carbon ions, resulting in decreased muon yield. Moreover, as illustrated in Figure 4A, the optimal points with a target density of approximately 600n_c undergo a laser-plasma interaction time exceeding 100T₀. In such cases, the interaction time surpasses the limits sustained by the RPA mechanism, and thus the ion charge is suboptimal. In contrast, the optimal points with a target density of approximately 200n_c experience a laser-plasma interaction time of approximately 50T₀. This results in higher energy and charge of the ions at this point, ultimately resulting in a greater yield of muons compared to the former situation. These findings confirm that the radiation pressure acceleration mechanism can produce an energetic high-charge carbon ion beam within a few tens of laser cycles, facilitating the increase of subsequent secondary particle yields. On the contrary, as we put the UUS points into the electron density-target thickness phase space, we can find that the data set has almost no regularity in the case of small amounts of data in Figure 4B. Hence, the data set sampled by BOS is more favourable and efficient for our investigation in this study.

FIGURE 3

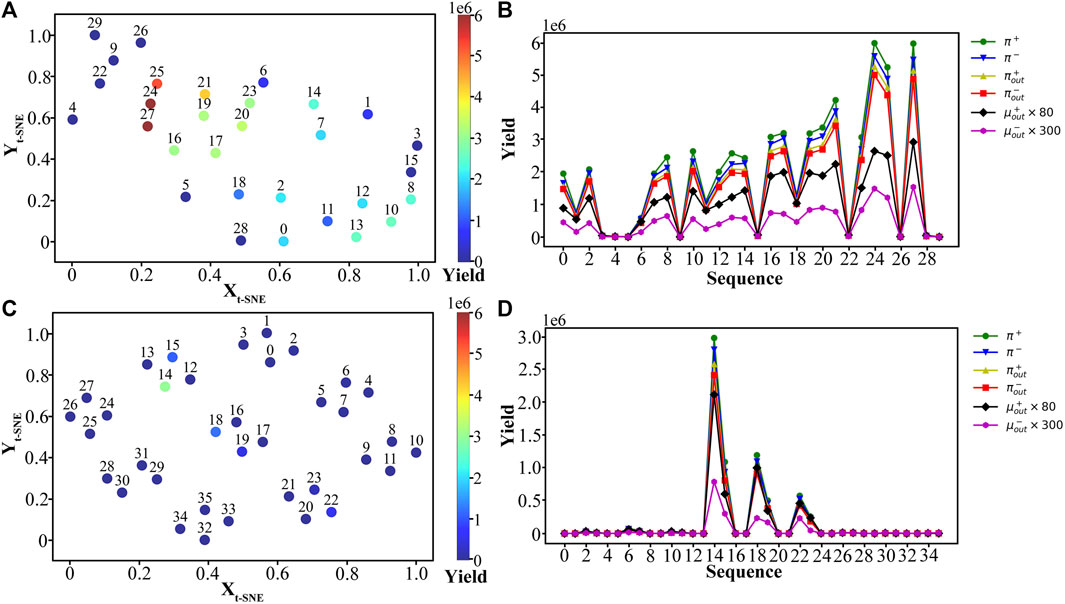
FIGURE 3. The t-SNE dimension reduction distribution and pion yield of BOS points (A) and UUS points (C) in four-dimensional parameter space, where the numbers are sample orders. The total yield of pions and the number of pion beams and muon beams according to the sequence of BOS (B) and UUS (D).

FIGURE 4

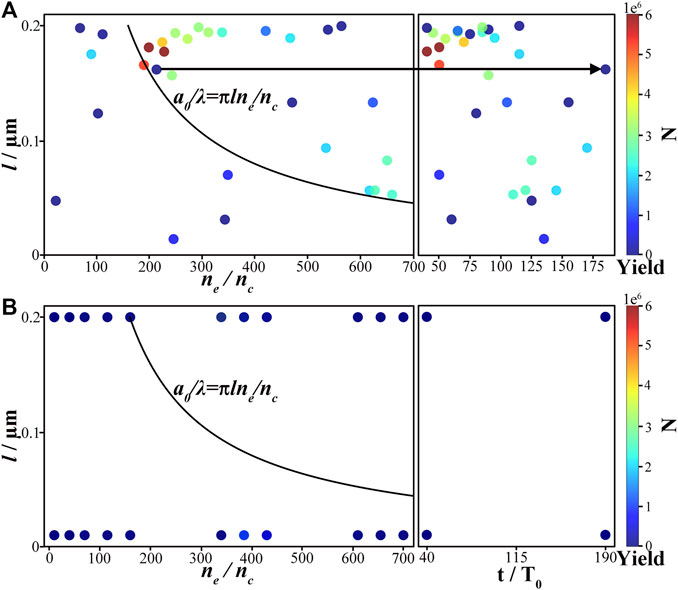
FIGURE 4. The relationship between the electron density n_e, the target thickness l and ion acceleration time t corresponding to (A) the BOS points and (B) the UUS points.

FIGURE 5

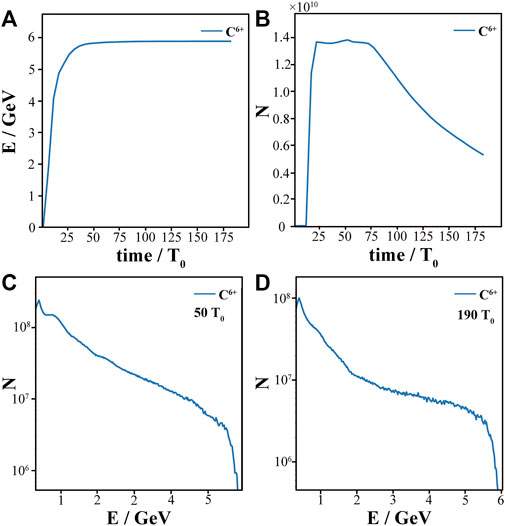
FIGURE 5. Evolution of the energy (A) and number (B) of the carbon ions in the simulation box. The energy spectrum of carbon ions at 50 T0 (C) and 190 T0 (D).

4 Discussion

For further investigation, we analyze the optimal muon source profile deduced by BOS and present the results in Figures 6, 7. Compared to the pure heavy ion targets, it has been demonstrated that by the use of a circularly polarized laser, a mixed target consisting of light and heavy ions can achieve higher ion velocities via the radiation pressure acceleration mechanism [52, 53]. It has been also observed that the higher the proton content in the mixed target, the better the acceleration of the heavy ions [53]. Therefore, the role of hydrogen ions in the target is to assist the carbon ions to form a more stable accelerating field structure, thus enhancing the energy and charge of the carbon ions, which are advantageous for muon production in the following stage. The results obtained from BOS are consistent with the aforementioned theory. We find that after a 10 Hz PW-class laser irradiates a 0.18 μm-thick CH target with a carbon ion density of 26.65 n_c and the hydrogen ion density of 38.44 n_c corresponding to an electron density n_e = 198.34n_c, the resulting carbon ion beam can be accelerated up to 6 GeV at 50T₀. Subsequently, it impinges on the graphite conversion target and produces 5.99 × 10⁶ pions in the target. The positive muon beam detected at the target rear has a mm-scale spot size, while the full width at half maximum (FWHM) of the beam duration is about 200 ps as obtained from the pulse duration fit using the kernel density estimation (KDE) based on the Gaussian kernel function as shown in Figure 7A, B.

FIGURE 6

FIGURE 6. The energy spectrum of the carbon ions which can generate the pions with a maximum yield.

FIGURE 7

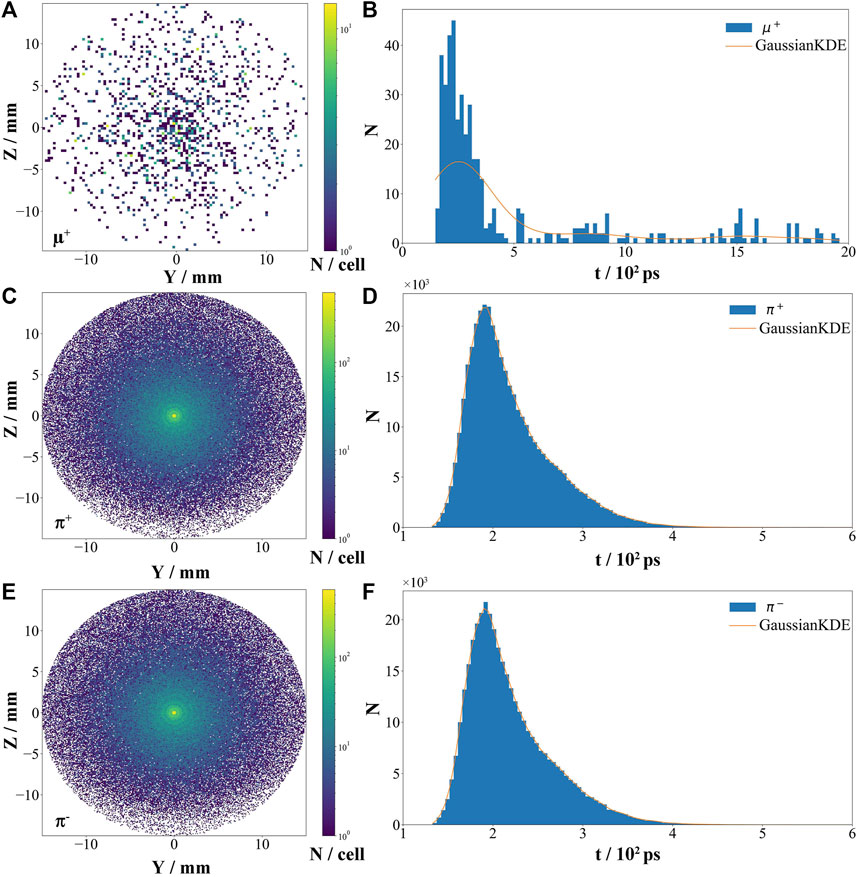
FIGURE 7. The flux density of μ⁺ beam (A), π⁺ beam (C) and π⁻ beam (E), the color represents the number of particles in each small grid. The pulse duration of μ⁺ beam (B), π⁺ beam (D) and π⁻ beam (F). The orange line in Figure (B, D, F) is the result of fitting with kernel density estimation based on the Gaussian kernel function.

Moreover, both the positive pion beam and negative pion beams have mm-sized beam spots with the corresponding pulse duration are only 60 ps at FWHM, as illustrated in Figures 7C–F. These excellent beam characteristics imply that the 10Hz-PW-laser-driven carbon-based muon source not only acts as a high-repetition-rate source but also shows promise as a high-density and ultra-short pulse muon source. The results imply that the BOS is an excellent method in the investigation of laser-driven muon sources and other laser-driven secondary particle sources such as positron sources [54] and neutron sources [55].On account of the limitation in computational resources, we have chosen to translate the 2D simulation results obtained from EPOCH2D into 3D by multiplying the results by 10^–6 [37] before inputting them into Geant4. This operation reduces the cost of calculation in the following simulations. It is worth noting, however, that there is a considerable difference between the 2D and 3D simulations. In order to assess the feasibility of this method, we carry out a full 3D simulation using the same parameters. The results demonstrate that the total pion yield in the 3D simulation is just 1.59 × 10⁶, that is because the acceleration of carbon ions is suppressed in the 3D simulation due to the serious instabilities such as Rayleigh-Taylor-like instability [49]. Though the cut-off energy is lower than 2D simulation results, the number of carbon ions exhibiting energy greater than 300 MeV is higher, as depicted in Figure 8A. Therefore, the π⁺ yield in the full 3D simulation still remains on the order of 10⁶. At the rear of the graphite target, the emitted pion beams are still on the millimeter scale with a pulse width of about 90 ps, as displayed in Figures 8B–E. Although this is slightly worse than the results calculated from the 2D simulation, it nevertheless falls within the same order of magnitude. Therefore, given that a series of full 3D simulations may be unsupported, the use of PIC simulation 2D results as substitutes in subsequent simulations proves to be a feasible approach.

FIGURE 8

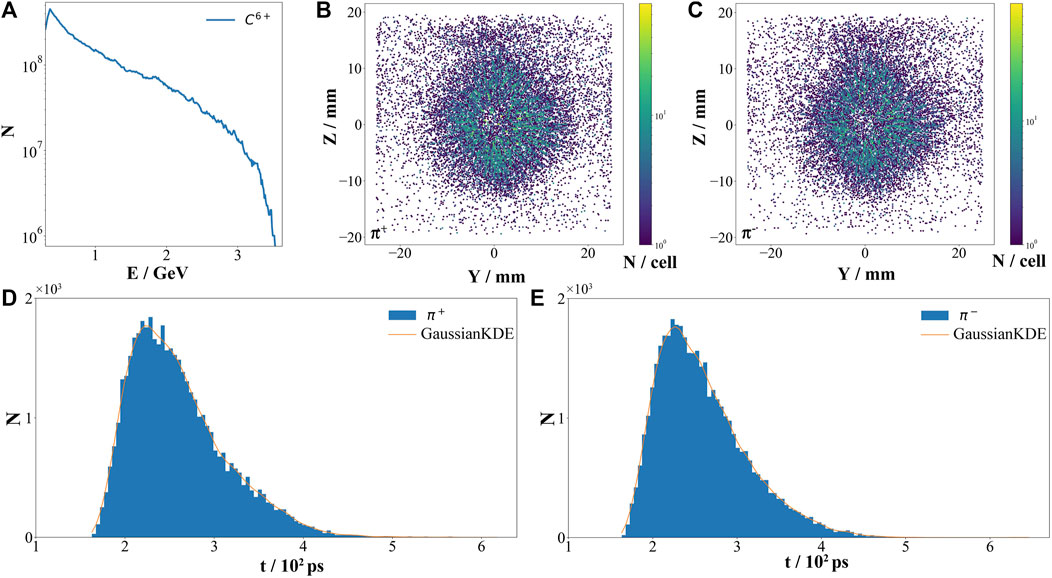
FIGURE 8. Full 3D simulation of carbon and pion beam properties. (A) Carbon ion energy spectrum. The flux densities of π⁺ beam (B) and π⁻ beam (C), the color represents the number of particles in each small grid. The pulse durations of π⁺ beam (D) and π⁻ beam (E). The orange lines in figure (D) (E) are the fitting result with the kernel density estimate based on the Gaussian kernel function.

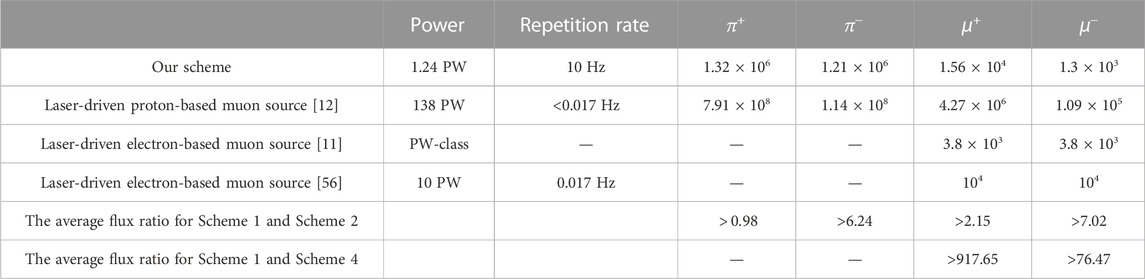
Finally, we obtained a mm-scale pion beam with a pulse width of about 90 ps at FWHM in a full 3D simulation. The results are summarized in Table 1. Adjacently, we compare the pion and muon beams produced using our scheme with those obtained from the laser-driven proton-based muon source described in Ref. [12] and the laser-driven electron-based muon source [11, 56]. As illustrated in the table, although the particle number of the laser-driven carbon-based muon source is smaller than that of the laser-proton-driven muon source, i.e., the instantaneous flux is smaller than that of the latter, the average flux of the laser-driven carbon-based muon source is comparable to the latter in π⁺, while π⁻ is 6 times larger than that of the latter, μ⁺ is 2 times higher than the latter, and μ⁻ is 7 times higher than the latter with a reduction in laser power by two orders. Thus this research provides guidance for the muon source design.

TABLE 1

TABLE 1. Comparison of full 3D simulation results of laser-driven muon sources.

5 Conclusion

The laser-driven ion acceleration and pion generation evolve many parameters of laser and targets, making the results unpredictable. Meanwhile, the whole system is highly sensitive to parameter changes, which can lead to a sudden change in the carbon ion beam quality and therefore, the pion and muon generation. These require a huge investigation cost in simulations and experiments. In this paper, we introduced an enhanced BOS via coupled with LHS, aimed at seeking the most optimal values in the multi-dimensional parameter space. We compared the results from 30 samplings by BOS with that from 36 samplings by UUS in the same parameter space and observed that BOS has a higher sampling efficiency and a more favourable resulting dataset for scientific research. Furthermore, following the results of BOS, it is found that a CH target with a thickness of 0.18 μm, a carbon ion density of 26.65 n_c and a hydrogen ion density of 38.44 n_c irradiated by a 10 Hz PW-class laser after 50 T₀ will generate an energetic high-charge carbon ion beam. Subsequently, through bombarding the graphite converter target, the carbon ion beam can produce a mm-scale 60-ps-duration π⁺ beam with number of 5.27 × 10⁶, a mm-scale 60-ps-duration π⁻ beam with number of 5 × 10⁶, a mm-scale 200-ps-duration μ⁺ beam with number 3.31 × 10⁴ and a μ⁻ beam with number of 4.97 × 10³ in 2D simulation. The full 3D simulation with the same parameters generates a mm-scale 90-ps-duration beam of 1.32 × 10⁶ π⁺, a mm-scale 90-ps-duration beam of 1.21 × 10⁶ π⁻, a beam of 1.56 × 10⁴ μ⁺ and a beam of 1.3 × 10³ μ⁻. Compared with the laser-driven proton-based muon source, the laser-driven carbon-based muon source has the comparable average flux of π⁺, 6 times that of π⁻, 2 times that of μ⁺, and 7 times that of μ −, with a reduction in laser power by two orders of magnitude. Therefore, the high-average-flux muon source is suitable for neutrino generation and fusion catalysis that require a large number of muons.

Data availability statement

The raw data supporting the conclusion of this article will be made available by the authors, without undue reservation.

Author contributions

Conceptualization: T-PY; methodology: RS and B-LW; software: RS, B-LW, LY, and X-JD; validation: T-PY, JZ and X-JD; writing—original draft preparation: RS; writing—review and editing: B-LW, JZ, G-XX, and T-PY; visualization: RS; supervision: T-PY and X-JD; project administration: T-PY. All authors contributed to the article and approved the submitted version.

Funding

This work was supported by the National Key R&D Program of China (Grant No. 2018YFA0404802), National Natural Science Foundation of China (Grant Nos. 12135009 and 12101608), The Hunan Provincial Innovation Foundation for Postgraduate (Grant Nos. CX20210007, CX20210062 and CX20220034), NSAF (Grant No. U2230208s) and The Science and Technology Innovation Program of Hunan Province (Grant No. 2020RC4020).

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

1. Ninomiya K, Nagatomo T, Kubo K, et al. Development of nondestructive and quantitative elemental analysis method using calibration curve between muonic x-ray intensity and elemental composition in bronze. Bull Chem Soc Jpn (2012) 85:228–30. doi:10.1246/BCSJ.20110151

CrossRef Full Text | Google Scholar

2. Jones SE, Anderson AN, Caffrey AJ, Van Siclen CD, Watts KD, Bradbury JN, et al. Observation of unexpected density effects in muon-catalyzed d-t fusion. Phys Rev Lett (1986) 56:588–91. doi:10.1103/PhysRevLett.56.588

PubMed Abstract | CrossRef Full Text | Google Scholar

3. Shahbaz A, Müller C, Staudt A, Bürvenich TJ, Keitel CH. Nuclear signatures in high-order harmonic generation from laser-driven muonic atoms. Phys Rev Lett (2007) 98:263901. doi:10.1103/physrevlett.98.263901

PubMed Abstract | CrossRef Full Text | Google Scholar

4. Giblin S, Cottrell S, King P, Tomlinson S, Jago S, Randall L, et al. Optimising a muon spectrometer for measurements at the isis pulsed muon source. Nucl Instr Methods Phys Res - section A (2014) 751:70–8. doi:10.1016/j.nima.2014.03.010

CrossRef Full Text | Google Scholar

5. Suerfu B, Tully CG. High resolution muon computed tomography at neutrino beam facilities. J Instrumentation (2016) 11:P02015. doi:10.1088/1748-0221/11/02/p02015

CrossRef Full Text | Google Scholar

6. Gorringe T, Hertzog D. Precision muon physics. Prog Part Nucl Phys (2015) 84:73–123. doi:10.1016/j.ppnp.2015.06.001

CrossRef Full Text | Google Scholar

7. Aoyama T, Asmussen N, Benayoun M, Bijnens J, Blum T, Bruno M, et al. The anomalous magnetic moment of the muon in the standard model. Phys Rep (2020) 887:1–166. doi:10.1016/j.physrep.2020.07.006

CrossRef Full Text | Google Scholar

8. Matsuzaki T, Ishida K, Nagamine K, Watanabe I, Eaton G, Williams W. The riken-ral pulsed muon facility. Nucl Instr Methods Phys Res - section A (2001) 465:365–83. doi:10.1016/S0168-9002(01)00694-5

CrossRef Full Text | Google Scholar

9. Zimmermann F. Lhc/fcc-based muon colliders. J Phys Conf Ser (2018) 1067:022017. doi:10.1088/1742-6596/1067/2/022017

CrossRef Full Text | Google Scholar

10. Bulanov SV, Esirkepov TZ, Migliozzi P, Pegoraro F, Tajima T, Terranova F. Neutrino oscillation studies with laser-driven beam dump facilities. Nucl Instr Methods Phys Res Section A-accelerators Spectrometers Detectors Associated Equipment (2004) 540:25–41. doi:10.1016/j.nima.2004.11.013

CrossRef Full Text | Google Scholar

11. Rao BS, Jeon JH, Kim HT, Nam CH. Bright muon source driven by gev electron beams from a compact laser wakefield accelerator. Plasma Phys Controlled Fusion (2018) 60:095002. doi:10.1088/1361-6587/aacdea

CrossRef Full Text | Google Scholar

12. Sha R, Cheng JH, Li DA, Huang YS, Zhao J, Hu YT, et al. Dense short muon source based on laser-ion accelerators. The Eur Phys J A (2022) 58:249. doi:10.1140/epja/s10050-022-00900-w

CrossRef Full Text | Google Scholar

13. Cartlidge E. The light fantastic. Science (2018) 359:382–5. doi:10.1126/science.359.6374.382

PubMed Abstract | CrossRef Full Text | Google Scholar

14. Nakahara K, Miyake Y, Shimomura K, Strasser P, Nishiyama K, Kawamura N, et al. The super omega muon beamline at j-parc. Nucl Instr Methods A (2009) 600:132–4. doi:10.1016/j.nima.2008.11.106

CrossRef Full Text | Google Scholar

15. Eaton GH. The isis pulsed muon facility. Z Für Physik C Particles Fields (1992) 56:S232–9. doi:10.1007/bf02426802

CrossRef Full Text | Google Scholar

16. Daniels J, Deshmukh A, Magana A, Nakamura K, Syversrud D, Tóth C (2013). Bella laser and operations. Proceedings of the PAC2013, Pasadena, CA USA.December 2013.

Google Scholar

17. Zeil K, Kraft SD, Bock S, Bussmann M, Cowan TE, Kluge T, et al. The scaling of proton energies in ultrashort pulse laser plasma acceleration. New J Phys (2010) 12:045015. doi:10.1088/1367-2630/12/4/045015

CrossRef Full Text | Google Scholar

18. Haefner CL, Bayramian AJ, Betts SM, et al. High average power, diode pumped petawatt laser systems: A new generation of lasers enabling precision science and commercial applications. Opt + Optoelectronics (Proceedings SPIE) (2017) 10241:1024102. doi:10.1117/12.2281050

CrossRef Full Text | Google Scholar

19. Danson CN, Haefner CL, Bromage J, Butcher T, Chanteloup JCF, Chowdhury EA, et al. Petawatt and exawatt class lasers worldwide. High Power Laser Sci Eng (2019) 7:e54. doi:10.1017/hpl.2019.36

CrossRef Full Text | Google Scholar

20. Jung D, Yin L, Gautier DC, Wu HC, Letzring S, Dromey B, et al. Laser-driven 1 gev carbon ions from preheated diamond targets in the break-out afterburner regime. Phys Plasmas (2013) 20:083103. doi:10.1063/1.4817287

CrossRef Full Text | Google Scholar

21. Nishiuchi M, Sakaki H, Esirkepov TZ, Nishio K, Pikuz TA, Faenov AY, et al. Acceleration of highly charged gev fe ions from a low-z substrate by intense femtosecond laser. Phys Plasmas (2015) 22:033107. doi:10.1063/1.4913434

CrossRef Full Text | Google Scholar

22. Nishiuchi M, Dover N, Hata M, Sakaki H, Kondo K, Lowe H, et al. Dynamics of laser-driven heavy-ion acceleration clarified by ion charge states. Phys Rev Res (2020) 2:033081. doi:10.1103/physrevresearch.2.033081

CrossRef Full Text | Google Scholar

23. Palaniyappan S, Huang C, Gautier DC, Hamilton CE, Santiago MA, Kreuzer C, et al. Efficient quasi-monoenergetic ion beams from laser-driven relativistic plasmas. Nat Commun (2015) 6:10170. doi:10.1038/ncomms10170

PubMed Abstract | CrossRef Full Text | Google Scholar

24. Clark K, Zepf B, Tatarakis M, Beg FN, Machacek A, et al. Energetic heavy-ion and proton generation from ultraintense laser-plasma interactions with solids. Phys Rev Lett (2000) 85:1654–7. doi:10.1103/physrevlett.85.1654

PubMed Abstract | CrossRef Full Text | Google Scholar

25. Wang P, Gong Z, Lee SG, Shou Y, Geng Y, Jeon C, et al. Super-heavy ions acceleration driven by ultrashort laser pulses at ultrahigh intensity. Phys Rev X (2021) 11:021049. doi:10.1103/physrevx.11.021049

CrossRef Full Text | Google Scholar

26. Braun-Munzinger P, Stachel J. Pion production in heavy-ion collisions. Annu Rev Nucl Part Sci (1987) 37:97–131. doi:10.1146/annurev.ns.37.120187.000525

CrossRef Full Text | Google Scholar

27. Bungau A, Cywinski R, Bungau C, King P, Lord J. Simulations of surface muon production in graphite targets. Phys Rev Spec Topics-accelerators Beams (2013) 16:014701. doi:10.1103/physrevstab.16.014701

CrossRef Full Text | Google Scholar

28. Bungau A, Cywinski R, Bungau C, King PJC, Lord JS. Target optimization studies for surface muon production. Phys Rev Spec Topics-accelerators Beams (2014) 17:034701. doi:10.1103/physrevstab.17.034701

CrossRef Full Text | Google Scholar

29. Radovic A, Williams M, Rousseau D, Kagan M, Bonacorsi D, Himmel A, et al. Machine learning at the energy and intensity frontiers of particle physics. Nature (2018) 560:41–8. doi:10.1038/s41586-018-0361-2

PubMed Abstract | CrossRef Full Text | Google Scholar

30. Emma C, Edelen A, Hogan MJ, O’Shea B, White GR, Yakimenko V. Machine learning-based longitudinal phase space prediction of particle accelerators. Phys Rev Acc Beams (2018) 21:112802. doi:10.1103/physrevaccelbeams.21.112802

CrossRef Full Text | Google Scholar

31. Gaffney JA, Brandon S, Humbird KD, Kruse MKG, Nora RC, Peterson JL, et al. Making inertial confinement fusion models more predictive. Phys Plasmas (2019) 26:082704. doi:10.1063/1.5108667

CrossRef Full Text | Google Scholar

32. Duris JP, Kennedy D, Hanuka A, Shtalenkova J, Edelen A, Baxevanis P, et al. Bayesian optimization of a free-electron laser. Phys Rev Lett (2020) 124:124801. doi:10.1103/physrevlett.124.124801

PubMed Abstract | CrossRef Full Text | Google Scholar

33. Shalloo RJ, Dann SJD, Gruse JN, Underwood CID, Antoine AF, Arran C, et al. Automation and control of laser wakefield accelerators using bayesian optimization. Nat Commun (2020) 11:6355. doi:10.1038/s41467-020-20245-6

PubMed Abstract | CrossRef Full Text | Google Scholar

34. Jalas S, Kirchen M, Messner P, Winkler P, Hübner L, Dirkwinkel J, et al. Bayesian optimization of a laser-plasma accelerator. Phys Rev Lett (2021) 126:104801. doi:10.1103/physrevlett.126.104801

PubMed Abstract | CrossRef Full Text | Google Scholar

35. Lu ZW, Hou XD, Wan F, Yi S, Lv C, Zhang B, et al. Diagnosis of ultrafast ultraintense laser pulse characteristics by machine-learning-assisted electron spin. Matter Radiat Extremes (2023) 8:034401. doi:10.1063/5.0140828

CrossRef Full Text | Google Scholar

36. Mockus J, Mockus L. Bayesian approach to global optimization and application to multiobjective and constrained problems. J Optimization Theor Appl (1991) 70:157–72. doi:10.1007/bf00940509

CrossRef Full Text | Google Scholar

37. Arber T, Bennett K, Brady C, Lawrence-Douglas A, Ramsay MG, Sircombe NJ, et al. Contemporary particle-in-cell approach to laser-plasma modelling. Plasma Phys Controlled Fusion (2015) 57:113001. doi:10.1088/0741-3335/57/11/113001

CrossRef Full Text | Google Scholar

38. Shaw B, Steinke S, van Tilborg J, Leemans WP. Reflectance characterization of tape-based plasma mirrors. Phys Plasmas (2016) 23:063118. doi:10.1063/1.4954242

CrossRef Full Text | Google Scholar

39. Agostinelli S, Allison J, Amako K, Apostolakis J, Araujo H, Arce P, et al. Geant4—A simulation toolkit. Nucl Instr Methods Phys Res (2003) 506:250–303. doi:10.1016/s0168-9002(03)01368-8

CrossRef Full Text | Google Scholar

40. Bertini HW. Low-energy intranuclear cascade calculation. Phys Rev (1963) 131:1801–21. doi:10.1103/physrev.131.1801

CrossRef Full Text | Google Scholar

41. Boudard A, Cugnon J, David JC, Leray S, Mancusi D. New potentialities of the liège intranuclear cascade model for reactions induced by nucleons and light charged particles. Phys Rev C (2013) 87:014606. doi:10.1103/physrevc.87.014606

CrossRef Full Text | Google Scholar

42. Rodríguez-Sánchez JL, David JC, Mancusi D, Boudard A, Cugnon J, Leray S. Improvement of one-nucleon removal and total reaction cross sections in the liège intranuclear-cascade model using Hartree-Fock-bogoliubov calculations. Phys Rev C (2017) 96:054602. doi:10.1103/physrevc.96.054602

CrossRef Full Text | Google Scholar

43. Mancusi D, Boudard A, Cugnon J, David JC, Kaitaniemi P, Leray S. Extension of the liège intranuclear-cascade model to reactions induced by light nuclei. Phys Rev C (2014) 90:054602. doi:10.1103/physrevc.90.054602

CrossRef Full Text | Google Scholar

44. Jones DR, Schonlau M, Welch WJ. Efficient global optimization of expensive black-box functions. J Glob Optimization (1998) 13:455–92. doi:10.1023/a:1008306431147

CrossRef Full Text | Google Scholar

45. Baudin M, Dutfoy A, Iooss B, Popelin AL (2017). Title: Open turns: An industrial software for uncertainty quantification in simulation. Available at: https://arxiv.org/abs/1501.05242.

Google Scholar

46. Schulz E, Speekenbrink M, Krause A. A tutorial on Gaussian process regression: Modelling, exploring, and exploiting functions. J Math Psychol (2018) 85:1–16. doi:10.1016/j.jmp.2018.03.001

CrossRef Full Text | Google Scholar

47. Roussel R, Gonzalez-Aguilera JP, Kim YK, Wisniewski EE, Liu W, Piot P, et al. Turn-key constrained parameter space exploration for particle accelerators using bayesian active learning. Nat Commun (2021) 12:5612. doi:10.1038/s41467-021-25757-3

PubMed Abstract | CrossRef Full Text | Google Scholar

48. van der Maaten L, Hinton GE. Visualizing data using t-sne. J Machine Learn Res (2008) 9:2579–605.

Google Scholar

49. Pegoraro F, Bulanov SV. Photon bubbles and ion acceleration in a plasma dominated by the radiation pressure of an electromagnetic pulse. Phys Rev Lett (2007) 99:065002. doi:10.1103/PhysRevLett.99.065002

PubMed Abstract | CrossRef Full Text | Google Scholar

50. Daido H, Nishiuchi M, Pirozhkov AS. Review of laser-driven ion sources and their applications. Rep Prog Phys (2012) 75:056401. doi:10.1088/0034-4885/75/5/056401

PubMed Abstract | CrossRef Full Text | Google Scholar

51. Shen XF, Qiao B, Pukhov A, Kar S, Zhu SP, Borghesi M, et al. Scaling laws for laser-driven ion acceleration from nanometer-scale ultrathin foils. Phys Rev E (2021) 104:025210. doi:10.1103/physreve.104.025210

PubMed Abstract | CrossRef Full Text | Google Scholar

52. Zhang X, Shen B, Ji L, Wang F, Jin Z, Li X, et al. Ion acceleration with mixed solid targets interacting with circularly polarized lasers. Phys Rev Spec Topics-accelerators Beams (2009) 12:021301. doi:10.1103/physrevstab.12.021301

CrossRef Full Text | Google Scholar

53. Ji L, Shen B, Zhang X, Wang F, Jin Z, Li X, et al. Generating monoenergetic heavy-ion bunches with laser-induced electrostatic shocks. Phys Rev Lett (2008) 101:164802. doi:10.1103/physrevlett.101.164802

PubMed Abstract | CrossRef Full Text | Google Scholar

54. Zhao J, Hu YT, Zhang H, Lu Y, Hu LX, Shao FQ, et al. Multistage positron acceleration by an electron beam-driven strong terahertz radiation. Photonics (2023) 10:364. doi:10.3390/photonics10040364

CrossRef Full Text | Google Scholar

55. Martinez B, Chen SN, Bolaños S, Blanchot N, Boutoux G, Cayzac W, et al. Numerical investigation of spallation neutrons generated from petawatt-scale laser-driven proton beams. Matter Radiat Extremes (2021) 7:024401. doi:10.1063/5.0060582

CrossRef Full Text | Google Scholar

56. Calvin L, Tomassini P, Doria D, Martello D, Deas RM, Sarri G. Laser-driven muon production for material inspection and imaging. Front Phys (2023) 11:1177486. doi:10.3389/fphy.2023.1177486

CrossRef Full Text | Google Scholar