- School of Mathematics and Physics, Lanzhou Jiaotong University, Lanzhou, China
The fractional stochastic vibration system is quite different from the traditional one, and its application potential is enormous if the noise can be deployed correctly and the connection between the fractional order and the noise property is unlocked. This article uses a fractional modification of the well-known van der Pol oscillator with multiplicative and additive recycling noises as an example to study its stationary response and its stochastic bifurcation. First, based on the principle of the minimum mean square error, the fractional derivative is equivalent to a linear combination of damping and restoring forces, and the original system is simplified into an equivalent integer order system. Second, the Itô differential equations and One-dimensional Markov process are obtained according to the stochastic averaging method, using Oseledec multiplicative ergodic theorem and maximal Lyapunov exponent to judge local stability, and judging global stability is done by using the singularity theory. Lastly, the stochastic D-bifurcation behavior of the model is analyzed by using the Lyapunov exponent of the dynamical system invariant measure, and the stationary probability density function of the system is solved according to the FPK equation. The results show that the fractional order and noise property can greatly affect the system’s dynamical properties. This paper offers a profound, original, and challenging window for investigating fractional stochastic vibration systems.
1 Introduction
Fractional derivative [1, 2] is an extension of the theory of integer derivatives, and the study of fractional derivatives has a history of over 300 years. Some new materials have appeared, e.g., viscoelastic materials, nanomaterials, cement mortar, 3D-printed materials, and porous materials [3–8], which are different from either a solid or a fluid, and their constitutive relation is extremely difficult to be expressed correctly by the traditional calculus though much effort has been made to solve the problem, for example, using the fractal viscoelastic model [9] and the fractal rheological model [10]; the intractable constitutive relation has not yet been solved.
Considering its memory property, we consider that fractional calculus might be the best candidate for stochastic dynamical systems [11, 12]. Stochastic disturbances are widespread in nature, and fractional stochastic systems have become a hot spot in both mathematics and physics to deal with noise excitation. For example, energy-harvesting devices [13–15] are always subject to random excitation, and a fractional model can effectively reveal the bifurcation properties and multiple attractors of the energy-harvesting system, for example, Ref. [16]. Fractional models for Gaussian white noise also caught much attention [17–21], and the fractional convolution kernel neural network is a suitable mathematical tool for fault diagnosis [22–24]. Duffing oscillator [25, 26] is extended to its fractional partner under noise [27, 28]. Van der Pol oscillator [29] is another widely used model for the analysis of fractional stochastic P-bifurcation [30, 31].
In reality, noise exists in all aspects of practical applications, especially in nonlinear systems. The properties of stationary response, energy-harvesting efficiency, stability, and bifurcation will be greatly affected by noise excitation. At present, the research on the dynamic behavior of systems driven by recycling noise has attracted widespread attention from domestic and foreign scholars and achieved fruitful results, especially in the birhythmic biological system [32], stochastic resonance in asymmetric bistable systems [33], and the double entropic stochastic resonance phenomenon [34]. In this article, the fractional van der Pol model with recycling noise is adopted to investigate its dynamical properties.
2 Model description
Balthazar van der Pol is a famous electronic engineer in the Netherlands. In 1927, he first deduced the famous van der Pol equation in order to describe the oscillation effect of triodes in electronic circuits, as shown below:
Afterward, as a classic nonlinear dynamic system, it is often used in mathematics and some nonlinear dynamic systems to demonstrate its dynamic behavior characteristics. In continuous research, the highest number of nonlinear terms considered is also constantly increasing, and there are also various methods for solving approximate solutions of such equations [35, 36]. From the classical van der Pol equation, changing the order of the equation can obtain systems with different dynamic behaviors, thereby better obtaining the dynamic behavior characteristics of the system. Therefore, we use the following equation to introduce the fractional generalized van der Pol model with multiplicative and additive recycling noise:
where
There are other definitions of fractional derivatives, for example, two-scale fractal derivative [37–41] and He’s fractional derivative [42]. The Caputo fractional derivative has memory property [43, 44], so it is used for the present study.
The
where
In order to identify
According to the minimum mean square method [44], we have
Equation 6 leads to the following equations:
Assuming that
and
Considering Eq. 8, 9, we re-write Eq. 7 in the form
For the same reason, we have
Hence
To simplify Eq. 10 further, we use the following asymptotic integrals
In view of Eq. 11, the integral averaging of Eq. 10 with respect to
Hence, the equivalent system (4) can be written in the form
where
3 Model processing
Now the problem becomes relatively simple; we assume that the solution of Eq. 13 can be expressed as [49].
where
We re-write Eq. 13 in the form
By Eq. 15 and the stochastic averaging method [50], Eq. 16 becomes
where
The recycling noise is a stationary process and can be approximated by a 2-D diffusion process. After stochastic averaging, the drift and diffusion coefficients are as follows:
where
For the deterministic averaging of
The corresponding Itô SDE is
where
The one-dimensional Markov Process can be expressed as:
where
4 Stochastic stability analysis
4.1 The local stochastic stability
Considering the case of
Therefore, it is obtained that
Then the approximate solution of the Lyapunov exponent of Itô stochastic differential equation is obtained
When
4.2 The global stochastic stability
4.2.1 Linear Itô stochastic stability
Judging global stability by the singularity theory,
And the following conclusions are drawn, as shown in Table 1.
4.2.2 Stability of nonlinear Itô stochastic differential equation
When
Conclusion: when
5 Stochastic bifurcation analysis
5.1 D-bifurcation
If
Equation 27 is the only strong solution of Eq. 26 with
Let
At this time, Eq. 27 has a non-trivial stationary state and a fixed-point equilibrium state. Assuming the invariant measures of these two kinds of stationary states are
The Lyapunov exponent of
Substituting Eq. 30 into Eq. 31, here
Invariant estimate
Let
5.2 P-bifurcation
5.2.1 Stochastic P-bifurcation under additive recycling noise
When additive noise just exists,
the corresponding boundary conditions are
In view of Eq. 35, the stationary probability density of the amplitude is
where
In view of Eq. 23, from Eq. 36, we obtain
where
The original system response meets
5.2.1.1 Influence of fractional order
As fractional damping is a combination of the equivalent stiff and equivalent damping, the fractional order is of paramount importance; its value can be calculated by He-Liu’s fractal formulation [52] for practical applications. According to Eq. 12, when
Setting
When
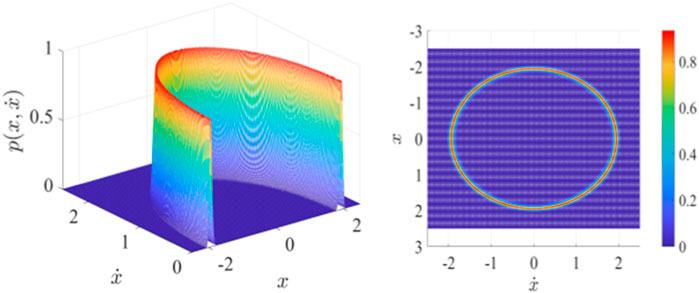
FIGURE 1. Joint probability density function section and top view of Eq. 13 when
When
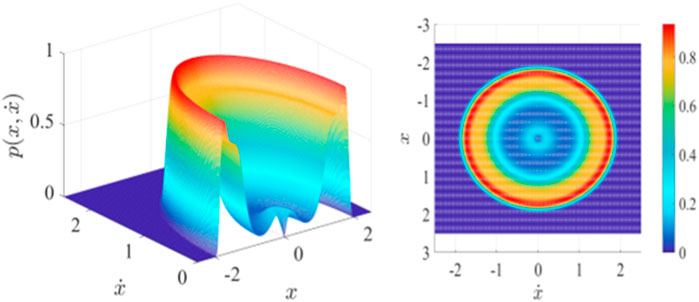
FIGURE 2. Joint probability density function section and top view of Eq. 13 when
When
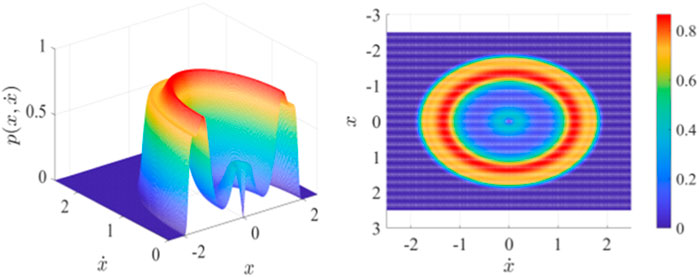
FIGURE 3. Joint probability density function section and top view of Eq. 13 when
When
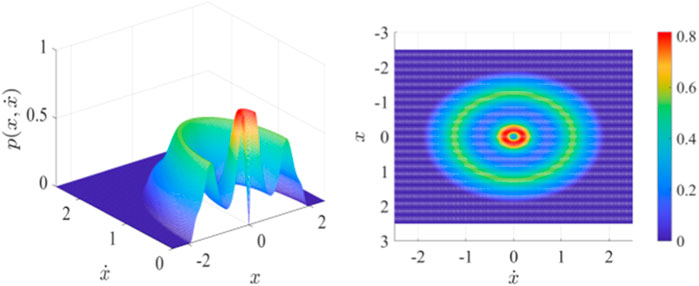
FIGURE 4. Joint probability density function section and top view of Eq. 13 when
Based on the above discussions, we conclude that the fractional order can cause stochastic P-bifurcation behavior in the system. From Figure 5, we find that an increasing fractional order will change the stationary response from a single mode to a dual mode and then to a tristable mode. The peak value changes from a single peak to two peaks and then to three peaks, so stochastic P-bifurcation occurs. Increasing the value of
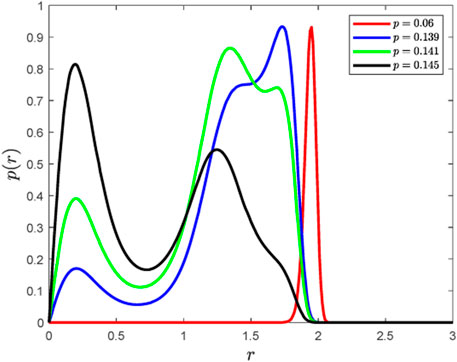
FIGURE 5. Stationary probability density function diagram of Eq. 13 when
5.2.1.2 Influence of noise intensity
Keeping the above parameters unchanged, and fixing
When
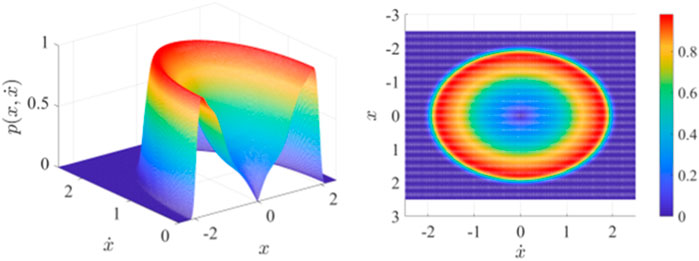
FIGURE 6. Joint probability density function section and top view of Eq. 13 when
When
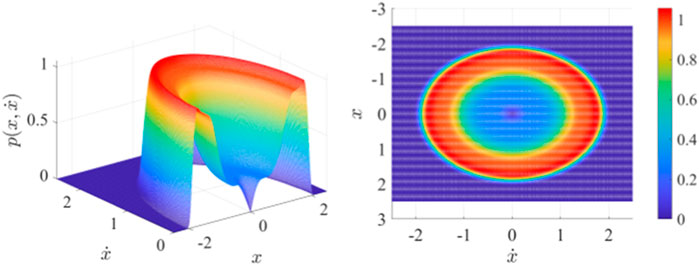
FIGURE 7. Joint probability density function section and top view of Eq. 13 when
When
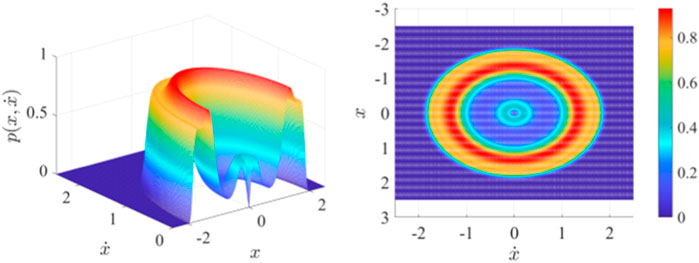
FIGURE 8. Joint probability density function section and top view of Eq. 13 when
When
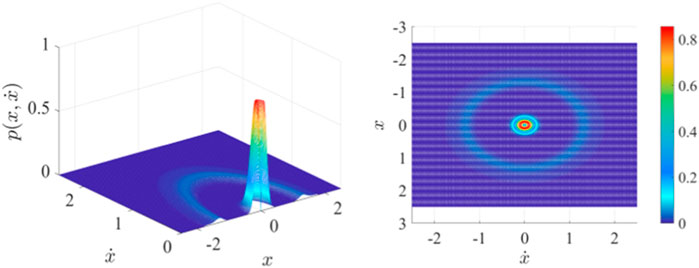
FIGURE 9. Joint probability density function section and top view of Eq. 13 when
Based on the above discussions, it can be verified that changing the noise intensity affects greatly stochastic P-bifurcation property. From Figure 10, it can also be seen that with noise intensity being reduced, the stationary response of the system switches from a single mode to a dual mode and then to a tristable mode. The peak value of the stationary probability density function curve changes from a single peak to two peaks and then three peaks, so stochastic P-bifurcation occurs. Decreasing the value of
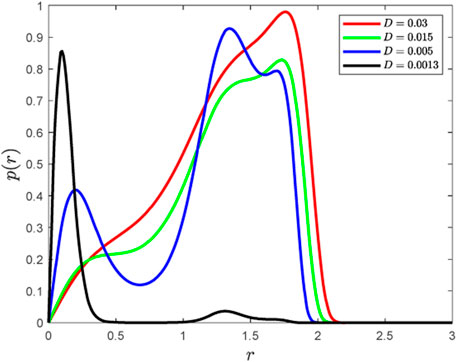
FIGURE 10. Stationary probability density function diagram of Eq. 13 when
5.2.2 Additive and multiplicative recycling noise
When
where
In view of Eq. 23, from Eq. 42, we have
where
Keeping the above parameters unchanged, we draw the joint probability density function section and top view of Eq. 13 under the influence of different fractional orders and noise intensity.
When
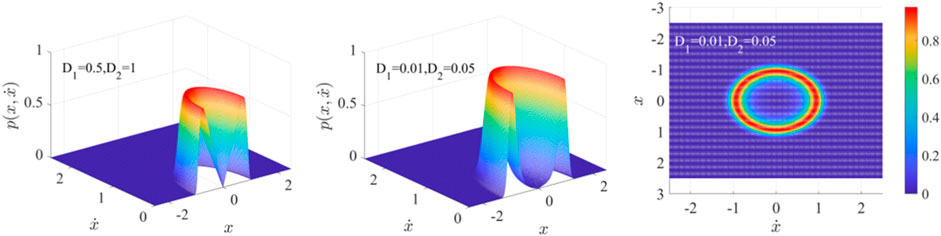
FIGURE 11. Joint probability density function section and top view of Eq. 13 when
When
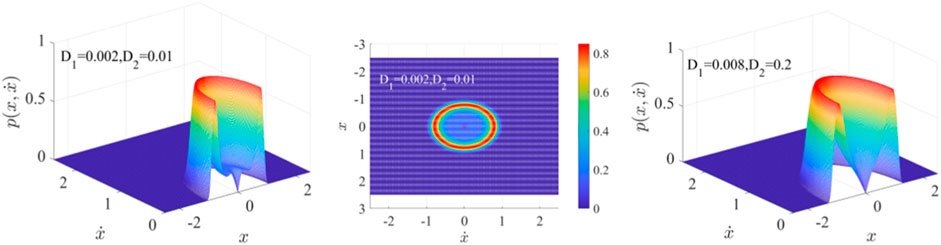
FIGURE 12. Joint probability density function section and top view of Eq. 13 when
When

FIGURE 13. Joint probability density function section and top view of Eq. 13 when
6 Conclusion
In this paper, the stationary response and the stochastic bifurcation of the fractional van der Pol equation under multiplicative and additive recycling noise excitations are investigated. By the least square method, we obtain an equivalent integral nonlinear stochastic system. The Itô differential equation and One-dimensional Markov process are obtained according to the stochastic averaging method. We discuss the local and global stochastic stability and analyze the conditions for inducing D-bifurcation and P-bifurcation in the system. The analysis shows that when
Data availability statement
The original contributions presented in the study are included in the article/Supplementary material, further inquiries can be directed to the corresponding author.
Author contributions
J-GZ: supervision, writing–review and editing, funding acquisition, investigation, and project administration. FW: writing–original draft, writing–review and editing, and software. H-NW: writing–review and editing and software. All authors contributed to the article and approved the submitted version.
Funding
This study was supported by the key project of the Gansu Province natural science foundation of China (No. 23JRRA882).
Conflict of interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Publisher’s note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
References
1. He JH. A tutorial review on fractal spacetime and fractional calculus. Int J Theor Phys (2014) 53:3698–718. doi:10.1007/s10773-014-2123-8
2. He JH. Fractal calculus and its geometrical explanation. Phys (2018) 10:272–6. doi:10.1016/j.rinp.2018.06.011
3. He CH, Liu C. Fractal approach to the fluidity of a cement mortar. Nonlinear Engineering-modeling Appl (2022) 11(1):1–5. doi:10.1515/nleng-2022-0001
4. Zuo YT, Liu HJ. Fractal approach to mechanical and electrical properties of graphene/sic composites. Facta Universitatis: Ser Mech Eng (2021) 19(2):271–84. doi:10.22190/fume201212003z
5. He CH, Liu C. Fractal dimensions of a porous concrete and its effect on the concrete’s strength. Facta Universitatis Ser Mech Eng (2023) 21(1):137–50. doi:10.22190/FUME221215005H
6. Jankowski P. Detection of nonlocal calibration parameters and range interaction for dynamic of FGM porous nanobeams under electro-mechanical loads. Facta Universitatis Ser Mech Eng (2022) 20(3):457–78. doi:10.22190/fume210207007j
7. He CH, Shen Y, Ji FY, He JH. Taylor series solution for fractal Bratu-type equation arising in electrospinning process. Fractals (2020) 28(1):2050011. doi:10.1142/s0218348x20500115
8. Liu FJ, Zhang T, He CH, Tian D. Thermal oscillation arising in a heat shock of a porous hierarchy and its application. Facta Universitatis Ser Mech Eng (2022) 20(3):633–45. doi:10.22190/fume210317054l
9. Liang YH, Wang KJ. A new fractal viscoelastic element: Promise and applications to Maxwell-Rheological model. Therm Sci (2021) 25(2):1221–7. doi:10.2298/tsci200301015l
10. Zuo YT. Effect of Sic particles on viscosity of 3-D print paste a fractal rheological model and experimental verification. Therm Sci (2021) 25(3):2405–9. doi:10.2298/tsci200710131z
11. Long Y, Xu BB, Chen DY, Ye W. Dynamic characteristics for a hydro-turbine governing system with viscoelastic materials described by fractional calculus. Appl Math Model (2018) 58:128–39. doi:10.1016/j.apm.2017.09.052
12. Wang L, Xue LL, Xu W, Yue XL. Stochastic P-bifurcation analysis of a fractional smooth and discontinuous oscillator via the generalized cell mapping method. Int J Non-Linear Mech (2017) 96:56–63. doi:10.1016/j.ijnonlinmec.2017.08.003
13. He CH, Amer TS, Tian D, Abolila AF, Galal AA. Controlling the kinematics of a spring-pendulum system using an energy harvesting device. J Low Frequency Noise: Vibration Active Control (2022) 41(3):1234–57. doi:10.1177/14613484221077474
14. He CH, Ei-Dib YO. A heuristic review on the homotopy perturbation method for non-conservative oscillators. J Low FrequCency Noise, Vibration Active Control (2022) 41(2):572–603. doi:10.1177/14613484211059264
15. He JH, Ei-Dib YO. The reducing rank method to solve third-order Duffing equation with the homotopy perturbation. Numer Methods Differential Equations (2021) 37(2):1800–8. doi:10.1002/num.22609
16. Zhang WT, Xu W, Niu LZ, Tang YN. Bifurcations analysis of a multiple attractors energy harvesting system with fractional derivative damping under random excitation. Commun Nonlinear Sci Numer Simulation (2023) 118:107069. doi:10.1016/j.cnsns.2022.107069
17. Hu DL, Mao XC, Han L. Stochastic stability analysis of a fractional viscoelastic plate excited by Gaussian white noise. Mech Syst Signal Process (2022) 177:109181. doi:10.1016/j.ymssp.2022.109181
18. Li YJ, Wu ZQ, Lan QX, Cai YJ, Xu HF, Sun YT. Stochastic transition behaviors in a Tri-Stable van der Pol oscillator with fractional delayed element subject to Gaussian White Noise. Therm Sci (2022) 26(3):2713–25. doi:10.2298/tsci2203713l
19. Li YJ, Wu ZQ, Lan QX, Cai YJ, Xu HF, Sun YT. Transition behaviors of system energy in a bi-stable van Ver Pol oscillator with fractional derivative element driven by multiplicative Gaussian white noise. Therm Sci (2022) 26(3):2727–36. doi:10.2298/tsci2203727l
20. Li YJ, Wu ZQ, Wang F, Zhang GQ, Wang YC. Stochastic P-bifurcation in a generalized Van der Pol oscillator with fractional delayed feedback excited by combined Gaussian white noise excitations. J Low Frequency Noise, Vibration Active Control (2021) 40(1):91–103. doi:10.1177/1461348419878534
21. Din A, Ain QT. Stochastic optimal control analysis of a mathematical model: Theory and application to non-singular kernels. fractal and fractional (2022) 6:279. doi:10.3390/fractalfract6050279
22. Zhu R, Wang MX, Xu SY, Li K, Han QP, Tong X, et al. Fault diagnosis of rolling bearing based on singular spectrum analysis and wide convolution kernel neural network. J Low Frequency Noise, Vibration Active Control (2022) 41(4):1307–21. doi:10.1177/14613484221104639
23. Kuo PH, Tseng YR, Luan PC, Yau HT. Novel fractional-order convolutional neural network based chatter diagnosis approach in turning process with chaos error mapping. Nonlinear Dyn (2023) 111:7547–64. doi:10.1007/s11071-023-08252-w
24. Kuo PH, Chen YW, Hsieh TH, Jywe WY, Yau HT. A thermal displacement prediction system with an automatic Lrgtvac-PSO optimized branch Structured bidirectional GRU neural network. IEEE Sensors Journa (2023) 23:12574–86. doi:10.1109/JSEN.2023.3269064
25. He JH, Jiao ML, Gepreel KA, Khan Y. Homotopy perturbation method for strongly nonlinear oscillators. Mathematics Comput Simulation (2023) 204:243–58. doi:10.1016/j.matcom.2022.08.005
26. He JH, Jiao ML, He CH. Homotopy perturbation method for fractal Duffing oscillator with arbitrary conditions. Fractals (2022) 30. doi:10.1142/S0218348X22501651
27. Chen LC, Zhu WQ. Stochastic jump and bifurcation of Duffing oscillator with fractional derivative damping under combined harmonic and white noise excitations. Int J Non-Linear Mech (2011) 46:1324–9. doi:10.1016/j.ijnonlinmec.2011.07.002
28. Chen LC, Zhu WQ. Stationary response of duffing oscillator with fractional derivative damping under combined harmonic and wide band noise excitations. Chin J Appl Mech (2010) 3:517–21.
29. He CH, Tian D, Moatimid GM, Salman HF, Zekry MH. Hybrid Rayleigh–van der pol–duffing oscillator: Stability analysis and controller. J Low Frequency Noise, Vibration Active Control (2022) 41(1):244–68. doi:10.1177/14613484211026407
30. Li YJ, Wu ZQ. Stochastic P-bifurcation in a tri-stable Van der Pol system with fractional derivative under Gaussian white noise. J Vibroengineering (2019) 21:803–15. doi:10.21595/jve.2019.20118
31. Li YJ, Wu ZQ, Lan QX, Hao Y, Zhang XY. Stochastic P bifurcation in a tri-stable van der Pol oscillator with fractional derivative excited by combined Gaussian white noises. J Vibration Shock (2021) 40(16):275–93. doi:10.21595/jve.2019.20118
32. Chamgoué AC, Yamapi R, Woafo P. Bifurcations in a biorhythmic biological system with time-delayed noise. Nonlinear Dyn (2013) 73:2157–73. doi:10.1007/s11071-013-0931-7
33. Wu YZ, Sun ZK. Residence-times distribution function in asymmetric bistable system driven by noise recycling. Acta Phys Sin (2020) 69(12):120501. doi:10.7498/aps.69.20201752
34. Guo XY, Cao TQ. Phenomenon of double entropic stochastic resonance with recycled noise. Chin J Phys (2022) 77:721–32. doi:10.1016/j.cjph.2021.10.020
35. He KY, Nadeem M, Habib S, Sedighi HM, Huang DH. Analytical approach for the temperature distribution in the casting-mould heterogeneous system. Int J Numer Methods Heat Fluid Flow (2021) 32:1168–82. doi:10.1108/HFF-03-2021-0180
36. Fang JH, Nadeem M, Habib M, Karim S, Wahash HA. A new iterative method for the approximate solution of klein-gordon and sine-gordon equations. J Funct Spaces (2022) 2022:1–9. doi:10.1155/2022/5365810
37. He JH, Kou SJ, He CH, Zhang ZW, Gepreel KA. Fractal oscillation and its frequency-amplitude property. Fractals (2021) 29(4):2150105. doi:10.1142/s0218348x2150105x
38. He JH, Moatimid G, Zekry M. Forced nonlinear oscillator in a fractal space. Facta Universitatis, Ser Mech Eng (2022) 20(1):001–20. doi:10.22190/fume220118004h
39. Tian D, Ain QT, Anjum N, He CH, Cheng B. Fractal N/MEMS: From pull-in instability to pull-in stability. Fractals (2021) 29:2150030. doi:10.1142/S0218348X21500304
40. He CH. A variational principle for a fractal nano/microelectromechanical (N/MEMS) system. Intermational J Numer Methods Heat Fluid Flow (2023) 33(1):351–9. doi:10.1108/hff-03-2022-0191
41. Ain QT, Sathiyaraj Karim S, Nadeem M, Mwanakatwe PK, Kandege Mwanakatwe P. ABC fractional derivative for the alcohol drinking model using two-scale fractal dimension. Complexity (2022) 2022:1–11. doi:10.1155/2022/8531858
42. Wang Y, An JY. Amplitude-frequency relationship to a fractional Duffing oscillator arising in microphysics and tsunami motion. J Low Frequency Noise Vibration Active Control (2019) 38(3-4):1008–12. doi:10.1177/1461348418795813
43. Mendes EM, Salgado GH, Aguirre LA. Numerical solution of Caputo fractional differential equations with infinity memory effect at initial condition. Commun Nonlinear Sci Numer Simulation (2019) 69:237–47. doi:10.1016/j.cnsns.2018.09.022
44. Zeng HJ, Wang YX, Xiao M, Wang Y. Fractional solitons: New phenomena and exact solutions. Front Phys (2023) 11:1177335. doi:10.3389/fphy.2023.1177335
45. Chen LC, Wang WH, Li ZS, Zhu WQ. Stationary response of Duffing oscillator with hardening stiffness and fractional derivative. Int J Non-Linear Mech (2013) 48:44–50. doi:10.1016/j.ijnonlinmec.2012.08.001
46. Li W, Zhang MT, Zhao JF. Stochastic bifurcations of generalized Duffing-van der Pol system with fractional derivative under colored noise. Chin Phys B (2017) 26:090501. doi:10.1088/1674-1056/26/9/090501
47. Chen LC, Li ZS, Zhuang QQ, Zhu WQ. First-passage failure of single-degree-of-freedom nonlinear oscillators with fractional derivative. J Vibration Control (2013) 19:2154–63. doi:10.1177/1077546312456057
48. Chen LC, Zhu WQ. Stochastic response of fractional-order van der Pol oscillator. Theor Appl Mech Lett (2014) 4:013010. doi:10.1063/2.1401310
49. Spanos PD, Zeldin BA. Random vibration of systems with frequency-dependent parameters or fractional derivatives. J Eng Mech (1997) 123(3):290–2. doi:10.1061/(asce)0733-9399(1997)123:3(290)
50. Zhu WQ. Nonlinear stochastic dynamics and control: Hamilton theoretical framework. Beijing, China: Science Press (2003).
51. Oseledec VI. A multiplicative ergodic theorem. Lyapunov characteristic numbers for dynamical systems. Trans Mosc Math. Soc (1968) 19(2):197–231.
52. He CH, Liu C. Fractal dimensions of a porous concrete and its effect on the concrete’s strength. Facta Universitatis Ser Mech Eng (2023) 21(1):137–50. doi:10.22190/FUME221215005H
Keywords: van der Pol system, fractional derivative, recycling noise, stochastic averaging method, stochastic bifurcation
Citation: Zhang J-G, Wang F and Wang H-N (2023) Fractional stochastic vibration system under recycling noise. Front. Phys. 11:1238901. doi: 10.3389/fphy.2023.1238901
Received: 12 June 2023; Accepted: 18 July 2023;
Published: 02 August 2023.
Edited by:
Ji-Huan He, Soochow University, ChinaReviewed by:
Muhammad Nadeem, Qujing Normal University, ChinaYajie Li, Henan University of Urban Construction, China
Ain Qura Tul, Guizhou University, China
Copyright © 2023 Zhang, Wang and Wang. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Jian-Gang Zhang, WmhhbmdqZzc3MTU3NzZAMTI2LmNvbQ==
 Jian-Gang Zhang
Jian-Gang Zhang Fang Wang
Fang Wang