Dynamics analysis of the two-layer complex propagation network with individual heterogeneous decreased behavior

Due to the differences in society stratum, personal profession, and social acceptability, information propagation can be impacted by the contact capabilities of individuals. Importantly, we found that with the changes in individual psychology, their response to a phenomenon will gradually weaken. This phenomenon is called heterogeneous decreased behavior and applied in the fields of economics, sociology, and ecology. In the social network, people show a gradually decreasing degree of interest for information, named individual heterogeneous decreased behavior (IHDB). We structure a two-layer network model to describe individual behavioral contact and propose a threshold function to represent IHDB. Meanwhile, we use partition theory to explain the information propagation mechanism. Through experiments, it is demonstrated that there is a continuous information outbreak in the ultimate adoption size when individuals exhibit a positive IHDB. However, when individuals exhibit a passive IHDB, there is a discontinuous information outbreak in the ultimate adoption size. Eventually, our experiments show that the theoretical analysis coincides with the results of the simulations.

1 Introduction

1.1 Research background

With the persistent exploration of the information propagation mechanism, researchers have discovered the influencing factors of different individual behaviors on information outbreak [1–9]. Individual behavior is mainly affected by individual psychology. For example, in information propagation, some people show positive adoption, while others show negative adoption [10, 11]. These behaviors are not only applied in information propagation but also in other fields, such as economics, ecology, and medicine. By investigating abundant literature works, we found that there is a latent behavioral phenomenon in multiple fields. Particularly, in investment, when the investment quota is increased, the additional income brought by an increase in one unit of investment will decrease [12–15]. In agricultural production, when the number of chemical fertilizers increases, the additional yield that can be brought by a unit of chemical fertilizers will decrease [16, 17]. In medicine, when the dose of drugs increases, the treatment effect of drugs on patients will decrease [18, 19]. In the field of education, the additional educational effects that can be brought about by one unit of educational resources will be reduced [20, 21]. In summary, this behavior is called a decreasing behavior which is applied in multiple fields. For propagation dynamics, the paper aims to explore the impact mode of decreasing behavior on information propagation.

Based on our survey, we found that the phenomenon of decreased behaviors also exists in information propagation. For example, for advertising effect, at the beginning, advertising may attract people’s attention, but over time, the interest degree of people in advertising will gradually decrease [22, 23]. For media marketing, people’s interest degree in the same type of content will also decrease [24, 25]. For teaching, learning motivation of students for the same knowledge will decrease [26, 27]. In summary, in information propagation, if the same information is repeatedly received, the interest degree of people will decrease, which is closely related to individual psychology [28]. Therefore, this paper defines the phenomenon as an individual heterogeneous decreasing behavior, which is called IHDB, to explore its impact on information propagation mechanisms.

1.2 Main contributions

In this study, we found that people can only closely contact with a small number of friends due to the differences in society stratum, personal profession, and social acceptability [29–31]. For instance, a user can face difficulty to connect with all of his/her friends in a short period of time. Furthermore, several social media platforms, such as Twitter, Instagram, Tinder, and WhatsApp, are used frequently by many individuals [32–34]. Therefore, this paper considers the two-layer contacted network to explore the individual contact capacity which needs to be considered to analyze the information propagation mechanism.

More importantly, information propagation will be influenced by the individual adoption behaviors [35, 36]. According to the explanation given in Section 1.1, we found that the individual interest in behavior adoption is closely related to the proportion of neighbors who adopt the behavior. The individual heterogeneous decreasing behavior (IHDB) illustrates that when more and more neighbors transmit a same piece of information to the individual, the passion degree of the individual to receive the information gradually decreases.

The advantages of the IHDB compared to other behaviors are as follows: i) More accurate simulation of reality: IHDB reflects different responses and response degrees of the individual in information acceptance. This is closer to the real situation because the response of a person is gradually weakened in each receiving information, which will affect the information propagation process. ii) More accurate prediction of information propagation: By considering IHDB, you can more accurately predict the spread trend of information in the networks. With the proportion of neighbors in adoption state changes, the individual behavior spreads more passively or slowly. This difference can be reflected in the model, thereby providing more accurate diffusion forecasts. iii) Planning more targeted propagation strategies: The consideration of IHDB can help decision-makers formulate more targeted information dissemination strategies. By understanding the mental characteristics and behaviors of people, we can make better customized strategies for different types of information and improve the effect of information propagation. iv) Research and identification of crucial factors: Simulation of IHDB can help researchers identify the impact factors. By observing the IHDB in the individual, it is possible to determine the factors that play a key role in the information dissemination network so as to intervene or use these factors to promote information propagation.

Enlightened by the aforementioned overview, we consider individual limited contact capacity, capture the IHDB, and define a non-rule trapezoidal-like threshold function to illustrate the IHDB feature. The non-rule trapezoidal-like threshold function displays a slow and non-linear rising, subsequently maintaining a horizontal line. In addition, we provide a partition theory to analyze the information propagation mechanism based on limited contact and IHDB. Finally, through the theoretical analysis and experimental simulation, this paper reveals the information propagation mechanism.

The remainder of this paper is organized as follows: in Section 2, we put forward a probability adoption threshold model for information propagation on the two-layer contacted network. Section 3 exhibits a division theory based on limited contact and IHDB function model. Section 4 uses simulations and theoretical assessments to validate the information propagation mechanism. Finally, Section 5 summarizes the results, and Section 6 reports the conclusion.

2 Information propagation model

2.1 Related work

A two-layered network model with N nodes is set up to explore the impacts of individual contact capability and IHDB characteristics on information propagation. Layers A and B represent two independent social network layers. Since the nodes connecting the various tiered networks are one-to-one correspondences, the same node is present in each layer. Then, the degree vector of node i is represented by $\overrightarrow{k_i}=(k_i^A,k_i^B)$, where $k_i^X$ represents a node degree. The degree distribution $P(\vec{k})$ of the network is represented by the degree vector $\vec{k}$. Furthermore, the degree distributions P_X(k^X) of $P(\vec{k})$ can be broken down in accordance with the uncorrelated feature. Considering the independence of P_A(k^A) and P_B(k^B), $P(\vec{k})=P_A(k^A)P_B(k^B)$.

This paper establishes a two-layer social network model to explore a novel information propagation mechanism by exploiting S–A–R (susceptible–adopted–recovered) propagation theory, as illustrated in Figure 1A. The explanation of the S–A–R model theory is as follows: a node in the susceptible state is denoted as the S-state, in the adopted state is denoted as the A-state, and in the recovered state is denoted as the R-state. Specifically, the individuals in the S-state cannot propagate information, but they can receive it from their A-state neighbors. The A-state individuals have adopted a piece of information and will transmit it to their neighbors in the S-state. The individuals in the R-state no longer receive information and exit the whole propagation process. If an individual transforms its state in the X-layer in the two-layer network model, it will change to the same state in other layers.

FIGURE 1

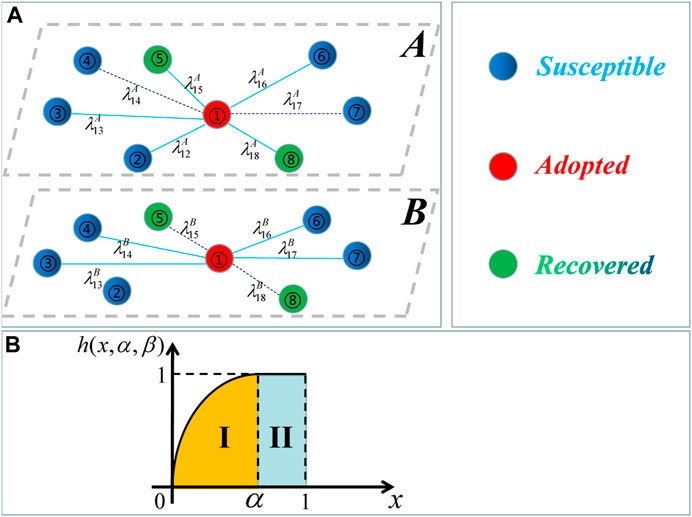
FIGURE 1. (A) Diagram of S–A–R propagation on the two-layer social network. Node 1 in the adopted state can transmit information to its neighbors in the susceptible state. Symbol λ represents the transmission probability in the social network. The dotted line means that the information has been transmitted in the last time step such as node 1 and its neighbors 4, 7 in layer A and node 1 and its neighbors 5, 8 in layer B. The solid line denotes that the information has not been transmitted along the corresponding edges. (B) Numerical function of a non-rule trapezoidal-like behavior. Symbol h denotes the proportion of information that a node in the adopted state has obtained its degree. Symbol α denotes the IHDB parameter.

This paper first considers that the contact ability of individuals can be set as C. If C < k_i, where k_i is the degree of individual i, an individual that has been adopted who can only contact some of its neighbors. However, it can contact all of its neighbors if C ≥ k_i. The probability of information transmission in the network can be set as λ. The probability that the information is received by the neighbor j in the S-state can be denoted as $\frac{\lambda C}{k_j^X}$(X ∈ {A, B}).

m^X is the total amount of information that the individual in the S-state has successfully received in the layer X. At the beginning, there is no information spreading on the multiple-layered network, the reason why the j value $m_j^X$ of the individual in the S-state is 0. When a neighbor i in the A-state effectively spreads information to individual j along the related link in the A-layer or B-layer, the total information bits of individual j will rise by 1 at each time step, i.e., $m_j^X\to m_j^X+1$. To explain the IHDB on information propagation, a non-rule trapezoidal-like function is proposed to illustrate the individual behavioral adoption in the whole network:

$h_X\left(x,\alpha ,\beta \right)=\left\{\begin{array}{cc}\hfill {\left(\frac{x}{\alpha }\right)}^{\beta },\hfill & \hfill 0\le x<\alpha ,0<\beta <1\hfill \\ \hfill 1,\hfill & \hfill \alpha \le x<1,\hfill \end{array}\right.(1)$

where x represents the proportion between the receiving information of an individual and the number of its contacted neighbors and parameter α represents the IHDB variable. In region I of Figure 1B, the behavioral adoption probability rises slowly to 1 based on the increase in x. In region II of Figure 1B, the adoption probability remains at 1.

2.2 Propagation mechanism

We randomly select a portion of ρ₀ individuals to act as the individuals (seeds) in the A-state at the beginning of information propagation and all other individuals to act as S-state individuals. Each A-state individual randomly chooses C of its neighbors to whom information is transferred in layer A(B) with probability λ^A(λ^B). The total amount of information that individual j in the S-state effectively gets from layer X is $m_j^X\to m_j^X+1$. Due to non-redundancy in information propagation, the information will not then be repeated through the same edge. Additionally, the individual in the susceptible state of X will accept the information and transmit to the adoption state with possibility $h_X(\frac{m^X}{k^X},\alpha ,\beta )$ at every time step. The S-state individual then changes to the corresponding state in other layers. Following successful information spreading, when the individual lost interest in information, the individuals in the adoption state transfer disinterested information and change to the recovery state with probability γ. In the two-layered contacted network, once there is no individual in the A-state, the information spreading process eventually comes to an end.

3 Theoretical analysis

We explore the novel IHDB properties of non-redundant information memory on two-layer networks by investigating literature works [37, 38]. Then, in order to mathematically investigate the information propagation mechanism, we propose an information propagation theory including individual limited contact and IHDB. The ultimate spreading size is defined as the proportion of individuals in the recovery state when the information spreading progress has ended. We introduce the initialization state [39] in which the individual can receive information but cannot transmit it outside.

The probability that an edge in layer X(X ∈ (A, B)) has not seen information propagation toward its S-state neighbor j up to time t is represented by ${\theta }_{k_j^X}^X(t)$. With a degree of $k_j^X$, the probability that i and j are neighbors in layer X is represented by the expression $\frac{k_j^{X}P(k_j^X)}{⟨k^X⟩}$. As a result, at time t, the individual i cannot receive the information by its neighbors in the X-layer with probability

${\theta }_A\left(t\right)={\displaystyle \sum _{k_j^A=0}}\frac{k_j^{A}P\left(k_j^A\right)}{⟨k^A⟩}{\theta }_{k_j^A}^A\left(t\right),(2)$

${\theta }_B\left(t\right)={\displaystyle \sum _{k_j^B=0}}\frac{k_j^{B}P\left(k_j^B\right)}{⟨k^B⟩}{\theta }_{k_j^B}^B\left(t\right),(3)$

respectively.

Until time t, the probability that an individual in the S-state possessing $\overrightarrow{k_i}=(k_i^A,k_i^B)$ will cumulatively take m_X bits of information in the A-layer or B-layer can be expressed as

${\varphi }_{m_A}^A\left(k_i^A,t\right)=\left(\begin{array}{c}\hfill k_i^A\hfill \\ \hfill m_A\hfill \end{array}\right){\theta }_A{\left(t\right)}^{k_i^A-m_A}{\left[1-{\theta }_A\left(t\right)\right]}^{m_A},(4)$

${\varphi }_{m_B}^B\left(k_i^B,t\right)=\left(\begin{array}{c}\hfill k_i^B\hfill \\ \hfill m_B\hfill \end{array}\right){\theta }_B{\left(t\right)}^{k_i^B-m_B}{\left[1-{\theta }_B\left(t\right)\right]}^{m_B},(5)$

respectively.

Individual i with m_X pieces of information in layer X, according to the IHDB features and the adoption threshold function, has not adopted the information and remained in the S-state with a probability ${\displaystyle \prod _{j=0}^{m_X}}[1-h_X(\frac{j}{k_i^X},\alpha ,\beta )]$. While getting m_X bits of information from those of layer X, the probability that an individual remains in the S-state at time t can be expressed as

$\begin{array}{c}{\tau }_{m_X}^X\left(k_i^X,t\right)={\displaystyle \sum _{m_X=0}^{k_i^X}}{\varphi }_{m_X}^X\left(k_i^X,t\right){\displaystyle \prod _{j=0}^{m_X}}\left[1-h_X\left(\frac{j}{k_i^X},\alpha ,\beta \right)\right]\hfill \\ ={\displaystyle \sum _{m_X=0}^{⌊\alpha k_i^X⌋}}{\varphi }_{m_X}^X\left(k_i^X,t\right){\displaystyle \prod _{j=0}^{m_X}}\left[1-{\left(\frac{j}{\alpha k_i^X}\right)}^{\beta }\right]\hfill \\ +{\displaystyle \sum _{m_X=⌈\alpha k_i^X⌉}^{k_i^X}}{\varphi }_{m_X}^X\left(k_i^X,t\right){\displaystyle \prod _{j=0}^{⌈\alpha k_i^X⌉}}\left[1-{\left(\frac{j}{\alpha k_i^X}\right)}^{\beta }\right]{\displaystyle \prod _{j=⌈\alpha k_i^X⌉}^{m_X}}\left(1-1\right)\hfill \\ ={\displaystyle \sum _{m_X=0}^{⌊\alpha k_i^X⌋}}{\varphi }_{m_X}^X\left(k_i^X,t\right){\displaystyle \prod _{j=0}^{m_X}}\left[1-{\left(\frac{j}{\alpha k_i^X}\right)}^{\beta }\right].\hfill \end{array}(6)$

As a result, the S-state individual i gets m_A and m_B pieces of information until time t and continues to be in the S-state possessing the probability

$\begin{array}{c}s\left(\vec{k},t\right)=\left(1-{\rho }_0\right){\displaystyle \sum _{m_A=0}^{k_i^A}}{\varphi }_{m_A}^A\left(k_i^A,t\right){\displaystyle \prod _{j=0}^{m_A}}\left[1-h_A\left(\frac{j}{k_i^A},\alpha ,\beta \right)\right]\hfill \\ \times {\displaystyle \sum _{m_B=0}^{k_i^B}}{\varphi }_{m_B}^B\left(k_i^B,t\right){\displaystyle \prod _{j=0}^{m_B}}\left[1-h_B\left(\frac{j}{k_i^B},\alpha ,\beta \right)\right]\hfill \\ =\left(1-{\rho }_0\right){\tau }_{m_A}^A\left(k_i^A,t\right){\tau }_{m_B}^B\left(k_i^B,t\right).\hfill \end{array}(7)$

The probability that a piece of information would have accumulated in the X-layer by time t when the S-state individual has not received information is expressed as

${\eta }_X={\displaystyle \sum _{k_i^X}}{P}_X\left(k_i^X\right){\tau }_{m_X}^X\left(k_i^X,t\right).(8)$

As a result, the percentage of the S-state individuals in the multi-layer network at time t is denoted as

$S\left(t\right)={\displaystyle \sum _{\vec{k}}}P\left(\vec{k}\right)s\left(\vec{k},t\right)=\left(1-{\rho }_0\right){\eta }_A{\eta }_B.(9)$

All of the model’s individuals can only alternate between three states; therefore, ${\theta }_{k_j^X}^X(t)$ can be transformed to

${\theta }_{k_j^X}^X\left(t\right)={\xi }_{S,k_j^X}^X\left(t\right)+{\xi }_{A,k_j^X}^X\left(t\right)+{\xi }_{R,k_j^X}^X\left(t\right),(10)$

where the probability that a neighbor of individual j is in the S-state, A-state, or R-state and has not sent the information to i by time t in layer X is represented by ${\xi }_{S,k_j^X}^X(t)$, ${\xi }_{A,k_j^X}^X(t)$, and ${\xi }_{R,k_j^X}^X(t)$, respectively.

Individual i in the initialization state cannot contact its neighbors due to the cavity theory. The degree vector of individual j is $\overrightarrow{k_j}=(k_j^A,k_j^B)$. The S-state individual j can receive information from all neighbors in layer A with the exception of individual i of layer A and $k_j^B$ neighbors of layer B if individual in the S-state i links its neighbor j of layer A. The probability for the individual j with degree $\overrightarrow{k_j}=(k_j^A,k_j^B)$ is indicated by ${\varsigma }_{n_A}^A(k_j^X-1,t)$ who receives n_A bits of information by its neighbors in the A-layer cumulatively up to time t. The probability ${\varsigma }_{n_X}^X(k_j^X-1,t)$ can be denoted as

$\begin{array}{c}{\varsigma }_{n_X}^X\left(k_j^X-1,t\right)={\displaystyle \sum _{n_X=0}^{k_j^X-1}}{\varphi }_{n_X}^X\left(k_j^X-1,t\right){\displaystyle \prod _{j=0}^{n_X}}\left[1-h_X\left(\frac{j}{k_j^X},\alpha ,\beta \right)\right]\hfill \\ ={\displaystyle \sum _{n_X=0}^{⌊\alpha k_j^X⌋}}{\varphi }_{n_X}^X\left(k_j^X-1,t\right){\displaystyle \prod _{j=0}^{n_X}}\left[1-{\left(\frac{j}{\alpha k_i^X}\right)}^{\beta }\right]\hfill \\ +{\displaystyle \sum _{n_X=⌈\alpha k_j^X⌉}^{k_j^X-1}}{\varphi }_{n_X}^X\left(k_j^X-1,t\right){\displaystyle \prod _{j=0}^{⌈\alpha k_j^X⌉}}\left[1-{\left(\frac{j}{\alpha k_i^X}\right)}^{\beta }\right]{\displaystyle \prod _{j=⌈\alpha k_j^X⌉}^{n_X}}\left(1-1\right)\hfill \\ ={\displaystyle \sum _{n_X=0}^{⌊\alpha k_j^X⌋}}{\varphi }_{n_X}^X\left(k_j^X-1,t\right){\displaystyle \prod _{j=0}^{n_X}}\left[1-{\left(\frac{j}{\alpha k_i^X}\right)}^{\beta }\right].\hfill \end{array}(11)$

j with ${\vec{k}}_j=(k_j^A,k_j^B)$ is also more likely to have acquired n_B bits of information from neighbors in layer B at time t by ${\tau }_{n_B}^B(k_j^B,t)$. Following the accumulation of n_A and n_B bits of information, the probability that j will stay in the susceptible state is given as

$\begin{array}{c}{\mathrm{\Theta }}_A\left(\vec{k},t\right)={\displaystyle \sum _{n_A=0}^{k_j^A-1}}{\varphi }_{n_A}^A\left(k_j^A-1,t\right){\displaystyle \prod _{j=0}^{n_A}}\left[1-h_A\left(\frac{j}{k_j^A},\alpha ,\beta \right)\right]\hfill \\ \times {\displaystyle \sum _{n_B=0}^{k_j^B}}{\varphi }_{n_B}^B\left(k_j^B,t\right){\displaystyle \prod _{j=0}^{n_B}}\left[1-h_B\left(\frac{j}{k_j^B},\alpha ,\beta \right)\right]\hfill \\ ={\varsigma }_{n_A}^A\left(k_j^A-1,t\right){\tau }_{n_B}^B\left(k_j^B,t\right).\hfill \end{array}(12)$

The probability that j in layer B will continue to be in the susceptible state after receiving all of the n_A and n_B bits of information is $\overrightarrow{k_j}$ when the individual i in the S-state interacts with j by a degree of $\overrightarrow{k_j}$ is expressed as

$\begin{array}{c}{\mathrm{\Theta }}_B\left(\vec{k},t\right)={\displaystyle \sum _{n_A=0}^{k_j^A}}{\varphi }_{n_A}^A\left(k_j^A,t\right){\displaystyle \prod _{j=0}^{n_A}}\left[1-h_A\left(\frac{j}{k_j^A},\alpha ,\beta \right)\right]\hfill \\ \times {\displaystyle \sum _{n_B}^{k_j^B-1}}{\varphi }_{n_B}^B\left(k_j^B-1,t\right){\displaystyle \prod _{j=0}^{n_B}}\left[1-h_B\left(\frac{j}{k_j^B},\alpha ,\beta \right)\right]\hfill \\ ={\tau }_{n_A}^A\left(k_j^A,t\right){\varsigma }_{n_B}^B\left(k_j^B-1,t\right).\hfill \end{array}(13)$

So, the probability that individual i and individual j in the S-state are linked by an edge can be expressed as

${\xi }_{S,k_j^X}^X\left(t\right)=\left(1-{\rho }_0\right)\frac{{\displaystyle \sum _{\overrightarrow{k_j}}}{k}_j^X{P}_X\left(\overrightarrow{k_j}\right){\mathrm{\Theta }}_X\left(\overrightarrow{k_j}t\right)}{⟨k^X⟩},(14)$

where $\frac{k_j^X{P}_X(\overrightarrow{k_j})}{⟨k^X⟩}$ defines the normal degree of the X-layer and $⟨k^X⟩$ represents the probability that individual i is next to j possessing $k_j^X$.

The evolutionary equation of ${\xi }_{R,k_j^X}^X(t)$ and ${\xi }_{A,k_j^X}^X(t)$ of layer X can be examined in the following expression. An A-state individual possessing degree $k_j^X$ chooses $\frac{C}{k_j^X}$ of its neighbors and contacts them. The probability of information transmission is λ. As a result, the probability that rumor will spread from individual j to its neighbors can be denoted by $\frac{\lambda C}{k_j^X}$. The following expression defines how ${\theta }_{k_j^X}^X(t)$ is evolved in layer X:

$\frac{d{\theta }_{k_j^X}^X\left(t\right)}{dt}=-\frac{\lambda C}{k_j^X}{\xi }_{A,k_j^X}^X\left(t\right).(15)$

Individuals in the adoption state cease spreading information and move to the recovered state with γ. The calculation for the evolution of ${\xi }_{R,k_j^X}^X(t)$ is

$\frac{d{\xi }_{R,k_j^X}^X\left(t\right)}{dt}=\gamma {\xi }_{A,k_j^X}^X\left(t\right)\left(1-\frac{\lambda C}{k_j^X}\right).(16)$

Combining Eqs 15, 16 with the original conditions ${\theta }_{k_j^X}^X(0)=1$ and ${\xi }_{R,k_j^X}^X(0)=0$, the development of ${\xi }_{R,k_j^X}^X(t)$ in layer X(X ∈ {A, B}) is

${\xi }_{R,k_j^X}^X\left(t\right)=\gamma \left[1-{\theta }_{k_j^X}^X\left(t\right)\right]\left[\frac{k_j^X}{\lambda C}-1\right].(17)$

Combining Eq. 10, Eq. 14, and Eq. 17 will derive

$\begin{array}{c}{\xi }_{A,k_j^X}^X\left(t\right)={\theta }_{k_j^X}^X\left(t\right)-{\xi }_{S,k_j^X}^X\left(t\right)-{\xi }_{R,k_j^X}^X\left(t\right)\hfill \\ ={\theta }_{k_j^X}^X\left(t\right)-\left(1-{\rho }_0\right)\frac{{\displaystyle \sum _{\overrightarrow{k_j}}}{k}_j^X{P}_X\left(\overrightarrow{k_j}\right)\mathrm{\Theta }\left(\overrightarrow{k_j}t\right)}{⟨k^X⟩}-\gamma \left[1-{\theta }_{k_j^X}^X\left(t\right)\right]\left(\frac{k_j^X}{\lambda C}-1\right).\hfill \end{array}(18)$

Substituting Eq. 18 into Eq. 15, it is possible to rewrite the evolution of ${\theta }_{k_j^X}^X(t)$ in layer X(X ∈ {A, B}) as

$\begin{array}{c}\frac{d{\theta }_{k_j^X}^X\left(t\right)}{dt}=-\frac{\lambda C}{k_j^X}\left\{{\theta }_{k_j^X}^X\left(t\right)-\left(1-{\rho }_0\right)\frac{{\displaystyle \sum _{\overrightarrow{k_j}}}{k}_j^X{P}_X\left(\overrightarrow{k_j}\right)\mathrm{\Theta }\left(\overrightarrow{k_j}t\right)}{⟨k^X⟩}-\gamma \left[1-{\theta }_{k_j^X}^X\left(t\right)\right]\left(\frac{k_j^X}{\lambda C}-1\right)\right\}\hfill \\ =\left(1-{\rho }_0\right)\frac{\lambda C}{k_j^X}\frac{{\displaystyle \sum _{\overrightarrow{k_j}}}{k}_j^X{P}_X\left(\overrightarrow{k_j}\right)\mathrm{\Theta }\left(\overrightarrow{k_j}t\right)}{⟨k^X⟩}+\gamma \left(1-\frac{\lambda C}{k_j^X}\right)-\left[\gamma +\frac{\lambda C}{k_j^X}\left(1-\gamma \right)\right]{\theta }_{k_j^X}^X\left(t\right).\hfill \end{array}(19)$

In the whole network, the expression for state change of the individuals is given as follows:

$\frac{dR\left(t\right)}{dt}=\gamma A\left(t\right),(20)$

$\frac{dA\left(t\right)}{dt}=-\frac{dS\left(t\right)}{dt}-\gamma A\left(t\right).(21)$

As a result, S(t), A(t), and R(t), which represent the nodes’ states at every given time step, can be calculated by combining and iterating Eqs 9, 20, 21, respectively.

While t → ∞, the nodes’ states in the network will not become any longer, meaning that $\frac{d{\theta }_{k_j^X}^X(t)}{dt}\to 0$. R(∞) is also the ultimate propagation size. Currently, the entire network consists solely of individuals in the S-state and the R-state. To determine R(∞), we must determine ${\theta }_{k_j^X}^X(\infty )$ as

${\theta }_{k_j^X}^X\left(\infty \right)={\xi }_{S,k_j^X}^X\left(\infty \right)+\gamma \left[1-{\theta }_{k_j^X}^X\left(\infty \right)\right]\left[\frac{k_j^X}{\lambda C}-1\right].(22)$

Then, by combining and iterating Eqs 9, 22, S(∞) and R(∞) are derived.

The crucial propagation probability is our next problem of concern. Moving the left side of Eq. 22 to the right side, it can be denoted as

$F\left[{\theta }_{k_j^X}^X\left(\infty \right)\right]={\xi }_{S,k_j^X}^X\left(\infty \right)-{\theta }_{k_j^X}^X\left(\infty \right)+\gamma \left[1-{\theta }_{k_j^X}^X\left(\infty \right)\right]\left[\frac{k_j^X}{\lambda C}-1\right].(23)$

At the critical point ${\theta }_c^X(\infty )$, $F[{\theta }_{k_j^X}^X(\infty )]$ is tangent to the abscissa. The critical condition can be denoted as

${\left.\frac{dF}{d{\theta }_{k_j^X}^X\left(\infty \right)}\right|}_{{\theta }_c^X\left(\infty \right)}=0.(24)$

Therefore, the critical information propagation probability is

$\lambda =\frac{\gamma }{A+\gamma +1},(25)$

where

${\left.\frac{d{\xi }_{S,k_j^X}^X\left(\infty \right)}{d{\theta }_{k_j^X}^X\left(\infty \right)}\right|}_{{\theta }_c^X\left(\infty \right)}=0.(26)$

4 Parameter settings

This section simulates and evaluates the developed model through testing on a multiple-layered contacted network such as ER [40] and SF networks [41]. The experiment is carried out in the ER network and the SF network with 10,000 nodes. Additionally, each layer network has $⟨k_X⟩=10$ as an average degree of X ∈ {A, B}. Furthermore, for convenience, the probability of information transmission can be given at λ_A = λ_B = λ. The experiment was conducted using double-layer contacted networks. In an ER network, there is an equal possibility of a connection forming between any two nodes, and the degrees of the nodes in layer X follow $P_X(k_X)=e^{-⟨k_X⟩}\frac{{⟨k⟩}^{k_X}}{k_X!}$. In SF networks, the degree distribution variability of nodes is negatively correlated with the degree exponent v. In an SF network, where ${\zeta }_X=\frac{1}{\sum _{k_X}{k_X}^{-v}}$, the degrees of nodes follow $P_X(k_X)={\zeta }_X{k}_X^{-v}$. Additionally, a relatively small number of seeds (ρ₀ = 0.001) and a recovered probability γ = 1.0 cause A-state nodes to move to the R-state.

Furthermore, for further explanation of the critical condition in our scenario, the relative variance is unitized and written as follows:

$\chi =N\frac{⟨R{\left(\infty \right)}^2⟩-{⟨R\left(\infty \right)⟩}^2}{⟨R\left(\infty \right)⟩},(27)$

where $⟨\dots ⟩$ stands for the mean set. The important parameters of the ultimate adoption size are implied by χ.

5 Experiments and discussion

5.1 Numerical analysis of the two-layer ER network

In Figure 2, with the unit transmission probability λ and the adoption threshold parameters α and β, we first investigate how the proportion of individuals in the three states of S-state, A-state, and R-state has changed with time.

FIGURE 2

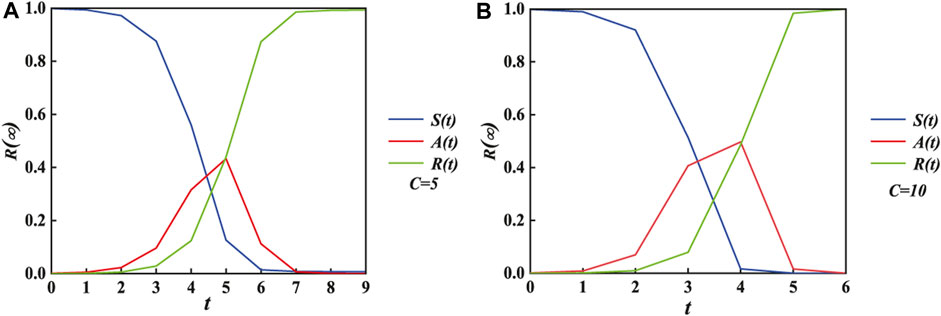
FIGURE 2. Individual status has changed three stages over time. For the same condition, the propagation time spends nine steps in subgraph (A) setting C = 5 and six steps in subgraph (B) setting C = 10. By comparison, the increase in the individual contact capacity accelerates the propagation process. The other variables include α^A = α^B = 0.1, β^A = β^B = 0.1, and λ^A = λ^B = 0.5.

Then, as shown in Figures 2A, B, R(t), which represents the ultimate spreading size, changes to 1 at the end, while S(t) increasingly decreases from 1 to 0 and A(t) progressively drops to 0 over time. As the increase in parameter C in subgraph (a) to subgraph (b), the evolution time costed steadily decreases from 9 to 6, while R(∞), which denotes the ultimate spreading size, increases at the same step t. The time progress demonstrates that information outbreak on a two-layered contacted network can be accelerated by enhancing contact ability of individuals.

Figure 3 displays the roles of unit transmission probability in each individual’s eventual adoption size with various IHDB values α in the subgraphs. The ultimate spreading size R(∞) spreads to a global network as λ rises, as shown in Figure 3A (β = 0.5) and (b) (β = 0.9). Furthermore, Figures 3A, B also indicate how IHDB can affect the propagation phase transition. In subgraph (a), the pattern of R(∞) always shows a second-order growth of continuous phase transition for any IHDB behavior exhibited by the individual (α^A = α^B = 0.1, 0.5, 0.9). The pattern of R(∞) in subgraph (b) indicates a second-order phase transition in the continuous propagation pattern when an individual exhibits a positive IHDB such as α^A = α^B = 0.1. This suggests that, when there is a small λ, a positive IHDB can result in widespread behavioral propagation. When α^A = α^B = 0.5, R(∞) also shows the same propagation phenomenon. While an individual exhibits a weak IHDB, R(∞) exhibits a first-order increase in the discontinuous pattern, i.e., α^A = α^B = 0.9.

FIGURE 3

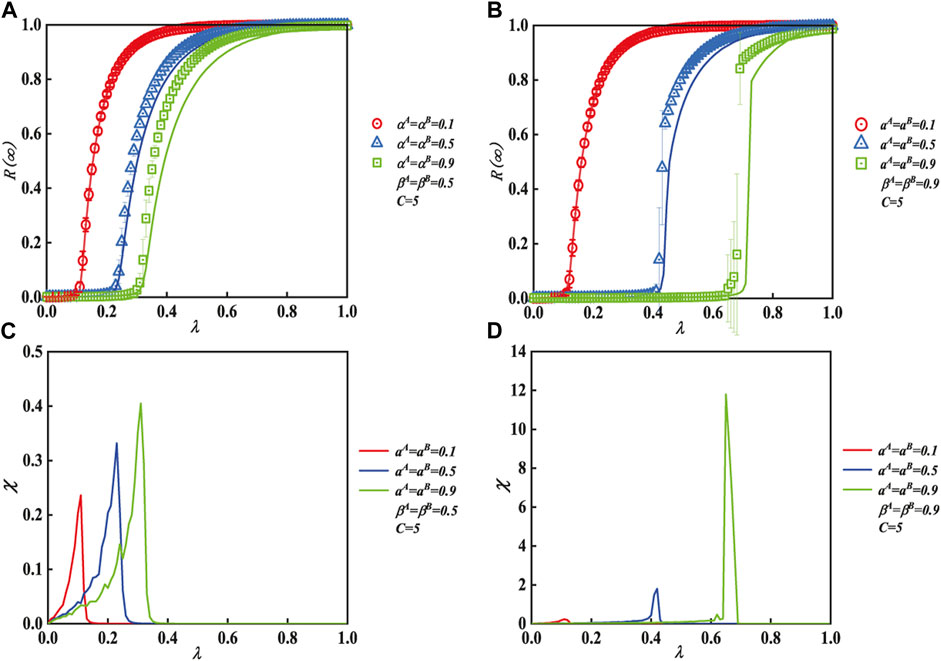
FIGURE 3. Effects of unit transmission probability of a multi-layer ER network on each individual’s ultimate spreading size while using various IHDB parameters. Subgraphs (A) (β = 0.5) and (B) (β = 0.9) demonstrate how the IHDB parameter affects the propagation pattern. The critical values of subgraphs (C) and (D) show the relative deviations and the critical values of (A) and (B), respectively.

Figure 3C displays the relative variances and critical information propagation probability of (a) and (b) individually (d). The global adoption will emerge from the deviation of behavioral propagation, which is represented by the top values of relative variance χ. Additionally, the numerical values of the simulation (symbols) agree with our theoretical analyses (lines).

For the two-layer contacted ER network, Figure 4 exhibits the joint impacts of variable (λ, α) on R(∞). Figure 4 (a) with β^A = β^B = 0.5 and (b) with β^A = β^B = 0.9 depict the effects of (λ, α) on the dissemination of information. In subgraph (a), the phase transition shows a continuous pattern in the whole area. Then, in subgraph (b), the image can be divided into two parts. In area I, a second-order continuous increase can be seen in the R(∞) pattern. The critical value between region I and region II is α* = 0.61. In area II, a first-order discontinuous increase can be seen in the R(∞) pattern. Additionally, the individual contact capability parameter is set at C = 5.

FIGURE 4

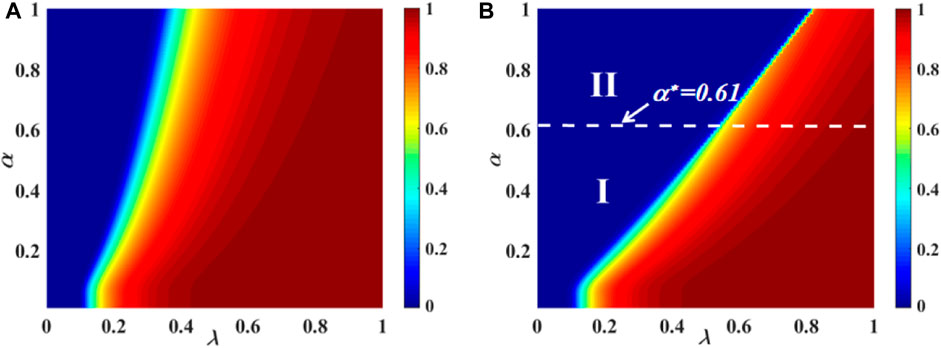
FIGURE 4. Impact of the unit transmission probability and the dynamic IHDB parameter α on each person’s final spreading size for an ER network with numerous layers of contacts. The impacts of subgraphs (A) (β^A = β^B = 0.5) and (B) (β^A = β^B = 0.9) on the ultimate spreading size are shown with varying IHDB parameters. In subgraph (A), the phase transition shows a continuous pattern in the whole area. In subgraphs (B), the phase transition shows two areas: the continuous second-order pattern in area I and the discontinuous first-order pattern in area II.

The joint impacts of variable plane (λ, β) on R(∞) for the two-layered ER network are shown in Figure 5. Figures 5A, B depict the effects of (λ, β) on information propagation, respectively, with α^A = α^B = 0.5 and α^A = α^B = 0.9. In subgraph (a), the image can be divided into two parts. There is a second-order continuous increase pattern in region I of R(∞) phase transition. The critical value between region I and region II is β* = 0.95. There is a first-order discontinuous increase pattern in region II of R(∞). Then, in subgraph (b), the image can also be divided into two parts. In area I, R(∞) exhibits a second-order continuous spreading. The critical value between region I and region II is β* = 0.78. In area II, R(∞) exhibits a first-order discontinuous spreading. Additionally, the individual contact capability parameter is set at C = 5.

FIGURE 5

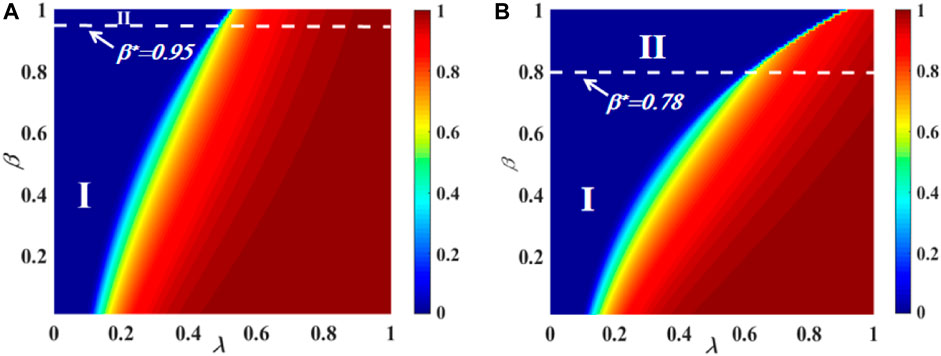
FIGURE 5. Integrative roles of the dynamic IHDB parameter α and transmission probability in each individual’s ultimate spreading size for a multiple-layered contacted ER network. The impacts of subgraphs (A) (α^A = α^B = 0.5) and (B) (α^A = α^B = 0.9) on the ultimate spreading size are shown with varying IHDB parameters. In subgraph (A), the phase transition shows a continuous pattern in the whole area. In subgraph (B), the phase transition shows two areas: the continuous second-order pattern in area I and the discontinuous first-order pattern in area II.

5.2 Numerical analysis of the two-layer SF network

Figure 6 depicts the influence of IHDB variable α and transmission probability λ on the ultimate spreading size of the multi-layer contacted SF network. In each subgraph, the fundamental parameters include C = 5 and β^A = β^B = 0.9. Figures 6A, B show how the ultimate adoption size R(∞) grows as λ increases until it achieves global adoption. When α^A = α^B = 0.1 and α^A = α^B = 0.5, the final spreading size shows a continuous spreading with second-order. However, R(∞) pattern exhibits a discontinuous spreading with first-order when α^A = α^B = 0.9. Then, the same growth pattern is also exhibited in subgraph (b) (v = 4). Moreover, compared with subgraph (b) (v = 4), subgraph (a) (v = 2) shows an incomplete global adoption because of strong heterogeneous degree distribution. Additionally, the numerical values of the simulation (symbols) match those of our theoretical analyses (lines).

FIGURE 6

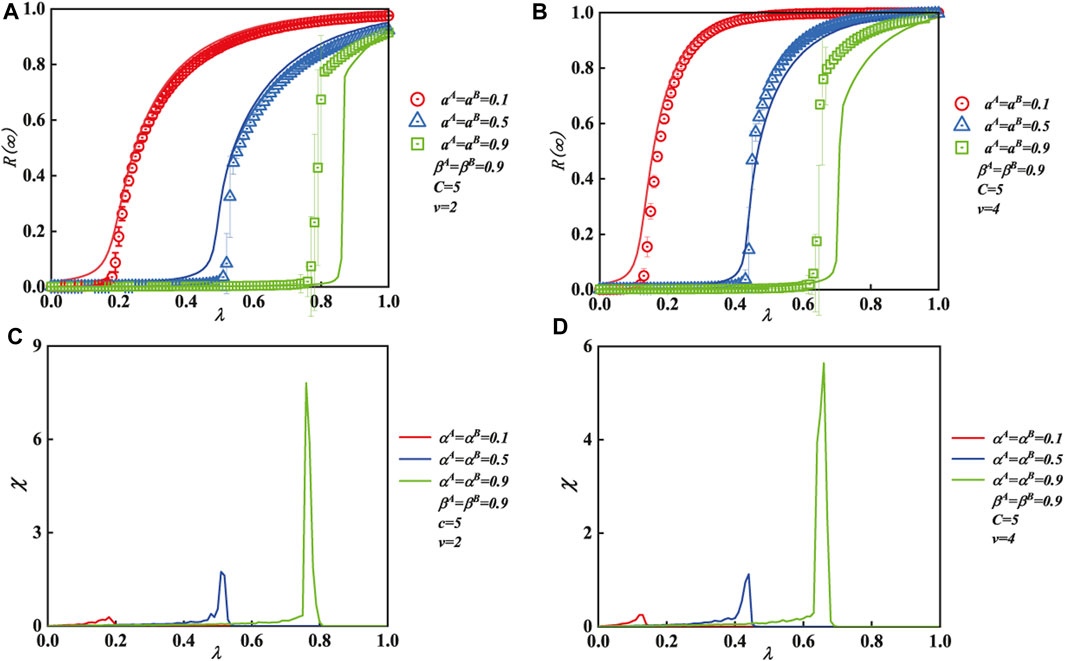
FIGURE 6. Effect of the unit transmission chance and the IHDB parameter α on each person’s ultimate spreading size for the multiple contacted SF network The IHDB parameter (β^A = β^B = 0.9) and the same contact capacity of people (C = 5) are applied to each subgraph. The vertical subgraphs use a unique degree distribution exponent as well, with subgraphs (A) and (B) corresponding to v = 2, 4, respectively. Subgraphs (A) and (B) display the effects on the ultimate spreading size with unit transmission probability λ. The critical values of subgraphs (C) and (D) show the relative deviations and the critical values of (A) and (B), respectively.

For the multiple-layered contacted SF network, Figure 7 shows the effect of R(∞) on the behavioral parameter plane (λ, β). The subgraphs (a) and (b), and (c) and (d) are set as the identical contact capacity of individuals by C = 5 and C = 10, respectively. The subgraphs (a) and (b), and (c) and (d) demonstrate the growth tendency of R(∞). In subgraph (a) with v = 2 and C = 5, the image can be divided into three parts. In the phenomenon of eventual information outbreak R(∞), area I displays a second-order continuous propagation pattern. The critical value between region I and region II is β* = 0.85. Area II exhibits a first-order discontinuous phase transition in the pattern of R(∞). The critical value between region II and region III is β** = 0.99. In area III, the R(∞) pattern does not exhibit information outbreak. In subgraph (b) with v = 2 and C = 10, the image can be divided into two parts. The R(∞) pattern of individual final spreading size in area I displays a second-order continuous increase. The critical value between region I and region II is β* = 0.75. In the pattern of R(∞), area II displays a first-order discontinuous increase. In subgraph (c) with v = 4 and C = 5, the image can be divided into two parts. While showing the pattern of information outbreak scale R(∞), area I displays a second-order continuous propagation pattern. The critical value between region I and region II is β* = 0.8. A first-order discontinuous increase in area II’s pattern of R(∞) is visible. In subgraph (d) with v = 4 and C = 10, the image can be divided into two parts. In the pattern of individual eventual spreading size R(∞), area I displays a second-order continuous increase. The critical value between region I and region II is β* = 0.85. Area II exhibits a first-order discontinuous phase transition in the pattern of R(∞). Furthermore, the heterogeneous degree distribution alters the information propagation but cannot alter the pattern of phase transition. Because there are some hub people in the multi-layer contacted SF network, when it exhibits a strong heterogeneous degree distribution (v = 2), there is a pattern of information suppression in the phase transition.

FIGURE 7

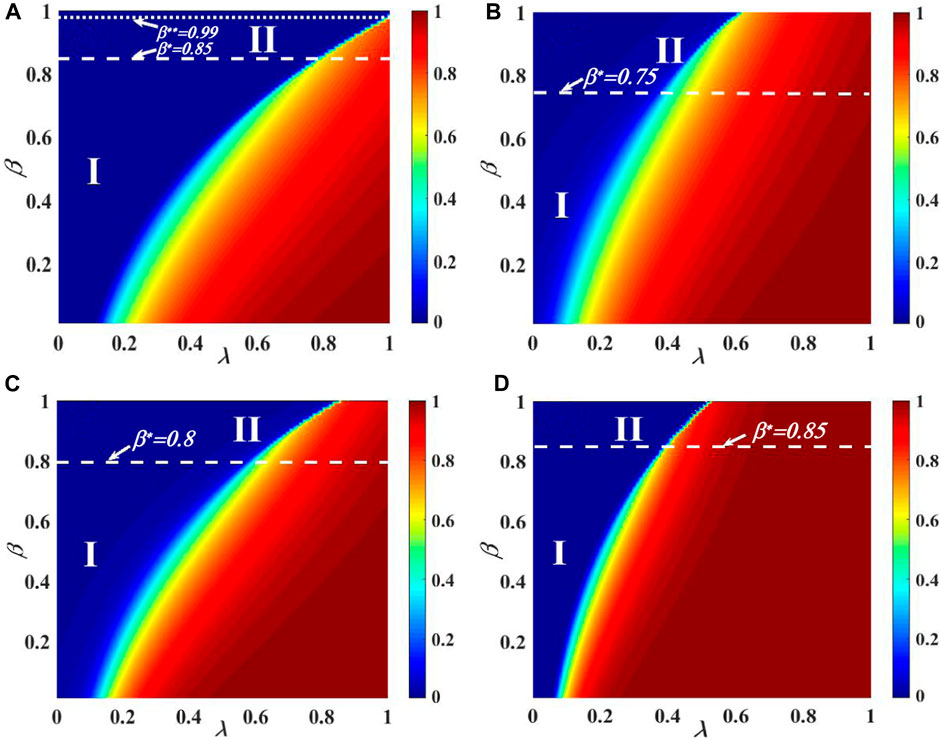
FIGURE 7. Combined effect of the unit transmission chance and the IHDB parameter β on the ultimate information outbreak for the two-layer contacted SF network. The influence of (λ, β) on the ultimate adoption size is shown in subgraphs (A) and (B) with v =2 and subgraphs (C) and (D) with v = 4, respectively. In subgraph (A) with C = 5, the phase transition shows three areas: the continuous second-order pattern in area I, the discontinuous first-order pattern in area II, and the static pattern in area III. In subgraph (B) with C = 10, the phase transition shows two areas: the continuous second-order pattern in area I and the discontinuous first-order pattern in area II. In subgraph (C) with C = 5, the phase transition shows two areas: the continuous second-order pattern in area I and the discontinuous first-order pattern in area II. In subgraph (D) with C = 10, the phase transition shows two areas: the continuous second-order pattern in area I and the discontinuous first-order pattern in area II.

5.3 Numerical analysis of the two-layer ER–SF network

Figure 8 exhibits the impact of IHDB variable α and transmission probability λ on the final spreading scope for the two-layer contacted ER–SF network. In each subgraph, the fundamental parameters include C = 5 and β^A = β^B = 0.9. Figures 8A, B (v^B = 2 and v^B = 4) show how the final spreading scope R(∞) grows as λ increases until it achieves global adoption. When α^A = α^B = 0.1 and α^A = α^B = 0.5, the final outbreak pattern shows a second-order continuous propagation. However, the R(∞) pattern shows a first-order discontinuous pattern when α^A = α^B = 0.9. In addition, the numerical values of the simulation (symbols) match those of our theoretical analyses (lines).

FIGURE 8

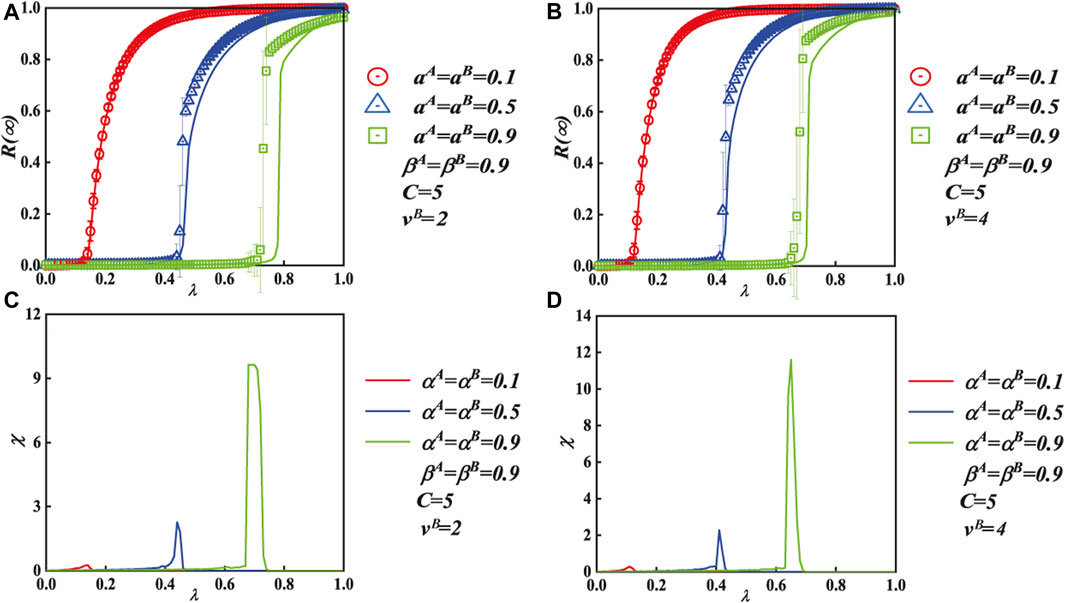
FIGURE 8. Effect of the unit transmission chance and the IHDB parameter α on each person’s ultimate spreading size for the two-layer contacted ER–SF network. The IHDB parameter (β^A = β^B = 0.9) and the same contact capacity of people (C = 5) are applied to each subgraph. The vertical subgraphs use a unique degree distribution exponent as well, with subgraphs (A) and (B) corresponding to the SF layer with v^B = 2, 4, respectively. Subgraphs (A) and (B) display the effects on the ultimate spreading size with unit transmission probability λ. The critical values of subgraphs (C) and (D) show the relative deviations and the critical values of (A) and (B), respectively. The initial seed is set at ρ = 0.001.

For the two-layer contacted ER–SF network, Figure 9 shows the effect of R(∞) on the behavioral parameter plane (λ, β). The subgraphs (a) and (b) are set as the identical contact capacity of individuals by C = 5. The subgraphs (a) and (b) demonstrate the growth tendency of R(∞). In subgraph (a) with v = 2, the image can be divided into two parts. In the phenomenon of eventual information outbreak R(∞), area I displays a second-order continuous propagation pattern. The critical value between area I and II is β* = 0.86. Area II exhibits a first-order discontinuous phase transition in the pattern of R(∞). In subgraph (b) with v = 4, the image can be divided into two parts. The R(∞) pattern of individual final spreading size in area I displays a second-order continuous increase. The critical value between region I and region II is β* = 0.9. In the pattern of R(∞), area II displays a first-order discontinuous increase.

FIGURE 9

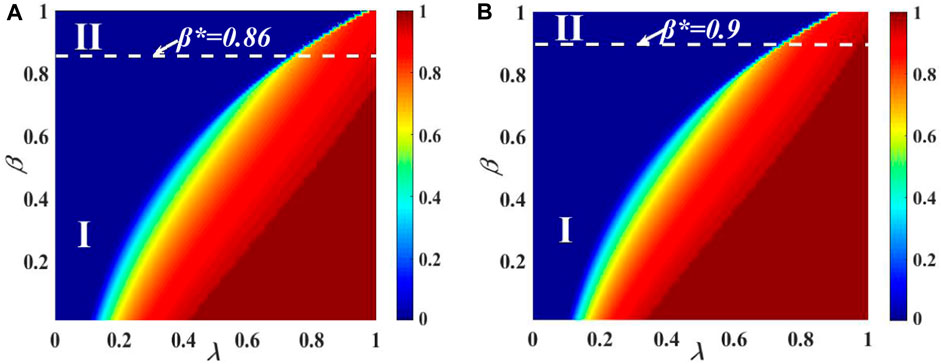
FIGURE 9. Combined effect of the unit transmission chance and the IHDB parameter β on the ultimate information outbreak for the two-layer contacted ER–SF network. The influence of (λ, β) on the ultimate adoption size is shown in subgraph (A) with v = 2 and subgraph (B) with v = 4, respectively. In subgraph (A), the phase transition shows two areas: the continuous second-order pattern in area I and the discontinuous first-order pattern in area II. In subgraph (B), the phase transition also shows two areas: the continuous second-order pattern in area I and the discontinuous first-order pattern in area II. Other parameters are set at C = 5, α^A = α^B = 0.9, and ρ₀ = 0.001.

6 Conclusion

Researchers have explored how transmission probability, information type, individual psychology, and heterogeneous behaviors affect information propagation mechanisms. In the research on information propagation, we found that individual behavior depends on individual psychology to show positive or negative, linear or non-linear adoption. In this paper, we explore how individual psychology affects the information propagation.

This paper considers the individual contact capacity, which affects the information outbreak. More importantly, we found that an individual can show the heterogeneous decreasing behavior on information propagation, which is called IHDB. Then, we proposed a non-rule trapezoidal-like probability function on the two-layer network model. Meanwhile, we proposed a novel generalized edge-based compartmental theory to analyze the information propagation mechanism. Finally, the propagation pattern on the two-layer contacted ER and SF networks was revealed by the simulation and theoretical analysis. When IHDB changes, the phenomenon of the ultimate information outbreak first increases continuously in the second-order phase transition and then increases discontinuously in the first-order phase transition. Additionally, increasing the number of contacted neighbors makes it easier for propagation information and changing the propagation pattern. Furthermore, the heterogeneous degree distribution also has influence on information spreading but has not altered the phase transition pattern. This paper demonstrates the impact of individual heterogeneous decreasing behavior on information propagation. We also present a heuristic theory to describe how individual behavior affects the propagation of information.

Data availability statement

The original contributions presented in the study are included in the article/Supplementary Material; further inquiries can be directed to the corresponding author.

Author contributions

YT: conceptualization, methodology, visualization, investigation, and writing—review and editing. HT: methodology, supervision, and formal analysis. XZ: conceptualization, methodology, and formal analysis. QC: formal analysis and supervision. All authors contributed to the article and approved the submitted version.

Funding

This work was supported by the National Key R&D Program of China under Grant No. 2020YFB1807800 and the BUPT Excellent Ph.D. Students Foundation under Grant No. CX2022209.

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

1. Peng H, Peng W, Zhao D, Wang W. Impact of the heterogeneity of adoption thresholds on behavior spreading in complex networks. Appl Maths Comput (2020) 386:125504. doi:10.1016/j.amc.2020.125504

CrossRef Full Text | Google Scholar

2. Cui Y, Wei R, Tian Y, Tian H, Zhu X. Information propagation influenced by individual fashion-passion trend on multi-layer weighted network. Chaos, Solitons and Fractals (2022) 160:112200. doi:10.1016/j.chaos.2022.112200

CrossRef Full Text | Google Scholar

3. Yang Q, Zhu X, Tian Y, Wang G, Zhang Y, Chen L. The influence of heterogeneity of adoption thresholds on limited information spreading. Appl Maths Comput (2021) 411:126448. doi:10.1016/j.amc.2021.126448

CrossRef Full Text | Google Scholar

4. Cui Q, Hu X, Ni W, Tao X, Zhang P, Chen T, et al. Vehicular mobility patterns and their applications to internet-of-vehicles: A comprehensive survey. SCIENCE CHINA-Information Sci (2022) 65(1–42):211301. doi:10.1007/s11432-021-3487-x

CrossRef Full Text | Google Scholar

5. Wang Z, Guo Q, Sun S, Xia C. The impact of awareness diffusion on sir-like epidemics in multiplex networks. Appl Maths Comput (2019) 349:134–47. doi:10.1016/j.amc.2018.12.045

CrossRef Full Text | Google Scholar

6. Zhao D, Li L, Peng H, Luo Q, Yang Y. Multiple routes transmitted epidemics on multiplex networks. Phys Lett A (2014) 378:770–6. doi:10.1016/j.physleta.2014.01.014

CrossRef Full Text | Google Scholar

7. Zhou L, Huang M, Tan F, Zhang Y. Mean-square bounded synchronization of complex networks under deception attacks via pinning impulsive control. Nonlinear Dyn (2023) 111:11243–59. doi:10.1007/s11071-023-08448-0

CrossRef Full Text | Google Scholar

8. Yao W, Wang C, Sun Y, Gong S, Lin H. Event-triggered control for robust exponential synchronization of inertial memristive neural networks under parameter disturbance. Neural Networks (2023) 164:67–80. doi:10.1016/j.neunet.2023.04.024

PubMed Abstract | CrossRef Full Text | Google Scholar

9. Fei Y, Liu L, Xiao L, Li K, Cai S. A robust and fixed-time zeroing neural dynamics for computing time-variant nonlinear equation using a novel nonlinear activation function. Neurocomputing (2019) 350:108–16. doi:10.1016/j.neucom.2019.03.053

CrossRef Full Text | Google Scholar

10. Li W, Jiang L, Perc M. A limited mobility of minorities facilitates cooperation in social dilemmas. Appl Maths Comput (2021) 391(125705):125705. doi:10.1016/j.amc.2020.125705

CrossRef Full Text | Google Scholar

11. Perc M, Jordan JJ, Rand DG, Wang Z, Boccaletti S, Szolnoki A. Statistical physics of human cooperation. Phys Rep (2017) 687:1–51. doi:10.1016/j.physrep.2017.05.004

CrossRef Full Text | Google Scholar

12. Faff R, Ho YK, Lin W, Yap CM. Diminishing marginal returns from R&amp;D investment: Evidence from manufacturing firms. Appl Econ (2013) 45:611–22. doi:10.1080/00036846.2011.608644

CrossRef Full Text | Google Scholar

13. Gauriot R, Heger SA, Slonim R. Altruism or diminishing marginal utility? J Econ Behav Organ (2020) 180:24–48. doi:10.1016/j.jebo.2020.09.030

CrossRef Full Text | Google Scholar

14. Hirschauer N, Jantsch A, Musshoff O. Developing business ethics theory and integrating economic analysis into business ethics teaching–a conceptualization based on externalities and diminishing marginal utility. Rev Soc Economy (2018) 76:43–72. doi:10.1080/00346764.2017.1333132

CrossRef Full Text | Google Scholar

15. Ahl RE, Cook E, McAuliffe K. Having less means wanting more: Children hold an intuitive economic theory of diminishing marginal utility. Cognition (2023) 234:105367. doi:10.1016/j.cognition.2023.105367

PubMed Abstract | CrossRef Full Text | Google Scholar

16. Liobikienė G, Butkus M. Determinants of greenhouse gas emissions: A new multiplicative approach analysing the impact of energy efficiency, renewable energy, and sector mix. J Clean Prod (2021) 309:127233. doi:10.1016/j.jclepro.2021.127233

CrossRef Full Text | Google Scholar

17. Chandio AA, Jiang Y, Gessesse AT, Dunya R. The nexus of agricultural credit, farm size and technical efficiency in sindh, Pakistan: A stochastic production frontier approach. J Saudi Soc Agric Sci (2019) 18:348–54. doi:10.1016/j.jssas.2017.11.001

CrossRef Full Text | Google Scholar

18. Jebeli SSH, Barouni M, Orojloo PH. Estimating the marginal effect of socioeconomic factors on the demand of specialty drugs. Glob J Health Sci (2015) 7(28).doi:10.5539/gjhs.v7n2p28

CrossRef Full Text | Google Scholar

19. Park T, Griggs SK, Chung PD. Characteristics of patients using specialty medications. Res Soc Administrative Pharm (2018) 14:901–8. doi:10.1016/j.sapharm.2017.10.007

CrossRef Full Text | Google Scholar

20. Cordis AS, Muzatko S. Higher education spending and cpa exam performance. J Account Educ (2021) 55:100727. doi:10.1016/j.jaccedu.2021.100727

CrossRef Full Text | Google Scholar

21. Ng ES, McGinnis Johnson. Game of loans J. Game of loans: The relationship between education debt, social responsibility concerns, and making a career choice in the public, private, and nonprofit sectors. Nonprofit Voluntary Sector Q (2020) 49:292–315. doi:10.1177/0899764019867773

CrossRef Full Text | Google Scholar

22. Chae I, Bruno HA, Feinberg FM. Wearout or weariness? Measuring potential negative consequences of online ad volume and placement on website visits. J Marketing Res (2019) 56:57–75. doi:10.1177/0022243718820587

CrossRef Full Text | Google Scholar

23. Agrawal D. Effect of brand loyalty on advertising and trade promotions: A game theoretic analysis with empirical evidence. Marketing Sci (1996) 15:86–108. doi:10.1287/mksc.15.1.86

CrossRef Full Text | Google Scholar

24. Issock Issock PB, Mpinganjira M, Roberts-Lombard M. Investigating the relevance of the traditional marketing mix across different stages of change: Empirical evidence from household recycling. J Soc Marketing (2021) 11:489–506. doi:10.1108/jsocm-11-2020-0221

CrossRef Full Text | Google Scholar

25. Götz O, Hoelter AK, Krafft M. The role of sales and marketing in market-oriented companies. J Personal Selling Sales Manage (2013) 33:353–71. doi:10.2753/PSS0885-3134330401

CrossRef Full Text | Google Scholar

26. Fonseca R, Michaud PC, Zheng Y. The effect of education on health: Evidence from national compulsory schooling reforms. SERIEs (2020) 11:83–103. doi:10.1007/s13209-019-0201-0

CrossRef Full Text | Google Scholar

27. Asem EK, Rajwa B. Impact of combination of short lecture and group discussion on the learning of physiology by nonmajor undergraduates. Adv Physiol Educ (2023) 47:1–12. doi:10.1152/advan.00022.2022

PubMed Abstract | CrossRef Full Text | Google Scholar

28. Li X, Hsee CK. The psychology of marginal utility. J Consumer Res (2021) 48:169–88. doi:10.1093/jcr/ucaa064

CrossRef Full Text | Google Scholar

29. Gelardi V, Le Bail D, Barrat A, Claidiere N. From temporal network data to the dynamics of social relationships. Proc R Soc B (2021) 288:20211164. doi:10.1098/rspb.2021.1164

PubMed Abstract | CrossRef Full Text | Google Scholar

30. Koltsova OY, Mararitsa LV, Terpilovskii MA, Sinyavskaya YE. Social signature in an online environment: Stability and cognitive limits. Comput Hum Behav (2021) 122:106856. doi:10.1016/j.chb.2021.106856

CrossRef Full Text | Google Scholar

31. Kojaku S, Hébert-Dufresne L, Mones E, Lehmann S, Ahn Y-Y. The effectiveness of backward contact tracing in networks. Nat Phys (2021) 17:652–8. doi:10.1038/s41567-021-01187-2

PubMed Abstract | CrossRef Full Text | Google Scholar

32. Zhu X, Tian H, Chen X, Wang W, Cai S. Heterogeneous behavioral adoption in multiplex networks. New J Phys (2018) 20:125002. doi:10.1088/1367-2630/aaf25d

CrossRef Full Text | Google Scholar

33. Li H, Zhang X, Zhao C. Explaining social events through community evolution on temporal networks. Appl Maths Comput (2021) 404:126148. doi:10.1016/j.amc.2021.126148

CrossRef Full Text | Google Scholar

34. Tan F, Zhou L, Lu J, Quan H, Liu K. Adaptive quantitative control for finite time synchronization among multiplex switched nonlinear coupling complex networks. Eur J Control (2023) 70:2023:100764. doi:10.1016/j.ejcon.2022.100764

CrossRef Full Text | Google Scholar

35. Zhu X, Wang W, Cai S, Stanley HE. Optimal imitation capacity and crossover phenomenon in the dynamics of social contagions. J Stat Mech Theor Exp (2018) 2018:063405. doi:10.1088/1742-5468/aac914

CrossRef Full Text | Google Scholar

36. Nian F, Yu X, Cao J, Luo L. Phase transition in information propagation on high-order networks. Int J Mod Phys B (2020) 34(21):2050203. doi:10.1142/s0217979220502033

CrossRef Full Text | Google Scholar

37. Yu X, Yang Q, Ai K, Zhu X, Wang W. Information spreading on two-layered multiplex networks with limited contact. IEEE Access (2020) 8:104316–25. doi:10.1109/access.2020.2999495

CrossRef Full Text | Google Scholar

38. Wang W, Liu Q, Liang J, Hu Y, Zhou T. Coevolution spreading in complex networks. Phys Rep (2019) 820:1–51. doi:10.1016/j.physrep.2019.07.001

PubMed Abstract | CrossRef Full Text | Google Scholar

39. Wang S, Lv W, Zhang J, Luan S, Chen C, Gu X. Method of power network critical nodes identification and robustness enhancement based on a cooperative framework. Reliability Eng Syst Saf (2021) 207:107313. doi:10.1016/j.ress.2020.107313

CrossRef Full Text | Google Scholar

40. Iacopini I, Petri G, Barrat A, Latora V. Simplicial models of social contagion. Nat Commun (2019) 10:2485. doi:10.1038/s41467-019-10431-6

PubMed Abstract | CrossRef Full Text | Google Scholar

41. Cimini G, Squartini T, Saracco F, Garlaschelli D, Gabrielli A, Guido C. The statistical physics of real-world networks. Nat Rev Phys (2019) 1:58–71. doi:10.1038/s42254-018-0002-6

CrossRef Full Text | Google Scholar