A novel grid multi-structure chaotic attractor and its application in medical image encryption

Grid multi-scroll/wing chaotic systems are complex non-linear dynamic systems, which are widely used in secure communication. The grid multi-scroll/wing chaotic systems are usually realized by using the function control method, which has a complex realization method, many control parameters, and a simple unit attractor structure. In this paper, based on the Hopfield neural network, a memristive Hopfield neural network model is proposed by using the memristor synapse control method. The model can generate novel grid multi-structure chaotic attractors, which have the characteristics of a simple implementation method, few control parameters, and complex unit attractor structure. Firstly, the generation mechanism of the grid multi-structure chaotic attractors is analyzed by the equilibrium points and stability. Secondly, its basic dynamical characteristics including the Lyapunov exponent spectrum, fractal dimension, time series, power spectrum, bifurcation diagram, and Poincaré section are analyzed. Thirdly, an analog circuit of the neural network model is designed and realized by Multisim. Finally, combined with the chaos encryption principle, an image encryption scheme is designed based on the generated grid multi-structure attractors. Experimental results show that compared with the existing schemes, the proposed scheme has larger information entropy, higher key sensitivity, and a good application prospect.

1 Introduction

Chaos theory is an important discovery of human natural science in the 20th century and has been widely concerned in the fields of non-linear circuits, neural networks, information security, and so on [1–3]. Chaotic attractors are the core of chaos theory, which corresponds to the motion of a disordered steady state in a chaotic system. Since Lorenz [4] discovered the first double-wing attractor in 1962, the construction of complex attractors in chaotic systems has been an important topic in the field of chaos research. After years of exploration, many chaotic systems with different types of attractors have been discovered [5–8], but a complete theoretical model has not yet been developed. The study of chaotic attractors is a very important and key link in the study of chaos theory. From the whole research process, the study of chaotic attractors has just started, and more chaotic attractors are still to be explored and discovered. Furthermore, the wide application of chaotic signals generated by chaotic attractors in the field of information security is another reason that attracts many researchers.

At present, there are three types of chaotic attractors found at home and abroad: 1) Self-excited attractors and hidden attractors. The chaotic attractors discovered earlier are closely related to the unstable equilibrium point of the system and are called self-excited attractors, such as the classical Lorenz attractors [4], Chua’s attractors [9], Chen attractors [10], Lv attractors [11] and so on [12–16]. With the deepening of research on self-excited attractors, some scholars have found that there is an attractor basin of chaos that does not intersect with any open small neighborhood of the equilibrium point of the system, which is called a hidden attractor [17]. In recent years, various hidden attractors have been proposed, such as the hidden attractor of no equilibrium point [18], the hidden attractor of a stable equilibrium point [19], and the hidden attractor of infinite equilibrium points [20]. 2) transient chaotic attractors, chaotic attractors, and hyperchaotic attractors. Chaotic systems can be characterized by the Lyapunov exponent, and chaotic attractors can be divided into different types according to the maximum Lyapunov exponent spectrum. In general, a transient chaotic attractor is defined as the existence of a positive Lyapunov exponent in finite time [21]. The attractor has a positive Lyapunov exponent in infinite time and is called a chaotic attractor. Hyperchaotic attractors are defined as the simultaneous existence of two or more positive Lyapunov exponents in infinite time [22]. In the past few decades, the research on transient chaotic attractors, chaotic attractors, and hyperchaotic attractors has been fruitful [23–25]. 3) Double scroll/wing attractor, multi-scroll/wing attractor, and grid multi-scroll/wing attractor. Double scroll/wing attractors are classical chaotic attractors with special scroll and dynamic trajectories of butterfly wings. Many simple chaotic systems can produce double scroll/wing attractors, such as Chua’s system, Lorenz system, Sprott system [26], Jerk circuit [27], and so on [28, 29]. With the deepening of research on double scroll/wing attractors, various functions such as periodic function [30], piecewise linear function [31], and multistage logic pulse function [32] have been used to expand double scroll/wing attractors in multiple directions to generate multi-scroll/wing attractors [33–35] and grid multi-scroll/wing attractors [36–38]. Among them, the grid multi-scroll/wing attractor has flexible adjustability and high complexity and has a very broad application prospect in secure communication and chaos control [39, 40], so it has become a research hotspot in academia.

The artificial neural network is a kind of non-linear system with complex dynamic characteristics [41, 42]. In recent years, the study of neural network dynamics has gradually become a new research hotspot in the intersection of physics, mathematics, computer science, and neuroscience [43–45]. Among them, Hopfield neural network is a complex non-linear system with chaotic behaviors [46]. Due to its chaotic characteristic, various Hopfield neural network models with different neurons and synaptic weights have been proposed and analyzed [47–50]. In particular, memristive Hopfield neural networks have attracted much attention because of their complex chaotic behavior and potential applications in image encryption. For example, Lin et al. [51] constructed a memristive Hopfield neural network with an arbitrary number of scroll attractors. Yu et al. [52, 53] designed two different memristive Hopfield neural networks which can generate multi-double-scroll attractors. Furthermore, Lai et al. [54] proposed a memristive Hopfield neural network with grid multi-scroll attractors. Meanwhile, the memristive neural network is used to design an image encryption scheme. Although the grid multi-scroll/wing attractor has excellent characteristics, the existing grid multi-scroll/wing attractor implementation methods are complex, the unit structure is simple, and the control parameters are many, and the exploration in recent years seems to indicate that the research of grid multi-scroll/wing attractor is difficult to make updated progress.

To solve these problems, this paper proposes a new method for the generation of novel grid multi-structure chaotic attractors controlled by memristor synapses based on the Hopfield neural network. This method is based on the neural network with complex dynamic characteristics, which successfully gets rid of the scroll/wing attractor unit structure, and makes it appear a more complex and changeable chaotic attractor unit structure. In addition, only two memristor synaptic control parameters are needed to adjust the grid size of the chaotic attractor. The basic dynamic characteristics of the new grid multi-structure attractor are studied by theoretical analysis and numerical simulation. At the same time, the existence of the attractor is verified from the aspect of the circuit. Finally, a scheme of grid multi-structure attractor image encryption is designed based on chaotic encryption theory. The experimental results show that the chaotic attractor exhibits complex dynamic characteristics, so it has better encryption performance and effect in image encryption.

The rest of this paper is organized as follows. Section 2 constructs a memristive Hopfield neural network. Section 3 analyzes the dynamical behaviors of the neural network. Section 4 designs and implements an analog neural network circuit. Section 5 designs a medical image encryption scheme. Section 6 concludes the article.

2 Construction of grid multi-structure attractors

2.1 Introduction of memristor and Hopfield neural network

A memristor is a non-linear circuit element with synaptic memory properties [55], often described in terms of voltage and current relationships. In this paper, a multi-piecewise non-linear flux-controlled memristor model is introduced [51], which can be expressed as

$\left\{\begin{array}{l}i=\left(a+b\phi \right)v\\ \dot{\phi }=cv-dh\left(\phi \right)\end{array}\right.(1)$

where a, b, c, and d represent the four positive parameters of the memristor, and W(φ) = (a + bφ) represents the memristor conductance associated with the memristor state variable φ. In addition, h(φ) is the internal state variable function of the memristor, which can be expressed as

$h\left(\phi \right)=\left\{\begin{array}{c}{h}_1\left(\phi \right)\\ h_2\left(\phi \right)\end{array}\right.(2)$

where

$h_1\left(\phi \right)=\left\{\begin{array}{l}\phi ,N=0\\ \begin{array}{l}\phi -{\displaystyle \sum _{i=1}^N}\left(\mathrm{s}\mathrm{g}\mathrm{n}\left(\phi +\left(2i-1\right)\right)+\mathrm{s}\mathrm{g}\mathrm{n}\left(\phi -\left(2i-1\right)\right)\right)\\ \mathrm{N}=\mathrm{1,2,3},\dots \end{array}\end{array}\right.(3)$

$h_2\left(\phi \right)=\left\{\begin{array}{l}\phi -\mathrm{s}\mathrm{g}\mathrm{n}\left(\phi \right),\mathrm{M}=0\\ \begin{array}{l}\phi -\mathrm{s}\mathrm{g}\mathrm{n}\left(\phi \right)-{\displaystyle \sum _{j=1}^M}\left(\mathrm{s}\mathrm{g}\mathrm{n}\left(\phi +2j\right)+\mathrm{s}\mathrm{g}\mathrm{n}\left(\phi -2j\right)\right)\\ M=\mathrm{1,2,3},\dots \end{array}\end{array}\right.(4)$

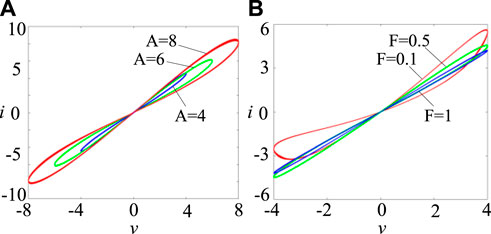
the sgn(.) is a symbolic function, N and where M are the two control parameters of the memristor. To verify that the above mathematical model is a memristor model, consider the case when N = 3. With fixed memristor parameters a = 1, b = 0.05, c = 2.2, d = 1.2, φ₀ = 0, the pinched hysteresis loop of the memristor is simulated by MATLAB R2017a when sinusoidal voltage v = Asin(2πFt) is applied at both ends of the memristor. The simulation results are shown in Figure 1. Under different excitation amplitude A, the pinched hysteresis loop of the model always passes through the origin of the voltage and current plane. With the increase of voltage frequency F, the area of the pinched hysteresis loop of the memristor decreases gradually. When the voltage frequency increases to infinity, the pinched hysteresis loop shrinks to a one-valued function. In summary, the proposed mathematical model satisfies the three characteristics of the memristor and is a memristor model.

FIGURE 1

FIGURE 1. Pinched hysteresis loop characteristics of the memristor. (A) F = 0.1. (B) A = 4.

The Hopfield neural network can produce complex chaotic phenomena and is a classical model for studying chaotic dynamics. A Hopfield neural network with n neurons can be expressed as [46]

${\mathrm{C}}_i{\dot{v}}_i=-\frac{v_i}{R_i}+{\displaystyle \sum _{j=1}^n}{w}_{ij}\tanh \left(v_j\right)+I_i\left(i,j\in N^{*}\right)(5)$

where, C_i, v_i, and R_i respectively represent the membrane capacitance, membrane voltage and membrane resistance of neuron i. w_ij represents the synaptic connection weight from neuron j to neuron i, and tanh(.) is the neuronal activation function. In addition, I_i represents the external bias current of the neuron. Generally speaking, the dynamic behavior of the Hopfield neural network is closely related to its synaptic weight coefficient. According to neural network model (Eq. 5), a Hopfield neural network model with four neurons is constructed by selecting appropriate synaptic weight coefficients, let C_i = 1, R_i = 1, I_i = 0, and its expression is as follows

$\left\{\begin{array}{l}{\dot{x}}_1=-x_1+3\tanh \left(x_2\right)+3\tanh \left(x_3\right)-13\tanh \left(x_4\right)\\ {\dot{x}}_2=-x_2-\tanh \left(x_1\right)+1.5\tanh \left(x_2\right)+7\tanh \left(x_3\right)-5\tanh \left(x_4\right)\\ {\dot{x}}_3=-x_3-4\tanh \left(x_2\right)+1.8\tanh \left(x_3\right)+4\tanh \left(x_4\right)\\ {\dot{x}}_4=-x_4+0.7\tanh \left(x_1\right)+2\tanh \left(x_4\right)\end{array}\right.(6)$

where x_i (i = 1, 2, 3, 4) is the membrane voltage of neuron i.

2.2 Construction of single-directional multi-structure attractors

Memristors have synaptic memory and programmability and can be used to simulate neural synapses [55]. When replacing the resistive synapses between neuron 3 and neuron 1 in the neural network (6) with the multi-piecewise non-linear memristor (1) described above, a memristive Hopfield neural network can be constructed as follows

$\left\{\begin{array}{l}{\dot{x}}_1=-x_1+3\tanh \left(x_2\right)+\rho W\left(\phi \right)\tanh \left(x_3\right)-13\tanh \left(x_4\right)\\ {\dot{x}}_2=-x_2-\tanh \left(x_1\right)+1.5\tanh \left(x_2\right)+7\tanh \left(x_3\right)-5\tanh \left(x_4\right)\\ {\dot{x}}_3=-x_3-4\tanh \left(x_2\right)+1.8\tanh \left(x_3\right)+4\tanh \left(x_4\right)\\ \begin{array}{l}{\dot{x}}_4=-x_4+0.7\tanh \left(x_1\right)+2\tanh \left(x_4\right)\\ \dot{\phi }=c\tanh \left(x_3\right)-dh\left(\phi \right)\end{array}\end{array}\right.(7)$

where, ρ represents the memristor synaptic coupling strength, ρW(φ) = ρ(a + bφ) represents the memristor synaptic coupling weight.

When a = 1, b = 0.01, c = 2.2, d = 1.2, ρ = 3, the initial value (0.1, 0.1, 0.1, 0.1, 0.1), the system in theρ-axis can produce n structure attractor. Taking N = 3 and M = 3 respectively, the numerical simulation results of 7-structure chaotic attractor and 8-structure chaotic attractor are obtained according to the system (7), as shown in Figure 2. From the attractor substructure in Figure 2, it is not difficult to find that, unlike the multi-scroll/wing chaotic attractor, the multi-structure chaotic attractor contains the unit structure attractor with multiple trajectory-disorder, rather than the conventional scroll/wing.

FIGURE 2

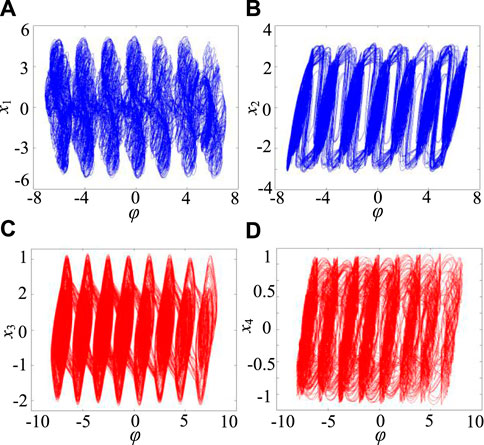
FIGURE 2. Multi-structure chaotic attractor of system (7). (A) 7-structure attractor on the φ-x₁ plane. (B) 7-structure attractor on the φ-x₂ plane. (C) 8-structure attractor on the φ-x₃ plane. (D) 8-structure attractor on the φ-x₄ plane.

2.3 Construction of grid multi-structure attractors

Further studies show that the chaotic attractor can be reconstructed and expanded in different directions by using other synapses in the same type of multi-segment non-linear memristor synaptic replacement system (7), and the grid multi-structure chaotic attractor can be constructed. The system model is as follows

$\left\{\begin{array}{l}{\dot{x}}_1=-x_1+3\tanh \left(x_2\right)+{\rho }_{1}W\left({\phi }_1\right)\tanh \left(x_3\right)-13\tanh \left(x_4\right)\\ {\dot{x}}_2=-x_2-\tanh \left(x_1\right)+1.5\tanh \left(x_2\right)+7\tanh \left(x_3\right)-{\rho }_{2}W\left({\phi }_2\right)\tanh \left(x_4\right)\\ {\dot{x}}_3=-x_3-4\tanh \left(x_2\right)+1.8\tanh \left(x_3\right)+4\tanh \left(x_4\right)\\ \begin{array}{l}{\dot{x}}_4=-x_4+0.7\tanh \left(x_1\right)+2\tanh \left(x_4\right)\\ {\dot{\phi }}_1=c\tanh \left(x_3\right)-dh\left({\phi }_1\right)\\ {\dot{\phi }}_2=c\tanh \left(x_4\right)-dh\left({\phi }_2\right)\end{array}\end{array}\right.(8)$

where ρ_i represents the memristor synaptic coupling strength, ρ_iW(φ_i) = ρ_i(a + bφ_i) represents the memristor synaptic coupling weight.

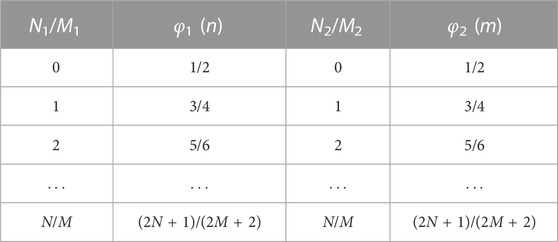
Select a = 1, b = 0.01, c = 2.2, d = 1.2, ρ₁ = 3, ρ₂ = 5, and the initial value is (0.1, 0.1, 0.1, 0.1, 0.1). By taking different memristor control parameters N_i and M_i, the n × m grid multi-structure chaotic attractor can be obtained from system (8), as shown in Figure 3. Obviously, by controlling the two control parameters of the two memristor synapses, a grid multi-structure chaotic attractor of arbitrary size can be obtained, as shown in Table 1. Therefore, compared with the existing multi-parameter function control methods of grid multi-scroll/wing chaotic attractors [30–32], the proposed control method of grid multi-structure chaotic attractors is greatly simplified. In addition, by comparing the structure of system (7) and system (8), we can see that: Only one memristor synapse is introduced in system (7), so that the attractor expands horizontally in the direction of introducing the magnetic flux variable φ, while system (8) introduces two memristor synapses at the same time, so that the attractor expands simultaneously in both directions of the magnetic flux variable φ1 and the magnetic flux variable φ2, thus forming a more complex grid multi-structure chaotic attractor. This is a phenomenon that has not been seen in many chaotic structures before.

FIGURE 3

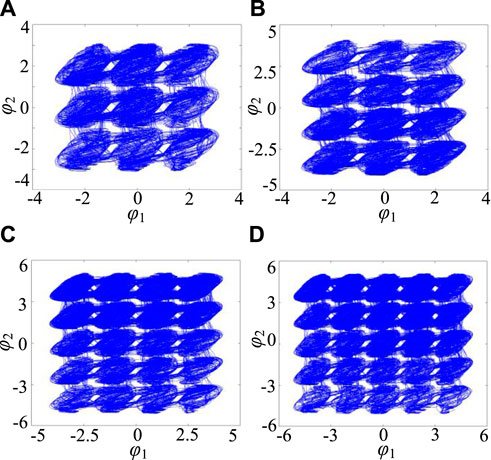
FIGURE 3. Grid multi-structure chaotic attractor of system (8). (A) 3 × 3-structure attractor (N₁ = 1, N₂ = 1). (B) 3 × 4-structure attractor (N₁ = 1, M₂ = 1). (C) 4 × 5-structure attractor (M₁ = 1, N₂ = 2). (D) 5 × 5-structure attractor (N₁ = 2, N₂ = 2).

TABLE 1

TABLE 1. Relation between memristor synaptic control parameters and grid attractors.

3 Basic dynamics analysis

In this section, the dynamic generation mechanism and chaotic characteristics of system (8) are analyzed by dynamic analysis method and numerical simulation.

3.1 Equilibrium points and their stabilities

The equilibrium point is a necessary condition for the generation of self-excited chaos, which can reveal the formation mechanism of chaos attractor from the system level. If the right-hand side of Eq. 8 is equal to 0, the equilibrium state equation of the system can be obtained as follows

$\left\{\begin{array}{l}-x_1+3\tanh \left(x_2\right)+{\rho }_{1}W\left({\phi }_1\right)\tanh \left(x_3\right)-13\tanh \left(x_4\right)=0\\ -x_2-\tanh \left(x_1\right)+1.5\tanh \left(x_2\right)+7\tanh \left(x_3\right)-{\rho }_{2}W\left({\phi }_2\right)\tanh \left(x_4\right)=0\\ -x_3-4\tanh \left(x_2\right)+1.8\tanh \left(x_3\right)+4\tanh \left(x_4\right)=0\\ \begin{array}{l}-x_4+0.7\tanh \left(x_1\right)+2\tanh \left(x_4\right)=0\\ c\tanh \left(x_3\right)-dh\left({\phi }_1\right)=0\\ c\tanh \left(x_4\right)-dh\left({\phi }_2\right)=0\end{array}\end{array}\right.(9)$

Equation 9 is a sixth-order equation, using the MATLAB platform to solve the equilibrium point by graphical analysis method. To have resistance control parameters N₁ = N₂ = 1 as an example, set a = 1, b = 0.01, c = 2.2, d = 1.2, ρ₁ = 3, ρ₂ = 5, Eq. 9 can be converted to

$\left\{\begin{array}{l}\begin{array}{l}{x}_3=\mathrm{atanh}\left(dh\left({\phi }_1\right)/\mathrm{c}\right)\\ x_4=\mathrm{atanh}\left(dh\left({\phi }_2\right)/\mathrm{c}\right)\\ x_1=\mathrm{atanh}\left(\left(x_4-2\tanh \left(x_4\right)\right)/0.7\right)\end{array}\\ x_2=\mathrm{atanh}\left(\left(-x_3+1.8\tanh \left(x_3\right)+4\tanh \left(x_4\right)\right)/4\right)\\ f_1\left({\phi }_1,{\phi }_2\right)=-x_1+3\tanh \left(x_2\right)+{\rho }_{1}W\left({\phi }_1\right)\tanh \left(x_3\right)-13\tanh \left(x_4\right)=0\\ f_2\left({\phi }_1,{\phi }_2\right)=-x_2-\tanh \left(x_1\right)+1.5\tanh \left(x_2\right)+7\tanh \left(x_3\right)-{\rho }_{2}W\left({\phi }_2\right)\tanh \left(x_4\right)=0\end{array}\right.(10)$

The functions f₁ and f₂ are drawn in MATLAB R2017a, as shown in Figure 4, where f₁ is represented by a green curve and f₂ by a red curve. It can be observed from the figure that f₁ and f₂ have 25 intersection points in different positions, that is, the system (8) has 25 equilibrium points at this time. Near the equilibrium point, the Jacobian matrix of the system can be expressed as

$J=\left[\begin{array}{cccccc}-1& 3m_2& {\rho }_{1}W\left({\phi }_1\right)m_3& -13m_4& {\rho }_{1}b\tanh \left(x_3\right)& 0\\ -m_1& -1+1.5m_2& 7m_3& -{\rho }_{2}W\left({\phi }_2\right)m_4& 0& -{\rho }_{2}b\tanh \left(x_4\right)\\ 0& -4m_2& -1+1.8m_3& 4m_4& 0& 0\\ 0.7m_1& 0& 0& -1+2m_4& 0& 0\\ 0& 0& c{m}_3& 0& -d{h}^{\prime }\left({\phi }_1\right)& 0\\ 0& 0& 0& c{m}_4& 0& -d{h}^{\prime }\left({\phi }_2\right)\end{array}\right](11)$

where m_i = sech²(x_i), i = 1, 2, 3, 4. Through numerical calculation, these 25 equilibrium points have three different stability, namely, unstable saddle coke of indicator 4 (yellow), unstable saddle coke of indicator 5 (blue), and unstable saddle coke of indicator 6 (black), as shown in Table 2. Obviously, system (8) generates 9 single structure attractors in the neighborhood of 9 unstable saddle focal points with index-4, 10 unstable saddle focal points with index-5 produce bond bands in the direction of φ₁ and φ₂, and 4 unstable saddle focal points with index-6 play a role in strengthening the connection in the diagonal direction. Finally, under the action of 25 unstable equilibrium points, a 3 × 3 grid multi-structure chaotic attractor phenomenon is generated, as shown in Figure 4. A large number of simulation results show that with the increase of the control parameters N₁/M₁ and N₂/M₂ of the two memristic synapses, the equilibrium point of the system will gradually expand along the φ₁ and φ₂ axes, resulting in a larger number of grid multi-structure chaotic attractors on the φ₁-φ₂ phase plane.

FIGURE 4

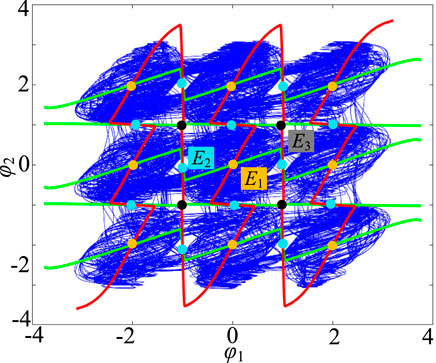
FIGURE 4. Function f₁ and f₂ curves, equilibrium point, and superposition diagram of 3 × 3 structure attractor.

TABLE 2

TABLE 2. Representative equilibrium points of system (8), corresponding to eigenvalues and types of equilibrium points.

3.2 Lyapunov exponents and Kaplan-Yorke dimension

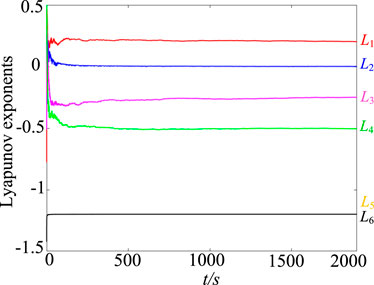
Lyapunov exponent spectrum analysis is an important method to study the dynamical characteristics of chaotic systems. It reveals the chaotic characteristics of the system from the perspective of the average exponential rate of convergence or divergence between adjacent orbits in the phase space of the system. Under the condition of multi-structure attractor generation in a 3 × 3 grid, six Lyapunov indices of the system were obtained by using the Wolf’s Jacobian-based method, as shown in Figure 5. Where L₁ = 0.2146, L₂ = 0.0015, L₃ = −0.2608, L₄ = −0.5047, L₅ = −1.201, L₆ = −1.202. Obviously, it is not difficult to find that system (8) has a positive Lyapunov exponent; a Lyapunov exponent is approaching 0; The sum of all Lyapunov exponents is negative. Therefore, under these conditions, the system is chaotic. The Kaplan-Yorke dimension corresponding to its Lyapunov index is

$D_{KY}=j+\frac{1}{\left|L_{j+1}\right|}{\displaystyle \sum _{i=1}^j}{L}_i=2+\frac{L_1+L_2}{\left|L_3\right|}=2.8286(12)$

FIGURE 5

FIGURE 5. Lyapunov exponents of system (8).

Obviously, the Kaplan-Yorke dimension of the system is fractional, which further proves that the grid multi-structure attractors generated by the system are chaotic.

3.3 Time series and power spectrum

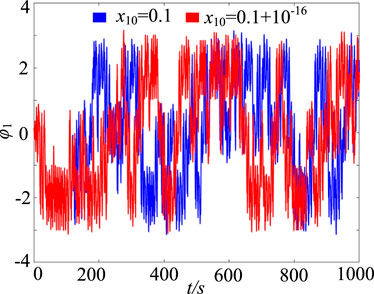
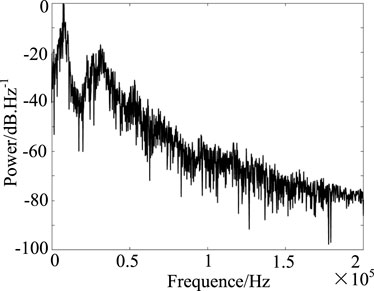
When system parameters are kept unchanged, the timing waveform of system (8) in the direction of state variable φ₁ is shown by the blue curve in Figure 6. It can be seen from the figure that its motion trajectory oscillates randomly in a certain region and has distinct aperiodic characteristics. In addition, after slightly changing the initial value x₁₀, the time-domain waveform obtained by system (8) is shown by the red curve in Figure 6. It is not difficult to see that when the initial values are 0.1 and 0.1 + 10⁻¹⁶ respectively, there is no obvious difference between the two timings in (0, 120 s) time, but when t is greater than 120 s, they show completely different time evolution tracks. Therefore, even with a size adjustment of 10⁻¹⁶ for x₁₀, the trajectory of the system can make a huge difference, which means that the motion state of the system is not only aperiodic but also extremely sensitive to initial conditions. To further verify its non-periodicity, the power spectrum of system (8) is shown in Figure 7. It can be seen that the system exhibits a continuous power spectrum similar to a noise signal in a limited frequency range, which indicates that the system has obvious aperiodic chaotic characteristics.

FIGURE 6

FIGURE 6. Time domain waveform of state variable φ₁.

FIGURE 7

FIGURE 7. Power spectrum of system (8).

3.4 Bifurcation diagrams and Poincaré maps

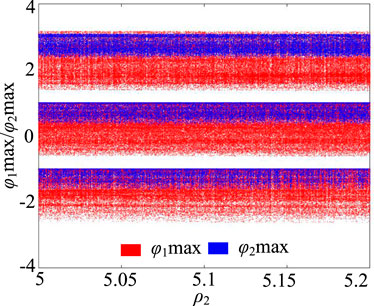
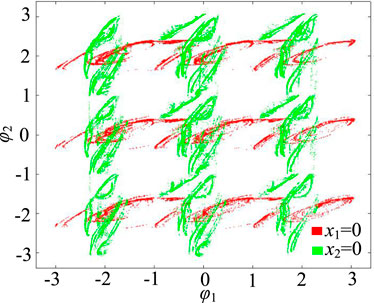
The bifurcation diagram is an important tool to describe the dynamic state of chaotic systems with parameter variation. Figure 8 shows the structure of local branch forks within the range of parameter ρ₂∈[5, 5.2], where red is the bifurcation in the direction of state variable φ₁, and blue is the bifurcation in the direction of state variable φ₂. It can be seen from Figure 8 that there are pieces of quasi-random points in the bifurcation diagram, indicating that the system is in a chaotic state. More importantly, different from the general chaotic bifurcation structure, the bifurcation diagram of system (8) presents three parallel bifurcation structures simultaneously in the directions of φ₁ and φ₂, and they are all in a chaotic state. This means that the system generates a 3 × 3 grid multi-structure chaotic attractor. In addition, Figure 9 shows the Poincaré map of a 3 × 3 grid multi-structure chaotic attractor in the φ₁-φ₂ phase plane. Among them, the red section diagram is generated by the x₁ = 0 section, and the green section diagram is generated by the x₂ = 0 section. Through observation, it is not difficult to find that the Poincare map of system (8) shows a series of irregular dense points, which further proves that the grid multi-structure attractors have complex chaotic characteristics.

FIGURE 8

FIGURE 8. Bifurcation diagram of system (8) with ρ₂.

FIGURE 9

FIGURE 9. Poincaré maps of system (8) in the plane φ₁-φ₂.

4 Circuit implementation and verification

Circuit realization is one of the effective ways to verify the mathematical model [56]. In general, chaotic systems can be implemented by analog or digital circuits to generate chaotic signals [57, 58]. In this section, we first design the physical circuit of system (8) and then verify the existence of grid multi-structure chaotic attractors by Multisim simulation.

4.1 Circuit design

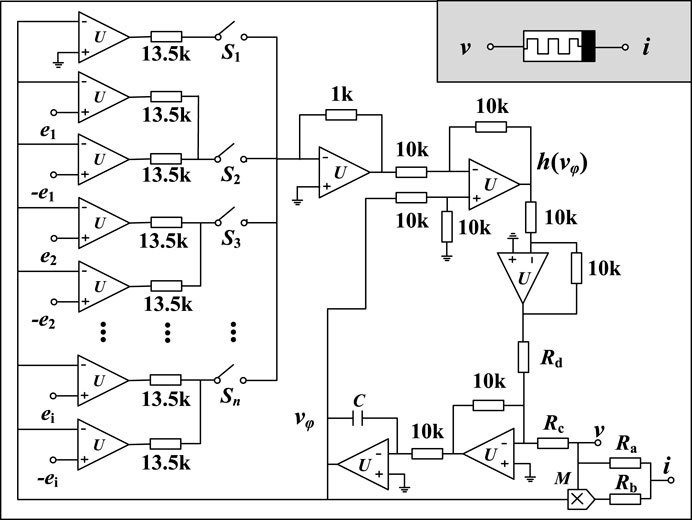
First, a multi-segment non-linear memristor circuit is designed, as shown in Figure 10. Where, the internal state equation h(φ) of the memristor is realized by a non-linear function generator, e1, e2,..., e_i is the control voltage, S1, S2,..., Sn is the selection switch. By selecting the corresponding control voltage and switch, the memristor function under different control parameters can be realized, as shown in Table 3.

FIGURE 10

FIGURE 10. Memristor circuit.

TABLE 3

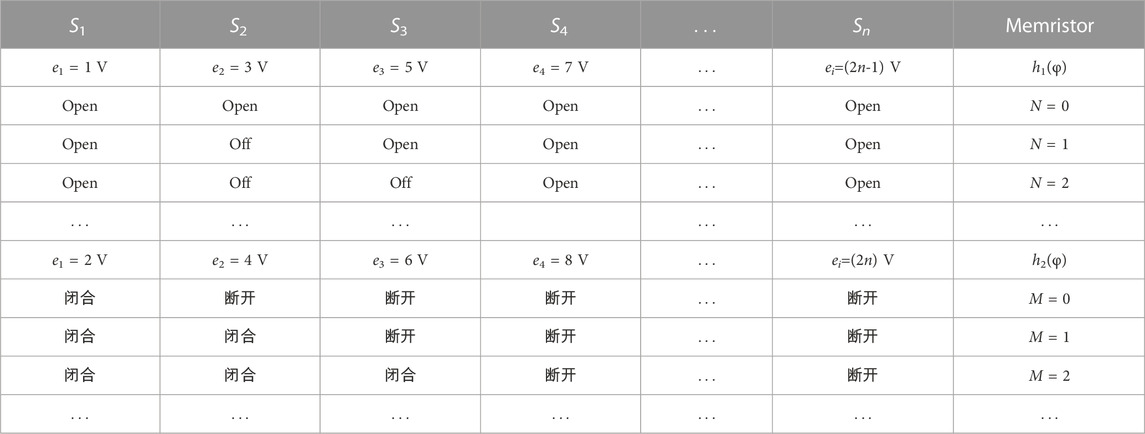
TABLE 3. Different memristor types realized by selecting the combination of switch and control voltage.

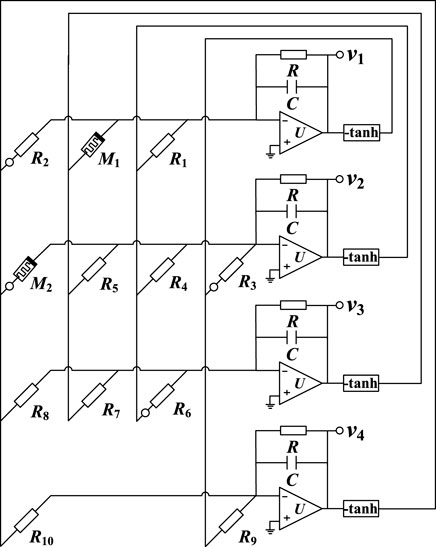
Then, based on the memristor circuit, the physical circuit of system (8) is realized, as shown in Figure 11. Where the neuron activation function tanh(.) The equivalent circuit is available in Ref. [47]. In addition, the four neuronal membrane voltages are simulated by the four capacitor voltages of the circuit, and the fixed synaptic weight coefficients are simulated using resistors R₁–R₁₀. The memristor synaptic weight is achieved by the memristor. According to Kirchhoff’s current law, the circuit equation of system (8) can be expressed as

$\left\{\begin{array}{l}RC{\dot{v}}_1=-v_1+\frac{R}{R_1}\tanh \left(v_2\right)+R\left(\frac{1}{R_{a1}}+\mathrm{g}\frac{v_{\phi 1}}{R_{b1}}\right)\tanh \left(v_3\right)-\frac{R}{R_2}\tanh \left(v_4\right)\\ RC{\dot{v}}_2=-v_2-\frac{R}{R_3}\tanh \left(v_1\right)+\frac{R}{R_4}\tanh \left(v_2\right)+\frac{R}{R_5}\tanh \left(v_3\right)-R\left(\frac{1}{R_{a2}}+\mathrm{g}\frac{v_{\phi 2}}{R_{b2}}\right)\tanh \left(v_4\right)\\ RC{\dot{v}}_3=-v_3-\frac{R}{R_7}\tanh \left(v_2\right)+\frac{R}{R_8}\tanh \left(v_3\right)+\frac{R}{R_9}\tanh \left(v_4\right)\\ \begin{array}{l}RC{\dot{v}}_4=-v_4+\frac{R}{R_{10}}\tanh \left(v_1\right)+\frac{R}{R_{11}}\tanh \left(v_4\right)\\ RC{\dot{v}}_{\phi 1}=\frac{R}{R_c}\tanh \left(v_3\right)-\frac{R}{R_d}h\left(v_{\phi 1}\right)\\ RC{\dot{v}}_{\phi 2}=\frac{R}{R_c}\tanh \left(v_3\right)-\frac{R}{R_d}h\left(v_{\phi 2}\right)\end{array}\end{array}\right.(13)$

FIGURE 11

FIGURE 11. Physical circuits of system (8).

4.2 MULTISIM simulation

The physical circuit of system (8) is implemented and simulated on the Multisim14.0 platform. In this section, we first design the physical circuit of system (8) and then verify the existence of grid multi-structure chaotic attractors by Multisim simulation. Set capacitance C = 1 nF, R = 10 kΩ. Fixed synaptic weight coefficient according to system (8), setting R₁ = R/w₁₂ = 3.3 kΩ, R₂ = R/w₁₄ = 0.77 kΩ, R₃ = R/w₂₁ = 10 kΩ, R₄ = R/w₂₂ = 6.7 kΩ, R₅ = R/w₂₃ = 1.4 kΩ, R₆ = R/w₃₂ = 2.5 kΩ, R₇ = R/w₃₃ = 5.7 kΩ, R₈ = R/w₃₄ = 2.5 kΩ, R₉ = R/w₄₁ = 14.3 kΩ, R₁₀ = R/w₄₄ = 5 kΩ. In addition, the resistance of the memristor circuit R_a = R/ρa, R_b = gR/ρb, R_c = R/c, R_d = R/d. When the system parameters a = 1, b = 0.01, c = 2.2, d = 1.2, ρ₁ = 3, ρ₂ = 5, R_a1 = 3.3 kΩ, R_b1 = 34 kΩ, R_a2 = 2 kΩ, R_b2 = 20 kΩ, R_c = 4.5 kΩ, R_d = 8.4 kΩ can be solved. Set the initial voltage of the five capacitor voltages to (0.1V, 0.1V, 0.1V, 0.1V). By setting the corresponding switching and control voltage according to Table 3, the system circuit can generate a grid multi-structure chaotic attractor consistent with the numerical simulation results, as shown in Figure 12. By comparing the results of Figure 12 and Figure 13, it can be found that the results obtained by Multisim circuit simulation and Matlab numerical simulation are almost exactly the same, thus verifying the grid multi-structure chaotic attractor characteristics of system (8).

FIGURE 12

FIGURE 12. Experiment results. (A) 3 × 3-structure attractor. (B) 4 × 5-structure attractor.

FIGURE 13

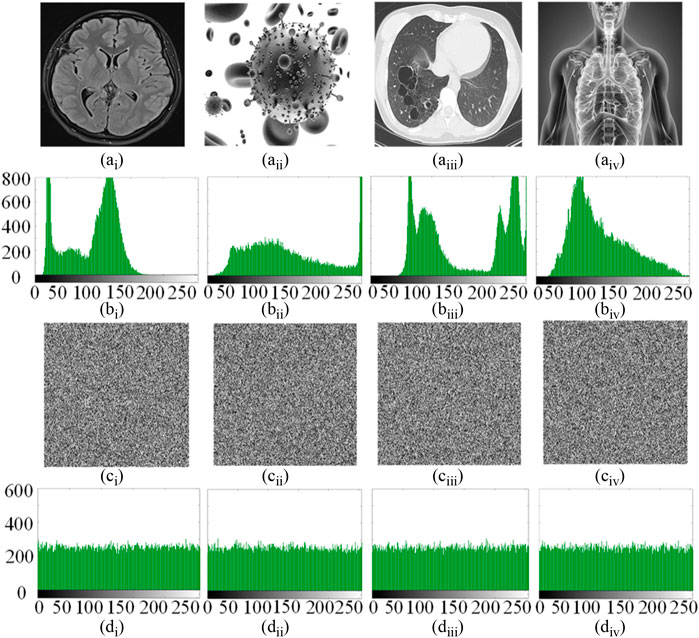
FIGURE 13. Encryption results. (Ai–iv) Original images. (Bi–iv) Histograms of the original images. (Ci–iv) Encrypted images. (Di–iv) Histograms of the encrypted images.

5 Medical image encryption applications

Chaotic signals have the characteristics of ergodic, initial value sensitivity, high randomness, etc., and are mainly used for the key generation of secure communication [59, 60]. Generally, the more chaotic the attractor trajectory of chaotic systems, the more sensitive the initial conditions, the higher the randomness of the key generated, and the better the encryption performance. Based on the above analysis results, the grid multi-structure chaotic attractor proposed in this paper has a complex structure, high initial value sensitivity, and strong chaos randomness, which can greatly improve the communication encryption effect and crack difficulty.

5.1 Image encryption scheme

In this section, a new image encryption scheme is designed based on the grid multi-structure chaotic attractor. The specific encryption steps are as follows:

Step 1. Set (a, b, c, d, ρ₁, ρ₂, x₂₀, x₃₀, x₄₀, φ₁₀, φ₂₀, N₁, N₂) = (1, 0.01, 2.2, 1.2, 3, 5, 0.1, 0.1, 0.1, 0.1, 0.1, 0.1, 1, 1), discarded number N₀ = 1000, time step Δt = 0.002, based fourth-order Runge-Kutta algorithm, the system (8) is continuously iterated 256 × 256 times. For each iteration, we can get six values x₁(i), x₂(i), x₃(i), x₄(i), φ₁(i), φ₂(i).

Step 2. The following preprocessing is performed on the six chaotic sequences to produce two distinct sets of sequences, respectively

$K_1\left(i\right)=x_{1i}+x_{2i}+x_{3i}+x_{4i}(14)$

$K_2\left(i\right)=\mathrm{mod}\left(\mathrm{f}\mathrm{l}\mathrm{o}\mathrm{o}\mathrm{r}\left(\left(\left(x_{1i}+x_{2i}+x_{3i}+x_{4i}+{\phi }_{1i}+{\phi }_{2i}\right)/6\right)*{10}^{15}\right),256\right)(15)$

Step 3. The index sequence index is obtained by arranging the sequence K1 in ascending order. Then, the index sequence is replaced and encrypted with the original image pixels successively to obtain the replaced image P1 as follows

$P_1\left(i\right)=P\left(\mathrm{i}\mathrm{n}\mathrm{d}\mathrm{e}\mathrm{x}\left(K_1\left(i\right)\right)\right)(16)$

Step 4. The pixels of the sequence K2 and the diagram P1 to be encrypted are different or encrypted as follows

$\mathrm{C}\left(i\right)=P_1\left(i\right)\oplus K_2\left(i\right)(17)$

5.2 Encryption performance analysis

In order to prove the effectiveness and security of the above encryption algorithm, the following tests are carried out on the MATLAB R2017a platform. In the experiment, four 256 × 256 medical images were used as original images, which were brain image, virus image, lung image, and chest image, as shown in Figures 13Ai–Aiv. The key space, histogram, correlation coefficient, information trail, key sensitivity, noise and data loss attacks of the encryption system are analyzed below.

(1) Keyspace analysis. The secret key space is an important index to evaluate the encryption system. Generally speaking, the larger the key space of the encryption system, the stronger the resistance to external brute force attacks. The designed encryption algorithm uses the above 11 parameters as the secret key, making it difficult to decrypt illegally. In the experiment, all bytes are double-precision data, so the secret key space of the encryption system is (10¹⁶)¹¹ = 10¹⁷⁶ ≈ 2⁵²⁸. Obviously, this key space is much larger than the minimum key space value of 2¹⁰⁰ to resist various brute force attacks.

(2) Histogram analysis. Histogram is a key index to evaluate the intensity distribution of pixel values in an image. The more average the histogram distribution of the image, the stronger the resistance to statistical attacks. Figure 13 shows the original image, the original image histogram, the encrypted image, and the encrypted image histogram of the four medical images respectively. Figures 13Ci–Civ look confusing and completely lose the information of the original images. In addition, by comparing Figures 14Bi–Biv and Figures 13Di–Div, we can see that the histogram of the encrypted image is very different from that of the original images. The histogram distribution of the original image is completely inconsistent and uneven, while the histogram distribution of the encrypted image is very average. Therefore, the designed encryption algorithm has good security against statistical analysis attacks.

(3) Correlation analysis. The correlation coefficient is an important index of image robustness. It represents the correlation between two adjacent pixels in an image. Usually, the correlation coefficient of the original image in all directions is relatively large, close to 1. The correlation of the encrypted image should be as small as possible, close to zero. In general, the correlation coefficient of the image can be calculated by the following formula

${\rho }_{xy}=\frac{{\displaystyle \sum _{i=1}^N}\left(x_i-E\left(x\right)\right)\left(y_i-E\left(y\right)\right)}{\sqrt{{\displaystyle \sum _{i=1}^N}{\left(x_i-E\left(x\right)\right)}^2}\sqrt{{\displaystyle \sum _{i=1}^N}{\left(y_i-E\left(y\right)\right)}^2}}(18)$

where x and y represent two adjacent pixel values, and N represents the total number of pixels. E(x) and E(y) represent the average values of pixels x_i and y_i, respectively. In order to calculate the correlation coefficient between the original image and the encrypted image, 10,000 pixels are randomly selected for analysis. Table 4 shows the phase relation values of the four original images and the encrypted images. As can be seen from Table 4, although the correlation coefficients of the four original images are close to 1 in the vertical, horizontal, and diagonal directions, after encryption, the correlation coefficients of the four encrypted images are very close to 0. Therefore, the designed encryption algorithm can greatly reduce the correlation of images, so as to effectively resist statistical attacks.

(4) Entropy analysis. Information entropy is an important index to describe the degree of image uncertainty. In general, the larger the information origin value, the higher the randomness of the image information. An ideal value for grayscale images is 8. Therefore, a good encryption algorithm should make the information descent of the encryption graph as close to 8 as possible. Information origin can be calculated by the following formula

$H\left(P\right)={\displaystyle \sum _{i=0}^{2^N-1}}P\left(x_i\right){\log }_2\frac{1}{P\left(x_i\right)}(19)$

where N represents the bit depth of image P, and P(x_i) represents the occurrence probability of pixel xi. Table 5 shows the information origin values of the four original and encrypted graphs. Obviously, compared with the origin of the original graph, the origin value of the encrypted graph is not only greatly improved, but also very close to the ideal value of 8. Therefore, the encryption algorithm has good encryption performance.

(5) Sensitivity analysis. The sensitivity of the key is an important index to evaluate the security performance of encryption algorithms. A good encryption algorithm should be as sensitive to the key as possible. When the keys a, b, c, d, ρ, φ₀, and N are fixed and the values of the keys x₁₀, x₂₀, x₃₀, and x₄₀ are changed, the key sensitivity of the four images is measured. The experimental results are shown in Figure 15. For the small change of the secret key, even with the disturbance of 10–16, the decrypted image still cannot decrypt the encryption diagram correctly. As shown in Table 6, compared with the existing similar work, the secret key sensitivity value of the image encryption algorithm based on multi-scroll memristor HNN in literature [34] is 10⁻⁹, and the secret key sensitivity value of the image encryption algorithm based on multi-scroll chaotic system in literature [35] is 10⁻¹². The designed image encryption algorithm based on multi-structure attractor memristor HNN has great advantages in terms of secret key sensitivity.

(6) Data loss and noise attacks. Noise and data loss attacks can be used to evaluate the robustness of cryptosystems. On the one hand, the image is prone to sudden and strong noise interference in the transmission process, which will produce noise and affect the correct decryption of the image. Therefore, for image encryption systems, resisting noise attacks is a very important performance index. Here, different proportions of salt and pepper noise are added to the encrypted image, as shown in Figures 15Ai–Aiii. Then the secret key is used to decrypt the encrypted image, as shown in Figures 15Bi–Biii. It can be observed that although some pixels of the decrypted image are changed after the addition of salt and pepper noise, most of the main information of the original image can still be obtained. Therefore, the noise has very little effect on the decryption process of the designed encryption algorithm. On the other hand, it is easy to lose some data in the process of encrypted image transmission. Therefore, a good encryption algorithm should be robust to partial data loss. Here, the data of different sizes of the encryption graph is cut out, as shown in Figures 15Ci–Ciii. Then, using the secret key to decrypt it, the results are shown in Figures 15Di–Diii. Obviously, although the encrypted graph has lost some data information, it can still recover most of the original image information through the decryption process. Therefore, the experimental results show that the designed encryption algorithm has strong resistance to data loss attacks.

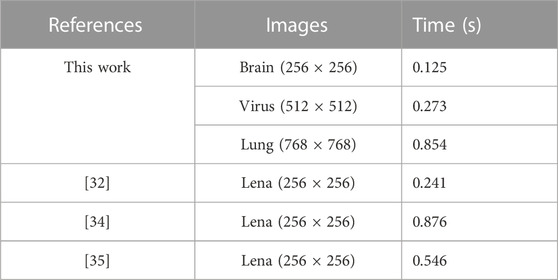
(7) Encryption time analysis. Regardless of the security performance, encryption time is also very important, especially in emergency medical care applications. The time test of the scheme is operated using MATLAB R2017a on a PC with Windows 10 64-bit operation system, 2.5 GHz CPU, and 8 GB RAM. All medical images are tested, and the comparison results of one round of encryption execution time are listed in Table 7. It is clear that the execution time of our scheme is shorter than the other schemes.

FIGURE 14

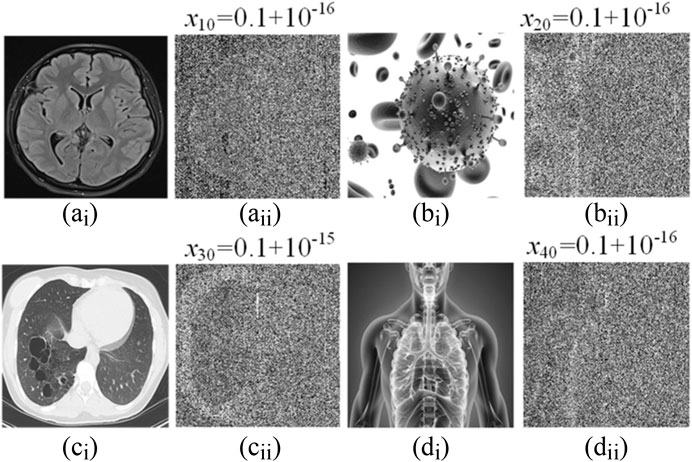
FIGURE 14. Test results of key sensitivity. (Ai–Di) Accurate decrypted images with right secret keys. (Aii–Dii) Inaccurate decrypted images with wrong secret keys.

TABLE 4

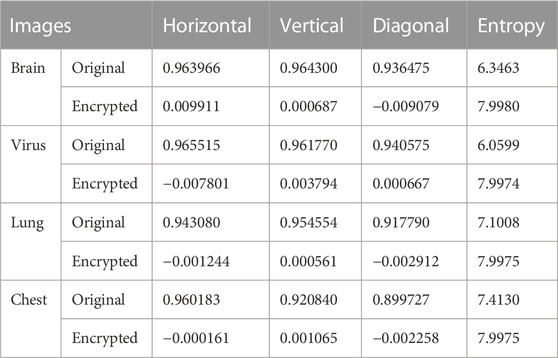
TABLE 4. Correlation coefficient and information origin between the original image and the encrypted image.

TABLE 5

TABLE 5. Comparison of information entropy of different encryption schemes.

FIGURE 15

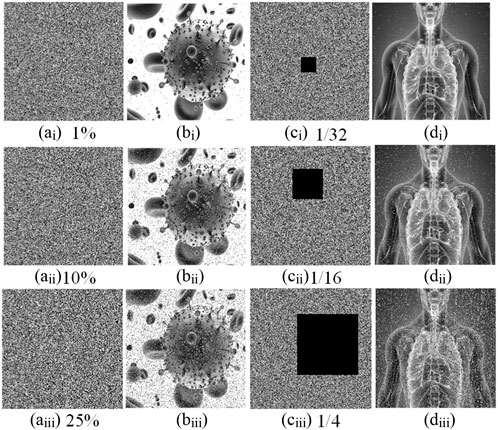
FIGURE 15. Test results of data loss and noise attacks. (Ai–iii) The encrypted images with 1%, 10%, and 25% salt and pepper noise, respectively. (Bi–iii) Corresponding decrypted images. (Ci–iii) The encrypted images with 1/32, 1/16, and 1/4 data loss, respectively. (Di–iii) Corresponding decrypted images.

TABLE 6

TABLE 6. Comparison of key sensitivity of different encryption schemes.

TABLE 7

TABLE 7. Comparison results of the encryption time.

The above experimental results show that the designed medical image encryption algorithm based on a multi-structure chaotic attractor has a larger key space and higher key sensitivity, can effectively resist various internal and external attacks, and can be applied to protect image data better in practical information communication.

6 Conclusion

Based on the chaotic property of the Hopfield neural network and the memristor synapse control method, a grid multi-structure attractor chaotic system is proposed in this paper. Its complex and varied chaotic structure provides a new idea for the study of new grid chaotic attractors. The basic dynamic analysis, such as equilibrium point, Lyapunov exponential spectrum, power spectrum, bifurcation diagram, and Poincare cross section, shows that the multi-structure chaotic attractor has the characteristics of simple implementation, few control parameters, complex unit topology, expandable unit structure, and complex chaotic dynamics. At the same time, based on the chaotic circuit design method, the circuit simulation of the chaotic attractor is realized, and the feasibility of the system circuit is verified. Finally, combined with the study of chaotic image encryption theory, an image encryption scheme based on the grid multi-structure attractor is designed. The experimental results show that the new grid multi-structure chaotic attractor has certain advantages in encrypted communication and has a good application prospect. The next step will consider introducing multiple memristor synapses into neural networks to construct n-dimensional grid multi-structure chaos attractors to improve the complexity of chaotic systems.

Data availability statement

The original contributions presented in the study are included in the article/Supplementary Material, further inquiries can be directed to the corresponding author.

Author contributions

ZH: Methodology, Software, Writing–original draft. HL: Data curation, Formal Analysis, Validation, Investigation, Writing–review and editing. CW: Conceptualization, Funding acquisition, Writing–review and editing.

Funding

The author(s) declare financial support was received for the research, authorship, and/or publication of this article. This work is supported by the National Natural Science Foundation of China (62271197, 61971185, and 62201204), the China Postdoctoral Science Foundation (2022M71104), and the Natural Science Foundation of Hunan Province (2023JJ40168).

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

1. Pham VT, Volos C, Jafari S, Wei Z, Wang X. Constructing a novel no-equilibrium chaotic system. Int J Bifurcation Chaos (2014) 24(05):1450073. doi:10.1142/s0218127414500734

CrossRef Full Text | Google Scholar

2. Lai Q, Kuate PDK, Liu F, Iu HHC. An extremely simple chaotic system with infinitely many coexisting attractors. IEEE Trans Circuits Syst Express Briefs (2019) 67(6):1129–33. doi:10.1109/tcsii.2019.2927371

CrossRef Full Text | Google Scholar

3. Wen Z, Wang C, Deng Q, Lin H. Regulating memristive neuronal dynamical properties via excitatory or inhibitory magnetic field coupling. Nonlinear Dyn (2022) 110(4):3823–35. doi:10.1007/s11071-022-07813-9

CrossRef Full Text | Google Scholar

4. Lorenz EN. Deterministic nonperiodic flow. J Atmos Sci (1963) 20(2):130–41. doi:10.1175/1520-0469(1963)020<0130:dnf>2.0.co;2

CrossRef Full Text | Google Scholar

5. Fan W, Chen X, Wang Y, Chen B, Wu H, Xu Q. Hidden firing patterns and memristor initial condition-offset boosting behavior in a memristive Hindmarsh-Rose neuron model. Front Phys (2023) 11:1160419. doi:10.3389/fphy.2023.1160419

CrossRef Full Text | Google Scholar

6. Sun J, Li C, Lu T, Akgul A, Min F. A memristive chaotic system with hypermultistability and its application in image encryption. Ieee Access (2020) 8:139289–98. doi:10.1109/access.2020.3012455

CrossRef Full Text | Google Scholar

7. Lin H, Wang C, Du S, Yao W, Sun Y. A family of memristive multibutterfly chaotic systems with multidirectional initial-based offset boosting. Chaos, Solitons & Fractals (2023) 172:113518. doi:10.1016/j.chaos.2023.113518

CrossRef Full Text | Google Scholar

8. Sahoo S, Roy BK. A new multi-wing chaotic attractor with unusual variation in the number of wings. Chaos, Solitons & Fractals (2022) 164:112598. doi:10.1016/j.chaos.2022.112598

CrossRef Full Text | Google Scholar

9. Chua LO, Lin GN. Canonical realization of Chua's circuit family. IEEE Trans Circuits Syst (1990) 37(7):885–902. doi:10.1109/31.55064

CrossRef Full Text | Google Scholar

10. Chen G, Ueta T. Yet another chaotic attractor. Int J Bifurcation chaos (1999) 9(07):1465–6. doi:10.1142/s0218127499001024

CrossRef Full Text | Google Scholar

11. Lv J, Chen G. A new chaotic attractor coined. Int J Bifurcation chaos (2002) 12(03):659–61.

Google Scholar

12. Wang Q, Tian Z, Wu X, Tan W. Coexistence of multiple attractors in a novel simple jerk chaotic circuit with CFOAs implementation. Front Phys (2022) 10:41. doi:10.3389/fphy.2022.835188

CrossRef Full Text | Google Scholar

13. Njitacke ZT, Sone ME, Fozin TF, Tsafack N, Leutcho GD, Tchapga CT. Control of multistability with selection of chaotic attractor: Application to image encryption. Eur Phys J Spec Top (2021) 230(7-8):1839–54. doi:10.1140/epjs/s11734-021-00137-6

CrossRef Full Text | Google Scholar

14. Yan D, Wang L, Duan S, Chen J, Chen J. Chaotic attractors generated by a memristor-based chaotic system and Julia fractal. Chaos, Solitons & Fractals (2021) 146:110773. doi:10.1016/j.chaos.2021.110773

CrossRef Full Text | Google Scholar

15. Liu T, Yan H, Banerjee S, Mou J. A fractional-order chaotic system with hidden attractor and self-excited attractor and its DSP implementation. Chaos, Solitons & Fractals (2021) 145:110791. doi:10.1016/j.chaos.2021.110791

CrossRef Full Text | Google Scholar

16. Gong LH, Luo HX, Wu RQ, Zhou NR. New 4D chaotic system with hidden attractors and self-excited attractors and its application in image encryption based on RNG. Physica A: Stat Mech its Appl (2022) 591:126793. doi:10.1016/j.physa.2021.126793

CrossRef Full Text | Google Scholar

17. Leonov GA, Kuznetsov NV, Vagaitsev VI. Localization of hidden Chuaʼs attractors. Phys Lett A (2011) 375(23):2230–3. doi:10.1016/j.physleta.2011.04.037

CrossRef Full Text | Google Scholar

18. Zhang S, Wang X, Zeng Z. A simple no-equilibrium chaotic system with only one signum function for generating multidirectional variable hidden attractors and its hardware implementation. Chaos (2020) 30(5):053129. doi:10.1063/5.0008875

PubMed Abstract | CrossRef Full Text | Google Scholar

19. Chen M, Wang C, Bao H, Ren X, Bao B, Xu Q. Reconstitution for interpreting hidden dynamics with stable equilibrium point. Chaos, Solitons & Fractals (2020) 140:110188. doi:10.1016/j.chaos.2020.110188

CrossRef Full Text | Google Scholar

20. Li C, Peng Y, Tao Z, Sprott JC, Jafari S. Coexisting infinite equilibria and chaos. Int J Bifurcation Chaos (2021) 31(05):2130014. doi:10.1142/s0218127421300147

CrossRef Full Text | Google Scholar

21. Bo-Cheng B, Zhong L, Jian-Ping X. Transient chaos in smooth memristor oscillator. Chin Phys B (2010) 19(3):030510. doi:10.1088/1674-1056/19/3/030510

CrossRef Full Text | Google Scholar

22. Lin H, Wang C, Cui L, Sun Y, Zhang X, Yao W. Hyperchaotic memristive ring neural network and application in medical image encryption. Nonlinear Dyn (2022) 110(1):841–55. doi:10.1007/s11071-022-07630-0

CrossRef Full Text | Google Scholar

23. Wang FP, Wang FQ. Multistability and coexisting transient chaos in a simple memcapacitive system. Chin Phys B (2020) 29(5):058502. doi:10.1088/1674-1056/ab7e98

CrossRef Full Text | Google Scholar

24. Lin H, Wang C, Yu F, Sun J, Du S, Deng Z, et al. A review of chaotic systems based on memristive Hopfield neural networks. Mathematics (2023) 11(6):1369. doi:10.3390/math11061369

CrossRef Full Text | Google Scholar

25. Li S, Wu Y, Zheng G. Adaptive synchronization for hyperchaotic liu system. Front Phys (2022) 9:812048. doi:10.3389/fphy.2021.812048

CrossRef Full Text | Google Scholar

26. Sprott JC. Some simple chaotic flows. Phys Rev E (1994) 50(2):647–50. doi:10.1103/physreve.50.r647

PubMed Abstract | CrossRef Full Text | Google Scholar

27. Sprott JC. A new chaotic jerk circuit. IEEE Trans Circuits Syst Express Briefs (2011) 58(4):240–3. doi:10.1109/tcsii.2011.2124490

CrossRef Full Text | Google Scholar

28. Li C, Yang Y, Yang X, Zi X, Xiao F. A tristable locally active memristor and its application in Hopfield neural network. Nonlinear Dyn (2022) 108(2):1697–717. doi:10.1007/s11071-022-07268-y

CrossRef Full Text | Google Scholar

29. Zhou W, Wang G, Iu HHC, Shen Y, Liang Y. Complex dynamics of a non-volatile memcapacitor-aided hyperchaotic oscillator. Nonlinear Dyn (2020) 100:3937–57. doi:10.1007/s11071-020-05722-3

CrossRef Full Text | Google Scholar

30. Yang Y, Huang L, Xiang J, Guo Q. Three-dimensional sine chaotic system with multistability and multi-scroll attractor. IEEE Trans Circuits Syst Express Briefs (2022) 69(3):1792–6. doi:10.1109/tcsii.2021.3126227

CrossRef Full Text | Google Scholar

31. Wang N, Li C, Bao H, Chen M, Bao B. Generating multi-scroll Chua’s attractors via simplified piecewise-linear Chua’s diode. IEEE Trans Circuits Syst Regular Pap (2019) 66(12):4767–79. doi:10.1109/tcsi.2019.2933365

CrossRef Full Text | Google Scholar

32. Hong Q, Li Y, Wang X, Zeng Z. A versatile pulse control method to generate arbitrary multidirection multibutterfly chaotic attractors. IEEE Trans Computer-Aided Des Integrated Circuits Syst (2018) 38(8):1480–92. doi:10.1109/tcad.2018.2855121

CrossRef Full Text | Google Scholar

33. Lai Q, Wan Z, Zhang H, Chen G. Design and analysis of multiscroll memristive hopfield neural network with adjustable memductance and application to image encryption. IEEE Trans Neural Networks Learn Syst (2022) 1–14. doi:10.1109/tnnls.2022.3146570

CrossRef Full Text | Google Scholar

34. Lin H, Wang C, Yu F, Xu C, Hong Q, Yao W, et al. An extremely simple multiwing chaotic system: Dynamics analysis, encryption application, and hardware implementation. IEEE Trans Ind Electron (2020) 68(12):12708–19. doi:10.1109/tie.2020.3047012

CrossRef Full Text | Google Scholar

35. Zhang S, Li C, Zheng J, Wang X, Zeng Z, Peng X. Generating any number of initial offset-boosted coexisting Chua's double-scroll attractors via piecewise-nonlinear memristor. IEEE Trans Ind Electron (2021) 69(7):7202–12. doi:10.1109/tie.2021.3099231

CrossRef Full Text | Google Scholar

36. Escalante RJ, Campos E. A class of piecewise linear systems without equilibria with 3-D grid multiscroll chaotic attractors. IEEE Trans Circuits Syst Express Briefs (2018) 66(8):1456–60.

Google Scholar

37. Ding PF, Feng XY, Wu CM. Novel two-directional grid multi-scroll chaotic attractors based on the Jerk system. Chin Phys B (2020) 29(10):108202. doi:10.1088/1674-1056/ab9dea

CrossRef Full Text | Google Scholar

38. Azam A, Aqeel M, Sunny DA. Generation of multidirectional mirror symmetric multiscroll chaotic attractors (MSMCA) in double wing satellite chaotic system. Chaos, Solitons & Fractals (2022) 155:111715. doi:10.1016/j.chaos.2021.111715

CrossRef Full Text | Google Scholar

39. Peng X, Zeng Y. Image encryption application in a system for compounding self-excited and hidden attractors. Chaos, Solitons & Fractals (2020) 139:110044. doi:10.1016/j.chaos.2020.110044

CrossRef Full Text | Google Scholar

40. Lin H, Wang C, Sun Y. A universal variable extension method for designing multiscroll/wing chaotic systems. IEEE Trans Ind Electron (2023) 1–13. doi:10.1109/TIE.2023.3299020

CrossRef Full Text | Google Scholar

41. Xu C, Wang C, Jiang J, Sun J, Lin H. Memristive circuit implementation of context-dependent emotional learning network and its application in multitask. IEEE Trans Computer-Aided Des Integrated Circuits Syst (2021) 41(9):3052–65. doi:10.1109/tcad.2021.3116463

CrossRef Full Text | Google Scholar

42. Liao M, Wang C, Sun Y, Lin H, Xu C. Memristor-based affective associative memory neural network circuit with emotional gradual processes. Neural Comput Appl (2022) 34(16):13667–82. doi:10.1007/s00521-022-07170-z

CrossRef Full Text | Google Scholar

43. Jiang D, Njitacke ZT, Nkapkop JDD, Tsafack N, Wang X, Awrejcewicz J. A new cross ring neural network: Dynamic investigations and application to WBAN. IEEE Internet Things J (2022) 10(8):7143–52. doi:10.1109/jiot.2022.3228748

CrossRef Full Text | Google Scholar

44. Zhou C, Wang C, Yao W, Lin H. Observer-based synchronization of memristive neural networks under DoS attacks and actuator saturation and its application to image encryption. Appl Maths Comput (2022) 425:127080. doi:10.1016/j.amc.2022.127080

CrossRef Full Text | Google Scholar

45. Zhou C, Wang C, Sun Y, Yao W, Lin H. Cluster output synchronization for memristive neural networks. Inf Sci (2022) 589:459–77. doi:10.1016/j.ins.2021.12.084

CrossRef Full Text | Google Scholar

46. Hopfield JJ. Neurons with graded response have collective computational properties like those of two-state neurons. Proc Natl Acad Sci (1984) 81(10):3088–92. doi:10.1073/pnas.81.10.3088

PubMed Abstract | CrossRef Full Text | Google Scholar

47. Bao B, Chen C, Bao H, Zhang X, Xu Q, Chen M. Dynamical effects of neuron activation gradient on Hopfield neural network: Numerical analyses and hardware experiments. Int J Bifurcation Chaos (2019) 29(04):1930010. doi:10.1142/s0218127419300106

CrossRef Full Text | Google Scholar

48. Lin H, Wang C, Chen C, Sun Y, Zhou C, Xu C, et al. Neural bursting and synchronization emulated by neural networks and circuits. IEEE Trans Circuits Syst Regular Pap (2021) 68(8):3397–410. doi:10.1109/tcsi.2021.3081150

CrossRef Full Text | Google Scholar

49. Isaac SD, Njitacke ZT, Tsafack N, Tchapga CT, Kengne J. Novel compressive sensing image encryption using the dynamics of an adjustable gradient Hopfield neural network. Eur Phys J Spec Top (2022) 231(10):1995–2016. doi:10.1140/epjs/s11734-022-00472-2

CrossRef Full Text | Google Scholar

50. Chen C, Min F, Zhang Y, Bao H. ReLU-type Hopfield neural network with analog hardware implementation. Chaos, Solitons & Fractals (2023) 167:113068. doi:10.1016/j.chaos.2022.113068

CrossRef Full Text | Google Scholar

51. Lin H, Wang C, Sun Y, Tang Z, Xie F, Chen D, et al. Analysis of outer membrane vesicles indicates that glycerophospholipid metabolism contributes to early symbiosis between Sinorhizobium fredii HH103 and soybean. IEEE Trans Circuits Syst Express Briefs (2022) 70(1):311–22. doi:10.1094/MPMI-11-21-0288-R

CrossRef Full Text | Google Scholar

52. Yu F, Kong X, Mokbel AAM, Yao W, Cai S. Complex dynamics, hardware implementation and image encryption application of multiscroll memeristive Hopfield neural network with a novel local active memeristor. IEEE Trans Circuits Syst Express Briefs (2022) 70(1):326–30. doi:10.1109/tcsii.2022.3218468

CrossRef Full Text | Google Scholar

53. Yu F, Shen H, Yu Q, Kong X, Sharma PK, Cai S. Privacy protection of medical data based on multi-scroll memristive Hopfield neural network. IEEE Trans Netw Sci Eng (2022) 10(2):845–58. doi:10.1109/tnse.2022.3223930

CrossRef Full Text | Google Scholar

54. Lai Q, Wan Z, Kuate PDK. Generating grid multi-scroll attractors in memristive neural networks. IEEE Trans Circuits Syst Regular Pap (2022) 70(3):1324–36. doi:10.1109/tcsi.2022.3228566

CrossRef Full Text | Google Scholar

55. Strukov DB, Snider GS, Stewart DR, Williams RS. The missing memristor found. nature (2008) 453(7191):80–3. doi:10.1038/nature06932

PubMed Abstract | CrossRef Full Text | Google Scholar

56. Xia Z, Wang C, Jin J, Du S, Lin H, Yang H. Novel AM/FM/ASK/FSK/PSK/QAM signal generator based on a digitally programmable CDTA. Circuits, Systems, Signal Process. (2015) 34(5):1635–53. doi:10.1007/s00034-014-9921-3

CrossRef Full Text | Google Scholar

57. Liu X, Wang J. The simplest memristor circuit with hyperchaos. Front Phys (2022) 10:904200. doi:10.3389/fphy.2022.904200

CrossRef Full Text | Google Scholar

58. Wang M, An M, He S, Zhang X, Ho-Ching Iu H, Li Z. Two-dimensional memristive hyperchaotic maps with different coupling frames and its hardware implementation. Chaos (2023) 33(7):073129. doi:10.1063/5.0154516

PubMed Abstract | CrossRef Full Text | Google Scholar

59. He S, Liu J, Wang H, Sun K. A discrete memristive neural network and its application for character recognition. Neurocomputing (2023) 523:1–8. doi:10.1016/j.neucom.2022.12.014

CrossRef Full Text | Google Scholar

60. Zhu W, Sun K, He S, Wang H, Liu W. A class of m-dimension grid multi-cavity hyperchaotic maps and its application. Chaos, Solitons & Fractals (2023) 170:113370. doi:10.1016/j.chaos.2023.113370

CrossRef Full Text | Google Scholar

61. Sambas A, Vaidyanathan S, Zhang X, Koyuncu I, Bonny T, Tuna M, et al. A novel 3D chaotic system with line equilibrium: Multistability, integral sliding mode control, electronic circuit, FPGA implementation and its image encryption. IEEE Access (2022) 10:68057–74. doi:10.1109/access.2022.3181424

CrossRef Full Text | Google Scholar

62. Sambas A, Vaidyanathan S, Tlelo-Cuautle E, Abd-El-Atty B, El-Latif AAA, Guillen-Fernandez O, et al. A 3-D multi-stable system with a peanut-shaped equilibrium curve: Circuit design, FPGA realization, and an application to image encryption. IEEE Access (2020) 8:137116–32. doi:10.1109/access.2020.3011724

CrossRef Full Text | Google Scholar