- 1School of Automation and Software Engineering, Shanxi University, Taiyuan, China
- 2College of Intelligence and Computing, Tianjin University, Tianjin, China
- 3School of Mathematical Sciences, Shanxi University, Taiyuan, China
- 4Institute of Computing Technology, China Academy of Railway Sciences Co., Ltd., Haidian, China
- 5Postgraduate Department China Academy of Railway Sciences, Beijing, China
As a new technology and application mode, the Internet of Things has an important impact on social life and economic development. In recent years, low-cost optimization of network transmission to solve the congestion problem of multi-layer communication networks has become one of the research hotspots. In this paper, a multi-dimensional communication data transmission model based on a multi-layer network is proposed. It then uses cooperative evolutionary game theory to calculate revenue, update weights, and adapt neighbors. Finally, the attention mechanism is dynamically introduced to share the weights of the multi-layer network, and the multi-dimensional communication propagation and routing strategies in the Internet of Things are studied and analyzed. The experimental results show that the model proposed in this paper has higher game revenue and application value than traditional single-layer network game theory. In particular, the indicators of cooperation rate, stable state, and maximum cooperation rate are better than the latter. The research results of this paper have important reference value for solving the problems of cooperation dilemma, social stickiness, and synergy in multi-layer networks.
1 Introduction
The Internet of Things (IoT) is a network composed of a large number of intelligent devices that can communicate with each other through wireless communication technology, collect and process various data [1], and provide various services for human beings. The application scenarios of IoT are very varied, including smart home, smart transportation, smart medical care, smart industry and so on. However, IoT also faces many challenges, such as huge number of devices, complex and diverse data, dynamic network structure, security and privacy protection [2] and so on.
In order to effectively analyze and manage IoT systems, complex network theory provides a powerful tool. Complex networks are networks composed of a large number of nodes and edges, which can have different attributes and functions, and the structure and dynamics of the networks have complex characteristics, such as small-world effect, scale-free property, community structure and so on [3]. Complex networks can describe various entities and relationships in IoT, such as devices, data, services, users and so on.
However, traditional complex network models often only consider the single-layer network structure, while ignoring the multi-layered, multi-dimensional and multi-typed network features in IoT. For example, devices in IoT can be divided into different layers according to their functions, locations, types and so on. Moreover, there are interactions and influences between different layers. Therefore, single-layer network models cannot fully reflect the actual situation and characteristics of IoT systems. To solve this problem, a new complex network model has emerged in recent years - multi-layer networks [4] (Multilayer Networks, MLN). Multi-layer networks are network structures composed of multiple single-layer networks. Each single-layer network represents a specific dimension or type of entity or relationship. Moreover, there are also cross-layer links or couplings between different single-layer networks. Multi-layer networks can effectively describe the multi-layered, multi-dimensional and multi-typed network features in IoT, and can reveal the interactions and influences between different layers of IoT systems. Networks can be used to describe many complex relationship structures, and provide expressions for their interactions. Social relationships, traffic routes, and other types of interactions [5, 6] can be represented by networks, which can reveal attributes from structural information. Such networks are only composed of one type of entity. However, networks that ignore relationship types oversimplify the complexity of system structure attributes. Many systems in modern society can be described by complex networks, such as power grids, transportation networks, and social networks. Alleviating traffic congestion in such network systems is an important problem. Therefore, it is very important to use multi-layer networks to construct complex systems with multiple types of connections or subsystems. Previous research results have proved the difference between networks and aggregated networks under attack in robustness [7]. Ignoring the diversity of networks will lead to information loss and inaccurate interpretation. It is also particularly important to explore the similarities and differences between layers, and it is essential for many application fields to be able to measure the similarity between layers in multi-layer networks [8], such as propagation processes, behavioral and information diffusion [9], link detection in multi-layer networks [10], community detection, etc. Recently, the concepts of multiple community detection and centrality have become an active research topic, which shows that many research results can be obtained by studying such rich structures. In addition, effective traffic allocation strategies are of great importance for alleviating traffic congestion in multi-layer networks. At the micro level, the role of local node structure is considered. At the macro level, the difference in transmission speed among layers is considered. Gao et al. proposed an effective multi-layer network traffic flow allocation [11] strategy. Dong et al. extended the range of available paths, combined with a congestion avoidance mechanism, and proposed a LEO constellation network load balancing routing algorithm based on extended link state, which realized the balanced distribution of business load, reduced link congestion and packet loss rate, and improved the throughput of LEO satellite network [12]. Zhu et al. proposed a multipath routing algorithm based on an improved breadth-first search, which determined the optimal path from multiple shortest paths according to the inter-satellite network, business and node bandwidth capacity [13]. Wang et al. proposed a wireless sensor network ant colony routing algorithm based on adaptive residual energy threshold [14] (ATRE-ARA). The search angle correction pheromone heuristic function was introduced to limit the search path and reduce the node energy cost. In order to solve the problem of link congestion and network performance degradation in some areas, Dong et al. discussed the optimization problem of load balancing routing algorithm [15] and the local optimization problem caused by routing decision based on local link state. The extended local link state load balancing routing algorithm uses the path congestion state to determine the routing, avoids local optimization, and improves the network performance through routing calculation and link congestion state exchange mechanism.
In the previous research results on cooperative games, prisoner’s dilemma game [16] have been widely applied in the interaction of network individuals, and competition and cooperation relationship has been formed between individuals. Each individual can choose cooperation or defection. They can get reward R when they cooperate with each other, and get reward P when they defect each other. If one party chooses to defect and the other party chooses to cooperate, the cooperating party gets S and the defecting party gets
In networks of different levels, cooperation between nodes that pay a cost to associate with another node can constitute a basic component of nature and human society [21]. All individuals should act selfishly to maximize their own fitness, thereby ensuring a better survival rate. Therefore, the emergence and maintenance of cooperation in a competitive world is a difficult problem, and explaining the evolution of cooperation between selfish individuals is the core problem of social science and IoT environment [22]. Evolutionary game theory provides a powerful theoretical framework for solving these two problems [23]. Compared with traditional game theory, evolutionary game theory has become a powerful tool for studying various self-organizing behaviors in natural, social, and economic systems. Cooperation is common in behaviors, which is also necessary for the generation and maintenance of order in IoT systems. Understanding how individuals produce cooperation has always been a challenging problem, especially considering the social dilemma that is not conducive to cooperation in social science. Prisoner’s dilemma games [24], snowdrift games, public goods problems are used to simulate the interaction between selfish individuals, and how to solve social dilemmas through self-organization. Based on these games, people have discovered many mechanisms that promote cooperation, including reputation and punishment, network reciprocity [25], success-driven migration, random interaction patterns, memory mechanisms, etc. Zhang et al. introduced a noise element into fitness measurement, which is determined by the parameter that controls the degree of noise. The considered noise-induced mechanism significantly promoted cooperative behavior, which may help explain the emergence of cooperation within populations. Li et al. proposed a new game model with heterogeneous random interaction effects [26] and found that this simple setting has different impacts on the evolution of cooperation in different social dilemmas. The stronger the heterogeneity of interaction probabilities, the more conducive it is to the development of cooperation. Pi et al. studied a memory-based snowdrift game on a network and proposed two strategy updating rules based on profiteers and conformists under the consideration of historical strategies [27], memory strength, payoff information, and memory length. The results show that memory strength, memory length, and consistency ratio can promote the level of cooperation on the network. In these works, since the focus is on the emergence of cooperation, there is no need to include any failure mechanism. That is to say, in this process, no individual is eliminated from the game; obviously this assumption does not apply to real situations. In existing research on network evolutionary games [28], the payoff of individuals is determined by their own and opponent’s strategies according to certain rules. All players are imitating their neighbors to get more payoffs. A failure or elimination mechanism should be added in the game rules. Specifically, assign each individual a fault tolerance parameter, which is the minimum payoff required for individual survival. In some previous studies, an individual’s death usually accompanies the birth of a new individual due to competition between individual neighbors [29] or imitating strategies of those neighbors with stronger adaptability. Although the assumption that death and birth occur at the same time is suitable for solving problems such as whether natural selection favors cooperation and what kind of topology promotes cooperation. The content you want to translate is about constructing a new resource-based conditional interaction model from a micro perspective [30]. Limited resources can not only be redistributed among populations, but the resources owned by players also affect whether they can interact with each other. And it was found that there is an optimal acceptable tolerance interval, which changes with the value of the cost-benefit ratio, making the promotion of cooperation most obvious. When exploring how evolutionary games affect social and economic models of cascading failures and emergence of cooperation [31], in the case of defectors’ existence, individuals are prone to defect for higher instantaneous benefits. In a relatively short period of time, a cascading process of individual death occurs, which even spreads to the whole network, leading to complete extinction. It shows that when most individuals cooperate, the system can maintain a healthy state because large-scale cascading events are impossible. Pi et al. introduced the similarity between players into the strategy updating rules [32] to explore the evolutionary game process, including strategy updating, player type transformation, and dynamic evolution of network structure, and explored the influence of conformists and profiteers on the evolution of cooperation in multiple games. Zeng et al. assumed that individuals follow a probability distribution of normal distribution and exponential distribution and found that a higher standard deviation usually inhibits cooperation in WPDs but promotes cooperation in SDGs [33]. Rationality can survive and make profits through cooperation, which naturally solves the social dilemma of profit and cooperation. Evolutionary game pays more attention to the dynamic process of reaching a steady state and allows trial and error to reach equilibrium. Especially many evolutionary game models are used to study the persistence and emergence of cooperation, such as prisoner’s dilemma game, snowdrift game, public goods game, etc. Nowak and May’s pioneering work [34], on spatial lattice, cooperators can form tight clusters to resist invaders’ invasion, which has a significant impact on cooperative behavior within structured populations. Inspired by this, outside regular lattice, people have done a lot of research on various topological networks, especially scale-free networks [35], small world networks, ER random networks, multi-layer coupled networks, etc.
Therefore, in order to solve the communication network congestion and optimize the network transmission capacity at a low cost, this paper proposes a multi-dimensional communication data transmission model based on a multi-layer network. Then, cooperative evolutionary game theory is used to calculate payoff, update weight, and adapt neighbor. Finally, the attention mechanism is dynamically introduced to share the weight value of the multi-layer network, and the multi-dimensional communication propagation and routing selection strategy in IoT are studied and analyzed.
The remaining work is organized as follows: Chapter 2 introduces the establishment of a multi-dimensional communication data transmission model based on multi-layer networks and specifically describes how to use cooperative evolutionary game theory to calculate revenue, update weights, and adapt neighbors. Chapter 3 uses the Monte Carlo method to study and analyze multi-dimensional communication propagation and routing selection strategies in the Internet of Things. Chapter 4 concludes that the model in this paper can significantly improve cooperation efficiency.
2 The multidimensional data transmission model based on multilayer networks
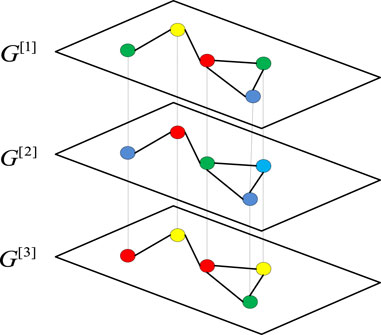
2.1 Multilayer network topology
Consider a multilayer network consisting of
2.2 Single-layer network routing selection strategy
In the signal propagation process of various communication devices in the Internet of Things, the routing selection strategy is crucial. Using game theory to model the routing selection strategy is one of the main methods. The main idea is that routing nodes will calculate the cumulative payoff with their neighbor nodes through game evolution and choose efficient routing as the transmission path based on the payoff expectation. For convenience, set the node with high routing selection expectation as cooperators and set the node with low routing selection expectation as defectors. In this paper, we will use a small world network as the underlying topology and dynamically realize network evolution based on the Monte Carlo principle [36]. On this basis, each routing node will update its selection strategy synchronously.
2.2.1 Routing node cooperation game payoff calculation
For each given complex network, each node will play the role of router and host, and they all have the ability to generate, accept and forward packets. At the beginning of network evolution game, each node
The payoff expectations of them in prisoner’s dilemma game are as follows:
where
The iterative algorithm of prisoner’s dilemma evolutionary game is realized by Monte Carlo simulation experiment method. First, randomly select a node
where
2.2.2 Routing node cooperation evolution weight update rule
If the average shared payoff of node
Of course, this weight will also be shared to other nodes in other network layers in the subsequent network evolution process.
2.2.3 Routing node adaptation transmission neighbor
After the evolutionary game is over, the focal player accumulates all the payoffs and updates the strategy synchronously, choosing an adaptive neighbor node according to the update rule determined by the Fermi function. In other words, the focal player may choose or not choose the opponent according to probability. Then, the probability of the focal player adopting neighbor’s strategy is defined as:
Where
Finally, each random focal player selects multiple neighbors for an evolutionary game continuously before selecting an adaptive neighbor. If the selection is successful, it will replace their cooperation intention
2.3 Multi-dimensional information sharing based on attention mechanism
The multi-layer construction of the Internet of Things covers the perception layer, the network layer, the cloud platform layer, and the application layer. These layers are connected and interact with each other through various protocols and interfaces, jointly realizing the functions and applications of the Internet of Things. Therefore, the information sharing of the multi-layer Internet of Things refers to the exchange and utilization of data between different levels of the Internet of Things, in order to improve the efficiency and value of the Internet of Things. For this purpose, the evolutionary real-time weights of different layers need to be shared with other network layers. First, the obtained weights
Next, simulate a new core layer to replace the new weight
Then, grab the cooperation ratio parameter
(1) Calculate the similarity: Use the cooperation level to calculate the value similarity of two nodes, which is regarded as the attention score of the node:
(2) Translate the attention score into numerical values, and divide the node cooperation value contribution:
(3) Calculate the attention aggregation score according to
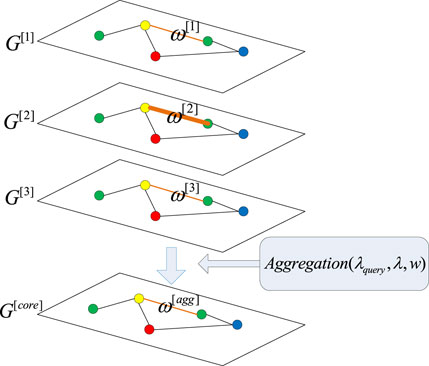
The whole process of the attention mechanism oriented multi-dimensional information aggregation algorithm is shown in Figure 2, where
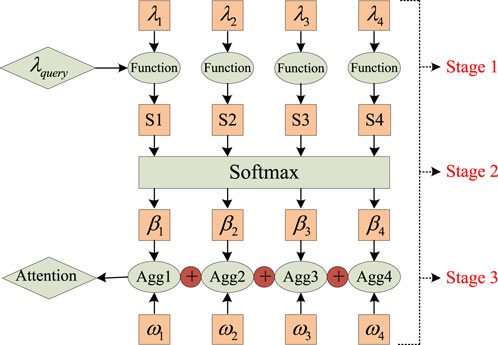
FIGURE 2. The flow of the attention mechanism oriented multi-dimensional information aggregation algorithm.
Equations 7–9 fit the game details between “roles” from a micro perspective, while the cooperation effect of multi-layers from a macro perspective requires the introduction of the concept of auxiliary layer and core layer, where the core layer is the simulation layer with attention weights. The evolution model of the auxiliary layer and the core aggregation layer is shown in Figure 3, where
3 Simulation results and analysis
3.1 Sensitivity analysis of experimental parameters
Figure 4A shows the evolution curves of the cooperation level with time steps under different betrayal benefits. It can be observed that when the value of
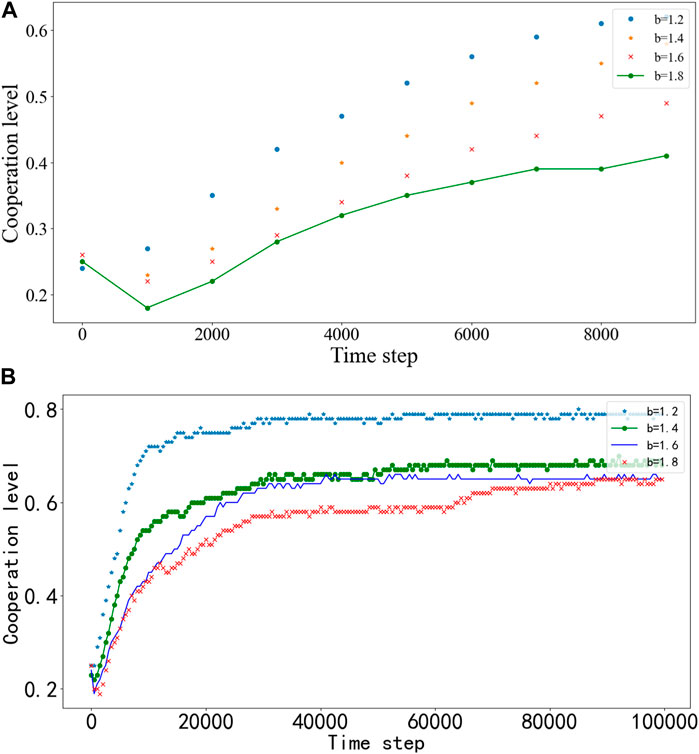
FIGURE 4. (A) The change trend of different values of b on the cooperation rate within 10,000 steps of MCS. (B) The effect of different b values on the stable state of the network.
Figure 5 shows the influence of network node number and weight update parameter on network cooperation level. In Figure 5A, the influence of different network node numbers on cooperation degree when
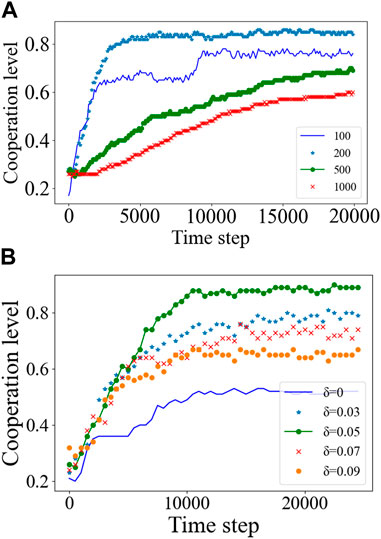
FIGURE 5. (A) The influence of different node numbers on the degree of cooperation. (B) The influence of different update parameter
3.2 The distribution of cooperative tendencies of network nodes in the experiment
Figure 6 shows the cooperation level of network nodes in small world network, BA scale-free network, and random network. It can be found that: in ER random network, the game method in this paper has the most significant effect, greatly promoting the efficiency of cooperation. In addition, there are more outliers when MCS = 2,000, which is caused by the individuals who are not in the cluster being invaded by betrayers, and there are still some nodes that do not adopt a cooperative attitude after most nodes communicate smoothly.
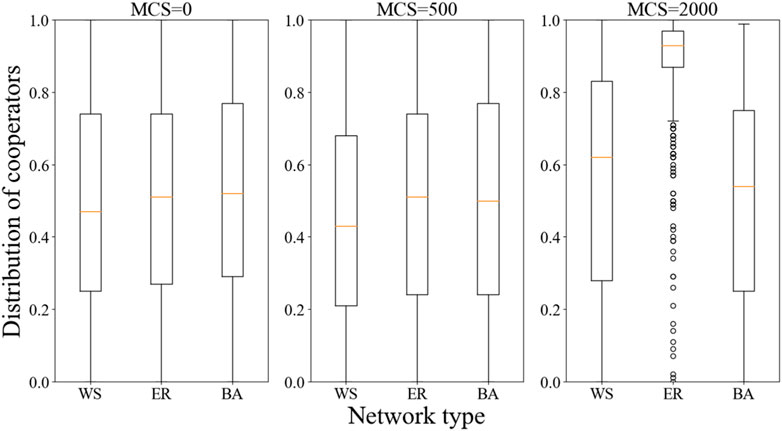
FIGURE 6. The distribution of network node cooperation tendency in small world network, BA scale-free network, and random network.
This paper realizes the information sharing of multi-layer network based on Monte Carlo principle, which is essentially the sharing of local random information. In other words, the change of each node is random, and the information sharing is to assign the node weight that has not been updated in the unit time step to the node weight that has been optimized by the adjacent layer through the attention mechanism, and the node here is the node of the same entity in different layers. Through the comparative experiments of traditional game, game with link weight, and multi-layer network sharing weight game (Table 1), it is found that the model provided in this paper has better performance than the other two in cooperation rate, maximum cooperation rate, and stable state.

TABLE 1. Comparison of game efficiency of traditional game, game with link weight, and game with multi-layer network sharing weight (The model of this paper).
Figure 7 shows the cooperative evolutionary game process of the multi-layer network based on the small-world network over time. Figures 7A–D are the partial layers (auxiliary layers) in the multi-layer network, with MCS being 50, 500, 1,000, 5,000, and 15,000 respectively. Figures 7E–H are the evolution process of the core layer of the shared cooperation network with attention score at the same step length. It can be clearly seen that the defection nodes in the core layer are higher than those in the auxiliary layer at the initial state, and the trend of cooperation level increase over time is significantly higher than that of all auxiliary layers. This indicates that the attention mechanism has a good effect of weight sharing and promotes the cooperation of network nodes. In summary, the attention mechanism can improve the overall cooperation level of the network, and the cooperation tendency of local network nodes may be lower than that of a small part of the layer nodes. This reflects that once a certain level in the communication network fails, it may also affect the information transmission of other data layers in this area.
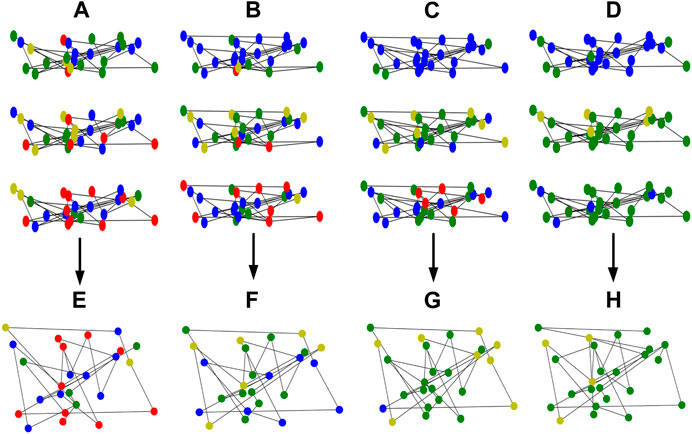
FIGURE 7. Cooperative evolutionary game process of the multi-layer network based on the small-world network over time.
Finally, this paper explores the distribution of the cooperation rate of shared network nodes guided by the attention mechanism (Figure 8). Compared with the literature [29, 37], the cooperation efficiency guided by the attention mechanism has obvious advantages. It is easy to see that when MCS = 0, the cooperation level and cooperation median of the three auxiliary layers and the core layer are quite similar. However, when MCS reaches 5,000, due to the randomness of network update, the cooperation level between the three auxiliary layers is different, and the cooperation rate of the core layer also begins to have a significant upward trend. In addition, although the overall cooperation rate of the core layer is higher than that of the auxiliary layer, its cooperation median is significantly higher than that of the auxiliary layer, indicating that the attention mechanism can improve an individual’s cooperation tendency faster from a micro level. It is worth noting that Aux2 has a higher overall cooperation score than other layers, but its median is much lower than other layers. This is because a rapid increase in node cooperation will also bring some individual defection. When MCS = 15,000, the cooperation tendency of all network layers has been concentrated between 0.6 and 0.85, and the cooperation nodes of the core layer have exceeded 0.9. This phenomenon indicates that individuals in the network gradually form clusters to resist invaders. And when MCS = 5,000, the core layer also caused some node defection due to rapid cooperation, but these defection nodes increased their cooperation tendency at a lower rate in MCS = 15,000. In summary, this shows that the model proposed in this paper has great reference value for the network cooperation level.
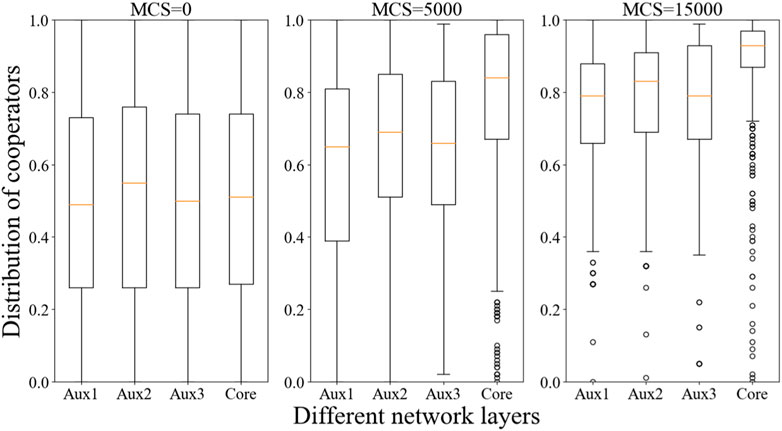
FIGURE 8. Box plot of node cooperation tendency distribution of multi-layer cooperation network based on small-world network.
4 Conclusion and prospect
In this paper, a new communication data transmission mode is proposed based on the multi-layer network framework. Each node calculates the payoff based on the prisoner’s dilemma game with its neighbors and introduces a link weight self-adjustment algorithm driven by benefits. Using random skew selection, each node independently selects a game route and an adaptive route, and introduces the attention mechanism to share the multi-layer weights. The paper explores the communication transmission and routing selection strategy in the multi-dimensional Internet of Things. The experimental results show that the proposed model can ensure that high-yield neighbors are more frequently selected as cooperative partners by using appropriate random skew selection. At the same time, introducing the attention mechanism can quickly find high-yield neighbor partners and provide support for weight allocation. Compared with the traditional prisoner’s dilemma game and the single-layer network with link weight, the multi-layer shared network with attention mechanism has significant advantages in terms of cooperative game rate, maximum cooperation rate, and cooperative steady state, which are 0.00000292, 0.00000301, and 16,011 respectively.
In summary, this paper extends the single-layer network cooperation mode and enriches the evolutionary game dynamics theory. In addition, the model has strong scalability, which can be shared based on inter-layer similarity factors. It can also set the multi-layer network as the same network layer at different times, giving the model a time memory mechanism. Therefore, in future work, we can focus on these aspects of research, which will provide some reference for the information transmission efficiency of the Internet of Things.
Data availability statement
The original contributions presented in the study are included in the article/Supplementary Materials, further inquiries can be directed to the corresponding author.
Author contributions
JW: Conceptualization, Methodology, Writing–original draft. KS: Data curation, Methodology, Writing–original draft. GY: Investigation, Writing–review and editing. WB: Data curation, Methodology, Writing–original draft. XW: Formal Analysis, Writing–review and editing.
Funding
This work was supported by the National Natural Science Foundation of China-China State Railway Group Co., Ltd.; Railway Basic Research Joint Fund (Grant No.U2268217); Research Project of China Academy of Railway Sciences Group Co., Ltd. (Grant No. 2021YJ136 and No. 2023YJ125); China Postdoctoral Science Foundation (No.2021M692400), Fundamental Research Program of Shanxi Province (No. 202203021221017), the special fund for Science and Technology; Innovation Teams of Shanxi Province (No. 202204051002015), Key Laboratory of Complex Systems and Data Science of Ministry of Education. The funder was not involved in the study design, collection, analysis, interpretation of data, the writing of this article, or the decision to submit it for publication.
Conflict of interest
Authors GY and WB were employed by China Academy of Railway Sciences Co., Ltd.
The remaining authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Publisher’s note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
References
1. Laghari AA, Wu K, Laghari RA, Ali M, Khan AA. Retracted article: A review and state of art of internet of things (IoT). Arch Computat Methods Eng (2022) 29:1395–413. doi:10.1007/s11831-021-09622-6
2. Chowdhury MZ, Shahjalal M, Ahmed S, Jang YM. 6G wireless communication systems: Applications, requirements, technologies, challenges, and research directions. IEEE Open J Commun Soc (2020) 1:957–75. doi:10.1109/ojcoms.2020.3010270
3. Yang K, Li J, Liu M, Lei T, Xu X, Wu H, et al. Complex systems and network science: A survey. J Syst Eng Elect (2023) 34:543–73. doi:10.23919/jsee.2023.000080
4. Li C, Zhang LJ. A blockchain based new secure multi-layer network model for internet of things. IEEE Int Congress Internet Things (2017) 34:33–41. doi:10.1109/IEEE.ICIOT.2017.34
5. Appel G, Grewal L, Hadi R, Stephen AT. The future of social media in marketing. J Acad Marketing Sci (2020) 48:79–95. doi:10.1007/s11747-019-00695-1
6. Nauman A, Qadri YA, Amjad M, Zikria YB, Afzal MK, Kim SW. Multimedia internet of things: A comprehensive survey. IEEE Access (2020) 8:8202–50. doi:10.1109/access.2020.2964280
7. Zhang W, Xia Y, Ouyang B, Jiang L. Effect of network size on robustness of interconnected networks under targeted attack. Physica A (2015) 435:80–8. doi:10.1016/j.physa.2015.05.011
8. Ghawi R, Pfeffer J. A community matching based approach to measuring layer similarity in multilayer networks. Social Networks (2022) 68:1–14. doi:10.1016/j.socnet.2021.04.004
9. Bródka P, Musial K, Jankowski J. Interacting spreading processes in multilayer networks: A systematic review. IEEE Access (2020) 8:10316–41. doi:10.1109/access.2020.2965547
10. Jalili M, Orouskhani Y, Asgari M, Alipourfard N, Perc M. Link prediction in multiplex online social networks. R Soc Open Sci (2017) 4(2):160863. doi:10.1098/rsos.160863
11. Gao L, Shu P, Tang M, Wang W, Gao H. Effective traffic-flow assignment strategy on multilayer networks. Phys Rev E (2019) 100:012310. doi:10.1103/physreve.100.012310
12. Dong C, Xu X, Liu A, Liang X. Load balancing routing algorithm based on extended link states in LEO constellation network. China Commun (2022) 19:247–60. doi:10.23919/jcc.2022.02.020
13. Zhu H, Yuan Z, Zhu X. An adaptive routing algorithm for inter-satellite networks based on the combination of multipath transmission and Q-Learning. Process. (2023) 11:167. doi:10.3390/pr11010167
14. Wang G, Sun M, Sun H, Zhang Y, Teng Z. An adaptive threshold of remaining energy based ant colony routing algorithm. J Northwest Polytechnical Univ (2022) 40(2):442–9. doi:10.1051/jnwpu/20224020442
15. Xu X, Dong C, Liu A. Optimization of load balancing routing algorithm based on extended localized link states in low earth orbit satellite networks. Int J Satellite Commun Networking (2021) 39(5):591–604. doi:10.1002/sat.1403
16. Yang W, Binghong W. Evolution of cooperation on spatial network with limited resource. PLoS ONE (2015) 10(8):e0136295. doi:10.1371/journal.pone.0136295
17. Zhu P, Guo H, Zhang H, Han Y, Wang Z, Chu C. The role of punishment in the spatial public goods game. Nonlinear Dyn (2020) 102:2959–68. doi:10.1007/s11071-020-05965-0
18. Dong Y, Guo S, Liu J, Yang Y. Energy-efficient fair cooperation fog computing in mobile edge networks for smart city. IEEE Internet Things J (2019) 6:7543–54. doi:10.1109/jiot.2019.2901532
19. Xia C, Ding S, Wang C, Wang J, Chen Z. Risk analysis and enhancement of cooperation yielded by the individual reputation in the spatial public goods game. IEEE Syst J (2017) 11:1516–25. doi:10.1109/jsyst.2016.2539364
20. Lee W, Kim M, Cho DH. Deep cooperative sensing: Cooperative spectrum sensing based on convolutional neural networks. IEEE Trans Vehicular Tech (2019) 68:3005–9. doi:10.1109/tvt.2019.2891291
21. Ohtsuki H, Hauert C, Lieberman E, Nowak MA. A simple rule for the evolution of cooperation on graphs and social networks. Nature (2006) 441(7092):502–5. doi:10.1038/nature04605
22. Fang L, Shi G, Wang L, Li Y, Xu S, Guo Y. Incentive mechanism for cooperative authentication: An evolutionary game approach. Inf Sci (2020) 527:369–81. doi:10.1016/j.ins.2019.07.030
23. Taylor C, Fudenberg D, Sasaki A, Nowak M. Evolutionary game dynamics in finite populations. Bull Math Biol (2004) 66(6):1621–44. doi:10.1016/j.bulm.2004.03.004
24. Bennich T, Weitz N, Carlsen H. Deciphering the scientific literature on sdg interactions: A review and reading guide. Sci Total Environ (2020) 728:138405. doi:10.1016/j.scitotenv.2020.138405
25. Zhang GQ, Sun QB, Wang L. Noise-induced enhancement of network reciprocity in social dilemmas. Solitons & Fractals (2013) 51(2):31–5. doi:10.1016/j.chaos.2013.03.003
26. Li X, Hao G, Zhang Z, Xia C. Evolution of cooperation in heterogeneously stochastic interactions. Solitons & Fractals (2021) 150:111186. doi:10.1016/j.chaos.2021.111186
27. Pi B, Li Y, Feng M. An evolutionary game with conformists and profiteers regarding the memory mechanism. Physica A: Stat Mech its Appl (2022) 597:127297. doi:10.1016/j.physa.2022.127297
28. Shirsendu P, Simone R, Francesca P. Reputation and punishment sustain cooperation in the optional public goods game. Phil Trans R Soc B (2021) 376:20200293. doi:10.1098/rstb.2020.0293
29. Li X, Sun S, Xia C. Reputation-based adaptive adjustment of link weight among individuals promotes the cooperation in spatial social dilemmas. Appl Math Comput (2019) 361:810–20. doi:10.1016/j.amc.2019.06.038
30. Li X, Han W, Yang W, Wang J, Xia C, Li H, et al. Impact of resource-based conditional interaction on cooperation in spatial social dilemmas. Physica A (2022) 594:127055. doi:10.1016/j.physa.2022.127055
31. Wang WX, Lai YC, Armbruster D. Cascading failures and the emergence of cooperation in evolutionary-game based models of social and economical networks. Chaos (2011) 21(3):033112. doi:10.1063/1.3621719
32. Pi B, Zeng Z, Feng M, Kurths J. Evolutionary multigame with conformists and profiteers based on dynamic complex networks. Chaos: Interdiscip J Nonlinear Sci (2022) 32(2):023117. doi:10.1063/5.0081954
33. Zeng Z, Li Q, Feng M. Spatial evolution of cooperation with variable payoffs. Chaos: Interdiscip J Nonlinear Sci (2022) 32(7):073118. doi:10.1063/5.0099444
34. Nowak MA, May RM. Evolutionary games and spatial chaos. Nature (1992) 359(6398):826–9. doi:10.1038/359826a0
35. Holme P. Rare and everywhere: Perspectives on scale-free networks. Nat Commun (2019) 10:1016. doi:10.1038/s41467-019-09038-8
36. Arellano M, Bond SR, Arellano B. Some tests of specification for panel data: Monte Carlo evidence and an application to employment equations. Rev Econ Stud (1991) 58(2):277–97. doi:10.2307/2297968
Keywords: internet of things, multi-layer network, enhanced prisoner’s dilemma, Monte Carlo simulation, attention mechanism
Citation: Wang J, Su K, Yang G, Bai W and Wang X (2023) Research on multi-layer network routing selection strategy based on cooperative evolutionary game in IoT environment. Front. Phys. 11:1274578. doi: 10.3389/fphy.2023.1274578
Received: 08 August 2023; Accepted: 11 September 2023;
Published: 28 September 2023.
Edited by:
Minyu Feng, Southwest University, ChinaReviewed by:
Juan Wu, Xi’ an University of Finance and Economics, ChinaXiaopeng Li, Tianjin University of Technology, China
Copyright © 2023 Wang, Su, Yang, Bai and Wang. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Guoyuan Yang, eWFuZ19neTIwMjNAMTI2LmNvbQ==
 Jianrong Wang
Jianrong Wang Kaixuan Su3
Kaixuan Su3 Guoyuan Yang
Guoyuan Yang Wei Bai
Wei Bai