Quantum image encryption algorithm based on four-dimensional chaos

1 Introduction

Quantum information and quantum computation, an interdisciplinary field of quantum physics and information science, have advanced quickly and made incredible strides in quantum communication, quantum cryptography, quantum computer, and other areas [1–3]. Quantum image processing is a branch of quantum information that deals with creating quantum protocols and algorithms to store, alter, and retrieve visual data [4–6]. Although the field is still in its infancy, it has already produced significant contributions to image processing, including quantum image watermarking [7, 8], quantum image encryption [9–12], and quantum image steganography and disambiguation [12, 13]. In order to hide image data and perform pre- or post-processing for secret storage and transfer, image encryption is frequently utilized. Its primary goal is to disorganize an ordered real-world image, which can greatly increase image security.

On one hand, cryptography is never a one-time thing. After quantum computers showed their subversive superiority, they had a huge impact on modern cryptosystems. One way to counter the threat of quantum computers is to use one-time password (OTP) [14] encryption that Shannon demonstrated, which is theoretically unconditionally secure [15], i.e., it cannot be cracked by any means. The encryption and decryption process of an OTP is very simple. First, before encryption, the two sides of encryption and decryption share a string of keys. During the encryption process, the sender needs to encrypt the message bitwise with the key or obtain ciphertext. To ensure the unconditional security of the OTP, the sender and receiver need to ensure that the key length is consistent with the message length, and each bit of the key can only be used once, so the encryption problem is transformed into the problem of how to provide the shared secret for both the sender and the receiver. Face-to-face key sharing is an effective method, but it is difficult to meet the user needs in many situations, such as remote encryption tasks and temporary encryption tasks. Quantum key distribution (QKD) provides a remote, real-time, and theoretically unconditional security shared key scheme. The first QKD protocol was proposed by Bennett and Brassard in 1984 and is, therefore, known as the BB84 protocol [16]. Subsequently, its theoretical safety was proved by many scholars [17–21]. In [22], an efficient quantum digital signature protocol is proposed, which uses asymmetric quantum keys obtained by secret sharing, a general hash, and a PAD. In addition, the author constructs the first quantum security network which integrates information theory secure communication, digital signature, secret sharing, and conference key negotiation and proves the advantage of this signature efficiency through experiments.

The Arnold transformation’s effective scrambling effect is widely used in the realm of image encryption [23]. However, it has a fatal flaw where it can be easily cracked after numerous iterations. Chaos provides good encryption technology of confusion and diffusion, establishing a new encryption method, due to its simplicity and efficiency, extreme sensitivity to initial conditions, autocorrelative quick attenuation, non-periodicity, ergodicity, and randomly like characteristics. Theoretically, chaotic high-dimensional systems are more prone to experience hyper-chaos. Rossler proposed the hyperchaotic Rossler system and introduced the idea of hyper-chaos [24]. A hyperchaotic system [25] has a higher application value in secure communication than a general chaotic system since it has many Lyapunov exponents, and the prediction of the dynamic behavior of the system is more challenging.

With the emergence of quantum image processing, various image encryption technologies have emerged one after another. [26] introduced dual random phase coding in quantum cryptography research, laying the foundation for future progress. In the same year, [27] significantly improved the key size and algorithm performance. Although some encryption methods, such as Arnold, Fibonacci, and Hilbert scrambling [28], are relatively less complex, [29–31] applied them to quantum circuits in 2014. Recently, Zhou N R et al. have become proficient in encrypting complex quantum images by means of a number of columns of effective encryption [32–34]. Due to the random qubit rotation of quantum Fourier transform, the calculation becomes more challenging. However, these methods have certain limitations and often face computational challenges and difficulty in maintaining sufficient key space to resist advanced attacks. In contrast, our method uses a chaotic system for image encryption [24, 25, 35]. The integration of chaos encryption technology provides multiple benefits, including enhanced security, non-deterministic image generation, and the ability to reduce pixel correlation and, therefore, be more resilient against a variety of attacks. This represents an important shift toward more robust and secure quantum image encryption methods.

This research proposes a quantum image encryption method based on four-dimensional chaos to encrypt the image. The picture encryption is then for the first time realized using the key set from four-dimensional chaotic systems to act on the entwine color information and coordinate information. After combining the quantum Arnold transform with another encryption key created by the four-dimensional chaotic system, the encryption operator is then obtained. After applying the encryption operator on the encrypted image created in the first phase, the final encryption is realized. Additionally, this scheme’s image processing operations, such as Arnold scrambling and gray value encryption, can be realized by quantum circuits, suggesting that this plan has a promising chance of being put into practice on quantum devices. The following is a summary of this paper’s main contributions:

(1) In the scrambling stage, the image encryption scheme combined with the chaotic system is used to eliminate the periodic interference of the Arnold transform encryption.

(2) The encryption structure of position scrambling and pixel gray value scrambling fusion is designed to improve the complexity and randomness of the encryption system.

(3) It is theoretically verified that using quantum computing, quantum image encryption can significantly reduce the computing space.

2 Theoretical basis

2.1 Four-dimensional hyperchaotic Lorenz system

In non-linear dynamical systems, which are both acyclic and non-convergent and have a highly sensitive dependency on initial values, chaotic phenomena are deterministic, stochastic-like processes. The three-dimensional Lorenz system serves as the foundation for the building of the four-dimensional Lorenz system, which uses some of its characteristics or variables to introduce the fourth dimension while maintaining the system’s ability to satisfy chaotic dynamics [36]. Its definition is shown in Eq. 1:

$\left\{\begin{array}{c}\dot{x}=\alpha \left(-x+y\right)+w\hfill \\ \dot{y}=\gamma x-y-xz\hfill \\ \dot{z}=xy-\beta z\hfill \\ \dot{w}=-yz+rw\hfill \end{array}\right..(1)$

The prerequisites of possessing at least one four-dimensional phase space and at least two positive Lyapunov exponents must be met by hyperchaotic systems [35–37]. According to Wang’s method [38], the system will exhibit hyperchaotic behavior when the initial parameters are set as follows: α = 10, β = 8/3, and γ = 28; −1.52 ≤ r ≤ −0.06 [the control parameters in Eq. 1]. Additionally, the initial values of x, y, z, and w can be freely chosen. The Lorenz hyperchaotic system can be discretized using the Python software application by setting and using the Runge–Kutta method, as shown in Figure 1. r = −1 is taken as the control parameter at this point. The system’s Lyapunov index comprises λ₁ = 0.3381, λ₂ = 0.1586, λ₃ = 0, and λ₄ = −15.1752, which demonstrates that hyper-chaos has taken place.

FIGURE 1

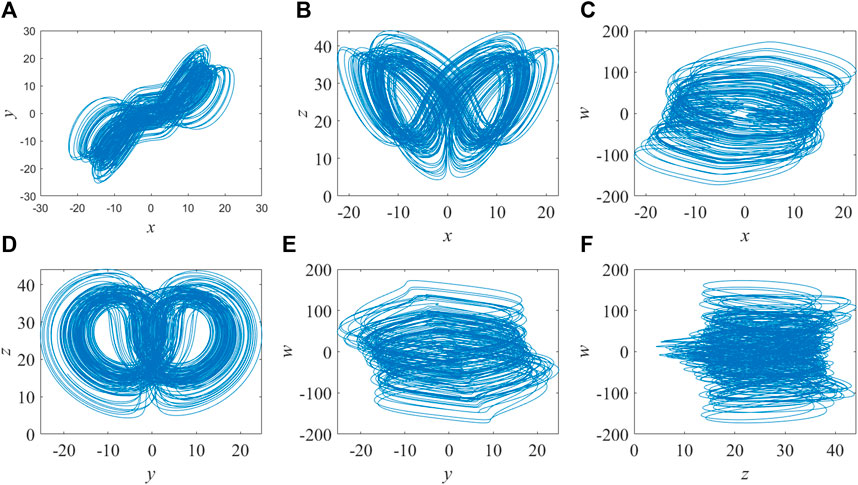
FIGURE 1. Projections of the Lorenz attractor when the parameter is set as r = −1. (A) x-y plane. (B) x-z plane. (C) x-w plane. (D) y-z plane. (E) y-w plane. (F) z-w plane.

2.2 Generalized quantum image representation

Quantum parallelism and quantum entanglement, two fundamental concepts in quantum mechanics, can be used in quantum image processing. These concepts have benefits for image storage, storage space optimization, processing task acceleration, computing resource optimization, and information security transmission. In this paper, we adopted Jiang Nan’s generalized quantum image representation technique, also known as the generalized quantum image representation (GQIR) [38, 39], which builds on the NEQR quantum image representation [40] by storing the image through two sets of entangled quantum sequences to increase the size of the original image from 2ⁿ × 2ⁿ to any size H × W. From an image of size H × W and grayscale range [0, 2^(q−1)], the quantum state representation of this image can be formulated as in Eq. 2:

$|\mathrm{\Psi }\rangle =\frac{1}{{\sqrt{2}}^{\text{h}+w}}{\displaystyle \sum _{Y=0}^{h-1}}{\displaystyle \sum _{X=0}^{w-1}}|G_{YX}^i\rangle \otimes |YX\rangle ,(2)$

where |YX⟩ represents coordinate information and $\left|G_{YX}^i\right.⟩$ represents gray information. |YX⟩ and $\left|G_{YX}^i\right.⟩$ are shown in Eq. 3:

$\begin{array}{c}|YX\rangle =|Y\rangle |X\rangle =|y_0{y}_1\dots y_{h-1}\rangle |x_0{x}_1\dots x_{w-1}\rangle ,y_i,x_i\in \left\{\mathrm{0,1}\right\}\hfill \\ |G_{YX}^i\rangle =|G_{YX}^0{G}_{YX}^1\dots G_{YX}^{q-1}\rangle ,G_{YX}^i\in \left\{\mathrm{0,1}\right\},\hfill \end{array}(3)$

where i = 0, 1, …, q − 1. The values of h and ω can be formulated as in Eq. 4:

$h=\left\{\begin{array}{c}\left[{\log }_2\right.H⌉,H>1\hfill \\ 1,H=1\hfill \end{array}\right.,w=\left\{\begin{array}{c}⌈{\log }_{2}W⌉,W>1\hfill \\ 1,W=1\hfill \end{array}\right.(4)$

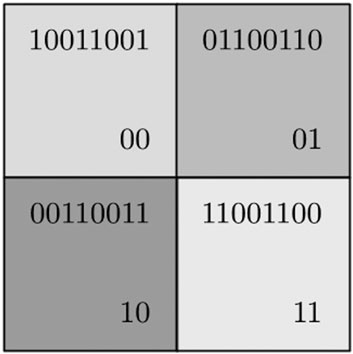
Compared with classical methods, quantum representation can significantly reduce the image storage space. For the size of 2ⁿ × 2ⁿ clear image, the classic image representation method needs 8 × 2ⁿ × 2ⁿ + n² number of bits, compared with the number of quantum bits required for quantum image representation, 2n + q bits (q is the image color depth). Figure 2 shows a simple image presented by GQIR, in which the gray value is 2 × 2. In addition, Figure 3 represents the quantum circuit of the image.

$\begin{array}{cc}\hfill |I\rangle =& \frac{1}{2}\left[|10011001\rangle \otimes |00\rangle +|01100110\rangle \otimes |01\rangle \right.\hfill \\ \hfill & \left.+|00110011\rangle \otimes |10\rangle +|11001100\rangle \otimes |11\rangle \right]\hfill \end{array}.$

FIGURE 2

FIGURE 2. GQIR of a simple graph.

FIGURE 3

FIGURE 3. Preparation circuit of the GQIR quantum image.

Combined with quantum mechanical measurement theory [41], the corresponding information on image in the quantum state |Ψ⟩ can be obtained using the measurement operator $\widehat{L}$ to measure the quantum state, so the measurement operator position information is given by $\widehat{L}$. $\widehat{L}$ is shown in Eq. 5:

$\widehat{L}={\displaystyle \sum _{Y=0}^{H-1}}{\displaystyle \sum _{X=0}^{W-1}}|YX\rangle \langle YX|I^{\otimes q},(5)$

where I^⊗q is the tensor product of the q identity matrix used for gray information on each pixel.

The gray information measurement operator $\widehat{C}$ is shown in Eq. 6:

$\widehat{C}={\displaystyle \sum _{c^{\prime }=0}^{2^q-1}}C|c^{\prime }\rangle \langle c^{\prime }|,(6)$

where c′ represents eigenvalues of C. After the operator is applied to the image, image information can be accurately observed.

2.3 Arnold transformation

The pixel coordinates are changed by the transformation matrix, and such a transformation belongs to affine transformation. The affine transformation can be expressed by Eq. 7:

$\left[\begin{array}{c}\hfill x^{\prime }\hfill \\ \hfill y^{\prime }\hfill \end{array}\right]=\left[\begin{array}{cc}\hfill a\hfill & \hfill b\hfill \\ \hfill c\hfill & \hfill d\hfill \end{array}\right]\left[\begin{array}{c}\hfill x\hfill \\ \hfill y\hfill \end{array}\right]\left(\mathrm{mod}N\right).(7)$

This paper will consider the Arnold transformation as an example position transformation of image pixels [42]. For a two-dimensional Arnold transformation, suppose there is a square grid image, which has a size of N × N, represented by I (x, y), (x,y)^T is used to represent the position coordinates of pixels. The values of x and y are integer values (x, y = 0, 1, …, N), mapping to new point addition and multiplication (mod N) via the operations in Eq. 8:

$\left[\begin{array}{c}\hfill x^{\prime }\hfill \\ \hfill y^{\prime }\hfill \end{array}\right]=\widehat{A}\left[\begin{array}{c}\hfill x\hfill \\ \hfill y\hfill \end{array}\right]\left(\mathrm{mod}N\right),\widehat{A}=\left[\begin{array}{cc}\hfill 1\hfill & \hfill 1\hfill \\ \hfill 1\hfill & \hfill 2\hfill \end{array}\right],(8)$

where ${\left(x^{\prime },y^{\prime }\right)}^{\text{T}}$ is the coordinate of the image transformed by the Arnold transform.

In addition, Arnold transformation is a reversible transformation, which means that pixel position coordinates after transformation can be restored without error, and its inverse transformation meets the requirement of $\widehat{A}{\widehat{A}}^{-1}={\widehat{A}}^{-1}\widehat{A}=I$. Inverse transformation can be expressed by Eq. 9:

$\left[\begin{array}{c}\hfill \mathrm{x}\hfill \\ \hfill \mathrm{y}\hfill \end{array}\right]={\widehat{A}}^{-1}\left[\begin{array}{c}\hfill {\mathrm{x}}^{\prime }\hfill \\ \hfill {\mathrm{y}}^{\prime }\hfill \end{array}\right]\left(\mathrm{mod}N\right),{\widehat{A}}^{-1}=\left[\begin{array}{cc}\hfill 2\hfill & \hfill -1\hfill \\ \hfill -1\hfill & \hfill 1\hfill \end{array}\right].(9)$

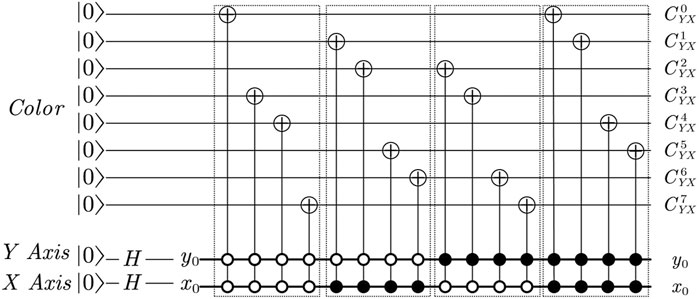
2.4 Quantum adder

A quantum adder [43] is needed in the process of Arnold transformation of image position coordinates, as shown in Figure 4. A function that the quantum adder can achieve is |a, b⟩ → |a, a + b⟩.

FIGURE 4

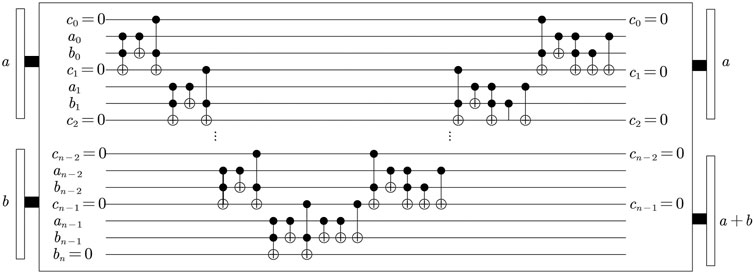
FIGURE 4. Plain adder network. All transits are calculated in the first step up to the last transit, which determines the result’s most significant digit. Then, all of these operations (aside from the final one) are undone in the reverse order, and the digit total is computed appropriately.

It is worth noting that after passing the adder, the image is no longer rectangular and will exceed the scope. Therefore, the quantum modular N adder should also be designed based on the adder network, in which the specific implementation method is given [43].

3 Improved algorithm of quantum image encryption

This section will provide a detailed introduction to the four-dimensional Lorenz chaos-based quantum image encryption technique. Figure 5 shows the encryption procedure.

FIGURE 5

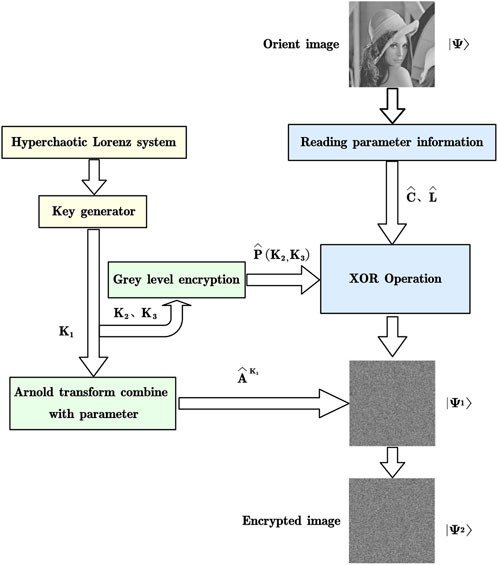
FIGURE 5. Encryption process of the quantum image. Key 1 is controlling the number of Arnold transformation, and keys 2 and 3 are controlling grayscale encryption.

3.1 Quantum image encryption

Step 1: In this initial step, the configuration process commences by selecting the control parameters for the system. We choose the values of the control parameters in the equations as follows: α = 10, β = 8/3, γ = 28, and r = −1. Furthermore, we set the initial value for the start of the motion to x (0), y (0), z (0), and w (0).

Step 2: We choose the w variable in Eq. 1 as the non-linear controller and randomly initialize the time of motion w (t₀). We set the discrete time t_n to correspond to each image point of the original image. We, therefore, denote the three generated chaotic signals as follows: K₁ = x (t_n), K₂ = y (t_n), and K₃ = z (t_n).

Step 3: The random grayscale encryption operator generated by the keys K₂ and K₃ is used to carry out modular operation P_n(Y, X). XOR operation is carried out on P_n(Y, X) and the corresponding points on the original image to hide the original information about the image. Finally, the quantum state containing grayscale information is normalized to obtain an encrypted image of $\left|{\mathrm{\Psi }}^{\prime }\right.⟩$. The specific calculation process can be formulated as in Eq. 10:

$\begin{array}{cc}\hfill P_n\left(Y,X\right)& =\text{\hspace{0.17em}floor\hspace{0.17em}}\left[\frac{K_{n_2}+1}{K_{n_2}+K_{n_3}+2}\times 10^{14}\right]\mathrm{mod}256\hfill \\ \hfill |{\mathrm{\Psi }}^{\prime }\rangle & =\frac{1}{{\sqrt{2}}^{h+w}}{\displaystyle \sum _{Y=0}^{h-1}}{\displaystyle \sum _{X=0}^{w-1}}|G_{YX}^{\prime i}\rangle \otimes |YX\rangle \hfill \\ \hfill |G_{YX}^{\prime i}\rangle & =|G_{YX}^{\prime 0}{G}_{YX}^{\prime 1}\dots {G_{YX}^{\prime 255}⟩}_Y,G_{YX}^{\prime i}\in \left\{\mathrm{0,1}\right\}\hfill \\ \hfill |G_{YX}^{n-1}\rangle & =|\frac{g_{YX}^{n-1}+P_{n-1}\left(Y,X\right)+2}{512}\rangle ,g_{YX}^n\in \left\{\mathrm{0,1},\dots ,255\right\}.\hfill \end{array}(10)$

Step 4: The generalized Arnold transform operator ${\widehat{A}}^{K_1}$ containing the key K₁ is applied to the primary encrypted image $\left|{\mathrm{\Psi }}^{\prime }\right.⟩$ after gray information hiding to obtain the final encrypted image $\left|{\mathrm{\Psi }}^{\prime \prime }\right.⟩$. The specific calculation process can be formulated as in Eq. 11:

$\begin{array}{cc}\hfill |{\mathrm{\Psi }}^{\prime \prime }\rangle & =\frac{1}{{\sqrt{2}}^{h+w}}{\displaystyle \sum _{Y=0}^{H-1}}{\displaystyle \sum _{X=0}^{W-1}}|G_{YX}^{\prime i}\rangle \otimes {\widehat{A}}^{K_1}|YX\rangle \hfill \\ \hfill & =\frac{1}{{\sqrt{2}}^{h+w}}{\displaystyle \sum _{Y=0}^{H-1}}{\displaystyle \sum _{X=0}^{W-1}}|G_{YX}^{\prime i}\rangle \otimes |Y^{\prime }{X}^{\prime }\rangle .\hfill \end{array}(11)$

Here, the generalized Arnold transform operator $\widehat{A}{K}_1$ is used to modify the encrypted image $\left|{\mathrm{\Psi }}^{\prime }\right.⟩$. This operation enhances the security of the encryption process. The resulting image $\left|{\mathrm{\Psi }}^{\prime \prime }\right.⟩$ encapsulates the concealed grayscale information, making it highly secure and suitable for safe transmission or storage.

3.2 Image decryption

The decryption process, which essentially is the reverse of the encryption process, and the specific decryption steps are as follows:

Step 1: In the first step, the necessary system control parameters and initial values are obtained. Keys required for the decryption process are generated in this phase.

Step 2: In the second step, the image decryption process begins by applying the inverse of the Arnold transform operator, denoted as ${\widehat{A}}^{-1}$, to the operator ${({\widehat{A}}^{-1})}^{K_1}$ of Arnold and the key inverse operation. This operation is performed on the encrypted image $\left|{\mathrm{\Psi }}^{\prime \prime }\right.⟩$. The resulting image $\left|{\mathrm{\Psi }}_R^{\prime }\right.⟩$ is obtained in Eq. 12.

$\begin{array}{cc}\hfill \left|{\mathrm{\Psi }}_R^{\prime }\right.⟩& ={\left({\widehat{A}}^{-1}\right)}^{K_1}\left|{\mathrm{\Psi }}^{\prime \prime }\right.⟩\hfill \\ \hfill & =\frac{1}{{\sqrt{2}}^{h+w}}{\displaystyle \sum _{Y=0}^{H-1}}{\displaystyle \sum _{X=0}^{W-1}}\left|G_{YX}^{\prime i}\right.⟩\otimes {\left({\widehat{A}}^{-1}\right)}^{K_1}|YX\rangle .\hfill \end{array}(12)$

Step 3: The gray encryption operator P_n(Y, X) generated by the key is used to restore the gray information about the image $\left|{\mathrm{\Psi }}_R^{\prime }\right.⟩$ and obtain the original image $\left|{\mathrm{\Psi }}_R\right.⟩$ before encryption, which can be calculated by Eq. 13:

$\left|G_{YX}^{n-1}\right.⟩=\left|\frac{512\times G_{YX}^{\prime n-1}-P_{n-1}\left(Y,X\right)-1}{256}\right.⟩,\left|G_{YX}^i\right.⟩=\left|G_{YX}^0{G}_{YX}^1\cdots G_{YX}^{q-1}\right.⟩.(13)$

This step effectively reverses the grayscale encryption process, allowing the retrieval of the original image $\left|{\mathrm{\Psi }}_R\right.⟩$ before encryption.

Figure 5 represents the entire flow of encryption. In the schematic representation, K₁ is the positional encryption operator used for Arnold’s disarrangement. K₂ and K₃ are image pixel-value encryption operators, which are used to obtain new pixel-value encryption results by performing modulo operations on gray values and then XOR operations on the original image pixels. Finally, the encrypted image is assembled at the pixel locations to obtain a complete encrypted image. All the encryption operators are derived from four-dimensional chaotic equations.

4 Simulation experiment and analysis

The Python platform is used in this paper to simulate the encryption system. Lena, Pepper, and Baboon, three common grayscale images with a size of 512 × 512, are chosen as test items, and the encryption algorithm is examined from several angles, including information entropy, histogram, correlation, and key sensitivity, respectively.

4.1 Experimental results

In the experiment, we selected the following key to simulate the encryption algorithm and set the initial parameter, $w\left(t_0\right)$ α = 10, β = 8/3, γ = 28, r = −1, $K_1=x\left(t_0\right)=1.1$, $K_2=y\left(t_0\right)=2.2$, and $K_3=z\left(t_0\right)=3.3$. Figure 6 displays the encryption and decryption outcomes. The illustration demonstrates how well the encryption technique can both encode and decode the original picture.

FIGURE 6

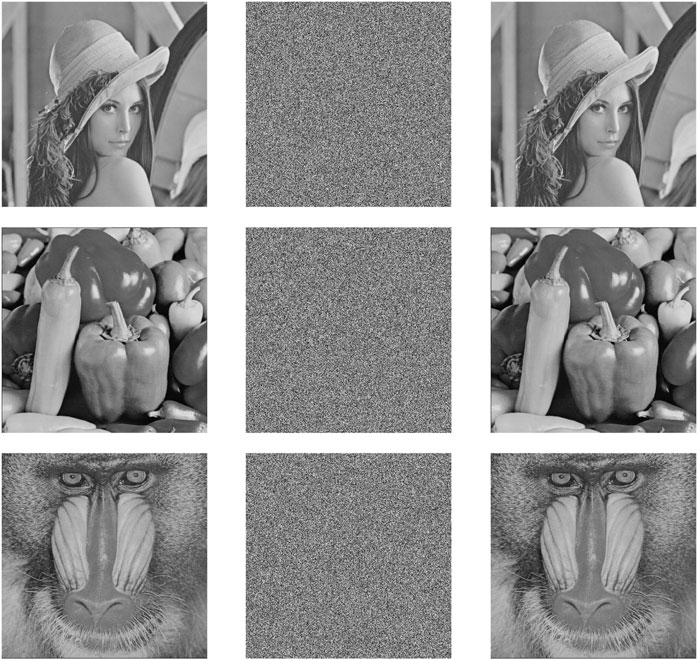
FIGURE 6. Comparison for encryption and decryption results. The first column shows plaintext images; the second column shows encrypted images; and the third column shows decrypted images.

4.2 Information entropy analysis

Information entropy reflects a measure of the richness of image information. In general, the greater the image information entropy, the richer the amount of information is and the higher the quality. From the point of view of image encryption, information entropy is considered from the statistical characteristics of the whole source and represents the overall characteristics of the source in an average sense. When the information entropy of an image approaches the ideal value, it shows that the more uniform the spatial distribution of the gray image is, the more notable the encryption effect is.

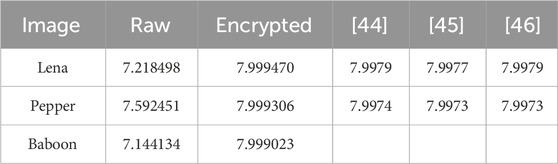
For the image with a gray level of 256, the information entropy of the ciphertext image is closer to 8 bits, indicating that it has less visual information [44]. To process encrypted grayscale images, the data are first read into memory. Then, the frequency of occurrence for each grayscale level is collected by traversing each pixel. Using these frequencies, the probability of each grayscale level pixel is calculated by dividing the frequency by the total number of pixels. Finally, the information entropy is calculated using Eq. 14:

$H\left(m\right)=-{\displaystyle \sum _{i=0}^{255}}P\left(m_i\right){\log }_{2}P\left(m_i\right),(14)$

where m_i is the i-th gray level for the digital image I with 256 gray levels, and P (m_i) is the emergence probability of m_i. Table 1 shows the comparison of the information entropy of the original image and encrypted image. The data show that the information entropy of the three images can reach above 7.999 bits after encryption, indicating that the system has better encryption and can effectively resist the statistical attack.

TABLE 1

TABLE 1. Information entropy of the original and encrypted images.

4.3 Histogram analysis

The image’s histogram clearly illustrates how the pixel values are distributed across the composition [47]. Figure 7 shows the comparison of the histogram distribution of an image before and after encryption. Figures 7A, B, C show the uneven distribution on the original image. After encryption, Figure 1D, E, F show that the histogram distribution of the ciphertext image is basically uniform, and by analyzing the statistical characteristics of the image or no useful statistical information can be obtained by performing any statistical analysis on it. This shows that the encryption system can withstand the histogram analysis.

FIGURE 7

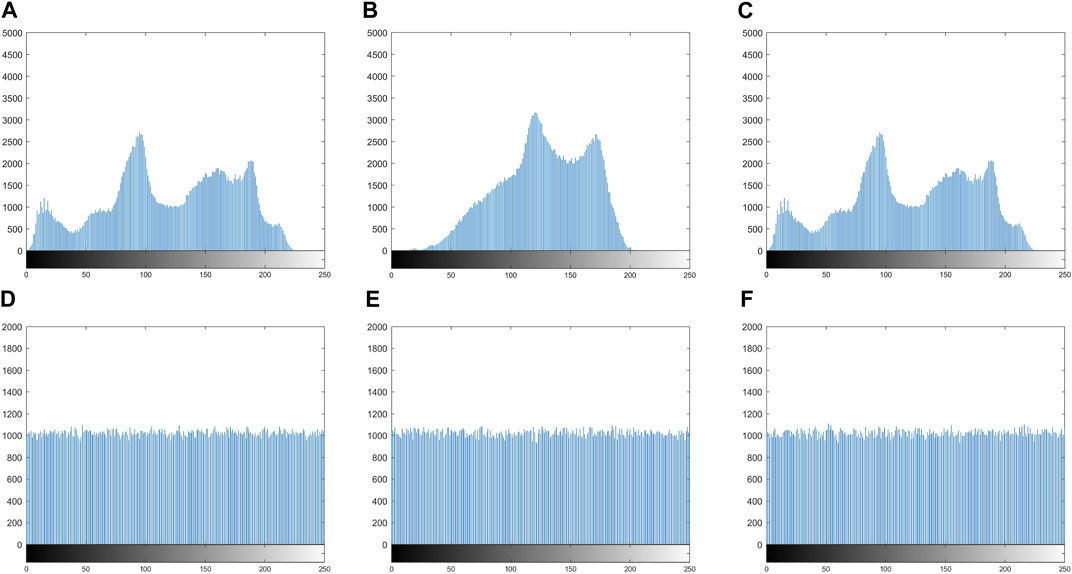
FIGURE 7. Histogram analysis of plaintext and ciphertext. Plaintext: (A) Lena, (B) Pepper, and (C) Baboon; ciphertext: (D) Lena, (E) Pepper, and (F) Baboon.

4.4 Correlation analysis

The redundancy quality of the image establishes a significant link between nearby image pixels. Moreover, the correlation of adjacent pixels is often used to reflect the correlation degree of pixel values of adjacent positions of an image, including horizontal, vertical, and diagonal directions. For a good encryption algorithm, the adjacent pixel correlation of the ciphertext will approach zero. Therefore, correlation can be used as an evaluation criterion to judge the image encryption effect. The calculation method of an adjacent relation of image pixels is shown in Eq. 15:

${\rho }_{\text{xy}}=\frac{{\displaystyle {\sum }_{\text{n},\mathrm{m}=1}^{\text{N}}}\left({\mathrm{x}}_n-\bar{X}\right)\left({\mathrm{y}}_m-\bar{Y}\right)}{\sqrt{{\displaystyle {\sum }_{\text{n},\mathrm{m}=1}^{\text{N}}}{\left({\mathrm{x}}_n-\bar{X}\right)}^2{\left(y_m-\bar{Y}\right)}^2}}.(15)$

In the information entropy of the original image and the encrypted image, $\bar{X}$ and $\bar{Y}$ are the average values of two adjacent pixels, N is the total number of pairs of adjacent pixels, and x_n and y_m are the values of the two adjacent pixels, respectively.

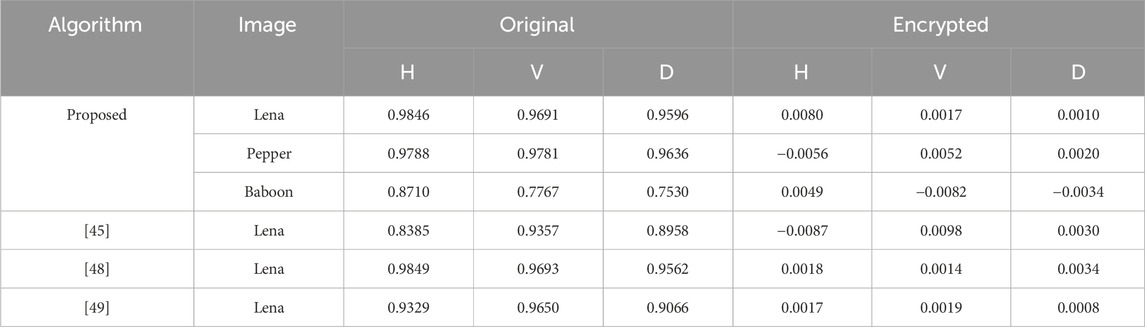
In total, 10,000 pairs of adjacent pixels are randomly selected to test the correlation in terms of distribution of adjacent pixels in horizontal, vertical, and diagonal directions. In three orientations, the correlation coefficients between plaintext and ciphertext pixels are examined. The experimental results of the correlation of adjacent pixels are shown in Table 2, and the analysis is shown in Figure 8.

TABLE 2

TABLE 2. Correlation comparison of the adjacent pixel analysis.

FIGURE 8

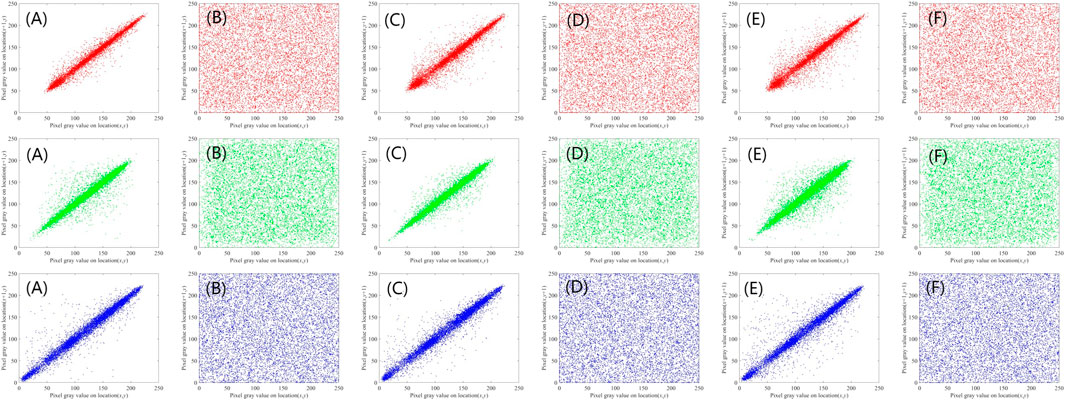
FIGURE 8. Correlation analysis of plaintext and ciphertext: (A) Horizontal direction of the original image. (B) Horizontal direction of the encrypted image. (C) Vertical direction of the original image. (D) Vertical direction of the encrypted image. (E) Diagonal direction of the original image. (F) Diagonal direction of the encrypted image.

By observing the data presented in Table 2, we can see that the pixel correlation of the plaintext image is very close to 1, indicating that it has a strong correlation. After the encryption algorithm, the pixel distribution of the ciphertext image is uniform, and the correlation is weak. It shows that the quantum image Arnold transformation is combined with the chaos system to control the parameters, and the encrypted image obtained after XOR operation on the related pixel method can effectively reduce the correlation between image pixels. The observed data presented in Table 2 not only underscore the enhanced security aspects of the encryption algorithm but also lend itself to a robustness analysis. The robustness of an encryption algorithm is of paramount importance to ensure that the encrypted data remain secure and intact under various conditions and potential threats. Here, we delve into a more granular assessment of the algorithm’s robustness:

It can also be seen from Table 2 that images before encryption are vulnerable to various types of attacks. However, after applying the encryption algorithm, the pixel distribution of the ciphertext image becomes more uniform, and the correlation is significantly weakened. This increased robustness against pixel-level correlation attacks is a key aspect of algorithm security.

Moreover, the combination of the quantum image Arnold transform with the chaos system-controlled parameters, followed by the XOR operation on related pixels, proves to be a robust approach to reduce the correlation between image pixels. This algorithm is designed to withstand common attacks such as differential cryptanalysis and brute-force decryption attempts. The utilization of chaos-based control parameters adds an extra layer of complexity to the encryption process, making it resistant to attacks that rely on predictable patterns.

In addition to addressing the pixel correlation, it is important to note that the algorithm also exhibits resistance to other potential vulnerabilities. For instance, it has been tested against known attacks, including differential attacks and frequency analysis, and has shown a high degree of robustness. The algorithm’s robustness is further bolstered by its ability to maintain the security of the encrypted image even when subjected to potential quantum computing-based attacks.

4.5 Analysis of a differential attack

The plaintext sensitivity of image encryption methods is frequently evaluated using a differential attack [50]. Key sensitivity in the context of ideal multimedia encryption means that a change of one bit in the key should result in a completely different encryption result. The beginning state of the chaotic mapping and the sensitivity of the control parameters are related to the key sensitivity of chaotic cryptography in general. Sensitivity was assessed using the number pixel change rate (NPCR) and uniform average change intensity (UACI). NPCR and UACI are acronyms for the “number of pixels changed” and “average intensity of changes,” respectively, between two encrypted images.

When a pixel in a plaintext image changes, the encryption result should ideally approach the standard value in order to resist a differential attack. NPCR = 99.6094% and UACI = 33.4635% are their corresponding standard values, which can be determined using Eq. 16:

$\left\{\begin{array}{c}NPCR:N\left(C_1,C_2\right)=\frac{{\displaystyle {\sum }_{i,j}}D\left(i,j\right)}{W\times H}\times 100\%\hfill \\ \hfill \\ UACI:U\left(C_1,C_2\right)=\frac{1}{W\times H}{\displaystyle {\sum }_{i,j}}\frac{\left|C_1\left(i,j\right)-C_2\left(i,j\right)\right|}{255}\times 100\%\hfill \end{array}\right..(16)$

The width and height of the two images are, respectively, expressed as W and H; D (i, j) is defined by Eq. 17:

$D\left(i,j\right)=\left\{\begin{array}{c}0,C_1\left(i,j\right)=C_2\left(i,j\right)\hfill \\ \hfill \\ 1,C_1\left(i,j\right)\ne C_2\left(i,j\right)\hfill \end{array}\right.,(17)$

where the pixel values of the two ciphertexts at point (i, j) are represented by C₁ (i, j) and C₂ (i, j).

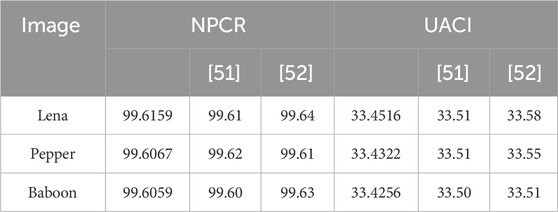
The value of K′ can be obtained by changing a bit of K, and then, two ciphertext images can be obtained using the same plaintext with the key. Table 3 represents the comparison for the NPCR and UACI values of the ciphertext before and after the change. The experimental data show that the NPCR and UACI values of our scheme are close to the ideal value.

TABLE 3

TABLE 3. Analysis results of chosen-plaintext attacks (%).

4.6 Key space and sensitivity analysis

A secure encryption method must provide a sufficiently large key space to ensure that the attacker cannot find the safe secret key in a timely manner. To survive powerful attacks, the key space should be greater than 2¹²⁸. The effective precision of chaotic system parameters in this paper can be obtained in 10⁻¹⁶. The key space for the picture algorithm can be reached in 10¹⁴⁰ ≫ 2¹²⁸. We can, therefore, conclude that the encryption system’s key space is sufficiently large to resist destructive attacks.

We also performed sensitivity analyses on related keys at the same time. Figure 9 illustrates the great sensitivity of this technique by showing that even a very minor key deviation prevents the right image from being decrypted.

FIGURE 9

FIGURE 9. Comparison of decryption results of similar keys. (A) The original unencrypted image. (B) The result after the deviation of key r₁ is 10⁻¹⁶. (C) The result after the deviation of key K₁ is 10⁻¹⁶. (D) The result after the deviation of K₂ is 10⁻¹⁷. (E) The result after the deviation of key K₃ is 10⁻¹⁸. (F) After decryption by the correct key Image.

5 Conclusion

This study puts out a four-dimensional chaos-based quantum image encryption technique. The algorithm addresses the shortcomings of Arnold transformation periodicity, small key space, and the lack of resistance to statistical analysis and proposes a reliable and effective encryption scheme. It does this by making full use of the characteristics of Arnold transform transposition, ergodicity, and randomness of the four-dimensional chaotic system. The four-dimensional Lorenz system gives encryption algorithms a key space that is large enough to withstand strong attacks. The approach first calculates the coordinates of the pixels’ scrambled values during the encryption phase using a quantum Arnold transform with a key and then performs a linear transformation of the values of the pixels using a quantum chaotic sequence. Finally, the displacement process is completely finished, and all pixels are traversed to produce ciphertext images. The complexity and randomness of the encryption technique are significantly increased when this type of displacement is used in conjunction with the pixel gray value encryption with a key. The simulation results of the encryption algorithm were analyzed from multiple perspectives, including information entropy, histogram, correlation, and key sensitivity. Finally, it was demonstrated that the experimental results were highly satisfactory. The image encryption procedures are all carried out via reversible quantum logic gates in order to further enhance the quality of the decrypted image. The approach can restore the original image with great fidelity, provided that the key is entirely accurate.

This method demonstrates the ability to resist various attacks, including statistical and brute force attacks, resulting in scrambled images with enhanced security and usability. The image encryption process is achieved exclusively through reversible quantum logic gates, further enhancing the quality of decrypted images when the key is precisely accurate [53–55]. However, it is important to note that four-dimensional chaos systems often require more complex computations, which may lead to higher computational complexity, particularly in real-time applications. In our future work, we plan to explore a symmetrically optimized quantum circuit to simplify the image representation and reduce computational complexity, creating a robust and highly adaptable image encryption method.

Data availability statement

The original contributions presented in the study are included in the article/Supplementary Material, all data are reasonably available from the authors.

Ethics statement

Written informed consent was obtained from the individual(s) for the publication of any potentially identifiable images or data included in this article.

Author contributions

X-DL: conceptualization, methodology, software, investigation, formal analysis, and writing–original draft; Q-HC: methodology, validation, and writing–review and editing; R-SZ: methodology, software, formal analysis, and writing–review and editing. G-ZL: visualization and investigation; SG: resources, supervision, and writing–original draft; L-LW: visualization and editing; X-KF: conceptualization, funding acquisition, resources, supervision, and writing–review and editing. All authors contributed to the article and approved the submitted version.

Funding

This project is supported by the 2021 key project of Shandong undergraduate teaching reform (grant no. Z2021114); innovation training program for college students in Shandong Province (grant nos 202110429213 and 202210429015); the Natural Science Foundation of Shandong Province, China (grant no. ZR2021MF049); and the Joint Fund of Natural Science Foundation of Shandong Province (grant no. ZR2022LLZ012).

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

1. Charles HB, David PD. Quantum information and computation. Nature (2000) 404:247–55. doi:10.1038/35005001

PubMed Abstract | CrossRef Full Text | Google Scholar

2. Shor PW. Algorithms for quantum computation: discrete logarithms and factoring proceedings. In: Proceedings of the 35th Annual Symposium on Foundations of Computer Science; November, 1994; Santa Fe, NM, USA (1994). p. 124–34.

Google Scholar

3. Grover LK. A fast quantum mechanical algorith for database search. In: Proceedings of the twenty-eighth annual ACM symposium on Theory of Computing; May, 1996; Philadelphia, Pennsylvania, USA (1996). p. 212–9.

Google Scholar

4. Yan F, Chen K-H, Venegas-Andraca SE, Zhao J-P. Quantum image rotation by an arbitrary angle. Quan Inf Process (2017) 16(11):282–20. doi:10.1007/s11128-017-1733-5

CrossRef Full Text | Google Scholar

5. Zhang W-W, Gao F, Liu B, Wen QY, Chen H. A watermark strategy for quantum images based on quantum fourier transform. Quan Inf Process (2013) 12:793–803. doi:10.1007/s11128-012-0423-6

CrossRef Full Text | Google Scholar

6. Song X-H, Wang S, Liu S, El-Latif AAA, Niu X-M. A dynamic watermarking scheme for quantum images using quantum wavelet transform. Quan Inf Process (2013) 12:3689–706. doi:10.1007/s11128-013-0629-2

CrossRef Full Text | Google Scholar

7. Song X-H, Wang S, El-Latif AAA, Niu X-M. Dynamic watermarking scheme for quantum images based on hadamard transform. Multimedia Syst (2014) 20:379–88. doi:10.1007/s00530-014-0355-3

CrossRef Full Text | Google Scholar

8. Miyake S, Nakamae K. A quantum watermarking scheme using simple and small-scale quantum circuits. Quan Inf Process (2016) 15:1849–64. doi:10.1007/s11128-016-1260-9

CrossRef Full Text | Google Scholar

9. Yang Y-G, Xia J, Jia X, Zhang H. Novel image encryption/decryption based on quantum fourier transform and double phase encoding. Quan Inf Process (2013) 12(11):3477–93. doi:10.1007/s11128-013-0612-y

CrossRef Full Text | Google Scholar

10. Song X-H, Wang S, El-Latif AAA, Niu X-M. Quantum image encryption based on restricted geometric and color transformations. Quan Inf Process (2014) 13:1765–87. doi:10.1007/s11128-014-0768-0

CrossRef Full Text | Google Scholar

11. Zhou N-R, Hua T-X, Gong L-H, Pei DJ, Liao QH. Quantum image encryption based on generalized arnold transform and double random-phase encoding. Quan Inf Process (2015) 14:1193–213. doi:10.1007/s11128-015-0926-z

CrossRef Full Text | Google Scholar

12. Jiang N, Zhao N, Wang L. Lsb based quantum image steganography algorithm. Int J Theor Phys (2016) 55:107–23. doi:10.1007/s10773-015-2640-0

CrossRef Full Text | Google Scholar

13. Zhang T-J, Abd-El-Atty B, Amin M, El latif AAA. Qislsqb: a quantum image steganography scheme based on least significant qubit. DEStech Trans Comp Sci Eng (2017). doi:10.12783/dtcse/mcsse2016/10934

CrossRef Full Text | Google Scholar

14. Vernam GS. Cipher printing telegraph systems for secret wire and radio telegraphic communications. Trans Am Inst Electr Eng (1926) 45:109–15. doi:10.1109/jaiee.1926.6534724

CrossRef Full Text | Google Scholar

15. Shannon CE. Communication theory of secrecy systems. Bell Syst Tech J (1949) 28(4):656–715. doi:10.1002/j.1538-7305.1949.tb00928.x

CrossRef Full Text | Google Scholar

16. Bennett CH, Brassard G. Quantum cryptography: public key distribution and coin tossing. Theor Comp Sci (2014) 560:7–11. doi:10.1016/j.tcs.2014.05.025

CrossRef Full Text | Google Scholar

17. Ekert AK. Quantum cryptography based on bell’s theorem. Phys Rev Lett (1991) 67:661–3. doi:10.1103/physrevlett.67.661

PubMed Abstract | CrossRef Full Text | Google Scholar

18. Xie Y-M, Lu Y-S, Weng C-X, Cao X-Y, Jia Z-Y, Bao Y, et al. Breaking the rate-loss bound of quantum key distribution with asynchronous two-photon interference. PRX Quan (2022) 3:020315. doi:10.1103/prxquantum.3.020315

CrossRef Full Text | Google Scholar

19. Diffie W, Hellman M. New directions in cryptography. Trans Inf Theor (1976) 22(6):644–54. doi:10.1109/tit.1976.1055638

CrossRef Full Text | Google Scholar

20. Benioff P. Quantum mechanical Hamiltonian models of turing machines. J Stat Phys (1982) 29(29):515–46. doi:10.1007/bf01342185

CrossRef Full Text | Google Scholar

21. Liu G-Z, Li W, Fan X-K, Li Z, Wang Y-X, Ma H-Y. An image encryption algorithm based on discrete-time alternating quantum walk and advanced encryption standard. Entropy (2022) 24:608. doi:10.3390/e24050608

PubMed Abstract | CrossRef Full Text | Google Scholar

22. Yin H-L, Fu Y, Li C-L, Weng C-X, Li B-H, Gu J, et al. Experimental quantum secure network with digital signatures and encryption. Natl Sci Rev (2022) 9(4):nwac228. doi:10.1093/nsr/nwac228

CrossRef Full Text | Google Scholar

23. Toda M, Ryogo K, Saitô N. Statistical physics I. Berlin, Germany: Springer (2015).

Google Scholar

24. Rossler OE, An equation for hyperchaos. Phys Lett A (1979) 71(2):155–7. doi:10.1016/0375-9601(79)90150-6

CrossRef Full Text | Google Scholar

25. Wang X-Y, Wang M-J. A hyperchaos generated from lorenz system. Physica A: Stat Mech its Appl (2008) 387(14):3751–8. doi:10.1016/j.physa.2008.02.020

CrossRef Full Text | Google Scholar

26. Yang Y-G, Xia J, Jia X, Zhang H. Novel image encryption decryption based on quantum fourier transform and double phase encoding. Quan Inf Process (2013) 12(9):3477–93. doi:10.1007/s11128-013-0612-y

CrossRef Full Text | Google Scholar

27. El-Latif AAA, Li L, Wang N, Han Q, Niu X-M. A new approach to chaotic image encryption based on quantum chaotic system, exploiting color spaces. Signal Process. (2023) 93. doi:10.1016/j.sigpro.2013.03.031

CrossRef Full Text | Google Scholar

28. Jiang N, Wang L, Wu W-Y. Quantum hilbert image scrambling. Int J Theor Phys (2014) 53:2463–84. doi:10.1007/s10773-014-2046-4

CrossRef Full Text | Google Scholar

29. Jiang N, Wu W-Y, Wang L. The quantum realization of arnold and fibonacci image scrambling. Quan Inf Process (2014) 13(5):1223–36. doi:10.1007/s11128-013-0721-7

CrossRef Full Text | Google Scholar

30. Jiang N, Wang L. Analysis and improvement of the quantum arnold image scrambling. Quan Inf Process (2014) 13(7):1545–51. doi:10.1007/s11128-014-0749-3

CrossRef Full Text | Google Scholar

31. Goggin ME, Sundaram B, Milonni PW. Quantum logistic map. Phys Rev A (1990) 41(10):5705–8. doi:10.1103/physreva.41.5705

PubMed Abstract | CrossRef Full Text | Google Scholar

32. Yang Y-G, Tian J, He L, Zhou Y-H, Shi W-M. Novel quantum image encryption using one-dimensional quantum cellular automata. Inf Sci (2016) 345:257–70. doi:10.1016/j.ins.2016.01.078

CrossRef Full Text | Google Scholar

33. Liu X-B, Xixao D, Liu C. Double quantum image encryption based on arnold transform and qubit random rotation. Entropy (2018) 20:867. doi:10.3390/e20110867

PubMed Abstract | CrossRef Full Text | Google Scholar

34. Ying M. Foundations of quantum programming. Amsterdam, Netherlands: Elsevier Science (2016).

Google Scholar

35. Liu H-J, Wang X-Y. Color image encryption using spatial bit-level permutation and high-dimension chaotic system. Opt Commun (2011) 284(15):3895–903. doi:10.1016/j.optcom.2011.04.001

CrossRef Full Text | Google Scholar

36. Lin R-Gand L An image encryption scheme based on lorenz hyperchaotic system and rsa algorithm. Security Commun Networks (2021) 1–14. doi:10.1155/2021/5586959

PubMed Abstract | CrossRef Full Text | Google Scholar

37. Shi J-J, Chen T, Chen S-H, Li Q, Shi R-H. Quantum image chaotic cryptography scheme based on arnold transforms. J Elect Inf Tech (2022) 44(9):4284–93. doi:10.11999/JEIT211143

CrossRef Full Text | Google Scholar

38. Chen S-S, Hu J, Wang C-P, Lü J-H. Adaptive synchronization of uncertain rössler hyperchaotic system based on parameter identification. Phys Lett A (2004) 321(1):50–5. doi:10.1016/j.physleta.2003.12.011

CrossRef Full Text | Google Scholar

39. Jiang N, Wu W-Y, Luo W, Zhao N. Quantum image pseudocolor coding based on the density-stratified method. Quan Inf Process (2015) 14(5):1735–55. doi:10.1007/s11128-015-0986-0

CrossRef Full Text | Google Scholar

40. Zhang Y, Lu K, Gao Y-H, Wang M. Neqr: a novel enhanced quantum representation of digital images. Quan Inf Process (2013) 12(7):2833–60. doi:10.1007/s11128-013-0567-z

CrossRef Full Text | Google Scholar

41. Sakurai JJ, Napolitano J. Modern quantum mechanics. London, United Kingdom: Pearson Education Limited (2011).

Google Scholar

42. Dyson F, Falk H. Period of a discrete cat mapping. The Am Math Monthly (1992) 99:603–14. doi:10.1080/00029890.1992.11995900

CrossRef Full Text | Google Scholar

43. Vedral V, Barenco A, Ekert A. Quantum networks for elementary arithmetic operations. Phys Rev A (1996) 54:147–53. doi:10.1103/physreva.54.147

PubMed Abstract | CrossRef Full Text | Google Scholar

44. Annaby MH, Rushdi MA, Nehary EA. Image encryption via discrete fractional fourier-type transforms generated by random matrices. Signal Processing: Image Commun (2016) 49:25–46. doi:10.1016/j.image.2016.09.006

CrossRef Full Text | Google Scholar

45. Zhou S. A quantum image encryption method based on dnacnot. IEEE Access (2020) 8:178336–44. doi:10.1109/access.2020.3027964

CrossRef Full Text | Google Scholar

46. Zia U, McCartney M, Scotney B, Martinez J, AbuTair M, Memon J, et al. Survey on image encryption techniques using chaotic maps in spatial,transform and spatiotemporal domains. Int J Inf Secur (2023) 21:917–35. doi:10.1007/s10207-022-00588-5

CrossRef Full Text | Google Scholar

47. Chen J-X, Zhang Y, Qi L, Fu C, Xu L-S. Exploiting chaos-based compressed sensing and cryptographic algorithm for image encryption and compression. Opt Laser Tech (2018) 99:238–48. doi:10.1016/j.optlastec.2017.09.008

CrossRef Full Text | Google Scholar

48. Wang X-Y, Liu L. Application of chaotic josephus scrambling and rna computing in image encryption. Multimedia Tools Appl (2021) 80(1):23337–58. doi:10.1007/s11042-020-10209-9

CrossRef Full Text | Google Scholar

49. Fang P, Liu H, Wu C, Liu M. A survey of image encryption algorithms based on chaotic system. Vis Comp (2023) 39:1975–2003. doi:10.1007/s00371-022-02459-5

CrossRef Full Text | Google Scholar

50. Zhu C-X. A novel image encryption scheme based on improved hyperchaotic sequences. Opt Commun (2012) 285(1):29–37. doi:10.1016/j.optcom.2011.08.079

CrossRef Full Text | Google Scholar

51. Butt KK, Li G-H, Masood F, Khan S. A digital image confidentiality scheme based on pseudo-quantum chaos and lucas sequence. Entropy (2020) 22(11):1276. doi:10.3390/e22111276

PubMed Abstract | CrossRef Full Text | Google Scholar

52. Ismail Abdelfatah R. Quantum image encryption using a self-adaptive hash function-controlled chaotic map (sahf-ccm). IEEE Access (2022) 10:107152–69. doi:10.1109/access.2022.3212899

CrossRef Full Text | Google Scholar

53. Wang J, Geng YC, Han L, Liu JQ. Quantum image encryption algorithm based on quantum key image. Int J Theor Phys (2019) 58:308–22. doi:10.1007/s10773-018-3932-y

CrossRef Full Text | Google Scholar

54. Zhou RG, Wu Q, Zhang MQ, Shen CY. Quantum image encryption and decryption algorithms based on quantum image geometric transformations. Int J Theor Phys (2013) 52:1802–17. doi:10.1007/s10773-012-1274-8

CrossRef Full Text | Google Scholar

55. Wang Z, Xu M, Zhang Y. Review of quantum image processing. Arch Comput Methods Eng (2022) 29(2):737–61. doi:10.1007/s11831-021-09599-2

CrossRef Full Text | Google Scholar