Polarization characteristics and structural modifications of Cu nanoparticles under high electric fields

High electric fields affect the diffusion dynamics of atoms on a metal surface, causing biased surface diffusion that possibly leads to the growth of intensively field emitting protrusions and consequent vacuum breakdown (VBD). The scientific understanding of this process, as well as other fundamental VBD initiation mechanisms, is far from complete. Here we investigate the exact atomic behaviour of metal surfaces exposed to extremely high electric fields using density functional theory (DFT). Previous theories describe the field-surface dynamics in terms of the effective dipole moments and polarizability of surface atoms, disregarding higher-order (hyperpolarizability) terms. The validity of this approximation has been evaluated only for electric fields up to 3 GV/m, due to computational limitations of the plane-wave DFT basis used in previous works. In this work, we test the validity of this approximation for a much wider field range, relevant for VBD and field emission (FE), using Cu nanoparticles as our test structures. We find that although such high fields can change the entire structure of Cu nanoparticles, their energetics are described very precisely by the permanent dipole moment and polarizability terms. Thus, we show that neglecting the hyperpolarizability terms is valid even for field values that exceeds the range that is relevant for intense FE and VBD. This work lays a solid foundation for further developing atomic-level simulation models for electric field-induced surface diffusion on metal surfaces and its effects on protrusion growth and VBD initiation.

Introduction

The behaviour of metal surfaces is modified by the influence of external electric fields, which can alter the interatomic interactions in a complex manner [1–3]. This results in electric fields playing a key role in the diffusion dynamics of the atoms on metal surfaces, resulting in various types of field induced surface modifications, with significant implications in various technologies. For instance, vacuum arcs, also known as vacuum breakdowns, are detrimental for a wide range of technologies, such as particle accelerators, fusion reactors, vacuum switches, electron sources, etc. [4–8] Despite years of study, the physical mechanisms leading to vacuum breakdown remain unclear. Although it is quite established that VBD is initiated from field enhancing protrusions on the metal surface that acts as intense field emitters, their formation mechanisms remain unknown. One of the most plausible explanations is field-induced growth of nano-protrusions on metal surfaces by biased diffusion. Similar effects can also be detrimental for the stability of field emitting electron sources. Meanwhile, if the field-induced surface modifications can be clearly understood and reliably modelled, it will offer possibilities for the controllable manipulation, nanopatterning and fabrication of surface structures.

The diffusion behaviour of adatoms on metal surfaces under external electric fields attracts the wide attention of both theoretical and experimental studies. Tsong and Kellogg [9–11] proposed a formula to describe the biased diffusion of an adatom in the presence of non-uniform fields, assuming that the modification of its migration barriers by the field is determined by the atomic polarization characteristics. Their formulae provided a strong qualitative understanding of how the migration barriers and the binding energies are modified in the presence of a high electric field. Yet, the atomic polarization characteristics were not rigorously defined for a non-isolated adatom that interacts and shares its charge with other surface atoms in its vicinity. This issue was recently tackled by the development of a complete theory [12, 13] that considers the entire charge redistribution on the surface. This theory defined rigorously and exactly the relevant effective atomic dipole characteristics, based on the systemic dipole characteristics of a slab system, which can be calculated by density functional theory methods. Although this method has been successful in describing the polarization characteristics and the biased diffusion dynamics for low fields up to a few GV/m, it is not clear whether higher-order hyper-polarizability terms can be neglected for higher electric fields.

In the present work, we investigate the behaviour of Cu nanoparticles under high electric field to verify the validity of neglecting hyper-polarizability terms. We compare the total energy of the nanoparticles under electric field as calculated directly by density functional theory (DFT) and by the polarization formula. We verify that leaving out hyper-polarizability terms is a valid approximation for applied fields up to 15 GV/m. In addition, we show that Cu nanoparticles are subjected to significant structural modifications when exposed to high electric fields, which due to their non-diffusion properties as well.

Simulation methods

We performed DFT calculations by combining the Vienna Ab initio Simulation Package (VASP) [14] 6.3.0 and Gaussian 16 package. All our calculations were performed with the Perdew–Burke–Ernzerhof (PBE) [15] generalized gradient approximation (GGA) [16, 17] for both VASP and Gaussian calculations. In VASP, the wave functions are expanded in a plane-wave basis sets, using the projector augmented wave (PAW) method [18]. The cut-off energy was set to 600 eV, and a single gamma-point grid sampling was used for Brillouin zone integration, as the simulation cell size was larger than 30 Å × 30 Å × 30 Å. The electronic convergence criterion was set to 10^–5 eV, ionic relaxation was run until the maximum interatomic force was less than 0.01 eV/Å, and σ = 0.2 was chosen for the Methfessel-Paxton smearing scheme [19]. Gaussian uses a localized basis set. The PBE functional was used in conjunction with the triple zeta valence polarization (TZVP) [20, 21] basis set.

Nanoparticle structure relaxation with and without field

We simulated four distinct types of Cu nanoparticle structures, shown in Figure 1. The simulated NP structures include a simple atomic dimer (a, e), a 14-atom cube (b, f), two stacked 23-atom cubes (c, g) and three stacked 32-atom cubes (d, h) with Cu atoms at the corner and at the centre of the faces in the FCC positions. We started by relaxing the structures without field using the Gaussian DFT simulation package. The relaxed structures are shown on the left-hand side (a-d) of Figure 1.

FIGURE 1

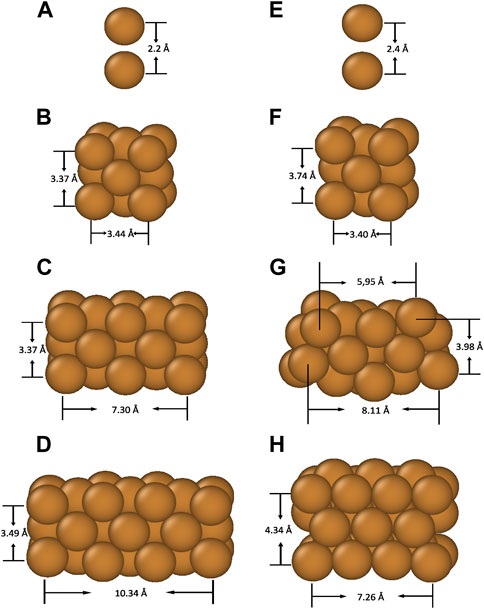
FIGURE 1. From top to bottom, side views of Cu dimer (A,E), single cube NP (B,F), two stacked cubes NP(C,G) and three stacked cubes NP (D,H), respectively. Bond lengths are marked by solid lines. Structures (A), (B), (C), and (D) are relaxed without field, while (E) and (F) are relaxed under a 15 GV/m applied field, (G) under a 2 GV/m field, and (H) under 1 GV/m. In all cases the field is applied vertically along the positive z-axis.

Then, to demonstrate the significance a high electric field plays in the dynamics of such atomic structures, we applied a strong electric field in the upward (+z) direction and relaxed the structures under the influence of the field, as shown on the right-hand side (e-h) of Figure 1.

For the Cu atom dimer, we find that the bond length (minimum energy distance) increases from 2.2 Å at zero field to 2.4 Å at a field of 15 GV/m. For the 1-cube NP, the bond lengths along the direction of an applied field (the vertical axis) are elongated by about 9%, while on the contrary, the bond lengths perpendicular to the direction of an applied field (the horizontal axis) are shortened by about 1%, causing the cube to be tetragonally distorted. In the case of 2-cube NP, a field of 2 GV/m is sufficient to cause significant structural deformation as shown in Figure 1G. The applied field exerts a strong external force on leading to atoms at the corner move upwards, thus bending the whole NP structure. Finally, for the 3-cube NP, even 1 GV/m field is sufficient to cause a complete reconstruction of the NP, as shown in Figure 1H. We see that the NP compactifies along the horizontal axis and stretches along the vertical axis. The most top face centre Cu atoms corresponding to that in ideal FCC positions move upwards along + z-axis and the atoms at corner move towards the middle to reach energy minimum.

Polarization characteristics

The total diploe moment $p$ of a system of atoms under an applied field $F$ can be expressed as [11]

$p\left(F\right)=\mu +\alpha F+O\left(F^2\right)(1)$

where $\mu$ and $\alpha$ are the permanent diploe moment and polarizability of a given atomic system (set of atomic positions), respectively. The total energy $U$ of a given system under high electric fields can be then obtained in terms of $\mu$ and $\alpha$ as [11]

$U=U_0-\mu F-\frac{1}{2}\alpha F^2+O\left(F^3\right)(2)$

where $U_0$ is the total energy in the absence of an external field. The parameters $\mu$ and $\alpha$, similarly to $U_0$ depend on the atomic structure and can be calculated for any atomic structure by using DFT in the presence of an applied field. However, it is not clear what is the field range for which higher order $O\left(F^3\right)$ (also known as hyperpolarizability) terms can be neglected. Previous DFT calculations [11] have shown that $O\left(F^2\right)$, $O\left(F^3\right)$ in Eqs 1, 2 can be neglected for electric field strengths up to 3 GV/m. Here we shall investigate whether this approximation is valid for higher field strengths as well.

The commonly used DFT package VASP, can perform accurate calculations when electric fields range from 0 to $\pm$ 3 GV/m, using the dipole layer method introduced by Neugebauer [22]. However, this method becomes unreliable when the applied field is larger than about 3 GV/m, as the electrons tunnel through the surface barrier and accumulate at the artificial potential well introduced near the dipole layer, thus leading to an unreliable result, especially in the calculation of the dipole moment of the system. Due to the limitations of the abovementioned method, we used the Gaussian package for high-field calculations, as the latter is capable of tackling DFT calculations with 15 GV/m field due to its localized basis wavefunctions. However, this basis is appropriate for simulating non-periodic, isolated structures, rather than the periodic slab models that are typically used for such calculations and are more representative of the interaction of high fields with large-scale metal surfaces. As we are here more interested in assessing the general behaviour of the polarization characteristics of metal surface structures exposed to high electric fields, we simulate different Cu nanoparticles, which can reveal typical characteristics, while remaining appropriate for the localized basis set of Gaussian.

To investigate the effect of hyper-polarizability terms at extremely high fields, we combine two widely used DFT calculation approaches and packages (VASP and GAUSSIAN), in a process schematically represented in the flow chart of Figure 2. For each relaxed structure of Figure 1, we use GAUSSIAN to directly calculate the total energy of a given atomic system for fields up to 15 GV/m and fit a parabola through them to obtain the optimum values for $\mu ,\alpha$ according to Eq. 2 that reproduce the calculated energy values. To validate different computational approaches, we also use VASP to calculate the polarization coefficients $\mu$ and $\alpha$ from only low-field (<3 GV/m) simulations. We can then substitute $\mu$ and $\alpha$ obtained by both methods into Eq. 2 to obtain the total field-induced energy in the entire field range, while disregarding hyper-polarizability terms. Finally, we compare the energy-field curves obtained by the three different methods to validate the more general, up-scalable, and computationally efficient method of Eq. 2. Note that the total energy $U$, $U^{\prime }$, $U^{″}$ , coefficients $\mu$ and $\alpha$ are uniquely dependent on the atomic positions, thus the atomic positions displayed in Figure 1 are kept fixed at each field increment step, ensuring that the extraction of $\mu ,\alpha$ for is valid for the given system and three different evaluation methods are comparable.

FIGURE 2

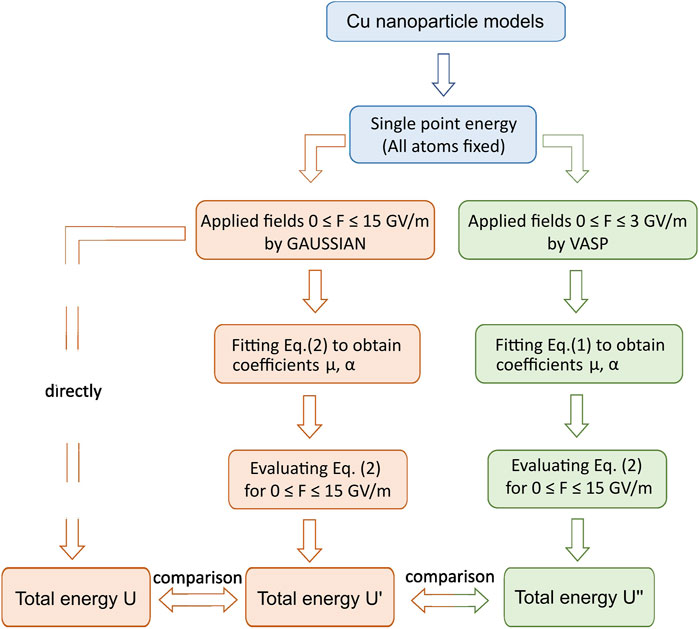
FIGURE 2. Workflow to illustrate the procedures of Cu nanoparticle simulations conducted in this work.

The results of the three different evaluation methods are presented in Figure 3, where we plot the field-induced energy of all simulated NP structures as a function of the applied field. The total energies of GAUSSIAN calculations ($U$) are plotted as dots, while the curves obtained by Eq. 2 by neglecting hyper-polarizability terms are given by lines, with dashed lines representing $\mu ,\alpha$ calculated by GAUSSIAN (i.e., $U^{\prime }$ of Figure 2) and solid lines representing $\mu ,\alpha$ values calculated by VASP (i.e., $U^{″}$ of Figure 2). Table 1 summarizes the corresponding values of $\mu ,\alpha$ obtained by the two different methods and the two different DFT software. The values obtained from VASP by fitting the dipole Equation 1 are listed as on the left hand side columns, while the corresponding values by fitting energy Eq. 2 from GAUSSIAN total energies, are given in the right hand side columns. The permanent dipole moments of structures (a), (b), (c), (d), (e) are zero due to their symmetry, while structures (f), (g), (h), relaxed under field lose their symmetry and obtain a non-zero permanent dipole moment. For all values, the error margin corresponds to the square root of the corresponding element of the curve fitting covariance matrix. Finally, the values of polarizability per atom (obtained from GAUSSIAN) are listed in the last column.

FIGURE 3

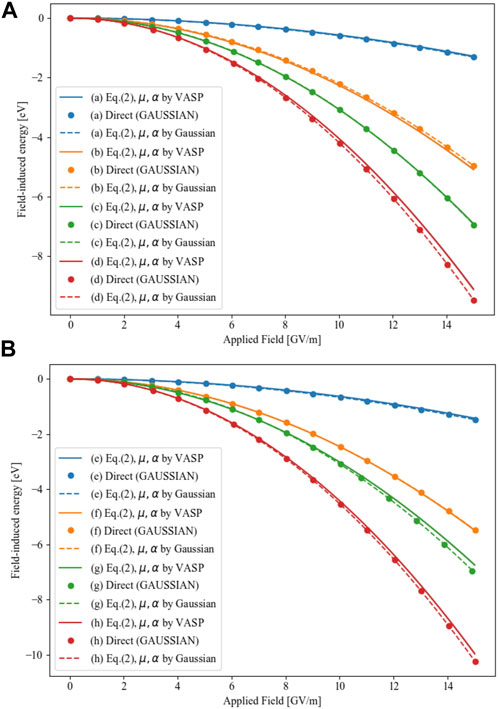
FIGURE 3. The field-induced energy of all simulated NP structures as a function of the applied field, structures in (A) are those relaxed without field, while structures in (B) are those relaxed after applied fields, all of them correspond to the labels of Figure 1.

TABLE 1

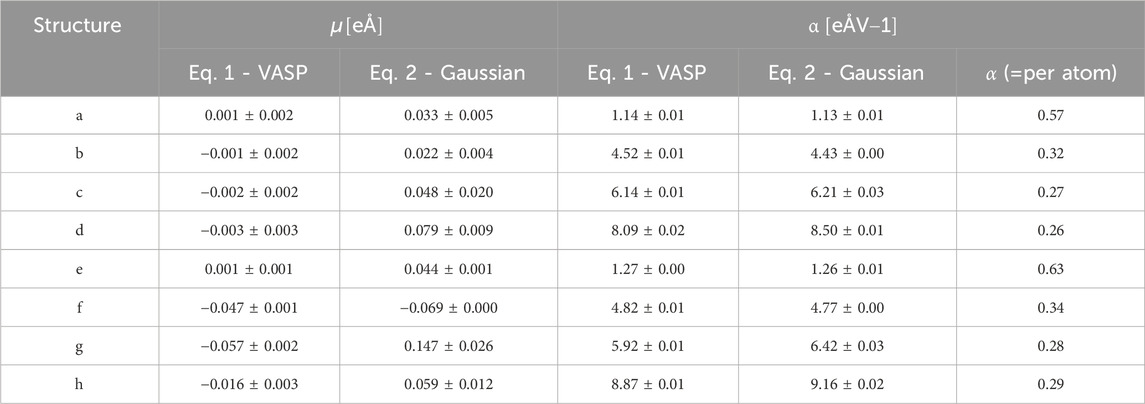
TABLE 1. The dipole moment µ and polarizability α of different NP structures as obtained from VASP by fitting the dipole Eq. 1 are listed as on the left-hand side columns, while the corresponding values by fitting energy Eq. 2 from GAUSSIAN total energies are given in the right-hand side columns, polarizability α per atom from GAUSSIAN are listed in the rightest column.

We clearly see that the $U$ values perfectly follow the parabolic shape of the $U^{\prime }$ curve. The deviation between the two does not exceed a 0.025 eV, clearly showing the irrelevance of hyperpolarizability terms in the <15 GV/m field range. Furthermore, the two different calculation approaches are in very good agreement when the applied field is less than 12 GV/m, with small deviations for higher field values (>12 GV/m). The slight differences are clearly attributable to the differences in the calculated polarization characteristics, as the two methods have different accuracies and the DFT methods use different basis sets.

To investigate the impact of the field on the potential energy landscape, in Figure 4 we show the total energy of the dimer system as a function of the interatomic distance for three different field values, comparing the direct GAUSSIAN calculation versus Eq. 2. The energy of the Cu dimer at 1.5 Å distance without applied field is set to be the reference (0 eV). We see that the two calculation methods are in very good agreement even for the F = 15 GV/m (blue curve). Therefore, the computationally efficient and more scalable method based on VASP is found to be reliable for the calculation of the potential energy landscape. Finally, we see that the potential well, i.e., the minimum of the curves gradually disappears with the field increased up for F = 15 GV/m.

FIGURE 4

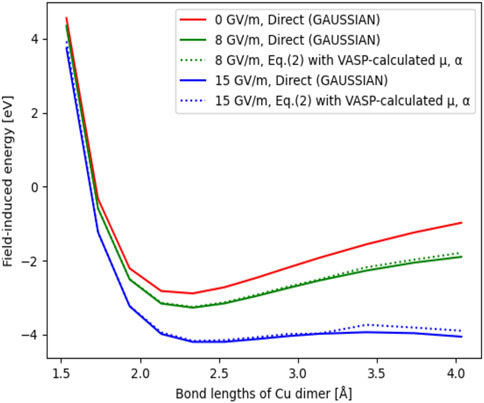
FIGURE 4. Total energy of Cu dimer as a function of the interatomic distance ranging from 1.5 Å to 4.0 Å. Solid curves are total energy curves obtained by GAUSSIAN, dash curves are total energies obtained by evaluating Eq. 2 using VASP-calculated $\mu ,\alpha$.

Discussion

Our results show that disregarding the hyperpolarizability terms is valid for electric field values at least up to 15 GV/m, which is the relevant range for vacuum breakdown and electron emission. This validates the calculation approach for surface dynamics based on Eq. 2, as introduced by Kyritsakis et. al [12]. According to our simulations, Cu nanoparticle structures change dramatically when exposed to applied fields, after significant structural modifications, their total energies are still sufficiently described very precisely by the permanent dipole moment µ and polarizability terms α. We can see that the total energy curves by neglecting hyperpolarizability terms coincide perfectly with total energy curves including these terms, especially when applied fields less than 12 GV/m. The permanent dipole moment µ and the polarizability α presented in Table 1 show good agreements with each other. Note that µ, α obtained from VASP are based on Eq. 1, i.e., calculated by fitting a straight line on the dipole-field curve obtained from VASP, while µ, α obtained from GAUSSIAN are obtained by Eq. 2, i.e., by fitting a parabola to the calculated energy-field curve. The agreement of these parameters confirm that the first two terms are sufficient to predict U and $p_z$. Our results for Cu nanoparticles have confirmed that the validity of neglecting the hyperpolarizability terms for field values close to intense FE and VBD.

A noteworthy finding is that the polarizability per atom of all nanoparticles is very similar, inlying in the range of 0.26–0.34 eÅV^-1, with the exception of the dimer system, where it is significantly larger Since the polarizability of a system represents the effective “atomic volume of repelling the field” (see analysis in Ref. [12], Appendix A), it is expected that the polarizability per atom would be quite close for all systems that form a cohesive metallic structure, since each atom introduces roughly the same field-free volume to the system. On the other hand, the dimer is expected to give higher polarizability per atom, since the number of atoms is not enough to establish a metallic behaviour and the entirety of the electronic density is displaced under field, as contrasted to “bulkier” systems, where only a part of only the surface atoms polarizes under field. Finally, we note that upon relaxation, all systems move towards higher polarizability values, as expected from Eq. 2, where increased polarizability under field contributes to the reduction of the system energy.

Conclusion

In conclusion, we investigate the behaviour of Cu nanoparticles of various atomic structures under high electric field. We compare the field-induced energy as predicted by the polarization characteristics of each structure − µ and α by disregarding hyper-polarizability terms. Our results show that hyperpolarizability terms are negligible in the investigated range below 15 GV/m, which is relevant for electron emission and vacuum breakdown phenomena. Furthermore, we show that reliable values for $\mu$ and $\alpha$ can be obtained from low-field calculations of the dipole moment of a structure, which is accessible in the more computationally efficient and up-scalable plane-wave-basis density functional theory approach. Finally, we find that the atomic structures like the investigated nanoparticles undergo significant structural modifications when exposed to such high electric fields, demonstrating the importance of the accurate incorporation of high electric fields in atomistic simulations.

Data availability statement

The raw data supporting the conclusion of this article will be made available by the authors, without undue reservation.

Author contributions

YW: Investigation, Writing–original draft, Data curation, Visualization. AK: Conceptualization, Supervision, Writing–original draft, Writing–review and editing, Methodology, Validation, Data curation, Formal Analysis, Visualization. VZ: Funding acquisition, Resources, Writing–review and editing, Project administration, Supervision, Conceptualization, Investigation.

Funding

The author(s) declare that financial support was received for the research, authorship, and/or publication of this article. The current study was supported by the European Union’s Horizon 2020 program, under Grant No. 856705 (ERA Chair ‘MATTER’) and by the Estonian Research Council’s grant RVTT3.

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

1. Veske M, Parviainen S, Zadin V, Aabloo A, Djurabekova F. Electrodynamics—molecular dynamics simulations of the stability of Cu nanotips under high electric field. J Phys D: Appl Phys (2016) 49:215301. doi:10.1088/0022-3727/49/21/215301

CrossRef Full Text | Google Scholar

2. Kyritsakis A, Veske M, Eimre K, Zadin V, Djurabekova F. Thermal runaway of metal nano-tips during intense electron emission. J Phys D: Appl Phys (2018) 51:225203. doi:10.1088/1361-6463/aac03b

CrossRef Full Text | Google Scholar

3. Parviainen S, Djurabekova F. Molecular dynamics simulations of ion irradiation of a surface under an electric field. Nucl Instr Methods Phys Res Section B: Beam Interactions Mater Atoms (2014) 339:63–6. doi:10.1016/j.nimb.2014.03.009

CrossRef Full Text | Google Scholar

4. The Vacuum Interrupter. Theory, design, and application (2023). Available at: https://www.routledge.com/The-Vacuum-Interrupter-Theory-Design-and-Application/Slade/p/book/9780367531720 (Accessed November 30, 2020).

Google Scholar

5. Mazurek B, Nowak A, Tyman A. X-ray emission accompanying cathode microdischarge. IEEE Trans Electr Insul (1993) 28:488–93. doi:10.1109/14.231530

CrossRef Full Text | Google Scholar

6. McCracken GM. A review of the experimental evidence for arcing and sputtering in tokamaks. J Nucl Mater (1980) 93–94:3–16. doi:10.1016/0022-3115(80)90299-8

PubMed Abstract | CrossRef Full Text | Google Scholar

7. Clic T. The compact linear collider (CLIC) - 2018 summary report (1970). 58.39 MB.

Google Scholar

8. Boland MJ, Felzmann U, Giansiracusa PJ, Lucas TG, Rassool RP, Balazs C, et al. Updated baseline for a staged compact linear collider. Geneva: CERN (2016).

Google Scholar

9. Tsong TT, Walko RJ. Measurements of the polarizability of tungsten adatoms on tungsten (110) planes. Physica Status Solidi (a) (1972) 12:111–7. doi:10.1002/pssa.2210120111

CrossRef Full Text | Google Scholar

10. Tsong TT. Measurement of the polarizabilities and field evaporation rates of individual tungsten atoms. J Chem Phys (1971) 54:4205–16. doi:10.1063/1.1674660

CrossRef Full Text | Google Scholar

11. Tsong TT, Kellogg G. Direct observation of the directional walk of single adatoms and the adatom polarizability. Phys Rev B (1975) 12:1343–53. doi:10.1103/physrevb.12.1343

CrossRef Full Text | Google Scholar

12. Kyritsakis A, Baibuz E, Jansson V, Djurabekova F. Atomistic behavior of metal surfaces under high electric fields. Phys Rev B (2019) 99:205418. doi:10.1103/physrevb.99.205418

CrossRef Full Text | Google Scholar

13. Baibuz E, Kyritsakis A, Jansson V, Djurabekova F. Polarization characteristics of adatoms self-diffusing on metal surfaces under high electric fields. arXiv (2022). No. arXiv:2201.03460. doi:10.48550/arXiv.2201.03460

CrossRef Full Text | Google Scholar

14. Kresse G, Furthmüller J. Efficient iterative schemes for ab initio total-energy calculations using a plane-wave basis set. Phys Rev B (1996) 54:11169–86. doi:10.1103/physrevb.54.11169

PubMed Abstract | CrossRef Full Text | Google Scholar

15. Perdew JP, Burke K, Ernzerhof M. Generalized gradient approximation made simple. Phys Rev Lett (1996) 77:3865–8. doi:10.1103/physrevlett.77.3865

PubMed Abstract | CrossRef Full Text | Google Scholar

16. Ceperley DM, Alder BJ. Ground state of the electron gas by a stochastic method. Phys Rev Lett (1980) 45:566–9. doi:10.1103/physrevlett.45.566

CrossRef Full Text | Google Scholar

17. Perdew JP, Zunger A. Self-interaction correction to density-functional approximations for many-electron systems. Phys Rev B (1981) 23:5048–79. doi:10.1103/physrevb.23.5048

CrossRef Full Text | Google Scholar

18. Blöchl PE. Projector augmented-wave method. Phys Rev B (1994) 50:17953–79. doi:10.1103/physrevb.50.17953

CrossRef Full Text | Google Scholar

19. Methfessel M, Paxton AT. High-precision sampling for brillouin-zone integration in metals. Phys Rev B (1989) 40:3616–21. doi:10.1103/physrevb.40.3616

PubMed Abstract | CrossRef Full Text | Google Scholar

20. Schäfer A, Horn H, Ahlrichs R. Fully optimized contracted Gaussian basis sets for atoms Li to Kr. J Chem Phys (1992) 97:2571–7. doi:10.1063/1.463096

CrossRef Full Text | Google Scholar

21. Schäfer A, Huber C, Ahlrichs R. Fully optimized contracted Gaussian basis sets of triple zeta valence quality for atoms Li to Kr. J Chem Phys (1994) 100:5829–35. doi:10.1063/1.467146

CrossRef Full Text | Google Scholar

22. Neugebauer J, Scheffler M. Adsorbate-substrate and adsorbate-adsorbate interactions of Na and K adlayers on Al(111). Phys Rev B (1992) 46:16067–80. doi:10.1103/physrevb.46.16067

PubMed Abstract | CrossRef Full Text | Google Scholar