Evolutionary modeling and analysis of opinion exchange and epidemic spread among individuals

The opinions of individuals within a group about an ongoing epidemic play a crucial role in the dynamics of epidemic spread. People’s acceptance of others' opinions also changes with the changing epidemic situation and the dynamics of communication between individuals, how individuals' opinions and acceptance of others' views on epidemics affect the spread of epidemics has become an unresolved issue. In this study, we construct a two-layer coupled network that integrates the Hegselmann-Krause (HK) continuous opinion model with an epidemic model. This framework takes into account the evolutionary game of opinion acceptance among individuals within the group. We investigate the dynamic interaction between opinion exchange among individuals and the spread of the epidemic and derive the epidemic spread threshold of the model using the Quasi-Mean-Field (QMF) approach. The results indicate that under different infection rates, individuals in the group spontaneously form varying levels of opinion about the epidemic, which in turn evolve into different final infection states for the group. The higher the infection rate, the faster a positive and unified opinion forms. Promoting communication among individuals within the group can, to some extent, inhibit the spread of the epidemic. However, due to the diversity and complexity of information in the real world, the phenomenon of “delayed epidemic prevention” often occurs.

1 Introduction

Infectious diseases not only pose a serious threat to individual health but also have significant impacts on public health security at the community level and globally [1, 2]. Consequently, many scholars have conducted research and analysis on the spread of infectious diseases. During the 2003 outbreak of SARS, people adopted simple self-protection measures after obtaining information about SARS, such as reducing travel, avoiding crowded places, frequent handwashing, staying at home, and wearing masks. Along with mandatory measures from the government or health departments, these actions effectively controlled the spread of the disease [3–6]. Devi et al. [7] developed a SEI Q 1 Q 2 R model with fuzzy parameters for COVID-19 and computed the basic reproduction number using the next-generation matrix method and used it for further study of model prediction. Moran Duan et al. [8] focused on age heterogeneity in epidemiologic models and considered the effect of pharmacologic interventions on disease transmission. Yang et al. [9] proposed a heterogeneous disease-behavior-information spreading model to study how infection risk is affected by information diffusion, behavioral changes, and disease spread. Sarafa et al. [10] introduced time-varying exposure rates in epidemic modeling, taking into account that exposure rates and social contact patterns vary by age and time.

The role of information dissemination can contribute to knowledge dissemination, social communication, decision support, etc., as well as assisting governments in the performance of their functions [11–13]. People usually acquire relevant information about social events, share interests, discuss trending topics, and express their opinions [14]. An opinion is a view, attitude, or evaluation of a thing, event, or issue by an individual or group of individuals, which is subjective and not necessarily based on factual or scientific evidence, and which can be construed as a discrete choice [15]. At the same time, individuals in society are often influenced by the opinions and information of others. Through frequent interactions, they promote the spread of opinions within social networks, a process that exhibits typical characteristics of complex systems such as complexity, uncertainty, and openness [16]. People’s viewpoints and opinions have a profound impact on various aspects of society, from personal life to national security, from business operations to public policy, the dissemination of online information and discussion is shaping modern society [17]. Meanwhile, the complexity, diversity, and sudden negative impacts of public opinion are often overlooked. For instance, rumors about COVID-19 confused people worldwide, rumors about the scientific and political sphere affecting society. Many important results have been achieved in the study of opinion dissemination among individuals in social networks [18, 19]. Street et al. [20] proposed a novel Multipath Asynchronous Threshold (MAT) model, modeling influence decay on diffusion paths, time decay, and individual diffusion dynamics, to study influence diffusion modeling and maximization problems in the context of viral marketing. Zhao et al. [21] constructed a comprehensive bounded confidence model to simulate the evolution of followers? Opinions under two advertising opinion leaders. They found that the weight of advertising influence has a dual effect on the evolution of followers? Opinions, and the information transmission probability of opinion leaders significantly impacts collective opinion evolution. Li et al. [22] developed two opinion dynamics models to study the evolution of public opinion among decision-makers and other related individuals on social media. They then proposed a consensus-reaching process based on public opinion management to handle the public opinion formed by all related groups. Liu et al. [23] proposed a new Negative Feedback SIR (NFSIR) model for social network information dissemination by analyzing the characteristics of social networks and the social attributes of propagators and combining it with traditional epidemiological models. They constructed an information transmission tree according to the evolution mechanism of information interaction and established differential equations for transmission dynamics, revealing the complex interactions and mutual influences between user relationships, social communities, and information in cyberspace. Wang et al. [24] proposed an algorithm for constructing a two-layer social network, considering the weights of strong and weak tie networks and individuals' subjective emotional tendencies. They introduced the E-HK, WHK, and E-WHK models to study the impact of emotional tendencies on opinion dissemination and evolution. Su et al. [25] studied a continuous-time model of opinion separation on signed networks by combining Degroot’s positive and negative weighting rules to describe the influence of neighbors and Jadbabaies leader-follower reflection mechanism to describe followers' trust/distrust relationships with leaders.

Complex Network Theory Provides a Framework and Tools for Modeling and Analyzing the Spread of Infectious Diseases and Information [9, 26, 27]. Researchers have conducted extensive studies on the spread of infectious diseases [10, 28, 29] and information [30–32] within complex network frameworks. Sun et al. [33] investigated the effect of resource diffusion on disease transmission in two-layer higher-order networks. Their results showed that expanding resource dispersion on 2-simplexes can inhibit the spread and outbreak of infectious diseases. Li et al. [34] modeled the spread of a multi-informative infectious disease on a two-layer network by considering both local and global information as well as individual differences. Huang et al. [35] investigated whether people believe more in social influences or risk perceptions when faced with asymptomatic infections, and developed a model of infectious disease in a multilayer network topology. Xia et al. [36] proposed a SIQRS model with quarantine, investigated its evolution on a simple complex, and derived transmission thresholds and steady-state infection proportions as well as their stability conditions using the QMF method. Wang et al. [37] constructed a two-layer metapopulation network model and explored the group-perceived information transmission on the spatial spread of epidemics. Huo et al. [38] proposed a three-layer coupled network model in order to investigate the influence of government policies on the co-evolution of information transmission, vaccination behavior and disease transmission, in which the information, behavior and infectious disease layers considered the influence of government policies.

Previous studies often dichotomize individuals' awareness or concepts of disease, yet real-world information and people’s opinion states tend to be continuous values, the acceptance of others' opinions has not been taken into consideration. Therefore, this paper constructs a two-layer coupled network that integrates a continuous opinion model with an epidemic model, incorporating individuals' varying receptiveness to others' opinions, investigating the co-evolution of dynamic opinion exchange among individuals regarding epidemics and the spread of infectious diseases within the group. The main contributions of this paper are as follows: (1) Combining the HK continuous opinion model with an epidemic model, we constructed a two-layer coupled network. The upper layer represents the HK opinion model, and the lower layer represents the epidemic spread model. By introducing the epidemic spread situation into the opinion update function of the HK model, we studied the dynamic interaction between individual opinion changes and epidemic spread. (2) Considering the openness of individuals within the group to others' opinions, we introduced the evolutionary game of opinion acceptance attitudes. (3) Using the QMF approach, we derived the dynamic epidemic spread threshold of the model. The structure of the paper is as follows: Chapter two introduces the model, Chapter 3 analyzes the epidemic spread threshold using QMF, Chapter 4 presents the simulation results, and Chapter 5 provides the conclusion.

2 Model introduction

Exchange of views on epidemics plays a crucial role in determining how an epidemic spreads within a community. When people discuss their perspectives on the severity of an epidemic, the effectiveness of preventive measures, and their experiences, these conversations can both promote widespread adherence to public health guidelines and foster skepticism and misinformation. Constructive dialogue that spreads accurate information can raise awareness and encourage collective action, thereby slowing the spread of the disease. Conversely, if exchanges are filled with misinformation or fear, they can lead to resistance against recommended behaviors, such as vaccination, or encourage social distancing, thereby accelerating the spread of the epidemic. Whether through social media, community discussions, or interpersonal conversations, the nature and content of these exchanges can significantly influence public perceptions and behaviors, ultimately affecting the trajectory of the epidemic.

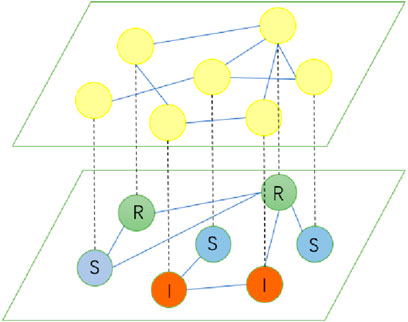
This paper considers the dynamic interaction between changes in individual opinions within a group and the spread of an epidemic, establishing a two-layer coupled infectious disease model (as shown in Figure 1), we represent people’s opinions as a series of continuous values and use game theory to represent changes in people’s receptive attitudes toward opinions. The first layer is the individual opinion propagation layer, and the second layer is the SIRS disease transmission layer. The individual opinion propagation layer is modeled using the HK propagation model, assuming that the opinion values of individuals can be positive or negative. The sign of the opinion value represents the pro or con opinions about the epidemic (such as the degree of epidemic control), correct or incorrect epidemic response knowledge, true information, or rumors. Assume there are $N$ individuals in the network, with individuals $i$ and $j$ having opinions $X_i\left(t\right)$ and $X_j\left(t\right)$ at time $t$, respectively, and $j\in N_i$ represents the set of neighbors of node $i$. If individual $j$ is within the communication radius $ϵ$ of individual $i$, it means that communication can occur between individuals, exchanging their respective opinion values about the epidemic, that is:

$\left|X_i\left(t\right)-X_j\left(t\right)\right|<ϵ$

Figure 1

Figure 1. Epidemiological modeling in conjunction with the HK model.

Due to the fact that different individuals may experience different changes in opinion after communicating with others, this paper considers individual heterogeneity by classifying individuals $i$ into those who are open to opinion exchange (open), meaning they are easily influenced by others' opinions, and those who are persistent (persist), meaning they retain their own opinions regardless of whether others' opinions are correct or incorrect. Thus, their opinion value will remain the same as the previous time step. When individual $i$ exchanges opinions with their neighbors, they can communicate with neighbors who meet the trust radius. Let $z\left(t\right)$ denote the current epidemic prevalence rate, then the opinion update function for individual $i$ is as follows:

$z\left(t\right)=I\left(t\right)/\left(I\left(t\right)+S\left(t\right)+R\left(t\right)\right)$

$\left\{\begin{array}{l}{X}_i\left(t+1\right)=\frac{{\displaystyle \sum _{j\in Ni}}{X}_j\left(t\right)}{n_j}+z\left(t\right)\left(\mathit{max}\left\{X_j\left(t\right)\right\}-X_i\left(t\right)\right),open\\ X_i\left(t+1\right)=X_i\left(t\right),persist\end{array}\right.$

where $n_j$ is the number of neighbors.

Individuals within a communication radius of $ϵ$ communicate with each other, and their attitudes affect whether their opinion values are updated and the benefits obtained from communication. Individuals' obtained benefits affect attitudes toward subsequent opinion exchanges, and this changes in attitudes toward acceptance of others' opinions is described through game theory. Suppose the payoff for individual i after exchanging with j is the change in their opinion value, defined as $O_i\left(t\right)=X_j\left(t\right)-X_i\left(t\right)$. Thus, $O_i\left(t\right)$ can be positive or negative. Additionally, the cost of communication C (such as time cost, economic cost, or emotional cost) must be considered. Assuming that people with open attitudes can be influenced by positive or negative opinions, the payoff matrix $M$ for individual i and the payoff function ${\pi }_i\left(t\right)$ are defined as follows:

${\pi }_i\left(t\right)={\displaystyle \sum _{j\in Ni}}{S}_{i}M{S_j}^T$

where $s_i$ and $s_j$ represent the strategies of nodes $i$ and $j$, respectively, with $s_i,s_j\in \left\{O,P\right\},O=\left(1,0\right),P=\left(0,1\right)$. $j\in N_i$ represents the set of neighbors of node $i$.

Assume that individual $i$ randomly selects one of its neighbors to imitate their “open” or “persist” attitude toward opinion acceptance. Let $K_i$ denote the ease or difficulty with which an individual changes their strategy. Considering individual heterogeneity, assume that $K_i\in U\left[0.1,0.9\right]$. The probability of strategy transition for individual $i$ is then given by:

$P_i\left(s_i\to s_j\right)=1/\left(1+e^{-\frac{{\pi }_j\left(t\right)-{\pi }_i\left(t\right)}{K_i}}\right)$

The second layer is the physical transmission layer of the infectious disease, where individuals may be in one of three states: Susceptible (S-state), Infectious (I-state), or Recovered (R-state). S-state represents individuals susceptible to the epidemic, I-state represents individuals who are infected and show clinical symptoms, and R-state represents individuals who have recovered from the disease. Assume that R-state individuals still have a risk of infection and can revert to the S-state. An individual’s opinion value regarding the epidemic affects their transition probabilities across all states of the epidemic. Assume that S-state individuals in the group become infected at a rate ${\beta }_i\left(t\right)$ to become I-state individuals. If an individual holds a negative opinion, their infection probability increases, while it decreases with a positive opinion. I-state individuals recover to the R-state at a recovery rate ${\mu }_i\left(t\right)$. If an individual holds a negative opinion, their recovery probability decreases, while it increases with a positive opinion. R-state individuals revert to the S-state at an immunity loss probability ${\sigma }_i\left(t\right)$. If an individual holds a negative opinion, this probability increases, while it decreases with a positive opinion.

$\left\{\begin{array}{l}{\beta }_i\left(t\right)=\left(1-0.125{\left(X_i\left(t\right)\right)}^3-0.075X_i\left(t\right)\right)\beta ,S\to I\\ {\mu }_i\left(t\right)=\left(1+0.05{\left(X_i\left(t\right)\right)}^3+0.05X_i\left(t\right)\right)\mu ,I\to R\\ {\sigma }_i\left(t\right)=\left(1-0.05{\left(X_i\left(t\right)\right)}^3-0.05X_i\left(t\right)\right)\sigma ,R\to S\end{array}\right.$

3 Model analysis

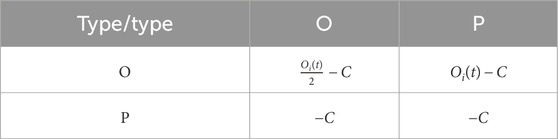
This section uses the QMF approach to analyze the epidemic spread threshold under dynamic interaction of individual opinions. Let $A_{ij}$ be the adjacency matrix of the epidemic layer in the second layer. The probabilities that node $i$ is in the Susceptible state $S_i\left(t\right)$, Infectious state $I_i\left(t\right)$, and Recovered state $,R_i\left(t\right)$ at time t can be expressed by the dynamic Equations 1–3:

$\frac{d{S}_i\left(t\right)}{dt}=-S_i\left(t\right){\displaystyle \prod _{j=1}^N}{A}_{ij}{I}_j\left(t\right){\beta }_j\left(t\right)+R_i\left(t\right){\sigma }_i\left(t\right)(1)$

$\frac{d{I}_i\left(t\right)}{dt}=S_i\left(t\right){\displaystyle \prod _{j=1}^N}{A}_{ij}{I}_j\left(t\right){\beta }_j\left(t\right)-I_i\left(t\right){\mu }_i\left(t\right)(2)$

$\frac{d{R}_i\left(t\right)}{dt}=I_i\left(t\right){\mu }_i\left(t\right)-R_i\left(t\right){\sigma }_i\left(t\right)(3)$

If $\beta$ ≤ ${\beta }^c$, when the epidemic spread reaches its steady state, only a finite number of individuals in the system will be infected, and the number of infected individuals will not increase as the network size increases. This implies that for any time $t$, the infection density $I_i\left(t\right)$ $\to 0$ holds. When the epidemic threshold is reached, for all $i$ and $t$, $I_i\left(t\right)=ϵ\ll 1$. Ignoring higher-order terms in (2), i.e., $I_i{\left(t\right)}^2=o\left(I_i\left(t\right)\right)=0,I_i\left(t\right)I_j\left(t\right)=o\left(I_i\left(t\right)\right)=0$, the probability of node $i$ being in the Susceptible state is $S_i\left(t\right)=1-I_i\left(t\right)\approx 1$. Equation 2 then becomes:

$\frac{d{I}_i\left(t\right)}{dt}={\displaystyle \sum _{j=1}^N}{A}_{ij}{I}_j\left(t\right){\beta }_j\left(t\right)-I_i\left(t\right){\mu }_i\left(t\right)$

$={\displaystyle \sum _{j=1}^N}\left(A_{ij}{\beta }_j\left(t\right)-{\mu }_i\left(t\right){\delta }_{ij}\right)I_j\left(t\right)(4)$

where ${\delta }_{ij}$ is the element of the identity matrix.

The average infection rate at time $t$ can be calculated as $\beta \left(t\right)=\frac{{\sum }_{j=1}^N{\beta }_j\left(t\right)}{N}$, and the average recovery rate as $\mu \left(t\right)=\frac{{\sum }_{j=1}^N{\mu }_i\left(t\right)}{N}$. Equation 4 is represented as Equation 5:

$\frac{d{I}_i\left(t\right)}{dt}=\beta \left(t\right){\displaystyle \sum _{j=1}^N}\left(A_{ij}-\frac{\mu \left(t\right)}{\beta \left(t\right)}{\delta }_{ij}\right)I_j\left(t\right)(5)$

Let $\mathrm{A}=A_{ij}$ represent the elements of the matrix $\mathrm{A}$. The solution to the above equations is transformed into solving for the eigenvalues of matrix $\mathrm{A}$. When the largest eigenvalue of matrix A is greater than 0, the infection density will grow exponentially over time, leading to a global epidemic spread in the system. Let ${\Delta }_{\max }\left(\mathrm{A}\right)$ denote the largest eigenvalue of matrix A. The epidemic spread threshold of the system at time t is given by Equation 6:

${\beta }^c\left(t\right)=\frac{\mu \left(t\right)}{{\Delta }_{\max }\left(\mathrm{A}\right)}(6)$

substituting the expression for ${\mu }_i\left(t\right)$ yields Equation 7:

${\beta }^c\left(t\right)=\frac{\mu {\displaystyle \sum _{\mathrm{i}=1}^N}\left(1+0.05{\left(X_i\left(t\right)\right)}^3+0.05X_i\left(t\right)\right),}{N{\Delta }_{\max }\left(\mathrm{A}\right)}(7)$

4 Numerical simulation

This paper uses Monte Carlo simulations to analyze the spread of epidemics under dynamic interaction of individual opinions through the synchronized update mechanism on a BA-BA network, and the results are the average of 100 independent realizations. The initial setup consists of a total of 2000 nodes, with 1,000 nodes in each layer, and an average degree of $k=8$. Nodes in the lower layer are connected to their corresponding nodes in the upper layer. The initial proportions of Susceptible (S) and Infectious (E) individuals are 98% and 2%, respectively. Each node chooses to adopt an “Open” or “persist” attitude towards communication with neighbors with a probability of 50%. In order to investigate the effect of opinion values evolving over time on epidemics, this paper does not limit the size of opinion values, which represents the emergence of new scientific studies or new rumors about epidemics as time advances, and this co-evolutionary phenomenon is investigated in this paper. The initial parameter settings for the model are as follows: $X_i\left(\mathrm{t}=0\right)\sim U\left[-1,1\right],\mathrm{\epsilon }=0.5,\beta =0.5,\mathrm{\sigma }=0.5,\mathrm{\mu }=0.4,C=0.05$.

Figure 2A shows the evolution of the proportions of different states in the epidemic layer over time, while Figure 2B illustrates the evolution of the opinion layer over time, where each curve represents the change in an individual’s opinion value over time. From Figure 2A, it can be observed that when the epidemic transmission rate is low, the overall level of positive opinion values regarding the epidemic within the group is not high and is quite dispersed. This corresponds to a relatively low level of awareness and knowledge about epidemic prevention among individuals in reality. Figure 2B shows that although most individuals remain in the susceptible state under stable conditions, there is always a certain proportion of individuals who are in the infectious state. This suggests that people’s differing opinions about epidemics cause them to spread.

Figure 2

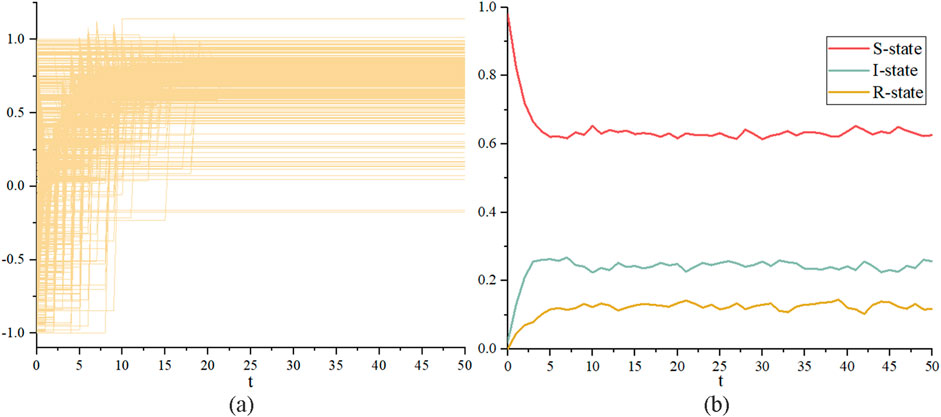
Figure 2. Evolution of system state over time for $\beta =0.2$. (A) Individual's opinion values. (B) The proportions of S, I, R states.

When $\beta =0.5$, as shown in Figure 3A, after some time of opinion exchange among individuals, all individuals develop a more unified opinion regarding the epidemic, and the opinion values are relatively high. Figure 3B Shows that the proportion of the S-state in the epidemic layer has significantly increased, reaching 90%, while the proportion of infected individuals is relatively low.

Figure 3

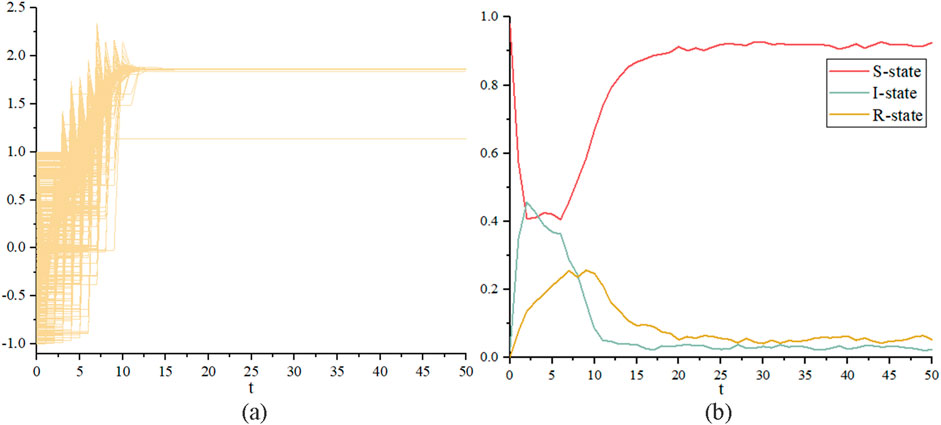
Figure 3. Evolution of system state over time for $\beta =0.5$. (A) Individual's opinion values. (B) The proportions of S, I, R states.

When $\beta =0.8$, that is, under high infection rates of the disease, Figure 4A shows that the group’s opinion values are extremely unified and have reached the highest value observed in the experiment. Additionally, the group’s opinion values stabilize more quickly and at a higher level compared to Figure 3A. Figure 4B indicates that the proportion of the S-state in the epidemic layer has reached 100% in the stable state, with no infected individuals present. Combining Figures 2–4, it can be seen that only under high infection rates can individuals within the group form a unified and positive opinion about the epidemic. Otherwise, individuals will have divergent opinions on the epidemic, and the epidemic situation will continue to spread. This suggests that external interventions are needed to control the spread of epidemics.

Figure 4

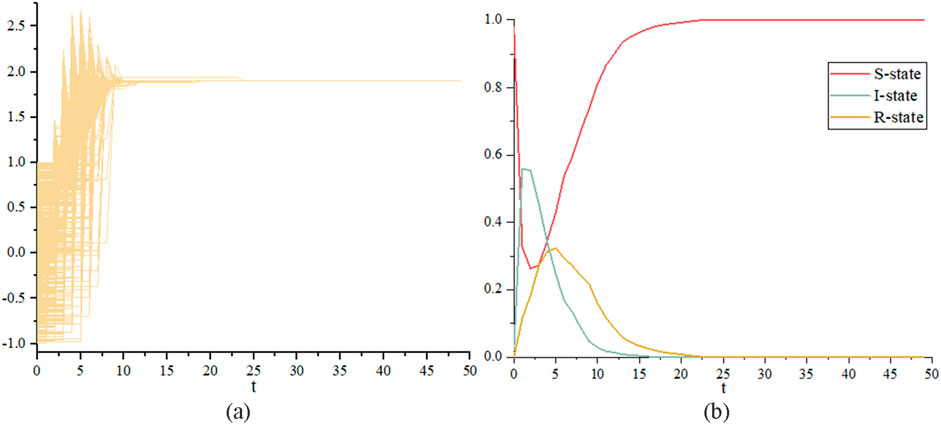
Figure 4. Evolution of system state over time for $\beta =0.8$. (A) Individual's opinion values. (B) The proportions of S, I, R states.

When $\mathrm{\epsilon }=0.1$, that is, when the communication radius is relatively small, Figure 5A shows that it is difficult for the group’s opinion values to unify, and they remain at a relatively low level. Figure 5B Indicates that the proportion of individuals in the S-state is almost equivalent to that in the I-state, with the proportion of infected individuals remaining at 40% in the stable state.

Figure 5

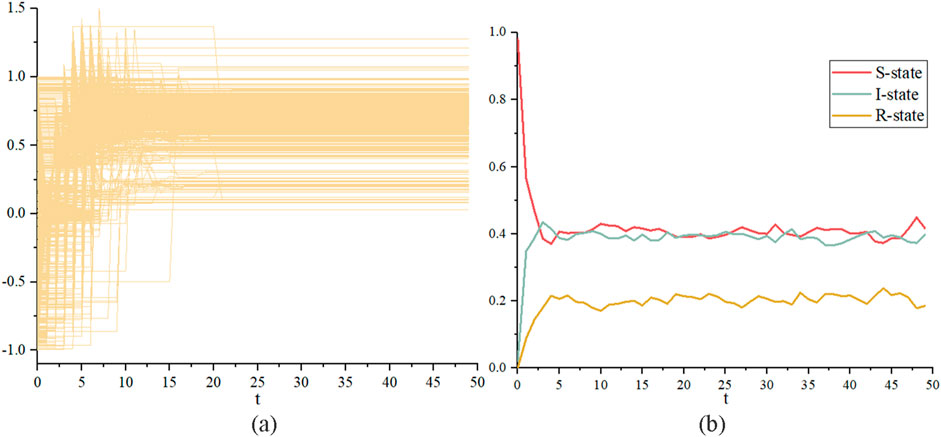
Figure 5. Evolution of system state over time for $\mathrm{\epsilon }=0.1$. (A) Individual's opinion values. (B) The proportions of S, I, R states.

When $\mathrm{\epsilon }=0.2$, Figure 6A shows that as the communication radius increases, the overall opinion value of the group rises and gradually converges towards a uniform opinion. Over time, all individuals' opinion values increase to a higher and more unified level. Figure 6B indicates that the proportion of individuals in the S-state also gradually increases, while the proportion of infected individuals decreases over time. The number of S-state individuals is higher compared to Figure 5A. However, even though a more unified and higher opinion value is formed, the epidemic has already spread. The speed at which the group forms a positive opinion about the epidemic cannot keep up with the spread of the epidemic, resulting in a situation where it is too late for the entire group to address the epidemic, leading to widespread and uncontrollable spread within the group.

Figure 6

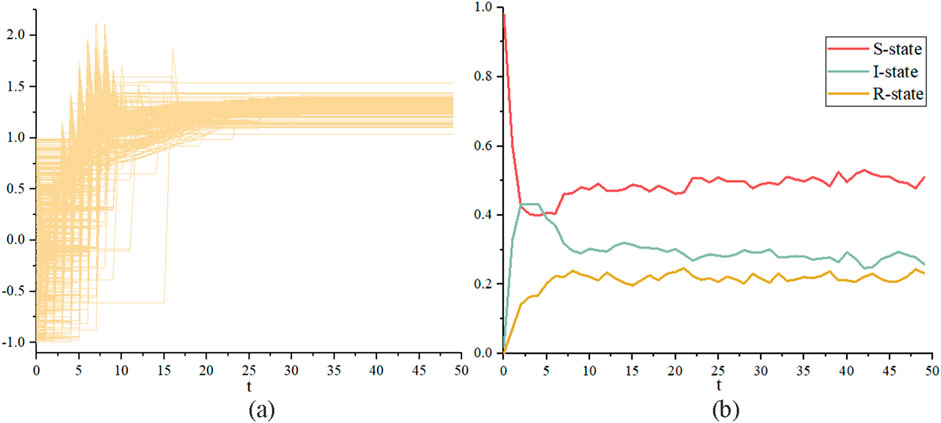
Figure 6. Evolution of system state over time for $\mathrm{\epsilon }=0.2$. (A) Individual's opinion values. (B) The proportions of S, I, R states.

When $\mathrm{\epsilon }=0.3$, Figure 7A shows that the opinion values are more unified and higher compared to Figure 6A. Figure 7B indicates that the proportion of individuals in the S-state is also higher compared to Figure 6A, while the proportion of individuals in the I-state is lower. Similar to Figure 6, individual opinion values gradually increase to a higher level over time, and the proportion of S-state individuals also gradually rises. However, by this time, the epidemic has already spread. Even though a positive and unified opinion about the epidemic is eventually formed, it cannot control the spread of the epidemic. Combining Figures 5–7, it can be seen that facilitating communication among individuals within the group can somewhat suppress the spread of the epidemic. However, changes in the group’s opinion often lag behind the spread of the epidemic, resulting in a phenomenon of ‘epidemic response lag.'

Figure 7

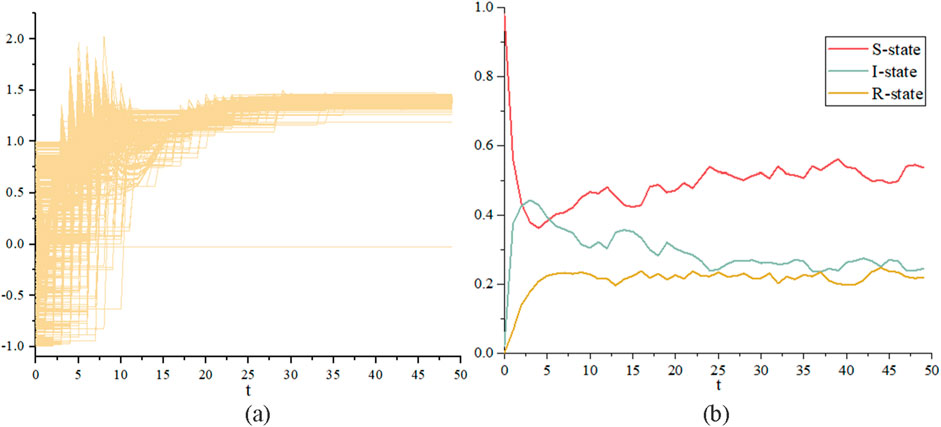
Figure 7. Evolution of system state over time for $\mathrm{\epsilon }=0.3$. (A) Individual's opinion values. (B) The proportions of S, I, R states.

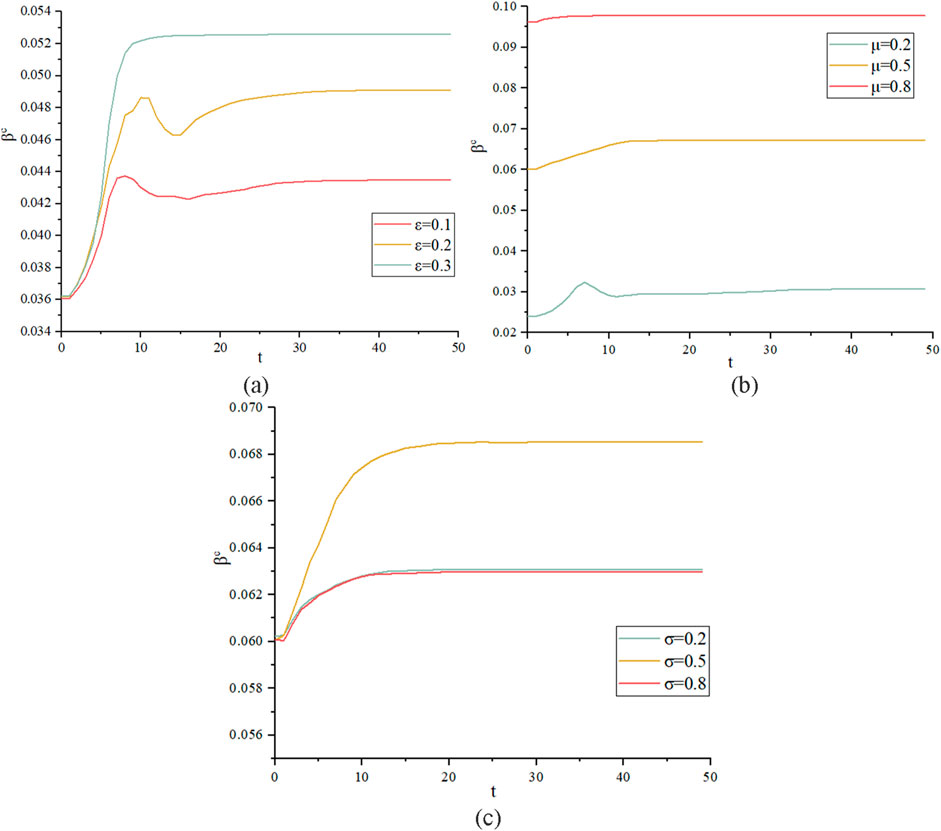
As shown in Figure 8A, when the communication radius $\mathrm{\epsilon }$ is increased, the epidemic threshold significantly rises. Additionally, as the dynamics of the two-layer coupled network evolve, the threshold also changes continually, stabilizing as the dynamic network reaches equilibrium. Figure 8B indicates that as $\mathrm{\mu }$ increases, the dynamic epidemic outbreak threshold also increases significantly. Figure 8C shows that the epidemic outbreak thresholds for $\mathrm{\sigma }=0.2$ and $\mathrm{\sigma }=0.8$ exhibit similar developmental trends. This similarity may be due to the fact that the development trends of group opinion values are similar under these two parameter settings.

Figure 8

Figure 8. Dynamic epidemic outbreak thresholds for different $\mathrm{\epsilon },\mathrm{\mu },\mathrm{\sigma }$. (A) $\mathrm{\epsilon }=0.1,0.2,0.3$. (B) $\mathrm{\mu }=0.2,0.5,0.8$. (C) $\mathrm{\sigma }=0.2,0.5,0.8$.

5 Conclusion

The perspectives of individuals within a population play a crucial role in the dynamics of epidemic spread. People’s views on an epidemic can influence their behaviors, such as adherence to public health guidelines, acceptance of vaccinations, and compliance with social distancing measures. Understanding the evolution of individuals' opinions on an epidemic is vital for controlling its spread and ensuring the success of public health interventions. Therefore, this paper establishes a two-layer coupling of the HK continuous opinion model and the epidemic model, using QMF to derive the epidemic dynamic spreading threshold, examining the dynamic interactions between individual opinion exchanges and epidemic spread within a population. The results show that under different infection rates, individuals within the population spontaneously form varying degrees of opinion on the epidemic, which then evolve into different final infection states for the group. Higher infection rates lead to faster formation of a positive and unified opinion value. The communication radius of individuals within the population significantly affects the development trend and threshold of the epidemic; a smaller communication radius makes it difficult to form a high-level and unified opinion. Promoting communication among individuals within the population can partially suppress epidemic spread, but due to the presence of diverse positive and negative information in the real world, changes in group opinion often lag behind the speed of epidemic spread, leading to a phenomenon of ‘epidemic control lag.' The communication radius between individuals, recovery rate, and immune loss probability all affect the epidemic spreading threshold in different ways. To control the spread of an epidemic, it is not only necessary to promote communication within the group, but also to increase external intervention in controlling the disease when the transmission rate is high. The limitation of this paper is that it does not capture more complex real-world phenomena such as polarization, media influence, or echo chambers. In the future, factors such as individual knowledge levels, learning, mobility, and time-varying network topology can be integrated and taken into account in epidemic transmission.

Data availability statement

The original contributions presented in the study are included in the article/supplementary material, further inquiries can be directed to the corresponding author.

Author contributions

RZ: Formal Analysis, Investigation, Methodology, Validation, Writing–original draft. XC: Conceptualization, Methodology, Validation, Writing–review and editing. BL: Investigation, Validation, Writing–review and editing.

Funding

The author(s) declare that financial support was received for the research, authorship, and/or publication of this article. The author(s) declare financial support was received for the research, authorship, and/or publication of this article. This paper Supported by China Postdoctoral Science Foundation (No. 2021M692400), Fundamental Research Program of Shanxi Province (No. 202203021221017, No. 202303021212360), Science and technology innovation project of colleges and universities in Shanxi Province (No.2023L379), Shanxi Province Higher Education Science and Technology Innovation Platform Project (No.2022P016). The funder was not involved in the study design, collection, analysis, interpretation of data, the writing of this article, or the decision to submit it for publication.

Conflict of interest

All authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Generative AI statement

The author(s) declare that no Generative AI was used in the creation of this manuscript.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

1. Morens DM, Gregory K, Anthony S. The challenge of emerging and re-emerging infectious diseases. Nature (2004) 430(6996):242–9. doi:10.1038/nature02759

PubMed Abstract | CrossRef Full Text | Google Scholar

2. Moghadas SM. Modelling the effect of imperfect vaccines on disease epidemiology. Discrete Continuous Dynamical Syst Ser B (2004) 4:999–1012. doi:10.3934/dcdsb.2004.4.999

CrossRef Full Text | Google Scholar

3. Lau J, Yang X, Tsui H, Kim JH. Monitoring community responses to the SARS epidemic in Hong Kong: from day 10 to day 62. J Epidemiol and Community Health (2003) 57(11):864–70. doi:10.1136/jech.57.11.864

CrossRef Full Text | Google Scholar

4. Tan XD, Li S, Wang C, Chen X, Wu X. Severe acute respiratory syndrome epidemic and change of people's health behavior in China. Health Educ Res (2004) 19(5):576–80. doi:10.1093/her/cyg074

PubMed Abstract | CrossRef Full Text | Google Scholar

5. Zhang HF, Wang C, Wu ZX, Wang BH, Zhou T. Braess's paradox in epidemic game: better condition results in less payoff. Scientific Rep (2013) 3(1):3292. doi:10.1038/srep03292

CrossRef Full Text | Google Scholar

6. Perra N, Balcan D, Gonçalves B, Vespignani A. Towards a characterization of behavior-disease models. PloS one (2011) 6(8):e23084. doi:10.1371/journal.pone.0023084

PubMed Abstract | CrossRef Full Text | Google Scholar

7. Sweatha S, Sindu D. Prediction and decision making in corona virus using fuzzy mathematical model. J Intell and Fuzzy Syst Preprint (2024) 1–14. doi:10.3233/JIFS-231945

CrossRef Full Text | Google Scholar

8. Duan M, Jin Z. The heterogeneous mixing model of COVID-19 with interventions. J Theor Biol (2022) 553:111258. doi:10.1016/j.jtbi.2022.111258

PubMed Abstract | CrossRef Full Text | Google Scholar

9. Yang Y, Zhang Q, Ruan Z, Cao Z, Xuan Q, Zeng DD. Effect of heterogeneous risk perception on information diffusion, behavior change, and disease transmission. Phys Rev E (2020) 102(4):042314. doi:10.1103/PhysRevE.102.042314

PubMed Abstract | CrossRef Full Text | Google Scholar

10. Iyaniwura SA, Falcão RC, Ringa N, Adu PA, Spencer M, Taylor M, et al. Mathematical modeling of COVID-19 in British Columbia: an age-structured model with time-dependent contact rates. Epidemics (2022) 39:100559. doi:10.1016/j.epidem.2022.100559

PubMed Abstract | CrossRef Full Text | Google Scholar

11. Yin XC, Wang H, Yin P, Zhu H. Agent-based opinion formation modeling in social network: a perspective of social psychology. Physica A: Stat Mech its Appl (2019) 532:121786. doi:10.1016/j.physa.2019.121786

CrossRef Full Text | Google Scholar

12. Alshahrani G, Mohammed S, Sameh A, Mekouar S, Huang S. Efficient algorithms based on centrality measures for identification of top-k influential users in social networks. Inf Sci (2020) 527:88–107. doi:10.1016/j.ins.2020.03.060

CrossRef Full Text | Google Scholar

13. Wang JK, Wang XH, Li F. Evolutionary game model of public opinion information propagation in online social networks. IEEE access (2020) 8:127732–47. doi:10.1109/access.2020.3006150

CrossRef Full Text | Google Scholar

14. Statista. Number of social networks users worldwide from 2010 to 2021 (2021). Available from: https://www.statista.com/statistics/278414/number-ofworldwide-social-network-users/ (Accessed June 06, 2024).

Google Scholar

15. Martins J, André CR. Continuous opinions and discrete actions in opinion dynamics problems. Int J Mod Phys C (2008) 19(04):617–24. doi:10.1142/s0129183108012339

CrossRef Full Text | Google Scholar

16. Zhu J, Jie F, Tang W, Zhang H. Dynamic parameter calibration framework for opinion dynamics models. Entropy (2022) 24(8):1112. doi:10.3390/e24081112

PubMed Abstract | CrossRef Full Text | Google Scholar

17. Li Y, Wang JK. Cross-network propagation model of public opinion information and its control in coupled double-layer online social networks. Aslib J Inf Management (2022) 74(2):354–76. doi:10.1108/ajim-04-2021-0126

CrossRef Full Text | Google Scholar

18. Wang JK, Wang XH, Li Y. A discrete electronic word-of-mouth propagation model and its application in online social networks. Physica A: Stat Mech Its Appl (2019) 527:121172. doi:10.1016/j.physa.2019.121172

CrossRef Full Text | Google Scholar

19. Pan LL, Shao HB, Li DW. Peer selection in opinion dynamics on signed social networks with stubborn individuals. Neurocomputing (2022) 477:104–13. doi:10.1016/j.neucom.2021.12.105

CrossRef Full Text | Google Scholar

20. Wang WJ, Nick S. Modeling and maximizing influence diffusion in social networks for viral marketing. Appl Netw Sci (2018) 3:1–26. doi:10.1007/s41109-018-0062-7

PubMed Abstract | CrossRef Full Text | Google Scholar

21. Chen J, Kou G, Wang H, Zhao Y. Influence identification of opinion leaders in social networks: an agent-based simulation on competing advertisements. Inf Fusion (2021) 76:227–42. doi:10.1016/j.inffus.2021.06.004

CrossRef Full Text | Google Scholar

22. Yang C, Guo R, Ding RX, Xu J, Li MN. Managing public opinion in consensus-reaching processes for large-scale group decision-making problems. J Oper Res Soc (2021) 73(11):2480–99. doi:10.1080/01605682.2021.1993760

CrossRef Full Text | Google Scholar

23. Liu XY, He D, Yang L, Liu C. A novel negative feedback information dissemination model based on online social network. Physica A: Stat Mech its Appl (2019) 513:371–89. doi:10.1016/j.physa.2018.09.032

CrossRef Full Text | Google Scholar

24. Han S, Tu LL, Wang XJ. The influence of emotional tendency on the dissemination and evolution of opinions in two-layer social networks. Physica A: Stat Mech its Appl (2024) 641:129729. doi:10.1016/j.physa.2024.129729

CrossRef Full Text | Google Scholar

25. Liang HL, Yuan F, Zhou Z, Su H. Opinion separation in leader–follower coopetitive social networks. Neurocomputing (2021) 434:90–7. doi:10.1016/j.neucom.2020.12.079

CrossRef Full Text | Google Scholar

26. Pastor S, Romualdo PS, Claudio C, Piet VM, Alessandro V. Epidemic processes in complex networks. Rev Mod Phys (2015) 87(3):925–79. doi:10.1103/revmodphys.87.925

CrossRef Full Text | Google Scholar

27. Moreno DM, Romualdo PS, Alessandro V. Epidemic outbreaks in complex heterogeneous networks. Eur Phys J B-Condensed Matter Complex Syst (2002) 26:521–9. doi:10.1140/epjb/e20020122

CrossRef Full Text | Google Scholar

28. Bradshaw W, William J, Huggins JH, Lloyd AL, Esvelt KM. Bidirectional contact tracing could dramatically improve COVID-19 control. Nat Commun (2021) 12(1):232. doi:10.1038/s41467-020-20325-7

PubMed Abstract | CrossRef Full Text | Google Scholar

29. Van M, Piet A, Jasmina O, Robert K. Virus spread in networks. IEEE/ACM Trans Networking (2008) 17(1):1–14. doi:10.1109/tnet.2008.925623

CrossRef Full Text | Google Scholar

30. Chen DB, Gao H, Lü L, Zhou T. Identifying influential nodes in large-scale directed networks: the role of clustering. PloS one (2013) 8(10):e77455. doi:10.1371/journal.pone.0077455

PubMed Abstract | CrossRef Full Text | Google Scholar

31. Feng ML, Liu L, Chen J, Xia C. Heterogeneous propagation processes between awareness and epidemic on signed multiplex networks. Chaos, Solitons and Fractals (2024) 183:114858. doi:10.1016/j.chaos.2024.114858

CrossRef Full Text | Google Scholar

32. Gallotti R, Valle F, Castaldo N, Sacco P, De Domenico M. Assessing the risks of ‘infodemics’ in response to COVID-19 epidemics. Nat Hum Behav (2020) 4(12):1285–93. doi:10.1038/s41562-020-00994-6

PubMed Abstract | CrossRef Full Text | Google Scholar

33. Sun QY, Wang D, Zhao D, Xia C, Perc M. Diffusion of resources and their impact on epidemic spreading in multilayer networks with simplicial complexes. Chaos, Solitons and Fractals (2022) 164:112734. doi:10.1016/j.chaos.2022.112734

CrossRef Full Text | Google Scholar

34. Li DD, Xie W, Han D, Sun M. A multi-information epidemic spreading model on a two-layer network. Inf Sci (2023) 651:119723. doi:10.1016/j.ins.2023.119723

CrossRef Full Text | Google Scholar

35. Huang H, Xu Y, Xing J, Shi T. Social influence or risk perception? A mathematical model of self-protection against asymptomatic infection in multilayer network. Chaos, Solitons and Fractals (2023) 166:112925. doi:10.1016/j.chaos.2022.112925

CrossRef Full Text | Google Scholar

36. Chen JX, Xia CY, Perc M. The SIQRS propagation model with quarantine on simplicial complexes. IEEE Trans Comput Soc Syst (2024) 11:4267–78. doi:10.1109/tcss.2024.3351173

CrossRef Full Text | Google Scholar

37. Zhang KB, Hong X, Han Y, Wang B. Interplay of simplicial information propagation and epidemic spreading on multiplex metapopulation networks. Chaos, Solitons and Fractals (2024) 180:114490. doi:10.1016/j.chaos.2024.114490

CrossRef Full Text | Google Scholar

38. Wu BJ, Huo L. The influence of different government policies on the co-evolution of information dissemination, vaccination behavior and disease transmission in multilayer networks. Chaos, Solitons and Fractals (2024) 180:114522. doi:10.1016/j.chaos.2024.114522

CrossRef Full Text | Google Scholar