Computational modeling and thermal analysis of magnetized nanofluid flow with physio-chemical interaction and chemical reaction between two non-parallel walls

Abstract

The study of how energy undergoes changes in physio-chemical interactions involving Al₂O₃ and γ-Al₂O₃ with water and C₂H₆O₂ within converging and diverging channels is of great significance, given its potential applications in today’s advanced technology. We have used two types of oxide nanoparticles, namely, Al₂O₃ and γ- Al₂O₃, with water and C₂H₆O₂. The purpose of this study is to investigate an innovative comparative magnetohydrodynamic (MHD) nanofluid flow and heat transport with the impact of thermal radiation on water and ethylene glycol (EG) suspended with Al₂O₃ and γ-Al₂O₃ nanoparticles. A novel comparison of concentration of Al₂O₃–H2O, γ-Al₂O₃–H₂O, and γ Al₂O₃–C₂H₆O₂ nanofluids is investigated under the influence of chemical reactions. The system of nonlinear ordinary differential equations was obtained via a similarity transformation and then solved using the homotopy analysis method (HAM) in Mathematica. The temperature and velocity profiles are obtained numerically for a range of controlling parameter values, including the volume percentage of nanomaterials, the magnetic effect parameter M, the radiation parameter Rd, and Eckert number Ec in convergent/divergent channels. The concentration profiles of Al₂O₃–H₂O, γ-Al₂O₃–H₂O, and γ-Al₂O₃–C₂H₆O₂ tri-nanofluids are calculated numerically for governing parameter values, including those accounting for chemical reactions. The investigation’s findings indicate that there is greater heat transport in γ-Al₂O₃–C₂H₆O₂ and γ-Al₂O₃–H₂O than in Al₂O₃–H₂O. We have demonstrated that there is good agreement between the current results and those found in the literature for various values of the magnetic field parameter, thermal radiation parameter, and nanoparticle volume fraction.

1 Introduction

In the realm of thermo science and thermal engineering, substantial advancements have been made in the pursuit of enhancing heat transfer. One notable approach involves the incorporation of additives into liquids. This strategy becomes particularly relevant when the inherent characteristics of the flowing fluids themselves pose constraints on the efficiency of heat transfer. To address this, solid additives are introduced into the base liquids, effectively modifying the properties of transport, dynamics of flow, and thermal transmission characteristics of these fluids (Zimparov, 2002). In addition to detailing the historical progression within this particular field, Hetsroni and Rozenblit (1994) conducted a study focusing on the thermal interplay between a turbulent flow containing particles and a heated plate. Their research centered on a liquid–solid blend comprising water and polystyrene particles.

Nanofluids, which consist of colloidal suspensions of nanoscale particles distributed steadily and intermittently into traditional fluids, were developed as a solution to the primary issue of heat transfer augmentation. This newly created category is known as nanofluids. The efficiency of energy transport in nanofluids is influenced by both the characteristics and size of the nanoscale particles, along with the volume percentage of solids. Several experimental studies have highlighted that nanofluids exhibit significantly higher thermal conductivity than conventional pure fluids (Wang et al., 1999; Lee et al., 1999; Xuan and Li, 2003). These findings suggest that nanofluids hold substantial potential for enhancing heat transfer processes. In contrast to traditional methods of improving heat transfer, which involve adding millimeter- or micrometer-sized particles to fluids, nanofluids are expected to be an optimal choice for practical applications. This is due to the minuscule size of the nanoparticles, which allows nanofluids to behave much like pure fluids, resulting in minimal or negligible increases in pressure drop. Choi and Eastman (1995) made an earlier contribution in this direction. Later, Eastman at el. (2001) showed that ethanol glycol-based copper nanofluid has higher thermal conductivity than pure ethanol glycol. Xuan and Li (2003) experimentally showed that Cu–water nanofluid can enhance the heat transfer process compared to pure-based liquid. The magnetohydrodynamic (MHD) fluid flow and heat transfer of hybrid nanofluid under thermal radiation were investigated by Chamkha et al. (2019), who developed a model for nanofluids that incorporates the Roseland distribution estimate, Brownian motion, and thermophoresis, expanding the understanding of these complex phenomena. Mohamed and Wahid (Abdel-wahed, 2017) investigated the effects of nonlinear thermal radiation and magnetic fields on nanofluid flow and temperature over a moving surface.

Hybrid nanofluids represent a specialized category within the broader domain of nanofluids, characterized by the deliberate blending of two or more distinct nanoparticle types into a base fluid. Nanofluids, in their general definition, encompass finely dispersed nanoparticles at the nanometer scale, entrained within a base fluid, which can be either a liquid or a gas. Notably, hybrid nanofluids derive their nomenclature from their unique composition, whereas multiple nanoparticle variants coexist within the same base fluid. The engineering of hybrid nanofluids is oriented toward imbuing them with distinctive and tailored properties, rendering them particularly suitable for a diverse array of applications. Of paramount significance among these applications are domains such as heat transfer, cooling systems, and energy generation, where the exigencies of thermal management and energy efficiency are critical. Numerous scholarly investigations have delved into the realm of hybrid nanofluids, each offering unique perspectives and findings. Notably, Hanif et al. (2020a) provided a complete entropy analysis, focusing on unsteady mixed convection in a magneto-hybrid nanofluid flowing over an inverted cone enclosed by a porous media. Khan and Rasheed (2021) investigated thermal properties in detail using silicon dioxide and molybdenum disulfide in a three-dimensional heated surface framework. Furthermore, Hanif et al. (2021) studied the effectiveness of hybrid nanofluids in the presence of heat radiation—specifically, in a heated cone under the influence of a magnetic field. The numerical analysis was performed using the Crank–Nicolson method. Hanif et al. (2020b) used numerical analysis to account for varying viscosities in water-based hybrid nanofluid flows around an inverted permeable cone by incorporating the effects of a magnetic field and radiative heat flux. Saqib et al. (2019) investigated the velocity and temperature of a hybrid nanofluid with nanoparticles of alumina and copper. They used Laplace transformation and fractional Caputo–Fabrizio derivative to calculate their outcomes.

The MHD, often called hydromagnetics or magnetofluid dynamics, studies fluid dynamics in electrically conducting mediums. The MHD field can be traced back to the pioneering work of Hannes Alfvén, a luminary in plasma physics who was awarded the Nobel Prize in Physics in 1970 for his efforts. The core assumption of magnetohydrodynamics is that magnetic fields can create electric currents within a flowing, conductive fluid. Consequently, these induced currents engender forces within the fluid, which reciprocally lead to alterations in the magnetic field itself, shaping the fundamental dynamics of MHD. The application of MHD on the nanofluid flow can alter its behavior. Keeping in view the significance of the MHD application, it has attracted the interest of many researchers. In several boundary value issues, researchers have employed the MHD flow with stretched surfaces to enhance thermal performance. Nourazar et al. (2017) investigated one such case. When different nanoparticles were suspended in a base fluid, they studied the flow of a nanofluid. When the magnetic parameter increases, they discovered an increase in the temperature profile. Babu et al. (2018) explained the nanofluid flow issue under the influence of heat radiation, where the MHD flow was induced by stretching a sheet. Venkateswarlu and Narayana (2019) presented the MHD flow across a porous flat plate and used slip effects to analyze the resulting model’s thermo-physical properties. Dehghani et al. (2019) investigated water–Al₂O₃ nanofluid mixed convection in a grooved channel with internal heat production in solid cylinders using numerical modeling of magneto hydrodynamics (MHD. The influence of a non-uniform magnetic field on the ferrofluid flow and heat transfer in plain and wavy channels was investigated by Mousavi et al. (2020). They discovered that the channel with wavy walls had a stronger magnetic field impact on the flow field and heat transfer than the channel with plain walls.

Thermal radiation, often referred to as heat radiation, entails the emission of electromagnetic waves in the form of heat by an object owing to its temperature. This phenomenon holds a fundamental status within the realms of physics and engineering, assuming a pivotal function across diverse domains, encompassing heat transfer, energy systems, and materials science. The extensive use of thermal radiation in the domains of physics and engineering, particularly concerning the design of mechanical components, spacecraft technology, and gas turbine systems, has bestowed paramount significance upon it. England and Emery (1969) investigated the impact of thermal radiation on a vertical flat plate with the laminar-free convection boundary layer flow for both non-absorbing and absorbing gases. Furthermore, Reddy (2019) investigated unsteady MHD-free convection flow through an isothermal porous vertical plate. They used the numerical technique Ritz finite element method to solve their problem. Their finding showed that velocity and temperature reduced for higher radiation parameters. Samad and Mansur-Rahman (1970) investigated unsteady MHD free convection flow with the influence of thermal radiation and chemical reactions through an infinite isothermal porous vertical plate. They also used the numerical technique known as the Ritz finite element method. They found that the velocity profile was enhanced by large thermal and mass Grashof numbers, while the velocity profile decreased for large magnetic parameters. Roja (2022) studied magnetohydrodynamic Powell–Eyring hybrid nanofluid flow in a vertical porous channel, accounting for porous media effects, magnetism, convective circumstances, dissipation energy, heat generation, and radiation. Their findings show that entropy generation increases with the Grashof number, Biot number, and radiation parameter but decreases with magnetism, Darcy number, and Eyring–Powell factors. The data revealed that increased radiation was associated with a decrease in liquid temperature and an increase in entropy. Rashad et al. (2023) studied MHD Cu–Fe₃O₄/ethylene glycol (EG) nanofluids in a permeable media using the Powell–Eyring fluid model. Their findings indicated that increasing both the radiation and magnetic field increased the fluid’s velocity. On the other hand, it was discovered that the radiation effect alone increased the temperature of the boundary layer. Furthermore, many investigators have studied how radiation affects the transfer of heat. These include analyses of Cu/H₂O laminar flows in vertical channels (Mostafazadeh et al., 2019), MHD flows of Cu/H₂O amongst parallel plates (Dogonchi et al., 2016), and MHD flows of GO/H₂O in permeable channels for nanofluids (Dogonchi et al., 2017). Additionally, investigations encompassed MHD flows of CuO–Al₂O₃/H₂O across two different geometries (Ashwinkumar et al., 2021), MHD flows of Al₂O₃–Ag/H₂O over a stretching sheet (Shoaib et al., 2020), and MHD flows of Williamson MoS₂–ZnO/EG over a permeable stretching sheet for hybrid nanofluids (Yahya et al., 2021).

The interaction of heat and mass transfer in conjunction with chemical reactions is a highly significant area of study, garnering substantial interest in recent times. This multidisciplinary field finds applications across various industries, including the design of chemical processing equipment, safeguarding crops from freezing damage, food processing, and the operation of cooling towers. The mechanism of an unsteady flow across an infinite vertical plate with a constant heat and mass transfer was studied by Das et al. (1994) in relation to the impact of the first-order homogeneous chemical reaction. The impact of the chemical reaction and injection on the flow characteristics in an unstable upward motion of an isothermal plate was explored by Muthucumaraswamy and Ganesan (2001). Chamkha (2003) investigated MHD flow over a uniformly stretched vertical permeable surface in the presence of heat generation/absorption and a chemical reaction. Rahman and Sattar (2005) investigated the MHD convective flow of micropolar fluid via a rotating vertical porous plate when heat production and/or absorption were present. The analytical solution for an unstable MHD-free convection flow via a semi-infinite vertical permeable moving plate with a heat source and chemical reaction was discovered by Ibrahim et al. (2008). Rahman et al. (2009a) investigated heat transport over a non-stretching sheet in a micropolar fluid with temperature-dependent fluid characteristics. Rahman et al. (2010) and Rahman et al. (2009b) studied heat transmission in micropolar fluid down an inclined plate with varying fluid characteristics under various boundary conditions. Recently, Akbarzadeh (2018) and Yadav (2019) used linear stability analysis to investigate the impact of chemical reactions on convective instability in a horizontal layer of nanofluids. They noticed that increasing the chemical reaction parameter (K₁) increases the system’s stability.

Radiative nanofluid flow between two non-parallel walls is one of the significant research motivations. This flow is also called the Jeffery–Hamel flow or flow amongst converging/diverging channels. The Jeffrey–Hamel flow is a specific type of non-parallel flow that occurs between two walls, with a gap that changes steadily along the direction of the fluid flow. This flow has significantly enhanced our understanding of non-parallel flows, boundary layer behavior, and turbulence phenomena. Its significance spans multiple fields, from applied research in microfluidics and numerical simulations to basic research in fluid dynamics. It is relevant to many biological, environmental, and engineering applications. It facilitates improvements in heat transfer, drag reduction, mixing, turbulence modeling, and the comprehension of natural processes, which eventually result in increased effectiveness, performance, and sustainability across a range of industries. Alharbi and Adnan (2022) presented a unique heat transfer model for two types of nanofluids and two host solvents. They found that the nanofluids based on Al₂O₃ and C₂H₆O₂ have significantly higher conductivity than other nanofluids. Adnan et al. (2022) investigated the energy storage efficiency of tri-hybrid nanofluids (Al₂O₃–CuO–Cu/H₂O) and hybrid nanofluids (Al₂O₃–CuO–H₂O), taking into account the effects of unique viscous dissipation mechanisms. In another study, Adnan et al. (2023) investigated the ternary hybrid nanofluid (Al₂O₃–CuO–Fe₃O₄)/C₂H₆O₂ flow, with a viscous dissipation effect in slippery converging/diverging channels. They found that ternary hybrid nanofluid has superior heat transfer characteristics compared to simple hybrid nanofluid. Boudjemline et al. (2023) considered the pressure-driven flow of an expanding tube containing a non-Newtonian Oldroyd-B nanofluid. Rawat et al. (2023) investigated a hybrid nanofluid flow in a Darcy–Forchheimer porous medium between two rotating discs. They emphasized the importance of non-uniform heat source/sink and the Cattaneo–Christov model in comprehending the complex flow behavior. Most relevant research studies are as follows: Adnan (2022), Gaffar et al. (2018), Grigore et al. (2017), Pirvut et al. (2018), Sudhagar et al. (2017), Sumithra et al. (2023), Aich et al. (2023), Rushi Kumar et al. (2023), Ismail et al. (2024), and Khan et al. (2024). Abdelsalam et al. (2023a), Abdelsalam et al. (2023b), Abdelsalam and Zaher (2023), El Koumy et al. (2012), Abdelsalam and Bhatti (2023), and Abdelsalam et al. (2024) investigated nanofluid flow, considering different nanoparticles with rheological properties by applying various mathematical models in different geometries.

In the current work, we consider a novel comparison of heat transfer and fluid velocity in water and EG dispersed by Al₂O₃ and Al₂O₃ nanoparticles between converging and diverging channels under MHD and thermal radiation effects. We also investigate novel comparative concentration profiles for Al₂O₃–H₂O, -Al₂O₃–H₂O, and Al₂O₃–EG under the impact of chemical reactions and the Schmidt number (Sc).

2 Problem formulations

2.1 Physical modeling

The flow of nanofluid between two non-parallel barriers is shown in Figure 1.

FIGURE 1

2.2 Mathematical modeling

2.2.1 Conservation equations for nanofluids

The continuity equation, the Navier–Stokes equations, and concentration equation in polar coordinates are as follows (Abdelsalam et al., 2023b; Abdelsalam and Zaher, 2023; El Koumy et al., 2012):

Here, Equation 1 represents the law of conservation of mass. Equations 2–4 represent the equation of momentum and equation for energy, correspondingly. Equation 5 represents the concentration field.

3 Thermo-physical properties

The thermo-physical characteristics of nanofluids are inherently contingent upon the thermo-physical attributes of both nanoparticles and base fluids. In the context of our ongoing nanofluid research, we consider the specific heat capacity, density, thermal conductivity, and electrical conductivity of the base fluids and particles. The pertinent values for these thermo-physical properties are presented in Table 1. Table 2 presents the shape factor, sphericity, and shape of the nanomaterials. The nanofluid models and their empirical correlations are provided in Tables 3, 4.

TABLE 1

Model					Pr	Shape
	997.1	4,179		0.613	6.96
	1,116.6	2,382		0.249	204
	3,970	765		40	…….

Thermo-physical properties of base fluids and materials (Abdelsalam and Bhatti, 2023; Abdelsalam et al., 2024; Dogonchi and Ganji, 2016).

TABLE 2

Nanomaterial’s shape	Shape factor	Sphericity	Shape
Brick	3.7	0.811
Cylinder	4.9	0.625
Sphere	3.0	1.000
Platelet	5.7	0.526
Blade	8.6	---
Tetrahedron	4.06	---
Hexahedron	3.72

Attributes for different shape factors (Adnan et al., 2023; Boudjemline et al., 2023; Adnan, 2022; Gaffar et al., 2018).

3.1 Boundary conditions

The feasible boundary conditions for this model are as follows:

4 Non-dimensionalization

We use similarity transformation to reduce the given modeled equation. The appropriate transformations of similarity are specified as (Abdelsalam and Bhatti, 2023; Abdelsalam et al., 2024; Dogonchi and Ganji, 2016)

Integrating Equation 1, we obtain Equation 9 as follows:

4.1 Final version of the model equations

By using the empirically derived correlations for the nanofluids and incorporating self-similar variables as defined in Equation 8, the flow model becomes nonlinear and coupled.

The initial and boundary conditions in the dimensionless form for the current problem can be articulated as follows:

4.2 Physical parameters

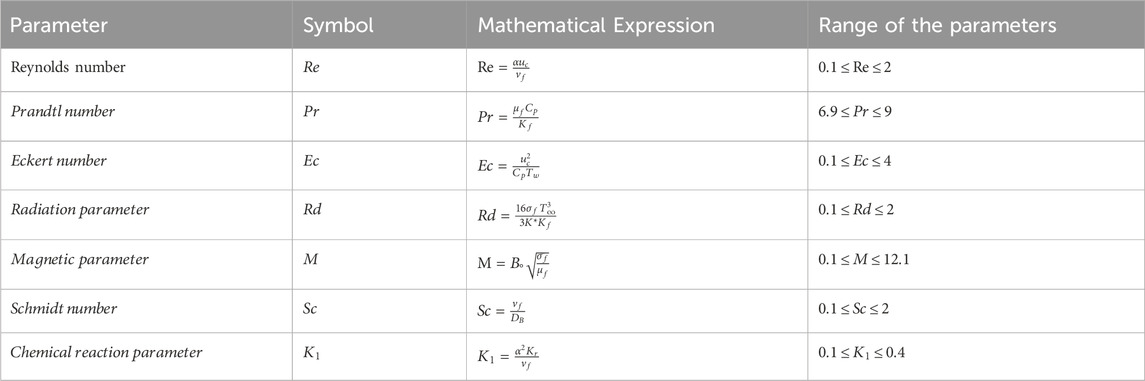
The physical parameters used in the modeled equations are explained in the following section, along with their symbols and mathematical forms.

5 Quantities of engineering interest

5.1 Calculation of the coefficient of skin friction

Surface drag forces result when fluids are in motion; such forces are characterized by the coefficient factor of friction . It is defined in Equation 20:

The terms , and represent the wall shear stress, fluid density, and the fluid stretching velocity, respectively. The coefficients of skin friction for the used nanofluids are calculated as given in Equations 21–23:

5.2 Nusselt number

The Nusselt number characterizes local heat conduction and convective heat transfer at a fixed position, relating heat transfer coefficients to thermal conductivity. The term is formally defined in Equation 24 as follows:

The local Nusselt numbers for given nanofluids are calculated as given in Equations 25–27 as follows:

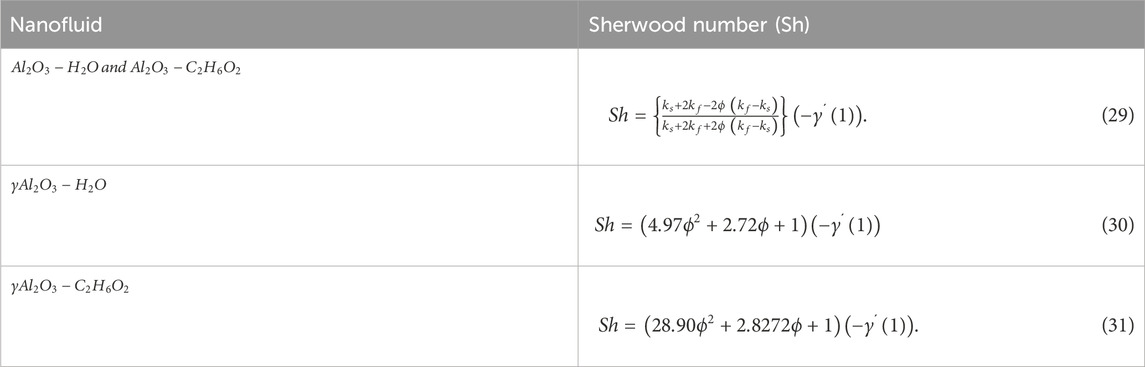
5.3 Calculation of the Sherwood number (Sh)

In the case of a mass transfer, the analogous Sherwood number provides a convective diffusion description similar to that used for heat transfer, involving mass transfer coefficient values and species diffusivity terms. is defined in Equation 28 as follows:

The Sherwood numbers for the used nanofluids are calculated as given in Equations 29–31 as follows:

6 Solution methodology

The homotopy analysis method (HAM) is applied to solve Equations 10–12, 13–15, and 16–18, subject to the boundary conditions given in Equation 19. The flowchart illustrating the HAM is shown in Figure 2.

FIGURE 2

The auxiliary parameter-containing solutions modify and regulate the rate of convergence of the solutions. The following Equation 32 represents how the primary guesses are chosen.

We consider the linear operators to be , which are defined in Equation 33 as follows:

These operators possess the following characteristics, as given in Equation 34:

where are the constants in the general solution. The resultant non-linear operatives are given in Equations 35–37 as follows:

The zeroth-order problems from Equations 10–12, 13–15, and 16–18 provide an overview of the fundamental concepts of the HAM, as presented in Equations 38–40:

The equivalent boundary conditions are given in Equation 41 as follows:

The incorporating parameter is denoted by , and are used to regulate the solution’s convergence. When , we obtain Equation 42 as follows:

The Taylor’s series expansion of about p = 0 is given in Equation 43 as follows:

where Equation 44 presents the following:

In order to ensure that Equation 31 converges at p = 1, the secondary constraints are selected. Substituting in Equation 31, we acquire Equation 45 as follows:

The following Equation 46 is satisfied by the -order problem:

The corresponding boundary conditions are given in Equation 47 as follows:

Here, Equations 48–50 present the following:

where

7 Result and discussion on physical parameters

Semi-analytical solutions were found for the converted radial momentum, energy, and concentration Equations 2, 4, 5, according to the boundary constraints Equations 6, 7 using HAM in Mathematica. The effects of a variety of factors on velocity and temperature profiles for Al₂O₃–H₂O, -Al₂O₃–H₂O, and Al₂O₃–EG are examined, including nanoparticle volume fraction the magnetic parameter M, the radiation parameter Rd, and the Eckert number Ec in convergent/divergent channels. We examined the effects of governing parameter values, such as chemical reactions and the Schmidt number, on the concentration profiles for Al₂O₃–H₂O, -Al₂O₃–H₂O, and γ-Al₂O₃–C₂H₆O₂ nanofluids. Table 1 provides an overview of the thermo-physical characteristics of the nanofluids. Table 2 exhibits the behavior of skin friction for various parameters. Table 3 shows the impact of and Ec. Table 4 provides variation in the Sherwood number for K₁ and Sc.

7.1 Velocity field

Figures 3a, b display the trend of a magnetic parameter with respect to the velocity of the nanofluid for Al₂O₃–H₂O, -Al₂O₃–H₂O, and γ-Al₂O₃–C₂H₆O₂ in divergent/convergent channels, respectively. The magnetic parameter plays an important role in the flow performance of nanofluids. Here are several reasons why the magnetic parameter is important in the nanofluid flow. It affects the velocity, pressure circulation, and heat transmission characteristics of the nanofluid. We can use the magnetic parameter to control and manipulate the flow performance of nanofluids. It is augmented by the heat transfer of nanofluids. It also affects the rheological properties of nanofluids. It is used in biomedical applications for targeted drug delivery, hyperthermia therapy, and magnetic resonance imaging (MRI). The fluid flow is slowed by Lorentz forces, which are created by larger physical changes in the magnetic parameter. The overall nanofluid velocity decreases with the increasing magnetic parameter M for both divergent and convergent channels. Figure 3a indicates a fast decrease in the velocity of Al₂O₃–H₂O, followed by -Al₂O₃–H₂O and γ-Al₂O₃–C₂H₆O₂, respectively. The impact of the solid volume fraction () on the velocity of the fluid is shown in Figures 4a, b. The solid volume fraction () is a precarious parameter that ominously influences the nanofluid flow behavior, thermal assets, stability, and act of nanofluids. Careful management and optimization are needed for comprehending the full potential of nanofluid-based technologies in several engineering, biomedical, and environmental applications. Physically, adding nanoparticles to the pure fluid causes the fluid’s density to increase, which makes it harder for the fluid to pass through the channel. Figure 4a shows that an increase in the volume fraction of solids in the diverging channel results in a reduction in the fluid velocity. Figure 4b, on the other hand, shows a reverse pattern for the convergent channel, i.e., as the solid volume percentage increases, so does the velocity. The impact of diverging/converging channels on the velocity profile of nanofluids is exhibited in Figures 5a, b, respectively. Figure 5a shows that variation in the diverging channel () causes a decrease in the velocity of the nanofluids. Moreover, a greater decrease in velocity was observed for Al₂O₃–H₂O, -Al₂O₃–H₂O, and γ-Al₂O₃–C₂H₆O₂. On the other hand, the velocity increases with variations in the converging channel , as shown in Figure 5b.

FIGURE 3

FIGURE 4

FIGURE 5

7.2 Temperature field

Over the desired domain, the temperature of the nanofluids was strongly influenced by the flow parameters. Consequently, the behavior of the temperature θ(η) versus the magnetic number M for Al₂O₃–H₂O, -Al₂O₃–H₂O, and γ-Al₂O₃–C₂H₆O₂ was depicted in Figures 6a, b. A careful analysis of the data revealed that the used nanofluids’ temperature increases with an increas in the magnetic field strength. Through the physical imposition of a dissipation function in the model, energy is transferred from high-temperature particles to lower-temperature particles by improving the fluid’s internal energy. As a result, the temperature of the nanofluids increases overall. There is a noticeable increase in γAl₂O₃–C₂H₆O₂ and Al₂O₃–H₂O compared to -Al₂O₃–H₂O. The impact of the solid volume fraction (φ) on the temperature profile of fluid through divergent and convergent channels is shown in Figures 7a, b, respectively. Figure 7a suggests that an increase in the solid volume fraction in the diverging channels leads to a decrease in temperature distribution. Moreover, there is a sharp decrease in temperature for Al₂O₃–H₂O, followed by -Al₂O₃–H₂O. However, the least decrease in temperature is observed for γ-Al₂O₃–C₂H₆O₂. It is evident from Figure 7b that the temperature distribution is favored by an increase in the solid volume fraction in the convergent channel. However, there is least augmentation in temperature observed for -Al₂O₃–H₂O. The influence of divergent and convergent channels on the fluid temperature distribution is depicted in Figures 8a, b, respectively. The plotted result analysis shows that temperature increases for more diverging walls (Figure 8a) and decreases for convergent walls (Figure 8b). The temperature increases significantly in γ-Al₂O₃–C₂H₆O₂ and -Al₂O₃–H₂O compared to Al₂O₃–H₂O for divergent walls. Similarly, temperature considerably decreases in γ-Al₂O₃–C₂H₆O₂ and -Al₂O₃–H₂O compared to Al₂O₃–H₂O for convergent walls. Figures 9a, b illustrate how variations in the Eckert number affect the temperature distribution in diverging and converging channels. The Eckert number plays a vital role in influencing numerous features of nanofluid flow behavior, along with heat transfer and thermal performance. It is very important in terms of kinetic and thermal energy in the fluid flow, permitting engineers and researchers to design and enhance nanofluid systems for several real-world applications. A careful examination of the data revealed that the used nanofluids’ temperature increases by strengthening their Eckert numbers. The model’s imposed dissipation function physically increases the fluid’s internal energy, facilitating the movement of energy from particles with higher temperatures to those with lower temperatures. As a result, the temperature of the nanofluids increases overall. The temperature increases noticeably in Al₂O₃–H₂O, followed by γ-Al₂O₃–C₂H₆O₂ and -Al₂O₃–H₂O, respectively. The effect of increasing Rd on the temperature profile is shown in Figures 10a, b. The graph shows that as heat radiation is steadily increased, the temperature profile decreases for the divergent channel (Figure 10a). It is due to the fact that the presence of the radiation parameter leads to thinning of the thermal layer. However, for the convergent channel (Figure 10b), temperature increases for the increase in the radiation parameter.

FIGURE 6

FIGURE 7

FIGURE 8

FIGURE 9

FIGURE 10

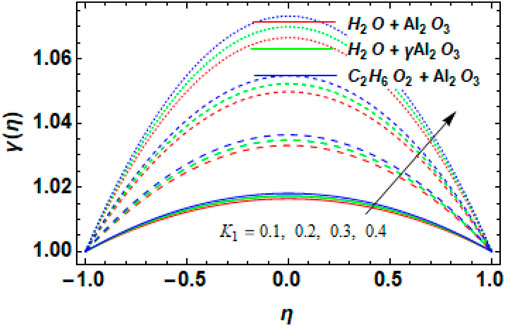
7.3 Concentration field

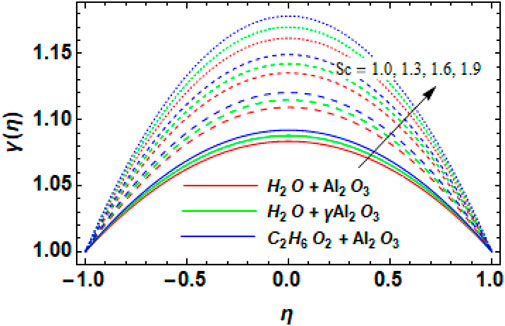
Figure 11 shows the impact of the increasing on the concentration profile . The figure reveals that increasing the value of the chemical reaction parameter results in increasing the concentration profile. Moreover, there is a significant increase observed in the concentration profiles of γ-Al₂O₃–C₂H₆O₂, followed by -Al₂O₃–H₂O and Al₂O₃–H₂O, respectively. The reason for this is that in this case, an increase in the chemical reaction parameter causes the rate of reaction to increase. The faster conversion of reactants into products as a result of the higher reaction rate has an impact on the nanofluid concentration. Higher reaction rates result in higher concentrations of nanoparticles because the reaction parameter affects the production or consumption of nanoparticles in the nanofluid. The behavior of increasing Sc versus the concentration profile is exhibited in Figure 12. It is evident from the figure that, overall, all used nanofluids exhibit an enhanced concentration profile with increasing values of the Schmidt number.

FIGURE 11

FIGURE 12

7.4 Discussion on the graphical and numerical analysis of physical quantities

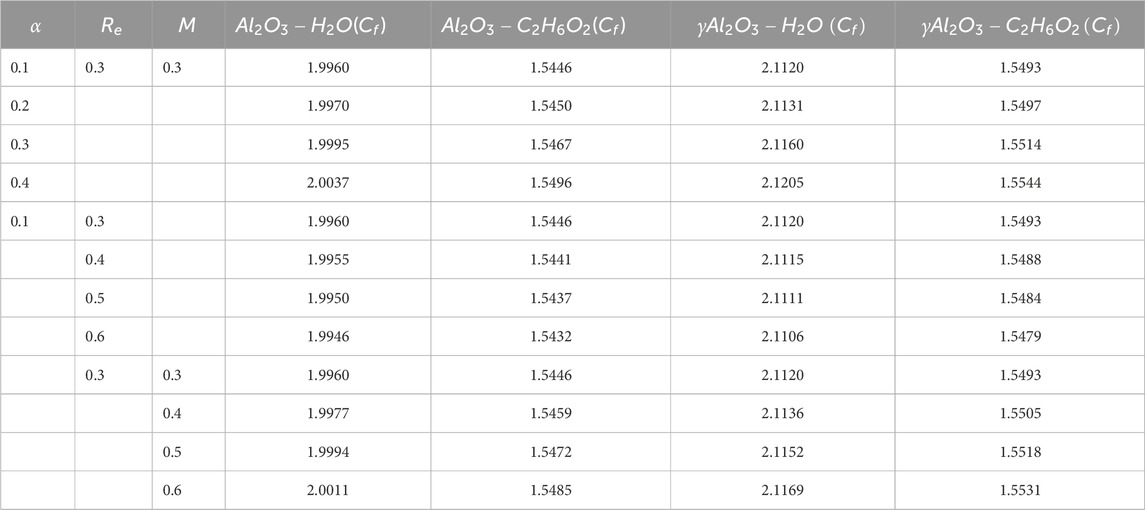
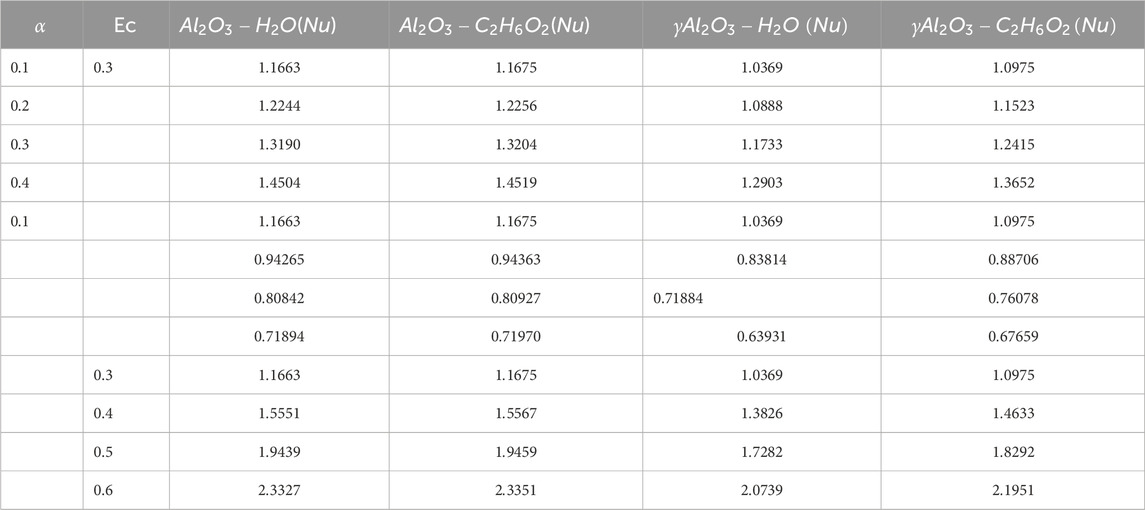
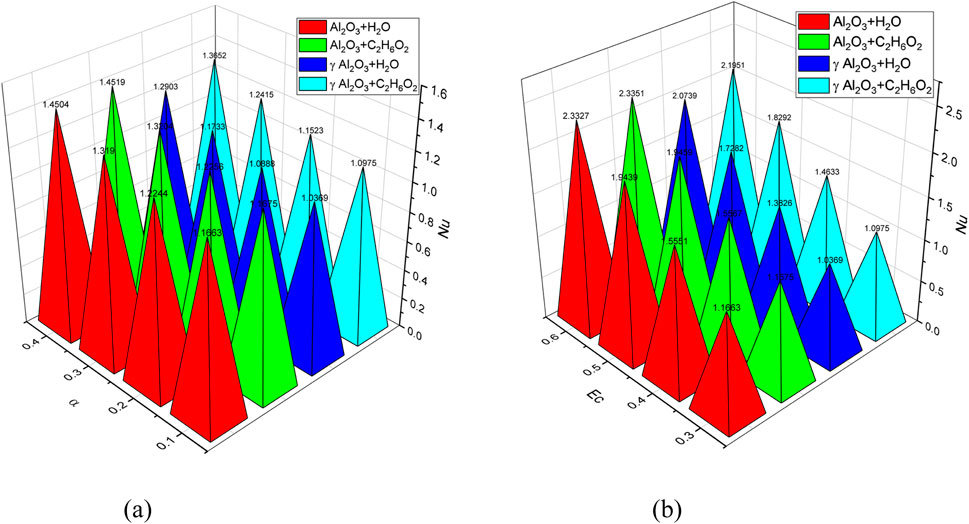
Table 5 exhibits the trend of skin fiction for increasing values of , , and M for , , , and . The table shows that skin friction increases with increasing values of for all nanofluids while keeping the values of and M constant. A similar trend is observed in skin friction in all used nanofluids for increasing values of and M. Table 6 shows the behavior of the Nusselt number Nu for the increasing values of and the Eckert number Ec. Table 6 shows that as the values of and Ec are increased separately, the Nusselt number increases for all nanofluids used. This indicates that the nanofluids have faster heat transfer ability. Table 7 indicates the trend of the Sherwood number for K₁ and Sc. A rapid increase in the Sherwood number is observed for increasing values of K₁ by fixing Sc for all used nanofluids. Similarly, a significant enhancement in the Sherwood number is also observed in all nanofluids for increasing values of Sc when the value of K₁ is kept constant.

Figure 13a exhibits the trend of C_f for increasing values of An overall enhancement in skin friction is observed for increasing values of for nanofluids , , , and . It is further observed that more enhancement is observed in skin friction for , followed by and , respectively. Figure 13b shows the evolution of C_f for increasing values of the Reynolds number (Re). Skin friction for used nanofluids is decreased for increasing values of the Reynolds number. Figure 13c shows an increased behavior of Cf for increasing values of the magnetic parameter (M) for all used nanofluids, i. e., , , and . Figure 14a demonstrates the trend of Nu for increasing values of It is observed from the figure that generally Nu has an increasing trend for increasing values of for , , and nanofluids. This is due to the fact that the cross-sectional area increases and that the fluid velocity decreases with a greater angle of divergence. Because there is more surface area available for heat exchange, heat transmission is improved. As a result, as the angle of divergence increases, the Nusselt number also increases. In addition, shows more increasing behavior, followed by and , respectively. Variations in Nu for increasing values of Ec are depicted in Figure 14b. A sharp enhancement is observed in the Nusselt number of , , and nanofluids by increasing the Eckert number. This indicates that the mentioned nanofluids have a higher rate of heat transfer. Moreover, the graph also shows that the used nanofluids exhibit more or less a similar behavior in their enhancement of the Nusselt number. Figure 15a depicts the trend of Sh for increased values of . A similar and minor enhancement is observed in Sh for all used nanofluids, i.e., , , and when is increased. Figure 15b depicts the variation in Sh for increased values of Sc. Overall, there is an increased trend observed in Sh for increased values of Sc for used nanofluids. Figures 16a–c show the h-curve graphs of (F ), , and for Al₂O₃–H₂O, -Al₂O₃–H₂O, and γ-Al₂O₃–C₂H₆O₂.

FIGURE 13

FIGURE 14

FIGURE 15

FIGURE 16

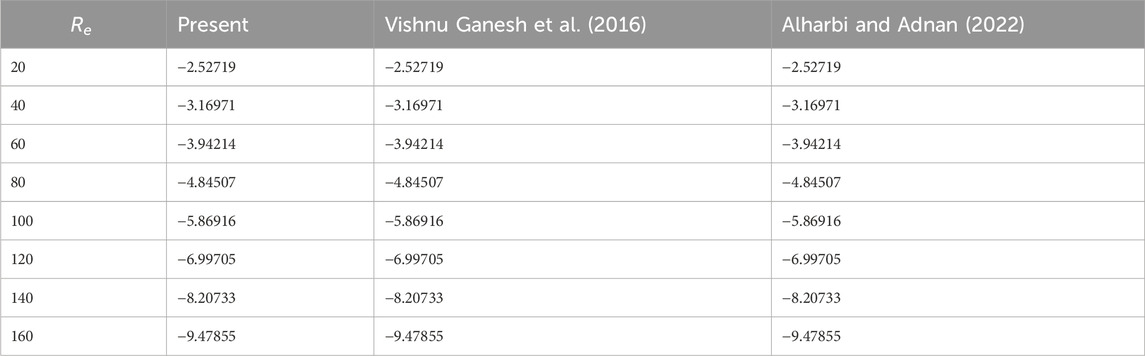
7.5 Validation of the results

Adequate comparison and discussion on the results with the existing literature for , with different values of R_e are presented. The Table 8 shows that the present results agree with those of previous studies by Khalid and Adnan (2022) and Vishnu Ganesh et al. (2016).

8 Conclusion

References

• 1

  Abdelsalam S. I. Abbas W. Megahed A. M. Said A. A. M. (2023a). A comparative study on the rheological properties of upper convected Maxwell fluid along a permeable stretched sheet. Heliyon9 (12), e22740. 10.1016/j.heliyon.2023.e22740

  • CrossRef
  • Google Scholar

• 2

  Abdelsalam S. I. Alsharif A. M. Abd Elmaboud Y. Abdellateef A. I. (2023b). Assorted kerosene-based nanofluid across a dual-zone vertical annulus with electroosmosis. Heliyon9 (5), e15916. 10.1016/j.heliyon.2023.e15916

  • CrossRef
  • Google Scholar

• 3

  Abdelsalam S. I. Bhatti M. M. (2023). Unraveling the nature of nano-diamonds and silica in a catheterized tapered artery: highlights into hydrophilic traits. Sci. Rep.13 (1), 5684. 10.1038/s41598-023-32604-6

  • CrossRef
  • Google Scholar

• 4

  Abdelsalam S. I. Magesh A. Tamizharasi P. Zaher A. Z. (2024). Versatile response of a Sutterby nanofluid under activation energy: hyperthermia therapy. Int. J. Numer. Methods Heat. Fluid Flow.34 (2), 408–428. 10.1108/HFF-04-2023-0173

  • CrossRef
  • Google Scholar

• 5

  Abdelsalam S. I. Zaher A. Z. (2023). Biomimetic amelioration of zirconium nanoparticles on a rigid substrate over viscous slime — a physiological approach. Appl. Math. Mech.44 (9), 1563–1576. 10.1007/s10483-023-3030-7

  • CrossRef
  • Google Scholar

• 6

  Abdel-wahed M. S. (2017). Nonlinear Rosseland thermal radiation and magnetic field effects on flow and heat transfer over a moving surface with variable thickness in a nanofluid. Can. J. Phys.95 (3), 267–273. 10.1139/cjp-2016-0345

  • CrossRef
  • Google Scholar

• 7

  Adnan (2022). Heat transfer inspection in [(ZnO-MWCNTs)/water-EG(50:50)] _hnf with thermal radiation ray and convective condition over a Riga surface. Waves Random Complex Media, 1–15. 10.1080/17455030.2022.2119300

  • CrossRef
  • Google Scholar

• 8

  Adnan Alharbi K. A. M. Ashraf W. Eldin S. M. Yassen M. F. Jamshed W. (2023). Applied heat transfer modeling in conventional hybrid (Al₂O₃-CuO)/C₂H₆O₂ and modified-hybrid nanofluids (Al₂O₃-CuO-Fe₃O₄)/C₂H₆O₂ between slippery channel by using least square method (LSM). AIMS Math.8 (2), 4321–4341. 10.3934/math.2023215

  • CrossRef
  • Google Scholar

• 9

  Adnan Guedri K. Raizah Z. Tag-Eldin E. Ashraf W. Khan U. et al (2022). Thermal efficiency in hybrid (Al2O3-CuO/H2O) and tri-hybrid (Al2O3-CuO-Cu/H2O) nanofluids between converging/diverging channel with viscous dissipation function: numerical analysis. Front. Chem.10, 960369. 10.3389/fchem.2022.960369

  • CrossRef
  • Google Scholar

• 10

  Aich W. Almujibah H. Shukhratovich Abdullaev S. Bani-Fwaz M. Z. Hassan A. M. (2023). Thermal performance of radiated annular extended surface using advanced nanomaterials influenced by various physical controlling parameters for nucleate boiling case. Case Stud. Therm. Eng.51, 103524. 10.1016/j.csite.2023.103524

  • CrossRef
  • Google Scholar

• 11

  Akbarzadeh P. (2018). The onset of MHD nanofluid convection between a porous layer in the presence of purely internal heat source and chemical reaction. J. Therm. Anal. Calorim.131 (3), 2657–2672. 10.1007/s10973-017-6710-9

  • CrossRef
  • Google Scholar

• 12

  Alharbi K. A. M. Adnan A. (2022). Thermal investigation and physiochemical interaction of H ₂ O and C ₂ H ₆ O ₂ saturated by Al ₂ O ₃ and γAl ₂ O ₃ nanomaterials. J. Appl. Biomater. Funct. Mater.20, 228080002211364. 10.1177/22808000221136483

  • CrossRef
  • Google Scholar

• 13

  Ashwinkumar G. P. Samrat S. P. Sandeep N. (2021). Convective heat transfer in MHD hybrid nanofluid flow over two different geometries. Int. Commun. Heat. Mass Transf.127, 105563. 10.1016/j.icheatmasstransfer.2021.105563

  • CrossRef
  • Google Scholar

• 14

  Babu D. H. Ajmath K. A. Venkateswarlu B. Narayana P. V. S. (2018). Thermal radiation and heat source effects on MHD non-Newtonian nanofluid flow over a stretching sheet. J. Nanofluids8 (5), 1085–1092. 10.1166/jon.2019.1666

  • CrossRef
  • Google Scholar

• 15

  Boudjemline A. Ahmad I. Rehman S. Hashim Khedher N. B. (2023). Jeffery-Hamel flow extension and thermal analysis of Oldroyd-B nanofluid in expanding channel. J. Non-Equilib. Thermodyn.48 (1), 75–90. 10.1515/jnet-2022-0052

  • CrossRef
  • Google Scholar

• 16

  Chamkha A. J. (2003). Mhd flow of a uniformly stretched vertical permeable surface in the presence of heat generation/absorption and a chemical reaction. Int. Commun. Heat. Mass Transf.30 (3), 413–422. 10.1016/S0735-1933(03)00059-9

  • CrossRef
  • Google Scholar

• 17

  Chamkha A. J. Dogonchi A. S. Ganji D. D. (2019). Magneto-hydrodynamic flow and heat transfer of a hybrid nanofluid in a rotating system among two surfaces in the presence of thermal radiation and Joule heating. AIP Adv.9 (2), 025103. 10.1063/1.5086247

  • CrossRef
  • Google Scholar

• 18

  Choi S. U. S. Eastman J. A. (1995). Enhancing thermal conductivity of fluids with nanoparticles.

  • Google Scholar

• 19

  Das U. N. Deka R. Soundalgekar V. M. (1994). Effects of mass transfer on flow past an impulsively started infinite vertical plate with constant heat flux and chemical reaction. Forsch. Im. Ingenieurwes.60, 284–287. 10.1007/BF02601318

  • CrossRef
  • Google Scholar

• 20

  Dehghani M. S. Toghraie D. Mehmandoust B. (2019). Effect of MHD on the flow and heat transfer characteristics of nanofluid in a grooved channel with internal heat generation. Int. J. Numer. Methods Heat. Fluid Flow.29 (4), 1403–1431. 10.1108/HFF-05-2018-0235

  • CrossRef
  • Google Scholar

• 21

  Dogonchi A. S. Alizadeh M. Ganji D. D. (2017). Investigation of MHD Go-water nanofluid flow and heat transfer in a porous channel in the presence of thermal radiation effect. Adv. Powder Technol.28 (7), 1815–1825. 10.1016/j.apt.2017.04.022

  • CrossRef
  • Google Scholar

• 22

  Dogonchi A. S. Divsalar K. Ganji D. D. (2016). Flow and heat transfer of MHD nanofluid between parallel plates in the presence of thermal radiation. Comput. Methods Appl. Mech. Eng.310, 58–76. 10.1016/j.cma.2016.07.003

  • CrossRef
  • Google Scholar

• 23

  Dogonchi A. S. Ganji D. D. (2016). Investigation of MHD nanofluid flow and heat transfer in a stretching/shrinking convergent/divergent channel considering thermal radiation. J. Mol. Liq.220, 592–603. 10.1016/j.molliq.2016.05.022

  • CrossRef
  • Google Scholar

• 24

  Eastman J. A. Choi S. U. S. Li S. Yu W. Thompson L. J. (2001). Anomalously increased effective thermal conductivities of ethylene glycol-based nanofluids containing copper nanoparticles. Appl. Phys. Lett.78 (6), 718–720. 10.1063/1.1341218

  • CrossRef
  • Google Scholar

• 25

  El Koumy S. R. Barakat E. S. I. Abdelsalam S. I. (2012). Hall and porous boundaries effects on peristaltic transport through porous medium of a maxwell model. Transp. Porous Media94 (3), 643–658. 10.1007/s11242-012-0016-y

  • CrossRef
  • Google Scholar

• 26

  England W. G. Emery A. F. (1969). Thermal radiation effects on the laminar free convection boundary layer of an absorbing gas. J. Heat. Transf.91 (1), 37–44. 10.1115/1.3580116

  • CrossRef
  • Google Scholar

• 27

  Gaffar S. A. Prasad V. R. Kumar B. Anwar O. (2018). Computational modelling and solutions for mixed convection boundary layer flows of nanofluid from a non-isothermal wedge. J. Nanofluids7 (5), 1024–1032. 10.1166/jon.2018.1522

  • CrossRef
  • Google Scholar

• 28

  Gao J. Liu J. Yue H. Zhao Y. Tlili I. Karimipour A. (2022). Effects of various temperature and pressure initial conditions to predict the thermal conductivity and phase alteration duration of water based carbon hybrid nanofluids via MD approach. J. Mol. Liq.351, 118654. 10.1016/j.molliq.2022.118654

  • CrossRef
  • Google Scholar

• 29

  Grigore N. Pirvut V. Mihai I. Mitariu S. I. C. Sava M. Hasegan A. (2017). Polymer ligating clips in urologic laparoscopic surgery. Mater. Plast.54 (2), 295–297. 10.37358/MP.17.2.4836

  • CrossRef
  • Google Scholar

• 30

  Hanif H. Khan I. Shafie S. (2020a). Heat transfer exaggeration and entropy analysis in magneto-hybrid nanofluid flow over a vertical cone: a numerical study. J. Therm. Anal. Calorim.141 (5), 2001–2017. 10.1007/s10973-020-09256-z

  • CrossRef
  • Google Scholar

• 31

  Hanif H. Khan I. Shafie S. (2020b). A novel study on time-dependent viscosity model of magneto-hybrid nanofluid flow over a permeable cone: applications in material engineering. Eur. Phys. J. Plus135 (9), 730. 10.1140/epjp/s13360-020-00724-x

  • CrossRef
  • Google Scholar

• 32

  Hanif H. Khan I. Shafie S. (2021). A novel study on hybrid model of radiative Cu–$$\hbox {Fe}_3\hbox {O}_4$$/water nanofluid over a cone with PHF/PWT. Eur. Phys. J. Spec. Top.230 (5), 1257–1271. 10.1140/epjs/s11734-021-00042-y

  • CrossRef
  • Google Scholar

• 33

  Hetsroni G. Rozenblit R. (1994). Heat transfer to a liquid—solid mixture in a flume. Int. J. Multiph. Flow.20 (4), 671–689. 10.1016/0301-9322(94)90038-8

  • CrossRef
  • Google Scholar

• 34

  Ibrahim F. S. Elaiw A. M. Bakr A. A. (2008). Effect of the chemical reaction and radiation absorption on the unsteady MHD free convection flow past a semi infinite vertical permeable moving plate with heat source and suction. Commun. Nonlinear Sci. Numer. Simul.13 (6), 1056–1066. 10.1016/j.cnsns.2006.09.007

  • CrossRef
  • Google Scholar

• 35

  Ismail B. S. B. Yaseen M. Rawat S. K. Pant M. (2024). Designing machine learning based intelligent network for assessment of heat transfer performance of ternary hybrid nanofluid flow between a cone and a disk: case of MLP feed forward neural network. Comput. Math. Appl.169, 17–38. 10.1016/J.CAMWA.2024.06.003

  • CrossRef
  • Google Scholar

• 36

  Khalid A. M. A. Adnan (2022). Thermal investigation and physiochemical interaction of H2O and C2H6O2 saturated by Al2O3 and γAl2O3 nanomaterials. J. Appl. Biomater. Funct. Mater.20, 22808000221136483. 10.1177/22808000221136483

  • CrossRef
  • Google Scholar

• 37

  Khan H. Yaseen M. Rawat S. K. Khan A. (2024). Insights into the significance of ternary hybrid nanofluid flow between two rotating disks in the presence of gyrotactic. Microorganisms. 10.1142/S1793292024501108

  • CrossRef
  • Google Scholar

• 38

  Khan M. Rasheed A. (2021). Slip velocity and temperature jump effects on molybdenum disulfide MoS2 and silicon oxide SiO2 hybrid nanofluid near irregular 3D surface. Alex. Eng. J.60 (1), 1689–1701. 10.1016/j.aej.2020.11.019

  • CrossRef
  • Google Scholar

• 39

  Lee S. Choi S. U.-S. Li S. Eastman J. A. (1999). Measuring thermal conductivity of fluids containing oxide nanoparticles. J. Heat. Transf.121 (2), 280–289. 10.1115/1.2825978

  • CrossRef
  • Google Scholar

• 40

  Mostafazadeh A. Toghraie D. Mashayekhi R. Akbari O. A. (2019). Effect of radiation on laminar natural convection of nanofluid in a vertical channel with single- and two-phase approaches. J. Therm. Anal. Calorim.138 (1), 779–794. 10.1007/s10973-019-08236-2

  • CrossRef
  • Google Scholar

• 41

  Mousavi S. M. Biglarian M. Darzi A. A. R. Farhadi M. Afrouzi H. H. Toghraie D. (2020). Heat transfer enhancement of ferrofluid flow within a wavy channel by applying a non-uniform magnetic field. J. Therm. Anal. Calorim.139 (5), 3331–3343. 10.1007/s10973-019-08650-6

  • CrossRef
  • Google Scholar

• 42

  Muthucumaraswamy R. Ganesan P. (2001). Effect of the chemical reaction and injection on flow characteristics in an unsteady upward motion of an isothermal plate. J. Appl. Mech. Tech. Phys.42, 665–671. 10.1023/A:1019259932039

  • CrossRef
  • Google Scholar

• 43

  Nourazar S. S. Hatami M. Ganji D. D. Khazayinejad M. (2017). Thermal-flow boundary layer analysis of nanofluid over a porous stretching cylinder under the magnetic field effect. Powder Technol.317, 310–319. 10.1016/j.powtec.2017.05.010

  • CrossRef
  • Google Scholar

• 44

  Padmaja K. Rushi Kumar B. Bég O. A. Bég T. A. (2023). Cross diffusion and higher order chemical reaction effects on hydromagnetic copper-water nanofluid flow over a rotating cone with porous medium. J. Multiscale Model.14. 23500063. 10.1142/S1756973723500063

  • CrossRef
  • Google Scholar

• 45

  Pirvut M. V. Grigore N. Mihai I. Priporeanu A. T. Racheriu M. Cretu D. et al (2018). Comparative study between polydioxanone unidirectional barbed suture and absorbable polyglactin running suture in partial nephrectomy. Mater. Plast.55 (1), 82–90. 10.37358/MP.18.1.4968

  • CrossRef
  • Google Scholar

• 46

  Rahman M. M. Aziz A. Al-Lawatia M. A. (2010). Heat transfer in micropolar fluid along an inclined permeable plate with variable fluid properties. Int. J. Therm. Sci.49 (6), 993–1002. 10.1016/j.ijthermalsci.2010.01.002

  • CrossRef
  • Google Scholar

• 47

  Rahman M. M. Rahman M. A. Samad M. A. Alam M. S. (2009a). Heat transfer in a micropolar fluid along a non-linear stretching sheet with a temperature-dependent viscosity and variable surface temperature. Int. J. Thermophys.30 (5), 1649–1670. 10.1007/s10765-009-0656-5

  • CrossRef
  • Google Scholar

• 48

  Rahman M. M. Sattar M. A. (2005). Magnetohydrodynamic convective flow of a micropolar fluid past a continuously moving vertical porous plate in the presence of heat generation/absorption. J. Heat. Transf.128 (2), 142–152. 10.1115/1.2136918

  • CrossRef
  • Google Scholar

• 49

  Rahman M. M. Uddin M. J. Aziz A. (2009b). Effects of variable electric conductivity and non-uniform heat source (or sink)on convective micropolar fluid flow along an inclined flat plate with surfaceheat flux. Int. J. Therm. Sci.48 (12), 2331–2340. 10.1016/j.ijthermalsci.2009.05.003

  • CrossRef
  • Google Scholar

• 50

  Rashad A. M. Nafe M. A. Eisa D. A. (2023). Heat generation and thermal radiation impacts on flow of magnetic eyring–powell hybrid nanofluid in a porous medium. Arab. J. Sci. Eng.48 (1), 939–952. 10.1007/s13369-022-07210-9

  • CrossRef
  • Google Scholar

• 51

  Rawat S. K. Yaseen M. Khan U. Kumar M. Eldin S. M. Alotaibi A. M. et al (2023). Significance of non-uniform heat source/sink and cattaneo-christov model on hybrid nanofluid flow in a Darcy-forchheimer porous medium between two parallel rotating disks. Front. Mater.9, 1097057. 10.3389/fmats.2022.1097057

  • CrossRef
  • Google Scholar

• 52

  Reddy B. P. (2019). Radiation and chemical reaction effects on unsteady MHD free convection parabolic flow past an infinite isothermal vertical plate with viscous dissipation. Int. J. Appl. Mech. Eng.24 (2), 343–358. 10.2478/ijame-2019-0022

  • CrossRef
  • Google Scholar

• 53

  Roja A. (2022). Scrutinization of entropy on MHD Eyring–Powell C71500–Ti ₆ Al ₄ V nanoparticles suspended in a C ₂ H ₆ O ₂ −H ₂ O hybrid base fluid with heat generation. Heat. Transf.51 (1), 193–209. 10.1002/htj.22302

  • CrossRef
  • Google Scholar

• 54

  Samad M. A. Mansur-Rahman M. (1970). Thermal radiation interaction with unsteady MHD flow past a vertical porous plate immersed in a porous medium. J. Nav. Archit. Mar. Eng.3 (1), 7–14. 10.3329/jname.v3i1.924

  • CrossRef
  • Google Scholar

• 55

  Saqib M. Khan I. Shafie S. (2019). Application of fractional differential equations to heat transfer in hybrid nanofluid: modeling and solution via integral transforms. Adv. Differ. Equ.2019 (1), 52. 10.1186/s13662-019-1988-5

  • CrossRef
  • Google Scholar

• 56

  Shoaib M. Raja M. A. Z. Sabir M. T. Islam S. Shah Z. Kumam P. et al (2020). Numerical investigation for rotating flow of MHD hybrid nanofluid with thermal radiation over a stretching sheet. Sci. Rep.10 (1), 18533. 10.1038/s41598-020-75254-8

  • CrossRef
  • Google Scholar

• 57

  Sudhagar P. Kameswaran P. K. Rushi Kumar B. (2017). Magnetohydrodynamics mixed convection flow of a nanofluid in an isothermal vertical cone. J. Heat. Transf.139 (3), 034503. 10.1115/1.4035039

  • CrossRef
  • Google Scholar

• 58

  Sumithra A. Rushi Kumar B. Sivaraj R. Öztop H. F. (2023). Thermal analysis of magnetic Iron-Oxide nanoparticle with combination of Water and Ethylene Glycol passes through a partially heated permeable square enclosure. J. taibah Univ. Sci.17 (1), 2257366. 10.1080/16583655.2023.2257366

  • CrossRef
  • Google Scholar

• 59

  Venkateswarlu B. Narayana P. V. S. (2019). Variable wall concentration and slip effects on MHD nanofluid flow past a porous vertical flat plate. J. Nanofluids8 (4), 838–844. 10.1166/jon.2019.1632

  • CrossRef
  • Google Scholar

• 60

  Vishnu Ganesh N. Abdul Hakeem A. K. Ganga B. (2016). A comparative theoretical study on Al2O3 and γ-Al2O3 nanoparticles with different base fluids over a stretching sheet. Adv. Powder Technol.27 (2), 436–441. 10.1016/j.apt.2016.01.015

  • CrossRef
  • Google Scholar

• 61

  Wang X. Xu X. Choi S. U. S. (1999). Thermal conductivity of nanoparticle - fluid mixture. J. Thermophys. Heat. Transf.13 (4), 474–480. 10.2514/2.6486

  • CrossRef
  • Google Scholar

• 62

  Xuan Y. Li Q. (2003). Investigation on convective heat transfer and flow features of nanofluids. J. Heat. Transf.125 (1), 151–155. 10.1115/1.1532008

  • CrossRef
  • Google Scholar

• 63

  Yadav D. (2019). The onset of longitudinal convective rolls in a porous medium saturated by a nanofluid with non-uniform internal heating and chemical reaction. J. Therm. Anal. Calorim.135 (2), 1107–1117. 10.1007/s10973-018-7748-z

  • CrossRef
  • Google Scholar

• 64

  Yahya A. U. Salamat N. Huang W.-H. Siddique I. Abdal S. Hussain S. (2021). Thermal charactristics for the flow of Williamson hybrid nanofluid (MoS2 + ZnO) based with engine oil over a streched sheet. Case Stud. Therm. Eng.26, 101196. 10.1016/j.csite.2021.101196

  • CrossRef
  • Google Scholar

• 65

  Zimparov V. (2002). Energy conservation through heat transfer enhancement techniques. Int. J. Energy Res.26 (7), 675–696. 10.1002/er.810

  • CrossRef
  • Google Scholar