Two-dimensional coronene fractals: modified reverse degree indices, comparative analysis of information entropy and predictive modeling of spectral properties

Topological characterization through graph-theoretical methods translates chemical and structural data into quantitative values that represent the molecular system. Our research explores the use of topological indices to study fractal structures. Molecular fractals are complex geometric configurations that exhibit self-similarity at different levels and systematically formed by repeating a fundamental unit. This study focuses on coronene-based molecular fractals, where coronene, a benzenoid molecule with a symmetrical graphite-like structure, finds applications in organic semiconductors, sensors, and molecular electronics, due to its unique electronic and optical properties. Additionally, information entropy is employed to evaluate and compare the structural complexities of coronene fractals. Spectra-based energetic properties such as total $\pi$-electron energy, HOMO-LUMO energy gaps, spectral diameter, delocalization and resonance energies are calculated to assess their kinetic and thermodynamic stability. Furthermore, predictive models are provided for estimating spectral characteristics across higher-dimensional coronene fractal structures.

1 Introduction

Benzenoid hydrocarbons are a group of polycyclic compounds consisting of six-member linked rings, characterized by their aroma and unique physicochemical properties. These substances create powerful inter-molecular bonds by acting in single and double bonds alternatively (Hill et al., 2004). Higher-order structural co-ordination is indicated by larger $\pi$-conjugated complexes. These characteristics primarily make them useful for applications in opto-electronic devices, nanomaterials, and natural semiconductors (Pisula et al., 2010; Pisula et al., 2011). Coronene, a planar molecule with seven peri-fused benzene rings, is well-known for having delocalized $\pi$-electrons, extended conjugation, and extreme symmetry (Newman, 1940; Robertson and White, 1945; Popov and Boldyrev, 2012). It serves as a fundamental polycyclic aromatic hydrocarbon (PAH) model for studying larger PAHs, graphene quantum dots, and graphene nanoflakes. Coronene-based structures enable precise theoretical investigations and bridge PAHs with graphene materials (Santa Daría et al., 2024; Tachikawa and Lund, 2022). It has a well-defined structure, fluorescence, and electronic properties which makes it a benchmark in theoretical and experimental studies. Coronene fractals exhibit exceptional electronic, optical, and energy-related properties, with strong $\pi$-electron delocalization enhancing charge transport and stable $\pi$-conjugation improving the performance of capacitors and batteries (Demir and Üngördü, 2023; Sanyal et al., 2013; Dobrowolski et al., 2011). Molecular stacking and employers are further enhanced by its symmetrical and planar architecture (Fedotov et al., 2013).

Fractal geometry, which explores recurring patterns at different scales, has evolved from describing physical theories to serve various applications such as complexes in medical and molecular engineering, neural networks, and laptop graphics, etc (Kirkby, 1983). Extensive research has been carried out using fractal methods. These deterministic fractals arise by combining benzene with hierarchical structure sequences, making them a significant tool for advancing nanotechnology and biotechnology (Uahabi and Atounti, 2015). Clar aromatic sextet theory is a concept introduced by Erich Clar to describe the electronic structure of polycyclic aromatic hydrocarbons (PAHs). It is particularly useful for understanding resonance, stability, and reactivity in PAH systems (Hosoya, 2005). Fractal molecular architecture, often analyzed through Clar’s system and golden ratio measurements, exhibits scaling properties that demonstrate its adaptability and potential (Lee and Chang, 1996). Studies of coronene-based fractals have shown that they can serve as supports for advanced nanomaterials (Nisha and Senthil Kumar, 2020). Despite significant advances in theoretical research, the integration of these complex systems remains a challenge, requiring further research (Kumar et al., 2017). Recent work emphasis on the unique aromatic properties and scaling behavior of fractal benzenoids, emphasizes their importance in development and fabrication of high-performance nanomaterials for optical and electronic device applications (Duan et al., 2021).

In computational chemistry, topological indices considered as are important tools that provide information on the chemical and structural characteristics of molecules (Estrada and Uriarte, 2001; Kumar and Das, 2024). Among these, the degree-based Zagreb index and the distance-based Wiener index have been crucial in forecasting molecular characteristics, including stability and boiling points (Wiener, 1947; Gutman and Trinajstić, 1972). In this article, we utilize modified reverse degree-based indices that incorporate a variable parameter, “$k$,” which potentially alters the graph’s degree sequence. Unlike traditional methods with fixed-degree sequences, this approach allows customization of the “$k$,” value to better correlate with specific datasets and their properties. This method is not limited to specific indices and can be applied to all degree-based indices. Notably, as the “$k$,” value increases, these modified indices exhibit a high correlation with the physicochemical characteristics of corona, blood cancer, and heart disease treatment drug molecules (Arockiaraj et al., 2023a; Arockiaraj et al., 2023b; Arockiaraj et al., 2024). In addition, they are used for stability analysis in advanced materials like carbon nanosheets, metal-organic frameworks, and pent-heptagonal nanostructures (Abul Kalaam and Berin Greeni, 2024). Further, employing hybrid models allows for more precise predictions of molecular activity (Arockiaraj et al., 2023c).

Entropy analysis is a fundamental method in the field of information theory, which offers special insights into the complexity and stability of molecules. Shannon’s entropy measures structural randomness (Dehmer, 2008; Shannon, 1948), while graph entropy is related to the vertices and edges of molecular graphs, which makes it easier to analyze a system using graph structures. Higher entropy of a structure constitutes more disorderness in the macrostructure, which reduces structural stability. However, high entropy materials, such as high-entropy alloys (HEAs), exhibit unique properties due to their high configurational entropy, which can result in the formation of stable disordered solid solutions. While high entropy promotes disorderness, it can also contribute to distinctive structural stabilities and desirable properties. For instance, HEAs are known for their high strength, ductility, and resistance to wear and corrosion.

Research articles focused on molecular fractals have explored various structural and topological aspects (Malik et al., 2023; Xu and Liu, 2025; Yogalakshmi and Easwaramoorthy, 2024). Recent studies on coronene fractals have examined degree and degree-sum properties, reverse degree-based indices, and coronene frameworks, as discussed in (Arockiaraj et al., 2022; Ullah et al., 2024; Khabyah et al., 2023). This study explores coronene fractal structures, analyzing their entropy levels and complexity through modified reverse degree-based indices. By delving into their structural and spectral features, it aims to deepen our understanding of their stability, complexity, and overall properties.

2 Methodology

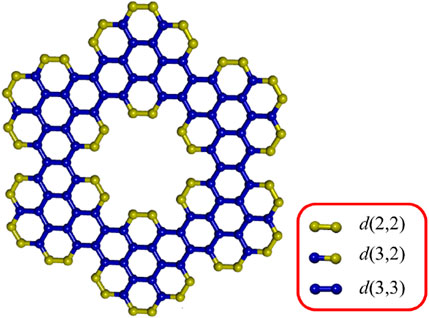
In this study, we examine three configurations of coronene fractals modeled as two-dimensional molecular graph structure and is represented by $G$, with $|V(G)|$ and $|E(G)|$ denote the number of vertices and edges, respectively. The degree of a vertex $a\in V(G)$ denoted as $d(a)$, indicates the number of vertices directly connected to $a$. The maximum degree, $\mathrm{\Delta }(G)$, represents the highest connectivity among all vertices in the graph $G$. Recent modification in reverse degree is done by introducing a parameter $k$ (with $k\ge 1$) that enhance the graph degree sequence to closely predict properties (Arockiaraj et al., 2023a). The modified reverse degree, represented $M_k\mathfrak{R}d(a)$, is defined as follows:

$M_k\mathfrak{R}\left(d(a)\right)=\left\{\begin{array}{cc}\mathrm{\Delta }\left(G\right)-d(a)+k\hfill & :k\le d(a)\hfill \\ \mathrm{\Delta }\left(G\right)-d(a)+k\left(mod\mathrm{\Delta }\left(G\right)\right)\hfill & :k>d(a)\hfill \end{array}\right.$

Modified reverse degree-based topological indices, $M_k\mathfrak{R}TI$, are employed to characterize coronene fractals by evaluating atom connectivity and providing insights into their molecular structure. For a graph $G$, the formulation of $M_k\mathfrak{R}TI$ is given as:

$M_k\mathfrak{R}TI\left(G\right)={\displaystyle \sum _{ab\in E\left(G\right)}}{M}_k\mathfrak{R}TI\left(d\left(a\right),d\left(b\right)\right)={\displaystyle \sum _{ab\in E\left(G\right)}}TI\left(M_k\mathfrak{R}\left(d\left(a\right)\right),M_k\mathfrak{R}\left(d\left(b\right)\right)\right),$

where $ab$ represents the edge connecting vertices $a$ and $b$. This formula provides an intensive evaluation by using the contributions of all edges inside the graph. The edge set $E(G)$ is divided into equivalent subsets, such that $E(G)={\bigcup }_{i=1}^n{E}_i$. Each subset of $E_i$, where $ab\in E_i$ and $i=\mathrm{1,2},\dots ,n$, groups edges based on vertex connectivity in $G$. For any subset $E_i$, the corresponding $M_k\mathfrak{R}TI$ is calculated as:

$M_k\mathfrak{R}TI\left(E_i\right)=|E_i|\times TI\left(M_k\mathfrak{R}\left(d\left(a\right)\right),M_k\mathfrak{R}\left(d\left(b\right)\right)\right),$

where $|E_i|$ represents the number of edges in subset $E_i$, and $TI(M_k\mathfrak{R}(d(a)),M_k\mathfrak{R}(d(b)))$ evaluates the contribution of modified reverse degree for the connected vertices.

The total $M_k\mathfrak{R}TI$ for graph $G$ is obtained by summing the contributions from all subsets $E_i$:

$M_k\mathfrak{R}TI\left(G\right)={\displaystyle \sum _{i=1}^n}|E_i|\times TI\left(M_k\mathfrak{R}\left(d\left(a\right)\right),M_k\mathfrak{R}\left(d\left(b\right)\right)\right)$

The topological index functions based on the modified reverse degree are outlined below.

• Modified reverse first Zagreb index $(M_k\mathfrak{R}{M}_1)$:

$M_k\mathfrak{R}{M}_1\left(d\left(a\right),d\left(b\right)\right)=M_k\mathfrak{R}\left(d\left(a\right)\right)+M_k\mathfrak{R}\left(d\left(b\right)\right)(1)$

• Modified reverse second Zagreb index $(M_k\mathfrak{R}{M}_2)$:

$M_k\mathfrak{R}{M}_2\left(d\left(a\right),d\left(b\right)\right)=M_k\mathfrak{R}\left(d\left(a\right)\right)\times M_k\mathfrak{R}\left(d\left(b\right)\right)(2)$

• Modified reverse forgotten index $(M_k\mathfrak{R}F)$:

$M_k\mathfrak{R}F\left(d\left(a\right),d\left(b\right)\right)={\left(M_k\mathfrak{R}\left(d\left(a\right)\right)\right)}^2+{\left(M_k\mathfrak{R}\left(d\left(b\right)\right)\right)}^2(3)$

• Modified reverse Sombor index $(M_k\mathfrak{R}S)$:

$M_k\mathfrak{R}S\left(d\left(a\right),d\left(b\right)\right)=\sqrt{{\left(M_k\mathfrak{R}\left(d\left(a\right)\right)\right)}^2+{\left(M_k\mathfrak{R}\left(d\left(b\right)\right)\right)}^2}(4)$

• Modified reverse geometric arithmetic index $(M_k\mathfrak{R}GA)$:

$M_k\mathfrak{R}GA\left(d\left(a\right),d\left(b\right)\right)=\frac{2\cdot \sqrt{M_k\mathfrak{R}\left(d\left(a\right)\right)\times M_k\mathfrak{R}\left(d\left(b\right)\right)}}{M_k\mathfrak{R}\left(d\left(a\right)\right)+M_k\mathfrak{R}\left(d\left(b\right)\right)}(5)$

• Modified reverse hyper-Zagreb index $(M_k\mathfrak{R}HZ)$:

$M_k\mathfrak{R}HZ\left(d\left(a\right),d\left(b\right)\right)={\left(M_k\mathfrak{R}\left(d\left(a\right)\right)+M_k\mathfrak{R}\left(d\left(b\right)\right)\right)}^2(6)$

• Modified reverse harmonic index $(M_k\mathfrak{R}H)$:

$M_k\mathfrak{R}H\left(d\left(a\right),d\left(b\right)\right)=\frac{2}{M_k\mathfrak{R}\left(d\left(a\right)\right)+M_k\mathfrak{R}\left(d\left(b\right)\right)}(7)$

• Modified reverse first redefined Zagreb index $(M_k\mathfrak{R}Re{Z}_1)$:

$M_k\mathfrak{R}Re{Z}_1\left(d\left(a\right),d\left(b\right)\right)=\frac{M_k\mathfrak{R}\left(d\left(a\right)\right)+M_k\mathfrak{R}\left(d\left(b\right)\right)}{M_k\mathfrak{R}\left(d\left(a\right)\right)\times M_k\mathfrak{R}\left(d\left(b\right)\right)}(8)$

• Modified reverse second redefined Zagreb index $(M_k\mathfrak{R}Re{Z}_2)$:

$M_k\mathfrak{R}Re{Z}_2\left(d\left(a\right),d\left(b\right)\right)=\frac{M_k\mathfrak{R}\left(d\left(a\right)\right)\times M_k\mathfrak{R}\left(d\left(b\right)\right)}{M_k\mathfrak{R}\left(d\left(a\right)\right)+M_k\mathfrak{R}\left(d\left(b\right)\right)}(9)$

• Modified reverse bi-Zagreb index $(M_k\mathfrak{R}BM)$:

$M_k\mathfrak{R}BM\left(d\left(a\right),d\left(b\right)\right)=M_k\mathfrak{R}\left(d\left(a\right)\right)+M_k\mathfrak{R}\left(d\left(b\right)\right)+\left(M_k\mathfrak{R}\left(d\left(a\right)\right)\times M_k\mathfrak{R}\left(d\left(b\right)\right)\right)(10)$

• Modified reverse tri-Zagreb index $(M_k\mathfrak{R}TM)$:

$M_k\mathfrak{R}TM\left(d\left(a\right),d\left(b\right)\right)={\left(M_k\mathfrak{R}\left(d\left(a\right)\right)\right)}^2+{\left(M_k\mathfrak{R}\left(d\left(b\right)\right)\right)}^2+\left(M_k\mathfrak{R}\left(d\left(a\right)\right)\times M_k\mathfrak{R}\left(d\left(b\right)\right)\right)(11)$

• Modified reverse geometric bi-Zagreb index $(M_k\mathfrak{R}GBM)$:

$M_k\mathfrak{R}GBM\left(d\left(a\right),d\left(b\right)\right)=\frac{\sqrt{M_k\mathfrak{R}\left(d\left(a\right)\right)\times M_k\mathfrak{R}\left(d\left(b\right)\right)}}{M_k\mathfrak{R}\left(d\left(a\right)\right)+M_k\mathfrak{R}\left(d\left(b\right)\right)+M_k\mathfrak{R}\left(d\left(a\right)\right)\times M_k\mathfrak{R}\left(d\left(b\right)\right)}(12)$

3 Evaluation of modified reverse degree indices

We explore three coronene fractal configurations: ZHCF$(n)$, AHCF$(n)$, and RCF$(m,n)$, as illustrated in Figures 1, 2. The structural parameters for these configurations are given by: $|V(\text{ZHCF}(n))|=126n^2+6n$ and $|E(\text{ZHCF}(n))|=171n^2+3n$; for AHCF, these are $|V(\text{AHCF}(n))|=378n^2-366n+120$ and $|E(\text{AHCF}(n))|=513n^2-507n+168$; and for RCF, they are $|V(\text{RCF}(m,n))|=84mn+2m+46n$ and $|E(\text{RCF}(m,n))|=114mn+m+59n$. All configurations share a maximum vertex degree of 3. The modified reverse degree metrics for each vertex are as follows:

$M_1\mathfrak{R}\left(d\left(a\right)\right)=\left\{\begin{array}{cc}2\hfill & :d\left(a\right)=2\hfill \\ 1\hfill & :d\left(a\right)=3\hfill \end{array}\right.$

$M_2\mathfrak{R}\left(d\left(a\right)\right)=\left\{\begin{array}{cc}3\hfill & :d\left(a\right)=2\hfill \\ 2\hfill & :d\left(a\right)=3\hfill \end{array}\right.$

$M_3\mathfrak{R}\left(d\left(a\right)\right)=\left\{\begin{array}{cc}1\hfill & :d\left(a\right)=2\hfill \\ 3\hfill & :d\left(a\right)=3\hfill \end{array}\right.$

Figure 1

Figure 1. The degree based enumeration of coronene fractal structure.

Figure 2

Figure 2. Configurations of coronene fractals (a) ZHCF(3) (b) AHCF(2) (c) RCF(5,3).

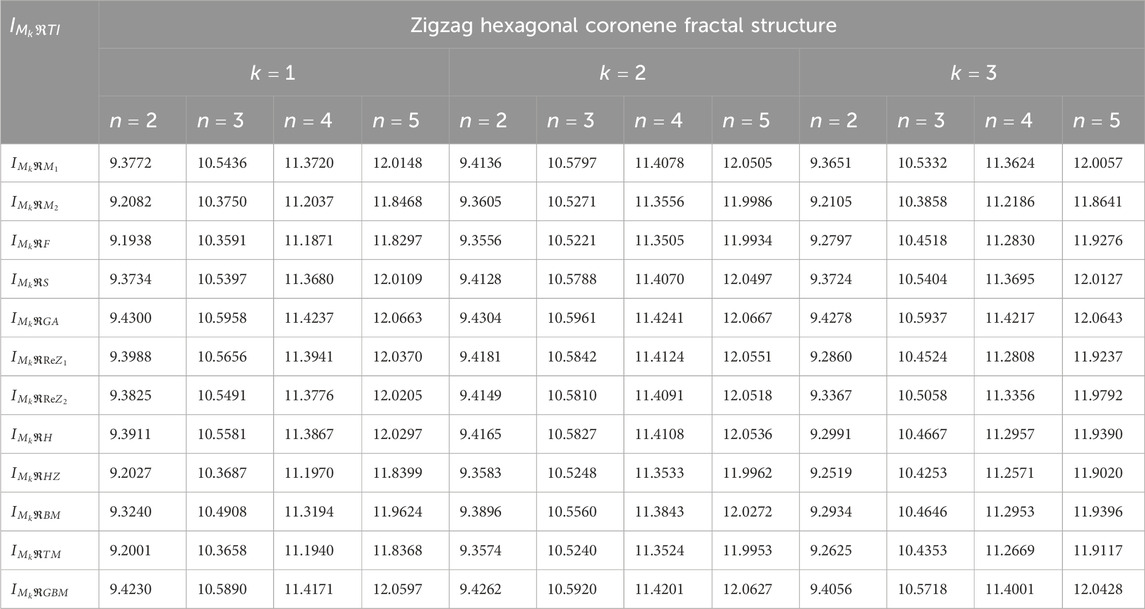
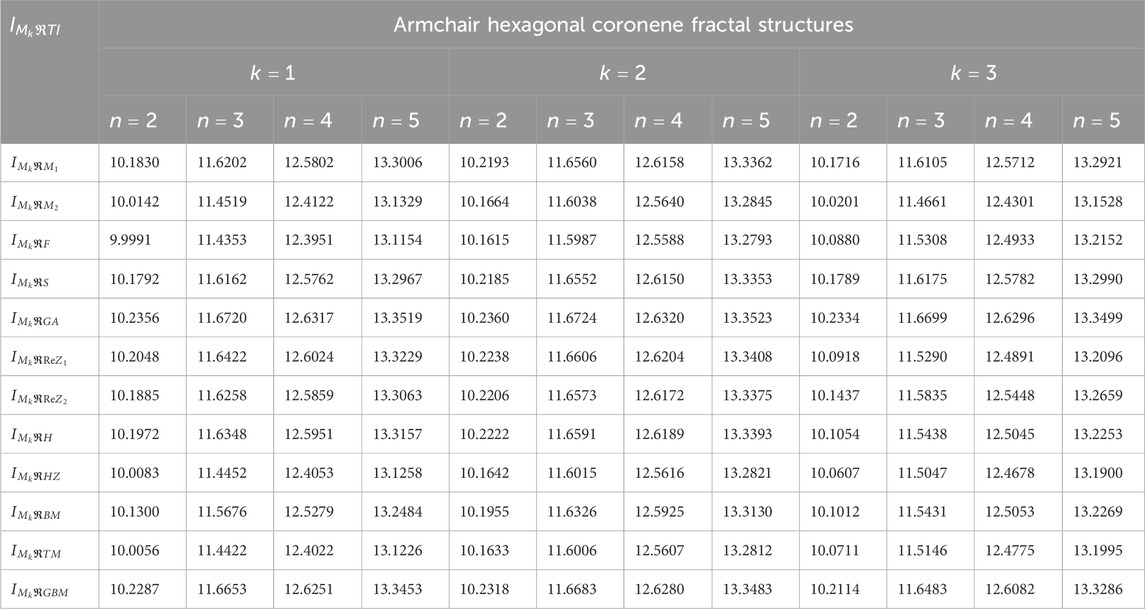
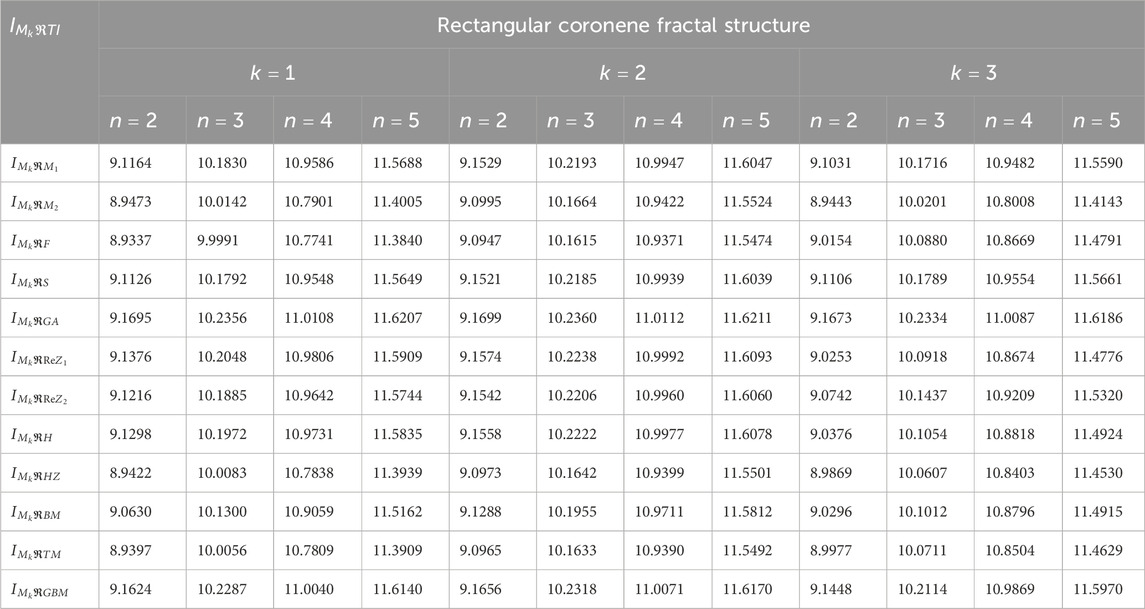
To calculate the modified reverse topological indices, edge partitioning is used, as illustrated in Figure 1, for three configurations of coronene fractals based on their standard vertex degrees, as detailed in Table 1. Each index involves complex computations with varying parameters. For instance, the calculation of the first Zagreb-based index is demonstrated using ZHCF coronene structures for different values of $k=\mathrm{1,2,3}$. When the variable parameter is set to $k=1$, the degree pairs (2,2), (2,3), and (3,3) are modified to (2,2), (2,1), and (1,1), respectively. Therefore,

$\begin{array}{ll}\hfill M_1\mathfrak{R}{M}_1\left(ZHCF\left(n\right)\right)& =|E\left(\mathrm{2,2}\right)|\times M_1\mathfrak{R}d\left(\mathrm{2,2}\right)+|E\left(\mathrm{2,3}\right)|\times M_1\mathfrak{R}d\left(\mathrm{2,3}\right)+|E\left(\mathrm{3,3}\right)|\times M_1\mathfrak{R}d\left(\mathrm{3,3}\right)\hfill \\ \hfill & =\left(18n^2+6n\right)\times \left(2+2\right)+\left(36n^2+12n\right)\times \left(2+1\right)+\left(117n^2-15n\right)\times \left(1+1\right)\hfill \\ \hfill & =414n^2+30n\hfill \end{array}$

Table 1

Table 1. Degree based edge partition of three configurations of coronene fractals.

For $k=2$ the degree classes are modified into (3,3), (3,2), and (2,2). Therefore,

$\begin{array}{ll}\hfill M_2\mathfrak{R}{M}_1\left(ZHCF\left(n\right)\right)& =|E\left(\mathrm{2,2}\right)|\times M_1\mathfrak{R}d\left(\mathrm{2,2}\right)+|E\left(\mathrm{2,3}\right)|\times M_1\mathfrak{R}d\left(\mathrm{2,3}\right)+|E\left(\mathrm{3,3}\right)|\times M_1\mathfrak{R}d\left(\mathrm{3,3}\right)\hfill \\ \hfill & =\left(18n^2+6n\right)\times \left(3+3\right)+\left(36n^2+12n\right)\times \left(3+2\right)+\left(117n^2-15n\right)\times \left(2+2\right)\hfill \\ \hfill & =756n^2+36n\hfill \end{array}$

Similarly for $k=3$ the degree classes are modified into (1,1), (1,3), and (3,3). Therefore,

$\begin{array}{ll}\hfill M_3\mathfrak{R}{M}_1\left(ZHCF\left(n\right)\right)& =|E\left(\mathrm{2,2}\right)|\times M_1\mathfrak{R}d\left(\mathrm{2,2}\right)+|E\left(\mathrm{2,3}\right)|\times M_1\mathfrak{R}d\left(\mathrm{2,3}\right)+|E\left(\mathrm{3,3}\right)|\times M_1\mathfrak{R}d\left(\mathrm{3,3}\right)\hfill \\ \hfill & =\left(18n^2+6n\right)\times \left(1+1\right)+\left(36n^2+12n\right)\times \left(1+3\right)+\left(117n^2-15n\right)\times \left(3+3\right)\hfill \\ \hfill & =882n^2+30n\hfill \end{array}$

The modified reverse degree-based indices illustrated in Equations 1–12, combined with the edge partitioning present in Table 1, are employed to compute the $M_k\mathfrak{R}TI$ for three configurations of coronene fractals. The results, corresponding to the variable parameters $k=\mathrm{1,2}$, and 3, are summarized in Tables 2–4.

Table 2

Table 2. Modified reverse degree indices of ZHCF structure for variable parameters $k$ = 1, 2, and 3.

Table 3

Table 3. Modified reverse degree indices of AHCF structure for variable parameters $k$ = 1, 2, and 3.

Table 4

Table 4. Modified reverse degree indices of RCF structure for variable parameters $k$ = 1, 2, and 3.

4 Evaluation of graph entropy

A mathematical foundation for assessing a system’s randomness and uncertainty is provided by Shannon’s concept of entropy, which quantifies the content of possibility distributions. For a discrete random variable $(x_1,x_2,\dots ,x_n)$ with chances $(h(x_1),h(x_2),\dots ,h(x_n))$, thus Shannon’s entropy $(\mathcal{H})$, is expressed as:

$\mathcal{H}=-{\displaystyle \sum _{i=1}^n}h\left(x_i\right){\log }_{2}h\left(x_i\right),$

where $h(x_i)=\frac{N_i}{N}$, $N_i$ represents the frequency of a specific outcome $x_i$, and $N$ is the total number of outcomes (Shannon, 1948). The information obtained from measuring the system is captured by using the logarithm base-2 to validate the entropy values in bits. This equation has a significant analogy to thermodynamic entropy, which quantifies the randomness of states in a physical system (Mowshowitz and Dehmer, 2012; Sabirov and O-sawa, 2015). In Physics, thermodynamic entropy is used to assess microstates, while Shannon’s entropy is generally applicable to abstract systems, such as graphs, and allows for the analysis of their structural complexity using attributes like vertices and edges (Mowshowitz, 1968).

Based on this foundation, incorporating topological indices into the entropy framework appears as a robust approach to assess molecular complexity. This approach focuses on graph edges and uses topological indices $(TIs)$, which are mathematical structural characterization of molecular graphs (Arockiaraj et al., 2023d). The probability given to each edge of a molecular graph $G$, with edges $ab\in E(G)$ is defined as $\frac{f(ab)}{M_k\mathfrak{R}TI}$, where $f(ab)$ is a modified reverse degree-based function and $M_k\mathfrak{R}TI$ is the associated index. The graph entropy is expressed as:

$I_{M_k\mathfrak{R}TI}=-{\displaystyle \sum _{ab\in E\left(G\right)}}\frac{f\left(ab\right)}{M_k\mathfrak{R}TI}{\log }_2\left(\frac{f\left(ab\right)}{M_k\mathfrak{R}TI}\right).$

Further the graph entropy equation simplifies as:

$I_{M_k\mathfrak{R}TI}={\log }_2\left(M_k\mathfrak{R}TI\left(G\right)\right)-\frac{1}{M_k\mathfrak{R}TI\left(G\right)}{\displaystyle \sum _{ab\in E\left(G\right)}}f\left(ab\right){\log }_{2}f\left(ab\right).$

By employing specific topological indices, the simplified representation makes it easier to calculate graph entropy for a molecular graphs of coronene fractals. For example, the modified first Zagreb index applied to a ZHCF$(n)$ structure. The result of substituting into the entropy formula is:

$I_{M_k\mathfrak{R}{M}_1}={\log }_2\left(M_k\mathfrak{R}{M}_1\right)-\frac{1}{M_k\mathfrak{R}{M}_1}{\displaystyle \sum _{ab\in E\left(G\right)}}f\left(ab\right){\log }_{2}f\left(ab\right).$

Employing degree-based edge partitions presented in Table 1, the entropy of ZHCF$(n)$ when $k=1$ and $M_1\mathfrak{R}{M}_1$ is:

$\begin{array}{ll}\hfill I_{M_1\mathfrak{R}{M}_1}\left(\text{ZHCF}\left(n\right)\right)& ={\log }_2\left(414n^2+30n\right)-\frac{1}{414n^2+30n}\left[18n^2+6n\times \left(4\times {\log }_2\left(4\right)\right)\right.\hfill \\ \hfill & \left.+36n^2+12n\times \left(3\times {\log }_2\left(3\right)\right)+\left(117n^2-15n\right)\times \left(2\times {\log }_2\left(2\right)\right)\right]\text{For\hspace{0.17em}}n=2,\text{\hspace{0.17em}we\hspace{0.17em}obtain:}{I}_{M_1\mathfrak{R}{M}_1}\left(\text{ZHCF}\left(2\right)\right)\hfill & ={\log }_2\left(1716\right)-\frac{1}{1716}\left[2346.82110036\right]=9.37722247\hfill \end{array}$

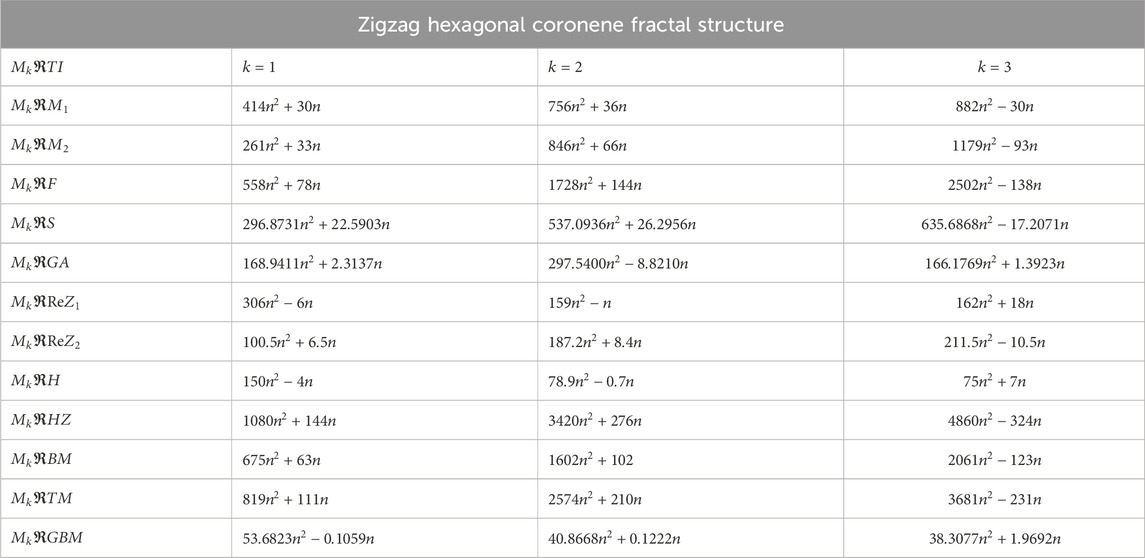
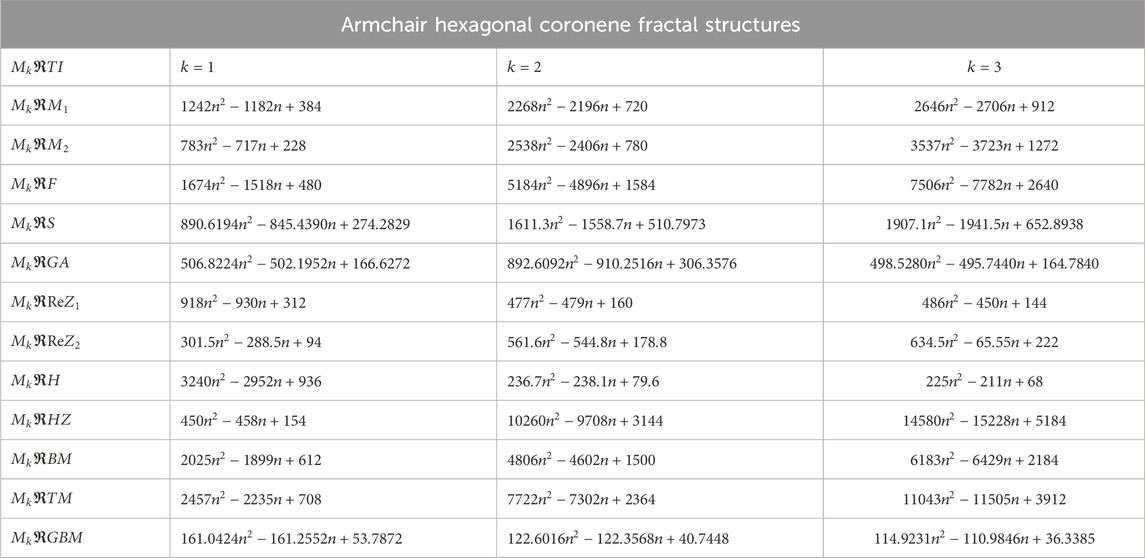
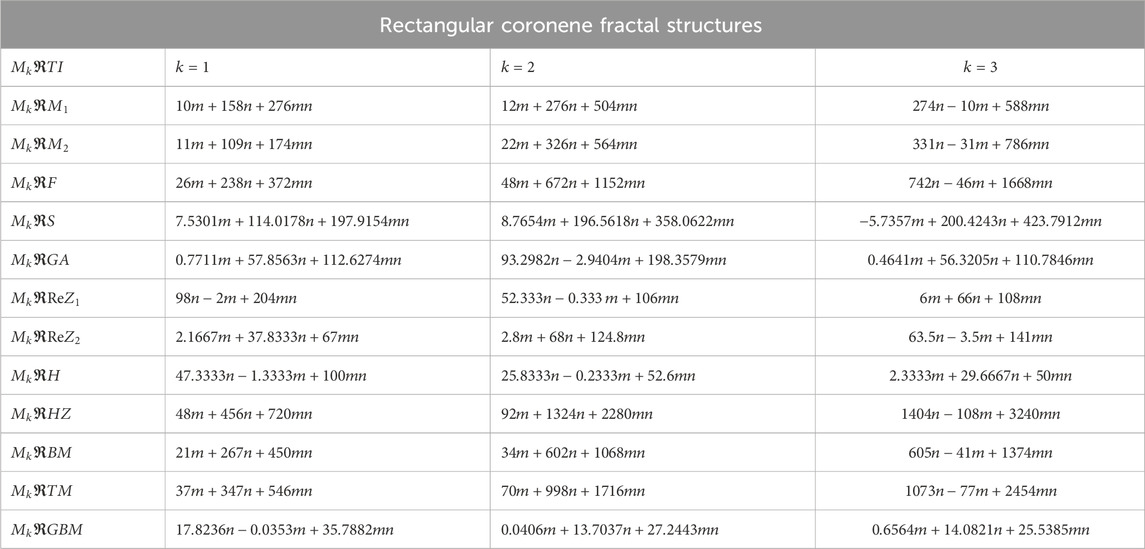
The entropy expressions for all configuration of coronene fractals are too extensive to display. Therefore, Tables 5–7 present the comparison of numerical values of modified reverse degree-based entropy levels for the fractal structures. For rectangular coronene fractals, we assume $m=n$.

Table 5

Table 5. Comparison of entropy levels for ZHCF at $k=1$, $k=2$, and $k=3$.

Table 6

Table 6. Comparison of entropy levels for AHCF at $k=1$, $k=2$, and $k=3$.

Table 7

Table 7. Comparison of entropy levels for RCF where $(m=n)$ at $k=1$, $k=2$, and $k=3$.

The entropy stages provided in Tables 5–7 monitor dynamic variation throughout the three configurations of coronene fractals for $k=\mathrm{1,2}$, and 3. Notably, entropy values continually peaks at $k=2$ in comparison to $k=1$ and $k=3$. The entropy measures differ slightly in their decimal values across all indices. Among the configurations, AHCF demonstrates slightly higher entropy values than the other coronene structures, while RCF exhibits lower entropy values, indicating greater structural stability. However, direct comparisons of complexity measures across these fractal structure are complicated by differences in the number of edges. We utilize relative measures, including structural information content (SIC) and bond information content (BIC), derived from the computed entropy values. These metrics provide a exact evaluation of the structural complexity and stability of the three coronene fractal configurations.

4.1 Relative complexity metrics

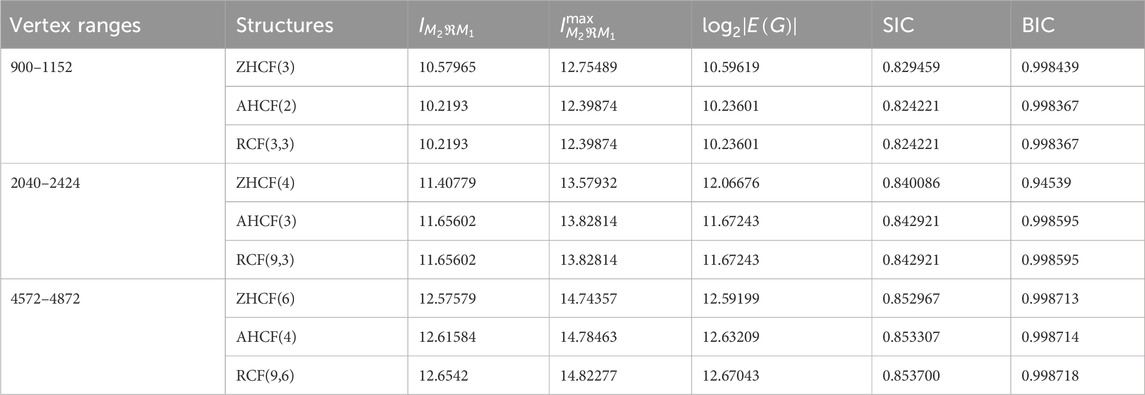
This subsection offers numerical and graphical estimation of complexity across the configurations of coronene fractals, emphasizing the importance of accounting for molecular size differences. Since graph entropy values are depending on the size of the molecular graph, the application of relative complexity measures has become essential for higher comparisons among molecular systems of varying dimensions (Dehmer, 2008). To address this, two normalized measures, namely structural information content (SIC) and bond information content (BIC), are introduced. Graph entropy alone may not adequately reflect structural complexity, especially for systems with differing dimensional sizes, highlighting the necessity of employing relative metrics (Bonchev and Trinajstić, 1982; Sabirov and Shepelevich, 2021). The maximum entropy concept is used to establish these metrics, where the limiting entropy value for $I_{M_k\mathfrak{R}TI}$ is defined as $I_{M_k\mathfrak{R}TI}^{\text{max}}={\log }_2(M_k\mathfrak{R}TI)$ (Junias et al., 2024). This leads to SIC, which quantifies molecular structure and the most useful information, as shown below:

${\text{SIC}}_{M_k\mathfrak{R}TI}=\frac{I_{M_k\mathfrak{R}TI}}{I_{M_k\mathfrak{R}TI}^{\text{max}}}.(13)$

Similarly, BIC includes a molecular graph where edges are counted to compute relative complexity. The formula for the BIC normalizes the entropy using the logarithmic scale of the total number of edges, as shown here:

${\text{BIC}}_{M_k\mathfrak{R}TI}=\frac{I_{M_k\mathfrak{R}TI}}{{\log }_2|E\left(G\right)|}.(14)$

From Equations 13, 14, we calculate the SIC and BIC measures for coronene fractals. The analysis focuses on the entropy values of the Zagreb index when $k=2$, where $I_{M_k\mathfrak{R}TI}=I_{M_2\mathfrak{R}{M}_1}$ providing insight into the relative complexity assessment between the fractals. For example the ZHCF(3) system with $|E(G)|=1548$, the Zagreb index value $I_{M_k\mathfrak{R}TI}=I_{M_2\mathfrak{R}{M}_1}=10.57965167$ and $I_{M_k\mathfrak{R}TI}^{\text{max}}={\log }_2(M_2\mathfrak{R}{M}_1)={\log }_2(6912)$. The values calculated by equations for SIC and BIC are as follows.

${\text{SIC}}_{M_2\mathfrak{R}{M}_1}=\frac{I_{M_2\mathfrak{R}{M}_1}}{{\log }_2\left(M_2\mathfrak{R}{M}_1\right)}=\frac{10.57965167}{12.7548875}=0.829458642$

${\text{BIC}}_{M_2\mathfrak{R}{M}_1}=\frac{I_{M_2\mathfrak{R}{M}_1}}{{\log }_2|E\left(G\right)|}=\frac{10.57965167}{10.59618976}=0.998439242$

The SIC and BIC measures for other coronene fractals across various vertex ranges, are presented in Table 8. These relative complexity measures offer a comparative analysis of complexity across different sizes, with values ranging from 0 to 1, where 1 indicates the highest complexity and 0 the lowest. The SIC and BIC measures, are shown in Table 8, with a graphical comparison in Figure 3.

Table 8

Table 8. Relative complexity measures of three classes of coronene structures.

Figure 3

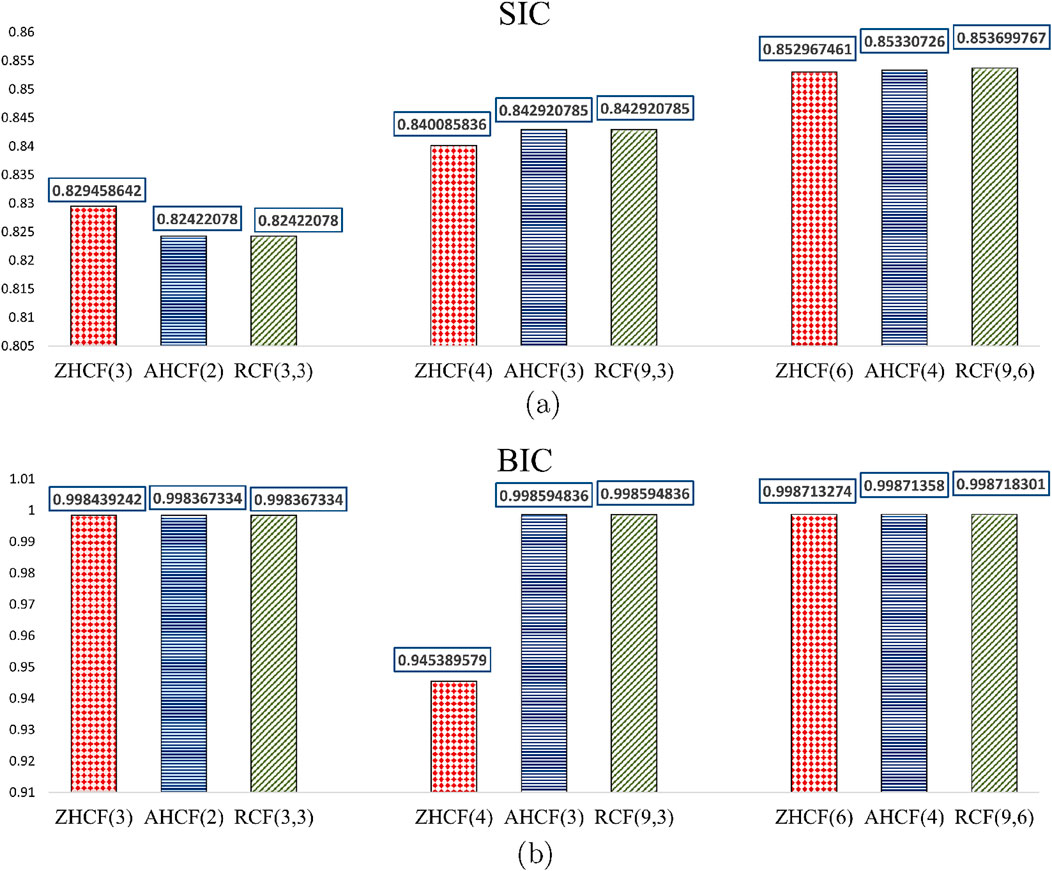
Figure 3. Graphical comparison of complexity measures among zigzag, armchair and rectangular coronene fractals. (a) Comparison of SIC measures across the range of k values for coronene fractals. (b) Comparison of BIC measures across the range of k values for coronene fractals.

Table 8; Figure 3 show that RCF and AHCF exhibit similar complexity values at small scales. However, with increasing size, the rectangular fractals exhibits slightly higher complexity compared to armchair configuration, while the zigzag-based coronene exhibits lower complexity than all other configurations because BIC is evaluated based on number of bonds in molecular graph and SIC obtained from maximum entropy. These two analyzes facilitate better comparisons, and help to determine the most appropriate indicator of complexity measures for molecular system.

From Figure 3; Tables 5–8, greater entropy variations are observed among the three configurations for smaller structures, while for the largest structure, all configurations approach the 2D graphitic sheet, and their entropy values converge to a limit. However, two types of isentropic structures exist: AHCF(2) and RCF(3,3) have the same number of vertices (900) and edges (1206); similarly, AHCF(3) and RCF(9,3) share the same number of vertices (2424) and edges (3264). Thus, we use spectral properties for a more conclusive analysis of stability.

5 Analysis of spectral properties in coronene fractals

This section focuses on the spectral properties of coronene fractals, using metrics derived from their graph spectra. Since these structures are two-dimensional and satisfy the Coulson-Rushbrook theorem, this method is more effective for analysis. It is not practical to perform complete $Abinitio$ calculations for complex systems such as AHCF(3) and RCF(9,3) with 2424 vertices and spectral eigenvalues (Arockiaraj et al., 2022). Consequently, machine learning techniques are needed to efficiently estimate stability in large, fractal structures. Significant spectal and energy properties such as total $\pi$-electron energy, spectral diameter, HOMO-LUMO energy gap, delocalization energy, and resonance energy, are determined by combinatorial analysis of graph spectra (Prabhu et al., 2024). These parameters provide valuable insights into the thermodynamic and kinetic stability of the coronene fractals under investigation.

The total $\pi$-electron energy $\left({\mathcal{E}}_{\pi }\right)$ is a critical measure of electronic stability in conjugated systems (Gutman and Trinajstić, 1972; Gutman, 1978). For coronene fractals, including zigzag, armchair, and rectangular patterns, ${\mathcal{E}}_{\pi }$ is calculated using the eigenvalues $({\lambda }_i)$ of the graph spectra of the molecular graph (Kalaam et al., 2024; Graovac et al., 1977). For a system with $p$ atoms:

${\mathcal{E}}_{\pi }=\left\{\begin{array}{cc}2{\displaystyle \sum _{i=1}^{p/2}}{\lambda }_i,\hfill & \text{if\hspace{0.17em}}p\text{\hspace{0.17em}is\hspace{0.17em}even},\hfill \\ {\lambda }_{\left(p+1\right)/2}+2{\displaystyle \sum _{i=1}^{\left(p-1\right)/2}}{\lambda }_i,\hfill & \text{if\hspace{0.17em}}p\text{\hspace{0.17em}is\hspace{0.17em}odd}.\hfill \end{array}\right.$

The $\pi$-electron distribution depends on whether $p$ is even or odd.

The HOMO-LUMO energy gaps, defined as the difference between the highest molecular orbital (HOMO) denoted ${\lambda }_H$ and the lowest unoccupied molecular orbital (LUMO) denoted ${\lambda }_L$. It plays an important role in analyzing molecular reactivity and kinetic stability. These difference is calculated by subtracting the lowest positive eigenvalue from the highest negative eigenvalue from the graph spectrum, expressed as ${\mathrm{\Delta }}_G={\lambda }_H-{\lambda }_L$ (Wu et al., 2018; Li et al., 2013). Larger HOMO-LUMO energy differences indicate increased kinetic stability and low chemical reactivity, as more energy is required to transfer an electron from HOMO to LUMO, thus decreasing the chemical reactivity however this difference does not directly reflect thermodynamic stability.

Thermodynamic stability is closely related to parameters such as delocalization and resonance energies, which generally increase with molecule size, increasing the stability. The delocalization energy ${({\mathcal{E}}_{\text{Deloc}})}_{\text{per\hspace{0.17em}bond}}$, is calculated as ${({\mathcal{E}}_{\text{Deloc}})}_{\text{per\hspace{0.17em}bond}}={\mathcal{E}}_{\pi }-|V(G)|$. Kekul$\acute{e}$ counts (KC), which reflect the number of Kekul$\acute{e}$ resonance structures in coronene fractals, are used to compute resonance energies as coronene fractals are benzenoid systems and bipartite graphs. Thus (KC) is derived from the square root of the constant term of the characteristic polynomial (Balasubramanian, 2023). According to Herndon’s definition of resonance, $\mathcal{R}{\mathcal{E}}_{\text{per\hspace{0.17em}bond}}=\frac{1}{|V(G)|}\left.\left(1.185\times \ln (\text{KC})\right)\right)$ (Herndon and Ellzey, 1974). The increase in size of the coronene fractals increases both delocalization and resonance energies. Because of the stabilization of the molecular orbitals (Mazouin et al., 2022), the HOMO-LUMO energy gap decreases with increasing molecular size. The spectral diameter $\mathcal{S}\mathcal{D}$ is calculated as the difference between the maximum and minimum eigenvalues: $\mathcal{S}\mathcal{D}={\lambda }_{max}-{\lambda }_{min}$. These graph spectra based energy properties were assessed using programs such as newGRAPH and MATLAB software (Stevanović et al., 2021; MATLAB, 2022). Table 9 displays the results, which are given in $\beta$ units.

Table 9

Table 9. Energetic properties of three classes of polycyclic aromatic hydrocarbons.

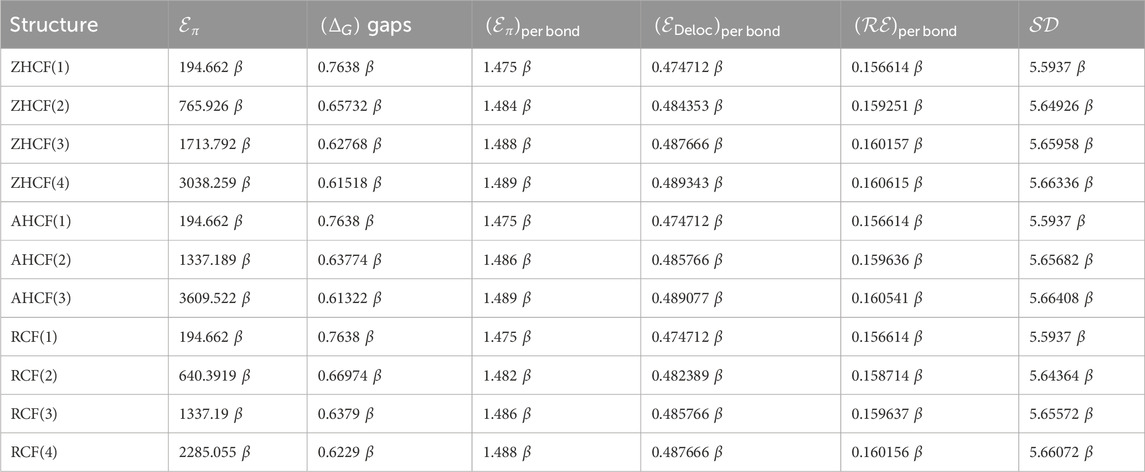
The data present in Table 9; Figure 4 show that the HOMO-LUMO energy gaps decrease as the size of coronene structures increase. This suggests that larger structures have more electronic delocalization and resonance energy, which results in lower energy differences between the highest occupied molecular orbital (HOMO) and the lowest unoccupied molecular orbital (LUMO). Meanwhile, both delocalization and resonance energy show an increasing trend, reflecting enhanced stability and conjugation within these structures. Among the fractal configurations analyzed, the rectangular coronene fractals have the largest HOMO-LUMO energy gaps, suggesting high kinetic stability, lower reactivity, and the lowest delocalization and resonance energies. On the other hand, armchair coronene fractals display the smallest HOMO-LUMO energy gaps, indicating less kinetic stability, larger chemical reactivity, higher electron delocalization, and resonance energies, all of which lead to greater stability with efficient electron transfer. This study emphasizes the significance of structural configuration on stability and reactivity in coronene fractals.

Figure 4

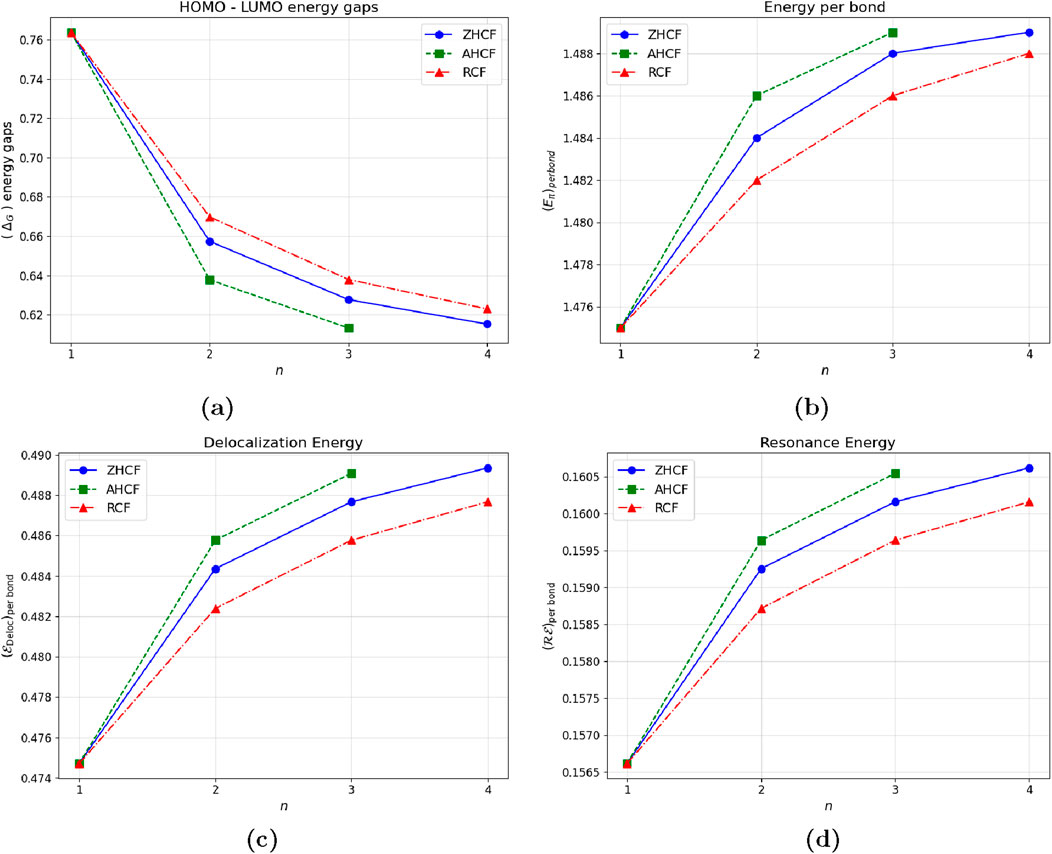
Figure 4. Graphical representation of energetic properties across kekulene tessellations. (a) HOMO-LUMO energy gap (b) Energy per bond (c) Delocalization energy per bond (d) Resonance energy per bond.

6 Predictive models

The prediction of the spectral properties of chemical structure by graph-entropy measures utilizes structure-property models which play an important role in characterizing and prediction chemical properties using topological indices (Raza et al., 2024; Rauf et al., 2022) These models offer a cost-effective alternative to experimental studies, offering reliability, accuracy and robustness (Hayat et al., 2019). For coronene fractals, we examine the relationship between spectral features and entropy measurements obtained from the reverse degree-based indices. Our findings show that there is a better correlation between the entropy measures and spectral properties, except for the HOMO-LUMO energy gap, which exhibits negative correlation due to its decrease in energy gaps with increasing system size. As noted in the previous section, the first Zagreb index was employed to compare relative complexity measures among the structures. We found that entropy measures associated with $M_2\mathfrak{R}{M}_1$ demonstrate the strongest correlation with spectral characteristics. Linear regression analysis was used to develop predictive models for spectral properties. The linear regression equation given as $P=R\cdot (I_{M_k\mathfrak{R}TI})+c$, where $P$ is the spectral properties, $R$ is the regression coefficient, and $c$ is the regression constant. The statistical parameters such as $r^2$, $r^2$, $F$-values, and $S.E$ are utilized to validate model’s performance.

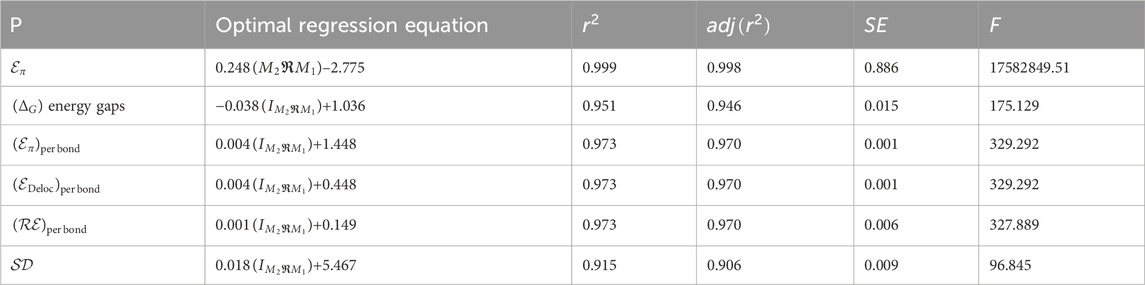
The regression models optimized to predict spectral characteristics are given detailed in Table 10 and illustrated in Figure 5. The selection was based on their unique performance indicators, such as $r^2$, adjusted $r^2$, high $F$-values, in addition to reduced error (SE) objectives. These metrics confirm the reliability and accuracy of the models. The developed models are particularly effective in estimating the energy value of high-aspect ratio coronene explosions. An efficient method based on linear regression was used to ensure accurate predictions while minimizing computational complexity.

Table 10

Table 10. Statistically derived optimal regression models for predicting energetic properties.

Figure 5

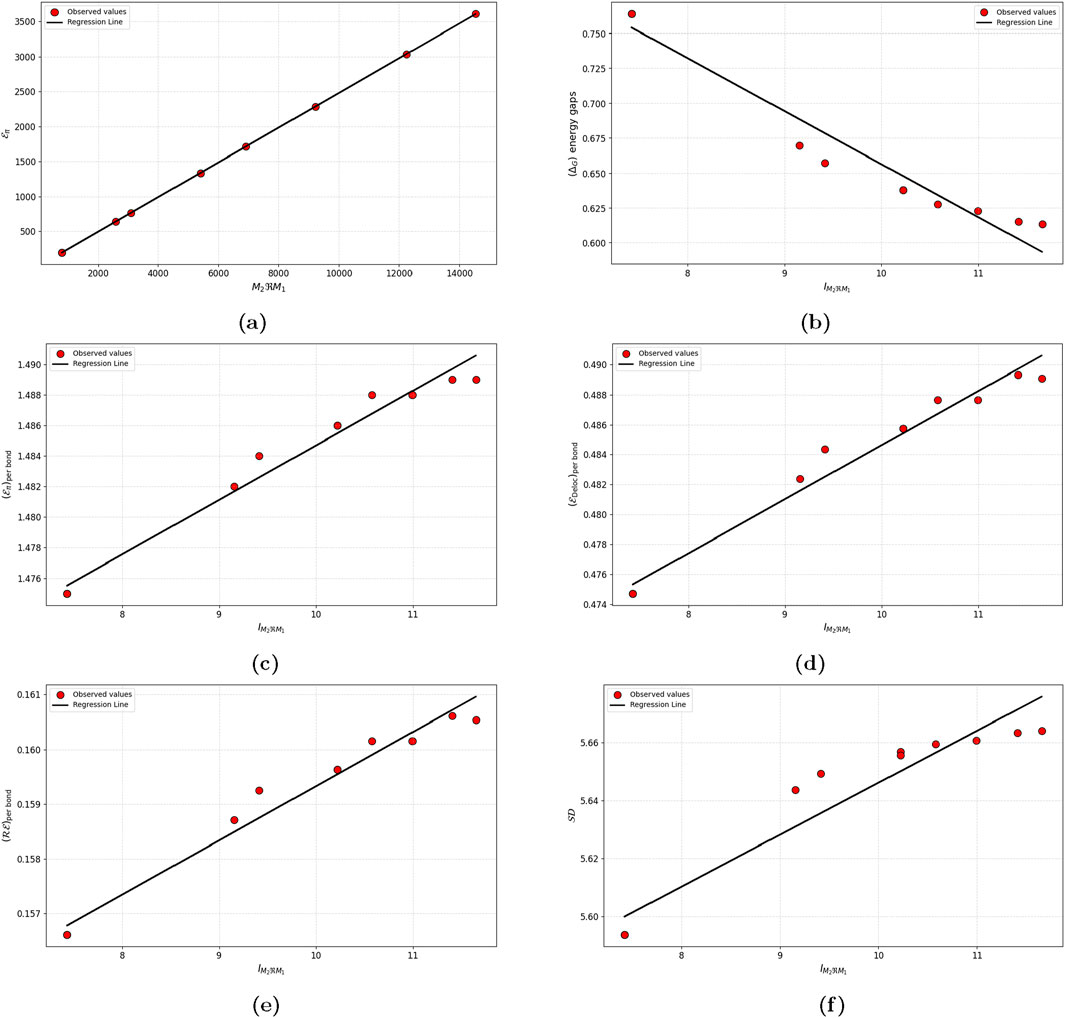
Figure 5. Linear regression models for the energetic properties. (a) Total π electron energy (b) Homo-Lumo energy gap (c) Energy per bond (d) Delocalization energy (e) Resonance energy per bond (f) Spectral diameter.

7 Conclusion

In this paper, we develop topological expressions based on modified reverse degree-based indices for three configurations of two-dimensional coronene fractals. These indices capture structural complexities and are effective in predicting physico-chemical properties. The computed indices function as graph-based metrics for evaluating entropy levels and relative complexity. The resulting entropy values offer insights into the structural challenges of these fractal systems, providing a foundation for further investigation into their properties. When paired with graph spectra, these approaches form a comprehensive machine learning framework for efficiently and accurately computing the spectral and thermodynamic properties of fractals and other two-dimensional materials. By integrating graph-theoretic methods with advanced statistical techniques, this study contributes to the development of improved computational chemistry algorithms, particularly for QSAR and QSPR studies aimed at predicting the stability and characteristics of complex chemical systems.

Data availability statement

The original contributions presented in the study are included in the article/supplementary material, further inquiries can be directed to the corresponding author.

Author contributions

AK: Conceptualization, Formal Analysis, Methodology, Writing – original draft. AG: Investigation, Methodology, Supervision, Validation, Writing – review and editing.

Funding

The author(s) declare that no financial support was received for the research and/or publication of this article.

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Generative AI statement

The author(s) declare that no Generative AI was used in the creation of this manuscript.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Abul Kalaam, A. R., and Berin Greeni, A. (2024). Comparative analysis of modified reverse degree topological indices for certain carbon nanosheets using entropy measures and multi criteria decision-making analysis, Int. J. Quantum Chem. 124(1), pe.27326, doi:10.1002/qua.27326

CrossRef Full Text | Google Scholar

Arockiaraj, M., Greeni, A. B., and Kalaam, A. A. (2023a). Linear versus cubic regression models for analyzing generalized reverse degree based topological indices of certain latest corona treatment drug molecules, Int. J. Quantum. Chem. 123(10), pe.27136, doi:10.1002/qua.27136

CrossRef Full Text | Google Scholar

Arockiaraj, M., Greeni, A. B., and Kalaam, A. A. (2023b). Comparative analysis of reverse degree and entropy topological indices for drug molecules in blood cancer treatment through QSPR regression models. Polycycl. Aromat. Compd., 1–18. doi:10.1080/10406638.2023.2271648

CrossRef Full Text | Google Scholar

Arockiaraj, M., Greeni, A. B., Kalaam, A. A., Aziz, T., and Alharbi, M. (2024). Mathematical modeling for prediction of physicochemical characteristics of cardiovascular drugs via modified reverse degree topological indices. EPJE 47 (8), 53. doi:10.1140/epje/s10189-024-00446-3

PubMed Abstract | CrossRef Full Text | Google Scholar

Arockiaraj, M., Jency, J., Abraham, J., Ruth Julie Kavitha, S., and Balasubramanian, K. (2022). Two-dimensional coronene fractal structures: topological entropy measures, energetics, NMR and ESR spectroscopic patterns and existence of isentropic structures. Mol. Phys. 120 (11), e2079568. doi:10.1080/00268976.2022.2079568

CrossRef Full Text | Google Scholar

Arockiaraj, M., Jency, J., Mushtaq, S., Shalini, A. J., and Balasubramanian, K. (2023d). Covalent organic frameworks: topological characterizations, spectral patterns and graph entropies. J. Math. Chem. 61, 1633–1664. doi:10.1007/s10910-023-01477-5

CrossRef Full Text | Google Scholar

Arockiaraj, M., Paul, D., Clement, J., Tigga, S., Jacob, K., and Balasubramanian, K. (2023c). Novel molecular hybrid geometric-harmonic-Zagreb degree based descriptors and their efficacy in QSPR studies of polycyclic aromatic hydrocarbons. SAR QSAR Environ. Res. 34, 569–589. doi:10.1080/1062936x.2023.2239149

PubMed Abstract | CrossRef Full Text | Google Scholar

Balasubramanian, K. (2023). Topological indices, graph spectra, entropies, Laplacians, and matching polynomials of n-dimensional hypercubes. Symmetry 15 (2), 557. doi:10.3390/sym15020557

CrossRef Full Text | Google Scholar

Bonchev, D., and Trinajstić, N. (1982). Chemical information theory: structural aspects. Int. J. Quantum Chem. 22 (16), 463–480. doi:10.1002/qua.560220845

CrossRef Full Text | Google Scholar

Dehmer, M. (2008). Information processing in complex networks: graph entropy and information functionals. Appl Math Comput. 201, 82–94. doi:10.1016/j.amc.2007.12.010

CrossRef Full Text | Google Scholar

Demir, C., and Üngördü, A. (2023). The design of push-pull substituted coronene molecules for optoelectronic applications. Mater. Chem. Phys. 301, 127631. doi:10.1016/j.matchemphys.2023.127631

CrossRef Full Text | Google Scholar

Dobrowolski, M. A., Ciesielski, A., and Cyrański, M. K. (2011). On the aromatic stabilization of corannulene and coronene. Phys. Chem. Chem. Phys. 13 (46), 20557–20563. doi:10.1039/c1cp21994d

PubMed Abstract | CrossRef Full Text | Google Scholar

Duan, Q., An, J., Mao, H., Liang, D., Li, H., Wang, S., et al. (2021). Review about the application of fractal theory in the research of packaging materials. Materials 14 (4), 860. doi:10.3390/ma14040860

PubMed Abstract | CrossRef Full Text | Google Scholar

Estrada, E., and Uriarte, E. (2001). Recent advances on the role of topological indices in drug discovery research. Curr. Med. Chem. 8 (13), 1573–1588. doi:10.2174/0929867013371923

PubMed Abstract | CrossRef Full Text | Google Scholar

Fedotov, P. V., Chernov, A. I., Talyzin, A. V., Anoshkin, I. V., Nasibulin, A. G., Kauppinen, E. I., et al. (2013). Optical study of nanotube and coronene composites. J. Nanoelectron. Optoelectron. 8 (1), 16–22. doi:10.1166/jno.2013.1428

CrossRef Full Text | Google Scholar

Graovac, A., Gutman, I., and Trinajstić, N. (1977). Topological approach to the chemistry of conjugated molecules. Berlin: Springer-Verlag.

Google Scholar

Gutman, I. (1978). The energy of a graph. Ber. Math. Stat. Sekt. Forschungszentrum Graz 103, 1–22.

Google Scholar

Gutman, I., and Trinajstić, N. (1972). Graph theory and molecular orbitals. Total π-electron energy of alternant hydrocarbons. Chem. Phys. Lett. 17 (4), 535–538. doi:10.1016/0009-2614(72)85099-1

CrossRef Full Text | Google Scholar

Hayat, S., Imran, M., and Liu, J. B. (2019). Correlation between the Estrada index and π-electronic energies for benzenoid hydrocarbons with applications to boron nanotubes. Int. J. Quantum Chem. 119 (23), e26016. doi:10.1002/qua.26016

CrossRef Full Text | Google Scholar

Herndon, W. C., and Ellzey, M. L. (1974). Resonance theory. V. Resonance energies of benzenoid and nonbenzenoid π systems. J. Am. Chem. Soc. 96 (21), 6631–6642. doi:10.1021/ja00828a015

CrossRef Full Text | Google Scholar

Hill, J. P., Jin, W., Kosaka, A., Fukushima, T., Ichihara, H., Shimomura, T., et al. (2004). Self-assembled hexa-peri-hexabenzocoronene graphitic nanotube. Science 304 (5676), 1481–1483. doi:10.1126/science.1097789

PubMed Abstract | CrossRef Full Text | Google Scholar

Hosoya, H. (2005). “Clar’s aromatic sextet and sextet polynomial,” in Advances in the theory of benzenoid hydrocarbons (Springer Berlin Heidelberg), 255–272.

CrossRef Full Text | Google Scholar

Junias, J. S., Clement, J., Rahul, M. P., and Arockiaraj, M. (2024). Two-dimensional phthalocyanine frameworks: topological descriptors, predictive models for physical properties and comparative analysis of entropies with different computational methods. Comput. Mater. Sci. 235, 112844. doi:10.1016/j.commatsci.2024.112844

CrossRef Full Text | Google Scholar

Kalaam, A. A., Greeni, A. B., and Arockiaraj, M. (2024). Modified reverse degree descriptors for combined topological and entropy characterizations of 2D metal organic frameworks: applications in graph energy prediction. Front. Chem. 12, 1470231. doi:10.3389/fchem.2024.1470231

PubMed Abstract | CrossRef Full Text | Google Scholar

Khabyah, A., Ahmad, A., Azeem, M., Ahmad, Y., and Koam, A. N. (2023). Reverse-degree-based topological indices of two-dimensional coronene fractal structures, Phys. Scr. 99(1), pe.015216, doi:10.1088/1402-4896/ad10db

CrossRef Full Text | Google Scholar

Kirkby, M. J. (1983). The fractal geometry of nature. Benoit B. Mandelbrot. W. H. Freeman and co., San Francisco, 1982. No. of pages: 460. Price: £22.75 (hardback). Earth Surf. Process. Landforms 8, 406. doi:10.1002/esp.3290080415

CrossRef Full Text | Google Scholar

Kumar, A., Duran, M., and Solá, M. (2017). Is coronene better described by Clar’s aromatic π-sextet model or by the AdNDP representation?. J. Comput. Chem. 38 (18), 1606–1611. doi:10.1002/jcc.24801

PubMed Abstract | CrossRef Full Text | Google Scholar

Kumar, V., and Das, S. (2024). On structure sensitivity and chemical applicability of some novel degree-based topological indices. Comput. Chem. 92 (1), 165–203. doi:10.46793/match.92-1.165k

CrossRef Full Text | Google Scholar

Lee, J. S., and Chang, K. S. (1996). Applications of chaos and fractals in process systems engineering. J. Process Control 6 (2-3), 71–87. doi:10.1016/0959-1524(95)00051-8

CrossRef Full Text | Google Scholar

Li, X., Li, Y., Shi, Y., and Gutman, I. (2013). Note on the HOMO-LUMO index of graphs. MATCH Commun. Math. Comput. Chem. 70 (1), 85–96.

Google Scholar

Malik, M. A., Imran, M., and Adeel, M. (2023). On distance-based topological indices and co-indices of fractal-type molecular graphs and their respective graph entropies. PLoS One 18 (11), e0290047. doi:10.1371/journal.pone.0290047

PubMed Abstract | CrossRef Full Text | Google Scholar

MATLAB (2022). MATLAB version: 9.13.0 (R2022b), Natick, Massachusetts: The MathWorks Inc.

Google Scholar

Mazouin, B., Schöpfer, A. A., and von Lilienfeld, O. A. (2022). Selected machine learning of HOMO-LUMO gaps with improved data-efficiency. Mater. Adv. 3 (22), 8306–8316. doi:10.1039/d2ma00742h

PubMed Abstract | CrossRef Full Text | Google Scholar

Mowshowitz, A. (1968). Entropy and the complexity of graphs: I. An index of the relative complexity of a graph. Bull. Math. Biophys. 30, 175–204. doi:10.1007/bf02476948

PubMed Abstract | CrossRef Full Text | Google Scholar

Mowshowitz, A., and Dehmer, M. (2012). Entropy and the complexity of graphs revisited. Entropy 14 (3), 559–570. doi:10.3390/e14030559

CrossRef Full Text | Google Scholar

Newman, M. S. (1940). A new synthesis of coronene. J. Am. Chem. Soc. 62 (7), 1683–1687. doi:10.1021/ja01864a014

CrossRef Full Text | Google Scholar

Nisha, S., and Senthil Kumar, A. (2020). π-Self-assembly of a coronene on carbon nanomaterial-modified electrode and its symmetrical redox and H₂O₂ electrocatalytic reduction functionalities. ACS Omega 5 (20), 11817–11828. doi:10.1021/acsomega.0c01258

PubMed Abstract | CrossRef Full Text | Google Scholar

Pisula, W., Feng, X., and Müllen, K. (2010). Tuning the columnar organization of discotic polycyclic aromatic hydrocarbons. Adv. Mater. 22 (33), 3634–3649. doi:10.1002/adma.201000585

PubMed Abstract | CrossRef Full Text | Google Scholar

Pisula, W., Feng, X., and Müllen, K. (2011). Charge-carrier transporting graphene-type molecules. Chem. Mater. 23 (3), 554–567. doi:10.1021/cm102252w

CrossRef Full Text | Google Scholar

Popov, I. A., and Boldyrev, A. I. (2012). Chemical bonding in coronene, isocoronene, and circumcoronene. Eur. J. Org. Chem. 2012 (18), 3485–3491. doi:10.1002/ejoc.201200256

CrossRef Full Text | Google Scholar

Prabhu, S., Arulperumjothi, M., Manimozhi, V., and Balasubramanian, K. (2024). Topological characterizations on hexagonal and rectangular tessellations of antikekulenes and its computed spectral, nuclear magnetic resonance and electron spin resonance characterizations. Int. J. Quantum Chem. 124 (7), 27365. doi:10.1002/qua.27365

CrossRef Full Text | Google Scholar

Rauf, R. A., Naeem, M., and Bukhari, S. U. (2022). Quantitative structure–property relationship of Ev-degree and Ve-degree based topological indices: physico-chemical properties of benzene derivatives. Int. J. Quantum Chem. 122 (5), e26851. doi:10.1002/qua.26851

CrossRef Full Text | Google Scholar

Raza, Z., Arockiaraj, M., Maaran, A., and Shalini, A. J. (2024). A comparative study of topological entropy characterization and graph energy prediction for Marta variants of covalent organic frameworks. Front. Chem. 12, 1511678. doi:10.3389/fchem.2024.1511678

PubMed Abstract | CrossRef Full Text | Google Scholar

Robertson, J. M., and White, J. G. (1945). 164. The crystal structure of coronene: a quantitative X-ray investigation. J. Chem. Soc. (Resumed), 607–617. doi:10.1039/jr9450000607

CrossRef Full Text | Google Scholar

Sabirov, D. S., and O-sawa, E. (2015). Information entropy of fullerenes. J. Chem. Inf. Model. 55 (8), 1576–1584. doi:10.1021/acs.jcim.5b00334

PubMed Abstract | CrossRef Full Text | Google Scholar

Sabirov, D. S., and Shepelevich, I. S. (2021). Information entropy in chemistry: an overview. Entropy 23 (10), 1240. doi:10.3390/e23101240

PubMed Abstract | CrossRef Full Text | Google Scholar

Santa Daría, A. M., González-Sánchez, L., and Gómez, S. (2024). Coronene: a model for ultrafast dynamics in graphene nanoflakes and PAHs. PCCP 26 (1), 174–184. doi:10.1039/d3cp03656a

CrossRef Full Text | Google Scholar

Sanyal, S., Manna, A. K., and Pati, S. K. (2013). Effect of imide functionalization on the electronic, optical, and charge transport properties of coronene: a theoretical study. J. Phys. Chem. C 117 (2), 825–836. doi:10.1021/jp310362c

CrossRef Full Text | Google Scholar

Shannon, C. E. (1948). A mathematical theory of communication. Bell Syst. Tech. J. 27 (3), 3–55. doi:10.1145/584091.584093

CrossRef Full Text | Google Scholar

Stevanović, L., Brankov, V., Cvetković, D., and Simić, S. (2021). newGRAPH: a fully integrated environment used for research process in graph theory. Available online at: http://www.mi.sanu.ac.rs/newgraph/index.html.

Google Scholar

Tachikawa, H., and Lund, A. (2022). Structures and electronic states of trimer radical cations of coronene: DFT-ESR simulation study. PCCP 24 (17), 10318–10324. doi:10.1039/d1cp04638a

PubMed Abstract | CrossRef Full Text | Google Scholar

Uahabi, K. L., and Atounti, M. (2015). Applications of fractals in medicine. Ann. Univ. Craiova-Math. Comput. Sci. Ser. 42 (1), 167–174.

Google Scholar

Ullah, A., Nazir, M., Zaman, S., Hamed, Y. S., and Jabeen, S. (2024). Fractal configurations of zigzag hexagonal type coronoid molecules: graph-theoretical modeling and its impact on physicochemical behavior, Phys. Scr. 100(1), pe.015237, doi:10.1088/1402-4896/ad9a1f

CrossRef Full Text | Google Scholar

Wiener, H. (1947). Structural determination of paraffin boiling points. J. Am. Chem. Soc. 69, 17–20. doi:10.1021/ja01193a005

PubMed Abstract | CrossRef Full Text | Google Scholar

Wu, Y., Yang, Y., and Ye, D. (2018). A note on median eigenvalues of bipartite graphs. MATCH Commun. Math. Comput. Chem. 80 (3), 853–862.

Google Scholar

Xu, S. A., and Liu, J. B. (2025). Entropies and degree-based topological indices of coronene fractal structures. Fractal Fract. 9 (3), 133. doi:10.3390/fractalfract9030133

CrossRef Full Text | Google Scholar

Yogalakshmi, K., and Easwaramoorthy, D. (2024). A new approach for generalized fractal dimensions based on topological indices for pyracyclene and pentahexoctite networks. IEEE Access 12, 166176–166187. doi:10.1109/access.2024.3489218

CrossRef Full Text | Google Scholar