QSPR graph model to explore physicochemical properties of potential antiviral drugs of dengue disease through novel coloring-based topological indices

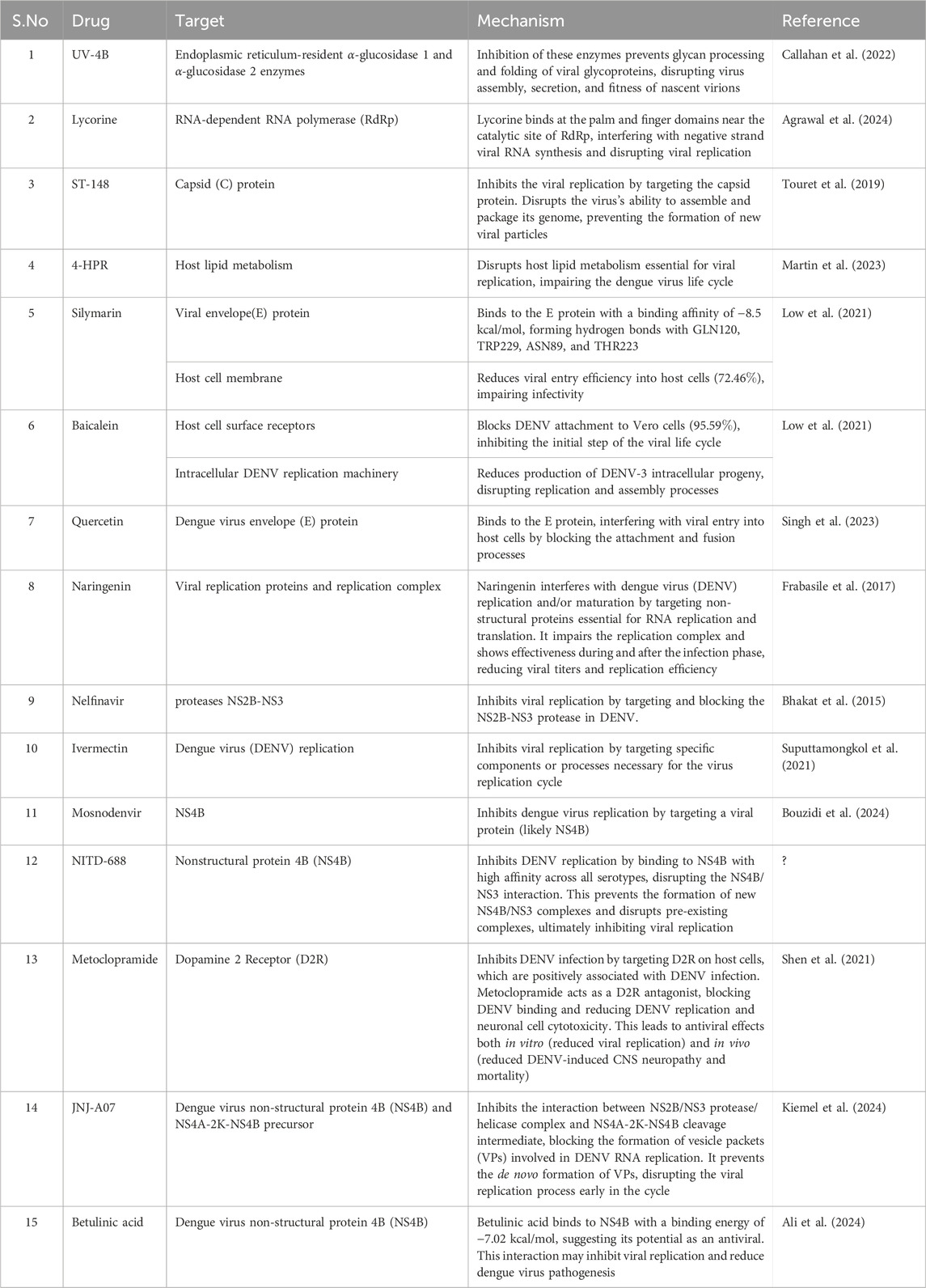
Dengue is a viral disease transmitted to humans through mosquito bites. Researchers have investigated various drugs with potential antiviral properties against it. Some of the promising antiviral drugs include UV-4B (N-9-methoxynonyl-1-deoxynojirimycin), Lycorine, ST-148, 4-HPR, Silymarin, Baicalein, Quercetin, Naringenin, Nelfinavir, Ivermectin, Mosnodenvir (JNJ-1802), NITD-688, Metoclopramide, JNJ-A07 and Betulinic acid. The chemical structure of a drug can be modelled as an isomorphic molecular graph $G(V,E)$, considering the atoms as the vertex set $V(G)$ and the bonds between the pair of atoms as the edge set $E(G)$. Graph coloring and topological indices serve as a powerful tools for analyzing the isomorphic molecular graph, providing the structural characterization and computational studies. In this article, two types of coloring-based topological indices viz., chromatic topological indices and induced color-based topological indices, are introduced. Linear regression is employed in the QSPR(Quantitative Structure Property Relationship) analysis to examine the dengue antivirals through the computed topological indices of the aforementioned drugs. The results of the QSPR analysis reveal that the induced color-based indices provide better predictions of the physicochemical properties of dengue-treating drugs.

1 Introduction

An infectious virus called dengue infects people through the bite of infected mosquito species called Aedes. Tropical and subtropical regions are particularly at risk for dengue fever, which poses a significant public health threat. The signs and symptoms of dengue include high fever, severe headache, joint and muscle pain, rash, mild bleeding, pain behind the eyes, nausea, vomiting and mild respiratory problems. In severe cases, the symptoms may worsen and the individual may experience intense abdominal pain, persistent vomiting, rapid breathing, lethargy, restlessness, bleeding from the nose or gums, blood in vomit or stools and even organ failure. It also lead to drop in platelet count, which increases the risk of bleeding. It is hard to diagnose dengue fever since the symptoms of dengue is similar to many viral infections. Hence it is advised to run laboratory tests, such as reverse transcription-polymerase chain reaction (RT-PCR) or serological tests to diagnose and differentiate dengue from other infections. Numerous drugs have been evaluated through in vitro, in vivo and clinical studies to identify potential antivirals for dengue. In addition to these efforts, Dengvaxia, the first licensed dengue vaccine, has been developed to provide partial protection against dengue virus, although it is not a therapeutic antiviral. Furthermore, investigational drugs like JNJ-A07 and JNJ-1802, that target the dengue virus non-structural protein 4B (NS4B), have shown promising results in pre-clinical and clinical studies, demonstrating potent pan-serotype activity and potential to inhibit viral replication effectively. Several drugs have shown potential antiviral activity against the dengue virus, including UV-4B (N-9-methoxynonyl-1-deoxynojirimycin), Lycorine, ST-148, 4-HPR, Silymarin, Baicalein, Quercetin, Naringenin, Nelfinavir, Ivermectin, Mosnodenvir (JNJ-1802), NITD-688, Metoclopramide, JNJ-A07, and Betulinic acid. The targets and mechanisms of these drugs in combating the dengue virus are summarized in Table 1.

Table 1

Table 1. The target and mechanism of the considered potential antiviral drugs of dengue.

Chemical graph theory (Wagner and Wang, 2018) is a part of graph theory which combines the principles of chemistry and graph theory. In chemical graph theory, the molecular structure of a chemical compound can be modelled in terms of an isomorphic molecular graph $G(V,E)$ with atoms as vertex set $V(G)$ and the bonds between the atoms as an edge set $E(G)$. The degree of an atom(vertex) $v$, denoted by $d(v)$, is the number of bonds(edges) incident to the atom $v$ and the neighborhood of an atom $v$, denoted by $N(v)$, is the set of all atoms that are adjacent to $v$.

Topological index of a molecular structure is a numerical value computed based on the structure of a molecule graph. It converts the qualitative or abstract information of a molecule into a quantitative form. Various types of topological indices have been developed based on the different parameters of the molecular graph structures. These include distance-based indices, degree-based indices, neighborhood-based indices and connectivity-based indices. The Quantitative Structure-Property Relationship (QSPR) analysis of a molecular graph is carried out through the topological indices to establish mathematical relationships between the structural features of chemical compounds and their physical or chemical properties.

In recent studies, researchers have employed the Quantitative Structure-Property Relationship (QSPR) analysis using various topological indices to predict the physicochemical and ADMET (Absorption, Distribution, Metabolism, Excretion, and Toxicity) properties of diverse drug compounds. Among the various topological index variants, degree-based and neighborhood degree-based indices have been widely employed to evaluate their predictive capabilities for drug-like compounds. For instance, Tamilarasi and Balamurugan (2025) utilized these indices to predict the properties of antifungal drugs, while Arockiaraj et al. (2025) applied them to analyze compounds used in the treatment of lung cancer. Similarly, degree-based indices have been employed in the QSPR modeling of drugs targeting heart disease Kuriachan and Parthiban (2025); Hasani and Ghods (2024), blood cancer Zaman et al. (2024) and tuberculosis Abubakar et al. (2024). Their application extends to respiratory diseases as well, with studies exploring treatments for asthma Balasubramaniyan and Chidambaram (2023) and COVID-19 Ugasini Preetha et al. (2024); Das et al. (2023). It is noteworthy that these degree-based indices have been widely applied across various diseases, highlighting their utility and predictive power. In addition to degree-based indices, distance-based topological indices have also proven effective. For instance, Sardar and Hakami (2024) employed the distance-based indices to predict properties of drugs used in Alzheimer’s disease, while Huang et al. (2023) focused on anticancer agents. Recent literature also highlights the use of more specialized topological variants. Density-based indices were applied to study monkeypox-related drugs Kalaimathi and Balamurugan (2023), while reverse-sum Revan indices found use in analyzing antifiloviral drugs Tamilarasi and Balamurugan (2022). Thilsath parveen and Siddiqui (2024) explored domination distance-based indices and Shi et al. (2025) investigated temperature-based indices to model the properties of anticancer compounds.

In graph theory (Bondy and Murty, 2008), a graph coloring of the graph $G(V,E)$ is an assignment of colors to the elements of the graph such as vertices or edges or both. The coloring of each element of the graph holds significance in its own distinct manner. In this article, the vertex coloring of a graph is considered. The vertex coloring $c:V(G)\to \mathbb{N}$, where $\mathbb{N}$ is the set of natural numbers, is said to be proper if no two adjacent vertices have the same color. Here, the set of natural numbers represents the set of colors. The minimum number of colors used to color the vertices of the graph is called as chromatic number and it is denoted as $\chi (G)$. The graph coloring helps to study the structural properties of graphs by analysing the relationship between the number of colors used to color the graphs and various graph parameters such as vertex degree, connectivity, independent number, neighborhood set and more.

The graph coloring finds various applications in chemistry, particularly in representing molecular structures. The assignment of colors to the vertices helps in differentiating the types of atoms or functional groups within a molecule (Huckvale et al., 2023; Jin et al., 2020). In reaction network analysis, vertices are represented as chemicals and the two vertices are connected by an edge if the two chemicals are reactive with each other. Coloring these vertices facilitates the separation of reactive chemicals, aiding the chemical manufacturing industry in efficiently (optimally) storing non-reactive chemicals together in their warehouses. The minimum number of colors used determines the minimum number of compartments or rooms required for storing the chemicals. Graph coloring is also applicable in conformational analysis, enabling the identification of structural similarities or differences. Different isomers can be colored distinctly, contributing to the systematic exploration of atom alignments in a molecular structure.

The topological indices based on graph coloring can provide a comprehensive understanding of the molecular graphs, facilitating the prediction of the physical and chemical properties of the molecules. Therefore, the chromatic topological indices emerges in the field of chemical graph theory. Unlike traditional indices, these coloring-based indices provide an alternate method for analyzing molecular structures, to understand how the arrangement of colors influences the molecular properties.

The notion of chromatic topological indices was introduced by Johan kok et al. in (Kok et al., 2016). For any color set, $C=\{c_1,c_2,\dots ,c_l\}$ and the coloring ${\varphi }_t(G)$ for $1\le t\le l!$ of a graph $G$, Johan kok et al. (Kok et al., 2016) introduced the indices viz., first chromatic Zagreb index $M_1^{{\varphi }_t}(G)$, second chromatic Zagreb index $M_2^{{\varphi }_t}(G)$ and third chromatic Zagreb index $M_3^{{\varphi }_t}(G)$. The arrangement of colors in a graph is categorized as ${\varphi }^{-}$ and ${\varphi }^{+}$ coloring. In ${\varphi }^{-}$ coloring, colors are assigned to the vertices in increasing order, maximizing the usage of each color before proceeding to the next color. In ${\varphi }^{+}$ coloring, colors are assigned to the vertices in decreasing order, maximizing the usage of each color before proceeding to the next color.

In (Albina and Manonmani (2022); (2021); (Kok et al. (2017); Rose and Naduvath (2018)) the chromatic topological indices of some classes of graphs were determined. Following this, Smitha) Rose and Sudev Naduvath introduced several variants of chromatic indices viz., chromatic total irregularity index (Rose and Naduvath, 2020a), injective chromatic zagreb indices (Rose and Naduvath, 2019), injective chromatic total irregularity index (Rose and Naduvath, 2019), equitable chromatic zagreb indices (Rose and Naduvath, 2020b) and equitable chromatic irregularity index (Rose and Naduvath, 2020b). In (Rose and Naduvath, 2019) and (Rose and Naduvath, 2020b), they computed the injective and equitabe chromatic Zageb indices and injective and equitabe chromatic total irregularity index for the Mycielskian graphs of path and cycle. Later, in (Rose and Naduvath, 2020a), they computed the chromatic total irregularity index for path and cycle.

Motivated by the exploration of various coloring-based topological indices, six new chromatic topological indices and ten new induced color-based topological indices are introduced in this article. The induced color-based indices distinguish themselves by providing a unique method to analyze the molecular structures through the color sum of the vertices.

The coloring-based topological indices have not yet been explored especially in the context of their effectiveness in predicting properties through QSPR analysis. To address this research gap, the performance of chromatic topological indices and induced color-based indices are investigated in this article in the context of molecular graph modeling for QSPR analysis. The coloring techniques considered, namely, the proper vertex coloring and sigma coloring have distinct theoretical significance in structural analysis of the molecular structures. The relevance of these coloring techniques and their foundational importance are discussed in detail in the Section 3.1.

Specifically, the induced color-based and chromatic topological indices are computed for 15 potential antivirals of dengue disease. QSPR analysis is performed through these indices and linear regression to explore the physicochemical properties of dengue antivirals. Further, the comparative analysis of the two types of indices is performed to identify the potential indices to predict the properties of drugs.

2 Isomorphic molecular graph

The concept of isomorphic molecular graph of a chemical structure is discussed in this section.

2.1 Motivation

Wiener (1947) introduced two topological indices, namely, Wiener index and polarity index for alkane molecules. He considered the skeletal structures of alkanes and represented them as molecular graphs to predict their boiling points. In the skeletal structures, the hydrogen atoms bonded to carbon atoms are not explicitly shown. Researchers have extensively computed various topological indices for chemical compounds to predict their properties, often using simplified molecular graph representations. These simplifications typically involve depleting hydrogen atoms and treating double and triple bonds as a single edges. Computing the Wiener index for the simplified molecular graph of a chemical compound does not affect the index value, as the Wiener index is a distance-based topological indices. Later, Ivan Gutman and Oskar E. Polansky (Gutman and Polansky, 2012) introduced the concept of a complete molecular graph, where the molecular graph includes hydrogen atoms but multiple bonds are still represented as single edges. The absence of double or triple bonds in the graph, however, leads to the non-existence of the corresponding chemical structure. Moreover, this simplification particularly affects the degree-based topological indices, as the degree of a vertex varies depending on the multiplicity of its bonds. Consequently, indices calculated using this simplified approach may yield misleading data. These limitations are addressed by W Tamilarasi et al., in (Tamilarasi and Balamurugan, 2024) by introducing an accurate representation of chemical structure as an isomorphic molecular graph. In this representation, double bonds are represented as two parallel edges, triple bonds as three parallel edges and hydrogen atoms are preserved in their adjacency. This approach preserves the unique structural characteristics of the molecule, allowing for accurate comparison and analysis. Therefore, in this article, the isomorphic molecular graph is considered to represent the chemical structure of the potential antivirals of dengue.

Definition 1:. (Tamilarasi and Balamurugan, 2024). Let $M$ be a molecular structure of a chemical molecule. The isomorphic molecular graph of $M$ is a graph $G(V,E)$ in which the atoms of $M$ including hydrogen atoms are considered as the vertex set $V(G)$ and the bonds between the atoms in $M$ are considered as the edge set $E(G)$, where the single bonds are represented as single edge, double bonds as two parallel edges and triple bonds as three parallel edges.

An example of isomorphic molecular graph is shown in Figure 1.

Figure 1

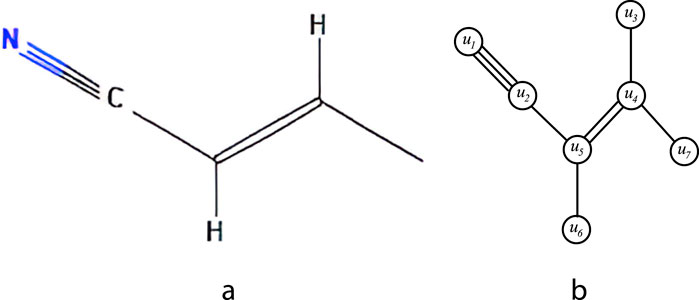
Figure 1. (a) Chemical structure of 2-butenenitrile (b) Isomorphic molecular graph of 2-butenenitrile.

3 Sigma coloring of isomorphic molecular graph and its significance

In this section, the concept of vertex coloring relevant to this article is discussed. Furthermore, the concept of sigma coloring and its significance are presented with appropriate examples.

Definition 2:. Let $G(V,E)$ be the isomorphic molecular graph. The vertex coloring $c$ of $G$ is said to be proper vertex coloring if no two adjacent vertices are assigned with the same color.

Definition 3:. Let $G(V,E)$ be a graph with vertex set $V$ and edge set $E$. Let $C=\{c_1,c_2,\dots ,c_{\ell }\}$ be the set of colors used to color the vertices of $G$. A ${\varphi }^{-}$ coloring is a vertex coloring in which the colors in $C$ are assigned in an order starting from the first color $c_1$. The color $c_1$ is assigned to the maximum possible number of vertices, followed by the color $c_2$ is assigned to the maximum possible number of the remaining uncolored vertices. This process is continued sequentially with $c_3,c_4,\dots ,c_{\ell }$ until all vertices in $V$ are colored.

Definition 4:. Let $G(V,E)$ be a graph with vertex set $V$ and edge set $E$. Let $C=\{c_1,c_2,\dots ,c_{\ell }\}$ be the set of colors used to color the vertices of $G$. A ${\varphi }^{+}$ coloring is a vertex coloring in which the colors in $C$ are assigned in order starting from the last color $c_{\ell }$. The color $c_{\ell }$ is assigned to the maximum possible number of vertices, followed by the color $c_{\ell -1}$ is assigned to the maximum possible number of remaining uncolored vertices. This process is continued sequentially with $c_{\ell -2},c_{\ell -3},\dots ,c_1$ until all vertices in $V$ are colored.

Definition 5:. Let $G(V,E)$ be a graph with vertex set(atom set) $V(G)$ and edge set (bond set) $E(G)$. The neighborhood of a vertex(atom) $v$ is defined as the set of vertices(atoms) that are adjacent to $v$. The cardinality of $N(v)$ denoted as $|N(v)|$ is defined as the number of vertices(atoms) in $N(v)$.

Definition 6:. (Chartrand et al., 2010) Let $G(V,E)$ be a isomorphic molecular graph, where $V(G)$ represents the vertex set(atom set) and $E(G)$ represents the edge set(bond set). Let $c:V(G)\to \mathbb{N}$ be a vertex(atom) coloring function, where $\mathbb{N}$ is a set of natural numbers. The color sum of the atom $v\in V(G)$, denoted by $\sigma (v)$ is the sum of colors of the neighbor atoms of $v$. The coloring $c$ is called sigma coloring if $\sigma (u)\ne \sigma (v)$ for any two atoms(vertices) $u$ and $v$ that shares a common bond(edge). The minimum number of colors needed for sigma coloring is called as sigma chromatic number of $G$ and it is denoted by $\sigma (G)$.

Throughout the article, the values inside the circles represent the proper vertex coloring, while the values outside the circles correspond to the sigma coloring. In sigma coloring, the values outside the brackets is the initial color assigned to the vertex and the values inside the bracket denote the color sum of the vertex.

Example 1:. The chemical structure of dopamine is shown in Figure 2a and the vertex coloring and sigma coloring of the isomorphic molecular graph of Dopamine are shown in Figure 2b.

Figure 2

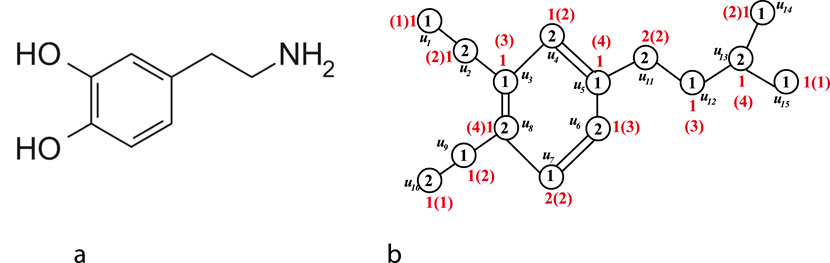
Figure 2. (a) Chemical structure of Dopamine (b) Vertex coloring and sigma coloring of isomorphic molecular graph of Dopamine.

3.1 Motivation and significance of sigma coloring

In the sigma coloring of an isomorphic molecular graph $G$, adjacent atoms can be assigned with the same color. Consequently, atoms of the same type can share the same color to distinguish them from atoms of other types. For example, consider the molecules cyclohexane, cyclohexene, cyclohexadiene and benzene. These molecules differ in their structures based on the number of double bonds present. The chemical structure of these molecules are provided in the Supplementary Material.

Let type 1 carbon atoms be those with a single bond and type 2 carbon atoms be those with a double bond. Cyclohexane contains only type 1 carbon atoms, cyclohexene and cyclohexadiene contain both type 1 and type 2 carbon atoms, while benzene contains only the type 2 carbon atoms. The objective is to distinguish each type of atom through sigma coloring. Initially, the atoms of the isomorphic molecular graph are colored and the color sum of atoms are calculated. If no two adjacent atoms have the same color sum then the type of carbon atom are effectively distinguished based on the assigned colors.

If two adjacent carbon atoms in the isomorphic molecular graphs of cyclohexane, cyclohexene, cyclohexadiene and benzene share a double bond then they are assigned with different colors; otherwise, adjacent carbon atoms are assigned the same color. Hydrogen atoms in the molecule are colored such that the sum of the colors of neighboring atoms of any two adjacent atoms remains distinct.

Let $c:V(G)\to \{\mathrm{1,2}\}$ be the vertex coloring of the isomorphic molecular graphs of cyclohexane, cyclohexene, cyclohexadiene and benzene. All atoms are colored in accordance with the aforementioned procedures. The values inside the circle represent the vertex color and the values outside the circle represent the color sum. Observe from Figure 3 that no two adjacent atoms have same color sum. Hence the atoms of the molecules can be differentiated by its types through the sigma coloring. The differentiation of the types are as follows.

Figure 3

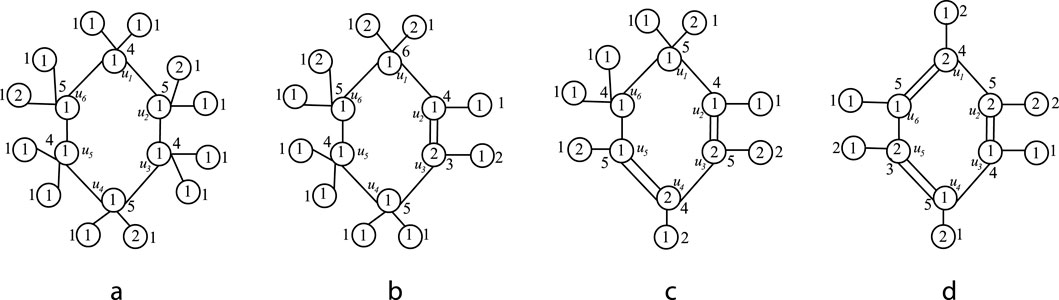
Figure 3. (a) Sigma coloring of isomorphic molecular graph of Cyclohexane (b) Sigma coloring of isomorphic molecular graph of Cyclohexene (c) Sigma coloring of isomorphic molecular graph of Cyclohexadiene (d) Sigma coloring of isomorphic molecular graph of benzene.

Define the cyclic sequence of carbon atom $S$ as $S:c(u_1),c(u_2),c(u_3),c(u_4),c(u_5),c(u_6),c(u_1)$.

$•$ The cyclic sequence $S$ of cyclohexane is $S:\mathrm{1,1,1,1,1,1,1}$. From this color sequence, the atoms represented as $u_1,u_2,u_3,u_4,u_5,u_6$ are the carbon atoms with single bond, since all the atoms are colored with same color.

$•$ The cyclic sequence $S$ of cyclohexene is represented as $S:\mathrm{1,1,2,1,1,1,1}$. From this color sequence, it is observed that two adjacent pairs of atoms, namely, $u_2,u_3$ and $u_3,u_4$, are colored with different colors,$1$ and 2. This implies the presence of two double bonds. However, carbon atoms can only form up to four covalent bonds. Therefore, there can be only one double bond, and it must be either the pair $(u_2,u_3)$ or $(u_3,u_4)$. In this case, $(u_2,u_3)$ represents carbon atoms of type 2, while all other atoms are of type 1.

$•$ The cyclic sequence $S$ of cyclohexdiene is $S:\mathrm{1,1,2,2,1,1,1}$. From this color sequence, it is observed that $u_2,u_3$ and $u_4,u_5$ are colored with different colors and all other pair of atoms are colored with same color. Therefore there exist 2 double bonds.

$•$ The cyclic sequence $S$ of benzene is $S:\mathrm{2,2,1,1,2,1,2}$. From this color sequence, it can be observed that the atoms in the pairs $(u_2,u_3),(u_4,u_5),(u_5,u_6)$ and $(u_6,u_1)$ are colored differently. As the same reasoning of cyclohexene, it can be concluded that, $(u_2,u_3),(u_4,u_5)$, and $(u_6,u_1)$ are of type 2.

From the sigma coloring of cyclohexene and benzene, it is observed that if there is an odd pair of type 2 carbon atoms, then there is a pair of carbon atoms where one is of type 1 and the other is of type 2, and they are colored differently. That is,

$•$ If two adjacent atoms have the same color, then at least one atom among them is of type 1.

$•$ If two atoms have different colors, then both atoms are of type 2.

$•$ In certain cases, such as when an even pair ($k$ pair) of atoms are colored with different colors, there are either an even number of atoms ($2k$ atoms) of type 2 or $2k-2$ atoms of type 2.

Unlike other colorings, sigma coloring employs the minimum number of colors. In this approach, any natural numbers can be used to color the atoms(vertices), but the number of colors considered must be minimal. Therefore, the atoms(vertices) in the isomorphic molecular graph can be assigned(colored) with numbers associated with the atoms present in the molecule such as atomic number, mass number oxidation state and so on. For instance, considering the atomic number of all the atoms in a molecule, among them choose the minimum number of colors that satisfies sigma coloring. This shows that sigma coloring allows us to incorporate numerical data associated with the atoms to color the vertices of the graph. Thus, sigma coloring proves to be an effective method for studying molecules.

The following is the general observation of sigma coloring of graphs, which will be used in the proof of the theorem.

Observation 1:. (Chartrand et al. 2010) Let G be a molecular graph. Then $\sigma (G)=1$ if and only if every two adjacent atoms of $G$ have different degrees.

4 Chromatic and induced color-based topological indices

Let $G(V,E)$ be an isomorphic molecular graph, where $V$ represents the atom set and $E$ represents the set of bonds. The ten new induced color-based topological indices and six new chromatic topological indices are introduced in this article and are defined in Table 2.

Table 2

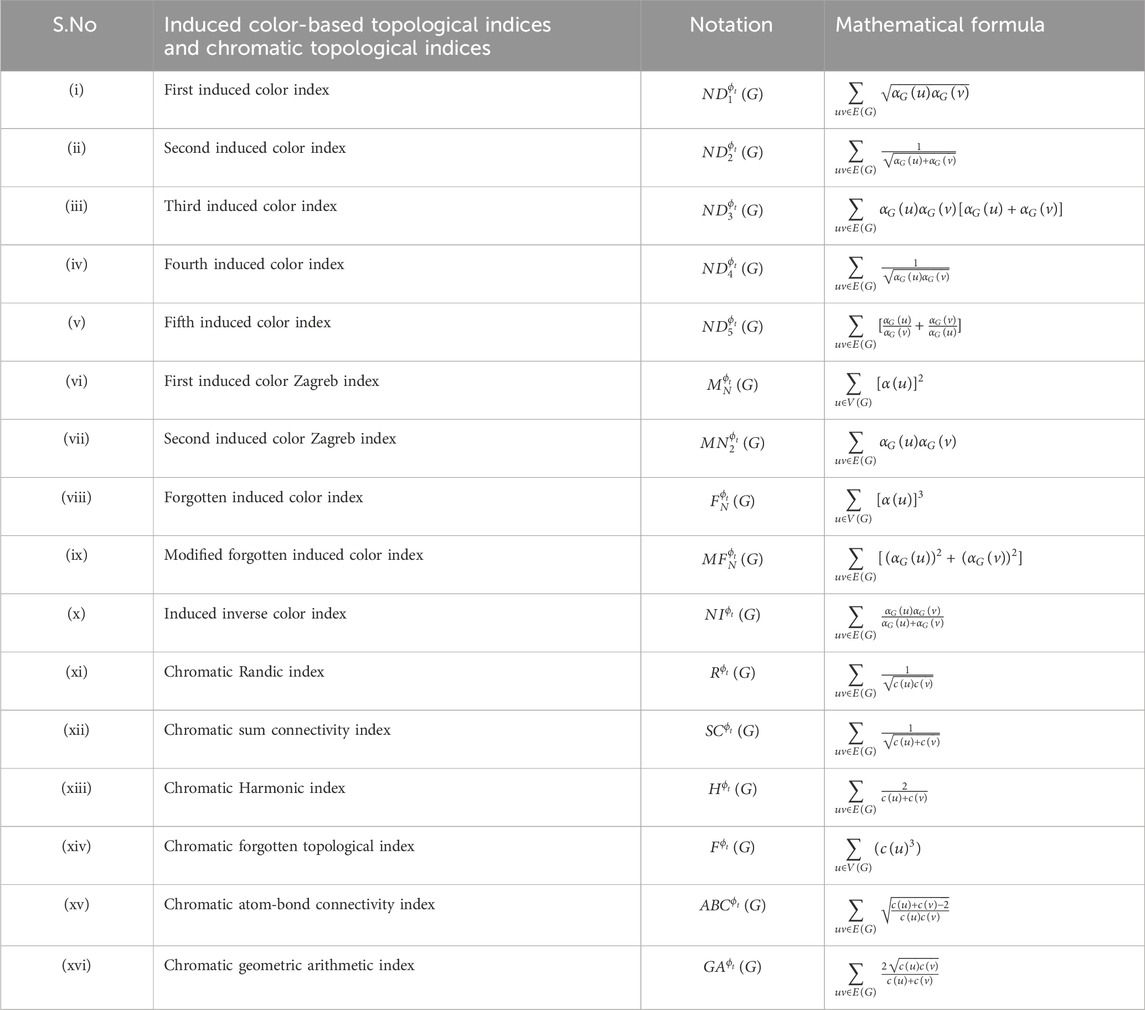
Table 2. Induced color-based topological indices and chromatic topological indices with their notations and mathematical formulas.

The induced color-based topological indices are computed using the graph coloring variants, where the vertex colors are derived from an initial assignment of vertex or edge colors. Examples of some of such variants include sigma coloring, closed sigma coloring, additive coloring, modular coloring, closed modular coloring, antimagic labeling and lucky labeling. In induced color based topological indices, $\alpha (u)$ represents the induced vertex color. The chromatic topological indices are determined using the proper vertex coloring technique, where $c(u)$ represents the color assigned to the vertex u.

The induced color-based topological indices capture the influence of neighboring vertices or incident edges, whereas chromatic indices utilize graph coloring attributes to represent molecular features.

Let $C=\{c_1,c_2,\dots ,c_l\}$ be the set of colors used to color the vertices of graph that satisfies the condition of the employed coloring. Let each vertex $u\in V(G)$ is assigned a color $c(u)=c_j$ for $1\le j\le l$. Let ${\varphi }_t:C\to \{\mathrm{1,2},\dots ,l\}$ denote the $t^{t}h$ permutation of numbers $\{\mathrm{1,2},\dots ,l\}$, for $1\le t\le l!$. The value of $t$ ranges from 1 to $l!$, since $\varphi$ is a permutation function using $l$ colors,. Then, for each such ${\varphi }_t$, the novel induced color-based topological indices and chromatic topological indices are defined in Table 2.

Let $C=\{c_1,c_2,\dots ,c_l\}$ be a proper vertex coloring of a graph $G$, where each vertex $u\in V(G)$ is assigned a color $c(u)=c_j$ for $1\le j\le l$. Let ${\varphi }_t:C\to \{\mathrm{1,2},\dots ,l\}$ denote the $t^{t}h$ permutation of numbers $\{\mathrm{1,2},\dots ,l\}$, for $1\le t\le l!$. The value of $t$ ranges from 1 to $l!$, since $\varphi$ is a permutation function using $l$ colors. Then, for each such ${\varphi }_t$, the chromatic topological indices introduced by Kok et al. (2016) and Rose and Naduvath (2020a) are defined as follows:

1. The first chromatic Zagreb index of $G$ is defined as, $M_1^{{\varphi }_t}$ = ${\displaystyle {\sum }_{j=1}^l}\theta (c_j)j^2$, where $\theta (c_j)$ is the number of vertices colored with the color $c_j$ in $G$.

2. The second chromatic Zagreb index of $G$ is defined as, $M_2^{{\varphi }_t}$ = ${\displaystyle {\sum }_{uv\in E(G)}}c(u)c(v)$

3. The chromatic irregularity index of $G$ is defined as, $M_3^{{\varphi }_t}$ = ${\displaystyle {\sum }_{uv\in E(G)}}|c(u)-c(v)|$

4. The chromatic total irregularity index of $G$ is defined as, $M_4^{{\varphi }_t}$ = ${\displaystyle {\sum }_{uv\in E(G)}}\frac{1}{2}|c(u)-c(v)|$

Let ${\varphi }^{-}$ denote the permutation ${\varphi }_t$ that yields the minimum value of the topological index among all l! possible permutations and let ${\varphi }^{+}$ refers to the permutation ${\varphi }_t$ that gives the maximum value. Let InV be the topological index value correspond to the given permutation. Then, the relationship between the topological index value is given by

$In{V}^{{\varphi }^{-}}\le In{V}^{{\varphi }_t}\le In{V}^{{\varphi }^{+}}$

These topological indices form the basis for QSPR analysis to improve the predictive accuracy of analysis in determining the physicochemical properties of antiviral drugs of dengue. The induced color-based topological indices are computed using a graph coloring variant known as sigma coloring, while the chromatic topological indices are calculated using the proper vertex coloring.

5 Methodology

A systematic approach is employed to analyze the properties of potential antiviral drugs for dengue disease through the Quantitative Structure-Property Relationship (QSPR) graph modelling by considering the topological descriptors of the isomorphic molecular graphs of the drugs. The methodology consists of the following key steps:

1. Data Collection and Isomorphic Molecular Graph Construction

  Potential antiviral drugs for dengue were selected based on their efficacy. The molecular structures of these drugs were obtained from publicly available database PubChem whose URL is pubchem.ncbi.nlm.nih.gov. Each chemical structure was then modelled as an isomorphic molecular graph.

2. Computation of Topological Indices

  The chromatic and induced color-based topological indices of the molecular graphs were computed through two distinct coloring approaches namely, proper vertex coloring and sigma coloring respectively.

3. QSPR Analysis

  The QSPR analysis was conducted to explore the relationship between the computed topological indices of molecular graphs and physicochemical properties of antiviral drugs used for dengue treatment. Linear regression analysis was performed using the Statistical Package for the Social Sciences (SPSS) software, applying statistical methods to evaluate the strength and significance of these correlations.

4. Statistical Analysis and Descriptor Evaluation

  The predictive capability of the computed indices was assessed using the following statistical parameters:

$•$ Correlation coefficient $(R^2)$: Measures the strength of association between variables.

$•$ Significance tests ($p$-values): Determine the reliability of the observed relationships.

$•$ Standard error values: Evaluate the accuracy and precision of the model.

$•$ Y-randomization test: Ensures that the QSPR analysis results are not obtained by chance.

The most effective indices were identified based on their predictive power and statistical significance, offering a robust framework for understanding the molecular properties of antiviral drugs used in dengue treatment.

6 Computation of chromatic and induced color-based topological indices of potential antivirals of dengue

In this section, the ${\varphi }^{-}$ and ${\varphi }^{+}$ chromatic and induced color-based topological indices of potential antivirals of dengue disease are computed through proper vertex coloring and sigma coloring respectively. The two coloring scheme ${\varphi }^{-}$ and ${\varphi }^{+}$ are employed to investigate how the order of color assignment influence the predictive power of the topological indices. The chemical structure of the considered potential antivirals of the dengue disease are obtained from the National Center for Biotechnology Information (NCBI) whose URL is pubchem.ncbi.nlm.nih.gov and they are provided in the Supplementary Material.

6.1 Computation of chromatic topological indices

Let $G(V,E)$ be an isomorphic molecular graph with vertex set $V(G)$ and edge set $E(G)$ and let $c:V(G)\to \{c_1,c_2,\dots ,c_l\}$ be the vertex coloring of $G$. The following steps are followed to color the vertices of the isomorphic molecular graphs of potential antivirals of dengue such that the vertex coloring is a proper vertex coloring.

1. Partition the vertices into independent sets.

2. Compute ${\varphi }^{-}$ proper vertex coloring of $G$.

    The color $c_1$ is assigned to the vertices in the independent set with the highest cardinality, followed by the color $c_2$, which is assigned to the vertices in the independent set with the second-highest cardinality. This process is repeated until all vertices of the graph are colored, ensuring that the coloring satisfies the condition of proper vertex coloring.

3. Compute the ${\varphi }^{+}$ proper vertex coloring of $G$.

    The color $c_l$ is assigned to the vertices in the independent set with the highest cardinality, followed by the color $c_{l-1}$, which is assigned to the vertices in the independent set with the second-highest cardinality. This process is repeated until all vertices of the graph are colored, ensuring that the coloring satisfies the condition of proper vertex coloring.

Theorem 1:. Let $G$ be the isomorphic molecular graph of Lycorine. The chromatic topological indices of $G$ through ${\varphi }^{-}$ and ${\varphi }^{+}$ proper vertex coloring are as follows:

$M_1^{{\varphi }^{-}}(G)=74,M_2^{{\varphi }^{-}}(G)=69,M_3^{{\varphi }^{-}}(G)=32,M_4^{{\varphi }^{-}}(G)=16$, $R^{{\varphi }^{-}}(G)=19.519,S{C}^{{\varphi }^{-}}(G)=16.251,H^{{\varphi }^{-}}(G)=18.3,F^{{\varphi }^{-}}(G)=154,$ $AB{C}^{{\varphi }^{-}}(G)=20.834,G{A}^{{\varphi }^{-}}(G)=27.168.\hspace{0.17em}{M}_1^{{\varphi }^{+}}(G)=154,M_2^{{\varphi }^{+}}(G)=157,$ $M_3^{{\varphi }^{+}}(G)=32,M_4^{{\varphi }^{+}}(G)=16,R^{{\varphi }^{+}}(G)=12.944,S{C}^{{\varphi }^{+}}(G)=13.388,$ $H^{{\varphi }^{+}}(G)=12.433,F^{{\varphi }^{+}}(G)=414,AB{C}^{{\varphi }^{+}}(G)=20.834,G{A}^{{\varphi }^{+}}(G)=27.999$.

Proof. Let $G$ be the isomorphic molecular graph of Lycorine representing the 25 atoms and 29 bonds as vertices and edges respectively. Let $V(G)=\{u_1,u_2,\dots ,u_{25}\}$ be the atom(vertex) set of $G$. The chemical structure of lycorine is shown in Figure 4a. The independent sets of the graph $G$ are as follows:

$\begin{array}{c}{A}_1=\left\{u_1,u_4,u_7,u_9,u_{10},u_{12},u_{14},u_{15},u_{17},u_{19},u_{21},u_{23}\right\},\hfill \\ A_2=\left\{u_3,u_5,u_6,u_8,u_{13},u_{16},u_{18},u_{20},u_{22},u_{24},u_{25}\right\},\hfill \\ A_3=\left\{u_2,u_{11}\right\}.\hfill \end{array}$

The graph $G$ can be colored with three colors because the vertices of $G$ can be partitioned into three independent sets. Let $c:V(G)\to \{1,2,3\}$ be the vertex coloring of $G$. From the sets A₁, A₂ and A₃, it is observed that $|A_1|=12,|A_2|=11$ and $|A_3|=2$. Thus, $|A_1|>|A_2|>|A_3|$. Now we have to prove that $c$ is a proper vertex coloring of $G$.

Figure 4

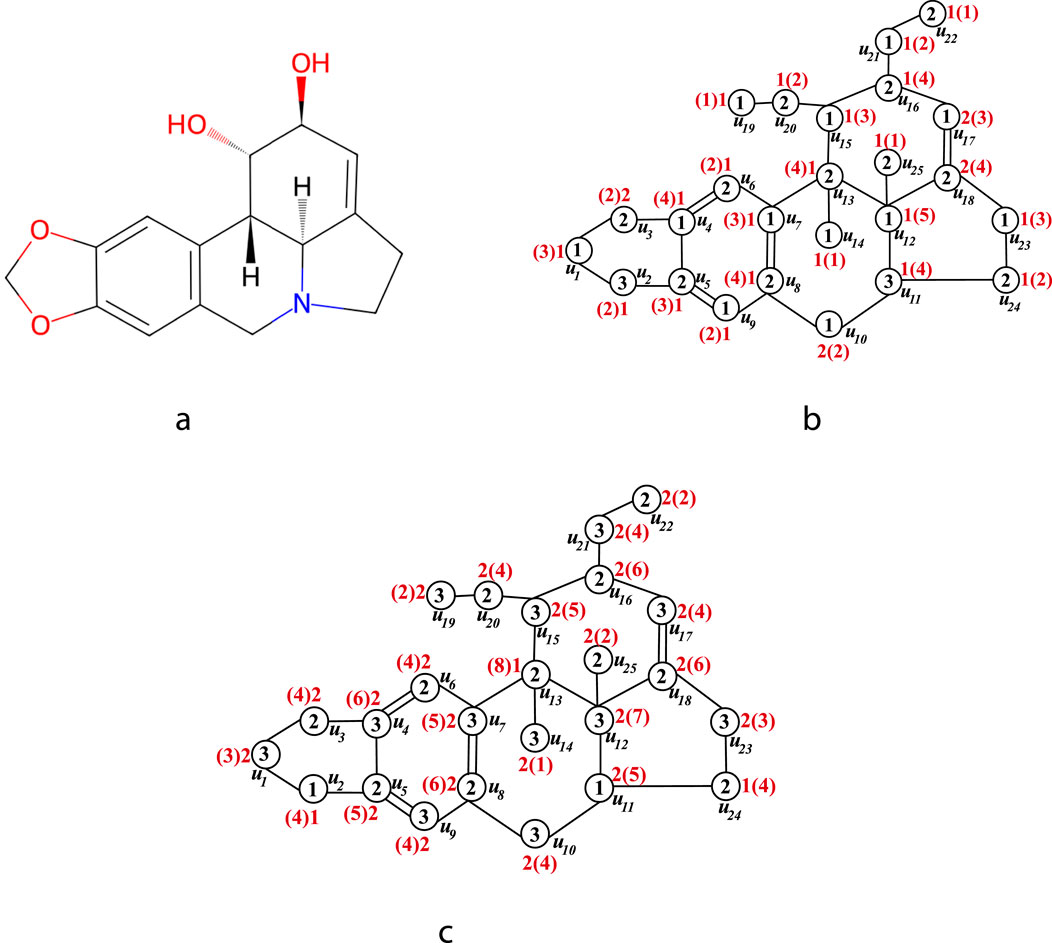
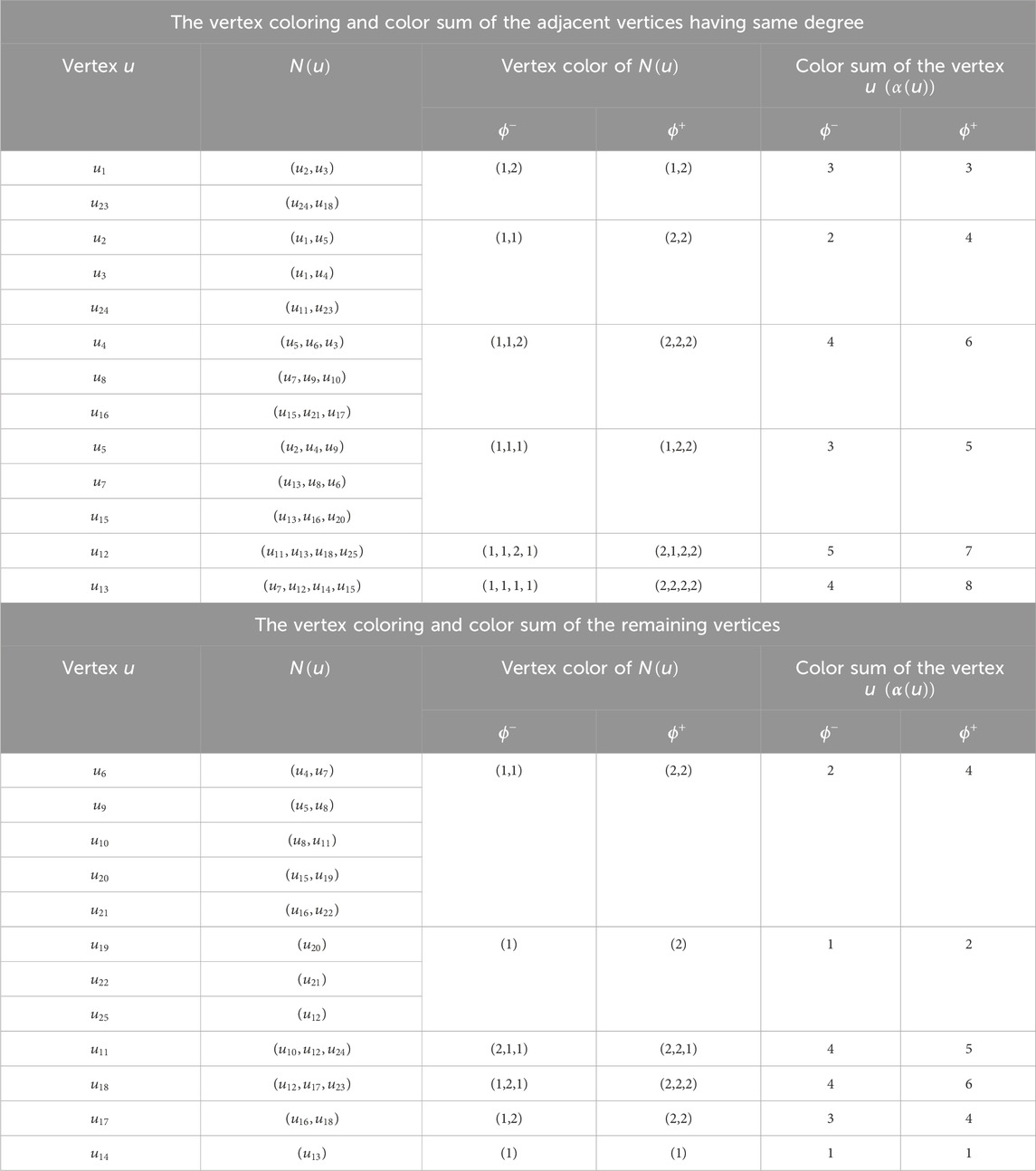
Figure 4. (a) The chemical structure of lycorine (b) The ${\varphi }^{-}$ vertex coloring and ${\varphi }^{-}$ sigma coloring of the isomorphic molecular graph of lycorine. (c) The ${\varphi }^{+}$ vertex coloring and ${\varphi }^{+}$ sigma coloring of the isomorphic molecular graph of lycorine.

6.1.1 Case 1. ${\mathit{\varphi }}^{-}$ coloring

In the case of ${\varphi }^{-}$ coloring, the vertices in $A_1,A_2$ and $A_3$ are colored with the colors 1, 2 and 3 respectively. This coloring yields the proper vertex coloring. The ${\varphi }^{-}$ proper vertex coloring of $G$ is shown in Figure 4b. Using these proper vertex color, the chromatic topological indices of $G$ are computed.

The number of vertices colored 1, 2 and 3 are 12, 11 and 2 respectively. Similarly, the number of end vertices of an edge with the color pair (1,2), (1,3) and (2,3) are 24, 3 and 2 respectively. Using the mathematical expressions presented in the Table 2 and in Section 4, the following chromatic topological indices are computed.

$\begin{array}{ll}\hfill M_1^{{\varphi }^{-}}\left(G\right)& ={\displaystyle \sum _{j=1}^l}\theta \left(c_j\right)j^2=12\left(1^2\right)+11\left(2^2\right)+2\left(3^2\right)=74.\hfill \\ \hfill M_2^{{\varphi }^{-}}\left(G\right)& ={\displaystyle \sum _{uv\in E\left(G\right)}}c\left(u\right)c\left(v\right)=24\left(2\right)+3\left(3\right)+2\left(6\right)=69.\hfill \\ \hfill M_3^{{\varphi }^{-}}\left(G\right)& ={\displaystyle \sum _{uv\in E\left(G\right)}}|c\left(u\right)-c\left(v\right)|=24\left(1\right)+3\left(2\right)+2\left(1\right)=32.\hfill \\ \hfill M_4^{{\varphi }^{-}}\left(G\right)& ={\displaystyle \sum _{uv\in E\left(G\right)}}\frac{1}{2}|c\left(u\right)-c\left(v\right)|=12+3+1=16\hfill \\ \hfill R^{{\varphi }^{-}}\left(G\right)& ={\displaystyle \sum _{uv\in E\left(G\right)}}\frac{1}{\sqrt{c\left(u\right)c\left(v\right)}}=\frac{24}{\sqrt{2}}+\frac{3}{\sqrt{3}}+\frac{2}{\sqrt{6}}=19.519\hfill \\ \hfill S{C}^{{\varphi }^{-}}\left(G\right)& ={\displaystyle \sum _{uv\in E\left(G\right)}}\frac{1}{\sqrt{c\left(u\right)+c\left(v\right)}}=\frac{24}{\sqrt{3}}+\frac{3}{\sqrt{4}}+\frac{2}{\sqrt{5}}=16.251\hfill \\ \hfill H^{{\varphi }^{-}}\left(G\right)& ={\displaystyle \sum _{uv\in E\left(G\right)}}\frac{2}{c\left(u\right)+c\left(v\right)}=\frac{2\left(24\right)}{3}+\frac{2\left(3\right)}{4}+\frac{2\left(2\right)}{5}=18.3\hfill \\ \hfill F^{{\varphi }^{-}}\left(G\right)& ={\displaystyle \sum _{u\in V\left(G\right)}}\left(c{\left(u\right)}^3\right)=12\left(1^3\right)+11\left(2^3\right)+2\left(3^3\right)=154\hfill \\ \hfill AB{C}^{{\varphi }^{-}}\left(G\right)& ={\displaystyle \sum _{uv\in E\left(G\right)}}\sqrt{\frac{c\left(u\right)+c\left(v\right)-2}{c\left(u\right)c\left(v\right)}}=24\sqrt{\frac{1}{2}}+3\sqrt{\frac{2}{3}}+2\sqrt{\frac{3}{6}}=20.834\hfill \\ \hfill G{A}^{{\varphi }^{-}}\left(G\right)& ={\displaystyle \sum _{uv\in E\left(G\right)}}\frac{2\sqrt{c\left(u\right)c\left(v\right)}}{c\left(u\right)+c\left(v\right)}=2\left(\frac{24\sqrt{2}}{3}\right)+2\left(\frac{3\sqrt{3}}{4}\right)+2\left(\frac{2\sqrt{6}}{5}\right)=27.168\hfill \end{array}$

6.1.2 Case 2. ${\mathit{\varphi }}^{+}$ coloring

In the case of ${\varphi }^{+}$ coloring, the vertices in $A_1,A_2$ and $A_3$ are colored with the colors 3, 2 and 1 respectively. This coloring yields the proper vertex coloring. The ${\varphi }^{+}$ proper vertex coloring is shown in Figure 4c. Using these vertex colors, the chromatic topological indices of $G$ are computed.

The number of vertices colored 1, 2 and 3 are 2, 11 and 12 respectively. Similarly, the number of end vertices of an edge with the color pairs (1,2), (1,3) and (2,3) are 2, 3 and 24 respectively. Using the mathematical expressions presented in the Table 2 and in Section 4, the following chromatic topological indices are computed.

$\begin{array}{ll}\hfill M_1^{{\varphi }^{+}}\left(G\right)& ={\displaystyle \sum _{j=1}^l}\theta \left(c_j\right)j^2=12\left(9\right)+11\left(4\right)+2=154\hfill \\ \hfill M_2^{{\varphi }^{+}}\left(G\right)& ={\displaystyle \sum _{uv\in E\left(G\right)}}c\left(u\right)c\left(v\right)=24\left(6\right)+3\left(3\right)+2\left(2\right)=157\hfill \\ \hfill M_3^{{\varphi }^{+}}\left(G\right)& ={\displaystyle \sum _{uv\in E\left(G\right)}}|c\left(u\right)-c\left(v\right)|=24\left(1\right)+3\left(2\right)+2\left(1\right)=32\hfill \\ \hfill M_4^{{\varphi }^{+}}\left(G\right)& ={\displaystyle \sum _{uv\in E\left(G\right)}}\frac{1}{2}|c\left(u\right)-c\left(v\right)|=12+3+1=16\hfill \\ \hfill R^{{\varphi }^{+}}\left(G\right)& ={\displaystyle \sum _{uv\in E\left(G\right)}}\frac{1}{\sqrt{c\left(u\right)c\left(v\right)}}=\frac{24}{\sqrt{6}}+\frac{3}{\sqrt{3}}+\frac{2}{\sqrt{2}}=12.944\hfill \\ \hfill S{C}^{{\varphi }^{+}}\left(G\right)& ={\displaystyle \sum _{uv\in E\left(G\right)}}\frac{1}{\sqrt{c\left(u\right)+c\left(v\right)}}=\frac{24}{\sqrt{5}}+\frac{3}{\sqrt{4}}+\frac{2}{\sqrt{3}}=13.388\hfill \\ \hfill H^{{\varphi }^{+}}\left(G\right)& ={\displaystyle \sum _{uv\in E\left(G\right)}}\frac{2}{c\left(u\right)+c\left(v\right)}=\frac{48}{5}+\frac{6}{4}+\frac{4}{3}=12.433\hfill \\ \hfill F^{{\varphi }^{+}}\left(G\right)& ={\displaystyle \sum _{u\in V\left(G\right)}}\left(c{\left(u\right)}^3\right)=12\left(3^3\right)+11\left(2^3\right)+2\left(1^3\right)=414\hfill \\ \hfill AB{C}^{{\varphi }^{+}}\left(G\right)& ={\displaystyle \sum _{uv\in E\left(G\right)}}\sqrt{\frac{c\left(u\right)+c\left(v\right)-2}{c\left(u\right)c\left(v\right)}}=24\sqrt{\frac{3}{6}}+3\sqrt{\frac{2}{3}}+2\sqrt{\frac{1}{2}}=20.834\hfill \\ \hfill G{A}^{{\varphi }^{+}}\left(G\right)& ={\displaystyle \sum _{uv\in E\left(G\right)}}\frac{2\sqrt{c\left(u\right)c\left(v\right)}}{c\left(u\right)+c\left(v\right)}=2\left(\frac{24\sqrt{6}}{5}\right)+2\left(\frac{3\sqrt{3}}{4}\right)+2\left(\frac{2\sqrt{2}}{3}\right)=27.999\hfill \end{array}$

In a similar manner, the chromatic topological indices for the isomorphic molecular graphs of UV-4B (N-9-methoxynonyl-1-deoxynojirimycin), ST-148, 4-HPR, Silymarin, Baicalein, Quercetin, Naringenin, Nelfinavir, Ivermectin, Mosnodenvir (JNJ-1802), NITD-688, Metoclopramide, JNJ-A07 and Betulinic acid are computed. The ${\varphi }^{-}$ and ${\varphi }^{+}$ proper vertex coloring of the isomorphic molecular graphs of the considered potential antivirals of dengue disease are provided in the Supplementary Material and their computed chromatic topological indices are tabulated in Table 3.

Table 3

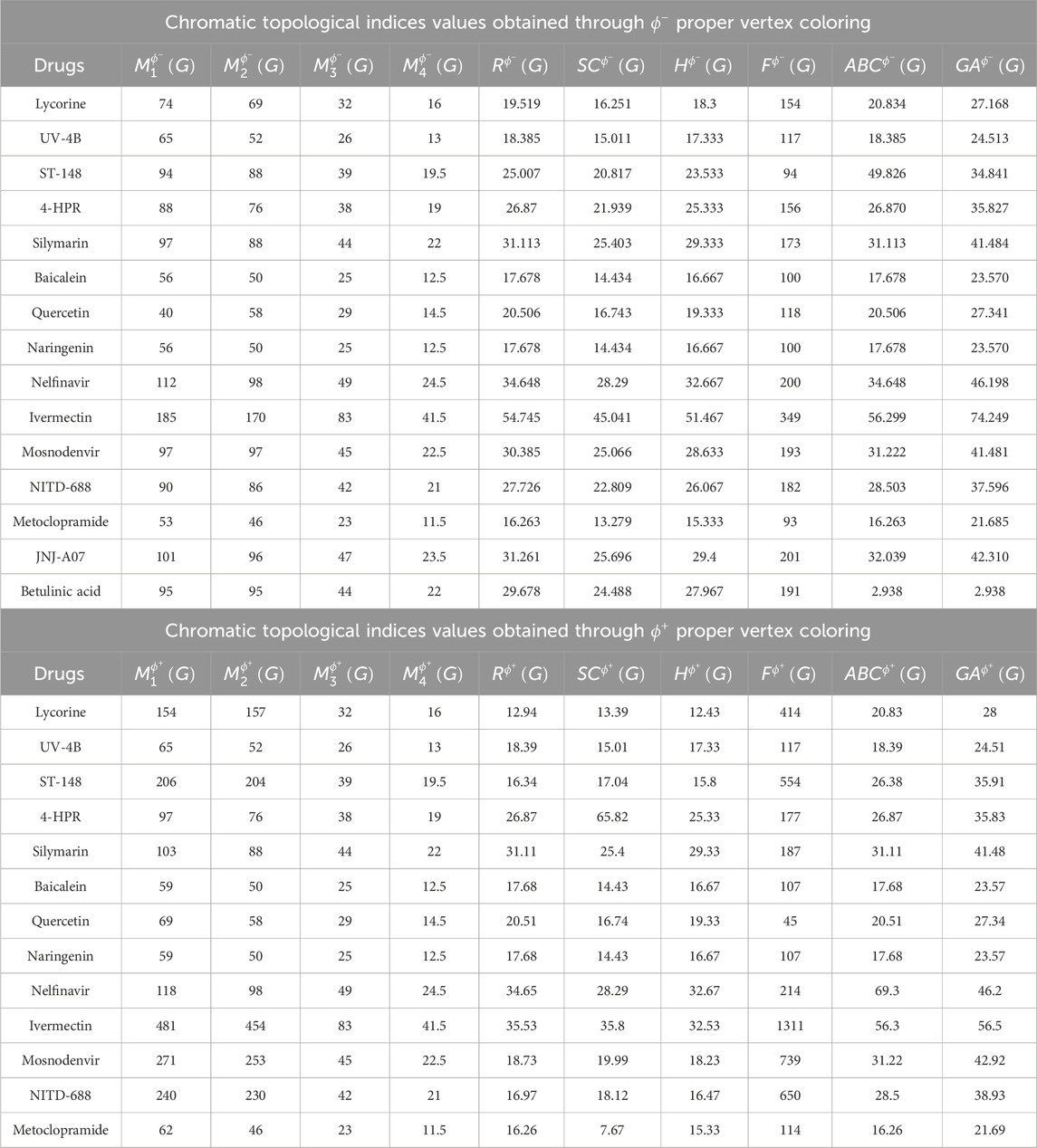
Table 3. The computed chromatic topological indices through ${\varphi }^{-}$ and ${\varphi }^{+}$ proper vertex coloring of 15 potential antivirals of dengue disease.

6.2 Computation of induced color-based topological indices

Let $c:V(G)\to \{c_1,c_2,\dots ,c_l\}$ be the vertex coloring of $G$. The following steps are followed to color the vertices of isomorphic molecular graph of the considered antivirals of dengue, such that the vertex coloring $c$ is a sigma coloring.

1. If two adjacent vertices, say $u$ and $v$, have different degrees, then the vertices in $N(u)$ and $N(v)$ can be colored with the same color such that $\sigma (u)\ne \sigma (v)$.

2. If two adjacent vertices, say $u$ and $v$, have equal degree, then atleast one vertex in $N(u)$ or $N(v)$ must be assigned with the different color such that $\sigma (u)\ne \sigma (v)$.

Theorem 2:. Let $G$ be the isomorphic molecular graph of Lycorine. The induced color based topological indices of the graph $G$ through ${\varphi }^{-}$ and ${\varphi }^{+}$ sigma coloring are as follows:

$N{D}_1^{{\varphi }^{-}}(G)=85.139,N{D}_2^{{\varphi }^{-}}(G)=12.022,N{D}_3^{{\varphi }^{-}}(G)=1820,$$N{D}_4^{{\varphi }^{-}}(G)=10.674,N{D}_5^{{\varphi }^{-}}(G)=69.933,M_N^{{\varphi }^{-}}(G)=211,$$M{N}_2^{{\varphi }^{-}}(G)=267,F_N^{{\varphi }^{-}}(G)=739,M{F}_N^{{\varphi }^{-}}(G)=607$ and $N{I}^{{\varphi }^{-}}(G)=41.081$

$N{D}_1^{{\varphi }^{+}}(G)=136.948,N{D}_2^{{\varphi }^{+}}(G)=9.447,N{D}_3^{{\varphi }^{+}}(G)=6104,$$N{D}_4^{{\varphi }^{+}}(G)=6.367,N{D}_5^{{\varphi }^{+}}(G)=69.833,M_N^{{\varphi }^{+}}(G)=532,$$M{N}_2^{{\varphi }^{+}}(G)=683,F_N^{{\varphi }^{+}}(G)=2874,M{F}_N^{{\varphi }^{+}}(G)=1521\mathrm{a}\mathrm{n}\mathrm{d}N{I}^{{\varphi }^{+}}(G)=66.604$.

Proof. Let $G$ be the isomorphic molecular graph of Lycorine where 25 atoms and 29 bonds are represented as vertices and edges respectively. Let $V(G)=\{u_1,u_2,\dots ,u_{25}\}$ be the vertex set of $G$. The chemical structure of lycorine is shown in Figure 4a. By Observation 1, we have the inequality.

$\sigma \left(G\right)\ge 2.$

Let $c:V(G)\to \{\mathrm{1,2}\}$ be the vertex coloring of $G$. Now we have to prove that $c$ is a sigma coloring of $G$.

From the isomorphic molecular graph of $G$, it is observed that $d(u_1)=d(u_3),d(u_1)=d(u_2),d(u_4)=d(u_5),d(u_7)=d(u_8),$ $d(u_{12})=d(u_{13}),d(u_{15})=d(u_{16})\mathrm{a}\mathrm{n}\mathrm{d}d(u_{23})=d(u_{24})$. By following the steps 1 and 2, the vertices with the same degree and different degrees are assigned colors as shown in Table 4.

Table 4

Table 4. The vertex coloring and color sum of the vertices for ${\varphi }^{-}$ and ${\varphi }^{+}$ sigma coloring of $G$.

By comparing the $\alpha (u)$ values in Table 4 for any two adjacent vertices in $G$, it is observed that adjacent vertices with the same degree and distinct degree have distinct color sums. Thus $c$ is both ${\varphi }^{-}$ sigma coloring and ${\varphi }^{+}$ sigma coloring. The ${\varphi }^{-}$ and ${\varphi }^{+}$ sigma coloring of $G$ are shown in Figures 4b,c respectively.

Using the $\alpha (u)$ value from Table 4, the induced color based topological indices are calculated for both ${\varphi }^{-}$ coloring and ${\varphi }^{+}$ coloring. Table 5 present the values necessary for the efficient computation of induced color-based topological indices in ${\varphi }^{-}$ sigma coloring.

Table 5

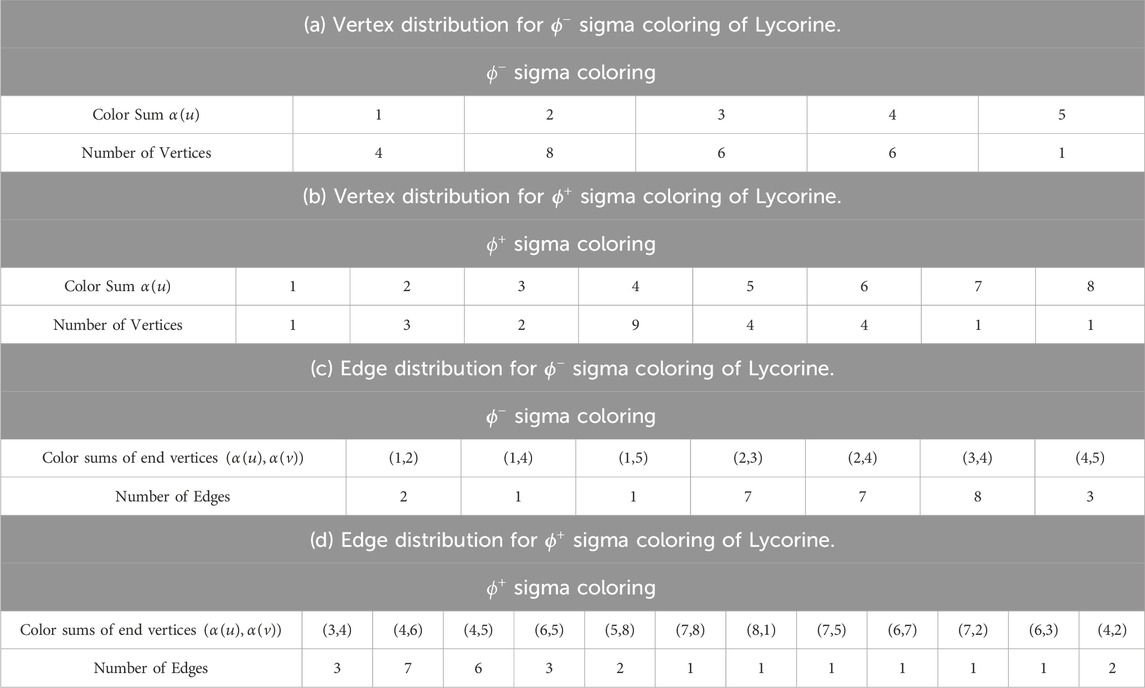
Table 5. The vertex and edge distribution based on color sums of vertices in ${\varphi }^{-}$ and ${\varphi }^{+}$ sigma coloring of Lycorine.

The following are the induced color-based indices of $G$ obtained through ${\varphi }^{-}$ sigma coloring.

$\begin{array}{ll}\hfill N{D}_1^{{\varphi }^{-}}\left(G\right)& ={\displaystyle \sum _{uv\in E\left(G\right)}}\sqrt{\alpha \left(u\right)\alpha \left(v\right)}\hfill \\ \hfill & =2\sqrt{2}+1\sqrt{4}+\sqrt{5}+7\sqrt{6}+7\sqrt{8}+8\sqrt{12}+3\sqrt{20}\hfill \\ \hfill & =85.139\hfill \end{array}$

$\begin{array}{ll}\hfill N{D}_2^{{\varphi }^{-}}\left(G\right)& ={\displaystyle \sum _{uv\in E\left(G\right)}}\frac{1}{\sqrt{\alpha \left(u\right)+\alpha \left(v\right)}}\hfill \\ \hfill & =\frac{2}{\sqrt{3}}+\frac{1}{\sqrt{5}}+\frac{1}{\sqrt{6}}+\frac{7}{\sqrt{5}}+\frac{7}{\sqrt{6}}+\frac{8}{\sqrt{7}}+\frac{3}{\sqrt{9}}\hfill \\ \hfill & =12.022\hfill \\ \hfill N{D}_3^{{\varphi }^{-}}\left(G\right)& ={\displaystyle \sum _{uv\in E\left(G\right)}}\alpha \left(u\right)\alpha \left(v\right)\left[\alpha \left(u\right)+\alpha \left(v\right)\right]\hfill \\ \hfill & =\left(2\times 2\times 3\right)+\left(1\times 4\times 5\right)+\left(1\times 5\times 6\right)\hfill \\ \hfill & +\left(7\times 6\times 5\right)+\left(7\times 8\times 6\right)+\left(8\times 12\times 7\right)\hfill \\ \hfill & +\left(3\times 20\times 9\right).\hfill \\ \hfill & =1820\hfill \\ \hfill N{D}_4^{{\varphi }^{-}}\left(G\right)& ={\displaystyle \sum _{uv\in E\left(G\right)}}\frac{1}{\sqrt{\alpha \left(u\right)\alpha \left(v\right)}}\hfill \\ \hfill & =\frac{2}{\sqrt{2}}+\frac{1}{\sqrt{4}}+\frac{1}{\sqrt{5}}+\frac{7}{\sqrt{6}}+\frac{7}{\sqrt{8}}+\frac{8}{\sqrt{12}}+\frac{3}{\sqrt{20}}\hfill \\ \hfill & =10.674\hfill \end{array}$

$\begin{array}{ll}\hfill N{D}_5^{{\varphi }^{-}}\left(G\right)& ={\displaystyle \sum _{uv\in E\left(G\right)}}\left[\frac{\alpha \left(u\right)}{\alpha \left(v\right)}+\frac{\alpha \left(v\right)}{\alpha \left(u\right)}\right]\hfill \\ \hfill & =2\left[\frac{1}{2}+\frac{2}{1}\right]+1\left[\frac{1}{4}+\frac{4}{1}\right]+\left[\frac{1}{5}+\frac{5}{1}\right]+7\left[\frac{2}{3}+\frac{3}{2}\right]+8\left[\frac{3}{4}+\frac{4}{3}\right]\hfill \\ \hfill & =+3\left[\frac{4}{5}+\frac{5}{4}\right]+7\left[\frac{2}{4}+\frac{4}{2}\right]\hfill \\ \hfill & =69.933\hfill \\ \hfill M_N^{{\varphi }^{-}}\left(G\right)& ={\displaystyle \sum _{u\in V\left(G\right)}}{\left(\alpha \left(u\right)\right)}^2\hfill \\ \hfill & =4\left(1^2\right)+8\left(2^2\right)+6\left(3^2\right)+6\left(4^2\right)+1\left(5^2\right)\hfill \\ \hfill & =211\hfill \\ \hfill M{N}_2^{{\varphi }^{-}}\left(G\right)& ={\displaystyle \sum _{uv\in E\left(G\right)}}\alpha \left(u\right)\alpha \left(v\right)\hfill \\ \hfill & =2\left(2\right)+1\left(4\right)+1\left(5\right)+7\left(6\right)+7\left(8\right)+8\left(12\right)+3\left(20\right)\hfill \\ \hfill & =267\hfill \\ \hfill F_N^{{\varphi }^{-}}\left(G\right)& ={\displaystyle \sum _{u\in V\left(G\right)}}{\left(\alpha \left(u\right)\right)}^3\hfill \\ \hfill & =4\left(1^3\right)+8\left(2^3\right)+6\left(3^3\right)+6\left(4^3\right)+1\left(5^3\right)\hfill \\ \hfill & =739\hfill \end{array}$

$\begin{array}{ll}\hfill M{F}_N^{{\varphi }^{-}}\left(G\right)& ={\displaystyle \sum _{uv\in E\left(G\right)}}\left(\alpha {\left(u\right)}^2+\alpha {\left(v\right)}^2\right)\hfill \\ \hfill & =2\left(1^2+2^2\right)+1\left(1^2+4^2\right)+1\left(1^2+5^2\right)+7\left(2^2+3^2\right)\hfill \\ \hfill & +7\left(2^2+4^2\right)+8\left(3^2+4^2\right)+3\left(4^2+5^2\right)\hfill \\ \hfill & =607\hfill \\ \hfill N{I}^{{\varphi }^{-}}\left(G\right)& ={\displaystyle \sum _{uv\in E\left(G\right)}}\frac{\alpha \left(u\right)\alpha \left(v\right)}{\alpha \left(u\right)+\alpha \left(v\right)}\hfill \\ \hfill & =2\left(\frac{1\times 2}{1+2}\right)+\left(\frac{1\times 4}{1+4}\right)+\left(\frac{1\times 5}{1+5}\right)+7\left(\frac{2\times 3}{2+3}\right)\hfill \\ \hfill & +7\left(\frac{2\times 4}{2+4}\right)+8\left(\frac{3\times 4}{3+4}\right)+3\left(\frac{4\times 5}{4+5}\right)\hfill \\ \hfill & =41.081\hfill \end{array}$

The Table 5 presents the values necessary for the efficient computation of induced color-based topological indices in ${\varphi }^{+}$ sigma coloring.

The following are the induced color-based indices of $G$ obtained through ${\varphi }^{+}$ sigma coloring of $G$.

$\begin{array}{ll}\hfill N{D}_1^{{\varphi }^{+}}\left(G\right)& ={\displaystyle \sum _{uv\in E\left(G\right)}}\sqrt{\sigma \left(u\right)\sigma \left(v\right)}=136.948\hfill \\ \hfill N{D}_2^{{\varphi }^{+}}\left(G\right)& ={\displaystyle \sum _{uv\in E\left(G\right)}}\frac{1}{\sqrt{\sigma \left(u\right)+\sigma \left(v\right)}}=9.447\hfill \\ \hfill N{D}_3^{{\varphi }^{+}}\left(G\right)& ={\displaystyle \sum _{uv\in E\left(G\right)}}\sigma \left(u\right)\sigma \left(v\right)\left[\sigma \left(u\right)+\sigma \left(v\right)\right]=6104\hfill \\ \hfill N{D}_4^{{\varphi }^{+}}\left(G\right)& ={\displaystyle \sum _{uv\in E\left(G\right)}}\frac{1}{\sqrt{\sigma \left(u\right)\sigma \left(v\right)}}=6.367\hfill \\ \hfill N{D}_5^{{\varphi }^{+}}\left(G\right)& ={\displaystyle \sum _{uv\in E\left(G\right)}}\left[\frac{\sigma \left(u\right)}{\sigma \left(v\right)}+\frac{\sigma \left(v\right)}{\sigma \left(u\right)}\right]=69.833\hfill \\ \hfill M_N^{{\varphi }^{+}}\left(G\right)& ={\displaystyle \sum _{u\in V\left(G\right)}}{\left(\sigma \left(u\right)\right)}^2=532\hfill \\ \hfill M{N}_2^{{\varphi }^{+}}\left(G\right)& ={\displaystyle \sum _{uv\in E\left(G\right)}}\sigma \left(u\right)\sigma \left(v\right)=683\hfill \\ \hfill F_N^{{\varphi }^{+}}\left(G\right)& ={\displaystyle \sum _{u\in V\left(G\right)}}{\left(\sigma \left(u\right)\right)}^3=2874\hfill \\ \hfill M{F}_N^{{\varphi }^{+}}\left(G\right)& ={\displaystyle \sum _{uv\in E\left(G\right)}}\left(\sigma {\left(u\right)}^2+\sigma {\left(v\right)}^2\right)=1521\hfill \\ \hfill N{I}^{{\varphi }^{+}}\left(G\right)& ={\displaystyle \sum _{uv\in E\left(G\right)}}\frac{\sigma \left(u\right)\sigma \left(v\right)}{\sigma \left(u\right)+\sigma \left(v\right)}=66.604\hfill \end{array}$

In Figure 4, the values inside the circles represent the proper vertex coloring, while the values outside the circles correspond to the sigma coloring. In sigma coloring, the numbers outside the brackets indicate the initial vertex color, whereas the numbers inside the brackets represent the vertex color sum.

In similar manner, the induced color based topological indices are calculated for UV-4B (N-9-methoxynonyl-1-deoxynojirimycin), ST-148, 4-HPR, Silymarin, Baicalein, Quercetin, Naringenin, Nelfinavir, Ivermectin, Mosnodenvir (JNJ-1802), NITD-688, Metoclopramide, JNJ-A07 and Betulinic acid. The ${\varphi }^{-}$ and ${\varphi }^{+}$ sigma coloring of the isomorphic molecular graphs of potential antivirals of dengue are provided in the Supplementary Material and their computed induced color based topological indices are tabulated in Table 6.

Table 6

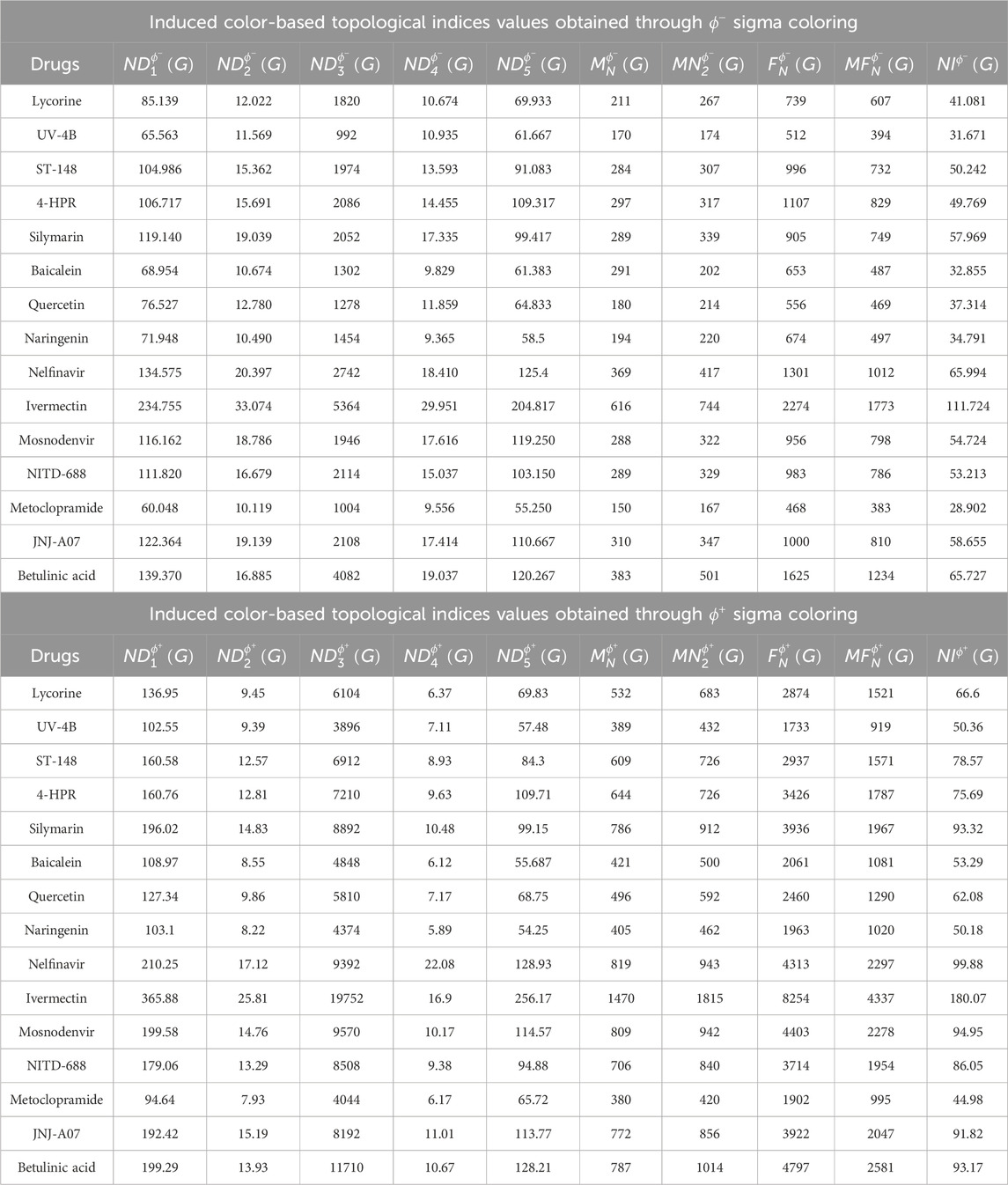
Table 6. The computed induced color-based topological indices through ${\varphi }^{-}$ and ${\varphi }^{+}$ sigma coloring of 15 potential antivirals of dengue.

7 QSPR analysis for physicochemical properties of potential antivirals of dengue

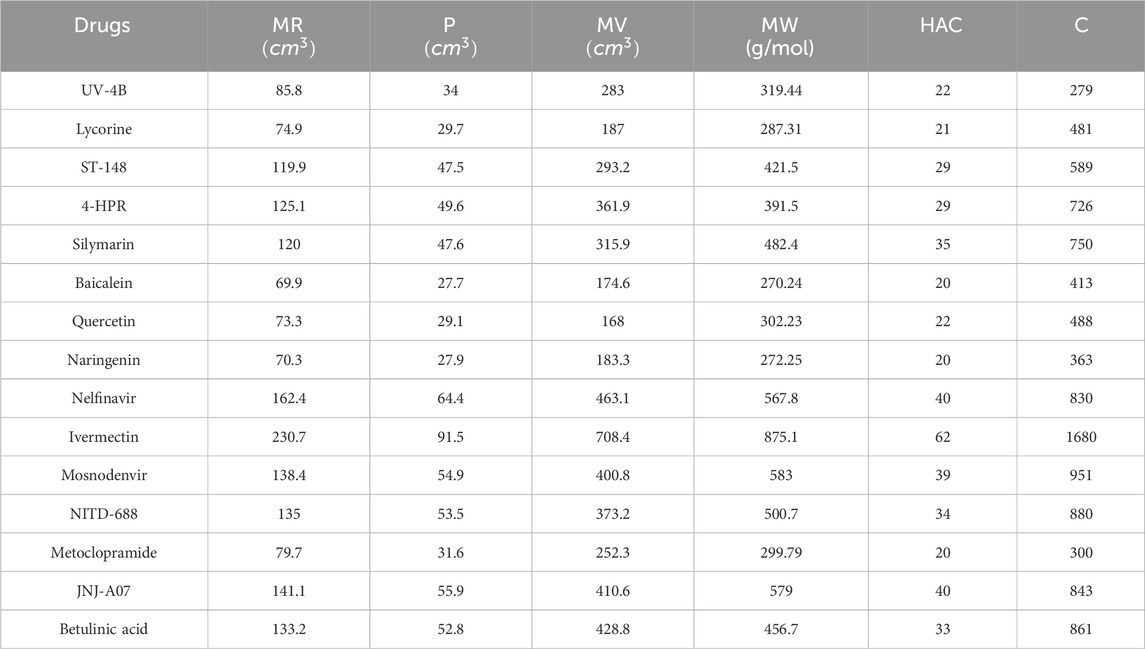
The QSPR analysis is carried out between the computed topological indices and physicochemical properties of antiviral drugs for dengue disease, namely, UV-4B (N-9-methoxynonyl-1-deoxynojirimycin), Lycorine, ST-148, 4-HPR, Silymarin, Baicalein, Quercetin, Naringenin, Nelfinavir, Ivermectin, Mosnodenvir (JNJ-1802), NITD-688, Metoclopramide, JNJ-A07 and Betulinic acid. The physicochemical properties of these drugs are tabulated in Table 7 and they were obtained from the database www.chemspider.com. The properties considered for the QSPR analysis include Molar Refraction (MR)$(c{m}^3)$, Polarizability (P) $(c{m}^3)$, Molar Volume (MV) $(c{m}^3)$, Molecular weight (MW) $(g/mol)$, Heavy Atom Count (HAC) and Complexity(C).

Table 7

Table 7. Physicochemical properties of potential antivirals of dengue.

The linear regression $Y=A+B(X)$ is used in QSPR analysis to explore the physicochemical properties of the aforementioned drugs. Here, $Y$ represents the physicochemical property, $X$ denotes the computed topological index and $A$ and $B$ are constants. The statistical parameters include $R^2$ (coefficient of determination), $R$ (correlation coefficient), $F$ (F-statistics) and $SE$ (standard error), which collectively evaluate the model’s performance. Specifically, $R^2$ measures the proportion of the variance in the dependent variable explained by the regression model, $R$ indicates the strength and direction of the linear relationship between the predicted and actual value, $F$ tests the overall significance of the regression model and $SE$ quantifies the average deviation of the observed values from the predicted value. The QSPR graph model maximizes $R^2,R$ and $F$ values and minimizes $SE$ value in the statistical analysis. The squared correlation coefficient values $(R^2)$ determined between the indices and physicochemical properties of potential antiviral drugs are presented in the form of heatmaps and are shown in Figure 5. The best-fitting and most predictable linear regression equations, having the maximum $R^2$ values, are summarized in Table 8. It is noted that the physicochemical properties hold great significance since $R>0.8$ and the p-value is less than 0.05. Compared to other regression models, linear regression analysis demonstrates significant outcomes, with a high coefficient value and a smaller standard error.

Figure 5

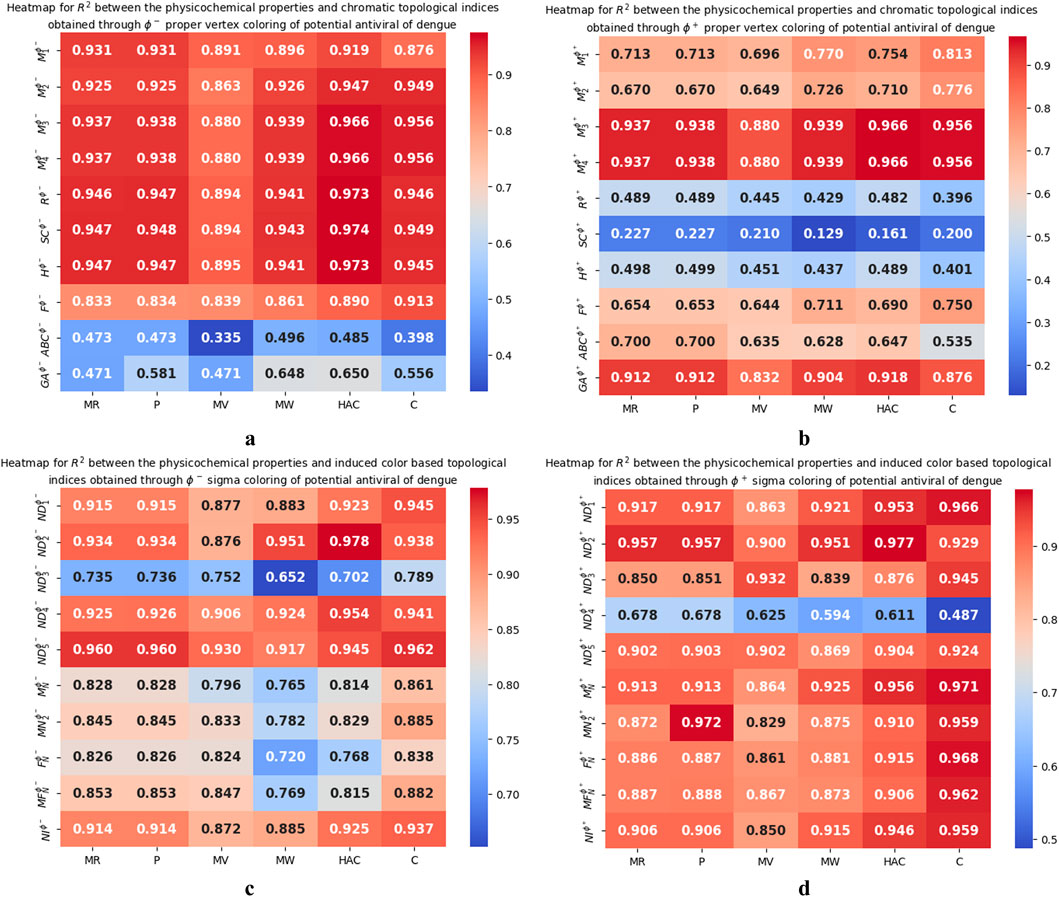
Figure 5. (a) Heatmap of $R^2$ between the physicochemical properties and ${\varphi }^{-}$ chromatic topological indices (b) Heatmap of $R^2$ between the physicochemical properties and ${\varphi }^{+}$ chromatic topological indices (c) Heatmap of $R^2$ between the physicochemical properties and ${\varphi }^{-}$ induced color-based topological indices (d) Heatmap of $R^2$ between the physicochemical properties and ${\varphi }^{+}$ induced color-based topological indices.

Table 8

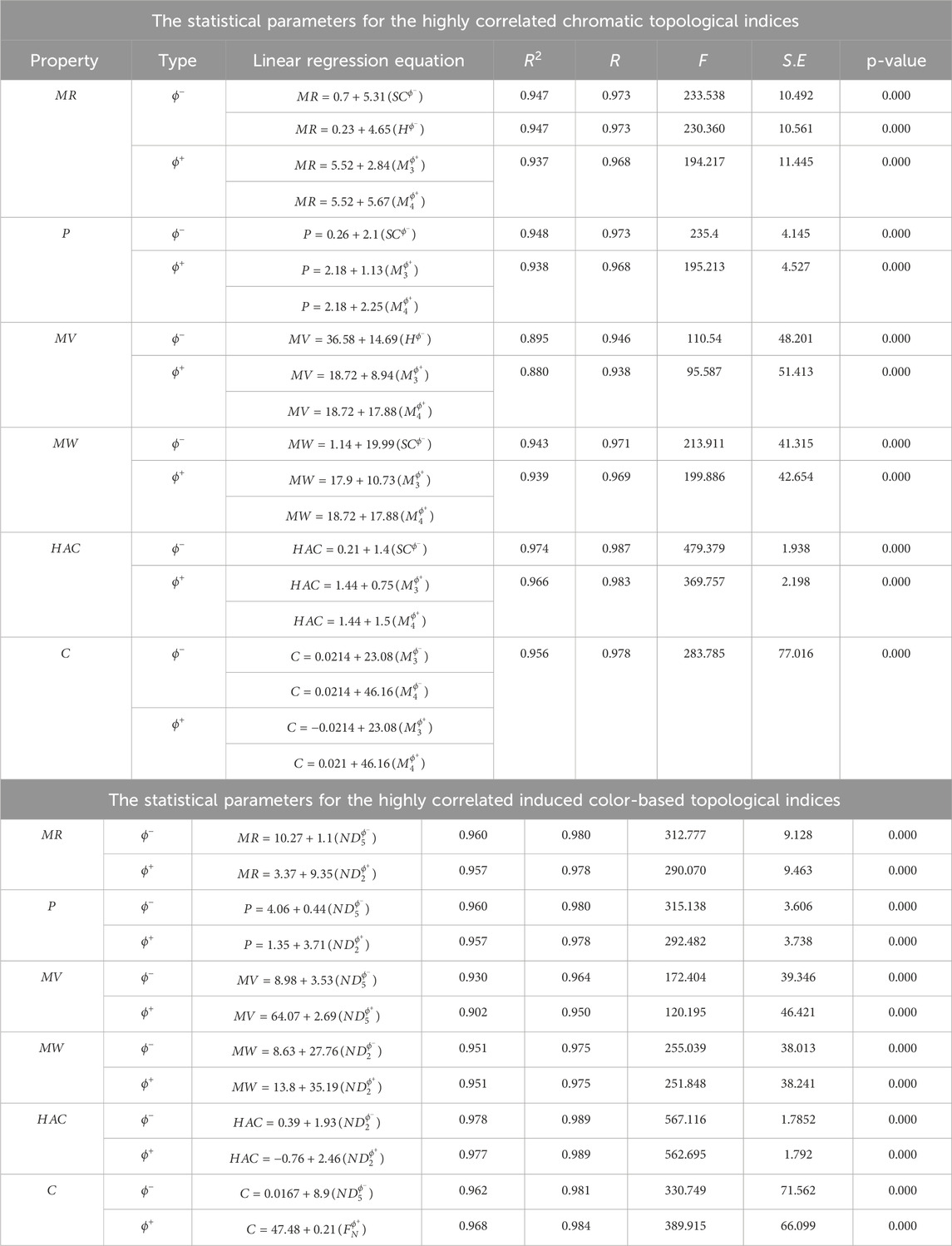
Table 8. The statistical parameters for the highly correlated chromatic topological indices and induced color-based topological indices.

The $R^2$ values obtained through chromatic topological indices and induced color-based indices are compared and analyzed. The results show that the induced color-based indices significantly outperform chromatic topological indices. The curve fits between the computed induced color-based topological indices and drug properties, obtained through linear regression with the highest $R^2$ values and $p<0.05$, are illustrated in Figure 6.

Figure 6

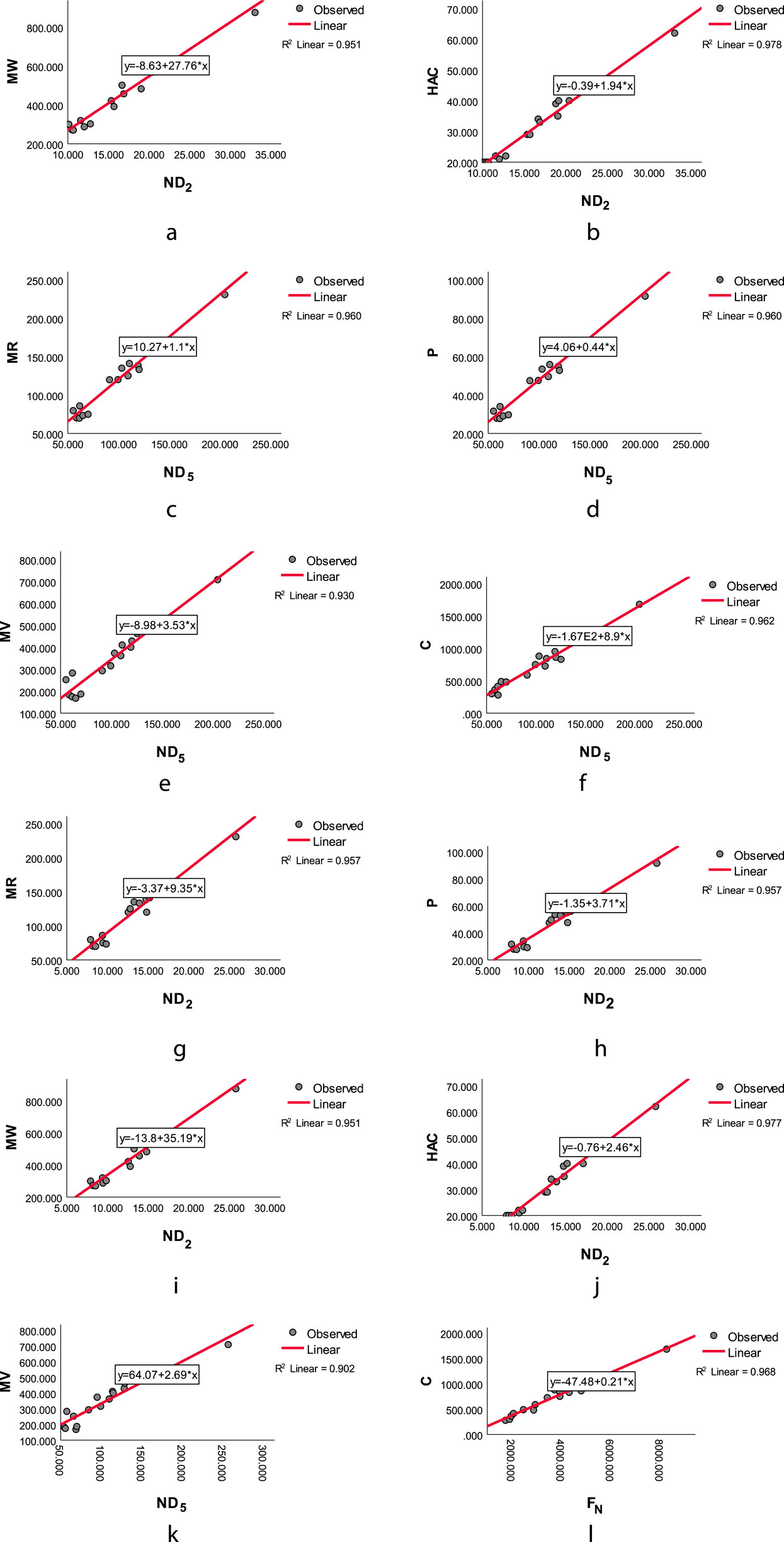
Figure 6. The linear regression curve of (a) ${\varphi }^{-}$ second induced color index$(N{D}_2^{{\varphi }^{-}})$ with Molar Weight (MW) (b) ${\varphi }^{-}$ second induced color index$(N{D}_2^{{\varphi }^{-}})$ with Heavy Atom Count(HAC) (c) ${\varphi }^{-}$ fifth induced color index$(N{D}_5^{{\varphi }^{-}})$ with Molar Refraction(MR) (d)+ ${\varphi }^{-}$ fifth induced color index$(N{D}_5^{{\varphi }^{-}})$ with Polarizability(P) (e) ${\varphi }^{-}$ fifth induced color index$(N{D}_5^{{\varphi }^{-}})$ with Molar Volume (MV) (f) ${\varphi }^{-}$ fifth induced color index$(N{D}_5^{{\varphi }^{-}})$ with Complexity (C) (g) ${\varphi }^{+}$ second induced color index$(N{D}_2^{{\varphi }^{+}})$ with Molar Refraction (MR) (h) ${\varphi }^{+}$ second induced color index$(N{D}_2^{{\varphi }^{+}})$ with Polarizability (P) (i) ${\varphi }^{+}$ second induced color index$(N{D}_2^{{\varphi }^{+}})$ with Molar Weight(MW) (j) ${\varphi }^{+}$ second induced color index$(N{D}_2^{{\varphi }^{+}})$ with Heavy Atom Count(HAC) (k) ${\varphi }^{+}$ fifth induced color index$(N{D}_5^{{\varphi }^{+}})$ and ${\varphi }^{+}$ Forgotten induced color index $(F_N^{{\varphi }^{+}})$ with Molar Volume (MV) (l) ${\varphi }^{+}$ fifth induced color index$(N{D}_5^{{\varphi }^{+}})$ and ${\varphi }^{+}$ Forgotten induced color index $(F_N^{{\varphi }^{+}})$ with Complexity (C).

8 Y-randomization test

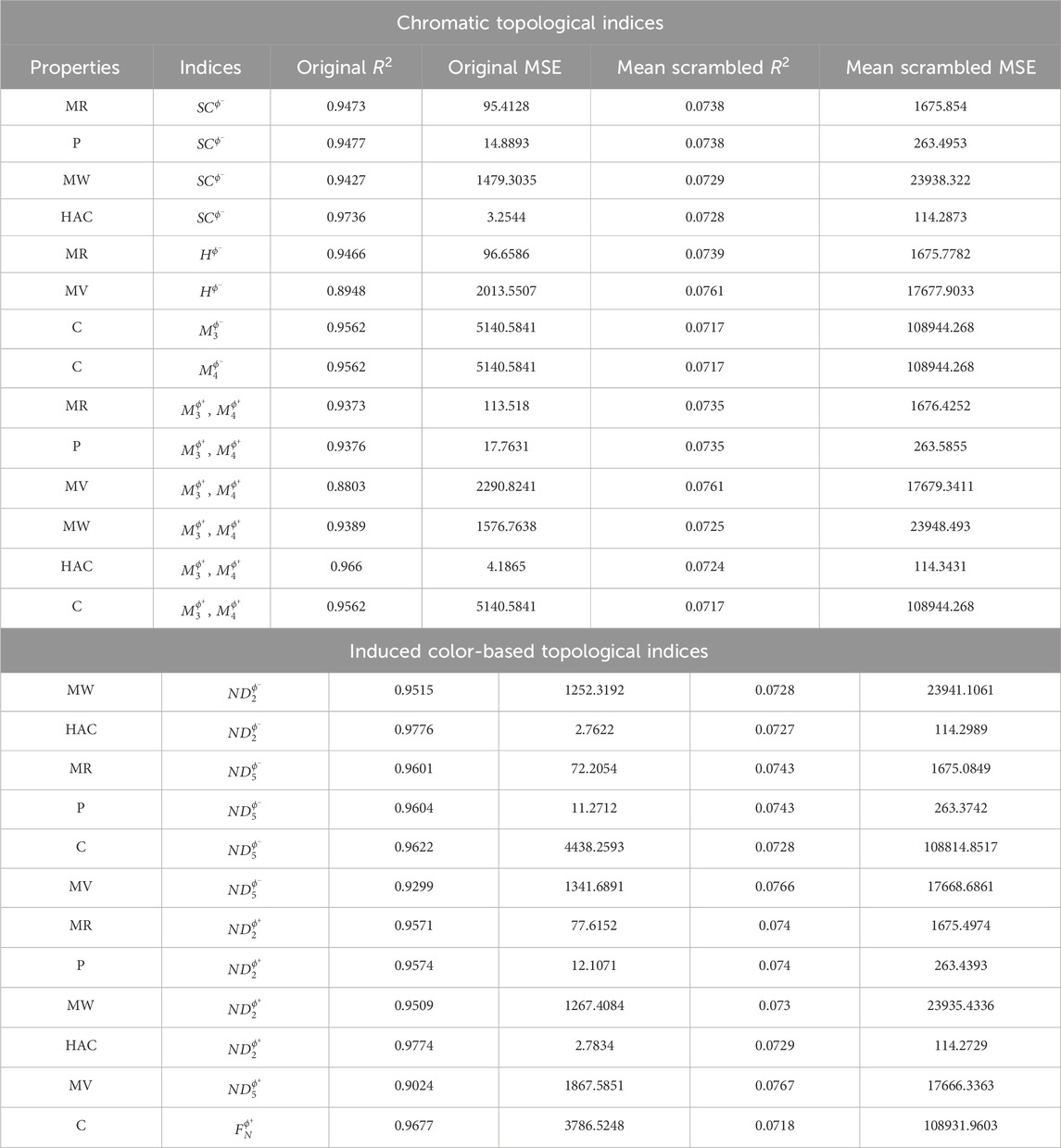
The Y-randomization test (also known as response permutation test) is performed to ensure that the developed QSPR analysis is not influenced by chance correlations. This test is a crucial validation technique in QSPR analysis to assess whether the observed relationship between the physicochemical properties and the computed topological indices are statistically significant.

In this procedure, the dependent variable (Y-values), representing the physicochemical properties, is randomly shuffled, while the independent variables (X-values), representing the topological indices, remain unchanged. A linear regression is then trained on the randomized dataset, and its coefficient of determination $(R^2)$ is compared with that of the original model. A significant drop in $R^2$ value after randomization indicates that the original model captures meaningful structure-property relationships.

The original and scrambled $R^2$ values and the original and scrambled mean squared error (MSE) for the proposed QSPR analysis are summarized in Table 9.

Table 9

Table 9. Comparison of original and scrambled R² and mean squared error value.

8.1 Inference from Y-randomization test

(i) The original R²; values for the physicochemical properties of potential antivirals of dengue disease are consistently high, with most values close to or exceeding 0.8. This indicates that the regression models effectively explain a significant proportion of variance in the observed data. Additionally, the original MSE values are low, demonstrating the accuracy of the predictions.

(ii) The mean scrambled R²; values remain consistently low (approximately 0.07 across all properties), suggesting a weak or nonexistent relationship between the scrambled observed values and the predicted values. Furthermore, the mean scrambled MSE values are substantially higher than the original MSE values, confirming that randomization disrupts predictive accuracy.

(iii) The substantial difference between the original and scrambled R²; values, along with the significant difference in MSE values, underscores that the predictive performance of the analysis is not attributable to random chance.

These results affirm that the regression models effectively capture meaningful relationships between the computed topological indices and the physicochemical properties of the considered dengue-treating drugs. Consequently, the Y-randomization test validates the statistical significance and robustness of the QSPR linear regression analysis.

9 Results and discussion

The chromatic topological indices that yield the highest correlation in the QSPR analysis for the physicochemical properties of UV-4B (N-9-methoxynonyl-1-deoxynojirimycin), Lycorine, ST-148, 4-HPR, Silymarin, Baicalein, Quercetin, Naringenin, Nelfinavir, Ivermectin, Mosnodenvir (JNJ-1802), NITD-688, Metoclopramide, JNJ-A07 and Betulinic acid are as follows:

(i) The ${\varphi }^{-}$ chromatic sum connectivity index $(S{C}^{{\varphi }^{-}})$ shows an excellent corrlation coefficient of Molar Refraction(MR), Polarizability (P), Molar weight(MW) and Heavy Atom Count(HAC).

(ii) The ${\varphi }^{-}$ chromatic harmonic index $(H^{{\varphi }^{-}})$ is the best suitable index to predict Molar Refraction(MR) and Molar Volume(MV).

(iii) The ${\varphi }^{-}$ chromatic irregularity index $(M_3^{{\varphi }^{-}})$ and ${\varphi }^{-}$ chromatic total irregularity index $(M_4^{{\varphi }^{-}})$ are the best indices for the prediction of Complexity (C).

(iv) The ${\varphi }^{+}$ chromatic irregularity index $(M_3^{{\varphi }^{+}})$ and ${\varphi }^{+}$ chromatic total irregularity index $(M_4^{{\varphi }^{+}})$ are the best suited indices for predicting Molar Refraction (MR), Polarizability (P), Molar Volume (MV), Molar Weight(MW), Heavy Atom Count(HAC) and Complexity (C).

The induced color-based topological indices that yield the highest correlation the QSPR analysis for the physicochemical properties of UV-4B (N-9-methoxynonyl-1-deoxynojirimycin), Lycorine, ST-148, 4-HPR, Silymarin, Baicalein, Quercetin, Naringenin, Nelfinavir, Ivermectin, Mosnodenvir (JNJ-1802), NITD-688, Metoclopramide, JNJ-A07 and Betulinic acid are as follows:

(i) The ${\varphi }^{-}$ second induced color index $(N{D}_2^{{\varphi }^{-}})$ is highly correlated with the properties, Molar Weight(MW) and Heavy Atom Count(HAC).

(ii) The ${\varphi }^{-}$ fifth induced color index $(N{D}_5^{{\varphi }^{-}})$ is the best suited index to predict Molar Refraction (MR), Polarizability(P), Complexity (C) and Molar Volume(MV).

(iii) The ${\varphi }^{+}$ second induced color index $(N{D}_2^{{\varphi }^{-}})$ is the best suited index to predict Molar Refraction (MR), Polarizability(P), Molar Weight(MW) and Heavy Atom Count(HAC).

(iv) The ${\varphi }^{+}$ fifth induced color index $(N{D}_5^{{\varphi }^{+}})$ is the best one for the prediction of the property Molar Volume(MV).

(v) The ${\varphi }^{+}$ forgotten induced color index $F_N^{{\varphi }^{+}}$ is highly correlated with the property Complexity (C).

9.1 Comparison of chromatic topological indices and induced color-based topological indices

The predictive capabilities of the newly introduced chromatic topological indices and induced color-based topological indices are compared to analyze their ability to model physicochemical properties. Notably, the induced color-based topological indices demonstrated consistently higher correlations, with $R^2$ values mostly exceeding 0.8, indicating more robust relationships with physicochemical properties. In contrast, chromatic topological indices exhibited greater variability in correlation strengths, with $R^2$ values ranging from 0.3 to 0.9. This significant difference suggests that the induced color-based indices can serve as more reliable predictors of physicochemical properties of chemical molecule. Additionally, from Figure 5, it is observed that the induced color-based indices consistently showed strong correlations across various property combinations, while chromatic indices displayed greater fluctuations in correlation strengths. The minimum $R^2$ values for induced color-based indices remained relatively high, ranging from 0.7 to 0.8, compared to the minimum $R^2$ values for chromatic indices, which ranged from 0.3 to 0.4. This difference in minimum $R^2$ values further emphasizes the strong predictive capability of induced color-based indices. These findings of QSPR analysis indicate that the induced color-based topological indices serve as an effective tool for modeling and predicting the physicochemical properties in chemical molecule.

10 Conclusion

Ten novel induced color-based topological indices and six chromatic-based topological indices were introduced to analyze the molecular structures of the antiviral drugs of dengue. The induced color-based indices were computed through sigma coloring, while chromatic topological indices were derived from proper vertex coloring. The QSPR analysis was performed between the physicochemical properties of dengue treating drugs and the computed topological indices of their molecular structures of the drugs. The results showed that the specific induced color-based indices such as the second induced color index $\left(N{D}_2^{{\varphi }_t}\right)$, fifth induced color index $\left(N{D}_5^{{\varphi }_t}\right)$ and forgotten induced color index $\left(F_N^{{\varphi }_t}\right)$ exhibited strong correlations with the properties. A comparative analysis between chromatic index and induced color-based index indicated that the induced color-based indices offer stronger correlations, suggesting their superior ability to capture structural features relevant to drug properties. Furthermore, the Y-randomization test confirmed that the QSPR analysis was not influenced by chance correlation. The findings of our work established the induced color-based indices as reliable predictors of the physicochemical properties of dengue antiviral drugs. The analysis using the color-based topological indices provide a foundation for further exploration in drug design and molecular property prediction.

11 Future work

(i) QSPR graph model proposed in this article can be extended to other chemical molecules and drugs to explore their properties

(ii) The Quantitative Structure-Activity Relationship(QSAR) and Quantitative Structure-Toxicity Relationship(QSTR) analysis can be performed between the computed topological indices and other properties through the induced color-based topological indices and chromatic topological indices for the potential antivirals of dengue.

(iii) The analysis of isomorphic molecular graph of chemical molecules through color based topological indices will provide us with the best model to predict the properties of the molecules.

Data availability statement

The original contributions presented in the study are included in the article/Supplementary Material, further inquiries can be directed to the corresponding author.

Author contributions

CY: Formal Analysis, Writing – original draft, Software, Data curation, Conceptualization, Investigation, Validation, Writing – review and editing, Methodology. BB: Writing – original draft, Supervision, Methodology, Writing – review and editing, Conceptualization, Validation, Formal Analysis.

Funding

The author(s) declare that financial support was received for the research and/or publication of this article. The article processing fee for open access is funded by the Vellore Institute of Technology, Chennai, India.

Acknowledgments

The authors thank the Vellore Institute of Technology, Chennai, India-600127 for the financial support and encouragement to carry out this research work. Also the authors would like to thank the reviewers and editor for their valuable comments and suggestions for the improvement of this article.

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Generative AI statement

The author(s) declare that no Generative AI was used in the creation of this manuscript.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Supplementary material

The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fchem.2025.1599715/full#supplementary-material

References

Abubakar, M. S., Aremu, K. O., Aphane, M., and Amusa, L. B. (2024). A qspr analysis of physical properties of antituberculosis drugs using neighbourhood degree-based topological indices and support vector regression. Heliyon 10, e28260. doi:10.1016/j.heliyon.2024.e28260

PubMed Abstract | CrossRef Full Text | Google Scholar

Agrawal, T., Siddqui, G., Dahiya, R., Patidar, A., Madan, U., Das, S., et al. (2024). Inhibition of early rna replication in chikungunya and dengue virus by lycorine: in vitro and in silico studies. Biochem. Biophysical Res. Commun. 730, 150393. doi:10.1016/j.bbrc.2024.150393

PubMed Abstract | CrossRef Full Text | Google Scholar

Albina, A., and Manonmani, A. (2021). Chromatic topological indices of VPH(m,n) and nanotorusn and nanotorus. Int. Adv. Res. J. Sci. Eng. Technol. 8, 123–127. doi:10.17148/IARJSET.2021.8622

CrossRef Full Text | Google Scholar

Albina, A., and Manonmani, A. (2022). Computation of chromatic zagreb indices of nanotubes and nanotori. AIP Conf. Proc. 2385, 130041. doi:10.1063/5.0071149

CrossRef Full Text | Google Scholar

Ali, S., Ali, U., Safi, K., Naz, F., Jan, M. I., Iqbal, Z., et al. (2024). In silico homology modeling of dengue virus non-structural 4b (ns4b) protein and its molecular docking studies using triterpenoids. BMC Infect. Dis. 24, 688. doi:10.1186/s12879-024-09578-5

PubMed Abstract | CrossRef Full Text | Google Scholar

Arockiaraj, M., Jeni Godlin, J., Radha, S., Aziz, T., and Al-Harbi, M. (2025). Comparative study of degree, neighborhood and reverse degree based indices for drugs used in lung cancer treatment through qspr analysis. Sci. Rep. 15, 3639. doi:10.1038/s41598-025-88044-x

PubMed Abstract | CrossRef Full Text | Google Scholar

Balasubramaniyan, D., and Chidambaram, N. (2023). On some neighbourhood degree-based topological indices with qspr analysis of asthma drugs. Eur. Phys. J. Plus 138, 823. doi:10.1140/epjp/s13360-023-04439-7

CrossRef Full Text | Google Scholar

Bhakat, S., Delang, L., Kaptein, S., Neyts, J., Leyssen, P., and Jayaprakash, V. (2015). Reaching beyond hiv/hcv: Nelfinavir as a potential starting point for broad-spectrum protease inhibitors against dengue and chikungunya virus. RSC Adv. 5, 85938–85949. doi:10.1039/C5RA14469H

CrossRef Full Text | Google Scholar

Bondy, J. A., and Murty, I. U. S. R. (2008). Graph theory. Springer Publishing Company.

Google Scholar

Bouzidi, H. S., Sen, S., Piorkowski, G., Pezzi, L., Ayhan, N., Fontaine, A., et al. (2024). Genomic surveillance reveals a dengue 2 virus epidemic lineage with a marked decrease in sensitivity to mosnodenvir. Nat. Commun. 15, 8667. doi:10.1038/s41467-024-52819-z

PubMed Abstract | CrossRef Full Text | Google Scholar

Callahan, M., Treston, A. M., Lin, G., Smith, M., Kaufman, B., Khaliq, M., et al. (2022). Randomized single oral dose phase 1 study of safety, tolerability, and pharmacokinetics of iminosugar uv-4 hydrochloride (uv-4b) in healthy subjects. PLOS Neglected Trop. Dis. 16, e0010636. doi:10.1371/journal.pntd.0010636

PubMed Abstract | CrossRef Full Text | Google Scholar

Chartrand, G., Okamoto, F., and Zhang, P. (2010). The sigma chromatic number of a graph. Graphs Comb. 26, 755–773. doi:10.1007/s00373-010-0952-7

CrossRef Full Text | Google Scholar

Das, S., Rai, S., and Kumar, V. (2023). On topological indices of molnupiravir and its qspr modelling with some other antiviral drugs to treat covid-19 patients. J. Math. Chem. 62, 2581–2624. doi:10.1007/s10910-023-01518-z

CrossRef Full Text | Google Scholar

Frabasile, S., Koishi, A. C., Kuczera, D., Silveira, G. F., Verri Jr, W. A., Duarte dos Santos, C. N., et al. (2017). The citrus flavanone naringenin impairs dengue virus replication in human cells. Sci. Rep. 7, 41864. doi:10.1038/srep41864

PubMed Abstract | CrossRef Full Text | Google Scholar

Gutman, I., and Polansky, O. E. (2012). Mathematical concepts in organic chemistry. Berlin, Heidelberg: Springer.

Google Scholar

Hasani, M., and Ghods, M. (2024). Topological indices and qspr analysis of some chemical structures applied for the treatment of heart patients. Int. J. Quantum Chem. 124, e27234. doi:10.1002/qua.27234

CrossRef Full Text | Google Scholar

Huang, L., Wang, Y., Pattabiraman, K., Danesh, P., Siddiqui, M. K., and Cancan, M. (2023). Topological indices and qspr modeling of new antiviral drugs for cancer treatment. Polycycl. Aromat. Compd. 43, 8147–8170. doi:10.1080/10406638.2022.2145320

CrossRef Full Text | Google Scholar

Huckvale, E. D., Powell, C. D., Jin, H., and Moseley, H. N. (2023). Benchmark dataset for training machine learning models to predict the pathway involvement of metabolites. Metabolites 13, 1120. doi:10.3390/metabo13111120

PubMed Abstract | CrossRef Full Text | Google Scholar

Jin, H., Mitchell, J. M., and Moseley, H. N. (2020). Atom identifiers generated by a neighborhood-specific graph coloring method enable compound harmonization across metabolic databases. Metabolites 10, 368. doi:10.3390/metabo10090368

PubMed Abstract | CrossRef Full Text | Google Scholar

Kalaimathi, M., and Balamurugan, B. (2023). Topological indices of molecular graphs of monkeypox drugs for qspr analysis to predict physicochemical and admet properties. Int. J. Quantum Chem. 123, e27210. doi:10.1002/qua.27210

CrossRef Full Text | Google Scholar

Kiemel, D., Kroell, A.-S. H., Denolly, S., Haselmann, U., Bonfanti, J.-F., Andres, J. I., et al. (2024). Pan-serotype dengue virus inhibitor jnj-a07 targets ns4a-2k-ns4b interaction with ns2b/ns3 and blocks replication organelle formation. Nat. Commun. 15, 6080. doi:10.1038/s41467-024-50437-3

PubMed Abstract | CrossRef Full Text | Google Scholar

Kok, J., Sudev, N., and Jamil, M. K. (2016). Chromatic zagreb indices for graphical embodiment of colour clusters. Indonesian J. Comb. doi:10.19184/ijc.2019.3.1.6

CrossRef Full Text | Google Scholar

Kok, J., Sudev, N., and Mary, U. (2017). On chromatic zagreb indices of certain graphs. Discrete Math. Algorithms Appl. 9, 1750014. doi:10.1142/S1793830917500148

CrossRef Full Text | Google Scholar

Kuriachan, G., and Parthiban, A. (2025). Computation of domination degree-based topological indices using python and qspr analysis of physicochemical and admet properties for heart disease drugs. Front. Chem. 13, 1536199. doi:10.3389/fchem.2025.1536199

PubMed Abstract | CrossRef Full Text | Google Scholar

Low, Z. X., OuYong, B. M., Hassandarvish, P., Poh, C. L., and Ramanathan, B. (2021). Antiviral activity of silymarin and baicalein against dengue virus. Sci. Rep. 11, 21221. doi:10.1038/s41598-021-98949-y

PubMed Abstract | CrossRef Full Text | Google Scholar

Martin, A. J., Shackleford, D. M., Charman, S. A., Wagstaff, K. M., Porter, C. J., and Jans, D. A. (2023). Increased in vivo exposure of n-(4-hydroxyphenyl) retinamide (4-hpr) to achieve plasma concentrations effective against dengue virus. Pharmaceutics 15, 1974. doi:10.3390/pharmaceutics15071974

PubMed Abstract | CrossRef Full Text | Google Scholar

Rose, S., and Naduvath, S. (2018). Chromatic topological indices of certain cycle related graphs. Contemp. Stud. Discrete Math. 2, 57–68. doi:10.48550/arXiv.1810.02875

CrossRef Full Text | Google Scholar

Rose, S., and Naduvath, S. (2019). Some results on injective chromatics topological indices of some graphs. South East Asian J. Math. & Math. Sci. 15, 115–128.

Google Scholar

Rose, S., and Naduvath, S. (2020a). Chromatic Zagreb and irregularity polynomials of graphs. Jordan J. Math. Statistics (JJMS) 13, 487–503. doi:10.1142/s1793830921500610

CrossRef Full Text | Google Scholar

Rose, S., and Naduvath, S. (2020b). On equitable chromatic topological indices of some mycielski graphs. Creative Math. & Inf. 29, 221–229. doi:10.37193/CMI.2020.02.13

CrossRef Full Text | Google Scholar

Sardar, M. S., and Hakami, K. H. (2024). Qspr analysis of some alzheimer’s compounds via topological indices and regression models. J. Chem. 2024, 5520607. doi:10.1155/2024/5520607

CrossRef Full Text | Google Scholar

Shen, T.-J., Hanh, V. T., Nguyen, T. Q., Jhan, M.-K., Ho, M.-R., and Lin, C.-F. (2021). Repurposing the antiemetic metoclopramide as an antiviral against dengue virus infection in neuronal cells. Front. Cell. Infect. Microbiol. 10, 606743. doi:10.3389/fcimb.2020.606743

PubMed Abstract | CrossRef Full Text | Google Scholar

Shi, X., Kosari, S., Ghods, M., and Kheirkhahan, N. (2025). Innovative approaches in qspr modelling using topological indices for the development of cancer treatments. PloS one 20, e0317507. doi:10.1371/journal.pone.0317507

PubMed Abstract | CrossRef Full Text | Google Scholar

Singh, S., Verma, A. K., Thakur, G., Sharma, S., and Awasthi, A. (2023). Quercetin: a putative eco-friendly wide spectrum antiviral against dengue. Macromol. Symp. 410, 2200199. doi:10.1002/masy.202200199

CrossRef Full Text | Google Scholar

Suputtamongkol, Y., Avirutnan, P., Mairiang, D., Angkasekwinai, N., Niwattayakul, K., Yamasmith, E., et al. (2021). Ivermectin accelerates circulating nonstructural protein 1 (ns1) clearance in adult dengue patients: a combined phase 2/3 randomized double-blinded placebo controlled trial. Clin. Infect. Dis. 72, e586–e593. doi:10.1093/cid/ciaa1332

PubMed Abstract | CrossRef Full Text | Google Scholar

Tamilarasi, W., and Balamurugan, B. (2024). New reverse sum revan indices for physicochemical and pharmacokinetic properties of anti-filovirus drugs. Front. Chem. 12, 1486933. doi:10.3389/fchem.2024.1486933

PubMed Abstract | CrossRef Full Text | Google Scholar

Tamilarasi, W., and Balamurugan, B. (2025). Qspr and qstr analysis to explore pharmacokinetic and toxicity properties of antifungal drugs through topological descriptors. Sci. Rep. 15, 18020–18025. doi:10.1038/s41598-025-01522-0

PubMed Abstract | CrossRef Full Text | Google Scholar

Tamilarasi, W., and Balamurugan, B. J. (2022). Admet and quantitative structure property relationship analysis of anti-covid drugs against omicron variant with some degree-based topological indices. Int. J. Quantum Chem. 122, e26967. doi:10.1002/qua.26967

CrossRef Full Text | Google Scholar

Thilsath parveen, S., Balamurugan, B. J., and Siddiqui, M. K. (2024). Exploring the properties of antituberculosis drugs through qspr graph models and domination-based topological descriptors. Sci. Rep. 14, 1–25. doi:10.1038/s41598-024-73918-3

CrossRef Full Text | Google Scholar

Touret, F., Baronti, C., Goethals, O., Van Loock, M., De Lamballerie, X., and Querat, G. (2019). Phylogenetically based establishment of a dengue virus panel, representing all available genotypes, as a tool in dengue drug discovery. Antivir. Res. 168, 109–113. doi:10.1016/j.antiviral.2019.05.005

PubMed Abstract | CrossRef Full Text | Google Scholar

Ugasini Preetha, P., Suresh, M., Tolasa, F. T., and Bonyah, E. (2024). Qspr/qsar study of antiviral drugs modeled as multigraphs by using ti's and mlr method to treat covid-19 disease. Sci. Rep. 14, 1–14. doi:10.1038/s41598-024-63007-w

PubMed Abstract | CrossRef Full Text | Google Scholar

Wagner, S., and Wang, H. (2018). Introduction to chemical graph theory. Chapman and Hall/CRC.

Google Scholar

Wiener, H. (1947). Structural determination of paraffin boiling points. J. Am. Chem. Soc. 69, 17–20. doi:10.1021/ja01193a005

PubMed Abstract | CrossRef Full Text | Google Scholar

Zaman, S., Yaqoob, H. S. A., Ullah, A., and Sheikh, M. (2024). Qspr analysis of some novel drugs used in blood cancer treatment via degree based topological indices and regression models. Polycycl. Aromat. Compd. 44, 2458–2474. doi:10.1080/10406638.2023.2217990

CrossRef Full Text | Google Scholar