Quantum-like modeling of cognition

This paper begins with a historical review of the mutual influence of physics and psychology, from Freud's invention of psychic energy inspired by von Boltzmann' thermodynamics to the enrichment quantum physics gained from the side of psychology by the notion of complementarity (the invention of Niels Bohr who was inspired by William James), besides we consider the resonance of the correspondence between Wolfgang Pauli and Carl Jung in both physics and psychology. Then we turn to the problem of development of mathematical models for laws of thought starting with Boolean logic and progressing toward foundations of classical probability theory. Interestingly, the laws of classical logic and probability are routinely violated not only by quantum statistical phenomena but by cognitive phenomena as well. This is yet another common feature between quantum physics and psychology. In particular, cognitive data can exhibit a kind of the probabilistic interference effect. This similarity with quantum physics convinced a multi-disciplinary group of scientists (physicists, psychologists, economists, sociologists) to apply the mathematical apparatus of quantum mechanics to modeling of cognition. We illustrate this activity by considering a few concrete phenomena: the order and disjunction effects, recognition of ambiguous figures, categorization-decision making. In Appendix 1 of Supplementary Material we briefly present essentials of theory of contextual probability and a method of representations of contextual probabilities by complex probability amplitudes (solution of the “inverse Born's problem”) based on a quantum-like representation algorithm (QLRA).

1. Introduction

Recently, scientists working in various disciplines (physicists, psychologists, economists, sociologists) started to apply the mathematical apparatus of quantum mechanics (QM), [1, 2] especially quantum probability calculus [3] (based on Born's rule), to multi-disciplinary problems [4–36]. Some physicists regard such an activity as totally “illegal.” They argue that the mathematical apparatus of QM was designed specifically for description of particular physical phenomena and it cannot be used in, e.g., psychology. Why? Some elaborate that the apparatus of QM is relevant to micro phenomena only (though this viewpoint is debatable even in the quantum physics community). One aim of this paper is to convince physicists, especially those working in the quantum information theory and quantum probability, that applications of the methods of QM to cognition can be justified. We show that the present sharp separation of subjects of physics and psychology/cognition is only a peculiarity of the present moment, that 19th and the first part of 20th century were characterized by mutual influence of physical and psychological theories and the fruitful exchange of ideas between the brightest representatives from both sides. One of the best known examples is the impact made by psychology on QM which resulted in borrowing the principle of complementarity [37] by Niels Bohr from William James' book [38], see also books of Plotnitsky [39–41]. It may be less known that, in turn, the idea of complementarity was elaborated by James under the influence of the 19th century studies in thermodynamics which led him (as well as later Freud [42, 43]) to the notion of psychic energy; initially, complementarity in psychology was about complementarity of different representations of psychic energy [38].

Meanwhile, we point out that quantum-like modeling of cognition considered here must be distinguished from theories of physical quantum brain in the spirit of Hameroff [44], Penrose [45, 46]. We work in the purely operational framework: it was found that some experimental studies in cognitive psychology, economics, and social science generate statistical data which match well quantum description of measurements and the corresponding probabilistic outputs (see e.g., [4, 5, 9, 13, 14, 18]). Therefore, it is natural to model cognition with the aid of QM formalism. The quantum cognition project does not try to explain the physiological origin of quantum rules for information processing and probability, similarly to Copenhageners in QM (following Bohr [37]). As in physics, this approach does not exclude a possibility to go beyond the operational quantum formalism. However, for the moment, there is no commonly accepted “prequantum model of cognition,” cf., however, with Khrennikov [47].

In this paper we also mark the turning points in the development of mathematical models for laws of thought starting with the book of Boole [48] and considering the foundations of classical probability theory as established by Kolmogorov [49] in 1933.

Then, we briefly review the violations of the laws of classical logic and probability in quantum statistical experiments, in particular we discuss the probabilistic structure of the two slit experiment [50] and adress no-go theorems [1, 51, 52] (von Neumann, Kochen-Specker, Bell), see also [53]. We demonstrate that such violations (including the interference effect) also occur in statistics collected in cognitive experiments. This similarity with effects in quantum physics convinced scientists from physics and cognitive science to apply the mathematical apparatus of QM to modeling of cognition. For illustration we use two concrete applications [12–18]: the order and disjunction effects. The paper is concluded with a short review of recent research in quantum(-like) cognition, in particular, cognitive applications of the theory of open quantum systems [23, 24, 30, 31] and positive operator valued measures [4, 7, 36].

We remark that the use of the mathematical apparatus of QM for problems of cognition is motivated not only by the existence of non-classical statistical data collected in cognitive psychology, but also by similarities of basic features of (1) states of a system under study and (2) possible observations performed on the system, in physics and cognition. First feature concerns the representation of a state (e.g., a mental state) as a superposition of other (basis) states. In quantum(-like) modeling of cognition, superpositions play the crucial role because they represent states of very deep uncertainty which can not be modeled by classical probability distributions. Secondly, the representation of incompatible quantum physical observables by non-commuting operators also corresponds well to psychological intuition, since the majority of observables used in psychology, in particular, in the theory of decision making, exhibit the order effect. The property of entanglement of the states of two (or more) different systems is crucial for most peculiar QM effects (such as quantum teleportation and quantum computing). Entanglement also plays an important role in cognitive studies but as an exhibition of contextuality of cognitive phenomena (in the spirit of Cabello [54]) rather than physical non-locality (see also [53, 55–58]).

The problem of a proper interpretation of a quantum state (represented by a wave function) is still one of the most intriguing problems of quantum foundations [53]. The present situation is characterized by a huge diversity of interpretations (which can be considered as a sign of deep foundational crisis). Working with applications of the QM formalism in new fields of science one also meets this problem. In QM there are, roughly speaking, two big classes of interpretations: (a) quantum state is a physical state of an individual system; (b) quantum state is a special (probabilistic) representation of information about the results of possible measurements on an ensemble of (identically prepared) systems. The first one can be called the physical interpretation and the second one the information interpretation. Recently, the latter became very popular in quantum information theory and led (in its extreme forms) to subjective interpretation of quantum states, including quantum Bayesianism of Fuchs [59–61] and the information interpretation of Zeilinger [62, 63], Brukner [64]. Such interpretations match the ideology of quantum(-like) cognition. (Though, as we have seen in QM, the problem of interpretation is very complex, and it would be too risky to try to fix firmly the interpretation of quantum(-like) states used in cognitive studies.) Meanwhile, there is one crucial difference between conventional QM and quantum cognition. In QM, in accordance with Bohr's views, there is a system and an observer, the latter considered as external with respect to the system. This ideology, although working successfully in experimental studies of micro-world phenomena, is problematical where the possibility of separation between a system under observation and the observer is questionable, e.g., in quantum cosmology. Trying to solve this problem, the problem of interpretation of the “wave function of the Universe,” Hugh Everett proposed the many worlds interpretation of the wave function, probably the most exotic among all interpretations. In fact, in quantum cognition we meet the same problem. The brain is a self-observer; here it is not easy to separate the system under measurement from the observer. However, it seems that the information interpretation in the spirit of Zeilinger-Brukner-Fuchs gives a possibility to resolve it: in the brain, one information subsystem makes predictions about the result of the observation on another information subsystem. Still, the problem of interpretation of the “mental wave function” is complicated. In this paper, we do not keep to any fixed interpretation, while we are most sympathetic to the information interpretation. At the same time we are very cautious (maybe, too cautious) with respect to the use of the many worlds interpretation for quantum cognition, in spite of novel possibilities and yet unexplored ways.

2. From Psychology to Physics and Back

Reviewing a variety of definitions from dictionaries and encyclopedias, we believe that we can safely state the following. Physics is the science that deals with the properties of matter. Psychology is the science that deals with mental processes and behavior. In accordance with the views of Rene Descartes there are two basic types of substance, material and mental, and one is not reduced to the other¹. Although during the last century physical reductionism captured the headlines in psychology, Descartes' ideology still penetrates the body of modern science. Naturally, physics and psychology are considered as different fields of science as they can be, each with its specific theoretical and experimental methodologies. It seems that there is nothing or very little in common between them. Most physics students would probably not like to spend their time studying psychology courses and vice versa. However, developments in physics and psychology are connected much stronger than one can imagine. We can point to a few big names who contributed to establishing a connection between the two most fundamental sciences (one about nature and the other about psyche): Hermann von Helmholtz (Figure 1), Sigmund Freud (Figure 2), Gustav Theodor Fechner, William James (Figure 4), Niels Bohr (Figure 3), Carl Jung, Wolfgang Pauli, Albert Einstein,.…

FIGURE 1

Figure 1. Hermann von Helmholtz.

FIGURE 2

Figure 2. Sigmund Freud.

FIGURE 3

Figure 3. Niels Bohr.

FIGURE 4

Figure 4. William James.

Freud was strongly influenced by works of von Helmholtz on thermodynamics and especially on the energy conservation law². He noted similarities between thermodynamics and the human psyche and developed a kind of mental thermodynamics known as psycho-dynamics [42, 43]. Freud actively used the notion of psychic energy (libido) and the law of its conservation. (Primarily libido represents the sexual energy. However, according to Freud, the sexual energy is one of the forms of the psychic energy which can be transformed into other forms.) At the first stage of his psycho-dynamical studies Freud was influenced by the ideas of Fechner: considering physical facts (related to human body) and mental facts as sides of one reality. Fechner concluded that both physical and mental phenomena has to be described by the same mathematical apparatus [65]. (This remark is very important for us as foretelling the main idea of this paper: behavior of both mind and matter nicely fits the framework of the mathematical formalism of quantum theory).

The notion of psychic energy played an important role in theorizing of James [38]. Following physicists (who at that time were already using the field theory) he started to operate with the notion of psychic field. This psychic field as well as a physical field can have different modes. This analogy led James [38] to the fundamental principle of complementary of information belonging to different modes of consciousness (the words of James are italicized):

“It must be admitted, therefore that in certain persons, at least, the total possible consciousness may be split into parts which coexist but mutually ignore each other, and share the object of knowledge beteen them. More remarkable still, they are complementary. Give an object to one of the consciousnesses, and by this very act you remove it from the other or others. Barring a certain common fund of information, like the command of language, etc., what the upper self knows the under self is ignorant of, and vice versa.”

Above we pointed to the “knowledge transfer” in one direction, from physics to psychology. However, the opposite also took place. In particular, the principle of complementarity was invented in quantum physics by Bohr under the strong influence of James' “Principles of Psychology” [38] (cf. the above citation with the principle of complementarity in QM).

Now we point to the famous correspondence between Pauli and Jung [66] on comparative analysis of foundations of physics and psychology. These letters were written in a free style of discussion between friends (and, in part, a patient and a psychoanalyst)³. This freedom allowed them to express (in psychoanalytic manner) many thoughts which would be never presented in formal scientific discussions and publications. From the letters it is clear that Jung was deeply influenced by quantum theory in Pauli's presentation; e.g., Jung wrote to Pauli:

“As the phenomenal world is an aggregate of the processes of atomic magnitude, it is naturally of the greatest importance to find out whether, and if so how, the photons (shall we say) enable us to gain a definite knowledge of the reality underlying the mediative energy processes Light and matter both behave like separate particles and also like waves. This …obliged us to abandon, on the plane of atomic magnitudes, a causal description of nature in the ordinary space-time system, and in its place to set up invisible fields of probability in multidimensional spaces.”

Inspired by acausal features of quantum mechanics, Jung developed his famous theory of synchronicity [67]; the theory about the experiences of two or more events as meaningfully related, where they are unlikely to be causally related (The subject sees it as a meaningful coincidence). The use by quantum physicists of “invisible fields of probability on multidimensional spaces” strongly supported Jung's interest in psychic fields, invisible, probabilistic, and defined not on the physical space time R⁴, but on some kind of “mental space,” cf. [68]. This was a clue to unification of psychic and quantum physical fields in one psycho-physical field. The idea was very appealing to both Pauli and Jung and it was one of the topics of their correspondence. Jung also discussed field models with Einstein, and Einstein's attempts to create a unified pure field model of physical reality (see e.g., [69]), also supported Jung's studies on psychical fields. Finally, however, neither the Einstein dream about a purely field description of physical reality nor the Jung-Pauli dream about the unified (quantum) psycho-physical field found a rigorous mathematical realization.

Our discussion on mutual influence of physics and psychology can be shortly represented as the following (of course, incomplete) diagram:

[Hess, Joule, Clausius, and von Helmholtz] → [Freud, Fechner, James] → [Bohr] ↔ [Pauli] ↔ [Jung] ← [Einstein]…

3. Modeling of Cognition with Classical-nonclassical Logic vs. Classical-nonclassical Probability

Now we concentrate on problems in cognition (keeping in mind our ultimate goal—the quantum modeling in cognitive psychology). Recall that “cognition” usually treats psychological functions of an indvidual from the viewpoint of information processing. (Sometimes “cognition” is treated more tendentiously as the “science of mind”). We shall use mathematics as an instrument for linkage of cognition and physics.

3.1. From Boolean Logic to Kolmogorovian Probability

In 19th century George Boole wrote the book “An Investigation of the Laws of Thought on Which are Founded the Mathematical Theories of Logic and Probabilities” [48], see also [70]. This was the first mathematical model of the thinking process based on the laws of reasoning nowadays known as the Boolean logic. The role of Boolean logic in modern science is impossible to overestimate, it plays the crucial role in information theory, decision making, artificial intelligence, digital electronics. Boolean logic is the basic mathematical model of classical logic.

One of the most important features of Boolean logic is that it serves as the basis of the modern probability theory [49]: representation of events by sets, subsets of some set Ω, the so-called sample space, or space of elementary events. The system of sets representing events, say ${F}$, allows operations of Boolean logics; ${F}$ is the so-called σ-algebra of sets⁴. It is closed with respect to the (Boolean) operations of (countable) union, intersection, and complement (or in logical terms “and,” “or,” “no”). Thus, the first lesson for a physics student is that by applying any theorem of probability theory, e.g., the law of large numbers, one has to be aware that paradigm of Boolean logic is being used. The set-theoretic model of probability was presented by Kolmogorov in 1933 [49]; it is based on the following two natural (from the Boolean viewpoint) axioms:

• (AK1) events are represented as elements of a σ-algebra and operations on events are described by Boolean logic;

• (AK2) probability is represented as a probabilistic measure.

We remind that a probabilistic measure p is a (countably) additive function on a σ-algebra ${F}$: $p({\cup }_{j=}^{\infty }{A}_j)=\sum _{j=}^{\infty }p(A_j)$ for A_j ∈ ${F}$, A_i ∩ A_j = ∅, i ≠ j, which is valued in [0, 1] and normalized by 1. We also recall the definition of a random variable as a measurable function, a : Ω → R⁵. In classical probability theory random variables represent observables.

Thus, the second lesson for a physics student is that probability is an axiomatic theory, as, e.g., geometry. (My experience of probabilistic discussions with physicists is that only a few of them understand this. Majority tries to treat probability heuristically, e.g., as frequency. This approach may work well in applied research, e.g., with experimental data. However, it may lead to paradoxic conclusions in foundational studies, as e.g., in the case of violation of Bell's inequality, see [53], for details)⁶.

3.2. Formula of Total Probability, Bayesian Analysis

One of the basic laws of the Kolmogorovian model, the formula of total probability (FTP), will play very important role in our further considerations. Before addressing FTP, we point to an exceptional role which is played by conditional probability in the Kolmogorov model. This sort of probabilities is not derived in any way from “usual probability”; conditional probability is per definition given by the Bayes formula:

$\begin{array}{ll}p(B|C)=p(B\cap C)/p(C),p(C)>0.& (1)\end{array}$

By Kolmogorov's interpretation it is the probability of an event B to occur under the condition that an event C has occurred. One can immediately see that this formula is one of strongest exhibitions of the Boolean structure of the model; one cannot even assign conditional probability to an event without using the Boolean operation of intersection.

Let us consider a countable family of disjoint sets A_k belonging to ${F}$ such that their union is equal to Ω and p(A_k) > 0, k = 1, …. Such a family is called a partition of the space Ω.

Theorem 1 Let {A_k} be a partition. Then, for every set B ∈ ${F}$, the following formula of total probability holds

$\begin{array}{ll}p(B)={\displaystyle \sum _{k}p}(A_k)p(B|A_k)& (2)\end{array}$

Especially interesting for us is the case where a partition is induced by a discrete random variable a taking values {α_k}. Here, A_k = = {ω ∈ Ω: a(ω) = α_k}. Let b be another discrete random variable. It takes values {β_j}. For any β_j, we have

$\begin{array}{ll}p(b={\beta }_j)={\displaystyle \sum _{k}p}(a={\alpha }_k)p(b={\beta }_j|a={\alpha }_k).& (3)\end{array}$

This formula plays a crucial role in classical decision theory: knowing probabilities of the a-variable and the corresponding conditional probabilities for the b-variable one can obtain the “total probability” for any value of the latter. We also point out that FTP is the cornerstone for the Bayesian procedure for probability updating which is also widely used in decision making.

3.3. Probability-geometry: Comparison of Evolutions

To understand better the role of the axiomatic nature of the modern set-theoretic model of probability it is useful to make comparison with another axiomatic theory - geometry. We can learn a lot from history of development of geometry. Of course, the biggest name in geometry is Euclid. His axiomatics of geometry was considered as the only possible for about 2000 years. It became so common that people started to identify Euclidean model of geometry with physical space. In particular, Immanuel Kant presented deep philosophic arguments [71] that physical space is Euclidean. The Euclidean dogma was rejected as the result of internal mathematical activity, the study of a possibility of derivation of one of axioms from others. This axiom was the famous fifth postulate: given a line and a point not on the line, there is precisely one line parallel to the given one and containing the given point. Nikolay Ivanovich Lobachevsky was the first to understand that this postulate can be replaced with one of its negations. This led him to a new geometric axiomatics, the model which nowadays is known as Lobachevsky geometry (or hyperbolic geometry). Thus, the Euclidean geometry started to be treated as just one of possible models of geometry. This discovery revolutionized, first, mathematics (with contributions of Gauss, Bolyai, and especially Riemann) and then physics (Minkowski, Einstein, Hilbert).

This geometry lesson tells us that there is no reason to expect that the Kolmogorovian model is the only possible axiomatic model of probability. One can expect that by modifying the Kolmogorovian axioms in the same spirit as Lobachevsky modified the Euclidean axiomes, mathematicians could create non-Kolmogorovian models of probability which may be useful for various applications, in particular in physics. However, in the case of probability the historical pathway of development of geometry was not repeated. Mathematicians did not have 2000 years to rethink the Kolmogorovian axiomatics…

3.4. Non-Kolmogorovian Nature of Quantum Probability; No-go Theorems

New physics, QM, intervened brutally in the mathematical kingdom. The probabilistic structure of QM did not match classical probability theory based on the set-theoretic approach of Kolmogorov. At the first stage of development of QM this mismatching was not so visible. The first sign can be seen in Born's rule:

$\begin{array}{ll}p(x)=|\psi (x){|}^2,& (4)\end{array}$

where ψ(x) is the wave function and p(x) is the probability to detect a particle at point x. The wave function is primary here, not the probability. What is encoded in these complex amplitudes pre-existing behind probabilities obtained in quantum measurements? One of the most evident consequences of Equation (4) is violation of the formula of total probability (FTP), one of the basic laws of classical probability theory, see Section 4 for details. In the two slit experiment constructive and destructive interference of the wave functions corresponding to passing through different slits is probabilistically represented as violation of FTP, so to say, interference of probabilities. (Moreover, in QM only such interference of probabilities can be observed, nothing closer to probability amplitudes, since “quantum waves” are not directly approachable).

John von Neumann was the first to pay attention to the peculiar probabilistic structure of QM as compared to the probabilistic structure of classical statistical mechanics [1]. In particular, he generalized Born's rule to quantum observables represented by Hermitian operators. For an observable represented by an operator with purely discrete spectrum, the probability to obtain the value λ as the result of measurement is given as

$\begin{array}{ll}p(\lambda )=\Vert P_{\lambda }\psi {\Vert }^2,& (5)\end{array}$

where P_λ is the projector corresponding to the eigenvalue λ. (Here $A={\displaystyle {\sum }_{\lambda }\lambda }{P}_{\lambda }).$

In his seminal book [1] von Neumann pointed out that, opposite to classical statistical mechanics where randomness of the results of measurements is a consequence of variability of physical parameters such as, e.g., the position and momentum of a classical particle, in QM the assumption about the existence of such parameters (for the moment, probably, still hidden and unapproachable by the existing measurement devices) leads to a contradiction. This statement presented in Von Neumann [1] is known as von Neumann no-go theorem, theorem about impossibility to go beyond the description of quantum phenomena based on quantum states: it is impossible to construct a theoretical model providing a finer description of those phenomena than given by QM⁷. Thus, von Neumann was sure that it is impossible to construct a classical probability measure on the space of some hidden variables which would reproduce probabilities obtained in quantum measurements. Later this statement was confirmed by other no-go theorems, e.g., of Kochen and Specker [51] and Bell [52].

3.5. Quantum Logic

These “theorems” are consequences of the mathematical structure of QM. While classical probability theory is based on the set-theoretical description, QM is founded on the premise that events are associated with subspaces (or orthogonal projectors on these subspaces) of a vector space, complex Hilbert space. The adoption of subspaces as the basis for predicting events also entails a new logic, the logic of subspaces (projectors), which relaxes some of the axioms of classical Boolean logic (e.g., commutativity and distributivity).

First time this viewpoint that QM is based on a new type of logic, quantum logic, was expressed in the book of Von Neumann [1], where he treated projectors corresponding to the eigenvalues of quantum observables (represented by Hermitian operators) as propositions (see also [72]). The explicit formulation of logic of QM as a special quantum logic is based on the lattice [73] of all orthogonal projectors. For reader's convenience, below we present the mathematical structure of quantum logic (see [74], for details). However, in principle one can jump directly to Section 3.6.

3.5.1. Logical Operations on for Projectors

For an orthogonal projector P, we set H_P = P(H), its image, and vice versa, for subspace L of H, the corresponding orthogonal projector is denoted by the symbol P_L.

The set of orthogonal projectors is a lattice with the order structure: P ≤ Q iff H_P ⊂ H_Q or equivalently, for any ψ ∈ H, 〈ψ|Pψ〉 ≤ 〈ψ|Qψ〉.

We recall that the lattice of projectors is endowed with operations “and” (∧) and “or” (∨). For two projectors P₁, P₂, the projector R = P₁ ∧ P₂ is defined as projector onto the subspace H_R = H_P1 ∩ H_P2 and the projector S = P₁ ∨ P₂ is defined as projector onto the subspace H_R defined as the minimal linear subspace containing the set-theoretic union H_P1 ∪ H_P2 of subspaces H_P1, H_P2: this is the space of all linear combinations of vectors belonging these subspaces. The operation of negation is defined as the orthogonal complement: $P^{\perp }=\left\{y\in H:\langle y|x\rangle =0forallx\in H_P\right\}.$

In the language of subspaces the operation “and” coincides with the usual set-theoretic intersection, but the operations “or” and “not” are non-trivial deformations of the corresponding set-theoretic operations. It is natural to expect that such deformations can induce deviations from classical Boolean logic.

Consider the following simple example. Let H be two dimensional Hilbert space with the orthonormal basis (e₁, e₂) and let $v=(e_1+e_2)∕\sqrt{2}.$ Then P_v ∧ P_e1 = 0 and P_v ∧ P_e2 = 0, but P_v ∧ (P_e1 ∨ P_e2) = P_v. Hence, for quantum events, in general the distributivity law is violated:

$\begin{array}{ll}P\wedge (P_1\vee P_2)\ne (P\wedge P_1)\vee (P\wedge P_2)& (6)\end{array}$

As can be seen from our example, even mutual orthogonality of the events P₁ and P₂ does not help to save the Boolean laws⁸.

We remark that for commuting projectors quantum logical operations have the Boolean structure. Thus, non-commutativity can be considered as algebraic representation of non-classicality of quantum logic. In particular, for a single observable (with purely discrete spectrum) $A=\sum _{\lambda }\lambda P_{\lambda },$ projectors corresponding to different eigenvalues are orthogonal and, hence, commutative. Therefore, deviations from classical logic and probability can be found only through analysis of results of a few incompatible measurements.

The idea that cognition and quantumness have something in common has been discussed during last 80 years, starting with the philosophic studies of Alfred North Whitehead.

3.6. Toward Quantum Modeling of Cognition

As we have seen, quantum logic relaxes some of the axioms of classical Boolean logic, e.g., commutativity and distributivity. Human judgments are not always commutative (order effects are pervasive) and often violate the probabilistic implications of the distributive axiom. The principles of QM resonate with deeply rooted psychological intuitions and conceptions about human cognition and decision. Therefore, it is natural to try to use the mathematical apparatus, developed to describe the aforementioned quantum deformations of Boolean logics, to model cognition and, in particular, to apply quantum measurement theory to model decision making. Also, the mathematical apparatus of QM is actively applied to probabilistic problems of psychology, cognitive science, social science, economics, and finances (see e.g., the monographs [4–7]).

We remark that non-commutativity of incompatible observables can be considered as the algebraic representation of the principle of complementarity. Thus, the loop in the inter-relation of physics and psychology was finally closed: complementarity came back to psychology, but in the advanced mathematical form.

We remark that in QM probabilities can only be expressed through elements of quantum logics, see Equation (5). Thus, non-classicality is a statistical effect. In the same way non-classicality of human reasoning can be observed only as a statistical effect. In fact, such an effect has been well known in psychology for long, but it was interpreted as irrational behavior of people which was statistically exhibited in the form of various probability fallacies. Their role (both in psychology and economics) was emphasized in the influential Tversky (over 30,000 citations), Kahneman (Nobel prize in economics) research program [77]: the conjunction and disjunction fallacies, order effects in decisions, over- and under- extension errors in conceptual combinations, and ambiguous concepts [78, 79].

In author's works [4, 10] it was pointed out that violation of FTP can serve as a statistical test of non-classicality of data generated by both physical and cognitive phenomena. The coefficient of interference expressed in the probabilistic terms, see Equation (9) Section 4 can be interpreted as quantitative measure of non-classicality (non-Kolmogorovness). These papers deal with an important case of dichotomous observables of the inverse Born problem: a complex probability amplitude ψ is reconstructed with the aid of the interference coefficient, see Appendix 1 in Supplementary Material for a detailed presentation. This constructive wave function method is especially important for cognitive applications. In QM the space geometry is often used to construct the corresponding wave functions, e.g., for a free particle with a fixed momentum p, ψ(x) = e^ixp; generally one can use the Schrödinger equation in R³ with a potential V(x) and initial and boundary conditions. The main problem of the quantum cognition project is that a proper notion of mental space has not yet been elaborated (cf. [68]). We cannot directly use physics methods, such as introducing functions (e.g., energy) on physical space. A possibility to construct a “mental wave function” directly from data is properly justified. The author designed an algorithm for inversion of Born's rule, the so-called Quantum-like representation algorithm (QLRA) [4], see Section 8 for a few applications.

Author's article [10] served as the theoretical basis for a series of experiments on contextual effect (of Gestalt type) in recognition of ambiguous figures by Conte et al. [13, 14, 18], see Section 8.1 for brief presentation of these results. Analysis of obtained statistical data showed that classical FTP is violated and that the “belief state” of students participated in the experiment can be described by a complex amplitude ψ and observables by non-commutative Hermitian operators.

Busemeyer et al. performed extended studies [5, 12, 16, 25–27, 32–34], see also the monograph of Busemeyer and Bruza [5], on violation of FTP for well-known data on probability fallacies obtained in experiments by Shafir and Tversky, Hofstader, Grosson and other cognitive psychologists [80–84]. It was shown that such data can be modeled with the aid of the mathematical formalism of QM [5]. Besides, Busemeyer et al. lauched the project on quantum(-like) decision making; see also the pioneer work of Aerts and Aerts [8], the paper of Phothos and Busemeyer [16] and the series of works of Asano et al. [23, 24, 30, 31, 35].

4. Violation of Formula of Total Probability and Non-Kolmogorov Probability Theory

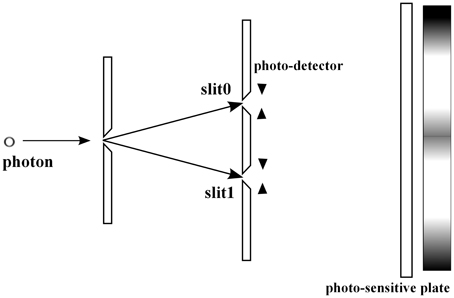
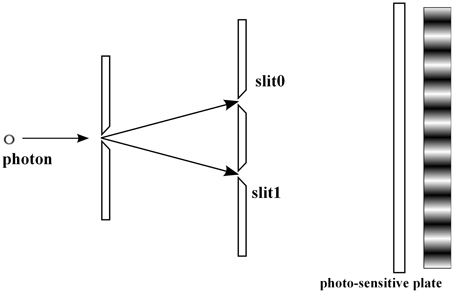
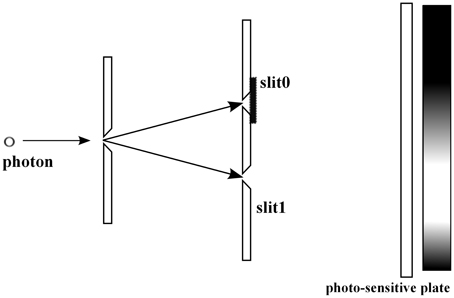
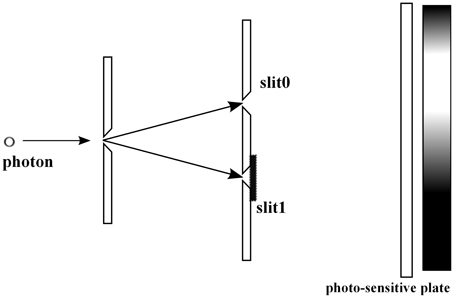
The two slit experiment is the basic example demonstrating that QM describes statistical properties of microscopic phenomena, to which the classical probability theory seems to be not applicable (see e.g., Feynman and Hibbs [50]). In this section, we consider the experiment with the symmetric setting: the slits are located symmetrically with respect to the source of photons, Figure 5. Consider a pair of random variables a and b. We select a as the slit variable, i.e., a = 0 (the photon passes through the upper slit), a = 1 (the photon passes through the lower slit), see Figure 5, and b as the position on the photo-sensitive plate, see Figure 5. Remark that the b-variable has the continuous range of values, the position x on the photo-sensitive plate.

FIGURE 5

Figure 5. Two slit experiment.

For the experimental context with both slits open, see Figure 6, by Born's rule Equation (4) the probability that a photon is detected at position x on the photo-sensitive plate is represented as

$\begin{array}{l}p(b=x)={\left|\frac{1}{\sqrt{2}}{\psi }_0(x)+\frac{1}{\sqrt{2}}{\psi }_1(x)\right|}^2=\frac{1}{2}{\left|{\psi }_0(x)\right|}^2\\ +\frac{1}{2}{\left|{\psi }_1(x)\right|}^2+\left|{\psi }_0(x)\right|\left|{\psi }_1(x)\right|\cos \theta ,& (7)\end{array}$

where ψ₀ and ψ₁ are two wave functions, whose absolute values |${{\psi }_i(x)}^2$| give the distributions of photons passing through the slit i = 0, 1, respectively, see Figures 7, 8

FIGURE 6

Figure 6. Context with both slits are open.

FIGURE 7

Figure 7. Context with only slit1 is open.

FIGURE 8

Figure 8. Context with only slit0 is open.

The term

$\begin{array}{l}\delta (x)=\left|{\psi }_0(x)\right|\left|{\psi }_1(x)\right|\cos \theta \end{array}$

represents quantitively the interference effect of two wave functions. Let us denote |${{\psi }_i(x)}^2$| by p(b = x|a = i), then Equation (7) is represented as

$\begin{array}{l}p(b=x)=p(a=0)p(b=x|a=0)+p(a=1)p(b=x|a=1)\\ +\delta (x),& (8)\end{array}$

where the “interference term” δ has the form:

$\begin{array}{ll}\delta (x)=\begin{array}{c}2\sqrt{p(a=0)p(b=x|a=0)p(a=1)}\\ \times p(b=x|a=1)\cos \theta .\end{array}& (9)\end{array}$

Here the values of probabilities p(a = 0) and p(a = 1) are equal to 1∕2, since we consider the symmetric setting. For a general experimental setting, p(a = 0) and p(a = 1) can be taken as the arbitrary non-negative values satisfying p(a = 0) + p(a = 1) = 1. In the above form, the classical probability law—FTP, see Equation (3),

$\begin{array}{ll}p(b=x)={\displaystyle \sum _{i}p}(a=i)p(b=x|a=i),& (10)\end{array}$

is violated, and the interference term Equation (9) quantifies the violation. The additional interference term appears not only in the two slit experiment, but in any experiment with arbitrary incompatible quantum observables represented by non-commuting Hermitian operators A, B : [A, B] ≠ 0 (see [53], for details).

Now consider two random variables of any origin, from physics, cognitive science, biology, sociology. Let FTP be violated. Of course, for a classical probabilist this is impossible, but plenty of such data exist, see Section 3.6. Here $p(b=x)\ne \sum _{i}p(a=i)p(b=x|a=i),$ i.e., a kind of (probabilistic) interference term appears:

$\begin{array}{ll}\delta (x)=p(b=x)-{\displaystyle \sum _{i}p}(a=i)p(b=x|a=i),& (11)\end{array}$

The point is that we cannot use the Kolmogorov probability model. For example, psychologists can look for special psychological explanations of such strange data, e.g., altruism. However, such a psychological “resolution” does not change the mathematical problem: how to describe such data mathematically? The previous analysis of quantum measurements of the interference type (more generally of pairs of incompatible quantum observables) demonstrated that the appearance of the interference type term matches the predictions of quantum probability theory, where probabilities are based on complex probability amplitudes. Therefore, it is natural to use this non-classical probability theory to model phenomena generating data with non-trivial interference terms which violate FTP. This was one of the starting points for quantum probability theory to impact mathematical modeling of cognition [4, 5, 10, 12].

We remark that (Equation 11) can be (tautologically) rewritten in the form similar to the formula for quantum interference (Equation 8) and the interference term can be always represented similarly: Equation (9):

$\begin{array}{ll}\delta (x)=2\lambda (x)\sqrt{p(a=0)p(b=x|a=0)p(a=1)p(b=x|a=1)}.& (12)\end{array}$

The only difference is that for arbitrary data we cannot guarantee that |λ(x)| ≤ 1. Thus, for arbitrary statistical data, we have FTP with the interference term:

$\begin{array}{l}p(b=x)={\displaystyle \sum _{i}p}(a=i)p(b=x|a=i)\hfill \\ +2\lambda (x)\sqrt{p(a=0)p(b=x|a=0)p(a=1)p(b=x|a=1)}. \hfill & (13)\hfill \end{array}$

5. Savage Sure Thing Principle, Disjunction Effect

STP [85] If you prefer prospect B₀ to prospect B₁ if a possible future event A happens, and you prefer prospect B₀ still if future event A does not happen, then you should prefer prospect B₀ despite having no knowledge of whether or not event A will happen.

Savage's illustration refers to a person deciding whether or not to buy a certain property shortly before a presidential election, the outcome of which could radically affect the property market. “Seeing that he would buy in either event, he decides that he should buy, even though he does not know which event will obtain,” [85], p. 21.

The crucial point is that the decision maker is assumed to be rational. Thus, the sure thing principle was used as one of foundations of rational decision making and rationality in general. It plays an important role in economics in the framework of Savage's utility theory. Mathematically Savage's STP is a simple consequence of FTP. Thus, this principle, widely used in economics, is mathematically based on the classical probability (and Boolean logic). In particular, the Bayes formula for conditional probabilities (Equation 1) plays the crucial role. Therefore, rationality determined by this principle is Bayesian rationality.

Experimentally observed [80, 81] violations of STP were interpreted by Shafir and Tversky as a new effect, the disjunction effect (see also Hofstader [82, 83] and Croson [84]). STP was also confronted by a number of famous (in cognitive psychology, economics, and decision making) paradoxes, Ellsberg, Allais, and Simpson paradoxes [6].

As was discovered by professor of cognitive psychology Jerome Busemeyer, statistical exhibiting the disjunction effect can be treated as non-classical, violating FTP, and hence these data has to be described by some non-Kolmogorovian probability model, e.g., quantum probability. Detailed analysis of data collected in Shafir and Tversky [81] and Tversky and Shafir [80] experiments as well as experiments of other cognitive psychologists was performed by the author Khrennikov [4]: FTP is violated; the corresponding quantum representations were constructed. Below we consider the simplest experiment.

In Section 8.3 we produce the quantum-like representation for statistical data obtained in one of experiments on disjunction effect which was performed by Tversky and Shafir [80]. By using the constructive wave function approach and QLRA, see Section 3.6 and Appendix 1 Supplementary Material, we construct the representation of data with the aid of a complex probability amplitude, “belief state,” “mental wave function,” such that experimental probabilities (frequencies) are given by the Born rule.

6. The General Scheme of Representation of Measurements in Quantum Physics and Cognition

In this section we repeat the discussion [36] on similarity between the schemes of representation of measurements in quantum physics and cognition.

On a very general level, QM accounts for the probability distributions of measurement results using two kinds of entities, called observables A and states ψ (of the system on which the measurements are made). Let us assume that measurements are performed in a series of consecutive trials numbered 1, 2, …. In each trial t the experimenter decides what measurement to make (e.g., what question to ask), and this amounts to choosing an observable A. Despite its name, the latter is not an observable per se, in the colloquial sense of the word. Still, it is associated with a certain set of values, which are the possible results one can get when measuring A. In a psychological experiment these are the responses that a participant is allowed to give, such as Yes and No.

The probabilities of these outcomes in trial t (conditioned on all the previous measurements and their outcomes) are computed as some function of the observable A and of the state ψ^(t) in which the system (a particle in quantum physics, or a participant in psychology) is at the beginning of trial t,

$\begin{array}{l}p(A=v\text{in trial }t|\text{measurements in trials }1,\dots ,t-1)=\\ F\left({\psi }^{\left(t\right)},A,v\right).& (14)\end{array}$

This measurement changes the state of the system, so that at the end of trial t the state is ψ^(t+1), generally different from ψ^(t). The change ψ^(t) → ψ^(t+1) depends on the observable A, the state ψ^(t), and the value v = v (A) observed in trial t,

$\begin{array}{ll}{\psi }^{\left(t+1\right)}=G\left({\psi }^{\left(t\right)},A,v\right).& (15)\end{array}$

On this level of generality, a psychologist will easily recognize in Equations (14, 15) a probabilistic version of the time-honored Stimulus-Organism-Response (S-O-R) scheme for explaining behavior [86]. This scheme involves stimuli (corresponding to A), responses (corresponding to v), and internal states (corresponding to ψ). It does not matter whether one simply identifies A with a stimulus, or interprets A as a kind of internal representation thereof, while interpreting the stimulus itself as part of the measurement procedure (together with the instructions and experimental set-up, that are usually fixed for the entire sequence of trials). What is important is that the stimulus determines the observable A uniquely, so that if the same stimulus is presented in two different trials t and t′, one can assume that A is the same in both of them.

QM is characterized by linear representation of observables—by Hermitian operators; pure states are represented by normalized vectors of complex Hilbert space H. Consider an observable which is mathematically represented by the Hermitian operator A with purely discrete spectrum: $A=\sum _{v}v{P}_v,$ where P_v is the projector onto the eigensubspace corresponding to the eigenvalue v. Then

$\begin{array}{l}p(A=v\text{ in trial }t|\text{measurements in trials }1,\dots ,t-1)=\\ F\left({\psi }^{\left(t\right)},A,v\right)=\Vert P_v{\psi }^{\left(t\right)}{\Vert }^2& (16)\end{array}$

and

$\begin{array}{ll}{\psi }^{\left(t+1\right)}=G\left({\psi }^{\left(t\right)},A,v\right)=\frac{P_v{\psi }^{\left(t\right)}}{\Vert P_v{\psi }^{\left(t\right)}\Vert }.& (17)\end{array}$

This state transform expresses the von Neumann-Lüders projection postulate of QM and represents the quantum state update as a back reaction on measurement.

Nowadays these transformations are actively used in psychology; for example, to describe the order effect [32].

7. Short Review on Various Directions of Research on Quantum Modeling of Cognition

As was emphasized in Khrennikov [4], some statistical data from psychology cannot be described by the standard von Neumann model in which observables are represented by Hermitian operators and state transformations (resulting from the back actions of measurements) by the von Neumann-Lüders projection postulate. As well as in quantum physics, one have to use generalized quantum observables represented by positive operator valued measures (POVMs) with corresponding state transformers [4, 36]. In quantum physics POVM-type observables naturally arise in the framework of theory of open quantum systems describing interaction of a quantum system with an environment; especially useful is the Markovian approximation in the form of the Gorini-Kossakowski-Sudarshan-Lindblad equation. This advanced formalism was widely applied to problems of cognition, in psychology, social and political sciences [23, 24, 30, 31, 87]. In this framework the process of decision making is represented as the process of interaction of a concrete psychological function with a mental environment: decision making as decoherence. This approach was used to model irrational behavior of players in games of the Prisoner's Dilemma type. In such games the rational behavior is associated with selection of the Nash equilibrium as the optimal strategy. However, there were found numerous experimental evidences that players can select strategies different from the Nash equilibrium [80, 81]. Such behaviors were modeled with the aid of theory of open quantum systems in a series of works of Asano et al. [23, 24, 30, 31].

As was already pointed out, no-go theorems play a crucial role in distinguishing classical and quantum probabilistic behaviors. In quantum physics the Bell-type inequalities are explored as experimental tests. In cognitive science the first experimental violation of a Bell-type inequality (in the form of the Wigner inequality) was reported in the article of Conte et al. [14, 18], see also [5]. In quantum physics the Leggett-Garg inequality was explored to test compatibility of macroscopic realism with QM. Harald Atmanspacher and Thomas Filk used this inequality [28] to study the problem of bistable perception (see also [88]).

Violations of the Bell-type inequalities can be coupled to the problem of contextuality, e.g., [53]. The contextual interpretation of the aforementioned results on violations of these inequalities in cognitive science and psychology is most natural. Cognition is irreducibly contextual. The contextual modeling of cognition was performed on the large scale in the monograph [4] in which a general contextual theory of probability was developed. Theory of contextual probability contains quantum probability as a special case. Recently Ehtibar Dzhafarov initiated extended studies on contextuality and Bell-type inequalities in psychology and psychophysics [89, 90].

8. Examples of Applications of the Mathematical Formalism of Quantum Theory

Here we present some examples of application the mathematical formalism of quantum theory to psychology and decision making.

8.1. Recognition of Ambiguous Figures

Let us explain our experiment on recognition of ambiguous figures [13], see also [4], and its connection with Gestalt psychology.

It is well known that, starting in 1912, Gestalt psychology moved a devastating attack against the structuralism formulations of perception in psychology. The classical structuralism theory of perception was based on a reductionistic and mechanistic conception that was assumed to regulate the mechanism of perception. For any perception there exists a set of elementary defining features that are at the same time necessary (each of them) and jointly sufficient in order to characterize perception also in cases of more complex conditions. The Gestalt approach introduced instead a holistic new approach, showing that the whole perception behavior of complex images can never be reduced to the simple identification and sum of elementary defining features defined in the framework of our experience.

During the 1920s and 1930s Gestalt psychology dominated in the study of perception. Its aim was to identify the natural units of perception, explaining it in a revised picture of the manner in which the nervous system works. Gestalt psychology's main contributions have provided some understanding of the elements of perception through the systematic investigation of some fascinating features, such as the causes of optical illusions, the manner in which the space around an object is involved in the perception of the object itself, and, finally the manner in which ambiguity plays a role in the identification of the basic laws of the perception.

In particular, Gestalt psychology also made important contributions to the question of how it is that sometimes we see movements even though the object we are looking at is not really moving. As we know, when we look at something we never see just the thing we look at. We see it in relation to its surroundings (underlying context). An object is seen against its background. In each case we distinguish between the figure, the object or the shape, and the space surrounding it, which we call background or ground, see Figures 9, 10, 11.

FIGURE 9

Figure 9. Ambiguity Figure 1A.

FIGURE 10

Figure 10. Ambiguity Figure 1B.

FIGURE 11

Figure 11. Ambiguity Figure 2.

The psychologist Rubin was the first to systematically investigate this phenomenon, and he found that it was possible to identify any well-marked area of the visual field as the figure, leaving the rest as the ground.

However, there are cases in which the figure and the ground may fluctuate and one is forced to consider the dark part as the figure and the light part as the ground, and vice versa, alternately.

Subjects of the experiment respond (recognize the image) based on subjective and context-dependent factors, and output of the experiment is principally probabilistic. The early work of Rubin, which observed the importance of the figure–ground relationship, marked the starting point from which Gestalt psychologists began to explain what today is known as the organizing principles of perception. A number of organizing or grouping principles emerged from such studies of ambiguous stimuli. Three identified principles may be expressed as similarity, closure and proximity. Gestalt psychologists attempted to extend their work also at a more physiological level, postulating the existence of a strong connection between the sphere of the experience and the physiology of the system, by admitting the well-known principle of isomorphism. This principle establishes that the subjective experience of a human being and the corresponding nervous event have substantially the same structure.

In our experiment, we examined subjects by Tests a and b in order to test quantum-like behavior. For Tests a and b we used the ambiguity figures of Figures 9, 10 as they were widely employed in Gestalt studies:

• (a) Are these segments equal?

• (b) Are these circles equal?

Thus, the a-test is based on the following cognitive task: look at Figure 9 and reply to question (a). The b-test is based on Figure 10: look a this figure and reply to question (b).

The reasons for using such ambiguity tests here for analyzing quantum-like behavior in perception may be summarized as it follows. First of all, the Gestalt approach was based on the fundamental acknowledgment of the importance of the context in the mechanism of perception. Quantum-like behavior also postulates this basic importance and role of the context in the evolution of the considered mechanism, see Section 4. Finally, we have seen that in ambiguity tests, the figure and the ground may fluctuate during the perception. Consequently, a non-deterministic (a quantum-like) behavior should be involved.

Ninety-eight medical students of University of Bari (Italy) were enrolled in this study, with about equal distribution of females and males, aged between 19 and 22 years, after giving their informed consent to participate in the experiment. In the first experiment a group of 53 students was subjected in part to Test b (presented with Test b only) and in part to Tests a and b (presented with Test a and soon after presented with Test b with prefixed time separation of about 2 s between the two tests). The same procedure was employed in the second and third experiments for groups of 24 and 21 students, respectively. All the students of each group were subjected to Test b or to Test a followed by Test b. The ambiguity figures of Test b or Test a followed by b appeared on a large screen for a time of only 3 s, and simultaneously the students were asked to mark on a previously prepared personal schedule their decision as to whether the figures were equal or not. Test a after Test b presentation had the objective of evaluating whether the perception of the first image (Test a) can alter the perception of the subsequent image (Test b). All the experiments were computer assisted and in each phase of the experiment the following probabilities were calculated:

$\begin{array}{l}{p}^b(+),p^b(-),p^a(+),p^a(-),\hfill \\ p(b=+|a=+),p(b=-|a=+),p(b=+|a=-),\hfill \\ p(b=-|a=-).\hfill \end{array}$

Here the role of context, say C, is played by the selection procedure of a sample for the experiment. All probabilities depend on C.

A statistical analysis of the results was performed in order to ascertain whether coefficients of interference λ_β are non-zero or zero in Tests b, a and b|a. The first experiment gave the following results

$\begin{array}{l}\text{Test}b:p^b(+)=0.6923;p^b(-)=0.3077,\hfill \\ \text{Test}a:p^a(+)=0.9259;p^a(-)=0.0741,\hfill \\ \text{Test}b|a:p(b=+|a=+)=0.68;p(b=-|a=+)=0.32,\hfill \\ p(b=+|a=-)=0.5;p(b=-|a=-)=\mathrm{0.5.}\hfill & (18)\hfill \end{array}$

The calculation of conditional probability gave the following result with regard to p^b(+):

$\begin{array}{ll}{p}^a(+)p(b=+|a=+)+p^a(-)p(b=+|a=-)=\mathrm{0.6666.}& (19)\end{array}$

The second experimentation gave the following results:

$\begin{array}{l}\text{Test}b:p^b(+)=0.5714;p^b(-)=0.4286,\hfill \\ \text{Test}a:p^a(+)=1.0000;p^a(-)=0.0000,\hfill \\ \text{Test}b|a:p(b=+|a=+)=0.7000;p(b=-|a=+)=\hfill \\ 0.3000,\hfill \\ p(b=+|a=-)=1.0000;p(b=-|a=-)=\mathrm{0.0000.}\hfill & (20)\hfill \end{array}$

The calculation of the conditional probability gave the following result with regard to p^b(+):

$\begin{array}{ll}{p}^a(+)p(b=+|a=+)+p^a(-)p(b=+|a=-)=\mathrm{0.7.}& (21)\end{array}$

Finally, the third experimentation gave the following results:

$\begin{array}{l}\text{Test}b:p^b(+)=0.4545;p^b(-)=0.5455,\hfill \\ \text{Test}a:p^a(+)=0.7000;p^a(-)=0.3000,\hfill \\ \text{Test}b|a:p(b=+|a=+)=0.4286;p(b=-|a=+)=\hfill \\ 0.5714;\hfill \\ p(b=+|a=-)=1.0000,p(b=-|a=-)=\mathrm{0.0000.}\hfill & (22)\hfill \end{array}$

The calculation of the conditional probability with regard to p^b(+) gave the following result:

$\begin{array}{ll}{p}^a(+)p(b=+|a=+)+p^a(-)p(b=+|a=-)=\mathrm{0.6000.}& (23)\end{array}$

The mean value ± SD of p^b(+) resulted in p^b(+) = 0.5727 ± 0.1189 in Test b and calculated using Equations (18), (20), and (22), while instead a mean value of 0.6556 ± 0.0509 resulted for p^b(+) when calculated in Test b|a and thus using Equations (19), (21), and (23). The two calculated mean values are different and thus give evidence of quantum-like behavior of cognitive mental states as they were measured by testing mental observables by Tests b, a, and b|a. Student's t-test showed that the probability that the obtained differences between the two estimated values of p^b(+) by Test b and by Test b|a are accidental, does not exceed 0.30. Thus, with probability 0.70 the coefficients of supplementarity are non-zero and, hence, students behave (think) in a quantum-like way (with respect to observables based on the ambiguous figures). We also found that these coefficients are bound by 1, so behavior is trigonometric, see Appendix 1 in Supplementary Material.

As the final step, we calculate cosθ_β on the basis of the coefficient of interference λ_β given by Equation (13) in Supplementary Material. In our experiments we obtained

$\begin{array}{l}\cos {\theta }_{+}=-0.2285,{\theta }_{+}=1.8013\end{array}$

and

$\cos {\theta }_{-}=0.0438,{\theta }_{-}=1.5270,$

which are quite satisfactory phase results indicating quantum-like behavior for the investigated mental states.

The above results present a preliminary evidence of the existence of quantum-like behavior in the dynamics of some mental states. Luckily, we were able to capture mental conditions of subjects in which the context influenced decision making in an essential way. We have established equivalence between quantum-like entities and corresponding cognitive entities.

As the performed experiment suggests a quantum-like behavior of cognitive entities, a consequence could be that cognitive entities as well as quantum entities exhibit a highly contextual nature. In the same manner as quantum entities are influenced by the routine physical act of measurement, cognitive entities are influenced by the act of measurement (decision). In the case of cognitive entities, the measurement is characterized by cognitive interaction.

Mathematical modeling of the experiment considered above was beased on a behavioral similarity between cognitive and quantum-like entities, so we were able to make direct use of an abstract quantum-like formalism and apply it to cognitive entities. Moreover, we were able to account for quantum-like dynamics of the cognitive entities. The numerical results of the previous experiment give us an opportunity to delineate basic features of cognitive entities not known in the past. Let us outline this approach in more detail. We can introduce a complex quantum-like amplitude, which represents the state of our cognitive entity expressed in relation to some selected mental observables. Let us suppose that we selected the mental observable b, belonging to a given cognitive entity. Suppose also that b can assume only two possible values (b = +, −). This complex quantum-like amplitude can be produced by QLRA, Appendix 1 in Supplementary Material. The Born rule holds

$\begin{array}{ll}|\psi (\pm ){|}^2=p^b(\pm ).& (24)\end{array}$

The complex quantum-like amplitude can represent the state of our cognitive entity in relation to the considered mental observable b.

The experiment indicates a methodological way for quantum-like processing of future experiments. We will briefly reconsider the case of the experiment we have performed, showing how to calculate quantum-like complex amplitudes and thus to give a quantum-like characterization of the state of the cognitive entity that was employed in the experiment. Let us consider in detail the model entities of our experiment. As we indicated previously, we managed to calculate two different values for cosθ(+) and cosθ(−), whose meaning is now clear. In our case, as we found above, cosθ₊ = −0.2285, θ₊ = 1.8013 and cosθ₋ = 0.0438, θ₋ = 1.5270, which nicely corresponds to quantum-like behavior of the investigated cognitive entity. As a final step, we present a detailed calculation of the quantum-like model of the mental state of the cognitive entity as characterized during the course of the experiment.

By using the obtained data, we can write a mental wave function ψ = ψ_C of the mental state C of the group of students who participated in the experiment—corresponding to a mental context denoted by the same symbol C. QLRA, see Appendix 1 in Supplementary Material, produces

$\begin{array}{l}\psi (\beta )=\sqrt{p(a=+)p(b=\beta |a=+)}\hfill \\ +e^{i\theta (\beta )}\sqrt{p(a=-)p(b=\beta |a=-)}.\hfill & (25)\hfill \end{array}$

The ψ is a function from the range of values {+, −} of the mental observable b to the field of complex numbers. Since b may assume only two values, such a function can be represented by two-dimensional vectors with complex coordinates. Our experimental data give

$\begin{array}{l}\psi (+)=\sqrt{0.8753\times 0.6029}\hfill \\ +e^{i\theta (+)}\sqrt{0.1247\times 0.5}\approx 0.7193+i0.2431\hfill & (26)\hfill \end{array}$

and

$\begin{array}{l}\psi (-)=\sqrt{0.8753\times 0.3971}\hfill \\ +e^{i\theta (-)}\sqrt{0.1247\times 0.5}\approx 0.5999+i\mathrm{0.2494.}\hfill & (27)\hfill \end{array}$

8.2. Quantum Representation of Order Effect in Psychology

For example, in a typical opinion-polling experiment, a group of participants is asked one question at a time, e.g., A = “Is Bill Clinton honest and trustworthy?” and then B = “Is Al Gore honest and trustworthy?” or in the opposite order, B and then A[91]. The corresponding probability distributions, p(A = i, B = j) - “first the B-question with the result j and then the A-question with the result i” and p(B = j, A = i) - “first the A-question with the result i and then the B-question with the result j” do not coincide.

For classical probability theory this is a problem. Here the observables A and B have to be represented by functions A, B : Ω → 0, 1 (random variables). Set A_i = {ω ∈ Ω : A(ω) = i}, B_j = {ω ∈ Ω : B(ω) = j}. Then

$\begin{array}{ll}p(A=i,B=j)=p(A_i\cap B_j)=p(B_j\cap A_i)=p(B=j,A=i).& (28)\end{array}$

The order effect is washed out as the result of commutativity of conjunction. For comparison with the quantum approach, it is useful to write the previous equality by using conditional probabilities:

$\begin{array}{cc}\begin{array}{l}p(A=i,B=j)=p(B=j)p(A=i|B=j)\hfill \\ =p(A=i)p(B=j|A=i)=p(B=j,A=i).\hfill \end{array}& (29)\end{array}$

In the quantum model of the opinion poll, observables are represented by Hermitian operators, $A=\sum _{i=0,1}i{P}_i,B=\sum _{j=0,1}j{Q}_j.$ Here

$\begin{array}{ll}p(A=i,B=j)\equiv p(B=j)p(A=i|B=j),& (30)\end{array}$

$\begin{array}{ll}p(B=j,A=i)\equiv p(A=i)p(B=j|A=i).& (31)\end{array}$

Opposite to Equation (29) which is a consequence of Equation (28), these are the definitions of the “sequential probabilities.” Here the joint probability distribution is, in general, not well defined. Quantum conditional probability is defined as the probability with respect to the state obtained as the update of the initial state ψ after the first measurement (and crucially dependent on the first measurement result)

$p(A=i|B=j)=\frac{\Vert P_i{Q}_j\psi {\Vert }^2}{\Vert Q_j\psi {\Vert }^2},p(B=j|A=i)=\frac{\Vert Q_j{P}_i\psi {\Vert }^2}{\Vert P_i\psi {\Vert }^2}.$

The order effect takes place if and only if $\parallel P_i{Q}_j\psi {\parallel }^2\ne \parallel Q_j{P}_i\psi {\parallel }^2,$ or 〈[P_i, Q_j]ψ|ψ〉 ≠ 0. If the operators do not commute, then such a state ψ exists.

8.3. “Hawaii Experiment”

Tversky and Shafir [80] considered the following psychological test demonstrating the disjunction effect. They showed that significantly more students report that they would purchase a non-refundable Hawaii vacation if they knew that they had passed or failed an important exam than report they would purchase if they did not know the outcome of the exam (So, a student is going to travel to Hawaii in any event, whether she passed exam or not, but only under the condition that she knows the result).

There can be introduced the following two variables; a = 1 (exam passed), a = 0 (exam failed) and b = 1 (go to Hawaii), b = 0 (not to go to Hawaii). The data [80] has the form:

p(b = 1) = 0.32 and hence p(b = 0) = 0.68 (these are the probabilities in the context of uncertainty). Then we also have p(a = 0) = p(a = 1) = 0.5. In the experiment 50% of students were informed that they passed/not passed the exam. The general structure of the experiment was the following. There were two groups of students; one was used for the unconditional measurement of the b-variable and generated the probabilities p(b = 0), p(b = 1) and the second group was used for the conditional measurement of b: under the conditions a = 1 or a = 0. The data collected in the second setting was

$\begin{array}{l}p(b=1|a=1)=0.54,p(b=1|a=0)=0.57;\hfill \\ p(b=0|a=1)=0.46,pb=0|a=0=\mathrm{0.43.}\hfill \end{array}$

The transition probabilities can be represented in the form of the following matrix: $P^{b|a}=\left(\begin{array}{ll}0.54\hfill & 0.57\hfill \\ 0.46\hfill & 0.43\hfill \end{array}\right).$ These data violate FTP and the degree of violation is given by the coefficients of interference, see Equation (11): δ(1) = 0.17, δ(0) = −0.17. (We remark that always ${\displaystyle {\sum }_x\delta }(x)=0).$ These coefficients can be represented in the form Equation (9) (as for interference of wave functions in the two slit experiment) with θ₁ = 1.3, θ₀ = 2. For dichotomous variables, the data easily allow to reconstruct the quantum(-like) state and observables, by using the constructive wave function approach and QLRA, see Appendix 1 in Supplementary Material. We present the formula giving the “belief state” ψ of students in the basis of eigenvectors of the Hermitian operator B representing the b-observable, i.e., B = diag(0, 1). It has the form: $\psi (x)=\sqrt{p(a=0)p(b=x|a=0)}+e^{i{\theta }_x}\sqrt{p(a=1)p(b=x|a=1)}.$ By inserting the values of probabilities and angles into this expression we obtain the vector with complex coordinates, x = 0, 1. The direct calculation shows that Born's rule Equation (4) holds, i.e., p(b = x) = |ψ(x)|², x = 0, 1. Thus, statistical data from this cognitive psychology experiment can be mathematically represented with the aid of the quantum formalism.

8.4. Categorization-decision Experiment

One of the most elucidating examples of quantum theory as applied to psychology is the experiment on interference of categorization in decision making. Statistical data collected in such experiments exhibits non-classical feature in the form of violation of FTP with high statistically significance. In particular, it is impossible model such data with the aid of classical Markov dynamics. Therefore, it is natural to proceed with the quantum-like model justifying violation of laws of classical probability theory. In coming presentation of this model we follow the paper [92].

Often decision makers need to make categorizations before choosing an action. For example, a military operator has to categorize an agent as an enemy before attacking with a drone. How does this overt report of the category affect the later decision? This paradigm was originally designed to test a Markov model of decision making that is popular in psychology [93]. Later it was adapted to investigate quantum-like interference effects in psychology [17, 92].

We begin by briefly summarizing the methods used in the experiments (see [92], for details). On each trial of several hundred training trials, the participant is first shown a picture of a face that may belong to a “good guy” category (category G) or a “bad guy” category (category B), and they have to decide whether to “attack” (action A) or “withdraw” (action W). The trial ends with feedback indicating the category and appropriate action that was assigned to the face on that trial. There are many different faces, and each face is probabilistically assigned to a category, and the appropriate action is probabilistically dependent on the category assignment. Some of the faces are usually assigned to the “good guy” category, while other faces are usually assigned to the “bad guy” category. The category is important because participants are usually rewarded (win points worth money) for “attacking” faces assigned to “bad guys” and they are usually punished (lose points worth money) for “attacking” faces assigned to the “good guys;” likewise they are usually rewarded for “withdrawing” from “good guys” and punished for “withdrawing” from “bad guys.” Participants are given ample training during which they learn to first categorize a face and then decide an action, and feedback is provided on both the category and the decision. Although the feedback given at the end of each trial is probabilistic, the optimal decision is to always “attack” when the face is usually assigned to a “bad guy” category, and always “withdraw” when the face is usually assigned to a “good guy” category. The key manipulation occurs during a transfer test phase which includes the standard “categorization–decision” (C-D) trials followed by either “category alone” (C-alone) trials or “decision alone” (D-alone) trials. For example, on a “decision alone” trial, the person is shown a face, and simply decides to “attack” or “withdraw,” and recieves feedback on the decision. The categorization of the face on the D-alone trials remains just as important to the decision as it is on C-D trials, and some implicit inference about the category is necessary before making the decision, but the person does not overtly report this implicit inference.

Note that the C-D condition in the psychology experiment allows the experimenter to observe which “path” the participant follows before reaching a final decision. This is analogous to a “double slit” physics experiment in which the experimenter observes which “path” a particle follows before reaching a final detector. In contrast, for the D-alone condition in the psychology experiment, the experimenter does not observe which “path” the decision maker follows before reaching a final decision. This is analogous to the “double slit” physics experiment in which the experimenter does not observe which “path” the particle follows before reaching a final detector⁹.

According to the Markov model proposed in Townsend et al. [93], for the D-alone condition, the person implicitly performs the same task as explicitly required by the C-D condition. More specifically, for the D-alone condition, once a face (denoted f) is presented, there is a probability that the person implicitly categorizes the face as a “good” or “bad” guy. From each category inference state, there is a probability of transiting to the “attack” or “withdraw” decision state. So the probablity of “attack” in the D-alone condition (denoted as p(A|f)) should equal the total probability of “attacking” in the C-D condition (denoted as p_T(A|f)). The latter is defined by the probability that the person categorizes a face as a “good guy” and then “attacks” plus the probability that the person categorizes the face as a “bad guy” and then “attacks” (p_T(A|f) = p(G ∩ A|f) + p(B∩A|f)). Using this categorization-decision paradigm, one can examine how the overt report of the category interferes with the subsequent decision. An interference effect of categorization on decision making occurs when the probability of “attacking” for D-alone trials differs from the total probability pooled across C-D trials. The Markov model for this task originally investigated by Townsend et al. [93] predicts that there should be no interference, and the law of total probability should be satisfied.

Beginning with our first study [17], we have conducted a series of four experiments on this paradigm (see 92, for review). All results of these experiments show similar results, but we briefly report a summary of findings from the fourth experiment that included 246 participants (a minimum 34 observations per person per condition). For a face more likely assigned to the “god guy” category (we denote these faces as g), the law of total probability is approximately satisfied (p_T(A|g) = 0.36, p(A|g) = 0.37). However, for a face more often assigned to the “bad guy” category (we denote these faces as b), the probability of “attack” (i.e., the optimal decision with respect to the average payoff) is systematically greater for the D-alone condition as compared to the C-D condition” violating the law of total probability (p(A|b) = 0.62 > p_T(A|b) = 0.56)¹⁰. More surprising, the probability of “attack” for the D-alone condition (which leaves the “good” or “bad” guy category unresolved) was even greater than the probability of “attack” given that the person previously categorized the face as a “bad guy” (p(A|b) = 0.62 > p(A|b, B) = 0.61) on a C-D trial! For some reason, the overt categorization response interfered with the decision by reducing the tendency to “attack” faces that most likely belonged to the “bad guy” category. These violations of the law of total probability contradict the predictions of the Markov model proposed by Townsend et al. [93] for this task.

A detailed quantum-like model for the categorization-decision task is presented in [17], and here we only present a brief summary following the paper [92]. The human decision system is represented by a unit length state vector |ψ〉 belonging to 4-dimensional Hilbert space spanned by four basis vectors. (Here we use Dirac's symbolic notations, see Appendix 2 in Supplementary Material).

Each basis vector represents one of the four combinations of categories and actions (e.g., |GA〉 is a basis vector corresponding to category G and action A). The state |ψ_f〉 = ψ_GA|GA〉 + ψ_GW|GW〉 + ψ_BA|BA〉 + ψ_BW|BW〉 is prepared by the face stimulus f that is presented during the trial. The question about the category is represented by a pair of projectors for good and bad categories C_G = |GA〉 〈GA| + |GW〉 〈GW|, C_B = (I − C_G). The question about the action is represented by a pair of projectors for attack and withdraw actions $D_A=U_{DC}|GA\rangle \langle GA|U_{DC}^{†}+U_{DC}|BA\rangle \langle BA|U_{DC}^{†},D_W=\left(I-D_A\right)$, where U_DC is a unitary operator of transformation from the categorization basis to the decision basis.

Following [92], we obtain that the probability of first categorizing the face as a “bad guy” and then “attacking” equals $p(B,A|f)=p\left(B\right)·p\left(A|B\right)={\Vert C_B|{\psi }_f\rangle \Vert }^2·{\Vert D_A|{\psi }_B\rangle \Vert }^2$, with $|{\psi }_B\rangle =\frac{C_B|{\psi }_f\rangle }{\Vert C_B|{\psi }_f\rangle \Vert }$, and combining the terms in the product we obtain $p(B,A|f)={\Vert D_A·C_B·|{\psi }_f\rangle \Vert }^2$; similarly, the probability of first categorizing the face as a “good guy” and then “attacking” equals $p(G,A|f)={\Vert D_A·C_G·|{\psi }_f\rangle \Vert }^2$; and so the total probability of attacking under the C-D condition equals $p_T(A|f)={\Vert D_A·C_G·|{\psi }_f\rangle \Vert }^2+{\Vert D_A·C_B·|{\psi }_f\rangle \Vert }^2$.

The probability of attack in the D-alone condition equals [92] $p(A|f)={\Vert D_A·|{\psi }_f\rangle \Vert }^2={\Vert D_A·\left(C_G+C_B\right)|{\psi }_f\rangle \Vert }^2={\Vert D_A·C_G|{\psi }_f\rangle +D_A·C_B|{\psi }_f\rangle \Vert }^2={\Vert D_A·C_G|{\psi }_f\rangle \Vert }^2+{\Vert D_A·C_B|{\psi }_f\rangle \Vert }^2+Int$, where Int = 2·Re[〈ψ_f|C_GD_AC_B|ψ_f〉]. If the projectors for categorization commute with the projectors for action (e.g., U_DC = I), then the interference is zero, Int = 0, and we obtain $p(A|f)={\Vert D_A·C_G|{\psi }_f\rangle \Vert }^2+{\Vert D_A·C_B|{\psi }_f\rangle \Vert }^2=p_T\left(A|f\right)$, and the law of total probability is satisfied. However, if the projectors do not commute (e.g., U_DC ≠ I), then we obtain an interference term. We can select the unitary operator U_DC which produces an inner product Int = −0.06, and account for the observed violation of the law of total probability.

9. Conclusion

We demonstrated that the mathematics developed to solve QM problems is highly suitable to solving particular problems (and paradoxes) in psychology and social sciences in general [6], cf. with the views of G. T. Fechner, see Section 1. The reason is that psychologists, like quantum physicists, must work with contextualized probabilistic systems that are highly sensitive to measurement, as well as “entangled” systems that are strongly interconnected and difficult to decompose into separate and independent parts. Our point (we call it the quantum-like paradigm [4], see also [94, 95]) is that the mathematical formalisms of quantum theory are highly suitable for such complex systems.

This inspires us to say that Descartes' dualism between the two substances, material and mental, can be resolved through construction of the general mathematical model based on quantum information and probability and applicable both to physics and cognition.

Conflict of Interest Statement

The author declares that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Acknowledgments

I would like to thank I. Basieva for fruitful discussions on the structure of this paper and inter-relation between physics and cognition and J. Busemeyer and E. Dzhafarov for discussions on analogy between quantum measurement theory and Stimulus-Organism-Response (S-O-R) scheme [96].

Supplementary Material

The Supplementary Material for this article can be found online at: http://journal.frontiersin.org/article/10.3389/fphy.2015.00077

Footnotes

1. ^It is also a Buddhist dogma that life is comprised of mind and matter.

2. ^Of course, when discussing this law we have to mention the works of Germain Henri Hess, James Prescott Joule, and Rudolf Clausius. But, for Freud, the influence of von Helmholtz's ideas was especially strong. He started his research in physiology under the supervision of Ernst Brucke who previously worked with Hermann von Helmholtz.

3. ^At the beginning Pauli wanted to discuss with Jung his psychical problems which might be a subject of psychoanalytic treatment. However, Jung smartly redirected Pauli to a young female psychoanalyst and the most part of Pauli-Jung correspondence is about psyche-physics inter-relation.

4. ^Here the symbol σ encodes “countable.” In American terminology such systems of subsets are called σ-fields.

5. ^Here measurability has the following meaning. The set of real numbers R is endowed with the Borel σ-algebra ${B}$: the minimal σ-algebra containing all open and closed intervals. Then for any A ∈ ${B}$ its inverse image a⁻¹(A) ∈ ${F}$. This gives a possibility to define on ${B}$ the probability distribution of a random variable, $p_a(A)=p(a^{-1}(A)).$

6. ^I see a big problem in the absence of mathematically advanced courses in probability theory for physics students. It seems that education in physics suffers from this problem throughout the world.

7. ^This theorem was criticized for unphysical assumptions used by von Neumann to approach his no-go conclusion; especially strong critique was from the side of Bell [52], the author of another famous no-go theorem; calmer critical arguments were presented by Ballentine [2]. (We also remark that, although in the modern literature the von Neumann statement is called “theorem,” in the German edition it was called an “ansatz”).

8. ^At first glance, representation of events by projectors/linear subspaces may look exotic because of the very common use of the set-theoretic representation of events in the modern classical probability theory. We want to fight this prejudice and support the view that alternatives are possible and sometimes desirable. The tradition to represent events by subsets was firmly established by Kolmogorov [49] only in 1933. We remark that before him the basic classical probabilistic models were not of the set-theoretic nature. For example, the main competitor of the Kolmogorov model, the von Mises frequency model [75], was based on the notion of a collective (see [76], for formulation of QM on the basis of the von Mises model).

9. ^We remark that here the picture of path is used only for illustrative purpose; therefore we placed path in quotation marks. In QM there is no such a concept as a “path” (trajectory) of a particle. We can only ascertain, and this is only statistically, a singular event of an electron “passing” through a slit. In fact this way of seeing the situation provides an even better parallel here.

10. ^This difference is statistically significant: t₍₂₄₅₎ = 4.41, p = 0.0004. Also the same effect was replicated in 4 independent experiment

References

1. Von Neumann J. Mathematische Grundlagen der Quantenmechanik. Berlin-Heidelberg-New York: Springer (1932). English translation: Mathematical Foundations of Quantum Mechanics. Princeton: Princeton University Press (1955).

Google Scholar

2. Ballentine LE. Quantum Mechanics. Englewood Cliffs, NJ: Prentice Hall (1989).

Google Scholar

3. Accardi L. Topics in quantum probability. Phys Rep. (1981) 71:169–92. doi: 10.1016/0370-1573(81)90070-3

CrossRef Full Text | Google Scholar

4. Khrennikov A. Ubiquitous Quantum Structure: From Psychology to Finance. Berlin; Heidelberg; New York, NY: Springer (2010).

Google Scholar

5. Busemeyer JR, Bruza PD. Quantum Models of Cognition and Decision. Cambridge: Cambridge University Press (2012).

Google Scholar

6. Haven E, Khrennikov A. Quantum Social Science. Cambridge: Cambridge University Press (2013).

Google Scholar

7. Asano M, Khrennikov A, Ohya M, Tanaka Y, Yamato I. Quantum Adaptivity in Biology: From Genetics to Cognition. Berlin-Heidelberg: Springer (2014).

Google Scholar

8. Aerts D, Aerts S. Applications of quantum statistics psychological studies of decision processes. Found Phys. (1994) 1:85–97. doi: 10.1007/BF00208726

CrossRef Full Text | Google Scholar

9. Atmanspacher H, Filk T, Römer H. Quantum zeno features of bistable perception. Biol Cybern. (2004) 90:33–40. doi: 10.1007/s00422-003-0436-4

PubMed Abstract | CrossRef Full Text | Google Scholar

10. Khrennikov A. On quantum-like probabilistic structure of mental information. Open Syst Inf Dyn. (2004) 11:267–75. doi: 10.1023/B:OPSY.0000047570.68941.9d

CrossRef Full Text | Google Scholar

11. Khrennikov A. The principle of supplementarity: a contextual probabilistic viewpoint to complementarity, the interference of probabilities, and the incompatibility of variables in quantum mechanics. Found Phys. (2005) 35: 1655–93. doi: 10.1007/s10701-005-6511-z

CrossRef Full Text | Google Scholar

12. Busemeyer JR, Wang Z, Townsend JT. Quantum dynamics of human decision making. J Math Psych. (2006) 50:220241. doi: 10.1016/j.jmp.2006.01.003

CrossRef Full Text | Google Scholar

13. Conte E, Todarello O, Federici A, Vitiello F, Lopane M, Khrennikov A, et al. Some remarks on an experiment suggesting quantum-like behavior of cognitive entities and formulation of an abstract quantum mechanical formalism to describe cognitive entity and its dynamics. Chaos Solitons Fractals (2007) 31:1076–88. doi: 10.1016/j.chaos.2005.09.061

CrossRef Full Text

14. Conte E, Khrennikov A, Todarello O, Federici A. A preliminary experimental verification on the possibility of Bell inequality violation in mental states. Neuroquantology (2008) 6:214–21. doi: 10.14704/nq.2008.6.3.178

CrossRef Full Text | Google Scholar

15. Haven E, Khrennikov A. Quantum mechanics and violation of the sure-thing principle: the use of probability interference and other concepts. J Math Psych. (2009) 53:378–88. doi: 10.1016/j.jmp.2009.01.007

CrossRef Full Text | Google Scholar

16. Pothos EM, Busemeyer JR. A quantum probability explanation for violations of rational decision making. Proc R Soc B (2009) 276:2171–78. doi: 10.1098/rspb.2009.0121

PubMed Abstract | CrossRef Full Text | Google Scholar

17. Busemeyer JR, Wang Z, Mogiliansky-Lambert A. Comparison of quantum and Markov models of decision making. J Math Psychol. (2009) 53:423–33. doi: 10.1016/j.jmp.2009.03.002

CrossRef Full Text

18. Conte E, Khrennikov A, Todarello O, Federici A. Mendolicchio L, Zbilut JP. Mental states follow quantum mechanics during perception and cognition of ambiguous figures. Open Syst Inf Dyn. (2009) 16:1–17. doi: 10.1142/S1230161209000074

CrossRef Full Text

19. Lambert-Mogiliansky A, Zamir S, Zwirn H. Type indeterminacy: a model of the K-T (Kahneman-Tversky)- man. J Math Psychol. (2009) 53:349–61. doi: 10.1016/j.jmp.2009.01.001

CrossRef Full Text | Google Scholar

20. Aerts D. Quantum structure in cognition. J Math Psych. (2009) 53:314–48. doi: 10.1016/j.jmp.2009.04.005

CrossRef Full Text | Google Scholar

21. Khrennikov A. A model of quantum-like decision-making with applications to psychology and cognitive science. Biosystems (2009) 95:179–87. doi: 10.1016/j.biosystems.2008.10.004

PubMed Abstract | CrossRef Full Text | Google Scholar

22. Khrennikov A. Classical and quantum probability for biologists-introduction. QP - PQ Quantum Probab White Noise Anal. (2010) 26:179–92.

23. Asano M, Ohya M, Khrennikov A. Quantum-like model for decision making process in two players game : a non-kolmogorovian model. Found Phys. (2011) 41:538–48. doi: 10.1007/s10701-010-9454-y

CrossRef Full Text | Google Scholar

24. Asano M, Ohya M, Tanaka Y, Basieva I, Khrennikov A. Quantum-like model of brain's functioning: decision making from decoherence. J Theor Biol. (2011) 281:56–64. doi: 10.1016/j.jtbi.2011.04.022

PubMed Abstract | CrossRef Full Text | Google Scholar

25. Trueblood JS, Busemeyer, JR. A quantum probability model for order effects on inference. Cogn Sci. (2011) 35:1518–52. doi: 10.1111/j.1551-6709.2011.01197.x

PubMed Abstract | CrossRef Full Text | Google Scholar

26. Busemeyer JR, Pothos EM, Franco R, Trueblood JS. A quantum theoretical explanation for probability judgment errors. Psych Rev. (2011) 118:193–218. doi: 10.1037/a0022542

PubMed Abstract | CrossRef Full Text | Google Scholar

27. Trueblood JS, Busemeyer JR. A quantum probability model of causal reasoning. Front Cogn. (2012) 2:289.

Google Scholar

28. Atmanspacher H, Filk T. Temporal nonlocality in bistable perception. In: Khrennikov A, Atmanspacher H, Migdall A, Polyakov S, editors. Proc. Int. Conference on Quantum Theory: Reconsiderations of Foundations - 6 Special Section: Quantum-like decision making: from biology to behavioral economics, AIP Conference Proceedings, Vol. 1508, Melville, NY (2012). p. 79–88.

29. Acacio de Barros J. Joint probabilities and quantum cognition. In: Khrennikov A, Atmanspacher H, Migdall A, Polyakov S, editors. Proc. Int. Conf. on Quantum Theory: Reconsiderations of Foundations - 6, Special Section: Quantum-like decision making: from biology to behavioral economics, AIP Conference Proceedings, Vol. 1508, Melville, NY (2012). p. 98–104.

30. Asano M, Ohya M, Tanaka Y, Basieva I, Khrennikov A. Quantum-like dynamics of decision-making. Physica A (2012) 391:2083–99.

Google Scholar

31. Asano M, Basieva I, Khrennikov A, Ohya M, Tanaka Y. Quantum-like dynamics of decision-making in prisoner's dilemma game. AIP Conf Proc. (2012) 1424:453–7.

Google Scholar

32. Wang Z, Busemeyer, JR. A quantum question order model supported by empirical tests of an a priori and precise prediction. Top Cogn Sci. (2013) 5:689–710.

PubMed Abstract | Google Scholar

33. Pothos EM, Busemeyer JR. Can quantum probability provide a new direction for cognitive modeling? Behav Brain Sci. (2013) 36:255–327.

PubMed Abstract | Google Scholar

34. Wang Z, Busemeyer JR, Atmanspacher H, Pothos EM. The potential of using quantum theory to build models of cognition. Top Cogn Sci. (2013) 5:689–710.

PubMed Abstract | Google Scholar

35. Asano M, Basieva I, Khrennikov A, Ohya M, Yamato I. Non-kolmogorovian approach to the context-dependent systems breaking the classical probability law. Found Phys. (2013) 43:895–911.

Google Scholar

36. Khrennikov A, Basieva I, Dzhafarov EN, Busemeyer JR. Quantum models for psychological measurements: an unsolved problem. PLoS ONE (2014) 9:e110909.

PubMed Abstract | Google Scholar

37. Bohr N. The philosophical writings of Niels Bohr, 3 vols. Woodbridge, CT: Ox Bow Press (1987).

Google Scholar

38. James W. The Principles of Psychology. New York, NY: Henry Holt and Co. (1890). Reprinted 1983, Boston: Harvard University Press.

39. Plotnitsky A. Niels Bohr and Complementarity: An Introduction. Berlin; New York, NY: Springer Scientific Publications (2012).

Google Scholar

40. Plotnitsky A. Epistemology and Probability: Bohr, Heisenberg, Schrdinger, and the Nature of Quantum-Theoretical Thinking, Springer Series Fundamental Theories in Physics. Berlin; New York, NY: Springer Scientific Publications (2009).

Google Scholar

41. Plotnitsky A. Reading Bohr: Physics and Philosophy, Springer Series Fundamental Theories in Physics. Dordrecht; Berlin; New York, NY: Springer Scientific Publications (2006).

Google Scholar

42. Freud S. The Ego and the Id. New York, NY: W.W. Norton and Company (1923).

Google Scholar

43. Freud S. The Interpretation of Dreams, Vols. 4, 5. Standard Edition 1954–1974. London: Hogarth Press (1900). 1627 p.

44. Hameroff S. Quantum coherence in microtubules. A neural basis for emergent consciousness? J Conscious Stud. (1994) 1:91–118.

Google Scholar

45. Penrose R. The Emperor's New Mind. Oxford: Oxford University Press (1989).

Google Scholar

46. Penrose R. Shadows of the Mind. Oxford: Oxford University Press (1994).

Google Scholar

47. Khrennikov A. Quantum-like model of processing of information in the brain based on classical electromagnetic field. Biosystems (2011) 105, 250–262.

PubMed Abstract | Google Scholar

48. Boole G. An Investigation of the Laws of Thought on Which are Founded the Mathematical Theories of Logic and Probabilities. London: Walton and Maberly (1854). Reprinted 1958, New York, NY: Dover Publications and 2009, Cambridge: Cambridge University Press.

Google Scholar

49. Kolmogoroff AN. Grundbegriffe der Wahrscheinlichkeitsrechnung. Berlin: Springer Verlag (1933). English translation: Kolmogorov AN. Foundations of Theory of Probability. New York, NY: Chelsea Publishing Company (1956).

Google Scholar

50. Feynman R, Hibbs A. Quantum Mechanics and Path Integrals. New York, NY: McGraw-Hill (1965).

Google Scholar

51. Kochen, S, Specker, E. The problem of hidden variables in quantum mechanical systems. J Math Mech. (1967) 17:59–87.

52. Bell J. Speakable and Unspeakable in Quantum Mechanics. Cambridge: Cambridge University Press (1987).

Google Scholar

53. Khrennikov A. Contextual Approach to Quantum Formalism. Berlin-Heidelberg: Springer (2009).

Google Scholar

54. Cabello A. Experimentally testable state-independent quantum contextuality. Phys Rev Lett. (2008) 101:210401.

PubMed Abstract | Google Scholar

55. Bartosik H, Klepp J, Schmitzer C, Sponar S, Cabello A, Rauch H, et al. Experimental test of quantum contextuality in neutron interferometry. Phys Rev Lett. (2009) 103:040403.

PubMed Abstract

56. Khrennikov A. Bell-boole inequality: nonlocality or probabilistic incompatibility of random variables? Entropy (2008) 10:19–32.

Google Scholar

57. Khrennikov A. Violation of bell's inequality and postulate on simultaneous measurement of compatible observables. J Comput Theor. Nanosci. (2011) 8:1006–10.

Google Scholar

58. Khrennikov A. Bell argument: locality or realism? Time to make the choice. AIP Conf Proc. (2012) 1424:160–75.

PubMed Abstract | Google Scholar

59. Fuchs CA. The anti-Växjö interpretation of quantum mechanics. In: Khrennikov AY editor. Quantum Theory: Reconsideration of Foundations, Vol. 2. Ser. Math. Model. Växjö: Växjö University Press (2002). p. 99–116.

60. Fuchs CA. Quantum mechanics as quantum information and only a little more. In: Khrennikov AY, editor. Quantum Theory: Reconsideration of Foundations, Vol. 2. Ser. Math. Model. Växjö: Växjö University Press (2002). p. 463–543

61. Fuchs CA. Delirium quantum (or, where I will take quantum mechanics if it will let me). In: Adenier G, Fuchs C, Khrennikov AY, editors. Foundations of Probability and Physics-3, AIP Conference Proceedings, Vol. 889. Melville, NY: AIP (2007). p. 438–62

62. Zeilinger A. Quantum teleportation and the non-locality of information. Phil Trans R Soc Lond. (1997) 1733:2401–4.

Google Scholar

63. Zeilinger A. A foundational principle for quantum mechanics. Found Phys. (1999) 29:631–43.

Google Scholar

64. Brukner C, Zeilinger A. Information invariance and quantum probabilities. Found Phys. (2009) 39:677–87.

Google Scholar

65. Fechner GT. In Sachen der Psychophysik. Wien: Breitkopf und Hrtel (1877).

Google Scholar

66. Meier CA, (ed.). Atom and Archetype: The Pauli/Jung Letters, 1932-1958. Princeton: Princeton University Press.

67. Jung C. Synchronicity: An Acausal Connecting Principle. Bollingen: Bollingen Foundation (1952).

Google Scholar

68. Khrennikov AY. Modelling of psychological behavior on the basis of ultrametric mental space: encoding of categories by balls. P-Adic Numbers Ultrametric Anal Appl. (2010) 2:1–20.

Google Scholar

69. Einstein A, Infeld L. Evolution of Physics: The Growth of Ideas from Early Concepts to Relativity and Quanta. New York, NY; Simon and Schuster (1961).

Google Scholar

70. Boole G. On the theory of probabilities. Phil Trans R Soc Lond. (1862) 152:225–42.

Google Scholar

71. Kant I. The Critique of Pure Reason. London: Penguin Classics (2008).

Google Scholar

72. Birkhoff G, von Neumann J. The logic of quantum mechanics. Ann Math. (1936) 37:823–843.

73. Birkhoff G. Lattice Theory. Providence: American Mathematical Society (1967).

Google Scholar

74. Beltrametti E, Cassinelli G. The Logic of Quantum Mechanics. Cambridge: Cambridge University Press (1981).

Google Scholar

75. Von Mises R. The Mathematical Theory of Probability and Statistics. London: AcademicPress (1964).

Google Scholar

76. Khrennikov A. Interpretations of Probability, 2nd Edn. Berlin: De Gruyter (2010).

Google Scholar

77. Tversky A, Kahneman D. Judgment under uncertainty: heuristics and biases. Science (1974) 185:1124–31.

PubMed Abstract | Google Scholar

78. Tversky A, Kahneman D. Causal schemas in judgments under uncertainty. In Fishbein M, editor. Progress in Social Psychology, Hillsdale, NJ: Erlbaum (1980), p. 49–72.

79. Tversky A, Kahneman D. Evidential impact of base rates. In: Kahneman D, Slovic P, Tversky A, editors. Judgment Under Uncertainty: Heuristics and Biases. New York, NY: Cambridge University Press (1982). p. 153–160.

PubMed Abstract

80. Tversky A, Shafir E. The disjunction effect in choice under uncertainty. Psych Sci. (1992) 3:305–9.

Google Scholar

81. Shafir E, Tversky A. Thinking through uncertainty: nonconsequential reasoning and choice. Cogn Psych. (1992) 24:449–474.

PubMed Abstract | Google Scholar

82. Hofstadter DR. Dilemmas for superrational thinkers, leading up to a luring lottery. Sci Am. (1983) 6:24–35.

83. Hofstadter DR. Metamagical Themes: Questing for the Essence of Mind and Pattern. New York, NY: Basic Books (1985).

84. Croson R. The disjunction effect and reasoning-based choice in games. Org Behav Hum Decis Process. (1999) 80:118–33.

Google Scholar

85. Savage LJ. The Foundations of Statistics. New York, NY: Wiley (1954).

Google Scholar

86. Woodworth RS. Psychology: A Study of Mental Life. New York, NY: H. Holt (1921).

87. Khrennikova P, Haven E, Khrennikov A. An application of the theory of open quantum systems to model the dynamics of party governance in the US Political System. Int J Theor Phys. (2014) 53:1346–60.

Google Scholar

88. Asano M, Hashimoto T, Khrennikov A, Ohya M, Tanaka Y. Violation of contextual generalization of the Leggett-Garg inequality for recognition of ambiguous figures. Phys Scr. (2014) T163, 014006.

Google Scholar

89. Dzhafarov EN, Kujala JV. Selectivity in probabilistic causality: where psychology runs into quantum physics. J Math Psych. (2012) 56:54–63.

Google Scholar

90. Dzhafarov EN, Kujala JV. Quantum entanglement and the issue of selective influences in psychology: an overview. Lect Notes Comp Sci. (2012) 7620:184–95.

Google Scholar

91. Moore DW. Measuring new types of question-order effects. Public Opin Q. (2002) 66:80–91.

Google Scholar

92. Busemeyer JR, Wang Z, Khrennikov A, Basieva I. Applying quantum principles to psychology. Phys Scr. (2014) T163:014007.

Google Scholar

93. Townsend JT, Silva KM, Spencer-Smith J, Wenger M. Exploring the relations between categorization and decision making with regard to realistic face stimuli Pragmat Cogn. (2000) 8:83–10.

Google Scholar

94. Asano M, Basieva I, Khrennikov A, Ohya M, Tanaka Y, Yamato I. Quantum-like model of diauxie in Escherichia coli: operational description of precultivation effect. J Theor Biol. (2012) 314:130–7.

PubMed Abstract | Google Scholar

95. Asano M, Basieva I, Khrennikov A, Ohya M, Tanaka Y, Yamato I. Quantum-like model of glucose effect on Escherichia coli growth. AIP Conf Proc. (2012) 1424:507–12.

Google Scholar

96. Dzhafarov EN, Kujala JV. On selective influences, marginal selectivity, and Bell/CHSH inequalities. Top Cogn Sci. (2014) 6:121–8.

PubMed Abstract | Google Scholar