Causal Scale of Rotors in a Cardiac System

Rotors of spiral waves are thought to be one of the potential mechanisms that maintain atrial fibrillation (AF). However, disappointing clinical outcomes of rotor mapping and ablation to eliminate AF raise a serious doubt on rotors as a macro-scale mechanism that causes the micro-scale behavior of individual cardiomyocytes to maintain spiral waves. In this study, we aimed to elucidate the causal relationship between rotors and spiral waves in a numerical model of cardiac excitation. To accomplish the aim, we described the system in a series of spatiotemporal scales by generating a renormalization group, and evaluated the causal architecture of the system by quantifying causal emergence. Causal emergence is an information-theoretic metric that quantifies emergence or reduction between micro- and macro-scale behaviors of a system by evaluating effective information at each scale. We found that the cardiac system with rotors has a spatiotemporal scale at which effective information peaks. A positive correlation between the number of rotors and causal emergence was observed only up to the scale of peak causation. We conclude that rotors are not the universal mechanism to maintain spiral waves at all spatiotemporal scales. This finding may account for the conflicting benefit of rotor ablation in clinical studies.

1. Introduction

The heart is a complex system consisting of five billion autonomous cardiomyocytes that interact with each other. This interaction leads to system behaviors at multiple scales. The dynamics of the rotating center (“rotor”) of spiral waves [1, 2] is a macro-scale, emergent behavior of the cardiac system that is reducible to but cannot easily be explained by the dynamics of the individual cardiomyocytes at the microscopic scale [3–6]. For example, the determinants of rotor dynamics include ionic currents [7], action potential duration (APD) restitution properties, conduction velocity (CV) restitution properties [8], wavefront curvature of spiral waves [9], heterogeneity and anisotropy of the media, and coexisting rotors [10, 11].

Currently, rotors are thought to be one of the potential mechanisms that maintains atrial fibrillation (AF) in human [12], and early clinical attempts to target rotors with interventional catheter ablation therapy to eliminate AF showed promising results [13–15]. However, recent clinical trials have been disappointing [16–20]. Apart from the technical limitations associated with rotor identification using clinically available systems [21], those negative findings raise a serious doubt on rotors as a macro-scale mechanism that causes the micro-scale behavior of individual cardiomyocytes to maintain spiral waves.

The micro- and macro-scale behaviors of a multi-scale system can be mathematically quantified by the information content of behaviors at each scale. For example, information-theoretic metrics such as the complexity profile [22] and the marginal utility of information [23] can quantitatively characterize the amount of information that is present in the system behavior at different scales. The downward causation [24–28] from macro- to micro-scale behaviors of the system is quantifiable as inter-scale downward information flow. We recently showed that the relationship between the number of rotors and downward information flow is nonlinear in a cardiac system [29]. At microscopic scales, higher numbers of rotors are associated with higher downward information flow. As the system description becomes more macroscopic, higher numbers of rotors are associated with lower downward information flow. This subtle but important finding suggests that rotors may not be a universal mechanism to maintain spiral waves at all scales. As the system is coarse-grained, rotors may lose their causal power to maintain spiral waves.

The aim of the study was to elucidate the causal relationship between rotors and spiral waves, and to identify the causal scale of rotors as a mechanism to maintain spiral waves. To accomplish the aim, we described rotors in a numerical model of cardiac excitation in a series of spatiotemporal scales by generating a renormalization group, and evaluate the causal architecture of the system by quantifying causal emergence. Causal emergence is an information-theoretic metric that quantifies emergence or reduction between micro- and macro-scale behaviors of a system by evaluating effective information at each spatiotemporal scale [30]. Effective information is a quantity that captures causal interactions of a system between its unconstrained repertoire of possible cause and a specific state of possible effect [31]. We hypothesized that a positive correlation between the number of rotors and causal emergence is not universally found in all the spatiotemporal scales of the cardiac system.

2. Materials and Methods

We perform the simulation and the data analysis using Matlab R2016b (Mathworks, Inc.).

2.1. Model of Spiral Waves

We used a modified Fitzhugh–Nagumo model to represent cardiac action potential [32, 33]. This model accurately reproduces important properties of cardiac systems, including slowed conduction velocity, unidirectional block due to wavefront curvature, and spiral waves [34].

$\begin{array}{ll}\frac{\partial v}{\partial t}=0.26v(v-0.13)(1-v)-0.1vr+I_{ex}+\nabla ·(D\nabla v)& (1)\end{array}$

$\begin{array}{ll}\frac{\partial r}{\partial t}=0.013(v-r)& (2)\end{array}$

where v is the transmembrane potential, r is the recovery variable, and I_ex is the external current [35]. D is the diffusion tensor, which is a diagonal matrix whose diagonal and off-diagonal elements are 1 and 0 mm²/ms, respectively, to represent a 2-D isotropic system [34]. We used an isotropic, homogeneous model to avoid confounding the causal archtecture by tissue anisotropy and inhomogeneity. We solved the model equations using a finite difference method for spatial derivatives and explicit Euler integration for time derivatives assuming Neumann boundary conditions. We generated 1,000 sets of a 2-D 120 × 120 isotropic lattice of components (= 11.9 × 11.9 cm) by inducing spiral waves with 40 random sequential point stimulations in 40 random components of the lattice (Supplementary Movie 1, section 3.2) [36]. In each component, we computed the time series for 10 s excluding the stimulation period with a time step of 0.063 ms, which was subsequently downsampled at a sampling frequency of 400 Hz.

We then defined the instantaneous phase ϕ(t) and the instantaneous amplitude A(t) of v(t) in each component via construction of the analytic signal ξ(t), which is a complex function of time [37].

$\begin{array}{ll}\xi (t)=v(t)+i{v}_H(t)=A(t)e^{i\varphi (t)}& (3)\end{array}$

Here, v_H(t) is the Hilbert transform of v(t)

$\begin{array}{ll}{v}_H(t)=\frac{1}{\pi }\text{p}.\text{v}.{\displaystyle {\int }_{-\infty }^{\infty }}\frac{v(\tau )}{t-\tau }d\tau & (4)\end{array}$

where p.v. indicates that the integral is taken in the sense of the Cauchy principal value. We defined the rotor of the spiral wave as a phase singularity [38], where the phase is undefined because all phase values converge. The phase singularity can be localized through calculation of the topological charge n_t [39, 40].

$\begin{array}{ll}{n}_t=\frac{1}{2\pi }{{\displaystyle \oint }}_c\nabla \varphi ·d\overrightarrow{l}& (5)\end{array}$

where $\varphi (\overrightarrow{r})$ is the local phase, and the line integral is taken over the path $\overrightarrow{l}$ on a closed curve c surrounding the singularity [41].

$\begin{array}{ll}{n}_t=\{\begin{array}{cc}+1\hfill & \mathrm{\text{counterclockwise rotor}}\hfill \\ -1\hfill & \mathrm{\text{clockwise rotor}}\hfill \\ 0\hfill & \mathrm{\text{elsewhere}}\hfill \end{array}\hfill & (6)\hfill \end{array}$

In this study, |n_t| was used to quantify the average number of rotors over the entire time series [42].

2.2. Renormalization Group

We generated a renormalization group of the system by a series of spatial and temporal transformation including coarse-graining and rescaling of the original microscopic description of the system. For each component, the time series of cardiac excitation was descretized to 1 when excited (during the APD at 90% repolarization, or APD₉₀) or 0 when resting (Figure 1A) [43]. Then we coarse-grained the system spatially and temporally with decimation by a factor of 2 (Figure 1B). Spatial decimation transforms a n × n lattice into a $\frac{n}{2}\times \frac{n}{2}$ lattice by extracting the top left component of each 2 × 2 block (Supplementary Movie 2). Temporal decimation downsampled the binary time series of each component by a factor of 2. Using a combination of iterative coarse-graining in spatial and temporal axes we created a renormalization group of a total of 36 spatiotemporal scales of the system. The renormalization group included spatial scales 1 (30 × 30 lattice), 2 (15 × 15 lattice), 3 (8 × 8 lattice), 4 (4 × 4 lattice), 5 (2 × 2 lattice), and 6 (1 × 1 lattice) (Figure 1C), and temporal scales 1 (400 Hz), 2 (200 Hz), 3 (100 Hz), 4 (50 Hz), 5 (25 Hz), and 6 (12 Hz) (Figure 1D).

FIGURE 1

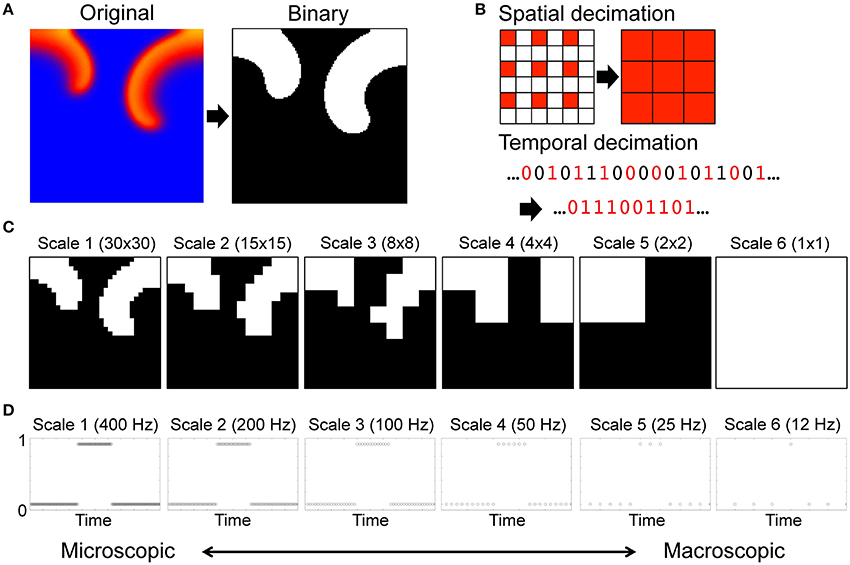
Figure 1. Renormalization of a cardiac system with spiral waves. (A) Original description of the system. For each component, the time series of cardiac excitation is descretized to 1 (black) when excited (during the APD at 90% repolarization, or APD₉₀) or 0 (white) when resting. (B) Spatial and temporal decimation. Spatial decimation takes the value of cardiac excitation (0 or 1) at each time point in the component at the top left corner of a block of 2 × 2 immediately adjacent components of the system, and assigns the value to the corresponding site in the system at the next scale. Temporal decimation downsamples the time series of cardiac excitation by a factor of 2. (C) Spatial scales. Spatial scales include scale 1 (30 × 30 lattice), scale 2 (15 × 15 lattice), scale 3 (8 × 8 lattice), scale 4 (4 × 4 lattice), scale 5 (2 × 2 lattice), and scale 6 (1 × 1 lattice). (D) Temporal scales. Each circle represents a data sampling point. Temporal scales include scale 1 (400 Hz), scale 2 (200 Hz), scale 3 (100 Hz), scale 4 (50 Hz), scale 5 (25 Hz), and scale 6 (12 Hz).

2.3. Effective Information

We treated each component on the lattice as a time-series process X. Entropy H of each time-series process X is

$\begin{array}{ll}H(X)=-{\displaystyle \sum _x}p(x){log}_{2}p(x)& (7)\end{array}$

where p(x) denotes the probability density function of the time series generated by X. Effective information quantifies the information generated when the system enters a specific state of possible effect Y out of its unconstrained probability distribution of possible cause X [31].

$\begin{array}{ll}EI(X\to Y)=I(X;Y)& (8)\end{array}$

$\begin{array}{ll}=H(X)+H(Y)-H(X,Y)& (9)\end{array}$

$\begin{array}{ll}={\displaystyle \sum _{x,y}}p(x,y){log}_2\frac{p(x,y)}{p(x)p(y)}& (10)\end{array}$

where X has a uniform probability distribution so that it provides the maximum entropy H(X)_max [44]. I(X; Y) is mutual information, p(x, y) and H(X, Y) denote the joint probability density function and the joint entropy of X and Y, respectively. Mutual information is originally a measure of statistical dependence to quantify how much information is shared between a source and a destination [45]. In this context, however, mutual information is applied between two time series of a system that is first perturbed into all possible states with equal probability and then observed as a sepcific state. Because of the system perturbations, mutual information here is a causal measure, and thus effective information of the system is a state-independent information-theoretic measure of a system's causal architecture [30].

One can describe a n × n lattice at time t as a binary string of length n × n. Therefore, the unconstrained repertoire of all possible causes X at time t₀ consists of 2ⁿ² possible states with equal probability 1/2ⁿ² at each time point. We defined the bin number b (b < 2ⁿ²) to calculate the probability distribution of X and Y, and we used b = 2¹⁰ = 1, 024 in this study. Analytically, because X has a uniform probability distribution, the probability that X falls in one of the b bins at each time point is 1/b. Therefore, entropy of X is equal to the maximum entropy (Figure 2A).

$\begin{array}{ll}H(X)=-{\displaystyle \sum _x}p(x){log}_{2}p(x)& (11)\end{array}$

$\begin{array}{ll}=b\times (-\frac{1}{b}{log}_2\frac{1}{b})& (12)\end{array}$

$\begin{array}{ll}={log}_{2}b& (13)\end{array}$

FIGURE 2

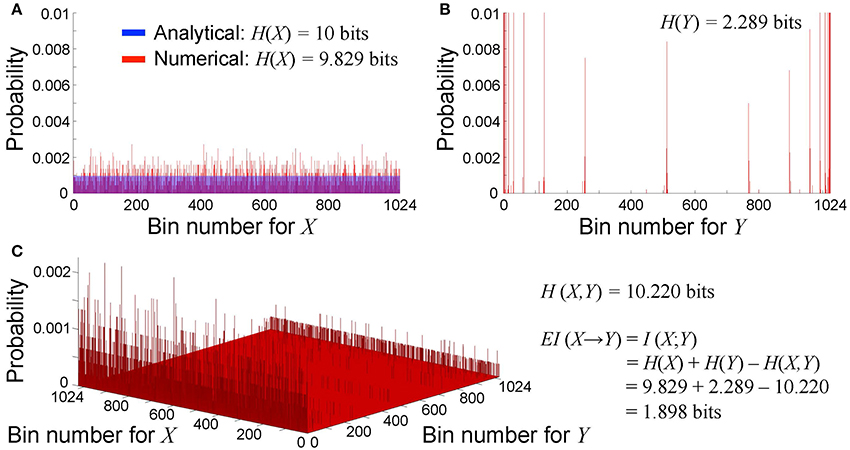
Figure 2. Probability distribution of cause X and effect Y. We define the bin number b = 2¹⁰ in this study. (A) Unconstrained probability distribution of possible cause X. Analytically, the probability of all bins is uniformly 1/b (shown in blue), and thus entropy is equal to the maximum entropy at log₂ b=10 bits. In contrast, numerically, the probability is non-uniform due to the discretization effect (shown in red). Entropy is 9.829 bits, which close to but not identical to the maximum entropy. (B) Probability distribution of a specific state of possible effect Y. The probability is non-uniform. Entropy is 2.289 bits in this case. (C) Bivariate probability distribution of cause X and effect Y. Joint entropy is 10.220 bits in this case. Effective information from case X to effect Y is equal to mutual information between X and Y, thus is calculated as 1.898 bits.

Numerically, X can be defined as a vector of uniformly distributed random numbers between 1 and 2ⁿ²−1 for a time series of finite duration. Due to the discretization effect, the probability is non-uniform. Entropy is close to but not identical to the maximum entropy (Figure 2A). We generated 1,000 sets of X at each scale to vaidate the robustness of our effective information measure in the cardiac system with rotors (section 3.1). Similarly, Y can be defined as a vector of decimal numbers between 1 and 2ⁿ²−1, each of which represents a specific state of the system with rotors (Figure 2B). Causal emergence is a difference in effective information between scales.

$\begin{array}{ll}CE=EI(X_m\to Y_m)-EI(X_n\to Y_n)& (14)\end{array}$

where m and n are different scales of the system description from the renormalization group. When scale m is more macroscopic than scale n(m > n), a positive CE indicates that the macroscopic behavior is emergence (downward causation), whereas a negative CE indicates that the macroscopic behavior is reduction (upward causation) [30]. In this study we quantified causal emergence with respect to the most microscopic system description with spatial scale = temporal scale = 1.

3. Results

3.1. Evaluation of Variance of Effective Information to Quantify Rotor Dynamics

First, we evaluated the variance of effective information to describe rotor dynamics at each spatiotemporal scale. This allowed us to vaidate the robustness of our effective information measure in the cardiac system with rotors. We repeated 1,000 numerical computations of X and Y in a representative spiral wave data set to calculate entropy H(X), H(Y), H(X, Y), then calculated EI(X → Y). Numerically, H(X) is not uniquely determined due to the discretization effect, but the variance was small (Figure 3). Spatial coarse-graining had minimal impact on the probability ditribution of H(X) from scales 1 through 4, but H(X) steeply fell in scales 5 and 6. In contrast, temporal coarse-graining gradually shifted the distribution of H(X) to the left. H(Y) was uniquely determined because it represents a specific state of the system regardless of the spatiotemporal scale (Figure 4). In this case, spatial coarse-graining clearly increased the distribution of H(Y) to the right, which peaked at scale 4 and decreased at scales 5 and 6. Similarly, temporal coarse-graining increased the distribution of H(Y) to the right, which peaked at scale 4 and decreased at scales 5 and 6. The relationship between the spatiotemporal coarse-graining and the probability distribution of joint entropy H(X, Y) was similar to that of H(X) (Figure 5), and the variance remained small. Effective infromation EI(X → Y) peaked at spatial scale of 4 and temporal scale 5, and the variance of EI(X → Y) remained small (Figure 6). This findings indicates that, despite the discretization effect, numerical computation of EI(X → Y) is robust with high reproducibility, and thus EI(X → Y) can be used to quantify the information of rotor dynamics at each spatiotemporal scale.

FIGURE 3

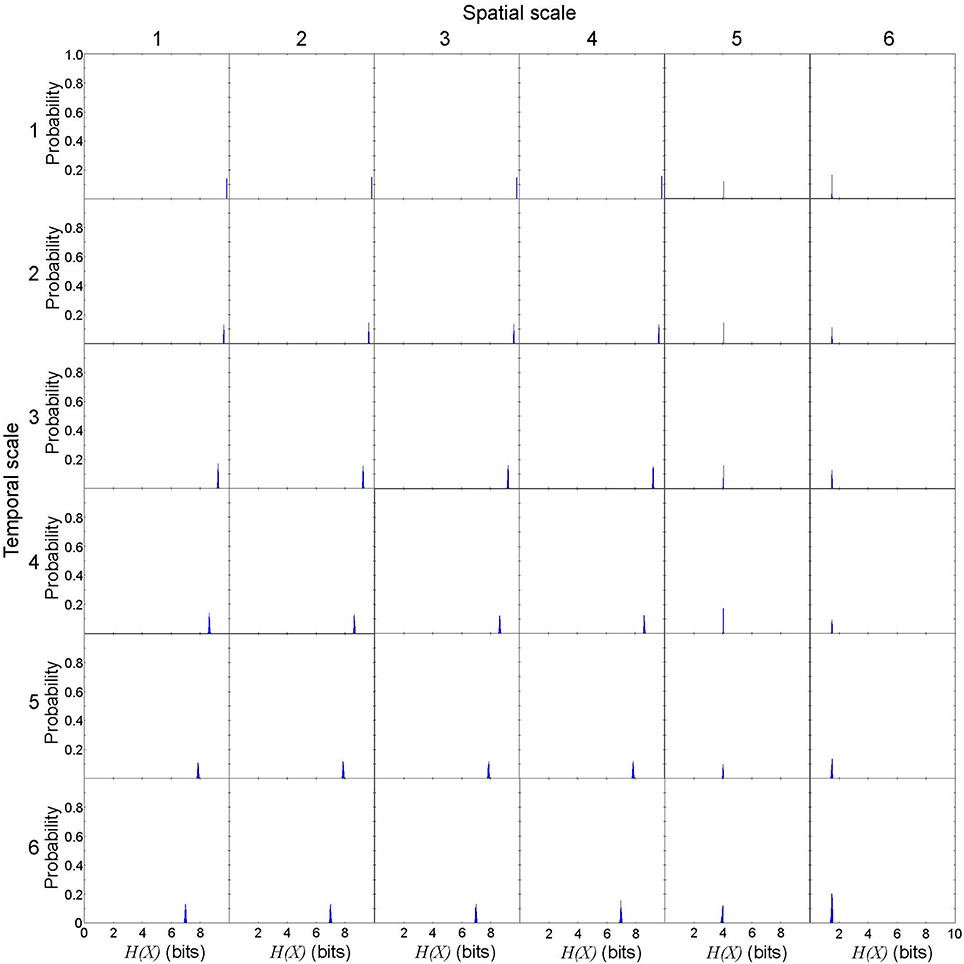
Figure 3. Entropy of unconstrained probability distribution of possible cause X in a representative spiral wave data set. H(X) is not uniquely determined due to the discretization effect, but the variance is small. Each subplot represents he probability distribution of H(X). The columns represent the spatial scales (1 through 6) and the rows represent the temporal scales (1 through 6).

FIGURE 4

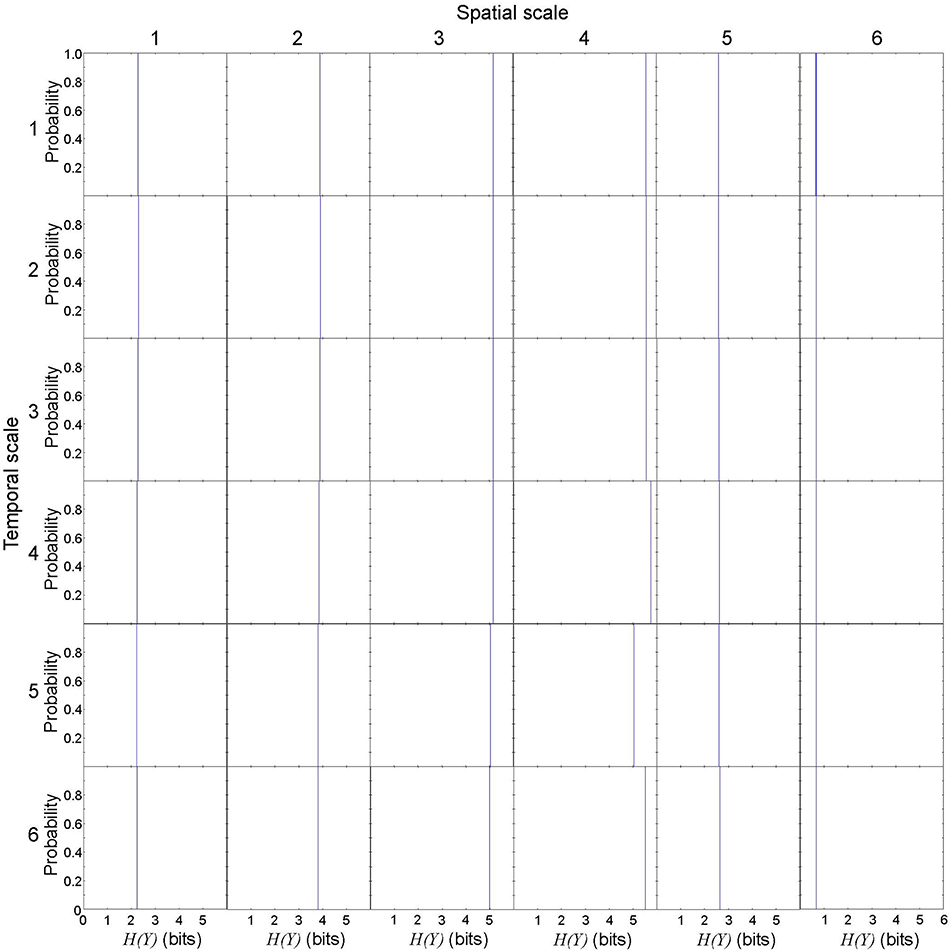
Figure 4. Entropy of specific state of possible effect Y in a representative spiral wave data set. H(Y) is uniquely determined because it represents a specific state of the system regardless of the spatiotemporal scale. Each subplot represents the probability distribution of H(Y). The columns represent the spatial scales (1 through 6) and the rows represent the temporal scales (1 through 6).

FIGURE 5

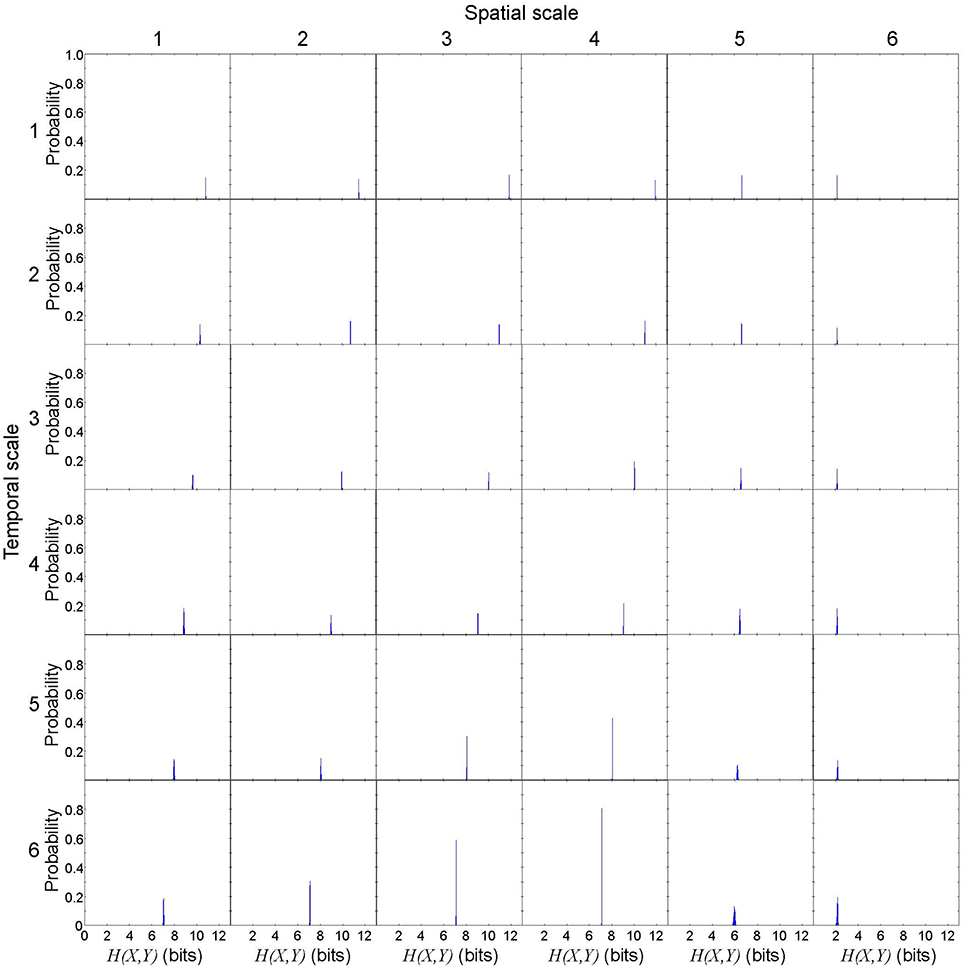
Figure 5. Joint entropy of cause X and effect Y in a representative spiral wave data set. H(X, Y) is not uniquely determined due to the discretization effect, but the variance is small. Each subplot represents the probability distribution of H(X, Y). The columns represent the spatial scales (1 through 6) and the rows represent the temporal scales (1 through 6).

FIGURE 6

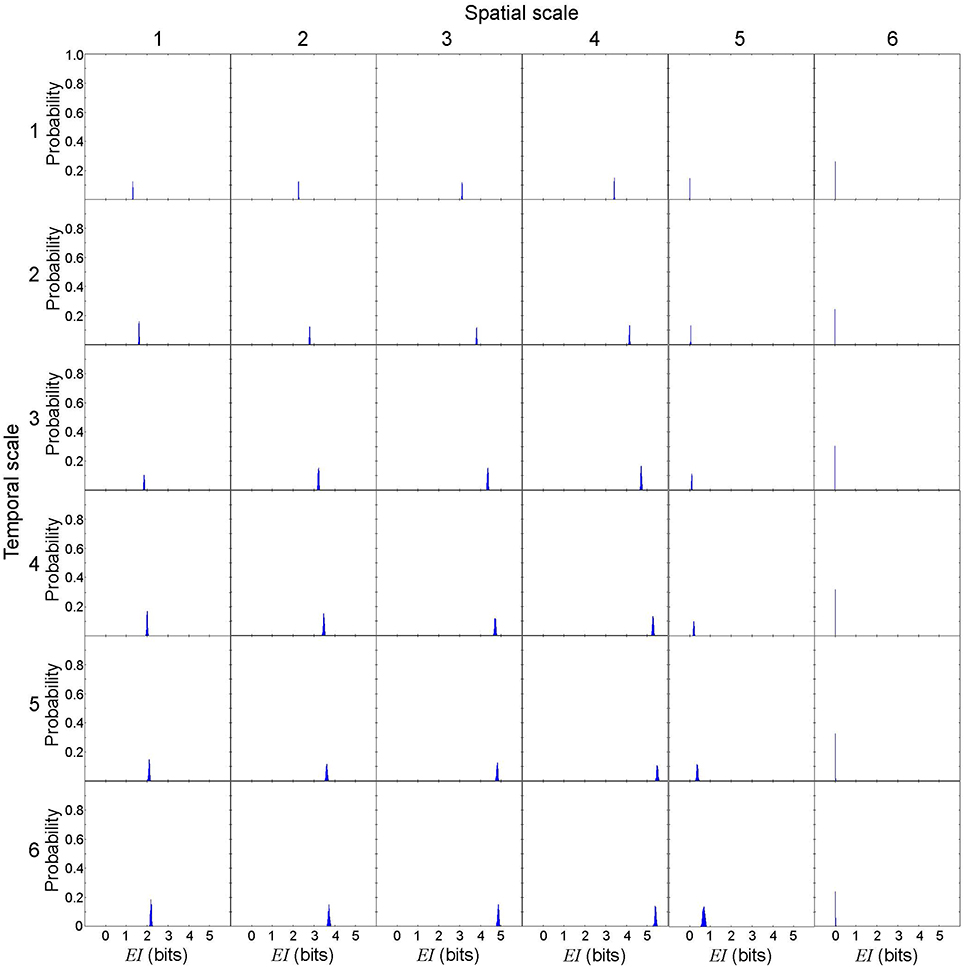
Figure 6. Effective information from cause X to effect Y in a representative spiral wave data set. EI(X → Y)[= I(X; Y) = H(X) + H(Y) − H(X, Y)] is not uniquely determined due to the discretization effect, but the variance is small. Each subplot represents the probability distribution of EI(X → Y). The columns represent the spatial scales (1 through 6) and the rows represent the temporal scales (1 through 6).

3.2. Evaluation of Effective Information in Aggregate Data Sets

Next, we quantified effective information to describe rotor dynamics at each spatiotemporal scale in 1,000 different sets of spiral waves with random initial conditions (Figure 7). This allowed us to analyze the causal architecture of the cardiac system with rotors in aggregate data sets, rather than focusing on one data set with a specific manifestation of rotor dynamics. Overall, effective information increased as the scale increased from microscopic to macroscopic descriptions of the system. However, effective information reached the global maximum at spatial scale = temporal scale = 4, beyond which effective information decreased (Figure 7). This finding indicates that the cardiac system with rotors has the most causal power at at spatial scale = temporal scale = 4. The behavior at this scale causes the behavior at more microscopic (downward causation) and macroscopic scales (upward causation). It is important to note that the scale of peak causation is not the most macroscopic scale (i.e., spatial scale = temporal scale = 6). We also found that the difference in effective information between scales was larger in spatial coarse-graining (Figure 7B) than that of temporal coarse-graining (Figure 7C), indicating that the impact of spatial coarse-graining on effective information was higher than that of temporal coarse-graining.

FIGURE 7

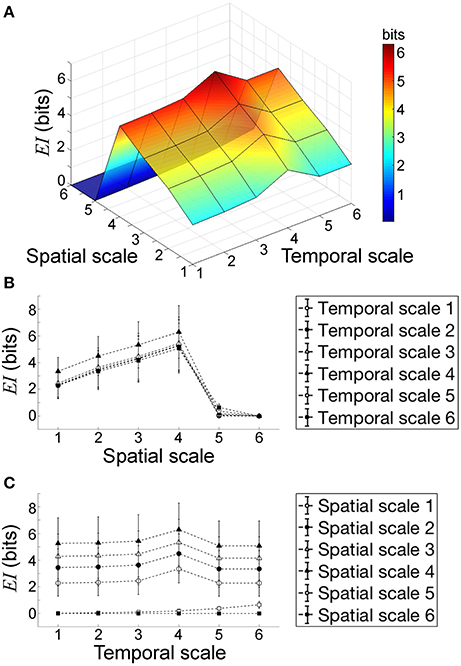
Figure 7. Effective information of the system in aggregate data sets. (A) Overview. Each point indicates the mean effective information EI(X → Y) of 1,000 data sets at each spatiotemporal scale. EI(X → Y) reaches the global maximum at spatial scale = temporal scale = 4. (B) Effective information vs. spatial scale. (C) Effective information vs. temporal. Each point indicates the mean of EI of 1,000 data sets at each spatiotemporal scale.

3.3. Relationship Between the Number of Rotors and Causal Emergence

Lastly, we evaluated the relationship between the number of rotors and causal emergence in the same 1,000 data sets used in section 3.1. This allowed us to relate the causal architecture of the cardiac system to rotor dynamics. The number of rotors ranged from 0 to 7, with a median of 3 (Figure 8). For system descriptions at spatial scale ≤ 4 and temporal scale ≤ 4, causal emergence was positive for all the data sets except a few where a rotor prematurely disappeared on its own (number of rotors ≤ 1, red dots in Figure 9). There was a significant positive correlation between the number of rotors and causal emergence. This finding indicates that rotor dynamics at those scales is an emergent behavior that causes the micro-scale behavior of the system. For system descriptions at spatial scale ≥ 5, causal emergence was negative for all the data sets, and there was a significant negative correlation between the number of rotors and causal emergence. This findings indicates that rotor dynamics at those scales is reducible to the micro-scale behavior of the system. For system descriptions at spatial scale = 1 and temporal scale ≥ 5, causal emergence scatters in positive and negative values. This finding indicates that the causal relationship at those scales is inconsistent. There was a significant negative correlation between the number of rotors and causal emergence at those scales, but the correlation coefficients were small (r = −0.089). For system descriptions at spatial scale = 2, 3, and 4 and temporal scale ≥ 5, causal emergence was almost always positive and there was a significant positive correlation between the number of rotors and causal emergence. This finding indicates that temporal coarse-graining has a smaller impact than spatial coarse-graining on the relationship between the number of rotors and causal emergence. This result is consistent with that of section 3.2.

FIGURE 8

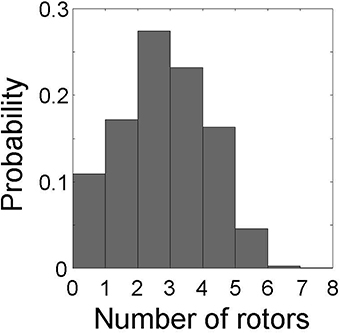
Figure 8. Probability distribution of the number of rotors. The number of rotors ranges from 0 to 7 in 1,000 data sets.

FIGURE 9

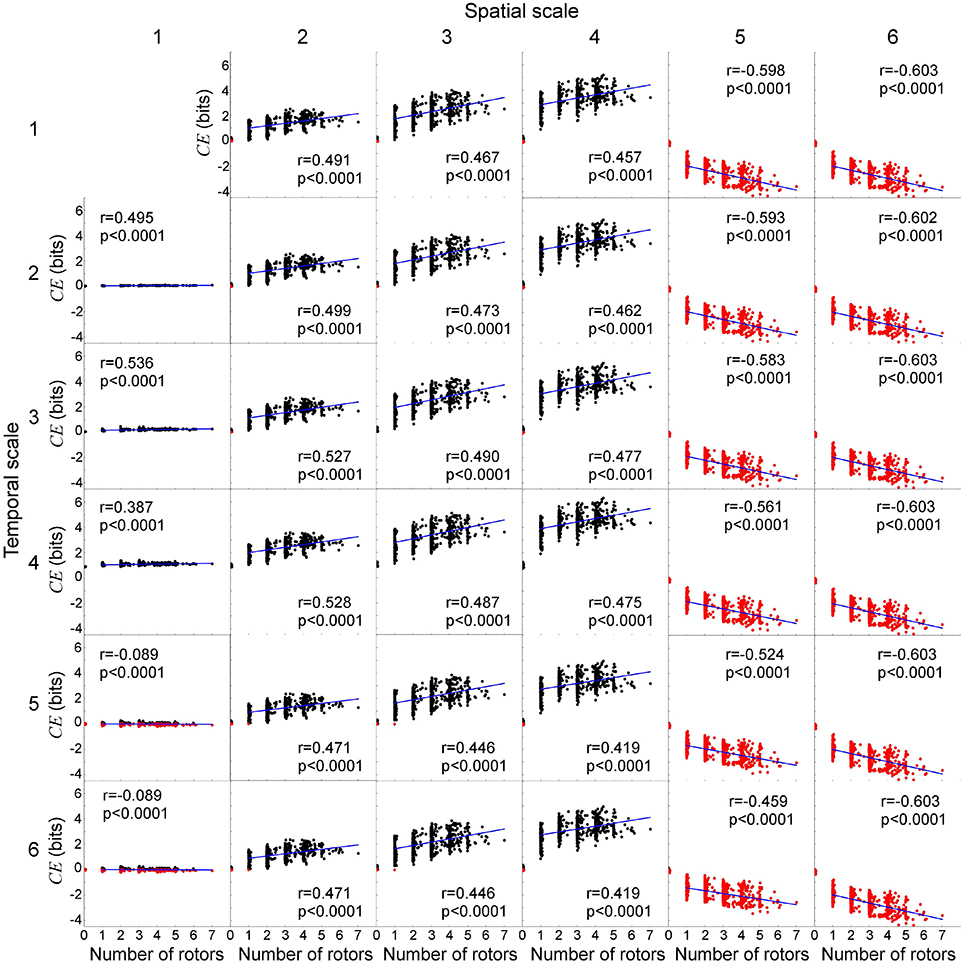
Figure 9. Number of rotors and causal emergence. We quantify causal emergence (CE) with respect to the most microscopic system description at spatial scale = temporal scale = 1. Each subplot represents an association between the number of rotors and CE at each spatiotemporal scale. Black dots indicate CE > 0 (emergence), whereas red dots indicate CE < 0 (reduction). Blue lines indicate linear fit for the number of rotors ≥1. The columns represent the spatial scales (1 through 6) and the rows represent the temporal scales (1 through 6).

4. Discussion

4.1. Main Findings

First, the numerical computation of effective information in the cardiac system with rotors is robust with high reproducibility (Figure 6), despite the discretization effect associated with random generation of the unconstrained probability distribution of possible cause X. Therefore, our effective information measure is a reasonable information-theoretic metric to quantify the information generated for specific dynamics in the cardiac system with rotors at each spatiotemporal scale.

Next, there is a spatiotemporal scale at which effective information peaks in the cardiac system with rotors (Figure 7). This finding indicates that the most causal power of the system does not lie in the most microscopic (i.e., spatial scale = temporal scale = 1) nor the most macroscopic scale (i.e., spatial scale = temporal scale = 6). In other words, both downward and upward causation coexist in the cardiac system with rotors.

Lastly, a positive correlation between the number of rotors and causal emergence is not universally found in all the spatiotemporal scales of the cardiac system (Figure 9). For example, the number of rotors and causal emergence were positively correlated only up to the scale of peak causation, beyond which the correlation is not universally positive. This finding indicates that rotors are not the universal causal mechanism to maintain spiral wave dynamics at all spatiotemporal scales.

4.2. Quantifying Causal Architecture of Cardiac Systems

Our study highlights several innovative aspects. First, we utilized a multi-scale approach by generating a renormalization group where we applied iterated coarse-graining and rescaling [46] to the microscopic description of the cardiac system to construct a series of robust and minimal macroscopic descriptions (Figure 1). In our previous work, we have successfully applied the renormalization group to a cardiac system to quantify inter-scale information flow [29]. In this study, we coarse-grained the system descriptions in both spatial and temporal scales to quantify macro-scale behaviors while reducing the number of degrees of freedom. This approach is different from a conventional and common belief that a detailed, high-resolution modeling with near-complete description of microscopic behaviors with infinite degrees of freedom is required to understand the macroscopic behavior of the cardiac system. Our results suggest that our approach is valid for achieving our aim to understand the macro-micro causal relationship between rotors and spiral waves in the cardiac system.

Second, we validated the robustness of effective information in a cardiac system (Figure 6). Effective information is equal to mutual information I(X; Y) between the source X and the destination Y [30]. Mutual information is a measure of statistical dependence between X and Y [45], and is not a causal measure. However, by choosing X as a uniform probability distribution such that it provides the maximum entropy H(X)_max [44], and Y as a specific state of dynamics, I(X; Y) becomes a causal measure to quantify the information generated from X to Y (Figure 2) [47]. Our results suggest that our effective information measure is robust with high reproducibility. Our results demonstrate that, because effective information sensitively captures the dynamics of the system, it is applicable to any multi-scale systems to quantify the causal architecture.

Lastly, we quantified causal emergence to evaluate the causal relationship between rotors and spiral waves to address whether rotors are the causal mechanism to maintain spiral waves, which is clinically important. Our result was unexpected; yes, rotors are the mechanism to maintain spiral waves, but not at all spatiotemporal scales. This result is consistent with our previous work evaluating inter-scale information flow [29]. Our result makes us reconsider a binary definition of a causal mechanism, where A either is or is not a cause of B. The binary definition of the causal mechanism may be both insensitive and simplistic, failing to capture important features of causal architecture. The finding that rotors are not the universal mechanism to maintain spiral waves at all scales may account for the conflicting benefit of rotor ablation in clinical studies, because the concept of scales has never been introduced as an independent variable in interventional catheter ablation therapy.

4.3. Clinical Implications

Successful treatment of arrhythmia requires targeted elimination of the mechanism that maintains arrhythmia, not the mechanism that triggers it. For example, in Wolff-Parkinson-White (WPW) syndrome, the ablation target is not the premature atrial complexes (PAC) that trigger atrioventricular reciprocating tachycardia (AVRT), one of the simplest forms of anatomical reentry. Instead, successful treatment of AVRT requires elimination of an accessory pathway (AP) connecting the atrium and the ventricle that maintains AVRT [48]. Because the mechanism that maintains AF remains unclear [12], catheter ablation of AF targets focal triggers mainly originating from the pulmonary veins (pulmonary vein isolation, PVI) [49, 50]. This approach remains far from curative, with recurrence rates up to 40% [51].

Our results suggest that the causal architecture analysis may guide the additional strategies of therapeutic intervention of AF, including the posterior wall isolation [52, 53], the stepwise approach [54–56], and the extensive ablation [57]. Those strategies, which are performed in addition to PVI, focus on segmenting the atria by linear lesions to reduce the mass of contiguous atrial tissue below an effective size needed to sustain fibrillation [58]. Up to now, those additional strategies have not produced significantly superior outcomes compared with the standard approach [51]. Because atrial segmentation disrupts the electrical conduction and changes the communication network topology within the atria [59], it is expected to alter the causal architecture of the system as well. Quantitative analysis of the causal architecture of the system using multi-electrode catheters may provide patient-specific diagnostic parameters that could potentially serve as a valid endpoint for therapeutic interventions. Further studies are required to link the causal architecture and clinical outcomes.

4.4. Limitations

We used a modified Fitzhugh-Nagumo model, which is a relatively simple model of excitable media. Because our aim was to study the causal relationship between rotors and spiral waves, we used an isotropic, homogeneous model to avoid confounding the causal architecture by tissue anisotropy and inhomogeneity. Further studies are required to assess the impact of tissue anisotropy and inhomogeneity on the causal relationship between rotors and spiral waves in a more realistic geometry of the heart.

4.5. Conclusions

Rotors are not the universal mechanism to maintain spiral waves at all scales in a cardiac system. This finding may account for the conflicting benefit of rotor ablation in clinical studies.

Author Contributions

HA, FP-C, MK, and ND: jointly conceived research; HA: designed and performed research, analyzed data, and wrote the manuscript; FP-C, MK, and ND: reviewed the manuscript and provided critical intellectual input.

Funding

This work was supported by the Fondation Leducq Transatlantic Network of Excellence (to HA).

Conflict of Interest Statement

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Supplementary Material

The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fphy.2018.00030/full#supplementary-material

Supplementary Movie 1. Random sequential point stimulations. We induce spiral waves by introducing 40 random sequential point stimulations in 40 random components of the lattice. In this example, random sequential point stimulations induce five spiral waves.

Supplementary Movie 2. Renormalzation group. The movie shows a renormalization group of the cardiac system with two spiral waves by a series of transformation including coarse-graining and length rescaling (scale 1 through 6). For each component, the time series of cardiac excitation is descretized to 1 (black) when excited (during the APD at 90% repolarization, or APD₉₀) or 0 (white) when resting.

References

1. Winfree A. Vortex action potentials in normal ventricular muscle. Ann NY Acad Sci. (1990) 591:190–207.

PubMed Abstract | Google Scholar

2. Jalife J, Berenfeld O. Molecular mechanisms and global dynamics of fibrillation: an integrative approach to the underlying basis of vortex-like reentry. J Theor Biol. (2004) 230:475–87. doi: 10.1016/j.jtbi.2004.02.024

PubMed Abstract | CrossRef Full Text | Google Scholar

3. Bedau MA. Weak emergence. Noûs (1997) 31:375–99.

Google Scholar

4. Seth AK. Measuring autonomy and emergence via Granger causality. Artif Life (2010) 16:179–96. doi: 10.1162/artl.2010.16.2.16204

PubMed Abstract | CrossRef Full Text | Google Scholar

5. Bar-Yam Y. Dynamics of Complex Systems. Reading, MA: Addison-Wesley (1997).

Google Scholar

6. Sayama H. Introduction to the Modeling and Analysis of Complex Systems. Geneseo, NY: State University of New York at Geneseo; Open SUNY Textbooks, Milne Library (2015).

Google Scholar

7. Qu Z, Xie F, Garfinkel A, Weiss JN. Origins of spiral wave meander and breakup in a two-dimensional cardiac tissue model. Ann Biomed Eng. (2000) 28:755–71. doi: 10.1114/1.1289474

PubMed Abstract | CrossRef Full Text | Google Scholar

8. Fenton FH, Cherry EM, Hastings HM, Evans SJ. Multiple mechanisms of spiral wave breakup in a model of cardiac electrical activity. Chaos (2002) 12:852–92. doi: 10.1063/1.1504242

PubMed Abstract | CrossRef Full Text | Google Scholar

9. Cabo C, Pertsov AM, Baxter WT, Davidenko JM, Gray RA, Jalife J. Wave-front curvature as a cause of slow conduction and block in isolated cardiac muscle. Circ Res. (1994) 75:1014–28.

PubMed Abstract | Google Scholar

10. Gray R. Theory of rotors and arrhythmias. In: Cardiac Electrophysiology: From Cell to Bedside. New York, NY: WB Saunders Co, Ltd. (2014). p. 341–50.

11. Biktashev VN. Drift of spiral waves. Scholarpedia (2007) 2:1836. doi: 10.4249/scholarpedia.1836

CrossRef Full Text | Google Scholar

12. Lip GYH, Fauchier L, Freedman SB, Van Gelder I, Natale A, Gianni C, et al. Atrial fibrillation. Nat Rev Dis Primers (2016) 2:16016. doi: 10.1038/nrdp.2016.16

CrossRef Full Text | Google Scholar

13. Narayan SM, Krummen DE, Shivkumar K, Clopton P, Rappel WJ, Miller JM. Treatment of atrial fibrillation by the ablation of localized sources: CONFIRM (Conventional Ablation for Atrial Fibrillation With or Without Focal Impulse and Rotor Modulation) trial. J Am Coll Cardiol. (2012) 60:628–36. doi: 10.1016/j.jacc.2012.05.022

PubMed Abstract | CrossRef Full Text | Google Scholar

14. Miller JM, Kowal RC, Swarup V, Daubert JP, Daoud EG, Day JD, et al. Initial independent outcomes from focal impulse and rotor modulation ablation for atrial fibrillation: multicenter FIRM registry. J Cardiovasc Electrophysiol. (2014) 25:921–9. doi: 10.1111/jce.12474

PubMed Abstract | CrossRef Full Text | Google Scholar

15. Narayan SM, Baykaner T, Clopton P, Schricker A, Lalani GG, Krummen DE, et al. Ablation of rotor and focal sources reduces late recurrence of atrial fibrillation compared with trigger ablation alone: extended follow-up of the CONFIRM trial (Conventional Ablation for Atrial Fibrillation With or Without Focal Impulse and Rotor Modulation). J Am Coll Cardiol. (2014) 63:1761–8. doi: 10.1016/j.jacc.2014.02.543

PubMed Abstract | CrossRef Full Text | Google Scholar

16. Haissaguerre M, Hocini M, Denis A, Shah AJ, Komatsu Y, Yamashita S, et al. Driver domains in persistent atrial fibrillation. Circulation (2014) 130:530–8. doi: 10.1161/CIRCULATIONAHA.113.005421

PubMed Abstract | CrossRef Full Text | Google Scholar

17. Benharash P, Buch E, Frank P, Share M, Tung R, Shivkumar K, et al. Quantitative analysis of localized sources identified by focal impulse and roter modulation mapping in atrial fibrillation. Circ Arrhythm Electrophysiol. (2015) 8:554–61. doi: 10.1161/CIRCEP.115.002721

CrossRef Full Text | Google Scholar

18. Gianni C, Mohanty S, Di Biase L, Metz T, Trivedi C, Gökoğlan Y, et al. Acute and early outcomes of focal impulse and rotor modulation (FIRM)-guided rotors-only ablation in patients with nonparoxysmal atrial fibrillation. Heart Rhythm (2016) 13:830–5. doi: 10.1016/j.hrthm.2015.12.028

PubMed Abstract | CrossRef Full Text | Google Scholar

19. Berntsen RF, Håland TF, Skårdal R, Holm T. Focal impulse and rotor modulation as a stand-alone procedure for the treatment of paroxysmal atrial fibrillation: a within-patient controlled study with implanted cardiac monitoring. Heart Rhythm (2016) 13:1768–74. doi: 10.1016/j.hrthm.2016.04.016

PubMed Abstract | CrossRef Full Text | Google Scholar

20. Buch E, Share M, Tung R, Benharash P, Sharma P, Koneru J, et al. Long-term clinical outcomes of focal impulse and rotor modulation for treatment of atrial fibrillation: a multicenter experience. Heart Rhythm (2016) 13:636–41. doi: 10.1016/j.hrthm.2015.10.031

PubMed Abstract | CrossRef Full Text | Google Scholar

21. Aronis KN, Berger RD, Ashikaga H. Rotors: how do we know when they are real? Circ Arrhythm Electrophysiol. (2017) 10:e005634. doi: 10.1161/CIRCEP.117.005634

CrossRef Full Text | Google Scholar

22. Bar-Yam Y. Multiscale complexity/entropy. Advs Complex Syst. (2004) 7:47–63. doi: 10.1142/S0219525904000068

CrossRef Full Text | Google Scholar

23. Allen B, Stacey BC, Bar-Yam Y. Multiscale information theory and the marginal utility of information. Entropy (2017) 19:273. doi: 10.3390/e19060273

CrossRef Full Text | Google Scholar

24. Campbell DT. ‘Downward causation’ in hierarchically organised biological systems. In: Ayala FJ, Dobzhansky T, editors. Studies in the Philosophy of Biology: Reduction and Related Problems. London: Palgrave (1974). p. 179–86.

Google Scholar

25. Auletta G, Ellis GF, Jaeger L. Top-down causation by information control: from a philosophical problem to a scientific research programme. J R Soc Interface (2008) 5:1159–72. doi: 10.1098/rsif.2008.0018

PubMed Abstract | CrossRef Full Text | Google Scholar

26. Davies PCW. The physics of downward causation. In: Clayton P, Davies PCW, editors. The Re-emergence of Emergence. Oxford: Oxford University Press (2006). p. 35–52.

27. Davies PCW. The epigenome and top-down causation. Interface Focus (2011) 2:42–8. doi: 10.1098/rsfs.2011.0070

PubMed Abstract | CrossRef Full Text | Google Scholar

28. Ellis GF. Top-down causation and emergence: some comments on mechanisms. Interface Focus (2011) 2:126–40. doi: 10.1098/rsfs.2011.0062

PubMed Abstract | CrossRef Full Text | Google Scholar

29. Ashikaga H, James RG. Inter-scale information flow as a surrogate for downward causation that maintains spiral waves. arXiv preprint arXiv:171110126. (2017).

Google Scholar

30. Hoel EP, Albantakis L, Tononi G. Quantifying causal emergence shows that macro can beat micro. Proc Natl Acad Sci USA. (2013) 110:19790–5. doi: 10.1073/pnas.1314922110

PubMed Abstract | CrossRef Full Text | Google Scholar

31. Tononi G, Sporns O. Measuring information integration. BMC Neurosci. (2003) 4:31. doi: 10.1186/1471-2202-4-31

PubMed Abstract | CrossRef Full Text | Google Scholar

32. Nagumo J, Arimoto S, Yoshizawa S. An active pulse transmission line simulating nerve axon. Proc IRE (1962) 50:2061–70.

Google Scholar

33. FitzHugh R. Impulses and physiological states in theoretical models of nerve membrane. Biophys J. (1961) 1:445.

PubMed Abstract | Google Scholar

34. Rogers JM, McCulloch AD. A collocation-Galerkin finite element model of cardiac action potential propagation. IEEE Trans Biomed Eng. (1994) 41:743–57.

PubMed Abstract | Google Scholar

35. Pertsov AM, Davidenko JM, Salomonsz R, Baxter WT, Jalife J. Spiral waves of excitation underlie reentrant activity in isolated cardiac muscle. Circ Res. (1993) 72:631–50.

PubMed Abstract | Google Scholar

36. Ashikaga H, James RG. Hidden structures of information transport underlying spiral wave dynamics. Chaos (2017) 27:013106. doi: 10.1063/1.4973542

PubMed Abstract | CrossRef Full Text | Google Scholar

37. Umapathy K, Nair K, Masse S, Krishnan S, Rogers J, Nash MP, et al. Phase mapping of cardiac fibrillation. Circ Arrhythm Electrophysiol. (2010) 3:105–14. doi: 10.1161/CIRCEP.110.853804

PubMed Abstract | CrossRef Full Text | Google Scholar

38. Winfree AT. When Time Breaks Down: The Three-Dimensional Dynamics of Electrochemical Waves and Cardiac Arrhythmias. Princeton, NJ: Princeton University Press (1987).

39. Goryachev A, Kapral R. Spiral waves in chaotic systems. Phys Rev Lett. (1996) 76:1619.

PubMed Abstract | Google Scholar

40. Mermin ND. The topological theory of defects in ordered media. Rev Moder Phys. (1979) 51:591.

Google Scholar

41. Bray MA, Wikswo JP. Use of topological charge to determine filament location and dynamics in a numerical model of scroll wave activity. IEEE Trans Biomed Eng. (2002) 49:1086–93. doi: 10.1109/TBME.2002.803516

PubMed Abstract | CrossRef Full Text | Google Scholar

42. Aronis KN, Ashikaga H. Impact of number of co-existing rotors and inter-electrode distance on accuracy of rotor localization. J Electrocardiol. (2018) 51:82–91. doi: 10.1016/j.jelectrocard.2017.08.032

PubMed Abstract | CrossRef Full Text | Google Scholar

43. Ashikaga H, Aguilar-Rodríguez J, Gorsky S, Lusczek E, Marquitti FMD, Thompson B, et al. Modelling the heart as a communication system. J R Soc Interface (2015) 12:20141201. doi: 10.1098/rsif.2014.1201

PubMed Abstract | CrossRef Full Text | Google Scholar

44. Jaynes ET. Information theory and statistical mechanics. Phys Rev. (1957) 106:620.

Google Scholar

45. Shannon CE. A mathematical theory of communication. Bell Syst Tech J. (1948) 27:623–56.

Google Scholar

46. Kadanoff LP. Scaling laws for Ising models near Tc. Physics (1966) 2: 263–72.

Google Scholar

47. Hoel EP. When the map is better than the territory. Entropy (2017) 19:188. doi: 10.3390/e19050188

CrossRef Full Text | Google Scholar

48. Page RL, Joglar JA, Caldwell MA, Calkins H, Conti JB, Deal BJ, et al. 2015 ACC/AHA/HRS Guideline for the Management of Adult Patients with Supraventricular Tachycardia: a Report of the American College of Cardiology/American Heart Association Task Force on Clinical Practice Guidelines and the Heart Rhythm Society. Heart Rhythm (2016) 13:e136–221. doi: 10.1161/CIR.0000000000000310

CrossRef Full Text | Google Scholar

49. Haissaguerre M, Jaïs P, Shah DC, Takahashi A, Hocini M, Quiniou G, et al. Spontaneous initiation of atrial fibrillation by ectopic beats originating in the pulmonary veins. N Engl J Med. (1998) 339:659–66.

PubMed Abstract | Google Scholar

50. Calkins H, Hindricks G, Cappato R, Kim YH, Saad EB, Aguinaga L, et al. 2017 HRS/EHRA/ECAS/APHRS/SOLAECE expert consensus statement on catheter and surgical ablation of atrial fibrillation. Heart Rhythm (2017) 14:e275–444. doi: 10.1016/j.hrthm.2017.05.012

PubMed Abstract | CrossRef Full Text | Google Scholar

51. Verma A, Jiang Cy, Betts TR, Chen J, Deisenhofer I, Mantovan R, et al. Approaches to catheter ablation for persistent atrial fibrillation. N Engl J Med. (2015) 372:1812–22. doi: 10.1056/NEJMoa1408288

PubMed Abstract | CrossRef Full Text | Google Scholar

52. Sanders P, Hocini M, Jaïs P, Sacher F, Hsu LF, Takahashi Y, et al. Complete isolation of the pulmonary veins and posterior left atrium in chronic atrial fibrillation. Long-term clinical outcome. Eur Heart J. (2007) 28:1862–71. doi: 10.1093/eurheartj/ehl548

PubMed Abstract | CrossRef Full Text | Google Scholar

53. Chen J, Off MK, Solheim E, Schuster P, Hoff PI, Ohm OJ. Treatment of atrial fibrillation by silencing electrical activity in the posterior inter-pulmonary-vein atrium. Europace (2008) 10:265–72. doi: 10.1093/europace/eun029

PubMed Abstract | CrossRef Full Text | Google Scholar

54. Jaïs P, Hocini M, Hsu LF, Sanders P, Scavee C, Weerasooriya R, et al. Technique and results of linear ablation at the mitral isthmus. Circulation (2004) 110:2996–3002. doi: 10.1161/01.CIR.0000146917.75041.58

PubMed Abstract | CrossRef Full Text | Google Scholar

55. Fassini G, Riva S, Chiodelli R, Trevisi N, Berti M, Carbucicchio C, et al. Left mitral isthmus ablation associated with PV isolation: long-term results of a prospective randomized study. J Cardiovasc Electrophysiol. (2005) 16:1150–6. doi: 10.1111/j.1540-8167.2005.50192.x

PubMed Abstract | CrossRef Full Text | Google Scholar

56. Scherr D, Khairy P, Miyazaki S, Aurillac-Lavignolle V, Pascale P, Wilton SB, et al. Five-year outcome of catheter ablation of persistent atrial fibrillation using termination of atrial fibrillation as a procedural endpoint. Circ Arrhythm Electrophysiol. (2015) 8:18–24. doi: 10.1161/CIRCEP.114.001943

PubMed Abstract | CrossRef Full Text | Google Scholar

57. Di Biase L, Burkhardt JD, Mohanty P, Mohanty S, Sanchez JE, Trivedi C, et al. Left atrial appendage isolation in patients with longstanding persistent AF undergoing catheter ablation: BELIEF trial. J Am Coll Cardiol. (2016) 68:1929–40. doi: 10.1016/j.jacc.2016.07.770

PubMed Abstract | CrossRef Full Text | Google Scholar

58. Panfilov AV. Is heart size a factor in ventricular fibrillation? Or how close are rabbit and human hearts? Heart Rhythm (2006) 3:862–4. doi: 10.1016/j.hrthm.2005.12.022

PubMed Abstract | CrossRef Full Text | Google Scholar

59. Tao S, Way SF, Garland J, Chrispin J, Ciuffo LA, Balouch MA, et al. Ablation as targeted perturbation to rewire communication network of persistent atrial fibrillation. PLoS ONE (2017) 12:e0179459. doi: 10.1371/journal.pone.0179459

PubMed Abstract | CrossRef Full Text | Google Scholar