Closed, Two Dimensional Surface Dynamics

We present dynamic equations for two dimensional closed surfaces and analytically solve it for some simplified cases. We derive final equations for surface normal motions by two different ways. The solution of the equations of motions in normal direction indicates that any closed, two dimensional, homogeneous surface with time invariable surface energy density adopts constant mean curvature shape when it comes in equilibrium with environment. In addition, we show that the shape equation is an approximate solution to our equation of motion in the normal direction and is valid for stationary or near to stationary shapes. As an example, we apply the formalism to analyze equilibrium shapes of micelles and explain why they adopt spherical, lamellar, and cylindrical shapes. Theoretical calculation for micellar optimal radius is in good agreement with all atom simulations and experiments.

1. Introduction

Biological systems exhibit a variety of morphologies and experience large shape deformations during a motion. Such “choreography” of shape motility is characteristic not only for all living organisms and cells [1] but also for proteins, nucleic acids, and to all biomacromolecules in general. Shape motility, which is a motion of two-dimensional surfaces, may be a result of active (by consuming energy) or passive (without consuming energy) processes. The time scale for shape dynamics may vary from slow (nanometer per nanoseconds) to very fast (nanometer per femtosecond) [2, 3]. Slowly moving surfaces are considered as overdamped systems. An example is cell motility. In that case one may use well developed the Helfrich formalism to describe the motion, where free energy expansion in powers of the curvature tensor gives coarse-grained modeling of membranes [4]. However, while the formalism [4] are applicable to slowly moving surfaces they are not applicable to fast moving surfaces, where biomolecules could be fitted. Surface dynamics for proteins or DNA [2, 3] may reach nm/fs range. So that surfaces may be represented as virtual three dimensional pseudo Riemannian manifolds. We derived fully generic equations of motions for three manifolds [5], but purposefully omitted lengthy discussion about motion of two-dimensional surfaces, which is a topic for this paper.

Currently, significant progress on fluidic models of membrane dynamics has already been made. The role of geometric constraints in self-assembly have been elucidated by linking together thermodynamics, interaction free energies, and geometry [6, 7]. The Helfrich formalism provides the foundation for a purely differential geometric approach whereby the membrane surface potential energy density is considered as a functional of the static curvature [4], see also review papers [8–10]. The model has been improved by adding force and torque balance equations [11, 12]. Specific dynamical equations accounting for bending as well as electrodynamic effects have also been reported [13–15]. Furthermore, active membrane theories, by including external forces, have extended the understanding of passive membranes [16–19].

Among the remarkable aspects of the fluid lipid membranes deduced from the large body of theoretical works [8–10], is that the physical behavior of a membrane on the length scale of its own thickness, in first approximation, can be expressed by a purely geometric Hamiltonian [4, 20, 21]. Associated Euler-Lagrange equations [22, 23], so called “shape equations,” are fourth order partial nonlinear differential equations, and finding a general analytical solution is typically difficult, even though it has been analytically [24] and numerically solved for some specific [25–32] and general cases [33, 34].

In fluid dynamics, material particles can be treated as a vertex of geometric figure and virtual layers as surfaces and equations of motion for such surfaces can be searched. We refer to the formalism as differentially variational surfaces (DVS) (or DVS formalism) [5].

In this paper, we propose different approach to the “shape choreography” problem. We use DVS formalism, tensor calculus of moving surfaces and the first law of thermodynamics to derive the final equation for the closed 2D surface dynamics (later on referred as a surface) and to solve it analytically for the equilibrium case. In other words, we derive generic equations of motions for closed two-dimensional surfaces and without any a priori symmetric assumptions, we show that constant mean curvature shapes are equilibrium solutions. In contrast to the Young-Laplace law these solutions, are universally correct descriptions of capillary surfaces as well as molecular surfaces. In addition, our equations of motions (20–25) are generic and exact. It advances our understanding of fluid dynamics because generalizes ideal magneto-hydrodynamic and Naiver-Stokes equations [5] and in contrast to Navier-Stokes, as we demonstrate in this paper, are trivially solvable for equilibrium shapes. To demonstrate the validity of these equations and their analytical solutions we apply them to micelles. Within our formalism it becomes simple task to show micelles lamellar, cylindrical, spherical shapes, and assert their optimal spherical radius.

For clarity, we shall give brief description of micelles and their structures. A micelle consists of monolayer of lipid molecules containing hydrophilic head and hydrophobic tail. These amphiphilic molecules, in aqueous environment, aggregate spontaneously into a monomolecular layer held together due to a hydrophobic effect [35, 36] (see also 5, 37–40) by weak non-covalent forces [41]. They form flexible, diverse surfaces with different topology, but remarkably in thermodynamic equilibrium conditions they are spherical, lamellar (plane), or cylindrical in shape.

2. Methods

In the section we provide basics of tensor calculus for moving surfaces and summarize the theorems we used directly or indirectly to derive equations for two-dimensional surface dynamics. Differential geometry preliminaries we used here are available in tensor calculus textbook [42] and in our work [5].

2.1. Basics of Differential Geometry

Let Sⁱ (i = 1, 2) be the coordinates of the moving surface S and X^α be the coordinates in the ambient Euclidean space (Figure 1). The surface is smooth enough for sufficient differentiability in space-time and it is expressed as X^α = X^α(t, Sⁱ) in the ambient coordinates. The surface equation for the position vector $\overrightarrow{R}$ is¹:

$\begin{array}{ll}\overrightarrow{R}=\overrightarrow{R}(X^{\alpha })=\overrightarrow{R}(t,S^i)& (1)\end{array}$

FIGURE 1

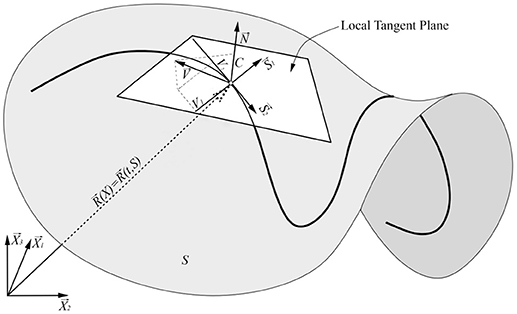
Figure 1. Graphical illustration of the arbitrary surface and its' local tangent plane. ${\overrightarrow{S}}_1,{\overrightarrow{S}}_2,\overrightarrow{N}$ are local tangent plane base vectors and local surface normal, respectively. ${\overrightarrow{X}}_1,{\overrightarrow{X}}_2,{\overrightarrow{X}}_3$ are arbitrary base vectors of the ambient Euclidean space and $\overrightarrow{R}=\overrightarrow{R}\left(X\right)=\overrightarrow{R}\left(t,S\right)$ is radius vector of the point. $\overrightarrow{V}$ is arbitrary surface velocity and C, V₁, V₂ display projection of the velocity to the $\overrightarrow{N},{\overrightarrow{S}}_1,{\overrightarrow{S}}_2$ directions, respectively.

A dot product of the covariant bases ${\overrightarrow{X}}_{\alpha }={\partial }_{\alpha }\overrightarrow{R}$ is a metric tensor:

$\begin{array}{ll}{X}_{\alpha \beta }={\overrightarrow{X}}_{\alpha }{\overrightarrow{X}}_{\beta }& (2)\end{array}$

where ${\partial }_{\alpha }=\partial /\partial X^{\alpha }$. The matrix inverse of the covariant metric forms the contravariant one: $X^{\alpha \beta }{X}_{\beta \gamma }={\delta }_{\gamma }^{\alpha }$ (the Kronecker delta ${\delta }_{\gamma }^{\alpha }$). In the ambient Euclidean space, due to mutual linear independence of the base vectors, the Christoffel symbols ${\Gamma }_{\beta \gamma }^{\alpha }={\overrightarrow{X}}^{\alpha }·{\partial }_{\beta }{\overrightarrow{X}}_{\gamma }$ are zeros and, therefore, covariant/contravariant derivatives become partial ones ∇_α = ∂_α.

The surface base vectors $\overrightarrow{S_i}={\partial }_i\overrightarrow{R}$ and metric tensors $S_{ij},S^{ij}$ are similarly defined

$\begin{array}{ll}{S}_{ij}={\overrightarrow{S}}_i·{\overrightarrow{S}}_j& (3)\end{array}$

where ${\partial }_i=\partial /\partial S^i$ and $S_{ab}{S}^{bc}={\delta }_a^c$. The surface Christoffel symbols given by ${\Gamma }_{jk}^i={\overrightarrow{S}}^i·{\partial }_j{\overrightarrow{S}}_k$ are not zeros and covariant/contravariant derivatives differ from partial ones ∇_i ≠ ∂_i. The space/surface Christoffel symbols form the basic concept for defining curvilinear derivatives on mixed space/surface tensors:

$\begin{array}{l}{\nabla }_i{T}_{\beta k}^{\alpha j}={\partial }_i{T}_{\beta k}^{\alpha j}+X_i^{\gamma }{\Gamma }_{\gamma \nu }^{\alpha }{T}_{\beta k}^{\nu j}-X_i^{\gamma }{\Gamma }_{\gamma \beta }^{\mu }{T}_{\mu k}^{\alpha j}+\\ {\Gamma }_{im}^j{T}_{\beta k}^{\alpha m}-{\Gamma }_{ik}^m{T}_{\beta m}^{\alpha j}& (4)\end{array}$

where $X_i^{\gamma }$ is the shift tensor, so that

${\overrightarrow{S}}_i=X_i^{\alpha }{\overrightarrow{X}}_{\alpha }$ and $S_{ij}={\overrightarrow{S}}_i·{\overrightarrow{S}}_j=X_i^{\alpha }{\overrightarrow{X}}_{\alpha }{X}_j^{\beta }{\overrightarrow{X}}_{\beta }=X_i^{\alpha }{X}_j^{\beta }{X}_{\alpha \beta }$. Note that in (4) the Christoffel symbols with Greek indexes are zeros.

Using (2, 4), one may directly prove metrilinic property of the surface metric tensor ∇_iS_mn = 0, from where follows ${\overrightarrow{S}}_m·{\nabla }_i{\overrightarrow{S}}_n=0$, meaning that ${\overrightarrow{S}}_m\perp {\nabla }_i{\overrightarrow{S}}_n$ are orthogonal vectors, therefore:

$\begin{array}{ll}{\nabla }_i{\overrightarrow{S}}_j=\overrightarrow{N}{B}_{ij}& (5)\end{array}$

where $\overrightarrow{N}$ is an unit surface normal and B_ij is the symmetric curvature tensor. The trace of the mixed curvature tensor is the mean curvature $B_i^i$ and the determinant is the Gaussian curvature. A particular case:

$\begin{array}{ll}{B}_i^i=\lambda & (6)\end{array}$

where λ is some non-zero constant is a sphere if the surface is closed. According to (5, 6), finding the curvature tensor non-directly implies identification of the surface.

2.2. Basics of Tensor Calculus for Moving Surfaces

All Equations written above are generally true for moving surfaces. We now turn to a brief review of definitions of coordinate velocity V^α, interface velocity C (which is the same as normal velocity), tangent velocity Vⁱ (Figure 1), time derivatives of the surface tensors and the space/surface integrals. The original definitions can be found in textbooks [42, 43].

Suppose that V^α is the coordinate velocity defined as:

$\begin{array}{ll}{V}^{\alpha }=\frac{\partial X^{\alpha }}{\partial t}& (7)\end{array}$

Then, given that the position vector $\overrightarrow{R}$ (1) is tracking the coordinate particle Sⁱ the surface velocity can be written as:

$\begin{array}{ll}\overrightarrow{V}=\frac{\partial \overrightarrow{R}(t,S^i)}{\partial t}=\frac{\partial \overrightarrow{R}}{\partial X^{\alpha }}\frac{\partial X^{\alpha }(t,S^i)}{\partial t}=V^{\alpha }{\overrightarrow{X}}_{\alpha }& (8)\end{array}$

Therefore, V^α is ambient component of the surface velocity $\overrightarrow{V}$. Taking into account (8) the surface normal velocity C can be represented as:

$\begin{array}{ll}C=\overrightarrow{V}·\overrightarrow{N}=V_{\alpha }{\overrightarrow{X}}^{\alpha }{N}^{\beta }{\overrightarrow{X}}_{\beta }=V_{\alpha }{N}^{\beta }{\delta }_{\beta }^{\alpha }=V_{\alpha }{N}^{\alpha }& (9)\end{array}$

C is called the interface velocity, is invariant and its sign depends on the choice of the surface normal. The surface velocity projection on the tangent plane (Figure 1) is Vⁱ the tangential velocity:

$\begin{array}{ll}{V}^i=V^{\alpha }{X}_{\alpha }^i& (10)\end{array}$

Taking (9, 10) into account one may write the surface velocity as $\overrightarrow{V}=C\overrightarrow{N}+V^i{\overrightarrow{S}}_i$.

FIGURE 2

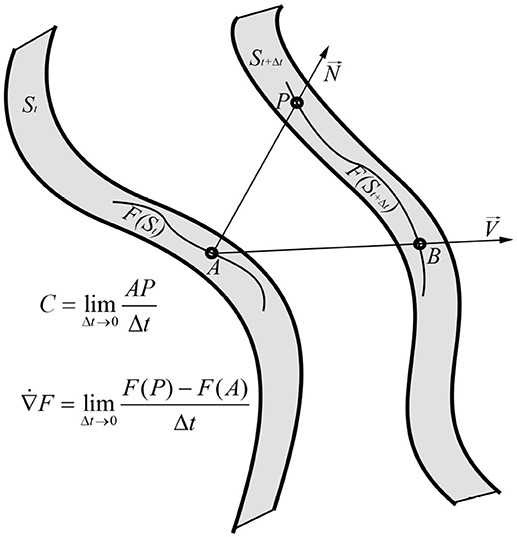
Figure 2. Geometric interpretation of the interface velocity C and of the curvilinear time derivative $\dot{\nabla }$ applied to invariant field F. A is arbitrary chosen point so that it lays on F(S_t) ∈ S_t curve and B is its' corresponding point on the S_t+Δt surface. P is the point where S_t surface normal, applied on the point A, intersects the surface S_t+Δt. By the geometric construction, for small enough Δt → 0, ∠APB → π/2, $\overrightarrow{AB}\approx \overrightarrow{V}\Delta t$, and $AP\approx \overrightarrow{V}\overrightarrow{N}\Delta t$. On other hand, by the same geometric construction the field F in the point B can be estimated as F(B) ≈ F(A)+Δt∂F/∂t, while from viewpoint of the S_t+Δt surface the F(B) value can be estimated as $F\left(P\right)+\Delta t{V}^i{\nabla }_{i}F$, where ∇_iF shows rate of change in F ∈ S_t+Δt and along the BP ≈ ΔtVⁱ.

The surface velocity in general and the interface velocity in particular has clear geometric interpretation. Suppose that the surfaces at the two nearby moments of time t, t+Δt are S_t, S_t+Δt. Then, for any arbitrarily chosen A ∈ S_t and the corresponding point B ∈ S_t+Δt the vector $\overrightarrow{AB}$ is approximately the surface velocity times increment of time: $\overrightarrow{AB}\approx \overrightarrow{V}\Delta t$ (Figure 2). If the P is the point where the surface normal $\overrightarrow{N}\in S_t$ intersects the surface S_t+Δt, then for infinitely small Δt, ∠APB → π/2 and $AP\to \overrightarrow{V}·\overrightarrow{N}\Delta t$, therefore:

$\begin{array}{ll}C={\displaystyle \underset{\Delta t\to 0}{lim}}\frac{AP}{\Delta t}& (11)\end{array}$

The interface velocity C is the instantaneous velocity of the interface in the normal direction.

2.3. Invariant Time Differentiation

Among the key definitions in calculus for moving surfaces, perhaps one of the most important is the invariant time derivative $\dot{\nabla }$. As we have already stated, invariant time derivative is already well defined in the literature [42, 43]. In this paragraph, we just give geometrically intuitive definition.

Let take smooth functional F defined on the surface F ∈ S_t. The invariant time derivative has to be defined so that: (1) it is free from choice of a reference frame (invariance) and (2) properly takes into account deformations along the normal. We explain importance of normal deformations in integration subsection. This can be achieved by following geometric construction: for an arbitrary chosen point A from the S_t surface A ∈ S_t let us find points B ∈ S_t+Δt and P so that the B is the intersection of the surface velocity to the S_t+Δt and the P is intersection of the surface normal to the S_t+Δt (Figure 2). Then, the invariant time derivative $\dot{\nabla }$ can be defined as:

$\begin{array}{ll}\dot{\nabla }F={\displaystyle \underset{\Delta t\to 0}{lim}}\frac{F(P)-F(A)}{\Delta t}& (12)\end{array}$

(12) is geometric, therefore must be an invariant. From the geometric construction (12) one can estimate value of F in point B, so that

$\begin{array}{ll}F(B)\approx F(A)+\Delta t\frac{\partial F}{\partial t}& (13)\end{array}$

B, P ∈ S_t+Δt are nearby points, therefore according to the definition of covariant derivative F(B) can be estimated as:

$\begin{array}{ll}F(B)\approx F(P)+\Delta t{V}^i{\nabla }_{i}F& (14)\end{array}$

since ∇_iF shows rate of change in F ∈ S_t+Δt and Δt·Vⁱ indicates BP. Determining F(A), F(P) values from (13, 14) and putting it in (12), gives

$\begin{array}{ll}\dot{\nabla }F=\frac{\partial F}{\partial t}-V^i{\nabla }_{i}F& (15)\end{array}$

The definition (15) extends for space/surface mixed tensors by the following formula:

$\begin{array}{l}\dot{\nabla }{T}_{\beta j}^{\alpha i}=\frac{\partial T_{\beta j}^{\alpha i}}{\partial t}-V^k{\nabla }_k{T}_{\beta j}^{\alpha i}+V^{\gamma }{\Gamma }_{\gamma \mu }^{\alpha }{T}_{\beta j}^{\mu i}-V^{\gamma }{\Gamma }_{\gamma \beta }^{\mu }{T}_{\mu j}^{\alpha i}\\ +{\dot{\Gamma }}_k^i{T}_{\beta j}^{\alpha k}-{\dot{\Gamma }}_j^k{T}_{\beta k}^{\alpha i}& (16)\end{array}$

where analog of the Christoffel symbol ${\dot{\Gamma }}_j^i$ for moving surfaces is defined by the formula ${\dot{\Gamma }}_j^i={\nabla }_j{V}^i-C{B}_j^i$. The derivative (16) satisfies: commutativity with the contraction, product and chain rules, metrilinic properties against the ambient metric and does not commute with the surface derivative [42]. According to (12) the invariant time derivative vanishes when applied to time independent scalars.

2.4. Time Differentiation of Integrals

The calculus of moving surfaces are effective due to two fundamental theorems about taking time derivatives of space and surface integrals [42]. In evaluation of the least action principle of the Lagrangian there is a central role for time differentiation of the surface and the space integrals, from where the geometry dependence is rigorously clarified.

Let the scalar field F = F(t, S) be defined on an Euclidean domain Ω which has the surface boundary S and the surface evolves with the interface velocity C while volume moves (expands or shrinks). Analogically suppose that the closed surface evolves and F = F(t, S) is again some scalar functional defined on the evolving surface S. Then, there are theorems for taking derivative of space and surface integrals from F integrand:

$\begin{array}{ll}\frac{d}{dt}{\displaystyle {\int }_{\Omega }}Fd\Omega ={\displaystyle {\int }_{\Omega }}\frac{\partial F}{\partial t}d\Omega +{\displaystyle {\int }_S}CFdS& (17)\end{array}$

$\begin{array}{ll}\frac{d}{dt}{\displaystyle {\int }_S}FdS={\displaystyle {\int }_S}\dot{\nabla }FdS-{\displaystyle {\int }_S}CF{B}_i^{i}dS& (18)\end{array}$

On the right hand side of (17, 18) the first terms indicate how the scalar field changes and the second terms show how geometry evolves. There are rigorous mathematical proofs of these formulas in the tensor calculus textbooks; we do not reproduce them here. Instead, we intuitively show why only interface velocity has to be taken into account. Rigorous mathematical proof follows from fundamental theorem of calculus

$\begin{array}{ll}\frac{d}{dt}{\displaystyle {\int }_a^{b(t)}}F(t,x)dx={\displaystyle {\int }_a^{b(t)}}\frac{\partial F(t,x)}{\partial t}dx+b^{\prime }(t)F(t,b(t))& (19)\end{array}$

In the case of volume integral or surface integral it can be shown that b′(t) is replaced by interface velocity C.

Intuitive explanation is pretty simple. Propose there is no interface velocity then closed surface velocity only has tangent component. For each given time tangent velocity (if there is no interface velocity) translates each point to its neighboring point and therefore, does not add new area to the closed surface (or new volume to the closed space, or new length to the closed curve). As so, tangential velocity just induces rotational movement (or uniform translational motion) of the object and can be excluded from additive terms in the integration. Perhaps, it is easier to understand this statement for one dimensional motion. Let's assume that material point is moving along some trajectory (some closed curve or loop), then, in each point, the velocity of the material point is tangential to the curve. Now one can translate this motion into the motion of the closed curve where the loop has only tangential velocity. In this aspect, the embedded loop only rotates (uniformly translates in the plane) without changing the length locally, therefore tangential velocity of the curve does not add new length to the curve (same is true for open curve with fixed ends).

3. General Equations of Surface Motions

Fully non-restrained and exact equations for moving three-dimensional surfaces in electromagnetic field, when the interaction with an ambient environment is ignored, reads

$\begin{array}{ll}\dot{\nabla }\rho +{\nabla }_i(\rho V^i)=\rho C{B}_i^i& (20)\end{array}$

$\begin{array}{l}{\partial }_{\alpha }(\rho V^{\alpha }(\dot{\nabla }C+2V^i{\nabla }_{i}C+V^i{V}^j{B}_{ij})\\ -V^{\alpha }(\frac{1}{4{\mu }_0}{F}_{\mu \nu }{F}^{\mu \nu }+A_{\mu }{J}^{\mu }))=fa& (21)\end{array}$

$\begin{array}{ll}{\displaystyle {\int }_S}\rho V_i(\dot{\nabla }{V}^i+V^j{\nabla }_j{V}^i-C{\nabla }^{i}C-C{V}^j{B}_j^i)dS={\displaystyle {\int }_{\Omega }}{f}^i{a}_{i}d\Omega & (22)\end{array}$

where ρ is the surface mass density, V^α, Vⁱ are coordinate and tangential components of the surface velocity, C is interface velocity, α = 0, 1, 2, 3 for Minkowski four-dimensional space-time ambient space, i = 0, 1, 2 for pseudo-Riemannian manifold (surface), B_ij is the surface curvature tensor, F^μν is electromagnetic tensor, $F^{\alpha }=J^{\alpha }-{\partial }_{\beta }{F}^{\beta \alpha }$, J^α is α component of $\overrightarrow{J}=\left(J^{\alpha }\right)$ four current, f, fⁱ are normal and tangential components of $\overrightarrow{F}=\left(F^{\alpha }\right)$, a, a_i are the normal and the tangential components of the $\partial \overrightarrow{A}/\partial t$ (here $\overrightarrow{A}=\left(A_{\alpha }\right)$ is four vector), S, Ω stand for the surface and the space integrals, respectively. The exact derivation of (20–22) is given in our work [5], we do not reproduce derivation of this set in this paper, rather just mention that first one is the consequence of mass conservation, second and third equations come from minimum action principle of a Lagrangian and imply motion in normal direction (21) and in tangent direction (22). For two dimensional surface dynamics, Minkowskian space becomes Euclidean, so that α = 1, 2, 3 and the surface is two-dimensional Riemannian manifold i = 1, 2. So that, after modeling the potential energy as a negative volume integral of the internal pressure and inclusion interaction with an environment, (20–22) further simplifies as

$\begin{array}{ll}\dot{\nabla }\rho +{\nabla }_i(\rho V^i)=\rho C{B}_i^i& (23)\end{array}$

$\begin{array}{l}{\partial }_{\alpha }(\rho V^{\alpha }(\dot{\nabla }C+2V^i{\nabla }_{i}C+V^i{V}^j{B}_{ij})\\ +V^{\alpha }(P^{+}+\Pi ))=-V^{\alpha }{\partial }_{\alpha }(P^{+}+\Pi )& (24)\end{array}$

$\begin{array}{ll}\rho V_i(\dot{\nabla }{V}^i+V^j{\nabla }_j{V}^i-C{\nabla }^{i}C-C{V}^j{B}_j^i)=0& (25)\end{array}$

where P⁺, Π are internal hydrodynamic and osmotic pressures, respectively. Derivation of (20–22) can be found in Svintradze [5]. We derive (23-25) in Appendix section. It is noteworthy that from the last equations set only the second equation (24) differs from the dynamic fluid film equations [42, 44]

$\begin{array}{ll}\rho (\dot{\nabla }C+2V^i{\nabla }_{i}C+V^i{V}^j{B}_{ij})=\sigma B_i^i& (26)\end{array}$

where σ is the surface tension. Equation (26) is only valid when the surface can be described with time invariable surface tension [42, 44], meaning that the surface is homogeneous and the surface tension is constant, while (24) does not have that restriction. Using (26) in (24) and taking into account that in equilibrium processes internal pressure is the same as external pressure, one gets exactly the same equation of motion in normal direction (39) as we get from using the first law of thermodynamics (see below).

$\begin{array}{ll}{\partial }_{\alpha }(\sigma V^{\alpha }{B}_i^i+(P^{+}+\Pi )V^{\alpha })=-({\partial }_{\alpha }{P}^{+}+{\partial }_{\alpha }\Pi )V^{\alpha }& (27)\end{array}$

It is worth of mentioning that (23–25) also follows from (20–22) if one applies same formalism as it is given in (30-32). Indeed, the space is 3D Euclidean so that α = 1, 2, 3 and the surface is 2D Riemannian (i = 1, 2) for relatively slowly moving surfaces and the potential energy could be written as:

$\begin{array}{l}U={\displaystyle {\int }_{\Omega }}(\frac{1}{4{\mu }_0}{F}_{\mu \nu }{F}^{\mu \nu }+A_{\mu }{J}^{\mu })\\ ={\displaystyle {\int }_{\Omega }}(-\frac{{ϵ}_0}{2}{E}^2+\frac{1}{{\mu }_0}{B}^2-q\phi +\overrightarrow{A}\overrightarrow{J})d\Omega & (28)\end{array}$

where $\overrightarrow{E},\overrightarrow{B}$ are electric and magnetic fields and $q,\phi ,\overrightarrow{A},\overrightarrow{J}$ are charge density, electric potential, magnetic vector potential and current density vector respectively. Using (30–32) formalism into account, we find

$\begin{array}{ll}dU=-(P^{+}+\Pi )d\Omega =(-\frac{{ϵ}_0}{2}{E}^2+\frac{1}{{\mu }_0}{B}^2-q\phi +\overrightarrow{A}\overrightarrow{J})d\Omega & (29)\end{array}$

Taking into account (29) and that the pressure comes from the normal force applied to the surface, we find $fa=-V^{\alpha }{\partial }_{\alpha }\left(P^{+}+\Pi \right)$ and in tangent direction $f^i{a}_i=0$, then (20–22) becomes (23–25). Electromagnetic potential energy can be generalized if one takes into account environment, which enters in energy terms as bound and free charges and electric/magnetic fields are replaced by polarization and magnetization vectors [5].

4. Results and Discussion

4.1. General Assumptions

In this section we apply basics of thermodynamics and fundamental theorems of calculus of moving surfaces to demonstrate shortest derivation of the equation, describing motion of homogeneous, closed two dimensional surface with time invariable surface tension at normal direction (27). We consider the system consisted of aqueous media with the formed closed surface in it (Figure 3). The system is isolated with constant temperature and there is no absorbed or dissipated heat on the surface; in other words, a process is adiabatic. According to the first law of thermodynamic, as far as there is no dissipated or absorbed heat, the change of the internal energy of the surface must be

$\begin{array}{ll}dE=\delta W& (30)\end{array}$

where δW is infinitesimal work done on the subsystem and dE is infinitesimal change of the internal energy. Because the temperature of the system is constant, the differential of the subsystems' internal energy can be remodeled as

$\begin{array}{ll}dE=dU& (31)\end{array}$

where U is the total potential energy of the surface. By the definition the elementary work done on the subsystem is

$\begin{array}{ll}\delta W=(P^{-}+\Pi )d\Omega & (32)\end{array}$

where, P⁻, Π are external hydrodynamic and osmotic pressures applied on the surface by the surroundings correspondingly and Ω is the volume that surface encloses with boundary of S surface area. Let's propose that the surface is homogeneous (i.e., material particles are homogeneously distributed on the surface) so that the total potential energy is integration of the potential energy per unit area over the surface, then

$\begin{array}{ll}dU=\sigma dS& (33)\end{array}$

where σ is the potential energy per unit area and is called surface tension in the paper. As far as we discuss simplest case of the system consisted of aqueous medium and single closed surface, we can suggest that the surface tension is not time variable. Using (30–33) after few lines of algebra, we fined

$\begin{array}{ll}{\displaystyle {\int }_S}\sigma dS={\displaystyle {\int }_{\Omega }}(P^{-}+\Pi )d\Omega & (34)\end{array}$

FIGURE 3

Figure 3. Graphical illustration of the isolated system containing aqueous solution. Water molecules are represented as red and white sticks. The system boundary is shown as white faces with black edges. The subsystem-micelle is closed surface, blue blob in the center of the system.

Assuming the surface is moving so that (34) stays valid for any time variations, then time differentiation of the left side must be equal to the time differentiation of the right integral. As far as on the right hand side we have space integral, time differentiation can be taken into the integral, using general theorems for differentiation of space and surface integrals (17–18), so that the integration theorem for the space integral which takes into account the volume motion holds, therefore:

$\begin{array}{l}\frac{d}{dt}{\displaystyle {\int }_{\Omega }}(P^{-}+\Pi )d\Omega ={\displaystyle {\int }_{\Omega }}({\partial }_{\alpha }{P}^{-}+{\partial }_{\alpha }\Pi )\frac{\partial X^{\alpha }}{\partial t}d\Omega \\ +{\displaystyle {\int }_S}C(P^{-}+\Pi )dS& (35)\end{array}$

To calculate a time derivative of the surface integral we have to take into account the theorem about time differentiation of the surface integral (18), from which follows that for the time invariable surface tension

$\begin{array}{ll}\frac{d}{dt}{\displaystyle {\int }_S}\sigma dS={\displaystyle {\int }_S}-\sigma C{B}_i^{i}dS& (36)\end{array}$

Where $C=V^{\alpha }{N}_{\alpha }$ is interface velocity, N_α is α component of the surface normal and V = ∂X^α/∂t is coordinate velocity, X^α is general coordinate and $B_i^i$ is the trace of the mixed curvature tensor generally known as mean curvature. After few lines of algebra putting (34–36) together, we find

$\begin{array}{ll}{\displaystyle {\int }_S}(\sigma C{B}_i^i+C(P^{-}+\Pi ))dS=-{\displaystyle {\int }_{\Omega }}({\partial }_{\alpha }{P}^{-}+{\partial }_{\alpha }\Pi )V^{\alpha }d\Omega & (37)\end{array}$

Generalized Gauss theorem converts the surface integral of the left hand side of (37) into space integral, so that

$\begin{array}{l}{\displaystyle {\int }_S{N}_{\alpha }}{V}^{\alpha }(\sigma B_i^i+P^{-}+\Pi )dS={\displaystyle {\int }_{\Omega }{\partial }_{\alpha }}(\sigma V^{\alpha }{B}_i^i\hfill \\ +(P^{-}+\Pi )V^{\alpha })d\Omega \hfill & (38)\end{array}$

Combination of (37) and (38) immediately gives equation of motion for surface in normal direction

$\begin{array}{ll}{\partial }_{\alpha }(\sigma V^{\alpha }{B}_i^i+(P^{-}+\Pi )V^{\alpha })=-({\partial }_{\alpha }{P}^{-}+{\partial }_{\alpha }\Pi )V^{\alpha }& (39)\end{array}$

For equilibrium processes internal and external pressures are identical P⁻ = P⁺, so that (39) becomes identical to the equation of motion in normal direction observed from master equations (23–27). Also, we should note that (39) is only valid for motion of the homogeneous surfaces with time invariable surface tension at the normal direction, therefore, it does not display any deformation in tangent directions. Equation (39) further simplifies when the surface comes in equilibrium with the solvent where divergence of the surface velocity ${\partial }_{\alpha }{V}^{\alpha }$ (stationary interface) along with ∂P/∂t (where P = P⁻+Π) vanishes, then the solution to (39), taking into account the condition (35), becomes

$\begin{array}{ll}{B}_i^i=-\frac{P}{\sigma }& (40)\end{array}$

The result (40) shows that the solution is constant mean curvatures (CMC) surfaces. Such CMC are rare and can be many if one relaxes the condition we restricted to the system. We consider isolated system where the surface is closed subsystem, these two preconditions mathematically mean that the surface we discuss is compact embedded surface in ℝ³. According to A. D. Alexandrov uniqueness theorem, if a compact surface embedded in ℝ³ has constant non-zero mean curvature then it is a sphere [45]. Correspondingly the solution (40) is a sphere (as far as we have compact two-manifold in the Euclidean space). When

$\begin{array}{ll}\frac{P}{\sigma }\ne 0& (41)\end{array}$

the surface is spheroid (or a cylinder if one relaxes compactness restriction making the cylinder infinitely long) and becomes plane (again when compactness argument is relaxed) or other zero mean curvature shape when compactness argument is not relaxed but contour of the surface remains fixed. This surprisingly simple and elegant derivation explains all the shapes surfaces can adopt in aqueous solution at equilibrium conditions². If the compactness condition is relaxed then (40) predicts that in addition to cylinder and plane all other CMC surfaces are also equilibrium shapes for moving surfaces. Taking into account that the surface tension in general can be a function of many variables, such as Gaussian curvature, bending rigidity, spontaneous curvature, molecules concentration, geometry of surfactant molecules and etc., then (39) may predict possible deformations of differently shaped surfaces and their wide range of static shapes. In fact, if considered that the surface tension, which is defined as potential energy per unit area, can be a function of mean curvature $\sigma =\sigma \left(B_i^i\right)$, then Taylor expansion of $\sigma \left(B_i^i\right)$ naturally rises all additional terms. These generalizations and temperature fluctuations can be included in the equations, but it is not scope of this paper and should be addressed separately. One may even propose σ as time independent the Helfrich Hamiltonian and then (39, 40) will become equation of static shapes for homogeneous surfaces with time invariable surface tension. In fact we clarify this statement in the following subsection.

4.2. Relevance to the Shape Equation

Here we give brief comparison of our equations of motions to the Helfrich formalism and show that the shape equation is a stationary approximate solution to the equation of the normal motion (39).

Let us propose that the system is overdamped, therefore variations in kinetic energy is much smaller than variations in the potential energy. Throughout of our equations we model potential energy as

$\begin{array}{l}U={\displaystyle {\int }_{\Omega }}{P}^{-}d\Omega \end{array}$

Assume that the Hamiltonian of the system $H={\int }_S\rho V^2/2dS+{\int }_{\Omega }{P}^{-}d\Omega$ is modeled as the free energy on the surface ${\int }_S\left({\sigma }_0+k/2{\left(B_i^i-K_0\right)}^2+k{K}_G\right)dS$, where σ₀ is classically defined constant surface tension, k is bending rigidity constant, K₀ is spontaneous curvature and K_G is the Gaussian curvature. This interpretation of the free energy is called spontaneous curvature model [8, 31]. As far as the system is overdamped, the variation of the kinetic energy is infinitely small, therefore in the first approximation $\delta {\int }_S\rho V^2/2dS\approx 0$ and we have

$\begin{array}{l}H={\displaystyle {\int }_S}\frac{\rho V^2}{2}dS+{\displaystyle {\int }_{\Omega }}{P}^{-}d\Omega \\ ={\displaystyle {\int }_S}({\sigma }_0+k/2{(B_i^i-K_0)}^2+k{K}_G)dS\\ \delta {\displaystyle {\int }_{\Omega }}{P}^{-}d\Omega =\delta {\displaystyle {\int }_S}({\sigma }_0+k/2{(B_i^i-K_0)}^2+k{K}_G)dS& (42)\end{array}$

For evaluation of the Hamiltonian variation, we note that according to the time differentiation of the space integrals (17) $\delta {\int }_{\Omega }{P}^{-}d\Omega ={\int }_{\Omega }\partial P^{-}/\partial td\Omega +{\int }_{S}C{P}^{-}dS$. On the other hand, the variation of the Helfrich free energy, which can be restricted to the normal variations [8], is

$\begin{array}{l}\delta {\displaystyle {\int }_S({\sigma }_0+k/2{(B_i^i-K_0)}^2+k{K}_G)}dS\\ ={\displaystyle {\int }_S\frac{\delta ({\sigma }_0+k/2{(B_i^i-K_0)}^2+k{K}_G)}{\delta N}}\frac{\delta N}{\delta t}dS\\ ={\displaystyle {\int }_S({\sigma }_0{B}_i^i-k(}{\nabla }_a{\nabla }^a{B}_i^i-\frac{1}{2}(B_i^i-K_0)[(B_i^i-K_0)B_i^i\\ -2{\left(B_i^i\right)}^2+4K_G]))CdS& (43)\end{array}$

where N is the normal coordinate and thus the interface velocity becomes C = ∂N/∂t. For stationary or near to stationary shapes ∂P⁻/∂t ≈ 0, taking into account (42, 43) and the variation of the ${\int }_{\Omega }{P}^{-}d\Omega$, we find

$\begin{array}{l}{\displaystyle {\int }_S({\sigma }_0{B}_i^i-k(}{\nabla }_a{\nabla }^a{B}_i^i-\frac{1}{2}(B_i^i-K_0)[(B_i^i-K_0)B_i^i\\ -2{\left(B_i^i\right)}^2+4K_G]))CdS={\displaystyle {\int }_{S}C}{P}^{-}dS& (44)\end{array}$

The last Equation (44) has to hold for any interface velocity C, therefore

$\begin{array}{l}{\sigma }_0{B}_i^i-k({\nabla }_a{\nabla }^a{B}_i^i-\frac{1}{2}(B_i^i-K_0)[(B_i^i-K_0)B_i^i\\ -2{\left(B_i^i\right)}^2+4K_G])=P^{-}& (45)\end{array}$

(45) is exactly the shape Equation [4, 8, 22, 23, 31]. Note that the shape Equation (45) can be obtained from the equation of motion in the normal direction (39) for near to stationary case. Indeed, according to (39) taking into account that the surface pressure can be modeled from (44, 45), we find

$\begin{array}{l}{\partial }_{\alpha }(\sigma B_i^i{V}^{\alpha }+({\sigma }_0{B}_i^i-k({\nabla }_a{\nabla }^a{B}_i^i-\frac{1}{2}(B_i^i-K_0)\\ [(B_i^i-K_0)B_i^i-2{\left(B_i^i\right)}^2+4K_G]))V^{\alpha })=-\frac{\partial P^{-}}{\partial t}& (46)\end{array}$

Taking into account that for stationary shapes $\partial P^{-}/\partial t=0,{\partial }_{\alpha }{V}^{\alpha }=0$, the last equation has trivial solution

$\begin{array}{l}{\sigma }_0^{,}{B}_i^i-k({\nabla }_a{\nabla }^a{B}_i^i-\frac{1}{2}(B_i^i-K_0)[(B_i^i-K_0)B_i^i\\ -2{\left(B_i^i\right)}^2+4K_G])=P_0& (47)\end{array}$

where ${\sigma }_0^{,},P_0$ are some constant surface tension and pressure respectively. These calculations formally establish that the shape equation is an approximate solution of our equations of motions constrained by the conditions: time invariable surface tension and stationary interfaces; and is valid only for overdamped systems. Note that the analytic solution (40) is exact and only valid for the surfaces in equilibrium with environment, while the shape equation is the approximate solution for stationary surfaces. It is no surprise that the stationary shapes are geometrically richer than equilibrium shapes. Equilibrium shapes can only adopt constant mean curvature.

4.3. Physical Application, Micelle

We can put Equation (39) and its solution (40) under the test for homogeneous micellar surface equilibrated with the aqueous solution. Based on (40) we can calculate minimal value of a micelle radius. The value of the trace of the mixed curvature tensor for a sphere is

$\begin{array}{ll}{B}_i^i=-\frac{2}{R}& (48)\end{array}$

where R is a radius.

Let's calculate value of the surface pressure when the micelle still can exist. Lipids in a micelle are confined in the surface by hydrophobic interactions with average energy in the range of hydrogen bonding. As far as values of hydrogen bonding energy are somewhat uncertain in the literature, by the first approximation we take average energy for the hydrogen bonding energy interval and assign it to the lipid molecule. Low boundary of the interval (minimum energy) for XH···Y hydrogen bond is about 1 kJ per mol (CH···C unit) and high boundary is about 161 kJ per mol (FH···F unit), the low and high values are taken according to references [46, 47]. Therefore, average energy is about (1+161)/2 = 81kJ/mol ≈ 13·10⁻²⁰J. To estimate hydrogen bonding energy per molecule with the undefined shape (lipid molecule) in the first approximation is to assign average energy to it and consider the spherical shape with the gyration radius. Of course it is low level approximation, but even such rough calculations produce reasonable results. After all these rough estimations the pressure to move one lipid from the surface, in order to induce critical deformations of the surface, is about average energy per the average volume of the lipid molecule

$\begin{array}{ll}P\approx \frac{3·13·10^{-20}}{4\pi r_G^3}\approx 3.1·10^{7}N/m^2& (49)\end{array}$

where $4\pi r_G^3/3$ is the estimated volume of a lipid molecule considered as sphere with the gyration radius r_G ≈ 1nm. On the other hand, the surface tension of a fluid monolayer at optimal packing of the lipids is about σ ≈ 3·10⁻²N/m [7, 48, 49], using these and (48, 49) in (40) the estimated micelle radius is

$\begin{array}{ll}R\approx \frac{2·3·10^{-2}}{3.1·10^7}=19.3\pm 0.1\AA & (50)\end{array}$

These calculations put the minimum radius in nanometer scale and is in very good agreement with experimental as well as computational frameworks [50, 51]. To further validate the (50) result, we ran a CHARMM based Micelle Builder simulation [52, 53] for 100 phospholipid molecules (DHPC lipids). The simulation result (Figure 4) generated a spherical micelle with diameter 38.5±0.1Å. These calculations indeed indicate that even such rough estimations produce reasonable accuracy.

FIGURE 4

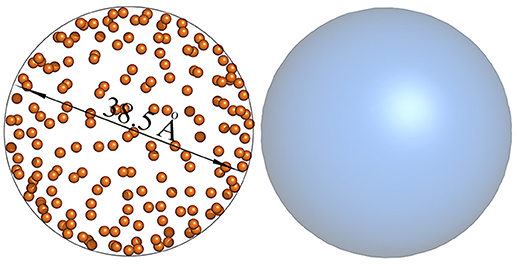
Figure 4. Simulated three dimensional coordinates of the micelle in aqueous solution display sphere with diameter 38.5Å. (Left) dihexanoylphosphatidylcholine (DHPC phospholipids) are modeled as orange balls. (Right) Gaussian mapping at contour resolution 8Å of the micelle shows spherical structure.

To get more convincing estimations it is necessary to take into account that neither lipids are spherical nor hydrophobic interactions per lipid are average energy of single hydrogen bond. In the second approximation lipids are no longer undefined spheres, but have well defined surfactant geometry. The Hydrophobic energy is no longer average energy of single hydrogen bond, but is 1 kJ per mol per −CH₂− unit. In all atom simulations we used dihexanoylphosphatidylcholine (DHPC) lipid molecule having 12−CH₂− units (Figure 5) per hydrophobic tail, so hydrophobic energy is about 12kJ/mol ≈ 1.99·10⁻²⁰J. Accurate calculation of the lipid molecule volume using cavity, channel and cleft volume calculator [54], gives the volume estimation of about 894ų. Using this value, one gets

$\begin{array}{ll}P\approx \frac{1.99·10^{-20}}{0.894·10^{-27}}\approx 2.22·10^{7}N/m^2& (51)\end{array}$

On other hand, using the same surface tension of a fluid monolayer at the optimal packing of the lipids, one gets R = 27 ± 0.1Å. All atom simulation also generates spherical structure with diameter 54 ± 0.1Å (Figure 5). There is still some uncertainty in this estimation because we assigned 1 kJ/mol energy per −CH₂− unit and we based on references data [46, 47], while in other literature it is mentioned that the hydrophobic interactions are about 4 kJ/mol per −CH₂− unit [55]. In our opinion, this discrepancy can be resolved if one calculates hydrophobic energy based on the potential energy

$\begin{array}{ll}U=-{\displaystyle {\int }_{\Omega }}\frac{{ϵ}_0}{2}{E}_{C{H}_2}^{2}d\Omega & (52)\end{array}$

where ${\overrightarrow{E}}_{C{H}_2}$ is electric field per −CH₂−, ϵ₀ is dielectric constant in the vacuum and Ω stands for the volume of the lipid molecules. Equation (52) directly emerges from $F_{\mu \nu }{F}^{\mu \nu }$ term written in the equations of motion (20–22 and 28–29). For electrostatics

$\begin{array}{ll}U={\displaystyle {\int }_{\Omega }}\frac{1}{4{\mu }_0}{F}_{\mu \nu }{F}^{\mu \nu }d\Omega =-{\displaystyle {\int }_{\Omega }}\frac{{ϵ}_0}{2}{E}_{C{H}_2}^{2}d\Omega & (53)\end{array}$

so one should go to the scrutiny of calculating electric field for each −CH₂− units, then take a sum of the electric field and square it (we are not going to do it in this paper). Also, one may ask why the hydrophilic interaction energy is not taken into account in these calculations. Hydrophilic head of the lipid molecule is in contact with water molecules so there is no work needed to drag it in aqueous solution from the lipids layer. Therefore, hydrophilic interaction energy can be neglected. The most work goes on overcoming hydrophobic interactions between lipid tails.

FIGURE 5

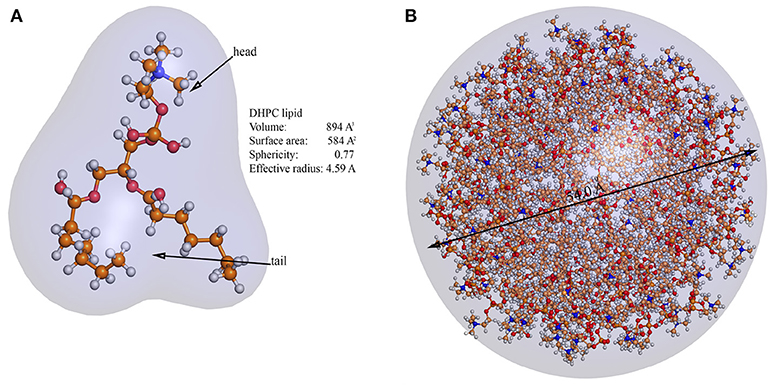
Figure 5. All atom simulation of DHPC micelle. (A) The figure shows a geometry of the DHPC surfactant molecule used in simulation and gives parametric description of volume, surface area, sphericity, and effective radius. (B) Indicates atomistic simulation result contoured by Gaussian map and the diameter of the micelle, measured by PyMol. The diameter of the simulated micelle appears to be 54.0Å with the uncertainty of the measurement 0.1Å.

5. Conclusion

We have presented a framework for the analysis of two dimensional surface dynamics (identified as micelle in the text) using first law of thermodynamics and calculus of moving surfaces. In final equations of normal motion (39,27) we assume that a surface is homogeneous and has time invariable surface tension. However, the general equations (23–25) do not have these constrains and indicate arbitrary motion along normal deformation, as well as into tangent directions, but are analytically more complex. The solution to the normal equations of motion in equilibrium conditions are surprisingly simple and display all possible equilibrium shapes. We applied the formalism to estimate micelle optimal radius and compared estimations to all atom simulations. Even for low-level approximations, we found remarkable agreement between theoretically calculated radius and one obtained from atomistic simulations and from experiments. One can readily apply the theory to any closed surfaces; such are vesicles, membranes, water droplets or soap films.

As a final remark, even though the analytic solution (40) looks like generalized Young-Laplace law, the difference is obvious. $B_i^i$ is a trace of mixed curvature tensor, known as mean curvature, and when the mean curvature is constant, it defines whole class of constant mean curvature (CMC) surfaces. Generalized the Young-Laplace law is a priori formulated for spherical morphologies and therefore in some particular cases can be obtained from (40) constant mean curvature shapes. The condition for holding the particular case is a compactness. However, the compactness argument can be relaxed in our derivation if the considered system is set to be much larger than the subsystem. Therefore, the solution (40) effectively predicts formation of all CMC surfaces while Young-Laplace law is correct for spherical structures alone. Also in derivation of Young-Laplace relation one of cornerstone idea is suggestion of spherical symmetries, while our derivation is free of symmetries and explains why CMC surfaces are such abundant shapes in nature, observable even on molecular levels. In fact, according to the results, any homogeneous closed surface with time invariable surface tension adopts CMC shape when it comes in equilibrium with environment.

Author Contributions

The author confirms being the sole contributor of this work and has approved it for publication.

Conflict of Interest Statement

The author declares that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Acknowledgments

We thank Dr. Frank Julicher (MPIPKS) and Dr. Erwin Frey (LMU), for stimulating discussions. The paper in it's current form was initiated at Aspen Center for Physics, which is supported by National Science Foundation grant PHY-1607611 and was partially supported by a grant from the Simons Foundation.

Supplementary Material

The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fphy.2018.00136/full#supplementary-material

Footnotes

1. ^Latin letters in indexes are related to the surface tensors and Greek letters are related to space tensors. Equations throughout the text are tensorial and repeated upper and lower indexes indicate Einstein summation convention, for instance $X_a{Y}^a=\Sigma X_a{Y}^a$.

2. ^Even though we set environment as aqueous, it enters into equations as osmotic pressure term, which due to a generality of arguments can be anything. Therefore, as a medium one may pick any liquid or gas.

References

1. Cahalan MD, Parker I. Choreography of cell motility and interaction dynamics imaged by two-photon microscopy in lymphoid organs. Annu Rev Immunol. (2008) 26:585–626. doi: 10.1146/annurev.immunol.24.021605.090620

PubMed Abstract | CrossRef Full Text | Google Scholar

2. Pal SK, Peon J, Bagchi B, Zewail AH. Biological water:â femtosecond dynamics of macromolecular hydration. J Phys Chem B (2002) 106:12376–95. doi: 10.1021/jp0213506

CrossRef Full Text | Google Scholar

3. Wan C, Fiebig T, Schiemann O, Barton JK, Zewail AH. Femtosecond direct observation of charge transfer between bases in DNA. Proc Natl Acad Sci USA. (2000) 97:14052–5. doi: 10.1073/pnas.250483297

PubMed Abstract | CrossRef Full Text | Google Scholar

4. Helfrich W. Elastic properties of lipid bilayers: theory and possible experiments. Z Naturforsch C (1973) 28:693–703.

PubMed Abstract | Google Scholar

5. Svintradze DV. Moving manifolds in electromagnetic fields. Front Phys. (2017) 5:37. doi: 10.3389/fphy.2017.00037

CrossRef Full Text | Google Scholar

6. Israelachvili JN, Mitchell DJ, Ninham BW. Theory of self-assembly of hydrocarbon amphiphiles into micelles and bilayers. J Chem Soc Faraday Trans 2 (1976) 72:1525–68.

Google Scholar

7. Israelachvili JN, Mitchell DJ, Ninham BW. Theory of self-assembly of lipid bilayers and vesicles. Biochim Biophys Acta (1977) 470:185–201.

PubMed Abstract | Google Scholar

8. Deserno M. Fluid lipid membranes: from differential geometry to curvature stresses. Chem Phys Lipids (2015) 185:11–45. doi: 10.1016/j.chemphyslip.2014.05.001

PubMed Abstract | CrossRef Full Text | Google Scholar

9. Lipowsky R, Sackmann E. Structure and Dynamics of Membranes. Amsterdam: Elsevier (1995).

Google Scholar

10. Seifert U. Configurations of fluid membranes and vesicles. Adv Phys. (1997) 46:13–137.

Google Scholar

11. Capovilla R, Guven J. Stresses in lipid membranes. J Phys A (2002) 35:6233. doi: 10.1088/0305-4470/35/30/302

CrossRef Full Text | Google Scholar

12. Fournier JB. On the stress and torque tensors in fluid membranes. Soft Matter. (2007) 3:883–8. doi: 10.1039/B701952A

CrossRef Full Text | Google Scholar

13. Scriven LE. Dynamics of a fluid interface equation of motion for newtonian surface fluids. Chem Eng Sci. (1960) 12:98–108.

Google Scholar

14. Arroyo M, DeSimone A. Relaxation dynamics of fluid membranes. Phys Rev E (2009) 79:031915. doi: 10.1103/PhysRevE.79.031915

PubMed Abstract | CrossRef Full Text | Google Scholar

15. Gao LT, Feng XQ, Yin YJ, Gao H. An electromechanical liquid crystal model of vesicles. J Mech Phys Solids (2008) 56:2844–62. doi: 10.1016/j.jmps.2008.04.006

CrossRef Full Text | Google Scholar

16. Salbreux G, Jülicher F. Mechanics of active surfaces. Phys Rev E (2017) 96:032404. doi: 10.1103/PhysRevE.96.032404

PubMed Abstract | CrossRef Full Text | Google Scholar

17. Ramaswamy S, Toner J, Prost J. Nonequilibrium fluctuations, traveling waves, and instabilities in active membranes. Phys Rev Lett. (2000) 84:3494–7. doi: 10.1103/PhysRevLett.84.3494

PubMed Abstract | CrossRef Full Text | Google Scholar

18. Chen HY. Internal states of active inclusions and the dynamics of an active membrane. Phys Rev Lett. (2004) 92:168101. doi: 10.1103/PhysRevLett.92.168101

PubMed Abstract | CrossRef Full Text | Google Scholar

19. Gov N. Membrane undulations driven by force fluctuations of active proteins. Phys Rev Lett. (2004) 93:268104. doi: 10.1103/PhysRevLett.93.268104

PubMed Abstract | CrossRef Full Text | Google Scholar

20. Canham PB. The minimum energy of bending as a possible explanation of the biconcave shape of the human red blood cell. J Theor Biol. (1970) 26:61–81.

PubMed Abstract | Google Scholar

21. Evans EA. Bending resistance and chemically induced moments in membrane bilayers. Biophys J. (1974) 14:923–31. doi: 10.1016/S0006-3495(74)85959-X

PubMed Abstract | CrossRef Full Text | Google Scholar

22. Zhong-Can OY, Helfrich W. Instability and deformation of a spherical vesicle by pressure. Phys Rev Lett. (1987) 59:2486–8. doi: 10.1103/PhysRevLett.59.2486

PubMed Abstract | CrossRef Full Text | Google Scholar

23. Zhong-Can OY, Helfrich W. Bending energy of vesicle membranes: general expressions for the first, second, and third variation of the shape energy and applications to spheres and cylinders. Phys Rev A (1989) 39:5280–8.

PubMed Abstract | Google Scholar

24. Mladenov IAM, Djondjorov PA, Hadzhilazova MT, Vassilev VM. Equilibrium configurations of lipid bilayer membranes and carbon nanostructures. Commun Theor Phys. (2013) 59:213–28. doi: 10.1088/0253-6102/59/2/14

CrossRef Full Text | Google Scholar

25. Svetina S, Žekš B. Membrane bending energy and shape determination of phospholipid vesicles and red blood cells. Eur Biophys J. (1989) 17:101–11.

PubMed Abstract | Google Scholar

26. Seifert U, Lipowsky R. Adhesion of vesicles. Phys Rev A (1990) 42:4768–71.

PubMed Abstract | Google Scholar

27. Lipowsky R. The conformation of membranes. Nature (1991) 349:475–81.

PubMed Abstract | Google Scholar

28. Seifert U, Berndl K, Lipowsky R. Shape transformations of vesicles: phase diagram for spontaneous-curvature and bilayer-coupling models. Phys Rev A (1991) 44:1182–202.

PubMed Abstract | Google Scholar

29. Jülicher F, Lipowsky R. Domain-induced budding of vesicles. Phys Rev Lett. (1993) 70:2964–7.

PubMed Abstract | Google Scholar

30. Jülicher F, Lipowsky R. Shape transformations of vesicles with intramembrane domains. Phys Rev E Stat Phys Plasmas Fluids Relat Interdiscip Topics (1996) 53:2670–83.

PubMed Abstract | Google Scholar

31. Jülicher F, Seifert U. Shape equations for axisymmetric vesicles: a clarification. Phys Rev E Stat Phys Plasmas Fluids Relat Interdiscip Topics (1994) 49:4728–31.

PubMed Abstract | Google Scholar

32. Miao L, Seifert U, Wortis M, Döbereiner HG. Budding transitions of fluid-bilayer vesicles: the effect of area-difference elasticity. Phys Rev E Stat Phys Plasmas Fluids Relat Interdiscip Topics (1994) 49:5389-407.

PubMed Abstract | Google Scholar

33. Heinrich V, Svetina S, Žekš B. Nonaxisymmetric vesicle shapes in a generalized bilayer-couple model and the transition between oblate and prolate axisymmetric shapes. Phys Rev E Stat Phys Plasmas Fluids Relat Interdiscip Topics (1993) 48:3112–23.

PubMed Abstract | Google Scholar

34. Kralj-Iglič V, Svetina S, Žekš B. The existence of non-axisymmetric bilayer vesicle shapes predicted by the bilayer couple model. Eur Biophys J. (1993) 22:97–103.

PubMed Abstract | Google Scholar

35. Chandler D. Interfaces and the driving force of hydrophobic assembly. Nature (2005) 437:640–7. doi: 10.1038/nature04162

PubMed Abstract | CrossRef Full Text | Google Scholar

36. Leikin S, Parsegian VA, Rau DC, Rand RP. Hydration forces. Annu Rev Phys Chem. (1993) 44:369–95.

PubMed Abstract | Google Scholar

37. Svintradze DV. Hydrophobic and hydrophilic interactions. Biophys J. (2010) 98:43a–4a. doi: 10.1016/j.bpj.2009.12.250

CrossRef Full Text | Google Scholar

38. Svintradze DV. Moving macromolecular surfaces under hydrophobic/hydrophilic stress. Biophys J. (2015) 108:512a. doi: 10.1016/j.bpj.2014.11.2807

CrossRef Full Text | Google Scholar

39. Svintradze DV. Cell motility and growth factors according to differentially variational surfaces. Biophys J. (2016) 110:623a. doi: 10.1016/j.bpj.2015.11.3342

CrossRef Full Text | Google Scholar

40. Svintradze DV. Geometric diversity of living organisms and viruses. Biophys J. (2017) 112:309a. doi: 10.1016/j.bpj.2016.11.1676

CrossRef Full Text | Google Scholar

41. Tanford C. The Hydrophobic Effect Formation of Micelles and Biological Membranes. New York, NY: Wiley-Interscience (1973).

Google Scholar

42. Grinfeld P. Introduction to Tensor Analysis and the Calculus of Moving Surfaces. New York, NY: Springer (2010).

Google Scholar

43. Hadamard J. Mmoire sur le problme danalyse relatif lquilibre des plaques elastiques encastres. Oeuvres, Hermann, Tome 2; 1968.

44. Grinfeld P. Exact nonlinear equations for fluid films and proper adaptations of conservation theorems from classical hydrodynamics. J Geom Symm Phys. (2009) 16:1–21.

Google Scholar

45. Alexandrov AD. Uniqueness theorem for surfaces in the large. Leningrad Univ 13, 19 (1958), 58. Am Math Soc Trans (Series 2). (1958) 21:412–6.

46. Larson J, McMahon T. Gas-phase bihalide and pseudobihalide ions. An ion cyclotron resonance determination of hydrogen bond energies in XHY-species (X, Y= F, Cl, Br, CN). Inorg Chem. (1984) 23:2029–33.

Google Scholar

47. Emsley J. Very strong hydrogen bonding. Chem Soc Rev. (1980) 9:91–124.

Google Scholar

48. Jähnig F. What is the surface tension of a lipid bilayer membrane? Biophys J. (1996) 71:1348–9.

PubMed Abstract | Google Scholar

49. Israelachvili JN. Intermolecular and Surface Forces: Revised Third Edition. Amsterdam: Academic Press (2011).

50. Feller SE, Zhang Y, Pastor RW. Computer simulation of liquid/liquid interfaces. II. Surface tension-area dependence of a bilayer and monolayer. J Chem Phys. (1995) 103:10267–76.

Google Scholar

51. Egberts E, Marrink SJ, Berendsen HJ. Molecular dynamics simulation of a phospholipid membrane. Eur Biophys J. (1994) 22:423–36.

PubMed Abstract | Google Scholar

52. Jo S, Kim T, Iyer VG, Im W. CHARMM-GUI: a web-based graphical user interface for CHARMM. J Comput Chem. (2008) 29:1859–65. doi: 10.1002/jcc.20945

PubMed Abstract | CrossRef Full Text | Google Scholar

53. Cheng X, Jo S, Lee HS, Klauda JB, Im W. CHARMM-GUI micelle builder for pure/mixed micelle and protein/micelle complex systems. J Chem Inf Model. (2013) 53:2171–80. doi: 10.1021/ci4002684

PubMed Abstract | CrossRef Full Text | Google Scholar

54. Voss NR, Gerstein M. 3V: cavity, channel and cleft volume calculator and extractor. Nucleic Acids Res. (2010) 38:W555–62. doi: 10.1093/nar/gkq395

PubMed Abstract | CrossRef Full Text | Google Scholar

55. Liu AL. Advances in Planar Lipids Bilayers and Liposomes, Vol. 4. Amsterdam: Academic Press; Elsevier (2011).

Google Scholar