- PoreLab, Department of Civil and Environmental Engineering, Norwegian University of Science and Technology, Trondheim, Norway
Modern soil mechanics (geotechnical engineering) was developed as a branch of civil engineering from the 1920's. While modern porous media physics was developed as a branch of physics and applied mathematics from roughly the same period of time. In soil mechanics the main concern is often on the deformations, resulting from mechanical, hydraulic, or thermal actions. In application of porous media physics the main concern is historically on the flow part, putting less emphasis on the mechanical part. However, deformation and flow are highly linked processes, especially in unconsolidated porous media (soil). This paper makes some links between concepts used in porous media physics, like the effective medium theory, and concepts in soil mechanics, like choice of stress measures. As an example, it shows that the use of Terzaghi effective stress is a matter of choice and can be consistently used also for cases where other effective stress measures are used in literature, like Biot effective stress. The requirement, to be consistent, is that the state variables considered, at the constitutive level, includes all relevant variables.
Introduction
Geotechnical engineering is the part of civil engineering concerns about the hydro-mechanical (or thermo-hydro mechanical) behavior of soils. In classical soil mechanics (geotechnical engineering) the basics principles used are:
• Equilibrium (Conservation of linear momentum)
• Mass balance (Conservation of mass)
• Heat balance (conservation of energy)
• Effective stress principle (Terzaghi or Bishop) for the stress carried by the soil skeleton and responsible for deformation.
• Stress-strain constitutive relations
• Darcy flow for the pore fluid(s)
• Fourier's law for heat conduction
The continuum approach is the most used approach to satisfy the momentum balance, compatibility, mass balance and heat balance equations. Deformation of and/or stresses (forces) acting on structures are one of the main problems for the geotechnical engineer to solve. In air-saturated soil systems (dry soils), when the loading rate is not too high (like the load coming from an explosion), the equilibrium equation is the only equation that should be solved. In water-saturated systems (and also in partially saturated systems), the volumetric deformation of the system is directly linked with the ability of the porous system for draining/absorbing of water, thus the mass balance equation should also be taken into account. Practical engineering problems involving non-isothermal conditions, e.g., artificial ground freezing projects, require the heat balance equation to be taken into account, too.
In classical soil mechanics, by assuming incompressible grains, the deformation of the system is considered as the result of the process of slippage, widening, and closing between granular medium particles. The slippage, widening, and closing between the granular materials will continue until reaching a locked state. Geotechnical engineers call this state as the “critical state” of the soil. At the onset of critical state, the volume of the system will be locked and the system can only be distorted. The critical state is a kind of geometrical state and can be found analytically. However, geotechnical engineers find this state experimentally, and use a mechanical constitutive framework to link the deformation gradients to an effective stress measure of the system [1].
The mechanical constitutive model is the key aspect of computational geotechnical engineering. Traditionally, in classical geotechnical engineering, these models are developed in the framework of plasticity theory. However, it is also possible to find deformation gradient- effective stress links, based on the effective medium theory. For the reader not used to the terminology, Effective Medium Theory (EMT) is a way to describe the macroscopic properties of a composite material from some sort of averaging of the multiple values of the constituents of this composite (e.g., [2–5]). The properties of the system are calculated from constituents' properties knowing the volume fraction of the constituents and geometrical details. This is typically used to find conductivities (hydraulic, thermal, or electric) in composite systems. In case of mechanical properties of material like rocks, EMT can be used to find elastic moduli of the composite from elastic moduli of the constituents (e.g., [6]). The volume fraction and the individual properties of the constituents are often the easy parts to establish, however, the geometry of the arrangement of the constituents is difficult to assess [7, 8]. Hence, effective medium theory will often result in rigorous upper and lower bounds from the extreme assumptions on geometrical arrangements and a representative model in between these two extremes, which needs experimental calibration.
This paper will give some relations between the macroscopic material behavior (i.e., constitutive laws) and the equivalent properties that can be obtained from effective medium theory. The main attempt is made on mechanical constitutive relations; however, it will also address the possibilities of using relations obtained from the use of effective medium theory for calculating hydraulic and thermal conductivities of the mixture.
Effective Medium Theory and Deformation Properties of Dry Soils
As an example of effective medium theory and the application to soil, the case of compressibility/stiffness is selected as a start point. For the case of soils, or to what is often in porous media physics referred to as “unconsolidated” porous materials, effective medium theory has been applied by several researchers to e.g., establish the dry bulk compressibility and shear modulus of the composite, assuming a system of spheres and the Hertz-Mindlin contact model (e.g., [9, 10]). In the geotechnical engineering community, a similar attempt, but under a different name “discrete element method,” have been made to find the deformation characteristics of the composite (e.g., [11–13]).
The dry bulk compressibility derived from effective medium theory, which will be a function of mean (effective) stress and/or porosity (or void ratio) in addition to the contact stiffness (grain compressibility) of the Hertz-Mindlin model, seems to be relatively in line with the measured values from course-graded soils (e.g., [14]). As seen from traditional geotechnical testing of sand samples under isotropic stress condition, the dry bulk compressibility, or the reciprocal property being the bulk stiffness, is shown to be a function of porosity and/or mean stress [1]. The empirical data typically gives that the bulk stiffness of sand varies with the square root of the mean stress, at least under the working stress levels normally encountered in geotechnical engineering practice. Houlsby et al. [15] derived a hyperelastic formulation, proposing a function for the elastic strain energy (Helmholtz free energy) and/or the complementary Gibbs free energy. The derivation from Houlsby et al. [15] gives not only the variation of the bulk stiffness under isotopic condition, as function of mean stress, but also the rest of the 4th order stiffness tensor and its stress dependency. As reviled from the hyperelastic description, under general stress condition, the stiffness is dependent on the general stress state not only the mean stress. However, the formulation gives, under the assumption of isotropic condition, a mean stress dependent bulk stiffness, that then agrees very well with the results obtained with effective medium theory [14]. It is worth noting, the power dependency according to hyperelasticity can vary between one (linear variation) and zero (constant stiffness), like the experimental finding of e.g., Janbu [16]. Effective medium theory under non-isotropic condition shows, as e.g., seen in Norris and Johnson [17], that the bulk compressibility will become a function of the tangential slip displacement in the contacts and the tangential contact stiffness in the Hertz-Mindlin model. This relates back to the general (shear) stress dependency found by Houlsby et al. [15] and will also generate coupling terms between bulk and shear stiffness in the medium in a similar way.
The Effective Stress Principle in Soils, Effect of Pore Fluid
The section above shows that the effective medium theory essentially produces similar results for dry granular media as those relations already used in soil mechanics when it comes to deformation of the medium. The natural next step would be to see the relationship between effective medium theory and an effective stress measure, in fully saturated soils. This is important since, in geotechnical engineering, the effective stress is considered as the only stress variable controlling the deformation of the soil. It is well-established, through experimental work and theory, that for saturated condition and for course-graded soils (i.e., sand and gravel) the effective stress principle of Terzaghi is valid (see for instance [18]). In the following, this concept is summarized. In saturated condition, due the small contact area between the relatively large grains, one may simply write up Equation (1) considering one component of normal stress and the buoyancy of the grains in water.
Where A is the total area of a cross section taken through the contact points, Aw is the area covered by water (note that water can be replaced by any other non-reactive pore-fluids), σ′ and σ are the effective and total normal stress respectively, pw and pam are the water and ambient pressures. This is in accordance with the expression found by Bishop [19]. Further setting Aw/A = 1 (i.e., ignoring the contact area between grains) and redefining total stress as σ – pam, and pore pressure as pw – pam, yields the Terzaghi effective stress as:
Note that, in the above, compression and pressure is considered as positive.
De Boer and Ehlers [20] used the concept of mixture theory and free energy to show that, when the constituents are considered as incompressible (incompressible grains and incompressible fluid) and that the fluid are considered to have negligible shear stress, the total partial solid stress tensor (acting over the whole area) is additively decomposed into the pore-liquid pressure and the effective stress tensor Equation (3). The above assumption holds, as the shear stiffness of the fluid is zero for Newtonian fluids and the viscosity times shear strain rate, in the fluid, is negligible or zero (which holds for the assumption of Darcy flow).
Where nS is the volume fraction of solid and pF is fluid pressure.
Similar for the partial pore-fluid stress tensor (acting over the whole area), the equation by de Boer and Ehlers yields:
where nF is the volume fraction of fluid, which in geotechnical engineering, in the case of saturated medium, is called porosity n (the ratio between pore volume and total volume).
When combining Equations (3, 4) in to the total stress of the effective medium, the following is obtained, since for saturated case nS + nF = 1:
This further clarifies, into the classical Terzaghi effective stress [21], by replacing fluid with water and omitting the index S for solid:
It will be for this effective stress that the constitutive equation, for the mechanical behavior of the saturated mixture, should be formulated.
For the case of partially saturated soil (which can be extended to the case of more than one type of pore fluid), Nikooee et al. [22] derived from a thermodynamic approach an analog stress to the Bishop effective stress [23]:
where pa is pore air pressure. Equation introduces the effective stress parameter χ. The parameter χ is a function of the water saturation (including the air entry value) and the specific air-water interfacial area. Notice the similarity of Equations (7) to if one sets χ = Aw/A. Other works, like that of Borja [24], show, by using mixture theory, that the parameter χ can be set to be equal to the degree of water saturation (Sw), meaning that the specific air-water interfacial area would only be dependent on the soil and degree of saturation and not if the soil is going through wetting or drying. This is probably an assumption that does not hold in reality and is easily proven incorrect by experimental testing (e.g., [25]). Others like the work of Jiang et al. [26] and Huyghe et al. [27] discuss the form of χ including the effect of wetting and drying. In addition, as discussed by e.g., Molenkamp et al. [28] and Manahiloh et al. [29], the Bishop effective stress actually should be take a form like Equation (8), as due to soil fabric, the effect of suction is not isotropic.
Where A is introduced to account for the anisotropic effect of suction due to the fabric tensor αij. The consequence of soil fabric leads to an effective stress measure that is dependent on the state variable (fabric). Therefore, it might be more appropriate to work with Terzaghi's definition of effective stress, Equation (6), and suction (pa – pw) as an independent stress variable, at the constitutive level.
As the effective stress is a well-established framework, working well for coarse graded soil and has solid theoretical explanations, the next step is to look into more of the fine graded soils like clay. Authors like Osipov [30] emphasizes on that the effective stress principle above does not consider the influence of any physicochemical forces on the effective stress. Mitchell and Soga [31] found that the effective stress principle can be modified to include the “far distance” attractive and repulsive electrostatic forces and the close distance chemical bounds. After integrating the effect of the close chemical bounding and the contact stresses, this results in the following expression for effective stress:
where A (capital α, not Latin A) is representing the integral of electrostatic attraction forces divided by area. However, the actual value of A is very difficult to assess. The size and the sign of which will be a function of particle orientation and distance, the double layer thickness etc. For water saturated clays, with no direct contact between particles, as in soft natural clays with fully open pore structure, A is equal to the integral over the local net disjoining/attractive pressure over the working areas, divided by the total area. The net A is then a function of the particle-to-particle distance, which in average is represented by the porosity of the clay (i.e., the volume fraction of free water). The link between this and the classical geotechnical terminology is what we experience as the effect of the pre-consolidation stress, pc′, of the clay. In terms of constitutive modeling, this allows for two options: A constitutive model formulated in terms of an effective stress considering ‘A’; or using the previous definition of effective stress, for saturated soils, and add an additional state variable being the pre-consolidation stress. The latter being the way it is often done in soil mechanics today. As an alternative, a measure of porosity can be used as state variable. For a denser clay, there might be formation of closed pores. In such case even for saturated condition, the χ (as the ratio “Aw/A”) parameter may locally be interpreted as less than one; and the local pore pressure might be higher than hydrostatic pressure, as the local encapsulated pressure cannot consolidate. Such behavior typical the case for e.g., smectite rich clays (swelling clays). However, this behavior may also be treated at a constitutive level considering Terzaghi effective stress [32], since the local effective stress is not needed for considering the macroscopic behavior of clay aggregates, and the microscopic effects (particle-particle interaction) can be included by state variables in the model (i.e., through fabric).
Constitutive Modeling and Choice of Effective Stress Measure
The relations between two physical quantities specified to a material are called constitutive relations. Examples of constitutive relations are that between potential differences and mean fluxes (fluid, electrical, heat etc.) or between deformation gradients and stresses (mechanical behavior). For soils, in the context of soil mechanics, there are three main constitutive relationships that needs to be addressed. Namely, for the hydraulic part (the hydraulic conductivity, i.e., the fluid flux due to the gradient in hydraulic potential, Darcy law, i.e., the 2nd order tensor, k), for the thermal part (the thermal conductivity, i.e., the heat flux due to temperature gradient, Fourier's law, i.e., the 2nd order tensor λ) and for the mechanical part (change in effective stress in relation to change in strain, i.e., the 4th order tangential stiffness tensor, D).
The hydraulic conductivity, k, is a function of the soil permeability (as a function of porosity and anisotropy) and the fluid viscosity (as a function of temperature). In addition, the gradient of hydraulic potential is linked through pressure gradient and density (the fluid density is also a function of temperature).
Even though the exact description on a macro level for establishing the effective hydraulic and thermal conductivity tensors are complicated, from the effective medium theory perspective, the derivation of it is the same for both consolidated and unconsolidated porous media.
The deformation properties of a dry porous media are discussed in a previous section. Accepting that the effective stress will be the only stress variable responsible for the mechanical behavior, the same constitutive rules will apply to saturated or partially saturated soils as for dry soils. Hence, the elastic stiffness relations found from effective medium theory applies also here. However, actually the elastic deformation of an unconsolidated porous medium (i.e., the elastic portion of strain in the soil material) normally only contributes with a small amount to the total deformation. Actually, most of the deformations within a soil material will be plastic deformations (strain that does not contribute to increase in internal reversible energy).
By the assumption of incompressible solid constituents, as shown by e.g., Gajo [33], the plastic strains in the medium (soil skeleton) can be found from a formulation considering a yield and potential surface that are formulated in terms of the effective stresses defined in the previous section.
In case of compressible constituents, the tradition in soil/rock mechanics community is to use the so-called Biot effective stress definition instead of Terzaghi effective stress. In accordance with Biot and Willis [34], the Biot effective stress, σ″ij, is defined in Equation.
Where α is the Biot parameter(assumed here as a constant). Note that when both the soil skeleton and the solid grains behave isotropically elastic, the volumetric deformation of the solid grains can be included into the Biot parameter, from the ratio of the bulk stiffness of the soil skeleton grain system to the bulk stiffness of solid grains. Which, then in saturated condition would be:
where K″ is bulk stiffness of the solid system (skeleton and grains) and KS is supposed to be the stiffness of the solid grains. Then, the volumetric deformation of the system can simply be calculated as:
where p″ is the mean Biot effective stress (p″ = σ″ii/3).
The other option is to use the Terzaghi effective stress principle for the soil skeleton, and the effective medium theory to find the effect of compressible constituents in the constitutive level. In this case, the total volumetric strain in the system is distributed into volumetric strain in the solid particles themselves and volumetric strain of the soil skeleton. While the volumetric strain in the soil skeleton is connected to the change in effective mean stress (p′), the volumetric strain in the solid particles is connected to the change in solid grains mean stress (ps). According to Equation (3) the stress in solid grains depends on both effective stress, p′, and pore pressure, pw. However, the solid stress in Equation (3) is acting over the whole area, and it could be rescaled on the solid surface forming the stress σS:
One can rewrite this equation in terms of mean stress rate as
where the Terzaghi definition is used:
and p is the total mean stress and p′ is the effective mean stress.
The increment in volumetric strain in the particles is related to pS through the bulk stiffness of the solid constituent, if the solid grains behave isotropically elastic.
where (εs)v is the volumetric strain of the particles and K is the actual effective bulk stiffness of the solid material.
The increment in volumetric strain in the skeleton is related to p′ through the bulk stiffness of the skeleton, if the skeleton behaves isotropically elastic.
where ε′v is the volumetric strain of the skeleton and K′ is the effective bulk stiffness of the soil skeleton. The total volumetric strain of the system then can be calculated as
Now, one can connect the Biot stiffness parameters to the effective stiffness parameters through: (full derivation is given in the Appendix)
Note that normally both K″ and K′ are function of n and/or p′. If K ≫ p′ then the relations are simplified to Equation (20), and only porosity dependency is present.
Giving the Biot coefficient, as a function of porosity, as follows:
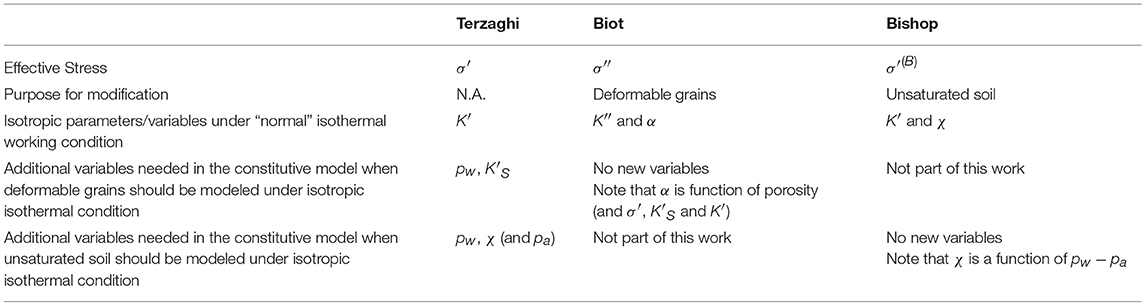
The difference between using the Biot effective stress measure and the Terzaghi effective stress is then simply the use of K′ or K″ for bulk stiffness of the soil skeleton alone or for the solid system in total, respectively, and KS or K for the grain contribution. It means that selection of the stress measure is a choice as long as one considers the effects at the constitutive level. Note that the above relation with Terzaghi effective stress definition can be extended to anisotropic elasticity, for the soil grains or the soil skeleton, by modifying Equations or respectively. Table 1 gives a brief summary of three of the stress measures, found in the article, and the connection with required variables.
Since soil actually does not behave in an isotropic linear elastic manner (see the section on effective medium theory and deformation properties of dry soils), the Biot definition of effective stress will be response dependent. Therefore, for a non-linear, anisotropic and/or inelastic material response, it is more convenient to have an effective stress measure that is independent of response (Equation, 6), i.e., the Terzaghi effective stress definition and solid stress as the stress state variables for the mechanical constitutive model.
Constitutive Modeling, Choice of Functions and State Variables
For e.g., soft clays, it is often found that there is a linear relationship between mean effective stress and elastic bulk stiffness, for small variation in porosity. Such an observation and others like it is essential information to be able to formulate constitutive models for the mechanical behavior of soils. However, the constitutive equations cannot be formulated in an arbitrarily manner, the following should apply (not in a specially ordered manner):
1. Behave in a deterministic manner or more strictly described: Principle of causality
2. Obey the 2nd law of thermodynamics (Entropy principle)
3. Behave objectively (Principle of material frame-indifference)
4. Preserve material symmetry, meaning that there is a consistency between material symmetry and constitutive equation.
5. Principle of equipresence, meaning that all constitutive equations should include the all the same state variables. Unless these are shown to have no effect. Or, that such a presence is in violation with physical laws (i.e., reduced by the other principles).
6. Finally, the constitutive behavior is to be described locally (Principle of local action). Which means that it is only the action on an infinitesimal space, which gives an effect in this infinitesimal space. However, deviation from this point is allowed in some cases, e.g., in order to use a continuum description for a local phenomenon.
Constitutive Model for the Mechanical Behavior
Houlsby and Puzrin [35] uses the fact that, in order to have a hyper-elastoplastic description of the mechanical behavior of a material, the constitutive equations should be formulated based on the 1st and 2nd law of thermodynamics. As a consequence of their derivation, it is possible to come up with a formulation of so called yield and potential surfaces, formulated in the conventional stress space (i.e., in terms of , pw, pa, θ, ∇θ, dθ/dt, ∇(dθ/dt), κ). Where θ is temperature and κ is a set of internal state variables. In the simplest form, κ is expressed simply by the plastic strain tensor, . Note that Houlsby and Puzrin uses the dissipative generalized stress “Xij“ to formulate the framework in their paper and also assuming that the mechanical work itself must be dissipative (to obey the 2nd law of thermodynamics). However, a transformation between a formulation in terms of the dissipative generalized stress and conventional stress tensor is possible. Normally, the elastoplastic description of soil materials is not derived from energy potentials and dissipation functions, but rather suggested expressions for yield surfaces, potential surfaces and hardening rules, for the plastic or viscoplastic part. For the elastic part, some uses a hypo-elastic description, in other case a hyper-elastic description is used (where the latter is definitely preferable).
Constitutive Relations for the Fluid Flow
Darcy's law, for quasi-static condition (steady state) of a single-phase flow in saturated porous media, gives that the fluid velocity tensor, w, over the total area, with respect to the soil skeleton grain system, is proportional to the difference in hydraulic potential:
Where:
and k is the hydraulic conductivity tensor (in geotechnical engineering, referred to as permeability tensor, which for isotropic condition is replaced by a single value k), vw is the actual velocity tensor of the water, v is the velocity tensor of the skeleton grain system, ρw is mass density of water, g is the gravitational tensor [0 0 –g]T. The hydraulic conductivity is found from:
where κ is the absolute permeability tensor and μw is dynamic viscosity of water. The absolute permeability tensor is expected to be a function of the porosity, n, and anisotropy/fabric α. μw and ρw are functions of temperature (θ) [and fluid pressure (pw)]. The geotechnical engineering practice is to establish this experimentally. However, effective medium theory can be used to establish such a relationship. For the case of partially saturated soil the concept of relative permeability as described in Brooks and Corey [36] is normally followed. A concept easily extended to anisotropic medium, e.g., [37].
Constitutive Relation for Heat Flow
Unlike the hydraulic conductivity, that depends on the absolute permeability tensor, a property of the pore space, and the properties of the fluid, the thermal conductivity depends on structure of the skeleton, properties the solid part, structure of the pores and properties of the pore fluid. Wang et al. [38] and Gong et al. [39] considered an isotropic representative volume and showed that an unified equation, for a modified effective medium theory model for the thermal conductivity of a two phase system (particular case of a multiphase system), is in accordance with Equation (25).
Where λ′ is the effective thermal conductivity, λS and λw are thermal conductivities of the solid and fluid (water), respectively, λm is the unknown effective medium conductivity parameter that gives the coupling, extremes being series, or parallel coupling (λm = 0 or λm = ∞). By setting λm = λ′, one retrieves a more original form of the EMT model (for electrical conductivity with spherical inclusions) by Landauer [40]. Note that λm likely itself will be porosity dependent, but this dependency is not significant, as discussed in e.g., Gong et al. [39] for the case of a sand, where empirical findings agreed well with the use of Equation (25). However, in general in a soil, it is expected that the thermal conductivity may not be isotropic, but expressed by a tensor (λ′). Which, also like the hydraulic conductivity, depends on the fabric tensor, α. Establishing the full λ′ tensor can be done following the procedure of a modified EMT with different structure in different directions, but little references to such work can be found in literature. Even from an experimental point of view, measurement of anisotropic thermal conductivity is challenging [41]. Finally, the Fourier law gives that the heat flux q is expressed as:
Note that in the above, properties as K and λS are assumed to be reflected by a single mineralogical composition. However, natural soil is composed of a variety of different minerals with varying KS and λS. The calculation of these two average quantities for the bulk of grains are ideal exercise in using EMT. For the case of effective bulk stiffness of the solid such a relation will be of the form of Equation (27) after modifying and extending the Landauer [40] relation.
Where n is the volume fraction of the solid constituent, i, and f is a geometrical factor between zero and infinity. For the effective (combined) solid thermal conductivity of the solid, , the following relation may be used:
Equations (27, 28) are not the exact form of the effective quantities for the solid, because it does not reflect on the anisotropy, but it is a simple suggestion as a start point.
Thermal Expansion
Based on the individual constituent the volumetric thermal expansion follows the Equation (29)
where αi is the volumetric thermal expansion of the constituent. However, for the solid grains when combined in a soil skeleton grain system, consisting of several different minerals, the thermal expansion coefficient is not necessary isotropic.
Final Governing Equations
Governing equations for a saturated porous media, in tensorial form, are presented below. The mass balance equation is written with an Eulerian description for the fluid phase with respect to the Lagrangian solid:
The first term in Equation (30) can be found by the bulk modulus of water (Kw):
Substituting Equations (18, 31, 29) in Equation (30), result in:
Considering Equations (16, 32) can be rewritten as:
Where the total volumetric strain is found from:
Introducing Equations (14, 34) into Equation (33) and rearranging, one find the final form of the mass balance equation as:
Where α′S, v and αw is the effective volumetric thermal expansion coefficient of solid and thermal expansion coefficient of water, respectively. The particular form of Equation (35) is chosen such that it includes the relative change in fluid pressure to solid stress through Equation (14), by the change in effective mean stress and/or due to change in porosity.
Equilibrium equation is written using the Terzaghi effective stress definition plus solid stress, stand for describing the hydro-mechanical behavior of a fully saturated system.
And finally for heat balance:
where Q is the total heat supply (or loss). CS and Cw are heat capacity of solid and fluid, respectively.
Conclusion
This article tries to connect the use of different concepts with porous media physics, like effective medium theory, to the classical concepts in soil mechanics/geotechnical engineering. The article demonstrates that the use of the Terzaghi effective stress principle is valid, for all types of geomaterials, as long as the constitutive model for the material behavior considers all relevant state variables. This means that there is no actual need for a Biot or Bishop effective stress, or any modification of such effective stress, to take into account of e.g., physiochemical forces, grain compressibility or the capillary suction in partially saturated soil. Especially since, the Biot parameter is anyway not a constant, but is deformation dependent, the physiochemical forces cannot be assessed properly and the capillary suction anyway must be treated as a state variable at constitutive level to account for soil fabric. For the case of compressible grains this article proposes a modified mass balance equation where the solid stress is included (rather that the Biot parameter). The understanding, of the geomaterials, obtained from effective medium theory and thermodynamics, shows that the conventional methodology, as used in modern numerical modeling in geotechnical engineering practice, is theoretically sound. This includes things like effective stress dependent stiffness, for the mechanical part, and the description of hydraulic and thermal conductivities where empirically based values fits with well with theoretical EMT studies, as recorded in various literature.
Data Availability
No datasets were generated or analyzed for this study.
Author Contributions
All authors made substantial contributions to the conception or design of the work, and were part of drafting the work or revising it critically for important intellectual content, thus approving the publication of the content. All authors agree to be accountable for all aspects of the work in ensuring that questions related to the accuracy or integrity of any part of the work are appropriately investigated and resolved.
Conflict of Interest Statement
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Acknowledgments
This work is supported by the Research council of Norway through its Centers of Excellence funding Scheme, project number 262644.
References
2. Johnson DL, Koplik J, Dashen R. Theory of dynamic permeability and tortuosity in fluid-saturated porous media. J Fluid Mechan. (1987) 176:379–402. doi: 10.1017/S0022112087000727
3. Burganos VN, Sotirchos SV. Diffusion in pore networks: effective medium theory and smooth field approximation. AICHE J. (1987) 33:1678–89. doi: 10.1002/aic.690331011
4. Brinkman HC. A calculation of the viscous force exerted by a flowing fluid on a dense swarm of particles. Appl Sci Res. (1947) A1:27.
5. Harris CK. Application of generalised effective-medium theory to transport in porous media. Transport Porous Media. (1990) 5:517–42. doi: 10.1007/BF01403480
6. Kuster GT, Toksöz MN. Velocity and attenuation of seismic waves in two-phase media: part i. Theoretical formulations. Geophysics. (1974) 39:587–606. doi: 10.1190/1.1440450
7. Makse HA, Gland N, Johnson DL, Schwartz LM. Why effective medium theory fails in granular materials. Phys Rev Lett. (1999) 83:5070–3. doi: 10.1103/PhysRevLett.83.5070
8. Garboczi EJ, Berryman JG. Elastic moduli of a material containing composite inclusions: effective medium theory and finite element computations. Mech Mater. (2001) 33:455–70. doi: 10.1016/S0167-6636(01)00067-9
9. Goddard JD. Nonlinear elasticity and pressure-dependent wave speeds in granular media. Proc R Soc London Series A Math Phys Sci. (1990) 430:105. doi: 10.1098/rspa.1990.0083
10. Makse HA, Gland N, Johnson DL, Schwartz L. The apparent failure of effective medium theory in granular materials. Phys Chem Earth Part A Solid Earth Geodesy. (2001) 26:107–11. doi: 10.1016/S1464-1895(01)00033-3
11. Dobry R, Tang-Tat NG A. Discrete modelling of stress-strain behaviour of granular media at small and large strains. Eng Comp. (1992) 9:129–43. doi: 10.1108/eb023853
12. Ting JM, Khwaja M, Meachum LR, Rowell JD. An ellipse-based discrete element model for granular materials. Int J Numer Anal Methods Geomechan. (1993) 17:603–23. doi: 10.1002/nag.1610170902
13. O'Sullivan C. Particle-based discrete element modeling: geomechanics perspective. Int J Geomech. (2011) 11:449–64. doi: 10.1061/(ASCE)GM.1943-5622.0000024
14. Johnson DL, Makse HA, Gland N, Schwartz L. Nonlinear elasticity of granular media. Phys B Conden Matter. (2000) 279:134–8. doi: 10.1016/S0921-4526(99)00700-0
15. Houlsby GT, Amorosi A, Rojas E. Elastic moduli of soils dependent on pressure: a hyperelastic formulation. Géotechnique. (2005) 55:383–392. doi: 10.1680/geot.55.5.383.66021
16. Janbu N. Soil compressibility as determined by oedometer and triaxial tests. Proc. ECSMFE Wiesbaden. (1963) 1:19–25.
17. Norris AN, Johnson DL. Nonlinear elasticity of granular media. J Appl Mech. (1997) 64:39–49. doi: 10.1115/1.2787292
18. Laloui L, Hutter K, Vulliet L. Thermodynamics of saturated and unsaturated soils. In: Biot Conference on Poromechanics. Louvain-La-Neuve (1998). p. 93–97.
20. de Boer R, Ehlers W. The development of the concept of effective stresses. Acta Mech. (1990) 83:77–92. doi: 10.1007/BF01174734
22. Nikooee E, Habibagahi G, Hassanizadeh SM, Ghahramani A. Effective stress in unsaturated soils: a thermodynamic approach based on the interfacial energy and hydromechanical coupling. Transport Porous Media. (2013) 96:369–96. doi: 10.1007/s11242-012-0093-y
23. Bishop AW, Blight GE. Some aspects of effective stress in saturated and partly saturated soils. Géotechnique. (1963) 13:177–97. doi: 10.1680/geot.1963.13.3.177
24. Borja RI. On the mechanical energy and effective stress in saturated and unsaturated porous continua. Int J Solids Struc. (2006) 43:1764–86. doi: 10.1016/j.ijsolstr.2005.04.045
25. Fredlund Delwyn G. Unsaturated soil mechanics in engineering practice. J Geotech Geoenviron Eng. (2006) 132:286–321. doi: 10.1061/(ASCE)1090-0241(2006)132:3(286)
26. Jiang Y, Einav I, Liu M. A thermodynamic treatment of partially saturated soils revealing the structure of effective stress. J Mech Phys Solids. (2017) 100:131–146. doi: 10.1016/j.jmps.2016.11.018
27. Huyghe JM, Nikooee E, Hassanizadeh SM. Bridging effective stress and soil water retention equations in deforming unsaturated porous media: a thermodynamic approach. Transport Porous Media. (2017) 117:349–365. doi: 10.1007/s11242-017-0837-9
28. Molenkamp F, de Jager RR F.A.Mathijssen JM. Stress measures affecting deformation of granular materials. Vadose Zone J. (2014) 13. doi: 10.2136/vzj2013.07.0130
29. Manahiloh KN, Muhunthan B, Likos WJ. Microstructure-based effective stress formulation for unsaturated granular soils. Int J Geomech. (2016) 16:D4016006. doi: 10.1061/(ASCE)GM.1943-5622.0000617
30. Osipov VI. Physicochemical Theory of Effective Stresses, Physicochemical Theory of Effective Stress in Soils. Cham: Springer International Publishing (2015). p. 39–54.
31. Mitchell JK, Soga K. Fundamentals of Soil Behavior, 3rd Edn. New York, NY: John Wiley and Sons Inc. (2005).
32. Mašín D, Khalili N. Swelling phenomena and effective stress in compacted expansive clays. Can Geotech J. (2015) 53:134–47. doi: 10.1139/cgj-2014-0479
33. Gajo A. Finite strain hyperelastoplastic modelling of saturated porous media with compressible constituents. Int J Solids Struc. (2011) 48:1738–53. doi: 10.1016/j.ijsolstr.2011.02.021
34. Biot M, Willis D. The elastic coeff cients of the theory of consolidation. J Appl Mech. (1957) 15:594–601.
35. Houlsby GT, Puzrin AM. A thermomechanical framework for constitutive models for rate-independent dissipative materials. Int J Plastic. (2000) 16:1017–47. doi: 10.1016/S0749-6419(99)00073-X
36. Brooks R, Corey T. HYDRAU uc Properties of Porous Media. Hydrology Papers, Colorado State University (1964). 24:37.
37. Bear J, Braester C, Menier PC. Effective and relative permeabilities of anisotropie porous media. Transport Porous Media. (1987) 2:301–16. doi: 10.1007/BF00165786
38. Wang J, Carson JK, North MF, Cleland DJ. A new approach to modelling the effective thermal conductivity of heterogeneous materials. Int J Heat Mass Transfer. (2006) 49:3075–83. doi: 10.1016/j.ijheatmasstransfer.2006.02.007
39. Gong L, Wang Y, Cheng X, Zhang R, Zhang H. A novel effective medium theory for modelling the thermal conductivity of porous materials. Int J Heat Mass Transfer. (2014) 68:295–8. doi: 10.1016/j.ijheatmasstransfer.2013.09.043
40. Landauer R. The electrical resistance of binary metallic mixtures. J Appl Phys. (1952) 23:779–84. doi: 10.1063/1.1702301
41. Li M, Kang JS, Hu Y. Anisotropic thermal conductivity measurement using a new Asymmetric-Beam Time-Domain Thermoreflectance (AB-TDTR) method. Rev Sci Instr. (2018) 89:084901. doi: 10.1063/1.5026028
Appendix
Derivation of the stiffness relation Equation (19).
Setting the rate of total stress in Equation (10) equal to the rate of total stress derived from Equation (6) combined with Equation (11) gives:
Taking the trace and inserting Equations (12, 17)
Combined with Equation (18)
Writing porosity change as:
Inserting Equation (A4) into Equation (14) and combining with Equation (16, 17)
Then, replacing the by using Equation (18) gives:
Which solved for gives:
Inserting the resulting Equation (A7) into Equation (A3) and rearranging gives:
Where, by grouping:
Which, finally gives Equation (19).
Keywords: soil mechanics, porous media physics, effective medium theory, effective stress, constitutive model
Citation: Grimstad G, Ghoreishian Amiri SA and Nordal S (2019) Relations and Links Between Soil Mechanics, Porous Media Physics, Physiochemical Theory, and Effective Medium Theory. Front. Phys. 7:41. doi: 10.3389/fphy.2019.00041
Received: 07 November 2018; Accepted: 06 March 2019;
Published: 01 April 2019.
Edited by:
Sergey G. Abaimov, Skolkovo Institute of Science and Technology, RussiaReviewed by:
Ignazio Licata, Institute for Scientific Methodology (ISEM), ItalyIrina Bayuk, Institute of Physics of the Earth (RAS), Russia
Copyright © 2019 Grimstad, Ghoreishian Amiri and Nordal. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Gustav Grimstad, Z3VzdGF2LmdyaW1zdGFkQG50bnUubm8=
 Gustav Grimstad
Gustav Grimstad Seyed Ali Ghoreishian Amiri
Seyed Ali Ghoreishian Amiri Steinar Nordal
Steinar Nordal