- 1Shenzhen Institutes of Advanced Technology, Chinese Academy of Sciences, Shenzhen, China
- 2Beijing Computational Science Research Center, Beijing, China
- 3Center for High Pressure Science and Technology Advanced Research, Shanghai, China
- 4Department of Physics, Beijing Normal University, Beijing, China
The discovery of superconductivity above 30 K in aromatic hydrocarbons in the past years has been an exciting event in condensed matter physics, chemistry, and materials. Superconductivity was realized by simply introducing electrons in the network made by carbon and hydrogen—the two components for organic systems. However, the accurate amount of doped electrons and their positions have not been established experimentally. No agreement has been reached for the mechanism of their superconductivity. Here, the first-principles theory with the combination of electron correlations is used to address these problems. Our calculations show that both the single-ring compound (benzene) and the two benzene ring compound (naphthalene) are superconductors with transition temperatures (Tc's) of 6.2 K and 5.8 K, respectively, after administration of potassium. By examining the existing experimental data carefully, we find that there exists a unique superconducting phase with Tc in the range of 5 − 7 K for all aromatic hydrocarbons. The almost constant low density of states at Fermi level with about two-electron doping accounts for this unified phase. The high density of states at Fermi level upon three-electron doping seems responsible for the high-Tc phase in these hydrocarbons with long benzene rings. Meanwhile, the electronic correlations also increase with an increasing number of benzene rings. These findings offer clues to the understanding of the superconductivity as well as to the search of new superconductors in this family.
1. Introduction
Organic materials with a crystal structure made primarily of a complex network based on carbon and/or hydrogen were postulated to superconduct with high transition temperature (Tc) and may even above room temperature [1]. Organic superconductors such as charge-transfer compounds are made up of electron donor molecules such as tetrathiafulvalene (TTF), bis-ethylenedithrio-TTF (BEDT-TTF, abbreviated as ET), and tetramethyltetraselenafulvalene (TMTSF) derivatives, as well as electron acceptor molecules such as tetracyanoquinodimethane (TCNQ) and fullerides [2–5], which were discovered many years ago and are being extensively studied. In 2010 and subsequent years, polycyclic aromatic hydrocarbons (PAHs) were found to exhibit superconductivity [6–9], and their discoveries have attracted great interest in these organic compounds. Experimental data showed that there usually exist multiple superconducting phases with different superconducting transition temperature Tc, and the highest Tc seems to increase with the number of benzene rings within the unit cell [6–9]. These compounds all have a superconducting phase with Tc ~ 5 − 7 K. In addition, spin-liquid state has been also realized in an ionic PAH [10]. Recently, the crystal structures of potassium-intercalated PAHs have been experimentally determined [11]. This information is very useful in theoretical studies on the superconducting phase and for understanding the driving force for superconductivity. However, a systematic study on the superconductivity in PAH, e.g., the relation between Tc and the number of benzene rings, is lacking. The issue of what is the exact amount of the cation intercalation or doping into the PAHs to induce superconductivity remains unsettled. Benzene−, being the simplest aromatic hydrocarbon, has six carbons on a ring and six hydrogens attached, i.e., C6H6. Other PAHs are made of more benzene rings. Thus, being the basic unit of PAH, solid benzene stands out as an ideal system to start with and address relevant issues. A natural question is whether such a compound could superconduct when doped by alkali atoms. If it superconducts, will its properties mimic those of all aromatic hydrocarbons? What factor is important for higher Tc? Exploring structures of doped solid benzene and examining corresponding phase stability, followed by the study of superconductivity, are the tasks of this work.
Solid benzene, whose crystallization characteristics have been extensively investigated [12–14], has a rich phase diagram with evolution into several phases by changing temperature and pressure. Liquid benzene crystallizes at room temperature and about 0.07 GPa, in an orthorhombic phase with space group Pbca (phase I), containing four formula units (f.u.) per unit cell [12]. At 1.4 GPa, a transition occurs from phase I to phase II (P43212), and then at 4 GPa, phase II transfers to phase III (P21/c), followed by phase IV (11 GPa) and phase V at higher pressures. Solid benzene has been found to be non-metallic and non-superconducting over a very broad pressure range. Upon heavy compression, solid benzene was predicted to undergo an insulator-to-metal transition in the pressure range of 180–200 GPa [15], suggesting that benzene is a possible superconductor under pressure. However, inherent to high-pressure techniques is the difficulty for experimental diagnosis and observation. Therefore, instead, we chose potassium (K) to dope solid benzene at ambient pressure and examine the possible realization of metallization and superconductivity. If doped solid benzene superconducts at ambient pressure, it would serve as an example to uncover the underlying origin of superconductivity in PAHs.
Although experimental studies on doping K into solid benzene have yet to be performed, the interaction between the benzene molecule and the K+ ion has already been observed experimentally as well as studied theoretically by López et al. [16], a resource which implies the feasibility of doping potassium into solid benzene. Notably, doping potassium has been shown to be the most effective and common method to induce superconductivity in PAHs [6–9]. One reason is that K has a relatively low melting point as compared to other alkali elements, which makes the chemical reaction and crystallization from liquid states of K and benzene suitable.
2. Materials and Methods
2.1. Structural Optimizations and Electronic Properties Calculation
All structural optimizations and electronic properties were calculated by using the Vienna ab initio simulation package (VASP) [17, 18]. In this work, the projector augmented wave (PAW) method [19] was adopted, and the exchange correlation energy was described by the Ceperley-Alder local density approximation (LDA) [20] as parameterized by Perdew and Zunger [21], which has been confirmed to be adequate by previous studies [22]. An energy cutoff of 500 eV was used for the plane wave basis sets. Thus, C-2p, H-1s, and K-3p4s were treated as valence states. The Brillouin zone (BZ) was sampled by 4 × 4 × 4 Monkhorst-Pack k-point grids during the optimization, and double k-point in the electronic structural calculations. The convergence thresholds were set as 10−6 eV in energy and 0.005 eV/Å in force. A conjugate-gradient algorithm was used to relax the ions into their instantaneous ground state.
2.2. Electron-Phonon Interaction and Relevant Parameter Calculations
To calculate electron-phonon interaction and relevant parameters, we used the QUANTUM-ESPRESSO package (QE) [23] with a cutoff energy of 60 and 450 Ry for wave functions and charge densities, respectively. Forces and stresses for the converged structures were optimized and checked to within the error allowance of the VASP and QE codes. Troullier-Martins norm-conserving scheme [24] was used to generate the pseudopotentials for C, H, and K atoms. An 8 × 8 × 8 Monkhorst-Pack k-point grid with Gaussian smearing of 0.03 Ry was used for the electron-phonon interaction matrix element calculations at 2 × 2 × 2 q-point mesh.
3. Results and Discussion
3.1. Prediction of Superconductivity in Benzene and Naphthalene
As a comparison and a check on accuracy, we start our investigation by looking at solid benzene. Figure 1A shows the optimized crystal structure of solid benzene from different orthographic directions, with crystal lattice constants a = 7.041 Å, b = 8.903 Å, and c = 6.357 Å at zero temperature and ambient pressure, which are 3–6% less than experimental values at 78 K [12]. If the effect of temperature is considered, the error between theoretical prediction and experimental measurement is acceptable. Solid benzene is a wide band gap insulator as shown in Figure S1A. Our calculated band gap of 4.1 eV is in good agreement with previous results [13]. From the reported data on PAHs, their superconductivity is highly sensitive to both the doping concentration and the cation positions in the unit cell. To examine both effects, we performed optimization studies on doped solid benzene, KxC6H6, by varying potassium contents (x = 1, 2, 3) and the position of K atoms in the unit cell. The optimized crystal lattice constants and atomic coordinates are summarized in Table S1. The formation energy (Ef) is a good indication for examining the stability. We calculated the formation energy of the doped system using the following:
where EKxC6H6 and EC6H6 is the total energy of the doped and host solid benzene, respectively. x is the number of doped K atoms. μK is the chemical potential of the K species. μK(bulk) can be obtained from the energy per K atom in the K metal with the bcc structure. When μK = μK(bulk), the doped element content is so rich that the related pure element phase can form. When Ef < 0, the doped compound can stably exist. The calculated result (see Figure S2) shows that K2C6H6 has lower formation energy than K1C6H6 and K3C6H6 in a certain region of chemical potential, and its associated negative sign suggests easier synthesis.
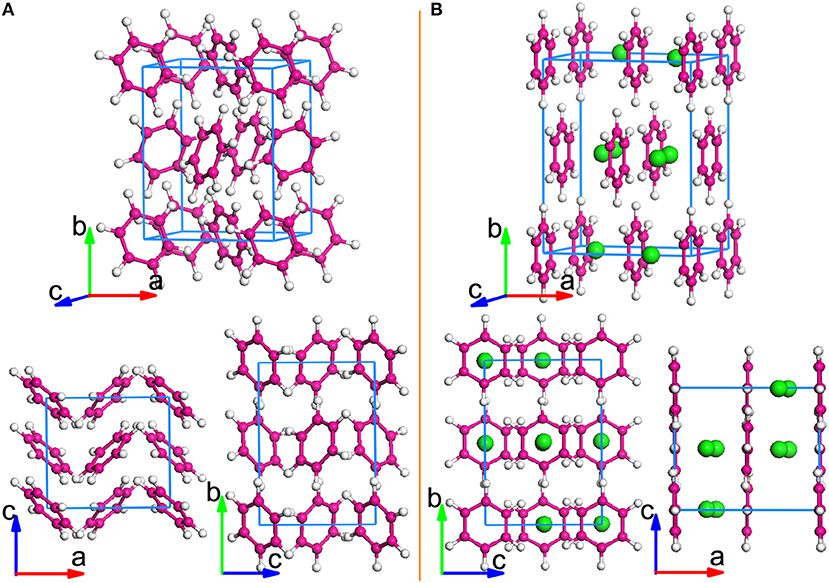
Figure 1. Crystal structures of undoped and K-doped benzene. (A) Optimized crystal structures of solid benzene. (B) Crystal structure of K-doped solid benzene K2C6H6. The structures are viewed from different axial directions. K-atoms are represented by Green spheres.
Figure 1B shows the optimized K2C6H6 crystal structure from different directions, with the following lattice constants: a = 8.605 Å, b = 10.705 Å, and c = 6.415 Å. When compared with the undoped case, we found that the lattice constants expand largely in the a and b directions. The insertion of eight K-atoms makes the volume expand by 26.9%. By K doping, a visible layered structure is formed, differing from that of the solid benzene. As shown in Figure 1B, all benzene rings are rotated and parallel to the bc-plane under the interaction of dopants, and K atoms are intercalated into two layers of benzene rings, occupying the Wyckoff 8c sites. The optimized structure of K2C6H6 is found to tend toward the higher symmetry of Fmmm from the lower Pbca symmetry. Significantly, as shown in Figure S3, the layered structure of K2C6H6 is similar to those of YbC6 and CaC6 [25]. This similarity indicates the possibility of superconductivity, because both YbC6 and CaC6 are known superconductors, with their Tc's reaching 6.5 K and 11.5 K, respectively [25, 26].
Once the crystal structure is determined, it is possible to obtain information about the electronic band structure. For K2C6H6, eight conduction bands (called CB1, CB2, …and CB8) along a high symmetry k-direction, Γ − Z − T − Y − S − X − U − R, of the Brillium zone are shown in Figure 2A. Specifically, under either Pbca or Fmmm symmetry, the lowest unoccupied molecular orbitals (LUMO) and LUMO+1 split into eight bands from Γ to Z, then they merge into four degenerate bands along the Z − T − Y − S − X − U directions, and further into two highly degenerated bands along the U − R direction. Electrons transferred from the K atoms to the C6H6 molecule occupy low energy orbitals and raise the Fermi level. Three bands—CB1, CB2, and CB3—are fully occupied by six of eight electrons, while the other three—CB4, CB5 and CB6—are partially filled by the remaining two electrons with Fermi level passing through. Both CB7 and CB8 are empty. Thus, K2C6H6 is metallic but in the low-spin state. Compared with the solid benzene, we noticed that the intermolecular distance along benzene rings becomes smaller on the bc-plane of K2C6H6. This effect enhances the intermolecular interaction and broadens the dispersion of energy bands. Analyzing the electronic characters near the Fermi level, as shown in Figure 2B, we found that the hole-like Fermi surfaces are formed by CB4 along the Γ − Z k-direction, while both CB5 and CB6 contribute the electron-like Fermi surfaces around the Y k-point. Fermi surface nesting is quite clear. Calculation of the projected density of states (PDOS) shows that the C-py and C-pz states are fully occupied and far below the Fermi level, while the C-px state has a large PDOS around the Fermi level, as shown in Figure 2C. Most PDOS of K-(s, px, py, pz) states are above the Fermi level, indicating the electrons transfer from K to C-px orbital. The large ratio of C-px PDOS over K PDOS follows that C-px electronic states contribute more to the Fermi surfaces.
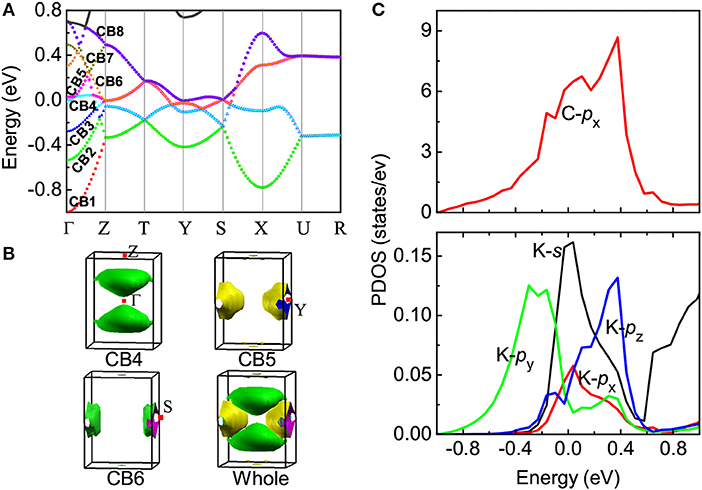
Figure 2. Electronic band structure of K2C6H6. (A) Energy band; (B) fermi surface; (C) projected density of states (PDOS), where zero energy denotes the Fermi level.
Next we examine whether this simplest aromatic hydrocarbon could exhibit superconductivity like other PAHs observed with superconductivity [6–9]. Assuming the pairing mechanism is still electron-phonon interaction mediated [22, 27], we evaluated the Eliashberg spectral function α2F(ω), the electron-phonon coupling integral λ(ω), and projected phonon density of states (PhDOS) of K2C6H6 as a function of frequency. The results are shown in Figure 3. The vibration in the low frequency range of 0–250 cm−1 comes mainly from K, C, and H atom modes as shown in Figure 3C. The appearance of phonon modes of C and H atoms in the region of low frequency implies a weak intermolecular interaction. The modes with moderate frequencies of 300–1450 cm−1 are formed by C and H vibrations (Figure 3C), which results from the intramolecular interaction. The total λ is 0.67, which is comparable to that of K3C22H14 [22] when assuming that the superconductivity in K3C22H14 is mainly mediated by the electron-phonon interaction. As shown in Figure 3B, we also noted that vibrational modes from C and H atoms contribute 58% and 19% to the total λ value, respectively, while the remaining 23% is provided by the dopant phonon modes. Following the modified McMillan equation of Allen and Dynes [28], with the obtained values of λ(ω) and logarithmic average of phonon frequencies ωlog, and a typical value of 0.10 for the Coulomb pseudopotential μ⋆, we obtained Tc = 6.2 K for K2C6H6.
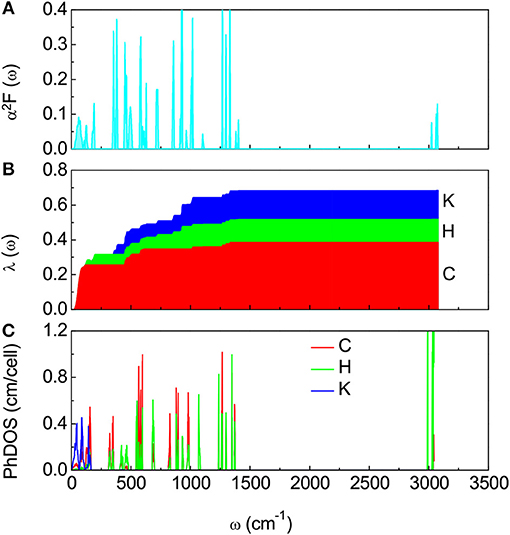
Figure 3. Electron-phonon coupling and phonon density of states of K2C6H6. (A) Electron-phonon coupling Eliashberg spectral function α2F(ω). (B) Electron-phonon coupling integral λ(ω) resolved by projections on C, H, and K phonons. (C) Phonon density of states (PhDOS) of K2C6H6 projected on C, H, and K modes.
The dominant contribution to the total λ from the vibrational modes of the C atoms in K2C6H6 shows some similarity with other C6-based or low-carbon-bearing compounds. In reality, CaC6 was discovered to exhibit superconductivity at 11.5 K [25]. Superconductivity has also been discovered in intercalation compounds of graphite with alkali metals AC8 (A = K, Rb, or Cs) [29]. The predicted Tc of 6.2 K in K2C6H6 is comparable to the temperature range of these low-carbon-based superconductors [25, 29].
Naphthalene (C10H8) is the second simple aromatic compound. Following the benzene crystal, a careful analysis on the 2-ring case also showed that K-doped naphthalene (KxC10H8) possesses a superconducting phase with Tc~5.2 K comparable to the doped solid benzene. The crystal structures induced by doping are shown in Figure S4 and the lattice parameters are listed in Table S2. K2C10H8 was identified to be a more stable phase from the calculated formation energy result shown in Figure S5. As observed in solid benzene, the doping of two electrons per molecule is the most stable. Different from the metallicity in K2C6H6, K2C10H8 is a semiconductor with a band gap about 0.75 eV. Similar to charged chrysene (C18H12) [30] and picene (C22H14), however, naphthalene would become a metal if doped with two electrons with a small amount of charge fluctuations (see [24] and Figures S6–S8). For charged K2C10H8, the Eliashberg spectral function α2F(ω) and the electron-phonon coupling integral λ(ω) as a function of frequency were also investigated (Figure S9). The values of λ = 0.64 and Tc = 5.8 K (μ⋆ = 0.1) were obtained for the K2C10H8 charged with the 0.1e per molecule. These calculated results on superconductivity of doped naphthalene have similarities with those of doped benzene.
3.2. Variation of Superconducting Transition Temperature Among Aromatic Hydrocarbons
By the same approach mentioned above, we have also investigated the superconductivity of K-doped phenanthrene (KxC14H10). The theoretically predicted Tc for this material is marked out in Figure 4, which is in good agreement with the experimental value. The calculated superconducting parameters of KxC14H10 are presented in Figure S10C and Table S3. A comparison of the predicted superconducting of benzene, naphthalene and phenanthrene with other PAHs reveals a common feature of aromatic hydrocarbons (Figure 4). Besides the reported high-Tc phases with Tc = 18 K for K-doped picene (KxC22H14) [6], 15 K for K-doped coronene (KxC24H12) [7], and 33 K for K-doped 1,2:8,9-dibenzpentacene (KxC30H18) [9], multi-superconducting phases in long-benzene-ring hydrocarbons were generally observed. A low Tc phase with almost the same Tc range, 5−7 K, exists in these hydrocarbon superconductors discovered so far [6–9]—5 K for KxC14H10 [8], 7 K for KxC22H14 [6, 7], and 7.4 K for KxC30H18 [9]—though several other transitions with higher Tc's were also observed. Tc of 5−7 K was also reported for KxC24H12 [7] in addition to three other transitions. Moreover, both Rb3C22H14 and Ca1.5C22H14 show the superconducting transition at temperatures around 7 K [6]. In particular, Sm-doped phenanthrene, chrysene and picene show the superconductivity around Tc~5 K [31]. It is important to note that the superconducting transitions were readily observed in the temperature range of 5−7 K for all reported aromatic hydrocarbons with various numbers of benzene rings. These observations are in good agreement with our current prediction for benzene, naphthalene, and phenanthrene, the relatively simple compounds of this series. So a natural question is what accounts for this most common low-Tc phase and why the compounds with multiple benzene rings have high-Tc phases.
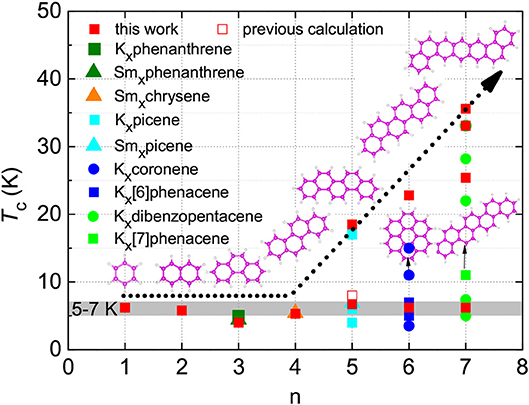
Figure 4. Superconducting transition temperatures of aromatic hydrocarbons. Variation of superconducting transition temperature Tc with the number of benzene rings (n) for various aromatic hydrocarbons. The gray region is the guide for eyes. Solid red squares represent our predicted results, while the hollow red square implies the predicted result by Casula et al. [22] Other data are taken from experiments.
For the number of benzene rings from one to seven, we have compared the growth situations of all aromatic hydrocarbons based on the calculated formation energies shown in Figures S11, S12. For K-doped phenanthrene shown in Figure S11C, similar to benzene and naphthalene, K2C14H10 is more stable in the chemical potential region satisfying Ef < 0. Hence, we suggest that the superconducting phase of Tc~5 K observed by experiment [8] is K2C14H10 instead of K3C14H10. For K-doped chrysene (KxC18H12), a four-benzene-ring system, our previous study [30] has indicated that K2C18H12 is the most stable case in the chemical potential region satisfying Ef < 0 (Also see Figure S11D). As a result, when intercalating two K atoms, the doped system is the most stable for benzene, naphthalene, phenanthrene, and chrysene. Here, we call them short-benzene-ring systems. Differing from these short-benzene-ring systems, satisfying Ef < 0, as shown in Figure S12A, K2C22H14 firstly obtains stable phase with the increase of K chemical potential, and then, under the K-rich limited condition, the high-concentration doping phase of K3C22H14 can also be obtained. The same situations also occur in K-doped [6]phenacene (KxC26H16) and KxC30H18 (See Figure S12). Thus we put picene, [6]phenacene, and 1,2;8,9-dibenzopentacene in the same class as long-benzene-ring systems. From these calculated results, for short-benzene-ring systems, the doping of two electrons is the most stable, while for long-benzene-ring systems, both the dopings of two and three electrons are, respectively, the more stable phase in the different regions of K chemical potential. Thus, the doping phases with different K contents can be obtained in long-benzene-ring systems. However, in all aromatic hydrocarbons, stability with two-electron doping is a common feature. The unified phases with two-electron dopant for all the studied compounds in this series are consistent with recent experiments [11].
With these analyses above, we are confident to conclude that the presence of the superconducting phase with Tc around 5 − 7 K is a common feature of all aromatic hydrocarbons. In most cases, the low-Tc phase was easily fabricated and more stable than the higher Tc phase [6, 7, 9]. Considering the fact that the cation concentration has never been experimentally identified by using the reliable neutron scattering or single crystal X-ray diffraction techniques, all the reported doping levels are an ideal chemical estimation based on the synthesis procedure. Our phase stability examination for K-doped aromatic hydrocarbons pins down the doping concentration of the exact two electrons for the stable superconducting phase of these hydrocarbons with Tc of 5 − 7 K. The superconducting phase with high-Tc is apparently the characteristic feature of long-benzene-ring systems, tending toward high-concentration doping such as three or more electrons.
In addition, we have investigated the density of states at Fermi level (N(EF)) to analyze the origin of this unified superconducting phase, since the stable phase of low-concentration doping can be obtained in all aromatic hydrocarbons. As shown in Figure 5, the low-concentration K2-doping results in small and comparable values on the N(EF) for all aromatic hydrocarbons. Moreover, the obtained ωlog values of 199.8 K for K2C6H6, 210.4 K for charged K2C10H8, and 193.7 K for K2C14H10 are also comparable in quantity with 207 K of K3C22H14 as shown in [19]. These results indicate that almost the same strength of electron-phonon coupling exists in all the K2-doping cases. Based on the superconductivity mediated by the electron-phonon interaction, we suggest that the unified superconducting phase of 5 − 7 K mainly comes from the low and the almost-same N(EF) value induced by two-electron doping. The electron-phonon interaction is enough to describe the superconductivity of this unified superconducting phase. With the help of the analysis of stability and DOS at the Fermi level above, we predict that the Tc of K-doped chrysene is in the range of 5 − 7 K as shown in Figure 4. Although a complete understanding of the mechanism of superconductivity in aromatic hydrocarbons is yet to be achieved, the common feature of the 5 − 7 K superconducting phase for all reported aromatic hydrocarbons provides important clues for understanding the superconductivity itself as well as for the search of new superconductors in this series.
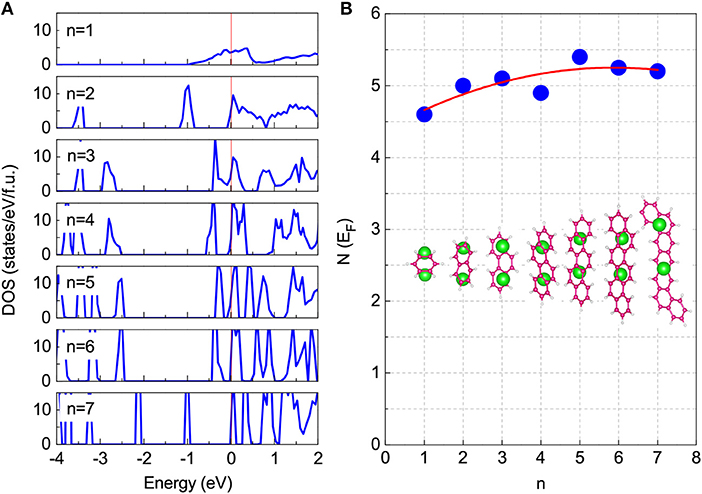
Figure 5. Total density of states (DOS) for K2-doped cases. n represents the number of benzene rings in system. These systems include K2C6H6 (n = 1), charged (K2C10H8)+0.1e (n = 2), K2C14H10 (n = 3), charged (K2C18H12)+0.1e (n = 4), charged (K2C22H14)+0.1e (n = 5), charged (K2C26H16)+0.1e (n = 6), and charged (K2C30H18)+0.1e (n = 7), respectively. (A) The results of DOS for K2-doped cases are presented. Zero energy denotes the Fermi level. (B) The DOS at Fermi level (N(EF)) varies with n. The corresponding structures are also inserted.
For long-benzene-ring systems, multi-doping concentrations are feasible. At a high-concentration doping level, as shown in Figure 6, K3-doping clearly leads to larger values of N(EF) compared with K2-doping. Within the framework of the BCS theory, K3-doping can drive a stronger electron-phonon interaction to exhibiting higher-Tc superconductivity. Hence, for each long-benzene-ring system, this high-Tc phase is related to the high N(EF) value induced by the three-electron doping. Regarding the enhancement of superconductivity among aromatic hydrocarbons, this is also related to the increase of the N(EF) with the number of benzene rings as shown in Figure 6B. Based on the discussion above combining the stability with the values of N(EF), we predicted that the Tc of K2-doped PAHs is in the range of 5 − 7 K, while the Tc of K3C22H14, K3C26H16, K3C30H18, K3.17C30H18, and K3.45C30H18 is 18.5, 22.8, 25.4, 33.1, and 35.6 K, respectively. These results, shown in Figure 4 (marked with solid red squares), are consistent with experiments.
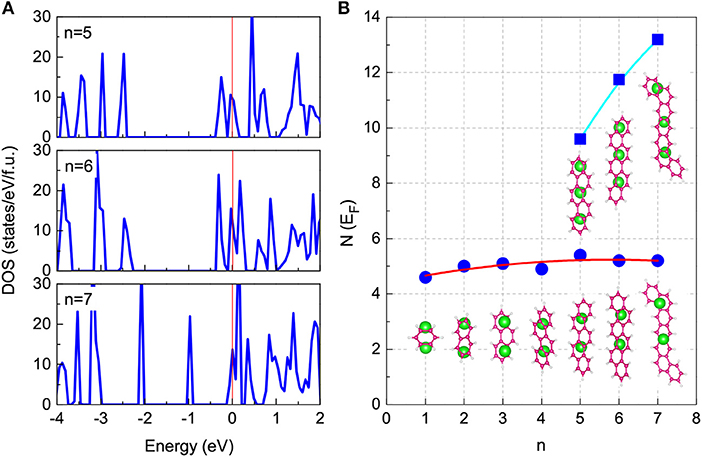
Figure 6. Total DOS for K3-doped cases with the long-benzene-ring chain. (A) The results of DOS for K3-doped cases of K3C22H14, K3C26H16, and K3C30H18 are presented. Zero energy denotes the Fermi level. (B) The N(EF) of K3-doped cases is compared with that of K2-doped cases. The corresponding structures are also inserted.
3.3. Electronic Correlations
In this section we address mechanism for high-Tc phases. Although electron-phonon interaction is still possible to account for higher transition temperatures with certain crystal structure, other possibilities exist. Like other superconductors such as cuprates, further investigations indicate that the electron-electron correlations seem to play an important role on superconductivity in these systems. In fact, this was similar to charge-transfer organic superconductors [32–37] and fullerides [3, 38], where the importance of electron correlations on superconductivity was emphasized. Magnetic measurements [8] on phenanthrene suggest the existence of local spin moments and indicate similar interplay between magnetism and superconductivity observed in fullerides [3].
To gain some insights on the exchange-correlation effects of electron-electron (e-e), we have carried out the series of calculations using the hybrid functionals method (HSE) [39, 40]. The exchange-correlation energy was written as
where μ is a screened Coulomb potential which splits the electron-electron exchange interaction into short-range (SR) and long-range (LR) components, the mixing coefficient ν represents the amount of exact/DFT exchange, indicating the extent of Fock exchange and reflecting the intensity of electronic correlation. Within the framework of the HSE method, the correlation interaction is still presented by the PBE functional form [41], the exchange interaction is separated into two parts—SR and LR. The LR exchange item is also described by PBE functional form, while the SR exchange item further splits into exact exchange and PBE forms. Both μ and ν are adjustable parameters; in this calculation, we adjusted them to investigate the extension of e-e interactions in PAH compounds.
For PAH crystal, the band gap is one of the electronic properties reflected by the exchange-correlation interactions. Usually, the LDA functional underestimates the value of band gap due to the incompletely counting of exchange-correlation effects. As mentioned above, the HSE functional can correct the exchange-correlation interaction in PAH compounds as possible as well. The parameter ν just describes the magnitude of the exchange-correlation effects by fitting the band gap between theoretical values and experimental ones. Table 1 lists out the parameters of μ and ν fitting experimental band gaps for the typical systems such as solid phenanthrene (3rings-A), chrysene [4rings-A(B)], picene (5rings-A), 1,2:5,6-dibenzanthracene (5rings-B), [6]phenacene (6rings-A), 1,2:7,8-dibenzanthracene (6rings-B), [7]phenacene (7rings-A), and 1,2:8,9-dibenzopentacene (7rings-B), respectively. Results show that the ratio ν of exact/DFT exchange becomes larger with the increase of the number of rings whether μ is 0.1 or 0.2, indicating the enhancement of electronic exchange-correlation interactions with the increase of the number of benzene rings.

Table 1. Based on the LDA, the calculated band gap (Eg) is smaller than the experimental one for each PAH. Reproducing the experimental band gap, the values of the μ and ν parameters are presented.
Another quantity to calculate is the effective Coulomb interaction, e.g., the Hubbard U. Combining the estimated Hubbard U with the calculated bandwidth of bands crossing the Fermi level (see the computational details in the Supplementary Material), we indeed found that the electron-electron correlation becomes important as the number of benzene rings increases, as shown in Figure 7. Multi-ring hydrocarbons are in favor of strong correlations and thus tend to have higher Tcs. It is therefore believed that both the electron-phonon interaction and electron-electron correlations work together to enhance Tc of the PAHs with increasing the number of benzene rings.
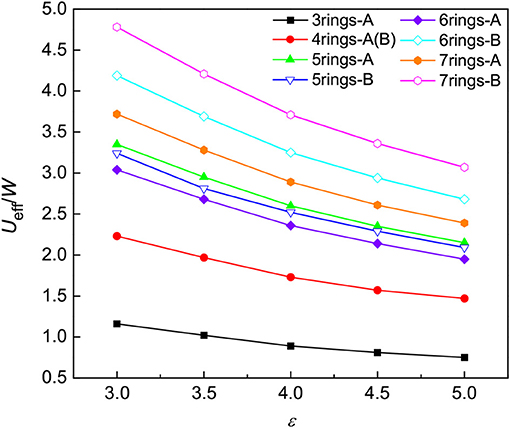
Figure 7. The electron-electron correlations of aromatic hydrocarbons. The effective electronic correlation parameter Ueff/W of two kinds of optimized structures is plotted as a function of the dielectric constant ε. The configuration with the zigzag arrangement of benzene rings is classified as A, such as phenanthrene and picene, while B denotes the configuration with the arrangement of benzene rings such as 1,2:8,9-dibenzpentacene and 1,2:5,6-dibenzanthracene.
4. Conclusions
In summary, carrying out first-principles calculations, we have investigated the crystal structures and possible superconductivity in potassium-doped solid benzene and naphthalene. Furthermore, we have analyzed the stability from formation energy, electronic structures near the Fermi level, and electronic correlations of K-doped PAHs. It was found that: (1) Solid benzene can be superconducting when doping with two K atoms; (2) the low Tc phase of 5 − 7 K is a common feature in all aromatic hydrocarbon superconductors—for this unique superconducting phase, the doping level is around two electrons in both short-benzene-ring and long-benzene-ring systems, and the electron-phonon interaction is enough to account; and (3) for higher Tc phases in long-benzene-ring systems, the doping level tends toward three electrons. Both the electron-phonon interaction and electron-electron correlations work together to enhance the Tc in long-benzene-ring systems.
Author Contributions
X-JC and H-QL designed research. G-HZ performed calculations. G-HZ, X-JC, and H-QL analyzed the results. G-HZ, X-JC, and H-QL wrote the first draft of the paper and all authors contributed to revisions. All authors reviewed the manuscript.
Funding
H-QL acknowledges financial support from NSAF U1530401 and computational resources from the Beijing Computational Science Research Center. The work was also supported by the Basic Research Program of Shenzhen under grant Nos. JCYJ20170818153404696 and JCYJ20180507182445460. Partial calculation was supported by the Special Program for Applied Research on Super Computation of the NSFC-Guangdong Joint Fund (the second phase) under Grant No. U1501501.
Conflict of Interest Statement
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Acknowledgments
The authors thank Z. B. Huang, C. Zhang, X. W. Yan, and C. L. Yang for valuable discussions.
Supplementary Material
The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fphy.2019.00052/full#supplementary-material
References
1. Ginzburg V. High-temperature superconductivity-dream or reality? Sov Phys Usp. (1976) 19:174–9. doi: 10.1070/PU1976v019n02ABEH005136
2. Hebard A, Rosseinsky M, Haddon R, Murphy D, Glarum S, Palstra T, et al. Superconductivity at 18 K in potassium-doped C60. Nature. (1991) 350:600–1. doi: 10.1038/350600a0
3. Ganin A, Takabayashi Y, Khimyak Y, Margadonna S, Tamai A, Rosseinsky M, et al. Bulk superconductivity at 38 K in a molecular system. Nat Mater. (2008) 7:367–71. doi: 10.1038/nmat2179
4. Jerome D, Mazaud A, Ribault M, Bechgarrd K. Superconductivity in a synthetic organic conductor (TMTSF)2PF6. J Phys. (1980) 41:L95–8.
5. Taniguchi H, Miyashita M, Uchiyama K, Satoh K, Mori N, Okamoto H, et al. Superconductivity at 14.2 K in layered organics under extreme pressure. J Phys Soc Jpn. (2003) 72:468–71. doi: 10.1143/JPSJ.72.468
6. Mitsuhashi R, Suzuki Y, Yamanari Y, Mitamura H, Kambe T, Ikeda N, et al. Superconductivity in alkali-metal-doped picene. Nature. (2010) 464:76–9. doi: 10.1038/nature08859
7. Kubozono Y, Mitamura M, Lee X, He X, Yamanari Y, Takahashi Y, et al. Metal-intercalated aromatic hydrocarbons: a new class of carbon-based superconductors. Phys Chem Chem Phys. (2011) 13:16476–93. doi: 10.1039/c1cp20961b
8. Wang X, Liu R, Gui Z, Xie Y, Yan Y, Ying J, et al. Superconductivity at 5 K in alkali-metal-doped phenanthrene. Nat Commun. (2011) 2:507–13. doi: 10.1038/ncomms1513
9. Xue M, Cao T, Wang D, Wu Y, Yang H, Dong X, et al. Superconductivity above 30 K in alkali-metal doped hydrocarbon. Sci Rep. (2012) 2:389. doi: 10.1038/srep00389
10. Takabayashi Y, Menelaou M, Tamura H, Takemori N, Koretsune T, Štefančič A, et al. π-electron S=1/2 quantum spin-liquid state in an ionic polyaromatic hydrocarbon. Nat Chem. (2017) 9:635–43. doi: 10.1038/nchem.2764
11. Romero F, Pitcher M, Hiley C, Whitehead G, Kar S, Ganin A, et al. Redox-controlled potassium intercalation into two polyaromatic hydrocarbon solids. Nat Chem. (2017) 9:644–52. doi: 10.1038/nchem.2765
12. Kozhin V, Kitaigorodskii A. Nizkotemperaturnye issledovaniya struktury aromaticheskikh soedinenii. 4. anizotropiya teplovogo rasshireniya v benzole. Zh Fiz Khim. (1955) 29:2074–5.
13. Thiéry M, Léger J. High-pressure solid-phases of benzene. 1. Raman and x-ray studies of C6H6 at 294 K up to 25 GPa. J Chem Phys. (1988) 89:4255–71. doi: 10.1063/1.454809
14. Ciabini L, Santoro M, Gorelli F, Bini R, Schettino V, Raugei S. Triggering dynamics of the high-pressure benzene amorphization. Nat Mater. (2007) 6:39–43. doi: 10.1038/nmat1803
15. Wen X, Hoffmann R, Ashcroft N. Benzene under high pressure: a story of molecular crystals transforming to saturated networks, with a possible intermediate metallic phase. J Am Chem Soc. (2011) 13:9023–35. doi: 10.1021/ja201786y
16. López E, Lucas J, de Andrés J, Albertí M, Bofill J, Bassi D, et al. Cross-section energy dependence of the [C6H6M]#43; adduct formation between benzene molecules and alkali ions (M = Li, Na, K). Phys Chem Chem Phys. (2011) 13:15977–84. doi: 10.1039/c1cp21889a
17. Kresse G, Furthmuller J. Efficiency of ab-initio total energy calculations for metals and semiconductors using a plane-wave basis set. Comput Mater Sci. (1996) 6:15–50. doi: 10.1016/0927-0256(96)00008-0
18. Kresse G, Furthmuller J. Efficient iterative schemes for ab Initio total-energy calculations using a plane-wave basis set. Phys Rev B. (1996) 54:11169–86. doi: 10.1103/PhysRevB.54.11169
19. Kresse G, Joubert D. From ultrasoft pseudopotentials to the projector augmented-wave method. Phys Rev B. (1999) 59:1758–75. doi: 10.1103/PhysRevB.59.1758
20. Ceperley D, Alder B. Ground state of the electron gas by a stochastic method. Phys Rev Lett. (1980) 45:566–9. doi: 10.1103/PhysRevLett.45.566
21. Perdew J, Zunger A. Self-interaction correction to density-functional approximations for many-electron systems. Phys Rev B. (1981) 23:5048–79. doi: 10.1103/PhysRevB.23.5048
22. Casula M, Calandra M, Profeta G, Mauri F. Intercalant and intermolecular phonon assisted superconductivity in K-doped picene. Phys Rev Lett. (2011) 107:137006. doi: 10.1103/PhysRevLett.107.137006
23. Giannozzi P, Baroni S, Bonini N, Calandra M, Car R, Cavazzoni C, et al. QUANTUM ESPRESSO: a modular and open-source software project for quantum simulations of materials. J Phys Condens Matter. (2009) 21:395502. doi: 10.1088/0953-8984/21/39/395502
24. Troullier N, Martins J. Efficient pseudopotentials for plane-wave calculations. Phys Rev B. (1991) 43:1993–2006. doi: 10.1103/PhysRevB.43.1993
25. Weller T, Ellerby M, Saxena S, Smith P, Skipper N. Superconductivity in the intercalated graphite compounds C6Yb and C6Ca. Nat Phys. (2005) 1:39–41.
26. Emery N, Hérold C, d'Astuto M, Garcia V, Bellin C, Marêché J, et al. Superconductivity of bulk CaC6. Phys Rev Lett. (2005) 95:087003. doi: 10.1103/PhysRevLett.95.087003
27. Kato T, Kambe T, Kubozono Y. Strong intramolecular electron-phonon coupling in the negatively charged aromatic superconductor picene. Phys Rev Lett. (2011) 107:077001. doi: 10.1103/PhysRevLett.107.077001
28. Allen P, Dynes R. Transition temperature of strong-coupled superconductors reanalyzed. Phys Rev B. (1975) 12:905–22. doi: 10.1103/PhysRevB.12.905
29. Hannay N, Geballe T, Matthias B, Andres K, Schmidt P, MacNair D. Superconductivity in graphitic compounds. Phys Rev Lett. (1965) 14:225–6. doi: 10.1103/PhysRevLett.14.225
30. Wang X, Zhong G, Yan X, Chen X, Lin H. First-principles prediction on geometrical and electronic properties of K-doped chrysene. J Phys Chem Solids. (2017) 104:56–61. doi: 10.1016/j.jpcs.2017.01.004
31. Artioli G, Hammerath F, Mozzati M, Carretta P, Corana F, Mannucci B, et al. Superconductivity in Sm-doped [n]phenacenes (n = 3, 4, 5). Chem Commun. (2015) 51:1092–5. doi: 10.1039/C4CC07879A
32. Kivelson S, Chapman O. Polyacene and a new class of quasi-one-dimensional conductors. Phys Rev B. (1983) 28:7236–43. doi: 10.1103/PhysRevB.28.7236
33. Karakonstatakis G, Berg E, White S, Kivelson S. Enhanced pairing in the checkerboard Hubbard ladder. Phys Rev B. (2011) 83:054508. doi: 10.1103/PhysRevB.83.054508
34. Giovannetti G, Capone M. Electronic correlation effects in superconducting picene from ab initio calculations. Phys Rev B. (2011) 83:134508. doi: 10.1103/PhysRevB.83.134508
35. Huang Z, Zhang C, Lin H. Magnetic instability and pair binding in aromatic hydrocarbon superconductors. Sci Rep. (2012) 2:922. doi: 10.1038/srep00922
36. Kim M, Min B, Lee G, Kwon H, Rhee Y, Shim J. Density functional calculations of electronic structure and magnetic properties of the hydrocarbon K3picene superconductor near the metal-insulator transition. Phys Rev B. (2011) 83:214510. doi: 10.1103/PhysRevB.83.214510
37. Ruff A, Sing M, Claessen R, Lee H, Tomic M, Jeschke H, et al. Absence of metallicity in K-doped picene: importance of electronic correlations. Phys Rev Lett. (2013) 110:216403. doi: 10.1103/PhysRevLett.110.216403
38. Duband P, Darling G, Dubitsky Y, Zaopo A, Rosseinsky M. The Mott-Hubbard insulating state and orbital degeneracy in the superconducting C fulleride family. Nat Mater. (2003) 2:605–10. doi: 10.1038/nmat953
39. Heyd J, Scuseria G, Ernzerhof M. Hybrid functionals based on a screened Coulomb potential. J Chem Phys. (2003) 118:8207–15. doi: 10.1063/1.1564060
40. Heyd J, Scuseria G. Efficient hybrid density functional calculations in solids: assessment of the Heyd-Scuseria-Ernzerhof screened Coulomb hybrid functional. J Chem Phys. (2004) 121:1187. doi: 10.1063/1.1760074
41. Perdew J, Burke K, Ernzerhof M. Generalized gradient approximation made simple. Phys Rev Lett. (1996) 77:3865. doi: 10.1103/PhysRevLett.77.3865
42. Bhatti M, Ali M, Shahid G, Saleh M. Characterization of phenanthrene single crystals. Turk J Phy. (2000) 24:673–9.
43. Roth F, Mahns B, Schofelder R, Hampel S, Nohr M, Buchner B, et al. Comprehensive studies of the electronic structure of pristine and potassium doped chrysene investigated by electron energy-loss spectroscopy. J Chem Phys. (2012) 137:114508. doi: 10.1063/1.4753999
44. Okamoto H, Kawasaki N, Kaji Y, Kubozono Y, Fujiwara A, Yamaji M. Air-assisted high-performance field-effect transistor with thin films of picene. J Am Chem Soc. (2008) 130:10470–1. doi: 10.1021/ja803291a
45. Chang N, Mori H, Chen X, Okuda Y, Okamoto T, Nishihara Y. Synthesis of substituted [6]Phenacenes through suzuki-miyaura coupling of polyhalobenzene with alkenylboronates and sequential intramolecular cyclization via C-H bond activation. Chem Lett. (2013) 42:1257–9. doi: 10.1246/cl.130584
Keywords: aromatic hydrocarbons, benzene, naphthalene, superconductivity, electron-phonon coupling, electronic correlations, first principles
Citation: Zhong G-H, Chen X-J and Lin H-Q (2019) Superconductivity and Its Enhancement in Polycyclic Aromatic Hydrocarbons. Front. Phys. 7:52. doi: 10.3389/fphy.2019.00052
Received: 29 November 2018; Accepted: 20 March 2019;
Published: 12 April 2019.
Edited by:
Shruba Gangopadhyay, University of Virginia, United StatesReviewed by:
Hamit Yurtseven, Middle East Technical University, TurkeyRui-Qin Zhang, City University of Hong Kong, Hong Kong
Soham Ghosh, University of California, Davis, United States
Copyright © 2019 Zhong, Chen and Lin. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Xiao-Jia Chen, eGpjaGVuQGhwc3Rhci5hYy5jbg==
Hai-Qing Lin, aGFpcWluZzBAY3NyYy5hYy5jbg==
 Guo-Hua Zhong
Guo-Hua Zhong Xiao-Jia Chen3*
Xiao-Jia Chen3* Hai-Qing Lin
Hai-Qing Lin