- Department of Physics and Astronomy, Vanderbilt University, Nashville, TN, United States
In the search for superheavy elements quasifission reactions represent one of the reaction pathways that curtail the formation of an evaporation residue. In addition to its importance in these searches quasifission is also an interesting dynamic process that could assist our understanding of many-body dynamical shell effects and energy dissipation thus forming a gateway between deep-inelastic reactions and fission. This manuscript gives a summary of recent progress in microscopic calculations of quasifission employing time-dependent Hartree-Fock (TDHF) theory and its extensions.
1. Introduction
The ongoing search for discovering new elements in the superheavy regime is perhaps the most exciting but at the same time challenging tasks in low-energy nuclear physics [1]. These searches were historically motivated by theoretical predictions of an island of stability, somewhat detached from the far end of the chart-of-nuclides [2–5], due to quantum mechanical shell closures. The experimental search for the so called superheavy elements (SHE) was initially done by using target projectile combinations that minimized the excitation energy of compound nuclei that was formed in reactions studied in the vicinity of the Coulomb barrier. For this reason these reactions are commonly referred to as cold fusion reactions and primarily involved closed shell nuclei, such as 208Pb target and projectiles in the chromium to zinc region. The cold fusion experiments were able to produce elements Z = 107–113 [6–8], but showed no indication that extending them to heavier elements were feasible. The identification of a SHE is done through the decay properties of a formed evaporation residue. In such reactions involving heavy elements the dominant reaction processes are quasifission (QF) and fusion-fission (FF), which are expected to strongly suppress the formation of an evaporation residue at higher excitation energies. For this reason it was a major surprise to observe that the so called hot fusion reactions, despite of their higher excitation energy, were able to synthesize elements Z = 113–118 [9, 10]. The hot fusion reactions utilized actinide targets with 48Ca projectiles. To further pursue the hot fusion reactions with heavier projectiles to reach elements Z > 120 requires a deeper understanding of the reaction pathways leading to an evaporation residue, particularly QF and FF components. In all of these reactions the evaporation residue cross-section is dramatically reduced due to the quasifission (QF) and fusion-fission (FF) processes. These processes occur during the reactions of heavy systems and correspond to excited fission channels in the classically allowed regime above the barrier and require a combination of statistical and truly dynamical approaches which are not necessarily confined to a collective subspace. Fusion-fission occurs after the formation of a composite system which then fissions due to its excitation, ultimately resulting in a fragment distribution that is peaked at equal mass breakup of the composite system. Quasifission occurs at a considerably shorter time-scale than fusion-fission [11–13] and is characterized by reaction fragments that differ significantly in mass from the original target/projectile nuclei. Quasifission for being one of the primary reaction mechanism that limits the formation of superheavy nuclei [14–16] has been the subject of intense experimental studies of [11–13, 17–24, 24–34]. Studies have also shown a strong impact of the entrance channel characteristics, including deformation [18, 19, 22, 23, 35–37] and shell structure [28] of the reactants. The final phase of the dynamics is also impacted by the fissility of the composite system [26, 29], its neutron richness [32], and by shell effects in the exit channel [12, 13, 20, 23, 24, 31, 38–40]. A number of theoretical approaches have been developed that describe the quasifission in terms of multi-nucleon transfer (MNT) processes [41–47]. Recently, time-dependent Hartree-Fock (TDHF) theory have proven to be an excellent tool for studying QF dynamics, and in particular mass-angle distributions and final fragment total kinetic energies (TKE) [31, 32, 34, 37, 45, 48–56]. While the fragments produced in TDHF studies are the excited primary fragments [57] a number of extensions based on the use of Langevin dynamics have been successfully applied to de-excite these fragments [55, 56, 58–60]. Theoretical studies of quasifission dynamics have taught us that dynamics themselves may be dominated by shell effects [47, 61]. Despite the apparent strong differences between fission and quasifission, it is interesting to note that similar shell effects are found in both mechanisms [54]. Quasifission can then potentially be used as an alternative mechanisms to probe fission mode properties. For instance, this could provide a much cheaper way than fusion-fission to test the influence of 208Pb shell effects in super-asymmetric SHE fission.
2. Microscopic Approaches
The underlying approach to study quasifission on a microscopic basis is the time-dependent Hartree-Fock (TDHF) theory [61–64]. Alternative approaches employ Langevin dynamics [65–67]. Indeed, the TDHF calculations of the quasifission process have yielded results that not only agree with the broad features of the experimental measurements but also shed insight into the relationship of the data to the properties of the participating nuclei. Such features include static deformation that induces dependence on the orientation of the nuclei with respect to the beam axis, shell effects that can predict the primary fragment charges, as well as the dependence of quasifission on neutron-rich nuclei. TDHF calculations give us the most probable reaction outcome for a given set of initial conditions (e.g., energy, impact parameter, orientation). However, quantum mechanically a collection of outcomes are possible for each of these initial conditions. In order to compute such distributions, one must go beyond TDHF and introduce methods to calculate distribution widths or fluctuations for these reactions. Much effort has been done to improve the standard mean-field approximation by incorporating the fluctuation mechanism into the description. At low energies, the mean-field fluctuations make the dominant contribution to the fluctuation mechanism of the collective motion. Various extensions have been developed to study the fluctuations of one-body observables. These include the time-dependent random phase approximation (TDRPA) approach of Balian and Vénéroni [68–72], the time-dependent generator coordinate method [73], or the stochastic mean-field (SMF) method [74, 75]. The effects of two-body dissipation on reactions of heavy systems using the time-dependent density matrix (TDDM) [76, 77] approach have also been recently reported [78, 79]. It is also possible to compute the probability to form a fragment with a given number of nucleons [80–83], but the resulting fragment mass and charge distributions are often underestimated in dissipative collisions [71, 84]. Recent reviews [47, 61] succinctly summarize the current state of TDHF (and its extensions) as it has been applied to various MNT reactions.
3. Insights From TDHF and Beyond
Experiments to discover new elements are notoriously difficult, with fusion evaporation residue (ER) cross-sections in pico-barns (for a recent experimental review see [85]). This cross-section is commonly expressed in the product form [86]
where σcap(Ec.m., L) is the capture cross-section at center of mass energy Ec.m. and orbital angular momentum L. PCN is the probability that the composite system fuses into a compound nucleus (CN) rather than breaking up via quasifission, and Wsur is the survival probability of the fused system against fission. It is thus clear that to have a good handle on the evaporation residue cross-section estimates it is important to understand each of these terms as well as possible. In this endeavor both theory and experiment can have a complementary role. Among these reaction mechanisms quasifission and fusion-fission can be on the order of millibarns, making it easier to study experimentally. However, the extraction of the PCN requires the proper disentangling of quasifission from fusion-fission [87–89] as it may be given by
Of these cross-sections fusion-fission arises from an excited and equilibrated composite system and therefore peaked around equal mass breakup as calculated in a statistical approach [14, 16, 90–92]. On the other hand, quasifission, which is a faster process and thus not fully equilibrated, could also contribute to the equal breakup regime. Consequently, experimental analysis could use assistance from theory to discern between the two processes. The capture cross-section, being the sum of quasifission, fusion-fission, and evaporation residue is relatively easy to measure or calculate and TDHF predictions using the density-constrained TDHF (DC-TDHF) approach have shown to give a relatively good results [52, 93]. Below, we discuss various aspects of the progress done in studying quasifission using TDHF and its extensions.
3.1. Mass Angle Distributions
Study of quasifission together with capture is intimately related to understanding the process for forming a compound nucleus, the quantity named PCN in Equation (1) [87]. Figure 1 shows the time-evolution of the 48Ca+249Bk reaction at Ec.m. = 234 MeV and orbital angular momentum L/ℏ = 60 [54] and the initial orientation of the 249Bk with respect to the collision axis β = 135°. For this orbital angular momentum and energy TDHF theory predicts quasifission. As the nuclei approach each other, a neck forms between the two fragments which grows in size as the system begins to rotate. Due to the Coulomb repulsion and centrifugal forces, the dinuclear system elongates and forms a very long neck which eventually ruptures leading to two separated fragments. In this case the final fragments are 203Au and 94Sr. While the outcome of such reactions in a single TDHF evolution vary greatly depending on the initial conditions, analysis of the fragments' properties can begin to suggest general behavior for systems undergoing quasifission. For example, the composition of the reaction products can be influenced by shell effects in the outgoing fragments [54] which can be inferred by the slight pear shape of the light outgoing fragment at the point of scission in Figure 1.

Figure 1. Quasifission in the reaction 48Ca+249Bk at Ec.m. = 234 MeV and orbital angular momentum L/ℏ = 60 and the orientation of the 249Bk with respect to the collision axis β = 135°. The darkening of tones depict increasing excitation.
However, the result from a single TDHF trajectory is difficult to extrapolate to the system as a whole so systematic investigations are often performed. As the reaction products predicted by TDHF give only the most probable outcome for any given collision geometry and energy, quantities like mass angle distributions produced by direct TDHF calculations result in collections of discrete points. By collecting data from large numbers of TDHF evolutions one can reveal deeper insights into the quasifission process. Recent studies of the 48Ca+249Bk reaction at Ec.m. = 234 MeV with the TDHF approach went beyond solely considering the extreme orientations of the deformed 249Bk nucleus by undertaking calculations spanning both a range of orientations and a range of angular momenta. The orientation of the deformed 249Bk was changed by 15° steps to cover the full range (0, π) with orbital angular momentum L changing in units of 10ℏ from 0 to quasielastic collisions. A total of 150 TDHF collisions were cataloged and analyzed. This allows for the study of correlations between, e.g., mass, angle, kinetic energy, as well as to predict distributions of neutron and proton numbers at the mean-field level.
In Figure 2A we plot the mass angle distribution (MAD) for this reaction. Figure 2B shows the corresponding yield in arbitrary units as a function of the mass ratio MR = M1/(M1+M2), where M1 and M2 are the masses of the final fragments. We note that the yields are strongly peaked at MR~0.33 and 0.67, with a full width at half maximum FWHM ≃ 0.1 corresponding to a standard deviation σMR≃ 0.042. The purpose of this figure is to compare quantitatively the relative contributions to the yields when going from central to peripheral collisions. For instance, we see that, because of the 2L+1 weighting factor, the most central collisions with L ≤ 20ℏ, which are found at backward angles, have the smallest contribution to the total yield. Despite the discrete nature of the data, the tight grouping of points indicates a peak in production probability in certain mass regions which will be discussed further in the next section.
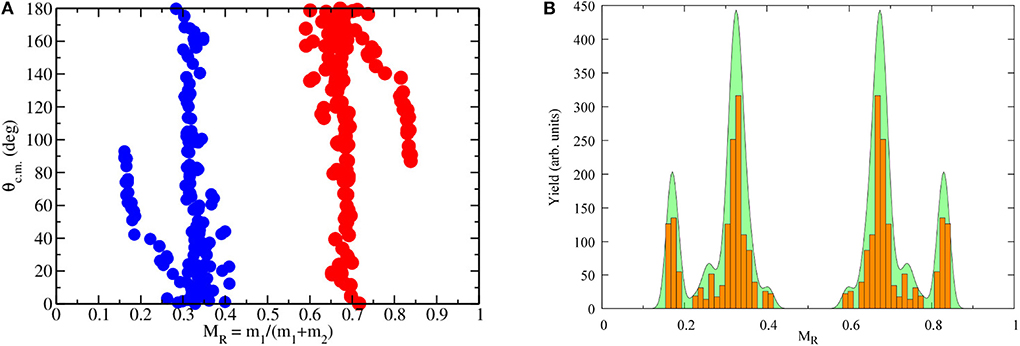
Figure 2. (A) TDHF MADs for quasifission in the reaction 48Ca+249Bk at Ec.m. = 234 MeV. (B) The yield (arb. units) as a function of mass ratio MR for the same reaction.
While nucleon transfer fluctuations can be calculated in TDHF, the ability to compare with experiment is still limited by the fact that TDHF vastly under predicts the widths of these distributions. Ideally, calculations would account for fluctuations in quantities, such as particle transfer, scattering angles, and total kinetic energies in the exit channel to more closely obtain what is observed experimentally. The simplest method for calculating these widths is the particle-number projection for the final fragments [81–83, 94]. However, these widths are still seriously underestimated. This is where extensions, such as TDRPA [68, 70–72] and SMF [74, 75] have proved to be vital theoretical tools for studying deep inelastic and quasifission reactions as both techniques provide methods to calculate both fluctuations and correlations of neutron and proton transfer based on a TDHF trajectory. Figure 3 shows predicted mass angle and mass energy distributions for the 176Yb+176Yb system from TDRPA. Production cross-sections are obtained by integrating the probabilities calculated from the predicted fluctuations over a range of impact parameters. Such calculations further extend the insight offered by the base TDHF theory and promise to be of great use for designing future MNT experiments.
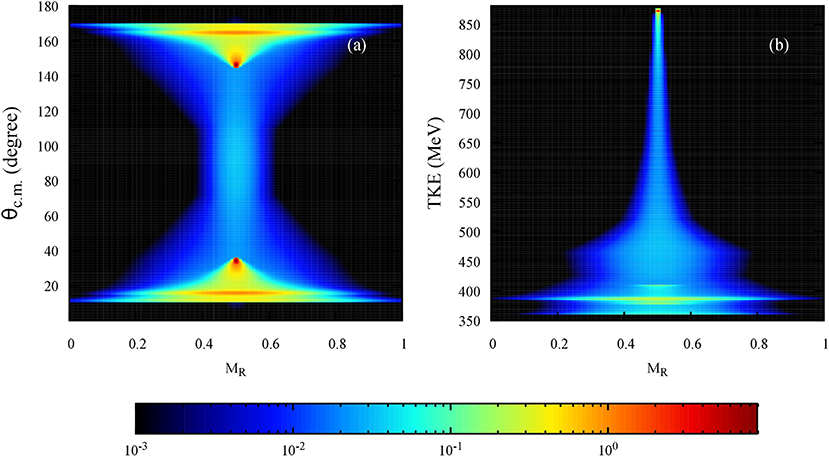
Figure 3. Mass angle (a) and mass energy (b) distributions predicted by TDRPA for the 176Yb+176Yb collision in the side-side orientation at Ec.m. = 880 MeV. Units are in millibarns per degree (a) and millibarns per MeV (b).
An alternate approach to TDRPA calculations for beyond the mean-field approximation can be formulated by incorporating the fluctuations in a manner that is consistent with the quantal fluctuation-dissipation relation, namely the SMF method [75]. In a number of studies it has been demonstrated that the SMF approach improves the description of nuclear collision dynamics by including fluctuation mechanisms of the collective motion. Most applications have been carried out in collisions where a di-nuclear structure is maintained. In this case it is possible to define macroscopic variables by a geometric projection procedure with the help of the window dynamics. The SMF approach gives rise to a Langevin description for the evolution of macroscopic variables. A limited study for central collisions was published in [95]. A general approach for non-central collisions has been developed [96] and used to calculate multi-nucleon transfer and heavy-isotope production in 136Xe+208Pb collisions [97, 98].
3.2. Deformed Shell Effects in Quasifission
Returning to the inference of shell effects influencing fragment production, this phenomenon can also be seen through thorough TDHF studies of a particular system and systematically analyzing the fragments produced for different impact parameters and deformation orientations. TDHF studies of quasifission dynamics have taught us that the dynamics of a system may be dominated by shell effects [47, 61]. An interesting finding of these TDHF studies is the prediction of the role of shell effects which favor the formation of magic fragments, in particular in the Z = 82 region in reactions involving an actinide collision partner [31]. This prediction has been later confirmed experimentally by Morjean et al. [99]. In addition, the calculations show that these shell effects strongly depend on the orientation of deformed actinide. Deformed shell effects in the region of 100Zr have also been invoked to interpret the outcome of TDHF simulations of 40, 48Ca+238U, 249Bk collisions [37, 52].
Such results are shown in Figure 4 for the reaction 48Ca+249Bk at Ec.m. = 234 MeV. Previous studies of the quasifission dynamics have taught us that dynamics may be dominated by shell effects [47, 54, 61]. These distributions are used to identify potential shell gaps driving quasifission. In Figure 4A we plot the charge yield obtained for this reaction. The right frame in Figure 4B shows the expected neutron yield distributions. One of the main driving features of this work was to show that shell effects similar to those observed in fission affect the formation of quasifission fragments. For this system the Z = 82 shell effect does not seem to play a major role contrary to previous TDHF observations for the Ca+U target projectile combinations. We also point out that mass-angle correlations could be used to experimentally isolate the fragments influenced by N = 56 octupole shell gaps [54, 100, 101]. We also find that more peripheral collisions are centered about the proton number Z = 40 confirming similar observations from past calculations [37] that the 100Zr region plays an important role in determining the lighter fragments due to the existence of strongly bound highly deformed Zr isotopes in this region [102].
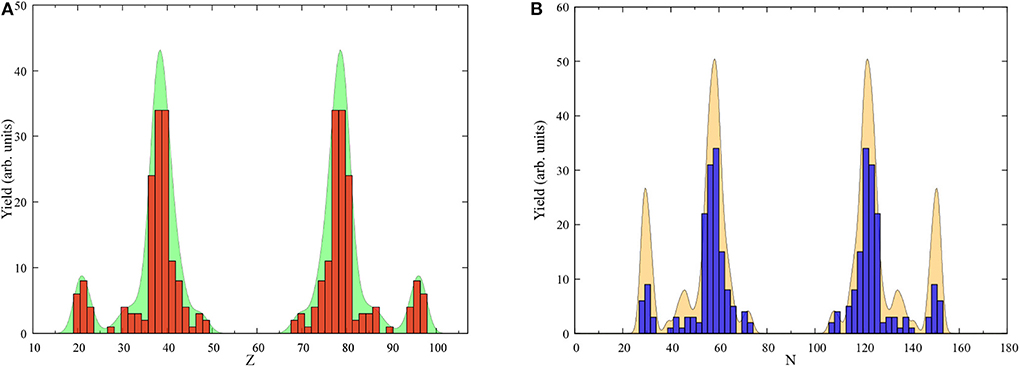
Figure 4. (A) Fragment charge yield (histogram) and (B) Neutron yields for the reaction 48Ca+249Bk at Ec.m. = 234 MeV. The smooth representations of the histograms are obtained by using a kernel density estimation with bandwidth 0.012.
3.3. Mass Equilibration
Due to long reaction times, the quasifission process is also suitable to study the time-scale of mass equilibration. Figure 5A shows the mass ratio, MR, of fragment masses as a function of contact time τ (1 zs = 10−21 s) at Ec.m. = 234 MeV for the 48Ca+249Bk reaction. We define the contact time as the time interval between the time t1 when the two nuclear surfaces (defined as isodensities with half the saturation density ρ0/2 = 0.07 fm−3) first merge into a single surface and the time t2 when the surface densities detach again. The dashed line shows a characteristic fit of a function in the form of c0+c1exp(−τ/τ0). Based on the quality of the fit and whether we exclude some extreme points from the fit or not, we obtain equilibration times between 8 and 10 zs. In Figure 5B we plot the ratio of final and initial mass difference between projectile-like fragment, APLF, and target-like fragment, ATLF, defined by,
as a function of contact time τ for the 48Ca+249Bk system at Ec.m. = 234 MeV. The points correspond to the impact parameters used, ranging from head-on collisions to more peripheral collisions and the full range of orientations angles for 249Bk. The horizontal lines on the right side of the figure indicate the net number of particles transferred between the target and the projectile. We note that more mass transfer happens at longer contact times as expected. From this figure we can also observe similar time-scale for mass equilibration. From these results (and others not shown here) we can conclude that mass equilibration takes substantially longer in comparison to other quantities, such as the equilibration of total kinetic energy (TKE) or N/Z equilibration. It is also interesting to observe that there is clustering of results around certain mass ratios. This is shown to be related to shell effects influencing the dynamical quasifission process in reference [54].
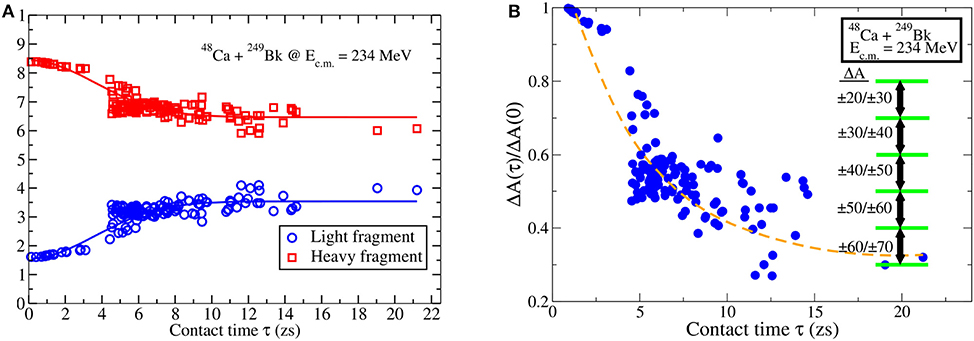
Figure 5. (A) Mass ratio of fragment masses as a function of contact time at Ec.m. = 234 MeV for the reaction 48Ca+249Bk. The solid lines show possible fits. (B) The ratio of the final and initial fragment masses as a function of contact time for the same reaction. The dashed line shows one possible fit.
3.4. Collective Landscape
Quasifission and fusion-fission could be used to help map out the non-adiabatic collective landscape between the fusion entrance channel and the fission exit channel. It has been demonstrated that the TDHF theory is able to provide a good simulation of the quasifission process. Calculated time-scales of quasifission indicate that while fast quasifission events are dominant, much slower events resulting in a split with equal mass fragments have also been observed. One of the open experimental questions is how to distinguish quasifission from fusion-fission. This is important for the calculation of the evaporation residue formation probability in superheavy element searches. In Figure 6 we show two such PESs calculated for the central collisions of the 40, 48Ca+238U systems, with the equatorial orientation of the 238U. The PES on the left of Figure 6 is for the 40Ca+238U system at Ec.m. = 211 MeV, while the PES on the right is for the 48Ca+238U system at Ec.m. = 203 MeV. Surfaces in Figure 6 are obtained by plotting the scattered β2, β3, and E data obtained from the DC-TDHF calculations for the time-evolution of the nuclear density. Since the scattered plot uses an extrapolation algorithm points far from the valleys may not be precise. A number of observations can be made from the PESs shown in Figure 6. First, we clearly see the valley corresponding to the incoming trajectory of the two nuclei. As the system forms a composite the energy rises to maximum, but most likely never makes it to the saddle point. The system spends a lot of time around this area undergoing complex rearrangements and finally starts to proceed down the quasifission valley.
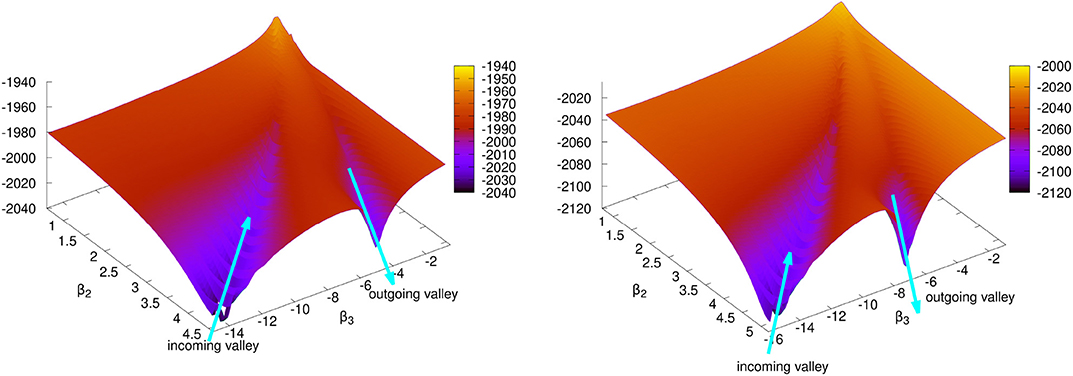
Figure 6. Plotted are the PESs calculated, using the DC-TDHF method, for central collisions of 40, 48Ca+238U, with the equatorial orientation of 238U. The PES on the left is for the 40Ca+238U system at Ec.m. = 211 MeV, while the PES on the right is for the 48Ca+238U system at Ec.m. = 203 MeV.
4. Summary
Quasifission reactions have emerged as an interesting and vibrant area of research in recent years as they teach us about dynamical many-body effects at much longer time-scales compared to other heavy-ion reactions. The persistence of shell effects for these time-scales has opened the possibility to view quasifission as a doorway process to fusion-fission and perhaps even fission. This wide applicability positions quasifission as a vital process in understanding nuclear reactions across the board. In advancing toward this goal, the TDHF theory and its extensions have emerged as an excellent theoretical tool to study these reactions. The success of TDHF results in replicating experiment is particularly impressive as the calculations contain no free parameters. Through the efforts of both theoretical and experimental study of quasifission, we have been able to identify a number of underlying physical phenomena affecting nuclear reactions, such as the dependence on mass-angle distributions on the orientation of deformed targets and the strong influence of shell effects in determination of reaction products. These predictions take steps toward a more complete understanding of dynamical processes in nuclear reactions and may be crucial in determining such quantities as the PCN by calibrating experimental angular distributions to that of the theory. To this end methods and techniques to discern between quasifission and fusion-fission may emerge, paving the way for future studies of neutron-rich nuclei and superheavy elements.
Data Availability Statement
The datasets generated for this study are available on request to the corresponding author.
Author Contributions
All authors listed have made a substantial, direct and intellectual contribution to the work, and approved it for publication.
Funding
This work was supported by the U.S. Department of Energy under grant No. DE-SC0013847.
Conflict of Interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
The handling editor declared a past co-authorship with one of the authors AU.
References
1. Christoph Düllmann E, Rolf–Dietmar Herzberg, Witold Nazarewicz, Yuri Oganessian. Special issue on superheavy elements. Nucl Phys A. (2015) 944:1–690. doi: 10.1016/j.nuclphysa.2015.11.004
2. Bender M, Rutz K, Reinhard PG, Maruhn JA, Greiner W. Shell structure of superheavy nuclei in self-consistent mean-field models. Phys Rev C. (1999) 60:034304. doi: 10.1103/PhysRevC.60.034304
3. Nazarewicz W, Bender M, Ćwiok S, Heenen PH, Kruppa AT, Reinhard PG, et al. Theoretical description of superheavy nuclei. Nucl Phys A. (2002) 701:165–71. doi: 10.1016/S0375-9474(01)01567-6
4. Ćwiok S, Heenen PH, Nazarewicz W. Shape coexistence and triaxiality in the superheavy nuclei. Nature. (2005) 433:705–9. doi: 10.1038/nature03336
5. Pei JC, Nazarewicz W, Sheikh JA, Kerman AK. Fission barriers of compound superheavy nuclei. Phys Rev Lett. (2009) 102:192501. doi: 10.1103/PhysRevLett.102.192501
6. Hofmann S, Heßberger FP, Ackermann D, Münzenberg G, Antalic S, Cagarda P, et al. New results on elements 111 and 112. Eur Phys J A. (2002) 14:147–57. doi: 10.1140/epja/i2001-10119-x
7. Münzenberg G, Morita K. Synthesis of the heaviest nuclei in cold fusion reactions. Nucl Phys A. (2015) 944:3–4. doi: 10.1016/j.nuclphysa.2015.06.007
8. Morita K. SHE research at RIKEN/GARIS. Nucl Phys A. (2015) 944:30–61. doi: 10.1016/j.nuclphysa.2015.10.007
9. Oganessian YT, Utyonkov VK. Superheavy nuclei from 48Ca-induced reactions. Nucl Phys A. (2015) 944:62–98. doi: 10.1016/j.nuclphysa.2015.07.003
10. Roberto JB, Alexander CW, Boll RA, Burns JD, Ezold JG, Felker LK, et al. Actinide targets for the synthesis of super-heavy elements. Nucl Phys A. (2015) 944:99–116. doi: 10.1016/j.nuclphysa.2015.06.009
11. du Rietz R, Hinde DJ, Dasgupta M, Thomas RG, Gasques LR, Evers M, et al. Predominant time scales in fission processes in reactions of S, Ti and Ni with W: zeptosecond versus attosecond. Phys Rev Lett. (2011) 106:052701. doi: 10.1103/PhysRevLett.106.052701
12. Tõke J, Bock R, Dai GX, Gobbi A, Gralla S, Hildenbrand KD, et al. Quasi-fission: the mass-drift mode in heavy-ion reactions. Nucl Phys A. (1985) 440:327–65. doi: 10.1016/0375-9474(85)90344-6
13. Shen WQ, Albinski J, Gobbi A, Gralla S, Hildenbrand KD, Herrmann N, et al. Fission and quasifission in U-induced reactions. Phys Rev C. (1987) 36:115–42. doi: 10.1103/PhysRevC.36.115
14. Sahm CC, Clerc HG, Schmidt KH, Reisdorf W, Armbruster P, Heßberger FP, et al. Hindrance of fusion in central collisions of heavy symmetric nuclear systems. Z Phys A. (1984) 319:113–8. doi: 10.1007/BF01415623
15. Gäggeler H, Sikkeland T, Wirth G, Brüchle W, Bögl W, Franz G, et al. Probing sub-barrier fusion and extra-push by measuring fermium evaporation residues in different heavy ion reactions. Z Phys A. (1984) 316:291–307. doi: 10.1007/BF01439902
16. Schmidt KH, Morawek W. The conditions for the synthesis of heavy nuclei. Rep Prog Phys. (1991) 54:949. doi: 10.1088/0034-4885/54/7/002
17. Hinde DJ, Hilscher D, Rossner H, Gebauer B, Lehmann M, Wilpert M. Neutron emission as a probe of fusion-fission and quasi-fission dynamics. Phys Rev C. (1992) 45:1229–59. doi: 10.1103/PhysRevC.45.1229
18. Hinde DJ, Dasgupta M, Leigh JR, Lestone JP, Mein JC, Morton CR, et al. Fusion-fission versus quasifission: effect of nuclear orientation. Phys Rev Lett. (1995) 74:1295–8. doi: 10.1103/PhysRevLett.74.1295
19. Hinde DJ, Dasgupta M, Leigh JR, Mein JC, Morton CR, Newton JO, et al. Conclusive evidence for the influence of nuclear orientation on quasifission. Phys Rev C. (1996) 53:1290–300. doi: 10.1103/PhysRevC.53.1290
20. Itkis MG, Äystö J, Beghini S, Bogachev AA, Corradi L, Dorvaux O, et al. Shell effects in fission and quasi-fission of heavy and superheavy nuclei. Nucl Phys A. (2004) 734:136–47. doi: 10.1016/j.nuclphysa.2004.01.022
21. Knyazheva GN, Kozulin EM, Sagaidak RN, Yu Chizhov A, Itkis MG, Kondratiev NA, et al. Quasifission processes in 40, 48Ca+144, 154Sm reactions. Phys Rev C. (2007) 75:064602. doi: 10.1103/PhysRevC.75.064602
22. Hinde DJ, Thomas RG, du Rietz R, Diaz-Torres A, Dasgupta M, Brown ML, et al. Disentangling effects of nuclear structure in heavy element formation. Phys Rev Lett. (2008) 100:202701. doi: 10.1103/PhysRevLett.100.202701
23. Nishio K, Ikezoe H, Mitsuoka S, Nishinaka I, Nagame Y, Watanabe Y, et al. Effects of nuclear orientation on the mass distribution of fission fragments in the reaction of 36S+238U. Phys Rev C. (2008) 77:064607. doi: 10.1103/PhysRevC.77.064607
24. Kozulin EM, Knyazheva GN, Dmitriev SN, Itkis IM, Itkis MG, Loktev TA, et al. Shell effects in damped collisions of 88Sr with 176Yb at the Coulomb barrier energy. Phys Rev C. (2014) 89:014614. doi: 10.1103/PhysRevC.89.014614
25. Itkis IM, Kozulin EM, Itkis MG, Knyazheva GN, Bogachev AA, Chernysheva EV, et al. Fission and quasifission modes in heavy-ion-induced reactions leading to the formation of Hs*. Phys Rev C. (2011) 83:064613. doi: 10.1103/PhysRevC.83.064613
26. Lin CJ, du Rietz R, Hinde DJ, Dasgupta M, Thomas RG, Brown ML, et al. Systematic behavior of mass distributions in 48Ti-induced fission at near-barrier energies. Phys Rev C. (2012) 85:014611. doi: 10.1103/PhysRevC.85.014611
27. Nishio K, Mitsuoka S, Nishinaka I, Makii H, Wakabayashi Y, Ikezoe H, et al. Fusion probabilities in the reactions 40, 48Ca+238U at energies around the Coulomb barrier. Phys Rev C. (2012) 86:034608. doi: 10.1103/PhysRevC.86.034608
28. Simenel C, Hinde DJ, du Rietz R, Dasgupta M, Evers M, Lin CJ, et al. Influence of entrance-channel magicity and isospin on quasi-fission. Phys Lett B. (2012) 710:607–11. doi: 10.1016/j.physletb.2012.03.063
29. du Rietz R, Williams E, Hinde DJ, Dasgupta M, Evers M, Lin CJ, et al. Mapping quasifission characteristics and timescales in heavy element formation reactions. Phys Rev C. (2013) 88:054618. doi: 10.1103/PhysRevC.88.054618
30. Williams E, Hinde DJ, Dasgupta M, du Rietz R, Carter IP, Evers M, et al. Evolution of signatures of quasifission in reactions forming curium. Phys Rev C. (2013) 88:034611. doi: 10.1103/PhysRevC.88.034611
31. Wakhle A, Simenel C, Hinde DJ, Dasgupta M, Evers M, Luong DH, et al. Interplay between quantum shells and orientation in quasifission. Phys Rev Lett. (2014) 113:182502. doi: 10.1103/PhysRevLett.113.182502
32. Hammerton K, Kohley Z, Hinde DJ, Dasgupta M, Wakhle A, Williams E, et al. Reduced quasifission competition in fusion reactions forming neutron-rich heavy elements. Phys Rev C. (2015) 91:041602(R). doi: 10.1103/PhysRevC.91.041602
33. Prasad E, Hinde DJ, Ramachandran K, Williams E, Dasgupta M, Carter IP, et al. Observation of mass-asymmetric fission of mercury nuclei in heavy ion fusion. Phys Rev C. (2015) 91:064605. doi: 10.1103/PhysRevC.91.064605
34. Prasad E, Wakhle A, Hinde DJ, Williams E, Dasgupta M, Evers M, et al. Exploring quasifission characteristics for 34S+232Th forming 266Sg. Phys Rev C. (2016) 93:024607. doi: 10.1103/PhysRevC.93.024607
35. Back BB, Fernandez PB, Glagola BG, Henderson D, Kaufman S, Keller JG, et al. Entrance-channel effects in quasifission reactions. Phys Rev C. (1996) 53:1734–44. doi: 10.1103/PhysRevC.53.1734
36. Umar AS, Oberacker VE. Dynamical deformation effects in subbarrier fusion of 64Ni+132Sn. Phys Rev C. (2006) 74:061601. doi: 10.1103/PhysRevC.74.061601
37. Oberacker VE, Umar AS, Simenel C. Dissipative dynamics in quasifission. Phys Rev C. (2014) 90:054605. doi: 10.1103/PhysRevC.90.054605
38. Morjean M, Jacquet D, Charvet JL, L'Hoir A, Laget M, Parlog M, et al. Fission time measurements: a new probe into superheavy element stability. Phys Rev Lett. (2008) 101:072701. doi: 10.1103/PhysRevLett.101.072701
39. Frégeau MO, Jacquet D, Morjean M, Bonnet E, Chbihi A, Frankland JD, et al. X-ray fluorescence from the element with atomic number Z = 120. Phys Rev Lett. (2012) 108:122701. doi: 10.1103/PhysRevLett.108.122701
40. Kozulin EM, Knyazheva GN, Itkis IM, Itkis MG, Bogachev AA, Krupa L, et al. Investigation of the reaction 64Ni+238U being an option of synthesizing element 120. Phys Lett B. (2010) 686:227–32. doi: 10.1016/j.physletb.2010.02.041
41. Adamian GG, Antonenko NV, Scheid W. Characteristics of quasifission products within the dinuclear system model. Phys Rev C. (2003) 68:034601. doi: 10.1103/PhysRevC.68.034601
42. Zagrebaev v, Greiner w. Shell effects in damped collisions: a new way to superheavies. J Phys G. (2007) 34:2265. doi: 10.1088/0954-3899/34/11/004
43. Aritomo Y. Analysis of dynamical processes using the mass distribution of fission fragments in heavy-ion reactions. Phys Rev C. (2009) 80:064604. doi: 10.1103/PhysRevC.80.064604
44. Zhao K, Li Z, Zhang Y, Wang N, Li Q, Shen C, et al. Production of unknown neutron–rich isotopes in 238U+238U collisions at near–barrier energy. Phys Rev C. (2016) 94:024601. doi: 10.1103/PhysRevC.94.024601
45. Sekizawa K, Yabana K. Time-dependent Hartree-Fock calculations for multinucleon transfer and quasifission processes in the 64Ni+238U reaction. Phys Rev C. (2016) 93:054616. doi: 10.1103/PhysRevC.93.054616
46. Sekizawa K. Enhanced nucleon transfer in tip collisions of 238U+124Sn. Phys Rev C. (2017) 96:041601(R). doi: 10.1103/PhysRevC.96.041601
47. Sekizawa K. TDHF theory and its extensions for the multinucleon transfer reaction: a mini review. Front Phys. (2019) 7:20. doi: 10.3389/fphy.2019.00020
48. David Kedziora J, Cédric Simenel. New inverse quasifission mechanism to produce neutron-rich transfermium nuclei. Phys Rev C. (2010) 81:044613. doi: 10.1103/PhysRevC.81.044613
49. Goddard PM, Stevenson PD, Rios A. Fission dynamics within time-dependent Hartree-Fock: deformation-induced fission. Phys Rev C. (2015) 92:054610. doi: 10.1103/PhysRevC.92.054610
50. Umar AS, Oberacker VE, Simenel C. Shape evolution and collective dynamics of quasifission in the time-dependent Hartree-Fock approach. Phys Rev C. (2015) 92:024621. doi: 10.1103/PhysRevC.92.024621
51. Umar AS, Oberacker VE. Time-dependent HF approach to SHE dynamics. Nucl Phys A. (2015) 944:238–56. doi: 10.1016/j.nuclphysa.2015.02.011
52. Umar AS, Oberacker VE, Simenel C. Fusion and quasifission dynamics in the reactions 48Ca+249Bk and 50Ti+249Bk using a time-dependent Hartree-Fock approach. Phys Rev C. (2016) 94:024605. doi: 10.1103/PhysRevC.94.024605
53. Wang N, Guo L. New neutron-rich isotope production in 154Sm+160Gd. Phys Lett B. (2016) 760:236–41. doi: 10.1016/j.physletb.2016.06.073
54. Godbey K, Umar AS, Simenel C. Deformed shell effects in 48Ca+249Bk quasifission fragments. Phys Rev C. (2019) 100:024610. doi: 10.1103/PhysRevC.100.024610
55. Sekizawa K. Microscopic description of production cross sections including deexcitation effects. Phys Rev C. (2017) 96:014615. doi: 10.1103/PhysRevC.96.014615
56. Sekizawa K, Hagino K. Time-dependent Hartree-Fock plus Langevin approach for hot fusion reactions to synthesize the Z = 120 superheavy element. Phys Rev C. (2019) 99:051602. doi: 10.1103/PhysRevC.99.051602
57. Umar AS, Oberacker VE, Maruhn JA, Reinhard PG. Microscopic calculation of precompound excitation energies for heavy-ion collisions. Phys Rev C. (2009) 80:041601. doi: 10.1103/PhysRevC.80.041601
58. Umar AS, Simenel C, Ye W. Transport properties of isospin asymmetric nuclear matter using the time-dependent Hartree–Fock method. Phys Rev C. (2017) 96:024625. doi: 10.1103/PhysRevC.96.024625
59. Guo L, Shen C, Yu C, Wu Z. Isotopic trends of quasifission and fusion-fission in the reactions 48Ca+239, 244Pu. Phys Rev C. (2018) 98:064609. doi: 10.1103/PhysRevC.98.064609
60. Jiang X, Wang N. Probing the production mechanism of neutron-rich nuclei in multinucleon transfer reactions. Phys Rev C. (2020) 101:014604. doi: 10.1103/PhysRevC.101.014604
61. Simenel C, Umar AS. Heavy-ion collisions and fission dynamics with the time–dependent Hartree-Fock theory and its extensions. Prog Part Nucl Phys. (2018) 103:19–66. doi: 10.1016/j.ppnp.2018.07.002
62. Negele JW. The mean-field theory of nuclear-structure and dynamics. Rev Mod Phys. (1982) 54:913–1015. doi: 10.1103/RevModPhys.54.913
63. Simenel C. Nuclear quantum many-body dynamics. Eur Phys J A. (2012) 48:152. doi: 10.1140/epja/i2012-12152-0
64. Stevenson PD, Barton MC. Low–energy heavy-ion reactions and the Skyrme effective interaction. Prog Part Nucl Phys. (2019) 104:142–64. doi: 10.1016/j.ppnp.2018.09.002
65. Zagrebaev VI, Karpov AV, Greiner W. Possibilities for synthesis of new isotopes of superheavy elements in fusion reactions. Phys Rev C. (2012) 85:014608. doi: 10.1103/PhysRevC.85.014608
66. Karpov AV, Saiko VV. Modeling near-barrier collisions of heavy ions based on a Langevin-type approach. Phys Rev C. (2017) 96:024618. doi: 10.1103/PhysRevC.96.024618
67. Saiko VV, Karpov AV. Analysis of multinucleon transfer reactions with spherical and statically deformed nuclei using a Langevin-type approach. Phys Rev C. (2019) 99:014613. doi: 10.1103/PhysRevC.99.014613
68. Roger Balian, Marcel Vénéroni. Fluctuations in a time-dependent mean-field approach. Phys Lett B. (1984) 136:301–6. doi: 10.1016/0370-2693(84)92008-2
69. Balian R, Vénéroni M. Correlations and fluctuations in static and dynamic mean-field approaches. Ann Phys. (1992) 216:351. doi: 10.1016/0003-4916(92)90181-K
70. Broomfield JMA. Calculations of Mass Distributions Using the Balian-Vénéroni Variational Approach. Guildford: University of Surrey (2009).
71. Simenel C. Particle-number fluctuations and correlations in transfer reactions obtained using the Balian-Vénéroni variational principle. Phys Rev Lett. (2011) 106:112502. doi: 10.1103/PhysRevLett.106.112502
72. Williams E, Sekizawa K, Hinde DJ, Simenel C, Dasgupta M, Carter IP, et al. Exploring zeptosecond quantum equilibration dynamics: from deep-inelastic to fusion-fission outcomes in 58Ni+60Ni reactions. Phys Rev Lett. (2018) 120:022501. doi: 10.1103/PhysRevLett.120.022501
73. Goutte H, Berger JF, Casoli P, Gogny D. Microscopic approach of fission dynamics applied to fragment kinetic energy and mass distributions in 238U. Phys Rev C. (2005) 71:024316. doi: 10.1103/PhysRevC.71.024316
74. Ayik S. A stochastic mean-field approach for nuclear dynamics. Phys Lett B. (2008) 658:174. doi: 10.1016/j.physletb.2007.09.072
75. Lacroix D, Ayik S. Stochastic quantum dynamics beyond mean field. Eur Phys J A. (2014) 50:95. doi: 10.1140/epja/i2014-14095-8
76. Tohyama M. Two-body collision effects on the low-L fusion window in 16O+16O reactions. Phys Lett B. (1985) 160:235–8. doi: 10.1016/0370-2693(85)91317-6
77. Tohyama M, Umar AS. Quadrupole resonances in unstable oxygen isotopes in time-dependent density-matrix formalism. Phys Lett B. (2002) 549:72–8. doi: 10.1016/S0370-2693(02)02885-X
78. Assié M, Lacroix D. Probing neutron correlations through nuclear breakup. Phys Rev Lett. (2009) 102:202501. doi: 10.1103/PhysRevLett.102.202501
79. Tohyama M, Umar AS. Two-body dissipation effects on the synthesis of superheavy elements. Phys Rev C. (2016) 93:034607. doi: 10.1103/PhysRevC.93.034607
80. Koonin SE, Davies KTR, Maruhn-Rezwani V, Feldmeier H, Krieger SJ, Negele JW. Time-dependent Hartree-Fock calculations for 16O+16O and 40Ca+40Ca reactions. Phys Rev C. (1977) 15:1359–74. doi: 10.1103/PhysRevC.15.1359
81. Simenel C. Particle transfer reactions with the time-dependent Hartree-Fock theory using a particle number projection technique. Phys Rev Lett. (2010) 105:192701. doi: 10.1103/PhysRevLett.105.192701
82. Sekizawa K, Yabana K. Time-dependent Hartree-Fock calculations for multinucleon transfer processes in 40, 48Ca+124Sn, 40Ca+208Pb, and 58Ni+208Pb reactions. Phys Rev C. (2013) 88:014614. doi: 10.1103/PhysRevC.88.014614
83. Scamps G, Lacroix D. Effect of pairing on one- and two-nucleon transfer below the Coulomb barrier: a time-dependent microscopic description. Phys Rev C. (2013) 87:014605. doi: 10.1103/PhysRevC.87.014605
84. Dasso CH, Dossing T, Pauli HC. On the mass distribution in time-dependent Hartree-Fock calculations of heavy-ion collisions. Z Phys A. (1979) 289:395–8. doi: 10.1007/BF01409391
85. Vardaci E, Itkis MG, Itkis IM, Knyazheva G, Kozulin EM. Fission and quasifission toward the superheavy mass region. J Phys G. (2019) 46:103002. doi: 10.1088/1361-6471/ab3118
86. Loveland W. Synthesis of transactinide nuclei using radioactive beams. Phys Rev C. (2007) 76:014612. doi: 10.1103/PhysRevC.76.014612
87. Yanez R, Loveland W, Barrett JS, Yao L, Back BB, Zhu S, et al. Measurement of the fusion probability, PCN, for hot fusion reactions. Phys Rev C. (2013) 88:014606. doi: 10.1103/PhysRevC.88.014606
88. Zhu L, Su J, Xie WJ, Zhang FS. Study of the dynamical potential barriers in heavy ion collisions. Nucl Phys A. (2013) 915:90–105. doi: 10.1016/j.nuclphysa.2013.07.003
89. Schmitt C, Mazurek K, Nadtochy PN. New procedure to determine the mass-angle correlation of quasifission. Phys Rev C. (2019) 100:064606. doi: 10.1103/PhysRevC.100.064606
90. Back BB. Complete fusion and quasifission in reactions between heavy ions. Phys Rev C. (1985) 31:2104–12. doi: 10.1103/PhysRevC.31.2104
91. Back BB, Esbensen H, Jiang CL, Rehm KE. Recent developments in heavy-ion fusion reactions. Rev Mod Phys. (2014) 86:317–60. doi: 10.1103/RevModPhys.86.317
92. Schmidt KH, Jurado B. Review on the progress in nuclear fission–experimental methods and theoretical descriptions. Rep Prog Phys. (2018) 81:106301. doi: 10.1088/1361-6633/aacfa7
93. Umar AS, Oberacker VE, Maruhn JA, Reinhard PG. Entrance channel dynamics of hot and cold fusion reactions leading to superheavy elements. Phys Rev C. (2010) 81:064607. doi: 10.1103/PhysRevC.81.064607
94. Scamps G, Hashimoto Y. Transfer probabilities for the reactions 14, 20O+20O in terms of multiple time-dependent Hartree-Fock-Bogoliubov trajectories. Phys Rev C. (2017) 96:031602. doi: 10.1103/PhysRevC.96.031602
95. Ayik S, Yilmaz O, Yilmaz B, Umar AS. Quantal nucleon diffusion: central collisions of symmetric nuclei. Phys Rev C. (2016) 94:044624. doi: 10.1103/PhysRevC.94.044624
96. Ayik S, Yilmaz B, Yilmaz O, Umar AS. Quantal diffusion description of multinucleon transfers in heavy–ion collisions. Phys Rev C. (2018) 97:054618. doi: 10.1103/PhysRevC.97.054618
97. Ayik S, Yilmaz B, Yilmaz O, Umar AS. Quantal diffusion approach for multinucleon transfers in Xe+Pb collisions. Phys Rev C. (2019) 100:014609. doi: 10.1103/PhysRevC.100.014609
98. Ayik S, Yilmaz O, Yilmaz B, Umar AS. Heavy-isotope production in 136Xe+208Pb collisions at Ec.m. = 514 MeV. Phys Rev C. (2019) 100:044614. doi: 10.1103/PhysRevC.100.044614
99. Morjean M, Hinde DJ, Simenel C, Jeung DY, Airiau M, Cook KJ, et al. Evidence for the role of proton shell closure in quasifission reactions from X-ray fluorescence of mass-identified fragments. Phys Rev Lett. (2017) 119:222502. doi: 10.1103/PhysRevLett.119.222502
100. Scamps G, Simenel C. Impact of pear-shaped fission fragments on mass-asymmetric fission in actinides. Nature. (2018) 564:382–5. doi: 10.1038/s41586-018-0780-0
101. Scamps G, Simenel C. Effect of shell structure on the fission of sub-lead nuclei. Phys Rev C. (2019) 100:041602. doi: 10.1103/PhysRevC.100.041602
Keywords: time-dependent Hartree-Fock, quasifission, superheavy elements, multi-nucleon transfer, time-dependent random phase approximation
Citation: Godbey K and Umar AS (2020) Quasifission Dynamics in Microscopic Theories. Front. Phys. 8:40. doi: 10.3389/fphy.2020.00040
Received: 03 January 2020; Accepted: 12 February 2020;
Published: 27 February 2020.
Edited by:
Paul Denis Stevenson, University of Surrey, United KingdomReviewed by:
Giuseppe Verde, National Institute for Nuclear Physics, ItalyKazuyuki Sekizawa, Niigata University, Japan
Copyright © 2020 Godbey and Umar. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: A. S. Umar, dW1hckBjb21wc2NpLmNhcy52YW5kZXJiaWx0LmVkdQ==
 Kyle Godbey
Kyle Godbey A. S. Umar
A. S. Umar