- 1Department of Information Systems, University of Lausanne, Lausanne, Switzerland
- 2Complex Systems Interdisciplinary Group (GISC), Department of Mathematics, Carlos III University of Madrid, Getafe, Spain
Public good games are a metaphor for modeling cooperative behavior in groups in the presence of incentives to free ride. In the model presented here agents play a public good game with their neighbors in a social network structure. Agents' decision rules in our model are inspired by elementary learning observed in laboratory and online behavioral experiments involving human participants with the same amount of information, i.e., when individuals only know their own current contribution and their own cumulated payoff. In addition, agents in the model are allowed to severe links with groups in which their payoff is lower and create links to a new randomly chosen group. Reinforcing the results obtained in network scenarios where agents play Prisoner's Dilemma games, we show that thanks to this relinking possibility, the whole system reaches higher levels of average contribution with respect to the case in which the network cannot change. Our setup opens new frameworks to be investigated, and potentially confirmed, through controlled human experiments.
1. Introduction
Public Good Games (PGG) are a well-known model for describing situations that require people or institutions to cooperate to achieve a goal that is considered beneficial to all. For instance, threats, such as global climate change, overfishing, deforestation, and natural resources depletion in general are fundamental social issues in which cooperation and self-restrain are required to achieve the best collective results [1]. However, cooperation is vulnerable to free-riding and, perhaps more commonly, fear to be exploited which in turn leads to selfish behavior. In fact, the best theoretical course of action from an individual point of view is to not cooperate [2, 3]. More precisely, linear PGG are multi-player games in which N ≥ 2 agents have the choice of voluntarily contribute to a common pool that will have an added value for each agent through a multiplication, also called enhancement, factor 1 < r < N and it will be enjoyed by all. Rationally, the best course of action and the dominant strategy for an agent is to avoid any contribution and to free-ride on the contribution of others. But if the number of non-contributing agents is large enough there will be no benefit from contributing and hence no public good provision. Indeed, the unique Nash equilibrium corresponds to zero contribution all around. Evolutionary game theory approaches [4] also have full defection as the stable state of the dynamics. However, game theory notwithstanding, it has been found in many controlled experiments conducted in the laboratory, or online, that subjects do contribute about half of their endowment in a one-shot game. If the game is iterated contributions decrease but, instead of vanishing, there is always a residual contribution of about 10–20% on the average. Literally hundreds of experiments have been performed to date on various aspects of PGG and it is almost impossible to cite them all. The following are some works from which further references can be found [5–10]. The general observed pattern is the steady decrease in contributions in iterated games as people learn the consequences of their actions. Variations of the basic game in which free-riders can be punished at a cost or rewards are provided to those who contribute show that contributions may again reach higher values [6, 7]. The role of punishment in social dilemma experiments has been recently reexamined in Li et al. [11]. Cognitive biases, when a decoy option is available in the social dilemma may also help to promote cooperation [12]. Such behaviors have been attributed to various causes by different authors and, indeed, what people do strongly depends on the information they are given about the other players' actions [13–19]. If people know who does what in the group, then they may condition their contribution on the action of others. If subjects start to free-ride this implies a progressive reduction of the contributions and people act as if they had pro-social preferences. In particular, the willingness to punish free-riders at a cost for the punisher shows that agents take into account the welfare of others to some extent when making their decisions [6]. But when there is no feedback for a participant, except her own payoff the steady reduction in contributions can be interpreted in a different way. Along these lines, Burton-Chellew et al. [8–10] run some experiments and suggested that payoff-based learning is sufficient to explain the results.
In the last two decades games in populations in which individuals are structured according to a network of contacts have attracted a lot of attention. This is natural as in everyday life each one of us belongs to several social networks, ranging from face-to-face interactions to pure web-based ones. A number of numerical simulation studies of the PGG game dynamics on network-structured populations have been published (e.g., see [20–25]) for two recent reviews. In most of the previous cases the numerical simulation models used were of the replicator dynamics type [24]. The results of these works do confirm that contributions go to zero in the long term in the average, until a critical value of the enhancement factor is reached. For larger values of the enhancement factor full cooperation is the stable state and it is reached at a rate that depends on the network structure and on the particular strategy update rule. It is difficult to underestimate the importance of theoretical and numerical models for our understanding of PGG dynamics. However, they contain a few unrealistic assumptions that prevent them from being equally useful in interpreting the results of laboratory experiments with human subjects. First of all, decision rules are homogeneous across the population and quite different from the behavioral rules that agents employ in laboratory and online experiments. In addition, for simplicity and mathematical convenience, individuals either contribute their full endowment or do not contribute at all. However, in experiments, participants usually receive a number of tokens and can choose how many to contribute to the common pool, i.e., contributions are a real, or more commonly, an integer variable, not a Boolean one. In a recent work [26], we made a first step to depart from standard replicator dynamics formulations toward individual decision and learning rules that are supposed to be closer to the way people make their decisions in the laboratory when playing a standard linear PGG game. Using a social network model for the population structure, we showed that a couple of simple models are able to qualitatively reproduce the average players' behavior observed in some laboratory experiments [8, 19]. As said above, the strategies effectively seen in experiments strongly depend on the kind and amount of the information available to the subjects. To keep the models as simple as possible, we targeted for inspiration experiments in which little information is provided. In Tomassini and Antonioni [26] the network was kept fixed, i.e., it was not possible to severe links or form new links. However, it has been previously shown both in simulation models [18, 27–30] as well as in experiments[13, 14, 17, 31–33] that the possibility of cutting contacts with unsuitable partners and forming new links with more promising ones is a simple mechanism that can lead to the emergence of cooperation in the two-person Prisoner's Dilemma game.
In the present study we extend the models presented in Tomassini and Antonioni [26] in such a way that unsatisfied agents have, in addition, the option of cutting a link with an unfavorable group and of joining another group and we investigate whether this possibility can lead to a higher average contribution. This extension is coherent with what we observe in society, where associations can usually be changed, and also serve as a simple form of punishment, or retaliation, that does not require complicated strategic considerations. With these elements in hand, we then proceed to a detailed numerical study of how contributions and the network itself evolve in time, and what are the main parameters governing the dynamical system. We believe that the approach presented here, given its behavior-oriented nature, can also suggest interesting and feasible settings for experimental work by using cheap numerical simulations.
The manuscript is organized as follows. We first describe the PGG model on coevolving social networks. This is followed by numerical simulation results and their discussion. A final section with further discussion and conclusions ends the paper.
2. Simulations Models
In this section we present the models for the population and group structures and for the strategic decisions of the individuals belonging to the population.
2.1. Population Structure
Social networks suggest a natural way of forming groups of agents for playing PGG games. The social network is generated according to the method described in Antonioni and Tomassini [34]. The network construction starts with a small kernel of nodes to which new nodes are added incrementally. A certain average degree is set at the beginning and each incoming node will form a number of links to existing nodes that is compatible with the given average degree. A parameter 0 ≤ α ≤ 1 determines the proportion of links that are made according to linear preferential attachment or according to a distance-based criterion. For α = 0 a new link is made to the closest existing node, i.e., the network is purely spatial. For α = 1 the link is made proportional to the degree of existing nodes by preferential attachment. For 0 < α < 1 links are space-dependent with probability α and degree-dependent with probability 1−α. For α = 0 the clustering coefficient is high and the degree distribution function of the network is peaked around the mean value. For α = 1 on the other hand, the degree distribution is fat-tailed and tends to a scale-free one with increasing network size [34, 35]. In our simulations we chose α = 0.3 which is an average value that was found in Antonioni and Tomassini [34] to lead to social network models with statistical features similar to those of some real-world social networks when the role of geographical space is taken into account. In any case, since the network will evolve in time, the particular initial state is not a critical factor. In Tomassini and Antonioni [26] we studied games on networks of mean degree four, six, and 12 in order to investigate the role of the average group size but we found that the group size distribution had little influence on the results; thus we performed our simulations for degree six only here. A recent experimental work [36] explicitly targets the influence of the group size, up to 1,000 interacting individuals, and gives further references.
Each agent in the network interacts with its first neighbors and it is the focal element in this group. The agent also participates in all the groups that have each neighbor as the focal element (see Figure 1 for a visual explanation of the group structure). If the degree of agent i in the graph is k, then the number of groups to which it participates is g = k + 1. A perhaps clearer way of dealing with multigroup membership is by using bipartite networks in which there are two disjoint sets of nodes: one set represents the agents and the other set represents the groups. An agent may have links to several groups but there cannot be links between groups or between agents (see e.g., [21, 37, 38]). In spite of the interest of this representation, in the present work we keep the standard agent network notation.
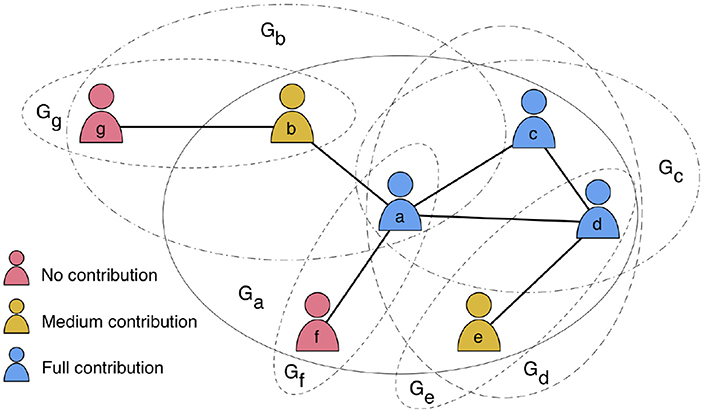
Figure 1. Visual representation of public goods games played on a network structure of seven nodes. Each PGG is centered in a focal node i and it is represented by a circle Gi. For example, the node a has four direct neighbors (b, c, d, f) and it participates in five PGGs, i.e., the circle Ga centered in a including its four neighbors, and other four PGGs represented by circles centered in its neighbors: Gb, Gc, Gd, Gf. Note that a node may indirectly interact with other nodes that are not direct neighbors. Colors represent the node contribution into the common pools in which it participates.
2.2. Public Goods Game and Behavioral Rules
We consider a standard linear PGG in which the sum of the contributions is equally shared between the members of the group independent of their respective contributions, after multiplication by the enhancement factor r > 1. The utility, or payoff, payoff πi of individual i after playing a round in all groups of which it is a member is:
in which we assume that i's endowment is 1 at the beginning of a round of play in each group and i's contribution ci is the same in all g groups in which i participates. The first term is what remains after contributing the amount 0 ≤ ci ≤ 1 in each of the g groups and the second term is the sum of i's gains over all g groups after multiplying by r and sharing the total amount among the members of the group whose size is |Nj|.
All agents decide their contribution and compute their payoff after having played in all their groups. Initial contribution are chosen randomly among the following set of values {0.0, 0.25, 0.50, 0.75, 1.0}, where 1.0 represents the total endowment contribution. In each round, a player has the same endowment of 1.0 in each group in which it is a member. We remark that this corresponds to the case in which each member contributes a fixed amount per game [20]. There is another possibility in which an individual contributes a fixed amount per member of the group to which it participates but we will not explore it here. The above framework is qualitatively similar to many experimental settings for the PGG. The quantitative difference is that participants usually receive a capital of 20–40 tokens that they can spend in integer amounts. Our simulated setting is an abstraction of those more detailed processes. This high-level process is schematized in Algorithm 1 (Play rounds).
After having played in all their groups and having got their utilities, agents must decide what to do next. To make the decision they use a number of very simple behavioral rules. Specifically, if an agent is satisfied, getting a payoff at least equal to the total contribution it made to the groups in which it is a member then, with probability 0.5 it will increase its contribution by 0.25 or, with probability 0.5, it will keep its contribution unchanged in the next step. The noisy decision helps introduce some heterogeneity in the agent's behavior and avoids mass population behavior, in agreement with what one observes in laboratory results where individual behaviors are rather variable. On the other hand, if the agent is unsatisfied because it got less than what it put in the common pool, then it will have two possible choices: either it decreases its contribution by 0.25 at the next time step, or it cuts a link to the group in which it gets the worst payoff. This is a form of escaping an unfavorable environment and it can be done freely, without paying a cost. Although the assumption of zero cost for relinking is probably not completely correct in a real world situation, it is an acceptable working hypothesis. The probabilities 1 − p of changing the contribution or p for joining another group are usually 0.5 but p can obviously be set to a different value in the simulations as a way of investigating the effect of the fluidity of connections on the system's behavior.
Once an agent a cuts a link, there are two ways to join another group: a can create a link to a random group, or to a group with probability proportional to the group's average payoff. The latter simulates uncertainty in the choice with a bias toward better groups. Clearly, the possibility of redirecting links requires more information than in the static model: besides the agent's own payoff and contribution, it is also given the identity of the player group in which it gets the worst payoff and, except in the random redirection, it also knows the average payoff of all groups but not in ranking order. The redirection is not done if the worst group is the one in which i is the focal element because in this case to change group i should cut all the links to its neighbors. It is also not done when the selected group j that i should join is already i's neighbor or it is i itself. For the sake of clarity, the above processes are summarized in pseudo-code form in Algorithms 2 (Decide next action) and 3 (Rewire link) for the random redirection case.
In our opinion, random redirection is much easier to set up in a laboratory experiment and should be the preferred choice in this case. It is also clear that the probability p should be a free parameter in an experiment in order to estimate it empirically from the observed relinking frequencies. On the whole, these rules constitute a simple reinforcement learning process in the sense that decisions that lead to better payoffs are maintained or reinforced while those that lead to negative results are weakened. Moreover, an agent can also act on its connections to try to improve its gains and, possibly, collective results.
Although the behavioral adaptation rules are extremely simple and certainly do not correspond in detail to the decisions made by human participants in an experiment, they were successful in the static network case to induce an average population behavior that was qualitatively similar to what was observed in experiments in which people had the same amount of information [26]. In the present study we extend the investigation to dynamic networks for which experimental results are lacking.
3. Results
In this section we discuss the results obtained by numerically simulating the behavioral model presented in the previous section. We first comment on the equilibrium contribution results and then we explore the nature of the topological transformations of the initial graphs in the dynamical model.
3.1. Evolution of the PGG Average Contribution
Figure 2 shows the average contribution during 40 interaction rounds for an enhancement factor r between 1.2 and 4.0 in steps of 0.2. The population size is 500 individuals connected in a social network of mean degree six built according to the model described in section 2.1 and Antonioni and Tomassini [34], giving a mean group size equal to seven and with an α value of 0.3. Some r values are redundant and are not shown for clarity. In each step of the 40 playing rounds individuals interact according to the schemas described in Algorithms 2 and 3. Results are averaged over 40 replicates by generating a new graph structure with the same simulation parameters and reinitializing randomly the individuals contributions before each repetition (see Algorithm 1). Figure 2A refers to the static case studied in Tomassini and Antonioni [26] while Figure 2B belongs to the dynamic case in which an unsatisfied agent can, with probability p = 0.5, cut a link to the group in which it gets the worst payoff and establish a new one to another randomly chosen group.
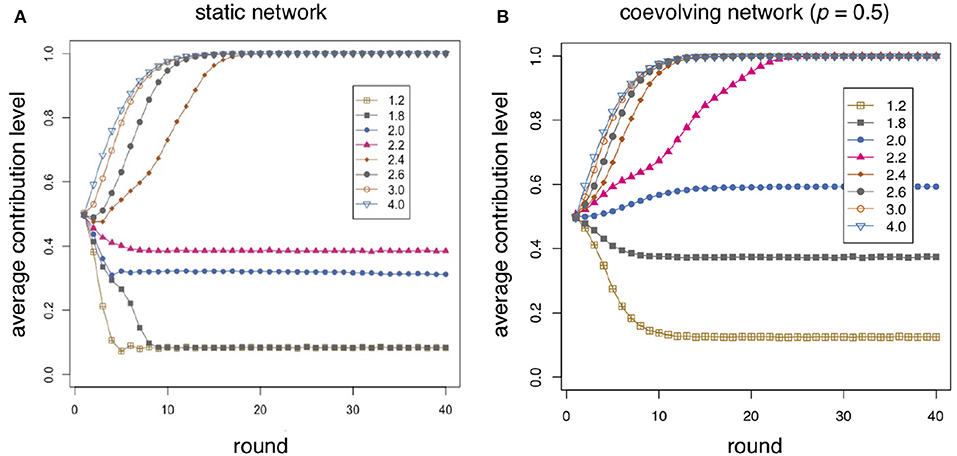
Figure 2. Average individual contribution as a function of round number for several values of the enhancement factor r as shown in the inset. The average is taken over 40 independent repetitions of 40 rounds on a network of size 500 and α = 0.3. (A) Static case, i.e., the network topology doesn't change during the simulation. (B) Coevolving network case, i.e., unsatisfied players may redirect a link to a random group with probability p = 0.5.
Initially, contributions are chosen randomly in the range [0, 1]. Therefore, in all cases the average value is about 0.5 at time step zero. This is the result of a stochastic process but it is also in line with results in experiments where subjects contribute about one-half of their endowment given that they still have no clue, or information, on the consequences of their choices. In the static case shown in Figure 2A contributions decline smoothly up to an r value of about 1.8, with a faster decay the lower r is. Again, this qualitatively also follows the trend found in experiments. And, as observed in most experiments, the pseudo-equilibrium value stabilizes around 0.1 and does not go to 0 as theory would tell us, in line with the experimental results of Burton-Chellew and West [8]. Above r = 2 there is an increase in average contribution, and for all r > 2.2 the stable state tends to full contribution after a short transient. Although the goal of the model is not to reproduce any particular set of results, we can say that, qualitatively, it correctly predicts the experimental behavior in Burton-Chellew and West [8] given the same amount of information.
When freedom of redirecting links is introduced the situation changes notably (see Figure 2B). The general behavior is the same as in the static case but the transition from low contribution (< 0.5) to high contribution sets in between r = 1.8 and r = 2.0 instead of r = 2.2 and r = 2.4 in the static case. Interestingly, at r = 1.8, the asymptotic average contribution remains at about 0.4 while, at r = 2.2, the final state is already one of full contribution. It is already well-known that models of the two-person PD in coevolving networks may attain states of full or almost full cooperation (see e.g., [27–30]) as a function of the strategy update rules and the game parameters. The emergence of cooperation through positive assortment between cooperators when redirecting links is allowed has been also confirmed experimentally (see e.g., [13, 14, 17, 31, 32]), and is admitted as being a reasonable explanation for the evolution of cooperation.
In Figure 3 we show how the rewiring frequency p affects the simulation results. When the rewiring probability is p = 0.2 (Figure 3A) the results are logically closer to the static case (see also Figure 2A) although the average contribution levels are still slightly better. On the other hand, in Figure 3B the probability of redirecting a link is p = 0.8. Increasing the rewiring probability is clearly beneficial for cooperation comparing the curves with those for p = 0.5 and especially with respect to the static case. Contributions reach and go beyond the 0.5 level already for r = 1.8 and full contribution is reached for r = 2.2 after only 10−15 steps in the average. The results shown in Figures 2B, 3 have been obtained with random redirection of a severed link. Payoff-proportional relinking gives very similar results and it is not shown here to save space.
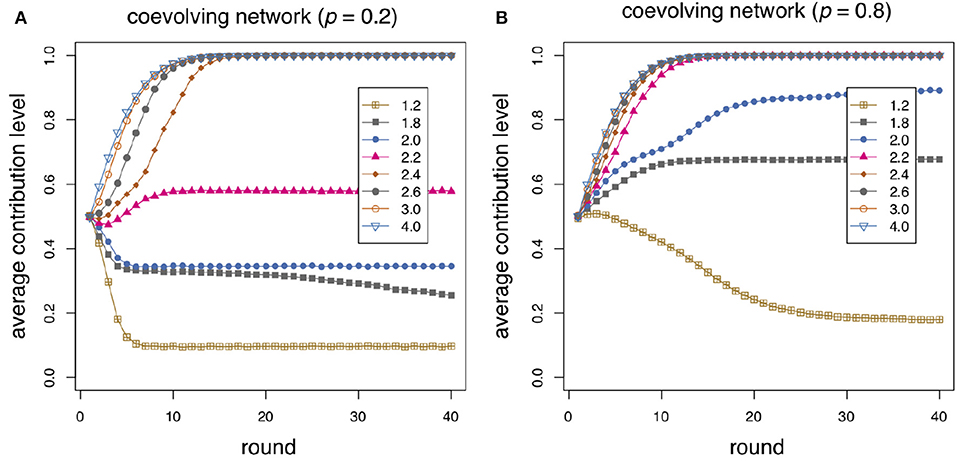
Figure 3. Average individual contribution as a function of round number for several values of the enhancement factor r as shown in the inset. The average is taken over 40 independent repetitions of 40 rounds on an initial network of size 500 and α = 0.3. (A) The probability of rewiring when an agent is unsatisfied is p = 0.2; (B) p = 0.8.
We are not aware of previous PGG coevolutionary models that use pseudo-behavioral adaptive rules similar to ours together with discrete amounts of contribution. However, there have been several studies on coevolutionary models of PGGs (e.g., [39–43]) based on replicator dynamics considerations under the form of payoff-monotone micro update rules and two-state agents. In general, these works show that switching links in unfavorable situations is a satisfactory strategy to use in PGG games for the evolution of cooperation in networks. Of course, coevolutionary rules involving factors other than the network structure are also possible and have been investigated in some cases (for a summary see Perc et al. [24]) but are not considered here.
3.2. Evolution of the Interaction Network
During a run of n playing rounds the original graph G1 evolves as a sequence of networks {G1, G2, …, Gn} in such a way that, in general, Gi ≠ Gj for any i, j ∈ {1, …, n} and i ≠ j, if the rewiring probability p > 0. In our model only the topology of the network may change. The average degree remains the same since a new connection is created only when an old one is deleted. It is useful to watch the topological changes in the evolving population of players by using standard network measures; here we use the average clustering coefficient 〈C〉, the average path length 〈L〉, and the degree distribution function (DDF), all of which are explained in Newman [35].
Let us begin with the degree distribution functions of initial and final network structures, shown in Figure 4. Figure 4A shows the DDF of one particular initial network which, as explained in section 2.1, is a social network model of 500 nodes, α = 0.3 and mean degree 〈k〉 ≈ 6. With a probability of rewiring p = 0.5, an agent represented by a network node may ask to rewire a link when unsatisfied. When cutting a link, the new connection is made at random and this means that, after a while, the graph evolves toward something that gets more similar to a random graph. One run comprises 40 rounds in our simulations. This is not enough to transform the original graph into a fully random graph but Figure 4B, which shows the DDF of the final network of a simulation for enhancement factor r = 1.2, indicates that the DDF has become narrower and more centered around the mean than the original one, as expected. Now, the amount of rewiring depends on the satisfaction of the agent, which in turn is a function of the enhancement factor r. As r increases, agents will be less prone to rewire their connections since they will be more satisfied in the average and, in this case, they will prefer to keep or increase their current contribution, as sketched in Algorithm 2. As a result, the DDF of the final network will be closer to the initial one. An example is shown in Figure 4C for a run with r = 2.4, starting from a DDF analogous to the one shown in Figure 4A.
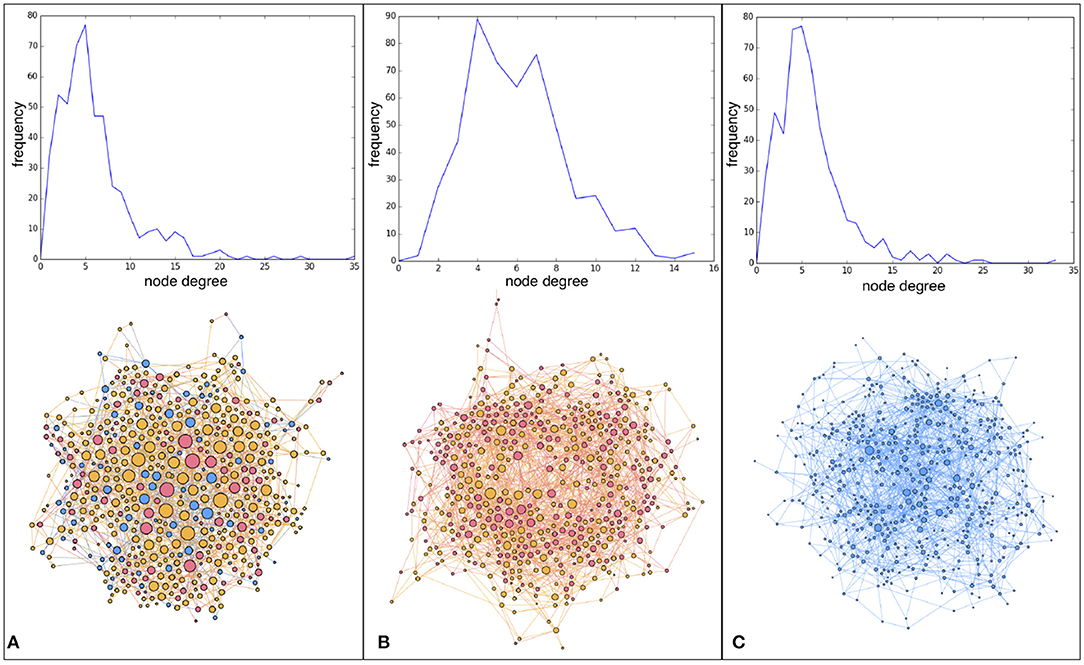
Figure 4. Degree distribution functions (DDFs) and graphical representation of the corresponding network structures. Node colors represent the node contribution to the common pools in which it participates: full contribution (blue), intermediate contribution (yellow), no contribution (red). Node size corresponds to the node degree. (A) DDF of an initial network of 500 nodes built according to the procedure described in Antonioni and Tomassini [34]. (B) DDF of the evolved network after 40 rounds of play with a link redirection probability p = 0.5 and an enhancement factor r = 1.2. (C) DDF of the final evolved network after 40 rounds of play having rewiring probability p = 0.5 and enhancement factor r = 2.4. Note the different scales in DDFs and figure zooms.
These trends are confirmed by the evolution of the other network metrics shown in Table 1. The values in the table refer to single treatments in which agents play the PGG for 40 rounds. It would be more adequate to show averages over many treatments although the trends are already recognizable and thus we limit ourselves to single examples just to convey the general idea.
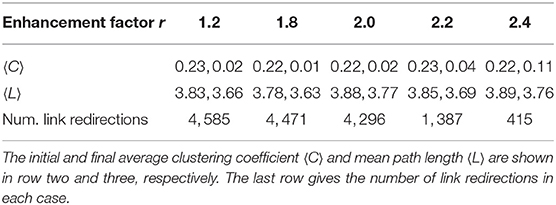
Table 1. Evolution of network statistics during a run of 40 rounds as a function of the enhancement factor r.
In Table 1 there are two entries for each line and each r value: the first refers to the initial network and the second refers to the evolved network after 40 rounds of play. The last row gives the number of link redirections for the corresponding value of r. For low values of r there is more rewiring and the average clustering coefficient 〈C〉 is small, following the trend in random graphs where it tends to zero when the graph size increases. When there is less rewiring as for r = 2.2, and especially r = 2.4, the final 〈C〉 is closer to the value of the original graph because the latter undergoes less randomization. The average path length 〈L〉 becomes a little shorter with the evolution but it is less affected and stays rather constant. The evolution of the average clustering coefficient during rounds is shown in more detail in Figure 5 for the same values of r as given in Table 1. Note that each curve corresponds to a single run of 40 game rounds in which a new initial graph of size 500, α = 0.3, mean degree ≈6, and probability of rewiring p = 0.5 is built for each value of r. This is the reason why there are some small fluctuations in the initial values of the average clustering coefficients. The shape of the curves confirm that rewiring activity stops earlier for higher values or r, as soon as players are satisfied. The curves for low r, where most players are unsatisfied, indicate that some network activity is present till the end of the run.
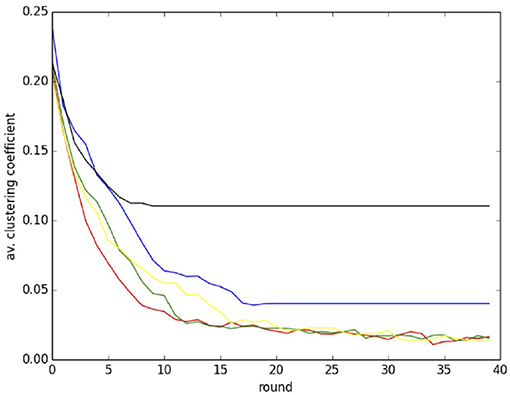
Figure 5. Evolution of the average clustering coefficient during a run of 40 rounds for the same r values as in Table 1. Color codes: r = 1.2, red; r = 1.8, green; r = 2.0, yellow; r = 2.2, blue; r = 2.4, black.
We conclude with some discussion of the differences in the network evolution found here with respect to the much more studied PD case, a good review of which is provided in Perc and Szolnoki [30]. Most models of PD on evolving networks start with a random network of agents and find at the end that the evolved networks are no longer random and that positive assortment of cooperators leads to cooperator clusters in which network reciprocity is at work, allowing cooperation to be widespread and stable. In order to compare with the static case, we started from a non-random network and allowed random relinking which requires minimal information. While contributions improve notably with respect to the fixed network, the topology evolves toward randomization. As a consequence, the initially existing communities tend to be destroyed progressively. It would certainly be interesting in future work to use more local rewiring rules, perhaps just limited to second neighbors in order to mitigate structure loss. Furthermore, from the point of view of the node properties, there is no analog of the cooperator clusters found in the binary PD case. The reason is 2-fold: first, we lack additivity in the multi-person PGG. A given agent plays with several players and in several groups at once and the groups are “intermingled,” as schematically shown in Figure 1. In addition, a node (agent) can no longer be characterized by a binary variable (C or D); rather, we have now several possible discrete values and this makes the concept of an assortative cluster more fuzzy.
3.3. PGG on a Real Social Network
In the previous sections we have discussed the results of playing a linear PGG with agents represented by the vertices of social network models. Those synthetic networks should be sufficiently representative of actual social networks. However, for the sake of completeness, it would be good to investigate how play evolves on a real social network. As an example, we chose a social network contained in the “Network Data Repository” [44]. The dataset contains all the Wikipedia voting data from the inception of Wikipedia till January 2008. Nodes represent Wikipedia users and an edge from node i to node j represents that user i voted on user j. The network has N = 889 nodes and 2, 914 edges, for a mean degree of 6.556 and an average clustering coefficient of 0.153. Its DDF has a rather long tail, probably representable by a stretched exponential or a power-law with an exponential cutoff, but given the size, we did not attempt to fit a function to it. Given the computational burden involved in the simulations, its relatively small size allowed us to run the PGG model with the same number of repetitions as before, i.e., 40 repetitions each one consisting of 40 rounds of play. In this way, the average results should be statistically comparable with those of section 3. Comparing results of Figures 6A,B shows that the coevolving scenario generally supports more cooperation with respect to the static one even for the real social network structure.
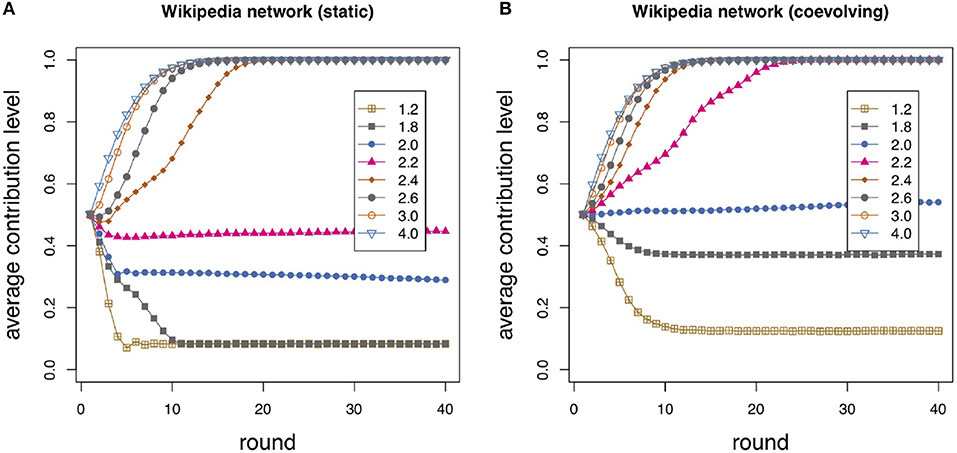
Figure 6. Wikipedia “who votes on whom” network (see text for details). Average individual contribution as a function of round number for several values of the enhancement factor r as shown in the inset. The average is taken over 40 independent repetitions of 40 rounds on the Wikipedia network using (A) p = 0 (static case); (B) p = 0.5 (coevolving).
4. Discussion and Conclusions
Realistic models of PGG dynamics have been proposed, both theoretical and based on numerical simulations. These models are essentially based on replicator dynamics ideas and either solve the corresponding differential equations, or numerically compute the population evolution. These theoretically justified approaches are a necessary first step toward an understanding of the game dynamics. However, the large amount of experimental data on PGGs that has been amassed in the last 20 years cannot be fully explained by existing theory alone. In fact, subjects in the laboratory make decisions in an individual manner, based on the amount of information available to them, and this leads in general to results that do not fully agree with the theoretical prescriptions. For this reason, we believe that a new class of models that incorporate decision making under uncertainty and admit individual variability and at least elementary learning capabilities is needed. In Tomassini and Antonioni [26] we made a first attempt in this direction and, under a very simple minimal information assumption, i.e., just agents' contribution and their own current aggregated payoff, we obtained results that were in good qualitative agreement with published experimental results. In Tomassini and Antonioni [26] the population structure was a static social model network. However, in everyday life associations between agents may change for various reasons, think for instance, of friendship, office colleagues, collaboration, and so on. In our computational PGG environment this is simulated by having unsatisfied agents cutting contacts with groups in which they are exploited and form new links to other groups.
In the present work we assumed a network structure that can evolve in time as a function of the above considerations. Indeed, it is well-known that contributions in PGG groups, which typically tend to decrease rather quickly in standard conditions, may increase again if a form of costly punishment of the free-riders is introduced (e.g., see [7]). In the present model an unsatisfied agent has the choice between decreasing the contribution to the public good or simply cutting a link to the group which generates the minimum payoff. The last option can be seen as a simple and cost-free form of punishment. The possibility of link redirection has been shown to be beneficial for cooperation in the Prisoner's Dilemma game, both in simulation as well as in experimental work with human subjects (see references in section 1). It was our hope that a similar mechanism could be equally useful in our pseudo-behavioral PGG model. Indeed, the results we obtained do confirm this. The average equilibrium contribution when link redirection is allowed is always better with respect to the one obtained with a fixed network for all values of the enhancement factor r. Furthermore, the transition from a non-cooperative to a cooperative system take place at lower values of r; the improvement is more substantial the larger the probability of redirecting links. We are not aware of laboratory or online experiments with the same characteristics as our model, thus we cannot compare our results with real data. However, because we kept our model particularly simple, an experiment with a similar setting would be easy to set up. In that context, having an easy way to change simulation model would be useful to facilitate parameter exploration before carrying out the actual experiment, which is usually expensive and time-consuming. In future work we plan to study other simple rule models for PGG based on different and richer information sets, such as the distribution of contributions in the group, reputational profiles and bipartite graph representation for agents and groups. Local rewiring and variants where cutting a link has a cost would also be interesting to investigate.
Data Availability Statement
The datasets generated for this study are available on request to the corresponding author.
Author Contributions
MT developed the code, performed the simulations, wrote the first draft of the manuscript. Both authors contributed the conception and design of the study, contributed to the manuscript revision, read, and approved the submitted version.
Funding
This work was supported by Ministerio de Ciencia, Innovación y Universidades/FEDER (Spain/UE) Grant No. PGC2018-098186-B-I00 (BASIC) and Ministerio de Economía y Competitividad of Spain Grant No. FJCI-2016-28276 (AA).
Conflict of Interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
References
1. Barrett S. Why Cooperate? The Incentive to Supply Global Public Goods. Oxford, UK: Oxford University Press (2007).
2. Hardin G. The tragedy of the commons. Science. (1968) 162:1243–8. doi: 10.1126/science.162.3859.1243
3. Olson M. The Logic of Collective Action: Public Goods and the Theory of Groups, Second Printing With New Preface and Appendix. Vol. 124. Cambridge, MA: Harvard University Press (2009).
5. Andreoni J. Cooperation in public-goods experiments: kindness or confusion? Am Econ Rev. (1995) 85:891–904.
6. Fehr E, Gächter S. Cooperation and punishment in public goods experiments. Am Econ Rev. (2000) 90:980–94. doi: 10.1257/aer.90.4.980
7. Fehr E, Gächter S. Altruistic punishment in humans. Nature. (2002) 415:137–40. doi: 10.1038/415137a
8. Burton-Chellew MN, West SA. Prosocial preferences do not explain human cooperation in public-goods games. Proc Natl Acad Sci USA. (2013) 110:216–21. doi: 10.1073/pnas.1210960110
9. Burton-Chellew MN, El Mouden C, West SA. Conditional cooperation and confusion in public-goods experiments. Proc Natl Acad Sci USA. (2016) 113:1291–6. doi: 10.1073/pnas.1509740113
10. Burton-Chellew MN, Nax HH, West A. Payoff-based learning explains the decline in cooperation in public goods games. Proc R Soc Lond B Biol Sci. (2018) 282:20142678. doi: 10.1098/rspb.2014.2678
11. Li X, Jusup M, Wang Z, Li H, Shi L, Podobnik B, et al. Punishment diminishes the benefits of network reciprocity in social dilemma experiments. Proc Natl Acad Sci USA. (2018) 115:30–5. doi: 10.1073/pnas.1707505115
12. Wang Z, Jusup M, Shi L, Lee J-H, Iwasa Y, Boccaletti S. Exploiting a cognitive bias promotes cooperation in social dilemma experiments. Nat Commun. (2018) 9:1–7. doi: 10.1038/s41467-018-05259-5
13. Antonioni A, Cacault MP, Lalive R, Tomassini M. Know thy neighbor: costly information can hurt cooperation in dynamic networks. PLoS ONE. (2014) 9:e110788. doi: 10.1371/journal.pone.0110788
14. Cuesta JA, Gracia-Lázaro C, Ferrer A, Moreno Y, Sánchez A. Reputation drives cooperative behaviour and network formation in human groups. Sci Rep. (2014) 5:7843. doi: 10.1038/srep07843
15. Barcelo H, Capraro V. Group size effect on cooperation in one-shot social dilemmas. Sci Rep. (2015) 5:1–8. doi: 10.1038/srep07937
16. Capraro V, Barcelo H. Group size effect on cooperation in one-shot social dilemmas II: curvilinear effect. PLoS ONE. (2015) 10:e0131419. doi: 10.1371/journal.pone.0131419
17. Antonioni A, Sánchez A, Tomassini M. Cooperation survives and cheating pays in a dynamic network structure with unreliable reputation. Sci Rep. (2016) 6:27160. doi: 10.1038/srep27160
18. Lozano P, Antonioni A, Tomassini M, Sánchez A. Cooperation on dynamic networks within an uncertain reputation environment. Sci Rep. (2018) 8:9093. doi: 10.1038/s41598-018-27544-5
19. Pereda M, Tamarit I, Antonioni A, Cuesta JA, Hernández P, Sánchez A. Large scale and information effects on cooperation in public good games. Sci Rep. (2019) 9:15023. doi: 10.1038/s41598-019-50964-w
20. Santos FC, Santos MD, Pacheco JM. Social diversity promotes the emergence of cooperation in public goods games. Nature. (2008) 454:213. doi: 10.1038/nature06940
21. Gómez-Gardeñes JM, Vilone D, Sánchez A. Disentangling social and group heterogeneities: public goods games on complex networks. Europhys Lett. (2011) 95:68003. doi: 10.1209/0295-5075/95/68003
22. Gómez-Gardeñes J, Romance M, Criado R, Vilone D, Sánchez A. Evolutionary games defined at the network mesoscale: the public goods game. Chaos. (2011) 21:016113. doi: 10.1063/1.3535579
23. Javarone MA, Antonioni A, Caravelli F. Conformity-driven agents support ordered phases in the spatial public goods game. Europhys Lett. (2016) 114:38001. doi: 10.1209/0295-5075/114/38001
24. Perc M, Gómez-Gardeñes J, Szolnoki A, Floría LM, Moreno Y. Evolutionary dynamics of group interactions on structured populations: a review. J R Soc Interface. (2013) 10:20120997. doi: 10.1098/rsif.2012.0997
25. Perc M, Jordan JJ, Rand DG, Wang Z, Boccaletti S, Szolnoki A. Statistical physics of human cooperation. Phys Rep. (2017) 687:1–51. doi: 10.1016/j.physrep.2017.05.004
26. Tomassini M, Antonioni A. Computational behavioral models for public goods games on social networks. Games. (2019) 10:35. doi: 10.3390/g10030035
27. Eguíluz VM, Zimmermann MG, Cela-Conde CJ, San Miguel M. Cooperation and the emergence of role differentiation in the dynamics of social networks. Am J Sociol. (2005) 110:977–1008. doi: 10.1086/428716
28. Santos FC, Pacheco JM, Lenaerts T. Cooperation prevails when individuals adjust their social ties. PLoS Comput Biol. (2006) 2:1284–91. doi: 10.1371/journal.pcbi.0020140
29. Pestelacci E, Tomassini M, Luthi L. Evolution of cooperation and coordination in a dynamically networked society. J Biol Theory. (2008) 3:139–53. doi: 10.1162/biot.2008.3.2.139
30. Perc M, Szolnoki A. Coevolutionary games–a mini review. Biosystems. (2010) 99:109–25. doi: 10.1016/j.biosystems.2009.10.003
31. Rand DG, Arbesman S, Christakis NA. Dynamic social networks promote cooperation in experiments with humans. Proc Natl Acad Sci USA. (2011) 108:19193–8. doi: 10.1073/pnas.1108243108
32. Wang J, Suri S, Watts DJ. Cooperation and assortativity with dynamic partner updating. Proc Natl Acad Sci USA. (2012) 109:14363–8. doi: 10.1073/pnas.1120867109
33. Gallo E, Yan C. The effects of reputational and social knowledge on cooperation. Proc Natl Acad Sci USA. (2015) 112:3647–52. doi: 10.1073/pnas.1415883112
34. Antonioni A, Tomassini M. A growing social network model in geographical space. J Stat Mech. (2017) 2017:093403. doi: 10.1088/1742-5468/aa819c
36. Pereda M, Capraro V, Sánchez A. Group size effects and critical mass in public goods games. Sci Rep. (2019) 9:5503. doi: 10.1038/s41598-019-41988-3
37. Smaldino PE, Lubell M. An institutional mechanism for assortment in an ecology of games. PLoS ONE. (2011) 6:e23019. doi: 10.1371/journal.pone.0023019
38. Peña J, Rochat Y. Bipartite graphs as models of population structures in evolutionary multiplayer games. PLoS ONE. (2012) 7:e44514. doi: 10.1371/journal.pone.0044514
39. Wu T, Fu F, Wang L. Individual's expulsion to nasty environment promotes cooperation in public goods games. Europhys Lett. (2009) 88:30011. doi: 10.1209/0295-5075/88/30011
40. Zhang CY, Zhang JL, Xie GM, Wang L. Coevolving agent strategies and network topology for the public goods games. Eur Phys J B. (2011) 80:217–22. doi: 10.1140/epjb/e2011-10470-2
41. Zhang HF, Liu RR, Wang Z, Yang HX, Wang BH. Aspiration-induced reconnection in spatial public-goods game. Europhys Lett. (2011) 94:18006. doi: 10.1209/0295-5075/94/18006
42. Li Y, Shen B. The coevolution of partner switching and strategy updating in non-excludable public goods game. Phys A Stat Mech Appl. (2013) 392:4956–65. doi: 10.1016/j.physa.2013.05.054
43. Li Z, Deng C, Suh IH. Network topology control strategy based on spatial evolutionary public goods game. Phys A Stat Mech Appl. (2015) 432:16–23. doi: 10.1016/j.physa.2015.02.101
Keywords: cooperation, PGG, dynamic networks, social networks, simulation model
Citation: Tomassini M and Antonioni A (2020) Public Goods Games on Coevolving Social Network Models. Front. Phys. 8:58. doi: 10.3389/fphy.2020.00058
Received: 27 November 2019; Accepted: 26 February 2020;
Published: 11 March 2020.
Edited by:
Valerio Capraro, Middlesex University, United KingdomReviewed by:
Zhen Wang, Northwestern Polytechnical University, ChinaSen Pei, Columbia University, United States
Copyright © 2020 Tomassini and Antonioni. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Marco Tomassini, bWFyY28udG9tYXNzaW5pQHVuaWwuY2g=; Alberto Antonioni, YWxiZXJ0by5hbnRvbmlvbmlAZ21haWwuY29t
 Marco Tomassini
Marco Tomassini Alberto Antonioni
Alberto Antonioni

