- 1Department of Physics, University of Washington, Seattle, WA, United States
- 2Los Alamos National Laboratory, Theoretical Division, Los Alamos, NM, United States
Significant progress in the understanding of the fission process within a microscopic framework has been recently reported. Even though the complete description of this important nuclear reaction remains a computationally demanding task, recent developments in theoretical modeling and computational power have brought current microscopic simulations to the point where they can provide guidance and constraints to phenomenological models, without making recourse to parameters. An accurate treatment compatible with our understanding of the inter-nucleon interactions should be able to describe the real-time dynamics of the fissioning system and could justify or rule out assumptions and approximations incompatible with the underlying universally accepted quantum-mechanical framework. Of particular importance are applications to observables that cannot be directly measured in experimental setups (such as the angular momentum distribution of the fission fragments, or the excitation energy sharing between the fission fragments, or fission of nuclei formed during the r-process), and their dependence of the excitation energy in the fissioning system. Even if accurate predictions are not within reach, being able to extract the trends with increasing excitation energy is important in various applications. The most advanced microscopic simulations of the fission process do not support the widely used assumption of adiabaticity of the large amplitude collective motion in fission, in particular for trajectories from the outer saddle toward the scission configuration. Hence, the collective potential energy surface and inertia tensor, which are the essential elements of many simplified microscopic theoretical approaches, become irrelevant. In reality, the dynamics of the fissioning system is slower than in the case of pure adiabatic motion by a factor of three to four times and is strongly overdamped. The fission fragment properties are defined only after the full separation, while in most of the current approaches no full separation can be achieved, which increases the uncertainties in describing fission-related observables in such methods.
1. The Past
In a matter of days after Hahn and Strassmann [1] communicated their yet unpublished results to Lise Meitner, she and her nephew Otto Frisch [2] understood that an unexpected and qualitatively new type of nuclear reaction has been put in evidence and they dubbed it nuclear fission, in analogy to cell divisions in biology. Until that moment in time nuclear fission was considered a totally unthinkable process [3, 4], “as excluded by the small penetrability of the Coulomb barrier [5], indicated by the Gamov's theory of alpha-decay” [2]. Meitner and Frisch [2] also gave the correct physical interpretation of the nuclear fission mechanism. They understood that Bohr's compound nucleus [6] is formed after the absorption of a neutron, which eventually slowly evolves in shape, while the volume remains constant, and that the competition between the surface energy of a nucleus and its Coulomb energy leads to the eventual scission. Meitner and Frisch [2] also correctly estimated the total energy released in this process to be about 200 MeV. A few months later Bohr and Wheeler [7] filled in all the technical details and the long road to developing a microscopic theory of nuclear fission ensued. In the years since, a few more crucial theoretical results have been firmly established: (i) the defining role of quantum shell effects [8, 9] and in particular the special role played by the pairing type of nucleon-nucleon interaction in shape evolution [10, 11]; (ii) the fact that the subsequent emission of neutrons and gammas can be described quite accurately using statistical methods [12, 13]; (iii) and that the non-relativistic Schrödinger equation should be adequate as well, as no genuine relativistic effects, such a retardation, are expected to play any noticeable role in fission dynamics.
Whether a fissioning nucleus undergoes either spontaneous fission or induced fission the time it takes the nucleus to evolve from its ground state shape until outside the barrier or past the outer saddle is very long in case of neutron induced fission ≈ (10−15) s. in comparison with the time the nucleus slides downhill until scission, which is estimated to be (10−20) s. Therefore, the saddle-to-scission stage of nuclear shape evolution is the fastest and arguably the most non-equilibrium stage of the nucleus dynamics from the moment a neutron has been captured and the stage which plays a crucial role in in determining the FFs properties. The many intricacies of the fission process, the multitude of aspects, which required a deep theoretical understanding, ultimately rooted in the quantum nature of this phenomenon defied the efforts of many generations of theorists, and a huge plethora of mostly phenomenological models have been put forward, often based on contradictory assumptions between models. The extensive range of assumptions, range from adiabatic evolution on top of which one adds (relatively weak) dissipation and fluctuations, to strongly overdamped motion, when the role of the collective inertia becomes irrelevant, to full statistical equilibrium near the scission configuration, and to mixing quantum and classical descriptions.
Microscopically inspired models are typically based on the (ill suited choice of words, as the our analysis shows) adiabatic approximation, which is often conflated with slow motion. The class of adiabatic transformations, during which only mechanical work is performed and no heat transfer or entropy production occurs, are only a subclass of slow motion or quasistatic processes. Theorists believed that the nuclear shape evolution until the moment of scission was so slow that individual nucleons had a sufficient time to adapt to avoided single-particle level crossings [14] and the entire nucleus would follow the lowest “molecular term,” using the Born-Oppenheimer chemical terminology [15] (see Figure 1). Following this assumption at first the generator coordinate method (GCM) has been introduced by Hill and Wheeler [14] and Griffin and Wheeler [18] and later on a related alternative approach, the adiabatic time-dependent Hartree-Fock (ATDHF) method [19–22]. GCM is still one of the most popular tools still in use in the microscopic theories of fission [22–29]. The GCM and ATDHF method have been shown to be basically equivalent [30], when GCM is defined with complex generator coordinates [31]. As however Goeke and Reinhard [30] succinctly state: “Usually the |q〉 is obtained by an educated guess using the preconceived knowledge of the process.” (Typically |q〉 stands for a generalized Slater determinant, aka Hartree-Fock-Bogoliubov many-nucleon wave function.) Even though many efforts have been dedicated to find a better way to choose the collective or generator coordinates the methods proved to be too difficult to implement in practice and the quality of the decoupling between collective and intrinsic degrees of freedom either too not very good or difficult to assess [32]. An exact separation between collective and intrinsic degrees of freedom (DoF) it is equivalent to an adiabatic evolution of the set of collective DoF. Then the collective DoF would always follow the lowest “molecular orbital” and only work would be performed on the intrinsic DoF, and thus with no heat transfer, and the intrinsic system would remain “cold” during the entire evolution.
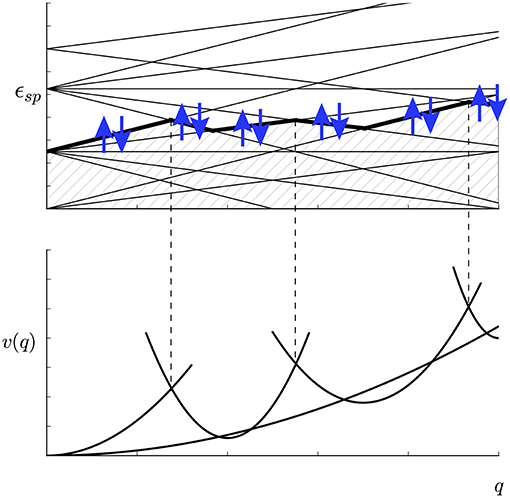
Figure 1. The schematic evolution of the single-particle nucleons levels (Upper panel) and of the total nuclear energy (Lower panel) as a function of deformation parameter q [10, 16, 17]. The thick line represents the Fermi level and the up/down arrows depict the Cooper pairs of nucleons on the Fermi level only, in time-reversed orbits (m, −m). This figure is reproduced from Bulgac et al. [17] under the terms of the American Physical Society copyright agreement.
2. The Present
Unfortunately until recently this crucial aspect of large amplitude collective nuclear dynamics, whether the large amplitude collective motion in fission is indeed adiabatic was never tested and, as our results unequivocally show, the adiabatic assumption is strongly violated. Surprisingly at first glance, we have recently shown that the evolution of the nuclear shape is in reality significantly slower that the adiabatic assumption would predict. One would naively expect that if the motion is even slower then at an avoided level crossing (see Figure 1), the probability that the system would follow the lower “molecular term” is even greater and thus the adiabatic assumption would be even more likely be valid. An analogy with a classical system can help and demonstrate just the opposite. If a railroad car is released on top of a hill, it will convert basically all the gravitational potential energy difference when reaching the bottom of the hill into kinetic energy. Thus, only pure mechanical work on the intrinsic DoF of the railroad car will occur with essentially no heat transfer or entropy production. This is an adiabatic process. However, if one were instead to block the wheels of the railroad car, the friction will slow down the car and almost the entire gravitational potential energy difference will be converted into heat, the wheels will get red hot, thus increasing the “intrinsic energy” of the car, and the speed of the car at the bottom of the hill would be rather small.
The only practical theoretical framework to consider in the treatment of the dynamics of large nuclei is the (Time-Dependent) Density Function Theory [(TD)DFT], which has been formulated a long time ago [33–38]. One of the main difficulties consist in constructing the energy density functional, for which no rigorous recipes exist, DFT and TDDFT arrive at the mathematical conclusion that the stationary or time-dependent solution of the many-body Schrödinger equation is in a one-to-one-to-one correspondence with the number density, an (arbitrary) applied one-body external potential, and that the number density can be obtained by solving the much simpler DFT or TDDFT equations. There is a continual debate in nuclear physics that DFT is not applicable to nuclei, which are self-bound isolated systems. At the same time however, no one would argue that DFT cannot describe neutrons and protons in the neutron star crust and deeper into the star. Neutrons are delocalized in the neutron star crust and below it. In the rod, slab, and tube phases in the neutron star crust and below both protons and neutrons are delocalized and in this respect they are similar to electrons in solids. One can imagine that in the future one might produce a nuclear trap using some kind of γ-lasers, similarly to what nowadays experiments are made with cold atoms. Until then one can mentally imagine that one can put an isolated nucleus in a spherical infinite square well-potential with a radius about 3…5× the nuclear radius (or even a harmonic potential) and compare the results of such a DFT treatment of the nucleus with the widely accepted DFT alter ego, the NEDF approach, a tool of choice in theoretical nuclear calculations. The results of the these two approaches are numerically indistinguishable under these conditions, and therefore the debate alluded above is merely pedantic. One deficiency of a pure DFT approach is that the number density alone cannot disentangle between a normal and a superfluid system, and one needs an order parameter, as one does in the case of magnetization. The practical local density approximation (LDA) [34], which is the local formulation of DFT, has to be augmented with the anomalous density [39, 40], and it was dubbed the superfluid LDA (SLDA). In Bulgac [39, 40] one can find detailed reviews of the developments, verification, and validation of TDSLDA for a variety of physical systems, ranging from cold atoms, nuclei, and to neutron star crust.
A (TD)DFT framework for nuclear structure and dynamics should satisfy several requirements (in this order of importance): (i) the DFT and the Schrödinger description of observables should be identical, as both in ultimate instance rely on the same inter particle interactions; (ii) both DFT and Schrödinger equations should describe correctly Nature, thus we need accurate interactions between nucleons; (iii) the numerical implementation of the (TD)DFT should faithfully reproduce the theory. At present we definitely do not have acceptable answers to the requirements (i) and (ii) and rely instead to a significant amount of phenomenology. The numerical implementation of DFT without any drastic physical restrictions became possible only relatively recently, with the advent of supercomputers [39, 40].
The TDSLDA is formulated in terms of Bogoliubov quasi-particle wave functions (qpwfs). The evolution of the qpwfs is governed by the equations:
where we have suppressed the spatial r and time coordinate t, and k labels the qpwfs (including the isospin) [ukσ (r, t), vkσ (r, t)], with σ = ↑, ↓ the z-projection of the nucleon spin. The single-particle (sp) Hamiltonian , and the pairing field Δ(r, t) are functionals of various neutron and proton densities, which are computed from the qpwfs, see Jin et al. [41] for technical details. No proton-neutron pairing is assumed in the present study, and the pairing field is singlet in character. A TDSLDA extension to a more complex pairing mechanisms is straightforward.
While a nuclear system evolves in time one can uniquely separate the energy into collective kinetic energy and intrinsic energy contributions [17] using the nuclear energy density functional (NEDF) (τ(r, t), n(r, t), …), in a similar manner as in hydrodynamics:
Above n(r, t) is the number density, τ(r, t) is the kinetic density energy, and p(r, t) = mn(r, t)v(r, t) are linear momentum and local collective/hydrodynamic velocity densities, and ellipses stand for various other densities. p(r, t)/n(r, t) is the position of the center of the local Fermi sphere in momentum space. The first term in Equation (2) is the collective/hydrodynamic energy flow Ecoll and the second term is the intrinsic energy Eint in the local rest frame. For the sake of simplicity we have suppressed the spin and isospin DoF, even though they are included in all the actual calculations. The collective energy Ecoll(t) is not vanishing only in the presence of currents and vanishes exactly for stationary states. The inertia tensor in Ecoll(t) in the case of irrotational collective motion is fully equivalent to the Werner-Wheeler inertial tensor [23]. The intrinsic energy Eint(t) is determined only by the fermionic matter distribution. The qualitative new result established in Bulgac et al. [17] and also illustrated here in Figure 2 is that in an fully unrestricted TDSLDA the collective flow energy is almost negligible until scission, in total discrepancy with what one would have naively expected if the adiabatic assumptions would be satisfied.
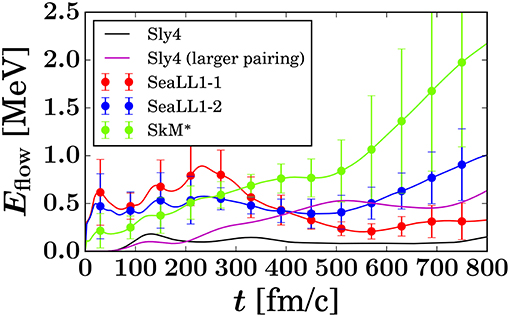
Figure 2. (Color online) the collective flow energy evaluated for NEDFs [42] realistic pairing SLy4 (dash-dot line), enhanced pairing SLy4* (dash line), and for SkM* (dotted and dash-dot lines with error bars), and SeaLL1 (solid and dashed lines with errors bars) sets [17]. The error bars illustrate the size of the variations due to different initial conditions in case of various SeaLL1-1,2 and SkM*-1,2 NEDFs used. In the case of realistic pairing NEDF Sly4 (larger pairing) the time has been scaled by a factor of 1/10. This figure is adapted from the results published in Bulgac et al. [17] under the Creative Commons CC BY license.
Our simulations point to an unexpectedly small Ecoll from saddle-to-scission, corresponding to a collective speed vcoll/c ≈ 0.002⋯0.004, significantly smaller than the Fermi velocity vF/c ≈ 0.25 (see Figure 2). Since in TDSLDA one simulates the one-body dynamics exactly, it is natural to discuss adiabaticity at the mean-field level. The transition rate between sp states is suppressed if the time to cross an avoided level-crossing configuration satisfies the restriction Δt ≪ ℏ/Δϵ ≈ 400 fm/c, where Δϵ = 1/ρsp(ϵF) is the average sp energy level spacing at the Fermi level. Since on the way from saddle-to-scission the time required is 1…3 × 103 fm/c and several dozen of avoided level crossings occur [16, 43], this condition is clearly violated. Somewhat surprisingly, the adiabatic assumption is also violated even in the case of SLy4 NEDF (see Bulgac et al. [42] and Figure 2), when the saddle-to-scission time is (104) fm/c as well. The collective motion is thus expected to be strongly overdamped. From saddle-to-scission the nucleus behaves as a very viscous fluid, the role of collective inertia is strongly suppressed, and the trajectories follow predominantly the direction of the steepest descent with the terminal velocity determined by the balance between the friction and the driving conservative forces (see Figure 2).
This result serves as the first microscopic justification for the assumption of the overdamped Brownian motion model [44–49] and partially to the scission-point model [50–53]. In both these phenomenological models it is assumed that the preformed FFs are in statistical equilibrium and that the collective energy flow is either vanishing or very small. The main difference is that in the scission-point model there is no mechanism to ensure that all equilibrium scission configurations could be reached dynamically, while the nucleus evolves from the saddle-to-scission. Moreover, the relaxed FF properties are defined only after the FFs become sufficiently well-separated, see below. It is equally unexpected that in the case of enhanced pairing, when the pairing condensates retain their long-range order throughout the entire saddle-to-scission evolution, the collective dynamics remains strongly overdamped.
While evolving from saddle-to-scission a nucleus encounters a large number of avoided level crossings and instead of following the lowest potential energy surface, as would happen in an adiabatic evolution, many transitions to higher excited levels occur. Similarly to what is known for decades in chemistry [54–56], one should consider not only the lowest potential energy surface, when initially the system could be found on the lowest with unit probability, but all “molecular terms,” which become populated during the evolution (see Figure 3). The separation between such potential energy surfaces reaches values of order (10) keV or even less, and only if the system traverses a level crossing in a time much longer than ≈ ℏ/10 keV ≈ 20, 000 fm/c or longer the nucleus will remain on the lowest potential energy surface. On the other hand the saddle-to-scission time is (103) fm/c and this is why the adiabatic assumption is in the final analysis strongly violated.

Figure 3. In nuclei the level density increases with the excitation energy quite fast, practically exponentially at energies of the order of the neutron separation energy, when [57, 58], and it reaches values of (105) MeV−1 and various potential energy surfaces, corresponding to different “molecular terms” display a large number of avoided level crossings. Here we illustrate the generic behavior of the collective energy levels (y-axis) as a function of a collective coordinate (x-axis), see Bulgac et al. [59] for details and a similar figure.
Why do pairing correlations play an important role in fission dynamics? In a static nuclear configuration each single-particle level is doubly-degenerate, due to the Kramers degeneracy. At the level crossing both nucleons on the highest occupied level (homo—highest occupied molecular orbital) would have to transition simultaneously to the lowest down-sloping level (lumo—lowest unoccupied molecular orbital) to ensure that the local momentum distribution remains approximately spherical, as otherwise it would acquire an oblate shape [10, 11, 14], while the shape of the nucleus becomes more prolate. Nucleon-nucleon interactions at low momentum transfer can be modeled with a reasonable accuracy with a zero-range δ-interaction, which favors the transitions between pairs of time-reversed orbitals, exactly as the Kramers degenerate orbitals (see Figure 1). The up-sloping levels are characterized by larger projections of the angular momentum on the fission axis, , and these levels should be depopulated, since in a FF the largest angular momenta are smaller, . While evolving from one level crossing to the next, the entire evolution is likely rather well-reproduced by a simple one-body dynamics, as each single-particle level occupation probability changes little. What one-body dynamics lacks is the contributions arising from the Boltzmann collision integral. However, at each level crossing the two-correlated nucleon pairs will undergo a collision, and at low energies transitions between pairs of time-reversed orbitals expected to dominate the collision rate. One should take with a grain of salt this simplistic picture of “collisions” and jumps between sp levels, as nothing happens instantaneously or at one point in space in quantum mechanics. In the presence of a Bose-Einstein condensate of nucleon Cooper pairs the nucleus has a superfluid component and pair transfers are enhanced due to the Bose enhancement factor. The dynamics of the nuclear systems then approaches the evolution of classical inviscid (no viscosity) or perfect fluid. An illustration of this behavior was exemplified in Figure 4 in Bulgac [40] and in Figure 4. When the magnitude of the pairing field was artificially increased from a realistic value to a value 3…4× larger the evolution time from saddle-to-scission decreased by a factor of ≈ 10 and at the same time the long range coherence of the pairing field across the entire nucleus survived. For realistic values of pairing strengths during the descent from the saddle-to-scission both proton and neutron pairing fields fluctuate both in space and time, long range order basically vanishes, but quite often it is revived.

Figure 4. These are some selected snapshots of the neutron/proton magnitudes (Left) and phases (Right) of pairing gaps (upper half/lower/half of each frame) in the case of realistic pairing strengths (upper panels) and enhanced pairing strength (lower panels), obtained in the case of SLy4 NEDF. This figure is adapted from the results published in Bulgac et al. [17] under the Creative Commons CC BY license.
Another important aspect which emerged from our TDSLDA fission simulations [17, 42], which is of significant importance in the implementation of various phenomenological models, concerns the shapes of FFs at scission and when they reach their relaxed shapes (see Figure 5). This behavior is apparently confirmed indirectly by experiments. In Langevin or Fokker-Planck [60–65], TDGCM [26, 66], and scission-point [50–53] models the calculation of the FFs yields consider only a very limited range of nuclear shapes. In particular in such simulations one never introduces the octupole FF moments. Our results, as well recent analysis by Scamps and Simenel [67], clearly demonstrate that the FFs emerge at scission octupole deformed and also with a significantly larger quadrupole deformation than the relaxed values. Moreover, even after scission the FFs there is a significant Coulomb interaction between them, which leads to the excitation of both low energy and giant resonances in FF [68, 69]. This interaction enables additional excitation energy exchange between the FFs after scission, and it also affects their total kinetic energy, a behavior also seen in our simulation, but yet not documented. In statistical scission-point models there is no dynamics, and only the competition between FFs configurations at the scission point are considered [50–53], a model to which our results lend partial support. However, the only shapes considered are quadrupole deformation of the relaxed FFs, which clearly is not what our dynamical simulation demonstrate.
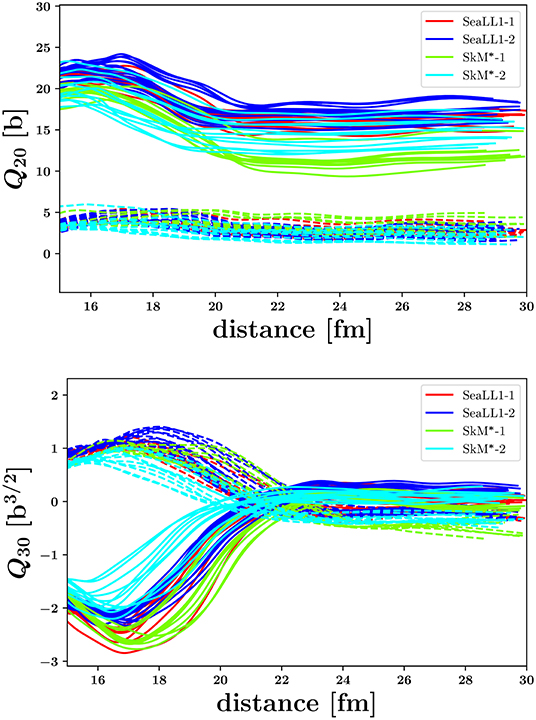
Figure 5. The evolution of the quadrupole and octupole moments of the FFs as a functions of their separation after scission [17]. Different lines correspond to different initial conditions and different NEDFs, see Bulgac et al. [17] more details. The solid/dashed lines are for the light/heavy FFs, respectively. This figure is adapted from the results published in Bulgac et al. [17] under the Creative Commons CC BY license.
Our simulations put in evidence another very important aspect, the mechanism of the excitation energy sharing between the FFs. As a rule the heavy FF emerges in the end cooler than the light FF, even though they have been in contact for quite a long time before scission. Moreover, when increasing the initial energy excitation of the fissioning nucleus we have established that only the heavy FF becomes hotter and that is reflected in the average neutron multiplicity number of emitted, and results which is in apparent agreement with experimental findings (see Figure 6). Experimentally it is extremely difficult to infer the excitation energies of the FFs, which are a crucial input in various statistical codes [70, 72, 73]. Bertsch et al. [74] argue that the FFs spin distribution, which determines the prompt gamma angular distribution, can be used to infer information of the excitation energy sharing between FFs. Randrup et al. [73] point to a pronounced anti-correlation between and mean total kinetic energy , which can be used reduce uncertainties in data analysis. Schmidt and Jurado [75, 76] suggested a phenomenological model, the “energy-sorting” mechanism based on the empirical constant temperature parametrization of the nuclear level densities due to Gilbert and Cameron [77]. In this “energy-sorting” model the FFs before scission have different temperatures, with a lower temperature of the heavy fragment, which would generate an energy flow from the light/hotter to the heavy/cooler fragment. Our simulations demonstrate however that the near scission the two FFs have properties quite different (shape, excitation energy, pairing correlations) from the properties of relaxed fragments. It is therefore problematic to relate the properties of excited isolated nuclei with the properties of FFs in contact before rupture.
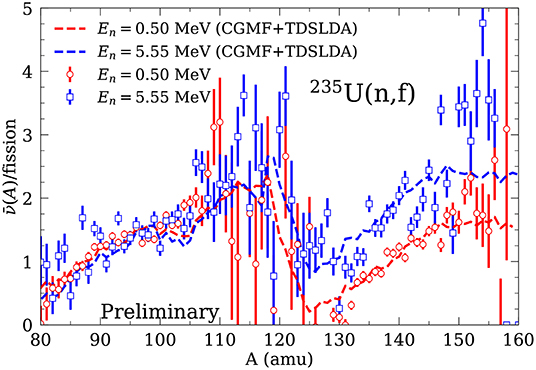
Figure 6. We compare here the average neutron multiplicity emitted by FFs using a CGMF simulation [70], which assumes an En dependence for the energy sharing extracted using the excitation energy sharing between the FFs in our calculation with NEDF SeaLL1, as a function of the equivalent incident neutron energy in 235U(n,f) reaction along with available experimental data [71]. Note that in this figure the parametrization was based on 240Pu calculations, while 236U calculations are in progress.
As we have mentioned above, the number of collective DoF and their character is a long standing problem in microscopic inspired theoretical and phenomenological models. The choice of collective DoF and their character is guided by the authors' intuition, their computational and other abilities, educated guess, imagination, and/or available resources [30]. It was never proven or demonstrated that a GCM representation of the nuclear wave function is ever accurate. The wave function of a many-fermion system in TDGCM is constructed according to the following prescription
where Φ(x|q) are (generalized) Slater determinants depending on nucleon spatial coordinates, spin, and isospin x = (x1, …, xA), xk = (rk, σk, τk) and parameterized by the collective coordinates q = (q1, …, qn), and where f(q, t) is the collective wave function. There is no criterion or small parameter which controls the accuracy of such a representation, that is
We have presented rather simple arguments that most likely such an accurate representation does not exist in general, particularly in fission large amplitude collective motion [17]. A rather simple estimate of the possible number of different shapes, and therefore of independent terms in Equation (3), shows that it is basically infinitely small in comparison with the number of possible terms in an exact multi-configurational Slater determinant representation of Ψexact. Can we check whether GCM is a good approximation for the saddle-to-scission evolution? Now we definitely can and we have the answer, and since
where T is the temperature of the intrinsic system, we know that the collective motion is strongly overdamped, that there is an irreversible energy flow from the collective/shape DoF to the intrinsic DoF, and that during the saddle-to-scission evolution the temperature of the intrinsic system increases, as does its (entanglement) entropy as well. We should also remember, that the evolution of the fissioning nucleus from saddle-to-scission is a truly non-equilibrium one, and the notion of a “slowly evolving” nuclear temperature T might be questionable. This suggest that in phenomenological calculations a more physically motivated choice for the potential energy surface would be one in which with increasing deformation one would increase the “temperature T,” so as to keep the “collective potential” energy V(q, T) essentially equal to the initial excitation energy of the compound nucleus. Basically this is the prescription that Randrup et al. [48, 49] have implemented lately.
There were indirect indication in microscopic approaches that the number of collective DoF can vary along the fission path. In the overwhelming majority of fission studies the only deformation of the nucleus close to the ground state is the axial symmetric quadrupole moment Q20, in spite of the fact that the Bohr-Mottelson five-dimensional collective Hamiltonian is one tool of choice to describe the low energy structure of open-shell nuclei [58, 78, 79]. Ryssens et al. [80] have shown in a beyond mean field calculation of the 1-dimensional fission path the nucleus 240Pu is axially deformed around the ground state configuration, it becomes triaxially deformed when it reaches the fission isomer region, and before it reaches the outer fission barrier it breaks the axial symmetry as well. We have recently developed a framework into which one can include fluctuations and dissipation in a quantum approach [81], which allows for shape fluctuations of any kind. What we observed that by allowing a bending mode to become active (see Figure 7), the mass and TKE distributions acquire shapes in quite nice agreement with observations. It was discussed quite some time ago that such bending modes might be responsible for the angular distributions of the FFs [82] and this type of distributions can be also extracted from TDSLDA calculations in the near future [74, 83]. Phenomenological or even TDGCM approaches do not consider so far such bending modes, which are definitely physically relevant for a large number of observables.
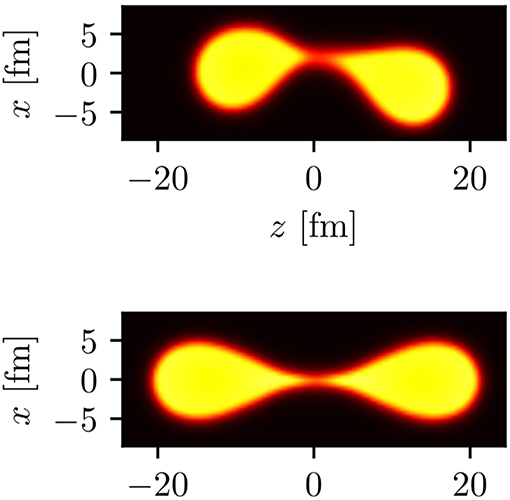
Figure 7. In the upper panel we show a typical scission configuration when unlimited type of fluctuations are allowed as compared to a typical TDSLDA scission configuration, in which axial symmetry is assumed in this case for 258Fm. This figure is reproduced form Bulgac et al. [81] under the terms of the American Physical Society copyright agreement.
3. What Are the Needs?
Nuclear fission is a complex process, in which a heavy nucleus evolves from a compact shape to a configuration in which two or more fragments are produced, and is accompanied by emission of prompt neutrons and gamma rays (and, eventually, electrons and antineutrinos). Most of the energy is released in form of kinetic energy of the fragments, while prompt neutrons emitted before beta decays play the main role in applications like energy production.
The dynamics of the nuclear system from the formation of compound nucleus until after the acceleration of FFs and prompt particle emission is too rapid to be experimentally resolved. On the other hand, the time scale of the weak interaction, which governs the decay of FFs in experiments toward stability ranges from seconds to minutes, and thus the dynamics involving beta decay toward stability, including delayed neutron and gamma emissions, can be decoupled from the initial more rapid part that is only governed by the strong interactions. Consequently, the fragment properties directly influence the properties of prompt fission and gamma rays, which have been the subject of comprehensive, albeit not exhaustive, experimental investigations over the years. Thus, at Los Alamos National Laboratory, experimental campaigns have investigated the prompt fission neutron spectra for neutron-induced fission of major actinides (235, 238U, 239Pu) for a large range of incident neutron energies using the ChiNu experimental setup [84, 85]. On the other hand, experiments that measure the average neutron multiplicity as a function of pre-fission neutron mass [86–91], which can be used to guide energy sharing in fission fragments, are more scarce, and for a limited number of reactions (usually spontaneous fission or neutron-induced fission with thermal neutrons). The surrogate reaction technique is used by Lawrence Livermore National Lab and Texas A&M to measure the 239Pu and 241Pu prompt fission neutron multiplicity (average and distribution) as a function of equivalent incident neutron energy [92, 93]. Complementary, significant resources have been devoted toward measuring the prompt fission gamma rays produced in the decay of fission fragments, after the neutron emission, at Los Alamos, using the DANCE calorimeter [94–97], and worldwide employing high-resolution detectors [98–102]. Such measurements complement existing measurements of prompt-gamma rays by Verbinski et al. [103], and many others [104–106]. Furthermore, data on total gamma production can be useful in evaluating the prompt fission gamma properties, if no other data exist, fission dominates, and the other gamma-producing channels can be modeled with reasonable accuracy [107].
In addition to detecting and measuring the products of decay of FFs, a concerted effort has been directed toward the direct measurement of the FF distributions. While simpler, the “2E” measurements [108–111] have the shortcoming that additional information is required to identify the mass of the fragment, hence the poor 4-6 amu resolution. Reducing such large uncertainties was the main argument for the construction of the SPIDER “2E–2v” experimental setup [112, 113] at the Los Alamos Neutron Science Center, which should start taking data in the near future. In this setup the two fragment kinetic energies and velocities are measured simultaneously and can achieve one mass unit resolution, as also demonstrated by similar setups, COSI FAN TUTTE at ILL, France and VERDI at JRC-Geel, Belgium. The Sofia experiment [114] at GSI has produced an extensive amount of experimental data with accuracies in mass and charge <1 mass unit, but suffer from the fact that a large range of excitation energies that cannot be disentangled is produced in Coulomb excitations. LLNL and LANL activation measurements at TUNL have provided invaluable data on the incident energy dependence of cumulative fission product yields [93, 115], and ongoing efforts are directed toward testing the Bohr hypothesis of independence between entrance and outgoing channels in a compound reaction by comparing fission yields in the 239Pu(n,f) and 240Pu(γ,f) reactions [116] that lead to the same fissioning system, at least in mass and charge. At CARIBOU, two projects are underway: (i) measurement of fission product properties (isomeric yield ratios, gamma-ray decay branching ratios, and β-delayed neutron emission properties) and (ii) improvements of the antineutrino spectrum simulations by performing measurements of the β-decay data using GAMASPHERE [117]. Other experiments related to the properties of FFs have concentrated on measuring the average total kinetic energy (TKE) of the fission fragments at the LANSCE WNR facility for energy from a few hundred keVs to 200 MeV [111, 113]. The High Rigidity Spectrometer [118] at FRIB [119] will allow to explore the fissioning of very neutron-rich nuclei, study their shell structure, the presence of superheavy, the limits of stability and the equation of state of neutron-rich nuclear matter, the neutron skins, and shed light on the nature of the r-process, so far an unknown territory.
Treating the evolution of a heavy nucleus from a compact configuration until the start of beta decays in the FFs, including prompt neutron and gamma emissions, is a complicated task, computationally unfeasible within a unified microscopic approach. Within this reality, one has to consider a mixture of approaches, in which the initial part of the fission process is treated within a microscopic framework that can inform more phenomenological treatments that model the emission of prompt neutrons and gamma rays, and whose results can be directly compared against a large set of experimental data. And the input from microscopic models does not necessarily need to be restricted to the fission process. The systematics of several physical quantities used in the phenomenological models of neutron and gamma emission is based on data for stable nuclei. Since the FFs are nuclei far from stability, it is important to investigate within more microscopic models the validity of various systematics far from stability, as prompt neutron and gamma observables are sensitive to ingredients like level densities, optical models, or gamma strength functions.
Several models have been proposed to describe the shape dynamics, and to some extent many of them are able to reproduce experimental quantities like the pre-neutron emission mass distributions, irrespective of the approximations involved. But, as noted above, the direct measurement of the FFs before neutron emission is not possible. Therefore, even before one goes into details regarding the validity of the approximations involved in theoretical models, one needs to consider the corrections involved in the analysis of the experimental data. The post-neutron emission FF mass distributions are obtained using information on average prompt neutron multiplicity as a function of the fragment mass, , either from measurements, where available, or from phenomenological models. Given the scarcity of the data, and the fact that these phenomenological models have been built in a systematics based on little data, the uncertainties arising from could be considerable. Another assumption is that no neutrons are emitted during scission or at neck rupture. It is conceivable that the number of neutrons emitted during the scission dynamics is not necessarily large, but how large is large? If the fraction of scission neutrons is significant, as some phenomenological models predict, citing the experimental prompt fission spectrum as evidence to support the claim [120–125], what is the impact on the experimental analysis? While these models are not universally accepted, a microscopic approach should be able to answer such a question, and the assumption of small numbers of neutrons emitted during scission should not be implicitly included in the model. Moreover, it would be rather impossible to asses the fraction of scission neutrons if the model does not follow the dynamics of the process until full separation.
All the codes that model the prompt neutron and gamma emissions have been built in the assumption that the neutron emission proceeds after the full acceleration of the fission fragments [70, 126–130]. This assumption can have significant consequences, as at full acceleration the neutrons are maximally boosted. If the emission occurs instead during the acceleration, then the prompt neutron spectrum in the lab frame can noticeably be altered.
In addition to validating assumptions in phenomenological codes, a reliable theoretical model should provide information on observables that cannot be measured, but are essential in modeling the neutron and gamma emission. Thus, while the total excitation energy available in the fragments can be determined from the Q-value and TKE, no additional constrains on how this energy is shared between the FFs are available. As the most efficient way to lower the energy in FFs is via neutron emission, can be used to parameterize the excitation energy sharing. However, such data are scarcely available, usually for a limited number of spontaneous and neutron-induced fission with thermal neutrons, and thus guidance from microscopic models on how the excitation energy is shared with increasing incident neutron energy is required not only for minor actinides, but even for induced fission reaction of major actinides 235, 238U and 239Pu isotopes.
Gamma emission competes with the neutron emission when the excitation energy in the nucleus is around the neutron separation energy. The spin of the fragments, which cannot be directly measured experimentally, determines the exact strength on the neutron-gamma competition. Only indirect information can be extracted regarding the spin distribution of the FFs from properties of prompt gamma rays, like average multiplicity, prompt gamma fission spectra [131], or isomeric ratios [132]. The measurements of gamma rays are also scarce with increasing the incident neutron energy. Experimentally, one observes an increase of the total prompt fission gamma energy released in fission [133], which has been interpreted as an increase of the average spin with the incident energy. However, only little experimental data exist and no microscopic model has been able to reproduce such trends.
The main message of this section is that experimentally one cannot isolate and measure properties of post-scission FFs, and any full model will have to include simulations of prompt neutron and gamma emission, in order to compare and validate against experimental data. Given that many quantities used in the modeling of prompt neutron and gamma emission are taken from data systematics, which in general is available only for nuclei close to stability, the reliability of the theoretical model near scission and beyond, until full separation, is very important. Such models should allow for a full separation of the fragments, and employ approximations that are validated and under control, as to reduce any uncertainties regarding the FF properties.
4. What Lessons Have We Learned so far and What Is the Most Likely Path to the Future?
While pairing is not the engine driving the fission dynamics, pairing provides the essential lubricant, without which the evolution may arrive rather quickly to a screeching halt [134–136]. So far we have not considered whether proton-neutron pairing might have a role in fission. It is very unlikely that a condensate of proton-neutron pairs exists in heavy nuclei, but as we have learned from our simulations, proton-neutron transitions with L = 0 between single-particle orbitals could be important as the neutron-neutron and proton-proton transitions with (S,L,T) = (0,0,1) at low excitation energies, even in the absence of a condensate of such pairs, see the discussion concerning Figures 1, 4.
TDSLDA framework for fission dynamics, while it does not incorporate fluctuations, has provided a lot of insight into the real quantum dynamics, and it revealed extremely valuable information into nuclear processes and quantities, which are either not easy or impossible to obtain in laboratory or observations: FFs excitation energies and angular momenta distributions prior to neutron and gamma emission, element formation in astrophysical environments, as well as other nuclear reactions in a parameter free approach. In particular, the excitation energy sharing mechanism between FFs and its evolution with the initial excitation energy of the compound nucleus was not accessible until now within a dynamic approach. Fluctuations, which are essential in order to reproduce mass and charge yields for example, can be now incorporated into a pure quantum framework [81].
The quality of the agreement with experimental data is surprisingly good, especially taking into account the fact that no attempt was made to reproduce any fission data. Basically all phenomenological NEDFs satisfy the most important requirements to describe the gross properties of nuclear fission: saturation, realistic surface tension and symmetry energy, Coulomb energy, realistic pairing and shell corrections energy. Nevertheless, the quality of existing NEDFs needs improving. One can make a strong argument that we have now a clear path from more phenomenology and adjusted parameters to more fundamental theory and increased predictive power [137].
Perhaps the most important aspect we have observed in all our simulations is the strong violation of the adiabatic assumption in fission large amplitude collective motion. Basically since the 1950's the adiabatic assumption was the main simplification included in all microscopic frameworks, GCM, ATDHF and a large majority of phenomenological models as well, such as the Langevin and the Fokker-Planck equations, where one needs to introduce a potential energy surface and an inertia tensor in the space of the collective variables. If the collective motion is overdamped, the inertia tensor becomes irrelevant, and moreover, considering only the lowest potential energy surface is physically unacceptable (see Figures 3, 2) and the corresponding discussion in section 2. As we have established in Bulgac et al. [81] the fluctuations, or equivalently the role of two-body collisions, does not affect this conclusion.
A somewhat unexpected result was the character of the energy sharing mechanism between the fission fragments, the fact that the heavy fragment is cooler than the light fragment and it has less excitation energy [17, 42]. And this conclusion is not a result of the fact that the heavy FF is closer to the double magic 132Sn nucleus. In the original experiment of Hahn and Strassmann [1] the heavy fragment had a charge closer to Z≈52−56, a fact recognized also by Meitner and Frisch [2, 138], and explained by Scamps and Simenel [67], this is due to a stabilization of the octupole deformation in FFs, also observed in our simulations [17, 42]. With increasing excitation energy of the fissioning nucleus the heavy FF appears to be the only one who absorb the increase and emits more neutrons (see Figure 6) and the accompanying discussion. The character of the excitation energy sharing mechanism has major consequences on the predicted spectrum of emitted neutrons and gammas.
Another important outcome was the clear indications that many more collective DoF appear to be relevant in fission than have ever been considered in either phenomenological or microscopically inspired models, such as GCM and ATDHF frameworks. At scission, both FFs are octupolly deformed. Moreover, the FFs attain their relaxed shapes only after the separation between them is ≈5…6 fm. No phenomenological or microscopically inspired approach on the market follow the FFs to such large separations. As we stressed in section 3 the spectrum of emitted neutrons is affected by the number of neutrons emitted before the full FFs acceleration. Another DoF, which appears to be relevant as well is the bending mode (see Figure 7 and Bulgac et al. [81]), the inclusion of which likely is going to influence the angular momentum distributions of the FFs [82].
We have pointed to several directions into which phenomenological models and theoretical models, such as GCM and ATDHF would have to be altered, in order to describe nuclear fission in a manner more consistent with theoretical expectations inferred from unrestricted quantum mechanical simulations (see section 3). We did not cover or mention all phenomenological models on the market and not all microscopically inspired theoretical frameworks, as this is not a review of such approaches, for which we recommend [129, 139].
Data Availability Statement
The datasets generated for this study are available on request to the corresponding author.
Author Contributions
All authors listed have made a substantial, direct and intellectual contribution to the work, and approved it for publication.
Funding
The work of AB and SJ was supported by U.S. Department of Energy, Office of Science, Grant No. DE-FG02-97ER41014 and in part by NNSA cooperative agreement DE-NA0003841. The work of IS was supported by the US Department of Energy through the Los Alamos National Laboratory. Los Alamos National Laboratory is operated by Triad National Security, LLC, for the National Nuclear Security Administration of U.S. Department of Energy (Contract No. 89233218CNA000001).
Conflict of Interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Acknowledgments
We thank many people with whom we had discussion over the years and for their input: I. Abdurrahman, G. F. Bertsch, P. Magierski, K. J. Roche, and N. Schunck. We thank G. F. Bertsch and J. Randrup who made a number of suggestions on our manuscript, which has been released as a preprint [140]. The TDSLDA calculations have been performed at the OLCF Summit and Titan, and CSCS Piz Daint, and for generating initial configurations for direct input into the TDSLDA code at OLCF Titan and Summit and NERSC Edison. This research used resources of the Oak Ridge Leadership Computing Facility, which was a U.S. DOE Office of Science User Facility supported under Contract No. DE- AC05-00OR22725 and of the National Energy Research Scientific computing Center, which was supported by the Office of Science of the U.S. Department of Energy under Contract No. DE-AC02-05CH11231. We acknowledge PRACE for awarding us access to resource Piz Daint based at the Swiss National Supercomputing Centre (CSCS), decision No. 2018194657. This work was supported by High Performance Computing Infrastructure in Japan, Project ID: hp180048. A series of simulations were carried out on the Tsubame 3.0 supercomputer at Tokyo Institute of Technology. This research used resources provided by the Los Alamos National Laboratory Institutional Computing Program.
References
1. Hahn O, Strassmann F. Über den Nachweis und das Verhalten der bei der Bestrahlung des Urans mittels Neutronen entstehenden Erdalkalimetalle. Naturwissenschaften. (1939) 27:11.
2. Meitner L, Frisch OR. Disintegration of uranium by neutrons: a new type of nuclear reaction. Nature. (1939) 143:239. doi: 10.1038/143239a0
3. Stuewer R. An Act of Creation: The Meitner–Frisch Interpretation of Nuclear Fission. Berlin: Neopubli GmbH (2010). Available online at: http://edition-open-access.de/proceedings/5/11/index.html
4. Pearson JM. On the belated discovery of fission. Phys Today. (2015) 68:40. doi: 10.1063/PT.3.2817
5. Fermi E, Amaldi E, d'Agostino O, Rasetti F, Segre E. Artificial radioactivity produced by neutron bombardment. Proc R Soc A. (1934) 146:249.
8. Strutinsky VM. Shell effects in nuclear masses and deformation energies. Nucl Phys A. (1967) 95:420.
9. Brack M, Damgaard J, Jensen AS, Pauli HC, Strutinsky VM, Wong CY. Funny Hills: the shell-correction approach to nuclear shell effects and its applications to the fission process. Rev Mod Phys. (1972) 44:320.
10. Bertsch G. The nuclear density of states in the space of nuclear shapes. Phys Lett B. (1980) 95:157.
11. Bertsch GF, Bulgac A. Comment on “spontaneous fission: a kinetic approach”. Phys Rev Lett. (1997) 79:3539.
14. Hill DL, Wheeler JA. Nuclear constitution and the interpretation of fission phenomena. Phys Rev. (1953) 89:1102.
16. Barranco F, Bertsch GF, Broglia RA, Vigezzi E. Large-amplitude motion in superfluid Fermi droplets. Nucl Data Sheets Phys A. (1990) 512:253.
17. Bulgac A, Jin S, Roche KJ, Schunck N, Stetcu I. Fission dynamics of 240Pu from saddle to scission and beyond. Phys Rev C. (2019) 100:034615. doi: 10.1103/PhysRevC.100.034615
18. Griffin JJ, Wheeler JA. Collective motions in nuclei by the method of generator coordinates. Phys Rev. (1957) 108:311.
20. Baranger M, Vénéroni M. An adiabatic time-dependent Hartree-Fock theory of collective motion in finite systems. Ann Phys. (1978) 114:123.
21. Villars F. Adiabatic time-dependent Hartree-Fock theory in nuclear physics. Nucl Phys A. (1978) 285:269.
22. Ring P, Schuck P. The Nuclear Many-Body Problem. 1st ed. No. 17 in Theoretical and Mathematical Physics Series. Berlin; Heidelberg; New York, NY: Springer-Verlag (2004).
24. Schunck N, Robledo LM. Microscopic theory of nuclear fission: a review. Rep Prog Phys. (2016) 79:116301. doi: 10.1088/0034-4885/79/11/116301
25. Goutte H, Berger JF, Casoli P, Gogny D. Microscopic approach of fission dynamics applied to fragment kinetic energy and mass distributions in 238U. Phys Rev C. (2005) 71:024316. doi: 10.1103/PhysRevC.71.024316
26. Regnier D, Dubray N, Schunck N, Verrière M. Fission fragment charge and mass distributions in 239Pu(n, f) in the adiabatic nuclear energy density functional theory. Phys Rev C. (2016) 93:054611. doi: 10.1103/PhysRevC.93.054611
27. Zdeb A, Dobrowolski A, Warda M. Fission dynamics of 252Cf. Phys Rev C. (2017) 95:054608. doi: 10.1103/PhysRevC.95.054608
28. Schunck N editor. Energy Density Functional Methods for Atomic Nuclei. Bristol: IOP Publishing (2019).
29. Younes W, Gogny DM, Berger JF. A Microscopic Theory of Fission Based on the Generator Coordinate Method. Vol. 950 of Lectures Notes in Physics. Berlin: Springer (2019).
30. Goeke K, Reinhard PG. The generator-coordinate-method with conjugate parameters and the unification of microscopic theories for large amplitude collective motion. Ann Phys. (1980) 124:249.
32. Dang GD, Klein A, Walet NR. Self-consistent theory of large-amplitude collective motion: applications to approximate quantization of nonseparable systems and to nuclear physics. Phys Rep. (2000) 335:93. doi: 10.1016/S0370-1573(99)00119-2
34. Kohn W, Sham LJ. Self-consistent equations including exchange and correlation effects. Phys Rev. (1965) 140:A1133–8.
35. Kohn W. Nobel lecture: electronic structure of matter—wave functions and density functionals. Rev Mod Phys. (1999) 71:1253–66.
36. Dreizler RM, Gross EKU. Density Functional Theory: An Approach to the Quantum Many–Body Problem. Berlin: Springer-Verlag (1990).
37. Marques MAL, Ullrich CA, Nogueira F, Rubio A, Burke K, Gross EKU editors. Time-Dependent Density Functional Theory. Vol. 706 of Lecture Notes in Physics. Berlin: Springer-Verlag (2006).
38. Marques MAL, Maitra NT, Nogueira FMS, Gross EKU, Rubio A editors. Fundamentals of Time-Dependent Density Functional Theory. Vol. 837 of Lecture Notes in Physics. Heidelberg: Springer (2012).
39. Bulgac A. Time-dependent density functional theory and the real-time dynamics of Fermi superfluids. Ann Rev Nucl Part Sci. (2013) 63:97. doi: 10.1146/annurev-nucl-102212-170631
40. Bulgac A. Time-dependent density functional theory for fermionic superfluids: from cold atomic gases, to nuclei and neutron star crust. Phys Status Solidi B. (2019) 2019:1800592. doi: 10.1002/pssb.201800592
41. Jin S, Bulgac A, Roche K, Wlazłowski G. Coordinate-space solver for superfluid many-fermion systems with the shifted conjugate-orthogonal conjugate-gradient method. Phys Rev C. (2017) 95:044302. doi: 10.1103/PhysRevC.95.044302
42. Bulgac A, Magierski P, Roche KJ, Stetcu I. Induced fission of 240Pu within a real-time microscopic framework. Phys Rev Lett. (2016) 116:122504. doi: 10.1103/PhysRevLett.116.122504
43. Bertsch GF, Younes W, Robledo LM. Scission dynamics with K partitions. Phys Rev C. (2018) 97:064619. doi: 10.1103/PhysRevC.97.064619
44. Weidenmüller HA, Zhang JS. Nuclear fission viewed as a diffusion process: case of very large friction. Phys Rev C. (1984) 29:879. doi: 10.1103/PhysRevC.29.879
45. Randrup J, Möller P. Brownian shape motion on five-dimensional potential-energy surfaces: nuclear fission-fragment mass distributions. Phys Rev Lett. (2011) 106:132503. doi: 10.1103/PhysRevLett.106.132503
46. Randrup J, Möller P, Sierk AJ. Fission-fragment mass distributions from strongly damped shape evolution. Phys Rev C. (2011) 84:034613. doi: 10.1103/PhysRevC.84.034613
47. Randrup J, Möller P. Energy dependence of fission-fragment mass distributions from strongly damped shape evolution. Phys Rev C. (2013) 88:064606. doi: 10.1103/PhysRevC.88.064606
48. Ward DE, Carlsson BG, Døssing T, Möller P, Randrup J, Åberg S. Nuclear shape evolution based on microscopic level densities. Phys Rev C. (2017) 95:024618. doi: 10.1103/PhysRevC.95.024618
49. Albertsson M, Carlsson BG, Døssing T, Møller P, Randrup J, Åberg S. Excitation energy partition in fission. Phys Lett B. (2020) 803:135276. doi: 10.1016/j.physletb.2020.135276
50. Wilkins BD, Steinberg EP. Semi-empirical interpretation of nuclear fission based on deformed-shell effects. Phys Lett B. (1972) 42:141.
51. Wilkins BD, Steinberg EP, Chasman RR. Scission-point model of nuclear fission based on deformed-shell effects. Phys Rev C. (1976) 14:1832.
52. Lemaître JF, Panebianco S, Sida JL, Hilaire S, Heinrich S. New statistical scission-point model to predict fission fragment observables. Phys Rev C. (2015) 92:034617. doi: 10.1103/PhysRevC.92.034617
53. Lemaître JF, Goriely S, Hilaire S, Sida JL. Fully microscopic scission-point model to predict fission fragment observables. Phys Rev C. (2019) 99:034612. doi: 10.1103/PhysRevC.99.034612
54. Tully JC, Preston RK. Trajectory surface hopping approach to nonadiabatic molecular collisions: the reaction of H+ with D2. J Chem Phys. (1971) 55:562.
56. Hammes-Schiffer S, Tully JC. Proton transfer in solution: molecular dynamics with quantum transitions. J Chem Phys. (1994) 101:4657.
57. Bethe HA. An attempt to calculate the number of energy levels of a heavy nucleus. Phys Rev. (1936) 50:332–41.
59. Bulgac A, Dang GD, Kusnezov D. Stochastic aspects of large amplitude collective motion. Phys Rep. (1996) 264:67.
60. Grangé P, Li JQ, Weidenmüller HA. Induced nuclear fission viewed as a diffusion process: transients. Phys Rev C. (1983) 27:2063.
61. Fröbrich P, Gontchar II. Langevin description of fusion, deep-inelastic collisions and heavy-ion-induced fission. Phys Rep. (1998) 292:131.
62. Sierk AJ. Langevin model of low-energy fission. Phys Rev C. (2017) 96:034603. doi: 10.1103/PhysRevC.96.034603
63. Ishizuka C, Usang MD, Ivanyuk FA, Maruhn JA, Nishio K, Chiba S. Four-dimensional Langevin approach to low-energy nuclear fission of 236U. Phys Rev C. (2017) 96:064616. doi: 10.1103/PhysRevC.96.064616
64. Sadhukhan J, Nazarewicz W, Schunck N. Microscopic modeling of mass and charge distributions in the spontaneous fission of 240Pu. Phys Rev C. (2016) 93:011304. doi: 10.1103/PhysRevC.93.011304
65. Sadhukhan J, Zhang C, Nazarewicz W, Schunck N. Formation and distribution of fragments in the spontaneous fission of 240Pu. Phys Rev C. (2017) 96:061301. doi: 10.1103/PhysRevC.96.061301
66. Regnier D, Dubray N, Schunck N. From asymmetric to symmetric fission in the fermium isotopes within the time-dependent generator-coordinate-method formalism. Phys Rev C. (2019) 99:024611. doi: 10.1103/PhysRevC.99.024611
67. Scamps G, Simenel C. Impact of pear-shaped fission fragments on mass-asymmetric fission in actinides. Nature. (2018) 564:382. doi: 10.1038/s41586-018-0780-0
68. Mustafa MG, Schmitt HW, Mosel U. Dipole excitations in fission fragments. Nucl Phys A. (1971) 178:9.
69. Simenel C, Umar AS. Formation and dynamics of fission fragments. Phys Rev C. (2014) 89:031601. doi: 10.1103/PhysRevC.89.031601
70. Becker B, Talou P, Kawano T, Danon Y, Stetcu I. Monte Carlo Hauser-Feshbach predictions of prompt fission gamma rays: application to n+235U, n+239Pu, and 252Cf (sf). Phys Rev C. (2013) 87:014617. doi: 10.1103/PhysRevC.87.014617
71. Müller R, Naqvi AA, Käppeler F, Dickmann F. Fragment velocities, energies, and masses from fast neutron induced fission of 235U. Phys Rev C. (1984) 29:885.
72. Randrup J, Vogt R. Calculation of fission observables through event-by-event simulation. Phys Rev C. (2009) 80:024601. doi: 10.1103/PhysRevC.80.024601
73. Randrup J, Talou P, Vogt R. Sensitivity of neutron observables to the model input in simulations of 252Cf(sf). Phys Rev C. (2019) 99:054619. doi: 10.1103/PhysRevC.99.054619
74. Bertsch GF, Kawano T, Robledo LM. Angular momentum of fission fragments. Phys Rev C. (2019) 99:034603. doi: 10.1103/PhysRevC.99.034603
75. Schmidt KH, Jurado B. Entropy driven excitation energy sorting in superfluid fission dynamics. Phys Rev Lett. (2010) 104:212501. doi: 10.1103/PhysRevLett.104.212501
76. Schmidt KH, Jurado B. Final excitation energy of fission fragments. Phys Rev C. (2011) 83:061601. doi: 10.1103/PhysRevC.83.061601
77. Gilbert A, Cameron AGW. A composite nuclear-level density formula with shell correction. Can J Phys. (1965) 43:1446.
78. Bertsch GF, Girod M, Hilaire S, Delaroche JP, Goutte H, Péru S. Systematics of the first 2+ excitation with the Gogny interaction. Phys Rev Lett. (2007) 99:032502. doi: 10.1103/PhysRevLett.99.032502
79. Delaroche JP, Girod M, Libert J, Goutte H, Hilaire S, Péru S, et al. Structure of even-even nuclei using a mapped collective Hamiltonian and the D1S Gogny interaction. Phys Rev C. (2010) 81:014303. doi: 10.1103/PhysRevC.81.014303
80. Ryssens W, Heenen PH, Bender M. Numerical accuracy of mean-field calculations in coordinate space. Phys Rev C. (2015) 92:064318. doi: 10.1103/PhysRevC.92.064318
81. Bulgac A, Jin S, Stetcu I. Unitary evolution with fluctuations and dissipation. Phys Rev C. (2019) 100:014615. doi: 10.1103/PhysRevC.100.014615
82. Moretto LG, Peqaslee GF, Wozniak GJ. Angular-momentum-bearing modes in fission. Nucl Phys A. (1989) 502:453c.
83. Bulgac A. Projection of good quantum numbers for reaction fragments. Phys Rev C. (2019) 100:034612. doi: 10.1103/PhysRevC.100.034612
84. Haight RC, Wu CY, Lee HY, Taddeucci TN, Perdue BA, O'Donnell JM, et al. The LANL/LLNL prompt fission neutron spectrum program at LANSCE and approach to uncertainties. Nucl Data Sheets. (2015) 123:130–4. doi: 10.1016/j.nds.2014.12.023
85. Kelly KJ, Devlin M, Gomez JA, O´Donnell JM, Taddeucci TN, Haight RC, et al. Measurements of the prompt fission neutron spectrum at LANSCE: the Chi-Nu experiment. EPJ Web Conf. (2018) 193:03003. doi: 10.1051/epjconf/201819303003
86. Maslin EE, Rodgers AL, Core WGF. Prompt neutron emission from U235 fission fragments. Phys Rev. (1967) 164:1520–7.
87. Nishio K, Nakagome Y, Yamamoto H, Kimura I. Multiplicity and energy of neutrons from 235U(nth,f) fission fragments. Nucl Phys A. (1998) 632:540–58.
88. Tsuchiya C, Nakagome Y, Yamana H, Moriyama H, Nishio K, Kanno I, et al. Simultaneous measurement of prompt neutrons and fission fragments for 239Pu(nth,f). J Nucl Sci Tech. (2000) 37:941. doi: 10.1080/18811248.2000.9714976
89. Batenkov OA, Boykov GA, Hambsch FJ, Hamilton JH, Jakovlev VA, Kalinin VA, et al. Prompt neutron emmision in the neutron-induced fission of 239Pu and 235U. AIP Conf Proc. (2005) 769:1003. doi: 10.1063/1.1945175
90. Göök A, Hambsch FJ, Vidali M. Prompt neutron multiplicity in correlation with fragments from spontaneous fission of 252Cf. Phys Rev C. (2014) 90:064611. doi: 10.1103/PhysRevC.90.064611
91. Göök A, Hambsch FJ, Oberstedt S, Vidali M. Prompt neutrons in correlation with fission fragments from 235U(n, f). Phys Rev C. (2018) 98:044615. doi: 10.1103/PhysRevC.98.044615
92. Akindele OA, Alan BS, Burke JT, Casperson RJ, Hughes RO, Koglin JD, et al. Expansion of the surrogate method to measure the prompt fission neutron multiplicity for 241Pu. Phys Rev C. (2019) 99:054601. doi: 10.1103/PhysRevC.99.054601
93. Wang BS, Harke JT, Akindele OA, Casperson RJ, Hughes RO, Koglin JD, et al. Determining the average prompt-fission-neutron multiplicity for 239Pu(n, f) via a 240Pu(α, α′f) surrogate reaction. Phys Rev C. (2019) 100:064609. doi: 10.1103/PhysRevC.100.064609
94. Ullmann JL, Bond EM, Bredeweg TA, Couture A, Haight RC, Jandel M, et al. Prompt γ-ray production in neutron-induced fission of 239Pu. Phys Rev C. (2013) 87:044607. doi: 10.1103/PhysRevC.87.044607
95. Chyzh A, Wu CY, Kwan E, Henderson RA, Gostic JM, Bredeweg TA, et al. Systematics of prompt γ-ray emission in fission. Phys Rev C. (2013) 87:034620. doi: 10.1103/PhysRevC.87.034620
96. Chyzh A, Wu CY, Kwan E, Henderson RA, Bredeweg TA, Haight RC, et al. Total prompt γ-ray emission in fission of 235U, 239, 241Pu, and 252Cf. Phys Rev C. (2014) 90:014602. doi: 10.1103/PhysRevC.90.014602
97. Jandel M, Rusev G, Bond EM, Bredeweg TA, Chadwick MB, Couture A, et al. Prompt fission gamma-ray studies at DANCE. Phys Proc. (2014) 59:101–6. doi: 10.1016/j.phpro.2014.10.016
98. Billnert R, Hambsch FJ, Oberstedt A, Oberstedt S. New prompt spectral γ-ray data from the reaction 252Cf(sf) and its implication on present evaluated nuclear data files. Phys Rev C. (2013) 87:024601. doi: 10.1103/PhysRevC.87.024601
99. Oberstedt A, Belgya T, Billnert R, Borcea R, Bryś T, Geerts W, et al. Improved values for the characteristics of prompt-fission γ-ray spectra from the reaction 235U(nth,f). Phys Rev C. (2013) 87:051602. doi: 10.1103/PhysRevC.87.051602
100. Lebois M, Wilson JN, Halipré P, Oberstedt A, Oberstedt S, Marini P, et al. Comparative measurement of prompt fission γ-ray emission from fast-neutron-induced fission of 235U and 238U. Phys Rev C. (2015) 92:034618. doi: 10.1103/PhysRevC.92.034618
101. Gatera A, Belgya T, Geerts W, Göök A, Hambsch FJ, Lebois M, et al. Prompt-fission γ-ray spectral characteristics from 239Pu(nth, f). Phys Rev C. (2017) 95:064609. doi: 10.1103/PhysRevC.95.064609
102. Makii H, Nishio K, Hirose K, Orlandi R, Léguillon R, Ogawa T, et al. Effects of the nuclear structure of fission fragments on the high-energy prompt fission γ-ray spectrum in 235U(nth, f). Phys Rev C. (2019) 100:044610. doi: 10.1103/PhysRevC.100.044610
103. Verbinski VV, Weber H, Sund RE. Prompt gamma rays from 235U(n, f), 239Pu(n, f), and spontaneous fission of 252Cf. Phys Rev C. (1973) 7:1173–85.
104. Peelle RW, Maienschein FC. Spectrum of photons emitted in coincidence with fission of 235U by thermal neutrons. Phys Rev C. (1971) 3:373–90.
105. Pleasonton F, Ferguson RL, Schmitt HW. Prompt gamma rays emitted in the thermal-neutron-induced fission of 235U. Phys Rev C. (1972) 6:1023–39.
106. Pleasonton F. Prompt γ-rays emitted in the thermal-neutron induced fission of 233U and 239Pu. Nucl Phys A. (1973) 213:413–25.
107. Stetcu I, Chadwick MB, Kawano T, Talou P, Capote R, Trkov A. Evaluation of the prompt fission gamma properties for neutron induced fission of 235;238U and 239Pu. Nucl Data Sheets. (2020) 163:261–79. doi: 10.1016/j.nds.2019.12.007
108. Straede C, Budtz-Jørgensen C, Knitter HH. 235U(n, f) Fragment mass-, kinetic energy- and angular distributions for incident neutron energies between thermal and 6 MeV. Nucl Phys A. (1987) 462:85–108.
109. Vivès F, Hambsch FJ, Bax H, Oberstedt S. Investigation of the fission fragment properties of the reaction 238U(n,f) at incident neutron energies up to 5.8 MeV. Nucl Phys A. (2000) 662:63–92. doi: 10.1016/S0375-9474(99)00413-3
110. Birgersson E, Oberstedt A, Oberstedt S, Hambsch FJ. Properties of the reaction 238U at the vibrational resonances. Nucl Phys A. (2009) 817:1–34. doi: 10.1016/j.nuclphysa.2008.12.001
111. Duke DL, Tovesson F, Laptev AB, Mosby S, Hambsch FJ, Bryś T, et al. Fission-fragment properties in 238U(n, f) between 1 and 30 MeV. Phys Rev C. (2016) 94:054604. doi: 10.1103/PhysRevC.94.054604
112. Tovesson F, Arnold CW, Bredeweg T, Jandel M, Laptev AB, Meierbachtol K, et al. SPIDER: a new instrument for fission yield measurement. In: Hamilton JH, Ramayya AV, editors. Proceedings of the Fifth International Conference on ICFN5. Singapore: World Scientific (2013). p. 361.
113. Meierbachtol K, Tovesson F, Duke DL, Geppert-Kleinrath V, Manning B, Meharchand R, et al. Total kinetic energy release in 239Pu(n, f) post-neutron emission from 0.5 to 50 MeV incident neutron energy. Phys Rev C. (2016) 94:034611. doi: 10.1103/PhysRevC.94.034611
114. Pellereau E, Taïeb J, Chatillon A, Alvarez-Pol H, Audouin L, Ayyad Y, et al. Accurate isotopic fission yields of electromagnetically induced fission of 238U measured in inverse kinematics at relativistic energies. Phys Rev C. (2017) 95:054603. doi: 10.1103/PhysRevC.95.054603
115. Gooden ME, Arnold CW, Becker JA, Bhatia C, Bhike M, Bond EM, et al. Energy dependence of fission product yields from 235U, 238U and 239Pu for incident neutron energies between 0.5 and 14.8 MeV. Nucl Data Sheets. (2016) 131:319–56. doi: 10.1016/j.nds.2015.12.006
116. Silano J, Tonchev A, Henderson R, Schunck N, Tornow W, Howell C, et al. Comparing fission-product yields from photon-induced fission of 240Pu and neutron-induced fission of 239Pu as a test of the Bohr hypothesis in nuclear fission. In: Proceedings of the Santa Fe Workshop on Fission Product Yields. Los Alamos, NM (2019).
117. Savard G. Fission product yield measurements using 252Cf spontaneous fission and neutron-induced fission on actinide targets at CARIBU. In: Talk at the International Workshop on Fission Product Yields. Los Alamos, NM (2019).
118. A High Rigidity Spectrometer fro FRIB. Available online at: hrs.lbl.gov/documents/HRS-WhitePaper122017.pdf
119. Facility for Rare Isotopes Beams. Available online at: www.frib.msu.edu
120. Carjan N, Rizea M. Scission neutrons and other scission properties as function of mass asymmetry in 235U(nth,f). Phys Rev C. (2010) 82:014617. doi: 10.1103/PhysRevC.82.014617
121. Carjan N, Hambsch FJ, Rizea M, Serot O. Partition between the fission fragments of the excitation energy and of the neutron multiplicity at scission in low-energy fission. Phys Rev C. (2012) 85:044601. doi: 10.1103/PhysRevC.85.044601
122. Rizea M, Carjan N. Dynamical scission model. Nucl Phys A. (2013) 909:50–68. doi: 10.1016/j.nuclphysa.2013.04.014
123. Carjan N, Rizea M. Similarities between calculated scission-neutron properties and experimental data on prompt fission neutrons. Phys Lett B. (2015) 747:178–81. doi: 10.1016/j.physletb.2015.05.050
124. Capote R, Carjan N, Chiba S. Scission neutrons for U, Pu, Cm, and Cf isotopes: relative multiplicities calculated in the sudden limit. Phys Rev C. (2016) 93:024609. doi: 10.1103/PhysRevC.93.024609
125. Carjan N, Rizea M. Structures in the energy distribution of the scission neutrons: finite neutron-number effect. Phys Rev C. (2019) 99:034613. doi: 10.1103/PhysRevC.99.034613
126. Vogt R, Randrup J. Event-by-event modeling of prompt neutrons and photons from neutron-induced and spontaneous fission with FREYA. Phys Proc. (2013) 47:82–7. doi: 10.1016/j.phpro.2013.06.013
127. Litaize O, Serot O, Berge L. Fission modelling with FIFRELIN. Eur Phys Jour A. (2015) 51:177. doi: 10.1140/epja/i2015-15177-9
128. Schmidt KH, Jurado B, Amouroux C, Schmitt C. General description of fission observables: GEF model code. Nucl Data Sheets. (2016) 131:107–221. doi: 10.1016/j.nds.2015.12.009
129. Schmidt KH, Jurado B. Review on the progress in nuclear fission–experimental methods and theoretical descriptions. Rep Prog Phys. (2018) 81:106301. doi: 10.1088/1361-6633/aacfa7
130. Talou P, Vogt R, Randrup J, Rising ME, Pozzi SA, Verbeke J, et al. Correlated prompt fission data in transport simulations. Eur Phys J A. (2018) 54:9. doi: 10.1140/epja/i2018-12455-0
131. Stetcu I, Talou P, Kawano T, Jandel M. Properties of prompt-fission γ rays. Phys Rev C. (2014) 90:024617. doi: 10.1103/PhysRevC.90.024617
132. Stetcu I, Talou P, Kawano T, Jandel M. Isomer production ratios and the angular momentum distribution of fission fragments. Phys Rev C. (2013) 88:044603. doi: 10.1103/PhysRevC.88.044603
133. Fréhaut J, Bertin A, Bois R. Mesure de pour la fission de 232Th, 235U et 237Np induite par des neutrons d'energie comprise entre 1 et 15 MeV. In: International Conference on Nuclear Data for Science and Technology. Antwerp; Dordrech: Reidel (1983). p. 78.
134. Goddard P, Stevenson P, Rios A. Fission dynamics within time-dependent Hartree-Fock: deformation-induced fission. Phys Rev C. (2015) 92:054610. doi: 10.1103/PhysRevC.92.054610
135. Goddard P, Stevenson P, Rios A. Fission dynamics within time-dependent Hartree-Fock. II. Boost-induced fission. Phys Rev C. (2016) 93:014620. doi: 10.1103/PhysRevC.93.014620
136. Tanimura Y, Lacroix D, Scamps G. Collective aspects deduced from time-dependent microscopic mean-field with pairing: application to the fission process. Phys Rev C. (2015) 92:034601. doi: 10.1103/PhysRevC.92.034601
137. Bulgac A, Jin S, Magierski P, Roche KJ, Schunck N, Stetcu I. Nuclear fission: from more phenomenology and adjusted parameters to more fundamental theory and increased predictive power. EPJ Web Conf. (2017) 163:00007. doi: 10.1051/epjconf/201716300007
139. Andreyev AN, Nishio K, Schmidt KH. Nuclear fission: a review of experimental advances and phenomenology. Rep Prog Phys. (2018) 81:016301.
Keywords: nuclear fission, total kinetic energy, total excitation energy, overdamped collective motion, adiabatic collective motion, average neutron multiplicity
Citation: Bulgac A, Jin S and Stetcu I (2020) Nuclear Fission Dynamics: Past, Present, Needs, and Future. Front. Phys. 8:63. doi: 10.3389/fphy.2020.00063
Received: 30 November 2019; Accepted: 27 February 2020;
Published: 18 March 2020.
Edited by:
Paul Denis Stevenson, University of Surrey, United KingdomReviewed by:
Giuseppe Verde, National Institute for Nuclear Physics, ItalyArmen Sedrakian, Frankfurt Institute for Advanced Studies, Germany
Copyright © 2020 Bulgac, Jin and Stetcu. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Aurel Bulgac, YnVsZ2FjQHV3LmVkdQ==
 Aurel Bulgac
Aurel Bulgac Shi Jin1
Shi Jin1 Ionel Stetcu
Ionel Stetcu