- 1Department of Physics “E. Pancini”, Università di Napoli Federico II, Naples, Italy
- 2Istituto Nazionale di Fisica Nucleare (INFN)-Sezione di Napoli, Naples, Italy
We demonstrate the possibility of creating optical beams with phase singularities engraved into exotic intensity landscapes imitating the shapes of a large variety of diverse plane curves. To achieve this aim, we have developed a method for directly encoding the geometric properties of a selected curve into a single azimuthal phase factor without passing through indirect encryption methods involving lengthy numerical procedures. The outcome is utilized to mold the optic axis distribution of a liquid-crystal-based inhomogeneous waveplate. The latter is finally used to sculpt the wavefront of an input optical gaussian beam via the Pancharatnam-Berry phase.
1. Introduction
Light sculpting has gained increasing importance in both fundamental and applied optics [1]. Engraving singularities in optical beams, in particular, has paved the way for multiple applications in both classical and quantum optics, most of which relate to the angular momentum of light. Singular Optics has gradually become an independent research field and now aspires to become a fundamental cornerstone of modern photonics. Optical singular beams have proven to be invaluable for non-contact manipulation over micro- and nanoscale [2, 3], which has enormous implications for modern nanophysics, crystal growth, and metamaterials, to give just a few examples. Furthermore, the infinite dimensionality of the orbital angular momentum (OAM) space has paved the way for increasing the data capacity of both free-space and fiber-optic communications [4] and for developing novel efficient protocols for classical [5] as well as quantum information processing [6–8]. No less important, optical singularities have been successfully utilized for super-resolution imaging [9, 10], on-chip optical switching [11–13], advanced microscopy [14, 15], and material machining [16–18].
Needless to say, the great potential of singular optics—and, more generally, of sculpted light—has been progressively unlocked over time, through the development of increasingly efficient and versatile tools for shaping the optical wavefronts. The most prominent technologies currently available for shaping spatial modes are computer-generated holograms (CGHs) displayed on spatial light modulators (SLMs)—based on dynamic phase control—and Pancharatnam-Berry phase (or geometric phase) Optical Elements (PBOEs). Indeed, several methods are nowadays available to fabricate geometric-phase optical elements for wavefront shaping, ranging from subwavelength metal stripe space-variant gratings [19] to multilayer plasmonic metasurfaces [20] and Spatially Varying Axis Plates (SVAPs) based on liquid crystals [21–26].
In the present paper, we introduce a method for designing SVAPs enabling the generation of scalar optical beams with non-linear azimuthal phase structures, giving birth to phase singularities engraved within non-cylindrically symmetric intensity profiles. Indeed, the cylindrical symmetry typical of the intensity profile of helical beams springs from their linear azimuthal phase profile, eiℓϕ. Helical beams have helical wavefronts —hence the name—and carry an OAM of ℏℓ per photon, ℓ being an integer, and ϕ the azimuthal polar angle around the beam propagation direction.There are multiple families of helical beams, which differ in their radial dependencies. Well-known examples are Laguerre-Gaussian (LG) beams [27, 28], Bessel and Bessel-Gaussian (BG) beams [29], and the wider class of Hypergeometric-Gaussian (HyG) beams [30], to name just a few. A helical beam with an azimuthal index ℓ has an ℓ-fold rotational symmetry, and its OAM spectrum accordingly includes only the component ℓ. With the light beam wavevector denoted as k, the azimuthal component of the linear momentum is ℏkϕ per photon: it does not depend on ϕ but only on the distance from the beam axis. The energy flux is therefore rotationally invariant around the beam axis, yielding the well-known cylindrically symmetric doughnut-shaped profile. An azimuthally non-uniform kϕ, in contrast, will break such symmetry and will give birth to an optical wavefront with a non-uniform helical phase structure, which will result, in its turn, in a non-cylindrically symmetric intensity profile. An OAM spectrum will broaden as a consequence of such symmetry breaking.
To impart a non-linear azimuthal structure, we have developed a phase design method aimed at encoding the geometric properties of a plane curve in order to create an intensity profile imitating the shape of the curve. We presently demonstrate that such an approach enables the direct determination of the phase profile required to reshape the intensity profile of a light beam as well as its OAM spectrum according to one's wishes. Here, in fact, we avoid passing through indirect methods for encoding the amplitude and phase of the target field into a single phase function [31], though the price to be paid is that only some features of the intensity profile and of the OAM spectrum will be precisely determined. Despite these apparent limitations, our method spontaneously leads us to introduce the concept of dark hollow beams with tailored intensity profiles or “Free-Form Dark-Hollow” (FFDH) Beams. A detailed study of the optical properties of FFDH beams will be reported elsewhere. Here, we focus on the generation of such beams by using the aforementioned SVAPs, of which q-plates [32] are probably the most famous examples. Liquid crystal-based SVAPs combine high conversion efficiency with exceptional manageability for overall high performance. Our SVAPs were fabricated by adopting a “direct-write approach," as defined in Kim et al. [21]. However, we would like to emphasize that our focus is presently on the method developed to determine the transmittance phase function. Specifically, an arbitrary superposition of azimuthal modes amounts to a complex function of ϕ with both an amplitude and a phase, i.e.,
Several approaches, mostly based on the Gerchberg-Saxton algorithm, are usually adopted to obtain a pure phase function providing an acceptable approximation for Equation (1) [33]. In what follows, we describe a method to directly generate a dark hollow beam in which the shape of the dark zone is basically inherited from the shape of a selected plane curve. This is achieved without resorting to inverse algorithms such as those mentioned above. They can be proved to be promising devices of potential interest for multiple applications ranging from super-resolution microscopy to directional selective trapping [34], as well as material processing and optical coronagraphy, not to mention the applications in classical and quantum communications [35, 36]. As an example, we consider the case of Stimulated Emission Depletion (STED) microscopy, in which super resolution is achieved by the selective deactivation of fluorophores through an excitation beam filling the internal zone of a doughnut-shaped de-excitation spot. Replacing the doughnut with an FFDH beam, the illumination area would acquire a non-circular shape, suitable for optimally sending photons to zones where they are really required and/or to prevent them from damaging the surrounding areas.
2. Free-Form Azimuthal Phase Shaping
The question arises of to what extent the transverse intensity profiles or the OAM spectrum of a light beam can be molded by manipulating a purely azimuthal phase factor eiψ(ϕ), ψ(ϕ) being an arbitrary function of the azimuthal coordinate ϕ. Such a phase factor does not enable the exploration of all the possible field distributions, even approximately, since ψ is assumed to be independent of the distance r from the beam axis [31, 37]. As above mentioned, in this work, we aim at introducing a toy method based on geometric intuition to determine the most appropriate azimuthal phase factor eiψ(ϕ) required to generate dark hollow beams with arbitrary shapes or, as we have baptized them, FFDH beams. To this purpose, we need a “dough cutter” for partitioning the plane around the beam axis into a number of sectors—“slicing the doughnut.” One can then distribute the transverse intensity of light among the several sectors according to one's wishes and necessities. Molding the intensity of light within each sector is necessary for tailoring the boundaries of the dark region around the axis—“shaping the hole of the doughnut.” The portions of light within different sectors can be disconnected from each other or not. Metaphors aside, our “dough cutter” is the azimuthal component ℏkϕ(ϕ) of the photon linear momentum as a function of ϕ, i.e.,
Assuming ψ(ϕ) is proportional to the orientation angle Θ(ϕ) of the unit normal to some plane curve γ described by ϕ-dependent parametric equations, then all the relevant features of kϕ(ϕ) can be gathered from the rotational symmetry properties of γ and from the local radius of curvature—the latter being related to both kϕ and its derivative. Such a geometric approach has the advantage that Θ(ϕ)—and therefore the plane curve it comes from—needs not to be determined, on a case-by-case basis, as a solution of an inverse problem. Rather, it can be helpful to use a representation of the curve in polar coordinates, with some free parameters that can be tuned to match as much as possible the target intensity profile.
2.1. Curve Selection
Multiple choices are available. Good options are Lamé curves or their generalizations. A Lamé Curve, also known as a superellipse [38], is a closed curve retaining the geometric properties of semi-major axis and semi-minor axis, typical of an ellipse, but with a different shape. In polar coordinates it is described by the equation
where a, b, and n are positive reals.
In 2003, J. Gielis introduced a single parametric equation—dubbed the “superformula”—describing multiple plane curves of the most varied kinds to study forms in plants and other living organisms [39]. The mathematical expression of the superformula, in polar coordinates, is
where ρ is the distance of a point of the curve γ from the origin of the coordinate system as a function of the azimuthal angle ϕ, m is an integer, n1, n2, and n3 are three integers controlling its local radius of curvature, and, finally, the positive real numbers a and b parameterize the radii of the circumferences respectively inscribed and circumscribed to the curve γ. For even m = 2k, Equation (4) describes a curve γ2k closing over the interval [0, 2π). γ2k is rotationally symmetric by an angle 2π/k. For odd m = 2k+1, γ2k+1 closes over the interval [0, 4π). When a = b and n1 = n2, γm exhibits an m-fold rotational symmetry Cm. As all the free parameters in Equation (4) can vary, the generated curves can be deeply diverse. No doubt the curves could be grouped according to a criterion based on the order of the their rotational symmetry. For m = 4, a = b, and n2 = n3>2, for instance, the superformula simply returns the superellipses first introduced by G. Lamé in 1818 [38]. For fixed values of m, a, and b, however, the signs and the absolute values of n1, n2, and n3 can dramatically change the topological properties of the curves. Besides, a peculiar feature of the superformula is the fact that, independently of m, when n2 = n3 = 2, it always degenerates into a circumference when a = b or into an ellipse otherwise. Here, we are not interested in the mathematical peculiarities of the superformula but rather in taking advantage of its “shape-shifter” capabilities.
Encrypting the geometrical properties of the selected curves into the optical phase. Assume γ(a, b, m, n1, n2, n3) is the curve described by the superformula for some values of the free parameters. The normal unit vector n = (nx, ny) of the curve is given by
where is the derivative of ρ with respect to ϕ. Denoting as Θ(ϕ) the angle that n forms with the x−axis, we set the optical phase ψ(ϕ) to be
Consequently, by varying the free parameters in Equation (4), multiple phase profiles can be designed and FFDHs accordingly generated. The realized phase profiles exhibit a modulation with the same symmetry properties as the curve γ. In the following, we show that the m-fold symmetry characterizing the phase modulation also affects the intensity profile of the generated beam. Light intensity, indeed, is expected to be equally partitioned among the m equally spaced sectors of the phase profile.
In Figure 1, this geometry-to-phase transfer procedure is sketched in the case a = b = 1, m = 5, n1 = 1/2, and n2 = n3 = 4/3. The rippled helical wavefront arising from Equation (6) is shown in Figure 2B for the same values of the parameters and is compared to the smooth helical wavefront corresponding to a doughnut beam with ℓ = 2 (Figure 2A). The latter can be easily shown to come from a circumference.
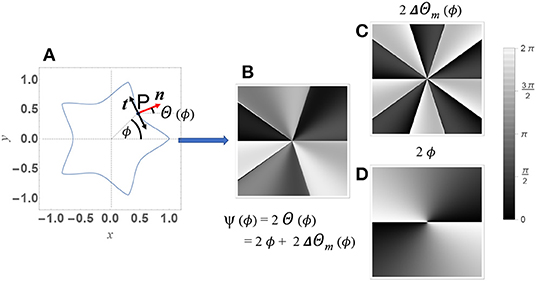
Figure 1. Schematic of the encryption procedure of the symmetry properties of a plane curve into the azimuthal phase of a light beam. In (A), as an example, we show t and n, i.e., the tangent and the normal unit vectors to the curve at the point P, respectively. n forms an angle Θ(ϕ) with the horizontal axis. In (B), we show the transverse phase profile ψ(ϕ) = 2Θ(ϕ; 1, 1, 5, 1/2, 4/3, 4/3) (Equation 6). The latter can be regarded as the superposition of the phase modulation 2ΔΘm(ϕ) (C) and the helical phase profile 2ϕ (D).
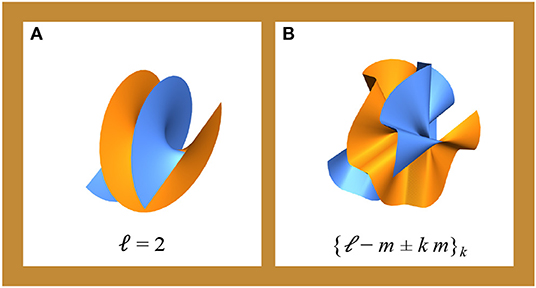
Figure 2. Helical wavefronts corresponding to a circumference (A) and to the curve represented in Figure 1A(B).
This structure primarily affects the OAM spectrum, which includes only the components (ℓ−m)±km, with k being an integer (Figure 3) and ℓ being the OAM index corresponding to the background helical mode. Specifically, in Figure 3, the OAM power spectrum of the generated FFDH is presented. In classical optics, the quantity is the fraction of the total power of the optical field component carrying an OAM proportional to l. In quantum optics, it is the probability that a photon in the beam carries an OAM of ℏl. The actual values of , as reported in Figure 3, have been determined numerically, by Fourier expansion of the azimuthal phase factor reported in Equation (5). The skew rays follow the paths dictated by kϕ.
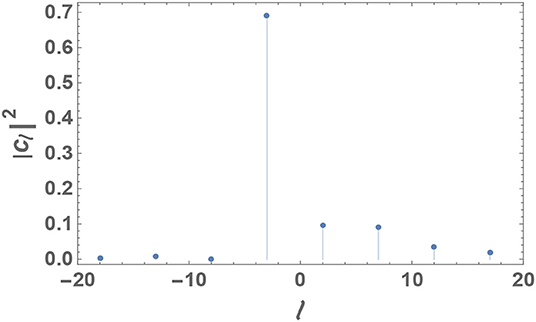
Figure 3. OAM power spectrum arising from the azimuthal phase profile corresponding to the parameter values a = b = 1, m = 5, n1 = 1/2, and n2 = n3 = 4/3.
3. Free-Form Azimuthal (FFA) SVAPs
We now focus on the experimental methods for generating optical beams with the phase structure prescribed by Equation (6). To reshape a TEM00 laser beam according to our wishes, we opted for a properly tailored SVAP. The latter is a half-wave retardation plate in which the direction-angle of of the optic axis is spatially variant [23, 24, 26]. When a circularly polarized input beam passes through the plate, it acquires a geometric phase factor . The sign in the exponent depends on the handedness of the incident beam polarization , which is reversed by the SVAP [25]. For a comprehensive view of the mechanism underlying wavefront reshaping via the Geometric or Pancharatnam-Berry Phase, we address the reader to Piccirillo et al. [25]. In essence, molding the phase of a SVAP amounts to patterning the optic-axis so that its direction-angle is locally equal to half the prescribed optical phase. In order to fabricate a liquid-crystal SVAP for generating FFDH beams, the optic-axis angular distribution must be set to
In Figure 4, we show the optic-axis pattern of a SVAP corresponding to Θ(ϕ; a = 1, b = 1, m = 5, n1 = 1/2, n2 = 4/3, n3 = 4/3) (Figure 4A) and, for comparison, the contribution to such a pattern of the modulation only (Figure 4B). Figure 5A shows a microscope image of the SVAP under crossed polarizers, with a birefringent λ-compensator inserted between the SVAP and the analyzer. The λ-compensator has a path difference of 550 nm and therefore introduces a π retardation at that wavelength. The fast axis forms a 45° angle to the axis of the analyzer. When the compensator is put in, the sample changes its color depending on its orientation. The changes in color are based on optical interference. This method fully unveils the optic axis pattern underlying the SVAP (Figure 4A) because, differently from the simple crossed-polarizers method, it enables the orthogonal orientations of the optic axis to be distinguished between.
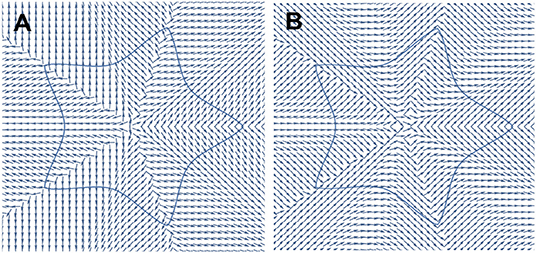
Figure 4. Optic axis patterns deduced from Equation (7) for the parameter values a = b = 1, m = 5, n1 = 1/2, and n2 = n3 = 4/3. (A) Optic axis pattern for a SVAP imparting to an input beam the geometric phase 2ϕ+2ΔΘm(ϕ) (Figure 1B). (B) Optic axis pattern for a SVAP imparting the geometric phase 2ΔΘm(ϕ) (Figure 1C).
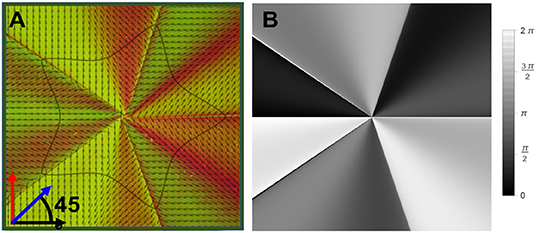
Figure 5. Experimental observation of the optic axis distribution of the SVAP (a = b = 1, m = 5, n1 = 1/2, and n2 = n3 = 4/3). (A) Microscope image of the SVAP between crossed polarizers + birefringent compensator plate at 45°. This image reveals the optic axis pattern underlying the SVAP (Figure 4A), which is displayed in the image overlay. The image was recorded when illuminating the sample with white light, sandwiched between crossed polarizers, and inserting, between the sample and the analyzer, a birefringent λ-compensator (λ = 550 nm) with the optic axis rotated by 45°. The arrows in the lower left corner sketch the axes orientations of the input linear polarizer (black arrow), the output analyzer (red arrow), and the λ-compensator (blue arrow). (B) Optical transverse phase profile associated with the optic axis pattern in (A)—the same as in Figure 1B—here replicated for the sake of comparison.
Though pure-phase holograms displayed on SLM could be used to create FFDH beams, fabricating optical devices based on Geometric Phase has proved to be not only the best-performing choice but also the most natural, since the unit normal distribution deduced from a generating curve is directly translated into an optic axis pattern. As an example, we have here chosen curves generated via the superformula to take advantage of a large variety of shapes grouped under the same equation. A similar method, however, can be applied to any other curve or family of curves.
4. Intensity profiles
As mentioned above, by adding a periodical azimuthal phase modulation to the phase of a helical beam, the cylindrical symmetry typical of the intensity profile of a doughnut is broken. In fact, each photon at distance r from the beam axis suffers a change in its azimuthal linear momentum kϕ that depends periodically on the orientation of the meridional plane it starts from. As kϕ has the same period as ρ(ϕ) in Equation (4), the resulting transverse intensity profile becomes periodic as well. What's more, the details of the profile of kϕ are inherited from the azimuthal rate of change of the unit vector normal to the curve, also meaning that the inflections of the intensity profiles will be inherited from the local curvature of the generating curve. This enables a one-to-one correspondence to be set between the geometric properties of the generating curve and the transverse intensity profile of the beam, especially as far as the dark region is concerned. In Figure 6A, we show the intensity profile of the beam experimentally generated for the parameter values a = b = 1, m = 5, n1 = 1/2, and n2 = n3 = 4/3 at distance z = 1 m from the SVAP for a circularly polarized input TEM00 Gaussian mode with a plane wavefront and radius w0 = (1.50±0.04) mm. For comparison, Figure 6B shows the theoretical intensity profile predicted by calculating the Fresnel transform of the optical field
for the same parameter values. The faint striped structure surrounding the core profile originates by diffraction from the abrupt azimuthal changes in the transverse phase profile shown in Figure 5B.
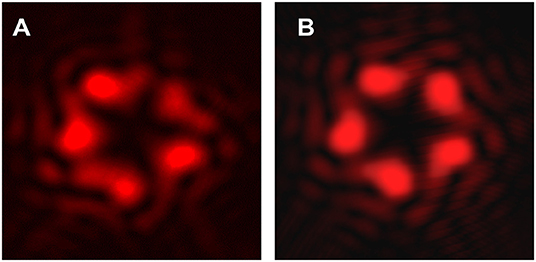
Figure 6. Comparison between the experimental (A) and theoretical (B) intensity profiles of the beam generated through the SVAP with the optic axis pattern shown in Figure 4A at distance z = 1 m, for the values a = b = 1, m = 5, n1 = 1/2, and n2 = n3 = 4/3 of the curve parameters and for an input gaussian beam with a plane wavefront and radius w0 = (1.50±0.04) mm.
5. Concluding remarks
We have shown the possibility of generating dark hollow beams with a large variety of intensity landscapes by using a single azimuthal phase factor without passing through numerical methods for optical field encryption. The method is based on a geometric approach in which the intensity profile around the beam axis is supposed to imitate the shape of a selected closed curve. Also, the OAM spectrum is affected by the shape of the generating curve. If the generating curve has m-fold rotational symmetry, the OAM spectrum will include only components with multiple of m within a global shift determined by the OAM index of the unperturbed helical mode. Liquid-crystal SVAPs turn out to be the most natural choice for implementing such a method, since the unit vector normal to the generating curve comes to be copied over the axis pattern. Applications of FFA SVAPs can be easily devised, in particular, for manipulating non-spherical objects trapped by optical tweezers—as unwanted rotations of micro-objects could then be avoided—as well as for increasing contrast in optical coronagraphy—as properly tailored dark-hollow beams with line singularities along radial directions could be exploited to split the intensity distribution around the optical axis.
Data Availability Statement
All datasets generated for this study are included in the article/supplementary material.
Author Contributions
All of the authors contributed to developing the method for designing Free-Form SVAPs introduced in this paper. BP fabricated and tested the SVAPs. All of the authors contributed to writing the paper.
Funding
This work was supported by the University of Naples Research Funding Program (DR no. 3425-10062015) and by the European Research Council (ERC) under grant no. 694683 (PHOSPhOR).
Conflict of Interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Acknowledgments
The authors thank Prof. L. Marrucci from the Department of Physics E. Pancini of the University of Naples for useful discussions.
References
1. Rubinsztein-Dunlop H, Forbes A, Berry MV, Dennis MR, Andrews DL, Mansuripur M, et al. Roadmap on structured light. J Opt. (2016) 19:013001. doi: 10.1088/2040-8978/19/1/013001
2. Taylor MA, Waleed M, Stilgoe AB, Rubinsztein-Dunlop H, Bowen WP. Enhanced optical trapping via structured scattering. Nat Photon. (2015) 9:669–73. doi: 10.1038/nphoton.2015.160
3. Dholakia K, Čižmár T. Shaping the future of manipulation. Nat Photon. (2011) 5:335–42. doi: 10.1038/nphoton.2011.80
4. Bozinovic N, Yue Y, Ren Y, Tur M, Kristensen P, Huang H, et al. Terabit-scale orbital angular momentum mode division multiplexing in fibers. Science. (2013) 340:1545–8. doi: 10.1126/science.1237861
5. Willner AE, Huang H, Yan Y, Ren Y, Ahmed N, Xie G, et al. Optical communications using orbital angular momentum beams. Adv Opt Photon. (2015) 7:66–106. doi: 10.1364/AOP.7.000066
6. Mair A, Vaziri A, Weihs G, Zeilinger A. Entanglement of the orbital angular momentum states of photons. Nature. (2001) 412:313–6. doi: 10.1038/35085529
7. Molina-Terriza G, Torres JP, Torner L. Twisted photons. Nat Phys. (2007) 3:305–10. doi: 10.1038/nphys607
8. Peacock AC, Steel MJ. The time is right for multiphoton entangled states. Science. (2016) 351:1152–3. doi: 10.1126/science.aaf2919
9. Maurer PC, Maze JR, Stanwix PL, Jiang L, Gorshkov AV, Zibrov AA, et al. Far-field optical imaging and manipulation of individual spins with nanoscale resolution. Nat. Phys. (2010) 6:912–8. doi: 10.1038/nphys1774
10. D'Aguanno G, Mattiucci N, Bloemer M, Desyatnikov A. Optical vortices during a superresolution process in a metamaterial. Phys Rev A. (2008) 77:043825. doi: 10.1103/PhysRevA.77.043825
11. Boriskina SV, Reinhard BM. Molding the flow of light on the nanoscale: from vortex nanogears to phase-operated plasmonic machinery. Nanoscale. (2012) 4:76–90. doi: 10.1039/C1NR11406A
12. Boriskina SV, Reinhard BM. Adaptive on-chip control of nano-optical fields with optoplasmonic vortex nanogates. Opt Express. (2011) 19:22305–15. doi: 10.1364/OE.19.022305
13. Kim H, Park J, Cho S-W, Lee S-Y, Kang M, Lee B. Synthesis and dynamic switching of surface plasmon vortices with plasmonic vortex lens. Nano Lett. (2010) 10:529–36. doi: 10.1021/nl903380j
14. Hell SW, Wichmann J. Breaking the diffraction resolution limit by stimulated emission: stimulated-emission-depletion fluorescence microscopy. Opt Lett. (1994) 19:780–2. doi: 10.1364/OL.19.000780
15. Novotny L, Beversluis MR, Youngworth KS, Brown TG. Longitudinal field modes probed by single molecules. Phys Rev Lett. (2001) 86:5251–4. doi: 10.1103/PhysRevLett.86.5251
16. Nivas JJ, Cardano F, Song Z, Rubano A, Fittipaldi R, Vecchione A, et al. Surface structuring with polarization-singular femtosecond laser beams generated by a q-plate. Sci Rep. (2017) 7:42142. doi: 10.1038/srep42142
17. Meier M, Romano V, Feurer T. Material processing with pulsed radially and azimuthally polarized laser radiation. Appl Phys A. (2007) 86:329–34. doi: 10.1007/s00339-006-3784-9
18. Rose P, Diebel F, Boguslawski M, Denz C. Airy beam induced optical routing. Appl Phys Lett. (2013) 102:101101. doi: 10.1063/1.4793668
19. Bomzon Z, Kleiner V, Hasman E. Pancharatnam-Berry phase in space-variant polarization-state manipulations with subwavelength gratings. Opt Lett. (2001) 26:1424–6. doi: 10.1364/OL.26.001424
20. Liu C, Bai Y, Zhao Q, Yang Y, Chen H, Zhou J, et al. Fully controllable pancharatnam-berry metasurface array with high conversion efficiency and broad bandwidth. Sci Rep. (2016) 6:34819. doi: 10.1038/srep34819
21. Kim J, Li Y, Miskiewicz MN, Oh C, Kudenov MW, Escuti MJ. Fabrication of ideal geometric-phase holograms with arbitrary wavefronts. Optica. (2015) 2:958–64. doi: 10.1364/OPTICA.2.000958
22. Jiang M, Yu H, Feng X, Guo Y, Chaganava I, Turiv T, et al. Liquid crystal pancharatnam–berry micro-optical elements for laser beam shaping. Adv Opt Mater. (2018) 6:1800961. doi: 10.1002/adom.201800961
23. Piccirillo B, D'Ambrosio V, Slussarenko S, Marrucci L, Santamato E. Photon spin-to-orbital angular momentum conversion via an electrically tunable q-plate. Appl Phys Lett. (2010) 97:241104. doi: 10.1063/1.3527083
24. Piccirillo B, Kumar V, Marrucci L, Santamato E. Pancharatnam-Berry phase optical elements for generation and control of complex light: generalized superelliptical q-plates. In: Galvez EJ, Glückstad J, Andrews DL, editors. Complex Light and Optical Forces IX, Vol. 9379. International Society for Optics and Photonics (SPIE) (2015). p. 22–30. doi: 10.1117/12.2078372
25. Piccirillo B, Picardi MF, Marrucci L, Santamato E. Flat polarization-controlled cylindrical lens based on the pancharatnam-berry geometric phase. Eur J Phys. (2017) 38:034007. doi: 10.1088/1361-6404/aa5e11
26. Alemán-Castaneda LA, Piccirillo B, Santamato E, Marrucci L, Alonso MA. Shearing interferometry via geometric phase. Optica. (2019) 6:396–9. doi: 10.1364/OPTICA.6.000396
27. Allen L, Beijersbergen MW, Spreeuw RJC, Woerdman JP. Orbital angular momentum of light and the transformation of Laguerre-Gaussian laser modes. Phys Rev A. (1992) 45:8185–9.
28. Allen L, Barnett SM, Padgett MJ. Optical Angular Momentum. Bristol: Institute of Physics Publishing (2003).
29. Jáuregui R, Hacyan S. Quantum-mechanical properties of bessel beams. Phys Rev A. (2005) 71:033411. doi: 10.1103/PhysRevA.71.033411
30. Karimi E, Piccirillo B, Marrucci L, Santamato E. Improved focusing with hypergeometric-gaussian type-II optical modes. Opt Express. (2008) 16:21069–75. doi: 10.1364/OE.16.021069
31. Bolduc E, Bent N, Santamato E, Karimi E, Boyd RW. Exact solution to simultaneous intensity and phase encryption with a single phase-only hologram. Opt Lett. (2013) 38:3546–9. doi: 10.1364/OL.38.003546
32. Marrucci L, Manzo C, Paparo D. Optical spin-to-orbital angular momentum conversion in inhomogeneous anisotropic media. Phys Rev Lett. Berlin (2006) 96:163905. doi: 10.1103/PhysRevLett.96.163905
33. Lu TH, Huang TD, Wang JG, Wang LW, Alfano RR. Generation of flower high-order poincarésphere laser beams from a spatial light modulator. Sci Rep. (2016) 6:39657. doi: 10.1038/srep39657
34. Porfirev A, Skidanov R. Dark-hollow optical beams with a controllable shape for optical trapping in air. Opt Express. (2015) 23:8373–82. doi: 10.1364/OE.23.008373
35. Piccirillo B, Piedipalumbo E, Marrucci L, Santamato E. Electrically tunable vector vortex coronagraphs based on liquid-crystal geometric phase waveplates. Mol Crystals Liquid Crystals. (2019) 684:15–23. doi: 10.1080/15421406.2019.1581707
36. Rubano A, Cardano F, Piccirillo B, Marrucci L. Q-plate technology: a progress review (invited). J Opt Soc Am B. (2019) 36:D70–87. doi: 10.1364/JOSAB.36.000D70
37. Forbes A, Dudley A, McLaren M. Creation and detection of optical modes with spatial light modulators. Adv Opt Photon. (2016) 8:200–27. doi: 10.1364/AOP.8.000200
38. Sokolov D. Lamé Curves. Encyclopedia of Mathematics. Springer Science+Business Media B.V.; Kluwer Academic Publishers (2001).
Keywords: geometric phase, wavefront sculpting, optical angular momentum, optical singularities, liquid crystals
Citation: Piccirillo B, Piedipalumbo E and Santamato E (2020) Geometric-Phase Waveplates for Free-Form Dark Hollow Beams. Front. Phys. 8:94. doi: 10.3389/fphy.2020.00094
Received: 30 November 2019; Accepted: 12 March 2020;
Published: 21 April 2020.
Edited by:
Uroš Tkalec, University of Ljubljana, SloveniaReviewed by:
Nina Kravets, UMR5798 Laboratoire Ondes et Matière d'Aquitaine (LOMA), FranceQi-Huo Wei, Southern University of Science and Technology, China
Copyright © 2020 Piccirillo, Piedipalumbo and Santamato. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Bruno Piccirillo, YnJ1bm8ucGljY2lyaWxsb0BmaXNpY2EudW5pbmEuaXQ=
 Bruno Piccirillo
Bruno Piccirillo Ester Piedipalumbo
Ester Piedipalumbo Enrico Santamato1
Enrico Santamato1