Polarization Correlation of Entangled Photons Derived Without Using Non-local Interactions

Entangled photons leaving parametric down-conversion sources exhibit a pronounced polarization correlation. The data violate Bell's inequality thus proving that local realistic theories cannot explain the correlation results. Therefore, many physicists are convinced that the correlation can only be brought about by non-local interactions. Some of them even assume that instantaneous influences at a distance are at work. Actually, assuming a strict phase correlation of the photons at the source the observed polarization correlation can be deduced from wave optical considerations. The correlation has its origin in the phase coupling of circularly polarized wave packets leaving the fluorescence photon source simultaneously. The enlargement of the distances between photon source and observers does not alter the correlation if the polarization status of the wave packets accompanying the photons is not changed on their way from the source to the observers. At least with respect to the polarization correlation of entangled photons the principle of locality remains valid.

1. Introduction

In 1935 Einstein et al. [1] initiated a discussion whether quantum mechanics is complete or not. In the following years one could not find concrete hints for the occurrence of hidden variables. In 1964 Bell [2] showed on the basis of two spin 1/2 particles that local realistic theories can principally not reproduce the results of quantum mechanics. In 1969 Clauser et al. [3] proposed an experiment to test local hidden variable theories with entangled photons. Already 3 years later Freedman and Clauser presented first measurements proving that local realistic theories were not able to describe the experimental results [4].

More elaborate experiments on the polarization correlation of entangled photons [5–12] showed that the experimental results are fully reproduced by quantum mechanics.

All experiments providing polarization correlation data with good statistics are performed in such a way that the detection processes of two distant observers are spacelikely separated. Thus, the publications on these experiments generally suggest that the results can only be induced by superluminal signals between the observers. Especially Salart et al. [9] emphasize that the violation of Bell's inequality seems to prove that quantum mechanics make use of non-local interactions.

Discrepancies between the results of local realistic theories and quantum mechanics are also discussed for more complicated quantum systems with more than two particles [13]. Many of these publications insinuate that faster-than-light communication might be possible. The drawback of all these attempts to prove the occurrence of non-local interactions is that until now no concrete results could be presented which reproduce the experimental findings.

In the last few years several recognized physicists try to prove that quantum mechanics does not use non-local interactions [14–21]. The authors show that some mathematical operations like the reduction of a quantum state seem to have non-local consequences. On closer examination these operations only cause changes of the observer's knowledge on the quantum state. The changes thus do not take place in physical space but merely in information space.

In fact, the results of the experiments with parametric down-conversion photon sources can be derived from wave optical and quantum statistical considerations without using superluminal signals. There are good arguments to assume that the experiments of Aspect and coworkers with entangled photons emerging from a specific decay cascade of calcium [5, 6] can also be explained without using non-local interactions. However, additional tests on the polarization status of the photons would be helpful in order to conclusively answer the question.

2. Photon Pairs Arising From Down-Conversion Sources

In the last 22 years several polarization correlation experiments with parametric down-conversion sources have been performed [7–12]. If necessary experimental details are taken from the doctor thesis of Weihs [22]. In a BBO crystal ultraviolet photons are converted into two phase coupled circularly polarized green photons with equal energies.

The circularly polarized wave packets are immediately decomposed into two linearly polarized wave packets with orthogonal polarization directions. The ordinary beam is vertically polarized. The extraordinary beam is horizontally polarized. Due to the different propagation directions the emission cones of ordinary and extraordinary beam appear on the exit plane as two off-centered circles which intersect each other at two points (see Figure 1). After traversing a compensation plate the reassembled circularly polarized wave packets leave nearly unchanged the two intersection zones.

FIGURE 1

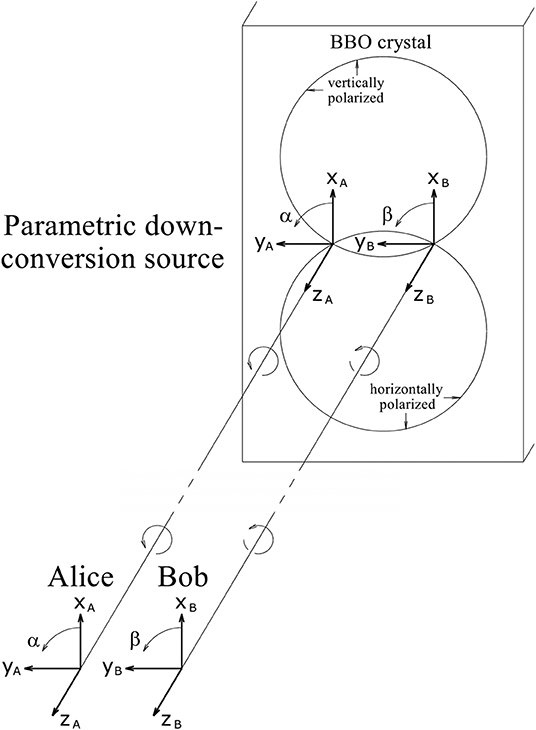
Figure 1. Schematic diagram of a simple experimental setup suited to determine polarization correlations. In the top right corner a BBO source is shown which provides entangled photons both rotating in the same direction. The coordinate systems of the observers Alice and Bob shown in the bottom left corner are both right-handed. The angles α and β indicate the orientations of the linear polarizations looked for by Alice and Bob, respectively. The thin lines between source and observers denote optical fibers. The distance between Alice and Bob is usually chosen large enough to ensure that two associated photon detection processes are spacelikely separated.

In the polarization correlation experiments with parametric down-conversion sources only the so-called singlet-configuration has been studied. In this configuration the polarization planes of associated photons rotate in the same direction. In statistical average about one half of the photon pairs rotate clockwisely, the other half counterclockwisely.

3. Detection of Polarized Photons by Alice and Bob

Photons emerging from the two exit sites of the source are guided by optical fibers to the observers. After leaving the optical fibers the wave packets traverse an electro-optical modulator arranged between two suitably oriented quarter-wave plates. In combination the three optically active elements twist linearly polarized waves by an arbitrarily choosable angle proportional to the applied voltage. The detector unit is fixed in space. The twist of the plane waves by the electro-optical modulator simulates a virtual twist of the detector unit. For the sake of convenience it will be assumed in the following that the twisting units are omitted and that the detectors are really twisted in space.

By the use of Wollaston prisms Alice and Bob split the incoming wave packets into two equally large components with orthogonal polarization directions. The linearly polarized components hit altogether four detectors which should be highly sensitive in order to detect nearly all incoming photons [11, 12]. When the apparatus is thoroughly adjusted the count rates of the detectors should no longer depend on the polarization direction.

In the four detector channels each registered pulse is saved together with an individual time stamp. After having finished the measurement the four data lists are compared in order to determine four coincidence rates namely I(α, β), I(α, β+90°), I(α+90°, β), and I(α+90°, β+90°). Let I₀ be the coincidence rate when the selecting filters are removed on both sides of the experiment. If the losses in the filters are negligible I₀ is also the coincidence rate summed up in the four channels. The two coincidence rates I(α, β) and I(α, β+90°) add up to I₀/2. The same is true for the coincidence rates I(α+90°, β) and I(α+90°, β+90°). Thereby one has to bear in mind that coincidence rates exhibit statistical uncertainties.

In this article particle as well as wave aspects will be addressed because the correlation of photons detected by Alice and Bob depends on the relative phase of the circularly polarized wave packets accompanying the photons. The derivation of the polarization correlation is mainly based on wave arguments but if necessary particle aspects will also be considered.

The terms “wave” and “light” are often used for convenience. In fact, a light beam will always be understood as a stream of independent wave packets with limited coherence length. Only wave packet pairs incorporating entangled photon pairs are strictly phase coupled when they leave the photon source. In the experiment of Weihs [22, p. 63] the coherence length has been estimated to be about 0.1 m. Thus, the wave packets leaving the photon source are very short in comparison with the distance between Alice and Bob thus precluding wave based non-local interactions between the observers.

4. Formal Derivation of the Polarization Correlation

In wave optics and quantum mechanics one often asks for the phase relation of interfering waves in the detection plane in order to get the interference pattern. In correlation experiments, however, one has to ask for the phase relation of two associated wave packets at the source. The relative phase at the source manifests itself in the overlap integral of the two normalized wave packets.

The two wave packets simultaneously leaving outputs A and B have a phase shift of ±90° at the source. The sign reveals which of the wave packets is leading. In Figure 1 the phase shift is indicated by twisted rotation vectors. If α≠β an additional phase shift of ±(α−β) has to be taken into account. The sign depends on the rotational direction of the two circularly polarized wave packets. Thus, the total phase shift of the two linearly polarized partial waves looked for by the two observers is

$\begin{array}{ll}\phi =\pm 90°\pm (\alpha -\beta ).& (1)\end{array}$

Neglecting the envelope function one has to evaluate the overlap integral of the two normalized functions

$\begin{array}{ll}\begin{array}{l}f(t)=\sqrt{\omega /\pi }sin(\omega t)\\ g(t)=\sqrt{\omega /\pi }sin(\omega t\pm 90°\pm (\alpha -\beta )).\end{array}& (2)\end{array}$

The second function divided by the normalizing factor can be converted by using trigonometrical addition theorems twice

$\begin{array}{l}\begin{array}{l}sin(\omega t\pm 90°\pm (\alpha -\beta ))=\\ sin(\omega t)cos(\pm 90°\pm (\alpha -\beta ))+\\ cos(\omega t)sin(\pm 90°\pm (\alpha -\beta ))=\\ \pm sin(\omega t)sin(\alpha -\beta )\\ \pm cos(\omega t)cos(\alpha -\beta )\end{array}(3)\end{array}$

By using the definite integrals

$\begin{array}{ll}\begin{array}{cc}\frac{\omega }{\pi }{\displaystyle {\int }_0^{2\pi /\omega }}sin(\omega t)sin(\omega t)dt& =1\\ \frac{\omega }{\pi }{\displaystyle {\int }_0^{2\pi /\omega }}sin(\omega t)cos(\omega t)dt& =0\end{array}& (4)\end{array}$

one can easily calculate the overlap integral

$\begin{array}{ll}{\displaystyle {\int }_0^{2\pi /\omega }}f(t)g(t)dt=\pm sin(\alpha -\beta ).& (5)\end{array}$

The (absolute) square of the overlap integral of the two normalized phase coupled wave packets is proportional to the coincidence rate. As has been explained in the previous chapter the coincidence rates I(α, β) and I(α, β+90°) add up to I₀/2. Therefore, the proportionality factor must be I₀/2.

Thus the coincidence rate is given by

$\begin{array}{ll}I(\alpha ,\beta )=I_{0}si{n}^2(\alpha -\beta )/2& (6)\end{array}$

and the correlation is given by

$\begin{array}{ll}C(\alpha ,\beta )=\frac{I(\alpha ,\beta )}{I(\alpha ,\beta )+I(\alpha ,\beta +90°)}=si{n}^2(\alpha -\beta ).& (7)\end{array}$

With this rather simple consideration the experimentally found correlations of entangled photons have been fully reproduced.

5. Working Out Quantum Statistical Aspects

Quantum statistics will become much clearer if each of the two circularly polarized light beams A and B leaving the source is formally splitted into two commensurate linearly polarized beams with orthogonal polarization directions. A circularly polarized wave can always be understood as the superposition of two equally sized linearly polarized partial waves with orthogonal polarization directions. The two partial waves are phase shifted with respect to each other by ±90°. The orientations of the linear polarizations ϑ and ϑ+90° can be freely chosen.

The photons contained in the two partial beams form two disjunct groups. If a photon has been assigned to a linearly polarized partial beam it will always stay in that beam. There is no intermixing between the two photon groups on their way from the source to the observers even if the photons and the accompanying wave packets traverse electro-optical modulators and quarter-wave plates.

All modern experiments are planned with the aim that selection and detection processes carried out by the two observers are spacelikely separated. Therefore, the splitting is performed just in front of the detectors. The rather late fixing of the angles α and β even concerns photons leaving the source much earlier. Thus, the splitting of the circularly polarized beams admittedly needs non-local information but certainly no non-local interaction because the two streams of photons propagating toward Alice and Bob are not modified by the repeated change of the detection angles. Before the photons reach the associated Wollaston prism the splitting procedure is a purely mathematical but not a physical process.

Due to their common origin entangled photon pairs are phase coupled when they leave the source. In case of parametric down-conversion processes the two entangled photons are in phase but the two associated circularly polarized wave packets are phase shifted by ±90°.

As the optical pathes from the source to Alice and Bob will generally not be balanced the initial phase information cannot be recovered by simply comparing the arrival times of the entangled photons. This would merely be impossible due to the limited time resolution of external clocks and to the jitter of the detection electronics.

Fortunately the two beams are equipped with synchronized internal clocks which can be easily read off by the observers. Within one wave cycle the polarization plane performs a full turn. Thus, the relative phase of the photons at the source up to multiples of 180° can be recovered from the difference of the polarization angles looked for by the two observers. The modulo 180° term comes from the 180° periodicity of the polarizer's transmittance.

The polarization correlation with due regard to the particle aspect will be derived in two steps. At first the case α = β will be discussed. This step covers the crucial point in the line of arguments explaining why the entangled photons are statistically distributed to only two of the four possible coincidence channels.

The two partial beams A(α) and B(α+90°) are in phase (or opposite in phase) at the source. The same is true for the partial beams A(α+90°) and B(α). As the photons are in phase at the source they must be found either in the coincidence channel A(α)/B(α+90°) or in the coincidence channel A(α+90°)/B(α). As the two coincidence channels are equivalent the probabilities to find the entangled photon pairs in these two coincidence channels must be equal.

In contrast, the partial beams A(α) and B(α) are phase shifted at the source by ± 90°. That means they are orthogonal to each other. The same is true for the partial beams A(α+90°) and B(α+90°). Therefore, there will be no coincidences in these two coincidence channels.

For each angle α the coincidence rates in the four conceivable channels are thus given by

$\begin{array}{ll}\begin{array}{l}I(\alpha ,\beta =\alpha +90°)=I_0/2\\ I(\alpha ,\beta =\alpha )=0\\ I(\alpha +90°,\beta =\alpha )=I_0/2\\ I(\alpha +90°,\beta =\alpha +90°)=0.\end{array}& (8)\end{array}$

The correlations C(α, β = α), C(α, β = α+90°), C(α+90°, β = α+90°), and C(α+90°, β = α) are either zero or unity. That means entangled photons are strictly anticorrelated. This statement is valid for each single pair of entangled photons, not only for a statistical ensemble of entangled photon pairs.

The considerations above prove that the two entangled photons are both contained either in the partial wave pair A(α) and B(α+90°) or in the partial wave pair A(α+90°) and B(α). Whether the photon is detected by detector A(α) or by detector A(α+90°) is purely accidental. One cannot predict which detector will be hit by individual photons. However, after the detection of the first photon of a photon pair for example on Alice's side it will be clear which one of the two detectors on Bob's side will be hit by the second photon.

Only the anti-correlation of entangled photons is predefined but not the polarization of individual photons [23]. This is why the polarization direction should not be thought of as an element of reality.

The phase relation of partial beams at the source thus leads to the strong polarization correlation although the information on the polarization status is not a hidden property of the photons. Einstein et al. [1] had claimed that a property equally found in two no longer interacting quantum states must be an element of reality. The pronounced polarization correlation of entangled photons seems to be a counterexample.

The wrong estimate of Einstein and his coworkers has entailed the erroneous approach of Bell [2] who assumed that the polarization directions are real properties of the photons. In fact, the phase coupling only predefines the interrelationship but not the property itself. In consequence Bell's inequalities are irrelevant.

The extension of the consideration to the case α≠β is rather trivial and exclusively rests on an optical law discovered by Etienne Louis Malus in 1810. Malus' law says: If light linearly polarized in direction γ traverses a polarization filter with its polarization axis oriented in direction δ its intensity is reduced by the factor

$\begin{array}{l}co{s}^2(\gamma -\delta ).\end{array}$

One cannot predict which one of the photons will traverse the polarization filter because Malus' law has a purely statistical character. The law is valid not only for light leaving a classical light source but also for laser light. That means it does not depend on second-order coherence properties of a photon stream. It is also experimentally proven in case of low intensity when the beam intensity is measured by single photon detectors. Brukner and Zeilinger explicitly show that Malus' law is also valid in the quantum regime [24]. In one of his recent publications Khrennikov has also used Malus' law when he derived the polarization correlation of entangled photons starting from quantum mechanical considerations [16, p. 3].

The first of Equation (8) means that if one of the entangled photons has been recorded by detector A(α) the associated photon will certainly be contained in the partial beam B(α+90°). Therefore, one has to apply Malus' law for γ = α+90° and δ = β. That means the coincidence rate I₀/2 is reduced by the factor cos²(α+90°−β) = sin²(α−β). Therewith the coincidence rate I(α, β) is given by

$\begin{array}{ll}I(\alpha ,\beta )=I_{0}si{n}^2(\alpha -\beta )/2.& (9)\end{array}$

in accordance with Equation (6).

The role of Alice and Bob can be exchanged. If the circularly polarized beams are splitted into partial beams linearly polarized in the directions β and β+90° the results presented above will be reproduced.

For α ≠ β Malus' law with its inherently statistical character has to be applied on Alice's or on Bob's side. In this case the correlation C(α, β) is larger than zero and smaller than unity. Thus, the correlation is not defined for a single pair of entangled photons but only for a sufficiently large group of entangled photon pairs.

As has been proven above the piece of information responsible for the emergence of the pronounced correlation is the phase shift of two associated wave packets when they leave the source. Traditionally quantum mechanics strictly takes into account phase differences of wave functions contained in a matrix element. Therefore, it can be assumed for sure that the phase difference of the two entangled photons will also be considered in quantum mechanics.

It is not relevant whether the correlation problem is handled classically or quantum mechanically. It is only relevant whether the phase information is used or not.

The calculations based on local realistic theories do not consider phase relations. They only try to reproduce the polarization correlation by assuming that the polarization directions of the entangled photons are encoded in the photons as hidden variables. In explaining the strong polarization correlation of entangled photons only their relative phase at the source is relevant.

6. General Remarks

The pronounced correlation of entangled photons is neither superprising nor mysterious. It solely depends on the initial phase shift of the circularly polarized waves accompanying the entangled photons. One only has to make sure that the polarization directions α and β looked for by the two observers are associated with corresponding polarization angles at the source. This condition is fulfilled in each of the experiments. Hereby it is not relevant at what time the polarization directions have been chosen. The purely conceptual splitting of the two partial beams and the detection of the photons have no effect on the parametric down-conversion process. The relative phase of the entangled photons has been fixed inside the source. The observers only decide which polarization directions they look for. There is no need for a superluminal information transfer between the observers. The distance between the observers is absolutely irrelevant.

The relative phase of entangled photons at the source could be declared to be a hidden variable finally revealed by the coincidence detection process. Hidden variables of this type can only be associated with wave packets but not with particles. The decisive point of the argumentation is that the wave intensity and thus also the coincidence rate is proportional to the (absolute) square of the scattering amplitude. Properties are only manifested after squaring the overlap integral. In particle based considerations properties directly act upon counting rates.

Bell's inequality is misleading because it attributes properties like polarization directions to particles and not to waves. Therefore, Bell cannot take into account phase differences of entangled photons. In future one should ignore violations of Bell's theorem because Bell's considerations are not adequate to describe wave phenomena.

7. Correlation of Photon Pairs in Triplet Configuration

A pronounced correlation of entangled photons should also be observable in triplet configuration. That means that the two circularly polarized waves are rotating in opposite directions. In this case the correlation cannot be derived as easily as in the singlet case. One can figure out that the triplet configuration arises from the singlet configuration by mirroring one of the circularly polarized waves at a vertical plane. This can be performed by a half-wave plate with the optical axis oriented in vertical direction. If the circularly polarized wave packets are phase shifted by ±90° the correlation should be

$\begin{array}{ll}C(\alpha ,\beta )=si{n}^2(\alpha +\beta ).& (10)\end{array}$

Thereby the origins of the angles α and β have to lie in the vertical plane. Preliminary measurements of Weihs [22, p. 72] support this result. For example if the two observers both look for polarization directions parallel to 45° the coincidence rate is at a maximum.

In a former publication [25] the sign in the correlation equation for the triplet configuration was minus instead of plus. The sign change has to do with the fact that Bob's coordinate system was left-handed in the previous article. In the consideration above both coordinate systems are right-handed.

8. Properties of Photon Pairs Arising From Atomic Sources

In the experiments with parametric down-conversion sources the two circularly polarized wave packets are phase shifted by ±90° leading to a strict anticorrelation of the linear polarizations. In contrast, in the experiments of Aspect et al. [5, 6] the two circularly polarized wave packets are in phase or opposite in phase. Therefore, the correlation is given by

$\begin{array}{ll}C(\alpha ,\beta )=co{s}^2(\alpha -\beta ).& (11)\end{array}$

The two photons produced by a decay cascade of calcium have different frequencies. Only if the rotational frequencies are equal one can define a phase shift. Thus, it should be tested in future experiments whether the rotational frequencies of the two entangled photons are equal or not. With respect to the rotational motion the coherence time of the two photons must be longer than the life time of the intermediate state of the decay cascade.

9. Does It Help to Postulate Non-local Interactions?

Is it really helpful to postulate a novel interaction which is in serious conflict with special relativity? Postulating an information transfer faster than light entails a wealth of new problems. An instantaneous influence at a distance requires that simultaneity can be strictly defined for distant locations in contrast to corresponding assertions of special relativity.

Even if such principal objections are ignored many practical problems arise. How could such a postulated interaction generate correct results? In correlation experiments the ratio of coincidence rates in two complementary channels I(α, β) and I(α, β+90°) has to be precisely defined. The newly postulated interaction has to redirect a well-specified percentage of stochastically arriving photons from one channel to the other one. The expected ratio of coincidences in the two channels depends on the difference of the polarization directions α and β? How does the postulated interaction get the information on the angles? In the experiments the twisting angles α and β are generated by applying voltages to electro-optical modulators. How could any theory whatsoever associate a voltage to an angle? The proportionality factor depends on the material, on the orientation of the crystal axis and numerous other experimental details.

Actually, in the optical fibers spurious birefringent effects occur which are manually compensated. How can the postulated new interaction know whether the apparatus is well-adjusted or not? By the way all the twisting processes are frequency dependent. Only light composed of photons like those used in the experiment can gain the information on the adjustment status and on the angles α and β.

The experiment of Salart et al. [9, p. 863] shows that the postulated “spooky” interaction must be at least 50,000 times faster than the speed of light. If the lengthes of the optical fibers differ distinctly from each other the superluminal signal has to wait quite a long, but an extremely well-defined time interval before it redirects individual pulses from one output to the other one. It will be extremely difficult to embed such a delayed reaction in a serious physical theory.

Data Availability Statement

All datasets generated for this study are included in the article/supplementary material.

Author Contributions

The author confirms being the sole contributor of this work and has approved it for publication.

Conflict of Interest

The author declares that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Acknowledgments

I thank Andrei Khrennikov for kindly reading my manuscript. I tried to consider his concerns with respect to quantum statistics.

References

1. Einstein A, Podolsky B, Rosen N. Can quantum-mechanical description of physical reality be considered complete? Phys Rev. (1935) 47:777–80.

Google Scholar

2. Bell JS. On the Einstein Podolsky Rosen Paradox. Physics. (1964) 1:195–200.

Google Scholar

3. Clauser JF, Horne MA, Shimony A, Holt RA. Proposed experiment to test local hidden-variable theories. Phys Rev Lett. (1969) 23:880–4.

Google Scholar

4. Freedman SJ, Clauser JF. Experimental test of local hidden-variable theories. Phys Rev Lett. (1972) 28:938–41.

Google Scholar

5. Aspect A, Grangier P, Roger G. Experimental tests of realistic local theories via Bell's theorem. Phys Rev Lett. (1981) 47:460–3.

Google Scholar

6. Aspect A, Grangier P, Roger G. Experimental realisation of Einstein-Podolsky-Rosen-Bohm Gedanken experiment: a new violation of Bell's inequalities. Phys Rev Lett. (1982) 49:91–4.

Google Scholar

7. Tittel W, Brendel J, Gisin B, Herzog T, Zbinden H, Gisin N. Experimental demonstration of quantum correlations over more than 10 km. Phys Rev A. (1998) 57:3229–32.

Google Scholar

8. Tittel W, Brendel J, Zbinden H, Gisin N. Violation of Bell's inequalities by photons more than 10 km apart. Phys Rev Lett. (1998) 81:3563–6.

Google Scholar

9. Salart D, Baas A, Branciard C, Gisin N, Zbinden H. Testing the speed of ‘spooky action at a distance'. Nature. (2008) 454:861–4. doi: 10.1038/nature07121

PubMed Abstract | CrossRef Full Text | Google Scholar

10. Weihs G, Jennewein J, Simon C, Weinfurter H, Zeilinger A. Violation of Bell's inequality under strict Einstein locality conditions. Phys Rev Lett. (1998) 81:5039–43.

Google Scholar

11. Giustina M, Versteegh MAM, Wengerowsky S, Handsteiner J, Hochrainer A, Phelan K, et al. (2015) Significant-Loophole-Free test of Bell's theorem with entangled photons. Phys Rev Lett. (2015) 115:250401. doi: 10.1103/PhysRevLett.115.250401

PubMed Abstract | CrossRef Full Text | Google Scholar

12. Shalm L, Meyer-Scott E, Christensen BG, Bierhorst P, Wayne MA, Stevens MJ, et al. Strong Loophole-Free test of local realism. Phys Rev Lett. (2015) 115:250402. doi: 10.1103/PhysRevLett.115.250402

PubMed Abstract | CrossRef Full Text | Google Scholar

13. Pan JW, Bouwmeester D, Daniell M, Weinfurter H, Zeilinger A. Experimental test of quantum nonlocality in three-photon Greenberger-Horne-Zeilinger entanglement. Nature. (2000) 403:515–9. doi: 10.1038/35000514

PubMed Abstract | CrossRef Full Text | Google Scholar

14. Khrennikov A. Get rid of nonlocality from quantum physics. Entropy. (2019) 21:806. doi: 10.3390/e21080806

CrossRef Full Text | Google Scholar

15. Khrennikov A. Quantum versus classical entanglement: eliminating the issue of quantum nonlocality. Found Phys. (2020) doi: 10.1007/s10701-020-00319-7

CrossRef Full Text | Google Scholar

16. Khrennikov A. Two faced Janus of quantum nonlocality. Entropy. (2020) 22:303. doi: 10.3390/e22030303

CrossRef Full Text | Google Scholar

17. Kupczynski M. Closing the door on quantum nonlocality. Entropy. (2018) 20:877. doi: 10.3390/e20110877

CrossRef Full Text | Google Scholar

18. Hess K. Bell's theorem and instantaneous influence at a distance. J Mod Phys. (2018) 9:1573–90. doi: 10.4236/jmp.2018.98099

CrossRef Full Text | Google Scholar

19. Hess K. Categories of nonlocality in EPR theories and the validity of Einstein's separation principle as well as Bell's theorem. J Mod Phys. (2019) 10:1209–21. doi: 10.4236/jmp.2019.1010080

CrossRef Full Text | Google Scholar

20. Boughn S. Making sense of Bell's theorem and quantum nonlocality. Found Phys. (2017) 47:640–57. doi: 10.1007/s10701-017-0083-6

CrossRef Full Text | Google Scholar

21. Griffiths RB. Nonlocality claims are inconsistent with Hilbert-space quantum mechanics. Phys Rev A. (2020) 101:022117. doi: 10.1103/PhysRevA.101.022117

CrossRef Full Text | Google Scholar

22. Weihs G. Ein Experiment zum Test der Bellschen Ungleichung unter Einsteinscher Lokalität (Dissertation), Universität Wien (1999). Available online at: https://www.uibk.ac.at/exphys/photonik/people/gwdiss.pdf (accessed March 1, 2020).

Google Scholar

23. Khrennikov A. Towards a resolution of dilemma: nonlocality or nonobjectivity. Int J Theor Phys. (2012) 51:2488–502. doi: 10.1007/s10773-012-1129-3

CrossRef Full Text | Google Scholar

24. Brukner Š, Zeilinger A. Malus' law and quantum information. Acta Phys Slov. (1999) 49:647–52.

Google Scholar

25. Jung K. Violation of Bell's inequality: must the Einstein locality really be abandoned? J Phys Conf Ser. (2017) 880:1–8. doi: 10.1088/1742-6596/880/1/012065

CrossRef Full Text | Google Scholar