- Faculté des Sciences de Base, Ecole Polytechnique Fédérale de Lausanne, EPFL SB IPHYS LQM, Lausanne, Switzerland
For half a century, the analysis of the size of national assemblies was dominated by the famous cube-root relation with the population. However, a revisitation of that historical work with a physicist’s approach reveals basic conceptual problems that fatally undermine its conclusions. Furthermore, the assembly size evaluation exceeds the accuracy of all power equations, which cannot be reliably used for political analysis.
Introduction
Could the “optimal” size for the national assembly of a country be evaluated with methods similar to physics research? This is a timely question: the debate about insufficient representation at the federal and state levels is raging in the USA. On the other side, there were recent initiatives to reduce the number of representatives in the national parliaments of many countries, including France, Hungary, Ireland, Japan, Mexico, the Netherlands, Portugal, Romania and the United Kingdom. And Italy just emerged from a referendum on this issue.
The classic reference is the 1972 work of Taagepera [1], who introduced the well-known cube-root formula to link A, the number of parliament members, and Po, the population:
where a is a constant.
Alternate approaches were later presented [2–5]. In particular, Auriol and Gary-Bobo [2] derived a square-root law and then empirically obtained a 0.4 exponent from recent data for 100 countries. And the foundations of the cube-root law were criticized: notably, Jacobs and Otjes [6] questioned the cause-effect sequence that supposedly leads to it.
The relation between A and Po size must be appreciated in a more general context [7–9]. Indeed, scaling power-law relations with the population were empirically and/or formally derived for other quantities like the number of election candidates [7, 8], patent production, personal income and the electrical cable length [9]. The general notion is that “similarly to large-scale physical thermodynamic systems, large groups of interacting humans may exhibit universal statistical properties” [7]. It is certainly not our scope here to challenge this notion, which is supported by a variety of facts and led to important contributions to the understanding of collective human phenomena. Our focused scope is to show that in the specific case of the cube-root relation for parliament members and population the derivation of Ref. [1] was flawed.
Furthermore, cube-root scaling laws have alternate mathematical explanations [10] with respect to [1] and were known as early as (at least) 1909 [11]. Therefore, our challenge of the classic derivation of Ref. [1] does not necessarily imply that the law itself is wrong.
Method
Taagepera’s work [1] remains a milestone in many experts' view, is known by a broad public and is often used in political debates. For example, it was publicized by the media as “scientific” support for one of the sides in the recent Italian referendum [4]. We thus decided to directly look at its derivation from a physicist’s prospective, and surprisingly found that the original work [1] is affected by four critical problems:
(1) The cube-root law was not derived from its data and the corresponding fit was arbitrarily forced.
(2) The theoretical steps that were used to derive Eq. 1 incorrectly evaluated one of its key factors.
(3) The model assumed that each representative spends on the average equal times for communications inside and outside the parliament, an arbitrary hypothesis that has unrealistic consequences.
(4) No evaluation of the “optimal” size based on a power law, including the cube-root one, can reach a meaningful accuracy.
Concerning the first problem, the original article [1] did mention a power law more general than Eq. 1:
However, it surprisingly argued against using it to fit the data: “The actual best fit of the data to an expression of the form A = aPon … could be worked out, but this would be a dead end… It is more fruitful to look for a plausible theoretical model which would fit the observed general trend”. This argument is fundamentally flawed from a physicist’s point of view: it considers only one hypothesis, renouncing a priori to demonstrate its superiority with respect to others.
Results
We analyzed the consequences of the above argument by applying the same fitting procedure as Ref. [1] to the data of its Table 1, i.e., a least-square fit of the logarithms. Using Eq. 2 instead of Eq. 1, i.e., an unrestricted fit (the solid line in Figure 1), we got:
The exponent n = 0.45 is actually closer to 0.5, the square-root law proposed by Auriol and Gary-Bobo [2], and to their empirical value 0.4.
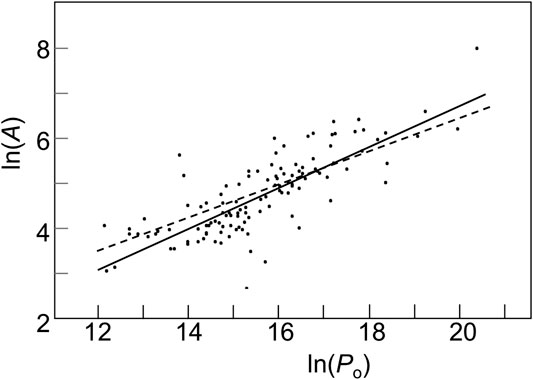
FIGURE. 1. Log-log plot of the original data of Taagepera [1]. The solid line is the best fit given by Eq. 3, whereas the dashed line is the (forced) fit with a cube-root law, leading to Eq. 4.
If one forces the same data set to be fitted by a cube-root law, the result is:
The corresponding fit (Figure 1, dashed line) is statistically inferior: the standard deviation, 250, is larger than for Eq. 3, 209.
To present the second and third of the problems affecting Ref. [1], we must consider the key steps in its derivation of the cube-root law. In a nutshell, the time spent in communications was considered as the essential factor in parliament effectiveness. And this time was linked to the number of communication channels.
Two kinds of channels were considered: first, those between each parliament member and his/her active constituency. The average number of such channels per member is:
Where kPo is the fraction of the population that is politically involved.
The second type of communication channels connects different members of the assembly, to discuss and implement the measures identified by the first type of channels. While communicating between them, two assembly members share the same channel, and it was argued in [1] that the total number of channels is in this case:
Which, except for unrealistically small assemblies, can be approximated as:
What is the relation between CC and CA? Ref. [1] simply assumed that for maximum effectiveness CC = CA, leading to:
That is, to the cube-root law of Eq. 1, with a = (2k)1/3.
However, this logic frame is affected by two conceptual problems. First, Eq. 5 applies to the channels between one member of the assembly and the corresponding constituency, whereas Eqs. 6 and 7 give the number of inter-assembly channels for all members. For one member, instead of Eqs. 6 and 7 one must use:
Which, assuming again that CC = CA, leads to:
Not a cube-root law but a square-root law [2].
To better understand why Eq. 9 is correct and Eqs. 6 and 7 are not, imagine that the inter-assembly “communication channels” are only used for speeches. A single assembly member shares with each speaker one channel, and the total number of his/her channels corresponds to the number of speakers, i.e., of representatives, and not to its square. This changes the cube-root law into a square-root law.
The other flaw in the above logic frame is that there is absolutely no evidence supporting its hypothesis that CC = CA. On the contrary, this assumption causes problems. In the original work of Ref. [1], it led to Eq. 8, and the corresponding forced best fit of Eq. 4 would give k ≈ 14%, which hopefully is too low. And would become a catastrophic 0.3% with the unrestricted best fit of Eq. 3.
The balance between different types of communications can actually change from country to country and evolves with time. For example, modern communication instruments can reduce CC. Symmetrically, effective negotiators can decrease CA. Thus, assuming a priori that CC = CA is arbitrary.
Supposing instead that CC/CA = x, Eqs. 8 and 10 become:
In both cases, the multiplication factor is a combination of k and x, which cannot be disentangled from each other by best-fitting the data. One could perhaps estimate k from independent information like literacy, party membership and voter participation. But evaluating x is extremely difficult because of its multiple, competing and evolving causes and the lack of data.
Discussion
The difficulties in evaluating x and k negatively impact the use of a power law to identify the “optimal” size of a national assembly. And other problems affect this approach.
Note that Ref. [1] tried to link the populations not to the “optimal” parliament sizes but to the real sizes, using data for countries of all kinds. Of these, many if not most were plagued by corruption, ineffective bureaucracy and/or authoritarian regimes. Thus, they could hardly lead to “optimal” values of A.
Hypothetically, one could try to extract an “optimal” value by using a subset of “good” countries, perhaps those with low indexes for corruption and bureaucratic ineffectiveness. However, not even filtering could solve the fourth problem affecting Ref. [1]: accuracy. In fact, any evaluation of A with a power law is very sensitive to the exponent. Taking the derivative of Eq. 2 one obtains:
(dA/dn) = aPon ln(Po) = A ln(Po) ,
since Po is large, an uncertainty dn, however small, is multiplied by a big factor ln(Po) and produces a large relative uncertainty dA/A. For example, the dn uncertainty ±0.03 from Eq. 3, with a population of just ≈617,000, would bring dA/A to ≈40%, large enough to accommodate most political preferences.
In short, accurately evaluating the “optimal” size of a national assembly is illusory. And trying to inject additional factors besides the population cannot solve the above problems.
At most, this kind of approach can identify the countries that strongly deviate from the “average”, as Ref. [2] did for France, the USA and Italy. However, without filtering the “average” is for a mix of “good” and “bad” countries, thus a deviation from it is not necessarily negative …and could even be positive!
In conclusion, we surprisingly found that the historical and very influential work of Taagepera [1] used a wrong equation to derive its famous cube-root law and arbitrarily assumed time equipartition between inter-assembly and assembly-constituency communications. An unrestricted best fit of the original data does not support the cube-root law and would favor instead a power law with an exponent larger than 1/3. These flaws fatally undermine the foundations of the cube-root law and disqualify - also for other reasons - its popular use to evaluate the “optimal” parliament size for a country.
Data Availability Statement
Publicly available datasets were analyzed in this study. This data can be found here: Reference 1 in the article.
Author Contributions
The author confirms being the sole contributor of this work and has approved it for publication.
Funding
Work supported in kind by the Ecole Polytechnique Fédérale de Lausanne (EPFL).
Conflict of Interest
The author declares that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
References
1. Taagepera R. The size of national assemblies. Soc Sci Res (1972) 1:385–401. The data extracted from this article and used here can be found in https://sciencehistory.epfl.ch/physics-and-sociology/
2. Auriol E, Gary-Bobo RJ. On the optimal number of representatives. Publ Choice (2012) 153:419–445. doi:10.1007/s11127-011-9801-3
3. Auriol E, Gary-Bobo RJ. The More the Merrier? Choosing the optimal number of representatives in modern democracies. Available at: https://voxeu.org/optimal-number-representatives-democracy (2007).
4. De Sio L, Angelucci G. 945 sono troppi? 600 sono pochi? Qual è il numero “ottimale” di parlamentari?. Available at: https://cise.luiss.it/cise/2019/10/09/945-sono-troppi-600-sono-pochi-quale-e-il-numero-ottimale-di-parlamentari (2019).
5. Jacobs K, Otjes S. Explaining reforms of assembly sizes. Available at: https://ecpr.eu/Filestore/PaperProposal/3bc100be-56fe-4efc-8d8c-a1f0b85e7f24.pdf (2014)
6. Jacobs K, Otjes S. Explaining the size of assemblies. A longitudinal analysis of the design and reform of assembly sizes in democracies around the world. Elect Stud (2015) 40:280–292. doi:10.1016/j.electstud.2015.10.001
7. Mantovani MC, Ribeiro HV, Moro MV, Picoli S, Mendes RS. Scaling laws and universality in the choice of election candidates. European Phys. Letters (2011) 96:48001. doi:10.1209/0295-5075/96/48001
8. Mantovani MC, Ribeiro HV, Lenzi EK, Picoli S, Mendes RS. Engagement in the electoral process: scaling laws and the role of political positions. Phys Rev. E (2013) 88:024802. doi:10.1103/PhysRevE.88.024802
9. Bettencourt LMA, Lobo HD, Kühnert C, West GB. Growth, innovation, scaling, and the pace of life in cities. Proc Natl Acad Sci Unit States Am (2007) 104: 7301–7306. doi:10.1073/pnas.0610172104
10. Kendall MG, Stuart A. The law of the cubic proportion in election results. Br J Sociol (1950) 1:183–196. doi:10.2307/588113
Keywords: cube-root law, assembly size, members of parliament, representatives, optimal parliament, Taagepera
Citation: Margaritondo G (2021) Size of National Assemblies: The Classic Derivation of the Cube-Root Law is Conceptually Flawed. Front. Phys. 8:614596. doi: 10.3389/fphy.2020.614596
Received: 06 October 2020; Accepted: 24 November 2020;
Published: 15 January 2021.
Edited by:
Haroldo V. Ribeiro, State University of Maringá, BrazilReviewed by:
Matjaž Perc, University of Maribor, SloveniaAngel Akio Tateishi, Federal Technological University of Paraná, Brazil
Eszter Bokanyi, Corvinus University of Budapest, Hungary
Copyright © 2021 Margaritondo. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Giorgio Margaritondo, Z2lvcmdpby5tYXJnYXJpdG9uZG9AZXBmbC5jaA==
 Giorgio Margaritondo
Giorgio Margaritondo