Stretched Exponential Dynamics in Online Article Views

Article view statistics offers a measure to quantify scientific and public impact of online published articles. Popularity of a paper in online community changes with time. To understand popularity dynamics of article views, we propose a decay dynamics based on a stretched exponential model. We find that a stretched exponent gradually decreases with time after online publication following a power-law scaling. Compared with a simple exponential or biexponential model, a stretched exponential model with a time-dependent exponent well describes long-tailed popularity dynamics of online articles. This result gives a useful insight into how popularity diminishes with time in online community.

Nowadays, many scientific journals promote online publication, which is efficient in rapidly and widely distributing scientific and public impact of scientific articles through online community. Once an open-access article is published on a journal website, the public can access the article immediately [1]. Article view statistics delivers useful statistical information of online published articles. Statistics of article page views is a useful alternative measure to quantify the impact of individual articles, independent of the journal impact factor [2–5]. Empirically, when an article receives attention, its daily page views would reach an initial peak and in turn diminish with time. We suppose that such a decay pattern in article page views would be similar to a relaxation process. On this basis, we assume there may be a popularity decay pattern for article page views, as suggested in a recent study on observations from six different PLoS journals [1]. It is a significant task to find out what mathematical model is appropriate for statistics in article page views.

In physics, a relaxation dynamics is a spontaneous evolution of out-of-equilibrium systems [6]. Glasses, for instance, usually show a relaxation dynamics toward equilibrium, which is commonly referred to as a physical aging [7]. Nonexponential relaxation dynamics, deviated from a simple exponential decay, ubiquitously appears as a relaxation dynamics in complex systems. Nonexponentiality in a relaxation dynamics is frequently described by a stretched exponential model [8–10] or the Kohlrausch-Williams-Watts (KWW) function [11, 12] (also known as the Weibull function [13]), expressed as $s=\text{exp}\left[-{\left(t/\alpha \right)}^{\beta }\right]$, where a physical quantity (s) monotonically decreases with time (t). This function is determined by two specific parameters: α is the characteristic lifetime corresponding to the specific time for $s=\text{exp}\left(-1\right)$ and β is the stretched exponent reflecting the degree of nonexponentiality (that is, the degree of deviation from the simple exponential decay). The simple exponential decay corresponds to $\beta =1$ and the classical stretched exponential decay holds in a condition of $0<\beta <1$ (here, β is an invariant constant). Particularly, the specific value of the stretched exponent β is associated with the underlying mechanism of the relaxation dynamics [7].

In this article, we utilize reliable statistical data for article page views that are available for online published articles in Scientific Reports and particularly we collect articles that were published after January 1, 2012. Data for daily page views including HTML views and PDF downloads were offered 48 h after online publication and updated daily. Here, we demonstrate a useful analysis methodology for evaluating nonexponentiality in article page views by applying the modified stretched exponential function, where the stretched exponent is modified to be time dependent and defined as $\beta \left(t\right)$ in $s=\text{exp}\left[-{\left(t/\alpha \right)}^{\beta \left(t\right)}\right]$ [14–19]. We find that the decay dynamics of article page views follows the modified stretched exponential model and particularly the stretched exponent gradually decreases with time following a power-law scaling. This finding suggests a possibility that popularity dynamics of online articles resembles a physical relaxation dynamics as can be frequently found in complex systems.

We collected the following two datasets: the first dataset comprised 42 articles from Scientific Reports published in 2012 and the second dataset comprised 19 articles published between January and May in 2015, showing more than 1,000 daily page views in a few days after online publication (see the supplementary tables). From the normalized page views described as $s=\text{exp}\left[-{\left(t/\alpha \right)}^{\beta \left(t\right)}\right]$, the characteristic lifetime α can be measured by detecting the interception point between $s\left(t\right)$ and $s\left(\alpha \right)=\text{exp}\left(-1\right)$. The estimate of the α value can be obtained from a linear regression from two neighboring data points that exist just above ($p+1$) and just below ($p-1$) the p [$\approx \text{exp}\left(-1\right)$] point for each s vs. t curve [18, 19]. The time-invariant (for the simple or the stretched exponential model) or the time-dependent stretched exponent (for the modified stretched exponential model) can be evaluated by identifying the time dependence of $\beta \left(t\right)=\text{ln}\left[-\text{ln}\left(s\right)\right]/\text{ln}\left(t/\alpha \right)$.

First, we counted the number of page views ($p_t$) at time t (days) that can be normalized by the number of initially maximized page views ($p_0$) at $t=0$. The normalized popularity is defined from the normalized page views as $s=p_t/p_0$. The initial popularity commonly decreases with time from the initial peak. For demonstration, the normalized page views for our two datasets are illustrated by the normal scales in Figures 1A,B. As seen here, the maximum peak can exist at the origin of time, indicating the initial attention, and the intermediate peaks can exist in the middle stage, indicating the intermediate attention. To examine whether the normalized page views have the power-law time dependence, we depicted the log-log plots in Figures 1C,D by respectively rescaling the normal scales in Figures 1A,B. Here, the straightness in the logarithmic scales is likely to change with time, suggesting a combination of a fast initial decay and a slow late decay. The possibility of two different time scalings is consistent with the previous observation [1]. The combination of fast and slow dynamics is manifested in the biexponential decay that is determined by two different time constants [20]. This result implies that a single power-law scaling of s vs. t is invalid in popularity dynamics of online articles.

FIGURE 1

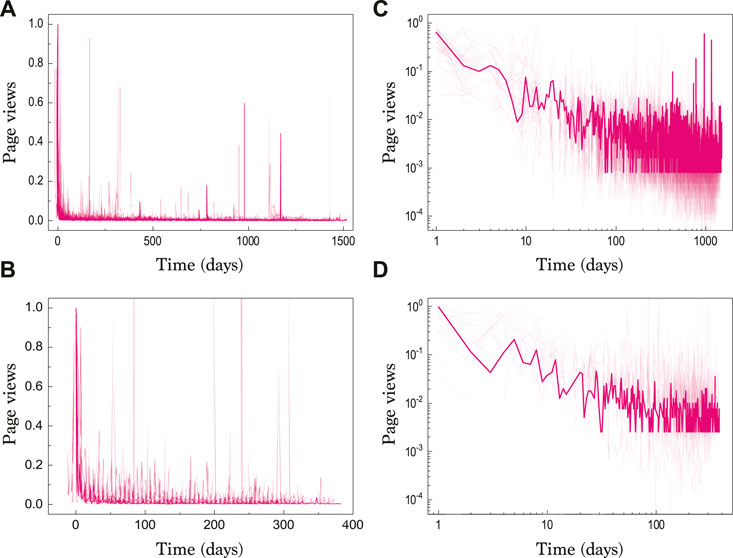
FIGURE 1. Statistics of article page views after online publication. The normalized page views are described in the normal scales (A,B) and in the lognormal scales (C,D). The first dataset is taken from 42 articles published in Scientific Reports in 2012 (A,C) and the second dataset from 19 articles published in Scientific Reports between January and May in 2015 (B,D), showing more than 1,000 views at the early stage of online publication. As a guide, the arbitrary selected data for srep00223 (A,C) and srep07971 (B,D) are marked with the solid line, respectively. Most interestingly, fast decays in the early stage and slow decays in the late stage can be observed.

Next, we tested the nonexponentiality in the normalized page views. To examine the nonexponentiality, the most feasible methodology is the application of the modified stretched exponential function $s=\text{exp}\left[-{\left(t/\alpha \right)}^{\beta \left(t\right)}\right]$. This function is quantified with the characteristic lifetime α and the time-dependent stretched exponent $\beta \left(t\right)$ [14, 15]. The modified stretched exponential function was invented to describe abnormal photoluminescence dynamics and human survival curves [16–19]. In general, the time-invariant (for the simple or the stretched exponential model) or the time-dependent stretched exponent (for the modified stretched exponential model) can be evaluated by identifying the time dependence of $\beta \left(t\right)=\text{ln}\left[-\text{ln}\left(s\right)\right]/\text{ln}\left(t/\alpha \right)$. The characteristic lifetime α can be measured by detecting the interception point between $s\left(t\right)$ and $s\left(\alpha \right)=\text{exp}\left(-1\right)$. The estimate of the α value can be obtained from a linear regression from two neighboring data points that exist just above ($p+1$) and just below ($p-1$) the p [$\approx \text{exp}\left(-1\right)$] point for each s vs. t curve [18, 19]. Here the time dependence of the stretched exponent is a good measure for testing the nonexponentiality of a decay curve and relevant to the relaxation time distribution [9].

As illustrated in Figures 2A,B, we are able to evaluate the nonexponentiality of the normalized page views for two different datasets published in Scientific Reports. Definitely, the stretched exponent significantly deviates from unity as $\beta \left(t\right)\ne 1$, indicating the nonexponentiality in the normalized popularity of online articles; that is, the simple exponential model is not valid. Most importantly, the stretched exponent decreases with time, showing a power-law time dependence for the lifetime after initial irregular changes. The long-tailed power-law time dependence of the $\beta \left(t\right)$ value can be formulated as $\beta \left(t\right)=\gamma t^{\delta }$ ($t>10$). From the representative data (srep00223 and srep07971) $t>10$, $\gamma =0.8096\pm 0.0132$ and $\delta =-0.1564\pm 0.0027$ (adj. $R^2=0.7049$) in Figure 2A and $\gamma =0.9589\pm 0.029$ and $\delta =-0.1807\pm 0.0064$ (adj. $R^2=0.7355$) in Figure 2B were estimated by a power-law fitting, as described by the bold line, respectively.

FIGURE 2

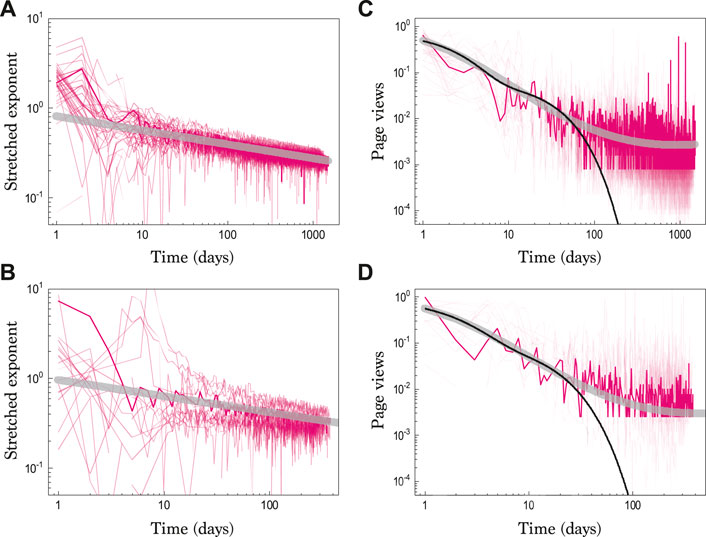
FIGURE 2. Time dependence of stretched exponents. The time-dependent stretched exponents $\beta \left(t\right)$ calculated from the normalized page views in Figure 1 show the nonexponentiality ($\beta \left(t\right)\ne 1$) and particularly the power-law time dependence as $\beta \left(t\right)=\gamma t^{\delta }$. The fitted power-law $\beta \left(t\right)$ curve is depicted by the bold line, respectively (A,B). Based on the fitting of $\beta \left(t\right)=\gamma t^{\delta }$, the normalized page views $s=\text{exp}\left[-{\left(t/\alpha \right)}^{\beta \left(t\right)}\right]$ are modeled as shown by the bold line (C,D), while the biexponential function (the black line) is inappropriate to the long-tailed popularity dynamics. For a guide, srep00223 (A,C) and srep07971 (B,D) are marked with the solid lines.

Based on the estimation for $\beta \left(t\right)=\gamma t^{\delta }$ in Figures 2A,B (the bold line), we are able to calculate the normalized page views with $s=\text{exp}\left[-{\left(t/\alpha \right)}^{\beta \left(t\right)}\right]$, which reveals the popularity dynamics of online articles. For two representative datasets, as demonstrated in Figures 2C,D, the calculated s curve (the bold line) agrees with the real data (the solid line) curve quite well, respectively. Particularly, the long-tailed popularity dynamics ($t>100$) is well described by this model.

We discuss a decay model in popularity dynamics of online articles. In fact, characterizing and modeling popularity dynamics is a difficult task, because online community consists of complex networks [21]. At any rate, popularity dynamics is likely to have a decay dynamics that consists of a short-term rapid decay and a long-tailed slow decay as expected from data in the literature [22–25]. On this basis, a recent study on article citation dynamics suggests a biexponential function, which fits the data better than the log-normal and the simple exponential models [20]. In the biexponential model, $s=A_1\text{exp}\left[-\left(t/{\tau }_1\right)\right]+A_2\text{exp}\left[-\left(t/{\tau }_2\right)\right]$, there must exist two different time constants ${\tau }_1$ and ${\tau }_2$. The coefficients $A_1$ and $A_2$ represent the relative contribution of two exponential decays. The biexponential function well explains the popularity dynamics including article citation, music, movie, and website page view for $t<100$ [20]. In Figures 2C,D, we incorporate the biexponential function to the calculated s curve (the bold line) (because of good fitting with high adj. $R^2>0.96$) instead of the real data (because of bad fitting with low adj. $R^2<0.86$). Interestingly, for short times ($t<50$), the biexponential function (the black line) is equal to our model (the bold line) but significantly deviates from the data and the modeled curve for long times ($t>50$). This analysis indicates that the biexponential decay is appropriate for the short-term dynamics but inappropriate for the long-tailed dynamics in popularity dynamics. Now, we presume that the origin of the modified stretched exponential function is a combination of multiple exponential functions that consist of multiple time constants as $s=\text{exp}\left[-{\left(t/\alpha \right)}^{\beta \left(t\right)}]\approx {{\displaystyle \sum }}^{\text{}}{A}_i\text{exp}[-\left(t/{\tau }_i\right)\right]$.

Our finding suggests that the relaxation dynamics in article page views resembles the physical relaxation dynamics as can be frequently found in complex systems. Social media are indeed complex systems that actively connect people every day. Interestingly, the temporal evolution of the stretched exponents in the normalized page views is identical in the luminescence decays, where the stretched exponents that are smaller than unity gradually decrease with time (see Refs. 14 and 15). The relaxation dynamics of public attention and physical excitation at the initial period would be alike with respect to the time evolution of impact and information propagation. A stochastic model for information propagation would be relevant to the nonexponentiality of page view statistics [1]. Our finding from selected datasets needs to be generalized from diverse datasets. Our analysis may not be suitable to describe the page view dynamics of not-so-popular articles because their peaks are weak. Further studies are required to search for a universal decay pattern in page views.

Long-time ($\sim$years) citation statistics are often alike with short-time ($\sim$days) page view statistics: there would be unpopular, popular, or revived articles (sleeping beauties) [26–28]. Scientific papers typically have a finite lifetime: their rate to attract citations achieves its maximum a few years after publication and then steadily declines [28]. The overall citation decays can be power-law or exponential [29–31]. We believe that the citation dynamics and the aging effect in citation networks [31–33] would be evaluated with the modified stretched exponential model, similar to the page view dynamics.

In conclusion, we present a useful statistical approach for article page views of online published articles. A significant finding is obtained: article page views usually decay over time after reaching initial peaks, especially exhibiting the nonexponentiality. A feasible methodology based on the stretched exponentiality is suggested for evaluation of the nonexponentiality. To understand popularity dynamics of article views, we propose a popularity decay dynamics based on a stretched exponential model. We find that a stretched exponent gradually decreases with time after online publication following a power-law scaling. Compared with a biexponential model, a stretched exponential model with a time-dependent exponent well describes long-tailed popularity dynamics of online articles. This result shows a general insight into how popularity decreases with time in online community.

Data Availability Statement

The raw data supporting the conclusions of this article will be made available by the authors, without undue reservation.

Author Contributions

YK and BW organized and conducted the research, analyzed the data, and wrote the manuscript.

Funding

This manuscript has been released as a pre-print at (https://arxiv.org/abs/1606.04972) (34). This research was supported by Basic Science Research Program through the National Research Foundation of Korea (NRF) funded by the Ministry of Education (NRF-2016R1D1A1B01007133, 2019R1A6A1A03033215) and also supported by the Korea Evaluation Institute of Industrial Technology funded by the Ministry of Trade, Industry, and Energy (20000423, Developing core technology of materials and processes for control of rheological properties of NanoInk for printed electronics) and by the MOTIE (Ministry of Trade, Industry, and Energy) in Korea, under the Fostering Global Talents for Innovative Growth Program (P0008746) supervised by the Korea Institute for Advancement of Technology (KIAT).

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Supplementary Material

The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fphy.2020.619729/full#supplementary-material

References

1. Yan KK, Gerstein M The spread of scientific information: insights from the web usage statistics in PLoS article-level metrics. PLoS One (2011) 6:e19917. doi:10.1371/journal.pone.0019917

PubMed Abstract | CrossRef Full Text | Google Scholar

2. Fox CS, Bonaca MA, Ryan JJ, Massaro JM, Barry K, Loscalzo J A randomized trial of social media from circulation. Circulation (2015) 131:28. doi:10.1161/CIRCULATIONAHA.114.013509

PubMed Abstract | CrossRef Full Text | Google Scholar

3. Gordon G, Lin J, Cave R, Dandrea R The question of data integrity in article-level metrics. PLoS Biol. (2015) 13:e1002161. doi:10.1371/journal.pbio.1002161

PubMed Abstract | CrossRef Full Text | Google Scholar

4. Feetham L Can you measure the impact of your research?. Vet. Rec. (2015) 176:542. doi:10.1136/vr.h2677

PubMed Abstract | CrossRef Full Text | Google Scholar

5. Wang X., Mao W., Xu S., Zhang C. Usage history of scientific literature: nature metrics and metrics of Nature publications. Scientometrics (2014) 98:1923–1933. doi:10.1007/s11192-013-1167-5

CrossRef Full Text | Google Scholar

6. Hodge IM. Physical aging in polymer glasses. Science (1995) 267:1945. doi:10.1126/science.267.5206.1945

PubMed Abstract | CrossRef Full Text | Google Scholar

7. Giordano VM, Ruta B Unveiling the structural arrangements responsible for the atomic dynamics in metallic glasses during physical aging. Nat. Commun. (2016) 7:10344. doi:10.1038/ncomms10344

PubMed Abstract | CrossRef Full Text | Google Scholar

8. Pavesi L, Ceschini M Stretched-exponential decay of the luminescence in porous silicon. Phys. Rev. B. (1993) 48:17625–17628. doi:10.1103/physrevb.48.17625

CrossRef Full Text | Google Scholar

9.W. Haase, and S. Wrobel, editors. Relaxation phenomena: liquid crystals, magnetic systems, polymers, high-Tc superconductors, metallic glasses. New York: Springer (2003).

CrossRef Full Text | Google Scholar

10. Yu Y, Wang M, Zhang D, Wang B, Sant G, Bauchy M Stretched exponential relaxation of glasses at low temperature. Phys. Rev. Lett. (2015) 115:165901. doi:10.1103/PhysRevLett.115.165901

PubMed Abstract | CrossRef Full Text | Google Scholar

11. Kohlrausch R. Theorie des elektrischen rckstandes in der leidener flasche. Pogg. Ann. Phys. Chem. (1854) 91:179214. doi:10.1002/andp.18541670103

CrossRef Full Text | Google Scholar

12. Williams G., Watts DC. Non-symmetrical dielectric relaxation behavior arising from a simple empirical decay function. Trans. Faraday Soc. (1970) 66:8085. doi:10.1039/tf9706600080

CrossRef Full Text | Google Scholar

13. Weibull WA. A statistical distribution function of wide applicability. J. Appl. Mech. (1951) 18:2931951

CrossRef Full Text | Google Scholar

14. Weon BM., Lee JL., Je JH. A unified decay formula for luminescence decays. J. Appl. Phys. (2005) 98:096101. doi:10.1063/1.2126120

CrossRef Full Text | Google Scholar

15. Weon BM., Je JH., Lee JL. Lifetime dispersion in a single quantum dot. Appl. Phys. A. (2007) 89:10291031. doi:10.1007/s00339-007-4239-7

CrossRef Full Text | Google Scholar

16. Weon BM, Je JH Plasticity and rectangularity in survival curves. Sci. Rep. (2011) 1:104. doi:10.1038/srep00104

PubMed Abstract | CrossRef Full Text | Google Scholar

17. Weon BM, Je JH Trends in scale and shape of survival curves. Sci. Rep. (2012) 2:504. doi:10.1038/srep00504

PubMed Abstract | CrossRef Full Text | Google Scholar

18. Weon BM. Tyrannosaurs as long-lived species. Sci. Rep. (2016) 6:19554. doi:10.1038/srep19554

PubMed Abstract | CrossRef Full Text | Google Scholar

19. Weon BM. Stretched exponential survival analysis for south korean females. Appl. Sci. (2019) 9:4230. doi:10.3390/app9204230

CrossRef Full Text | Google Scholar

20. Candia C., Jara-Figueroa C., Rodriguez-Sickert C., Barabási A-L., Hidalgo CA. The universal decay of collective memory and attention. Nat. Hum. Behav. (2019) 3:82–91. doi:10.1038/s41562-018-0474-5

PubMed Abstract | CrossRef Full Text | Google Scholar

21. Ratkiewicz J, Fortunato S, Flammini A, Menczer F, Vespignani A Characterizing and modeling the dynamics of online popularity. Phys. Rev. Lett. (2010) 105:158701. doi:10.1103/PhysRevLett.105.158701

PubMed Abstract | CrossRef Full Text | Google Scholar

22. Yeung CH, Cimini G, Jin CH Dynamics of movie competition and popularity spreading in recommender systems. Phys. Rev. E Stat. Nonlin. Soft Matter Phys. (2011) 83:016105. doi:10.1103/PhysRevE.83.016105

PubMed Abstract | CrossRef Full Text | Google Scholar

23. Abbas K, Shang M, Abbasi A, Luo X, Xu JJ, Zhang YX Popularity and novelty dynamics in evolving networks. Sci. Rep. (2018) 8:6332. doi:10.1038/s41598-018-24456-2

PubMed Abstract | CrossRef Full Text | Google Scholar

24. Wang D., Song C., Barabási A-L. Quantifying long-term scientific impact. Science (2013) 342:127–132. doi:10.1126/science.1237825

CrossRef Full Text | Google Scholar

25. Sinatra R, Wang D, Deville P, Song C, Barabási AL Quantifying the evolution of individual scientific impact. Science (2016) 354:aaf5239. doi:10.1126/science.aaf5239

PubMed Abstract | CrossRef Full Text | Google Scholar

26. Redner S Citation statistics from 110 years of physical review. Phys. Today (2005) 58:4954. doi:10.1063/1.1996475

CrossRef Full Text | Google Scholar

27. Redner S How popular is your paper? An empirical study of the citation distribution. Eur. Phys. J. B. (1998) 4:131134. doi:10.1007/s100510050359

CrossRef Full Text | Google Scholar

28. Ke Q, Ferrara E, Radicchi F, Flammini A Defining and identifying sleeping beauties in science. Proc. Natl. Acad. Sci. U.S.A. (2015) 112:7426. doi:10.1073/pnas.1424329112

PubMed Abstract | CrossRef Full Text | Google Scholar

29. Basu Hajra K., Sen P. Aging in citation networks. Physica A (2005) 346:4448. doi:10.1016/j.physa.2004.08.048

CrossRef Full Text | Google Scholar

30. Basu Hajra K., Sen P. Modelling aging characteristics in citation networks. Physica A (2006) 368:575582. doi:10.1016/j.physa.2005.12.044

CrossRef Full Text | Google Scholar

31. Wang M., Yu G., Yu D. Effect of the age of papers on the preferential attachment in citation networks. Physica A. (2009) 388:42734276. doi:10.1016/j.physa.2009.05.008

CrossRef Full Text | Google Scholar

32. Eom YH, Fortunato S Characterizing and modeling citation dynamics. PLoS One (2011) 6:e24926. doi:10.1371/journal.pone.0024926

PubMed Abstract | CrossRef Full Text | Google Scholar

33. Zeng A., Shen Z., Zhou J., Wu J., Fan Y., Wang Y, et al. The science of science: from the perspective of complex systems. Phys. Rep. (2017) 714-715:173.

CrossRef Full Text | Google Scholar

34. Kim Y., Cho K., Weon BM. Physical aging in article page views. arXiv:1606.04972 (2016).

CrossRef Full Text | Google Scholar