- 1School of Engineering and Physical Sciences, Institute of Biological Chemistry, Biophysics and Bioengineering, Heriot Watt University, Edinburgh, United Kingdom
- 2Optics and Photonics Research Group, Faculty of Engineering, University of Nottingham, Nottingham, United Kingdom
- 3School of Physics and Astronomy, University of Glasgow, Glasgow, United Kingdom
- 4Division of Biomedical Engineering, James Watt School of Engineering, University of Glasgow, Glasgow, United Kingdom
Microrheology with optical tweezers (MOT) measurements are usually performed using optical traps that are close to isotropic across the plane being imaged, but little is known about what happens when this is not the case. In this work, we investigate the effect of anisotropic optical traps on microrheology measurements. This is an interesting problem from a fundamental physics perspective, but it also has practical ramifications because in 3D all optical traps are anisotropic due to the difference in the intensity distribution of the trapping laser along axes parallel and perpendicular to the direction of beam propagation. We find that attempting viscosity measurements with highly anisotropic optical traps will return spurious results, unless the axis with maximum variance in bead position is identified. However, for anisotropic traps with two axes of symmetry such as traps with an elliptical cross section, the analytical approach introduced in this work allows us to explore a wider range of time scales than those accessible with symmetric traps. We have also identified a threshold level of anisotropy in optical trap strength of ~30%, below which conventional methods using a single arbitrary axis can still be used to extract valuable microrheological results. We envisage that the outcomes of this study will have important practical ramifications on how all MOT measurements should be conducted and analyzed in future applications.
Introduction
Optical tweezers (OT), first introduced by Ashkin et al. [1], exploit a tightly focussed laser beam with high intensity gradient to trap and move micro and nano-sized dielectric objects in 3D, by harnessing both the gradient and scattering forces. When calibrated, OT are exceptionally sensitive transducers capable of measuring forces in the pico-Newton range. Therefore, scientists have adopted them to study a wide range of physical and biophysical phenomena including molecular binding forces [2], organelle transport [3], flagellar motion [4], the mechanical properties of DNA [5], molecular motors [6, 7] and polymerases [8, 9], and the diffusion of proteins [10].
Another successful application of optical tweezers is in the field of “hybrid” microrheology, whereby an optically trapped bead acts as a probe, revealing the thermal fluctuations of the molecules in the suspending fluid. Microrheology with OT (MOT) has been used with growing popularity to study the rheology of complex biological materials such as the vitreous humor [11], biopolymer networks [12], and extracellular secretions from phytoplankton [13] at the microscale.
The physical principles underpinning MOT rely on the assumption that the probe bead is trapped within a symmetric quadratic potential of the form , where r is the displacement from the center of the trap and κ is the trap stiffness. The restoring force experienced by a trapped bead is thus given by F(r) = −κrr. Due to the thermal fluctuations of the molecules of the suspending fluid, the weakly trapped particle experiences Brownian motion and can randomly move away from the equilibrium position, which is usually coincident with the trap center. The statistical mechanics analysis of the particle dynamics can be exploited to calculate both the trap stiffness [14] and the linear micro-rheology properties of the medium surrounding the bead [15, 16].
At this point, it is important to remember that the strength of the trapping force is governed by the optical properties of both the bead and the suspending medium, and also by the intensity distribution of the laser beam in all 3 dimensions. The trapping force is therefore sensitive to any optical aberration in the instrument [17]. The dominant aberrations seen in optical instruments that can be described by primary Zernike polynomials are: (i) spherical aberration, (ii) coma, (iii) astigmatism, (iv) curvature of field, (v) distortion, and (iv) defocus. Of these, astigmatism and coma result from the optical path not being centered and have been shown to alter the ratio of trap stiffness along the two lateral axes, x and y perpendicular to the direction of beam propagation [17]. Spherical aberrations, field curvature and distortion have been shown to affect the axial position of the trap; but, while the first has a significant effect on trap stiffness along the two lateral axes, the latter two do not change its strength [18]. It is thus a common experience for researchers to spend a significant amount of time and effort at the start of any MOT measurement performing a series of alignment procedures to remove such aberrations and ensure an isotropic intensity distribution of the trapping beam in the x-y image plane. Adaptive optics (AO) methods exist for correcting aberrations and include the use of deformable membrane mirrors (controlled using an array of piezoelectric actuators) [19] and liquid crystal spatial light modulators (SLM) [20]. An SLM is a convenient choice when applied to a holographic optical tweezers (HOT) system where the aberrations can be corrected by using the same SLM that is used to control the position of the trap. Shack-Hartmann sensors can be used in combination with SLMs for providing a feedback loop to correct for aberrations in OT systems [20, 21], or can be simply controlled by adding the appropriate Zernike polynomials to the phase mask applied to the SLM [22]. Another means of deliberately introducing a degree of anisotropy to the optical trap is by exploiting the orientation of the linear polarization of the trapping beam [23, 24].
However, AO approaches can be time consuming and complex to implement, and many OT systems will not include these specialized features. Therefore, it is useful to identify an acceptable degree of anisotropy in an optical trap below which accurate MOT results can still be ensured. Moreover, when analyzing the 3D trajectory of an optically trapped probe bead, a degree of trap anisotropy is unavoidable because the point spread function is broader along the axial (z) direction than the lateral (x or y) directions. This is a consequence of the defocus aberration. With the development of new tools to perform microrheology in 3D [25], it is important to consider how this anisotropy may affect results.
Therefore, from a rheological perspective, it is useful to consider how microrheology measurements are affected by optical traps that are anisotropic, or even lacking an axis of symmetry. In this work, by using data from three different labs (and thus three different OT systems) alongside simulations, we have explored how to correctly extract the rheological properties of the suspending media from the statistical mechanics analysis of the trajectory of a probe particle confined within an anisotropic optical trap.
Materials and Methods
Experimental
The experimental data were collected independently from three different labs, each equipped with a different OT system. The labs are based at the University of Glasgow, University of Nottingham and Heriot Watt University.
OT System 1
The University of Glasgow (UoG) lab used an OT system based on a continuous wave, diode pumped solid state (DPSS) laser (Ventus, Laser Quantum), which provided up to 3 W at 1,064 nm. A nematic liquid crystal spatial light modulator (SLM) (BNS, XY series 512 × 512) was used to create the desired arrangement of optical traps and was also used to control the individual trap shape. The laser entered a custom-made inverted microscope which uses the same microscope objective lens (Nikon, 100x, 1.3 NA) to both focus the trapping beam and to image the thermal fluctuations of 5 μm diameter silica beads (Bangs Laboratories). Samples were mounted on a motorized microscope stage (ASI, MS-2000). A complementary metal-oxide semiconductor (CMOS) camera (Dalsa, Genie HM 1024 GigE) acquired high-speed images of a reduced field-of-view. These images were processed in real-time at up to ~3 kHz to calculate the center of mass of the bead using particle tracking software developed using LabVIEW (National Instruments), running on a standard desktop PC [22, 26].
OT System 2
At the University of Nottingham optical trapping was achieved by means of a continuous wave 1,064 nm 3 W DPSS laser (Ventus, Laser Quantum). The beam path was directed into an inverted microscope body (Eclipse Ti; Nikon) and focused using a high NA objective lens (Nikon, 100x, 1.3 NA). The same objective lens was used to collect images of the trapped polystyrene microspheres (Cat. No. 19814; Polysciences Inc.), in wide-field with illumination in transmission. Thermal fluctuations of the trapped polystyrene microspheres measuring 1.93 ± 0.05 μm in diameter, were detected using a fast CCD camera (DALSA Genie; Teledyne Technologies International Corp) at 600 Hz. Similar to Glasgow, particle tracking software written in LabVIEW (version 2013 32bit, National Instruments) was used to record the time-dependent position of the trapped microspheres in real time [26].
OT System 3
At Heriot Watt University optical trapping was achieved by means of a 1,064 nm laser (Opus, Laser Quantum). The beam path was directed into an inverted microscope body (IX73; Olympus) and focused using a high NA objective lens (Olympus, 60x, 1.2 NA). As with the Glasgow and Nottingham systems, this objective lens was also used to collect images of the trapped polystyrene microspheres in wide-field with transmission illumination. Thermal fluctuations of the polystyrene microspheres (Cat. No. 35-2B; Thermo Scientific Fluoromax), were detected using a CMOS camera (Orca Flash 4.0, Hamamatsu) at ~66 Hz. To obtain the z-coordinates of trapped beads a multiplane imaging system was employed [25]. In summary, a relay system was built between the microscope and camera, and a pair of curved diffraction gratings were placed at the telecentric position. This segmented the image into nine sub-images, each imaging a different depth in the sample. A full description of the systems may be found in references [27, 28]. Images were captured and saved using micromanager, then processed using Matlab (Matlab 2019b, MathWorks, Natick MA) [25].
Anisotropy
In system 1, an SLM was used to control both the position and shape of the optical trap. Here, patterns displayed on the SLM imparted an arbitrary phase function to the reflected light beam. Simple gratings effectively control the lateral position of the trap while anisotropy is introduced by the addition of astigmatism (using Zernike polynomials). In systems 2 and 3 anisotropy in the x-y plane resulted from slight, unintentional misalignments in the trapping optics within each system, which are generally present in all OT experiments. The anisotropy in the x-z plane, recorded by system 3, is an inevitable consequence of the defocus aberration, which causes the intensity distribution of a focal spot to extend further in the axial direction than in the lateral direction.
Computational Simulations
Simulations were carried out in Matlab (Matlab 2019b, MathWorks, Natick MA), and based on a modified version of code developed to model in 2D the trajectory of a bead trapped in a harmonic potential [29]. To summarize, the input parameters were temperature (T), bead radius (a), number of time-steps (N), frame rate (f), the optical trap strengths along the semi-major and semi-minor axes of the trap and , and the angle ϕ between the x' axis and the Cartesian x axis, as shown in Figure 1. A thermal velocity distribution is seeded such that it conforms to Maxwell-Boltzmann statistics. The velocity along the x and y axes due to the trap force is calculated iteratively and assumes that the bead will accelerate until it reaches a velocity such that drag force and trapping force will be balanced.
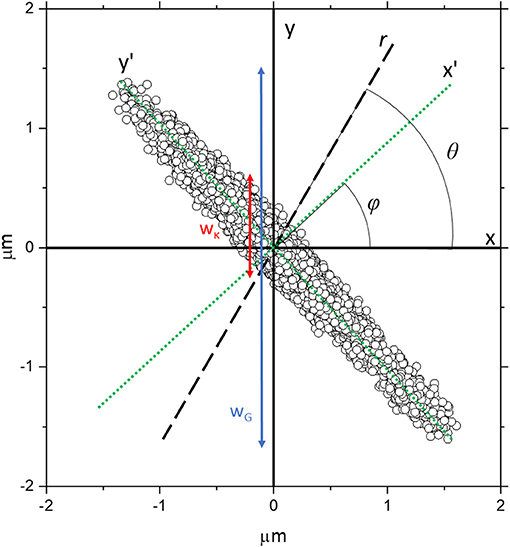
Figure 1. The trajectory obtained from the simulation of a bead confined within a highly asymmetric optical trap, with trap stiffnesses = 1 × 10−6 Nm−1 and = 1 × 10−8 Nm−1 along the x' and y' axes, respectively (green dotted lines), which are rotated by an angle ϕ relative to the Cartesian x and y axes. The black dashed line is an arbitrary direction r along which the analysis is being carried out and it is orientated at an angle θ from the x axis. The red line represents a rough estimate of wκ, the spread of particle coordinates due to the strength of the trap projected along y, whereas the blue line represents wG which is a rough estimate of the spread of particle coordinates projected along y due to the geometry of the trap.
In order to generate trajectory data akin to that of a particle trapped within a symmetric isotropic trap, we simply set = . In order to generate trajectories that are not aligned along the principal Cartesian axes, we set ϕ ≠ 0 and define the principal axes of the trap as x' = xcos ϕ + ysin ϕ and y' = ycos ϕ – xsin ϕ and calculate forces accordingly. For symmetric but anisotropic data with two axes of symmetry (e.g., with an ellipsoidal shaped scatter plot), we set ≠ . To generate traps that have <2 axes of symmetry we split the simulation into four quadrants, and set and independently in each quadrant, such that the restorative force acting on the bead varies depending on which quadrant of the bead enters.
Analysis
For both simulated and experimental data, we have performed rotational coordinate transformations to resample the bead trajectories multiple times as a function of the rotation angle θ. We have then calculated the normalized mean squared displacement (NMSD) for each of these data sets as a function of the lag-time (τ). From the analysis of the NMSD(τ) it is possible to determine the fluid's microrheological properties. The correct way to do this is the focus of this paper and is discussed hereafter.
Results and Discussion
Determining a Fluid's Viscosity From an Anisotropic Optical Trap
A means for measuring the suspending fluid viscosity (η) from an MOT measurement is to use Equation 1, which has been obtained by solving a generalized Langevin equation for a confined object undergoing Brownian motion within a symmetric quadratic potential [15]:
where NPAF(τ,r) is the normalized position autocorrelation function of the particle and NMSD(τ,r) is its normalized mean-squared-displacement, both evaluated along a direction r and as a function of the lag-time τ. The decay constant in Equation 1 is defined as follows:
Where a is the bead radius and κr is the trap strength in the direction defined by the vector, r. The trap strength can be calculated by applying the principle of equipartition of energy:
where kB is Boltzmann's constant, T is absolute temperature and <r2> is the variance in the bead position along the vector r. This approach has proved to be a very effective means for extracting the fluid viscosity when analyzing the 2D trajectory of a bead confined within a symmetric trap with a circular cross-section where only r = x or r = y are analyzed [15]. Interestingly, it is not clear in the literature whether this approach will be as effective when dealing with an OT system where the trap strength is anisotropic and the axes of maximum and minimum trap strength are not aligned along the Cartesian system of coordinates x and y; like the case shown in Figure 1. This latter represents an extreme case of an anisotropic trap that would not commonly be used in real MOT experiments, but it is simulated here to highlight any possible shortcomings of the analytical model introduced in this work to characterize asymmetric traps.
From data like those shown in Figure 1, one can calculate the variance of the bead displacement along the coordinate defined by the arbitrary axis r, i.e., <r2>, as plotted using circle symbols in Figure 2A and determine the trap strength via Equation 3 as function of the angle θ, as shown with circle symbols in Figure 2B. In the same diagrams we report two different fits whose derivation will be discussed later in the text. In Figure 2C we plot the relative viscosity (defined as the ratio between the calculated viscosity to that input into the simulation ηrel = η/ηinput) as a function of the angle θ as obtained by means of Equation 1 applied to the NPAF data. Interestingly, it can be seen that the relative viscosity strongly deviates from the value of one as θ is varied. This is inconsistent with the assumptions made in the model used for generating the simulated trajectory, which is based on a Newtonian fluid with a constant, isotropic viscosity. Therefore, these results demonstrate that the widely-used analytical method introduced by Tassieri et al. [15] is not applicable to study trajectories acquired from a highly asymmetric OT.
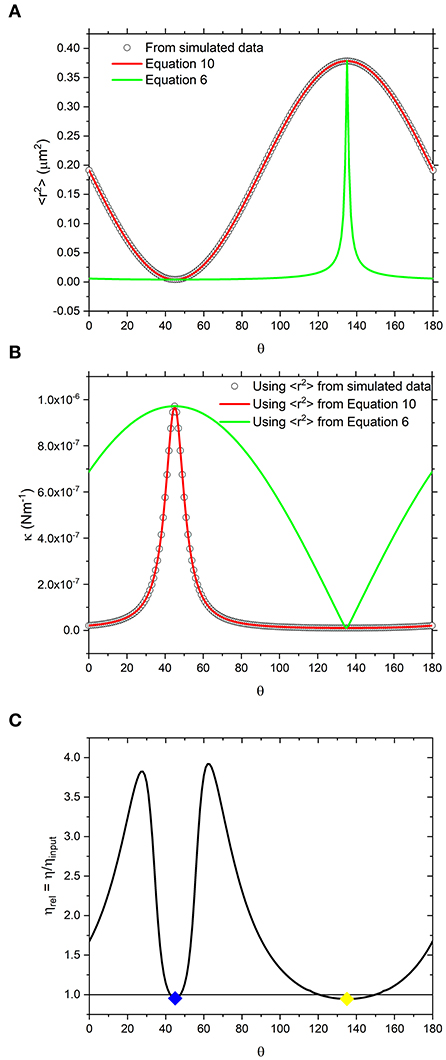
Figure 2. (A) White circles are values of <r2> obtained directly from simulated data shown in Figure 1, resampled at increments of Δθ = 1°. Alongside are lines representing the values calculated using equation 10 which is derived from the trap geometry (red) and equation 6 which is derived from a vector analysis of the forces acting on the bead (green). (B) the same as (A) but using the <r2> values reported in a) to calculate κ using equation 3. (C) Relative viscosity values obtained by fitting NPAF plots to equation 1. Blue and yellow diamonds are the values of relative viscosity, calculated at 45 and 135° which are the axes along which <r2> is minimized and maximized, respectively.
In order to elucidate such results, we have plotted the particle NMSD as function of the lag-time along different directions for the simulated data, as shown in Figure 3A. From the latter it is apparent that when r is aligned along x' and y', the curves return a single-exponential growth of the form of 1-exp(−λrτ), typical of symmetric traps. However, at intermediate angles, the curves show a multimodal growth. Hence, the erroneous estimation of the relative viscosity of the suspending fluid when using Equations 1–3. This is further corroborated graphically in Figure 3B, where the NPAFs evaluated from the simulated data (symbols) are compared against those calculated via Equation 1 (lines), with κr determined via Equation 3.
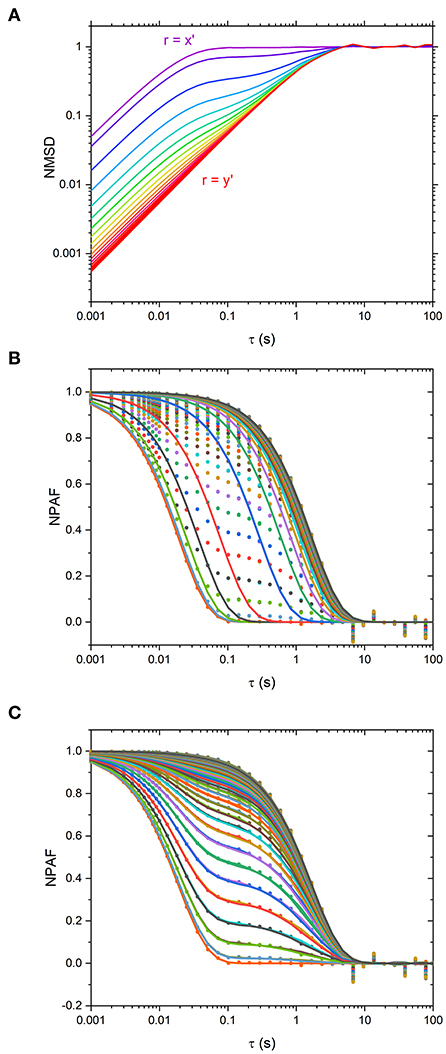
Figure 3. (A) Normalized mean squared displacement (NMSD) simulated data plotted at Δθ = 5° intervals from θ-ϕ = 0 o (purple, r = x' axis) to θ−ϕ = 90 o (red, r = y' axis). Traces are colored such that purple traces are aligned along x' and red aligned along y'. (B) Normalized Position Autocorrelation Function (NPAF) simulated data (dots) and fits to equation 1, the mono-exponential expression for NPAF, plotted at Δθ = 1° intervals (lines). (C) the same as in (B) but with fits to the multi-exponential expression for NPAF, Equation 15.
In order to understand why Equations 1 and 2 do not yield results that accurately describe the simulated data, we have considered the total restorative force acting on the trapped bead along a generic direction r:
Which implies,
If Equation 5 is combined with the expression for potential energy in an optical trap, , one can plot iso-potential lines (i.e., contour lines where the potential energy in the trap is constant) to better understand the shape of the trap. In Figure 4, we report the iso-potential line for E = kBT for the trap shown in Figure 1, along with an isotropic trap having the same mean trap strength.
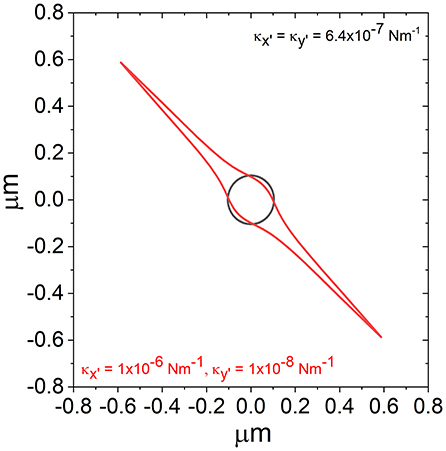
Figure 4. Iso-potential lines over which , for a trap of the same form as that shown in Figure 1 (red) and a trap with the same average value of κ but isotropic (black).
From Figure 4, it is possible to see that, while the iso-potential line for the isotropic trap (black) is isotropic, the iso-potential contour for the anisotropic trap is highly anisotropic. From looking at the scatter plot in Figure 1 it may be assumed that the potential is elliptical based on the shape produced by the simulated data points. However, while the scatter plot does not reveal the real density of the distribution of points in proximity of the trap center; the iso-potential lines better illustrates the actual shape of the trap, which is not elliptical, but is actually sharply pointed along the axis where the trap is weakest.
Although κ is difficult to directly observe experimentally, we can use the form of κ given in equation Equations 3 and 5 to obtain an expression of the variance as function of angle and trap stiffnesses:
where κx′ = kBT/<r2>min and κy′ = kBT/<r2>max. Interestingly, as shown by the green lines in Figures 2A,B, it is possible to see that Equation 6 does not reproduce the κ nor <r2> values obtained from the simulation.
To see why this is the case, let us now consider the variance of a particle trajectory by taking the coordinate aligned along an arbitrary direction r, such that:
and thus,
If expanded, the latter becomes:
It can be demonstrated both theoretically and experimentally that the third term on the right side of Equation 9 is negligible for most real experimental cases, and certainly null in the case of optically trapped beads suspended in a Newtonian fluid, whose dynamics are explored at time and length scales longer than nanoseconds and nanometers, respectively. Therefore, Equation 9 can be simplified as follows:
When Equation 10 is compared to the simulated data as shown in Figure 2A (red curve), the agreement is apparent. Notably, the κ values calculated using <r2> obtained by means of Equation 10 (red curve) instead of Equation 6 (green curve) are also in agreement with the data as shown in Figure 2B.
This demonstrates the crux of the problem; in MOT experiments it is difficult to directly evaluate the forces experienced by the bead and often researchers rely on the variance <r2> to act as a proxy measurement that can be fed into Equation 3 to determine κ. However, when a highly anisotropic trap is aligned such that sampling isn't along its semi-major or semi-minor axes (x' and y'), the <r2> values of the bead trajectory are greatly enlarged due to the geometry of the trap. Visually, this is probably best understood by looking at Figure 1, where the spread of data points due to the restorative force of the trap along y (wκ) is shown with a red arrow alongside the spread of data points due to the geometry of the trap along y shown by the blue arrow (wG). It follows that the variance measured along y [< r(θ = 90)2 >] will be approximately proportional to wG, whereas wκ will be approximately proportional to the value predicted by Equation 6. It is apparent that these will give significantly different values of <r2>.
By carefully considering the geometry of the optical trap, it is possible to still accurately describe the normalized position autocorrelation function. Let us consider the expression of the particle NPAF for an arbitrary direction r:
The numerator can be expanded as follows:
Thus,
where ax′ is the particle position autocorrelation function not normalized by the variance, such that
and cx′y′ is the cross-correlation function between the particle coordinates x' and y'. The denominator in Equation 11 can then be expressed by means of Equation 10; which gives,
We can obtain decay constant and by fitting Equation 1 along the axes where <r2> are minimized or maximized, then re-express Equation 14 as follows,
In Figure 3C are the NPAF values obtained using Equation 15 alongside the data obtained from simulations. It is apparent that Equation 15 describes the data very well-compared to the fit performed via Equation 3, as shown in Figure 3B.
At this point it is important to remember that numerous microrheology studies in literature have yielded excellent and accurate microrheological information without doing a full analysis of trap geometry even though, as discussed in the introduction, in real experiments it would be unusual for an optical potential to be perfectly isotropic due to slight optical aberrations. This suggests the existence of a degree of trap anisotropy below which measurements are unaffected. Therefore, it would be of interest to a broad audience of biophysicists and microrheologists to understand what level of anisotropy in an optical trap will result in an erroneous measurement of the fluid viscosity and thus require improvements in the beam shape or alignment, or the implementation of AO approaches we discussed earlier. In order to address this query, in Figure 5 we report the percentage anisotropy in the measured viscosity, ηanisotropy, as a function of percentage anisotropy in κ, κanisotropy, obtained using three different experimental OT systems. These measurements were carried out using a range of different values of , bead radius, a, number of time steps, N, and acquisition rate, f. As these data are somewhat sparse in themselves, simulations were also carried out with the input values derived from each of the experimental studies. The simulation outputs are also shown in the same figure using lines of the same color as the corresponding experimental data. For each simulated data set, these parameters remain constant while the input value of is varied. From Figure 5 it is possible to observe that for κanisotropy values lower than ~30%, the precise value of ηanisotropy differs for each of the different sets of simulations, but for all three sets ηanisotropy appears to be independent of κanisotropy in this <30% region. Therefore, Equation 1 is still a valid approach for microrheology purposes. This is not the case for anisotropy values higher than ~30%, where ηanisotropy increases proportionally to κanisotropy, and at which point the experimentalist may wish to improve the alignment of their system. Notably, the experimental data (solid symbols) in Figure 5 are in good agreement with those from simulations, especially for the data obtained from systems two and three. Interestingly, the experimental data obtained from system 1 appear to be offset compared to the simulations. We must admit that it is unclear to us what is the precise cause of this off-set; however, the behavior of the data is still consistent with a model where κanisotropy only has a strong effect on ηanisotropy at values above ~30%, as suggested by the simulations.
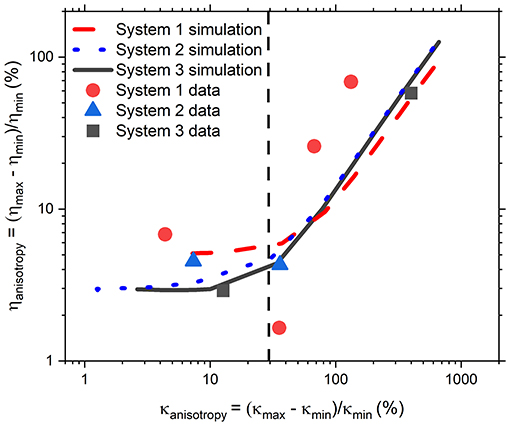
Figure 5. Anisotropy in η as a function of anisotropy in κ from experiments (filled symbols) and simulations (lines). Simulations were carried out to match the frame rate, temperature, bead size, and run length of the data from System 1 (experimental results red circles, simulations red dashed line), System 2 (experimental results blue triangles, simulations blue dotted line), and System 3 (experimental results black squares, simulations black solid line). Black dashed line is a rough judge of the level below which anisotropy in κ will have a discernible effect on the anisotropy in η.
Although we have identified a threshold level of anisotropy in κ below which microrheology measurements could be safely performed without performing a full rotational analysis of the trap, it is worth bearing in mind that sometimes levels of anisotropy above 30% are unavoidable. This is indeed the case when measurements are performed with OT in 3D where optical traps are highly anisotropic, due to the stretching of the intensity distribution of the laser along the axial or “z” dimension. Therefore, for 3D microrheology measurements, one would inevitably need to perform a full rotational analysis if the direction of trap beam propagation slightly deviates from the axis of z-tracking. Furthermore, the use of a highly anisotropic trap has the added advantage of exploring a wider range of low frequencies, as can be deduced from Figure 3A where the plateau region of the NMSD is achieved at longer times for the axis showing the weaker trap stiffness (y'). We could therefore speculate that this opens the door to the possibility of deliberately introducing anisotropy into the x-y plane to gain additional information on the viscoelastic properties of the surrounding medium. For scatter plots that have 2 axes of symmetry (such as the one shown Figure 1) the solution is straightforward. One could rotate the data by 180 degrees, sampling at regular increments of the angle θ, and find the axes for which <r2> is maximized and minimized. As shown in Figures 2B,C, at the angles where <r2> is maximized and minimized (i.e., 45 and 135° in this case), Equation 6 and Equation 10 return the same result because the NMSD curve is a single-exponential growth to a limit of the form 1- e−λτ, as shown in Figure 3C). The resulting ηrel values are marked as blue and yellow dots on Figure 2C), giving 95.3 and 94.5% of the expected value, respectively.
Optical Traps With One or Zero Axes of Symmetry
In this section, we focus our attention to optical traps which feature only 1 or 0 axes of symmetry. In practice, experimentalists should be able to avoid performing measurements where the trap shows such a degree of anisotropy. However, it is still of interest to understand these as they are the most general case from a phenomenological perspective. In this instance, we have used simulated data to explore the anisotropy, as this allowed us to control the degree of asymmetry of the trap in a systematic manner. However, in real experiments, scatter plots with a similar shape could be generated by (i) deliberately or otherwise introducing optical aberrations to the trap beam, (ii) passing the beam through a highly inhomogeneous media, or (iii) spatially filtering the trap beam. Simulated scatter plots from optical traps with a single axis of symmetry along the x-axis are shown in Figures 6A,B. In Figures 6D,E we plot <r2> and ηrel as a function of θ for these traps.
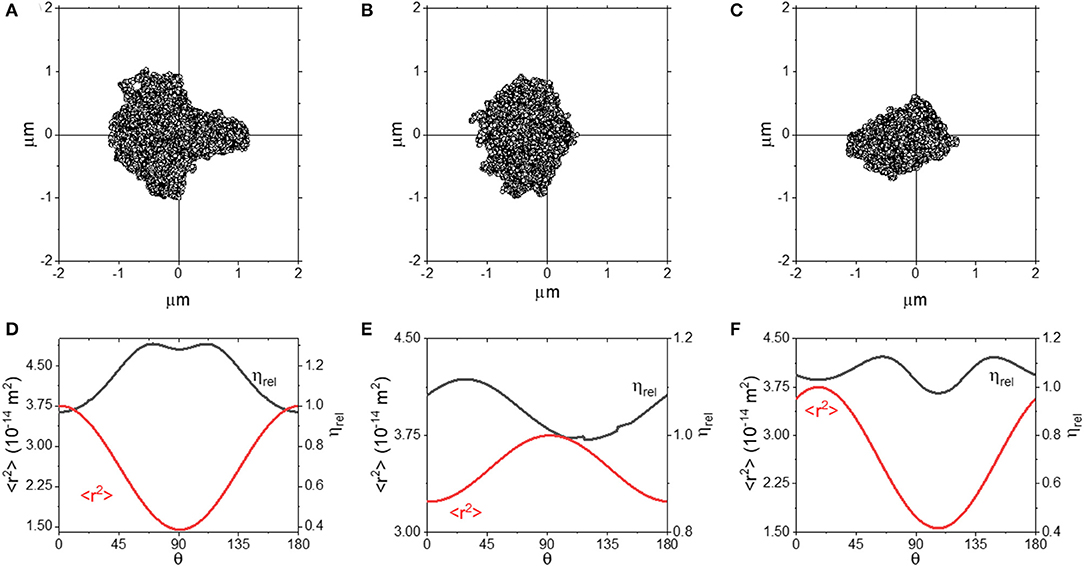
Figure 6. (A–C) Scatter plots for optical traps with 1 (A,B) or 0 (C) axes of symmetry. (D–F) plots of <r2> and ηrel as a function of θ for the plots shown in (A–C).
From Figure 6, we can see that both the scatter plots in (A) and (B) have an axis of symmetry running along the x axis, but are asymmetric in the y-axis. In both the cases, the ηrel curves are smooth and continuous, with a slight discontinuity in Figure 6E) around ~135°, most likely due to a slight quirk of the scatter plot distribution. Interestingly, we observe that ηrel is ~1 when <r2> is at its maximum, but not when <r2> is at its minimum, where ηrel is over-estimated by up to ~25%. We explore this approach further in Figures 6C,F, where we report the outcomes obtained from a trap with no axis of symmetry. We see that when measurements are performed along the direction where <r2> is maximized, ηrel is close to 1, and interestingly the same result is achieved also at the angle where <r2> is minimized. These results suggest that even by using an optical trap with significant aberrations, accurate microrheology would be achievable when a full rotational analysis is carried out and the axis of maximum <r2> is identified.
Conclusion
In this work, we have demonstrated that highly anisotropic optical traps may return spurious microrheology results if the shape of the trap is not considered carefully. Nonetheless, when performing a detailed analysis of the bead variance in all the possible directions of motion of the trapped particle, it is possible to successfully extract fluids' viscosity. In particular, we have demonstrated that, as long as the difference in optical trap strength between strongest and weakest axis remains lower than ~30% of the weakest trap strength, the conventional analytical approaches would still return an accurate measurement of the fluid viscosity with the stochastic nature of the measurement dictating the accuracy. This is not true anymore when the threshold is exceeded. For this case, we have provided a novel analytical model that allows an accurate measurement of the fluids' rheological properties over a wider range of accessible frequencies than symmetric optical traps.
Data Availability Statement
The raw data supporting the conclusions of this article will be made available by the authors, without undue reservation.
Author Contributions
MT and AM derived the analytical expressions. Simulations were carried out by AM. AM led the writing of the paper, but all authors contributed to the interpretation of results and contributed to the manuscript. The project was conceived and led by MT. All authors contributed to building the experimental systems, collecting data, and data analysis.
Conflict of Interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Acknowledgments
We acknowledge support via EPSRC grant Experiencing the micro-world - a cell's perspective (EP/R035067/1 – EP/R035563/1 – EP/R035156/1). MT and GG would like to thank Miles Padgett for his support and useful discussions. We also would like to acknowledge the immense contribution to this field of the late Arthur Ashkin, who sadly passed away while this paper was in preparation.
References
1. Ashkin A, Dziedzic JM, Bjorkholm JE, Chu S. Observation of a single-beam gradient force optical trap for dielectric particles. Opt Lett. (1986) 11:288–90. doi: 10.1364/OL.11.000288
2. Glass DG McAlinden N Millington OR Wright AJ. A minimally invasive optical trapping system to understand cellular interactions at onset of an immune response. PLoS ONE. (2017) 12:e0188581. doi: 10.1371/journal.pone.0188581
3. Ashkin A, Schutze K, Dziedzic JM, Euteneuer U, Schliwa M. Force generation of organelle transport measured in vivo by an infrared laser trap. Nature. (1990) 348:346–8. doi: 10.1038/348346a0
4. Block SM, Blair DF, Berg HC. Compliance of bacterial flagella measured with optical tweezers. Nature. (1989) 338:514–18. doi: 10.1038/338514a0
5. Wang MD, Landick R, Gelles J, Block SM. Stretching DNA with optical tweezers. Biophys J. (1997) 72:1335–46. doi: 10.1016/S0006-3495(97)78780-0
6. Svoboda K, Schmidt CF, Schnapp BJ, Block SM. Direct observation of kinesin stepping by optical trapping interferometry. Nature. (1993) 365:721–7. doi: 10.1038/365721a0
7. Finer JT, Simmons RM, Spudich JA. Single myosin molecule mechanics: piconewton forces and nanometre steps. Nature. (1994) 368:113–9. doi: 10.1038/368113a0
8. Yin H, Wang MD, Svoboda K, Landick R, Block SM, Gelles J. Transcription against an applied force. Science. (1995) 270:1653. doi: 10.1126/science.270.5242.1653
9. Wang MD, Schnitzer MJ, Yin H, Landick R, Gelles J, Block SM. Force and velocity measured for single molecules of RNA polymerase. Science. (1998) 282:902. doi: 10.1126/science.282.5390.902
10. Oddershede L, Dreyer JK, Grego S, Brown S, Berg-Sorensen K. The motion of a single molecule, the λ-receptor, in the bacterial outer membrane. Biophys J. (2002) 83:3152–61. doi: 10.1016/S0006-3495(02)75318-6
11. Watts F, Tan LE, Wilson CG, Girkin JM, Tassieri M, Wright AJ. Investigating the micro-rheology of the vitreous humor using an optically trapped local probe. J Opt. (2013) 16:015301. doi: 10.1088/2040-8978/16/1/015301
12. Ashworth JC, Thompson JL, James JR, Slater CE, Pijuan-Galito S, Lis-Slimak K, et al. Peptide gels of fully-defined composition and mechanics for probing cell-cell and cell-matrix interactions in vitro. Matrix Biol. (2020) 85–86:15–33. doi: 10.1016/j.matbio.2019.06.009
13. Guadayol Ò, Mendonca T, Segura-Noguera M, Wright AJ, Tassieri M, Humphries S. Microrheology reveals microscale viscosity gradients in planktonic systems. Proc Natl Acad Sci USA. (2020) 118:e2011389118. doi: 10.1073/pnas.2011389118
14. Berg-Sørensen K, Flyvbjerg H. Power spectrum analysis for optical tweezers. Rev Sci Instruments. (2004) 75:594–612. doi: 10.1063/1.1645654
15. Tassieri M, Giudice FD, Robertson EJ, Jain N, Fries B, Wilson R, et al. Microrheology with Optical Tweezers: measuring the relative viscosity of solutions ‘at a glance'. Sci Rep. (2015) 5:8831. doi: 10.1038/srep08831
16. Tassieri M, Evans RML, Warren RL, Bailey NJ, Cooper J. Microrheology with optical tweezers: data analysis. N J Phys. (2012) 14:115032. doi: 10.1088/1367-2630/14/11/115032
17. Roichman Y, Waldron A, Gardel E, Grier DG. Optical traps with geometric aberrations. Appl Opt. (2006) 45:3425–9. doi: 10.1364/AO.45.003425
18. Dutra RS, Viana NB, Maia Neto PA, Nussenveig HM. Absolute calibration of optical tweezers including aberrations. Appl Phys Lett. (2012) 100:131115. doi: 10.1063/1.3699273
19. Müllenbroich CM, McAlinden N, Wright AJ. Adaptive optics in an optical trapping system for enhanced lateral trap stiffness at depth. J Opt. (2013) 15:075305. doi: 10.1088/2040-8978/15/7/075305
20. Bowman RW, Wright AJ, Padgett MJ. An SLM-based Shack–Hartmann wavefront sensor for aberration correction in optical tweezers. J Opt. (2010) 12:124004. doi: 10.1088/2040-8978/12/12/124004
21. López-Quesada C, Andilla J, Martín-Badosa E. Correction of aberration in holographic optical tweezers using a Shack-Hartmann sensor. Appl Opt. (2009) 48:1084–090. doi: 10.1364/AO.48.001084
22. Bowman RW, Gibson GM, Linnenberger A, Phillips DB, Grieve JA, Carberry DM, et al. “Red Tweezers”: fast, customisable hologram generation for optical tweezers. Comp Phys Commun. (2014) 185:268–73. doi: 10.1016/j.cpc.2013.08.008
23. Dutra RS, Viana NB, Maia Neto PA, Nussenzveig HM. Polarization effects in optical tweezers. J Opt A Pure Appl Opt. (2007) 9:S221–7. doi: 10.1088/1464-4258/9/8/S15
24. So J, Choi JM. Tuning the stiffness asymmetry of optical tweezers via polarization control. J Korean Phys Soc. (2016) 68:762–7. doi: 10.3938/jkps.68.762
25. Matheson AB, Paterson L, Wright AJ, Mendonca T, Tassieri M, Dalgarno PA. Optical Tweezers with Integrated Multiplane Microscopy (OpTIMuM) – a new tool for 3D microrheology. Sci Rep. (2021) 11:5614. doi: 10.1038/s41598-021-85013-y
26. Gibson GM, Leach J, Keen S, Wright AJ, Padgett MJ. Measuring the accuracy of particle position and force in optical tweezers using high-speed video microscopy. Opt Exp. (2008) 16:14561–70. doi: 10.1364/OE.16.014561
27. Djidel S, Gansel JK, Campbell HI, Greenaway AH. High-speed, 3-dimensional, telecentric imaging. Opt Exp. (2006) 14:8269–77. doi: 10.1364/OE.14.008269
28. Dalgarno PA, Dalgarno HI, Putoud A, Lambert R, Paterson L, Logan DC, et al. Multiplane imaging and three dimensional nanoscale particle tracking in biological microscopy. Opt Exp. (2010) 18:877–84. doi: 10.1364/OE.18.000877
Keywords: microrheology, optical trapping, anisotropy, optical tweezers, simulations
Citation: Matheson AB, Mendonca T, Gibson GM, Dalgarno PA, Wright AJ, Paterson L and Tassieri M (2021) Microrheology With an Anisotropic Optical Trap. Front. Phys. 9:621512. doi: 10.3389/fphy.2021.621512
Received: 26 October 2020; Accepted: 15 March 2021;
Published: 16 April 2021.
Edited by:
Michael W. Berns, University of California, Irvine, United StatesReviewed by:
Qian Sun, Nankai University, ChinaElliot Botvinick, Beckman Laser Institute and Medical Clinic, United States
Copyright © 2021 Matheson, Mendonca, Gibson, Dalgarno, Wright, Paterson and Tassieri. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Andrew B. Matheson, YS5tYXRoZXNvbkBody5hYy51aw==; Manlio Tassieri, bWFubGlvLnRhc3NpZXJpQGdsYXNnb3cuYWMudWs=
 Andrew B. Matheson
Andrew B. Matheson Tania Mendonca
Tania Mendonca Graham M. Gibson3
Graham M. Gibson3 Amanda J. Wright
Amanda J. Wright Lynn Paterson
Lynn Paterson Manlio Tassieri
Manlio Tassieri