- 1Applied Physics Laboratory, The Johns Hopkins University, Laurel, MD, United States
- 2Institute for Research in Electronics and Applied Physics, University of Maryland, College Park, MD, United States
Magnetic reconnection is a fundamental process providing topological changes of the magnetic field, reconfiguration of space plasmas and release of energy in key space weather phenomena, solar flares, coronal mass ejections and magnetospheric substorms. Its multiscale nature is difficult to study in observations because of their sparsity. Here we show how the lazy learning method, known as K nearest neighbors, helps mine data in historical space magnetometer records to provide empirical reconstructions of reconnection in the Earth’s magnetotail where the energy of solar wind-magnetosphere interaction is stored and released during substorms. Data mining reveals two reconnection regions (X-lines) with different properties. In the mid tail (
1 Introduction
Charged particles, electrons and ions forming space plasmas usually drift in the ambient magnetic field making plasmas frozen in that field [1]. The frozen-in condition may be broken when oppositely directed field lines approach each other so closely that particles become unmagnetized and their orbits become different from conventional drift motions. As a result, magnetic field lines may change their connectivity near so-called X-lines in the process of magnetic reconnection. This process was introduced to explain major sources of space weather disturbances on the Sun, solar flares [2, 3] and coronal mass ejections (CMEs) [4]. It was also invoked by Dungey [5] to describe the structure of the Earth’s magnetosphere, the plasma bubble surrounding our planet and protecting its life from the hazardous stream of high-energy particles emitted by our star. According to Dungey, reconnection takes place on the day side of the magnetospheric boundary, the magnetopause, to provide the solar wind plasma entry into the magnetosphere through the reconnected magnetic flux tubes. Then the flux tubes reconnect again on the night side, in the region where the Earth’s dipole magnetic field lines are stretched in the antisunward direction forming the magnetotail. Finally, to explain a delayed explosive response of the polar regions of the magnetosphere to solar wind disturbances during substorms [6], Hones [7] proposed that the substorm explosions are powered by the unsteady reconnection in the tail due to the formation of another “near-Earth” X-line.
The magnetotail reconnection is important not only as a key element of the space weather chain. It occurs in space plasma practically in the absence of particle collisions. Similar collisionless reconnection processes are expected to occur in the solar corona during flares and CMEs, where in-situ observations are impossible [1]. They are also expected in sufficiently hot laboratory plasmas that are investigated on the way to controlled nuclear fusion [8]. Thus, the magnetotail represents a natural space laboratory for collisionless reconnection due to many dedicated missions, such as Geotail [9], Cluster [10], THEMIS [11] and MMS [12].
The magnetotail is also very interesting because it reveals different regimes of reconnection. On the one hand, it must experience steady reconnection, which was conjectured by Dungey [5] in his description of the magnetospheric convection cycle and later confirmed in observations of steady magnetospheric convection (SMC) regimes [13]. On the other hand, the magnetotail experiences unsteady reconnection during substorms [7].
Both the first-principle modeling and the empirical reconstruction of magnetotail reconnection are very difficult to perform because of its multiscale nature. It links global reconfigurations of the nightside magnetosphere to kinetic processes on the scales of ion or even electron gyroradii that provide irreversibility for global reconfigurations. As a result, its kinetic particle-in-cell (PIC) simulations describing the full dynamics of electrons and ions (largely protons) and their self-consistent electromagnetic fields [14] are usually limited to the immediate X-line vicinity [15] and the moments after the X-line formation in global magnetohydrodynamic models [16], where the reconnection onset is provided due to numerical or ad hoc plasma resistivity. Moreover, it is very difficult to take into account that the magnetotail itself becomes multiscale prior to the reconnection onset. In-situ observations suggest that it may contain thin (ion-scale) current sheets (TCS) embedded into a thicker current sheet (CS) [17–21]. The latter may also be split in two current layers forming bifurcated TCSs [19, 22–24].
The major problem in the empirical reconstruction of magnetotail reconnection, common to all in-situ space observations, is the extreme sparsity of these observations with fewer than a dozen probes available at any moment. To solve this problem, it has recently been proposed to mine data in the multi-mission database covering many years of historical spaceborne magnetometer observations [25, 26]. It was found that such a data-mining (DM) method resolves the formation of embedded TCSs in the growth phase of substorms and their decay after the substorm onset. It also resolves the formation of the near-Earth X-lines during substorms [27]. Here we show that the DM approach allows one to resolve the formation of two different X-lines in the magnetotail during substorms. Moreover, it becomes possible to quantitatively assess their steadiness. We also show that PIC simulations guided by the DM reconstruction of the magnetotail reproduce the formation of X-lines and reconnection regimes similar to those found in the DM analysis.
2 Data Mining Method
In the DM approach, the geomagnetic field is reconstructed using not only a few points of spaceborne magnetometer measurements available at the moment of interest, but also a much larger number of other measurements made at the
This approach resembles very much the “lazy-learning” pattern recognition technique known as the K-nearest neighbor (KNN) learning [28, 29]. At the same time, our DM approach differs from conventional KNN regression methods, where both finding the NNs (“mining”) and regressions (model fitting) are made in the same space. Here, as is illustrated in Figure 1, we first detect NNs as a (sub)set of
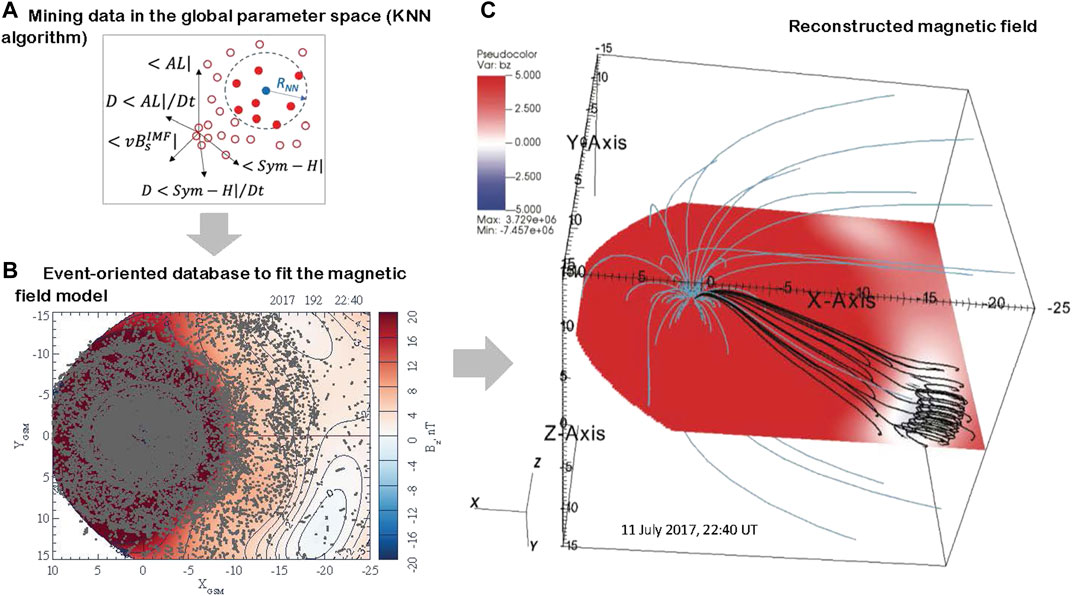
FIGURE 1. DM algorithm of the magnetic field reconstruction used in this study: (A) Nearest neighbor selection using KNN method. (B) The event-oriented subset of the database formed using the selected set of
The NN subset is formed by points
where
Here
In the 5-D space of the binning parameters (2)–(6), the
The conjecture that the substorm dynamics of the magnetosphere is coherent and hence the distribution of its magnetic field can be determined by a few control parameters had been formulated many years ago (e.g., [34], and refs. therein). Later, the singular spectrum analysis of substorms [35] revealed that the mean-field dynamics of the magnetosphere can be described as a motion on a folded 2-D surface in a 3-D state space formed by the average
The database consists of
At every moment of interest
where
The parameters
Another major group of currents are the field-aligned currents (FACs), connecting the ionosphere with the magnetopause and the tail CS. It is described in SST19 using a similar system of finite current elements [45], sufficiently flexible to reproduce the spiral FAC structure at low latitudes [46] whose night-side part is likely associated with the Harang discontinuity [47]. Each element of the FAC system is described as the magnetic field of two deformed conical surfaces corresponding to Region 1 (R1) and Region 2 (R2) FACs [48]. The size of each system is an adjustable parameter, while their azimuthal distribution is controlled by the relative contributions of two groups of basis functions with odd and even symmetry due to factors
Originally two groups of such FAC elements were proposed in [44] to describe R1 and R2 systems in their DM-based storm-time model, TS07D [36]. Later, it was proposed [45] to use more elements similar to the original TS07D FAC basis functions, shifted in latitude to describe more complex FAC distributions. Eventually, Stephens and coauthors [26] showed that the FAC system can be described with many details important for substorm reconstructions, including the Harang discontinuity and the substorm current wedge [49], with the following set of elements. It consists of
Thus, the resulting DM algorithm, which links the SST19 model with KNN binning, represents a typical “gray box” model combining empirical algorithms with physics-based constraints [50]. As is shown in [26, 27], it reproduces the multiscale CS thinning process with the formation of an ion-scale TCS (
The DM SST19 algorithm also describes the magnetic field dipolarization in the expansion phase (see, for example, Fig. 4 in [26]) with the formation of a substorm current wedge seen as a curl of the difference between the expansion and growth phase magnetic field distributions ([26], Fig. 10). The disappearance of TCS after the dipolarization can be seen, for instance, from the comparison of Fig. 12d in [27] with other panels in Fig. 12. It can also been seen from their Fig. 8f, where the relative strengths of thin and thick CSs are quantified by integrating the current density over the regions
The new DM reconstruction has a characteristic property of machine learning algorithms [29, 52]: given more data in the database it may provide more details about the magnetospheric structure and evolution. In particular, as is shown in [27], with adding to the database first two years of the MMS mission data (2016–2017), it becomes possible for the same SST19 model with the parameters
3 13 February 2008 Substorm: Steady and Unsteady X-Lines
In this section we describe the global structure and dynamics of reconnection on the example of a relatively small and short substorm (13 February 2008 02:05–02:55 UT) considered earlier in [27] with the reconstruction parameters
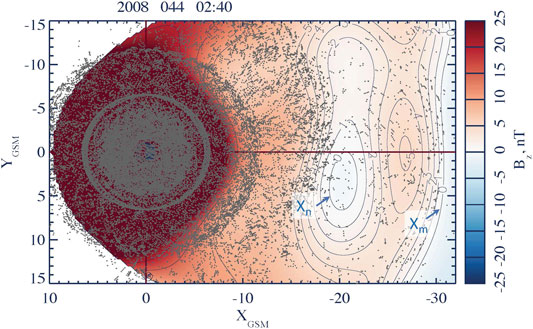
FIGURE 2. Two X-lines,
This global X-line reconstruction is quite unique. In fact, because of the extreme sparsity of in-situ space observations, such reconstructions were not available before the machine learning era. Earlier, Nagai et al. [53, 54] described the location and the dawn-dusk extension of X-lines using single-point observations. More recently, the reconstructions of the X-line vicinity were made by processing multi-probe MMS data with Grad-Shafranov [55] and polynomial [56] techniques. However, these were still very local reconstruction, largely limited to the size of the MMS tetrahedron (<30 km). Here we demonstrate for the first time how the DM approach based on the KNN algorithm resolves simultaneously two X-lines in the near-Earth and midtail regions.
The formation of transient near-Earth X-lines, which was proposed by Hones [7] as a mechanism of substorms, has been discussed since that time in many studies, including correlated multi-probe and remote sensing analyses (see, for instance [57, 58], and references therein). At the same time, persistent reconnection in the midtail around
This can be done using the Faraday’s law, which in the 2-D picture of reconnection takes the form
It suggests that the temporal variations of
The noon-midnight meridional maps of magnetic field lines presented in Figures 3, 4 reveal interesting distinctions of magnetic reconnection in the mid tail region and closer to Earth (
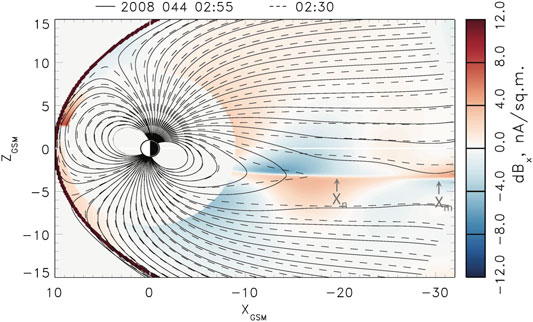
FIGURE 3. Color-coded variations of the x-component of the magnetic field between moments
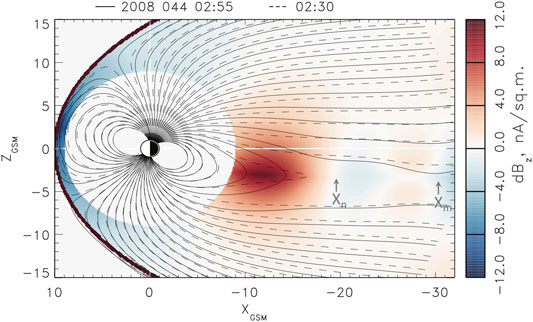
FIGURE 4. Color-coded variations of the z-component of the magnetic field between moments
The difference in
4 6 August 2017 Substorm: Complex Reconnection Picture Resolved Using Advanced DM Method
In this section we consider another substorm event with a more complex structure of dipolarizations and X-lines. It occurred on 6 August 2017 and is also interesting because of a possible X-line crossing detected by the MMS mission. Its signatures were the
where

FIGURE 5. Validation results (using MMS1 data with 5-min cadence) and analysis of the 6 August 2017 substorm. Panels (A–C) show observed (black lines) and reconstructed (red lines) values of the GSM magnetic field components, (D) the MMS1 probe ephemeris (X, Y, Z and the radial distance R (black solid, dashed, dotted and purple lines, (E)
Here
The weighted KNN approach is shown to result in better sensitivity of the model to variations of the magnetospheric state (e.g., storm or substorm phase) by using effectively much smaller numbers of NNs without overfitting [70]. Below we provide the DM reconstruction results with the parameters similar to those used in the previous section and with the weighting factor
The reconstruction summary for this substorm in the format used earlier in [26, 27] is presented in the right panels of Figure 5. Following [26], we consider the growth phase starting from the first point with
Figures 5H–J show weak storm activity: small and constant values of -
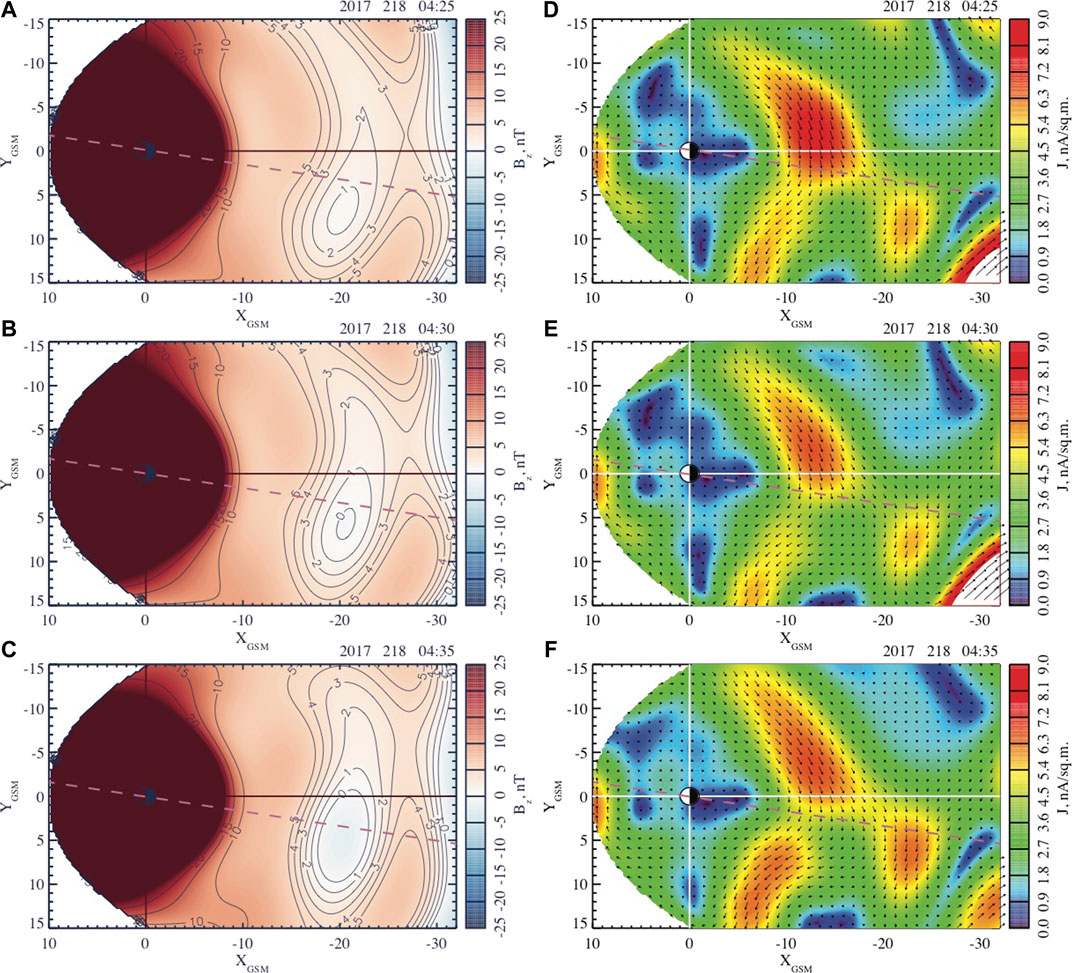
FIGURE 6. Distributions of the equatorial magnetic field
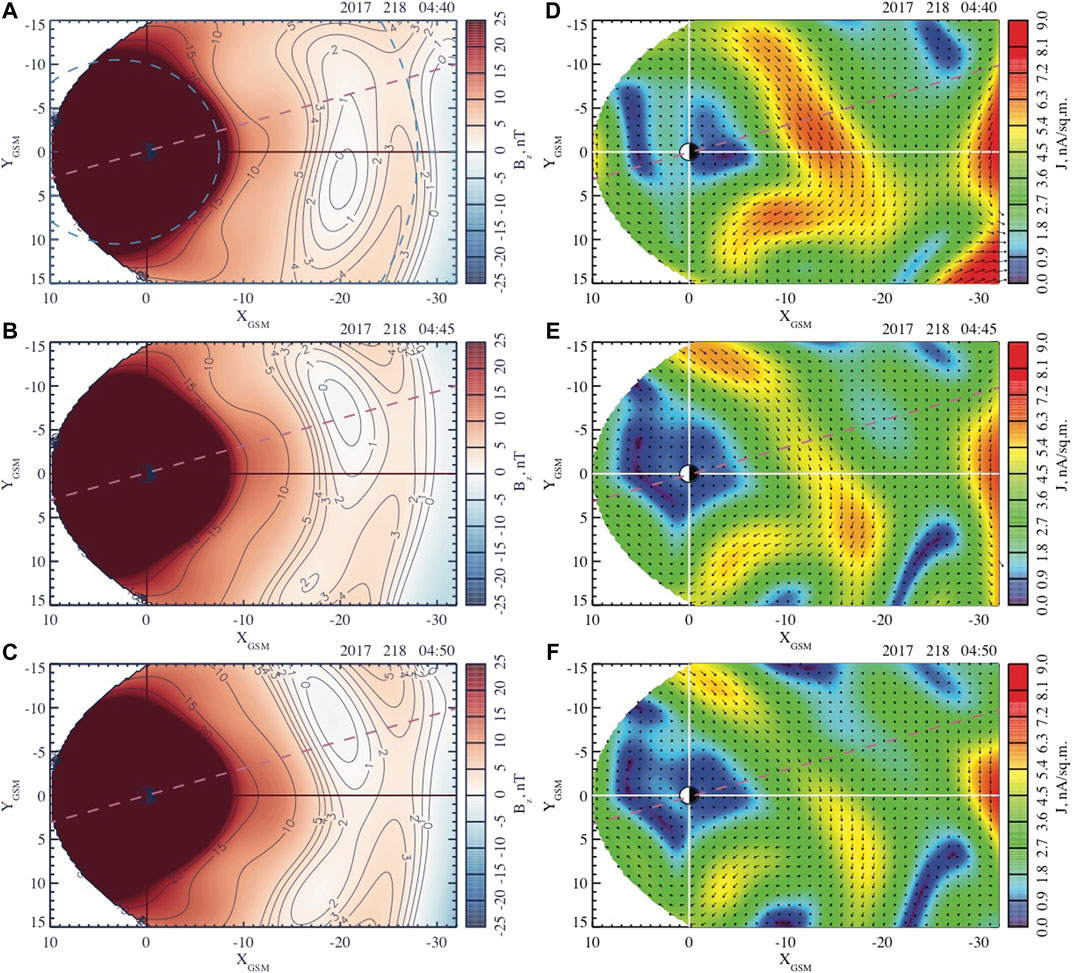
FIGURE 7. Distributions of the equatorial magnetic field
An interesting feature of this event is that the magnetic field dipolarization in the expansion phase has two sub-phases: 04:20–04:35 UT and 04:40–04:55 UT. Indeed, Figures 6, 7, which describe the evolution of the equatorial magnetic field and current, reveal two successive reconfigurations developing in the premidnight and postmidnight sectors. Figure 6 shows that during the first dipolarization a new X-line forms at
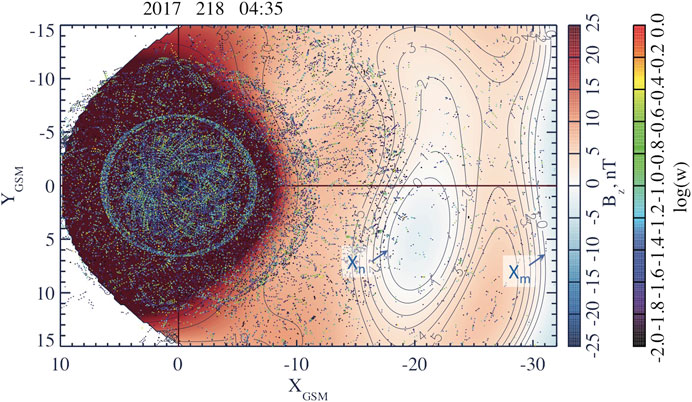
FIGURE 8. Two X-lines,
The second dipolarization described in Figure 7 causes stronger and more global changes of the near-Earth magnetic field (regions
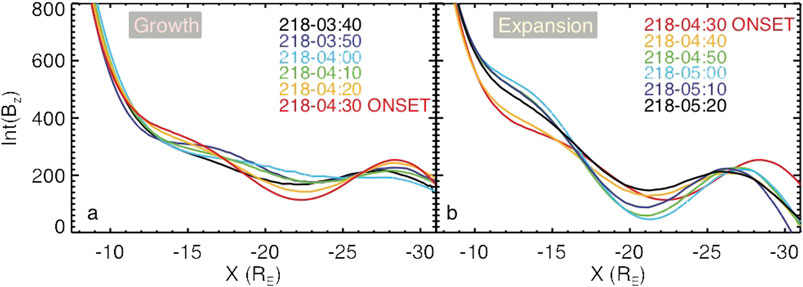
FIGURE 9. Analogs of Figs. 5n and 5o, now showing the line integral
To further investigate two dipolarizations occuring during this substorm, we present in Figures 10, 11 the meridional cuts of the cross current and in-plane magnetic field components
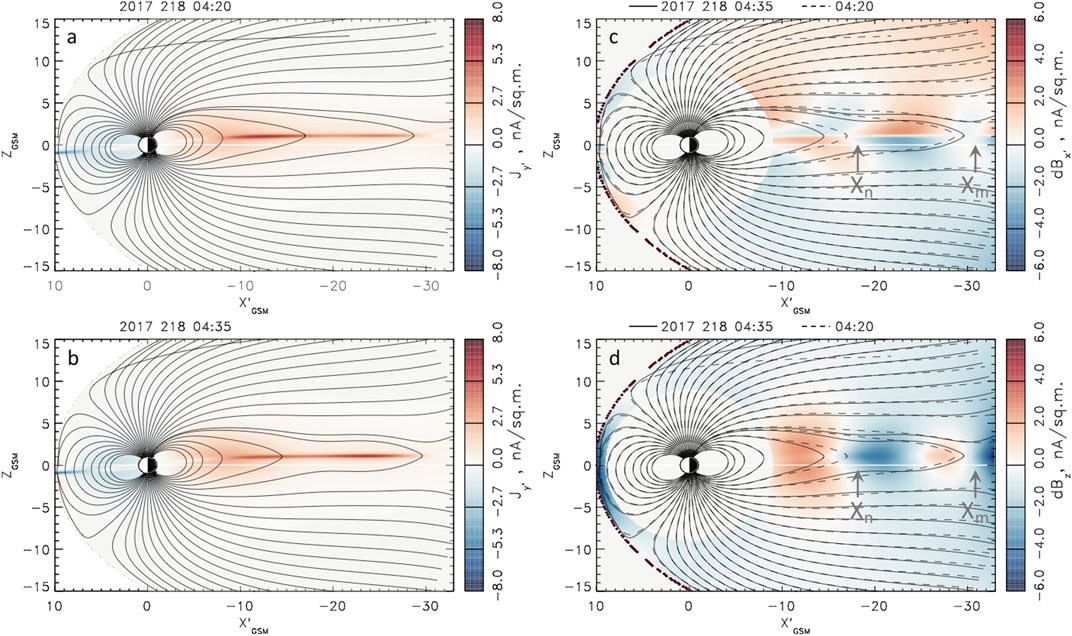
FIGURE 10. (A, B) Color-coded distributions of the current density component
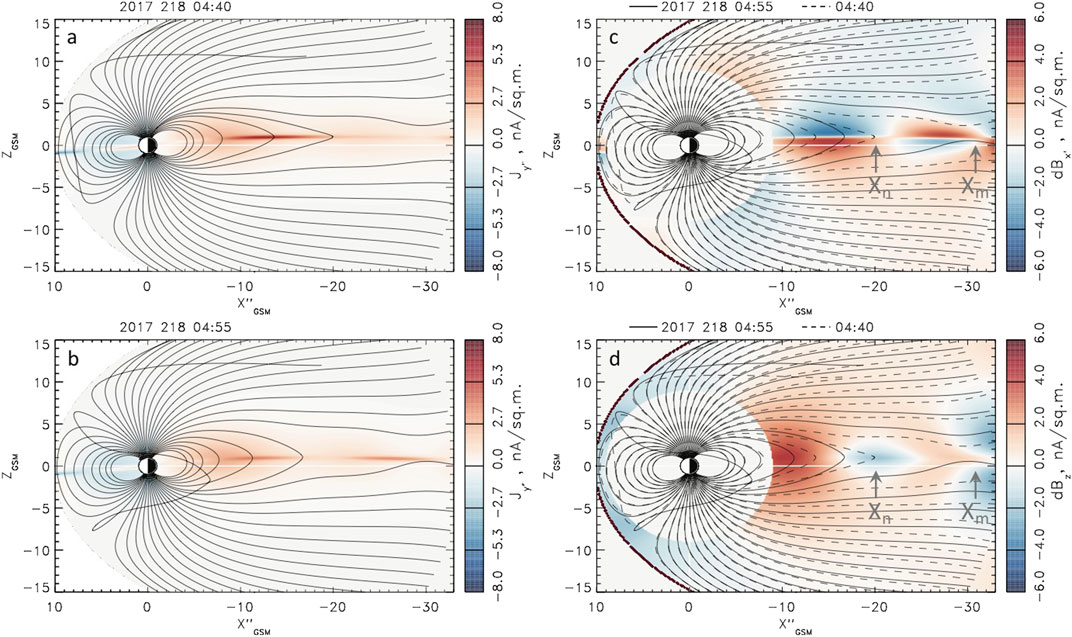
FIGURE 11. (A, B) Color-coded distributions of the current density component
As one can seen from the comparisons of Figures 10A,B, the first dipolarization is relatively weak, and it does not cause any significant flux redistribution, according to Figure 9B. During the first dipolarization, the magnetic field variations near
In contrast, during the second dipolarization, the (already shorter, less than
It is important to note that these processes of the tail thinning and dipolarization often occur under weak variations of the lobe magnetic field. Its weak variations in the growth phase were reported in [74–76] and they are seen in Figure 10C as well as in [27] (Figs. 12, 16, S4 and S13). Even rapid dipolarization processes shown in Figures 4, 11C are accompanied by more gradual lobe field variations, consistent with other data analyses [58, 74].
5 Kinetic Simulations of Magnetotail Reconnection Guided by Empirical Reconstructions
In order to understand the physical mechanisms of the formation of several X-lines in the magnetotail and their different reconnection regimes revealed in the DM analysis, we performed PIC simulations of the tail current sheet equilibrium sharing some of the observed pre-onset tail features. In particular, the reconstruction of the February 13 event discussed above in ([27], Fig. 8h) suggests that the near-Earth reconnection is preceded by the formation of a flux accumulation region near
The PIC simulations were performed using an open boundary modification [64, 80] of the explicit massively parallel code P3D [81] in a 3-D box with dimensions
The plasma parameters include the mass ratio
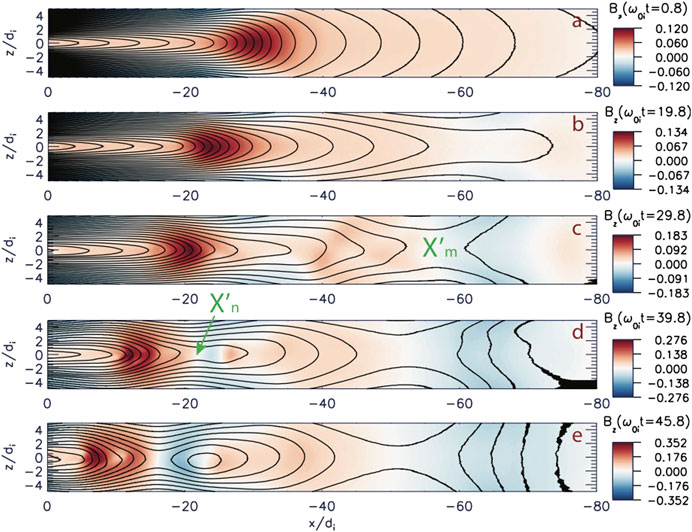
FIGURE 12. (A) The initial magnetic field configuration in PIC simulations of magnetotail reconnection, which is shown here as a color-coded distribution of the
In contrast to earlier simulations ([83], and refs. therein) that described spontaneous onset regimes, here we drive the system by imposing a weak external electric field
The external driving first results in the CS thinning and stretching, which are seen particularly well in the tailward part of the box (Figure 12B). It also causes the buildup of the plasma pressure in the region
It is very interesting that the magnetic field perturbations shown in Figure 12E strongly resemble the DM reconstructions of substorm dipolarizations shown in Figures 4, 10D, 11D with much stronger bipolar
Figure 13A shows that the electric field distributions around the X-lines are indeed drastically different. Around
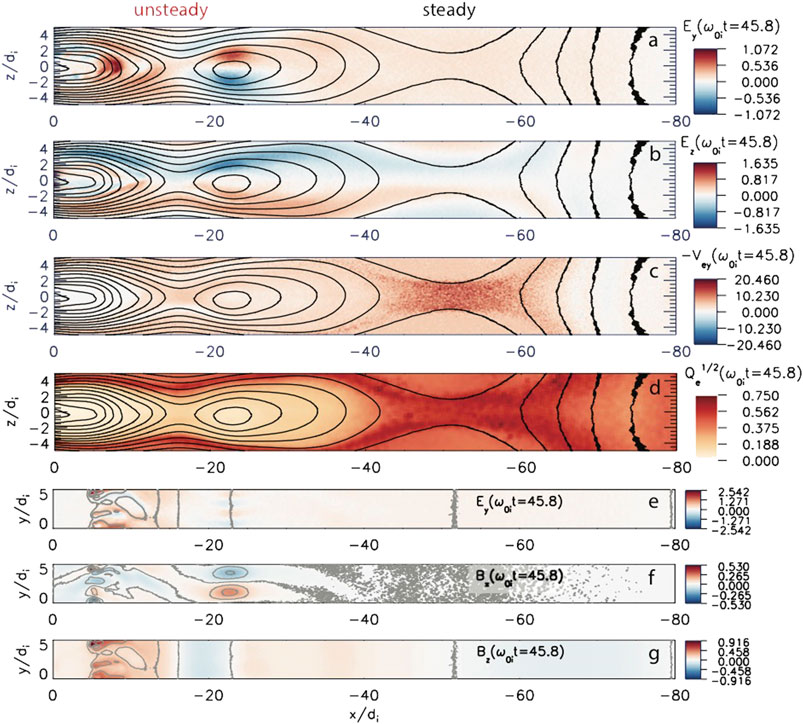
FIGURE 13. Steady and unsteady reconnection regions in weakly driven magnetoatail at the moment
At the same time, earthward of
In Figures 13B–D we present another group of signatures, which cannot be resolved using the DM analysis. Figure 13B shows the electric field directed toward the neutral plane
Finally, in Figure 14 we present the kinetic dissipation parameters for the unsteady part of this run and compare them with similar parameters inferred from MMS observations. In contrast to the steady-state reconnection area near
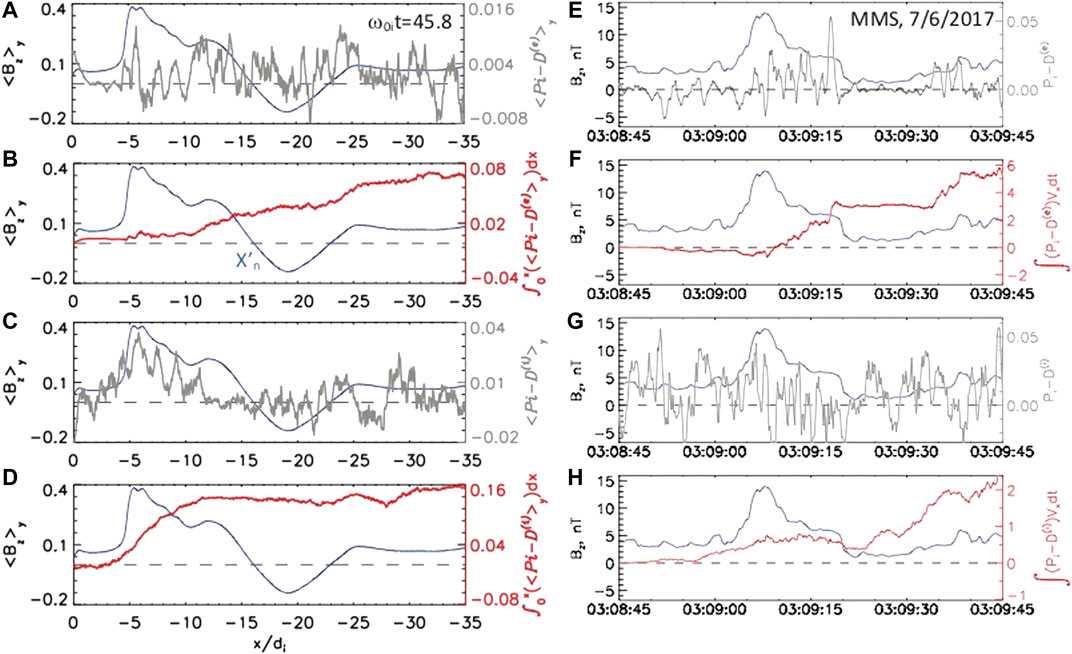
FIGURE 14. (A–D) Kinetic dissipation parameters in the unsteady reconnection region in PIC simulations (Figure 13) and (E–F) similar parameters derived from MMS observations of a DF on 6 July 2017 at
To solve this problem, it has recently been proposed [109] to employ the new kinetic parameter
In Figures 14A–D we present kinetic dissipation measures obtained in PIC simulations and averaged over the y direction
Figures 14E–H show the dissipation parameters similar to those in Figures 14A–D but now derived from MMS observations of a DF on 6 July 2017, a relatively rare case of a slow moving DF with the ion bulk flow speed smaller than 200 km/s. The four-probe sub-ion-scale MMS observations of the electromagnetic field and plasma parameters provide the unique opportunity to measure the kinetic dissipation parameters
In spite of these caveats, simulation and observation results presented in Figure 14 have interesting similarities. In particular, both simulations and data show the accumulation of positive
6 Discussion
6.1 Error Analysis of Empirical Reconstructions
In this study we provided a DM reconstruction of magnetic reconnection in the Earth’s magnetotail associated with its dipolarizations during substorms. A direct validation of this reconstruction can only be provided using a limited number of in-situ observations available at the moment of interest. This is an unavoidable feature of the DM method as a data discovery tool, which extracts from data the information (e.g., on the global structure of the magnetotail), which cannot be obtained by other methods. We simply have no real constellations of
FIGURE 15. The substorm part of the binning parameters (4)–(6)
Consistent with the analysis of the 13 February 2008 substorms [27], we have found that the relatively strong deviations of the binning parameters from their means over NNs take place for the solar wind parameter
An important source of uncertainty in the present NN approach may be the instrument errors and combining probes from different epochs. Fortunately, the accuracy of magnetic field measurements critical for our investigation (with a few nT accuracy necessary to resolve the
6.2 Implications for Local Reconnection Models and Tearing Stability
The concept of magnetic reconnection was introduced to explain explosive energy release and rapid changes of magnetic field topology associated with solar flares [2, 3], magnetospheric substorms [7, 108, 122] and laboratory current disruptions ([123], and refs. therein). But its theory turned out to be built mainly on models of steady-state reconnection regimes ([63, 124–127], and refs. therein). The few exceptions include the tearing instability theory [87, 108, 122, 128], and catastrophe models of coronal mass ejections and solar flares [129, 130].
At the same time, the description of transition from the slow evolution of the tail to its rapid reconfiguration has long been complicated by the almost universal tearing stability of the tail current sheet provided by magnetization of electrons due to nonzero northward magnetic field
In 1974 Schindler [108] hypothesized that the tail could become unstable even with magnetized electrons if the CS is sufficiently thin to demagnetize ions and provide their Landau dissipation. The corresponding tearing instability must be much faster compared to the electron tearing. However, later it was found [135] that magnetized electrons change the free energy of the tearing mode, and eventually Lembege and Pellat [131] showed that the corresponding sufficient stability condition coincides with the Wentzel–Kramers–Brillouin (WKB) approximation
A missing key for ion tearing destabilization was found relatively recently when it was discovered [77] that the stability condition derived by Lembege and Pellat [131] is only valid for constant
Despite this clarity in the tearing stability theory and consistent simulation results, until now, the role of EDMR and IDMR regimes in the actual magnetotail dynamics remained unclear. In particular, it is unknown if/when the driving (ultimately due to the solar wind) is sufficiently strong to squeeze the CS down to electron scales and to provide EDMR with the subsequent steady reconnection, and when (if any)
The present study provides interesting implications for the magnetotail stability and reconnection onset mechanisms. Our DM reconstructions suggest that both steady and unsteady reconnection regimes are possible in the magnetotail during substorms. At the same time, our PIC simulations guided by empirical reconstructions suggest that both IDMR and EDMR regimes are possible in the tail. Moreover, the former resembles the unsteady reconnection, while the latter becomes eventually steady, consistent with the classical fast and steady reconnection models ([62] and refs. therein).
6.3 Role of Thin Current Sheets
The use in Section 5 of isotropic plasma equilibria with shifted Maxwellian distributions for ions and electrons, inherited from the 1962 Harris solution [79], to explain the reconnection features found in our DM reconstructions may be questioned in view of another discovery in the DM analysis of substorms, namely the buildup of extended TCSs in the substorm growth phase and their decay in the expansion phase [26, 27] (see also Figures 10A,B, 11A,B of the present study).
The analysis of 2-D isotropic equilibrium models [136] suggests that they require strongly stretched magnetic field configurations (with sufficiently large values of the ratio
Indeed, three of four substorm events on 13 February 2008 considered in [27] had relatively small values of
However, this is not the case for the event considered in Section 3, whose specific features (the
One can also provide more general arguments why the isotropic 2-D models can still be used in the local stability analysis of the realistic magnetotail. First, statistical studies show that the tail plasmas away from the dipole region are weakly anisotropic [138, 139]. At the same time, the DM reconstructions demonstrate that the current of the embedded TCS in the late growth phase may be small, compared to the total current, as is seen, for instance, from Figure 5L (this is the case for all four 13 February 2008 events as is seen from Fig. 8f in [27]). This suggests that the embedded TCS features and underlying non-isotropic plasma properties may only serve to provide the formation of the ion-scale TCSs sufficiently far from Earth, where their local stability properties can still be realistically reproduced by PIC simulations with isotropic equilibria and open x-boundaries. This is consistent with the results of statistical studies based on Geotail data [140], which suggest that the near-Earth X-line mainly forms near the tailward edge of the TCS. This appears to be the case during the second dipolarization in the 6 August 2017 event (Figure 11), although this is likely not the case during the first dipolarization when the near-Earth X-line forms in the middle of a very long TCS (Figure 10). Besides, even if the initial TCS is relatively short because of the corresponding force balance, the simulations performed in Section 5 suggest that it becomes more stretched and closer to empirical TCS reconstructions due to the external driving. To conclude, while some substorm dipolarizations certainly require a generalization of the isotropic plasma approximation, as it was outlined in [136], others can still be described using the conventional class of isotropic CS models [78, 79].
7 Conclusion
In this study, we investigated for the first time the magnetotail reconnection picture using modern data-mining methods, which allow us to employ for the reconstruction not only the magnetic field measurements available at the moment of interest but also other events in the historical database when the magnetosphere was in similar global states (substorm phases). The DM reconstruction revealed two distinctly different regions of magnetic reconnection with weak and strong changes of the magnetic field geometry. For both the 13 February 2008 and the 6 August 2017 substorms considered in our study the near-Earth X-line appears near
In addition to earlier investigations, our DM reconstruction reveals that the near-Earth X-line (
Moreover, the DM analysis shows that reconnection regimes at near-Earth and midtail X-lines are different. The near-Earth X-line appears at the substorm onset and then disappears from that region or reappears in another near-Earth region, e.g., in the postmidnight sector (compare Figures 7A,B or Figures 2, 10 in [27]). In contrast, the midtail X-line, after its appearance within the reconstruction validity region (here
To understand the physical mechanisms of the formation of several X-lines in the magnetotail and their different reconnection regimes, we performed 3-D PIC simulations of a relatively long (
The reconnection picture in PIC simulations, guided by the DM reconstructions, is found to be surprisingly consistent with the empirical picture of the magnetotail reconnection. It also reveals two reconnection areas with distinctly different reconnection regimes, whose steadiness can now be checked using the explicit distributions of the electric field in the meridional plane (Figure 13A). It is found that farther in the tail, the reconnection process is steady and it reveals many signatures of the sustained collisionless reconnection process with the region of agyrotropic electron motion in its center. The corresponding dusk component of the electric field is broadly distributed in the meridional plane and hence it becomes effectively a global parameter of this reconnection regime. Its value
Both empirical and first-principle pictures of magnetotail reconnection still need further refinement. The present DM approach provides an empirical picture on the magnetotail on the time scales greater than 5 min and on the spatial scales larger than
Data Availability Statement
Publicly available datasets were analyzed in this study. This data can be found here: http://doi.org/10.5281/zenodo.4383387.
Author Contributions
Conceptualization, MSi; methodology, MSi, GS, TM and MSw; software, MSi, GS, TM and MSw; formal analysis, MSi, GS and TM; investigation, MSi, GS and TM; resources, MSi, GS and TM; data curation, MSi, GS and TM; writing–original draft preparation, MSi; writing–review and editing, MSi, GS, TM and MSw; visualization, MSi, GS and TM; supervision, MSi; project administration, MSi; funding acquisition, MSi. All authors have read and agreed to the published version of the manuscript.
Funding
This work was funded by NASA grants 80NSSC19K0074, 80NSSC19K0847, 80NSSC20K1271, 80NSSC19K0396 and 80NSSC20K1787, as well as NSF grants AGS-1702147 and AGS-1744269.
Conflict of Interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Acknowledgments
We acknowledge interesting and useful discussions of the obtained results with Nikolai Tsyganenko, Rumi Nakamura, Ferdinand Plaschke, Slava Merkin and Shin Ohtani. We thank the many spacecraft and instrument teams and their PIs who produced the data sets we used in this study, including the Cluster, Geotail, Polar, IMP-8, GOES, THEMIS, Van Allen Probes and MMS, particularly their magnetometer teams. We also thank the SPDF for the OMNI database for solar wind values, which is composed of data sets from the IMP-8, ACE, WIND, and Geotail missions, and also the WDC in Kyoto for the Geomagnetic indices. Simulations were made possible by the NCAR’s Computational and Information Systems Laboratory (doi:10.5065/D6RX99HX), supported by the NSF, as well as the NASA High-End Computing Program through the NASA Advanced Supercomputing Division at Ames Research Center.
Nomenclature
The following abbreviations are used in this manuscript:
CME Coronal Mass Ejection
CS Current Sheet
DM Data Mining
EDR Electron Diffusion Region
EDMR Electron Demagnetization Mediated Reconnection
FAC Field Aligned Current system
GSM Geocentric Solar Magnetospheric coordinate system
IDMR Ion Demagnetization Mediated Reconnection
KNN K Nearest Neighbors method
PIC Particle-In-Cell simulation method
R1,2 Region 1,2 field-aligned current
SMC Steady Magnetospheric Convection
TCS Thin Current Sheet
UT Universal Time
WKB Wentzel–Kramers–Brillouin approximation
References
1. Cassak PA. Inside the black box: magnetic reconnection and the magnetospheric multiscale mission. Space Weather (2016) 14:186–97. doi:10.1002/2015SW001313
3. Sturrock PA. Model of the high-energy phase of solar flares. Nature (1966) 211:695–7. doi:10.1038/211695a0
4. Forbes TG. A review on the genesis of coronal mass ejections. J Geophys Res Space Phys (2000) 105:23153–65. doi:10.1029/2000JA000005
5. Dungey JW. Interplanetary magnetic field and the auroral zones. Phys Rev Lett (1961) 6:47–8. doi:10.1103/PhysRevLett.6.47
6. Akasofu SI. The development of the auroral substorm. Planet Space Sci (1964) 12:273–82. doi:10.1016/0032-0633(64)90151-5
7. Hones EW. Transient phenomena in the magnetotail and their relation to substorms. Space Sci Rev (1979) 23:393–410. doi:10.1007/BF00172247
8. Ren Y, Yamada M, Ji H, Dorfman S, Gerhardt SP, Kulsrud R. Experimental study of the hall effect and electron diffusion region during magnetic reconnection in a laboratory plasma. Phys Plasmas (2008) 15:082113. doi:10.1063/1.2936269
9. Nishida A, Uesugi K, Nakatani I, Mukai T, Fairfield DH, Acuna MH. Geotail mission to explore earth’s magnetotail. Eos, Trans Am Geophys Union (1992) 73:425–9. doi:10.1029/91EO00314
10. Sharma AS, Nakamura R, Runov A, Grigorenko EE, Hasegawa H, Hoshino M, et al. Transient and localized processes in the magnetotail: a review. Ann Geophysicae (2008) 26:955–1006. doi:10.5194/angeo-26-955-2008
12. Burch JL, Moore TE, Torbert RB, Giles BL. Magnetospheric multiscale overview and science objectives. Space Sci Rev (2016) 199:5–21. doi:10.1007/s11214-015-0164-9
13. Sergeev VA, Pellinen RJ, Pulkkinen TI. Steady magnetospheric convection: a review of recent results. Space Sci Rev (1996) 75:551–604. doi:10.1007/BF00833344
14. Birdsall CK, Langdon AB. Plasma physics via computer simulation. New York: Taylor & Francis (2005).
15. Nakamura TKM, Genestreti KJ, Liu YH, Nakamura R, Teh WL, Hasegawa H, et al. Measurement of the magnetic reconnection rate in the Earth’s magnetotail. J Geophys Res Space Phys (2018) 123:9150–68. doi:10.1029/2018JA025713
16. Lapenta G, El Alaoui M, Berchem J, Walker R. Multiscale mhd-kinetic PIC study of energy fluxes caused by reconnection. J Geophys Res Space Phys (2020) 125:e2019JA027276. doi:10.1029/2019JA027276
17. Sergeev VA, Mitchell DG, Russell CT, Williams DJ. Structure of the tail plasma/current sheet at and its changes in the course of a substorm. J Geophys Res Space Phys (1993) 98:17345–65. doi:10.1029/93JA01151
18. Nakamura R, Baumjohann W, Runov A, Volwerk M, Zhang TL, Klecker B, et al. Fast flow during current sheet thinning. Geophys Res Lett (2002) 29:55–1–55–4. doi:10.1029/2002GL016200
19. Runov A, Sergeev VA, Nakamura R, Baumjohann W, Apatenkov S, Asano Y, et al. Local structure of the magnetotail current sheet: 2001 Cluster observations. Ann Geophysicae (2006) 24:247–62. doi:10.5194/angeo-24-247-2006
20. Petrukovich AA, Artemyev AV, Malova HV, Popov VY, Nakamura R, Zelenyi LM. Embedded current sheets in the Earth’s magnetotail. J Geophys Res Space Phys (2011) 116. doi:10.1029/2010JA015749
21. Sergeev VA, Angelopoulos V, Kubyshkina M, Donovan E, Zhou XZ, Runov A, et al. Substorm growth and expansion onset as observed with ideal ground-spacecraft THEMIS coverage. J Geophys Res (2011) 116:A00I26. doi:10.1029/2010JA015689
22. Hoshino M, Nishida A, Mukai T, Saito Y, Yamamoto T, Kokubun S. Structure of plasma sheet in magnetotail: double-peaked electric current sheet. J Geophys Res Space Phys (1996) 101:24775–86. doi:10.1029/96JA02313
23. Asano Y, Mukai T, Hoshino M, Saito Y, Hayakawa H, Nagai T. Evolution of the thin current sheet in a substorm observed by Geotail. J Geophys Res Space Phys (2003) 108. doi:10.1029/2002JA009785
24. Asano Y, Nakamura R, Baumjohann W, Runov A, Vörös Z, Volwerk M, et al. How typical are atypical current sheets? Geophys Res Lett (2005) 32. doi:10.1029/2004GL021834
25. Sitnov MI, Ukhorskiy AY, Stephens GK. Forecasting of global data-binning parameters for high-resolution empirical geomagnetic field models. Space Weather (2012) 10. doi:10.1029/2012SW000783
26. Stephens GK, Sitnov MI, Korth H, Tsyganenko NA, Ohtani S, Gkioulidou M, et al. Global empirical picture of magnetospheric substorms inferred from multimission magnetometer data. J Geophys Res Space Phys (2019) 124. doi:10.1029/2018JA025843
27. Sitnov MI, Stephens GK, Tsyganenko NA, Miyashita Y, Merkin VG, Motoba T, et al. Signatures of nonideal plasma evolution during substorms obtained by mining multimission magnetometer data. J Geophys Res Space Phys (2019) 124:8427–56. doi:10.1029/2019JA027037
28. Cover T, Hart P. Nearest neighbor pattern classification. IEEE Trans Inf Theor (1967) 13:21–7. doi:10.1109/TIT.1967.1053964
30. Tsyganenko NA. Effects of the solar wind conditions on the global magnetospheric configurations as deduced from data-based field models. Proceedings of the Third International Conference on Substorms (ICS-3) (1996), ESA SP-389, Versailles, France (1996).
31. Partamies N, Juusola L, Tanskanen E, Kauristie K. Statistical properties of substorms during different storm and solar cycle phases. Ann Geophysicae (2013) 31:349–58. doi:10.5194/angeo-31-349-2013
32. Davis TN, Sugiura M. Auroral electrojet activity index AE and its universal time variations. J Geophys Res (1896-19771966) 71:785–801. doi:10.1029/JZ071i003p00785
33. Hsu TS, McPherron RL. The characteristics of storm-time substorms and non-storm substorms. In: A Wilson, editor. Fifth international conference on substorms, 443. Noordwijk, Netherlands: ESA Special Publication (2000). p. 439.
34. Surjalal Sharma A. Assessing the magnetosphere’s nonlinear behavior: its dimension is low, its predictability, high. Rev Geophys (1995) 33:645–50. doi:10.1029/95RG00495
35. Sitnov MI, Sharma AS, Papadopoulos K, Vassiliadis D, Valdivia JA, Klimas AJ, et al. Phase transition-like behavior of the magnetosphere during substorms. J Geophys Res Space Phys (2000) 105:12955–74. doi:10.1029/1999JA000279
36. Sitnov MI, Tsyganenko NA, Ukhorskiy AY, Brandt PC. Dynamical data-based modeling of the storm-time geomagnetic field with enhanced spatial resolution. J Geophys Res Space Phys (2008) 113. doi:10.1029/2007JA013003
37. Burton RK, McPherron RL, Russell CT. An empirical relationship between interplanetary conditions and Dst. J Geophys Res (1896-19771975) 80:4204–14. doi:10.1029/JA080i031p04204
38. Runge J, Balasis G, Daglis IA, Papadimitriou C, Donner RV. Common solar wind drivers behind magnetic storm-magnetospheric substorm dependency. Scientific Rep (2018) 8:16987. doi:10.1038/s41598-018-35250-5
39. Sitnov MI, Sharma AS, Papadopoulos K, Vassiliadis D. Modeling substorm dynamics of the magnetosphere: from self-organization and self-organized criticality to nonequilibrium phase transitions. Phys Rev E (2001) 65:016116. doi:10.1103/PhysRevE.65.016116
40. Ukhorskiy AY, Sitnov MI, Sharma AS, Papadopoulos K. Global and multi-scale features of solar wind-magnetosphere coupling: from modeling to forecasting. Geophys Res Lett (2004) 31. doi:10.1029/2003GL018932
41. Pulkkinen TI, Baker DN, Fairfield DH, Pellinen RJ, Murphree JS, Elphinstone RD, et al. Modeling the growth phase of a substorm using the Tsyganenko model and multi-spacecraft observations: CDAW-9. Geophys Res Lett (1991) 18:1963–6. doi:10.1029/91GL02002
42. Kubyshkina MV, Sergeev VA, Pulkkinen TI. Hybrid input algorithm: an event-oriented magnetospheric model. J Geophys Res Space Phys (1999) 104:24977–93. doi:10.1029/1999JA900222
43. Tsyganenko NA, Andreeva VA. An empirical RBF model of the magnetosphere parameterized by interplanetary and ground-based drivers. J Geophys Res Space Phys (2016) 121:10,786–10,802. doi:10.1002/2016JA023217
44. Tsyganenko NA, Sitnov MI. Magnetospheric configurations from a high-resolution data-based magnetic field model. J Geophys Res Space Phys (2007) 112. doi:10.1029/2007JA012260
45. Sitnov MI, Stephens GK, Tsyganenko NA, Ukhorskiy AY, Wing S, Korth H, et al. Spatial structure and asymmetries of magnetospheric currents inferred from high-resolution empirical geomagnetic field models. Washington, D.C: American Geophysical Union (2017). p. 199–212. chap. 15. doi:10.1002/9781119216346.ch15
46. Iijima T, Potemra TA. The amplitude distribution of field-aligned currents at northern high latitudes observed by Triad. J Geophys Res (1896-19771976) 81:2165–74. doi:10.1029/JA081i013p02165
47. Harang L. The mean field of disturbance of polar geomagnetic storms. Terrestrial Magnetism Atmos Electricity (1946) 51:353–80. doi:10.1029/TE051i003p00353
48. Tsyganenko NA. A model of the near magnetosphere with a dawn-dusk asymmetry 1. Mathematical structure. J Geophys Res Space Phys (2002) 107:SMP 12–1–SMP 12–5. doi:10.1029/2001JA000219
49. McPherron RL, Russell CT, Aubry MP. Satellite studies of magnetospheric substorms on August 15, 1968: 9. Phenomenological model for substorms. J Geophys Res (1896-19771973) 78:3131–49. doi:10.1029/JA078i016p03131
50. Camporeale E. The challenge of machine learning in space weather: nowcasting and forecasting. Space Weather (2019) 17:1166–207. doi:10.1029/2018SW002061
51. Runov A, Angelopoulos V, Zhou XZ. Multipoint observations of dipolarization front formation by magnetotail reconnection. J Geophys Res Space Phys (2012) 117. doi:10.1029/2011JA017361
52. Kubat M. An introduction to machine learning. 1st ed. Incorporated: Springer Publishing Company (2015).
53. Nagai T, Fujimoto M, Nakamura R, Baumjohann W, Ieda A, Shinohara I, et al. Solar wind control of the radial distance of the magnetic reconnection site in the magnetotail. J Geophys Res Space Phys (2005) 110. doi:10.1029/2005JA011207
54. Nagai T, Shinohara I, Zenitani S. The dawn-dusk length of the x line in the near-earth magnetotail: Geotail survey in 1994-2014. J Geophys Res Space Phys (2015) 120:8762–73. doi:10.1002/2015JA021606
55. Hasegawa H, Sonnerup BUO, Denton RE, Phan TD, Nakamura TKM, Giles BL, et al. Reconstruction of the electron diffusion region observed by the Magnetospheric Multiscale Spacecraft: First results. Geophys Res Lett (2017) 44:4566–74. doi:10.1002/2017GL073163
56. Denton RE, Torbert RB, Hasegawa H, Dors I, Genestreti KJ, Argall MR, et al. Polynomial reconstruction of the reconnection magnetic field observed by multiple spacecraft. J Geophys Res Space Phys (2020) 125:e2019JA027481. doi:10.1029/2019JA027481
57. Baker DN, Pulkkinen TI, Angelopoulos V, Baumjohann W, McPherron RL. Neutral line model of substorms: Past results and present view. J Geophys Res Space Phys (1996) 101:12975–3010. doi:10.1029/95JA03753
58. Angelopoulos V, Runov A, Zhou XZ, Turner DL, Kiehas SA, Li SS, et al. Electromagnetic energy conversion at reconnection fronts. Science (2013) 341:1478–82. doi:10.1126/science.1236992
59. Imber SM, Slavin JA, Auster HU, Angelopoulos V. A THEMIS survey of flux ropes and traveling compression regions: location of the near-Earth reconnection site during solar minimum. J Geophys Res Space Phys (2011) 116. doi:10.1029/2010JA016026
60. Zhao S, Tian A, Shi Q, Xiao C, Fu S, Zong Q, et al. Statistical study of magnetotail flux ropes near the lunar orbit. Sci China Technol Sci (2016) 59:1591–6. doi:10.1007/s11431-015-0962-3
61. Shay MA, Drake JF. The role of electron dissipation on the rate of collisionless magnetic reconnection. Geophys Res Lett (1998) 25:3759–62. doi:10.1029/1998GL900036
62. Cassak PA, Liu YH, Shay M. A review of the 0.1 reconnection rate problem. J Plasma Phys (2017) 83:715830501. doi:10.1017/S0022377817000666
63. Liu YH, Hesse M, Guo F, Daughton W, Li H, Cassak PA, et al. Why does steady-state magnetic reconnection have a maximum local rate of order 0.1? Phys Rev Lett (2017) 118:085101. doi:10.1103/PhysRevLett.118.085101
64. Sitnov MI, Swisdak M. Onset of collisionless magnetic reconnection in two-dimensional current sheets and formation of dipolarization fronts. J Geophys Res (2011) 116:12216. doi:10.1029/2011JA016920
65. Nakamura R, Baumjohann W, Klecker B, Bogdanova Y, Balogh A, Rème H, et al. Motion of the dipolarization front during a flow burst event observed by Cluster. Geophys Res Lett (2002) 29:3–1–3–4. doi:10.1029/2002GL015763
66. Runov A, Angelopoulos V, Sitnov MI, Sergeev VA, Bonnell J, McFadden JP, et al. Themis observations of an earthward-propagating dipolarization front. Geophys Res Lett (2009) 36. doi:10.1029/2009GL038980
67. Sitnov MI, Swisdak M, Divin AV. Dipolarization fronts as a signature of transient reconnection in the magnetotail. J Geophys Res Space Phys (2009) 114. doi:10.1029/2008JA013980
68. Huang SY, Fu HS, Yuan ZG, Zhou M, Fu S, Deng XH, et al. Electromagnetic energy conversion at dipolarization fronts: Multispacecraft results. J Geophys Res Space Phys (2015) 120:4496–502. doi:10.1002/2015JA021083
69. Runov A, Angelopoulos V, Zhou XZ, Zhang XJ, Li S, Plaschke F, et al. A THEMIS multicase study of dipolarization fronts in the magnetotail plasma sheet. J Geophys Res Space Phys (2011) 116. doi:10.1029/2010JA016316
70. Sitnov MI, Stephens GK, Tsyganenko NA, Korth H, Roelof EC, Brandt PC, et al. Reconstruction of extreme geomagnetic storms: Breaking the data paucity curse. Space Weather (2020) 18:e2020SW002561. doi:10.1029/2020SW002561
71. Galeev AA. Spontaneous reconnection of magnetic field lines in a collisionless plasma. In: AA Galeev, and RN Sudan, editors. Handbook of plasma physics, Vol. 2. New York): North-Holland (1984). p. 305–35.
72. Sitnov MI, Buzulukova N, Swisdak M, Merkin VG, Moore TE. Spontaneous formation of dipolarization fronts and reconnection onset in the magnetotail. Geophys Res Lett (2013) 40:22–7. doi:10.1029/2012GL054701
73. Liu YH, Birn J, Daughton W, Hesse M, Schindler K. Onset of reconnection in the near magnetotail: PIC simulations. J Geophys Res Space Phys (2014) 119:9773–89. doi:10.1002/2014JA020492
74. Shukhtina MA, Dmitrieva NP, Sergeev VA. On the conditions preceding sudden magnetotail magnetic flux unloading. Geophys Res Lett (2014) 41:1093–9. doi:10.1002/2014GL059290
75. Artemyev AV, Angelopoulos V, Runov A, Petrokovich AA. Properties of current sheet thinning at x -10 to -12 RE. J Geophys Res Space Phys (2016) 121:6718–31. doi:10.1002/2016JA022779
76. Sun WJ, Fu SY, Wei Y, Yao ZH, Rong ZJ, Zhou XZ, et al. Plasma sheet pressure variations in the near-Earth magnetotail during substorm growth phase: themis observations. J Geophys Res Space Phys (2017) 122:12,212–12,228. doi:10.1002/2017JA024603
77. Sitnov MI, Schindler K. Tearing stability of a multiscale magnetotail current sheet. Geophys Res Lett (2010) 37:08102. doi:10.1029/2010GL042961
78. Schindler K. A selfconsistent theory of the tail of the magnetosphere. In: BM McCormac, editor. Earth’s magnetospheric processes. Dordrecht-Holland: D. Reidel) (1972). p. 200–9.
79. Harris E. On a plasma sheath separating regions of oppositely directed magnetic field. Il Nuovo Cimento Ser (1962) 23:115–21. doi:10.1007/BF02733547
80. Divin AV, Sitnov MI, Swisdak M, Drake JF. Reconnection onset in the magnetotail: Particle simulations with open boundary conditions. Geophys Res Lett (2007) 34:L09109. doi:10.1029/2007GL029292
81. Zeiler A, Biskamp D, Drake JF, Rogers BN, Shay MA, Scholer M. Three-dimensional particle simulations of collisionless magnetic reconnection. J Geophys Res (2002) 107:1230. doi:10.1029/2001JA000287
82. Sitnov MI, Merkin VG, Swisdak M, Motoba T, Buzulukova N, Moore TE, et al. Magnetic reconnection, buoyancy, and flapping motions in magnetotail explosions. J Geophys Res Space Phys (2014) 119:7151–68. doi:10.1002/2014JA020205
83. Sitnov M, Birn J, Ferdousi B, Gordeev E, Khotyaintsev Y, Merkin V, et al. Explosive magnetotail activity. Space Sci Rev (2019) 215:31. doi:10.1007/s11214-019-0599-5
84. Pritchett PL. Externally driven magnetic reconnection in the presence of a normal magnetic field. J Geophys Res Space Phys (2005) 110. doi:10.1029/2004JA010948
85. Pritchett PL. Onset of magnetic reconnection in the presence of a normal magnetic field: Realistic ion to electron mass ratio. J Geophys Res Space Phys (2010) 115. doi:10.1029/2010JA015371
86. Nishimura Y, Lyons LR. Localized reconnection in the magnetotail driven by lobe flow channels: Global MHD simulation. J Geophys Res Space Phys (2016) 121:1327–38. doi:10.1002/2015JA022128
87. Loureiro NF, Schekochihin AA, Cowley SC. Instability of current sheets and formation of plasmoid chains. Phys Plasmas (2007) 14:100703. doi:10.1063/1.2783986
88. Bessho N, Bhattacharjee A. Instability of the current sheet in the Earth’s magnetotail with normal magnetic field. Phys Plasmas (2014) 21:102905.
89. Pritchett PL. Instability of current sheets with a localized accumulation of magnetic flux. Phys Plasmas (2015) 22:062102. doi:10.1063/1.4921666
90. Sitnov MI, Merkin VG, Pritchett PL, Swisdak M. Distinctive features of internally driven magnetotail reconnection. Geophys Res Lett (2017) 44:3028–37. doi:10.1002/2017GL072784
91. Swisdak M. Quantifying gyrotropy in magnetic reconnection. Geophys Res Lett (2016) 43:43–9. doi:10.1002/2015GL066980
92. Pritchett PL, Coroniti FV. Structure and consequences of the kinetic ballooning/interchange instability in the magnetotail. J Geophys Res Space Phys (2013) 118:146–59. doi:10.1029/2012JA018143
93. Runov A, Sergeev VA, Baumjohann W, Nakamura R, Apatenkov S, Asano Y, et al. Electric current and magnetic field geometry in flapping magnetotail current sheets. Ann Geophysicae (2005) 23:1391–403. doi:10.5194/angeo-23-1391-2005
94. Petrukovich AA, Zhang T, Baumjohann W, Nakamura R, Runov A, Balogh A, et al. Oscillatory magnetic flux tube slippage in the plasma sheet. Ann Geophysicae (2006) 24:1695–704. doi:10.5194/angeo-24-1695-2006
95. Sergeev VA, Sormakov DA, Apatenkov SV, Baumjohann W, Nakamura R, Runov AV, et al. Survey of large-amplitude flapping motions in the midtail current sheet. Ann Geophys (2006) 24:2015–24. doi:10.5194/angeo-24-2015-2006
96. Panov EV, Sergeev VA, Pritchett PL, Coroniti FV, Nakamura R, Baumjohann W, et al. Observations of kinetic ballooning/interchange instability signatures in the magnetotail. Geophys Res Lett (2012) 39. doi:10.1029/2012GL051668
97. Gao JW, Rong ZJ, Cai YH, Lui ATY, Petrukovich AA, Shen C, et al. The distribution of two flapping types of magnetotail current sheet: implication for the flapping mechanism. J Geophys Res Space Phys (2018) 123:7413–23. doi:10.1029/2018JA025695
98. Sergeev VA, Angelopoulos V, Nakamura R. Recent advances in understanding substorm dynamics. Geophys Res Lett (2012) 39. doi:10.1029/2012GL050859
99. Pritchett PL, Coroniti FV. Formation of thin current sheets during plasma sheet convection. J Geophys Res Space Phys (1995) 100:23551–65. doi:10.1029/95JA02540
100. Hesse M, Winske D, Birn J. On the ion-scale structure of thin current sheets in the magnetotail. Physica Scripta (1998) T74:63–6. doi:10.1088/0031-8949/1998/t74/012
101. Birn J, Hesse M. Forced reconnection in the near magnetotail: onset and energy conversion in PIC and MHD simulations. J Geophys Res (2014) 119:290–309. doi:10.1002/2013JA019354
102. Lu S, Lin Y, Angelopoulos V, Artemyev AV, Pritchett PL, Lu Q, et al. Hall effect control of magnetotail dawn-dusk asymmetry: A three-dimensional global hybrid simulation. J Geophys Res Space Phys (2016) 121:11,882–11,895. doi:10.1002/2016JA023325
103. Phan TD, Shay MA, Eastwood JP, Angelopoulos V, Oieroset M, Oka M, et al. Establishing the context for reconnection diffusion region encounters and strategies for the capture and transmission of diffusion region burst data by MMS. Space Sci Rev (2016) 199:631–50. doi:10.1007/s11214-015-0150-2
104. Torbert RB, Burch JL, Phan TD, Hesse M, Argall MR, Shuster J, et al. Electron-scale dynamics of the diffusion region during symmetric magnetic reconnection in space. Science (2018) 362:1391–5. doi:10.1126/science.aat2998
105. Cozzani G, Retinò A, Califano F, Alexandrova A, Le Contel O, Khotyaintsev Y, et al. In situ spacecraft observations of a structured electron diffusion region during magnetopause reconnection. Phys Rev E (2019) 99:043204. doi:10.1103/PhysRevE.99.043204
106. Merkin VG, Sitnov MI, Lyon JG. Evolution of generalized two-dimensional magnetotail equilibria in ideal and resistive MHD. J Geophys Res Space Phys (2015) . doi:10.1002/2014JA020651
107. Birn J, Merkin VG, Sitnov MI, Otto A. MHD stability of magnetotail configurations with a hump. J Geophys Res Space Phys (2018) 123. doi:10.1029/2018JA025290
108. Schindler K. A theory of the substorm mechanism. J Geophys Res (1974) 79:2803–10. doi:10.1029/JA079i019p02803
109. Sitnov MI, Merkin VG, Roytershteyn V, Swisdak M. Kinetic dissipation around a dipolarization front. Geophys Res Lett (2018) 45:4639–47. doi:10.1029/2018GL077874
110. Yang Y, Matthaeus WH, Parashar TN, Wu P, Wan M, Shi Y, et al. Energy transfer channels and turbulence cascade in Vlasov-Maxwell turbulence. Phys Rev E (2017) 95:061201. doi:10.1103/PhysRevE.95.061201
111. Nakamura R, Amm O, Laakso H, Draper NC, Lester M, Grocott A, et al. Localized fast flow disturbance observed in the plasma sheet and in the ionosphere. Ann Geophysicae (2005) 23:553–66. doi:10.5194/angeo-23-553-2005
112. Zhou XZ, Angelopoulos V, Sergeev VA, Runov A. On the nature of precursor flows upstream of advancing dipolarization fronts. J Geophys Res Space Phys (2011) 116. doi:10.1029/2010JA016165
113. Eastwood JP, Goldman MV, Hietala H, Newman DL, Mistry R, Lapenta G. Ion reflection and acceleration near magnetotail dipolarization fronts associated with magnetic reconnection. J Geophys Res Space Phys (2015) 120:511–25. doi:10.1002/2014JA020516
114. Liu CM, Vaivads A, Graham DB, Khotyaintsev YV, Fu HS, Johlander A, et al. Ion-beam-driven intense electrostatic solitary waves in reconnection jet. Geophys Res Lett (2019) 46:12702–10. doi:10.1029/2019GL085419
115. Pollock C, Moore T, Jacques A, Burch J, Gliese U, Saito Y, et al. Fast plasma investigation for Magnetospheric Multiscale. Space Sci Rev (2016) 199:331–406. doi:10.1007/s11214-016-0245-4
116. Frank LA, Ackerson KL, Lepping RP. On hot tenuous plasmas, fireballs, and boundary layers in the Earth’s magnetotail. J Geophys Res (1896-19771976) 81:5859–81. doi:10.1029/JA081i034p05859
117. Balogh A, Carr CM, Acuña MH, Dunlop MW, Beek TJ, Brown P, et al. The Cluster magnetic field investigation: Overview of in-flight performance and initial results. Ann Geophysicae (2001) 19:1207–17. doi:10.5194/angeo-19-1207-2001
118. Frühauff D, Plaschke F, Glassmeier KH. Spin axis offset calibration on THEMIS using mirror modes. Ann Geophysicae (2017) 35:117–21. doi:10.5194/angeo-35-117-2017
119. Russell CT, Anderson BJ, Baumjohann W, Bromund KR, Dearborn D, Fischer D, et al. The magnetospheric multiscale magnetometers. Space Sci Rev (2016) 199:189–256. doi:10.1007/s11214-014-0057-3
120. Tsyganenko NA, Singer HJ, Kasper JC. Storm-time distortion of the inner magnetosphere: How severe can it get? J Geophys Res Space Phys (2003) 108. doi:10.1029/2002JA009808
121. Stephens GK, Sitnov MI, Ukhorskiy AY, Roelof EC, Tsyganenko NA, Le G. Empirical modeling of the storm time innermost magnetosphere using Van Allen Probes and THEMIS data: Eastward and banana currents. J Geophys Res Space Phys (2016) 121:157–70. doi:10.1002/2015JA021700
122. Coppi B, Laval G, Pellat R. Dynamics of the geomagnetic tail. Phys Rev Lett (1966) 16:1207–10. doi:10.1103/PhysRevLett.16.1207
123. Yamada M. Review of controlled laboratory experiments on physics of magnetic reconnection. J Geophys Res Space Phys (1999) 104:14529–41. doi:10.1029/1998JA900169
124. Sweet PA. 14. The neutral point theory of solar flares. Symp - Int Astronomical Union (1958) 6:123–34. doi:10.1017/S0074180900237704
125. Parker EN. Sweet’s mechanism for merging magnetic fields in conducting fluids. J Geophys Res (1896-19771957) 62:509–20. doi:10.1029/JZ062i004p00509
126. Petschek HE. Magnetic Field Annihilation. AAS-NASA Symposium on Physics of Solar Flares. NASA Spec. Publ. (1964) 50:425.
127. Birn J, Drake JF, Shay MA, Rogers BN, Denton RE, Hesse M, et al. Geospace Environmental Modeling (GEM) magnetic reconnection challenge. J Geophys Res Space Phys (2001) 106:3715–9. doi:10.1029/1999JA900449
128. Pucci F, Velli M. Reconnection of quasi-singular current sheets: the ideal tearing mode. ApJL (2014) 780:L19. doi:10.1088/2041-8205/780/2/l19
129. Forbes TG, Isenberg PA. A catastrophe mechanism for coronal mass ejections. Astrophysical J (1991) 373:294. doi:10.1086/170051
130. Cassak PA, Shay MA, Drake JF. Catastrophe model for fast magnetic reconnection onset. Phys Rev Lett (2005) 95:235002. doi:10.1103/PhysRevLett.95.235002
131. Lembege B, Pellat R. Stability of a thick two-dimensional quasineutral sheet. Phys Fluids (1982) 25:1995–2004. doi:10.1063/1.863677
132. Pellat R, Coroniti FV, Pritchett PL. Does ion tearing exist? Geophys Res Lett (1991) 18:143–6. doi:10.1029/91GL00123
133. Daughton W. The unstable eigenmodes of a neutral sheet. Phys Plasmas (1999) 6:1329–43. doi:10.1063/1.873374
134. Hesse M, Schindler K. The onset of magnetic reconnection in the magnetotail. Earth, Planets and Space (2001) 53:645–53.
135. Galeev AA, Zelenyi LM. Tearing instability in plasma configurations. Zhurnal Eksperimentalnoi i Teoreticheskoi Fiziki (1976) 70:2133–51.
136. Sitnov MI, Merkin VG. Generalized magnetotail equilibria: Effects of the dipole field, thin current sheets, and magnetic flux accumulation. J Geophys Res Space Phys (2016) 121:7664–83. doi:10.1002/2016JA023001
137. Rich FJ, Vasyliunas VM, Wolf RA. On the balance of stresses in the plasma sheet. J Geophys Res (1972) 77:4670–6. doi:10.1029/JA077i025p04670
138. Walsh AP, Owen CJ, Fazakerley AN, Forsyth C, Dandouras I. Average magnetotail electron and proton pitch angle distributions from Cluster PEACE and CIS observations. Geophys Res Lett (2011) 38. doi:10.1029/2011GL046770
139. Wang CP, Zaharia SG, Lyons LR, Angelopoulos V. Spatial distributions of ion pitch angle anisotropy in the near-Earth magnetosphere and tail plasma sheet. J Geophys Res Space Phys (2013) 118:244–55. doi:10.1029/2012JA018275
140. Asano Y, Mukai T, Hoshino M, Saito Y, Hayakawa H, Nagai T. Statistical study of thin current sheet evolution around substorm onset. J Geophys Res Space Phys (2004) 109. doi:10.1029/2004JA010413
141. Ieda A, Machida S, Mukai T, Saito Y, Yamamoto T, Nishida A, et al. Statistical analysis of the plasmoid evolution with Geotail observations. J Geophys Res Space Phys (1998) 103:4453–65. doi:10.1029/97JA03240
142. Nagai T, Shinohara I, Zenitani S, Nakamura R, Nakamura TKM, Fujimoto M, et al. Three-dimensional structure of magnetic reconnection in the magnetotail from Geotail observations. J Geophys Res Space Phys (2013) 118:1667–78. doi:10.1002/jgra.50247
143. Genestreti K, Fuselier S, Goldstein J, Nagai T, Eastwood J. The location and rate of occurrence of near-earth magnetotail reconnection as observed by Cluster and Geotail. J Atmos Solar-Terrestrial Phys (2014) 121:98–109. doi:10.1016/j.jastp.2014.10.005
144. Wang CP, Lyons LR, Nagai T, Samson JC. Midnight radial profiles of the quiet and growth-phase plasma sheet: The Geotail observations. J Geophys Res Space Phys (2004) 109:12201. doi:10.1029/2004JA010590
145. Machida S, Miyashita Y, Ieda A, Nosé M, Nagata D, Liou K, et al. Statistical visualization of the Earth’s magnetotail based on Geotail data and the implied substorm model. Ann Geophys (2009) 27:1035–46. doi:10.5194/angeo-27-1035-2009
146. Sergeev VA, Gordeev EI, Merkin VG, Sitnov MI. Does a local B-minimum appear in the tail current sheet during a substorm growth phase? Geophys Res Lett (2018) 0. doi:10.1002/2018GL077183
147. Liu J, Angelopoulos V, Runov A, Zhou XZ. On the current sheets surrounding dipolarizing flux bundles in the magnetotail: the case for wedgelets. J Geophys Res Space Phys (2013) 118:2000–2020. doi:10.1002/jgra.50092
Keywords: data mining and knowledge discovery, nearest neighbor method, magnetosphere, magnetotail, magnetic reconnection, space weather, particle-in-cell simulations
Citation: Sitnov M, Stephens G, Motoba T and Swisdak M (2021) Data Mining Reconstruction of Magnetotail Reconnection and Implications for Its First-Principle Modeling. Front. Phys. 9:644884. doi: 10.3389/fphy.2021.644884
Received: 22 December 2020; Accepted: 05 February 2021;
Published: 21 April 2021.
Edited by:
Enrico Camporeale, University of Colorado Boulder, United StatesReviewed by:
Thomas Berger, University of Colorado Boulder, United StatesAnton Artemyev, Space Research Institute (RAS), Russia
Copyright © 2021 Sitnov, Stephens, Motoba and Swisdak. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Mikhail Sitnov, TWlraGFpbC5TaXRub3ZAamh1YXBsLmVkdQ==
 Mikhail Sitnov
Mikhail Sitnov Grant Stephens
Grant Stephens Tetsuo Motoba
Tetsuo Motoba Marc Swisdak2
Marc Swisdak2