- 1Artificial Life Laboratory, Institute of Biology, University of Graz, Graz, Austria
- 2Institute of Mathematics and Scientific Computing, University of Graz, Graz, Austria
Vibratory signals play a major role in the organization of honeybee colonies. Due to the seemingly chaotic nature of the mechano-acoustic landscape within the hive, it is difficult to understand the exact meaning of specific substrate-borne signals. Artificially generated vibrational substrate stimuli not only allow precise frequency and amplitude control for studying the effects of specific stimuli, but could also provide an interface for human-animal interaction for bee-keeping-relevant colony interventions. We present a simple method for analyzing motion activity of honeybees and show that specifically generated vibrational signals can be used to alter honeybee behavior. Certain frequency-amplitude combinations can induce a significant decrease and other signals might trigger an increase in honeybees’ motion activity. Our results demonstrate how different subtle local modulatory signals on the comb can influence individual bees in the local vicinity of the emitter. Our findings could fundamentally impact our general understanding of a major communication pathway in honeybee colonies. This pathway is based on mechanic signal emission and mechanic proprio-reception of honeybees in the bee colony. It is a candidate to be a technologically accessible gateway into the self-regulated system of the colony and thus may offer a novel information transmission interface between humans and honeybees for the next generation of “smart beehives” in future beekeeping.
1 Introduction
Honeybees are not only economically valuable as producers of honey and wax, but most importantly they are highly efficient pollinators of wild flowers and hence they provide exceptionally important ecosystem services [1, 2]. Even beyond ecology, the economic dependency on honeybees for crop production is significant: While the demand for bee-pollinated crops is constantly on the rise, the recently reported steep increases in colony losses have raised concerns about the sustainability of honeybee populations and crop production [3].
The Western honeybee (Apis mellifera L.) has evolved a sophisticated communication system based on a set of very distinct locomotion behaviors, called “dances,” which involve the production and a localized emission of specific mechano-acoustic vibrational patterns. These specific dance types trigger very specific reactions or behavioral modulations in those animals that perceive the emitted stimuli. These dances form, in their totality, the “dance language” of the honeybees. Most notably the “waggle dance” is used for recruiting nest mates to a specific foraging source. A dancing bee communicates the location of a food source by a repeated figure-eight shaped movement. The direction of the linear waggle phase relative to gravity represents the direction of the food source relative to the sun, while the duration of each run increases with the distance of the food source [4]. To decode the information from such a dance, the observer bees have to closely follow the movements of the dancing bee. As the inside of a hive is usually dark, information cannot be transferred visually but instead via vibrations emitted during the waggling phase of each waggle dance circuit. The vibration signals are typically composed of a ca. 15 Hz body movement and a 200–300 Hz vibration produced by the flight muscles [5, 6]. It has been shown that these signals also travel through the comb which can act as an amplifier [7, 8]. Therefore the comb itself is the medium for sound transmission and the content of the cells affects the number of dance followers, with empty cells attracting more recruits [7, 9]. Other bees may not only interact with a dancer by following her runs but they can also interfere with the waggle dances and interrupt them. For example, if another bee encounters a dance advertising a food source that she already knows to be sub-optimal, she may send a “stop signal” [10]. In this case the bee bumps her head into the advertising dancer and emits another specific vibrational signal in parallel to the head-butting [11]. As a consequence, the dancing bee often stops advertising its food source. A similar effect of stopping the previously executed behavior can be triggered artificially in lab studies: When bees were stimulated with sinusoidal sound vibrations emitted onto the honeycomb, they reacted with spontaneous movement stops, what is called the “freezing response” [12–14]. While these stop and freezing signals are characterized by higher frequency vibrations, low frequency vibrations of ca. 10–40 Hz may be associated with increased activity levels of bees [15–17]. In addition, other signals and feedback mechanisms are involved in the coordination of foraging by the bee colony [18]. We pick up this line of research on the fundamental mechano-physical aspects of honeybee interaction. In our study, we aim to understand the effects of vibrations on the individual and collective behavior of honeybees. The main research question that drives our study is “How do specifically shaped vibration patterns on the combs alter the behavior of the bees that perceive these stimuli?.” The answers to this research question can offer insights into the recruitment processes that governs the individual foraging behavior and the collective foraging patterns that arise from them. This might be a door opening method for novel technology to boost the pollination service, and ultimately also the ecosystem service provided by a honeybee colony in a new generation of “smart beehives.”
2 Materials and Methods
Our basic concept in the setup of our experiments was initially inspired by the setup reported in [12] and further elaborated to reflect and incorporate the technological progress we can build upon. However, these innovations allowed us to make significant improvements in the research focus and in the level of detail of our observations: Instead of subjectively evaluating the bees’ behavioral responses, we use here a simple but effective pixel-based evaluation metric to measure the change in motion activity. This allowed us to quantify the behavioral responses instead of reporting only qualitative annotations. We refrained from using a modified loudspeaker to transfer the vibrational stimulus onto the comb via a physical/mechanical bridge, but integrated a thin piezoelectric loudspeaker into the honeycomb itself, to alter the natural environment on the honeycomb as little as possible.
2.1 Experimental Setup
All experiments were conducted on a small honeybee colony (approx. 1,500 bees) housed in a one-comb observation hive (see Figure 1E). The hive was located inside a building with the hive entrance being connected to the outside, allowing the bees to forage in a natural habitat. In our experimental setup, a commercially available food-grade plastic honeycomb, as frequently used by beekeepers, was modified in the following way: The outer frame elements of two plastic honeycombs were shortened on one side each and both were joined together to form a new combined double-layered honeycomb with a slim space in between the two middle layers to allow cables and devices to reside in this cavity (see Figure 1B). Into this cavity, which was approx 10 mm wide, four piezoelectric elements were inserted (see Figures 1A,D). One of these piezoelectric elements (Murata 7BB-27-4L0) served as the emitter of the vibration stimuli we tested here, while the other three elements were used for signal recording for control and adjustment purposes. The emitter was placed at a specific area of the comb, the so-called “dance floor region,” the region in the hive where the majority of forager recruitment dances happen. After these preparations, the honeycomb was covered with a thin layer of wax and placed in a conventional full-sized colony beehive for 10 weeks. During this time, it was fully accepted by bees and filled with cells containing brood, pollen and nectar and received the required chemical nest-scent which is important for acceptance of the comb. The honeycomb was then transferred into the experimental observation hive, replacing the original comb that the experimental colony had in usage up until then. We waited for additional 2 weeks for the experimental colony to fully accept the modified comb before starting to conduct the experiments. The experiments were recorded digitally as video with a Canon D5 camera (see Figure 1C). In the experiments we report here, a python script was used for the stimulus generation (see Figure 1G). We tested 19 different sinusoidal frequencies: From 50 to 750 Hz in 50 Hz steps, from 1000 to 2500 Hz in 500 Hz steps, and in addition, we examined the effect of white noise. We repeated the excitation for each stimulus 12 times. The intensities used for each frequency stimulus are shown in Figure 2C. In addition, we tested the effect of different amplitude levels on the bees’ response at 50, 500, and 5000 Hz and repeated each amplitude-frequency combination 10 times (shown in Figures 3D–F). These sinusoidal stimuli were passed through an audio amplifier (see Figure 1F) to the emitter inside the honeycomb. All experiments were carried out in continuous 30-min experiment cycles (see Figure 1L), which were recorded on video at 25FPS. Each cycle consisted of a series of 5 s long stimulus periods with vibrational emissions of specific frequencies and amplitudes, alternated by 10-s periods without any active stimulus emissions. The sequence of frequencies and amplitudes was produced in a randomized order.
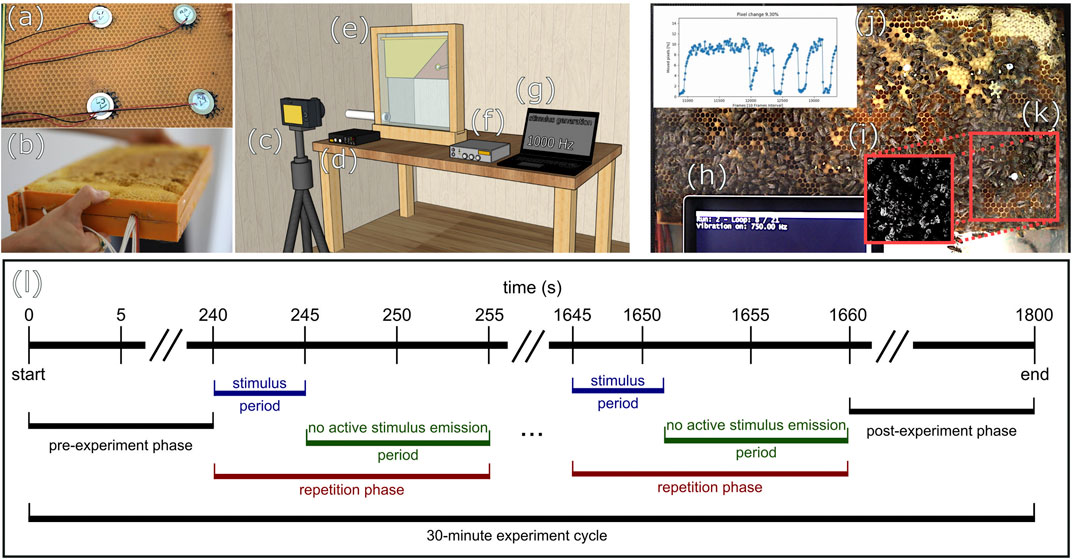
FIGURE 1. Modified honeycomb, experimental setup, and exemplary video frame with overlays (A) placement of piezoelectric elements on the inner side of the comb, (B) closed modified comb, (C) camera, (D) sound recorder, (E) observation beehive (position of vibration-emitter in diagram exposed), (F) amplifier, (G) frequency generation, (H) information on the actuation status, (I) motion detection in ROI: value changes between frames below (black) and above (white) threshold, (J) average PMI of ROI over time, (K) red markings indicate the position of ROI, (L) diagram of exemplary experiment cycle.
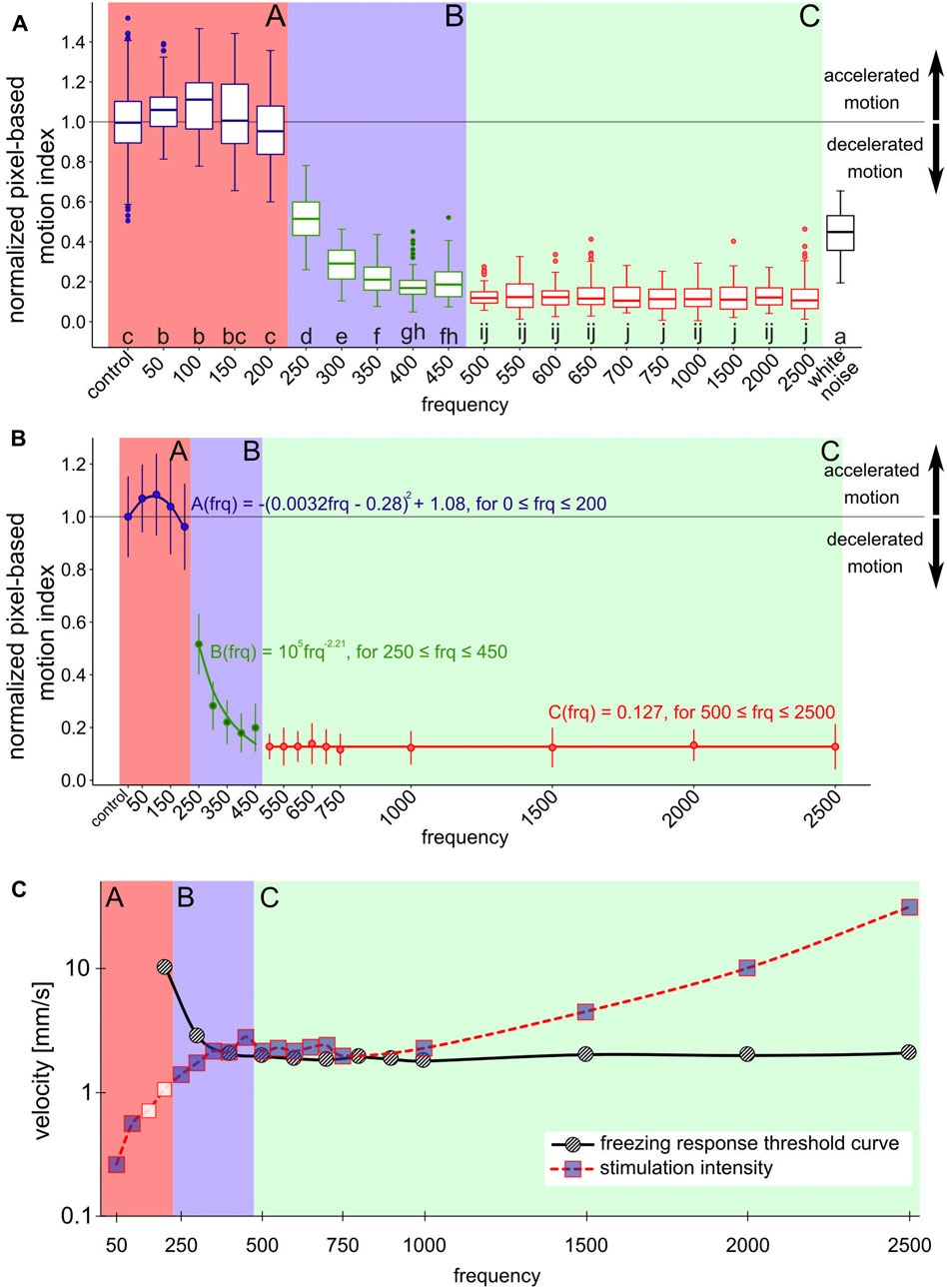
FIGURE 2. Normalized pixel-based motion index depending on the stimulus frequency (A) boxplots show the distribution of normalized PMI measurements to the respective frequency stimulus. 12 repetitions per frequency, each repetition phase consists of 5 s of stimulus, filmed at 25 FPS. 10 FPS are combined into one measurement, first and last measurement of each stimulus period were discarded. Same lowercase letters indicate non-significantly different data groups (pairwise Wilcoxon tests, Bonferroni–Holm adjusted p-value) [25]. Colored backgrounds indicate areas with related data groups. Section A: control to 200 Hz stimulus, high basic PMI; section B: 250–450 Hz stimulus, sharply decreasing PMI; section C: 500–2500 Hz stimulus, low PMI. Outside these ranges: white noise (B) shows the data as mean values and the corresponding standard deviation with correctly spaced frequency intervals. Models describing the courses of frequency dependence of the PMI were fitted to the mean values for the respective data groups in section A,B,C. Section A is described by a parabolic function, section B by a power function and section C by a line (C) shows the intensities of the stimulations at the respective frequencies (squares and red dotted line) measured at the position of the highest intensity on the surface of the comb. The figure also includes threshold curve of the freezing response (black solid line), data adopted from [14]. Incorporated into the dependency of frequency and displacement amplitude is also the change of PMI: blue fill color of the squares indicates a change in motion activity compared to control.
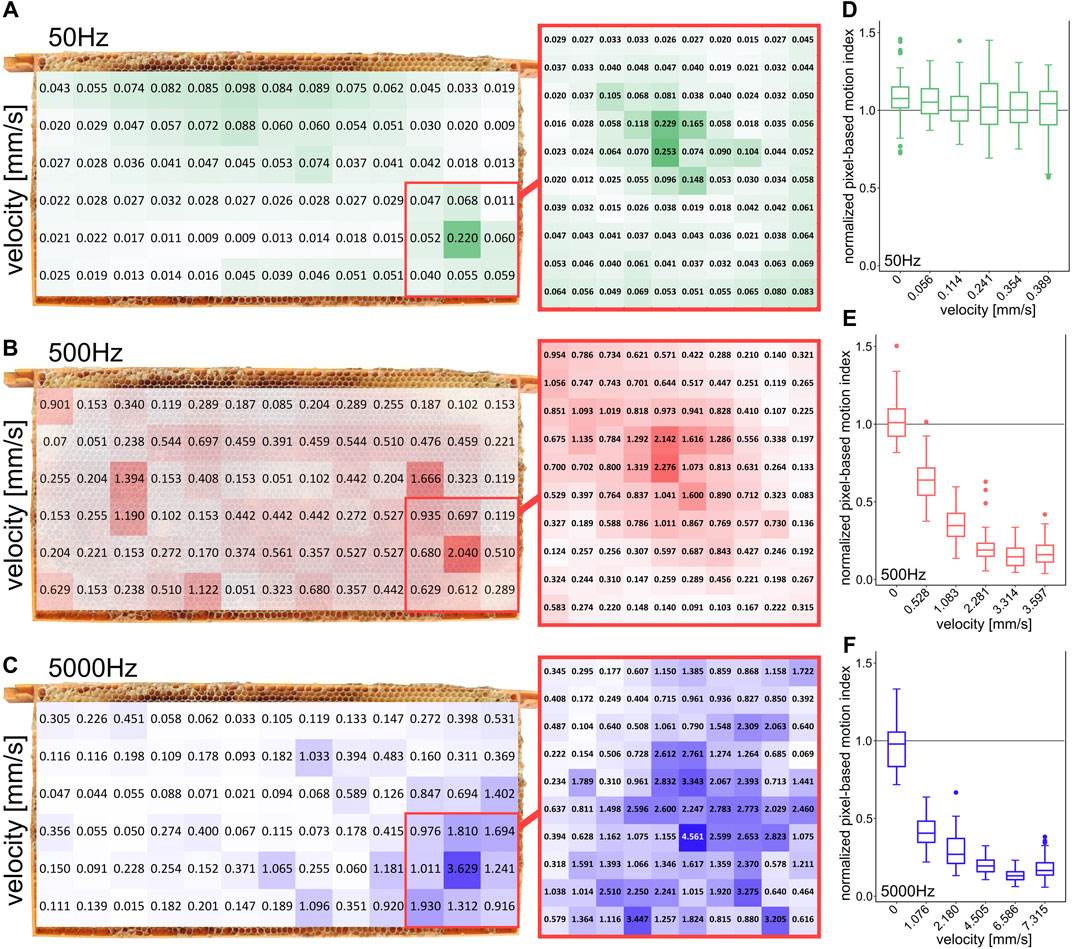
FIGURE 3. Spatial distribution of local vibration stimulation intensities and effect of stimulation intensity on changes in honeybee movement activity (A–C) local intensity measurements on the comb at 50, 500, and 5000 Hz, (D–F) normalized pixel-based motion index of bee activity in the region of interest depending on different signal intensities for 50, 500, and 5000 Hz (10 repetitions per group). Signal intensity measured at the comb position of maximum intensity at the corresponding frequency.
2.2 Optical Motion Activity Analysis
The experimental video recordings were processed after all experiments were completed. For the evaluation of the honeybees’ motion activity modulations induced by the vibrational patterns, we defined a pixel-based motion index (PMI) according to Eqs. 2, 3. A square-shaped region of interest (ROI) was defined around the emitter of the vibrational stimuli, with a size of 400 × 400 pixels in each frame, respectively, 10 × 10 cm on the comb. Within this ROI, the three color (red, green blue) channels were combined into one average gray-scale image array for each frame t as
Each array element value of the gray-scale
An exemplary frame of such a video recording with an indicated ROI is shown in Figures 1H–K. Figure 4 shows four example PMI arrays at different frequency excitations before arithmetic averaging of the arrays. The experiments were conducted over the course of 2 days at the end of August 2019. To account for differences in the general motion activity levels that the bees exhibited between experimental cycles, each

FIGURE 4. Comparison of
2.3 Intensity Measurements
The effects of different intensities on the motion activity of the bees at various frequencies (50, 500, and 5000 Hz) were measured (Figures 3D–F). For this purpose, intensities were chosen that were respectively lower and higher than the intensities used for the frequency-dependent experiments (which are shown in Figure 2C). The actual vibration intensity on the surface of a comb depends on the size of the comb, on the type of comb and foundation, on the housing and on the position of the measurement [8, 20]. Also the content of the comb, respectively the bees themselves, might influence the pervading vibrations [21]. To show the distribution of the vibration intensity on the comb surface, we measured the intensity for different frequencies (50, 500, 5000 Hz) in a 3 × 3 cm grid for the whole comb and a finer grid within the ROI (1 × 1 cm). Since intensity measurements with a laser vibrometer required direct, uninterrupted contact with the surface of the comb, these measurements could not be conducted in an inhabited hive. After the completion of the behavior experiments, the colony was removed from the comb and the bees were transferred to another hive. The same observation hive and the experimental comb, which still contained comb alterations of the bees affecting the vibration propagation (food in cells, potentially brood), was used for post-hoc evaluation. The intensity measurements were conducted at a later point in time, the comb was stored in a freezer in between. Changes that might alter the intensity of vibration on the front side of the comb can therefore not be ruled out. Hence, the distribution of vibration shown in Figures 3A–C can only indicate the actual distribution of vibration intensity in the live experimental setup. To prepare the intensity measurements, we put self-adhesive reflector tapes on the surface of the honeycomb at even intervals. We measured the intensity exactly at the center of each grid measurement point. We generated the vibration stimuli of the behavioral experiments with a piezotransducer and simultaneously recorded it with three surrounding piezoelectric sensors. To make the post-hoc laser-measurement evaluation as comparable as possible, the vibration generation was performed the same as in the behavior experiments and was additionally recorded by the same piezoelectric sensors. The intensities in these recordings were digitally measured to match with the previously digitally measured intensities of the behavior experiment recordings. The alignment showed comparable digital intensities at the different frequencies tested. After we were able to ensure similar vibration intensities through this step, we conducted more precise intensity measurements using a laser vibrometer (Polytec PDV 100), the measurements are shown in Figures 2C, 3. The data was transmitted to the Polytec Vibrometer software (V5.2.2) via the USB break-out box (VIB-E-220). In this software the magnitude was measured as velocity via fast Fourier transform.
2.4 Statistical Analysis
We used the software package R [22] with the RStudio IDE [23] for the majority of our analyses. The package collection tidyverse [24] was used for graphs and exploratory data analysis. For comparing effects of different frequency stimuli, a two sided pairwise Wilcoxon rank sum test with Bonferroni–Holm family wise error rate adjustment was used. Test results are represented as lowercase letters [25], whereas the same letters indicate a nonsignificant comparison
2.5 Code Availability
For reproducible code a public Github repository1 under MIT licence was created. It includes the exported dataset, session info with packages, the code used for the statistical analysis, and the exported pairwise comparison test results.
3 Results
3.1 Motion Activity Depending on the Stimulus Frequency
Figure 2 shows the normalized PMI (Eqs. 2, 3) in response to the frequency of the applied vibration. All data groups were compared pairwise (Figure 2A). This allowed us to classify the data into three distinct frequency-defined sections that share a common behavior: When bees were stimulated with frequencies located in section A (in the range of 50–200 Hz, respectively the control group), the observed bees in the ROI did not show a significantly reduced motion activity in the normalized PMI, but even a slight increase in activity at low frequencies, with a maximum at 100 Hz. Further increasing the frequency of the signal yielded a diminishing of the reaction back again to the level observed in the control group at the highest frequency in section A, which is 200 Hz. In contrast to that, when stimulating the bees with frequencies within section B (250–450 Hz) a different pattern was observed in the reaction of the bees: They exhibited a significant decrease in their normalized PMI with increasing frequencies. A further increase of frequencies covered by section C (500–2500 Hz) resulted in a low normalized PMI, independent of the exact frequency.
To further detail the observed dependencies of behavioral modulation and bees on the frequencies of the emitted stimuli, we fitted a set of regression functions for every section. These functions model the expected behavioral modulation of the PMI with respect to the tested vibrational frequencies (Figure 2B), in order to allow prediction of the honeybees’ responses to signals in the regions on the frequency band between the tested frequencies. The honeybees’ response to signals with frequencies in section A can be predicted by a parabolic function (
In addition to the effect of specific frequencies, we also tested the effect of white noise onto the bees’ motion behavior. As Figure 2A shows, this signal, which is composed by the definition of a collection, or a sum of all possible frequencies, triggered again a clear, but not a maximal, response in the honeybees’ motion modulation. We observed that this mixed-frequency signal reduced the PMI down to be about four times higher than the lowest observed PMI and was found to be a response similar to a clean sinusoidal signal of 250 Hz.
Exemplary results showcasing the different PMI for the control group, 100 Hz, white noise and 750 Hz are shown in Figures 4A–D.
3.2 Motion Activity Depending on the Stimulus Intensity
We also observed the influence of the signal’s amplitude onto the observable behavioral modulation of the recipients’ motion behavior. However, the actual vibration intensities on the comb surface varied significantly depending on various factors. To map an impression of the distribution of intensities on the surface of the honeycomb, we measured the intensities for three different frequencies at different locations (Figures 3A–C). The highest intensities were measured near the emitter in the center of the ROI for all frequencies. The emitter was placed in the inner side of the hollow honeycomb.
Figures 3D,E shows the dependence of the freezing response on the amplitude of the emitted sinusoidal signal. For three specific frequencies, the normalized PMI was determined for different intensity levels. At 50 Hz, no significant change in motion activity was detected regardless of the applied stimulus magnitude. At 500 Hz a reduction of motion activity between video frames was determined at a velocity of 0.528 mm/s and at 5000 Hz at a velocity of 1.076 mm/s. At 500 Hz and an intensity of more than 2.281 mm/s, respectively, at 5000 Hz and an intensity of more than 4.505 mm/s no further reduction of the PMI was detected.
3.3 Correlation of Frequency and Displacement Amplitude
In order to provide a final interpretation of our data and to see its standing within the existing body of literature, we conducted a post-hoc meta-analysis on reference data from literature, which is shown in Figure 2C. This graph depicts a 3Dimensional view of our data: The X-Y plane depicts the relationship between frequencies and displacement amplitude of the stimuli in our experiments (measured directly on the emitter). The color of the data points represents our experimental results in a summarized way: data points filled in blue indicate a significant response of honeybees to a stimulus compared to the control data set. In addition to that, a threshold curve for the freezing response, redrawn from [14], has been added as a reference data set to this graph.
4 Discussion
4.1 Stimuli Generation for Studying Honeybee Communication Pathways
Much research effort has been invested over the past 50 years to explore the effects of substrate-born vibrations in the honeybee colony [26–30]. One common approach of such studies has been to playback vibration signals onto the combs [31, 32]. However, these signals consist of a convolution of many frequencies, they are often modulated, and can be very complexly structured. Another approach has been to study the effects of pure-tone sinusoidal frequencies, such was the study that first reported on the freezing response of honeybees to these stimuli [12]. The study reports a decreased locomotive activity, especially with frequencies in a range of 500–1000 Hz. No such freezing response was reported at a frequency below 100 Hz or above 2500 Hz. The excitation of the subgenual organs of a honeybee is a mechanical energy transfer, thus the energy that the signal contains is expected to be important. This energy depends on the signal’s amplitude and on the frequency in combination, additionally affected by material properties in the medium it spreads and wave-based effects like interference patterns, harmonic oscillations, the geometry of the substrate and dampening effects. The behavioral response of the animals depends not only on the specific frequency, or a specific amplitude, but on the combination of these two and the measurement point on the honeycomb [14]. showed the threshold for the required signal amplitude. Such a threshold curve indicates the expected set of minimum signal prerequisites in order to expect a specific behavioral response (redrawn as a reference data set in Figure 2C). The stimulus intensities applied in our experiments can be grouped into three distinct regions: In the range of 50–300 Hz, the stimuli we generated were below the predicted behavior response threshold, thus if the prediction holds we should not have observed the responses that we did observe. In the region of 350–1000 Hz, the stimuli we generated were approximately at the threshold level of the behavioral response, thus also here the previous predictions we found in the existing literature need to be questioned, given that the behavioral responses we observed are too significant to assume that the sensorial or behavioral threshold was just matched. Such a match would suggest that we see weak to medium responses, as such thresholds differ across individuals and over time, thus we should expect only a fraction of the bees in the ROI reacting to such borderline signals. Only for signals in the 1500–2500 Hz range did the intensity of our signals lie above the threshold curve described in the literature and thus lead to the predicted behavioral responses. Studies have already shown that the physiological threshold of the subgenual organ of honeybees is lower than the behavioral threshold [33]. It is possible that the behavioral threshold to vibration intensity was underestimated so far due to the subjective assessment of the behavioral response.
In addition, our experiments potentially indicate that stimulus intensities well below the reported behavioral threshold for signals in the 50–100 Hz frequency range produce the opposite effect of a freezing response: The PMI showed a statistically significant increase in motion activity. This behavioral response to these vibrational stimuli was previously unknown and, to our knowledge, is the first time such a behavioral response to an artificial stimulus has been observed. Our finding result from statistical evaluation of the data and does not imply any behavioral/biological relevance of this stimulus response. In a second series of experiments measuring the effect of vibration intensity on behavioral modification, no increase in activity was detected with a pure tone of 50 Hz, regardless of intensity (see Figure 3D). Activating vibration signals are known to occur in natural honeybee colonies, in particular the shaking dance. This signal is reported to cause a non-specific increase in activity [16]. However, the frequencies associated with this signal are significantly lower (
4.2 Strengths and Weaknesses of the Applied PMI Metric
In contrast to the qualitative observer-based evaluation used in the literature so far, the rather objective, as it is based on a computer algorithm, and quantitative motion index metric used here allows for a simple pixel-based assessment of the observed honeybees’ motion activity. This analysis reveals more details in the evaluation of vibration signal effects on honeybee behavior. For example, without such a quantitative approach, it would not have been possible to generate a model, based on three regression functions, that allows predicting the bees’ responses to specific frequencies in a quantitative way. This is a fundamental new piece of evidence that can be utilized in technological approaches of human-honeybee interaction, for example in “smart beehives.” However, this method of assessment also has its weaknesses and does not evaluate strictly the actual stimulus-behaviour response of the bees themselves, but uses rather the resulting optical flow as a proxy for quantification of the video frames. But nevertheless, this simple method already allows quantification of changes in the overall movement patterns at certain areas on the comb over time, a feature that might suffice for informing mean-field model based approaches of this system in the future. For individual-based models the data would need to be extracted rather on an individual bee level, with sophisticated image tracking and individually marked bees. Such systems already exist and are proven to be effective with honeybees [34–36], however, these setups demand for much more sophisticated computer hardware than we used here, as our method could easily be performed in an all-in-one solution with a simple low-cost and low-energy computing solution, likely even operating on a live datastream and in a closed-loop setup in the near future.
In this work we show that artificially generated vibration patterns on the comb can affect the locomotor activity of bees. The surface of the honeycomb serves as a communication platform through which the vibrations are transmitted. Many factors influence the intensity of the signals on the surface of the honeycomb [8, 20, 21]. Also in our experiments, the intensity of the stimulus decreased very rapidly as a function of distance from the emitter, respectively, a very complex intensity pattern emerged, even within the ROI (see Figures 3A–C). Nevertheless, certain well-defined frequency-amplitude combinations result in significant downregulation of their motion, while others may result in upregulation. Understanding these responses could be a door opener for targeted interventions in the signal cascade of the colony. The dance floor, where the waggle dances occur, is not the only the location where information is passed on from returning foragers to the bees inside the colony, this information is also further processed by a network of interacting bees, shaping the foraging patterns of the colony as a whole [37]. By downregulating the locomotor activity of the bees on the dance floor via artificial vibrations, the information flow on the dance floor will be disturbed and changes in the foraging patterns of the colony may arise as a result of this intervention. Especially since small interventions in the worker allocation system, which is composed of many feedback loops [18], could alter individual feedbacks and thus change the way the system works. If these interventions could be triggered automatically in a controlled way when dances to potentially hazardous forage sites (like fields freshly sprayed with pesticides) were detected, a mechanism could be established to protect the colony from a potentially fatal foraging decision. Whether or not the potential upregulation of motion activity we observed at low frequencies could potentially be used to stimulate foraging activities requires further studies.
Data Availability Statement
The datasets presented in this study can be found at: https://github.com/martin-st/motion-analysis-of-honeybees.
Ethics Statement
According to the animal care principles of our institution and the current animal protection laws of Austria, experiments on insects do not fall under animal experiments requiring a permit. However, during our work we attach great importance to causing as little harm to the animals as possible.
Author Contributions
MS developed the core hypothesis in this article together with TS and HO. MS and HO conducted the experiments and generated the Python code to determine the pixel change. MS, HO, MB, and TS wrote the text of the article together in a collaborative effort. MS designed Figures 1, 4 with input of MB and TS. MS and HO designed Figures 2, 3 with input of MB and TS. HO performed the data analyses and implemented the R Code for Figures 2, 3. GH improved the PMI calculation performance by implementing multiprocessing.
Funding
This work was supported by the Field of Excellence “Complexity of Life in Basic Research and Innovation” (COLIBRI) at University of Graz and the EU H2020 FET-Proactive project “HIVEOPOLIS” (no. 824069).
Conflict of Interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Footnotes
1https://github.com/martin-st/motion-analysis-of-honeybees
References
1. Klein A-M, Vaissière BE, Cane JH, Steffan-Dewenter I, Cunningham SA, Kremen C, et al. Importance of Pollinators in Changing Landscapes for World Crops. Proc R Soc B (2007) 274:303–13. doi:10.1098/rspb.2006.3721
2. Gallai N, Salles J-M, Settele J, Vaissière BE. Economic Valuation of the Vulnerability of World Agriculture Confronted with Pollinator Decline. Ecol Econ (2009) 68:810–21. doi:10.1016/J.ECOLECON.2008.06.014
3. Kearns CA, Inouye DW, Waser NM. ENDANGERED MUTUALISMS: The Conservation of Plant-Pollinator Interactions. Annu Rev Ecol Syst (1998) 29:83–112. doi:10.1146/annurev.ecolsys.29.1.83
4. von Frisch K. The Dance Language And Orientation Of Bees (Cambridge, MA: Harvard University Press 2013) (1967) doi:10.4159/harvard.9780674418776
5. Esch H. Über die Schallerzeugung beim Werbetanz der Honigbiene. Z Vergl Physiol (1961) 45:1–11. doi:10.1007/bf00297754
6. Michelsen A, Towne WF, Kirchner WH, Kryger P. The Acoustic Near Field of a Dancing Honeybee. J Comp Physiol (1987) 161:633–43. doi:10.1007/bf00605005
7. Nieh JC, Tautz J. Behaviour-locked Signal Analysis Reveals Weak 200-300 Hz Comb Vibrations during the Honeybee Waggle Dance. J Exp Biol (2000) 203:1573–9. doi:10.1242/jeb.203.10.1573
8. Tautz J, Casas J, Sandeman D. Phase Reversal of Vibratory Signals in Honeycomb May Assist Dancing Honeybees to Attract Their Audience. J Exp Biol (2001) 204:3737–46. doi:10.1242/jeb.204.21.3737
9. Tautz J, Rohrseitz K. What Attracts Honeybees to a Waggle Dancer? J Comp Physiol A: Sensory, Neural Behav Physiol (1998) 183:661–7. doi:10.1007/s003590050289
10. Kietzman PM, Visscher PK. The Anti-waggle Dance: Use of the Stop Signal as Negative Feedback. Front Ecol Evol (2015) 3:14. doi:10.3389/fevo.2015.00014
11. Nieh JC. The Stop Signal of Honey Bees: Reconsidering its Message. Behav Ecol Sociobiol (1993) 33:51–6. doi:10.1007/bf00164346
12. Little HF. Reactions of the Honey Bee, Apis mellifera L., to Artificial Sounds and Vibrations of Known Frequencies1. Ann Entomol Soc America (1962) 55:82–9. doi:10.1093/aesa/55.1.82
13. Spangler HG. Suppression of Honey Bee Flight Activity with Substrate Vibration123. J Econ Entomol (1969) 62:1185–6. doi:10.1093/jee/62.5.1185
14. Michelsen A, Kirchner WH, Lindauer M. Sound and Vibrational Signals in the Dance Language of the Honeybee, Apis mellifera. Behav Ecol Sociobiol (1986) 18:207–12. doi:10.1007/bf00290824
15. Gahl RA. The Shaking Dance of Honey Bee Workers: Evidence for Age Discrimination. Anim Behav (1975) 23:230–2. doi:10.1016/0003-3472(75)90068-8
16. Schneider SS, Lewis LA. The Vibration Signal, Modulatory Communication and the Organization of Labor in Honey Bees, apis Mellifera. Apidologie (2004) 35:117–31. doi:10.1051/apido:2004006
17. Hrncir M, Maia-Silva C, Farina WM. Honey Bee Workers Generate Low-Frequency Vibrations that Are Reliable Indicators of Their Activity Level. J Comp Physiol A (2019) 205:79–86. doi:10.1007/s00359-018-1305-x
18. Anderson C, Ratnieks FLW. Worker Allocation in Insect Societies: Coordination of Nectar Foragers and Nectar Receivers in Honey Bee (Apis mellifera) Colonies. Behav Ecol Sociobiol (1999) 46:73–81. doi:10.1007/s002650050595
19. Mariano P, Salem Z, Mills R, Schönwetter-Fuchs-Schistek S, Correia L, Schmickl T. Evolving Robot Controllers for a Bio-Hybrid System. In: Artificial Life Conference Proceedings. (MIT Press) (2018) p. 155–62.
20. Sandeman D, Tautz J, Lindauer M. Transmission of Vibration across Honeycombs and its Detection by Bee Leg Receptors. J Exp Biol (1996) 199:2585–94. doi:10.1242/jeb.199.12.2585
21. Tautz J. Honeybee Waggle Dance: Recruitment success Depends on the Dance Floor. J Exp Biol (1996) 199:1375–81. doi:10.1242/jeb.199.6.1375
22.R Core Team. R. A Language and Environment for Statistical Computing. Vienna, Austria: R Foundation for Statistical Computing (2020).
23.RStudio Team. RStudio: Integrated Development Environment for R. Boston, MA: RStudio, PBC (2021).
24. Wickham H, Averick M, Bryan J, Chang W, McGowan L, François R, et al. Welcome to the Tidyverse. Joss (2019) 4:1686. doi:10.21105/joss.01686
25. Piepho H-P. An Algorithm for a Letter-Based Representation of All-Pairwise Comparisons. J Comput Graphical Stat (2004) 13:456–66. doi:10.1198/1061860043515
26. Simpson J. The Mechanism of Honey-Bee Queen Piping. Z für vergleichende Physiologie (1964) 48:277–82.
27. Ohtani T, Kamada T. ‘Worker Piping': The Piping Sounds Produced by Laying and Guarding Worker Honeybees. J Apicultural Res (1980) 19:154–63. doi:10.1080/00218839.1980.11100016
28. Hrncir M, Barth FG, Tautz J. 32 Vibratory and Airborne-Sound Signals in Bee Communication (Hymenoptera). Insect sounds Commun Physiol Behav Ecol Evol (2005) 421. doi:10.1201/9781420039337.CH32
29. Seeley T, Tautz Jx. r. Worker Piping in Honey Bee Swarms and its Role in Preparing for Liftoff. J Comp Physiol A: Sensory, Neural Behav Physiol (2001) 187:667–76. doi:10.1007/s00359-001-0243-0
30. Schlegel T, Visscher PK, Seeley TD. Beeping and Piping: Characterization of Two Mechano-Acoustic Signals Used by Honey Bees in Swarming. Naturwissenschaften (2012) 99:1067–71. doi:10.1007/s00114-012-0990-5
31. Michelsen A, Kirchner WH, Andersen BB, Lindauer M. The Tooting and Quacking Vibration Signals of Honeybee Queens: a Quantitative Analysis. J Comp Physiol (1986) 158:605–11. doi:10.1007/bf00603817
32. Kirchner W, Dreller C, Towne W. Hearing in Honeybees: Operant Conditioning and Spontaneous Reactions to Airborne Sound. J Comp Physiol A (1991) 168:85–9. doi:10.1007/bf00217106
33. Kilpinen O, Storm J. Biophysics of the Subgenual Organ of the Honeybee, apis Mellifera. J Comp Physiol A (1997) 181:309–18. doi:10.1007/s003590050117
34. Wario F, Wild B, Couvillon MJ, Rojas R, Landgraf T. Automatic Methods for Long-Term Tracking and the Detection and Decoding of Communication Dances in Honeybees. Front Ecol Evol (2015) 3:103. doi:10.3389/fevo.2015.00103
35. Boenisch F, Rosemann B, Wild B, Dormagen D, Wario F, Landgraf T. Tracking All Members of a Honey Bee colony over Their Lifetime Using Learned Models of Correspondence. Front Robot AI (2018) 5:35. doi:10.3389/frobt.2018.00035
36. Gernat T, Rao VD, Middendorf M, Dankowicz H, Goldenfeld N, Robinson GE. Automated Monitoring of Behavior Reveals Bursty Interaction Patterns and Rapid Spreading Dynamics in Honeybee Social Networks. Proc Natl Acad Sci USA (2018) 115:1433–8. doi:10.1073/pnas.1713568115
Keywords: honeybees, behavior, substrate-born communication, modulatory signals, freezing responds
Citation: Stefanec M, Oberreiter H, Becher MA, Haase G and Schmickl T (2021) Effects of Sinusoidal Vibrations on the Motion Response of Honeybees. Front. Phys. 9:670555. doi: 10.3389/fphy.2021.670555
Received: 21 February 2021; Accepted: 20 May 2021;
Published: 10 June 2021.
Edited by:
Natasha Mhatre, Western University, CanadaReviewed by:
Michael Hrncir, University of São Paulo, BrazilDamian Octavio Elias, University of California, Berkeley, United States
Copyright © 2021 Stefanec, Oberreiter, Becher, Haase and Schmickl. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Martin Stefanec, bWFydGluLnN0ZWZhbmVjQHVuaS1ncmF6LmF0
 Martin Stefanec
Martin Stefanec Hannes Oberreiter1
Hannes Oberreiter1 Thomas Schmickl
Thomas Schmickl