Densest-Packed Columnar Structures of Hard Spheres: An Investigation of the Structural Dependence of Electrical Conductivity

Identical hard spheres in cylindrical confinement exhibit a rich variety of densest-packed columnar structures. Such structures, which generally vary with the corresponding cylinder-to-sphere diameter ratio D, serve as structural models for a variety of experimental systems at the micro- or nano-scale. In this research, the electrical conductivity as a function of D has been studied for four different types of such columnar structures. It was found that, for increasing D, the electrical conductivity of each type of structures decreases monotonously, as a result of the system’s resistive components becoming more densely packed along the long axis of the cylindrical space. However, there exists a discontinuous rise in the system’s electrical conductivity at $D=1+\sqrt{3}/2$ (discontinuous zigzag-to-single-helix transition) and D = 2 (discontinuous double-helix-to-double-helix transition), respectively, as a result of the establishment of additional conducting paths upon an abrupt increase in the number of inter-particle contacts. This is not the case for the continuous single-helix-to-double-helix transition at $D=1+4\sqrt{3}/7$. The results, which tell us how the system’s electrical conductivity can be tuned through a variation of D, could serve as a guide for the development of quasi-one-dimensional materials with a structurally tunable electrical conductivity.

1 Introduction

Packing problems [1], which concern the optimal arrangements of objects in space, have historically been of great interest to both physicists and mathematicians. Such problems not only pose sufficient intellectual challenges for mathematicians [2], but they also yield solutions that physicists can use as theoretical models to understand the structures of matter [3–6]. Prominent examples include the application of the face-centered cubic (fcc) and hexagonal close-packed (hcp) structures as models for bulk crystal structures of solids [4] and the application of random close packings as models for bulk amorphous structures of liquids [3, 6]. In contrast to these examples for bulk systems, the past few decades have seen an uprising interest in the packings of particles in confined settings, such as those of particles confined within a two-dimensional box [7, 8], within a parallel strip [9–14], within a spherical container [15, 16], within a cylindrical container [17–36], onto a cylindrical surface [37], between parallel plates [38–46], within a wedge cell [47, 48], or within a flexible container [49]. In particular, for packings of identical spheres in cylindrical confinement, more than fifty densest-packed columnar structures have been discovered within a relatively narrow range of the cylinder-to-sphere diameter ratio D [17, 22, 24, 29, 30] where, intriguingly, many of such columnar structures exhibit unexpected chirality despite the simplicity of the confining cylindrical geometry. On the other hand, such columnar structures of spheres have been observed for a variety of experimental systems at both the micro- [50–56] and the nano-scale [57–63]. This problem of confined packings has recently been extended to shape-anisotropic particles [13, 14, 36, 37], for which a variety of confinement-induced crystal structures with specific orientational order have been discovered.

The research described above focussed on the structural aspects of the corresponding densest-packed arrangements of particles. For each densest-packed structure, those studies mainly involved a characterisation of the packing fraction and contact network and an investigation of the underlying mechanism of confinement-induced geometric frustration. Not only have the theoretical findings helped us understand better the structural properties of some existing experimental systems; they can also serve as a basis for the design of quasi-one-dimensional materials with designated physical properties. From the viewpoint of materials design, however, it is also important to understand how the macroscopic mechanical, electrical or optical properties of a system depend on the microscopic arrangements of its constituents, because an understanding of such structure-property relationships would allow those macroscopic properties to be tailored via a controlled microscopic assembly of the system’s constituents. Following this spirit, we have investigated how the electrical conductivity of a densest-packed columnar structure of identical spheres in cylindrical confinement depends on the underlying microscopic arrangement of spheres and how this property varies with the cylinder-to-sphere diameter ratio D. The structures investigated were the zigzag structures at $D\in (\mathrm{1,1}+\sqrt{3}/2)$, the single-helix structures at $D\in (1+\sqrt{3}/\mathrm{2,1}+4\sqrt{3}/7)$, the double-helix structures at $D\in (1+4\sqrt{3}/\mathrm{7,2})$, and the double-helix structures at $D\in (\mathrm{2,1}+3\sqrt{3}/5)$. Based on a resistor-network model [64–68] and certain symmetry considerations, an analytic expression that describes the electrical conductivity σ as a function of D has been derived for each type of structures. The results, which tell us how the system’s electrical conductivity can be tuned through a variation of D, could serve as a guide for the development of quasi-one-dimensional materials with a structurally tunable electrical conductivity.

This paper is organized as follows: In Section 2, we introduce the resistor-network model [67] as employed in our study of electrical conductivity. In Sections 3–5, we present an analytic derivation of the electrical conductivity σ as a function of D for, respectively, the zigzag structures at $D\in (\mathrm{1,1}+\sqrt{3}/2)$ (Section 3), the two types of helical structures at D < 2 (Section 4), and the double-helix structures at $D\in (\mathrm{2,1}+3\sqrt{3}/5)$ (Section 5). In Section 6, we summarize our results and discuss their implications.

2 Resistor-Network Model

For any pair of touching spheres with a potential difference Δψ and with a current I that flows from one sphere to the other, the inter-particle resistance R, which takes into account the bulk resistance of each sphere and the contact resistance between the spheres, is defined as

$R\equiv \left|\frac{\mathrm{\Delta }\psi }{I}\right|,(1)$

and is modelled by a resistor that joins the centres of the spheres. The contact resistance is thought to be arising from a negligibly small overlap between the spheres. Let d_c be the cross-sectional diameter of the overlap volume and d the diameter of either sphere. The ratio d_c/d is then a measure of the extent of inter-sphere overlap. Figure 1 shows that, as this ratio decreases, the inter-particle resistance R increases monotonously. We assume the value of d_c/d to be sufficiently small such that, while the value of R remains finite, any uncertainty in the value of D can be ignored.

FIGURE 1

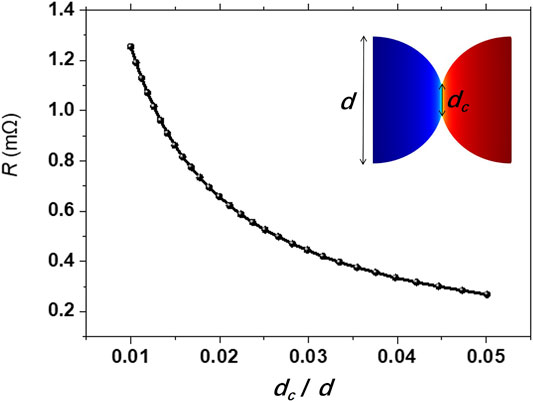
FIGURE 1. Plot of the inter-particle resistance R as a function of d_c/d for a pair of touching spheres, where d_c is the cross-sectional diameter of the overlap volume and d the diameter of either sphere. The results were obtained from COMSOL simulations. As the ratio d_c/d decreases, the inter-particle resistance R increases monotonously. In our resistor-network model, we assume the value of d_c/d to be sufficiently small such that, while the value of R remains finite, any uncertainty in the value of D can be ignored.

In principle, for such columnar structures, the electrical conductivity σ as a function of D can be derived by considering the spatial distribution of resistors within the confining cylindrical space. For any assembly of identical spheres, we take the value of R to be the same for any pair of touching spheres. Since our focus is on the conducting behaviour of the confined spheres, we simplify our problem by assuming all other regions of the confining cylindrical space to be electrically insulating, such that we only need to be concerned with the conducting paths across the assembly of spheres. For each type of structures, we replace each pair of touching spheres by a resistor, identify the corresponding spatial distribution of resistors, and apply Kirchhoff’s laws with some symmetry considerations to derive an analytic expression for the electrical conductivity of an infinitely long structure.

3 Zigzag Structures at $\mathit{D}\in (\mathrm{1,1}+\sqrt{3}/2)$

Consider the zigzag structures at $D\in (\mathrm{1,1}+\sqrt{3}/2)$, and assume each of them to be infinitely long. Figure 2 illustrates such a zigzag structure and the corresponding zigzag chain of resistors. At D < 2, the spheres of any columnar structure are distinguishable in terms of their vertical z-positions along the long axis of the cylindrical space. Taking advantage of this, we have indexed the spheres of the abovementioned zigzag structure in ascending order of their vertical positions. Any sphere i in such a zigzag structure is only in contact with its two nearest neighbours, i.e. spheres (i − 1) and (i + 1), such that the corresponding coordination number (C. N.) is 2. For any pair of neighbouring spheres, the centre-to-centre separation along the long axis of the cylindrical space is given by

${(\mathrm{\Delta }z)}_D=\sqrt{D(2-D)},(2)$

if the diameter of each sphere is taken to be unity. The electrical conductivity σ as a function of D can be derived by considering an equivalent linear chain of resistors, in which each resistive component occupies a cylindrical space of length (Δz)_D and cross-sectional area A_D = π(D/2)²:

${\sigma }^{\prime }\equiv \left(\frac{\pi R}{4}\right)\sigma =\frac{\sqrt{2-D}}{D^{3/2}}(3)$

where, for increasing D, the numerator and denominator of this expression for the rescaled conductivity σ′ decreases and increases, respectively. This corresponds to a monotonous decrease in σ′, as the columnar structure becomes thicker in diameter and the resistors inside become more densely packed along the long axis of the cylindrical space.

FIGURE 2

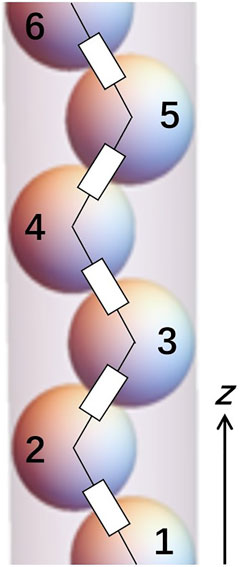
FIGURE 2. Schematic illustration of a zigzag structure at $D\in (\mathrm{1,1}+\sqrt{3}/2)$ and the corresponding zigzag chain of resistors. For any pair of touching spheres, the inter-particle resistance R, which takes into account the bulk resistance of each sphere and the contact resistance between the spheres, is modelled by a resistor that joins the centres of the spheres. The diameter of the confining cylindrical tube is just equal to D, if the diameter of each sphere is taken to be unity. The spheres are indexed in ascending order of their vertical z-positions.

4 Single- and Double-Helix Structures at D < 2

The single-helix structures at $D\in (1+\sqrt{3}/\mathrm{2,1}+4\sqrt{3}/7)$ and the double-helix structures at $D\in (1+4\sqrt{3}/\mathrm{7,2})$ are different from the zigzag structures at $D\in (\mathrm{1,1}+\sqrt{3}/2)$ in terms of their networks of inter-particle contacts, and for this reason we classify the zigzag-to-single-helix transition at $D=1+\sqrt{3}/2$ as a discontinuous structural transition. On the other hand, these two types of helical structures at D < 2 share the same network of inter-particle contacts, and therefore we classify the single-helix-to-double-helix transition at $D=1+4\sqrt{3}/7$ as a continuous structural transition. In each of those helical structures, be it a single- or a double-helix structure, each sphere is not only in contact with its two nearest neighbours but also in contact with its two next-nearest neighbours [e.g., sphere i in contact with spheres (i ± 1) and (i ± 2)] such that, for a coordination number of 4, there exist triplets of mutually touching spheres, in the form of {1, 2, 3}, {2, 3, 4}, {3, 4, 5}…, across the structure.

As illustrated in Figure 3, with additional resistors joining pairs of next-nearest neighbours, the resistor network of any single- or double-helix structure at D < 2 is no longer a simple chain of resistors and is therefore different from that of a zigzag structure. It reflects the presence of triplets of mutually touching spheres in the structure. But based on some symmetry considerations for an infinitely long structure, an equivalent linear chain of resistors can be derived from this more complex resistor network. The electrical conductivity σ as a function of D can then be derived be considering the length and cross-sectional area of the cylindrical space occupied by each resistive component in this equivalent circuit.

FIGURE 3

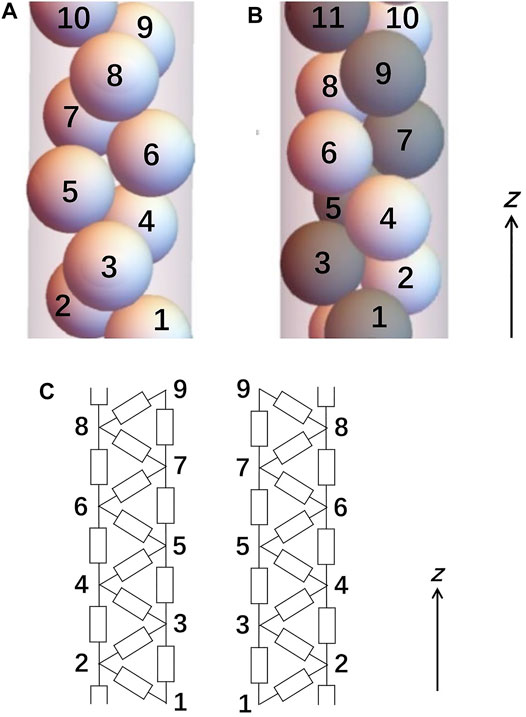
FIGURE 3. Schematic illustration of (A) a single-helix structure at $D\in (1+\sqrt{3}/\mathrm{2,1}+4\sqrt{3}/7)$ and (B) a double-helix structure at $D\in (1+4\sqrt{3}/\mathrm{7,2})$, as well as (C) the corresponding electrical circuit (i.e. a resistor network not drawn to scale) for either structure. The spheres in each structure are indexed in ascending order of their vertical z-positions. As shown in Panel (C), this electrical circuit, which corresponds to the presence of triplets of mutually touching spheres across each structure, can be presented in two equivalent versions that are mirror images of each other.

Consider the electrical circuit on the left-hand side of Figure 3C, and let I_i→j be the current that flows from sphere i to sphere j. Since this circuit is infinitely long, the circuital environment (i.e., the way a sphere is connected to all other components in the circuit) of sphere i ∈ (−∞, + ∞) is the same for respectively all even values of i and all odd values of i as a result of translational symmetry across the circuit. On the other hand, the equivalent mirror-symmetric circuit on the right-hand side of Figure 3C implies that the circuital environment is the same for all spheres regardless of whether their indices i are odd or even. It follows that the symmetry conditions

$I_{i\to (i+1)}=I_{(i+1)\to (i+2)}(4)$

and

$I_{i\to (i+2)}=I_{(i+2)\to (i+4)}(5)$

apply to any value of i. According to Kirchhoff’s current law, the total current that flows into any sphere i is equal to the total current that flows out of the same sphere:

$I_{\text{total}}=I_{(i-2)\to i}+I_{(i-1)\to i}=I_{i\to (i+1)}+I_{i\to (i+2)}.(6)$

This condition also follows naturally from the symmetry conditions I_(i−1)→i = I_i→(i+1) and I_(i−2)→i = I_i→(i+2), as described respectively by Eqs 4 and 5. On the other hand, let V_i→j = I_i→jR be the voltage across sphere i and sphere j. According to Kirchhoff’s voltage law, the voltage across any pair of spheres is path-independent, so that we can link up the voltages across nearest neighbours and those across next-nearest neighbours as follows:

$I_{i\to (i+2)}R=I_{i\to (i+1)}R+I_{(i+1)\to (i+2)}R.(7)$

A combination of Eqs 4 and 7 yields the following relation between I_i→(i+1) and I_i→(i+2):

$I_{i\to (i+2)}=2I_{i\to (i+1)},(8)$

such that the total current that flows across any sphere i is equal to

$I_{\text{total}}=3I_{i\to (i+1)}.(9)$

For any integer N, the voltage across sphere i and sphere (i + N) is a sum of the voltages across nearest neighbours:

$V_{i\to (i+N)}=N{V}_{i\to (i+1)}=N{I}_{i\to (i+1)}R.(10)$

This voltage can also be expressed in terms of the effective resistance R_i,(i+N) between sphere i and sphere (i + N):

$V_{i\to (i+N)}=3I_{i\to (i+1)}{R}_{i,(i+N)},(11)$

where, according to Eq. 9, 3I_i→(i+1) is the total current that flows across either sphere. A combination of the above expressions for V_i→(i+N) reveals a simple proportionality between R_i,(i+N) and R:

$R_{i,(i+1)}=\frac{R_{i,(i+N)}}{N}=\frac{R}{3}.(12)$

It follows that the electrical conductivity of any single- or double-helix structure at D < 2 can be obtained from an equivalent linear chain of resistors in which the resistance of each component is equal to R/3. For any single-helix structure at $D\in (1+\sqrt{3}/\mathrm{2,1}+4\sqrt{3}/7)$, each resistive component in the equivalent linear chain of resistors occupies a cylindrical space of length [35].

${(\mathrm{\Delta }z)}_D=\sqrt{\left(1+\frac{\sqrt{3}}{2}\right)-\frac{\sqrt{3}}{2}D}(13)$

and cross-sectional area A_D = π(D/2)², so that the electrical conductivity σ as a function of D is given by

${\sigma }^{\prime }\equiv \left(\frac{\pi R}{4}\right)\sigma =\frac{3}{\sqrt{2}}\frac{\sqrt{\left(2+\sqrt{3}\right)-\sqrt{3}D}}{D^2}.(14)$

For the double-helix structures at $D\in (1+4\sqrt{3}/\mathrm{7,2})$, a similar derivation using the condition [35].

${(\mathrm{\Delta }z)}_D=\frac{1}{2\sqrt{2}}\sqrt{1+\sqrt{1-{(D-1)}^2}}(15)$

yields the following expression for the electrical conductivity as a function of D:

${\sigma }^{\prime }\equiv \left(\frac{\pi R}{4}\right)\sigma =\frac{3}{2\sqrt{2}}\frac{\sqrt{1+\sqrt{1-{(D-1)}^2}}}{D^2}.(16)$

Like the case of zigzag structures, the rescaled conductivity σ′ of either type of helical structures at D < 2 decreases monotonously for increasing D, as the numerator and denominator in the corresponding expression decreases and increases, respectively.

5 Double-Helix Structures at $\mathit{D}\in (\mathrm{2,1}+3\sqrt{3}/5)$

For the double-helix structures at $D\in (\mathrm{2,1}+3\sqrt{3}/5)$, the electrical conductivity σ as a function of D can be derived in a manner similar to that for the two types of helical structures at D < 2. Here we need to consider a slightly different resistor network (Figure 4), because each sphere in such a double-helix structure is not only in contact with its two nearest neighbours and two next-nearest neighbours but also with one of its third-nearest neighbours (C. N. = 5). Take the structure in Figure 4 as an example. For any odd value of i, sphere i is in contact with sphere (i + 3), such that the consecutive quartet of spheres, {i, (i + 1), (i + 2), (i + 3)}, are in mutual contact and exhibit a tetrahedral configuration. This gives rise to the presence of quartets of mutually touching spheres, in the form of {1, 2, 3, 4}, {3, 4, 5, 6}, {5, 6, 7, 8}…, across the structure. Since sphere (i + 1) is not in contact with sphere (i + 4), the circuital environment of sphere i is different from that of sphere (i + 1), such that we should only consider the following conditions of translational symmetry for pairs of next-nearest neighbours:

$I_{i\to (i+1)}=I_{(i+2)\to (i+3)},(17)$

$I_{i\to (i+2)}=I_{(i+2)\to (i+4)}(18)$

and

$I_{i\to (i+3)}=I_{(i+2)\to (i+5)}.(19)$

According to Kirchhoff’s current law, the total current that flows across sphere i is given by

$I_{\text{total}}=I_{(i-2)\to i}+I_{(i-1)\to i}=\sum _{n=1}^3{I}_{i\to (i+n)},(20)$

which can also be written as

$I_{\text{total}}=I_{i\to (i+2)}+I_{(i+1)\to (i+2)}=\sum _{n=1}^3{I}_{i\to (i+n)}(21)$

according to the above symmetry conditions for next-nearest neighbours. This implies

$I_{i\to (i+1)}+I_{i\to (i+3)}=I_{(i+1)\to (i+2)}.(22)$

On the other hand, according to Kirchhoff’s voltage law, we have the following conditions for the path independence of voltages:

$V_{i\to (i+3)}=I_{i\to (i+3)}R=\sum _{n=1}^3{I}_{(i-1+n)\to (i+n)}R(23)$

and

$V_{i\to (i+2)}=I_{i\to (i+2)}R=I_{i\to (i+1)}R+I_{(i+1)\to (i+2)}R.(24)$

Using the symmetry condition I_{(i+2)→(i+3)} = I_i→(i+1), Eq. 23 can be written as

$I_{i\to (i+3)}R=2I_{i\to (i+1)}R+I_{(i+1)\to (i+2)}R.(25)$

Substituting Eq. 34 into Eq. 22 yields

$I_{i\to (i+1)}=0,(26)$

which implies

$I_{i\to (i+2)}=I_{(i+1)\to (i+2)}(27)$

and hence

$I_{\text{total}}=2I_{i\to (i+2)}(28)$

according to Eqs 21 and 24, respectively. For any integer N, the voltage across sphere i and sphere (i + 2N) is a sum of the voltages across next-nearest neighbours:

$V_{i\to (i+2N)}=N{V}_{i\to (i+2)}=N{I}_{i\to (i+2)}R.(29)$

This voltage can also be expressed in terms of the effective resistance R_i,(i+2N) between sphere i and sphere (i + 2N):

$V_{i\to (i+2N)}=2I_{i\to (i+2)}{R}_{i,(i+2N)}(30)$

for I_total = 2I_i→(i+2). A combination of Eqs 29 and 30 yields

$R_{i,(i+1)}\equiv \frac{R_{i,(i+2N)}}{2N}=\frac{R}{4}.(31)$

According to Eqs 12 and 31, there is a drop in the effective resistance R_i,(i+1) as the diameter ratio D increases beyond 2. This is attributed to the establishment of additional conducting paths across the system. For this type of helical structures, we have [69].

${(\mathrm{\Delta }z)}_D=\frac{\sqrt{1+\sqrt{9-8{(D-1)}^2}}}{4}.(32)$

The electrical conductivity σ as a function of D is then given by

${\sigma }^{\prime }\equiv \left(\frac{\pi R}{4}\right)\sigma =\frac{\sqrt{1+\sqrt{9-8{(D-1)}^2}}}{D^2},(33)$

where, as in the case of the other types of structures, the rescaled conductivity σ′ decreases monotonously for increasing D.

FIGURE 4

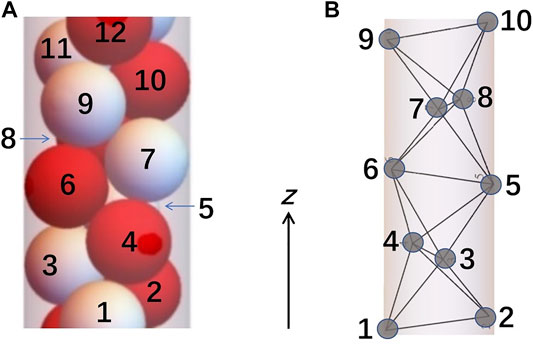
FIGURE 4. Schematic illustration of (A) a double-helix structure at $D\in (\mathrm{2,1}+3\sqrt{3}/5)$ and (B) the corresponding network of inter-particle contacts. The spheres in the structure are indexed in ascending order of their vertical z-positions. Each sphere is not only in contact with its two nearest neighbours and two next-nearest neighbours but also with one of its third-nearest neighbours, such that there exist quartets of mutually touching spheres, in the form of {1, 2, 3, 4}, {3, 4, 5, 6}, {5, 6, 7, 8}…, across the structure.

6 Results and Discussion

The rescaled electrical conductivity σ′ as a function of D has been derived for the zigzag structures at $D\in (\mathrm{1,1}+\sqrt{3}/2)$, the single-helix structures at $D\in (1+\sqrt{3}/\mathrm{2,1}+4\sqrt{3}/7)$, the double-helix structures at $D\in (1+4\sqrt{3}/\mathrm{7,2})$, and the double-helix structures at $D\in (\mathrm{2,1}+3\sqrt{3}/5)$. From the results, we have also found out how σ′ is related to the volume fraction V_F of spheres. As shown in Figure 5, for increasing D, the rescaled electrical conductivity σ′ decreases monotonously for each type of structures, as the resistive components of the system become more densely packed along the long axis of the cylindrical space. However, there exists a discontinuous rise in σ′ at $D=1+\sqrt{3}/2$ (discontinuous zigzag-to-single-helix transition) and D = 2 (discontinuous double-helix-to-double-helix transition), respectively, as a result of the establishment of additional conducting paths upon an abrupt increase in the number of inter-particle contacts. This is not the case for the continuous single-helix-to-double-helix transition at $D=1+4\sqrt{3}/7$. Figure 6 shows an auxillary plot of the volume fraction V_F of spheres as a function of D, where for each type of structures this volume fraction is given by [23].

$V_F=\frac{2}{3D^2{(\mathrm{\Delta }z)}_D}.(34)$

As indicated by the inset of Figure 6, this volume fraction is continuous across every structural transition, as different from the case of σ′. Figure 7 shows a plot of σ′ as a function of V_F. It was found that, for each type of helical structures, the rescaled electrical conductivity σ′ decreases monotonously for increasing V_F. For the zigzag structures at $D\in (\mathrm{1,1}+\sqrt{3}/2)$, however, this is only the case for a limited regime of σ′, where σ′ increases monotonously with V_F for all other values of σ′.

FIGURE 5

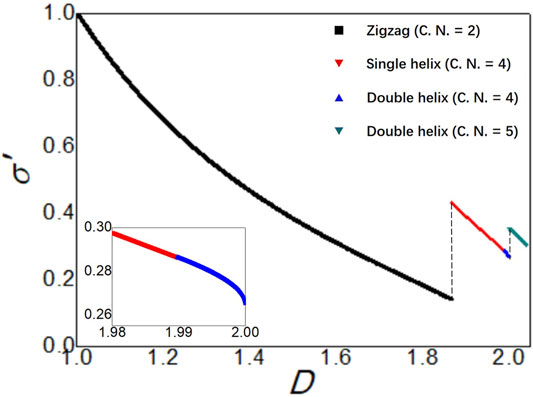
FIGURE 5. Plot of the rescaled electrical conductivity σ′ as a function of the cylinder-to-sphere diameter ratio D. The vertical dashed lines indicate a discontinuous rise in σ′ at $D=1+\sqrt{3}/2$ (discontinuous zigzag-to-single-helix transition) and D = 2 (discontinuous double-helix-to-double-helix transition), respectively.

FIGURE 6

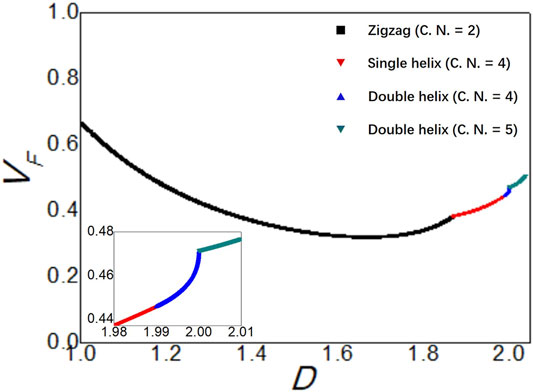
FIGURE 6. Plot of the volume fraction V_F of spheres as a function of the cylinder-to-sphere diameter ratio D. The inset indicates that this volume fraction is continuous across each structural transition.

FIGURE 7

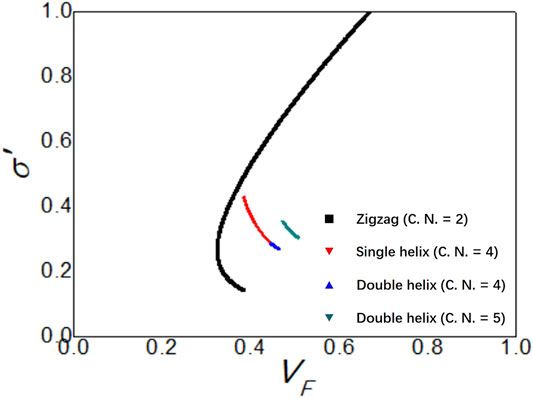
FIGURE 7. Plot of the rescaled electrical conductivity σ′ as a function of the volume fraction V_F of spheres. For each type of helical structures, σ′ decreases monotonously for increasing V_F. For the zigzag structures at $D\in (\mathrm{1,1}+\sqrt{3}/2)$, this is only the case for a limited regime of σ′, where σ′ increases monotonously with V_F for all other values of σ′.

The results presented in Figure 5 could serve as a guide for the development of quasi-one-dimensional materials with a structurally tunable electrical conductivity. Any such experimental system should be a densest-packed assembly of conducting spherical particles immersed in an insulating medium. Once the inter-particle resistance R between any pair of touching spheres is known, the system’s electrical conductivity can be tuned to any designated value through a variation of D. On the other hand, the relation between σ′ and V_F as presented in Figure 7 suggests that it is possible to characterise the volume fraction experimentally by means of electrical-conductivity measurements. In cases where the measured value of σ′ corresponds to two possible values of V_F, i.e to two possible types of columnar structures, the correct type of structures can be determined from the corresponding measured value of D.

Data Availability Statement

The original contributions of this study are all included in the article. Further inquiries can be directed to the corresponding author.

Author Contributions

This research was jointly completed by PM and her research supervisor H-KC. The manuscript was mainly written up by H-KC.

Funding

This work was supported by the Science, Technology and Innovation Commission of Shenzhen Municipality (Grants No. JCYJ20160531193515801 and No. ED11409002).

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s Note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

1. Aste T, Weaire D. The Pursuit of Perfect Packing. 2nd ed. Boca Raton: CRC Press (2008).

Google Scholar

2. Hales T. A Proof of the Kepler Conjecture. Ann Math (2005) 162:1065–185. doi:10.4007/annals.2005.162.1065

CrossRef Full Text | Google Scholar

3. Bernal JD. Geometry of the Structure of Monatomic Liquids. Nature (1960) 185:68–70. doi:10.1038/185068a0

CrossRef Full Text | Google Scholar

4. Chaikin PM, Lubensky TC. Principles of Condensed Matter Physics. Cambridge: Cambridge University Press (2000).

Google Scholar

5. Torquato S. Random Heterogeneous Materials: Microstructure and Macroscopic Properties. New York: Springer-Verlag (2002).

Google Scholar

6. Finney JL. Bernal's Road to Random Packing and the Structure of Liquids. Philos Mag (2013) 93:3940–69. doi:10.1080/14786435.2013.770179

CrossRef Full Text | Google Scholar

7. Aström JAM, Karttunen M. Cell Aggregation: Packing Soft Grains. Phys Rev E Stat Nonlin Soft Matter Phys (2006) 73:062301. doi:10.1103/PhysRevE.73.062301

PubMed Abstract | CrossRef Full Text | Google Scholar

8. Yao Z. Stress-Induced Ordering of Two-Dimensional Packings of Elastic Spheres. Phys Rev E (2020) 101:062904. doi:10.1103/PhysRevE.101.062904

PubMed Abstract | CrossRef Full Text | Google Scholar

9. Füredi Z. The Densest Packing of Equal Circles into a Parallel Strip. Discrete Comput Geom (1991) 6:95–106. doi:10.1007/bf02574677

CrossRef Full Text | Google Scholar

10. Ashwin SS, Bowles RK. Complete Jamming Landscape of Confined Hard Discs. Phys Rev Lett (2009) 102:235701. doi:10.1103/physrevlett.102.235701

PubMed Abstract | CrossRef Full Text | Google Scholar

11. Yamchi MZ, Ashwin SS, Bowles RK. Inherent Structures, Fragility, and Jamming: Insights from Quasi-One-Dimensional Hard Disks. Phys Rev E Stat Nonlin Soft Matter Phys (2015) 91:022301. doi:10.1103/PhysRevE.91.022301

PubMed Abstract | CrossRef Full Text | Google Scholar

12. Martínez-Ratón Y, Velasco E. Highly Confined Mixtures of Parallel Hard Squares: A Density-Functional-Theory Study. Phys Rev E (2019) 100:062604. doi:10.1103/PhysRevE.100.062604

PubMed Abstract | CrossRef Full Text | Google Scholar

13. Jin W, Wang Y, Chan H-K, Zhong Z. Confinement-Induced Columnar Crystals of Ellipses. Phys Rev Res (2021) 3:013053. doi:10.1103/physrevresearch.3.013053

CrossRef Full Text | Google Scholar

14. Basurto E, Gurin P, Varga S, Odriozola G. Anisotropy-Independent Packing of Confined Hard Ellipses. J Mol Liquids (2021) 333:115896. doi:10.1016/j.molliq.2021.115896

CrossRef Full Text | Google Scholar

15. Winkler A, Statt A, Virnau P, Binder K. Phase Transitions and Phase Equilibria in Spherical Confinement. Phys Rev E (2013) 87:032307. doi:10.1103/physreve.87.032307

CrossRef Full Text | Google Scholar

16. Curk T, Farrell JD, Dobnikar J, Podgornik R. Spontaneous Domain Formation in Spherically Confined Elastic Filaments. Phys Rev Lett (2019) 123:047801. doi:10.1103/PhysRevLett.123.047801

PubMed Abstract | CrossRef Full Text | Google Scholar

17. Pickett GT, Gross M, Okuyama H. Spontaneous Chirality in Simple Systems. Phys Rev Lett (2000) 85:3652–5. doi:10.1103/physrevlett.85.3652

PubMed Abstract | CrossRef Full Text | Google Scholar

18. Landry JW, Grest GS, Silbert LE, Plimpton SJ. Confined Granular Packings: Structure, Stress, and Forces. Phys Rev E Stat Nonlin Soft Matter Phys (2003) 67:041303. doi:10.1103/PhysRevE.67.041303

PubMed Abstract | CrossRef Full Text | Google Scholar

19. Landry JW, Grest GS. Granular Packings with Moving Side walls. Phys Rev E Stat Nonlin Soft Matter Phys (2004) 69:031303. doi:10.1103/PhysRevE.69.031303

PubMed Abstract | CrossRef Full Text | Google Scholar

20. Mueller GE. Numerically Packing Spheres in Cylinders. Powder Technol (2005) 159:105–10. doi:10.1016/j.powtec.2005.06.002

CrossRef Full Text | Google Scholar

21. Theuerkauf J, Witt P, Schwesig D. Analysis of Particle Porosity Distribution in Fixed Beds Using the Discrete Element Method. Powder Technol (2006) 165:92–9. doi:10.1016/j.powtec.2006.03.022

CrossRef Full Text | Google Scholar

22. Mughal A, Chan HK, Weaire D. Phyllotactic Description of Hard Sphere Packing in Cylindrical Channels. Phys Rev Lett (2011) 106:115704. doi:10.1103/physrevlett.106.115704

PubMed Abstract | CrossRef Full Text | Google Scholar

23. Chan HK. Densest Columnar Structures of Hard Spheres from Sequential Deposition. Phys Rev E Stat Nonlin Soft Matter Phys (2011) 84:050302. doi:10.1103/PhysRevE.84.050302

PubMed Abstract | CrossRef Full Text | Google Scholar

24. Mughal A, Chan HK, Weaire D, Hutzler S. Dense Packings of Spheres in Cylinders: Simulations. Phys Rev E Stat Nonlin Soft Matter Phys (2012) 85:051305. doi:10.1103/PhysRevE.85.051305

PubMed Abstract | CrossRef Full Text | Google Scholar

25. Chan H-K. A Hybrid Helical Structure of Hard-Sphere Packing from Sequential Deposition. Philos Mag (2013) 93:4057–69. doi:10.1080/14786435.2013.801568

CrossRef Full Text | Google Scholar

26. Mughal A. Screw Symmetry in Columnar Crystals. Philos Mag (2013) 93:4070–7. doi:10.1080/14786435.2013.817691

CrossRef Full Text | Google Scholar

27. Mughal A, Weaire D. Theory of Cylindrical Dense Packings of Disks. Phys Rev E Stat Nonlin Soft Matter Phys (2014) 89:042307. doi:10.1103/PhysRevE.89.042307

PubMed Abstract | CrossRef Full Text | Google Scholar

28. Yamchi MZ, Bowles RK. Helical Defect Packings in a Quasi-One-Dimensional System of Cylindrically Confined Hard Spheres. Phys Rev Lett (2015) 115:025702. doi:10.1103/PhysRevLett.115.025702

PubMed Abstract | CrossRef Full Text | Google Scholar

29. Fu L, Steinhardt W, Zhao H, Socolar JES, Charbonneau P. Hard Sphere Packings within Cylinders. Soft Matter (2016) 12:2505–14. doi:10.1039/c5sm02875b

PubMed Abstract | CrossRef Full Text | Google Scholar

30. Fu L, Bian C, Shields CW, Cruz DF, López GP, Charbonneau P. Assembly of Hard Spheres in a cylinder: A Computational and Experimental Study. Soft Matter (2017) 13:3296–306. doi:10.1039/c7sm00316a

PubMed Abstract | CrossRef Full Text | Google Scholar

31. Mughal A, Winkelmann J, Weaire D, Hutzler S. Columnar Structures of Soft Spheres: Metastability and Hysteresis. Phys Rev E (2018) 98:043303. doi:10.1103/physreve.98.043303

CrossRef Full Text | Google Scholar

32. Winkelmann J, Haffner B, Weaire D, Mughal A, Hutzler S. Corrected Article: Simulation and Observation of Line-Slip Structures in Columnar Structures of Soft Spheres [Phys. Rev. E 96, 012610 (2017)]. Phys Rev E (2018) 97:059902. doi:10.1103/PhysRevE.97.059902

PubMed Abstract | CrossRef Full Text | Google Scholar

33. Winkelmann J, Mughal A, Williams DB, Weaire D, Hutzler S. Theory of Rotational Columnar Structures of Soft Spheres. Phys Rev E (2019) 99:020602. doi:10.1103/PhysRevE.99.020602

PubMed Abstract | CrossRef Full Text | Google Scholar

34. Winkelmann J, Mughal A, Weaire D, Hutzler S. Equilibrium Configurations of Hard Spheres in a Cylindrical Harmonic Potential. EPL (2019) 127:44002. doi:10.1209/0295-5075/127/44002

CrossRef Full Text | Google Scholar

35. Chan H-K, Wang Y, Han H. Densest Helical Structures of Hard Spheres in Narrow Confinement: An Analytic Derivation. AIP Adv (2019) 9:125118. doi:10.1063/1.5131318

CrossRef Full Text | Google Scholar

36. Jin W, Chan H-K, Zhong Z. Shape-Anisotropy-Induced Ordered Packings in Cylindrical Confinement. Phys Rev Lett (2020) 124:248002. doi:10.1103/physrevlett.124.248002

PubMed Abstract | CrossRef Full Text | Google Scholar

37. Liu H, Zong Y, Zu M, Mason TG, Ye F, Zhao K. Curvature-Assisted Self-Assembly of Brownian Squares on Cylindrical Surfaces. J Colloid Interf Sci (2022) 605:863–70. doi:10.1016/j.jcis.2021.07.123

CrossRef Full Text | Google Scholar

38. Zangi R, Rice SA. Nature of the Transition from Two- to Three-Dimensional Ordering in a Confined Colloidal Suspension. Phys Rev E (2000) 61:660–70. doi:10.1103/physreve.61.660

CrossRef Full Text | Google Scholar

39. Cohen I, Mason TG, Weitz DA. Shear-Induced Configurations of Confined Colloidal Suspensions. Phys Rev Lett (2004) 93:046001. doi:10.1103/PhysRevLett.93.046001

PubMed Abstract | CrossRef Full Text | Google Scholar

40. García-Castillo A, Arauz-Lara JL. Static Structure of Confined Dumbbell-Sphere Colloidal Mixtures. Phys Rev E Stat Nonlin Soft Matter Phys (2008) 78:020401. doi:10.1103/PhysRevE.78.020401

PubMed Abstract | CrossRef Full Text | Google Scholar

41. Desmond KW, Weeks ER. Random Close Packing of Disks and Spheres in Confined Geometries. Phys Rev E Stat Nonlin Soft Matter Phys (2009) 80:051305. doi:10.1103/PhysRevE.80.051305

PubMed Abstract | CrossRef Full Text | Google Scholar

42. Camenen JF, Descantes Y, Richard P. Effect of Confinement on Dense Packings of Rigid Frictionless Spheres and Polyhedra. Phys Rev E Stat Nonlin Soft Matter Phys (2012) 86:061317. doi:10.1103/PhysRevE.86.061317

PubMed Abstract | CrossRef Full Text | Google Scholar

43. Oğuz EC, Marechal M, Ramiro-Manzano F, Rodriguez I, Messina R, Meseguer FJ, et al. Packing Confined Hard Spheres Denser with Adaptive Prism Phases. Phys Rev Lett (2012) 109:218301. doi:10.1103/PhysRevLett.109.218301

PubMed Abstract | CrossRef Full Text | Google Scholar

44. Chen D, Torquato S. Confined Disordered Strictly Jammed Binary Sphere Packings. Phys Rev E Stat Nonlin Soft Matter Phys (2015) 92:062207. doi:10.1103/PhysRevE.92.062207

PubMed Abstract | CrossRef Full Text | Google Scholar

45. Deißenbeck F, Löwen H, Oğuz EC. Ground State of Dipolar Hard Spheres Confined in Channels. Phys Rev E (2018) 97:052608. doi:10.1103/PhysRevE.97.052608

PubMed Abstract | CrossRef Full Text | Google Scholar

46. Jung G, Petersen CF. Confinement-Induced Demixing and Crystallization. Phys Rev Res (2020) 2:033207. doi:10.1103/physrevresearch.2.033207

CrossRef Full Text | Google Scholar

47. Ramiro-Manzano F, Bonet E, Rodriguez I, Meseguer F. Layering Transitions in Confined Colloidal Crystals: The Hcp-Like Phase. Phys Rev E Stat Nonlin Soft Matter Phys (2007) 76:050401. doi:10.1103/PhysRevE.76.050401

PubMed Abstract | CrossRef Full Text | Google Scholar

48. Liu B, Besseling TH, van Blaaderen A, Imhof A. Confinement Induced Plastic Crystal-to-Crystal Transitions in Rodlike Particles with Long-Ranged Repulsion. Phys Rev Lett (2015) 115:078301. doi:10.1103/PhysRevLett.115.078301

PubMed Abstract | CrossRef Full Text | Google Scholar

49. Maibaum L, Schmidt M, Löwen H. Colloids Confined to a Flexible Container. Phys Rev E Stat Nonlin Soft Matter Phys (2001) 63:051401. doi:10.1103/PhysRevE.63.051401

PubMed Abstract | CrossRef Full Text | Google Scholar

50. Moon JH, Kim S, Yi G-R, Lee Y-H, Yang S-M. Fabrication of Ordered Macroporous Cylinders by Colloidal Templating in Microcapillaries. Langmuir (2004) 20:2033–5. doi:10.1021/la0358015

CrossRef Full Text | Google Scholar

51. Li F, Badel X, Linnros J, Wiley JB. Fabrication of Colloidal Crystals with Tubular-Like Packings. J Am Chem Soc (2005) 127:3268–9. doi:10.1021/ja042928n

CrossRef Full Text | Google Scholar

52. Tymczenko M, Marsal LF, Trifonov T, Rodriguez I, Ramiro-Manzano F, Pallares J, et al. .Colloidal Crystal Wires. Adv Mater (2008) 20:2315–8. doi:10.1002/adma.200701526

CrossRef Full Text | Google Scholar

53. Vanapalli SA, Iacovella CR, Sung KE, Mukhija D, Millunchick JM, Burns MA, et al. Fluidic Assembly and Packing of Microspheres in Confined Channels. Langmuir (2008) 24:3661–70. doi:10.1021/la703840w

PubMed Abstract | CrossRef Full Text | Google Scholar

54. Meagher AJ, García-Moreno F, Banhart J, Mughal A, Hutzler S. An Experimental Study of Columnar Crystals Using Monodisperse Microbubbles. Colloids Surf A: Physicochemical Eng Aspects (2015) 473:55–9. doi:10.1016/j.colsurfa.2014.12.020

CrossRef Full Text | Google Scholar

55. Lee T, Gizynski K, Grzybowski BA. Non-Equilibrium Self-Assembly of Monocomponent and Multicomponent Tubular Structures in Rotating Fluids. Adv Mater (2017) 29:1704274. doi:10.1002/adma.201704274

PubMed Abstract | CrossRef Full Text | Google Scholar

56. Wu G, Cho H, Wood DA, Dinsmore AD, Yang S. Confined Assemblies of Colloidal Particles with Soft Repulsive Interactions. J Am Chem Soc (2017) 139:5095–101. doi:10.1021/jacs.6b12975

PubMed Abstract | CrossRef Full Text | Google Scholar

57. Mickelson W, Aloni S, Han W-Q, Cumings J, Zettl A. Packing C 60 in Boron Nitride Nanotubes. Science (2003) 300:467–9. doi:10.1126/science.1082346

PubMed Abstract | CrossRef Full Text | Google Scholar

58. Khlobystov AN, Britz DA, Ardavan A, Briggs GAD. Observation of Ordered Phases of Fullerenes in Carbon Nanotubes. Phys Rev Lett (2004) 92:245507. doi:10.1103/physrevlett.92.245507

PubMed Abstract | CrossRef Full Text | Google Scholar

59. Cong VT, Ganbold E-O, Saha JK, Jang J, Min J, Choo J, et al. .Gold Nanoparticle Silica Nanopeapods. J Am Chem Soc (2014) 136:3833–41. doi:10.1021/ja411034q

CrossRef Full Text | Google Scholar

60. Liang R, Xu J, Deng R, Wang K, Liu S, Li J, et al. .Assembly of Polymer-Tethered Gold Nanoparticles under Cylindrical Confinement. ACS Macro Lett (2014) 3:486–90. doi:10.1021/mz5002146

CrossRef Full Text | Google Scholar

61. Sanwaria S, Horechyy A, Wolf D, Chu C-Y, Chen H-L, Formanek P, et al. .Helical Packing of Nanoparticles Confined in Cylindrical Domains of a Self-Assembled Block Copolymer Structure. Angew Chem Int Ed (2014) 53:9090–3. doi:10.1002/anie.201403565

CrossRef Full Text | Google Scholar

62. Chen Z, Ye S, Evans SD, Ge Y, Zhu Z, Tu Y, et al. .Confined Assembly of Hollow Carbon Spheres in Carbonaceous Nanotube: A Spheres-In-Tube Carbon Nanostructure with Hierarchical Porosity for High-Performance Supercapacitor. Small (2018) 14:1704015. doi:10.1002/smll.201704015

PubMed Abstract | CrossRef Full Text | Google Scholar

63. Zhang F, Liu R, Wei Y, Wei J, Yang Z. Self-Assembled Open Porous Nanoparticle Superstructures. J Am Chem Soc (2021) 143:11662–9. doi:10.1021/jacs.1c04784

CrossRef Full Text | Google Scholar

64. Kirkpatrick S. Percolation and Conduction. Rev Mod Phys (1973) 45:574–88. doi:10.1103/revmodphys.45.574

CrossRef Full Text | Google Scholar

65. Swensen JP, Dollar AM. The Connectedness of Packed Circles and Spheres with Application to Conductive Cellular Materials. PLoS ONE (2012) 7:e51695. doi:10.1371/journal.pone.0051695

PubMed Abstract | CrossRef Full Text | Google Scholar

66. Birkholz O, Gan Y, Kamlah M. Modeling the Effective Conductivity of the Solid and the Pore Phase in Granular Materials Using Resistor Networks. Powder Technol (2019) 351:54–65. doi:10.1016/j.powtec.2019.04.005

CrossRef Full Text | Google Scholar

67. Ma P. A Theoretical Study of the Electrical Resistivities of Densest-Packed crystal Structures of Spheres in Cylindrical Confinement. Master thesis. Shenzhen: Harbin Institute of Technology (2020).

68. Birkholz O, Neumann M, Schmidt V, Kamlah M. Statistical Investigation of Structural and Transport Properties of Densely-Packed Assemblies of Overlapping Spheres Using the Resistor Network Method. Powder Technol (2021) 378:659–66. doi:10.1016/j.powtec.2020.09.056

CrossRef Full Text | Google Scholar

69. Wang Y. A Theoretical Study of Columnar Crystals. Master thesis. Shenzhen: Harbin Institute of Technology (2018).

Google Scholar