- 1Department of Aerospace Engineering, Indian Institute of Technology Kharagpur, India
- 2Department of Electrical Engineering, Institute of Infrastructure Technology Research and Management (IITRAM), Ahmedabad, India
- 3Department of Physics and Chemistry, Technical University of Cluj-Napoca, Cluj-Napoca, Romania
- 4Department of Automation, Technical University of Cluj-Napoca, Cluj-Napoca, Romania
This study provides an overview of the tab-controlled jets to understand and predict the influence of mixing promoting vortices at speeds ranging from subsonic to supersonic. A detailed description of various features of the circular jets controlled by tab-like vortex generators is provided. Here, both the experimental and the numerical investigations on the impacts of tabs on the mixing enhancement and noise suppression are presented. Following a brief introduction about subsonic and supersonic circular jets, this study discusses the influences of certain key parameters on mixing characteristics, including the effect of tab geometry, tab number, tab orientation, tab size, and tab position relative to nozzle outlet. Subsequently, their effect on noise suppression is also reviewed. The detrimental effect of tabs in terms of thrust penalty is described. Finally, the future direction of research on the tab-controlled jets is outlined.
1 Introduction
Over the last 40 years, there have been several experimental studies on tab-controlled jets. In the late 1980s, extensive studies of the tab-like vortex generators for mixing enhancement were carried out. At the same time, several researchers put effort into understanding the underlying flow mechanism behind the tab-controlled jets. Interestingly, these studies revealed that the tab could reduce the jet plume and turbulent mixing noise, a primary part of aircraft jet noise. In the mid-1990s, the investigations on tab-controlled jets received serious attention due to the practical implications of stringent noise regulations. With this in mind, various tab configurations in small- and large-scale models were evaluated and obtained encouraging results for jet noise reduction. However, the disadvantage associated with a tab-controlled jet is the thrust penalty. Even though the tab can be implemented actively, it can be protruded into the flow or withdrawn according to the requirement. A tab is a small metal plate situated perpendicular to the freestream, which notably alters the mixing and noise behavior of the flow field. The deployment of a tab at the nozzle outlet primarily aims to disturb the boundary layer to achieve the desired flow behavior. Essentially, tab-like vortex generators shed a pair of counter-rotating vortices that move in the axial downstream direction.
In contrast, a vortex generator of half delta-wing type generates only a plain vortex. The generated streamwise vortices produced from the tabs moving along the exhaust jet plume entrain the ambient fluid. Besides, the tabs are widely used to reduce screech and broadband noise in shock-containing supersonic jets. The broadband noise can be generated in the jet mixing layer when the large-scale structures communicate with the shock cells. Particularly, the screech tone is produced while the closed-loop acoustic feedback occurs between the shock wave and the noise from the turbulent structures developing at the mixing layer. Essentially, inserting a tab at the nozzle outlet disrupts the flow symmetry, a common phenomenon for all the tabs investigated. This disruption in flow symmetry leads to the mitigation of screech tone. In the tab-controlled supersonic jet, the shock cell structure is feebler, and the shock cell spacing is lesser, responsible for reducing the broadband shock-associated noise. However, the basic effect originates from the distribution of vorticity, which is changing due to the influence of tabs.
Furthermore, the tab shape, size, orientation, and location greatly influence the jet mixing and aeroacoustic noise characteristics. This study reviews tab-controlled circular jets’ mixing and aeroacoustic behavior in subsonic and supersonic speeds. This study includes the effect of the key parameters such as tab geometry, tab size, tab orientation at the nozzle outlet and its location from the nozzle outlet in mixing augmentation and noise mitigation. However, in the present study, the effects related to thermophysical–chemical phenomena (i.e., the density of the gas coming out of a nozzle and the release of heat from the jet) in the presence of additional geometry over the nozzle body (e.g., lobe geometry) are not taken into account. The present review aims to develop our understanding of the flow features of tab-controlled jets due to their vast applications in the aerospace industry.
2 Free Round Jets
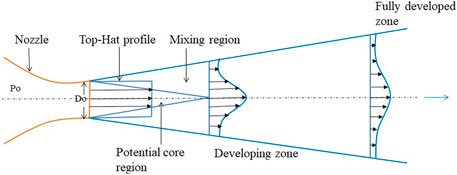
When the jet comes out a nozzle into the quiescent medium, the surrounding fluid is entrained toward the jet flow field. The jet spreads in a radial direction while flowing along the streamwise direction. As the jet stream propagates downstream, the high-speed jet flow’s velocity reduces because of mixing with the surrounding low-speed fluid or stagnant ambient fluid. Essentially, when the jet discharges from a confined space to its surroundings, the jet boundary develops a tangential separation surface. The other side of which the low speed or stagnant fluid persists. The tangential shear creates the large-scale vortices, which are proficient suction creators. The large-scale vortices engulf the surrounding low-speed fluid into the main flow. Therefore, the mass flow is increased rapidly across every cross section of the jet. This is essential because the pressure inside the jet is lesser than the external freestream [1]. Subsequently, the centerline velocity was reduced in the axial direction to support the momentum conservation. The large-scale vortices formed at the edge of the mixing layer moves chaotically both along and normal to the jet stream. This phenomenon exchanges the mass, momentum, and energy between adjacent fluid flows in the transverse direction—furthermore, large-scale turbulent structures break into relatively small-scale structures at the shear layer. Essentially, the small-scale vortices are the superior mixing enhancer that supports low momentum fluid to entrain into the mixing layer to achieve momentum from the higher momentum fluid. The velocity profile at the nozzle exit is similar to the top-hat shape. In the nearfield of the nozzle outlet, a finite region persists, which is not influenced by the mixing initiated at the shear layer. Hence, the nozzle exit velocity remains constant. The zone mentioned above is called the potential jet core in subsonic jets, as shown in Figure 1. When the viscous activity influences this zone, the top-hat velocity profile reduces in extent along the freestream.
Subsequently, the jet centerline velocity gradually reduces when flow crosses the potential core region. If the mixing is higher, there will be faster jet velocity decay. Normally, this velocity decay is characteristic decay, inversely proportional to the distance along the freestream direction from the nozzle outlet. Generally, the potential core region spreads to 6De, and the characteristic decay occurs from about 6De to 12De, where De represents the nozzle exit diameter. After that, the jet velocity decay is very minimal, and at a downstream distance of 30De, the velocity reaches almost zero. The region from 12De to 30De from the nozzle exit is the fully developed region. This region is also the self-similar region since the velocity profile structure is similar in the downstream region, even though the jet velocity gradually reduces.
Based on the vortex theory, the subsonic jet evolution from the nozzle can be explained as follows. When the flow discharges from the round nozzle, the azimuthal vortices are generated because of the Kelvin–Helmholtz instabilities, occurring at the edge of the mixing layer, which causes the generation of rolling-up vortex rings. Subsequently, the transition to secondary instabilities developed by either the resulting vortex rings or the leftover vorticity between the successive rings leads to streamwise vortices. Widnall and Sullivan [2] and Pierrehumbert and Widnall [3] observed periodic vortex rings and streamwise counter-rotating vortices in the near-field region. Furthermore, the study conducted by Martin and Meiburg [4] showed that both primary vortical structures (azimuthal vortices) and streamwise vortical structures interact at the end of the potential core region. This interaction causes the vortex rings to distort and eventually break into small-scale structures [5]. Soon after the breakdown of the vortex rings, the jet spreads linearly in the axial downstream direction. At these locations, the entrainments caused by the streamwise vortices are comparably higher than that due to the azimuthal vortices. This is because the azimuthal structures lose their energy quicker than the secondary structures in the streamwise direction. In this manner, the streamwise vortices play an important role in mixing in the axial downstream direction [6,7].
A subsonic jet consists of three zones: potential core region, characteristic region, and fully developed region. Since viscous action is not yet penetrated inside the jet, the jet velocity remains constant in the potential core region. In contrast, the supersonic jet is wave-dominated and governed by strong viscous action. Therefore, there is no potential core region in the supersonic jet. Instead, it is called the supersonic core region. Nevertheless, the other two regions, namely, the characteristic decay and fully developed regions, have similar characteristics as in the subsonic jet.
In the supersonic jet, the axial velocity is not constant in the core region like in the case of the subsonic jet. Instead, there are generations of shocks and expansion waves in the supersonic jet core region. Essentially, the supersonic jet core is defined as the extent of axial distance from the nozzle outlet to the location where characteristic decay starts or axial location up to which the waves prevail from the nozzle outlet [8]. According to the static pressure difference between the nozzle exit and the surrounding atmosphere where the jet is discharged, the expansion of the supersonic jet is classified into three categories: overexpansion, correct expansion, and underexpansion. Overexpansion of a jet can only be established when the convergent-divergent nozzle operates below the design nozzle pressure ratio. In this case, the pressure at the nozzle outlet is lesser than the surrounding atmospheric pressure. Essentially, the opposite family of oblique shocks is generated at the exit of the nozzle to increase the exit pressure level to the atmospheric pressure level by compressing the jet flow coming out of the nozzle, as shown in Figure 2A [9]. These opposite oblique shocks intersect at the jet centerline and reflect as the expansion waves from the jet boundary. Subsequently, the expansion waves are reflected as the compression waves. This continuous process causes the formation of periodic shock cell structures in the jet flow field.
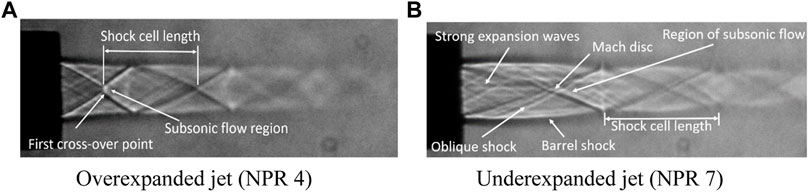
FIGURE 2. Shadowgraphic views of the uncontrolled Mach 1.75 jet [9].
The underexpansion condition is established when the convergent or convergent-divergent nozzle operates above the correct expansion pressure ratio. Essentially, in this situation, the opposite expansion waves are formed at the nozzle exit since the nozzle outlet pressure is more than the surrounding pressure, as illustrated in Figure 2B. These opposite expansion waves intersect at the jet centerline and reflect as the compression waves from the free boundaries. Again, these reflected compression waves cross and reflect as expansion waves from the jet boundary. Similar to the over-expansion case, this phenomenon results in the formation of the periodic wave structure. The ideal or correctly expanded condition, where the nozzle outlet pressure is the same as the surrounding pressure. Even though the flow is ideally expanded, the jet flow has to expand at the nozzle outlet to capture the free space. This causes the generation of expansion waves at the nozzle outlet. However, the strength of expansion waves for correctly expanded flow is lesser than underexpanded flow. Beyond the limiting nozzle pressure ratio, the intersecting shock point becomes an intersection zone resembling a Mach disk. The Mach disk acts as a normal shock through which the supersonic flow is brought to subsonic speed. The limiting level of underexpansion is determined by the settling chamber conditions and the nozzle geometry.
In most cases, the Pitot probe is utilized to estimate the pressure on the centerline of the jet axis. When the Pitot probe faces the supersonic flow, the detached bow shock is generated ahead of the probe. Hence, the measured total pressure by the Pitot probe is associated with the post-shock subsonic flow rather than the total pressure associated with the pre-shock supersonic flow [10,11]. Therefore, the measured post-shock pressure should be corrected from the pressure loss across the bow shock to obtain the pre-shock total pressure. It can be noted that since the supersonic jet core consists series of shocks and expansion waves, the Mach number rapidly varies at different points according to the waves of different strength existing in the core. Thus, estimating the pre-shock total pressure from shock loss is troublesome.
Moreover, the pressure measurement in the supersonic domain will cause measurement error owing to interference of the probe with the shock structures. Hence, the measurements in the supersonic domain are considered to be qualitative, which is helpful for the sake of comparison. Furthermore, the results are good enough to capture key aspects such as supersonic core length, shock cell spacing, and the number of shock cells. The centerline pressure decay of uncontrolled Mach 1.75 jet at overexpanded and underexpanded situations is presented in Figure 3.
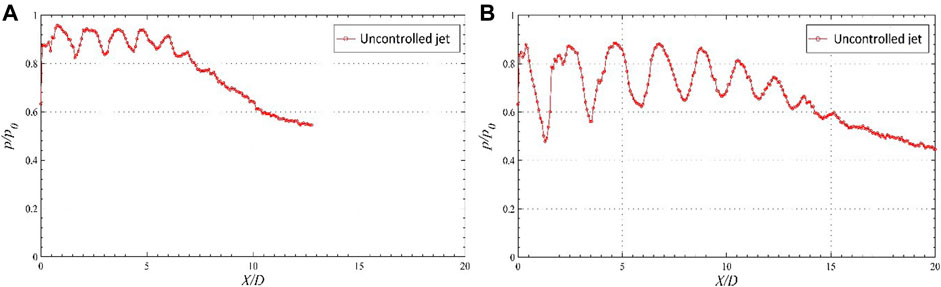
FIGURE 3. Centerline pressure decay for the uncontrolled Mach 1.75 jet [9].
The presence of shocks and expansion waves in the jet core region is confirmed by the peak and the foot of the pressure distributions in the centerline pressure decay. For an overexpanded jet, oblique shock waves are produced to match the nozzle outlet pressure with the ambient pressure (Figure 2A). The appearance of oblique shock waves at the nozzle outlet for the overexpanded jet causes total pressure to decrease, as shown in Figure 3A. Since a drop in overall pressure increases the Mach number upstream of the wave, the flow accelerates first after leaving the nozzle. Furthermore, the decrease in overall pressure approaches a minimum value at a certain downstream region, which is associated with the maximum flow speed. Essentially, this is the first shock intersection point or shock crossover point. Beyond this location, the subsonic jet starts accelerating due to the transport of momentum from the surrounding higher momentum fluid. As a result, the total pressure increases to its highest value, at which point the flow becomes again supersonic. When the flow exceeds supersonic levels, the pressure decreases before it reaches the second shock intersection point—the loop repeats, resulting in multiple shock cell configurations in the jet core. At the underexpansion condition, the core length for the free jet is higher, as shown in Figure 3B. Furthermore, shock cells are stretched, and the shocks and the expansion waves are intense because of the added effect of the underexpansion level and the flow relaxation effect.
When a jet comes out a nozzle to an ambient medium, it relaxes since it expands into a large infinite area from a small space. This relaxation process occurs through the formation of expansion waves at the nozzle exit. The relaxation effect is the only reason for the generation of expansion waves at the nozzle exit even though the jet is correctly expanded (pressure at the nozzle exit is in equilibrium with the ambient medium). On the other hand, when the jet is underexpanded, the pressure at the nozzle exit is more than the ambient pressure. Therefore, in underexpanded jets, strong expansion waves are produced due to both pressure gradient and the relaxation effect of Kaushik and Rathakrishnan [12].
3 Jet Controlled With Tabs
3.1 Subsonic Jet Controlled With Tabs
Bradbury and Khadem [13] experimentally investigated the parameters that affect jet development in low-speed subsonic jets. They have considered the flow parameters, including nozzle convergence angle, nozzle flow turbulence level, and boundary layer thickness at the nozzle exit. In addition to that, they have analyzed the effect of the tab on jet development. It was seen that the nozzle convergence angle, flow turbulence level, and boundary layer thickness have a negligible effect on jet development. On the contrary, the deployment of tabs at the nozzle outlet provides significant alteration in the development of the jet. These results from the azimuthal variation of flow angle and trailing vortices are generated from the tab. Thus, a significant reduction in the potential core region from 6D to 2D and faster decay of centerline velocity were obtained. They have also analyzed the effect of the ramp in the place of a tab and found that the tab has a greater effect than the ramp in distorting the jet. Zaman et al. [14] explored a quantitative and qualitative study for typical tab cases. The flow visualization images confirmed the significant effect of the delta tab on jet development.
When the tab number at the nozzle outlet is higher, intense interaction among the neighboring vortices occurs, eventually reducing their strength. In addition, the breakdown of streamwise vortices as the flow proceeds downstream causes the spreading of a jet, which eventually increases the surrounding fluid entrainment. Also, they identified the sources accountable for the production of streamwise vortices when the tabs are introduced. The dominant source of vorticity generation is the extreme pressure hill in front of the tab, generating a primary counter-rotating vortex pair moving in a streamwise direction. The static pressure distribution in front of the tab for streamwise vorticity generation as a primary source is schematically described in Figure 4. The wall static pressure distribution in the z-direction (Figure 4C), together with the strain rate corresponding to the boundary layer on the wall of the nozzle, generates pair of streamwise vortices, as illustrated in Figure 4A. In this case, the vorticity flux formed by the upstream static pressure distribution for incompressible flow is given as follows:
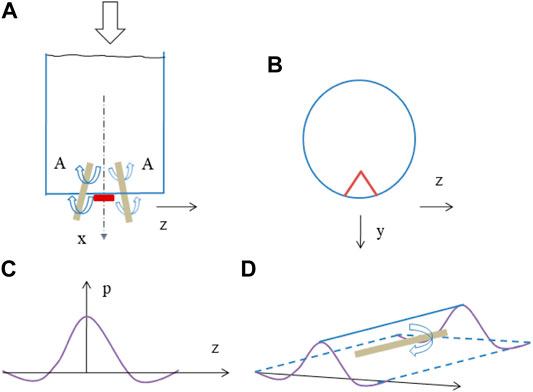
FIGURE 4. Schematic diagrams of the primary source of streamwise vorticity generation (A) and (B) the nozzle with a delta tab; (C) the vortex filament is emerging from the sides of a tab; (D) pressure distribution in front of the tab [14].
Besides, the rotation direction of the vortex pair from the pressure hill is positive, as sketched in Figure 4D. The second source of the streamwise vorticity generation is illustrated in Figure 5. The shedding of vortices from the sides of the tab is illustrated in Figure 5C. Essentially, the second source of the streamwise vorticity generation comes from the static pressure gradient across the tab surface, which is responsible for the fluid rolling along the tab edges from the high-pressure region to the low-pressure region, as shown in Figure 5D. In the above equation, the term ∂p/∂z represents the pressure gradient in the z-direction. In addition to that, the pressure gradient along the x-direction also exists under the action of tabs. This results in the generation of secondary spanwise vortices reoriented into streamwise vortices when it convects downstream. The vortex filament in the case of delta tab would be reoriented from ωy and ωz components to ωx through the terms of ωy (∂u/∂y) and ωz (∂u/∂z) in the vorticity transport equation, which is exhibited in Figures 5C,E,F.
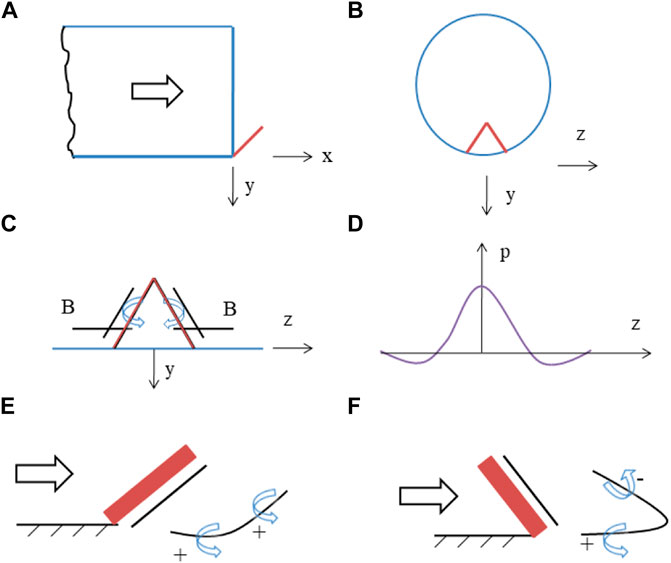
FIGURE 5. Schematic diagram of the second source of streamwise vorticity generation. (A), (B) Side view and front view of the nozzle attached with a delta tab; (C) front view of the emerging vortex filament from the edges of a tab; (D) lateral pressure gradient upstream of a tab; (E) for a delta tab, reoriented vortex filament by mean shear (F) for the tab with ϕ = 45⁰, only partially reoriented vortex filament by mean shear [14].
Gretta and Smith [15] examined the influence of passive mixing behavior through the tab to study the mechanism of redistribution of momentum and jet mixing in the tab’s wake region. They observed that the generated streamwise vortices cause transportation of near-wall boundary layer flow toward the free stream fluid and high-speed free stream fluid toward the wall surface. This causes an increased mixing which significantly thickens the turbulent boundary layer. Also, flow visualizations showed that the tab creates a wake region consisting of counter-rotating streamwise vortices enclosed by separate hairpin vortices, as shown in Figure 6.
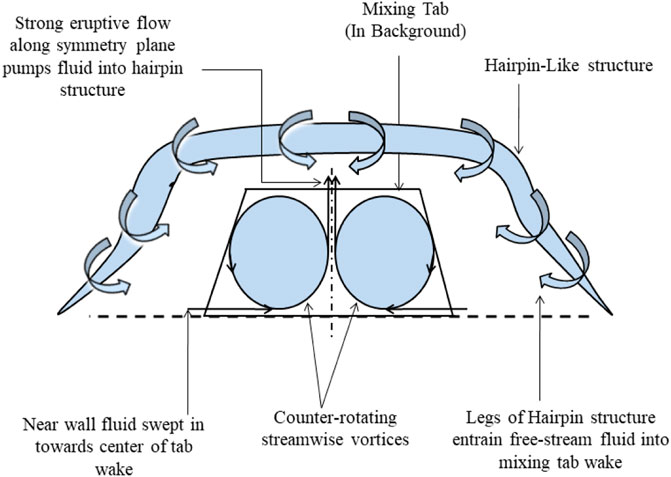
FIGURE 6. Fluid movement from the surface to the wake of the tab [15].
Later, Behrouzi and McGuirk [16] analyze the velocity field in the nozzle flow using the laser Doppler velocimetry (LDV) technique. They have considered several parameters like velocity ratio between the co-flowing jet and ambient medium, tab number, tab shape, and tab orientation angle to study jet core velocity decay and its spreading. They have observed that the orientation angle of the tabs, velocity ratio, and tab shape weakly affects the velocity decay. However, it was found that the tab number and the tab projected area significantly affect the jet mixing. Particularly, the optimum number of the tabs was found to be two. Zhang and Schneider [17] quantitatively investigated the mixing behavior of chemically reacting round jets to examine the influence of tabs and Reynolds number in the near-field jet mixing. They showed that the four tabs improve mixing more effectively than the two tabs even though two tabs induce faster velocity decay than four tabs. The jet mixing was a strong function of the number of tabs and the tab projected area. The spreading of the jet can be improved by inserting more tabs. However, the insertion of more tabs at the nozzle exit will result in high thrust loss. Thus, the optimum numbers of the tab were found to be 2 for better mixing enhancement. Besides, it was observed that the Reynolds number has no effect on molecular mixing for the fully turbulent jet. In contrast, the mixing rate is augmented with the Reynolds number when the jet is transitional. Additionally, they observed that the tab has an important impact on the turbulent jet than on the transitional jet.
Carletti et al. [18] examined the influence of the tabs for an axisymmetric jet surrounded by a cylindrical ejector. They have observed that adding streamwise large-scale vortices at the nozzle outlet increases the centerline velocity decay, mass entrainment, and the shear layer spreading rate within the ejector. Moreover, the generated streamwise vortices are dominated in the region that exists from the nozzle outlet to five times the exit diameter. Reeder and Samimy [19] carried out the experimental study, including the two-dimensional velocity measurements and flow visualization of a tab-controlled low-speed subsonic jet using the water-tunnel facility. The tab-induced distortion is essentially similar in both subsonic and supersonic jets since the compressibility effects play no role in the tab phenomenon. Therefore, the vortex structure formed in both water and air would be similar to the study of Reeder and Samimy [19]. The tab configuration considered in this investigation was similar to the study of Zaman et al. [20] and Samimy et al. [21], which includes the delta tab and inverted delta tab. The overall distortion pattern of the water jet with the deployment of the tab was found to be consistent with previous observations. The velocity measurements confirmed that the tabs shed the streamwise counter-rotating vortex pair. The second set of vortices was also generated from the delta tab that corresponds to a horseshoe vortex system. However, this second set of vortices at high-speed jets was not seen due to the smaller boundary layer thickness at the nozzle outlet. The third set of vortices, shed in the streamwise direction, was observed at the top edge of each inverted delta tab. The mixing enhancement was shown by the higher Reynolds stress levels and the flow visualization for the tab-controlled cases. They have also explained vortex dynamics behind delta tabs and inverted delta tabs. The schematic diagram of the vortex activity for the delta and the inverted delta tab is sketched in Figure 7. Since the delta tab has a broader base, the tab deforms the jet at a higher rate when compared to a simple rectangular tab.
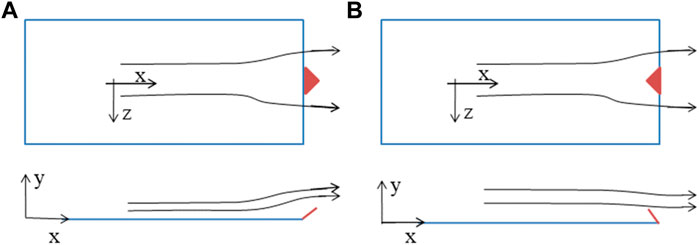
FIGURE 7. Schematic diagram of fluid vorticity dynamics to demonstrate the influence of (A) delta tab and (B) inverted delta tab [19].
Steffen et al. [22] numerically investigated the mixing effectiveness of the circular nozzle associated with the tab. In that study, the experimental work of Zaman et al. [14] was considered for comparative purposes. They have analyzed the centerline velocity decay and the axial profile of volume flux to study the jet mixing characteristics. It was found that these outcomes support the overall jet entrainment and the vorticity field behavior. Moreover, these findings have added further credibility to the statement made on the basic flow dynamics. Behrouzi and McGuirk [16] studied and compared the effect of the three-dimensional shape of tab geometry over the two-dimensional shape with a small thickness. The 3D tab geometry was chosen since it is associated with minimum pressure losses. They have used three different types of 3D tabs: drag reduction tabs, pivotable tabs, structurally stiffened tabs, and 2D plain tabs. All three investigated 3D tabs have the same projected area as the 2D plain tab. The drag reduction tab, which has a forebody shape to reduce the drag, allows shedding vortices from the tab’s edges. The pivotable tab of 10° incidence angle between jet flow and tab orientation was tested with minimal drag. The structurally stiffened tab with a stiffening web on the front was also investigated. Among the various tab configurations investigated, the 2D plain tab provides maximum reduction in core length as compared to 3D tabs.
Moreover, the stiffened tab performs slightly better than other 3D tabs configurations. It reduces the tab-associated drag by modifying its shape or reducing the incidence angle to the flow direction results in an increment in core length toward the uncontrolled jet. Furthermore, the 2D shape tab’s spreading was better than that for the 3D shape of the same tab projected area. They also observed that the splitting of jets causes widening of the contact area of the jet shear layer with the surroundings responsible for the higher mass entrainment. Later, Mi and Nathan [23] investigated the temperature field in the near-field and intermediate region of a slightly heated circular jet with zero, two, and four delta tabs at the nozzle exit. They have studied the statistics of scalar fluctuations in turbulent flow to understand the scalar mixing characteristics. They have observed that the tab-controlled jets modify the scalar mixing characteristics compared to undisturbed jets. The average temperature scalar field was found to be decays more quickly in the downstream distance due to the enhanced mixing rate between the jet and the surrounding medium. Behrouzi and McGuirk [24] examined the effect of velocity ratio, the number of tabs, tab shape, and orientation of the on-jet mixing enhancement in subsonic and supersonic speeds. They showed that the Mach number plays no role in the production of streamwise vorticity since the jet bifurcation follows a similar tendency in both the subsonic and supersonic flows. Also, it was found that tab number, tab width, and tab projected area strongly influence jet mixing. Again, the optimum tab number is two, which provides maximum distortion to a jet.
Carletti et al. [25] presented the jet mixing enhancement technique using half delta-wing vortex generators and compared its effectiveness with the plain tab and the deflector plates. They have varied the vortex generator’s shape, size, orientation, and location relative to the jet exit plane. It was observed that the centerline velocity decay for vortex generator-controlled jet is highly dependent upon the height and angle of attack of the vortex generator. However, the variation of centerline pressure decay is not sensitive to sweep angle and shape variations. Also, they indicated that the velocity distribution is symmetric when the tab is at 60° angle of attack.
On the other hand, it was found to be asymmetric at 30° angle of attack. Moreover, the half delta-wing tab produces a single vortex at an angle of attack lower than 40°, while the tab generates a streamwise vortex pair at the angle of attack higher than that. Nagata et al. [26] studied the control of a jet implementing three kinds of tabs: a half delta-wing tab at 30° angle of attack and delta tabs placed at an angle of attack of 45 and 90°. They observed that the velocity fluctuation exists on the suction side for the half delta-wing tab. At the same time, it is generated between the two tabs and downstream of the tabs when the delta tab is inclined at an angle of 90 and 45°, respectively. They also found a significantly modified velocity field when the half delta-wing tab is employed. Recently, Ito et al. [27] experimentally investigated the effect of half delta-wing tab on diffusion and mixing behavior of axisymmetric jet where the tabs are placed circumferentially at the nozzle outlet at the same interval. They have varied the tab number from 1 to 6. The mean velocity distribution observed that the mixing with the surrounding fluid enhanced, and the entrainment area significantly increased by installing the tabs. They found that mixing of the jet is more effective at a higher number of tabs; however, it is suppressed in the downstream region for 4, 5, and 6 tabs. Essentially, the greater number of tabs causes the suppression of entrainment and mixing. Also, it was observed from the mean temperature profile that the thermal diffusion is higher at a higher number of tabs at the nozzle outlet. However, in the downstream direction, it is equivalent or decreased in the case of tab-controlled jets. This is because of the enhancement of mixing, diffusion, and energy dissipation with the tab effects.
3.2 Supersonic Jet Controlled With Tabs
Ahuja and Brown [28] reported the behavior of heated/unheated underexpanded supersonic jets from a mixing point of view. The number of tabs at the nozzle exit was varied as one, two, three, and four. The core length reduction was maximum (maximum reduction in core length from 6D to 2D) when two identical tabs were positioned at 180° apart at the circular nozzle exit. Also, they have shown that the insertion of the tab causes the jet to depart greatly from the axisymmetry, which increases mass entrainment. Though the axisymmetric structures are suppressed with the introduction of tabs, the generation of other large-scale turbulent structures and their mutual interaction results in increased mixing. Moreover, the hydrodynamic excitation by the shedding of vortices and the enlarged area of the jet perimeter by the tab slow down the jet flow considerably. Zaman et al. [29] observed that the tabs have similar effects from the low subsonic to the underexpanded supersonic Mach numbers. They found that the generated streamwise vortices by the tab modify the structure of the jet flow field to escalate the jet spreading rate. The tab length comparable to 0.02D but higher than the efflux boundary layer thickness is responsible for the significant outcome. Moreover, it was observed from the Pitot pressure measurements that a considerable reduction in shock cell spacing and jet core length occurs when tabs are deployed. It was further observed that the different tab heights for a particular tab width are effective only if the tab height is not limited to the boundary layer thickness. Interestingly, the presence of each tab produces the counter-rotating streamwise vortices originating from the tip of the tab (trailing vortex) rather than from the base of the tab (necklace vortex). The generation of trailing vortices can be explained as follows: when the tab is positioned perpendicular to the flow, the oncoming boundary layer before the tab is lifted, and the incoming streamlines are at an angle of attack for the tab, which produces the resultant force acting radially outward from the jet axis. Moreover, they suggested that the tab provides lesser influence in the overexpanded condition since the adverse pressure gradient exists across the tab. In severely overexpanded conditions, the formation of shock waves inside the nozzle causes boundary layer separation, resulting in either negligible or adverse pressure gradient across the tab. Therefore, for the efficient operation of a tab, the pressure gradient across the tab should be favorable. Samimy et al. [30] conducted the experimental study on mixing characteristics by varying the tab number at the nozzle exit as one, two, and four. Interestingly, similar findings were documented in the previous work, which revealed that the tab induces significant jet distortion and jet bifurcation, specifically in the supersonic condition. Essentially, the pair of counter-rotating streamwise vortices distorts the jet cross section and entrains fluid significantly from the surroundings when two tabs are introduced. Therefore, significant distortion of jet causes a substantial increment in entrainment area, which eventually results in enhanced mixing for two tab cases. However, when four tabs are placed at the nozzle exit, four pairs of counter-rotating vortices are created and interact at 45° diametrical planes while the vortices grow downstream. There will be both suction and traction of fluid from the ambient and the mixing region, respectively. Hence, increasing the number of tabs beyond a certain limit reduces the entrainment rate. Zaman et al. [20] and Samimy et al. [21] considered the effect of triangular-shaped tabs on the mixing characteristics of supersonic jets. They have analyzed the tab of various geometries such as the rectangular end, circular end, and triangular end to examine their mixing ability.
Moreover, the tab is ineffective in producing jet distortion when the distance between the nozzle exit and the tab increases. Due to the spacing between the tab and nozzle, the upstream region of the tab can communicate the pressure signal with ambient which essentially reduces the pressure gradient across the tab. In contrast, jet mixing is significantly improved when the tab is deployed at the nozzle outlet. Ultimately, they found that the tilted triangular-shaped tab (i.e., apex inclined downstream), also known as the “delta tab,” produces significant distortion and mixing augmentation than the plain rectangular tab for the same blockage area. In addition, they inferred that the tab height should be greater than the boundary layer thickness to produce more distortion, and the width of the tab has a significant influence on jet distortion rather than tab height. It should be noted that most of the inferences observed here are based on qualitative analysis. Wishart et al. [31] discussed the significantly perturbed supersonic jet through a single point disturbance inside the nozzle. In their study, the tab is inclined upstream at an angle of 28° to the jet centerline. Furthermore, they put two tabs at both the symmetrical and asymmetrical positions. It is found that the placement of two tabs at a symmetrical position along nozzle exit diameter provides rapid jet development when compared to the asymmetrical positions. Seiner and Grosch [32] conducted an experimental and numerical investigation to study the jet mass flow entrainment rate by introducing streamwise vorticity by the prism-shaped tab-like devices. They have varied the tab number at the nozzle exit as 2, 4, and 6. It is interesting to see that the vortex strength decreases when the tab number increases; however, total vorticity remains constant. They revealed that the near-field jet mixing layer growth rate is enhanced with tab number; simultaneously, the smaller number of tabs causes the largest mass entrainment. Hari and Kurian [33] reported the experimental studies on the coaxial supersonic jet, where the annular convergent nozzle surrounds a plain C-D nozzle. They have used the tabs at the outlet of the C-D nozzle and convergent nozzle, which referred to the primary and the secondary tab, respectively. They have primarily focused on the mixing behavior of secondary tabs on dual supersonic streams. They have observed a lesser supersonic core length for the secondary tab-controlled jets than other cases. Also, the jet width and shear layer thickness were higher at each axial location for the tabbed nozzle. The Schlieren images support the pressure measurement values, which indicate an increase in jet width.
Moreover, the laser sheet images revealed the creation of streamwise vortices and the ejection of jet core fluid to the surroundings with the secondary tab-controlled nozzle. Furthermore, Kaushik and Rathakrishnan [12] studied the effect of limiting corrugated tab under overexpansion, nearly correct expansion, and underexpansion conditions. In that study, the rectangular, semicircular, and triangular corrugations were made along the simple rectangular tab edges. Their results demonstrated the efficacy of corrugated tab in promoting the mixing than that controlled with the simple rectangular tab. The percentage decrease in core length for plain tab and various corrugated tabs at different NPRs is tabulated in Table 1. The reduction in core length is found to be maximum for semicircular corrugation. This confirms the superiority of the semicircular corrugated tab over the other rectangular and triangular corrugated tabs ex-tending across the diameter of the nozzle outlet. The cause behind the improved performance of the semicircular corrugated tab can be explained as follows: the vortices produced by the corrugated tab are depended on the corrugation shape. In the presence of any sharp corners, the vortices, shed from the corner, being of the different families, would tend to interact among themselves. The interaction of vortices will result in the loss of their strength. Here, the semicircular corrugated tab is associated with only two corners. Moreover, the strength of the shock waves prevailing at the nozzle exit was significantly reduced, and the corrugated tabs shrink shock cells. The weakening of waves and shortening of cells would result in a decrease in shock-associated noise.

TABLE 1. Percentage reduction in supersonic core length of the limiting corrugated tabs at different NPRs [12].
Kaushik and Rathakrishnan [34] experimentally investigated the tab aspect ratio effect on mixing, promoting effectiveness at Mach 1.73 nozzle. They have used three different plain rectangular tabs with aspect ratios of 1.0, 1.5, and 2.0, placed diametrically opposite positions at the nozzle outlet. This study was conducted at adverse, zero, and favorable pressure gradient conditions. They found that the tab aspect ratio of 1.0 performs well than the tabs of other aspect ratios of 1.5 and 2.0. Notice that all the tabs show their maximum effectiveness at the zero-pressure gradient condition. The shadowgraphic images revealed that the shock strength effectively reduced in the supersonic jet core with the rectangular tabs of aspect ratio 1.0 related to the tabs of other aspect ratios.
A recent study by Thillaikumar et al. [9] revealed that the triangular corrugated tab of an aspect ratio of 1.5 is superior in reducing the supersonic core length by 99.7% at near correct expansion conditions. On the other hand, the semicircular corrugated tab with the same aspect ratio is the most effective in reducing jet asymmetry. The centerline pressure plot for the plain actuator and the rectangular, semicircular, and triangular tabs of aspect ratio 1.5 is shown in Figure 8, where the pressure decay for the triangular corrugated tab is maximum at the near correct expansion condition. The subsequent study of Jana and Kaushik [35], with the deployment of tabs of different corrugation shapes of aspect ratio 2, revealed that the core length decrement is maximum for rectangular tab at overexpansion conditions. However, the triangular and semicircular corrugated tab is the most effective in jet mixing in the far-field. They have concluded that the location of the corrugation geometry over a tab influences their mixing behavior.
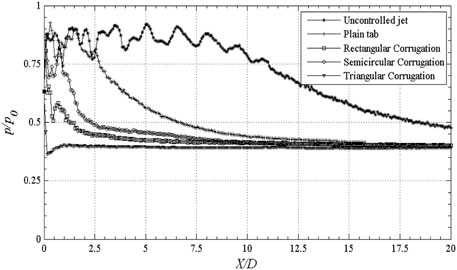
FIGURE 8. Centerline pressure decay for Mach 1.73 jet at near correct expansion condition [9].
3.3 Effect of Various Tab Parameters on Jet Mixing
3.3.1 Tab Orientation Angle on Jet Mixing
This section deals with the effect of the orientation angle of the tab at the nozzle exit. First, the employment of a tab at the nozzle exit has a noticeable effect in reducing the core length and enhancing the mixing performance. Similarly, the tab orientation angle of 45o downstream lean was superior in improving mixing than upstream inclination. The projected area is 50% higher than the inclined tab when the tab is perpendicular to the flow direction. Thus, the noticeable effect in entrainment was observed with tab orientation 90o for constant tab height. For the same projected area, the tab orientation angle of 45o with downstream lean provides a better effect in mixing than the upstream lean. This is due to the streamwise vortices generation with upstream and downstream inclined tabs.
3.3.2 Number of Tabs on Jet Mixing
The effect of the number of tabs in mixing enhancement is discussed in this section. A nozzle with one, two, three, and four tabs was investigated. The insertion of a single tab provides a substantial reduction in jet potential core length compared to the uncontrolled jet. Furthermore, an increment in tab number to two significantly reduces the potential core length and spreading of the jet cross section. Moreover, increasing the number of tabs to four and eight results in no such decrement length core length. When the tab number increases to four, the generated vortices are close enough, and the interaction occurs between them, resulting in the loss of their strength. This phenomenon reduces the ability to employ a larger number of tabs at the nozzle exit. However, when two tabs are employed, the generated vortices are further apart and can affect the cross-sectional distortion for a longer axial extent before they interfere with each other. This caused a significant reduction in core length and improved spreading in two tab cases.
3.3.3 Tab Geometry on Jet Mixing
Tab geometry effects on jet mixing are provided in this section—the tab of a uniform cross section of shed vortices of uniform size. However, the generation of varying sizes of vortices along the edges of the tab was found to be better from a mixing point of view. Thus, the tab geometry can be modified to shed vortices of varying sizes by changing the half width of the tab, in the case of triangular, trapezoidal, and corrugated geometry of half width varying along the edges of the tabs. The previous investigation found that the geometry of the tab has a substantial effect on the mixing enhancement of the jet.
3.3.4 Tab Location on Jet Mixing
It is a well-established fact that the insertion of a tab is always associated with thrust loss. Therefore, several investigations have been performed because of efficient jet mixing while minimizing the thrust loss by changing the tab position relative to the nozzle outlet. Reeder and Zaman [36] conducted a study by deploying the tab upstream and downstream of the nozzle outlet of the sonic underexpanded jets. With the help of static pressure measurements and Mie scattering measurements, they showed drastic changes in the jet flow field while varying the tab position relative to the nozzle outlet. Moreover, it was observed that the distortion of the jet is prominent for the tab position at the nozzle outlet or an upstream location from the nozzle exit. However, the jet distortion disappears when the tab location shifts downstream from the nozzle outlet.
Kweona et al. [37] examined the influence of wire tabs deployed across the diameter of a nozzle in a Mach 2.0 jet. They have altered the tab locations in the freestream direction downstream of the nozzle exit as xt* = 0.2, 1.0, 2.0, 3.0, and 6.0, where xt* is the nondimensional location of the tabs, deployed in the downstream direction from the nozzle exit. The significant decrement in screech tone, broadband noise, and overall sound pressure level for the tab location downstream of the nozzle outlet was observed. The tab locations were maintained within the three times nozzle exit diameters in this study. Besides, the optical visualization observed the weakened shock cell structures, reduced strength of shock cells, and improved spreading rate in the downstream direction. Recently, Arun kumar et al. [38] experimentally investigated the effect of tab positions in the mixing, relative to nozzle exit, at a supersonic jet Mach number of 2.0. It was observed that the location of the tab along the downstream direction has a huge impact on mixing capability based on the supersonic core length reduction. Furthermore, they revealed that the tab must be located behind the first shock interaction point, which causes a maximum core length reduction.
4 Tab Blockage Effects
Although the tab augments the mixing, two major consequences are related to the tab control. They are thrust loss due to area blockage and base drag due to the existence of tabs. First, the thrust loss associated with the deployment of tabs at the nozzle outlet was examined by Zaman et al. [14]. They have used a system enabling the measurement of single component force for jet thrust. They observed that the thrust loss increases with delta tabs at a constant pressure ratio. This study has maintained the blockage from 1.5 to 2% of the nozzle outlet area associated with each delta tab. The geometrical blockage associated with the tab can be defined as the ratio of the tab projected area perpendicular to the axis to the nozzle outlet area.
where As is the projected area of the tab, and An represents the cross-sectional area of the nozzle outlet. The related thrust loss with each delta tab due to flow distortion was calculated from 1 to 1.5% of ideal thrust. Behrouzi and McGuirk [16] investigated various 3D shapes of a tab to examine the thrust loss for the same projected area. It was found that the enhancement of mixing of the 2D tabs was higher related to the 3D tabs for the same projected area. Lovaraju and Rathakrishnan [39] quantify the thrust loss due to the insertion of tabs. As per the jet literature, the amount of thrust is approximately the blockage offered by the tabs [10]. In the present case, the blockage offered by the thin tab at the nozzle exit is 5%. Therefore, it can be said that the thrust loss associated due to deployment of tabs at the nozzle exit is roughly 5%. Later, Rathakrishnan [40] used the cross-wire tab with less than 10% blockage at various supersonic Mach numbers. Also, in the study, they revealed that the thrust loss occurred due to the tab being nearly equal to the projected area of the cross-wire. Also, they have suggested that the thinnest tab can be used to minimize the momentum thrust loss and drag associated with the tabs.
5 Jet Noise
In 1952, Lighthill first proposed the acoustic analogy model, a general theory to understand the jet noise phenomenon. An experimental investigation conducted by Sarohia and Massier [41] revealed the effect of large-scale structures on mixing and noise production in sub-sonic jet flows. They have observed that the large-scale structure prevails in the far-field location of the jet about 7D from the nozzle outlet. High-speed Schlieren images harmonized with the near-field pressure measurements show that merging adjacent organized large-scale structures in the jet shear layer results in an instantaneous peak of the near-field pressure signal. In 1981, Zaman and Hussain observed the initial toroidal structures and their breakdown into substructures at the end of the potential core region, which causes a large part of the aeroacoustic noise. They found that the coherent substructures are involved in the noise emission instead of coherent structures. Also, the nozzle’s flow condition influences the noise characteristics since it influences the mixing mechanism. Essentially, the subsonic jet power spectrum is dominated by a single broad maximum with no distinct frequencies, which is essentially only because of turbulent mixing.
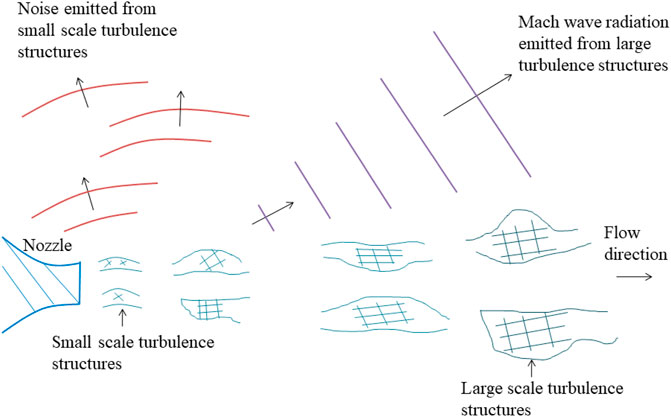
The noise behavior of supersonic jets is quite complex compared to subsonic jets. But, surprisingly, the generation of supersonic jet noise is well established than their subsonic counterparts. Rather, it is quite simple to predict the noise directivity and spectral characteristics in supersonic jets. From the available literature, it is well understood that both the turbulent structures of fine and the large-scale are the reason for the generation of aeroacoustic noise. Figure 9 schematically indicates the noise emission from small- and large-scale turbulent structures. However, the relative noise intensity of these structures is strongly dependent on temperature and the jet Mach number. In the case of cold subsonic jets, the turbulent structures travel at subsonic convective Mach number compared to the ambient sound speed. Thus, they are not very effective in large-scale turbulent noise. Therefore, the subsonic jet noise is primarily generated by the fine-scale structures only.
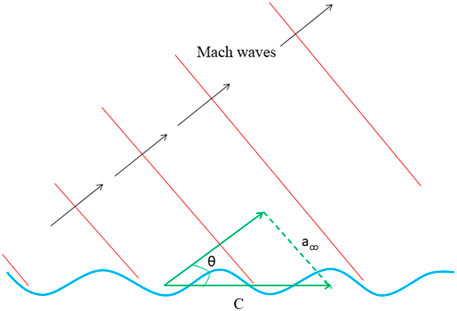
In contrast, the large-scale structures travel at a supersonic convective velocity relative to the ambient sound velocity for supersonic jets at elevated temperatures. This causes the generation of intense noise, which is much higher than the noise radiated by the small-scale turbulent structures. Therefore, large-scale structures are a primary cause of supersonic jet noise radiation. In the view of the stochastic instability wave model, the instability waves present in the jet field and the large-scale turbulent structures are statistically alike. This concept approximates the physical problem of instability waves as a wavy wall. This wavy wall has the same wave speed and wavelength as instability waves. For a wavy wall, if the transmission speed is supersonic when compared to the ambient sound speed, this results in noise emission appearing as Mach waves, as shown in Figure 10. The intense noise emission direction in the wavy wall analogy can be estimated by the jet’s most amplified instability wave speed in the Mach wave relation.
Moreover, the Strouhal number at the most augmented instability wave and the peak of emitted noise should be similar. Tam et al. [42] found good agreement in investigating these relationships. Also, McLaughlin et al. [43] calculated the frequencies of most amplified instability waves over a range of jet Mach numbers and found good agreement with experimental results.
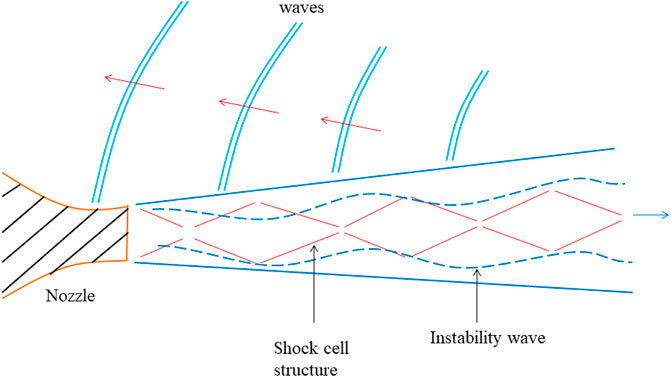
Moreover, when the jet expands imperfectly into the atmosphere, the quasiperiodic shock cell structures are formed in the supersonic jet core. This causes the generation of another noise component known as shock-associated noise. Shock-associated noise is additionally subclassified into two components such as screech tone and broadband shock-associated noise. Therefore, the imperfect supersonic jet expansion produces three noise components: turbulent mixing noise, screech noise, and broadband shock-associated noise. The turbulent mixing noise can be produced through instability waves and large-scale turbulent structures present in the jet shear layer. At the same time, screech and broadband noise are produced because the shock cells interact with shear layer instability waves [44]. The noise spectrum of imperfectly expanded supersonic jets was estimated by Seiner [45]. Screech tone is represented by maximum peak and is associated with its harmonics. Sometimes, fourth or fifth harmonics can be noticed. The low-frequency zone in the left side to the screech frequency is the turbulent mixing noise, and the high-frequency peak right to the screech tone is termed broadband shock-associated noise.
Interestingly, the relative magnitude of three noise components is strongly dependent on the noise measurement direction. The intensity and the spectral and directional characteristics are strongly dependent on the ratio of the jet to ambient temperature and jet Mach number. Increasing the supersonic flow velocity increases the difference in maximum noise level between the principal part and the background noise. On the other hand, at constant Strouhal and Mach numbers, the increment in maximum noise level has no appreciable growth with the rise in the jet temperature. However, the increase in temperature widens the maximum noise sector. Therefore, the total noise radiation from the jet is higher at elevated temperatures. At a low Strouhal number, more radiated noise leads to broadening the peak in the noise spectrum. The peak broadband noise frequency is associated with convection velocity in the jet mixing layer and spacing between shock cells.
Moreover, the amplitude depends upon the measurement distance to jet diameter ratio, nozzle geometry, and off-design parameter. The off-design parameter can be defined as β = |Me2—Md2|1/2, where Me is the jet exit Mach number, and Md’s design Mach number. Higher imperfection in jet expansion level from the design Mach number results in increased strength of shock cell structures that leads to increment in noise levels. Powell [46] first identified the screech tone in supersonic jets. They showed that the peak might influence the spectrum over broadband shock-associated noise and turbulent mixing noise. They have explained the acoustic feedback process responsible for these discrete tones, exhibited in Figure 11. Sound propagation in the upstream direction results in the interaction with the nozzle lip which forces the instabilities present in the jet shear layer near the nozzle outlet. These Kelvin–Helmholtz instability waves propagate along the streamwise direction and develop quickly in the jet shear layer by taking energy from the bulk jet flow. Afterward, the interaction between K-H instability waves and periodic shock cell structures emit aeroacoustic noise. The sound travels outside the jet shear layer toward the nozzle outlet in broadband shock-associated noise. Once the acoustic waves reach the nozzle lip, the new instability waves are formed and propagate in the streamwise direction, and the feedback loop is closed.
6 Jet Noise Suppression by Tabs
Tanna [47] first investigated the effect of tab in eliminating the noise, which is an effective method to reduce the screech tone. They believed that the symmetry of the nozzle exit is important in establishing the screech feedback loop between the nozzle outlet and shock cell structures. Besides, installing a tab at the nozzle exit distorts the symmetry. Norum and Seiner [48] performed the aeroacoustic measurements in the near- and far-field cold supersonic jets. The behavior of the noise field is distinctive in near- and far-field regions. To extract the overall behavior of the noise field, it is essential to measure the noise in near- and far-field locations. The near-field and far-field noise measurements are generally performed by deploying the microphones at the nozzle exit and around the 40De location from the nozzle exit. However, in this case, the microphones were deployed parallel to the jet centreline axis at a radial distance of 140 mm. They have used a tab at the nozzle tip to control shock-associated noise. They found that the tab deployment at the nozzle exit substantially impacts shock noise emission. The far-field acoustic data of power spectral density showed that the tab effectively eliminates the convergent nozzle’s screech. Besides, using a tab results in exceedingly high-frequency broadband noise in a convergent-divergent nozzle. They also observed the 10 percent reduction in shock cell spacing with tab-controlled supersonic jets compared with uncontrolled jets. The near-field acoustic measurements showed that the peak noise is generated downstream of shock cells since the shock cell spacing decreases in the downstream distance. Seiner and Yu [49] reported the near-field and far-field noise spectra with an inserted tab at the nozzle outlet in the overexpansion and underexpansion supersonic jet conditions. In this study, the microphones were positioned at a radius of 2.68De distance from the nozzle exit. Meanwhile, in far-field measurements, the microphone was deployed at 90° to the nozzle jet axis at a distance of 61.5De. They showed that in the overexpanded nozzle, with the insertion of a tab, the upstream near-field region is influenced by the screech, and the broadband noise component dominates the downstream region. It is found that the last few shock structures primarily contribute to noise generation. However, this feature happened in the vicinity of the end of the initial supersonic shear layer in an expanded system. Ahuja and brown (1989) studied the effects of tabs in screech noise reduction. They have measured the near-field pressure spectrum in the plane of the nozzle outlet with a microphone located one inch from the nozzle lip. Using the acoustic measurements, they showed that the screech tone is 130 dB greater than the background broadband jet noise. However, the presence of tab in supersonic underexpanded jets eliminated the screech noise. Also, the maximum noise reduction was observed with four tabs at the nozzle exit. Samimy et al. [30] studied the far-field noise characteristics of a jet controlled with tabs. They have considered flow conditions from subsonic to highly underexpanded supersonic conditions. Their study has varied the number of tabs as one, two, and four. The microphone was located at the nozzle outlet plane and at a distance of 135De from the jet axis, where De represents the nozzle outlet diameter. Also, the noise spectra measurements were taken at two azimuthal angles (ϕ) of 0° and 90° for one and two tab cases, and 0° and 45° for four-tab cases, with respect to the tab location (ϕ = 0°). Note that, the acoustic measurements can be performed at different polar and azimuthal angles to investigate the noise directivity pattern. The jet noise radiation is uniform in all directions at a polar angle below 110° to the jet centreline axis at the nozzle exit. In this region, the uniform background noise is generated by the fine-scale structures in the jet field. But, at a polar angle above 130°, the generation of large-scale structures dominates the noise radiation. Samimy et al. [30] found that both the screech noise and the harmonics present in the uncontrolled jet were eliminated by tabs. They have observed that with the four tabs case, the overall sound pressure level decreases about 6.5 dB, and, with one and two tab cases, the sound pressure level was dropped about 1–3 dB based on the measurement plane. Besides, it was noted that the tab performs effectively for all the underexpanded conditions, while this was not the case for the overexpanded jet. Ahuja et al. [50] evaluated the performance of tabs in jet noise suppression located at the nozzle outlet. It was observed that the plain supersonic jet from the circular exit is noisiest. However, the tabs deployment at the nozzle outlet eliminates all the screech noise and reduces the shock-associated noise by 10 dB. However, the tab-controlled jets produce additional high-frequency noise related to the uncontrolled circular nozzle. Also, it is found that the addition of a tab increases the broadband noise at all frequencies for subsonic conditions. They have explained that the tab thickens the mixing layer that resists the instability waves responsible for the screech [51]. Samimy et al. [21] conducted the far-field noise measurements for one and four tabs located at the exit of the axisymmetric jet. This study is similar to the work carried out by Samimy et al. [30]. It is found that the tab eliminated the screech components, and the influence is more prominent with four tabs.
Moreover, it was noted that the broadband level of the noise decreased over most of the frequency range of spectrum for the four tabs case. Kobayashi et al. [52] conducted a detailed study of tab size effects on jet thrust loss and noise suppression in heated and cold underexpanded supersonic jets. They have used a conical convergent nozzle operated without tabs and with a pair of tabs to study noise’s spectral and directivity characteristics. The jet gas temperature ratios were changed for all cases from 303 to 773 K. The smaller tabs efficiently reduced the jet noise. The maximum decrease in acoustic power level and overall sound pressure level was observed to be 4.3 and 7 dB, respectively, at the jet gas temperature of 773 K. However, they found the noise reduction level of 6 dB in acoustic power level and 9.7 dB in overall sound pressure level for the cold jet. They noted that the polar angle direction of the maximum noise reduction shifted from 90o to 30o polar angle position estimated from the jet axis at an increased jet temperature. Also, they have observed a significant noise reduction per percentage thrust loss of 16.4 dB/% (overall sound pressure level) and 10.4 dB/% (acoustic power level) with the smallest size tab. Furthermore, it was observed that increasing the number of tabs eliminates the screech tone and reduces the shock and turbulent mixing noise. At polar angle 30°, the maximum noise reduction was achieved with a larger number of tabs. Zaman and Hussain [53] studied the influence of delta tabs on the far-field noise spectra. This study used four delta tabs at the nozzle outlet for the noise measurements and a no-tab case. Interestingly, the delta tab eliminates the screech component and its harmonics. In overall noise level, about 5 dB reduction was estimated at an azimuthal angle ψ = 0° for the delta tab-controlled case. Also, the broadband noise was decreased over the most frequency spectrum in addition to the screech component. Like a simple tab, the delta tab also provides similar results as Samimy et al. [21] reported. However, in this study, they did not compare the noise spectra of the delta tab with the simple tab. Furthermore, Reeder and Samimy [19] observed a reduction in screech tone with the deployment tabs at the nozzle exit or upstream of the nozzle exit locations. Saiyed and Bridges [54] experimented by studying the performance of the low bypass ratio turbofan engine model by employing the tabs. They have analyzed the tab effect on effective perceived noise level (EPNL) and far-field noise spectra. In this study, the tab size, placement, combination of tabs and mixers, and blockage were kept into account. It is observed that at high power, the deployment of tabs at only the core nozzle reduces 1 EPN dB. At constant blockage, the higher penetration of the tab gives small noise benefits compared to a smaller tab. Also, the high-frequency noise induced by the tabs was not observed in this case.
Furthermore, installing tabs on both the core and the exhaust nozzle provides a 2 EPN dB drop of noise irrespective of power. This formation has a little higher tab-induced high-frequency noise. Then, it is found that the combination of exhaust nozzle and core mixer tabs reduces the noise level of 2 dB compared to the core mixer alone at low frequency with the expense of tab-induced high-frequency noise. Also, it is observed that the interaction of tabs with incoming turbulence plays a vital role in the EPNLs. Tam and Zaman [55] presented the experimental data of subsonic jet noise to show a good agreement of the experimental values with the similarity spectra consisting of large turbulence structures/instability waves noise and fine-scale turbulence noise. They have investigated non-axisymmetric nozzle shapes such as elliptic, rectangular, lobed, and tabbed nozzles with the same nozzle exit area along with circular nozzle. They showed that the geometric modifications into rectangular and elliptic shapes are not an efficient way to suppress the noise. Moreover, they found that the large-scale turbulent structures and the noise radiated in all directions are suppressed from the lobed nozzle. In addition to that, the tab-controlled jet effectively reduces the noise from the large-scale structures, and the reduction is higher for a large number of tabs. Both large- and fine-scale structures generate the turbulent mixing noise. Of these, large-scale turbulent structures dominate the radiation of mixing noise. The tab deployment at the nozzle outlet suppresses the large-scale structures in the jet shear layer. Therefore, the suppression of large-scale structures eventually results in mitigating turbulent mixing noise. Hileman and Samimy [56] studied the effect of the delta tab on modifying the correctly expanded supersonic jet of Mach 1.3 ejected from the circular exit. They have used a single tab and two tabs, where delta tabs are positioned at the opposite sides of the nozzle outlet. The far-field acoustic data were taken at an angle of 30°, 60°, and 90° to assess the impact of the delta tab on radiated noise field. Irrespective of the microphone location, the insertion of the tab caused an increment in high-frequency noise on the tab side (ϕ = 0°) of the jet relative to other sides of the jet (ϕ = 90° and 180°). It was observed that the counter-rotating vortices in the streamwise direction produced by the tabs are responsible for the emitted sound in high frequency along the tab direction. Also, it was found that the tab regulates the creation of spanwise roll-up, which has a strong impact on maximum noise at 30° in the downstream direction. Hussain et al. [57] examined the effect of the perforated tab on the acoustic field of convergent nozzle covering Mach numbers from subsonic and supersonic. They used a triangular tab and circular perforation to study the far-field noise characteristics. Also, the low-frequency noise was reduced with the tabs in both subsonic and supersonic jets with the expense of tab-induced high-frequency noise. From the noise directivity pattern, it was observed that the overall noise level was increased in subsonic jets with the insertion of tabs except the far downstream polar angle above 150° angle. Moreover, in underexpanded jets, the overall noise level was reduced in all directions without the penalty of high-frequency noise. André et al. [58] reported the experimental data to study the impact of the tab on broadband shock-associated noise in underexpanded supersonic jets. In this study, the screech was suppressed nonintrusively with a notched nozzle configuration to study the broadband noise alone. It was shown that the broadband hump shifted toward high frequencies for both tabbed jet and notched jet. Furthermore, the amplitude of the hump was reduced for the tabbed jet compared to the notched nozzle. Moreover, it has been noted that the higher broadband shock-associated noise peak frequency for the tab-controlled jet comes from the shortening of the shock cells, while the notched jet comes from the screech suppression. The noise directivity shows that the insertion of tab reduces the noise level at polar angle 110°, which indicates the reduction in turbulent mixing noise. Ashwin Kumar et al. [59] investigated the effect of the triangular and inverted triangular tab on subsonic, sonic, and supersonic noise characteristics. The simple rectangular tab is also considered for comparative purposes. It was observed that the placement tabs disturb the acoustic feedback loop, thus eliminating the screech. Furthermore, the generation of large-scale structures is also inhibited, leading to reduced turbulent mixing noise and shock-associated noise. The inverted triangular tab was better in reducing the noise level over the Mach number range investigated. Moreover, at supersonic conditions, the inverted triangular saw reduces the broadband shock noise level by 12 dB compared to 7 dB for the triangular tab. Furthermore, the directivity pattern of the overall sound pressure level indicates that the inverted triangular tab reduces the noise level relative to the triangular tab.
7 Discussion and Conclusion
When a supersonic jet comes out of a convergent–divergent nozzle, it diverges to conserve the momentum. The large eddies are generated at the jet boundary due to the shearing action between the jet and the surrounding lower momentum or stagnant fluid. These large eddies entrain the outer fluid inside the jet; consequently, the jets slow down to keep the momentum constant. Because of the circular nozzle, the azimuth vortices of the same size are shed into the jet. Moreover, the shock cell structures are also present in the jet being supersonic. Thus, the vorticity–vorticity and vorticity–shock interactions are inevitable. These interactions are essentially responsible for jet mixing augmentation, and hence, the jet flow gets diffuse into the surroundings. Once a pair of plain tabs are introduced, the additional vortices in transverse directions (perpendicular to the jet axis) are also shed along with the azimuth vortices from the nozzle exit. This essentially makes the nozzle exit noncircular.
Furthermore, the vortices shed by the tab augment the entrainment at their location compared to the axis perpendicular to the deployment. Because of the relative difference in entrainment along these two axes, the axis switch phenomenon occurs at the downstream location, which directly indicates mixing enhancement. Moreover, it is seen in the jet literature that the vortices of mixed size are efficient mixing promoters compared to the vortices of the same size. Therefore, once the corrugations are provided on the tab edges, the early axis switch phenomenon occurs due to the shedding of mixed-size vortices. Hence, efficient mixing is obtained as compared to the tabs without corrugations. Several researchers establish that the enhanced mixing directly indicates noise attenuation.
In this article, the influence of vortex-inducing tabs on the mixing and acoustic characteristics of circular jets has been reviewed. The effect of various tab parameters such as tab geometry, tab aspect ratio, tab orientation, tab number, and tab position relative to nozzle exit has been explored. It is observed that the increase in the number of tabs at the nozzle outlet causes faster velocity decay than the uncontrolled jets. It has been observed that the tab height should be higher than the boundary layer thickness for effective mixing. Interestingly, the tab width is a vital parameter than tab height. However, the tab orientation angle has more impact than the tab shape; the triangular tab leaning downstream, called a “delta tab,” has the superior effect in jet mixing. These tabs generate counter-rotating stream-wise vortices that influence jet development significantly. Furthermore, the recent development of the half-delta wing tab shows that it produces a single vortex and produces counter-rotating vortices while deploying a pair of tabs of opposite signs adjacently. The tab orientation responsible for generating the co-rotating vortices shows an improved jet mixing relative to the counter-rotating vortices configuration. Moreover, improved mixing can be achieved for increased tab height and angle of attack. Furthermore, the tab eliminates the screech noise by interrupting the symmetry of the jet at the outlet of a supersonic nozzle. The insertion of a tab reduces the strength of the shock waves and shortens the shock cell spacing, reducing the broadband noise level. Specifically, the noise level decreases with increasing the number of tabs up to 4; furthermore, an increase in tab number at the nozzle exit results in an increment of high-frequency noise. However, an increase in the tab height for the same blockage area has small noise benefits relative to the smaller tab. Several investigations concentrated on the rectangular tab and delta tab separately in reducing the jet noise at supersonic speeds. However, a direct comparison of the impact of various types of tab geometry on the jet noise level needs to be examined.
Though several aspects of jet mixing and their control mechanisms have been revealed in the last few decades, the vortex dynamics of the tab-controlled circular jet are yet to be addressed. How does the tab insertion at the circular nozzle exit change the coherent structures in the free round jet? How does this variation alter the flow structure and its downstream growth? What is the physical mechanism behind the jet manipulation using the tab? Those phenomena are yet to be answered for a thorough understanding of the jet control mechanism. In addition, the following issues are yet to be addressed to understand the influence of the tab on jet noise. What is the effect of the delta tab and half delta-wing tab on turbulent mixing noise and shock-associated noise? How do the various tab parameters such as tab geometry, tab number, tab orientation, tab height, and tab position relative to the nozzle outlet affect the jet noise at both subsonic and supersonic levels? Extensive experimental studies are required to answer the issues mentioned above, along with the appropriate numerical analysis.
8 Novelty and Innovation Statement
Supersonic vehicles are increasingly attracting research interests due to their inherent benefits in various areas. Several investigations have been conducted in the supersonic flow regimes to improve the performance of supersonic aircraft. Particularly, jet control and the associated noise reduction techniques are the essential areas of research to improve the stealth capability of a military aircraft and enhance passengers’ comfort in a transport plane. Therefore, this review article aims to give an overview of recent technological advancements in jet control and noise characteristics. Although review literature is available primarily on jet control and jet noise, integrated review work on jet control and the associated aeroacoustic characteristics is hardly found. Since jet control is closely connected to jet noise reduction, a thorough examination of jet control and its impact on jet noise is required to comprehend the flow physics. The review discussed the basic physics of jet and aeroacoustic noise, recent advancements to control it, and the gray areas in this field where further research can be conducted. Therefore, the review work will provide the reader with an indication of the direction they can move ahead.
Author Contributions
TT reviewed the literature associated with the mixing behavior of jets and prepared the first draft. MK reviewed the manuscript and supervised the study. DD revised the manuscript. MU edited the revised version. VM finalized the manuscript.
Conflict of Interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Publisher’s Note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
References
1. Wygnanski I, Fiedler H. Some Measurements in the Self-Preserving Jet. J Fluid Mech (1969) 38:577–612. doi:10.1017/s0022112069000358
2. Widnall SE, Sullivan JP. On the Stability of Vortex Rings. J Proc R Soc Lond A. Math Phys Sci (1973) 332:335–53.
3. Pierrehumbert RT, Widnall SE. The Structure of Organized Vortices in a Free Shear Layer. J Fluid Mech (1981) 102:301–13. doi:10.1017/s0022112081002656
4. Martin JE, Meiburg E. Numerical Investigation of Three-Dimensionally Evolving Jets Subject to Axisymmetric and Azimuthal Perturbations. J Fluid Mech (1991) 230:271–318. doi:10.1017/s0022112091000794
5. Verzicco R, Orlandi P. Direct Simulations of the Transitional Regime of a Circular Jet. Phys Fluids (1994) 6:751–9. doi:10.1063/1.868313
6. Grinstein FF, Gutmark EJ, Parr TP, Hanson‐Parr DM, Obeysekare U. Streamwise and Spanwise Vortex Interaction in an Axisymmetric Jet. A Computational and Experimental Study. Phys Fluids (1996) 8:1515–24. doi:10.1063/1.868927
7. Liepmann D, Gharib M. The Role of Streamwise Vorticity in the Near-Field Entrainment of Round Jets. J Fluid Mech (1992) 245:643–68. doi:10.1017/s0022112092000612
9. Thillaikumar T, Jana T, Kaushik M. Experimental Assessment of Corrugated Rectangular Actuators on Supersonic Jet Mixing. Actuators (2020) 9:1–24. doi:10.3390/act9030088
10. Kaushik M. Innovative Passive Control Techniques for Supersonic Jet Mixing. 1st ed. Germany: Lambert Academic Publishing (2012).
11. Kaushik M, Rathakrishnan E. Corrugated Tab for Supersonic Jet Mixing. Int Rev Mech Eng (2014) 8:983–91.
12. Kaushik M, Rathakrishnan E. Corrugated Limiting Tab for Jet Mixing. Int J Turbo Jet-Engines (2013) 30:359–73. doi:10.1515/tjj-2013-0016
13. Bradbury LJS, Khadem AH. The Distortion of a Jet by Tabs. J Fluid Mech (1975) 70:801–13. doi:10.1017/s0022112075002352
14. Zaman KBMQ, Reeder MF, Samimy M. Control of an Axisymmetric Jet Using Vortex Generators. Phys Fluids (1994) 6(2):778–93. doi:10.1063/1.868316
15. Gretta WJ, Smith CR. The Flow Structure and Statistics of a Passive Mixing Tab. J Fluids Eng (1993) 115:255–63. doi:10.1115/1.2910133
16. Behrouzi P, McGuirk JJ. Experimental Studies of Tab Geometry Effects on Mixing Enhancement of an Axisymmetric Jet. JSME International Journal Ser B, Fluids Thermal Engineering (1998) 41:908–17. doi:10.1299/jsmeb.41.908
17. Zhang S, Schneider SP. Quantitative Molecular‐mixing Measurements in a Round Jet with Tabs. Phys Fluids (1995) 7:1063–70. doi:10.1063/1.868549
18. Carletti MJ, Rogers CB, Parekh DE. Use of Streamwise Vorticity to Increase Mass Entrainment in a Cylindrical Ejector. AIAA J (1995) 33:1641–5. doi:10.2514/3.12704
19. Reeder MF, Samimy M. The Evolution of a Jet with Vortex-Generating Tabs: Real-Time Visualization and Quantitative Measurements. J Fluid Mech (1996) 311:73–118. doi:10.1017/s0022112096002510
20. Zaman KBMQ, Reeder MF, Samimy M. Supersonic Jet Mixing Enhancement by 'delta Tabs. In: AIAA/ASME/SAE/ASEE 28th Joint Propulsion Conference and Exhibit; 1992 Jul 6–8; Nashville, TN. Nashville, TN (1992). AIAA-92-3548. doi:10.2514/6.1992-3548
21. Samimy M, Zaman KBMQ, Reeder MF. Effect of Tabs on the Flow and Noise Field of an Axisymmetric Jet. AIAA J (1993) 31:609–19. doi:10.2514/3.11594
22. Steffen CJ, Reddy DR, Zaman KBMQ. Numerical Modeling of Jet Entrainment for Nozzles Fitted with Delta Tabs. Reno, NV, U.S.A: AIAA Paper (1997).
23. Mi J, Nathan GJ. Effect of Small Vortex-Generators on Scalar Mixing in the Developing Region of a Turbulent Jet. Int J Heat Mass Transfer (1999) 42:3919–26. doi:10.1016/s0017-9310(99)00087-3
24. Behrouzi P, McGuirk JJ. Effect of Tab Parameters on Near-Field Jet Plume Development. J Propulsion Power (2006) 22:576–85. doi:10.2514/1.15473
25. Carletti MJ, Rogers CB, Parekh DE. Parametric Study of Jet Mixing Enhancement by Vortex Generators, Tabs and Deflector Plates. Am Soc Mech Eng Fluids Eng Division Conf (1996) 237:303–12.
26. Nagata K, Sakai Y, Shirosawa M, Kubo T. Active Control of an Axisymmetric Turbulent Jet Using Moving Delta Tabs (Effects of the Delta Tabs Oscillating in Phase). Jfst (2008) 3:292–302. doi:10.1299/jfst.3.292
27. Ito Y, Miura K, Sakai Y, Iwano K. Enhancement and Suppression of Mixing and Diffusion in an Axisymmetric Jet by Half delta-wing Tabs. Int J Heat Mass Transfer (2018) 118:1218–30. doi:10.1016/j.ijheatmasstransfer.2017.11.053
28. Ahuja KK, Brown WH. Shear Flow Control by Mechanical Tabs. In: AIAA 2nd Shear Flow Conference; 1989 Mar 13–16; Tempe, AZ. Tempe, AZ (1989). AIAA-89-0994. doi:10.2514/6.1989-994
29. Zaman KBMQ, Samimy M, Reeder MF. Effect of Tabs on the Evolution of an Axi-Symmetric Jet. In: 8th Symposium on Turbulent Shear Flows; 1991 Sept 9–11. Munich, Germany (1991). Paper 25-5.
30. Samimy M, Zaman KBMQ, Reeder MF. Supersonic Jet Mixing Enhancement by Vortex Generators. In: AIAA/ASME/SAE/ASEE 27th Joint Propulsion Conference and Exhibit; 1991 Jun 24–26; Sacramento, CA. Sacramento, CA (1991). AIAA-91-2263.
31. Wishart DP, Krothapalli A, Mungal MG. Supersonic Jet Control via Point Disturbances inside the Nozzle. AIAA J (1993) 31:1340–1. doi:10.2514/3.11773
32. Seiner JM, Grosch CE. Mixing Enhancement by Tabs in Round Supersonic Jets. In: 4th AIAA/CEAS Aeroacoustics Conference; 1998 Jun 2–4. Toulouse, France (1998). AIAA-98-2326.
33. Hari S, Kurian J. Effectiveness of Secondary Tabs for Supersonic Mixing. Experiments in Fluids (2001) 31:302–8. doi:10.1007/s003480100285
34. Kaushik M, Rathakrishnan E. Corrugated Tab Aspect Ratio Effect on Supersonic Jet Mixing. Int J Turbo Jet-Engines (2015) 32:265–73. doi:10.1515/tjj-2014-0032
35. Jana T, Kaushik M. Performance of Corrugated Actuator-Tabs of Aspect Ratio 2.0 on Supersonic Jet Mixing Enhancement. J Mech Sci Technol (2021) 35(3):1087–97. doi:10.1007/s12206-021-0222-z
36. Reeder MF, Zaman KBMQ. Impact of Tab Location Relative to the Nozzle Exit on Jet Distortion. AIAA J (1996) 34:197–9. doi:10.2514/3.13044
37. Kweon Y-H, Miyazato Y, Aoki T, Kim H-D, Setoguchi T. Control of Supersonic Jet Noise Using a Wire Device. J Sound Vibration (2006) 297:167–82. doi:10.1016/j.jsv.2006.03.033
38. Arun Kumar P, Aileni M, Rathakrishnan E. Impact of Tab Location Relative to the Nozzle Exit on the Shock Structure of a Supersonic Jet. Phys Fluids (2019) 31:076104. doi:10.1063/1.5111328
39. Lovaraju P, Rathakrishnan E. Subsonic and Transonic Jet Control with Cross-Wire. AIAA J (2006) 44:2700–5. doi:10.2514/1.17637
40. Rathakrishnan E. Experimental Studies on the Limiting Tab. AIAA J (2009) 47:2475–85. doi:10.2514/1.43790
41. Sarohia V, Massier PF. Experimental Results of Large-Scale Structures in Jet Flows and Their Relation to Jet Noise Production. AIAA J (1978) 16:831–5. doi:10.2514/3.60969
42. Tam CKW, Chen P, Seiner JM. Relationship between the Instability Waves and Noise of High-Speed Jets. AIAA J (1992) 30:1747–52. doi:10.2514/3.11132
43. McLaughlin DK, Barron WD, Vaddempudo AR. Acoustic Properties of Supersonic Helium/air Jets at Low Reynolds Number. Aachen, Germany: AIAA Paper (1992).
44. Tam CKW, Tanna HK. Shock Associated Noise of Supersonic Jets from Convergent-Divergent Nozzles. J Sound Vibration (1982) 81:337–58. doi:10.1016/0022-460x(82)90244-9
45. Seiner M. Advances in High Speed Jet Aeroacoustics. In: 9th Aeroacoustics Conference; 1984 Oct 10–15. Williamsburg, VA, U.S.A (1984).
46. Powell A. On the Mechanism of Choked Jet Noise. Proc Phys Soc B (1953) 66:1039–56. doi:10.1088/0370-1301/66/12/306
47. Tanna HK. An Experimental Study of Jet Noise Part II: Shock Associated Noise. J Sound Vibration (1977) 50:429–44. doi:10.1016/0022-460x(77)90494-1
48. Norum TD, Seiner JM. Location and Propagation of Shock Associated Noise from Supersonic Jets. In: AIAA 6th Aeroacoustics Conference; 1980 Jun 4–6; Connecticut. Hartford, Connecticut (1980). AIAA-80-0983. doi:10.2514/6.1980-983
49. Seiner JM, Yu JC. Acoustic Near Field and Local Flow Properties Associated with Broadband Shock Noise. In: AlAA 7th Aeroacoustics Conference; 1981 Oct 5–7; Palo Alto, CA. Palo Alto, California (1981). AIAA-81-1975.
50. Ahuja KK, Manes JP, Massey KC, Calloway AB. An Evaluation of Various Concepts of Reducing Supersonic Jet Noise. In: AIAA 13th Aeroacoustics Conference; 1990 Oct 22–24; Tallahassee, FL. Tallahassee, FL (1990). AIAA-90-3982. doi:10.2514/6.1990-3982
51. Tam CKW. Jet Noise Generated by Large-Scale Coherent Motion. Aeroacoustics of Flight Vehicles. Theor Pract (1991) 1:311.
52. Kobayashi H, Oinuma H, Sawamura T, Outa E. Effects of Tab Size on Supersonic Underexpanded Cold and Heated Jet Noise Suppression and Jet Thrust Loss. In: 15th Aeroacoustics Conference; 1993 Oct 25–27. Long Beach, CA, U.S.A (1993). AIAA-93-4348.
53. Zaman KBMQ, Hussain AKMF. Turbulence Suppression in Free Shear Flows by Controlled Excitation. J Fluid Mech (1981) 103:133–59. doi:10.1017/s0022112081001274
54. Saiyed NH, Bridges JE. Tabs and Mixers for Reducing Low Bypass Ratio Jet Noise. In: 5th AIAA/CEAS Aeroacoustics Conference and Exhibit; 1999 May 10–12. Bellevue, WA, U.S.A (1999). AlAA 99-1966.
55. Tam CKW, Zaman KBMQ. Subsonic Jet Noise from Nonaxisymmetric and Tabbed Nozzles. AIAA J (2000) 38:592–9. doi:10.2514/3.14449
56. Hileman J, Samimy M. Effects of Vortex Generating Tabs on Noise Sources in an Ideally Expanded Mach 1.3 Jet. Int J Aeroacoustics (2003) 2:35–63. doi:10.1260/147547203322436935
57. Hussain GF, Nasser AS, Nawaz MM, Mondal BK, Karthikeyan N. Effect of Perforated Tabs on the Noise Field of an Axisymmetric Jet. Amm (2013) 307:250–6. doi:10.4028/www.scientific.net/amm.307.250
58. André B, Thomas Castelain. T, Bailly C. Effect of a Tab on the Aerodynamical Development and Noise of an Underexpanded Supersonic Jet. Comptes Rendus Mecanique (2013) 341:659–66. doi:10.1016/j.crme.2013.08.001
Keywords: centerline pressure decay, supersonic jet core, jet mixing, streamwise vortices, Mach number
Citation: Thangaraj T, Kaushik M, Deb D, Unguresan M and Muresan V (2022) Survey on Vortex Shedding Tabs as Supersonic Jet Control. Front. Phys. 9:789742. doi: 10.3389/fphy.2021.789742
Received: 17 November 2021; Accepted: 23 December 2021;
Published: 01 February 2022.
Edited by:
Antonio F. Miguel, University of Evora, PortugalReviewed by:
Tamal Jana, Jain University, IndiaKarthick S. K., Technion Israel Institute of Technology, Israel
Copyright © 2022 Thangaraj, Kaushik, Deb, Unguresan and Muresan. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Dipankar Deb, ZGlwYW5rYXJkZWJAaWl0cmFtLmFjLmlu
 Thillaikumar Thangaraj
Thillaikumar Thangaraj Mrinal Kaushik
Mrinal Kaushik Dipankar Deb
Dipankar Deb Mihaela Unguresan3
Mihaela Unguresan3